Abstract
Motivation: Statistical analyses of genome-wide association studies (GWAS) require fitting large numbers of very similar regression models, each with low statistical power. Taking advantage of repeated observations or correlated phenotypes can increase this statistical power, but fitting the more complicated models required can make computation impractical.
Results: In this article, we present simple methods that capitalize on the structure inherent in GWAS studies to dramatically speed up computation for a wide variety of problems, with a special focus on methods for correlated phenotypes.
Availability: The R package ‘boss’ is available on the Comprehensive R Archive Network (CRAN) at http://cran.r-project.org/web/packages/boss/
Contact: voorma@u.washington.edu
Supplementary information: Supplementary data are available at Bioinformatics online.
1 INTRODUCTION
In analysis of genome wide association studies (GWAS), it is standard to fit very large numbers of very similar regression models. A general form of commonly used models is
where 1≤i≤n indexes subjects in the study, yi is the subject's outcome of interest, Xi is a vector of subject-specific adjustment variables, gi is the set of genotype-dependent variables and ϵi is an error term. The genotype-dependent variables gi vary from model to model, within one analysis, but the adjustment variables Xi remain identical within each analysis. If the errors are uncorrelated, standard ordinary least squares (OLS) or generalized linear models (GLM) efficiently estimate genetic effects βg. However, when the errors are correlated notably, greater efficiency can be obtained, by incorporating this structure into the model. For instance, if repeated measures on an individual are available, either generalized estimating equations (GEE) or mixed models can increase power relative to an analysis that uses a single phenotype measure for each individual (Liang and Zeger, 1993). Similarly, when subjects are related, kinship can be incorporated into a mixed model to increase power (Kang et al., 2008). A single GEE or mixed model analysis involves negligible computing effort, but the number of analyses carried out often extends into several millions, meaning more complicated GEE and mixed models computation with standard methods can be infeasible.
Some computational speedups are available, by capitalizing on the similarity of each regression, meaning one can obtain genome-wide estimates at a substantially reduced computational cost. For example, Auchenko et al. (2007) introduced an approximation to the Maximum Likelihood Estimate for mixed models which is currently implemented in ProbABEL. In their approach, both phenotypic correlation and non-genetic effects are estimated once and assumed constant across all models in an analysis. When the inclusion of genotype does not change these parameters, the inference is close to that obtained from the full fit, but can be misleadingly inaccurate when genotype is correlated with non-genetic covariates.
In another example, rather than fixing both non-genetic effects and variance structure, Kang et al. (2008, 2001) proposed mixed model methods where the variance structure of phenotype is fixed over all markers in which case simple modifications to Generalized Least Squares procedures can give fast computation of the results (Meyer and Tier, 2011). This is more complicated to implement and slower than the ProbABEL approximation, but makes less assumptions about the nature of the genetic association. However, one drawback of a mixed model approach is that results may be invalid if either the correlation structure or the covariate–phenotype relationship is not well specified.
If the phenotype correlation is due to repeated observations on an individual, then GEE models provide powerful testing, which does not require us to correctly specify either the correlation structure or the phenotype–covariate relationships, that may be complicated (Diggle, 2002). However, there are no software packages that can currently implement this on a genome-wide scale in reasonable amounts of time.
In this article, we explore two approaches that substantially reduce the computation required for a broad class of statistical models. Each exploits two important features of GWAS analyses: (i) few covariates are different in each regression and (ii) little variation in phenotype is explained by genotype at a particular locus. Our first approach exploits symmetry in the estimation of single marker models. For ordinary least squares, it is ~20 times faster than current implementations, and for mixed models it can reduce computation by a factor of a few hundred.
Our second approach is based on matrix decompositions and applies to a broader class of models, including those with multiple markers, and allows model-robust variance estimation. In the case of linear mixed models, it aligns with a proposal by Meyer and Tier (2011). The speedup for this approach is not large for GEE and GLM models with few covariates or observations, but in our tests estimation in GEE models was 60–80 times faster than currently implemented GEE packages in R. Although these computational approaches are approximations, estimation in practice is almost identical to traditional methods, as we demonstrate. The two approaches have the unifying feature that they are based on classical one-step approximations, suggesting the name boosted one-step statistics (BOSS).
2 APPROACH
First, consider estimation of the effect of a single genotype variable g=[g1… gn]T on a phenotype Y=[y1… yn]T adjusted for p subject−specific covariates xj=[xj1… xjn]T, j=1… p. Denote the model matrix Xg=[1n, x1,… xp, g]=[X, g]. If the outcomes are independent and continuous, we get coefficients by computing the OLS estimate
This is sufficiently simple to perform on a genome-wide scale, and there is software available to do so (Aulchenko et al., 2007; Purcell et al., 2007). For more complicated models, such as mixed models, GLM or GEE, we can estimate the coefficients through iteratively re-weighted least squares (IWLS) that repeatedly calculates
where Wk is a matrix of weights and 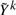 is a modified phenotype at the kth iteration of this procedure. The details of how this arises and the exact scheme by which these are updated are not important for this discussion, and the interested reader can refer e.g. Diggle (2002) and McCullagh and Nelder (1989). It suffices to note that, at each iteration, Wk and Yk differ from Wk−1 and Yk−1 in ways that only depend on the fitted values at the current iteration. Since it can be assumed that genotype has little effect on these fitted values, we can estimate Wk and
is a modified phenotype at the kth iteration of this procedure. The details of how this arises and the exact scheme by which these are updated are not important for this discussion, and the interested reader can refer e.g. Diggle (2002) and McCullagh and Nelder (1989). It suffices to note that, at each iteration, Wk and Yk differ from Wk−1 and Yk−1 in ways that only depend on the fitted values at the current iteration. Since it can be assumed that genotype has little effect on these fitted values, we can estimate Wk and 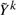 in the absence of genotype and substantially lower the number of iterations required to converge. In fact, for the models we consider one iteration of the IWLS algorithm is typically sufficient. This can be considered an instance of a so-called ‘one-step approximation’, which are well known to be asymptotically equivalent to fully converged solutions (Lehmann and Casella, 1998; Lipsitz et al., 1994). Here, since the one step is based on a model with nearly identical fitted values to the model of interest, the practical performance is superior to classically implemented one-step estimators, as we demonstrate in Section 4. The accuracy decreases with the strength of the genetic effect, but our simulations suggest that this loss in accuracy occurs far beyond the threshold of genome-wide significance. That is when there are genome-wide significant results, both BOSS and traditional tests will identify them, but the exact size of the effect may differ slightly when it is very large.
in the absence of genotype and substantially lower the number of iterations required to converge. In fact, for the models we consider one iteration of the IWLS algorithm is typically sufficient. This can be considered an instance of a so-called ‘one-step approximation’, which are well known to be asymptotically equivalent to fully converged solutions (Lehmann and Casella, 1998; Lipsitz et al., 1994). Here, since the one step is based on a model with nearly identical fitted values to the model of interest, the practical performance is superior to classically implemented one-step estimators, as we demonstrate in Section 4. The accuracy decreases with the strength of the genetic effect, but our simulations suggest that this loss in accuracy occurs far beyond the threshold of genome-wide significance. That is when there are genome-wide significant results, both BOSS and traditional tests will identify them, but the exact size of the effect may differ slightly when it is very large.
This procedure is already used in mixed models, although is not identified as such. There W is proportional to the inverse variance–covariance matrix of phenotype induced by random effects. The details of this model are explored by (Kang et al., 2010). BOSS applies the same idea to GLM and GEE.
The use of one-step estimators takes advantage of the fact that genotype at a particular loci explains little of the variation in complicated phenotypes, but does not use the fact that only one variable changes in each regression. Sections 3 and 4 outline two methods used by BOSS which perform one-step estimation quickly by avoiding calculations that do not involve g. The first applies to single marker models and allows only model-based standard errors. The second is slower, but applies more generally and allows computation of robust test statistics.
To make the remaining discussion simpler, we first express this weighted least-squares problem as an OLS problem. If we decompose the matrix W as a square root, i.e. W=DTD, we see that the above procedure is equivalent to regressing DXg=[DX, Dg] on 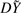 . In general, W is an n×n matrix, making this factorization difficult, slow and memory-intensive. However, W will often have structure. For GLM it is a diagonal matrix, so we only need to store a vector of length n. For GEE and mixed models, W is typically composed of small blocks corresponding to independent clusters of observations, so we need only to store and factorize these blocks. For some mixed model problems, W may be dense, and difficult to factorize in this way, but as shown in the Supplementary Appendix we can reduce the effective dimension to the number of random effects terms using the spectral decomposition. The factorization will need to be performed only once, but the multiplication D g will need to be performed for each marker. So, where the weight matrix is sufficiently simple to factorize and handle, speed in one-step estimation will come from fast implementations of OLS.
. In general, W is an n×n matrix, making this factorization difficult, slow and memory-intensive. However, W will often have structure. For GLM it is a diagonal matrix, so we only need to store a vector of length n. For GEE and mixed models, W is typically composed of small blocks corresponding to independent clusters of observations, so we need only to store and factorize these blocks. For some mixed model problems, W may be dense, and difficult to factorize in this way, but as shown in the Supplementary Appendix we can reduce the effective dimension to the number of random effects terms using the spectral decomposition. The factorization will need to be performed only once, but the multiplication D g will need to be performed for each marker. So, where the weight matrix is sufficiently simple to factorize and handle, speed in one-step estimation will come from fast implementations of OLS.
3 METHODS
In this section, we describe fast implementations for one-step estimation. In the previous section, we demonstrated how this can be phrased in terms of fast OLS, so we will restrict our discussion to that case.
3.1 A fast algorithm for GWAS with single markers
Typically, we model a quantitative trait Y as an outcome variable with genotype g and covariates X as predictors. That is we form the model
where ϵ ~(0, var[Y|X+g]). With model-based approaches, we assume that var[Y|X+g] does not change with X and g. After fitting the model via OLS, the output is used to test the hypothesis Ha0: βg=0.
However, if we swap Y and g to form the model
The hypothesis test Hb0: γy=0 is equivalent to the previous test that βg=0 and yields identical P-values when one uses model-based standard errors. (A straightforward proof of this is given in the Supplementary Appendix.) While this formulation may seem unnatural, it leads to simplified calculations. Almost all of the computational effort involved in regression is spent on the matrix of covariates, and using g as an outcome allows us to do this work only once, before we examine genotype.
To use this result in a GWAS setting, we first denote the new matrix of predictors Xy=[X, y] and 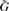 to be an n×m matrix of genotypes for the entire GWAS (in practice we may break this up into more manageable chunks). The test statistics can then be computed by:
to be an n×m matrix of genotypes for the entire GWAS (in practice we may break this up into more manageable chunks). The test statistics can then be computed by:
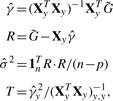 |
where R · R indicates element-wise multiplication. Here, T is a vector of χ2 test statistics, identical to those computed with traditional methods.
It is notable that this technique yields test statistics, but not regression coefficients. In typical GWAS, only a tiny fraction of these coefficients might be of interest, and they could be computed without special techniques, at minor computational cost. However, regression coefficients could be approximated, genome wide, by using the identity (Peng et al., 2009)
By setting 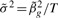 , we can get an estimate of the variance and report a coefficient-standard error pair that are close approximations to the truth (because the genetic effect can be assumed to be small) and whose ratio gives the same test statistic as the full regression. The approximation is worse when
, we can get an estimate of the variance and report a coefficient-standard error pair that are close approximations to the truth (because the genetic effect can be assumed to be small) and whose ratio gives the same test statistic as the full regression. The approximation is worse when 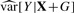 is much different than
is much different than 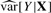 , but this difference is typically negligible, as we demonstrate in Section 4. Furthermore, as noted by Zhong and Prentice (2010), interpretation of coefficients near the significance threshold is difficult due to the ‘winner's curse’ bias. Thus, when differences between this method and OLS exist, they are likely small compared to bias.
, but this difference is typically negligible, as we demonstrate in Section 4. Furthermore, as noted by Zhong and Prentice (2010), interpretation of coefficients near the significance threshold is difficult due to the ‘winner's curse’ bias. Thus, when differences between this method and OLS exist, they are likely small compared to bias.
3.2 Efficient GWAS using Cholesky updates
The method described in the previous section, while very fast for the models described, has some limitations. It only allows us to use model-based standard errors and thus relies on parametric assumptions; in GWAS settings, these are not likely to be checked, nor is there good power to detect important model misspecification (Janssen, 2000). When our model is not correct, either in how, we specify the variance structure or the mean structure, results can be misleading. In main-effects analysis with independent outcomes, the model-based analysis may be appropriate, but there is little work exploring the impacts of misspecification of variance structure (Voorman et al., 2011). Furthermore, it does not give us fitted values that we can use in subsequent IWLS iterations, if desired. In this section, we explore a method based on well-known matrix decompositions which, while slower, overcomes these limitations.
We start with the case of a single marker, which is later generalized to multiple marker models. In order to distinguish between those variables that are the same in each regression and those that differ, denote the model matrix as Xg=[1n, x1,… xp−1, g]=[X, g]. The bottleneck calculation of each fit is a matrix inversion of the form
This matrix inversion is typically done by first factorizing XgTXg to a form which makes inversion very simple. This factorization comprises the bulk of the computation involved in a regression. In this case, all but one column of Xg remains unchanged between markers. Rather than computing the inverse for each marker, we can simply update the factorization calculated without genotype; this can be done easily using the Cholesky decomposition of XT X.
Formally, we denote L as the lower-triangular Cholesky factorization of XT X. We want to augment L with rows corresponding composed of a p-vector lgT and a scalar c to form the updated Cholesky decomposition Lbg
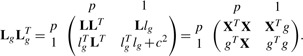 |
Since L is lower triangular, solving the system of equations Llg=XTg is straightforward. We then set cTc=gTg− lTglg. For p variables and n observations, this updating can be done with O(p2+np) calculations, rather than O(p3+np2) calculations, the cost of a typical OLS fit. [The same approach is used by Efron et al. (2004) in the LARS algorithm to successively add covariates to a model]. The benefit of this approach is small when there are few covariates or observations, but becomes substantial in larger models and studies, which is precisely when computational speed becomes an issue in GWAS. The application of this procedure to mixed model equations was recently noticed by Meyer and Tier (2011). Our discussion extends the results to a still broader class of models.
The approach for main-effects GWAS outlined above easily extends to the situation where multiple markers or interactions are included. These terms can be subsequently added using the same method, which gives the matrix inverse using the same order of computation as standard matrix inversion (Efron et al., 2004; Golub and Van Loan, 1996).
3.3 Missing data
One drawback of pre-computing before genotype is observed is that it is more difficult to adapt the analysis to peculiarities for any single regression. For example, if a subject is missing genotype data, the quantities computed without genotype will still contain this subject's information. If this constitutes only one observation, rank-one downdating algorithms can compute the appropriate factorization efficiently, to which the genotype of the remaining observations can be added as described above (Dongarra, 1979). If there are many missing observations, as would be the case with repeated measures, this downdating may be applied repeatedly; however, it may be more straightforward to conduct a naive analysis. In practice, linkage disequilibrium allows one to accurately impute missing genotype data, so this is not a large concern (Scheet and Stephens, 2006; Browning and Browning, 2009; Howie et al., 2009). The methods used by BOSS can accommodate uncertain genotype, given by a continuous variable, without modification. Currently, BOSS ignores missing genotype, which is equivalent to imputing a value of 0. Observations with missing non-genetic covariates are dropped from the analysis by BOSS.
3.4 Meta-analyses
It is common in GWAS analyses to pool effect estimates and associated standard errors from multiple study centers. Since meta-analyses typically do not require that all study centers use the same estimator of an effect, the one-step estimators produced by BOSS can be considered compatible with those produced by other software. Furthermore, in the range of scenarios where it would be beneficial to meta-analyse results, that is, when the effect is modest, one should expect BOSS estimates to nearly identical to traditional estimators.
4 RESULTS
4.1 Timing comparisons
We implemented the above methods in R and compared the timings using synthetic data (R Development Core Team, 2009). We simulated data for n=2000 subjects and averaged time over m=1000 simulated genetic markers, which is sufficient to accurately estimate the relative speeds. For GEE and mixed models, we generated three observations per patient. For GEE, we modeled the variance structure with an exchangeable working correlation matrix, and for mixed models we used a random intercept and one random slope. To make calculations as fair as possible, we implemented OLS directly with matrix inversion, which is twice as fast as the specialized code in the ‘lm()’ function; we used ‘glm.fit()’ for logistic regression, ‘geese()’ from the ‘geepack’ package for GEE calculations and ‘lmer()’ from the ‘lme4’ package for mixed models (Bates and Maechler, 2009; R Development Core Team, 2009; Yan, 2002; Yan and Fine, 2004). All comparisons were carried out on a Macbook pro with a 2.8 GHz Intel Dual Core i7. The timing comparisons are given in Table 1.
Table 1.
Timing comparisons, given in seconds per 1000 SNPs
| Naive method | BOSS-chol | BOSS-swap | |
|---|---|---|---|
| OLS | 1.29 | 0.74 | 0.059 |
| OLS - GxE | 1.39 | 1.07 | – |
| Logistic reg. | 7.68 | 0.82 | 0.062 |
| GEE - linear, exch. | 325 | 5.38 | 0.31 |
| GEE - logistic, exch. | 383 | 5.27 | 0.31 |
| Linear mixed models | 360 | 2.62 | 0.48 |
For OLS, the Cholesky updating method is twice as fast as traditional methods, while the swap method is 20 times as fast. The advantage of the Cholesky updating is less pronounced for GxE analyses, but more so for logistic regression. For logistic regression, the swap method is about 125 times faster than the naive method.
For repeated measures, the Cholesky method is 60 times faster than traditional methods for GEE with continuous outcomes 70 times faster for GEE with binary outcomes, and about 137 times faster for linear mixed models. If we do not want to use robust variance estimates, the ‘swap’ method gives GEE and mixed model estimates 1000 and 750 times faster, respectively, than standard code.
4.2 Accuracy of the one-step estimator
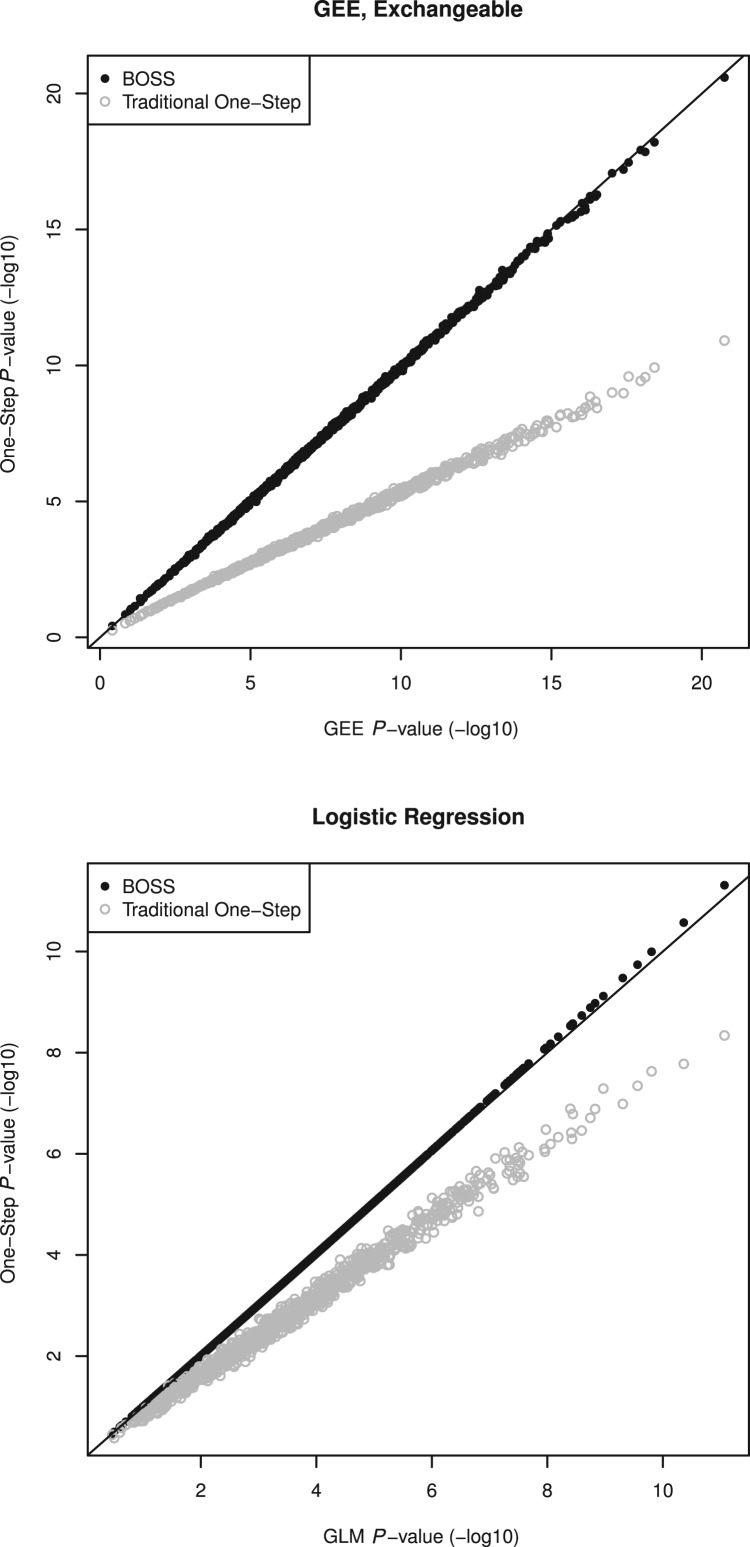
In general, we found that the P-values from BOSS approximations are extremely accurate, which agrees with what (Kang et al., 2010) demonstrated for mixed models. Figure 1 displays results for logistic regression and GEE with exchangeable working correlation. Genotype was simulated away from the null to demonstrate that there is little difference between the two methods, even for small P-values. The simulations are described in more detail in the Supplementary Appendix. For logistic regression, the traditional one-step approximation is not sufficiently accurate for genome-wide significant associations. For GEE, traditional one-step approximation is the same as estimation with an independence working correlation. Although both the independence and exchangeable working correlations are consistent for arbitrary correlation structures, we see that correctly modelling correlation structure increases power.
Fig. 1.
Comparison of P-values obtained with BOSS and those obtained with the fully converged model. Results are also displayed for the conventional one-step approximations
There is no clear choice for a threshold to identify when further iterations may be beneficial. Since the accuracy of the approach depends on the change in the fitted values, iterating further either when within-cluster or overall fitted values change relative to the model fitted without genotype. However, since the approximations are so close, the simplest and most practical approach is performing subsequent iterations when the approximate P-values fall below a certain threshold, say pone−step<;1/m where m is the number of tests. In this way, we would not expect to perform subsequent iterations in a study where genotype has no effect, and when an association is present in the data the P-value reported will be as accurate as possible.
4.3 Accuracy of approximations in the single marker method
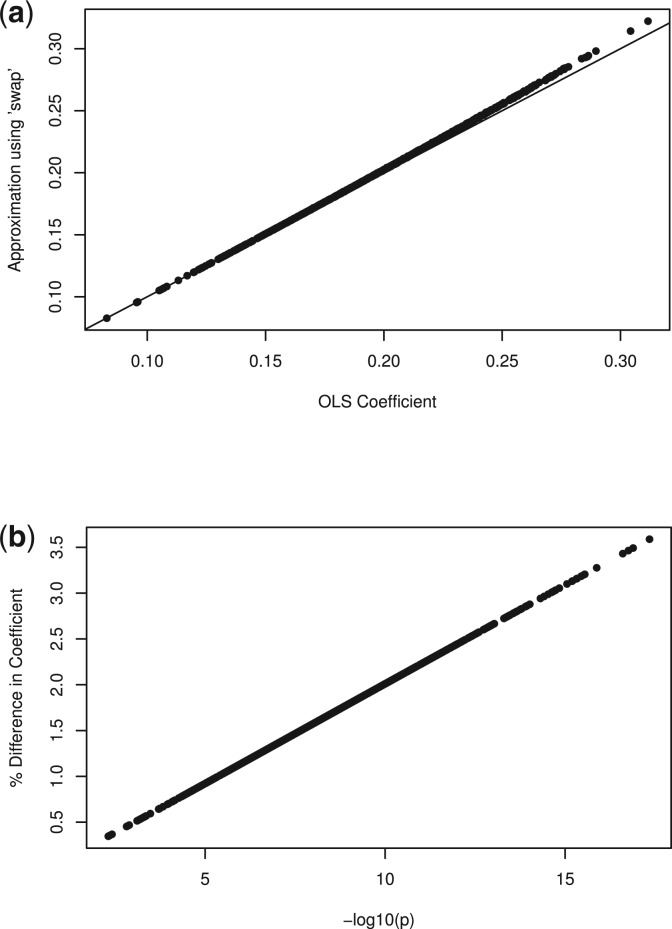
First, as discussed in the previous section, the single marker method calculates a coefficient-standard error pair, which is different from the OLS estimate, but gives identical Wald statistics. We simulated 1000 genotypes for 2000 subjects away from the null hypothesis and computed both the OLS 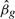 and the described approximation. Figure 2 demonstrates that this approximation is very close to the truth, even when the genetic effect is large. We see that genotype with p≈10−8 differs from the standard OLS coefficient by about 1%. Since var [Y|X]≥var [Y|X+G], we know that the approximation is an overestimate, but we see that it is by a very small amount.
and the described approximation. Figure 2 demonstrates that this approximation is very close to the truth, even when the genetic effect is large. We see that genotype with p≈10−8 differs from the standard OLS coefficient by about 1%. Since var [Y|X]≥var [Y|X+G], we know that the approximation is an overestimate, but we see that it is by a very small amount.
Fig. 2.
Comparison of approximate coefficients to the OLS estimates using ‘swap’ method. (a) The approximate against the OLS estimate directly. (b) The error in the approximation, as a percent of the OLS coefficient, against the P-value. Herein, the approximate coefficient, with its associated variance, yields identical inference to the OLS estimate
5 CONCLUSION
In this article, we provided general computational methods that capitalize on the structure of genome-wide association studies to increase speed. BOSS is composed of two distinct procedures, but each takes advantage of two important features of genome-wide association studies (i) few variables change from analysis to analysis and (ii) genotype at each locus explains a small component of variation in phenotype. Recognizing this, we demonstrated that one could perform nearly exact estimation and testing in a wide variety of statistical models fit with IWLS including GLM, GEE and mixed models, for a lower computational cost than currently implemented least squares. This had also been noticed in mixed models, but our contribution allows the analyst to use a much broader set of tools, and for single marker models we provide a method which is substantially faster (Meyer and Tier, 2011). In particular, it is now feasible to take advantage of repeated measures with GEE and doubly robust standard errors on a genome-wide scale.
Funding: National Institutes of Health/National Heart, Lung, and Blood Institute training [T32 HL07183-34, in part] and research [R01 HL074745].
Conflict of Interest: none declared.
REFERENCES
- Aulchenko Y., et al. Genomewide rapid association using mixed model and regression: a fast and simple method for genomewide pedigree-based quantitative trait loci association analysis. Genetics. 2007;177:577. doi: 10.1534/genetics.107.075614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bates D., Maechler M. lme4: Linear Mixed-effects Models using S4 Classes. 2009 R package version 0.999375-31 http://CRAN.R-project.org/package= lme4. [Google Scholar]
- Browning B., Browning S. A unified approach to genotype imputation and haplotype-phase inference for large data sets of trios and unrelated individuals. Am. J. Hum. Genet. 2009;84:210–223. doi: 10.1016/j.ajhg.2009.01.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diggle P. Analysis of Longitudinal Data. Vol. 25. USA: Oxford University Press; 2002. [Google Scholar]
- Dongarra J. LINPACK: Users' Guide. Philadelphia, Pennsylvania, USA: Society for Industrial Mathematics; 1979. Number 8. [Google Scholar]
- Efron B., et al. Least angle regression. Ann. Stat. 2004;32:407–499. [Google Scholar]
- Golub G., Van Loan C. Matrix Computations. Vol. 3. Baltimore, Maryland, USA: Johns Hopkins Univ Pr.; 1996. [Google Scholar]
- Howie B., et al. A flexible and accurate genotype imputation method for the next generation of genome-wide association studies. PLoS Genetics. 2009;5:e1000529. doi: 10.1371/journal.pgen.1000529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Janssen A. Global power functions of goodness of fit tests. Ann. Stat. 2000;28:239–253. [Google Scholar]
- Kang H., et al. Efficient control of population structure in model organism association mapping. Genetics. 2008;178:1709. doi: 10.1534/genetics.107.080101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kang H., et al. Variance component model to account for sample structure in genome-wide association studies. Nat. Genet. 2010;42:348–354. doi: 10.1038/ng.548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lehmann E., Casella G. Theory of Point Estimation. Vol. 31. New York, New York, USA: Springer Verlag; 1998. [Google Scholar]
- Liang K., Zeger S. Regression analysis for correlated data. Annual review of public health. 1993;14:43–68. doi: 10.1146/annurev.pu.14.050193.000355. [DOI] [PubMed] [Google Scholar]
- Lipsitz S., et al. Performance of generalized estimating equations in practical situations. Biometrics. 1994;50:270–278. [PubMed] [Google Scholar]
- McCullagh P., Nelder J.A. Generalized Linear Models. 2. Boca Raton, Florida, USA: Chapman and Hall/CRC; 1989. [Google Scholar]
- Meyer K., Tier B. ‘snp snappy’: a strategy for fast genome wide association studies fitting a full mixed model. Genetics. 2011;190:275–277. doi: 10.1534/genetics.111.134841. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng J., et al. Partial correlation estimation by joint sparse regression models. J. Am. Stat. Assoc. 2009;104:735–746. doi: 10.1198/jasa.2009.0126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Purcell S., et al. Plink: a tool set for whole-genome association and population-based linkage analyses. Am. J. Hum. Genet. 2007;81:559–575. doi: 10.1086/519795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Development Core Team. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing; 2009. [Google Scholar]
- Scheet P., Stephens M. A fast and flexible statistical model for large-scale population genotype data: applications to inferring missing genotypes and haplotypic phase. Am. J. Hum. Genet. 2006;78:629–644. doi: 10.1086/502802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Voorman A., et al. Behavior of qq-plots and genomic control in studies of gene-environment interaction. PloS one. 2011;6:e19416. doi: 10.1371/journal.pone.0019416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan J. geepack: Yet another package for generalized estimating equations. R-News. 2002;2/3:12–14. [Google Scholar]
- Yan J., Fine J.P. Estimating equations for association structures. Stat. Med. 2004;23:859–880. doi: 10.1002/sim.1650. [DOI] [PubMed] [Google Scholar]
- Zhong H., Prentice R. Correcting winner's curse in odds ratios from genomewide association findings for major complex human diseases. Genet. Epidemiol. 2010;34:78–91. doi: 10.1002/gepi.20437. [DOI] [PMC free article] [PubMed] [Google Scholar]