Protein dynamics and photon echoes

Chemical reactions involve motions along particular coordinates—the reaction coordinate—and very often require that a free energy barrier is surmounted. The motion of solvent molecules with respect to reactants and products provides the energy to surmount the barrier along the reaction coordinate and take away the excess energy of the newly formed product. These same motions also can impede the reactive process (“friction”) and produce fluctuations in the height and shape of the potential energy barrier. Naturally, these fluctuations occur on the timescale of the nuclear motions in the solvent, which vary from 10⁻¹⁵ to 10⁻¹⁰ s in typical liquids. Thus, the study of these fluctuations in the time domain requires the use of femtosecond spectroscopy.

In the past 10 years, much progress has been made in measuring and understanding the dynamics of the interactions of solutes and their solvent hosts (1, 2). The extraordinarily rapid timescale on which water accommodates change in the charge distribution of solutes (70% of the relaxation is complete in 30–40 fs) has been observed and described theoretically (3, 4). The majority of such studies use electronic spectroscopies such as fluorescence up-conversion and photon echo spectroscopy. The focus often has been on solvation of polar molecules in polar solvents—this is driven by coulombic interactions between the solute and the solvent. Because of the long range of the coulomb force, such measurements gloss over the details of individual interactions, an approximation that is likely quite good in homogenous fluids such as water. Indeed, this approach leads to the free energy parabolas of Marcus Theory for electron transfer and the linear response behavior of systems to perturbation. Proteins, and thus biological reactions, are quite a different story. They are strongly heterogeneous and show fluctuations over a huge range of timescales (5), and specific interactions often lie at the heart of, for example, their catalytic behavior. In an impressive technical advance, Lim et al. (6) have extended the three-pulse stimulated echo technique to the infrared to study fluctuations in the vibrational frequencies of small molecules and ions in proteins. In contrast to the frequencies of electronic transitions, vibration frequencies are likely to be mostly sensitive to their local environment. As a consequence, the new results of Lim et al. (6) provide a glimpse of the microscopic protein structure changes around their probe molecules and could open the way to a much improved understanding of protein substrate interactions.

Up to now, such understanding has been almost wholly the domain of the computer simulation community, and experimental feedback on the predictions of such work has been indirect or simply lacking. A nice example of simulation of the mechanistic implication of fluctuations is given by Zhou et al. (7). Their simulation of acetylcholinesterase (AchE) implicates the fluctuations of residues forming a narrow “gate” in the channel leading to the active site in the selectivity of the enzyme. The gate opens less frequency for larger substrates that require larger fluctuations to pass through the channel. For the natural substrate (acetylcholine), the gate is likely to open one or more times during any diffusional encounter with AchE, giving rise to hydrolysis at a rate close to the diffusion controlled rate characteristic of a permanently open gate. But an increase in the effective radius of the substrate by only 0.4 Å over the natural substrate decreases the reaction rate by three orders of magnitude (7). This type of dynamic selectivity is unlikely to be unique, and the possibility of experimental study of such fluctuations—perhaps by binding a probe in the gate—is very intriguing. To appreciate the information content of the experiment of Lim et al. (6), a brief description of how it works seems to be in order.

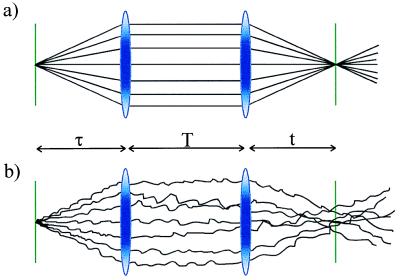
The key features of the three-pulse photon echo method used by Lim et al. (6) can be understood by means of an analogy to ray optics as shown in Fig. 1. The three pulses define three time periods, τ, T, and t, of which only the first two are under experimental control. The first pulse initiates events, and, during the first time period, the system propagates as a superposition between two quantum levels. Such superpositions, or coherences, evolve with an oscillatory component e^−iω_12t where ω₁₂(=E₁₂/ћ reflects the energy difference between the two levels involved. In a system with a distribution of energy levels, for an individual molecule, α, we can write:

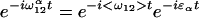where ɛ_α is the offset of the frequency of molecule α from the mean value <ω₁₂>. The distribution of ɛ_α values, f(ɛ_α), describes the inhomogeneous distribution. Focusing on the inhomogeneous contribution, we can define an electronic phase factor φ_α = ɛ_αt; in other words, the phase evolves linearly with time after the first interaction with a slope determined by the inhomogeneous parameter ɛ_α. For n molecules, we will get n lines with different slopes fanning out from the initial value created by the first pulse (Fig. 1a). The second pulse in the echo sequence produces a population (diagonal density matrix). Because there is no energy difference between a state and itself, the phase stays constant after the second interaction with the light (Fig. 1a). Finally, the third pulse produces a coherence with a phase factor −ɛ_αt. The sign change comes about because the second superposition is the Hermitian conjugate of the first (8); so now, in the third time period, the rays will change sign but retain the same magnitude. Thus, the final interaction refocuses the rays at a time t equal to the duration of the first time period, τ. The refocused beam constitutes the photon echo.

Figure 1.

Ray optics analogy for the three-pulse stimulated photon echo experiment. The rays represent the phase evolution of the quantum system. (a) After the initial pulse (τ = 0), the rays fan out with slopes determined by the value of the offset from the mean frequency of individual members of the inhomogeneous distribution. The second pulse (first lens) collimates the rays by converting the superposition into a population state. The third pulse (second lens) refocuses the rays by converting the population state to the Hermitian conjugate of the first superposition state. The echo intensity is proportional to the square of the field amplitude and thus depends on the amount of constructive interference generated by the third (rephasing) pulse. For a wide inhomogeneous distribution, the constructive interference is restricted to a very short time interval at around t = τ, depicted by the sharpness of focus produced by the second lens. (b) The disruption of the smooth phase evolution during the population period, T, and during the two coherence periods (τ and t) leads to a loss of refocusing ability. Thus, by recording the photon echo as a function of the population period, the fluctuations in the inhomogeneous distribution (“spectral diffusion”) can be followed.

So far, we have described a system without external interactions. Fig. 1b depicts the situation in which interactions with the environment alter the transition frequencies of the molecule. Dephasing processes change the slope of the rays during periods t and τ whereas spectral diffusion—the evolution of the inhomogeneous distribution referred to by Lim et al. (6)—occurs during the population period T. An attractive aspect of the three-pulse stimulated echo is that the population period can be long (compared with the short-lived superposition states), thus giving a long period for the system to report on the fluctuations it is receiving. Clearly, all of the fluctuations shown in Fig. 1b diminish the refocusing (“rephasing”) ability of the third pulse, decreasing the echo intensity. However, following the lead of Silvestri et al. (9), Lim et al. (6) recorded the two symmetry-related echo signals obtained by interchanging the time order of pulses one and two (see Fig. 1 of ref. 6). It turns out that the position of the maximum of the echo signal (integrated over the time period t), or, more generally, its first moment, is a very sensitive measure of the memory the system retains for the transition frequency it had at the moment of the initial excitation.

The results of Lim et al. (6) for azide ion bound to carbonic anhydrase II and hemoglobin, and CO bound to myoglobin, are of relevance to current debates concerning the role of protein fluctuations in enzyme catalysis, for example, involving hydrogen transfer (10), in the rebinding of small molecules to their ligands (11 and references therein), and on long range biological electron and energy transfer (12, 13). Lim et al. (6) find that memory of the inhomogeneous distribution is retained for much longer timescales in the protein environment than for the same ions in aqueous solution. The new results provide a real challenge to theorists because the fluctuations in vibrational frequency involve changes in the electronic nature of the small molecule probes. Modeling them requires highly specific calculations and therefore results in detailed descriptions of the timescale, amplitude, and molecular nature of active site fluctuations in proteins.