Probing the Elasticity of DNA on Short Length Scales by Modeling Supercoiling under Tension

Abstract

The wormlike-chain (WLC) model is widely used to describe the energetics of DNA bending. Motivated by recent experiments, alternative, so-called subelastic chain models were proposed that predict a lower elastic energy of highly bent DNA conformations. Until now, no unambiguous verification of these models has been obtained because probing the elasticity of DNA on short length scales remains challenging. Here we investigate the limits of the WLC model using coarse-grained Monte Carlo simulations to model the supercoiling of linear DNA molecules under tension. At a critical supercoiling density, the DNA extension decreases abruptly due to the sudden formation of a plectonemic structure. This buckling transition is caused by the large energy required to form the tightly bent end-loop of the plectoneme and should therefore provide a sensitive benchmark for model evaluation. Although simulations based on the WLC energetics could quantitatively reproduce the buckling measured in magnetic tweezers experiments, the buckling almost disappears for the tested linear subelastic chain model. Thus, our data support the validity of a harmonic bending potential even for small bending radii down to 3.5 nm.

Introduction

DNA bending on short length scales plays a crucial role in many biological processes. In eukaryotic cells, DNA is compacted with the help of nucleosomes in which the DNA is tightly wrapped around an 8-nm protein core (1). Permanently bent DNA sequences are thought to determine nucleosome positioning (2). In addition, the genomes of double-stranded DNA viruses are heavily bent to fit into the protein shell of the viral capsid (3,4). Transcription regulation involves many DNA binding proteins that induce sharp DNA bends (1). For example, the Lac-repressor causes the formation of stable DNA-loops with radii much smaller than the scale of the DNA bending persistence length (5,6).

To establish quantitative models of biological processes that involve DNA bending, a precise knowledge about the mechanical properties of DNA is essential. The so-called wormlike chain (WLC) is the most commonly used theoretical model to describe the elastic bending of DNA. It can be formulated by approximating the DNA as a chain of short, nanometer-sized rigid segments of length l, each of which has a bending energy assigned as

$$E_{\text{WLC}}=\frac{1}{2}\frac{p}{l}{k}_{\text{B}}T{\theta }_i^2,$$ (1)

where p = ∼150 bp is the DNA bending persistence length, θ_i is the angle between neighboring segments i and $i+1$, and k_BT is the thermal energy. The WLC model has been proven to accurately describe experiments that probe elastic DNA bending on length scales of the DNA persistence length and larger (7,8). These experiments were, however, insensitive to detect a nonharmonic bending potential that may be present at short length scales (9). First evidence for a significant deviation from the WLC energetics came from DNA cyclization using fragments shorter than 100 bp (10). These experiments revealed much higher DNA circle formation probabilities than classically predicted. This stimulated the development of a number of alternative models termed subelastic chain (SEC) models that, for large deflections, assume a reduced bending energy. This class of models includes the so-called kinkable WLC models (11,12), where the bending energy saturates at a threshold angle, as well as the linear SEC (LSEC) model that was obtained from mapping the angular distribution of DNA in AFM experiments (9). For the LSEC model, the bending energy of two consecutive 2.5-nm segments is given by

$$E_{\text{LSEC}}^{2.5\text{nm}}=\alpha \left|\theta \right|k_{\text{B}}T,$$ (2)

where α is a dimensionless scaling constant. The LSEC model has attracted considerable attention and has been corroborated (13,14) but also contradicted by subsequent work (15–17). The most severe challenge to the LSEC model have been more recent cyclization experiments (15) that revealed lower minicircle formation probabilities than originally measured (10). However, an unambiguous assessment of the limits of the WLC model is problematic due to 1), a limited number of techniques that are at all sensitive to the actual bending potential at short lengths, and 2), the fact that in all previous experiments, large angular deflections occurred only as statistically rare events.

Here, we model the behavior of supercoiled DNA under tension, where part of the DNA becomes permanently bent at large deflections, to test the success of different models of DNA bending elasticity. When twisting single DNA molecules (Fig. 1 a), e.g., using magnetic (18–20) or optical tweezers (21), the molecule extension remains initially almost constant. Once a critical torque is reached, the molecule buckles, which is seen as an abrupt extension decrease, and a superhelical (plectonemic) structure is formed. Additional turns are absorbed by the extruding superhelix in form of writhe (8), whereby the DNA extension decreases linearly with the number of added turns N (Fig. 1, b and e). The exact behavior of the DNA during supercoiling depends both on the applied force and on the ionic strength of the solution (19–24). The torque within the DNA increases linearly before the buckling transition, exhibits an abrupt decrease upon buckling, and remains constant afterwards (see Fig. 1, c and f) (19,21,22,25). The origin of the abrupt buckling is an energetic penalty due to the strongly bent end-loop of the plectoneme compared to the subsequent extrusion of the weaker bent superhelix (20,24,26). Thus, the end-loop serves as a nucleation barrier for the plectoneme formation. As we show here, the measured parameters of the abrupt buckling (20), such as the critical number of turns and the length jump, provide a sensitive benchmark for the energetics of DNA bending at large deflections.

Figure 1.

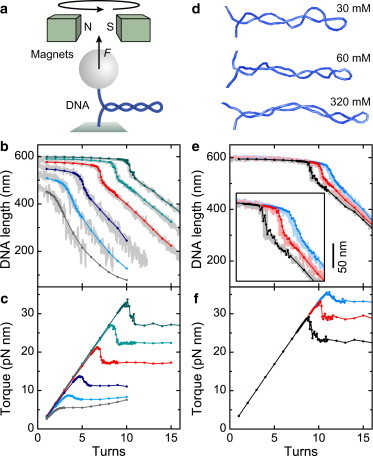
Supercoiling of DNA under tension. (a) Sketch of supercoiling experiments using magnetic tweezers. A DNA molecule is tethered between a surface and a magnetic bead under constant force and can be simultaneously twisted. (b) DNA length versus applied turns at different forces and 170 mM Na⁺. Simulations using WLC bending for stretching forces of 0.25, 0.5, 1.0, 2.0, 3.0, and 4.0 pN (bottom to top in gray, light blue, dark blue, red, light green, and dark green, respectively). The corresponding experimental supercoiling curves (taken from Maffeo et al. (22)) are shown behind (light gray). (c) Torque during DNA supercoiling for the simulations shown in panel b. (d) Snapshots of simulated supercoils at 1.0 pN and nine turns in the presence of 30, 60, and 320 mM monovalent ions. (e) DNA length versus applied turns at different ionic strength and a constant stretching force of 3.0 pN. Results from simulations for 30, 60, and 320 mM monovalent ions (blue, red, and black, respectively). Experimental data (taken from Brutzer et al. (20)) are shown behind (lighter color). (Inset) Enlarged view into the buckling region. (f) Torque during DNA supercoiling for the simulation curves shown in panel e. The experimental curves were slightly shifted in vertical direction for a better overlay with the simulation data.

Methods

Monte Carlo simulations

Monte Carlo simulations were carried out as described recently in Maffeo et al. (22). A brief description of the procedure is given in the main text; a detailed explanation can be found in the Supporting Material.

Analysis of the parameters of the buckling transition

For a precise analysis of the main parameters describing the buckling transition, i.e., the position of the buckling, the length, and the torque jump, we performed independent simulation runs and combined the results to increase the available number of events. Similarly to the previous analysis of experimental data (20), we analyzed the statistical occupancy, the mean DNA extension, and torque of the pre- and the postbuckling states around the buckling point. For this, we binned all DNA length and torque values obtained from the concatenated simulations and fitted double Gaussian curves to the resulting histograms (Fig. 2 a and see Fig. S1 a in the Supporting Material). From these fits, we obtained the mean DNA length and torque for the pre- and the postbuckling states as well as the occupancy of the postbuckling state p_post with respect to the number of applied turns N. The latter dependency can be theoretically described by an expression of the following form (20),

$$p_{\text{post}}\left(N\right)=\frac{1}{1+\text{exp}\left[A\left(N_{\text{b}}-N\right)\right]},$$ (3)

where N_b is the buckling position, i.e., the position at which the pre- and the postbuckling state are equally populated. The dimensionless parameter A describes the width of the transition (20). We fitted Eq. 3 to the occupancy data of the postbuckling state with A and N_b being free fit parameters (see Fig. 2 b and Fig. S1 b). Then we linearly interpolated the DNA lengths and the torque values of the pre- and postbuckling states around the buckling point to determine the length and the torque jumps at the position N_b (see Fig. 2 c and Fig. S1 c).

Figure 2.

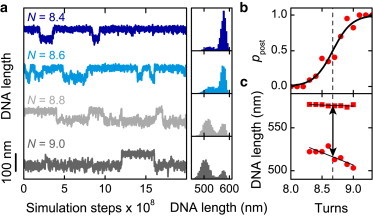
Analysis of the DNA length jump upon buckling from simulations carried out at 3.0 pN force and 170 mM monovalent salt. (a) DNA length versus simulation time at different numbers of turns N with corresponding histograms (shown on the right). Transitions between the pre- and the postbuckling state can be clearly seen. (b) Occupancy of the postbuckling state as function of the applied turns obtained from the histograms shown in panel a. (Solid line) Fit according to Eq. 3. (Dashed line) Buckling position N_b at which the DNA has the same probability to be in the pre- and the postbuckling state. (c) Mean DNA length of the pre- and the postbuckling state (squares and circles, respectively) as function of turns obtained from the histograms shown in panel a. (Arrow) Size of the length jump at the buckling position as obtained from linearly interpolating the DNA lengths (solid lines).

Once the torque jump ΔΓ is known, one can compute the energy barrier that has to be exceeded to nucleate a plectoneme. It corresponds to the triangular-shaped area formed by the torque overshoot in the torque-versus-angular-displacement plots (see Fig. 1 c and (20)):

$$E_{\text{loop}}-E_{\text{helix}}=\frac{1}{2}\frac{{\left(\Delta \Gamma \right)}^2·L_0}{C_{\text{S}}}.$$ (4)

The term E_loop denotes the free energy to form the first turn of writhe in the plectoneme, which comprises the additional energy for the end-loop formation. The term E_helix is the free energy for every subsequent turn of writhe within the plectoneme. The apparent torsion modulus C_S can be derived from linear fits of the torque-turn dependence in the prebuckling phase (see Fig. S2 and the Supporting Material). The energy barrier E_loop–E_helix is force- and salt-dependent, because ΔΓ increases with the applied stretching force and ionic strength (Fig. 3, d and h, and Brutzer et al. (20)).

Figure 3.

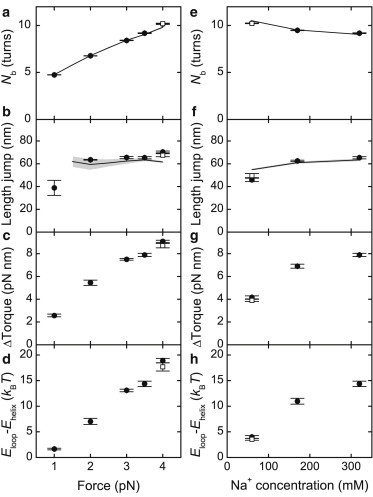
Parameters describing the buckling transition. Data from simulations that use the WLC model are shown (solid circles, 5-nm segments and open squares, 2.5-nm segments). Experimental data were taken from Brutzer et al. (20) (shown as lines; standard error of the measurements is depicted as shaded area if larger than the line width). The buckling parameters are shown as function of force at 320 mM Na⁺ (a–d) and as a function of ionic strength at constant stretching force of 3.5 pN (e–h). (a and e) Positions of the buckling point N_b. (b and f) Abrupt DNA length jump and (c and g) torque jump at the buckling point. (d and h) Energy difference between the formation energies E_loop and E_helix. E_loop–E_helix represents the energetic penalty to nucleate a plectonemic superhelix and was calculated using Eq. 4.

Analysis of the superhelix curvature

We analyzed the curvature of the simulated supercoils to determine the bending angle within the tightly bent end-loop. In a first step we applied an automatized plectoneme-detecting algorithm (27) and identified every segment that is part of the plectonemic superhelix. Subsequently we determined the apex of the plectonemic region, i.e., the position along the chain, which is at the center of the end-loop. Therefore, we determined for each segment i in the helical part of the plectoneme its nearest neighbor i + n on the opposite helix strand. Assuming the apex to be roughly located at index i + n/2 in a regular superhelix, we estimated the apex position by averaging the indexes of several segment pairs. Because the position of the plectoneme within the molecule varies during the simulation, we used the apex as a reference point to align the DNA segments of single simulation snapshots. In a third step we computed the bending angle θ between neighboring 5-nm segments within the plectoneme. For better resolution, this analysis was performed for the simulations with 2.5-nm segments, where segments i and i + 1 determined one 5-nm segment and segments i + 2 and i + 3 the neighboring 5-nm segment. We averaged the bending angles of the aligned DNA segments over several hundred simulation snapshots and different simulations and obtained mean bending angles for every segment pair relative to the apex position (see Fig. 5). We verified that the simulations using 5-nm segments gave identical results within error (not shown).

Figure 5.

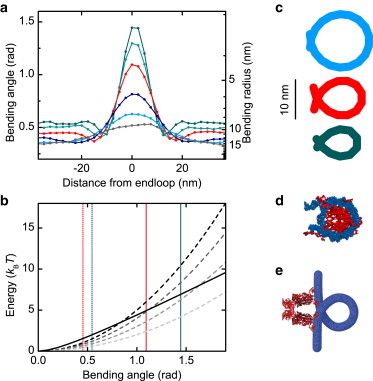
DNA bending within plectonemic supercoils. (a) Bending angles and radii between consecutive 5-nm segments around the plectoneme end-loop from simulations using the WLC model for forces between 0.25 and 4 pN at 170 mM Na⁺ (colors are as in Fig. 1b). The segments are aligned at the turning point of the superhelix. For better resolution the data were taken from simulations using 2.5-nm segments. (b) Comparison of bending energies as predicted by the LSEC model according to Eq. 5 (solid line) and the WLC model (Eq. 1) for persistence length of 50, 40, 30, and 20 nm (black to lighter-shaded dashed lines). Average angles within the plectonemic superhelix and maximum angles in the end-loop are shown (dotted and solid, vertical lines) at stretching force of 2.0 pN and 4.0 pN. (c) End-loop conformations from average bending angles at 0.5, 2, and 4 pN are shown in colors corresponding to panel a. (d) Visualization of a nucleosome based on PDB entry:1KX5 (32) and (e) a model of the Lac-repressor, derived from PDB entry:1JWL (33), the DNA loop is modeled purely graphically assuming a loop size of ∼93 bp (34). Biological models are to scale with end-loops derived from curvature analysis in panel c.

Results

To model previously published experimental supercoiling data (20,22), we carried out Monte Carlo simulations with a coarse-grained DNA model. We note that, recently, theoretical descriptions that include influences from DNA fluctuations also became available (24,28,29). However, these models exhibit considerable differences regarding the applied electrostatic potentials as well as the entropic free energy contributions from the fluctuations. In particular, the latter is a complex term that is still not well understood nor stringently validated. We therefore preferred simulations that naturally include fluctuations over theoretical modeling. The simulations were carried out as described before (22) (see also the Supporting Material).

In brief, the DNA was considered as a 645-nm-long chain consisting of 129 small cylindrical 5-nm segments (additional control simulations were also carried out for 2.5-nm segments, see below and the Supporting Material). The elastic properties of the DNA were described by harmonic potentials for twisting (torsional rigidity of 90 nm × k_BT (19,25,30,31)) as well as elastic stretching and by harmonic and nonharmonic potentials for bending (see below and the Supporting Material). The electrostatic interactions were modeled by approximating DNA as a homogeneously charged cylinder with 1.2-nm radius for which a Debye-Hückel potential is obtained that fits the exact solution of the Poisson-Boltzmann equation for DNA-DNA distances ≥0.5 nm (22). This potential, which uses only 42% of the full DNA charge (see Fig. S3), has previously been successfully applied to describe the force and salt dependence of the postbuckling slopes of the supercoiling curves (22). Electrostatic interactions between neighboring segments were excluded and assumed to be comprised in the persistence length of the DNA. A detailed description of the simulation procedure and used parameters are given in the Supporting Material.

Testing the WLC model

We first tested the classical harmonic potential for DNA bending for a persistence length of 50 nm. By performing simulations for different numbers of turns, we obtained curves matching those observed in the magnetic tweezers experiments over the whole range of forces and ionic strengths (Fig. 1).

The analysis of the slopes and torques of the postbuckling phase confirmed the good agreement of simulation results and experimental data (20) (see Fig. S4). The increase of the postbuckling torque at elevated turn numbers for forces of 0.5 pN and lower (Fig. 1 c) is in agreement with recent theoretical predictions (24,29). It arises, however, to a minor extent from multiple plectonemes but mostly from intrinsically bent or internally split single plectoneme configurations, which are hard to capture in theoretical models.

At a critical supercoiling density, transitions between stretched and supercoiled DNA states can be observed in the simulations (see Fig. 2) similarly to the ones found in experiments (20). For better comparison, we analyzed the buckling in detail and determined the position of the buckling point N_B, at which the pre- and the postbuckling states are equally populated, as well as the size of the abrupt DNA length jump at this point (see Fig. 2 and Fig. S1). A comparison with experimental data that were analyzed in the same manner (20) provided, within errors, quantitative agreement with our simulations (Fig. 3). We also determined the size of the torque jump upon buckling (see Fig. 3, and see Fig. S1 and Fig. S5) that agrees with experimental estimates (20,26) and calculated the force- and salt-dependent energy barrier (E_loop–E_helix) that has to be overcome to establish the initial plectonemic structure (20) (see Fig. 3, d and h, and see Methods). To analyze whether the coarse-graining can affect the obtained results, we performed a selected set of simulations using 2.5-nm DNA segments yielding very similar results for the buckling parameters (Fig. 3), for the postbuckling slopes and torques (see Fig. S4) as well as for the apparent torsional rigidity (see Fig. S2 and the Supporting Material). All the simulation results obtained so far confirm that the classical WLC model can quantitatively describe the buckling transition.

Testing alternative bending models

We next tested the bending potential given by the LSEC model (9). The original form of the LSEC potential was given for 2.5-nm segments (Eq. 2). To adapt this potential for 5-nm segments, the angular distributions for two consecutive 2.5-nm segments need to be convoluted (9) (see the Supporting Material), from which the following potential is obtained:

$$E_{\text{LSEC}}^{5\text{nm}}=\left(-\text{ln}\left(1+\alpha \left|\theta \right|\right)+\alpha \left|\theta \right|\right)k_{\text{B}}T.$$ (5)

Instead of the originally given value of 6.8 (9), we used α = 6.4, because this provides a much better agreement between the angular distributions of the LSEC model and the WLC model using p = 50 nm, calculated for DNA lengths of 30 nm and larger.

While the bending potential was replaced, we left all other parameters unchanged and repeated the simulations for various numbers of turns and stretching forces (Fig. 4, a and b). In stark contrast to WLC bending, the simulations using the LSEC potential reproduced the postbuckling slopes, but failed to describe the buckling transition. The buckling points shifted by up to two turns toward lower values. The size of the abrupt length jump (Fig. 4 a) decreased to about a third of the experimental value leading to a rather smooth buckling transition. Correspondingly the torque overshoot upon buckling appeared also to be largely reduced (Fig. 4 b) compared to the simulations using WLC bending. As a control, we additionally carried out simulations using 2.5-nm segments with the original formulation of the LSEC model providing a similarly suppressed buckling (not shown).

Figure 4.

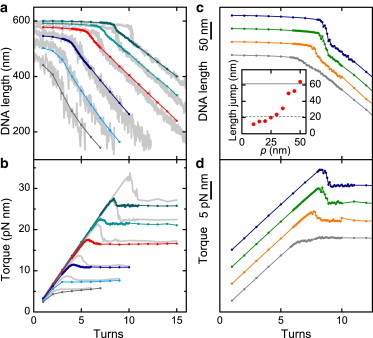
Simulations of DNA supercoiling under tension with alternative DNA models. (a) DNA length versus applied turns at different applied forces (0.25–4 pN) and 170 mM Na⁺ using the LSEC model (colored dots and lines, colors as in Fig. 1b). (Light gray) Experimental supercoiling curves. (b) Torque values for the simulations shown in panel a. Torque values from simulations using the WLC bending are shown behind (light gray). (c) DNA length versus applied turns from simulations using the WLC model where the bending persistence length was reduced locally to 20, 30, 40, and 50 nm (gray, orange, green, and dark-blue dots and lines, respectively) at 170 mM Na⁺ and 3.0 pN force. (Inset) Length jump as function of local persistence length (red circles), and length jump from experiments and from the LSEC model (solid and dashed line, respectively). (d) Torque values for the simulations shown in panel c. Curves in panels c and d were shifted with respect to each other by 40 nm and 5 pN nm, respectively, to improve clarity.

To better understand the influence of the bending rigidity within the end-loop on the abrupt buckling, we made a small part of a DNA chain with WLC bending energetics (p = 50 nm) more flexible by lowering the persistence length over a 30-nm stretch (six consecutive segments, corresponding approximately to the size of the end-loop) in the middle of the chain. We carried out simulations with local bending persistence lengths ranging from 50 to 10 nm. As expected, locally lowering the end-loop formation energy leads to a pronounced reduction of the abrupt length and torque decrease upon buckling (Fig. 4, c and d). To achieve an abrupt length and torque decrease as seen for the LSEC model, the persistence length has to be locally reduced to ∼25–30 nm (Fig. 4 c, inset). This shows that a greatly reduced buckling is only achieved if the DNA bending energetics is significantly altered.

End-loop formation

We also analyzed the mean curvature of several hundred simulated plectonemes, confirming high bending deflections in the end-loop and a moderate bending in the helical part (Fig. 5 a). For stretching forces above 2.0 pN, the end-loop shows bending angles between consecutive 5-nm segments that are >1 rad (corresponding to a bending radius of 5 nm) up to 1.4 rad (corresponding to a bending radius of 3.6 nm) at 4.0 pN.

As described above, the buckling transition arises due to the energetic offset between the formation energy of an end-loop and the subsequent formation of the superhelical plectoneme structure (20). The magnitude of this offset depends on the applied stretching force, the ionic strength of the solvent, and in the context of simulations, on the applied bending potential. If this offset is small, i.e., in the order of 1 k_BT, the extrusion of multiple end-loops and plectonemes becomes likely. Because the LSEC model provides considerably smaller bending energies for the end-loop compared to the WLC model, DNA configurations with multiple end-loops and plectonemes should occur more frequently that is corroborated by the simulations (Fig. 6).

Figure 6.

Snapshots from simulations with WLC and LSEC bending elasticity taken shortly after the buckling transition. The salt concentration is 170 mM, the forces are indicated in the figure. The radius of the visualized DNA was doubled to improve clarity. For the LSEC model, multiple plectonemes are frequently detected. This is due to the lower energy required to form the tightly bent end-loop compared to the WLC bending energetics (see text).

To additionally confirm that multiplectoneme states are due to a low energy difference between end-loop formation and superhelix extrusion, we carried out simulations at salt concentrations below 20 mM. With decreasing ionic strength, the growing electrostatic repulsion within the plectonemic superhelix lowers the offset imposed by the strong bending of the end-loop. As a consequence, the formation of multiple end-loops is preferred over a single superhelix (see Fig. S6 and Fig. S7 (three-dimensional models)). It even seems that only end-loops are forming and that plectoneme formation is suppressed, suggesting a negative energetic offset. The formation of multiple end-loops and plectonemes is accompanied by a complete loss of the abrupt buckling (see Fig. S6 b) as experimentally observed at low ionic strength (20) as well as an increasing, nonconstant postbuckling torque (see Fig. S6 c), as seen also for low forces at higher ionic strength (Fig. 1 c) and as recently predicted (24,29).

Discussion

In summary, we show here that the abrupt buckling, which occurs upon supercoiling DNA under tension, is quantitatively reproduced using a classical harmonic potential for bending deflections. The small bending radii that can be present in the end-loop of a plectoneme are similar to those obtained in the smallest protein-induced DNA loops known so far (Fig. 5, c–e).

The alternative LSEC model that assumes a reduced bending energy for large deflections fails to describe the buckling. The buckling is a robust benchmark for model assessment that is relatively insensitive to a particular value of the persistence length—a local reduction of the persistence length by 10 nm still provides a length jump being much larger than found for the LSEC model (Fig. 4 c). A global reduction of the persistence length has an even smaller effect on the length jump (not shown). This is different compared to other experiments, in particular DNA cyclization, that can be equally well described by both models, depending on the parameters taken (9,15).

Most importantly, the buckled state is based on a permanently tight DNA bend within the end-loop. Previous investigations of short-scale DNA elasticity, e.g., as measured by DNA cyclization, AFM, SAXS, and FRET (9,10,13,15,17), however, relied on the statistical frequency of rare, large bending deflections, which are more difficult to interpret and partially contradictory (Peters and Maher (35); compare Wiggins et al. (9) to Witz et al. (36); Yuan et al. (13) to Mastroianni et al. (17); and Mathew-Fenn et al. (37) to Becker and Everaers (38)).

In contrast to the original AFM studies that proposed the LSEC model (9), DNA bending within supercoils occurs in free solution. In fact it has been suggested that electrostatic immobilization of DNA on mica surfaces can affect the hydrogen bonding of complementary bases and the stacking of adjacent base pairs leading to more frequent local DNA denaturations and thus to a higher bending flexibility as measured by AFM (14). In line with this, investigations of DNA minicircles with cryo-electron microscopy, that avoid any surface immobilization, support a harmonic bending potential for DNA (39).

The large difference for WLC and LSEC model observed here arises from the extreme DNA bending within the end-loop at elevated forces with bending radii of 5 nm and smaller (Fig. 5 a). In this regime, the WLC and LSEC energetics diverge significantly (Fig. 5 b). This causes a much lower plectoneme nucleation barrier for the LSEC model and thus the greatly suppressed buckling.

We note that our simulation model does not account for the sequence-specific elasticity of DNA as recently measured (40). The presence of stretches of reduced bending rigidity could favor less extensive buckling at certain spots on the DNA. However, this appears to be negligible most likely due to the insensitivity of the buckling against changes of the persistence length (Fig. 4 c, inset). Though nonharmonic bending potentials for certain basepair stackings are suggested (14), it might be the averaging over many different stacking configurations that provide a mean harmonic potential for DNA bending according to the central limit theorem as long as the base stacking is not interrupted. The latter condition should be fulfilled even for the tight bends we obtain, because DNA helix disruptions have so far only been found for bending radii <3.5 nm (41).