Abstract
Motivation: Gene–gene interactions (epistasis) are thought to be important in shaping complex traits, but they have been under-explored in genome-wide association studies (GWAS) due to the computational challenge of enumerating billions of single nucleotide polymorphism (SNP) combinations. Fast screening tools are needed to make epistasis analysis routinely available in GWAS.
Results: We present BiForce to support high-throughput analysis of epistasis in GWAS for either quantitative or binary disease (case–control) traits. BiForce achieves great computational efficiency by using memory efficient data structures, Boolean bitwise operations and multithreaded parallelization. It performs a full pair-wise genome scan to detect interactions involving SNPs with or without significant marginal effects using appropriate Bonferroni-corrected significance thresholds. We show that BiForce is more powerful and significantly faster than published tools for both binary and quantitative traits in a series of performance tests on simulated and real datasets. We demonstrate BiForce in analysing eight metabolic traits in a GWAS cohort (323 697 SNPs, >4500 individuals) and two disease traits in another (>340 000 SNPs, >1750 cases and 1500 controls) on a 32-node computing cluster. BiForce completed analyses of the eight metabolic traits within 1 day, identified nine epistatic pairs of SNPs in five metabolic traits and 18 SNP pairs in two disease traits. BiForce can make the analysis of epistasis a routine exercise in GWAS and thus improve our understanding of the role of epistasis in the genetic regulation of complex traits.
Availability and implementation: The software is free and can be downloaded from http://bioinfo.utu.fi/BiForce/.
Contact: wenhua.wei@igmm.ed.ac.uk
Supplementary information: Supplementary data are available at Bioinformatics online.
1 INTRODUCTION
Genome-wide association studies (GWAS) have been successful in identifying a large number of trait-associated genetic loci (Hindorff et al., 2009), but are less successful in identifying much of the genetic variation (Maher, 2008). Gene–gene interactions (epistasis) are thought to be a potential source of unexplained genetic variation (Eichler et al., 2010; Gibson, 2010; Manolio et al., 2009; Zuk et al., 2012), but they remain largely unexplored in GWAS conducted so far. A major hurdle for studying epistasis in GWAS is the lack of widely accepted algorithms that are fast enough to effectively handle high-density single nucleotide polymorphism (SNPs) and can map different forms of epistasis while keeping false-positive rates (FPRs) under control (Wei et al., 2010). High-throughput tools are needed to make epistasis analyses routinely available in GWAS and ultimately improve our understanding of the role of epistasis in the genetic regulation of complex traits.
Significant efforts have been made to develop new tools and algorithms for epistasis detection in GWAS (Cordell, 2009) using either deterministic or stochastic methods, such as regression (Hemani et al., 2011; Kam-Thong et al., 2011; Liu et al., 2011; Schupbach et al., 2010; Wan et al., 2010), machine learning (Cattaert et al., 2010; Greene et al., 2010; Motsinger-Reif et al., 2010) and Bayesian-based approaches (Tang et al., 2009; Zhang and Liu, 2007). Most of these algorithms concern only GWAS for case–control (binary) disorders and still require substantial computing time to analyse epistasis in one trait in real GWAS data (Schupbach et al., 2010; Yung et al., 2011). Partial search strategies, based on biological knowledge (Emily et al., 2009) or filtering unimportant SNPs prior to analysis (Kam-Thong et al., 2011), are adopted in some studies in order to reduce excessive computing burden but risk missing some types of variation. Fast but comprehensive methods to analyse epistasis in GWAS conducted for many complex (i.e. continuous and quantitative) traits are lacking.
Previously, we showed that high-throughput analysis of epistasis in quantitative traits in GWAS was feasible using computers with general purpose graphics processing units (Hemani et al., 2011). We also suggested a search algorithm using the information of pre-identified loci in a full pair-wise genome scan to increase the power of detection of epistasis (Lam et al., 2009; Wei et al., 2010), which was applied successfully in recent studies for binary (Liu et al., 2011) and complex traits (Wei et al., 2011). These ideas are combined in a unique tool, BiForce, to support high-throughput epistasis analysis for either binary or quantitative traits on commonly used computer systems. Herein, we describe the algorithm and essential features of BiForce and compare the performance of BiForce with that of BOOST (Wan et al., 2010) in binary traits and PLINK (Purcell et al., 2007) in quantitative traits through simulation, both of which perform exhaustive pair-wise search based on regression-based statistics over commonly used computer systems as BiForce. We also demonstrate BiForce analysis of epistasis in real GWAS data, i.e. eight metabolic traits in the Northern Finland Birth Cohort 1966 (NFBC1966) (Sabatti et al., 2009) provided by dbGaP (http://www.ncbi.nlm.nih.gov/gap) and two disease traits provided by the Wellcome Trust Case Control Consortium (WTCCC) (https://www.wtccc.org.uk/ccc1/). It is hoped that with BiForce, the analysis of epistasis in GWAS will become a routine exercise thus facilitating accumulation of information on epistasis hence improving our understanding its role in the genetic regulation of complex traits.
2 METHODS
2.1 BiForce
BiForce is a multi-threaded Java implementation of a combined search algorithm (Lam et al., 2009; Wei et al., 2010) and it can be used on a single workstation or computer clusters through a friendly graphical user interface or the command line. It uses contingency table-based methods to calculate pair-wise SNP interactions, which makes BiForce applicable to either binary or quantitative traits (Supplementary Note 1). BiForce can perform full pair-wise genome scans very rapidly because of three computational achievements:
Bitwise data structures: SNP genotype data are converted into Boolean bit values and stored in memory-efficient Java BitSet arrays allowing missing genotypes to be handled easily.
Boolean bitwise operations: logical operations (e.g. AND) over the arrays of bit values make the calculation of SNP interactions (see below) extremely fast.
Multithread (and/or multi-core) parallelization: this makes full pair-wise genome scans feasible on a single workstation and portable across computer clusters.
The combined search algorithm includes two consecutive genome scans: single SNP-based genome-wide association tests (i.e. conventional GWAS) and pair-wise interaction tests of all SNP combinations. Single SNPs with marginal effects that are genome-wide significant (marginal SNPs) are identified in the first scan and used to detect interactions involving marginal SNPs (Wei et al., 2010). The 5% genome-wide significance thresholds are derived based on the Bonferroni correction for total number of tests performed. Given N to be the total number of SNPs in a study with K (K>0) marginal SNPs being identified, the thresholds are P=0.05/N for marginal SNPs, P=0.05/((N−1)×K) for interactions involving marginal SNPs (because each marginal SNP is tested against the full genome, and hence the total test is (N−1)×K) and P=0.05/(N×(N−1)/2) for a pair-wise genome scan (Evans et al., 2006; Lam et al., 2009).
Considering a pair of SNPs denoted as SNP1 and SNP2, the following genetic models are used to detect epistasis where genotypes of each SNP (i.e. homozygote of the minor allele, homozygote of the major allele and heterozygote) were fitted as fixed factors:
Model 1: y = μ + SNP1 + SNP2 + SNP1 × SNP2 + e
Model 2: y = μ + SNP1 + SNP2 + e,
where y is the trait of interest, μ is the model constant, SNP1 (or SNP2) is a fixed factor with three levels, SNP1×SNP2 is the interaction term and e is the random error term. The test of Model 1 against Model 2 (F ratio for quantitative traits and log-likelihood ratio for binary traits) is for the interaction between the two SNPs (i.e. four degrees of freedom). P-values were computed based on specific test statistic distributions and actual degrees of freedom (assumed fixed four degrees of freedom in disease traits).
BiForce is designed to provide fast screening of epistasis without pre-filtering of SNPs in GWAS. For disease traits, BiForce adopts the approximation step implemented in BOOST (Wan et al., 2010) as a default option to accelerate the exhaustive genome scan, which can be dismissed when necessary (i.e. using only log-likelihood ratio tests in the exhaustive scan). Quality control procedures applied in GWAS are required before using BiForce to analyse epistasis. Currently, BiForce can only work with SNPs located on autosomal chromosomes.
2.2 Experiments on simulation data
Simulation was used to test the performance of BiForce in binary traits in comparison with BOOST (Wan et al., 2010) and quantitative traits in comparison with PLINK (Purcell et al., 2007) using 500 replicates for every simulation scenario (Supplementary Note 2). For simplicity, in both comparison cases, we adopted the simulation design used in the BOOST paper (Wan et al., 2010), where BOOST was compared against PLINK using simulation generated by the program gs (Li and Chen, 2008) to measure the power of detection and the program genomeSIMLA (Dudek et al., 2006) for FPR estimates. The gs program generated SNP genotypes using HapMap data under the assumption of Hardy–Weinberg equilibrium, whereas the genomeSIMLA program generated genotype data based on the Affymetrix 500k SNP array to accommodate linkage disequilibrium in real GWAS. The simulation design used four two-locus interaction models each with marginal effects of the disease loci to generate epistatic scenarios. Briefly, considering two loci A (disease risk allele a) and B (disease risk allele b), Model 1 is a multiplicative model (Marchini et al., 2005); both Models 2 and 3 have the missing lethal genotype (i.e. the double homozygote of disease alleles aabb does not lead to disease) (Li and Reich, 2000); Model 2 differs from Model 3 mainly in the double heterozygous genotype AaBb that does not lead to disease and has been used to describe the genetics of handedness (Levy and Nagylaki, 1972; Neuman and Rice, 1992); Model 4 is a well known XOR (exclusive OR) model where only four single heterozygous genotypes (AABb, AaBB, Aabb and aaBb) lead to disease (Li and Reich, 2000; Moore and Williams, 2009) (Supplementary Note 2).
Following the design, the four epistatic models were used to generate epistatic scenarios for binary traits each with a fixed disease prevalence of 0.1, 1000 SNPs, a sample size of 800 or 1600 (with balanced design) and a minor allele frequency (MAF) of 0.1 or 0.2 or 0.4 for disease SNPs (assumed equal MAF for both loci). Disease heritability was set as 0.03 for Model 1 and 0.02 for Models 2–4. The gs program simulated SNP genotypes and samples (either 800 or 1600) for each epistatic scenario. To apply the simulation design to quantitative traits without the disease prevalence parameter while maintaining the interaction pattern, genotypes in the contingency table derived for each epistatic scenario for binary traits were scaled down to concern only MAF and heritability (Supplementary Note 2). The gs program simulated SNP genotypes and an R script was used to simulate samples for quantitative traits with a standardized distribution (mean of 0 and variance of 1) for each epistatic scenario (Supplementary Note 2). We randomly chose the chromosome 11 HapMap data for gs to simulate the epistatic scenarios. Power was calculated as the percentage of replicates with the simulated epistatic SNP pair detected as a significant signal out of the total of 500 replicates.
In addition, following the simulation design, the NULL scenarios were generated using the genomeSIMLA program to simulate 38 836 SNPs based on the SNP information of chromosome 1 from the Affymetrix 500k SNP array as the BOOST paper (Wan et al., 2010), with 1000 samples simulated by randomly sampling from a Bernoulli distribution for binary traits or from a Gaussian distribution (mean of 0 and variance of 1) for quantitative traits. An additional NULL scenario was used to examine FPRs where 1000 SNPs were randomly generated with MAFs uniformly distributed in [0.05, 0.5]. FPR was calculated as the percentage of the total number of significant SNP pairs detected out of 500 replicates.
2.3 High-throughput analyses of epistasis
BiForce was used to analyse epistasis in eight metabolic traits in the NFBC1966 cohort: C-reactive protein (CRP), diastolic blood pressure (DBP), glucose (GLU), high-density lipoprotein (HDL), insulin (INS), low-density lipoprotein (LDL), systolic blood protein (SBP) and triglycerides (TRI). Following the instructions given in the original GWAS (Sabatti et al., 2009), we firstly excluded individuals according to the phenotypic exclusion criteria and then undertook the procedures of quality control of genotype data and corrected each trait for the SexCOPG covariate (recoded according to gender, status of taking oral contraception and pregnancy) (Supplementary Note 3). Furthermore, each trait was normalized (instead of log transformed in the original GWAS (Sabatti et al., 2009)) using the ‘rntransform’ function and then corrected for relatedness using the ‘polygenic’ function both available in the GenABEL package (Aulchenko et al., 2007a) implemented in R (http://www.r-project.org/) and the resultant environmental residuals (i.e. pgresidualY) were used as the new trait values to test for association (Aulchenko et al., 2007b).
After the quality control and phenotype pre-processing, the NFBC1966 cohort had 323 697 autosomal SNPs and >4500 individuals (ranged from 4579 in INS to 5255 in CRP) in different traits. The consensus GWAS threshold (P = 5.0E-08) (McCarthy et al., 2008) was applied to identify marginal SNPs. Following the definitions in Section 2.1, with N as 323 697, the 5% genome-wide threshold P-values were derived as 9.54E-13 for the full pair-wise genome scan and 1.5E-07 for interactions with marginal SNPs if only one marginal SNP was detected (or 7.7E-07, 5.1E-08, 3.9E-08, 3.1E-08, 2.6E-08, 2.2E-08, 1.9E-08, 1.7E-08 and 1.5E-08, if 2–10 marginal SNPs were detected, respectively).
BiForce was also used to analyse two WTCCC datasets: bipolar disorder (BD) and Crohn's disease (CD) that were obtained initially for BiForce development with 1500 shared control individuals from the UK Blood Services (Consortium, 2007). All individuals were genotyped with the Affymetrix GeneChip 500K mapping array set. After excluding 153 individuals with non-European ancestry and quality control (Supplementary Note 3), in total 1458 shared controls, 1868 BD cases (347 004 SNPs) and 1752 CD cases (349 056 SNPs) were analysed for epistasis using BiForce. The 5% genome-wide threshold P-values were derived for the two traits similarly as for the metabolic traits.
3 RESULTS
3.1 Power and FPR on simulation experiments
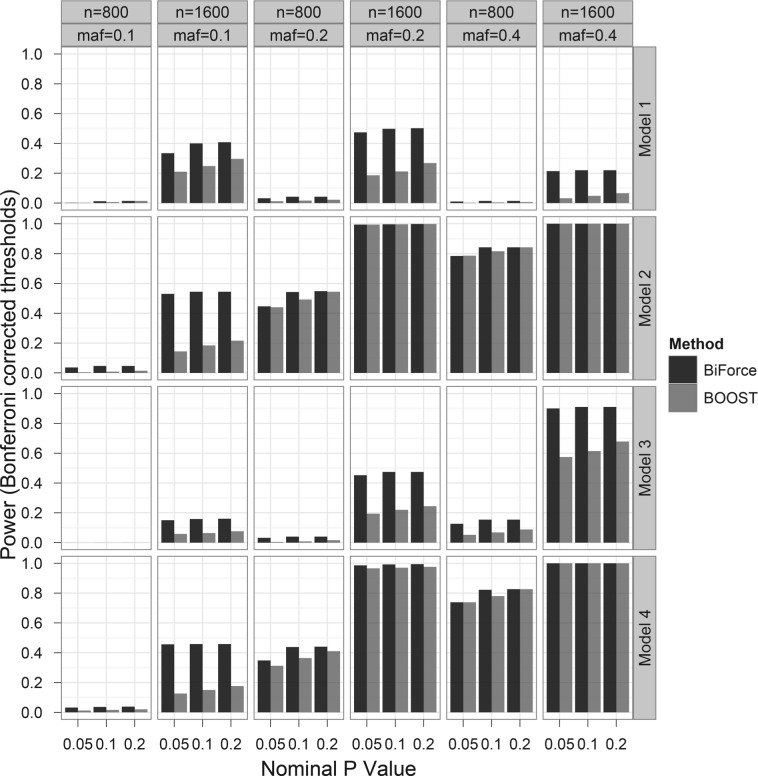
Figure 1 shows the comparison of power of detection of epistasis between BiForce and BOOST for binary traits. BiForce exhibited higher or similar power across all epistatic scenarios simulated. The BiForce power advantage over BOOST became more evident when the sample size was 1600, e.g. power more than doubled when MAF was 0.1 in Models 2–4, MAF was 0.2 and 0.4 in Model 1 and MAF was 0.2 in Model 3. The power gains in BiForce are attributable to the use of the combined search algorithm through detection of interactions involving marginal SNPs. If interactions involving marginal SNPs are ignored or when no marginal SNPs were involved in interactions, the power values from BiForce were almost identical to those from BOOST since both use log-likelihood ratio tests and a pair-wise genome scan.
Fig. 1.
Comparison of power of detection of epistasis in binary traits between BiForce and BOOST. Model 1: multiplicative model, Models 2 and 3: missing lethal genotype model (aabb does not lead to disease, AaBb does in Model 3 but not in Model 2), Model 4: exclusive OR model
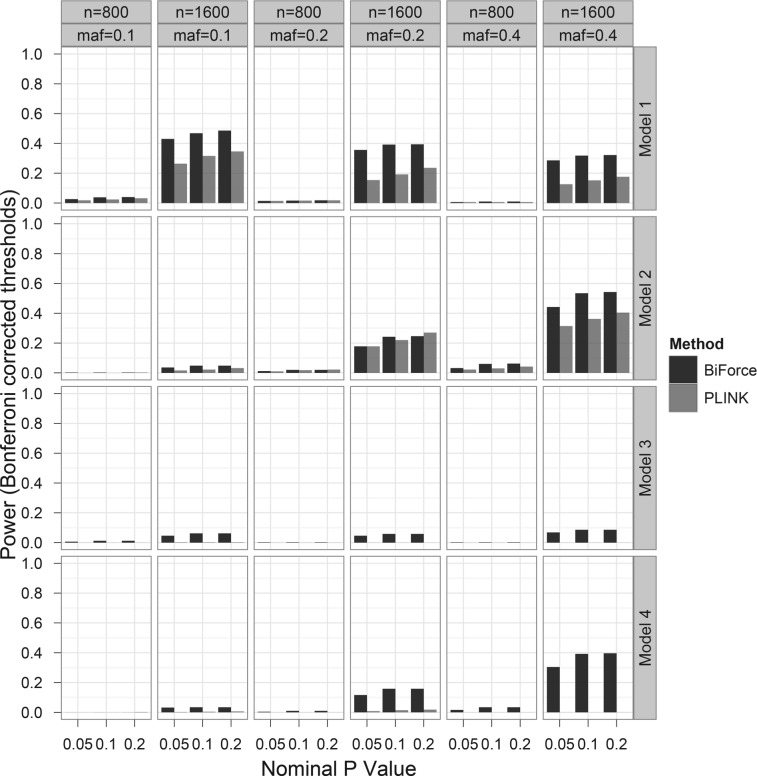
The power of detection of epistasis in quantitative traits was generally low across simulation scenarios (Fig. 2). With a sample size of 800, neither BiForce nor PLINK could detect epistatic signals. BiForce was clearly more powerful than PLINK in all the scenarios with a sample size of 1600. The reasons for the BiForce power gains include the use of the combined search algorithm as before as well as the genotype models. In contrast to the allelic models used in PLINK that can detect only additive–additive interactions, the genotype models used in BiForce can detect additional interaction components not captured by the allelic model (e.g. additive dominance).
Fig. 2.
Comparison of power of detection of epistasis in quantitative traits between BiForce and PLINK. Model 1: multiplicative model, Models 2 and 3: missing lethal genotype model (aabb does not lead to disease, AaBb does in Model 3 but not Model 2), Model 4: exclusive OR model
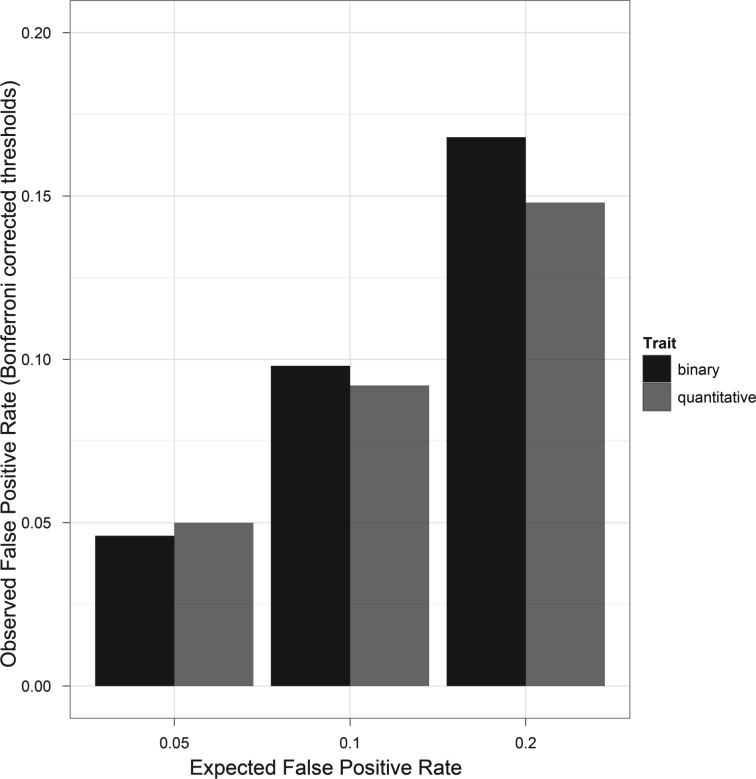
The simulation results of the NULL scenario generated by genomeSIMLA showed that BiForce could control FPR at the 5% genome-wide significance level (Fig. 3). The FPR values became slightly lower than the expected values as the Bonferroni-adjusted thresholds became liberal (i.e. 20%). In the NULL simulation scenario using random SNPs, the FPR of BiForce at the 5% genome-wide significance level was similar to that of BOOST and PLINK and close to 5%, with slightly inflation in quantitative traits when the Bonferroni-adjusted thresholds became liberal (Supplementary Note 4). Using thresholds adjusted to the same level of FPR of 5% made little differences to power profiles as shown in Figures 2 and 3 (Supplementary Note 4).
Fig. 3.
FPR profiles of BiForce in detection of epistasis in binary and quantitative traits
3.2 BiForce computational efficiency
We tested BiForce and BOOST in analysing datasets with 1000 samples and different numbers of SNPs on a single workstation (2.8 GHz Intel Core iMAC with 4 GB RAM and four CPU cores each with two threads) to give a fair comparison. In addition, the same tests were performed on a computer cluster of 32 nodes each with four CPU cores (two threads per core). BiForce was found to be about 30% faster than BOOST when using a single thread and 4–5-fold faster when using eight threads (Table 1). Using the computer cluster, BiForce was 315–330-fold faster than BOOST.
Table 1.
Computing performance (in h) comparison between BiForce and BOOST in analysing different GWAS datasets (1000 samples)a
| SNPs | BOOST | BiForce (1 thread) | BiForce (8 threads) | BiForce (cluster) |
|---|---|---|---|---|
| 100 k | 2.90 | 2.29 | 0.60 | 0.01 |
| 200 k | 11.61 | 8.89 | 2.29 | 0.29 |
| 300 k | 26.11 | 20.08 | 5.11 | 0.65 |
| 400 k | 46.36 | 35.97 | 8.83 | 1.16 |
| 500 k | 72.64 | 55.68 | 14.03 | 1.82 |
| 1000 k | 295.97 | 221.98 | 55.96 | 7.40 |
aBOOST, BiForce (one thread) and BiForce (eight threads) each ran on an iMAC workstation with 4 GB RAM and 4 Intel Cores each with two threads running at 2.8 GHz. BiForce (cluster) used a 32-node computer cluster each with 4 CPU cores (two threads per core).
The above tests were not feasible for quantitative traits because of very long PLINK computing times. Instead, we measured the number of pair-wise tests computed per second by BiForce and PLINK in the quantitative trait situation using 10 000 SNPs and 200 samples on the same workstation as before. BiForce computed 505 000 pair-wise tests per second when using a single thread (2 380 714 using eight threads), whereas PLINK computed only 2990 pair-wise tests per second, i.e. a 168- and 796-fold speed increase using one and eight threads, respectively.
We also tested BiForce on a large GWAS dataset with 500 000 SNPs and 5000 samples to give an idea of computing time in real GWAS data. In the binary trait case, BiForce took 118.18, 30.8 and 0.46 h using one thread and eight threads on the workstation and 256 threads on the computer cluster, respectively. In the quantitative trait case, BiForce took 293.24 and 6.81 h using eight threads on the workstation and 256 threads on the cluster, respectively. In contrast, FastEpistasis—a parallel extension of PLINK took 29, 4 or 0.5 days to analyse a GWAS dataset of the same size using 8, 64 or 512 MPI-bound processors, respectively (Schupbach et al., 2010); GBOOST—a graphical processing unit version of BOOST took 1.34 h to compute a smaller GWAS dataset of 351 542 SNPs and 5003 samples on a computer with Nvidia GeForce GTX 285 display card (i.e. 240 CPU cores) (Yung et al., 2011).
3.3 Epistasis in eight metabolic traits in NFBC1966
BiForce was used to analyse the eight metabolic traits in the NFBC1966 cohort over a local (MRC Human Genetics Unit) cluster of 32 computer nodes each with two Quad-cores (four threads per core) giving a total of 256 threads running at 2.53 GHz per thread. For each trait, BiForce splits the search into 32 small tasks each of which was analysed using two threads and took on average 10.5 h to complete. The whole analysis of eight traits was completed within a day (<24 h).
Using the threshold of P = 5.0E-08, we found 10, 4, 7, 4, 1 and 2 marginal SNPs associated with CRP, GLU, HDL, LDL, SBP and TRI, respectively, and none associated with DBP or INS (Supplementary Table S1). These results mostly agreed with the original GWAS (Sabatti et al., 2009) although we used genotype models (instead of allelic models) and the more rigorous rank transform of the data to normality (instead of the log-transform). BiForce discovered nine genome-wide significant epistatic SNP pairs of which five were for CRP (essentially two epistatic signals on chromosomes 1 and 12, respectively) and one was for each of GLU, HDL, LDL and TRI (Table 2). All the nine epistatic pairs were discovered as marginal SNP interactions (the first seven were between two marginal SNPs), while the rs3764261–rs1532624 pair in HDL was also detected through the pair-wise genome scan. All the epistatic SNPs had a relatively common MAF between 0.28 and 0.41. Interestingly, the interacting SNPs in each of the nine epistatic pairs are located very closely together (<1 Mb) with linkage disequilibrium (LD, in r2) in a range between 0.35 and 0.99. No significant epistatic signals were detected in DBP, INS and SBP.
Table 2.
Genome-wide significant epistatic pairs identified from the NFBC199 cohorta
| Trait | SNP1 | SNP2 | Pint | Distance | LD (r2) |
|---|---|---|---|---|---|
| CRP | rs1811472b (1q23.2; 0.41) | rs2592887b (1q23.2; 0.40) | 3.0E-12 | 10 590 | 0.86 |
| CRP | rs1811472b (1q23.2; 0.41) | rs2794520b (1q23.2; 0.36) | 3.5E-11 | 36 467 | 0.62 |
| CRP | rs2592887b (1q23.2; 0.40) | rs2794520b (1q23.2; 0.36) | 2.9E-12 | 25 877 | 0.70 |
| CRP | rs2650000b (12q24.31; 0.45) | rs7953249b (12q24.31; 0.48) | 2.6E-09 | 14 762 | 0.76 |
| CRP | rs1169300b (12q24.31; 0.32) | rs2464196b (12q24.31; 0.32) | 3.4E-10 | 4202 | 0.99 |
| GLU | rs560887b (2q31.1; 0.30) | rs563694b (2q31.1; 0.34) | 1.3E-08 | 10 923 | 0.81 |
| HDL | rs3764261b (16q13; 0.28) | rs1532624b (16q13; 0.41) | 2.0E-14 | 12 155 | 0.53 |
| LDL | rs157580b (19q13.32; 0.29) | rs405509 (19q13.32; 0.46) | 6.9E-10 | 13 570 | 0.35 |
| TRI | rs1260326b (2p23.3; 0.36) | rs780094 (2p23.3; 0.36) | 5.8E-08 | 10 297 | 0.95 |
aAll SNP pairs listed were detected as marginal SNP interactions, with the threshold of 1.5E-08 for CRP, 2.2E-08 for HDL, 3.9E-08 for GLU and LDL, 7.7E-07 for TRI; SNP1 (SNP2)—name, genomic location and MAF (the latter two in bracket) of the first (second) SNP; Pint—P-value of the interaction test; distance—the distance in base pairs between two SNPs; LD—linkage disequilibrium (in r2) between a pair of SNPs; the SNP pair in HDL was also detected via the pair-wise genome scan (P < 9.54E-13).
bThe marginal SNP.
3.4 Epistasis in two disease traits in WTCCC
BiForce was used to analyse two disease traits BD and CD in the WTCCC data over the same local computer cluster above. Using pre-defined genome-wide thresholds, we identified 3 and 25 marginal SNPs (Supplementary Table S2), 5 and 12 genome-wide significant SNP pairs (Table 3) in BD and CD, respectively. Two of these identified SNP pairs were detected as marginal SNP (rs4246045) interactions, and the remaining were detected only through full pair-wise genome scans. The SNP pairs of rs11162341–rs6658302, rs11096892–rs6531531 and rs2747436–rs29254 were identified in both BD and CD suggesting pleiotropic effects in these signals. Again, all the identified SNP pairs were local interactions in five loci: 1p31.1, 3q21.3, 4p15.1, 5q33.1 and 6p22.1, with SNP MAF ranged from 0.05 to 0.29 and LD ranged between 0.02 and 0.82. Similar observations were previously reported in the BOOST paper (in Table 3 without detailed information of epistatic pairs of SNPs) (Wan et al., 2010) where the total number of SNP pairs detected was slightly different possibly due to a doubled number of control samples and slight differences in the quality control procedure used.
Table 3.
Genme-wide significant epistatic pairs identified from the WTCCC datasetsa
| Trait | SNP1 | SNP2 | Pint | Distance | LD (r2) |
|---|---|---|---|---|---|
| BD | rs11162341 (1p31.1; 0.13) | rs6658302 (1p31.1; 0.25) | 1.7E-14 | 11 272 | 0.02 |
| BD | rs11096892 (4p15.1; 0.05) | rs6531531 (4p15.1; 0.28) | 9.1E-15 | 2196 | 0.03 |
| BD | rs4246045b (5q33.1; 0.14) | rs4958847 (5q33.1; 0.12) | 5.5E-09 | 62 490 | 0.82 |
| BD | rs11949556 (5q33.1; 0.12) | rs4246045b (5q33.1; 0.14) | 4.7E-09 | 52 704 | 0.82 |
| BD | rs2747436 (6p22.1; 0.29) | rs29254 (6p22.1; 0.06) | 4.2E-13 | 28 341 | 0.03 |
| CD | rs11162341 (1p31.1; 0.13) | rs6658302 (1p31.1; 0.25) | 3.1E-14 | 11 272 | 0.02 |
| CD | rs1735558 (3q21.3; 0.15) | rs6439119 (3q21.3; 0.24) | 2.2E-16 | 136 423 | 0.47 |
| CD | rs2248668 (3q21.3; 0.14) | rs6439119 (3q21.3; 0.24) | 8.9E-19 | 32 438 | 0.49 |
| CD | rs2811472 (3q21.3; 0.15) | rs6439119 (3q21.3; 0.24) | 8.0E-16 | 44 316 | 0.48 |
| CD | rs2811483 (3q21.3; 0.14) | rs6439119 (3q21.3; 0.24) | 4.8E-19 | 8514 | 0.50 |
| CD | rs2811484 (3q21.3; 0.14) | rs6439119 (3q21.3; 0.24) | 6.0E-19 | 8334 | 0.50 |
| CD | rs2811510 (3q21.3; 0.14) | rs6439119 (3q21.3; 0.24) | 6.3E-19 | 8675 | 0.50 |
| CD | rs2955125 (3q21.3; 0.14) | rs6439119 (3q21.3; 0.24) | 6.8E-19 | 2005 | 0.50 |
| CD | rs2955132 (3q21.3; 0.14) | rs6439119 (3q21.3; 0.24) | 1.1E-18 | 17 039 | 0.50 |
| CD | rs1554534 (3q21.3; 0.15) | rs6439119 (3q21.3; 0.24) | 8.8E-15 | 123 518 | 0.47 |
| CD | rs11096892 (4p15.1; 0.05) | rs6531531 (4p15.1; 0.28) | 2.8E-14 | 2196 | 0.03 |
| CD | rs2747436 (6p22.1; 0.29) | rs29254 (6p22.1; 0.06) | 3.4E-14 | 28 341 | 0.03 |
aThreshold for the pair-wise genome scan was 8.3E-13 for BD and 8.2E-13 for CD; threshold for marginal SNP interactions was 4.8E-08 in BD (three marginal SNPs were detected); SNP1 (SNP2)—name, genomic location and MAF (the latter two in bracket) of the first (second) SNP; Pint—P-value of the interaction test; distance—the distance in base pairs between two SNPs; LD—linkage disequilibrium (in r2) between a pair of SNPs.
bThe marginal SNP.
4 DISCUSSION
We have shown that BiForce is a unique tool that can support high-throughput analysis of epistasis in GWAS for either binary or quantitative traits. BiForce achieves great computational efficiency by integrating three major advances in computing (i.e. bitwise data structures, Boolean bitwise operations and multithreaded parallelization) with fast calculation of pair-wise interactions. The implementation of the combined search algorithm (i.e. using a less stringent threshold to detect marginal SNP interactions) increases the power of detection of epistasis. Through a series of performance tests, we showed that BiForce was more powerful and significantly faster than BOOST in binary traits and PLINK in quantitative traits. Using real GWAS datasets from the NFBC1966 and WTCCC cohorts, we demonstrated that BiForce could analyse multiple traits in a short time period and identified genome-wide significant epistasis signals.
The strategy of using a less stringent threshold for marginal SNP interactions is statistically justifiable and has been validated in simulations elsewhere (Kooperberg and Leblanc, 2008; Wei et al., 2010) and successfully applied in real data analyses (Evans et al., 2011; Strange et al., 2010; Wei et al., 2011). Our simulation results support the strategy and justify that BiForce is working as expected. BiForce differs from BOOST mainly in the strategy of detection of marginal SNP interactions, thus in binary traits the power of detection by BiForce should be higher than or equal to that from BOOST as shown in our simulation results (Fig. 1). BiForce differs from PLINK in the strategy of detection of marginal SNP interactions as well as the use of genotype models, and hence it is not straightforward to assess the individual impact of the strategy on the BiForce power gains in quantitative traits, especially when the power of detection was generally low (Fig. 2). However, with reference to the simulation results in the BOOST study (Wan et al., 2010) comparing BOOST (genotype models) against PLINK (allelic models), it is clear that the power advantage in BiForce over PLINK in scenarios using Model 1 with MAF of 0.2 and 0.4 (Fig. 2) can be mostly attributed to the strategy of detection of marginal SNP interactions because the model simulated favours the allelic models in these scenarios. Whereas in the scenario using Model 4 with MAF of 0.4, the BiForce power advantage (Fig. 2) can be attributed to the use of genotype models because as MAF increases towards 0.5 the model simulated generates less marginal effects and thus marginal SNP interactions are more difficult to be detected. Nevertheless, the power gains in BiForce are not surprising because all the four interaction models favour marginal effects to some extent. It is worth noting that allelic models implemented in PLINK may have some advantage over BiForce in situations where empty cells (i.e. no samples available in certain genotypes) in the nine-cell contingency table (Supplementary Note 1) are prevalent.
The NULL scenario simulation results (Fig. 3) further justify BiForce. Using 38 836 SNPs simulated from a subset of human genome (i.e. chromosome 1), the results suggest that BiForce has a good control of FPR at the 5% level when LD is present. Surprisingly, the FPR values became more deflated (i.e. lower than the expected nominal error rates of 10 and 20%) when using less stringent thresholds indicating the Bonferroni correction could be conservative. This phenomenon was also observed in the BOOST paper where it was suggested to be due to the LD among the SNPs simulated (i.e. correlated tests) because no FPR deflation was observed in the NULL simulation scenario using 1000 random SNPs (Wan et al., 2010). Our results of the NULL scenarios using 1000 random SNPs were in line with the BOOST results in binary traits but showed certain FPR inflation in quantitative traits using either BiForce or PLINK (Supplementary Note 4). Our results suggest that in addition to LD, the ratio of number of SNPs to number of samples in a study could be critical for the relevance of the significance thresholds based on Bonferroni correction under the assumption that all pair-wise tests are independent.
One may expect that in real GWAS concerning the full genome, the FPR at the 5% level may be further deflated because of a much increased ratio of SNPs to samples and the power of detection may be reduced owing to likely over-stringent Bonferroni-corrected thresholds. The problem can become severe as more and more SNPs are becoming available to GWAS. Therefore, the simulation results in this study may be taken as evidence for software comparisons but are not encouraged to be interpreted at the genome-wide level. A good alternative way to derive the genome-wide significance thresholds is to use permutation. Unfortunately, genome-wide permutation in real GWAS of epistasis would be computational prohibitive even for BiForce. Before the threshold issue is resolved, it is reasonable to use Bonferroni-corrected thresholds so that significant interactions identified from BiForce would contain less false positives than expected, which may be important to GWAS epistasis studies at the early stage. Nevertheless, considering that the Bonferroni-corrected thresholds may be over-stringent, BiForce allows user specified thresholds to be used in epistasis detection.
The generally low power of detection of epistasis in quantitative traits in simulation (Fig. 2) may be slightly discouraging. One possible reason for the low power could be that the scaling applied to genotype values (Section 2.2, Supplementary Note 2) might have reduced contrasts among them. However, it becomes obvious that a large proportion of existing GWAS have limited power to detect epistasis through pair-wise genome scans due to relatively small sample sizes used (Cordell, 2009; Gauderman, 2002; Wei et al., 2012; Zuk et al., 2012), particularly in quantitative traits (Yang et al., 2010). Indeed, the epistasis results of the NFNC1966 cohort (Table 2) suggest that excluding marginal SNP interactions, we could identify only one epistatic pair in HDL through pair-wise genome scans of eight metabolic traits despite that the sample size (5000) in the NFBC1966 cohort is reasonably big. In contrast, 3 and 12 SNP pairs were identified through pair-wise genome scans of the WTCCC BD and CD, respectively (sample size <3500; Table 3) suggesting WTCCC is slightly more powerful than NFBC1966. Considering that nine SNP pairs in CD could be regarded as one epistatic signal because they were mapped to the same genomic location (3q21.3), the power of detection in CD may not be much higher than that in BD (Table 3).
After BiForce analyses, the identified statistical significant interactions need to be tested for replication in other GWAS populations to avoid false positives (Wei et al., 2011, 2012). Nonetheless, statistical replication of the identified interactions and further understanding their underlying biology are beyond the focus of this article of presenting the computational efficiency of BiForce as a fast screening tool. BiForce users are recommended to firstly evaluate the epistasis results in the original GWAS population by re-testing the statistical significant epistatic signals jointly in models considering various covariates and potential population stratification if necessary and then identify independent and important epistatic SNP pairs for statistical replication and further analyses. Such re-tests are essential for binary traits because BiForce in its current form (based on contingency tables) is unable to accommodate covariates in binary traits. Covariates can be approximately dealt with in quantitative traits prior to BiForce analysis as demonstrated in the epistasis analyses of the eight metabolic traits in the NFBC1966 cohort.
Interestingly, all the significant epistatic pairs identified from the NFBC1966 and WTCCC cohorts reflect interactions between two closely located SNPs with a wide range of LD (Tables 2 and 3). The observation of rich local interactions could be taken as supporting the hypothesis that some genetic variation in complex traits may hide in epistasis between linked SNPs (Haig, 2011). However, one immediate question is whether these epistatic pairs are true interactions or mirroring marginal effects captured by haplotypes. The epistatic pairs identified in quantitative traits involve at least one marginal SNP (Table 2) whereas most of those identified in the two disease traits involving no marginal SNPs (Table 3). These results demonstrate that local interactions are not necessarily associated with marginal SNPs (e.g. none of the 25 marginal SNPs in CD listed in Supplementary Table S2 was involved in local interactions) or driven by high LD between SNPs. A haplotype effect could create an apparent statistical interaction when there is only a single causative variant segregating. However, it may be more likely to find an apparent local interaction caused by a haplotype effect when each SNP is in LD with a single causative variant, but LD between SNPs is low. This arises because the correlation between two SNPs in high LD means that fitting the two SNPs together may explain little additional variation over fitting just one SNP. Unfortunately, statistically distinguishing a haplotype effect from a genuine local interaction is likely to be very difficult especially when only a limited sample of the variants available in a region. A detailed study of genetic variation in the region and other approaches such as functional genetic studies may be needed to help disentangle local interactions and understand the underlying mechanisms, e.g. intragenic and extragenic regulation mechanisms (Rokop and Grossman, 2009) and interactions between coding and regulatory variants within a gene (Lappalainen et al., 2011).
With the performance presented, BiForce can remove the computational bottleneck in analysing epistasis in single GWAS populations. Indeed, BiForce has been used to analyse several other dbGaP GWAS datasets with different numbers of SNPs and samples (300–800k SNPs, 1800–6000 samples) in separate studies of epistasis, including those from the GAIN Collaborative Association Study of Psoriasis, GoKinD and GENEVA Diabetes studies. However, routine high-throughput analysis of epistasis with BiForce presents many new challenges. For example, we need fast pipelines to interpret epistatic signals identified from high-throughput analyses, perhaps making use of functional annotation to include biological meaning. We also need methods to make good use of sub-significant epistatic signals given that many GWAS may have low power to detect genome-wide significant signals (Gauderman, 2002). In this case, a method to support meta-analysis of epistasis in GWAS will be needed as BiForce is not applicable to imputed SNP genotype data in its current form.
Supplementary Material
ACKNOWLEDGEMENTS
We thank the editor and two anonymous reviewers for their valuable suggestions and comments. We are grateful for the assistance from the authors of the BOOST software. We thank Gibran Hemani for the R script to simulate quantitative phenotypes. We acknowledge data access to NHLBI STAMPEED study (Northern Finland Birth Cohort 1966, phs000276.v1.p1), GAIN Collaborative Association Study of Psoriasis (phs000019.v1.p1), NINDS Parkinson's Disease study (phs000089.v3.p2) and NHGRI GENEVA Diabetes Study (phs000091.v2.p1) via dbGaP (http://www.ncbi.nlm.nih.gov/gap) and Bipolar Disorder and Crohn's Disease studies via Wellcome Trust Case Control Consortium (https://www.wtccc.org.uk/ccc1/).
Funding: The Biotechnology and Biological Sciences Research Council (BB/H024484/1) and the Medical Research Council Core Fund. Funding for open access charge: BB/H024484/1.
Conflict of Interest: none declared.
Footnotes
† Both authors contributed equally to this work.
REFERENCES
- Aulchenko Y.S., et al. GenABEL: an R library for genome-wide association analysis. Bioinformatics. 2007a;23:1294–1296. doi: 10.1093/bioinformatics/btm108. [DOI] [PubMed] [Google Scholar]
- Aulchenko Y.S., et al. Genomewide rapid association using mixed model and regression: a fast and simple method for genomewide pedigree-based quantitative trait loci association analysis. Genetics. 2007b;177:577–585. doi: 10.1534/genetics.107.075614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cattaert T., et al. FAM-MDR: a flexible family-based multifactor dimensionality reduction technique to detect epistasis using related individuals. PLoS One. 2010;5:e10304. doi: 10.1371/journal.pone.0010304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Consortium T.W.T.C.C. Genome-wide association study of 14,000 cases of seven common diseases and 3,000 shared controls. Nature. 2007;447:661–678. doi: 10.1038/nature05911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cordell H.J. Detecting gene–gene interactions that underlie human diseases. Nat. Rev. Genet. 2009;10:392–404. doi: 10.1038/nrg2579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dudek S.M., et al. Data simulation software for whole-genome association and other studies in human genetics. Pac. Symp. Biocomput. 2006:499–510. [PubMed] [Google Scholar]
- Eichler E.E., et al. Missing heritability and strategies for finding the underlying causes of complex disease. Nat. Rev. Genet. 2010;11:446–450. doi: 10.1038/nrg2809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Emily M., et al. Using biological networks to search for interacting loci in genome-wide association studies. Eur. J. Hum. Genet. 2009;17:1231–1240. doi: 10.1038/ejhg.2009.15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evans D.M., et al. Two-stage two-locus models in genome-wide association. PLoS Genet. 2006;2:e157. doi: 10.1371/journal.pgen.0020157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evans D.M., et al. Interaction between ERAP1 and HLA-B27 in ankylosing spondylitis implicates peptide handling in the mechanism for HLA-B27 in disease susceptibility. Nat. Genet. 2011;43:761–767. doi: 10.1038/ng.873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gauderman W.J. Sample size requirements for association studies of gene–gene interaction. Am. J. Epidemiol. 2002;155:478–484. doi: 10.1093/aje/155.5.478. [DOI] [PubMed] [Google Scholar]
- Gibson G. Hints of hidden heritability in GWAS. Nat. Genet. 2010;42:558–560. doi: 10.1038/ng0710-558. [DOI] [PubMed] [Google Scholar]
- Greene C.S., et al. Multifactor dimensionality reduction for graphics processing units enables genome-wide testing of epistasis in sporadic ALS. Bioinformatics. 2010;26:694–695. doi: 10.1093/bioinformatics/btq009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haig D. Does heritability hide in epistasis between linked SNPs? Eur. J. Hum. Genet. 2011;19:123–123. doi: 10.1038/ejhg.2010.161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hemani G., et al. EpiGPU: exhaustive pairwise epistasis scans parallelized on consumer level graphics cards. Bioinformatics. 2011;27:1462–1465. doi: 10.1093/bioinformatics/btr172. [DOI] [PubMed] [Google Scholar]
- Hindorff L.A., et al. Potential etiologic and functional implications of genome-wide association loci for human diseases and traits. Proc. Natl. Acad. Sci. U S A. 2009;106:9362–9367. doi: 10.1073/pnas.0903103106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kam-Thong T., et al. EPIBLASTER-fast exhaustive two-locus epistasis detection strategy using graphical processing units. Eur. J. Hum. Genet. 2011;19:465–471. doi: 10.1038/ejhg.2010.196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kooperberg C., Leblanc M. Increasing the power of identifying gene × gene interactions in genome-wide association studies. Genet. Epidemiol. 2008;32:255–263. doi: 10.1002/gepi.20300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lam A.C., et al. A combined strategy for quantitative trait loci detection by genome-wide association. BMC Proc. 2009;3(Suppl. 1):S6. doi: 10.1186/1753-6561-3-s1-s6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lappalainen T., et al. Epistatic selection between coding and regulatory variation in human evolution and disease. Am. J. Hum. Genet. 2011;89:459–463. doi: 10.1016/j.ajhg.2011.08.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levy J., Nagylaki T. A model for the genetics of handedness. Genetics. 1972;72:117–128. doi: 10.1093/genetics/72.1.117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li J., Chen Y. Generating samples for association studies based on HapMap data. BMC Bioinformatics. 2008;9:44. doi: 10.1186/1471-2105-9-44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li W., Reich J. A complete enumeration and classification of two-locus disease models. Hum. Hered. 2000;50:334–349. doi: 10.1159/000022939. [DOI] [PubMed] [Google Scholar]
- Liu Y., et al. Genome-wide interaction-based association analysis identified multiple new susceptibility loci for common diseases. PLoS Genet. 2011;7:e1001338. doi: 10.1371/journal.pgen.1001338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maher B. Personal genomes: the case of the missing heritability. Nature. 2008;456:18–21. doi: 10.1038/456018a. [DOI] [PubMed] [Google Scholar]
- Manolio T.A., et al. Finding the missing heritability of complex diseases. Nature. 2009;461:747–753. doi: 10.1038/nature08494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marchini J., et al. Genome-wide strategies for detecting multiple loci that influence complex diseases. Nat. Genet. 2005;37:413–417. doi: 10.1038/ng1537. [DOI] [PubMed] [Google Scholar]
- McCarthy M.I., et al. Genome-wide association studies for complex traits: consensus, uncertainty and challenges. Nat. Rev. Genet. 2008;9:356–369. doi: 10.1038/nrg2344. [DOI] [PubMed] [Google Scholar]
- Moore J.H., Williams S.M. Epistasis and its implications for personal genetics. Am. J. Hum. Genet. 2009;85:309–320. doi: 10.1016/j.ajhg.2009.08.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Motsinger-Reif A.A., et al. Grammatical evolution decision trees for detecting gene–gene interactions. BioData Min. 2010;3:8. doi: 10.1186/1756-0381-3-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neuman R.J., Rice J.P. Two-locus models of disease. Genet. Epidemiol. 1992;9:347–365. doi: 10.1002/gepi.1370090506. [DOI] [PubMed] [Google Scholar]
- Purcell S., et al. PLINK: a tool set for whole-genome association and population-based linkage analyses. Am. J. Hum. Genet. 2007;81:559–575. doi: 10.1086/519795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rokop M.E., Grossman A.D. Intragenic and extragenic suppressors of temperature sensitive mutations in the replication initiation genes dnaD and dnaB of Bacillus subtilis. PLoS One. 2009;4:e6774. doi: 10.1371/journal.pone.0006774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sabatti C., et al. Genome-wide association analysis of metabolic traits in a birth cohort from a founder population. Nat. Genet. 2009;41:35–46. doi: 10.1038/ng.271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schupbach T., et al. FastEpistasis: a high performance computing solution for quantitative trait epistasis. Bioinformatics. 2010;26:1468–1469. doi: 10.1093/bioinformatics/btq147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strange A., et al. A genome-wide association study identifies new psoriasis susceptibility loci and an interaction between HLA-C and ERAP1. Nat. Genet. 2010;42:985–990. doi: 10.1038/ng.694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang W., et al. Epistatic module detection for case–control studies: a Bayesian model with a Gibbs sampling strategy. PLoS Genet. 2009;5:e1000464. doi: 10.1371/journal.pgen.1000464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wan X., et al. BOOST: a fast approach to detecting gene–gene interactions in genome-wide case–control studies. Am. J. Hum. Genet. 2010;87:325–340. doi: 10.1016/j.ajhg.2010.07.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wei W.H., et al. Controlling false positives in the mapping of epistatic QTL. Heredity. 2010;104:401–409. doi: 10.1038/hdy.2009.129. [DOI] [PubMed] [Google Scholar]
- Wei W., et al. Characterisation of genome-wide association epistasis signals for serum uric acid in human population isolates. PLoS One. 2011;6:e23836. doi: 10.1371/journal.pone.0023836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wei W., et al. Genome-wide analysis of epistasis in body mass index using multiple human populations. Eur. J. Hum. Genet. 2012 doi: 10.1038/ejhg.2012.17. 10.1038/ejhg.2012.1017 [doi] [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang J., et al. Comparing apples and oranges: equating the power of case–control and quantitative trait association studies. Genet. Epidemiol. 2010;34:254–257. doi: 10.1002/gepi.20456. [DOI] [PubMed] [Google Scholar]
- Yung L.S., et al. GBOOST: a GPU-based tool for detecting gene–gene interactions in genome-wide case control studies. Bioinformatics. 2011;27:1309–1310. doi: 10.1093/bioinformatics/btr114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y., Liu J.S. Bayesian inference of epistatic interactions in case–control studies. Nat. Genet. 2007;39:1167–1173. doi: 10.1038/ng2110. [DOI] [PubMed] [Google Scholar]
- Zuk O., et al. The mystery of missing heritability: genetic interactions create phantom heritability. Proc. Natl Acad. Sci. USA. 2012;109:1193–1198. doi: 10.1073/pnas.1119675109. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.