An expanded binding model for Cys₂His₂ zinc finger protein-DNA interfaces

Abstract

Cys₂His₂ zinc finger (C2H2-ZF) proteins comprise the largest class of eukaryotic transcription factors. The “canonical model” for C2H2-ZF protein–DNA interaction consists of only four amino acid - nucleotide contacts per zinc finger domain, and this model has been the basis for several efforts for computationally predicting and experimentally designing protein-DNA interfaces. Here, we perform a systematic analysis of structural and experimental binding data and find that, in addition to the canonical contacts, several other amino acid and base pair combinations frequently play a role in C2H2-ZF protein-DNA binding. We suggest an expansion of the canonical C2H2-ZF model to include one to three additional contacts, and show that a support vector machine approach including these additional contacts improves predictions of DNA targets of zinc finger proteins.

1. Introduction

The specific recognition of DNA by proteins is fundamental to the regulation of gene transcription. Transcription factors can be categorized structurally based upon the domains by which they bind DNA (Harrison, 1991). One such structural class consists of the Cys₂His₂ zinc finger (C2H2-ZF) proteins, which are the largest class of eukaryotic transcription factors. C2H2-ZF proteins have been extensively studied, with crystal structures and experimental studies having elucidated their highly conserved modular structure (Wolfe, 2000). Their ability to bind a range of DNA sequences has led to extensive systematic efforts to design novel protein-DNA proteins of desired specificity (Mandell & Barbas, 2006, Fu, 2009). Moreover, since C2H2-ZF domains occur in large numbers in eukaryotic genomes, with several hundred proteins known in the human genome (Venter, 2001), making progress towards predicting their DNA binding specificity will be a key step in uncoverinag protein regulatory networks. While there has been substantial progress in understanding C2H2-ZF protein-DNA interactions, considerable challenges remain in predicting the specificity of C2H2-ZF proteins and in designing new C2H2-ZF proteins that bind a particular site of interest.

Structural studies have revealed that each “finger” in a C2H2-ZF protein consists of a beta-beta-alpha structure, with the alpha-helix binding DNA in the major groove (Pavletich & Pabo, 1991). While the classical C2H2-ZF domain was first discovered in the Xenopus laevis TF-IIIA, the protein essential for correct initiation of transcription (Brown, 1984), the most studied protein in this family is the early growth factor EGR-1 (also known as Zif268). Initial co-crystal studies of Zif268 (Elrod-Erickson et al., 1996, Pavletich & Pabo, 1991) revealed the modular nature C2H2-ZF DNA binding, and it remains the most popular model system for understanding the determinants of C2H2-ZF DNA-binding specificity. Indeed, 16 out of 28 X-ray and NMR structures for C2H2-ZF structures in the Protein Data Bank (PDB) (Berman et al., 2000) are based on Zif268 or its variants, and Zif268 has proven to be a successful platform for designing proteins for recognizing specific DNA sequences (Mandell & Barbas, 2006).

Analysis of co-crystal structures of Zif268 proteins bound to DNA led to the formulation of the so-called “canonical binding model” (Elrod-Erickson et al., 1996) that suggests that binding specificity is limited to four amino acid - nucleotide contacts per zinc finger (ZF), as shown by solid arrows in Figure 1. The canonical binding model has been widely used to describe and predict C2H2-ZF protein–DNA binding interfaces (Benos et al., 2002, Kaplan et al., 2005, Persikov et al., 2009, Liu & Stormo, 2008, Endres & Wingreen, 2006), and as the basis for approaches for designing proteins to recognize specific DNA sequences (Mandell & Barbas, 2006, Kim & Berg, 1996, Segal et al., 2006, Sander et al., 2010). Thus, though derived from the Zif268 model system, the canonical model has been successfully used to model other members of the C2H2-ZF protein family.

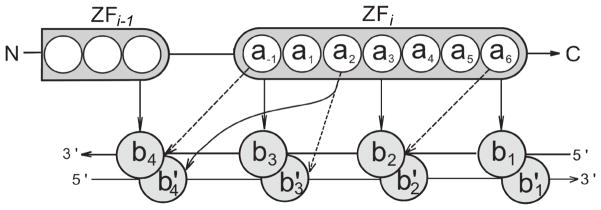
Figure 1.

Schematic representation of the C2H2-ZF protein–DNA interaction interface, with two successive fingers shown. Amino acids within the i-th finger are numbered according to their relative position from the start of the alpha helical domain, with a₋₁ denoting the residue immediately preceding the helix. Bases b₁, b₂, b₃, and b₄ are numbered sequentially from 5′ to 3′ of the primary DNA strand; the complementary bases are denoted by b₁′, b₂′, b₃′ and b₄′. The canonical binding model includes four amino acid - base contacts, and these contacts are represented by solid arrows. In the canonical model, amino acids a_−1, a₃ and a₆ contact consecutive bases in the primary strand, a₂ contacts a base on the complementary strand, and successive fingers bind overlapping 4 base pair subsites. Additional contacts for a proposed expanded binding model are shown by dashed arrows (see Results).

The merits and limitations of the canonical binding model have been considered in a variety of previous studies. C2H2-ZF proteins with low sequence similarity to Zif268 may have somewhat different arrangement of amino acid - base interactions (Wolfe et al., 1999, Wolfe et al., 2001, Iuchi, 2001). Indeed, alternate amino acid - base interactions were observed for C2H2-ZF proteins differing from the “classical” Zif268 protein (Wolfe et al., 2001). Geometric comparisons between C2H2-ZF structural interfaces have shown that there is notable variation in the docking arrangements of protein–DNA interfaces, and it has been argued that this may influence what contacts are possible at any given position (Pabo & Nekludova, 2000). Moreover, side-chain interactions within the zinc finger DNA binding domain also affect the DNA binding interface (Miller & Pabo, JMB 2001). More recent analysis of the C2H2-ZF DNA binding docking geometries in 21 X-ray co-crystal structures confirmed that despite overall structural similarity in C2H2-ZF domains and low backbone variation, a wide range of docking geometries exist between the protein and DNA molecules (Siggers & Honig, 2007). Nevertheless, a systematic analysis to determine whether additional determinants of C2H2-ZF DNA binding specificity should be included in the canonical model has yet to be undertaken.

We recently reported that support vector machines (SVMs) are a promising approach for predicting C2H2-ZF protein–DNA interactions when trained on a literature-derived experimental database of C2H2-ZF DNA binding and non-binding examples (Persikov et al., 2009). In the linear SVM model, the C2H2-ZF protein–DNA interaction interface was modeled by the pairwise amino acid - base interactions that make up the canonical structural interface. Alternatively, the SVM with a polynomial kernel captured dependencies between the canonical contacts and implicitly considers higher-order interactions amongst the amino acids and nucleotides in the binding interface. We found that a SVM utilizing a second degree polynomial kernel outperforms previously published prediction procedures as well as the linear SVM, suggesting a role for the importance of higher-order correlations between contacts in the canonical model. Similarly, a neural network approach for predicting C2H2-ZF protein-DNA interactions was found to have increased performance as compared a linear perceptron model (Liu & Stormo, 2008). A mechanistic understanding of what higher-order correlations are important requires further investigation of additional contacts to supplement those found in the canonical binding model. This will also help evaluate additional and/or alternative interactions important for DNA recognition by C2H2-ZF proteins different from the classical Zif268 structure, and can be utilized for better prediction and design of C2H2-ZF interfaces.

In this study, we analyze C2H2-ZF protein–DNA binding interfaces using several complementary approaches. First, we analyze all existing structural data of C2H2-ZF complexes with DNA to uncover all possible pair-wise contacts between amino acid side chains and nucleotides. Second, we perform a statistical analysis of our dataset of known C2H2-ZF interfaces to determine which contacts show evidence of functional constraint. Third, we analyze pre-trained SVM models to uncover which contacts are most important for predictions of binding and non-binding protein-DNA interfaces; this provides us with indirect information about which amino acid - nucleotide contacts are essential for DNA recognition by zinc fingers. This comprehensive analysis leads to an expansion of the canonical ZF protein–DNA binding model, with up to three additional proposed contacts (shown in Figure 1). Finally, as proof of principle, we show that simply using this expanded structural binding model instead of the canonical binding model improves predictions of DNA targets for C2H2-ZF proteins. Overall, our work advances our understanding of the determinants of C2H2-ZF protein-DNA specificity, and we anticipate that the expanded structural binding model will lead to further improvements in predicting and designing C2H2-ZF interfaces.

2. Methods

2.1. C2H2-ZF domain determination

All the protein sequences described in this work were analyzed for the presence of C2H2-ZF domains using the hmmsearch program, which is part of the HMMER 2.3.2 protein sequence homology search software (Eddy, 2008), along with the corresponding HMM profile provided by Pfam (Finn et al., 2010) for the ZF-C2H2 family (Pfam accession no. PF00096). To get confident predictions of ZF domains, the Pfam suggested gathering threshold of 17.7 for the HMMER bit scores was used.

2.2. Structural analysis

C2H2-ZF domains within protein sequences were identified as described above for 25 X-ray and 5 NMR entries for C2H2-ZF protein–DNA complexes listed in PDB. For those entries with both C2H2-ZF domains and co-complexed DNA, an amino acid and nucleotide pair were determined to be interacting as follows. The distance L between them was estimated as the distance between the closest heavy atom (nitrogen, carbon, or oxygen) of the amino acid side chain and the closest heavy atom of the corresponding nucleotide. Non-specific backbone interactions were not considered. If this interacting distance is less than 3.3Å, then the pair is considered as potentially interacting. This maximum allowable distance L_max = 3.3Å captures hydrogen-bonds (2.6–3.3Å) and van der Waals contacts (2.8–4.1Å), but will eliminate water-mediated interactions. Longer L_max values could instead be used; however, since the structural analysis is for uncovering evidence for expanding the canonical structural model, we chose to be conservative in identifying interacting amino acid and nucleotide pairs.

2.3. Mathematical representations of the structural interface

Experimental structural studies have shown that the alpha-helix in each zinc finger fits into the major groove of the DNA, and each consecutive finger contacts four base pairs which overlap by one DNA position (Pavletich and Pabo, 1991, Elrod-Erickson et al., 1996). In each zinc finger, the amino acid positions that contact DNA are denoted as a₋₁, a₂, a₃, and a₆, where the numbering of each position is derived by its position relative to the start of the alpha-helix (Figure 1). Assuming that only residues in one of these four positions can contact the four base pair site, as has been previously suggested and as we predominantly find in our structural analysis (see Results), C2H2-ZF protein–DNA binding can be represented by a pairwise contact-based structural model listing the amino acids and nucleotides present in each of sixteen possible contacts. This can be encapsulated in a feature vector x = {x_abc}, where x_abc =1 for every amino acid a ∈{Ala, Cys, …, Trp} and base b ∈ {a,c,g,t} at corresponding contact position c. In the case of the canonical binding model, this representation scheme leads to a feature space containing 320 dimensions representing all possible amino acids and nucleotides in the four canonical contacts (20 × 4 × 4). In contrast, an “all-contact model” will result in a feature space containing 1280 dimensions representing all possible abc combinations (20 amino acids × 4 bases × 16 contacts).

2.4. Statistical analysis of the experimental database

We previously built a literature-derived database of binding and non-binding configurations of C2H2-ZF proteins and DNA (Persikov et al., 2009); this database consists primarily of zinc finger Zif268 protein mutants whose specificity has been probed by in vitro randomization experiments such as SELEX and phage display. The database is available for download at http://compbio.cs.princeton.edu/zf/. From this database, 1312 positive examples (in which the given protein is known to bind to the given DNA) and 8081 negative examples (in which the protein does not bind the DNA) were extracted. Before our statistical analysis, each of these examples was split into individual ZF domains, and duplicates were removed.

We evaluated whether, for each of the 16 contacts, the distribution of nucleotides found in that contact position is significantly affected by which amino acid is present. That is, for each of the 16 contacts, we compared the distribution of nucleotides with the presence of every amino acid a, with the overall distribution on nucleotides in a given position. For statistical evaluation, we hypothesized for each contact that the distribution of nucleotides is independent of the amino acid occupying the corresponding contacting position. This null-hypothesis was tested by a χ² test as follows. The χ² values were computed as:

$${\chi }_{a,c}^2=\sum _b\frac{{(o_{a,b,c}-e_{a,b,c})}^2}{e_{a,b,c}}$$

where o_a,b,c is the number of observed ab contacts at the tested position c, and e_a,b,c is the corresponding expected number calculated from distribution of nucleotides at that position, assuming no preferential co-occurrence with respect to the amino acid (i.e., e_a,b,c is computed as fraction of the nucleotide position involved in the contact that is base b multiplied by the number of contact c amino acid-base pairs that involve amino acid a). ${\chi }_{a,c}^2$ was not computed if any of the e_a,b,c values were less than five, as significance values would be over-estimated in this case. We identified those amino acid and contact pairs whose ${\chi }_{a,c}^2$ values with three degrees of freedom led to an individual p-value of less than 10⁻⁵. Note that at most 320 significance tests were performed (16 contacts × 20 amino acids). Additionally, to determine which base pairs were over- and under-represented for each amino acid in the contact, we also computed log₂(o_a,b,c/e_a,b,c) in each case where e_a,b,c is at least 5.

2.5. Support Vector Machines

We have reported previously that support vector machines (SVMs) can be successfully applied to predict C2H2-ZF protein–DNA binding (Persikov et al., 2009). Given a dataset of training examples {x_i}, SVMs search for a weight vector w that best separates binding and non-binding examples (Vapnik, 1995, Cristianini and Shawe-Taylor, 2000). The trained weight vector w can then be used to make predictions for any feature vector x corresponding to a configuration of protein and DNA. Using a linear model and constraining the weight vector to go through the origin during training, the score for a particular C2H2-ZF protein–DNA configuration represented as x is computed as w·x. The more positive the abc-th dimension of the weight vector w, the more favorable the abc combination is scored for ZF protein–DNA binding. Similarly, the more negative the abc-th dimension, the more unfavorable the abc combination is scored. Combinations with w_abc=0 have no influence on the estimated binding propensity; note, however, that dimensions can be zero as a result of never observing particular amino acid - base pair combinations in the training set. As an alternate statistical approach to analyze the possible importance of all feasible amino acid - base pair combinations in determining C2H2-ZF protein–DNA binding, we trained a linear SVM in an all-contact model with a full pair-wise feature space containing 1280 dimensions (20 amino acids × 4 bases × 16 contacts). Though in previous work on zinc fingers (Persikov et al., 2009) and coiled coils (Fong et al., 2004), we utilized information about comparative binding affinities, here only positive and negative examples were used in the analysis in order to highlight any potential amino acid - nucleotide pair-wise interactions. Training was done after positive and negative examples in our data set were split into individual ZF domains, and duplicate entries were removed. The SVM-light software version 6.01 was used to train the SVMs (Joachims, 1999). For all experiments, the regularization parameter C was automatically chosen by SVM-light. The trained weight vector w was analyzed further, as described below, to uncover the amino acid - nucleotide contacts judged by the learning algorithm to be most favorable and unfavorable. We note that the weight vector learned by a SVM can be fully expressed with respect to a subset of the training examples (i.e., the support vectors); this means that the weight vector analysis implicitly analyzes only these important examples, and may therefore be more robust than the statistical analysis of the original database to outliers and closely related examples in the training set.

2.6. Evaluating amino acid–nucleotide contacts from weight vector analysis

We used two related approaches to evaluate the influence of each of the 16 contacts in the SVM trained weight vector using the all-contact model. In particular, a contact that is important for distinguishing between positive and negative examples of C2H2-ZF protein-DNA interfaces should have several amino acid-base pair combinations whose entries in the weight vector are either very high or very low, and the weight vector entries corresponding to the 80 different possible combinations of amino acids and base pairs for the contact should show a wide range of scores. To identify these cases, we first computed a mean and standard deviation over the entire weight vector using all non-zero w_abc dimensions; these were used to compute a Z-score for each non-zero w_abc entry. Additionally, for each contact c, we also computed the standard deviation of all the non-zero w_abc amino acid - base pair combinations.

2.7. Testing scenarios

2.7.1. Cross-validation testing

We performed cross-validation using the previously collected high-confidence experimental dataset (Persikov et al., 2009). In particular, we randomly selected 100 positive and 1000 negative examples from the initial database as a test set, and used the remaining examples as a training set. All examples involving proteins selected for the test set were filtered out of the training dataset. This procedure was repeated 1000 times and an averaged ROC curve is created for each method and binding model.

2.7.2. Transfac database testing

In addition to cross validation, the performances of the linear SVMs based on different structural binding models were also tested on the Transfac database. The Transfac database contains data on transcription factors, DNA sequences containing their experimentally-found binding sites, and regulated genes (Matys et al., 2003). The most recent public release (ver 7.0 – 2005-09-30) contains 244 C2H2-ZF proteins with their corresponding DNA binding sequences; the number of zinc fingers within each protein varies from 1 to 29 (as determined by HMMER). Linear SVMs were trained using the previously gathered experimental data set and assuming various models for C2H2-ZF binding specificity. When scoring a protein in Transfac, we ensure that the protein is not in the training set for the SVM methods. Due to difficulties in determining DNA binding configurations in proteins with numerous zinc fingers (Iuchi, 2001), the evaluation on Transfac was limited to proteins with three C2H2-ZF domains. This set consists of 311 three finger C2H2-ZF protein–DNA combinations, corresponding to 24 distinct proteins. Each of these proteins is assumed to bind a 10 base pair site. The Transfac data are analyzed in a similar manner to our previous work (Persikov et al., 2009). Briefly, the DNA fragment is scanned in 10 base pair windows. Each window is scored with the corresponding protein with the model being utilized, and the score for the given C2H2-ZF protein-DNA pair is set to the highest window score obtained. For each protein-DNA pair, we consider 1000 randomized DNA sequences of the length of the original DNA, and consider the rank of the score amongst the scores for these randomized sequences. If n_i is the number of randomized DNA sequences scoring higher than the original target DNA, then the rank is equal to n_i +1. We note that a p-value for each score can be calculated for every protein–DNA combination as p_i = n_i/1000. Since the ZF proteins come from a range of organisms, randomized DNA sequences are generated assuming that the nucleotides are equally probable. Finally, for each distinct protein, we consider all of its protein-DNA pairings in Transfac, and compute an average rank. Finally, we compare methods by utilizing box plots with the median, 2nd quartile, 3rd quartile and outliers of the averaged ranks shown. The differences between performances of two different prediction methods are judged by the Wilcoxon signed-rank test (Wilcoxon, 1945).

2.7.3. Evaluation of additional contacts by non-SVM methods

To test how adding an additional fifth contact to the canonical binding model affects prediction accuracy for other methods, we probed all possible additional contacts in turn to predict high-confidence data as described above by two non-SVM methods. The first approach, which we call SBGY95, is based on expert knowledge of biochemical principles (Suzuki et al., 1995), and can be used to evaluate any type of protein–DNA interaction interface. Chemical rules of protein–DNA binding are based on the inherent chemical compatibility of amino acids and bases, and weights are given to amino acid–base pairings. The numerical amino acid–base compatibilities (Fig. 1a in the original publication) are used to compute binding scores according to the assumed binding model for C2H2-ZF proteins. The second approach, which we call MGM98, is based on hydrogen bonding patterns extracted from co-crystal structures of various proteins in the PDB and NDB (Mandel-Gutfreund and Margalit, 1998). The log-odd scores (from Table 2 in the original publication) used in this method represent more general trends found in protein–DNA interactions, and can be applied to score any protein–DNA interface. For both of these methods, the four-contact canonical binding model is expanded by each of the additional contacts in turn. For any dataset, the performance of the resulting five contact models can be compared to the original canonical model on the known experimental database of positive and negative examples using the area under the ROC curve (AUC).

Table 2.

List of NMR structures for C2H2-ZF protein – DNA complexes gathered from the PDB

PDB_ID	Number of ZFs in protein	Number of models in structure
2JP9	4	20
2JPA	4	20
1TF3	3	22
1YUJ (1YUI)	1	50
2KMK	3	12

3. Results

3.1. Structural analysis of amino acid side chain–nucleotide contacts in protein–DNA complexes

3.1.1. Co-crystal structures

C2H2-ZF domains were identified within 25 crystal structures in the PDB, with 118 domains in 39 protein chains (Table 1). Additional analysis of the co-crystal structures showed that 100 ZF domains were in contact with the DNA (i.e., with at least one amino acid - nucleotide interacting pair). All amino acid residues starting from position a₋₄ to position a₉ were included in this analysis. While amino acids in certain positions were found not to interact with DNA, the four amino acids in the canonical model were found to make close contacts with multiple nucleotides (see supplementary Table S1). Interestingly, all 61 ZF-domains in co-crystal structures of the Zif268 protein or its variants make DNA contacts with at least one interaction with length < 3.3Å (excluding the unusual 1ZF chain from the 1MEY structure which had no co-crystal DNA partner). More variation was observed for non-Zif268 proteins with several C2H2-ZF domains making no DNA contact (Table 1).

Table 1.

X-ray structures gathered from the Protein Data Bank

Protein group	List of PDB structures	Number of ZFs in protein	Number of protein chains	Number of ZFs in all chains	Number of ZFs making DNA contacts
Zif268 family	1A1F, 1A1G, 1A1H, 1A1I, 1A1J, 1A1K, 1A1L, 1AAY, 1JK1, 1JK2, 1MEY, 1P47, 1ZAA, 1F2I, 1LLM	2–3	24	62	61
non-Zif268 family	1G2D, 1G2F, 2DRP, 1UBD, 2PRT, 2GLI, 1TF6, 2I13, 2WBS, 2WBU	2–6	15	56	39
Total:	25 structures		39	118	100

A key question in understanding C2H2-ZF protein-DNA interfaces is to identify which ZFs are binding DNA. It was proposed earlier that certain fingers in multi-ZF proteins do not participate in DNA recognition, but rather serve a different function (Schafer et al., 1994), and it is known that C2H2-ZF domains can mediate protein-protein and protein-RNA interactions (Brayer and Segal, 2008). While there are four proteins with X-ray structures that have more than three ZFs, we find that known C2H2-ZF protein-DNA interfaces consist of at most three ZFs sequentially contacting DNA. For each of the proteins with more than three ZFs crystallized, we found that not all the ZF domains participate in DNA binding. In the Wilms Tumor suppressor protein (WT1) only three ZFs are contacting DNA (2PRT structure), while the first ZF domain makes no contact with DNA. The first ZF domain is also not found to contact DNA for the NMR structures of the WT1 protein (2JP9 and 2JPA structures). For the YY1 human protein, one out of four ZF domains makes no DNA contact (1UBD structure). The human GLI oncogene (2GLI structure) contains five ZF domains (Pavletich and Pabo, 1993). However, the first two ZF domains were found not to contact DNA (with a closest backbone distance of 17.6Å), and only ZFs 3–5 were found to participate in DNA recognition. Similarly, in the Xenopus laevis TFIIIA protein (1TF6 structure) with 6 ZF domains, only the first three ZFs were observed to insert in the major groove of the DNA in the manner seen in other complexes. In contrast, fingers ZF4-ZF6 form a continuous platform-like surface, and were proposed to dock other components of the transcription complex (Nolte et al., 1998). The only protein with more than three consecutive fingers bound to consecutive bases of DNA was a four zinc finger protein, 1UBD. However, even in this case the binding was atypical. While ZFs 2–4 contact bases according to the canonical model, the first ZF makes only a single amino acid–base contact (Houbaviy et al., 1996). Thus, the vast majority of Cys₂His₂ proteins, as shown by co-crystal structures, bind DNA using at most three consecutive ZF domains.

3.1.2. NMR structures

In addition to X-ray co-crystal structures, five NMR structures were identified to contain C2H2-ZF domains. Every NMR structure represents the list of best models (see Table 2). In order to include the NMR data to the interaction matrix derived from the X-ray structures, we computed the number of contact occurrences in each NMR structure containing multiple models. For each of the five PDB entries, a contact was counted when it was observed in at least 50% of all models (see Table S2). This approach gave good agreement in contact counts between the original structures of GAGA factor (1YUJ) and its averaged model (1YUI). The latter averaged model, 1YUI, was excluded from further analysis because it represented the average structure of all NMR models listed in the 1YUJ structure (Omichinski et al., 1997).

3.1.3. Observed DNA contacts in C2H2-ZF structures

Canonical contacts were found to be most frequent among all potential contacts and were observed in ~60–80% of all DNA-interacting ZF domains. Interestingly, only amino acids occupying the “canonical” positions (a₋₁, a₂, a₃, and a₆) were found to contact DNA with occurrences >1% (Table S1). However, in addition to the contacts listed in the canonical binding model, these amino acids were observed to make alternative contacts with nucleotide partners (Table S1).

To represent the contacts in a compact form, we considered only four amino acid positions (a₋₁, a₂, a₃, a₆) and four nucleotide positions (b₁,b₂,b₃,b₄) (Table 3). We note that the presence of a given nucleotide in the complimentary chain (say the guanine in position b₃′) requires the presence of the complimentary base in the corresponding position (cytosine in the position b₃); thus, monitoring only nucleotide identities in the primary DNA chain gives all the necessary information about the complimentary chain. Moreover, whereas structural analysis can reveal whether the nucleotide on the primary or complementary strand is involved in a contact, the statistical approaches utilized next do not differentiate between these possibilities. Therefore, for a vector representation of the binding interface, we monitor nucleotides occupying only positions b₁, b₂, b₃, and b₄ (as Table S1 shows that positions b₀ and b₅ rarely are in contact with the ZF domain) and consider contacts with the primary and complementary bases together. Thus, the interaction matrix is a represented as 4×4 table including four rows for the amino acids in key positions (a₋₁,a₂,a₃,a₆) and four columns representing both nucleotides at positions (b₁,b₂,b₃,b₄) and their complements (Table 3). We find that the four canonical contacts a₋₁ b_3, a₂b_4, a₃ b₂ and a₆ b₁ were found more frequently than the other contacts. Moreover, contact a₂b₃ was frequently found in ZF protein-DNA interfaces, with most of the contacts with the complementary strand. Additionally, contacts a₋₁b₄ and a₆b₂ were observed frequently with contacts with both the primary and complementary strand. Thus a structural analysis finds that three non-canonical contacts are frequently found in C2H2-ZF protein-DNA interfaces; we show these contacts in Figure 1, with a₂b₃ illustrated as a contact with the complimentary strand and a₋₁b₄ and a₆b₂ illustrated as contacting either the primary or secondary strand. It should be noted that in addition to the contacts listed in Table 3, additional non-canonical contacts were observed in 1TF3 (contact a₆b₂) and 1YUJ structures (contact a₋₁b₂).

Table 3.

ZF protein–DNA interaction matrix of counts for interacting amino acid - base pairs within distances < 3.3Å as observed in 25 X-ray and 5 NMR structures. Only significant amino acid and nucleotide positions are shown; the top number gives the combined total of primary and complimentary chain contacts, and the bottom numbers give in parentheses the number of primary chain contacts followed by the number of complimentary DNA chain contacts. The seven most frequent contacts are highlighted; canonical contacts have darker shadings.

position		Base
		b4	b3	b2	b1
amino acid	a−1	26 (16/10)	81 (81/0)	11 (11/0)	0
	a2	61 (2/59)	21 (3/18)	3 (0/3)	1 (1/0)
	a3	0	1 (1/0)	79 (79/0)	5 (5/0)
	a6	2 (0/2)	1 (0/1)	27 (13/14)	58 (58/0)

3.2. The analysis of preferential amino acid - nucleotide occurrences

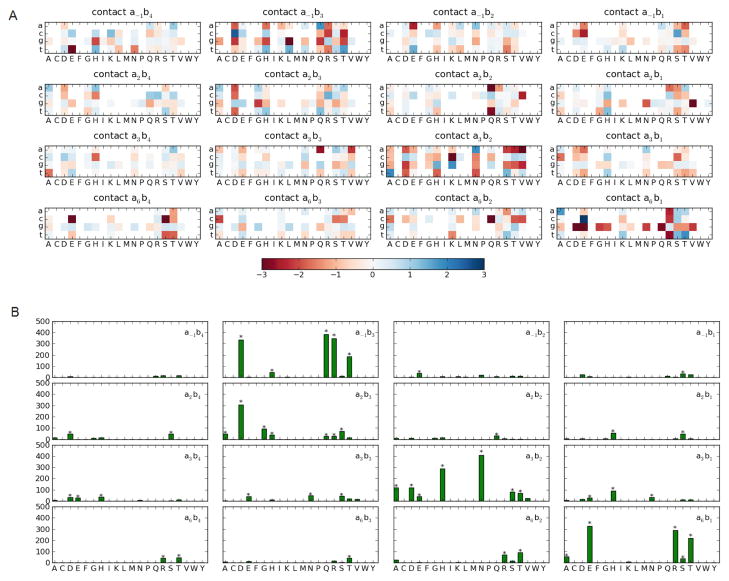
To gain further evidence for the importance of frequent non-canonical contacts observed in protein structures, we performed a statistical analysis of our experimental data set to check for a contact-dependent trend of preferential amino acid - base pair co-occurrences. Figure 2A shows a heat-plot showing the log-odds of the observed versus expected number of nucleotides for each amino acid in each contact (see Methods), as computed using all positive examples in the database. Preferentially high and low nucleotide occurrences are shown in blue and red respectively. Numerous distinct positive and negative preferences are evident (as indicated in Figure 2A by darker colors) in the canonical positions a₆b₁, a₃b₂ and a₋₁b₃, though strong preferences are observed in all the contact positions. To perform a rigorous analysis, we applied the χ² test to test whether the nucleotide distribution observed in a contact c for each amino acid is different from the overall nucleotide distribution found in that contact.

Figure 2.

(a) Heat plot of log-odd scores for observed versus expected nucleotide frequencies in positive examples for each amino acid in each of the 16 contacts (b) The corresponding χ² values, with stars denoting those tests that are significant at p-value < 10⁻⁵.

As seen from the Figure 2B, several χ² values are very large for four of the contacts. Using an individual p-value of 10⁻⁵, the null-hypothesis was more often rejected in the canonical positions a₆b₁, a₃b₂, a₋₁b₃ as well as the contact a₂b₃ than the other contacts. This statistical analysis suggests that amino acids in these contacts constrain the nucleotide composition, thus providing evidence that they are playing a role in determining C2H2-ZF protein–DNA binding specificity in this dataset. This is the expected result for the canonical contacts. Contact a₂b₃ was also identified by the structural analysis as frequently occurring in C2H2-ZF protein–DNA interfaces. We note that canonical contact a₂b₄ is not identified in this statistical analysis; however, a significant fraction of the data set is obtained from experiments that vary only the middle three nucleotides of a 9 or 10 base-pair binding site while keeping the base corresponding to b₄ fixed. For this reason, we may also not expect contact a₋₁b₄, which was identified by the structural analysis, to be found as a determinant of specificity in this statistical analysis. A similar analysis on the negative examples showed very little effect of amino acid - base pair preferences (see supplementary Figure S1).

3.3. Analysis of pre-trained full-contact SVM

To evaluate the favorability and unfavorability of all possible abc contacts for predicting ZF–DNA binding, we transformed the w_abc entries to z-scores with respect to the mean and standard deviation computed over all non-zero entries in the learned weight vector. Though high and low z-scores (> 2 or < −2, respectively) are apparent across the contacts (Figure 3), they are most frequent in the four canonical contacts and contact a₂b₃. Remarkably, even though all contacts are considered, the most favorable contacts involve amino acid - nucleotide pairings in the canonical binding model (data not shown). In agreement with earlier co-crystal analysis studies and in vitro binding experiments (Wolfe 2001), the full-contact SVM model considered the two most favorable interactions to be arginine contacting guanine when occupying positions a₋₁b₃ and a₆b₁.

Figure 3.

Heat-plot for each dimension of the learned full-contact SVM. Individual weight entries are z-score normalized. Positive z-scores, shown in blue, correspond to favorable interactions and negative z-scores, shown in red, correspond to unfavorable interactions.

If a contact is important in distinguishing between positive and negative ZF protein-DNA interfaces in the training set, we expect that different amino acid - nucleotide pairings should show relatively large variations in their corresponding weight vector entries. Conversely, contacts that are not important for distinguishing positive and negative ZF protein-DNA interfaces should show less variation. Thus, we ranked each of the 16 contacts according to the standard deviations of the weights observed in amino acid -nucleotide pairings (Figure 4). The canonical contacts (a₋₁b₃, a₂b₄, a₃b₂, and a₆b₁) showed the most variation, followed by contacts a₋₁b₄ and a₂b₃. The latter two were also observed frequently in co-crystal and NMR structures, with a₂b₃ showing evidence of functional constraint by the statistical analysis of the experimental dataset as well.

Figure 4.

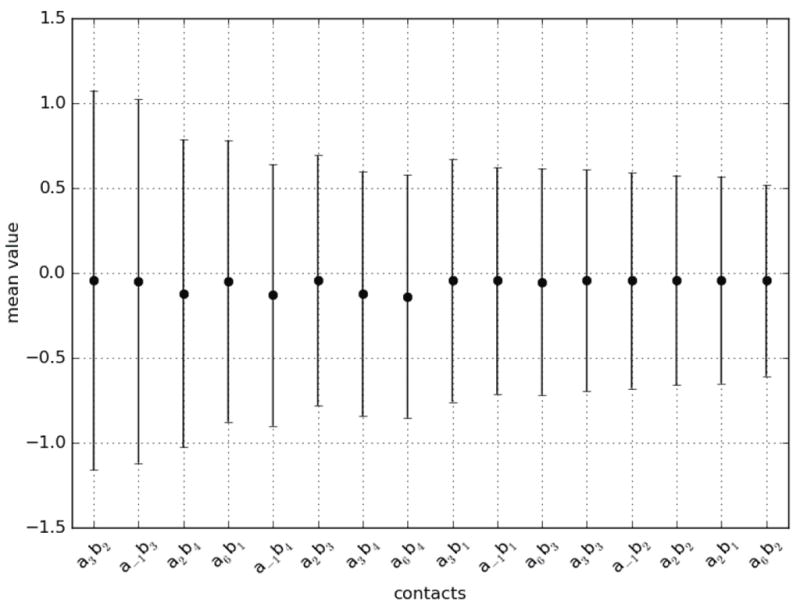
Mean and standard deviation of scores observed per contact for amino acid - nucleotide pairings. The contacts are listed with decreasing standard deviations. The four canonical contacts a₃b₂, a₋₁b₃, a₂b₄, and a₆b₁ show the greatest variation in the scores attributed to amino acid - nucleotide pairings, followed by a₋₁b₄ and a₂b₃, two of the contacts proposed by the structural analysis as playing a role in the ZF-DNA interface.

As a result of the structural analysis, the statistical analysis of the experimental database, and the analysis of the weight vector, we propose three new structural models as alternatives to the 4-contact canonical binding model which consists of contacts a₋₁b₃, a₂b₄, a₃b₂, a₆b₁ (solid arrows on Figure 1). The 5-contact model (the consensus model) includes the four canonical contacts and a₂b₃, as suggested by all the analyses. The 7-contact model (all arrows on Figure 1) includes the four canonical contacts and the contact a₂b₃ (as suggested by all analyses) along with a₋₁b₄ and a₆b₂, as suggested by structure analysis (with a₋₁b₄ supported by the weight vector analysis as well). Finally, the all-contact model includes all 16 possible contacts (see Figure 1 and Table 3).

3.4. Cross-validation test

If additional contacts are important for ZF protein–DNA binding, their inclusion should improve the performance of the linear SVM as compared to just considering the canonical contacts. To test this, linear SVMs trained based on different binding models were compared with the SVM trained based on the canonical model as well as with additional prediction methods as described previously (Persikov et al., 2009). The performance of all the methods was tested by holdout cross-validation using the high-confidence experimental database for ZF protein–DNA interactions. Consistent with the results we previously reported, all the SVM methods outperformed the previously published methods (data not shown). We instead focus here on comparing the performance of the linear SVM based on the newly proposed structural binding models.

The all-contact model, which assumes all 16 possible amino acid - nucleotide contacts, showed performance close to that of the polynomial SVM using the canonical model. The consensus model 5-contact model showed a notable increase in performance when compared to the canonical 4-contact model, and the 7-contact expanded model showed intermediate results between the canonical model and the consensus model (Figure 5). As the relative performance of the 5-contact and 7-contact model illustrates, performance of the SVM does not necessarily improve on all test sets with consideration of additional contacts. Nevertheless, both the 5-contact and 7-contact improve upon the basic canonical model, with a clear performance improvement evident with the inclusion of the single a₂b₃ contact.

Figure 5.

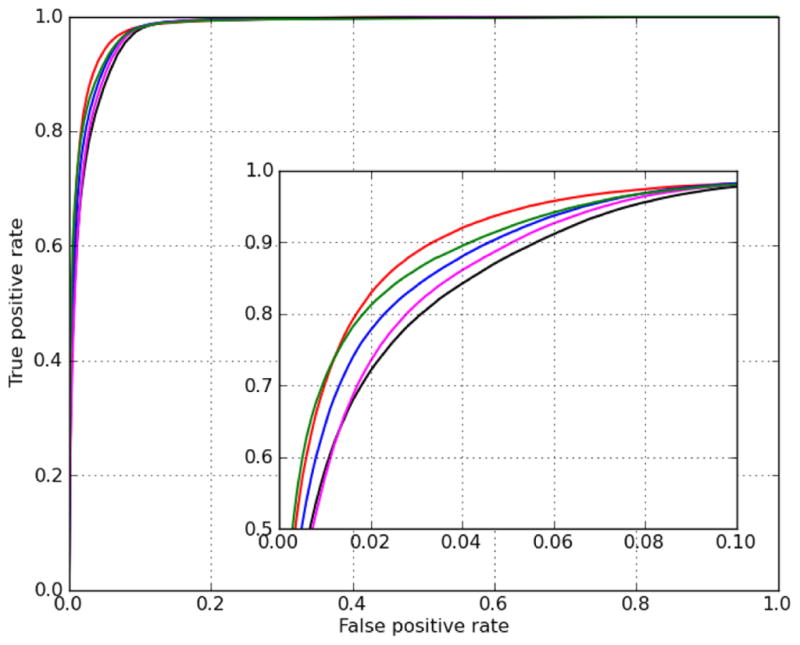
ROC curves for cross-validation testing of the polynomial SVM based on the canonical model (red) and linear SVMs based on various binding models: canonical model (black), 5-contact model (blue), 7-contact model (magenta), and all contact model (green).

To address the question of how different structural binding models may affect the performance of the polynomial SVM, we also trained and tested polynomial SVMs based on the 7-contact expanded model and the all-contact model (see supplementary Figure S3). Despite differences in the structural models, similar performance was observed across polynomial SVMs based on the canonical binding model and the expanded models. Therefore, we find no advantage to using the expanded models when the polynomial kernel is used. We also note that the performance of the all-contact linear SVM is very similar to that of the polynomial kernels. This finding is consistent with the hypothesis that amino acid – amino acid and nucleotide – nucleotide interactions do not play a major role in DNA recognition by C2H2-ZF proteins.

3.5. Predicting in vivo transcription factor binding sites listed in Transfac database

As an alternative to testing the performance of the binding models on the in vitro experimental training data set, we also consider the Transfac database of in vivo data on transcription factor–DNA binding (Matys et al., 2003). For each of the 24 three finger C2H2-ZF proteins in Transfac, we computed the average rank of the score of the DNA regions that are bound as compared to 1000 randomized DNA sequences (Figure 6). The linear SVM shows an increase in performance over the other models when using the 7-contact expanded structural binding model as measured by median ranks and the range of ranks (Figure 6). The 7-contact model shows better performance than the canonical (p≤0.05) and all-contact models (p≤0.02), as determined by the Wilcoxon signed rank test. This suggests an important role in predicting protein-DNA ZF interactions for the three additional contacts that are included in the expanded 7-contact model.

Figure 6.

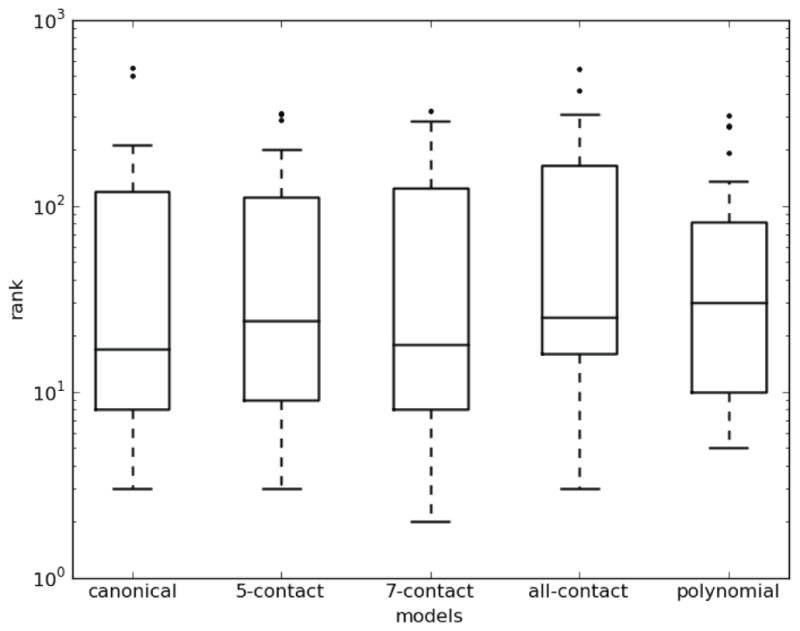
For each of five DNA-binding models utilized to train SVMs, we show box plots of the average ranks for each Transfac protein of the bound DNAs amongst 1000 randomized DNA sequences. Each box shows the median, 2^nd quartile, 3^rd quartile and outlier ranks. Lower ranks indicate better predictions.

3.6. Expanding structural binding models also leads to better performance of non-SVM methods

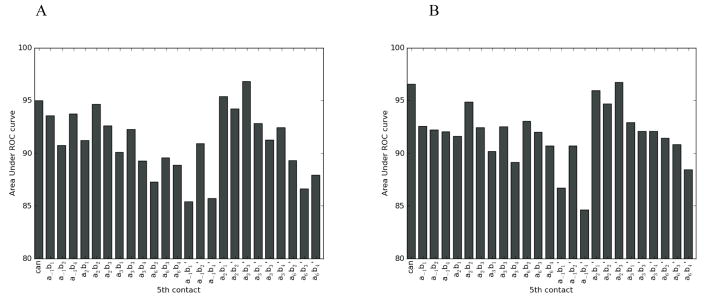
As an additional test to confirm whether the increased SVM performance originates from using an expanded structural binding model, we tested whether adding an additional contact affects the prediction quality by two non-SVM methods. The SBGY95 and MGM98 methods can be based on any structural model with specified amino acid - nucleotide interacting pairs. Note that since both of these approaches give a particular score to a specified amino acid - nucleotide contact, it is necessary to distinguish between contacts in the primary and complementary strand. Probing every additional 5th contact using these two approaches clearly indicated that only the a₂b₃′ contact results in consistently improved predictions when added to the canonical binding model. In particular, the area under the ROC curve increased from 94.8% to 97.8% for MGM98 and from 96.4% to 97.9% for SBGY95 (Figure 7) when adding this contact to the canonical binding model. The full ROC curves for the MGM98 and SBGY95 methods based on the canonical model and the model including the a₂b₃′ contact are shown in Figure S2. Therefore, application of the consensus 5-contact binding model in cross-validation leads to an improvement over a canonical binding model in SVM as well as in non-SVM methods. We note that the structural analysis indicates that the a₂b₃ contact primarily involves the nucleotide in the complementary strand and thus corresponds to a₂b₃′ here. On the other hand, the other two contacts frequently observed structural contacts (a₋₁b₄ and a₆b₂) involve either the primary and complementary strand approximately evenly; addition of just one additional contact for either of these in the SGBY95 and MGM98 methods would result in considering the incorrect amino acid - nucleotide contact about half the time. For this reason, we may not expect to see performance improvements using just one of these contacts at a time.

Figure 7.

Area under ROC curves on the experimental data set for adding all possible contacts to the canonical binding model for the (A) MGM98 and (B) SBGY95 methods. The “can” column gives the performance using the canonical binding model, and the other 24 columns consider each additional contact in turn. Contact a₂b₃ ′ is the consensus contact implicated by all analyses, and incorporating it to the canonical binding model improves predictions by both these methods.

4. Discussion

The C2H2-ZF protein family is arguably the best studied of all transcription factor structural classes, and this makes C2H2-ZFs an excellent model system for developing and applying computational approaches for predicting protein–DNA binding specificity. The canonical binding model was initially proposed over two decades ago, and has served well for studies of ZF specificity and for designing proteins to target DNA (Rebar and Pabo, 1994). However, it was later proposed that amino acids in both canonical and non-canonical positions can make alternate patterns of base contacts in different complexes (Wolfe et al., 2000). To systematically address this question, we tested how well the canonical binding model describes protein–DNA interfaces for a varied set of ZF proteins with a variable number of ZF domains. Our structural analysis confirmed that the canonical model is a good first approximation for describing the C2H2-ZF protein–DNA structural interface (solid arrows on Figure 1). The canonical model is appropriate for describing the majority of co-crystal structures analyzed, especially those based on the Zif268 protein and its variants. The protein and DNA backbones are structurally conserved throughout the co-crystal structures, creating a rigid framework for the recognition interface. Among all the amino acid positions, only the four amino acids occupying the canonical amino acid positions (a₋₁, a₂, a₃, and a₆) in the α-helical part of the ZF domain form close side-chain contacts to the DNA (Table S1). Therefore, the identities of these four amino acid residues likely modulate the docking geometry of the protein-DNA interface and determine DNA binding specificity in most cases without significantly affecting the structure of the ZF domain.

On the other hand, structural analysis also confirmed that pair-wise contacts between amino acids and nucleotides in C2H2-ZF protein-DNA interfaces can differ from that described by the canonical model. The most frequently observed alternative contact was between the side chain of the amino acid in position a₂ and nucleotide b₃′ of the complementary DNA chain (Table 3 and Figure 1). This interaction (contact a₂b₃) was detected in >20% of analyzed ZF – DNA complexes. This contact can perhaps be formed when the side chain size and/or other chemical preferences prevent a formation of a canonical contact between amino acid a₂ and nucleotide in position b₄′ (Figure 1). It may also be possible that the amino acid occupying position a₂ tends to simultaneously interact with nucleotides b₃′ and b₄′.

Despite several structures available for the ZF protein–DNA complexes, the amount and diversity of ZF proteins with known structures is still limited. As a result, we also wanted to re-evaluate the canonical binding model without using any structural data. An alternative approach to evaluate the ZF–DNA structural interface is to analyze previously collected experimental database including 1312 positive and 8081 negative examples of C2H2-ZF protein – DNA binding (Persikov et al., 2009), along with the weight vector of the linear SVM trained on this data. In accordance to our expectations, both of these statistical analyses confirmed the importance of the contacts in the canonical binding model. Moreover, both statistical approaches identify the a₂b₃ contact as important for ZF protein–DNA recognition. The addition of only this single contact to the canonical binding model (the consensus 5-contact model) results in consistently improved predictions in cross-validation testing (Figure 5). To confirm the general importance of the observed a₂b₃ contact, we also tested whether the inclusion of this contact into the binding model can also improve prediction methods not based on SVMs. Indeed, only adding the a₂b₃ contact to the canonical model consistently results in better performance of alternative methods based on stereochemical principles of amino acid–nucleotide binding preferences (SBGY95) (Suzuki et al., 1995) and based on the analyses of co-crystal structures of various protein-DNA complexes (MGM98) (Mandel-Gutfreund and Margalit, 1998) (Figures 7 and S2). Therefore, inclusion of contact a₂b₃ shows improvement in predicting DNA binding in a wide range of testing scenarios. Two more alternate contacts, a₋₁b₄ and a₆b₂, were observed in structures of ZF protein–DNA complexes. Contact a₋₁b₄ was also found to be important via weight vector analysis. Inclusion of these contacts, along with the canonical contacts and a₂b₃, in a 7-contact model resulted in improved performance of the SVM in cross-validation (Figures 5 and Figure S2) and an improvement in predicting experimental binding sites listed in the Transfac database (Figure 6).

We note that although the number of ZF domains in a single C2H2-ZF protein can be high (e.g., 29 for rOAZ, a rat Olf-1/EBF-associated 134-kDa zinc finger protein (Tsai and Reed, 1998)), our structural analysis suggests that only short domains, containing 2–4 ZFs, can act as a DNA recognition domain and bind to continuous DNA sequence. It was observed earlier that in proteins with multiple ZF domains, many domains do not participate in DNA recognition (Schafer et al., 1994, Nolte et al., 1998) but instead may serve an alternative (protein-binding or RNA-binding) function (Schafer et al., 1994) and/or recognize alternative DNA sequences (Nolte et al., 1998). The present analysis of the co-crystal structures confirmed that the Cys₂His₂ proteins bind DNA using 2–4 ZF domains. Three-finger ZF cluster appears to be an optimal for binding the DNA (Iuchi, 2001): while using only two fingers may not be sufficient for the binding specificity, the larger number of ZF domains will not result in a close protein – DNA contact. 3ZF clusters are to recognize the 10bp DNA sequences, resulting in specificity of one on a million DNA sequence variants (4¹⁰).

5. Major conclusion

We presented several lines of evidence that the canonical binding model should be modified for C2H2-ZF proteins. The analysis of co-crystal structures, the statistical analysis of an experimental dataset of C2H2-ZF protein–DNA binding interfaces, and the analysis of the SVM models trained on that experimentally derived database revealed the importance of three alternate contacts not previously considered in C2H2-ZF protein–DNA binding: a₂b₃, a₋₁b₄, and a₆b₂. Moreover, inclusion of these contacts improves the performance of ZF protein–DNA predictions in simple modifications to existing techniques. Overall, our work furthers our understanding of the determinants of C2H2-ZF protein–DNA specificity, and we expect that the expanded structural binding model will lead to further improvements in predicting and designing C2H2-ZF interfaces.