Combinatorial analysis for sequence and spatial motif discovery in short sequence fragments

Abstract

Motifs are over-represented sequence or spatial patterns appearing in proteins. They often play important roles in maintaining protein stability and in facilitating protein function. When motifs are located in short sequence fragments, as in transmembrane domains that are only 6–20 residues in length, and when there is only very limited data, it is difficult to identify motifs. In this study, we introduce combinatorial models based on permutation for assessing statistically significant sequence and spatial patterns in short sequences. We show that our method can uncover previously unknown sequence and spatial motifs in β-barrel membrane proteins, and that our method outperforms existing methods in detecting statistically significant motifs in this dataset. Lastly, we discuss implications of motif analysis for problems involving short sequences in other families of proteins.

I. Introduction

The identification of spatial and sequence motifs plays an important role in understanding protein stability and function. Often these motifs are embedded in short sequence fragments, as in the transmembrane domains of membrane proteins, which are usually only 6–20 residues in length. In studies of α-helical membrane proteins, Senes et al. discovered a large number of sequence motifs in transmembrane helices based on exhaustive permutation [1]. These sequence motifs were found to play important roles in the folding and assembly of TM helices. Examples include the well-known GxxxG motifs that promote the dimerization of Glycophorin A [1] and other Small-xxx-Small motifs [2].

Motifs are spatial or sequence patterns that are observed with much higher frequency than would be expected by chance, while antimotifs are patterns observed with much lower frequency. Here, spatial pattern refers to two interacting residues from short sequence fragments that are spatially adjacent. Examples of such sequence pairs are adjacent strands in a β-sheet, arranged parallel or antiparallel, or interacting α-helices in transmembrane proteins. Sequence pattern refers to two ordered residues along the N-to-C direction of a short sequence fragment, following the convention of Senes et al. [1]. These patterns can be expanded to involve an arbitrary number of residues.

Identifying motifs from sequence information is an important task, and there is a large body of literature on motif discovery (see the book by Robin et al. [3] and references within). For short sequence fragments, discovery of motifs is a challenging task, especially when the amount of available data is limited. The statistics of spatial motifs from short fragments cannot be approximated by a χ² distribution, as was used by Wouters and Curmi [4]. The χ² distribution requires assumptions of normality that are not generally true in short sequences when data is scarce. For sequence motifs, methods based on the binomial distribution, as was used by Hart et al. [5] and by Robin et al. [3], are also inappropriate. The binomial distribution requires unrealistic assumptions that become more apparent in short sequences, such as drawing from a universal residue population with replacement.

In this study, we present formulae for discovery of spatial motifs of interacting residue pairs and sequence motifs consisting of residues embedded in short-sequence fragments based on a combinatorial model called the permutation model [3]. This model relies on drawing from a population of residues without replacement, and was used by Senes et al. to study membrane proteins [1]. We are concerned with not only finding motifs in short sequences, but also calculating accurate p-values that determine the statistical significance of the identified motifs. We introduce modifiable combinatorial models for several different types of analyses. Specifically, we have derived analytical forms to describe all possible two-residue spatial motifs as well as for two-residue and multi-residue sequence motifs under a variety of conditions.

Our models use as input a dataset of short sequence fragments, and are designed to obtain optimal statistical power from small datasets. We believe that our methods represent a more robust alternative to earlier methods, a necessity when dealing with the smaller amount of information provided by short sequences. Our models can be applied generally to any set of interacting short sequence pairs for spatial motif discovery, and to any set of short sequences for sequence motif discovery. We illustrate the effectiveness of our models for motif discovery in β-barrel membrane proteins, of which only a small structural dataset exists [6]. We also compare these results to other existing models, in order to show that our models are more appropriate for datasets of short sequences.

II. Model and Methods

A. General model

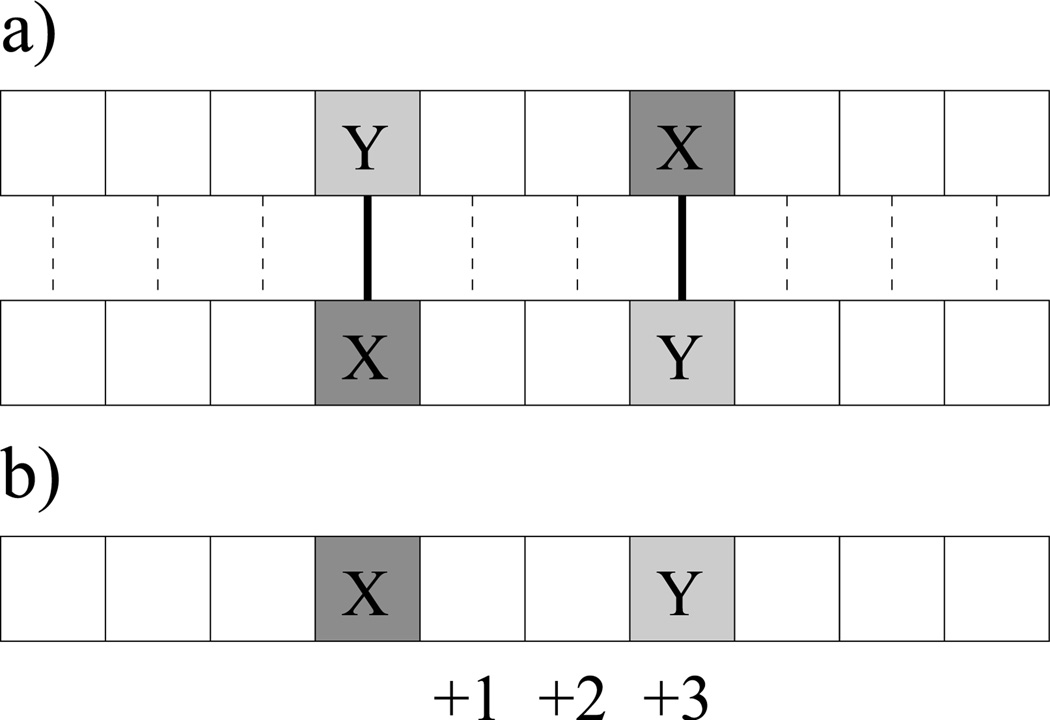
We introduce the definition of residue pair XY as some meaningful combination of two residues of amino acid types X and Y. We will focus on two major classes of pairs (Figure 1). We define a spatial interaction pair X-Y as a pattern in which a residue of type X is found interacting with a residue of type Y on two interacting sequences (Figure 1a). In this case, interacting sequences are assumed to be the same length, and each residue on one sequence interacts with exactly one residue on the other sequence, though different pairs of interacting sequences in a dataset may be of different lengths. We will introduce a method to relax the matching length requirement later. We define a sequence pair XYk as a pattern in which a residue of type Y is found at the k-th position from a residue of type X along a single sequence (Figure 1b).

Fig. 1.

Examples of spatial and sequence patterns. a) Two X-Y spatial patterns on interacting sequences. b) an XY3 sequence pattern.

We define the propensity P(X, Y) of residue pair XY as:

$$P(X,Y)=\frac{f_{\text{obs}}(X,Y)}{𝔼[f(X,Y)]},$$

where f_obs(X, Y) is the observed count of XY patterns, and 𝔼[f(X, Y)] is the expected count of XY patterns. We define a motif as a residue pair with propensity > 1.0 (or greater than some other predefined limit) and statistically significant, based on p-value. Similarly, an antimotif is a residue pair with propensity < 1.0 (or some other predefined limit) and statistically significant. The null model used to calculate 𝔼[f(X, Y)] is similar for both pair types: the residues within each sequence are exhaustively and independently permuted without replacement, and each permutation occurs with equal probability. We call this internally random. It is the same model used by Senes et al. [1], and is also called the permutation model in literature [3]. We will also introduce an alternative permutation model that is position-dependent, and examine an existing model based on permutation with replacement, called the Bernoulli model [3].

The focus of this paper is to determine explicit formulae to calculate 𝔼[f(X, Y)] for each pair type under different conditions. Where possible, we will also determine explicit probability distributions for f(X, Y), which will allow for the calculation of variance and p-values. Although these formulae are designed for single sequences, we will also describe how these models can be expanded to study whole datasets of short sequences.

All formulae presented have been verified through comparison to results obtained through full enumeration of permutations in order to ensure correctness.

B. Propensity of spatial interactions

To identify spatial motifs, we calculate the intersequence spatial propensity P(X, Y) for interacting pairs of residue types X and Y (Figure 1a):

$$P(X,Y)=\frac{f_{\text{obs}}(X,Y)}{𝔼[f(X,Y)]},$$

where f_obs(X, Y) is the observed count of X-Y contacts in the sequence pair, and 𝔼[f(X, Y)] is the expected count of X-Y contacts in a null model.

In order to calculate 𝔼[f(X, Y)], we use an internally random null model in which residues within each of the two sequences in a sequence pair are permuted exhaustively and independently, and each permutation occurs with equal probability. An X-Y contact forms if in a permuted sequence pair two interacting residues happen to be type X and type Y. 𝔼[f(X, Y)] is then the expected number of X-Y contacts in the sequence pair.

Null model for residues of the same type.

For cases in which X is the same as Y (i.e. X-X pairs), let x₁ be the number of residues of type X in the first sequence, x₂ the number of residues of type X in the second sequence, and l the length of the sequence pair (i.e. the length of either sequence). In the internally random null model, we randomly select residues from one sequence to pair up with residues from the other sequence. We wish to know ℙ_XX(i), the probability of exactly i = f(X, X) number of X-X contacts in this model. There are $\left(\begin{array}{c}\hfill l\hfill \\ \hfill x_2\hfill \end{array}\right)$ ways to place the x₂ residues of type X in the second sequence. Of these, i will each be paired with one of the x₁ residues of type X on the first sequence, and x₂ − i will each be paired with one of the l − x₁ non-X residues. There are $\left(\begin{array}{c}\hfill x_1\hfill \\ \hfill i\hfill \end{array}\right)\text{ and }\left(\begin{array}{c}\hfill l-x_1\hfill \\ \hfill x_2-i\hfill \end{array}\right)$ ways to do this, respectively. When multiplied together, we have that ℙ_XX(i) follows a hypergeometric distribution:

$${\mathbb{P}}_{\mathit{\text{XX}}}(i)=\frac{\left(\begin{array}{c}\hfill x_1\hfill \\ \hfill i\hfill \end{array}\right)\left(\begin{array}{c}\hfill l-x_1\hfill \\ \hfill x_2-i\hfill \end{array}\right)}{\left(\begin{array}{c}\hfill l\hfill \\ \hfill x_2\hfill \end{array}\right)}.$$ (1)

𝔼[f(X, X)] is then the expectation of the hypergeometric distribution:

$$𝔼[f(X,X)]=\frac{x_1{x}_2}{l}.$$

For statistical significance, two-tailed p-values can be calculated using the hypergeometric distribution for a dataset of sequence pairs (Section II-D).

Null model for residues of different types.

If the two contacting residues are not of the same type, i.e. X ≠ Y, the number of X-Y contacts in the internally random model for one sequence pair is the sum of two dependent hypergeometric variables, one variable for type X residues in the first sequence s₁ and type Y in the second sequence s₂, and another variable for type Y residues in s₁ and type X in s₂. The expected number of X-Y contacts 𝔼[f(X, Y)] is the sum of the two expected values:

$$𝔼[f(X,Y)]=𝔼[f(X,Y|X\in s_1,Y\in s_2)]+𝔼[f(X,Y|Y\in s_1,X\in s_2)]=\frac{x_1{y}_2}{l}+\frac{y_1{x}_2}{l},$$

where x₁ and x₂ are the numbers of residues of type X in the first and second sequence, respectively, y₁ and y₂ are the numbers of residues of type Y in the first and second sequence, and l is the length of the sequence pair. Despite the fact that the variables f(X, Y|X ∈ s₁, Y ∈ s₂) and f(X, Y|X ∈ s₂, Y ∈ s₁) are dependent (i.e. the placement of an X-Y pair may affect the probability of a Y-X pair in the same sequence pair), their expectations may be summed directly, because expectation is a linear operator.

However, because f(X, Y|X ∈ s₁, Y ∈ s₂) and f(X, Y|X ∈ s₂, Y ∈ s₁) are dependent, to determine the p-value for a specific observed number of X-Y contacts, a more detailed formula for the null model must be established. The probability of a specific number of X-Y contacts occurring in one sequence pair does not follow a simple hypergeometric distribution. Here we develop a general hypergeometric model based on the multinomial with three parameters to characterize such a probability. First, we define a 3-element multinomial function M(a, b, c) as:

$$M(a,b,c)\equiv \frac{a!}{b!c!(a-b-c)!},$$ (2)

where M(a, b, c) = 0 if a − b − c < 0. This represents the number of distinct permutations, without replacement, in a multiset of size a containing three different types of elements, with number count b, c, and a − b − c of each of the three element types.

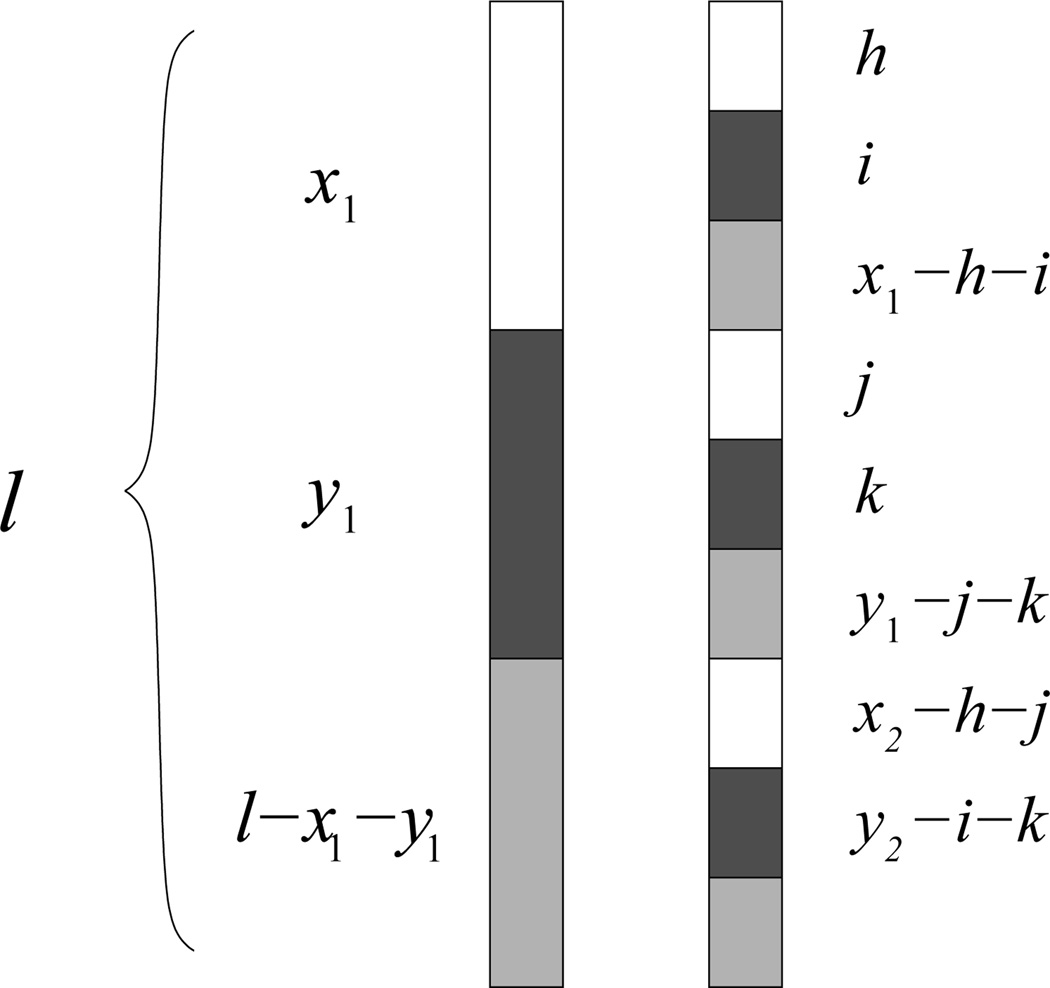
Consider residues in the first sequence of length l of a sequence pair. These l residues are of three types: x₁ count of type X residues, y₁ of type Y residues, and n₁ = l − x₁ − y₁ count of type “neither.” We now first fix the positions of residues on sequence 1, and permute exhaustively the l residues on sequence 2. We can fix one sequence in this way without loss of generality, because only the number, not the order, of residues pairs within a sequence pair is relevant for calculating ℙ_XY(i). Let x₂, y₂, and n₂ be the numbers of residues of type X, Y, and “neither” on sequence 2, respectively. There are M(l, x₂, y₂) ways to permute these residues.

Consider the residues on sequence 2 that match to the x₁ number of residues of type X on sequence 1 (Figure 2). These x₁ residues on sequence 2 consist of h number of type X residues, i number of type Y residues, and x₁ − h − i number of type “neither” residues. They can be permuted in M(x₁, h, i) different ways. Similarly, the y₁ residues on sequence 2 that match type Y residues in sequence 1 consist of j number of type X residues, k number of type Y residues, and y₁ − j − k of type “neither” residues, and thus the total number of permutations for these y₁ residues is M(y₁, j, k). Similarly, there are M(n₁, x₂ − h − j, y₂ − i − k) number of permutations to match the remaining n₁ = l − x₁ − y₁ of type “neither” residues on sequence 1.

Fig. 2.

Division of residues in spatial motif analysis when X ≠ Y. White = X, black = Y, gray = “neither” X or Y.

We characterize the probability ℙ(h, i, j, k) of intersequence matches: a) the x₁ type X residues on sequence 1 with h type X residues, i type Y residues, and x₁ − h − i type “neither” residues on sequence 2; b) the y₁ type Y residues on sequence 1 with j type X residues, k type Y residues, and y₁ − j − k type “neither” residues on sequence 2; and c) the remaining n₁ type “neither” residues on sequence 1 with x₂ − h − j type X residues, y₂ − i − k type Y residues, and the remaining type “neither” residues from sequence 2. Equivalently, ℙ(h, i, j, k) is the probability of h X-X contacts, i X-Y contacts, j Y-X contacts, and k Y-Y contacts occurring in a random permutation.

We introduce a higher order hypergeometric distribution for ℙ(h, i, j, k) as follows:

$$\mathbb{P}(h,i,j,k)=\frac{M(x_1,h,i)·M(y_1,j,k)·M(l-x_1-y_1,x_2-h-j,y_2-i-k)}{M(l,x_2,y_2)}.$$

The marginal probability ℙ_XY (m) that there are a total of i + j = m X-Y contacts in the internally random model, namely, the pairings in which a residue of type X in the first sequence is paired with a residue of type Y in the second sequence, summed with the pairings in which a residue of type Y in the first sequence is paired with a residue of type X in the second sequence, is:

$${\mathbb{P}}_{\mathit{\text{XY}}}(m)={\displaystyle \sum _{h=0}^{x_1}}{\displaystyle \sum _{i=0}^{x_1-h}}{\displaystyle \sum _{k=0}^{\stackrel{y_1-}{(m-i)}}}\mathbb{P}(h,i,m-i,k),$$

where again h is the number of matched X-X contacts, i the number of matched X-Y contacts, j = m − i the number of matched Y-X contacts, and k the number of matched Y-Y contacts. The remaining contacts involving residues of type “neither” will then automatically be assigned, since all matches involving X and Y have been accounted for. There are x₁ possible values for h, one for each residue of type X on sequence 1; x₁ − h possible values for i, once h has been determined; and y₁ − j = y₁ − (m − i) possible values for k, once i has been determined. The i number of X-Y contacts plus the m − i number of Y-X contacts will sum to the m number of contacts desired.

This closed-form formula is important, because it allows us to calculate p-values analytically for this null model. The run time is O(l⁴), due to the presence of 3 summations and l! in the summand. However, because this formula is intended for use with short sequences, this run time is not prohibitive. For much longer sequences, a null model based on the Bernoulli model is an appropriate substitute (Section II-F.1).

Adjustment for sequences of different length within a sequence pair.

The requirement for interacting sequences to be of the same length may be relaxed by introducing a 21st “dummy” amino acid type. All unpaired residues in the longer member of a sequence pair will be paired to this extra amino acid type, and our standard method can be applied to determine the propensity of unpaired amino acids (i.e. residues paired with the “dummy” amino acid type).

C. Propensity of sequence patterns

1) Propensity of two-residue sequence patterns

We introduce the propensity P(X, Y|k) for two ordered intrasequence residues of type X and type Y that are k positions away on the same sequence (Figure 1b). We call this pattern XYk following the convention established by Senes et al. [1]. For instance, AL3 represents AxxL, where “x” is any residue type. We define the propensity as:

$$P(X,Y|k)=\frac{f_{\text{obs}}(X,Y|k)}{𝔼[f(X,Y|k)]},$$

where f_obs(X, Y|k) is the observed count of XYk patterns, and 𝔼[f(X, Y|k)] is the expected count of XYk patterns.

In our null model, the sequences are internally random, i.e. the residues within each sequence are permuted exhaustively and independently, and each permutation occurs with equal probability. An XYk pattern forms if in a permuted sequence an X residue happens to be followed by a Y residue at the k-th position along the sequence in the N-terminal to C-terminal direction of the peptide.

To determine 𝔼[f(X, Y|k)], we can represent f(X, Y|k) as the sum of identical Bernoulli variables f_t(X, Y|k), each of which equals 1 if one of the x number of residues of type X occurs at position t in the sequence and one of the y number of residues of type Y occurs at position t + k, or equals 0 otherwise. Since an XYk pattern cannot occur if t > l − k, we concern ourselves only with the first l − k positions. As long as t ≤ l − k, the probability of an XYk pattern occurring at position t does not depend on t: there is a $\frac{x}{l}$ chance of an X residue occurring at position t and a $\frac{y}{l-1}$ chance of a Y residue occurring at position t + k, once the residue at position t is drawn. Thus,

$$𝔼[f_t(X,Y|k)]=\mathbb{P}[f_t(X,Y|k)=1]=\frac{x}{l}·\frac{y}{(l-1)}\text{ if }t\le l-k.$$

There are l − k such identical variables, and their expectations may be summed:

$$𝔼[f(X,Y|k)]=(l-k)\frac{\mathit{\text{xy}}}{l(l-1)},$$ (3)

where l is the length of the sequence, x is the number of residues of type X, and y is the number of residues of type Y. For XXk patterns, i.e. two residues of the same type displaced by k residues, the expectation is calculated as

$$𝔼[f(X,X|k)]=(l-k)\frac{x(x-1)}{l(l-1)},$$ (4)

as there will be x − 1 residues available to place the second X residue at position t + k after the first X residue is placed at t. Although these Bernoulli random variables are dependent (i.e. the placement of one XYk pattern will affect the probability of another XYk pattern), their expectations may be summed, because expectation is a linear operator. However, in order to calculate statistical significance in terms of p-values, special formulae must be derived to determine ℙ_XYk(i), the probability of the occurrence of i = f(X, Y|k) XYk patterns.

Null model for residues of different types if k = 1.

We first consider the case where X ≠ Y and k = 1 (i.e. pairs of different adjacent residues along a sequence). The number of ways to permute x number of X residues, y number of Y residues, and l − x − y number of type “neither” residues is $\frac{l!}{x!y!(l-x-y)!}$. We wish to enumerate how many of these permutations contain exactly i XY1 patterns.

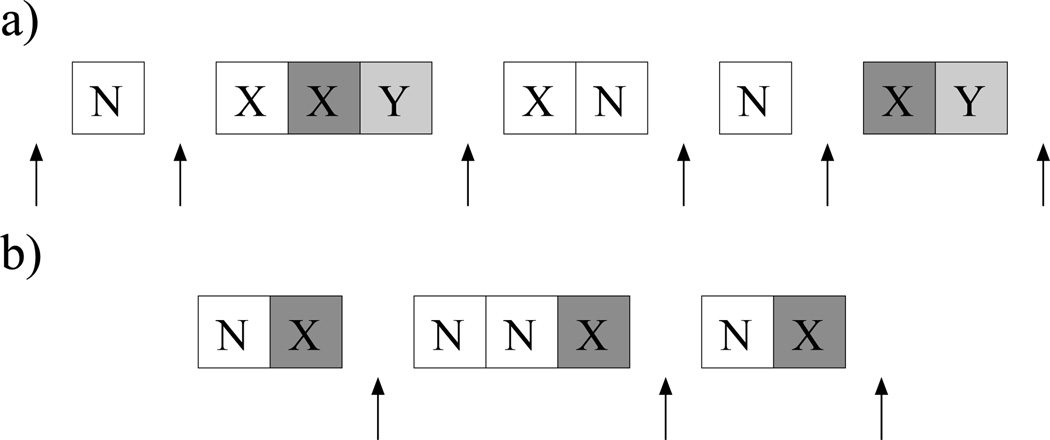
First, we place the x residues of type X and l − x − y residues of type “neither” in a subsequence of l − y residues. There are $\left(\begin{array}{c}\hfill l-y\hfill \\ \hfill x\hfill \end{array}\right)$ ways to arrange the X residues in this subsequence. Second, we select i of these X residues to participate in XY1 patterns. There are $\left(\begin{array}{c}\hfill x\hfill \\ \hfill i\hfill \end{array}\right)$ ways to do this. Next, we add a Y residue after each of these i X residues to complete the XY1 patterns (Figure 3a). We now have a subsequence of length l − y + i residues, and we have y − i residues of type Y left to complete the full sequence.

Fig. 3.

Examples of the internally random model for sequence motifs when k = 1 a) Example when X ≠ Y and k = 1. After placing l − y non-Y residues and i Y residues that form the desired number i of XY1 patterns, there are l − x − y + i + 1 “slots” in which to place the remaining Y residues so that no additional XY1 patterns are formed. b) Example when X = Y and k = 1. After placing l − x non-X residues and x − i X residues without forming an XX1 pattern, there are x − i “slots” in which to place the remaining i X residues so that each one forms a new XX1 pattern.

We view this subsequence as having a “slot” at the beginning position and after each residue, and add these y − i Y residues to the slots until the full sequence is obtained. We choose which slot in which to place each Y residue with replacement, so that some slots may contain more than one Y residue, and some may contain none. We may not, however, choose a slot just after an X residue without forming a new XY1 pattern or disrupting an already existing one (Figure 3a). There are thus l − x − y + i + 1 slots available: one after each reside of type “neither” (l − x − y), one after each Y in an XY1 pattern (+i), and one at the beginning of the subsequence (+1). Using the standard formula for choosing objects with replacement but without regard to order, the number of ways to place the remaining y − i residues of type Y in the l − x − y + i + 1 available slots is:

$$\left(\begin{array}{c}\hfill (l-x-y+i+1)+(y-i)-1\hfill \\ \hfill y-i\hfill \end{array}\right)=\left(\begin{array}{c}\hfill l-x\hfill \\ \hfill y-i\hfill \end{array}\right).$$

Combining these terms and simplifying, the probability of i XY1 patterns in one sequence follows a hypergeometric distribution:

$${\mathbb{P}}_{\mathit{\text{XY}}1}(i)=\frac{\left(\begin{array}{c}\hfill l-y\hfill \\ \hfill x\hfill \end{array}\right)\left(\begin{array}{c}\hfill x\hfill \\ \hfill i\hfill \end{array}\right)\left(\begin{array}{c}\hfill l-x\hfill \\ \hfill y-i\hfill \end{array}\right)}{\frac{l!}{x!y!(l-x-y)!}}=\frac{\left(\begin{array}{c}\hfill x\hfill \\ \hfill i\hfill \end{array}\right)\left(\begin{array}{c}\hfill l-x\hfill \\ \hfill y-i\hfill \end{array}\right)}{\left(\begin{array}{c}\hfill l\hfill \\ \hfill y\hfill \end{array}\right)}.$$

Null model for residues of the same type if k = 1.

When X = Y and k = 1, the probability of i XX1 patterns in one sequence follows a different distribution, and the proof is slightly different from the above case. There are $\left(\begin{array}{c}\hfill l\hfill \\ \hfill x\hfill \end{array}\right)$ ways to permute the x number of X residues in a sequence of length l, and we wish to enumerate how many permutations contain exactly i XX1 patterns.

First, place all residues that are not of type X in a subsequence of length l − x. There are now a total of l − x + 1 “slots” in which to place the x number of residues of type X: one after each residue, and one at the beginning of the subsequence. We choose x − i of these slots without replacement to be filled with exactly one residue of type X, in $\left(\begin{array}{c}\hfill l-x+1\hfill \\ \hfill x-i\hfill \end{array}\right)$ number of ways. This is to ensure that no XX1 pattern is formed in this step. In the next step, we can ensure that there are i XX1 patterns by placing the remaining i residues of type X only in slots following one of these already placed X residues (Figure 3b). There are thus x − i available slots, but we may choose them with replacement. There are $\left(\begin{array}{c}\hfill (x-i)+i-1\hfill \\ \hfill i\hfill \end{array}\right)=\left(\begin{array}{c}\hfill x-1\hfill \\ \hfill i\hfill \end{array}\right)$ ways to do this. Combining these terms, we have another hypergeometric distribution:

$${\mathbb{P}}_{\mathit{\text{XX}}1}(i)=\frac{\left(\begin{array}{c}\hfill l-x+1\hfill \\ \hfill x-i\hfill \end{array}\right)\left(\begin{array}{c}\hfill x-1\hfill \\ \hfill i\hfill \end{array}\right)}{\left(\begin{array}{c}\hfill l\hfill \\ \hfill x\hfill \end{array}\right)},$$ (5)

with the convention that $\left(\begin{array}{c}\hfill n\hfill \\ \hfill r\hfill \end{array}\right)$ if n < r.

Null model for residues of different types if x ≤ 2 or y ≤ 2.

If either x = 1 or y = 1, then

$${\mathbb{P}}_{\mathit{\text{XYk}}}(1)=𝔼[f(\mathit{\text{XY}}|k)]=(l-k)\frac{\mathit{\text{xy}}}{l(l-1)},$$

since the maximum possible number i of XYk patterns is 1, and

$$𝔼[f(\mathit{\text{XY}}|k)]=0·{\mathbb{P}}_{\mathit{\text{XYk}}}(0)+1·{\mathbb{P}}_{\mathit{\text{XYk}}}(1)={\mathbb{P}}_{\mathit{\text{XYk}}}(1).$$

This is the same as Equation (3). As a result, it is possible to determine ℙ_XYk(1) for all values of k if the number count of either one of the residue types is 1. For i = 0, we have simply:

$${\mathbb{P}}_{\mathit{\text{XYk}}}(0)=1-{\mathbb{P}}_{\mathit{\text{XYk}}}(1).$$

If x = 2 or y = 2, the probability of two XYk patterns is:

$${\mathbb{P}}_{\mathit{\text{XYk}}}(2)=\frac{\left[\right(\begin{array}{c}\hfill l-k\hfill \\ \hfill 2\hfill \end{array})-(l-2k)]}{\frac{l(l-1)(l-2)(l-3)}{x(x-1)y(y-1)}}.$$ (6)

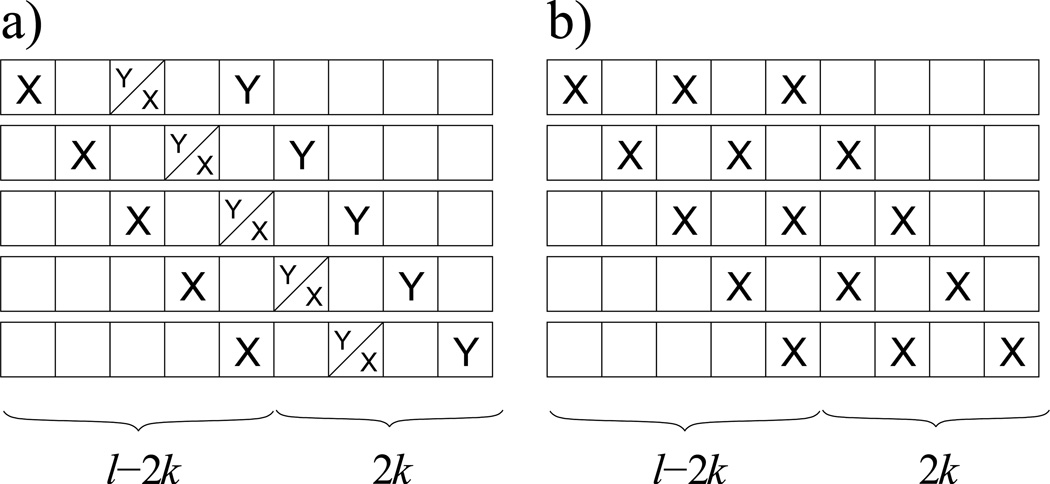
There are $\left(\begin{array}{c}\hfill l-k\hfill \\ \hfill 2\hfill \end{array}\right)$ positions in which to place two XYk patterns. However, the terminal residue of type Y in the first pattern overlaps with and forbids the placement of the initial residue of type X in the second pattern in l − 2k cases, in which the initial residue of type X in the first pattern is placed in one of the first l − 2k positions of the sequence (Figure 4a). Thus, there are $\left(\begin{array}{c}\hfill l-k\hfill \\ \hfill 2\hfill \end{array}\right)-(l-2k)$ possible ways to place two XYk patterns. Since there are $\frac{l(l-1)(l-2)(l-3)}{x(x-1)y(y-1)}$ possible ways to place two residues of type X and two resides of type Y, the probability of exactly two XYk residues is as shown in Equation (6).

Fig. 4.

a) Visual explanation of why there are l − 2k forbidden placements of 2 XYk patterns when either x = 2 or y = 2. The terminal Y residue of the first pattern interferes with the initial X residue of the second pattern. b) Visual explanation of why there are l − 2k possible ways to place 2 XXk patterns when x = 3 in sequence motif analysis.

Since there can only be a maximum of two XYk patterns when x = 2 or y = 2, it is possible to determine the probability of exactly one XYk pattern or zero patterns using the definition of expectation. Because $𝔼[f(\mathit{\text{XYk}})]={\displaystyle {\sum }_{i=0}^2}i·{\mathbb{P}}_{\mathit{\text{XYk}}}(i)=0·{\mathbb{P}}_{\mathit{\text{XYk}}}(0)+1·{\mathbb{P}}_{\mathit{\text{XYk}}}(1)+2·{\mathbb{P}}_{\mathit{\text{XYk}}}(2)$ and ℙ_XYk(0) + ℙ_XYk(1) + ℙ_XYk(2) = 1, we have:

$${\mathbb{P}}_{\mathit{\text{XYk}}}(1)=𝔼[f(\mathit{\text{XYk}})]-2{\mathbb{P}}_{\mathit{\text{XYk}}}(2),$$ (7)

$${\mathbb{P}}_{\mathit{\text{XYk}}}(0)=1-[{\mathbb{P}}_{\mathit{\text{XYk}}}(1)+{\mathbb{P}}_{\mathit{\text{XYk}}}(2)].$$ (8)

Null model for residues of the same type if x ≤ 3.

If x = 2, then the probability of one XXk pattern is:

$${\mathbb{P}}_{\mathit{\text{XXk}}}(1)=𝔼[f(\mathit{\text{XXk}})]=(l-k)\frac{x(x-1)}{l(l-1)},$$

since it is only possible to have one XXk pattern. Then:

$${\mathbb{P}}_{\mathit{\text{XXk}}}(0)=1-{\mathbb{P}}_{\mathit{\text{XXk}}}(1).$$

If x = 3, then the probability of exactly two XXk patterns is:

$${\mathbb{P}}_{\mathit{\text{XXk}}}(2)=\frac{l-2k}{\left(\begin{array}{c}\hfill l\hfill \\ \hfill x\hfill \end{array}\right)},$$

since there are only l − 2k positions in which to place an X ⋯ X ⋯ X pattern (i.e. the only way to obtain two XXk patterns if x = 3), and $\left(\begin{array}{c}\hfill l\hfill \\ \hfill x\hfill \end{array}\right)$ ways to place x residues of type X in a sequence of length l (Figure 4b). It is then possible to determine the remaining probabilities using expectation, as was done in Equations (7) and (8), since at most only two XXk patterns are possible when x = 3 (i.e. an X ⋯ X ⋯ X pattern, where “ ⋯” corresponds to k − 1 residues).

Null model for residues if k > 1, x > 2, and y > 2.

When k > 1, x > 2, and y > 2, the analytical formulae for ℙ_XYk(i) become very complicated. However, when the sequences in the dataset used are short, it is possible to fully enumerate all permutations of a sequence and calculate ℙ_XYk(i) and p-values exactly, as shown by Senes et al. [1]. Because x and y are usually small in short sequences, this situation should not occur frequently enough to adversely affect the computation time needed for motif analysis of short sequences.

2) Propensity of multi-residue sequence patterns

The model presented for two-residue sequence patterns may be expanded easily to determine 𝔼[f(X₀, X₁, X₂, …, X_n|k₁, k₂, …, k_n)], the expected number of a specific pattern containing n + 1 residues placed in a contiguous subsequence of k_n + 1 residues (k_n ≥ n). Here, X_i is the residue type of the i-th fixed residue in the pattern and k_i is the position of this residue from the 0-th residue (k₀ = 0). Any other position not specified by k_i can be any residue type. For example, the pattern (A, L, Y|2, 4) is written as AL2Y4 and represents AxLxY. A graphic example is shown in Figure 5. There are many examples of these multi-residue sequence motifs in proteins, including the GxGxxG NADH binding motif [7] and the RSxSxP 14-3-3 binding motif [8].

Fig. 5.

Example of a multi-residue sequence pattern as described in the text. This pattern contains 5 specified residues in a span of 10 residues. Here, X₀, X₁, X₂, X₃, and X₄ are specified amino acid types, and the corresponding k values are counted as the distance from the first position of the sequence (i.e. the position occupied by X₀). Thus, k₁ = 2, k₂ = 3, k₃ = 6, and k₄ = 9. All other residues (in white) are unspecified and may be any amino acid type. This pattern is written as (X₀, X₁, X₂, X₃, X₄ | 2, 3, 6, 9).

The expected value can be calculated as:

$$𝔼[f(X_0,X_1,X_2,\dots ,X_n|k_1,k_2,\dots ,k_n)]=(l-k_n)\frac{{\displaystyle {\prod }_{i=0}^n}[x_i-\#(𝕀(X_i))]}{\frac{l!}{(l-n-1)!}},$$ (9)

where x_i is the number of residues of type X_i, l is the length of the sequence, and #(𝕀(X_i)) is the number of times residue type X_i appears in the “subpattern” {X₀, X₁, X₂, …, X_i−1}.

Equation (9) is an extension of Equations (3) and (4).We can represent f(X₀, X₁, X₂, …, X_n|k₁, k₂, …, k_n) as the sum of identical Bernoulli variables f_t(X₀, X₁, X₂, …, X_n|k₁, k₂, …, k_n), each of which equals 1 if the appropriate pattern occurs at position t and 0 otherwise. For t > l − k_n, this value is always 0. For t ≤ l − k_n, the probability of the pattern does not depend on t. The probability that the i-th residue in the pattern is of type X_i is $\frac{x_i-\#(𝕀(X_i))}{l-i}$, as there will be l − i residues to choose from and x_i − #(𝕀(X_i)) residues of type X_i available after the first i residues have been placed. The function #(𝕀(X_i)) is necessary in case there are identical residue types in {X₀, X₁, ⋯, X_n}. Multiplying these probabilities, and then multiplying by l − k_n for the number of Bernoulli variables, results in the expected value in Equation (9).

D. Motif analysis on datasets of short sequences

The previous motif analyses are useful for determining propensities in a single short sequence or sequence pair. However, under most cases, sequence analysis must be performed on a dataset of multiple short sequences in order to attain sufficient statistical significance. This has the advantage of capturing within-sequence relationships on a scale large enough to obtain reliable p-values.

Because expectation is a linear operator, it is a simple matter to sum the expected values of each sequence to determine the expected value of the entire dataset:

$$𝔼[f{(X,Y)}_{\mathit{\text{dataset}}}]={\displaystyle \sum _{n=1}^m}𝔼[f{(X,Y)}_n],$$

where 𝔼[f(X, Y)_n] is the expected value of the n-th sequence in a dataset of m sequences. If each distribution f(X, Y)_n is independent among all sequences, the variance of the dataset may also be determined by summing the variances of each sequence.

To determine the probability distribution function for the dataset as a whole, ℙ[f(X, Y)_dataset], we follow the approach of Senes et al. [1]. First, the probability distributions of the first two sequences, ℙ₁ and ℙ₂, are combined into a single “database” distribution ℙ_db(2) as follows:

$${\mathbb{P}}_{\mathit{\text{db}}(2)}(i)={\displaystyle \sum _{j=0}^i}{\mathbb{P}}_1(j)·{\mathbb{P}}_2(i-j),$$

that is, the probability ℙ_db(2)(i) of i total patterns in the two sequences is the sum of the probabilities of all possible combinations of j patterns occurring in the first sequence and i − j patterns occurring in the second sequence. This new probability, ℙ_db(2)(i), can now be thought of as a single sequence distribution, and so the probability distribution for the entire dataset can be compiled using a recursive formula:

$${\mathbb{P}}_{\mathit{\text{db}}(n)}(i)={\displaystyle \sum _{j=0}^i}{\mathbb{P}}_{\mathit{\text{db}}(n-1)}(j)·{\mathbb{P}}_n(i-j),$$

where ℙ_n is the probability distribution for the n-th sequence, and ℙ_db(n) is the probability distribution for the first n sequences combined. When the recursion terminates at the last (m-th) sequence, ℙ_db(m)(i) = ℙ[f(X, Y)_dataset]. This function can be used to determine p-values for the entire dataset. It is recommended that two-tailed p-values are used, regarding the following hypothesis test:

$$H_0:f_{\text{obs}}(X,Y)=𝔼[f(X,Y)]$$

$$H_1:f_{\text{obs}}(X,Y)\ne 𝔼[f(X,Y)].$$

To calculate p-values, we use:

$$p=2·{\displaystyle \sum _{i=0}^{f_{\text{obs}}(X,Y)}}{\mathbb{P}}_{\mathit{\text{db}}(m)}(i)$$

when f_obs(X, Y) < 𝔼[f(X, Y)], and

$$p=2·{\displaystyle \sum _{i=f_{\text{obs}}(X,Y)}^{\mathit{\text{UB}}}}{\mathbb{P}}_{\mathit{\text{db}}(m)}(i)$$

when f_obs(X, Y) > 𝔼[f(X, Y)], where UB is an upper bound for all possible X-Y patterns in the dataset. Because i ≤ x and i ≤ y in each sequence under a permutation model, the sum of min(x, y) for each sequence is always an acceptable upper bound, though lower acceptable values may be used to reduce unnecessary computations. Because we are using two-tailed p-values, and because the distribution of f(X, Y) is not necessarily symmetric, it is possible for p > 1.0 if f_obs(X, Y) falls between 𝔼[f(X, Y)] and the median of f(X, Y). In that case, p is simply set to 1.0.

Multiple hypothesis testing for datasets of short sequences.

Using an alphabet of 20 amino acids, the spatial motif analysis requires 210 tests (for each possible unordered pair of amino acids), and the sequence motif analysis requires 400 tests (for each possible ordered pair of amino acids). Because of the high number of tests used, it is possible that some tests with p-values meeting the specified cut-off (usually p < 0.05) are only significant because multiple hypotheses are being tested, and not due to true statistical significance. This multiple hypothesis testing problem can be corrected using the standard Bonferroni method [9]. However, in datasets of short sequences, this method may be too conservative and overstate the effect of multiple hypothesis testing.

We have applied a more appropriate method of multiple hypothesis correction based on the Significance Analysis of Microarrays (SAM) method developed by Tusher et al. [10]. This method calculates the false discovery rate (FDR), which measures the proportion of significant test results that are due to random sampling [11].

The method is the same for spatial and sequence motif analysis. We randomly permute the residues of all sequences in a dataset, and calculate p-values from this dataset using the same model as was used on the true dataset. We do this 1,000 times and average the number of significant results from each permuted dataset. This method ensures that each dataset has exactly the same sequence lengths and amino acid distribution as the true dataset, but that all significant results are due only to random sampling. The ratio of this average to the number of significant results from the true dataset is the FDR. Their difference is the presumed number of truly statistically significant results in the dataset.

E. Positional null model

The previous motif analyses are based on an internally random null model in which the residues within each sequence are permuted, and each permutation is equally likely. This assumption can be problematic in certain cases where there are biases of residue types for certain positions in a sequence known a priori. For instance, aromatic residues tend to be favored at either end of a transmembrane α-helix or β-strand [12–14]. These single-residue biases may confound two-residue propensities without providing additional information into the preferences of these patterns. When such biases are known, it may be helpful instead to consider a null model that accounts for them.

We therefore introduce a positional null model. Instead of permuting residues across all positions within individual sequences, we permute residues across all sequences in a dataset within specific positions (Figure 6).We have adapted this null model for both spatial and sequence motifs. We describe our work in full in the Appendix.

Fig. 6.

Difference between a) an internally random null model for sequence motif analysis and b) a position-dependent null model. In both cases, only residues of the same shade are permuted with each other. In a), residues are permuted only within each sequence individually, while in b), residues are permuted across sequences but only within their specified position t.

F. Binomial null model

The methods we have developed in Sections II-B and II-C.1 are based on the permutation model, which relies on permuting sequences without replacement. Methods based on the Bernoulli model, which relies on permuting sequences with replacement, have been well-developed and applied to important problems of motif analysis in long sequences [3]. Here, we examine whether the permutation model is more powerful than the Bernoulli model for short sequences, where coupling effects are great. We introduce a binomial null model, which relies on permutation with replacement, for both spatial and sequence motif analysis, for the purpose of comparing its performance to our methods.

1) Binomial null model for spatial interaction pairs

To calculate propensities for spatial interaction pairs under a binomial null model, we permute each sequence in a sequence pair of length l with replacement. We wish to find the probability of exactly i X-Y pairs occurring in the permuted sequence pair, and the expectation 𝔼[f(X, Y)] of this probability distribution.

We first examine the case where X = Y. We can represent f(X, X) as the sum of l identical and independent Bernoulli variables f_t(X, X), each of which equals 1 if an X-X pair occurs at position t on the sequence pair, and 0 otherwise. The probability of a pair does not depend on t: the probability that a residue of type X will occur at position t on the first sequence is $\frac{x_1}{l}$, where x₁ is the number of residues of type X in the first sequence, and the probability that an X residue will occupy position t on the second sequence is similarly $\frac{x_2}{l}$, where x₂ is the number of X residues in the second sequence. Combining these terms:

$$\mathbb{P}[f_t(X,X)=1]=\frac{x_1{x}_2}{l^2}$$

for all positions t. Because these residues are drawn with replacement, these Bernoulli variables are independent, and therefore their sum, f(X, X), is a binomial distribution, and the probability of exactly i X-X pairs can be calculated as:

$${\mathbb{P}}_{\mathit{\text{XX}}}{(i)=l·(\frac{x_1{x}_2}{l^2})}^i·{(1-\frac{x_1{x}_2}{l^2})}^{l-i}.$$

The expected count of X-X pairs can be calculated using the standard expectation of the binomial distribution:

$$𝔼[f(X,X)]=l·\frac{x_1{x}_2}{l^2}=\frac{x_1{x}_2}{l}.$$

For the case where X ≠ Y, we similarly represent f(X, Y) as the sum of l Bernoulli variables f_t(X, Y) with the same characteristics. In this case, the probability that an X-Y occurs at position t is the sum of the probability that an X residue occurs at position t on the first sequence and a Y residue occurs at position t on the second sequence, with the probability conversely that a Y residue occurs at position t on the first sequence and an X residue occurs at position t on the second sequence:

$$\mathbb{P}[f_t(X,Y)=1]=\frac{x_1{y}_2}{l^2}+\frac{y_1{x}_2}{l^2}=\frac{x_1{y}_2+y_1{x}_2}{l^2},$$

where x₁ and y₁ are the number of residues of type X and Y, respectively, on the first sequence, and x₂ and y₂ are the number of residues of type X and Y on the second sequence. Again, these independent Bernoulli variables may be summed to a binomial distribution:

$${\mathbb{P}}_{\mathit{\text{XY}}}(i)=l·{(\frac{x_1{y}_2+y_1{x}_2}{l^2})}^i·{(1-\frac{x_1{y}_2+y_1{x}_2}{l^2})}^{l-i},$$

with expectation

$$𝔼[f(X,Y)]=l·\frac{x_1{y}_2+y_1{x}_2}{l^2}=\frac{x_1{y}_2+y_1{x}_2}{l}.$$

Note that the expected values for both cases are identical to the expected values obtained by our internally random model (Section II-B). This ensures that the p-values obtained by the two models can be compared directly to evaluate statistical power.

For datasets of multiple sequences, we combine the distributions for each single sequence into one database distribution from which to derive p-values, as described in Section II-D.

2) Binomial null model for sequence pairs

The binomial null model for sequence pairs is more complicated than that for spatial pairs, as the Bernoulli variables are no longer independent. This model has already been discussed in detail by Robin et al. [3]. For our purposes, we have chosen to use full enumeration in this study, by calculating the probability of each possible permutation of amino acids with replacement and summing those containing the specified number of XYk patterns. As with the spatial motif analysis, for datasets of multiple sequences, we combine the distributions for each single sequence into one database distribution from which to derive p-values, as described in Section II-D.

It is important to note, however, that the expected count of sequence patterns under a binomial null model differs from that under our internally random model. For the case where X = Y, we represent f(X, X|k) as the sum of Bernoulli variables f_t(X, X|k), as we did for our internally random model (Section II-C.1), each of which equals 1 if an XXk pattern occurs at position t, and 0 otherwise. Similarly, this variable equals 0 if t > l − k, and does not depend on t otherwise:

$$\mathbb{P}[f_t(X,X|k)=1]=\frac{x}{l}·\frac{x}{l}\text{ if }t\le l-k,$$

where x is the number of residues of type X in a sequence of length l. Since we draw with replacement, the probability that an X residue occurs at any position is simply $\frac{x}{l}$. As there are l − k identical Bernoulli variables, their expectations may be summed:

$$𝔼[f(X,X|k)]=(l-k)\frac{x^2}{l^2}.$$

We note that, since l ≥ x, this expectation is higher than the expectation under our internally random model (Equation 4):

$$(l-k)\frac{x^2}{l^2}\ge (l-k)\frac{x(x-1)}{l(l-1)},$$ (10)

with equality only in the trivial cases where x = l or x = 0. This reveals a particularly problematic aspect of the binomial null model. When x = 1, the expectation will be nonzero, even though it is impossible for a sequence with x = 1 to contain an XXk pattern. Under our internally random model, this expectation is appropriately zero.

For the case where X ≠ Y, we again represent f(X, Y|k) as the sum of Bernoulli variables f_t(X, Y|k), each of which equals 1 if an XYk pattern occurs at position t, and 0 otherwise. Again, this variable equals 0 if t > l − k, and does not depend on t otherwise:

$$\mathbb{P}[f_t(X,Y|k)=1]=\frac{x}{l}·\frac{y}{l}\text{ if }t\le l-k,$$

where y is the number of residues of type Y in the sequence. The expectation is then:

$$𝔼[f(X,Y|k)]=(l-k)\frac{\mathit{\text{xy}}}{l^2}.$$

This expectation is lower than the expectation under our internally random model (Equation 3):

$$(l-k)\frac{\mathit{\text{xy}}}{l^2}\le (l-k)\frac{\mathit{\text{xy}}}{l(l-1)},$$

with equality only in the trivial cases where x = 0 or y = 0.

III. Results

Most of the combinatorial null models discussed above have been applied to a real set of proteins, β-barrel membrane proteins, with considerable success [6, 14]. This set is an excellent example of a small dataset of short sequences that requires robust combinatorial models in order to discover significant motifs. Less than 30 non-homologous members of this family of proteins are represented in crystal structures, and transmembrane β-strands are on average 9–10 residues in length. We describe and discuss these results below. The most important feature of these models, their robustness, can be noted in the number of significant p-values.

We use the structures of 23 β-barrel membrane proteins with resolution of 3.0 Å or better as our dataset, comprising a total of 314 β-strands (Table I). All proteins share no more than 26% pairwise sequence identity. The average length of a sequence in this set is 9.8 residues. The run time of each program on the entire dataset was less than a minute on an Intel Core Duo E4400 processor at 2.0 GHz.

TABLE I.

Dataset of 23 β-barrel membrane proteins used for this study.

Protein	Organism	Architecture	Strands	PDB	ID
OmpA	E. coli	monomer	8	1BXW	[15]
OmpX	E. coli	monomer	8	1QJ8	[16]
NspA	N. meningitidis	monomer	8	1P4T	[17]
OmpW	E. coli	monomer	8	2F1T	[18]
PagP	E. coli	monomer	8	1THQ	[19]
OpcA	N. meningitidis	monomer	10	1K24	[20]
OmpT	E. coli	monomer	10	1I78	[21]
OMPLA	E. coli	dimer	12	1QD6	[22]
NalP	N. meningitidis	monomer	12	1UYN	[23]
FadL	E. coli	monomer	14	1T16	[24]
Porin	R. capsulatus	trimer	16	2POR	[25]
Porin	R. blastica	trimer	16	1PRN	[26]
OmpF	E. coli	trimer	16	2OMF	[27]
Omp32	C. acidovorans	trimer	16	1E54	[28]
LamB	S. typhimurium	trimer	18	2MPR	[29]
ScrY	S. typhimurium	trimer	18	1A0S	[30]
FepA	E. coli	monomer	22	1FEP	[31]
FhuA	E. coli	monomer	22	2FCP	[32]
FecA	E. coli	monomer	22	1KMO	[33]
BtuB	E. coli	monomer	22	1NQE	[34]
FptA	P. aeruginosa	monomer	22	1XKW	[35]
TolC	E. coli	trimer	4	1EK9	[36]
α-Hemolysin	S. aureus	heptamer	2	7AHL	[37]

A. Analysis of spatial motifs in β-barrel membrane proteins

Table II lists pairwise interstrand spatial motifs we discovered using the models described in Section II-B. These are divided into H-bonded and non-H-bonded pairs (see reference for definitions [14]). Only motifs significant at the threshold p-value of 0.05 are listed. Detailed biological implications of these motifs are described in the reference [14]. Current analysis has led to the discovery of exciting new roles for the motifs topping each list, G-Y in H-bonded pairs and W-Y in non-H-bonded pairs. The former is a result of “aromatic rescue” [38], the protection of the backbone atoms of glycine from solvent by tyrosine’s large side-chain. The latter motif, W-Y, appears frequently in the “aromatic belt” of β-barrel membrane proteins, and allows considerable van der Waals contacts between the two large side-chains.

TABLE 2.

Spatial H-bonded and non-H-bonded motifs in TM β-strand pairs significant at p < 0.05. Listed under “Permutation” are p-values from our internally random permutation model. Listed under “Binomial” are p-values from the alternative binomial model described in the text.

H-bonded				Non-H-Bonded
		p-Value				p-Value
Pair	Propensity	Permutation	Binomial	Pair	Propensity	Permutation	Binomial
GY	1.51	4.7 × 10−4	4.9×10−3	WY	2.71	1.2×10−9	1.1×10−6
ND	2.61	1.1×10−3	5.8×10−3	RY	2.28	6.1×10−3	1.8×10−2
GF	1.73	5.2×10−3	2.1×10−2	EF	2.58	6.6×10−3	3.2×10−2
KS	1.84	1.5×10−2	4.6×10−2	GV	1.60	7.3×10−3	2.1×10−2
ET	1.64	2.0×10−2	5.1×10−2	RE	1.83	9.9×10−3	3.3×10−2
RP	4.00	3.1×10−2	7.0×10−2	QG	1.53	2.7×10−2	7.4×10−2
IY	1.55	3.2×10−2	7.6×10−2	LL	1.38	3.6×10−2	9.8×10−2
				AA	1.49	3.6×10−2	7.9×10−2
				AL	1.31	4.1×10−2	8.3×10−2

Because there are 210 possible amino acid pairs in this analysis, we calculate the false discovery rate (FDR), as described in Section II-D, in order to estimate the number of significant results that are likely to be due to random sampling rather than true statistical significance. For the H-bonded motif analysis, random sampling produces an average of 4.16 significant results (motifs and antimotifs combined), compared with 9 significant results found in the true dataset (including antimotifs, not shown in Table II), which represents an FDR of 46%. For the non-H-bonded motif analysis, random sampling produces an average of 4.40 significant results, compared with 14 in the true dataset, which represents an FDR of 31%. These results imply that 4–5 results from the H-bonded analysis and 9–10 results from the non-H-bonded analysis are truly statistically significant, and, by extension, potentially biologically significant.

We compare the results from our motif analysis, based on the permutation model, to a binomial model, as described in Section II-F.1. For the H-bonded motif analysis, the binomial model produces 5 significant results (motifs and antimotifs combined), compared with 9 significant results found using our model. For the non-H-bonded motif analysis, the binomial model produces 9 significant results, compared with 14 found using our model. In Table II, we compare p-values from our model and from the binomial model. In every case, the p-value from our model is more significant than the p-value from the binomial model. It is clear from this comparison that our methods, based on the permutation model, outperform the binomial model on datasets of short sequences.

B. Analysis of sequence motifs in β-barrel membrane proteins

In Table III, we report the pairwise intrastrand sequence motifs we discovered with calculated propensities and p-values, as described in Section II-C.1 [6]. Our method allows us to calculate exact probability distributions using the formulae provided for 306 of the 314 sequences. Only 8 of the sequences required full enumeration to obtain exact distributions, either because x > 3 for an XXk pattern or x > 2 and y > 2 for an XYk pattern.

TABLE III.

Sequence motifs and antimotifs for k = 2 and p < 0.05 in TM β-strands.

Motifs			Antimotifs
Pair	Odds	p-Value	Pair	Odds	p-Value
LA2	1.83	3.7×10−6	YV2	0.48	3.8×10−3
GR2	2.08	6.8×10−6	WY2	0.14	5.4×10−3
AY2	1.87	3.0×10−5	YA2	0.51	9.6×10−3
LG2	1.68	1.3×10−4	YT2	0.40	1.3×10−2
VY2	1.63	1.7×10−3	EY2	0.00	1.7×10−2
AA2	1.63	3.0×10−3	LK2	0.19	3.5×10−2
VV2	1.50	5.8×10−3	RT2	0.42	4.0×10−2
PM2	5.62	1.1×10−2	QN2	0.00	4.5×10−2
AV2	1.57	1.2×10−2	VH2	0.00	4.8×10−2
IL2	1.79	1.3×10−2
ND2	2.28	1.4×10−2
LL2	1.42	1.4×10−2
IA2	1.72	1.7×10−2
GG2	1.32	1.8×10−2
VL2	1.48	2.2×10−2
GA2	1.54	2.2×10−2
YQ2	1.84	2.5×10−2
TV2	1.66	2.6×10−2
KW2	3.68	2.7×10−2
GV2	1.47	3.6×10−2
VP2	2.07	4.7×10−2

Although we inspected multiple k values, the most informative motifs occur when k = 2, because in this situation residues on β-strands are closest to each other. Significant (p < 0.05) motifs (propensity > 1.0) and antimotifs (propensity < 1.0) when k = 2 are displayed in Table III. Detailed biological implications of these motifs are published elsewhere [6], but we discovered a clear pattern of the amino acid tyrosine appearing in the second (C-terminal) position of motifs and in the first (N-terminal) position of antimotifs. We have called this phenomenon the aliphatic-Tyr dichotomy, because it occurs most often with aliphatic residues, and it may be involved in protein-lipid interactions.

Because there are 400 possible ordered amino acid pairs for each value of k in this analysis, we correct for multiple hypothesis testing by calculating the false discovery rate (FDR) as described in Section II-D, in order to estimate the number of significant results that are likely to be due to random sampling rather than true statistical significance. For the case when k = 2, random sampling produces an average of 8.68 significant results (motifs and antimotifs combined), compared with 30 significant results found in the true dataset (Table III), which represents an FDR of 29%. This result implies that 21–22 results from our analysis are truly statistically significant.

In addition to the standard null model, whose results are listed in Table III, we also utilized two other sequence motif null models in our study, specifically, the positional null model for sequence motifs (see Appendix), and the binomial model (Section II-F.2).

The analysis of position-dependent motifs was performed primarily to determine if single-residue position preference confounds the results listed in Table III. Motifs were found to be similar between the two null models, suggesting that there is little confounding effect. However, some antimotifs showed divergence, and therefore single-residue preference must be taken into account when discussing such antimotifs [6].

An analysis using the binomial model, as described in Section II-F.2, was performed to determine whether our methods, based on the permutation model, are more powerful than existing methods based on the Bernoulli (i.e. binomial) model for datasets of short sequences. Although the binomial method produces more statistically significant results than our method for this dataset (45 vs. 30), these results are misleading, as 19 of the 22 antimotifs discovered by the binomial method are of the form XX2 (i.e. X = Y). The only XX2 pattern not determined to be an antimotif, CC2, does not appear in the dataset, because cysteine is not found in transmembrane β-strands. By comparison, the antimotifs from our permutation method do not include any XX2 pairs, while 4 of the 21 over-represented motifs are of the form XX2 (Table III).

We investigate this discrepancy to determine which model is more effective. It is possible that, even though there were more significant results using the binomial method, these results may be due to random sampling. We calculate the false discovery rate (FDR) for the binomial method using the same sampling technique described in Section II-D. Using the same dataset, random sampling produces an average of 38.68 significant results, compared with 45 found in the true dataset, which represents an FDR of 86%. This is considerably worse than the FDR of 29% found for our internally random model, and suggests that only 6–7 of the results from the binomial method are truly significant. This compares unfavorably with the 21–22 significant results from our method (Table IV).

TABLE IV.

False discovery rates for sequence motif analysis under two competing models. “# Signif. Results”, number of significant results found in original dataset. “Avg. False Discoveries”, average number of significant results found after permuting residues in dataset 1,000 times. “FDR”, false discovery rate.

Model	# Signif. Results	Avg. False Discoveries	FDR
Permutation	30	8.68	29%
Binomial	45	38.68	86%

The reason for this discrepancy becomes apparent when the formulae for expectation between the two methods are compared (Inequality 10). Under a binomial model, a sequence with x = 1 will have a non-zero expected count of XXk patterns, even though it is impossible for an XXk pattern to form in the true sequence. By comparison, under our internally random model, the expected count of XXk patterns is zero if x = 1. In long sequences, such as whole genes or genomes, it is rare for x = 1, and therefore the binomial model is useful for its relative ease of calculation. In short sequences, however, x = 1 for most amino acids X very commonly. For example, in our dataset of 314 sequences, 142 sequences contain exactly one alanine residue, while only 60 contain more than one. It is clear that coupling effects from sampling with replacement introduce great unwanted bias in the results of the binomial method, as shown by its high FDR compared with our internally random model.

IV. Discussion

There are two well-known models for studying sequence motifs: the permutation model and the Bernoulli model [3]. A third model, the Markovian model, is a form of the Bernoulli model generalized to allow for dependence between nearby residues in a sequence. The internally random model proposed by Senes et al. in the context of studying transmembrane helices is based on the permutation model, with a sequence pattern containing two specified residues and a specified number of wildcard residues between them [1]. This model provides one of the most natural ways of building random sequences that share common characteristics with the observed sequence. It is well-suited for studying transmembrane helices and strands, as they are short sequences (< 20 residues) for which coupling effects are strong. However, this model is not normally used for long sequences, such as whole genes or genomes, because the methods for obtaining exact distributions of null models greatly increase in complexity for longer sequences [3]. In this situation, methods based on the Bernoulli model, including Markovian methods, are preferred [3]. For this reason, the permutation model is not widely used.

The difference between the permutation and Bernoulli models is determined by how sequences are permuted to obtain null models. In the permutation model, they are permuted without replacement, while in the Bernoulli model, they are permuted with replacement. In long sequences, the effects of this difference are negligible, and the power of the two models to discover motifs is similar [3]. However, in short sequences, this difference is significant, since not replacing withdrawn residues greatly affects the sampling space. It is well-known that, under the same conditions, the hypergeometric distribution, which relies on sampling without replacement, and which we have used in this study to derive formulae based on the permutation model, has a lower variance than the binomial distribution, which relies on sampling with replacement [39]. This difference translates into higher statistical power for hypothesis tests, and is greatest when the sample size (e.g., sequence length for biological sequences) is small. Although tests based on the hypergeometric distribution tend to be more computationally complex, this complexity is manageable in short sequences, and the statistical power takes priority. For this reason, we adopt the permutation model in our study of motifs in short sequences.

Several important results are known for the permutation model and have been applied to the study of motifs in nucleotide sequences. The total number of possible sequences for fixed nucleotide and dinucleotide compositions can be derived using Whittle’s formula [40], and further generalization using an embedding technique to fixed compositions of tri- and tetranucleotides exists [3]. In addition, the number of sequences containing a specific word at a specific position can also be computed exactly, and hence the expected number of occurrences of this word. However, while these fomulae are important for the study of nucleotide sequences that are based on a genetic code of trinucleotides, in which the third position is often degenerate, these results do not directly lead to discovery of biologically significant sequence motifs in short protein sequences, as there is no physical reason to adopt a null model of contiguous di- or tripeptides.

In general, the permutation model remains difficult, as it requires complex combinatorial analysis [3]. In fact, even when simulation instead of combinatorial analysis is employed to evaluate probabilities, it is not known how to generate permuted random sequences with equal probability while preserving various properties (e.g., the composition of di-nucleotide words) [3].

In this study, we have obtained useful results beyond existing literature based on the permutation model for the discovery of sequence motifs from fragments of very short length, as well as spatial interaction motifs when these fragments form interacting pairs. Our results are important for discovery of biologically significant motifs when only very limited data is available, as in β-barrel membrane proteins. Our results show that a number of important motifs can be successfully uncovered, and the results can be used to understand the mechanisms of membrane protein folding and to predict membrane protein structures [6, 14]. Finally, we show that our analytical methods for motif discovery outperform similar methods based on the Bernoulli model for a dataset of short sequences, due to higher statistical power and lower false discovery rate.

Sequence motif analyses have already been performed for transmembrane α-helices [1] and β-strands [6], and spatial motif analysis for transmembrane β-strands [¹⁴], with considerable success. There are still many problems for which such analysis may generate useful insights. Spatial motif analysis may reveal important residue interactions in α-helical membrane proteins, where helices are often packed closely together and at nearly coincidental axes. Both sequence and spatial analyses are appropriate for any dataset of β-strands from a family of β-sheets. In addition to transmembrane β-barrels, motifs in soluble β-barrels have been studied [14]. Lastly, sequence analysis may be useful for motif discovery in short sequences drawn from a family of proteins with similar structure or function, in an effort to determine common sites of function or locations essential to structural integrity.