Protective immunity to Schistosoma haematobium infection is primarily an anti-fecundity response stimulated by the death of adult worms

Abstract

Protective immunity against human schistosome infection develops slowly, for reasons that are not yet fully understood. For many decades, researchers have attempted to infer properties of the immune response from epidemiological studies, with mathematical models frequently being used to bridge the gap between immunological theory and population-level data on schistosome infection and immune responses. Here, building upon earlier model findings, stochastic individual-based models were used to identify model structures consistent with observed field patterns of Schistosoma haematobium infection and antibody responses, including their distributions in cross-sectional surveys, and the observed treatment-induced antibody switch. We found that the observed patterns of infection and antibody were most consistent with models in which a long-lived protective antibody response is stimulated by the death of adult S. haematobium worms and reduces worm fecundity. These findings are discussed with regard to current understanding of human immune responses to schistosome infection.

Schistosoma haematobium parasites infect more than 100 million people in sub-Saharan Africa and are responsible for a heavy burden of disease (1, 2). Protective immunity against schistosomes takes a long time to develop; the precise nature of the protective immune response and the reasons for its slow development are not fully understood, although several immune responses, antibodies in particular, have been associated with protection (3). Two hypotheses for the slow development of anti-S. haematobium immunity have been put forward: firstly, that dying worms are the main source of protective antigen, with exposure to dying worms delayed by long parasite life spans (4); secondly, that exposure to a certain threshold level of antigen is required before a protective response is stimulated (5).

There is a long history of using epidemiological data to understand the immune response to human schistosome infection (6, 7), and mathematical models have played an important role (8). A common approach has been testing the ability of models to reproduce patterns seen in field data (9–11). Robust patterns include the peaked age-intensity curve (7), the “peak shift” (infection peaking at a higher level and younger age in populations with higher exposure) (12), and an age-related switch in the S. haematobium-specific antibody response (13, 14) (note that this “switch” refers to a rapid change in the dominant antibody isotype, not isotype switching of individual B cells). Pattern-oriented modeling (POM), developed initially in ecology, uses multiple different patterns to discriminate between possible models (15). Previous work using POM with deterministic models could not distinguish between the two hypotheses for the slow development of immunity against S. haematobium but greatly narrowed down the range of model structures consistent with these field patterns (16). The combination of the life cycle stage that provided the main antigenic stimulus for each antibody response, and the life cycle stage targeted by each antibody response, was critical in determining whether all of these patterns could be reproduced (16). These previous models did not take into account heterogeneities in exposure to infection or look at the distribution of infection or antibody responses across populations nor the impact of treatment on the immune response.

Schistosomes are highly aggregated among their human hosts, such that many individuals harbor few or no schistosome worms, while a few carry heavy parasite loads (17). Previous modeling work suggests that this distribution arises from aggregation between individuals in their rates of infection (related to water exposure) (9), which observational studies confirm is highly heterogeneous (18). Aggregated worm burdens may also result from aggregation in the number of worms acquired per contact (10, 19). Levels of S. haematobium-specific antibody are also highly aggregated. Isotypes that demonstrate an age-related switch have a dichotomous relationship, with individuals rarely producing high levels of both isotypes (13, 20). As well as occurring naturally with age, this antibody switch is observed in younger children following praziquantel treatment (20, 21).

Here, we extend our earlier POM analysis (16), incorporating heterogeneous exposure into the successful model structures using stochastic individual-based models, and testing whether these models can also reproduce the distributions of S. haematobium infection and antibody seen in the field and the post-treatment antibody switch. We find that only a very limited set of models are capable of reproducing the field data, providing novel insights into the immunological processes that lead to these observed patterns.

Results

Baseline Analysis: Cross-Sectional Criteria.

The initial analysis used the baseline parameter values to assess whether each model could meet all of the “cross-sectional” criteria listed in Table 1. Only three of the different model structures tested were ever able to meet all of these criteria over a twofold change in population contact rate (Table 2). These models all included an antigen threshold and all had the nonprotective response stimulated by egg antigens, with the protective antibody response stimulated by antigen from cercariae, live worms or dying worms. In all three models the protective response reduced worm fecundity.

Table 1.

Criteria used to determine whether models replicated age-related and distributional patterns of infection and antibody seen in cross-sectional and post-treatment field data

Pattern identified in field data	Criterion applied to model output	Source
Cross-sectional
Prevalence of infection by urine test	Prevalence of egg positives 5–80% for 6–14 year olds and for 15–34 year olds	Refs. 14, 44
Peaked age intensity curve	Maximum level of infection occurs between age of 6–23 years old	Refs. 7, 14, 16, 44
Reduced infection level in adults	Infection level in 24–34 year old age group < 40% of peak age group	Refs. 7, 14, 16, 44
Peak shift	Peak infection intensity is lower and occurs in the same or older age group when infection rate is halved	Ref. 12
Aggregated egg output	Standardized variance (SV) of mean egg output 2–60 for whole population, for 6–14 year olds and for 15–34 year olds	Refs. 14, 44
Antibody switch	Spearman’s ρ for association between two antibody responses < -0.2	Refs. 13, 14, 20
Antibody switch after age of infection peak	Initial (nonprotective) antibody response first falls below its midpoint value in the same or a later age group than peak infection	Refs. 13, 14
Post-treatment
Antibody switch after treatment	A2 is ≥200% and A1 is ≤ 50% of respective pre-treatment levels at both 18 and 36 wk post-treatment	Ref. 20

Table 2.

Relative success of different model structures in meeting criteria

Immune mechanism	Life cycle stage			No. of parameter sets passing following criteria:
	Antigen for A2	Targeted by A2	Antigen for A1	Cross-sectional	Cross-sectional and post-treatment
Cross-regulation	Cercariae	Cercariae	Live worms	0	0
	Cercariae	Cercariae	Dying worms	0	0
	Cercariae	Cercariae	Eggs	0	0
	Live worms	Eggs	Cercariae	0	0
	Live worms	Eggs	Live worms	0	0
	Live worms	Eggs	Dying worms	0	0
	Live worms	Eggs	Eggs	0	0
	Dying worms	Cercariae	Live worms	0	0
	Dying worms	Cercariae	Eggs	0	0
	Dying worms	Eggs	Cercariae	0	0
	Dying worms	Eggs	Live worms	0	0
	Dying worms	Eggs	Dying worms	0	0
	Dying worms	Eggs	Eggs	0*	0
Antigen threshold	Cercariae	Cercariae	Live worms	0	0
	Cercariae	Cercariae	Dying worms	0	0
	Cercariae	Cercariae	Eggs	0	0
	Cercariae	Eggs	Eggs	22	0
	Live worms	Eggs	Eggs	254	0
	Dying worms	Eggs	Eggs	48	32
	Eggs	Eggs	Eggs	0	0

^*For this model, 12 individual parameter sets were able to meet all of the criteria, but none of these could meet the criteria over a twofold change in population infection rate.

One of the cross-regulation models was able to meet all of the cross-sectional criteria for 12 individual parameter sets, although not over a twofold change in population contact rate (Table 2). In this model the protective antibody response was stimulated by antigen from dying worms and reduced worm fecundity, and the nonprotective antibody response was stimulated by egg stage antigens.

Importance of Different Criteria.

The relative importance of the different criteria in excluding parameter combinations was assessed for the baseline analysis. The number of individual simulations passing each criterion, and passing each pair of criteria, was counted. For both cross-regulation and threshold models, the criteria least likely to be passed were the antibody switch (failed by 85% and 70% of simulations, respectively) and S. haematobium infection prevalence in both 6–14- and 15–34-year-olds (at least one of these prevalence criteria was failed by 86% and 90% of simulations for the cross-regulation and threshold models, respectively). Simulations that gave reduced infection levels in adults were more likely to pass the prevalence criteria, and those passing the prevalence criteria were in general more likely to pass the aggregation and antibody switch criteria. A number of trade offs were seen between different criteria; most notably, simulations passing the peak age criterion were less likely to pass the criterion for prevalence in 6–14-year-olds (this pair of criteria was failed by 97% of all simulations). The majority of simulations failed on multiple criteria, with only 5% failing on a single criterion alone. All of the criteria were found to be discriminatory.

Inclusion of Treatment.

The models that were able to meet all of the criteria over a twofold change in population contact rate were further analyzed for their ability to reproduce the observed antibody switch after treatment of children aged 6–15 years old. A range of different treatment efficacies and post-treatment levels of transmission reduction were investigated (see SI Text for details). Only the model with dying worm antigens stimulating the protective antibody response was able to reproduce the post-treatment antibody switch (Table 2) for a subset of the parameters that reproduced all of the cross-sectional data patterns. The number of parameter sets reproducing the post-treatment antibody switch was robust to the level of treatment efficacy and transmission reduction over the ranges explored. The cross-regulation model that was able to meet all of the cross-sectional criteria for individual parameter sets was also able to reproduce the antibody switch after treatment.

Sensitivity Analysis.

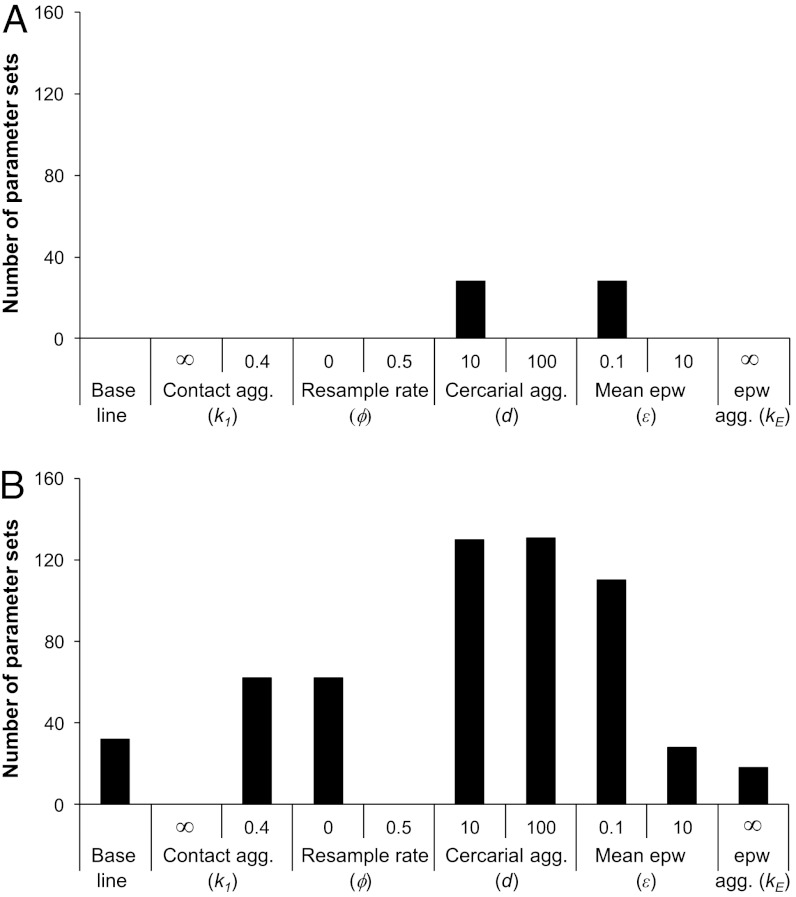
Sensitivity analysis was carried out on the two model structures which were able to reproduce the antibody switch after treatment: one with cross-regulation and one with an antigen threshold, which both had an anti-fecundity, dying worm-stimulated, protective antibody response and egg-stimulated, nonprotective antibody. Each of the parameters governing the stochastic model processes was varied separately in turn, while varying all other parameters over their full baseline ranges. Fig. 1 shows the number of parameter sets that were able to pass all of the cross-sectional and the post-treatment criteria over a twofold change in maximum contact rate when each of the stochastic process parameters was varied in turn. For the cross-regulation model (Fig. 1A), the criteria were only all passed with moderate cercarial aggregation (d = 10) or with low egg output per worm (ε = 0.1). For the antigen threshold model, it was found that both the aggregation of the underlying contact rates between individuals and the rate at which this contact level was resampled affected whether the models could meet all of the criteria. Poisson distributed contacts (k₁ = ∞) and frequent resampling of contact rates (ϕ = 0.5 y^-1) both prevented the models from reproducing field patterns (Fig. 1B). These results are not independent, because more frequent resampling of contact rates reduces the overall aggregation of contact between individuals. A moderate increase in aggregation of the underlying contact rate to the maximum level reported in ref. 22 (k₁ = 0.4), or perfect predisposition (ϕ = 0), both increased the number of parameter sets that were able to meet all of the criteria. Increased cercarial aggregation (d = 10, d = 100) and reduced egg output per worm (ε = 0.1) all increased the number of parameter sets meeting all criteria, while increased egg output (ε = 10) made little difference, and reducing the aggregation of eggs per worm found in urine (using a Poisson distribution, k_E = ∞) reduced the number of parameter sets able to meet all of the criteria.

Fig. 1.

Results of univariate sensitivity analysis. Panels show the number of parameter combinations tested that meet all criteria (cross-sectional and post-treatment) over a twofold change in maximal contact rate when the following parameters are changed individually as shown: the scale parameter for the gamma distribution from which individual contact rates are drawn (k₁), the probability with which contact rates are resampled (ϕ), the aggregation of cercariae acquired per contact (d), the mean number of eggs per worm per 10 mL urine (ε), and the scale parameter for the gamma distribution from which the number of eggs per worm is drawn (k_E). Baseline values are: k₁ = 0.5, ϕ = 0.05 y^-1, d = 1, ε = 1, k_E = 1. (A) Cross-regulation model, (B) antigen threshold model.

Parameter Distributions.

The decay rates for the two plasma cell populations in successful parameter sets (summed across the baseline and sensitivity analysis results) are shown in Fig. 2. Similar patterns were seen for both the cross-regulation model (Fig. 2A) and the antigen threshold model (Fig. 2B). For all of the successful parameter sets, there was relatively rapid decay of the initial antibody response (A₁) of 8–80 y^-1 (half-life 3.2–32 d), with slower decay of the protective antibody response (A₂) for almost all parameter combinations of 0.008–0.8 y^-1 (half-life of 10 mon–87 y). Within these ranges there was little apparent preference for particular values or combinations of the two decay rates. Four parameter combinations in the antigen threshold models had more rapid A₂ decay of 8 y^-1 (half-life 32 d).

Fig. 2.

Distribution of plasma cell decay rates in successful parameter combinations. The frequency of different combinations of decay rates for the two plasma cell populations are shown for models that were able to meet all of the cross-sectional and post-treatment criteria, in either the baseline or the univariate sensitivity analysis. (A) Cross-regulation models. (B) Antigen threshold models. Bars are drawn for all combinations of plasma cell decay rates that were used. Black bars indicate a frequency of 0, gray bars a frequency > 0.

Antibody Aggregation and Co-distributions.

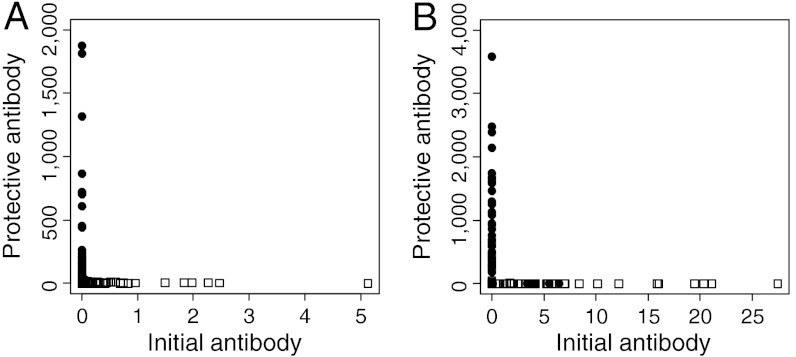
All of the models that passed all of the criteria gave aggregated distributions for both antibody responses. Visual inspection of antibody co-distributions for randomly selected parameter sets (Fig. 3) confirmed that the models had reproduced the dichotomous relationship which was seen in field data (20).

Fig. 3.

Antibody co-distributions in the model outputs, shown for two example parameter sets. (A) Cross-regulation model, parameters used: Λ_pmax = 25, 1/μ = 10, γ₁ = 80, γ₂ = 0.008, η = 0.256, ρ = 0.1, k₁ = 0.5, ϕ = 0.05, k_E = 1, d = 10. (B) Antigen threshold model, parameters used: Λ_pmax = 100, 1/μ = 6.5, γ₁ = 80, γ₂ = 0.08, η = 1.024, T = 250, k₁ = 0.5, ϕ = 0.05, k_E = 1, d = 100. White squares 0–14-year-olds, black circles 15–34-year-olds.

Discussion

As hypothesized, it was found that dying worms had to provide the main antigenic stimulus for a protective antibody response in order to reproduce field patterns of S. haematobium infection and antibody. Additionally, it was found that the protective antibody response had to reduce worm fecundity, and the nonprotective antibody response had to be stimulated by eggs. Other models most commonly failed because they could not reproduce the antibody switch or give plausible infection prevalence. Models including either cross-regulation or an antigen threshold were able to reproduce all of the pre- and post-treatment infection and antibody patterns. The analysis suggested that the B cell populations that produce the different antibody responses have different intrinsic decay rates, with the cells producing the initial antibody response decaying more rapidly than those producing protective antibody. It also showed that high aggregation in contact rates and low rates of change of contact rates (in line with levels measured in the field) are necessary for models to reproduce the observed data patterns.

The finding that dying worms provide the main source of protective antigen fits with several studies showing that praziquantel treatment, which kills adult schistosomes but has little effect on immature worms (23), can boost antibody responses associated with protection against reinfection (20, 24). The finding that protective immunity is likely to principally target fecundity is supported by the findings that lower levels of S. haematobium egg output were found relative to levels of circulating anodic antigen (a marker for worm burden) in adults than in children (25), and that S. haematobium fecundity is reduced by the immune response in mice (26). This analysis suggests that the most likely antigens to stimulate a protective response are ones that have their immune recognition boosted by treatment and that stimulate a primarily anti-fecundity response. Previously identified S. haematobium antigens that were only serologically recognized post-treatment include tropomyosin, paramyosin, triose phosphate isomerase, and glutathione S-transferase (GST) (27). Vaccinations of mice and natural mammalian hosts with S. japonicum tropomyosin and paramyosin lead to modest reductions in worm burden upon challenge, and often to an even greater reduction in egg output (28, 29), although this is not always seen (30, 31). One study has suggested that S. japonicum triose phosphate isomerase induces anti-fecundity effects (32), but other studies show a similar reduction in worm burden as in egg output (33), suggesting other immune targets. The antigen that has been most frequently associated with an anti-fecundity response is GST, which has been shown to reduce S. haematobium worm fecundity in baboons (34) as well as S. mansoni fecundity in mice (35) and S. japonicum fecundity in natural hosts (30).

For virtually all of the successful models, the B cell population producing protective antibody had a slower natural decay rate than the B cell population producing the initial (nonprotective) response. Short- and long-lived subsets of plasma B cells specific for a range of viral and bacterial antigens have been described, which have differing reported decay rates (36, 37). Different schistosome antigens may stimulate populations of plasma cells with differing decay rates.

The balance between different isotypes may also influence the expression of protection. Recent proteomics studies indicate that the isotypes IgA, IgE, IgG1, and IgG4 commonly recognise some schistosome antigens but also differentially recognise others and that heavily infected people do not have high ratios of IgG1/IgA or IgE/IgG4 (38).

It was found that relatively high levels of aggregation of individual contact rates had to be maintained, with low rates of change of individual contact rates, in order to reproduce field patterns. The values used in the baseline analysis, of k₁ = 0.5 and ϕ = 0.05 y^-1, which were both estimated from field data, were sufficient to reproduce all of the required patterns. Aggregation of cercarial acquisition increased the number of parameter sets for which models met all of the criteria but was not essential, and both reduced mean egg output per worm and increased aggregation of egg output also enhanced the ability of the models to meet the criteria, because both decrease the measured prevalence of infection. The level of aggregation of egg output used in most of the models was estimated from S. mansoni data (39), in the absence of similar estimates for S. haematobium. The reduced level of mean egg output per worm (0.1 per worm per 10 mL urine) that improved model performance is slightly lower than previous estimates (40, 41) but plausible given the considerable uncertainty in egg production rates for S. haematobium and variation in urine output. Exposure to cercariae is difficult to quantify directly, but there is no good evidence that exposure is highly aggregated (19) or, equivalently, that occasional large exposures are more likely than frequent small exposures (42). Aggregation in individual exposure levels was sufficient to explain antibody aggregation as well as aggregation in infection intensities, without needing to additionally consider other potential sources of antibody aggregation such as variability in individual immune competence, although such variability is not excluded.

In conclusion, this work has shown that observed pre-treatment, age-related patterns of S. haematobium infection and antibody and short-term, post-treatment changes in antibody levels, are consistent with the following immunological model. In younger, untreated individuals resident in endemic areas, secreted egg antigens stimulate an antibody response that is produced by short-lived plasma cells (with any associated memory B cell response also being short-lived) and is essentially nonprotective. Cumulative deaths of adult S. haematobium worms eventually release a sufficient quantity of antigens (such as GST) to stimulate a different antibody response that is produced by long-lived plasma cells (or is driven by antigen-independent stimulation of a long-lived memory B cell population) that reduces S. haematobium fecundity. The integration of immunological and epidemiological processes developed here provides powerful insights into the essential elements of a highly complex host-pathogen interaction, and we hope that this kind of analysis will also prove helpful for understanding other infectious diseases of humans.

Materials and Methods

Model.

An individual-based, stochastic, discrete-time model was used to describe changes in worm burden and the level of two separate antibody responses with age for people living in an area with stably transmitted endemic schistosome infection. The model structure, assumptions, and parameter values are all informed by current understanding of immune responses to human S. haematobium infection. Antibody responses are explicitly modeled because they have been well characterized, are frequently associated with protection, and have a clearly defined cellular source, B cells, for which the maturation pathways are well known. The immune response is modeled as populations of antibody-producing plasma B cells, but this may equivalently represent the dynamics of memory B cells with continual antigen-independent activation to short-lived plasma cells. T cells are assumed to contribute to the generation and maintenance of the antibody response but are not explicitly included. The model was based upon a framework used in earlier deterministic population-level models (16), with worm survival assumed to be approximately Gaussian distributed. The model structures used were those that met a panel of criteria over the greatest region of parameter space tested in the deterministic analysis (16) and had either cross-regulation of the short-lived antibody response or an antigen threshold for the longer-lived antibody response. Cross-regulation was included in this and our earlier models to test whether this was necessary to generate the switch in the antibody response. In the deterministic analysis, every possible combination of schistosome life-cycle stage stimulating and being targeted by the antibody response was considered (16); here we only look at those combinations that gave outputs in the deterministic analysis consistent with field data. In the deterministic framework, it was found that in general the shorter-lived antibody response (A₁) must have little or no protective effect, so it was assumed here that only the longer-lived antibody response (A₂) was protective.

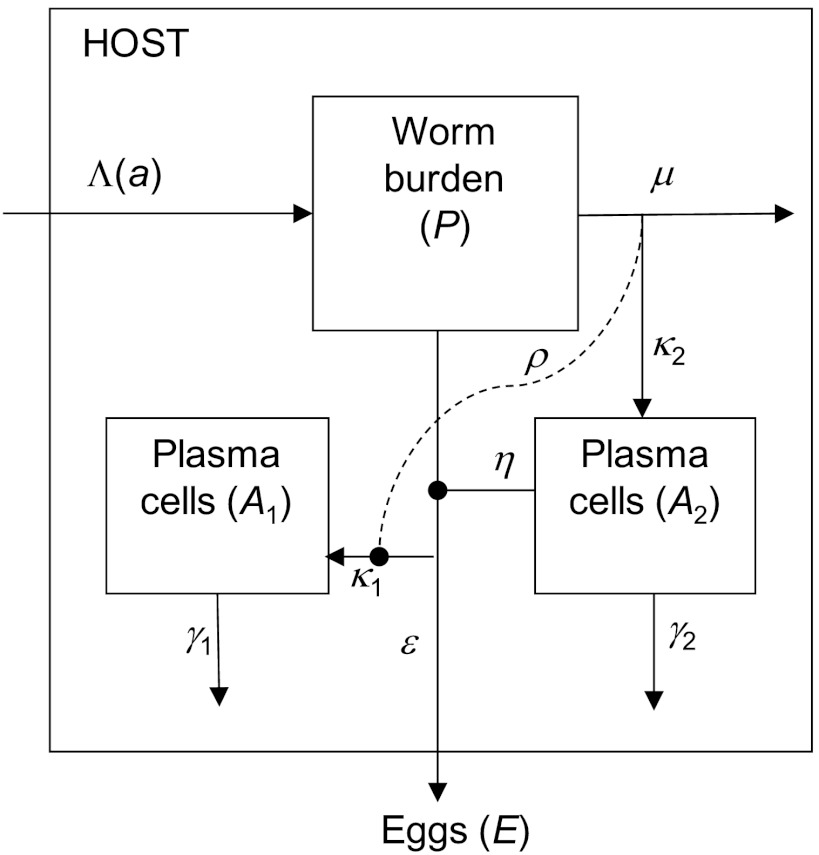
A schematic diagram of the model is shown in Fig. 4. Water contact, worm acquisition and death, and measured egg output are all modeled as stochastic processes, while antibody development and immune stimulation by egg antigens are modeled deterministically. In line with field observations (43), an individual’s contact rate (Λ(a)) is assumed to increase linearly with age up to age a_c and then remains constant at Λ_m. Λ_m varies between individuals and is drawn from a gamma distribution with a mean equal to the population average and shape parameter k₁. To allow for changes in contact rate due to moving house or school, this individual contact rate is reselected with a yearly probability ϕ. Daily contacts are Poisson distributed around Λ(a). It is assumed that d cercariae are acquired with a probability 1/d per contact. New cercariae may be killed upon entry into the host by an anti-reinfection antibody response; otherwise they become worms and pass through nine worm compartments to give approximately Gaussian distributed survival. The number of eggs within the host (E) is assumed to be proportional to current worm burden but reduced by anti-fecundity antibody. Measured egg output is calculated as the arithmetic mean of three separate “samples” (as is collected in the field), each drawn from a negative binomial distribution with mean εE(a) (where ε is the mean number of eggs output in 10 mL urine per worm per day) and aggregation parameter k_E. Two antibody responses (A₁ and A₂) are modeled as separate populations of plasma cells, each having a single life stage as its principal source of antigen: cercariae, live worms, dying worms, or (within-host) eggs. Each plasma cell population expands at a rate proportional to the level of antigen stimulating that response and decays exponentially. In models with cross-regulation, the growth rate of the nonprotective antibody response, A₁, is reduced as a function of the level of antigen stimulating the protective antibody response. For models with an antigen threshold, a cumulative tally of exposure to antigen is kept, and protective antibody (A₂) is only made if cumulative antigen exposure exceeds a threshold level. The model equations and a detailed description of the model are given in SI Text.

Fig. 4.

Schematic diagram of the model. This shows the main state variables, worm burden (P), and two populations of plasma cells (A₁ and A₂), with production of eggs (E). A single worm compartment is shown for clarity. Cross-regulation of the nonprotective response (of strength ρ) is shown by the dashed line.

For each population, separate simulations were run for 161 individuals, updated at daily steps, with infection and antibody levels recorded at a single age for each individual to give simulated cross-sectional data sets for comparison with field data (14).

The impact of treatment is assessed in the model by introducing a single round of praziquantel treatment (assumed to be at the WHO-recommended dose of 40 mg/kg body weight) for all individuals aged 6–15 years old. The effects of treatment are assumed to be (i) a decline in worm burden, (ii) a boost to the level of dying worm antigen (proportional to the number of worms killed by treatment), and (iii) a reduction in transmission after treatment, modeled as a reduction in the probability of infection per contact on all subsequent days.

Model Criteria.

Criteria were drawn up to test whether models could reproduce robust patterns of S. haematobium infection and antibody seen in field data. The following cross-sectional patterns were characterized: infection prevalence (by age), the peaked age intensity curve, reduced infection level in adults, the peak shift, aggregation of infection (by age), the antibody switch, and the age at which the antibody switch occurs. Changes in antibody levels after treatment were included in an additional criterion. Antibody aggregation was also assessed but was not included as a formal criterion, because the range of levels obtained from field data was too broad to be informative. The data and methods used to draw up the criteria for the peaked age intensity curve, reduced infection level in adults, the peak shift, the antibody switch, and the age of the antibody switch have been previously described (16). Prevalence and aggregation of S. haematobium infection were calculated from data from six Zimbabwean communities (14, 44, 45) for the whole population and for two age groups (6–14- and 15–34-year-olds) and used to determine ranges for the relevant criteria. Infection aggregation was characterized by the standardized variance, calculated as . For the post-treatment antibody switch, the extent of the switch and the length of time over which the antibody responses remained switched were analyzed using antibody data from treated children (20). The criteria are all listed and defined in Table 1, and the data and methods are described in more detail in SI Text.

Model Analysis.

Simulations were run for each of the successful combinations of antigen and antibody target identified from deterministic analysis (16). In the initial baseline analysis, the parameters governing the stochastic processes were kept constant and the parameters determining mean population infection rate, worm life span, antibody strength, strength of cross-regulation/antigen threshold level, and plasma cell decay rates were each varied across plausible ranges (see SI Text for details). All possible combinations of these parameters were used in turn, giving 4,725 parameter sets for each antigen-target combination. Each simulated cross-sectional dataset was analyzed in the same way as the field data used to draw up the criteria, and the POM approach was used to identify models that could simultaneously meet all of the cross-sectional criteria (more details about POM are given in SI Text). Successful parameter combinations had to meet these criteria over a twofold change in contact rate, because all of these patterns were identified in multiple populations with different levels of infection. Performance curves were drawn for a selection of parameter sets to determine how many replicate simulations were needed to obtain a stable estimate of the proportion of repeat simulations passing all of the criteria. Four-hundred repeat simulations were found to be sufficient. A threshold percentage of simulations passing all criteria was used to define “successful” parameter combinations; this threshold was set at 50%, which was found to provide a good level of discrimination while allowing that the criteria represent typical patterns, not hard-and-fast rules. No parameter combinations were accepted using a higher threshold of 95%.

Parameter sets meeting the cross-sectional criteria were tested for their ability to reproduce the treatment-induced antibody switch in 6–15-year-olds. Univariate sensitivity analysis was carried out on models that were able to reproduce both the cross-sectional and post-treatment patterns, varying each of the parameters governing the stochastic processes in the model in turn. These models were tested for their ability to reproduce both the cross-sectional and post-treatment patterns. Antibody distributions were assessed visually for a subset of the models that passed all of the criteria for qualitative comparison with the field data.