Virtual melting as a new mechanism of stress relaxation under high strain rate loading

Abstract

Generation and motion of dislocations and twinning are the main mechanisms of plastic deformation. A new mechanism of plastic deformation and stress relaxation at high strain rates (10⁹–10¹² s^-1) is proposed, under which virtual melting occurs at temperatures much below the melting temperature. Virtual melting is predicted using a developed, advanced thermodynamic approach and confirmed by large-scale molecular dynamics simulations of shockwave propagation and quasi-isentropic compression in both single and defective crystals. The work and energy of nonhydrostatic stresses at the shock front drastically increase the driving force for melting from the uniaxially compressed solid state, reducing the melting temperature by 80% or 4,000 K. After melting, the relaxation of nonhydrostatic stresses leads to an undercooled and unstable liquid, which recrystallizes in picosecond time scales to a hydrostatically loaded crystal. Characteristic parameters for virtual melting are determined from molecular dynamics simulations of Cu shocked/compressed along the 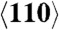and 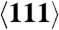directions and Al shocked/compressed along the 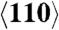direction.

Generation and motion of dislocations, twinning, and crystal–crystal phase transformations are the main mechanisms of plastic deformation and relaxation of nonhydrostatic stresses that are reflected in the deformation-mechanism maps (1, 2). Recent large-scale nonequilibrium molecular dynamics (NEMD) simulations of shockwave propagation in fcc metallic single crystals have revealed that for wave propagation along the 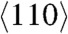and 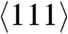directions, melting occurs at temperatures below the equilibrium melt temperature T_m(p) at the corresponding shock pressure p—e.g., for Cu by 20% in ref. 3 and by 7–8% (± 4%) in ref. 4. However, for shockwaves along the 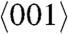direction, superheating is observed. A possible mechanism for the observed melting below T_m(p) has been attributed to solid-state disordering due to high defect densities. Indeed, a small reduction in the melt temperature due to defects has been reported (5). It has also been argued that anomalous plastic flow rather than bulk melt can explain the experimentally observed low melt temperatures of Ta under pressure (6). Here, we propose a new deformation mechanism, under which melting can occur at temperatures much below T_m(p) in materials subjected to high deviatoric stresses (such as those produced under shock loading and isentropic deformation) and compete with defect nucleation mechanisms, as will be shown here in the case of metals. We have developed a thermomechanical theory of melting under uniaxial deformation that predicts extremely large driving forces. The thermodynamic driving force for melting is due to the energy and work of nonhydrostatic stresses. The theory is quite general and not material-specific, and it is most applicable at deformation rates sufficiently high, where melting may proceed at rates faster than traditional mechanisms of plasticity. As a proof of concept, we have systematically studied melting under high strain rates in two fcc metals, Cu and Al, employing molecular dynamics (MD) methods that simulate quasi-isentropic and shockwave loading conditions. These simulations confirm for the first time that melting can occur at temperatures much below (by 80% or 4,000 K) T_m(p). After melting, the nonhydrostatic stresses relax, leading to an undercooled and unstable liquid, which for the metals studied here recrystallizes in ps time scales. Because the conditions for melting (nonhydrostatic stresses) disappear upon melting, and because of the short time scale involved, we have termed this new deformation mechanism virtual melting (VM). Because fcc metals can be easily deformed by traditional dislocation and twinning mechanisms, the strain rates at which VM is observed and confirmed via our MD simulations of Cu and Al crystals are necessarily high (approximately 10⁹–10¹² s^-1) and represent an upper bound in the regime of strain rates to study and confirm our thermodynamic predictions. For materials with suppressed plasticity (such as Si, Ge, high-strength materials, alloys, or complex organic molecules), VM may very well be observed at much lower strain rates. Because the thermodynamic VM formalism is quite general, in what follows we will primarily discuss our results for Cu and Al shocked or quasi-isentropically compressed along the 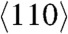direction and Cu shocked or quasi-isentropically compressed along the 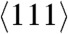direction. Simulation details are provided in SI Appendix. We find that the reduction of the melt temperature correlates with the magnitude of the nonhydrostatic (shear) stress at the shock front, which is consistent with thermodynamics.

Results and Discussion

Development of Thermodynamics of Melting Under Nonhydrostatic Conditions (see details in SI Appendix).

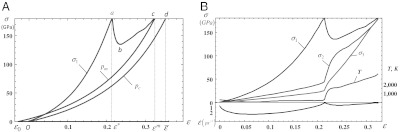
Fig. 1A shows, by way of example, the stress σ₁-uniaxial strain curve for a Cu single crystal loaded in the 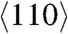direction. The data was obtained from quasi-isentropic MD simulations employing a well-tested embedded atom method (EAM) potential for Cu (7). Because in a planar shock, the two lateral strains are zero, the uniaxial strain ε = l/l₀ - 1 is equal to the volumetric strain, where l₀ and l are the initial and the current lengths of the sample, respectively. Melting starts at strain ε = ε^∗ and stress 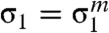, and it ends at strain ε = ε^m and at the same stress σ₁. Because the transformation proceeds under a variable stress tensor, classical thermodynamic approaches based on thermodynamic potential differences and thermodynamic equilibrium across an interface (8–10) are not applicable. In fact, the reduction of the thermodynamic melt temperature of the stress-free solid, T_m(0), caused by deviatoric stresses was estimated to be just 1 K (8, 10), which is why it was not considered as a possible reason for the reduction in T_m(0) in shockwaves. We here will consider a homogeneous transformation process in a finite volume, expanding on our advanced thermodynamic approach to crystal–crystal transformations (11, 12). Because melting is assumed to be the only dissipative process, the thermodynamic driving force per unit unloaded volume for the melting is equal to the total dissipation, as follows

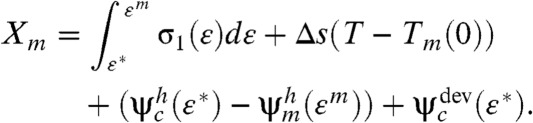[1]

Here, ψ^h and ψ^dev are the elastic energy of hydrostatic and deviatoric stresses (strains), Δs is the jump in entropy, T is the temperature at which the melting starts at ε = ε^∗, and subscripts c and m refer to crystalline and molten states, respectively. An increase in temperature during the deformation increases X_m and can be taken into account through an effective temperature (11). For simplicity, we neglect it and underestimate X_m. Let p_c(ε) and p_m(ε) be the pressure-volumetric strain equation of state of the crystalline and molten phases, respectively (Fig. 1A), with ε_c(p) and ε_m(p) being their inverse equations. The equation of state for the melt starts at point (ε = ε₀; σ₁ = 0), where ε₀ < 0 is the volumetric transformation strain at melting at pressure p = 0. After some manipulations, the condition X_m = 0 provides the equilibrium melt temperature under uniaxial straining :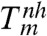

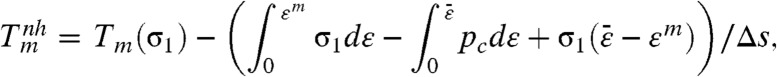[2]

where 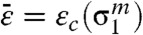and 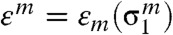(Fig. 1A). Geometrically, the magnitude of the negative mechanical part of the driving force for melting under hydrostatic conditions is equal to the area {Oε₀cd} between the equation of state for melt and crystal. This area characterizes the increase in the melt temperature under hydrostatic loading from T_m(0) = 1,357 K to 5,087 K (at 179.1 GPa) (see Table S1 in SI Appendix). The difference between the areas under the stress-strain curve σ₁(ε) {Oabcd} and {Od}, which represents the equation of state p_c(ε) for the single crystal, provides an additional driving force for melting due to non-hydrostatic loading (the term in parentheses in Eq. 2). This difference is almost three times larger than the area {Oε₀cd} and produces close to a threefold reduction in T_m(p) when compared with the increase associated with the hydrostatic pressure. All parameters for Cu and Al melting obtained from NEMD simulations of shock loading along the direction and for Cu along the 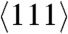direction can be found in Table S1 in SI Appendix.

Fig. 1.

(A) Stress-uniaxial strain curve of a Cu crystal until melting (σ₁, the same as in B) and equations of state of molten (p_m) and crystalline (p_c) phases. Area between curves {Oabcd} and {Od} is the additional driving force for melting due to nonhydrostatic loading. (B) Variation of normal stresses σ_i, temperature, and prescribed strain rate vs. uniaxial strain obtained using MD simulations for 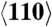shock loading of Cu.

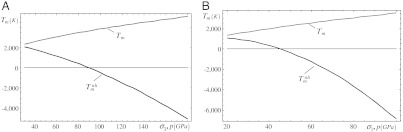
In Fig. 1B, melting commences at a peak stress σ^m = 179.1 GPa, corresponding to ε^∗ = 0.214, and ends at the same stress σ₁ = 179.1 GPa but at ε^m = 0.324. For this case, the reduction in the thermodynamic melt temperature calculated with the help of Eq. 2 is enormous (Fig. 2A): ΔT_m = 10074 K—i.e., from T_m(179.1) = 5,087 K to 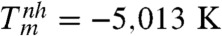. Reductions of similar orders of magnitude were found for Al, and for other loading directions (Fig. 2B and Table S1 in SI Appendix). It should be noted that a negative 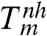does not imply the existence of a negative temperature: At this temperature the calculated thermodynamic driving force for melting due to nonhydrostatic stresses is zero. In order for melting to proceed within ps time scales, some overheating—which cannot be estimated using thermodynamics—is necessary. Furthermore, MD simulations (see below) have shown that melting can occur at least at 0.2T_m(p). The calculated reduction in the melt temperature ΔT_m vs. strain ε^∗ and corresponding stress σ₁(ε^∗) can be approximated by 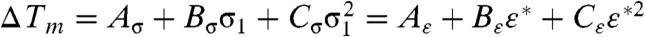. All constants for Cu and Al are listed in Table S3 in SI Appendix.

Fig. 2.

Calculated melting temperature under hydrostatic T_m and nonhydrostatic 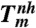conditions vs. pressure (uniaxial load) for shock loading of Cu (A) and Al (B) along the 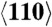direction.

MD Simulations.

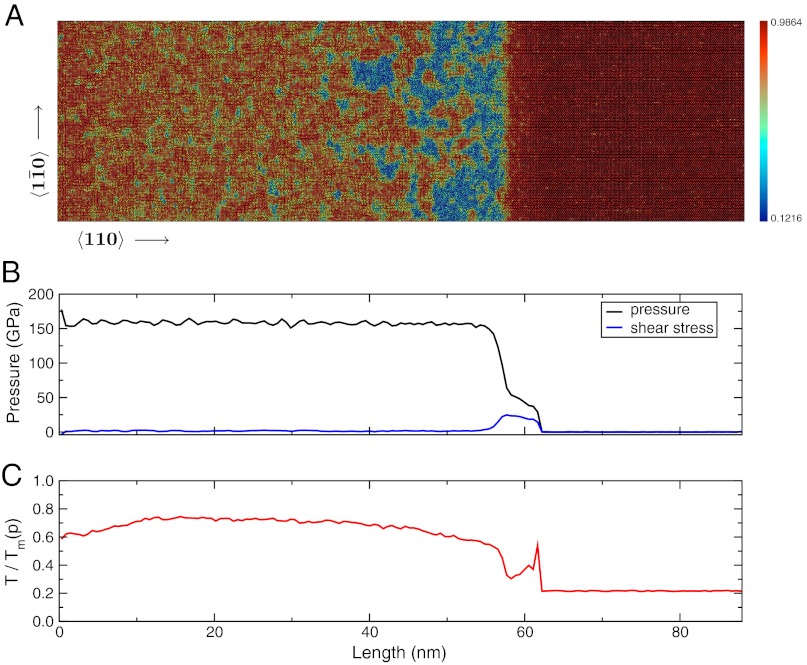
Fig. 3A shows a thin slice (about 20-Å thick) of the atomic configuration from an NEMD simulation of Cu shocked along the 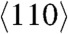direction to a pressure of 160 GPa (see also Movie S1). Liquid and solid atoms were identified with a local order parameter q₆, which measures the symmetry correlation of an atom with its neighbors (13, 14). Solid atoms (red) are well correlated with their neighbors, while liquid atoms (blue) are not. The material at the shock front melts at a temperature T ≃ 0.3T_m(p) at the corresponding pressure along the profile (Fig. 3 A–C) and recrystallizes behind the shock front at T ≃ 0.8T_m(p) and at a rate that increases with increase in T_m(p) - T. This is consistent with the behavior of an over-cooled liquid rather than amorphous solid (see SI Appendix). No evidence of dislocation or extended defects was found.

Fig. 3.

(A) Atomic configuration of Cu slab shocked to a pressure of 160 GPa (red atoms are solid, blue are liquid); (B and C) pressure and temperature profiles, respectively, along the shock direction. The temperature is normalized by the equilibrium melt temperature T_m(p) at the corresponding shock pressure along the profile.

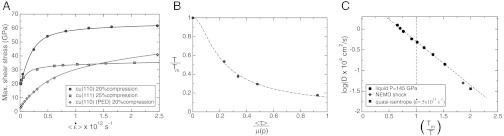
Fig. 4A shows the shear stress τ = 1/2(σ₁ - 1/2(σ₂ + σ₃)) as a function of strain rate for Cu compressed quasi-isentropically. The shear stress at 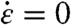corresponds to the elastic limit, which is characteristically high for defect-free crystals. The elastic limit can be lowered by introducing pre-existing dislocations (PED) (15). Data shown are for samples with defect densities approximately 10¹² cm^-2. Fig. 4B clearly shows a strong reduction in the melt temperature (even by 4,000 K) for quasi-isentropic compression with increasing shear stress. The final strain was fixed at 0.34, while the strain rate was varied and the temperature was controlled to a value that would yield the same maximum fraction of liquid atoms (25%) for all simulations. In shock compression, where the temperatures are higher, the fraction of pre-melted atoms behind the shock is significantly higher than 25% (Fig. 3A).

Fig. 4.

(A) Maximum shear stress vs. average strain rate in Cu defect-free and with pre-existing defects (PED), quasi-isentropically and uniaxially compressed to 0.20 and 0.25 along the 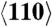and 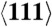directions. The PED crystal is nominally oriented along the 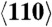direction. (B) Melting temperature (normalized by T_m(160) = 4816 K) vs. average shear stress (normalized by the shear modulus at p = 160 GPa) for defective Cu quasi-isentropically compressed to a final strain of 0.34 at different strain rates. (C) Diffusion coefficient of liquid Cu at a pressure of 145 GPa (circles) evaluated from the atomic mean-squared displacements. Also shown is the diffusion coefficient associated with a region behind the shock front for Cu shocked along 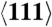to a pressure of 145 GPa (diamond) as well as Cu isentropically compressed along 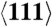to the same pressure at a strain rate of 5 × 10¹¹ s^-1 (square). The dashed line is a fit to the liquid data, extrapolated to lower temperatures.

Solid-state disordering has been proposed as the main mechanism of pre-melting in shock along the 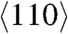and 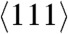orientations in Cu single crystals (4). In order to distinguish between a hot, amorphous solid or a supercooled liquid, the self-diffusion coefficient of the liquid region behind the shock front was computed from the mean-squared displacement. Fig. 4C shows the diffusion coefficient as a function of temperature at a pressure of 145 GPa for the liquid state of the EAM model Cu used in this work. Also shown is the diffusion coefficient of a region behind the shock front in a Cu slab shocked along the 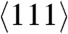direction to the same pressure. Because all points belong to the same Arrhenius line, these results confirmed that the region behind the shock front is a supercooled liquid rather than an amorphous solid. Note that VM was observed for isothermal 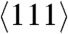loading of Cu even at 300 K (Table S1 in SI Appendix)—i.e., at T ≃ 0.055T_m(p). However, recrystallization is so fast that the diffusion coefficient could not be determined.

Conclusions

At high strain rates (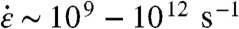 in metals) and high shear stresses, VM can compete with traditional defect nucleation mechanisms and therefore should be incorporated in the deformation-mechanism maps (1, 2). This prediction is based on a new thermomechanical theory of melting under uniaxial straining that is quite general and that can be applied to any material subjected to strain rates sufficiently large in order to allow melting to proceed faster than traditional mechanisms of plasticity. Virtual melting has been confirmed for the first time by MD simulations for the most critical case of fcc metals. For materials with suppressed plasticity, VM may be observed at lower strain rates and stresses than the ones sampled here [e.g., in a recent MD study (16) deformation of organic α-HMX crystal is shown to occur through generation and motion of dislocations for shock strengths up to 14 GPa and via formation of amorphous shear nanobands at higher pressure, which may be related to VM]. Our thermodynamic approach can be extended for amorphization and sublimation as well as for arbitrary 3D loading, in particular for pressure and shear experiments. The concept of the VM was introduced in refs. (17–20) as an intermediate step in crystal–crystal, crystal–amorphous, and crystal–gas transformations. Here, however, VM was for the first time directly observed in MD simulations of plastic straining. The driving force for VM in phase transformations in refs. (17–20) is due to the relaxation of the deviatoric stresses and also disappears upon melting, as in the case of VM here. This suggests that our results here indirectly support the plausibility of VM in phase transformation as well. Finally, while the sampled compression rates in our simulations of Cu and Al were necessarily high, they are close to what can be achieved in laser-driven shock experiments (21). However, due to the short time scales additional efforts are required for experimental verification of VM, particularly in metals. Such regimes are also relevant for nuclear explosion and meteorite impact as well as for planned experiments in large laser facilities such as the National Ignition Facilities at the Lawrence Livermore National Laboratory in the United States and the Laboratoire pour l’Utilisation des Lasers Intenses in France.

Materials and Methods

We have performed multimillion atom NEMD simulations of shockwave compression as well as smaller, Hugoniostat-method (22) and MD simulations of quasi-isentropic compression (15). The NEMD simulations comprised up to 12 million atoms arranged in a rectangular slab with periodic boundary conditions in the transverse directions. The procedure used to initiate a shockwave of a given strength is detailed in ref. 23. The systems studied were Cu and Al single crystals as well as Cu crystals with pre-existing defects. A detailed description of the MD simulations and methods is available in SI Appendix.