Abstract
Based upon an extensive single-channel data set, a Markov model for types I and II inositol trisphosphate receptors (IP3R) is developed. The model aims to represent accurately the kinetics of both receptor types of IP3R depending on the concentrations of inositol trisphosphate (IP3), adenosine trisphosphate (ATP), and intracellular calcium (Ca2+). In particular, the model takes into account that for some combinations of ligands the IP3R switches between extended periods of inactivity alternating with intervals of bursting activity (mode changes). In a first step, the inactive and active modes are modeled separately. It is found that, within modes, both receptor types are ligand-independent. In a second step, the submodels are connected by transition rates. Ligand-dependent regulation of the channel activity is achieved by modulating these transitions between active and inactive modes. As a result, a compact representation of the IP3R is obtained that accurately captures stochastic single-channel dynamics including mode changes in a model with six states and 10 rate constants, only two of which are ligand-dependent.
Introduction
The inositol trisphosphate receptor (IP3R) is an ion channel that releases calcium (Ca2+) from intracellular stores upon activation by inositol trisphosphate (IP3). This is essential for initiating and sustaining calcium oscillations in the cytosol, a most important signaling system that is responsible for various cell functions. Recently, it has been shown by Ionescu et al. (1) that the inositol trisphosphate receptor exhibits mode changes: rather than continuously adjusting its activity, the average open probability jumps between different activity levels even when ligand concentrations are kept constant. To the best of our knowledge, mode changes have been analyzed only qualitatively, and no quantitative model based on experimental data is yet available.
Only kinetic models that accurately represent the stochastic behavior of single IP3R channels depending on various ligands such as inositol trisphosphate, adenosine trisphosphate (ATP), and cytosolic calcium allow investigation of spatiotemporal phenomena such as the spatial transmission of calcium signals within and between cells by calcium waves. If IP3Rs are mainly regulated by mode switching, as suggested by Ionescu et al. (1), the initiation of waves by stochastic local calcium release from a single or a few IP3Rs may be possible at relatively low average open probabilities: In fact, as can be seen in the sample data set shown in Fig. 1 a, even when PO is as low as half of its maximum, the channel can exhibit high levels of activity for extended periods of time. Calcium released during such bursting events may be enough to trigger activation of neighboring IP3Rs due to the local elevation of calcium concentration, which in turn may initiate a calcium wave. Questions like this, which depend on a quantitatively accurate representation of the stochastic spatiotemporal dynamics of a cluster of IP3Rs, cannot be answered by simple qualitative interpretation of single-channel data—a quantitative model is required.
Figure 1.
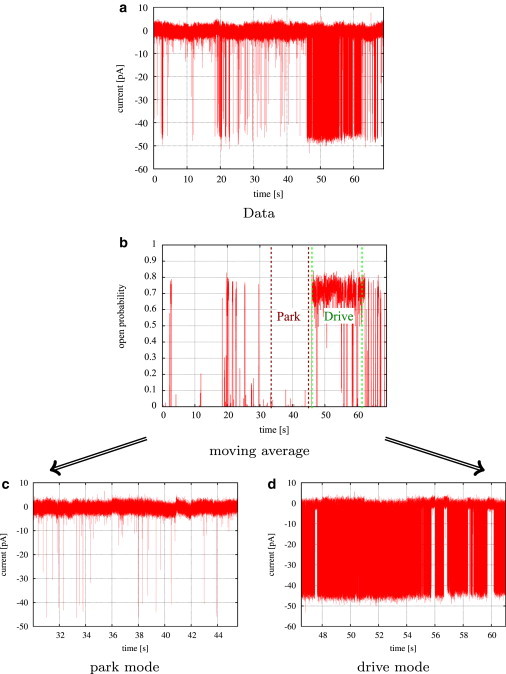
Identifying segments of similar activity by moving averages. (a) Data set collected from type II IP3R at 10 μM IP3, 5 mM ATP, and 50 nM Ca2+. (b) Approximation of average open probabilities by moving averages reveals two levels of activity. (c and d) Kinetics of characteristic segments of low activity (c) and high activity (d) were studied in more detail by Markov models.
A general difficulty of representing mode switching in a quantitative model is that even in data collected over an extended period of time, only few mode changes may occur. Thus, direct fitting of raw single-channel data is unlikely to capture the instantaneous transitions between different levels of activity. For this reason, in previous studies modes were modeled separately (2). Although this leads to accurate models of the kinetics within modes, representing the dynamics of mode switching requires an appropriate combination of these models.
In this work, we aim to represent IP3R kinetics including mode changes in a continuous-time Markov chain model. Similar to Gin et al. (2), we derive our model by statistical analysis of an extensive single-channel data set (3). Our study is—to the best of our knowledge—the first attempt to model ligand-dependent regulation of both type I and type II IP3Rs by IP3, ATP, and Ca2+. To overcome the difficulties mentioned above with including mode changes in a quantitative model we follow a hierarchical approach. In the first step, we study average channel activity estimated by moving averages. It is found that the channel jumps between low activity, characterized by an average probability close to zero, and high activity, with an open probability of ∼70%. These two levels of activity can be observed in data sets collected at various ligand concentrations and in both type I and type II IP3Rs.
While Ionescu et al. (1) saw ligand-independent levels of activity, we also fit segments, exhibiting high and low channel activity, to Markov models using an improved version of the algorithm published recently by Siekmann et al. (4) (see Section 1.4 in the Supporting Material). This method is based upon Markov chain Monte Carlo (MCMC), an approach that calculates probability distributions for all model parameters rather than, for example, the maximum-likelihood estimators (MLEs) that are common in more traditional algorithms (5–7). Thus, it can be assessed more confidently how well a model captures the experimental data; in particular, over-parameterized models are detected more easily (I. Siekmann, E. J. Crampin, and J. Sneyd, unpublished). The results obtained at this stage are very similar across all ligand concentrations, which indicates that the two levels of activity have ligand-independent kinetics.
Average open probability is a relatively coarse description of a data set that gives a rough idea of the average channel activity. A medium average open probability can emerge due to long open and closed intervals of similar length or to frequent short openings and closings, i.e., data sets with the same average level of activity may have very different kinetics. Therefore, we propose a more constrained definition of modes of an ion channel: A mode must exhibit not only the same average open probability but also the same kinetic behavior, at least approximately. According to this definition we have found two different modes. In analogy to the automatic gear change found in cars, we will refer to these modes more suggestively as park (inactive) and drive (highly active) modes.
Finally, the transitions between the modes are investigated: The kinetic models for park and drive modes are connected with transition rates that account for mode switching. Although the mode-specific submodels were inferred from segments, complete traces collected at certain ligand concentrations are used to fit the two additional rates. Thus, we obtain a model for modal gating where a ligand-dependent mode change (transition rates) switches between the ligand-independent park and drive modes. It is expected that the simple approach described here can be successfully applied to other ion channels exhibiting mode changes.
Methods
Experiments
Single IP3R potassium currents were measured in the on-nucleus patch-clamp configuration using PClamp 9 and an Axopatch 200B amplifier (Molecular Devices, Sunnydale, California). Pipette solution contained 140 mM KCl and 10 mM HEPES, with varying concentrations of IP3, ATP, BAPTA, and free Ca2+. Free-calcium concentrations were calculated using Max Chelator freeware and verified fluorometrically. Traces were consecutive 3-s sweeps recorded at −100 mV, sampled at 20 kHz, and filtered at 5 kHz. A minimum of 15 s of recordings was considered for data analyses. Pipette resistances were typically 20 MOhm and seal resistances were >5 GΩ. Details can be found in Wagner and Yule (3).
Segmentation
In this first step of our analysis, different levels of activity (quantified by different levels of average open probability, PO, calculated for a segment of an experimental trace) were identified in data sets collected at different ligand concentrations. At each data point i, an estimate of the average open probability, , was obtained by a moving average with a given window size of w data points (see Eq. A1 in the Supporting Material). Varying the window w over a wide range from 200 to 1000 data points did not change the activity levels that were found. Results for selected type II IP3R data sets are shown in Fig. S1. For the two different levels of PO (low activity, close to zero; high activity, ∼70%) that were found, representative segments were selected for further analysis. The process of selecting segments based upon the level of channel activity is shown in Fig. 1.
At this stage, no attempt is made for optimizing the localization of the change points; the main aim is to identify the activity levels present in the traces.
Submodels for modes
In this second step, representative data segments for high and low levels of activity were analyzed in more detail. Kinetics characteristic of a certain level of activity were investigated by Markov models. Segments representative for each of the distinct average open probabilities, PO, were fitted to Markov models with different numbers of open and closed states.
Starting from a model with one open and one closed state (Fig. 2 a), the number of states was extended until the likelihood of a more complex model was not improved in comparison to models with fewer states (Fig. 2, b–d). Also, if stationary probabilities of additional states were very low, this was taken as evidence that a model with fewer states was sufficient.
Figure 2.
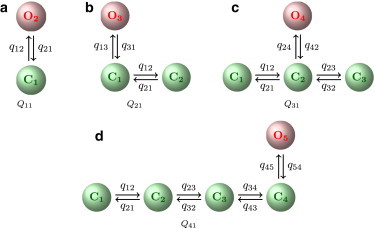
Models used for representing park- and drive-mode kinetics.
Examples for results are shown in Section 2 of the Supporting Material. For both type I and type II IP3Rs, the best model for the nearly inactive park mode had one open and one closed state (Fig. 2 a), whereas the best representation for the active drive mode was a model with one open and three closed states (Fig. 2 c). To determine whether the kinetics depends on ligands, models obtained for segments showing the same average open probability, PO, but taken from data sets collected at different ligand concentrations were compared (see Section 2.3 of the Supporting Material and Fig. S4).
All fits were performed using an improved version of the Markov chain Monte Carlo algorithm by Siekmann et al. (4). Thus, the results of these fits are not point estimates but a set of samples for each of the rate constants. These samples represent the probability distribution of the parameters, the so-called posterior distribution, which can be visualized by histograms (Fig. S2 and Fig. S3). By the posterior distribution (a concept from Bayesian statistics; see Siekmann et al. (4)), probabilities are assigned to a range of possible values for the rate constants instead of singling out a best estimate. This approach extracts more information from data and gives a better idea of parameter uncertainty than do traditional approaches like maximum likelihood estimators (MLEs). Nevertheless, statistical quantities like MLEs, mean values, and standard deviations can be calculated from these probability distributions. In Table S2, we have summarized mean values and standard deviations for the rate constants of both modes of both receptor types.
Model for modal gating
In the third step, kinetics of complete experimental traces were modeled. For this purpose, the kinetic models for park and drive modes obtained previously were connected by transition rates. The underlying assumption is that at each point of the experimental trace the IP3R is either in the park or the drive mode, and that an accurate model of the complete trace can be achieved by representing the transitions between these modes. Fig. 3 illustrates in a diagram how submodels for park and drive modes are obtained from segments of data. To determine the transition rates, a complete experimental trace from one representative cell for a given combination of ligands was used for fitting.
Figure 3.
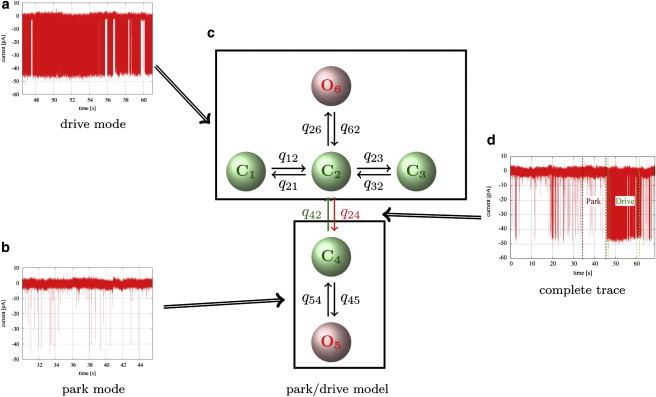
Kinetics of segments characteristic of the drive mode (a) and the park mode (b) were studied by Markov models. By comparing fits of models with different numbers of open and closed states and different topologies to segments from data sets at different ligand concentrations, it was found that the drive mode was best represented by a model with one open and three closed states (c, upper), whereas the best model for the park mode was a simple two-state model with one open and one closed state (c, lower). Interestingly, the rate constants obtained from these fits were very similar across a wide range of ligand concentrations, indicating that the kinetics of the channel within modes is independent of ligand concentration (see Fig. S4). The models for park and drive modes were connected by transition rates that were determined by fits to complete traces (d). The rate constants for the models representing park and drive modes were drawn from the probability distributions calculated from the previous fits. The transition rates q24 and q42 were sampled as described in more detail in the main text. Thus, probability distributions for all rate constants in c were calculated.
Samples for the transition rates were generated by the following algorithm:
-
1.
First, the submodels are initialized with a random sample from the posterior probability distributions for park and drive modes, which have been calculated previously (see Fig. S2 and Fig. S3 for examples of type II IP3R results).
-
2.
The transition rates are sampled using an improved version of the algorithm by Siekmann et al. (4) (see Section 1.4 in the Supporting Material (and I. Siekmann, E. J. Crampin, and J. Sneyd, unpublished)) while the other rates are kept constant. The algorithm is run long enough that convergence is ensured (for the data sets used for this study, usually between 3000 and 5000 iterations).
-
3.
The last values for the transition rates, together with the rates of the two submodels, are chosen as a sample of the probability distribution for the combined model for modal gating (Fig. 3 c).
-
4.
This process is repeated with different rate constants drawn from the probability distributions for park and drive modes until a sufficient number of samples is obtained (we usually generated 200 samples).
Results and Discussion
Mode changes in the IP3R
A data set collected from type II IP3R at 10 μM IP3, and 50 M Ca2+ clearly shows two different levels of activity (Fig. 1 a). Although the channel is mostly closed in the first part of the trace and opens only for short times at about t ≈ 47 s, the receptor seems to switch to a different mode, in which its behavior is characterized by frequent openings, interrupted by only short closed intervals.
This behavior is even more obvious if we take a look at the time series of estimated average open probabilities, (see Fig. S1 b). Initially, the estimated average open probability is nearly constantly zero, until it jumps to ∼70% at t ≈ 47 s. This clear separation of the trace into segments of two different average open probabilities is also exhibited at all other concentrations of cytosolic calcium (Fig. S1). Since the channel switches instantaneously between about zero and ∼70%, its overall activity is determined by the proportion of time that the IP3R opens with high average open probability. At low Ca2+ concentrations, is close to zero most of the time, but even at this low level of activity, quick transitions to PO ≈ 70% can be observed (Fig. S1 a). In contrast, at the two intermediate calcium concentrations, 0.2 μM and 1 μM, the IP3R seems to remain at PO ≈ 70% for most of the trace. In particular, at 0.2 μM there seem to be no transitions to the low level of PO (see Fig. S1, c and d). At higher Ca2+ concentrations, the channel switches frequently between both levels of PO (Fig. S1, e and f).
These results are similar for both IP3R types and across all combinations of ligand concentrations. This shows that the overall activity of the IP3R is regulated by the proportion of time the average open probability is at 70%.
Kinetics within segments
After segments characterized by high or low average open probability were identified, the channel kinetics within these segments was studied in more detail. Representative segments chosen from data sets obtained at different ligand concentrations were fitted to Markov models. For segments showing high channel activity, the best fit was obtained by a model with one open and three closed states (Fig. 2 c), whereas data showing low activity were represented best by a two-state model consisting of one open and one closed state (Fig. 2 a). These models were selected by starting with the simplest model, Q11 (Fig. 2 a), to which open and closed states were added. For segments with low activity, adding either open or closed states did not improve the likelihood.
Adding a second open state when fitting the data showing high activity always led to a very low stationary probability for this state; therefore, only models with one open state were considered. Adding up to three more closed states improved the likelihood, but adding a fourth closed state again decreased the likelihood (see Table S1).
Comparing the results of these fits for calcium concentrations in the physiological range (0.05 μM, 0.2 μM Ca2+, and 1 μM) suggests that the kinetics for both levels of activity is independent of ligands. Fig. S4 shows that means and standard deviations for all rate constants are very similar, which is also true for the histograms of the rate constants.
For other Ca2+concentrations, results are inconclusive, because the channel changes quickly between the two modes (see Fig. S1, in particular Fig. S1 e). Therefore, the segments that can be used for fitting are too short to lead to reliable results. Thus, as the simplest hypothesis, we assume that the kinetics is ligand-independent for both levels of average open probability. This is consistent with Ionescu et al. (1), who also found that kinetic parameters like average open and closed times were similar across different ligand concentrations. We conclude that the IP3R has two ligand-independent modes, one of which shows low activity (park mode), whereas the other shows a high level of activity (drive mode).
In the Supporting Material, the means of the rate constants for both models for both receptor types are listed in Table S2. As an example, the type II IP3R results are shown in Fig. S2 and Fig. S3.
Modal gating
Now, we aim to combine the submodels for park and drive modes, which appropriately describe data segments with low and high average open probabilities, with a model for complete data sets. This is achieved by linking the submodels for both modes with transition rates (i.e., the rate constants q24 and q42 in Fig. 3 c). It was decided to introduce only one pair of transition rates, because the data often only show a relatively low number of discernible transitions between park and drive modes. It is therefore unlikely that more than two parameters can be fitted. We further assumed that the transition rates should be between either two open or two closed states, because it seems not convincing that the channel has to open or close when it makes a transition to another mode. Since the open state O5 of the park model (Fig. 3 c) has a very low stationary probability, it was decided to place the link between two closed states. Otherwise, all transitions between the modes had to go through O5, which would increase the importance of this state. We considered only the possibility of connecting state C2 with the closed state C4 of the park mode—it is unlikely that the results would be different when connecting C4 to C1 or C3.
When fitting the data to this model, we sometimes observe divergence. According to the algorithm described above (Model for modal gating), new initial values for the rate constants q24 and q42 are chosen every 3000 iterations. Although in most cases the samples for both rates are distributed from 10−3 to 0.5 after just a few iterations, for some initial conditions, the samples quickly increase and it seems that they will not tend toward fixed values. In cases like these, the sample obtained at the end of the respective interval was omitted, because it is not representative for the posterior distribution. A possible reason for this phenomenon is that for some traces there is only a very low number of mode transitions. For type I IP3Rs, at high IP3 and calcium concentrations that led to the highest level of activity (i.e., at 5 mM ATP, 1 μM and 5 μM Ca2+; at 100 μM ATP, 1 μM and 10 μM Ca2+), the results were compromised so much by divergence that no fit for the transition rates could be obtained. For these data sets, the channel seems to remain in drive mode during the whole trace.
After dropping samples that are damaged by divergence, probability distributions are also obtained for the transition rates q24 and q42; one example is given in Fig. 4.
Figure 4.
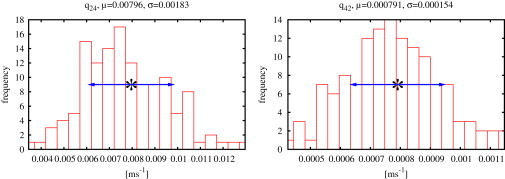
Results for type II IP3R at 10 M IP3, 5 M ATP, and 50 M Ca2+ for the rates q24 and q42 linking the two modes (Fig. 3). These histograms were obtained by a fit to one representative record from one cell for a given combination of ligands. Mean values, μ, and standard deviations, σ, of the probability distributions are shown above the histograms and indicated in the plot by asterisks and arrows.
Means and standard deviations of the fits for both types of the IP3R are shown in Figs. 5 and 6. With these mean values for transition rates and the ligand-independent rate constants (Table S2), a model for modal gating is obtained that can be used, for example, in dynamic models of calcium oscillations.
Figure 5.
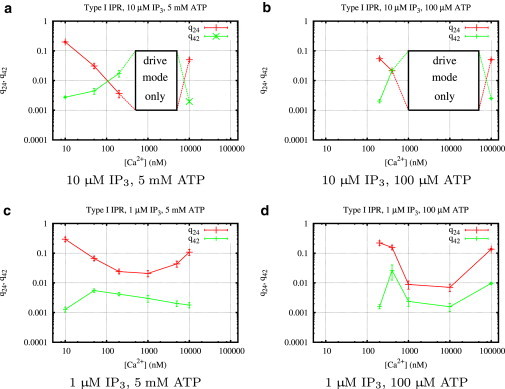
Calcium regulation of the transition rates q24 and q42 (Fig. 3) of type I IP3R for different concentrations of IP3, ATP, and Ca2+. Mean values and standard deviations of the transition rates were calculated from histograms (see Fig. 4 for an example) obtained from fits using the MCMC algorithm described in Section 1.4 of the Supporting Material.
Figure 6.
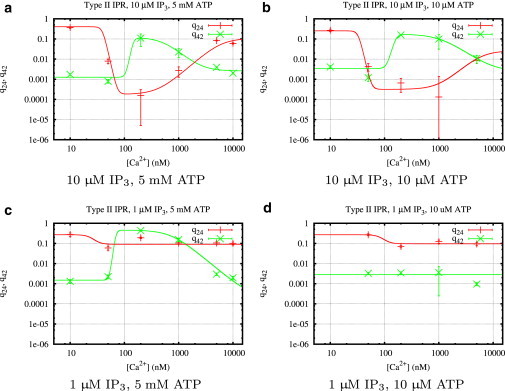
Calcium regulation of the transition rates q24 and q42 (Fig. 3c) of type II IP3R for different concentrations of IP3, ATP, and Ca2+. Mean values and standard deviations of the transition rates were calculated from histograms (see Fig. 4 for an example) obtained from fits using the MCMC algorithm described in Section 1.4 of the Supporting Material.
Statistical analysis of the model
At this point we have finished the construction of our model. It seems clear that the transition rates q24 and q42 are the key parameters for gaining a better understanding of the switching between park and drive modes. It is interesting to note that the average open probability, open and closed times, and expected sojourn times in park and drive modes are given by surprisingly simple functions. Moreover, many quantities depend only on the ratio or just one of the transition rates.
Average open, park, and drive probabilities
The stationary open probability, PO, as well as the probabilities of being in park mode or drive mode, and , depend only on the ratio of the transition rates. By taking advantage of detailed balance (Eq. A3 in the Supporting Material) and using the fact that the vector π of stationary probabilities must sum to one, it is easy to calculate π from the general model shown in Fig. 3. For the probabilities of park and drive modes we obtain
| (1) |
| (2) |
with
| (3) |
H is related to the expected number of transitions between states within park and drive modes; its value is similar for both types of the IP3R (for type I IP3Rs, H ≈ 0.27; for type II IP3Rs, H ≈ 0.22).
The expected open probability, PO, of the IP3R is simply the sum of the open probabilities for park and drive modes, and , weighted by and :
| (4) |
Since and can be calculated from the rates of the park and drive model summarized in Table S2, Eq. 4 depends only on ϕ. Fig. 7 shows PO, , and ; the parameters , , and H were calculated for the type I IP3R results. The parameter H marks a threshold for the relative contributions of both modes: if ϕ is well below H, the channel behavior is characterized by the park mode, whereas for ϕ > H, the drive mode becomes more important. Since H is ∼1/4, the transition rate q42 to the drive mode only has to be four times smaller than q24 for the drive mode to be more dominant.
Figure 7.
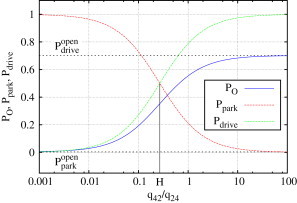
Open probability of the IP3R as a weighted sum of the open probabilities within park and drive modes, and (see Eq. 4). At the turning point, H, both modes contribute equally to the open probability, PO. This plot shows the results for type I IP3R; results for type II IP3R are similar.
Sojourn time distribution in park and drive modes
The expected time that the IP3R spends in park and drive modes can be computed using Laplace transforms, a method that avoids calculation of eigenvalues (9). The expected park and drive times depend only on the rate exiting the mode:
| (5) |
Since the ratio is low for both type I and type II IP3Rs, the expected time for sojourns in park mode is approximately .
Similarly, the expected time for staying in drive mode is
| (6) |
where
| (7) |
For type I IP3Rs, K ≈ 3.73 while for type II IP3R, K ≈ 4.59. The expected sojourn times in park and drive modes are shown in Fig. 8.
Figure 8.
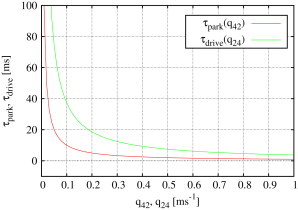
Expected sojourn times for park and drive modes (see Eqs. 5 and 6) depend only on the rate exiting the mode and are proportional to and , respectively. The plot shown here is based upon type I IP3R results; the corresponding graph for type II IP3R is similar.
The fact that both and can be regulated independently by varying the rate exiting park or drive modes shows that the model represents modal gating in a surprisingly simple way.
Expected open and closed times
The open-time distribution again depends on the ratio ϕ. In particular, the expected open times and are completely independent of the transition rates. For both type I and type II IP3Rs, q62 and q54 have very similar values. Thus, the total expected open time is approximately constant across all ligand concentrations (because it is given by an expression similar to Eq. 4).
Finally, the expected closed time, , is the only quantity that explicitly depends on both transition rates:
| (8) |
with
| (9) |
and
| (10) |
Again, all parameters in Eqs. 8−10 can be calculated from the ligand-independent rates summarized in Table S2, so that depends only on q24 and q42. A plot for is shown in Fig. 9.
Figure 9.
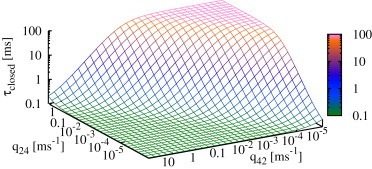
Expected closed time of the IP3R (see Eq. 8) depends on both transition rates, q24 and q42. It clearly shows that reaches a minimum if the tendency to switch to drive is high (low q24, high q42), whereas closed times increase for high q24 and low q42. This plot shows the results for type I IP3R; the type II IP3R results are similar.
In summary, these results show that the IP3R regulates its activity by adjusting the duration of closed times; instead of opening for longer times, open probability is increased by opening more frequently.
Type I IP3R: ATP shifts Ca2+-dependent open probability
Fig. 5 indicates that IP3 and ATP regulate type I IP3R in a complementary way. The ATP concentration seems to determine the range of calcium concentrations in which the channel is optimally activated. In this optimal range, IP3 increases the transition rate, q42, from park to drive mode and decreases the transition rate, q24, from drive to park. Therefore, IP3 mainly influences the shape of q24 and q42 as functions of calcium, whereas ATP shifts these curves along the Ca2+ axis, as previously shown by Mak et al. (10). Comparing the columns of Fig. 4, we see that at 5 mM ATP the optimal Ca2+ range is between 0.5 μM and 5 μM Ca2+, whereas lowering ATP shifts the optimal range to ∼1–10 μM Ca2+.
To see how the transition rates regulate channel behavior, we now turn to our results for the stationary open probability, PO (Fig. 7); according to our above analysis, it is easy to see how the well-known bell-shaped curve for calcium dependence (first observed by Bezprozvanny et al. (11)) is generated. The frequency of being in drive mode and therefore increasing PO gets higher for increasing values of the ratio . The bell-shaped Ca2+ dependency is formed because for all IP3 and ATP concentrations, q24 decreases as the Ca2+ concentration goes from low to intermediate and increases again in the intermediate to high concentration range, whereas q42 behaves in exactly the opposite way. This means that in Fig. 6 we move first from the left to the right along the ϕ axis and then back again. Plots for the Ca2+ dependencies for all ligand concentrations are shown in Fig. 9. At high IP3 (and optimal Ca2+), the park mode is switched off completely. Low IP3 has weaker influence on both rates (Fig. 5, c and d), so that in the optimal Ca2+ range, and .
Type II IP3R: only IP3 can suppress park mode and enhance drive mode
Looking at high IP3 and ATP first (Fig. 6 a), the curves of the transition rates q24 and q42 look similar to the corresponding results for type I IP3R (Fig. 5 a). A comparison of the open probability curves (Figs. 10 b and 11 b) confirms that both types seem to behave identically; at optimal Ca2+ concentrations, an increase of the rate q42 from park to drive and a simultaneous decrease of the rate q24 from drive to park activates the drive mode.
Figure 10.

Type I IP3R: average stationary probabilities in park and drive modes and overall average open probability, PO, depending on IP3, ATP, and Ca2+.
Figure 11.
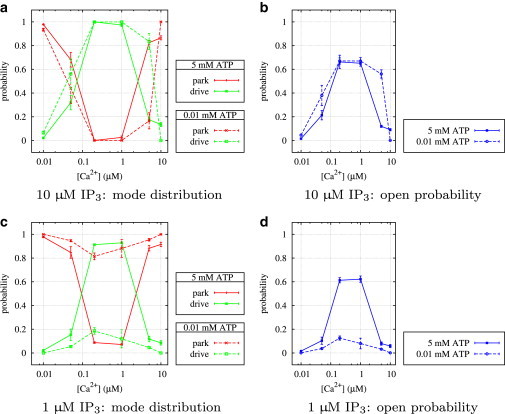
Type II IP3R: average stationary probabilities in park and drive mode, and overall average open probability, PO, depending on IP3, ATP, and Ca2+.
The different behavior of the two receptor types for other ligand combinations is mainly caused by highly different ATP regulation. Decreasing ATP to a concentration of 10 μM (i.e., one magnitude lower than for the parallel type I IP3R experiment) has no visible effect (Fig. 6 b), which indicates that the influence of ATP on the channel is dominated by IP3.
Fig. 6 c shows that ATP at low IP3 concentrations plays a similar role, but with a subtle difference. Although q42 is similar in shape to the corresponding curves at high IP3, the opposite rate q24 remains nearly constant for all Ca2+ concentrations. This suggests that down-regulating the park mode and up-regulating the drive mode are two independent mechanisms. Whereas ATP alone can only facilitate transitions to the drive mode, IP3 is able to both up-regulate the drive mode and down-regulate the park mode without requiring ATP. The open probability is only insignificantly lower than for high IP3 (Fig. 11 b and d); Fig. 11 c further shows that at optimal Ca2+ concentrations, the channel is seldom in park mode. Finally, at low ATP and IP3 (Fig. 6 d), the type II IP3R is essentially deactivated (Fig. 11 d).
Comparison of the IP3 type I and type II receptors
In summary, type I IP3R and type II IP3R are not very different as far as kinetics within park or drive mode are concerned; rather, they differ in how the transitions between park and drive modes are regulated.
In type I IP3Rs, IP3 and ATP play independent roles—whereas ATP determines the Ca2+ range in which the type I IP3R is optimally activated, the IP3 concentration defines how strong this activation is. In the type II IP3R, instead of shifting the optimal Ca2+ range, ATP facilitates activation of the channel by IP3.
Conclusion
A model for type I and type II IP3Rs that takes into account mode changes was constructed based upon an extensive set of experimental data. A recently developed statistical method (4) allows direct fitting of single-channel data to Markov models.
In contrast to most of the earlier models for IP3R channels (reviewed by Sneyd and Falcke (12), but see Gin et al. (2), which follows a similar approach), the states and the connections between them are not related to an underlying reaction scheme. Taking into account the binding and unbinding of different ligands (as, for example, in the classical de Young-Keizer model (13)) requires a large number of states and rate constants. Ion-channel data sets are time series of only two types of events (open and closed) that are unlikely to contain enough information to reliably fix these parameters, as observed previously by Sneyd et al. (14).
Theoretical studies of aggregated Markov models (i.e., models where several states represent open and closed events) further indicate that information on the model topology is lost because single-channel data only provide time series of openings and closings (15–17)—usually the data can constrain models only up to a class of equivalent models. This raises the question of how effectively biochemical processes can be encoded in the structure of aggregated Markov models. In conclusion, the authors believe that assuming mass-action kinetics is not sufficient for investigating underlying biochemical processes. Such investigations can be achieved more suitably by taking into account much more physical detail, as in models based on molecular dynamics.
The main assumption of our model is that modes and mode switching can be modeled in two steps. This crucial idea allows us to incorporate transitions between the two modes present in our data, although sometimes only a few mode switches occurred in an experimental trace. In this way, an accurate representation of single-channel kinetics including modal gating could be achieved by a compact Markov model consisting of only six states, eight ligand-independent rate constants, and two rates depending on IP3, ATP, and cytosolic Ca2+.
The small number of parameters makes this model particularly suitable to be used in dynamical models for Ca2+ oscillations. Since this model was obtained from steady-state data, it is a priori only valid if ligand concentrations change at a slower timescale than the transitions in the model, giving the model sufficient time to reach equilibrium after a ligand change. In a deterministic calcium model, the Markov model can be interpreted as a linear system of deterministic ordinary differential equations. The calcium-dependent transition rates for different combinations of IP3 and ATP can be obtained by interpolating the values shown in Figs. 5 and 6, and values for the ligand-independent rates are given in Table S2. Further studies will be required to investigate whether the IP3R model presented here will generate calcium oscillations by fast activation at low calcium and slow inhibition at high calcium concentrations, as in some earlier models. As mentioned in the Introduction, an interesting application of the full stochastic model could be the initiation of calcium waves by calcium puffs.
A particular strength of the modeling method used here is that MCMC calculates not just single values for each rate constant in the model but a set of samples that represent probability distributions. Probability distributions contain important information such as correlations between rate constants that cannot be obtained by most other approaches. We have no indications that correlations between parameters play an important role in the model presented here. For example, the standard deviations for PO, , and shown in Figs. 10 and 11 would be expected to increase if the covariance between rate constants was large. We have also examined cross-correlations between selected pairs of rate constants (results not shown) that further support the idea that rate constants are not strongly correlated. This suggests that the mean values provided for all rate constants are good representations of the underlying probability distributions. Nevertheless, it is possible to use the full probability distributions calculated with MCMC instead of reducing them to mean values if a particular application of the model depends crucially on possible interactions between the model parameters.
A tempting biological interpretation of the model presented here is to identify park and drive modes with two different conformations of the channel. Indeed, our model is structurally similar to the classical Monod-Wyman-Changeux model (18) for conformational changes. Monod et al. (18) considered two submodels (chains of four states) representing the kinetics of two different conformations that were connected by transition rates. Although the behavior within a conformational state in the Monod-Wyman-Changeux model is modified by ligand binding, transitions to the other conformational state are ligand-independent. In contrast, our model proposes ligand-independent kinetics for both park and drive modes, with the ligand-dependent transition rates determining in which of the two conformations the channel is found more often. Consistent with the idea of a conformational change, average sojourns in park and drive modes are on a longer timescale than open and closed times (due to the small values of the transition rates). It is also interesting to note that type I IP3R and type II IP3R differ mainly in modal gating, whereas park and drive modes of both receptor types are very similar, as can be seen by comparing the respective values in Table S2. It remains to be confirmed experimentally whether park and drive modes indeed correspond to structurally different states of the IP3R or if they result from another regulatory mechanism.
Acknowledgments
We thank Colin Fox for helpful suggestions on how to combine the models for park and drive modes. The very constructive comments from editor Ian Parker and two anonymous reviewers are gratefully acknowledged.
This work was supported by the National Institutes of Health Grant R01-DE19245.
Supporting Material
References
- 1.Ionescu L., White C., Mak D.O. Mode switching is the major mechanism of ligand regulation of InsP3 receptor calcium release channels. J. Gen. Physiol. 2007;130:631–645. doi: 10.1085/jgp.200709859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Gin E., Falcke M., Sneyd J. A kinetic model of the inositol trisphosphate receptor based on single-channel data. Biophys. J. 2009;96:4053–4062. doi: 10.1016/j.bpj.2008.12.3964. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Wagner, L. E., and D. I. Yule. 2012. Differential regulation of the InsP3 receptor type-1 and -2 single channel properties by InsP3, Ca2+ and ATP. J. Physiol.http://jp.physoc.org/content/early/2012/04/30/jphysiol.2012.228320.abstract. [DOI] [PMC free article] [PubMed]
- 4.Siekmann I., Wagner L.E., 2nd, Sneyd J. MCMC estimation of Markov models for ion channels. Biophys. J. 2011;100:1919–1929. doi: 10.1016/j.bpj.2011.02.059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Qin F., Auerbach A., Sachs F. Maximum likelihood estimation of aggregated Markov processes. Proc. Biol. Sci. 1997;264:375–383. doi: 10.1098/rspb.1997.0054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Qin F., Auerbach A., Sachs F. Idealization of single-channel currents using the segmental K-means method. Biophys. J. 1996;70:MP432. [Google Scholar]
- 7.Colquhoun D., Hawkes A.G., Srodzinski K. Joint distributions of apparent open and shut times of single-ion channels and maximum likelihood fitting of mechanisms. Philos. Trans. R. Soc. Lond. A. 1996;354:2555–2590. [Google Scholar]
- 8.Reference deleted in proof.
- 9.Colquhoun D., Hawkes A.G. On the stochastic properties of single ion channels. Proc. R. Soc. Lond. B Biol. Sci. 1981;211:205–235. doi: 10.1098/rspb.1981.0003. [DOI] [PubMed] [Google Scholar]
- 10.Mak D.O.D., McBride S., Foskett J.K. ATP regulation of type 1 inositol 1,4,5-trisphosphate receptor channel gating by allosteric tuning of Ca2+ activation. J. Biol. Chem. 1999;274:22231–22237. doi: 10.1074/jbc.274.32.22231. [DOI] [PubMed] [Google Scholar]
- 11.Bezprozvanny I., Watras J., Ehrlich B.E. Bell-shaped calcium-response curves of Ins(1,4,5)P3- and calcium-gated channels from endoplasmic reticulum of cerebellum. Nature. 1991;351:751–754. doi: 10.1038/351751a0. [DOI] [PubMed] [Google Scholar]
- 12.Sneyd J., Falcke M. Models of the inositol trisphosphate receptor. Prog. Biophys. Mol. Biol. 2005;89:207–245. doi: 10.1016/j.pbiomolbio.2004.11.001. [DOI] [PubMed] [Google Scholar]
- 13.De Young, G. W., and J. Keizer, 1992. A single-pool inositol 1,4,5-trisphosphate-receptor-based model for agonist-stimulated oscillations in Ca2+ concentration. Proc. Natl. Acad. Sci. 89:9895–9899. http://www.pnas.org/content/89/20/9895.abstract. [DOI] [PMC free article] [PubMed]
- 14.Sneyd J., Falcke M., Fox C. A comparison of three models of the inositol trisphosphate receptor. Prog. Biophys. Mol. Biol. 2004;85:121–140. doi: 10.1016/j.pbiomolbio.2004.01.013. [DOI] [PubMed] [Google Scholar]
- 15.Fredkin D.R., Rice J.A. On aggregated Markov processes. J. Appl. Probab. 1986;23:208–214. [Google Scholar]
- 16.Kienker P. Equivalence of aggregated Markov models of ion-channel gating. Proc. R. Soc. Lond. B Biol. Sci. 1989;236:269–309. doi: 10.1098/rspb.1989.0024. [DOI] [PubMed] [Google Scholar]
- 17.Bruno W.J., Yang J., Pearson J.E. Using independent open-to-closed transitions to simplify aggregated Markov models of ion channel gating kinetics. Proc. Natl. Acad. Sci. USA. 2005;102:6326–6331. doi: 10.1073/pnas.0409110102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Monod J., Wyman J., Changeux J.P. On the nature of allosteric transitions: a plausible model. J. Mol. Biol. 1965;12:88–118. doi: 10.1016/s0022-2836(65)80285-6. [DOI] [PubMed] [Google Scholar]
- 19.Metropolis N., Rosenbluth A.W., Teller E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953;21:1087–1092. [Google Scholar]
- 20.Hastings W.K. Monte Carlo sampling methods using Markov chains and their applications. Biometrika. 1970;57:97–109. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


