Partial molar volume, surface area, and hydration changes for equilibrium unfolding and formation of aggregation transition state: High-pressure and cosolute studies on recombinant human IFN-γ

Abstract

The equilibrium dissociation of recombinant human IFN-γ was monitored as a function of pressure and sucrose concentration. The partial molar volume change for dissociation was −209 ± 13 ml/mol of dimer. The specific molar surface area change for dissociation was 12.7 ± 1.6 nm²/molecule of dimer. The first-order aggregation rate of recombinant human IFN-γ in 0.45 M guanidine hydrochloride was studied as a function of sucrose concentration and pressure. Aggregation proceeded through a transition-state species, N*. Sucrose reduced aggregation rate by shifting the equilibrium between native state (N) and N* toward the more compact N. Pressure increased aggregation rate through increased solvation of the protein, which exposes more surface area, thus shifting the equilibrium away from N toward N*. The changes in partial molar volume and specific molar surface area between the N* and N were −41 ± 9 ml/mol of dimer and 3.5 ± 0.2 nm²/molecule, respectively. Thus, the structural change required for the formation of the transition state for aggregation is small relative to the difference between N and the dissociated state. Changes in waters of hydration were estimated from both specific molar surface area and partial molar volume data. From partial molar volume data, estimates were 25 and 128 mol H₂O/mol dimer for formation of the aggregation transition state and for dissociation, respectively. From surface area data, estimates were 27 and 98 mol H₂O/mol dimer. Osmotic stress theory yielded values ≈4-fold larger for both transitions.

Aggregation is of considerable concern to the medical, pharmaceutical, and biotechnology industries, as protein aggregation occurs in human diseases (1–4) and during the production, purification, and storage of protein products (5). Characterization of the conformational state(s) that lead(s) to aggregation is essential for a mechanistic understanding of the aggregation process.

Protein aggregation was once viewed as a nonspecific hydrophobically driven process involving the fully unfolded random coil (6–8). However, recent research has shown protein aggregation to follow distinct pathways involving folding intermediates (6, 7, 9). Thus, the folding pathway and aggregation processes are critically linked (7, 8). Characterization of the unfolding process, in conjunction with aggregation rate studies, should then provide insight into the mechanisms of protein aggregation and the role of folding intermediates therein. A major challenge in characterizing aggregation pathways is that under conditions that greatly favor the native state (e.g., physiological), the small populations of highly reactive aggregation-competent species and the transition states leading to these species may be inaccessible to available spectroscopic techniques. To populate putative aggregation-competent species at levels sufficient for spectroscopic measurement, conditions that greatly perturb the native state are typically used (e.g., pH <4.0). Furthermore, even if the aggregation-competent species populated under nonnative conditions is the same as that found under native conditions, the transition state that precedes the formation of the aggregation-competent species and that may determine the rates of aggregation may still be undetectable. Here, we use high hydrostatic pressure to characterize the equilibrium unfolding process and aggregation transition states that are found under conditions that favor the native state.

Pressure may be used to measure differences in partial molar volume between equilibrium states and between reactants and transition states. For proteins, the partial molar volume (V_i) is composed of (10):

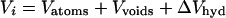1

where V_atoms and V_voids are the volumes of the constituent atoms and voids because of packing inefficiencies, respectively. ΔV_hyd is the volume change of the system resulting from protein–solvent interactions (11).

The change in partial molar activation volume (ΔV*) for protein aggregation is related to the reaction rate constant, k, by (12).

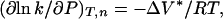2

where ΔV* (ml/mol) is the difference in partial molar volumes between the transition-state species (N*) and native state (N), P is pressure (MPa), R is the gas constant (ml MPa/mol K), and T is the temperature (K). An equivalent expression for two-state equilibrium processes is (12)

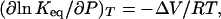3

where K_eq is the equilibrium constant, and ΔV is the difference in partial molar volumes between equilibrium species (ml/mol). Eqs. 2 and 3 both require the assumption of incompressibility or the use of concentration-independent units.

The homodimeric protein, recombinant human IFN-γ (rhIFN-γ) is an ideal system for characterization of aggregation and unfolding with high pressure. Dissociated monomers of rhIFN-γ aggregate (13) with first-order kinetics in the presence of nondenaturing concentrations of guanidine hydrochloride (Gdn⋅HCl) (14, 15). Aggregation can be modeled in the Lumry–Eyring framework, with rate limitation of the first step (A) explaining the first-order kinetics (14).

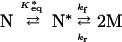A

B

where M is monomer, and M_x, M_y, and M_x+y are aggregates consisting of x, y, and x + y units of M, respectively. In this mechanism, N* is a transition state in equilibrium with N, and M is the aggregation-competent species. K^*_eq is the equilibrium constant between N and N*, k_f the forward rate constant for N* to 2 M, and k_r the reverse rate constant, which is negligible under aggregating conditions. Thus, for N to 2 M, k (min⁻¹), the commonly defined first-order rate constant, is equal to K^*_eqk_f.

Previously, addition of sucrose was used to manipulate surface tensions to measure the specific molar surface area changes for the N to N* transition (Δa*) (14). The present study presents the pressure and surface tension effects on the equilibrium unfolding and aggregation rate of rhIFN-γ. Results from these studies provide insight into the magnitude of structural changes required to form N* relative to those required for equilibrium unfolding. In addition, ΔV*, ΔV, Δa*, and Δa are used to estimate changes in hydration for transition-state formation and equilibrium unfolding. These values are compared with those calculated by using osmotic stress theory (16), an approach that has recently generated considerable controversy (17–19).

Materials and Methods

Materials.

Purified rhIFN-γ in 5 mM sodium succinate, pH 5.0, provided by Genentech, was stored at 4°C. Sodium succinate (5 mM), pH 5.0 (buffer), was used throughout. High-purity sucrose was from Pfanstiehl Chemicals. All other chemicals were reagent grade or higher from Sigma.

Equilibrium Dissociation/Unfolding.

Experiments were conducted at either 0.5 or 1.1 mg/ml rhIFN-γ in buffer containing 0.0, 0.125, 0.25, 0.50, 0.75, and 1.0 M sucrose. Sample solutions were prepared at least 8 h before the start of the experiment and stored at 4°C until use. Experiments were conducted by loading the samples into a high-pressure spectroscopy cell, equilibrating at 32°C, and collecting UV absorbance spectra at increasing, then decreasing, pressures between 0.1 and 250 MPa. Similar experiments without sucrose were conducted at Institut National de la Santé et de la Recherche Médicale (INSERM, Montpellier, France), up to 700 MPa. The pressure-induced transition was monitored by second-derivative UV (2D UV) spectroscopy (see below). After pressure increments of ≈10–20 MPa, rhIFN-γ reached an equilibrium conformation in 45 min. After returning to atmospheric pressure, pressure-induced transitions were 85–92% reversible.

Aggregation Reaction.

Aggregation was initiated by addition of Gdn⋅HCl solution to protein/sucrose solutions to yield solutions containing rhIFN-γ (1 mg/ml for 2D UV spectroscopy and 25 mg/ml for infrared spectroscopy), 0.45 M Gdn⋅HCl, and the desired sucrose concentration (0–1.5 M). At this level of Gdn⋅HCl, the native state of rhIFN-γ is still greatly favored over the denatured state, but aggregation is promoted by both an ionic strength effect and populating of N* (14). Aggregation at atmospheric pressure (28°C), in the absence of sucrose, was monitored by both 2D UV and IR spectroscopies, as described below. Investigations into the effects of sucrose and elevated pressures used 2D UV spectroscopy and solutions preequilibrated to 32°C. Aggregation was initiated, the reaction mixture was loaded into the high-pressure cell, and the system brought to the desired pressure. After thermal equilibration to 32°C (≈10 min after reaction initiation), 2D UV spectra were obtained as a function of time, as described below.

IR and 2D UV Spectroscopy.

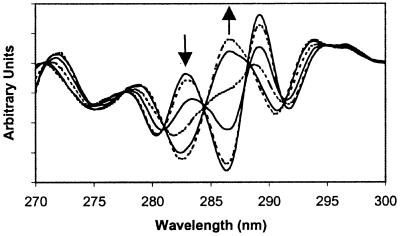
IR spectra were used to follow protein aggregation, collected by using a Nicolet Magna 750 spectrometer, and analyzed as previously described (20). UV absorption spectra were measured from 310 to 250 nm with a Perkin–Elmer Lambda 3B dual-beam spectrophotometer. The methods for the collection of absorption spectra and calculation of the second derivative are described elsewhere (15). Fraction native (f_N) protein was determined by 2D UV spectroscopy by calculating the difference between the maximum near 283 nm and the minimum near 286 nm (see Fig. 1), divided by this difference at atmospheric pressure [Max₂₈₃(P), −Min₂₈₆(P)]/[Max₂₈₃(atm) − Min₂₈₆(atm)].

Figure 1.

Selected 2D UV spectra of rhIFN-γ (1.1 mg/ml) at various pressures in 0.0 M sucrose, 32°C. The arrows indicate spectral trends with increasing P. Spectra were taken at pressures listed in order of 286 nm extremum position from bottom to top: 0.1, 60, 120, 150, 185, 225 MPa.

High-Pressure Equipment.

The high-pressure cell, designed in our laboratory, is made of 316 stainless steel, sealed with Buna-N 90 durometer o-rings, and has an optical port diameter of 6 mm and a pathlength of 7.65 mm. The cell has cylindrical sapphire windows (16 mm in diameter, 5.1 mm thick) and operates at pressures to 250 MPa. A manual pump generates pressure and a metallic gauge (accurate to ±2 MPa) is used to monitor pressure. Both the pump and gauge were purchased from High Pressure Equipment (Erie, PA). A piston separates the pressure-transmitting fluid from the sample.

Results

High-Pressure Characterization of Equilibrium Unfolding.

rhIFN-γ subunits each contain one tryptophan and four tyrosine residues (21). The region between 275 and 295 nm of the 2D UV spectrum reflects the microenvironments of tryptophan and tyrosine residues and is affected by the conformational state of proteins (22–24). Application of hydrostatic pressures of up to 250 MPa to solutions of rhIFN-γ in buffer results in significant changes in the 2D UV spectrum (Fig. 1). These changes are caused by alterations in the conformation of rhIFN-γ, because 2D UV spectra of tyrosine and tryptophan are minimally affected by pressure (25). In thermal and urea denaturation experiments with rhIFN-γ, 2D UV spectral changes were concomitant with the loss of secondary structure, as measured by circular dichroism spectroscopy at 222 nm (data not shown). Thus, the spectral changes observed with pressure result from the unfolding of rhIFN-γ.

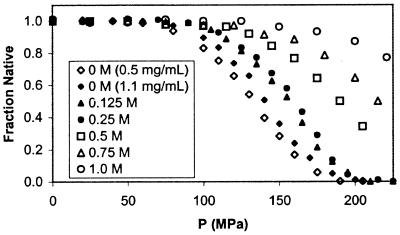
The intensity of the 2D UV spectrum at 286 nm was followed as a function of pressure, and the data were converted to f_N by baseline correction for the pre- and posttransition regions (26) (Fig. 2). Consistent with a two-state equilibrium process, the unfolding curve is sigmoidal, with midpoints at 133 and 140 MPa for samples containing 0.5 and 1.1 mg/ml rhIFN-γ, respectively.

Figure 2.

Equilibrium f_N rhIFN-γ vs. P as measured by 2D UV spectroscopy for various sucrose concentrations at 32°C. End states for the equilibrium process are native rhIFN-γ and dissociated monomer. The symbols ⋄ and ⧫ represent 0.5 and 1.1 mg/ml rhIFN-γ in 0 M sucrose solutions, respectively. Other experiments were conducted at 1.1 mg/ml.

An appropriate model is required to interpret equilibrium pressure data. We anticipate that the equilibrium unfolding transition we observed is coincident with dissociation of the native dimer into monomeric subunits:

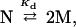4

where K_d (mol/L) is the equilibrium dissociation constant. The dependence of pressure-induced transitions on protein concentration can be used to verify this assumption in two ways. First, the pressure-induced dissociation for equilibrium processes is governed by (27):

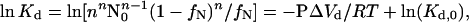5

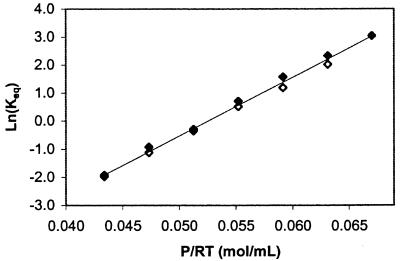
where n is the order of the reaction process (n = 2 for dimeric dissociation), N₀ is the initial native protein concentration, ΔV_d is the ΔV for dissociation, and K_d,0 is the dissociation constant at a reference temperature, pressure, and protein concentration. The pressure-induced process we monitored is dissociation, because a plot of ln(K_d) vs. P/RT for two protein concentrations (0.5 and 1.1 mg/ml) falls on a single line (Fig. 3), with a slope −ΔV_d = 207 ± 10 ml/mol of dimer at a 95% confidence level (note that all results are reported at a 95% confidence level). The value of ΔV_d is equivalent to ≈−0.350 mm³/molecule.

Figure 3.

Ln(K_eq) vs. P/RT for the equilibrium transition of rhIFN-γ in 0 M sucrose buffer monitored by 2D UV at 32°C. Concentrations of 0.5 mg/ml (◊) and 1.1 mg/ml (⧫) were run to determine whether the equilibrium process monitored was concentration dependent. Overlap of the data sets indicates the event is consistent with dissociation.

Second, for dimer dissociation, f_N vs. P curves at constant f_N are shifted by a pressure offset (ΔP) as a function of the protein concentration by (27):

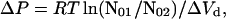6

where ΔP = (P₂ − P₁) and N₀₁ and N₀₂ are the initial protein concentrations for conditions 1 and 2, respectively. For denaturation not accompanied by dissociation (n = 1, Eq. 5), no pressure offset is expected as a function of protein concentration. As is evident in Fig. 2, there is a clear offset in pressure between the equilibrium unfolding curves for protein concentrations of 0.5 and 1.1 mg/ml. The ΔP observed in Fig. 2 matches that predicted from Eq. 6 (9.6 MPa), for a ΔV_d of −207 ml/mol of dimer, indicative of equilibrium dissociation of rhIFN-γ with pressure. After dissociation, no further transitions in protein conformation were observed at pressures up to 700 MPa (data not shown). Furthermore, the 2D UV spectrum of rhIFN-γ at pH 2.0, where the protein is known to be monomeric with significant loss of secondary structure (13), is very similar to that seen for the pressure-unfolded state (data not shown). Thus, the conformational state of rhIFN-γ at high pressure is a monomer with structure perturbed relative to N. It is emphasized that, because dissociation and unfolding are coincident, partial molar volume changes and specific molar surface area changes have contributions from both processes.

Sucrose Effect on Unfolding/Dissociation.

The specific molar surface area change on dissociation (Δa_d) can be calculated by monitoring the free energy change for dissociation as a function of the protein–water surface tension (20, 28):

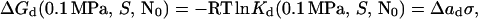7

where S is sucrose concentration (M), and σ is surface tension (mN/m). We varied surface tension by adding sucrose to solutions of rhIFN-γ. The surface tension increment of sucrose (δσ/δS) at the protein–water interface is assumed to be equivalent to that at the air–water interface (14, 28). To use Eq. 7, we must first calculate ΔG_d(0.1 MPa, S, N₀) at each sucrose concentration. For sucrose concentrations of 0.0, 0.125, and 0.25 M, the effect of pressure on f_N (Fig. 2) was used with Eq. 5 to yield ΔV_d and ΔG_d(0.1 MPa, S, N₀) (Table 1). ΔV_d is independent of both sucrose (i.e., surface tension) and protein concentrations and has an average value of −209 ± 13 ml/mol of dimer.

Table 1.

ΔV_d, P_1/2, and ΔG_d (0.1 MPa) for pressure-induced equilibrium dissociation of rhIFN-γ

Sucrose, M	rhIFN-γ, mg/mL	ΔVd,* mL/mol	P1/2,*† MPa	ΔGd (0.1 MPa),* kJ/mol
0.0	0.5	−200 (13)	133 (3)	27.2 (1.9)
0.0	1.1	−212 (13)	140 (3)	28.1 (1.9)
0.125	1.1	−208 (13)	154 (3)	30.3 (1.9)
0.25	1.1	−214 (13)	159 (3)	32.1 (1.9)
0.50	1.1		190 (3)‡	37.7 (1.9)§
0.75	1.1		215 (3)‡	43.0 (1.9)§
1.0	1.1		255 (3)‡	51.3 (1.9)§

^*Average of two runs at each sucrose level. The pooled standard deviation of each value from all complete unfolding curves was used to determine the 95% confidence intervals, which are in parentheses. 

^† Estimated at f_N = 0.50 from experimental data. 

^‡ Estimated by comparison of dissociation curves with completed dissociation curves. 

^§ Calculated by ΔG (0.1 MPa, S, 1.1 mg/mL) = −P_1/2ΔV_ave + RT ln(K[f_N(0.5)]), with ΔV_ave = −209 mL/mol. 

For sucrose concentrations above 0.25 M, the unfolding curves are incomplete because of stabilization of the protein by sucrose and pressure limitations of the equipment. However, estimation of f_N(P) for these solutions was possible because, for the solutions where the unfolding was complete, the posttransition slopes were identical. These posttransition slopes were used to calculate f_N for solutions with sucrose concentrations greater than 0.25 M. For these higher sucrose concentrations, an estimate of ΔG_d(0.1 MPa, S, N₀) (Table 1) was made by using P_1/2, the pressure where fn = 0.50, and ΔG_d(fn = 0.50, N₀) (Eqs. 5 and 7) according to:

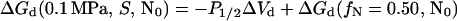8

Because ΔV_d is concentration independent at ≤0.25 M sucrose, ΔV_d is assumed to be constant at all sucrose concentrations. This method is accurate because, for complete dissociation curves (samples with ≤0.25 M sucrose), it produced P_1/2 values within 3 MPa (≈2%) of actual values.

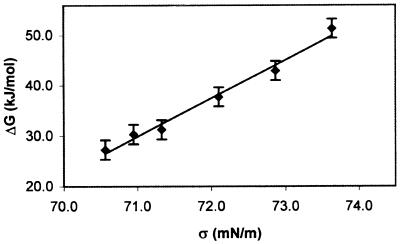
By using Eq. 7, a plot of ΔG_d(0.1 MPa, S, 1.1 mg/ml) vs. σ (Fig. 4) yields a line with a slope of 7.62 ± 1.0 kJ m/(mN mol) (R² = 0.98), equivalent to a Δa_d = 12.7 ± 1.6 mm²/molecule of dimer.

Figure 4.

ΔG_d(0.1 MPa, S, 1.1 mg/ml) of rhIFN-γ at 32°C vs. σ for the equilibrium dissociation. The variation of σ with sucrose concentration was obtained from Supran et al. (29). Error bars are 95% confidence limits based on the pooled standard deviation of ΔG_d(0.1 MPa, S, 1.1 mg/ml) from the intercept of ΔG_d vs. P plots for each sucrose concentration. Assuming the intercept is at 0.1 MPa introduces negligible error.

Monitoring rhIFN-γ Aggregation at High Pressure.

To understand pressure-dependent aggregation processes, a suitable in situ measurement technique is required. 2D UV spectroscopy is a convenient tool for protein structural characterization under high pressure. Previously, determination of residual soluble protein by size-exclusion HPLC and direct monitoring of secondary structural changes by IR spectroscopy have been used to follow rhIFN-γ aggregation at atmospheric pressure (14, 20). However, neither of these methods is convenient for high-pressure studies. We found that 2D UV spectroscopy also can be used to extract aggregation rate data. Rate constants for rhIFN-γ aggregation at atmospheric pressure (28°C) were 0.0077 ± 0.0007 min⁻¹ by IR spectroscopy and 0.0074 ± 0.0010 min⁻¹ by 2D UV spectroscopy. Therefore, we used the 2D UV spectroscopy method for determining the rate of aggregation for all high-pressure experiments.

Pressure Effect on the Aggregation Rate.

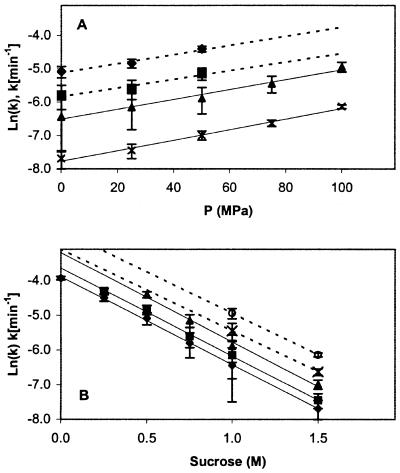
Fig. 5A is a plot of ln(k) vs. pressure for sucrose concentrations of 0.5, 0.75, 1.0, and 1.5 M. ln(k) increases linearly with increasing pressure and ΔV* for aggregation is independent of sucrose concentration (best-fit lines are parallel) averaging −41 ± 9 ml/mol of dimer, which is equivalent to −0.068 mm³/molecule. Because of the time delay in assembling the high-pressure cell and the rapid rate of pressure-induced aggregation at low sucrose concentrations, the reaction rate at pressure above 50 MPa and below sucrose concentrations of 0.75 M could not be determined accurately.

Figure 5.

(A) ln(k) vs. P at various sucrose concentrations (⧫, 0.5 M; ■, 0.75 M; ▴, 1.0 M; X, 1.5 M). (B) ln(k) vs. sucrose concentration at various P (⧫, 0.1 MPa; ■, 25 MPa; ▴, 50 MPa; X, 75 MPa; ○, 100 MPa). Reaction conditions were 1.0 mg/ml protein, 0.45 M Gdn⋅HCl, and 32°C. Error bars represent 95% confidence intervals on the rate constant. A best-fit line has been added for each sucrose (in A) and P (in B) level.

Sucrose Effect on the Aggregation Rate.

Kendrick et al. (14) used aggregation rates as a function of σ to determine Δa*, the specific molar surface area change between N and N*. Following their approach, we analyzed our pressure-dependent aggregation rates as a function of sucrose concentration and plotted ln(k) as a function of sucrose concentration (Fig. 5B). At all pressures tested, ln(k) for the aggregation reaction decreases linearly with increasing sucrose concentration. Because σ is linear in sucrose concentration (29) and no specific sucrose/pressure interaction is observed (best-fit lines are parallel), we assume that the effect of sucrose concentration on σ is independent of pressure. The slopes (−Δa*/RT) ln(k) vs. σ are independent of pressure (plots not shown), with a value corresponding to Δa* = 3.5 ± 0.2 mm²/molecule of dimer. This value of Δa* is in good agreement with that reported by Kendrick et al. (14), 3.85 ± 0.28 mm²/molecule of dimer at 25°C in the presence of 0.9 M Gdn⋅HCl, suggesting that Δa* is not a function of Gdn⋅HCl concentration, pressure or temperature.

Consistency of Results from Pressure and Sucrose Studies.

Under assumptions detailed in Table 2 ΔV and Δa can be interconverted. Measured and interconverted ΔV_d and ΔV*, and Δa_d and Δa* values are all internally consistent (Table 2).

Table 2.

Comparison of methods for the determination of ΔV^*, Δa^*, and Δn_W^* for the N to N^* transition and for the determination of ΔV, Δa, and Δn_W for dissociation equilibrium

Parameter	Hydrostatic P effects	σ effects	Osmotic pressure (π) effects
ΔV*, mL/mol dimer	−41 (9)†	−44	−176
Δa*, nm2/molecule	3.2	3.48 (0.15)‡	13.9
ΔnW*, mol H2O/mol dimer	25	27	108 (5)§
ΔV, mL/mol dimer	−209 (13)†	−160	−642
Δa, nm2/molecule	16.6	12.7 (1.6)‡	50.8
ΔnW, mol H2O/mol dimer	128	98	393 (52)§

Asterisks indicate values for the N to N* transition. Bolded values were calculated directly from the method indicated and are accompanied by 95% confidence limits in parentheses. 

^† ΔV* and ΔV were determined from the dependence of the aggregation rate and dissociation equilibrium on P, as described in the text. 

^‡ Δa* and Δa were determined from the dependence of the aggregation rate and dissociation equilibrium on σ, as described in the text. 

^§ Δn_W* and Δn_W were determined from the dependence of the aggregation rate and dissociation equilibrium constants on osmolality (16), δ[ln(k)]/δ[Osmolal] = −Δn_W/55.6, and δ[ln(K)]/δ[Osmolal] = −Δn_W/55.6, respectively. 

 Other values were obtained from (i) ΔV = Δn_W (ΔV_P,S/Γ_W,S + ΔV_W,S) and (ii) Δa = Δn_W/Γ_W,S. Γ_W,S is the protein surface density of water (7.75 molecule/nm²), assuming water at the protein surface is 18% more dense than bulk water (30) and cubic packing. Δn_W is the number of new water molecules at the protein surface, ΔV_P,S is the specific volume change of protein atoms for the transfer from protein interior to protein surface (0.2 ų/Ų of new protein surface area), and ΔV_W,S is the molecular volume change for water for the transfer from bulk solution to protein surface (−5.3 ų/molecule H₂O). Values for ΔV_P,S and ΔV_W,S were calculated from data presented in ref. 30. Activation parameters (ΔV*, Δa*, Δn_W*) are determined analogously to equilibrium parameters (ΔV, Δa, Δn_W). Our estimate of water surface density (ΔV_P,S/Γ_W,S + ΔV_W,S = 1.63 mL/mol) is consistent with results from molecular dynamics simulations for water at methane surfaces [2 mL/mol (46)]. 

Discussion

Pressure Effects on Dissociation and Aggregation.

Pressure destabilizes the native state of rhIFN-γ, favoring both dissociation and aggregation. Pressure-induced dissociation is expected, because pressure is commonly used to dissociate and unfold proteins (27). As such, ΔV in going from native to dissociated or unfolded states must be negative, as seen here for the dissociation and unfolding of rhIFN-γ. Negative values of ΔV (Eq. 1) arise from the filling of void spaces (ΔV_voids), and from the solvation of newly exposed protein surfaces (ΔΔV_hyd) at which the density of water is greater than that in bulk solution (30). Increased solvation increases the hydrodynamic volume (27), consistent with the measured increase in specific molar surface area (Δa). The ΔV_d of −209 ml/mol measured for rhIFN-γ is large for dimer dissociation, as typical values range from ≈50 to 170 ml/mol (27, 31, 32). However, considering the intertwined structure of the rhIFN-γ dimer, its high intersubunit surface area (21), and its concomitant dissociation and unfolding, a large ΔV_d is expected.

The pressure-induced aggregation of rhIFN-γ may seem counterintuitive, because pressure often dissociates multimeric proteins (27, 33–36). However, rhIFN-γ aggregates because the transition state, N*, has a smaller V_i than does N. Thus, the equilibrium favors N* at higher pressures, increasing the rate of formation of M (step A) and accelerating aggregation. As with equilibrium dissociation, formation of a more solvated species (N*) at pressure is explained by increases in solvent exposed protein surface area. The ΔV* of −41 ml/mol measured here is similar to ΔV* of other proteins for formation of transition states between native and unfolded conformations (37–39).

Sucrose Effect on Dissociation and Aggregation.

Exclusion of sucrose from the protein surface (28, 40–42) stabilizes rhIFN-γ against both pressure-induced dissociation and aggregation. By assuming the most compact state, the protein minimizes the thermodynamically unfavored sucrose/protein interaction (28, 40–42). The equilibria between 2 M and N (dissociation) and between N and N* (activation step for aggregation) are both shifted toward N, minimizing the solvent-accessible surface area.

Changes in specific molar surface area during dissociation and aggregation can be compared with the total protein surface area from the crystal structure of rhIFN-γ (21). Each monomer of rhIFN-γ consists of six α-helices. The helices intertwine to form a dimer (21) with an unusually high degree of intersubunit contact, in which the interface between monomers comprises 35–40% of the total surface area of the protein (14). Assuming the native structure of rhIFN-γ is globular with a hydrodynamic diameter of 3.70 nm (14), the measured Δa_d and Δa^* represent increases in solvent-exposed surface area relative to that of the native dimer of 30 and 8%, respectively.

Comparison Between the N to 2 M and N to N* Transitions.

Comparisons of ΔV_d and ΔV*, and Δa_d and Δa* provide insight into the degree of perturbation of the native state that is required for formation of the transition state for aggregation relative to that required for dissociation. ΔV* is 20% of ΔV_d, and Δa* is 30% of Δa_d. Thus, the transition state has a partial molar volume and specific molar surface area much more similar to that of the native state than to that of the dissociated state. Furthermore, because the increased surface exposure of N* is a small percentage of the intersubunit surface area, N* is most likely an associated, perturbed conformer of N that readily dissociates. Thus, changes in volume and surface area indicate that the formation of the transition state, which leads to the aggregate-competent monomer, requires only a minor perturbation in native structure relative to that occurring on dissociation and unfolding.

What are the implications of a transition state that is minimally perturbed from the native state for the formation of aggregates in vitro and in vivo? Our results support the contention (14) that, for at least some proteins, the transition state is part of the native-state ensemble, and its formation could result simply from dynamic fluctuations in the conformation of native protein molecules. Consistent with this suggestion are the observations that both in formulations of therapeutic proteins and human diseases, proteins aggregate under conditions greatly favoring the native state. From a molecular population standpoint, at any instant in time, finite concentrations of these transition-state species are always present. For protein therapeutics or in human diseases, time scales of interest can be years or even decades. With such long time scales, small but finite populations of aggregation-prone conformations can lead to substantial aggregation.

Changes in Hydration for the Transitions.

Our results for ΔV*, ΔV_d, Δa*, and Δa_d can address a recent controversy in the literature regarding the use of the osmotic stress model to calculate hydration state changes of reactions (17–19). By using the osmotic stress model (16), changes in waters of hydration between the native state and transition state (Δn^*_w) or between the native state and the equilibrium unfolded state (Δn_w) can be determined from reaction rate or equilibrium constants, respectively, as a function of osmolality. These changes can be estimated independently from changes in specific molar surface area and partial molar volume for the N to N* transition and the N to 2 M equilibrium. Our two independent techniques give consistent estimates of Δn^*_W and Δn_w, whereas the osmotic stress method gives estimates approximately four times greater (Table 2). This is because the osmotic stress method does not provide estimates of changes in monolayer water surface coverage as reported previously (16, 43) but is rather an estimate of differences in the water adsorption isotherm for two different protein states, defined relative to a Gibbs' dividing surface for a reference solute (e.g., sucrose). The number of waters participating in a process estimated by osmotic stress measurements thus depends on the characteristics (e.g., excluded volume) of the reference solute (17, 44, 45).

Abbreviations

rhIFN-γ

recombinant human IFN-γ

Gdn⋅HCl

guanidine hydrochloride

2D UV

second-derivative UV