Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2012 Oct 8;2:713. doi: 10.1038/srep00713

Entropy-driven liquid–liquid separation in supercooled water

V Holten 1, M A Anisimov 1,a
PMCID: PMC3465811  PMID: 23056905

Abstract

Twenty years ago Poole et al. suggested that the anomalous properties of supercooled water may be caused by a critical point that terminates a line of liquid–liquid separation of lower-density and higher-density water. Here we present a thermodynamic model based on this hypothesis, which describes all available experimental data for supercooled water with better quality and fewer adjustable parameters than any other model. Liquid water at low temperatures is viewed as an ‘athermal solution' of two molecular structures with different entropies and densities. Alternatively to popular models for water, in which liquid–liquid separation is driven by energy, the phase separation in the athermal two-state water is driven by entropy upon increasing the pressure, while the critical temperature is defined by the ‘reaction' equilibrium constant. The model predicts the location of density maxima at the locus of a near-constant fraction of the lower-density structure.

Cold and supercooled water have been the subject of intensive experimental, theoretical and computational studies for the last several decades. Still, the famous statement of 1972 by Franks ‘of all known liquids, water is probably the most studied and least understood'1 remains topical. This is especially true for metastable supercooled water, which is now a focal point of debates. On the other hand, there is a growing interest in the prediction of properties of supercooled water. In particular, in applied atmospheric science it is commonly accepted that the uncertainties in numerical weather prediction and climate models are mainly caused by poor understanding of properties of water in tropospheric and stratospheric clouds, where liquid water can exist in a deeply supercooled state2,3. Reliable prediction of properties of supercooled water is also important for cryobiology4.

A provocative, but thermodynamically consistent, view on the global phase behaviour of supercooled water was expressed in 1992 by Poole et al.5. According to this view, deeply in the supercooled region, just below the line of homogeneous ice nucleation, there could exist a critical point of liquid–liquid coexistence (LLCP) that would terminate the line of first-order transitions between two liquid aqueous phases, low-density liquid (LDL) and high-density liquid (HDL) (Fig. 1). The anomalies in the heat capacity, the compressibility, and the thermal-expansion coefficient experimentally observed upon supercooling6,7,8,9,10,11,12,13 thus might be associated with this critical point, even if it is inaccessible. The extension of the coexistence curve into the one-phase region is the Widom line14. The definition of the Widom line as given in Ref. 14 is ambiguous. However, we define the Widom line in an unambiguous way as the locus of stability minima and order-parameter fluctuation maxima15,16. This definition uniquely locates the Widom line along the line of zero ordering field near the critical point. While the maxima of different properties generally deviate from the Widom line upon departure from the critical point, the heat capacity maxima line appears to be close to the Widom line specifically for the liquid-liquid transition in supercooled water.

Figure 1. Hypothetical phase diagram of cold water.

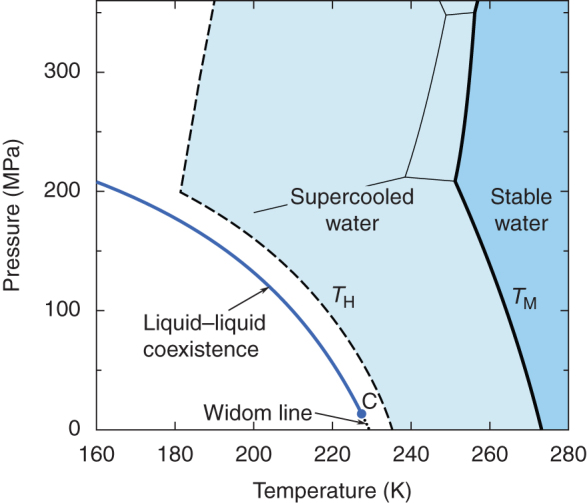
Figure 1

Open in a new tab

Supercooled water exists between the melting temperature17 TM and the homogeneous ice nucleation temperature18,19 TH. Below TH, there may exist a liquid–liquid critical point, marked by ‘C', which terminates a liquid–liquid coexistence curve. The location of this critical point is shown as predicted by our model. The adopted location of the liquid–liquid coexistence curve is close to similar suggestions of Mishima13,20 and Kanno and Angell7. The extension of the coexistence curve into the one-phase region is the line of maximum fluctuations of the order parameter, the Widom line14,15,16. Thin solid lines represent phase boundaries between the different ices21,22.

Intriguing liquid–liquid phase separation and the existence of the second critical point in water still remain a plausible hypothesis which needs further verification. In view of the inaccessibility of the LLCP to direct experiments, development of an equation of state, based on a solid physical concept and able to accurately describe all available experimental data, might help in resolving the supercooled-water dilemma.

In this paper, we offer an approach to thermodynamics of phase separation in supercooled water alternative to common views. Following Bertrand and Anisimov16, we assume that liquid water is a non-ideal athermal ‘solution' of two supramolecular arrangements, which undergoes phase separation driven by non-ideal entropy upon increase of the pressure. In the athermal two-state model, the non-ideality driven by entropy determines the critical pressure, whereas the critical temperature follows from the condition of ‘chemical reaction' equilibrium. We have developed an explicit equation of state, which is based on the athermal two-state model and which describes all available experimental data for supercooled water, both H2O and D2O, with better quality and with fewer adjustable parameters than any other model suggested so far. We have also shown that the popular two-state ‘regular-solution' scenario, in which phase separation is energy-driven, fails to describe the experimental data on water.

Results

How a pure liquid can unmix

The only possible fluid–fluid phase transition in simple one-component substances, such as argon or methane, is separation into liquid and gas. This transition is driven by attraction forces between molecules. The critical temperature of the liquid–gas separation is uniquely proportional to the depth of the intermolecular interaction potential, which is a superposition of the attraction and repulsion potentials. The simplest model of the liquid–gas transition is the lattice gas, which, despite its simplicity, reflects the most important features of fluid phase behaviour23. A central concept in physics of phase transitions is the notion of the order parameter24. The order parameter in fluids is the difference between the densities of liquid and vapour. Thus, in simple one-component fluids only one liquid phase and only one critical point are possible. To observe a liquid–liquid separation one needs a mixture of two or more species. Remarkably, the same lattice-gas model that describes the liquid–gas transition in pure substances can also explain liquid–liquid demixing in weakly-compressible binary solutions. In binary liquid solutions the order parameter is the difference in concentrations of two liquid phases, while the critical temperature is proportional to the difference in the depths of the interaction energies between like and unlike molecules.

However, such a simple fluid-phase behaviour is not a law of nature. As explained by Mishima and Stanley25, if the intermolecular potential of a pure fluid could exhibit two minima, the interplay between these minima may define the critical temperature Tc and pressure Pc of liquid–liquid separation. Application of this picture to water implies that the second, liquid–liquid, critical point is driven by molecular interaction energy just like the liquid–gas critical point. Another possibility is a double-step potential that depends on hydrogen-bond bending, as shown by Tu et al.26.

The hypothesized existence of two liquid states in pure water can be globally viewed in the context of polyamorphism, a phenomenon that has been experimentally observed or theoretically suggested in silicon, liquid phosphorus, triphenyl phosphate, and in some other molecular-network-forming substances27,28. Commonly, polyamorphism in such systems is described as energy-driven. However, there is an ambiguity in terminology adopted in Refs. 27 and 28, where the term ‘density, entropy-driven' is used for an energy-driven phase separation. There is an example of entropy-driven liquid polyamorphism, isotropic Blue Phase III in chiral liquid crystals29.

The thermodynamic relation between the molar volume change ΔV and the latent heat (enthalpy change) of phase transition, Q = TΔS (where ΔS is the molar entropy change) is given by the Clapeyron equation dP/dT = Q/TΔV = ΔS/ΔV. Therefore, the relation between the volume/density (ρ = 1/V) change and the latent heat/entropy change is controlled by the slope of the transition line in the P–T plane.

Two features make the second critical point in water phenomenologically different from the well-known gas–liquid critical point. The negative slope of the liquid–liquid phase transition line in the P–T plane in supercooled water (Fig. 1) means, in accordance with the Clapeyron equation, that the higher-density liquid water is the phase with larger entropy. A large value of this slope at the critical point (about 30 times greater than that for the gas–liquid transition at the critical point) indicates the significance of the entropy change with respect to the density change, and, correspondingly, the importance of the entropy fluctuations. Secondly, supercooled water tends to separate upon pressurizing. The relative significance of the entropy change, combined with a high degree of cooperativity of hydrogen bonds30, suggest that the liquid–liquid phase separation in water near the LLCP may be driven by entropy rather than by energy.

The topology of the liquid–liquid transition line in supercooled water is almost orthogonal to that of the liquid–vapour transition line near the critical point. This radically changes the relation between scaling fields and physical fields which theoretically describe the criticality (see Supplementary Fig. S1). In particular, this topology suggests that for supercooled water the ordering field is mostly associated with the temperature and the thermal field with the pressure. In turn, the order parameter is associated with the entropy, not with the density, thus the phase transition is entropically driven.

The Clapeyron equation itself does not provide an answer whether the liquid–liquid transition in pure substances is energy-driven or entropy-driven. To answer this question one should examine the source of non-ideality in the free energy. Bertrand and Anisimov16 introduced the concept of a ‘lattice liquid', as opposed to a lattice gas, an imaginary one-component liquid which exhibits liquid–liquid separation upon pressurizing with a vertical liquid–liquid transition line in the P–T plane, thus without the density change. The order parameter in a lattice liquid is the entropy and the ‘ordering field', conjugate to the order parameter, is the temperature. The phase transition in a lattice liquid is purely entropy-driven. The critical temperature (the same as the temperature of the liquid–liquid transition line) is defined by thermodynamic equilibrium as zero ordering field, but not by the interaction potential. In real water, as seen in Fig. 1, the slope of the hypothesized LDL–HDL transition line in supercooled water changes from very steep at higher temperatures to relatively flat at lower temperatures. It is thus tempting to assume that the liquid–liquid separation in water may represent a special kind of liquid polyamorphism, intermediate between two limiting cases: mostly entropy-driven phase separation (lattice liquid-like) near the critical point and mostly energy-driven (lattice gas-like) separation into two amorphous states observed in water at about 140 K31. We show in this paper that the actual behaviour of supercooled water appears to be much closer to the lattice-liquid behaviour than to the lattice-gas behaviour.

The entropy-driven separation of a lattice liquid can be further specified in terms of a two-state model16. The pure liquid is assumed to be a mixture of two interconvertible states or structures of the same molecules, whose ratio is controlled by thermodynamic equilibrium. The existence of two states does not necessarily mean that they can separate. If these states form an ideal ‘solution', the liquid will remain homogeneous at any temperature or pressure. However, if the solution is non-ideal, a positive excess Gibbs energy, GE = HE − TSE, would cause phase separation. If the excess Gibbs energy is associated with a heat of mixing HE, the separation is energy-driven. If the excess Gibbs energy is associated with an excess entropy SE, the separation is entropy-driven. The entropy-driven nature of such a separation means that the two states would allow more possible statistical configurations, and thus higher entropy, if they are unmixed.

Two-state models for liquid water have a long history, dating back to the 19th century32,33. More recently, two-state models have become popular to explain liquid polyamorphism27,28,34. Ponyatovsky et al.35 and Moynihan36 assumed that water could be considered as a ‘regular binary solution' of two states, which implies that the phase separation is driven by energy. Ponyatovsky et al.35 and Moynihan36 made an attempt to describe the thermodynamic anomalies with this model, but the agreement with experimental data was only qualitative.

Virtual liquid–liquid criticality in supercooled water

There is no direct experimental evidence of the LLCP in real water, but it is indirectly supported by thermodynamic arguments based on density measurements13 and by critical-like anomalies of thermodynamic response functions6,7,8. The known existence of two states of glassy water31, as well as experiments on nano-confined water, which does not crystallize37,38, are also consistent with the possibility of a ‘virtual' liquid–liquid separation. This possibility is also supported by simulations of some water-like models, such as ST239,40,41. The exact location of the liquid–liquid critical point in these models is uncertain30. Moreover, for the mW model42 it has been recently shown that spontaneous crystallization occurs before a possible liquid–liquid separation could equilibrate43,44. However, the anomalies observed in the metastable region of the mW model42,43,44,45 might still be associated with the existence of a virtual LLCP in the unstable region.

The first attempt to develop an equation of state for supercooled water, based on the assumption that the LLCP exists, and on the asymptotic theory of critical phenomena46,47, was made by Fuentevilla and Anisimov15 and further elaborated and clarified by Bertrand and Anisimov16. In particular, both works estimated the LLCP critical pressure below 30 MPa, much lower than most of simulated water-like models predicted. Holten et al.48 used the same asymptotic equation of state, also in a mean-field approximation49, but introduced the noncritical backgrounds of thermodynamic properties in a thermodynamically consistent way. The resulting correlation represents all available experimental data for supercooled water, H2O and D2O, within experimental accuracy, thus establishing a benchmark for further developments in this field. However, there is a concern regarding the application of the asymptotic theory to a broad range of temperatures and pressures including the region far away from the assumed critical point. Such an extension makes the description of experimental data inevitably semi-empirical since all non-asymptotic physical features are absorbed by the adjustable backgrounds of thermodynamic properties. This fact underlines the need to develop a closed-form theoretically-based equation of state which would satisfy the asymptotic critical anomalies and, at the same time, describe regular behaviour far away from the critical region.

Water as an athermal solution of two states

We assume pure liquid water to be a mixture of two interconvertible states or structures A (HDL) and B (LDL). The fraction of molecules in state B is denoted by x, and is controlled by the ‘reaction'

graphic file with name srep00713-m1.jpg

The states A and B could correspond to different arrangements of the hydrogen-bonded network50. The Gibbs energy per molecule G is the sum of the contributions from both states,

graphic file with name srep00713-m5.jpg

where µA and µB are the chemical potentials of A and B in the mixture. The variable x is conjugate to 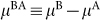Inline graphic. If A and B form an athermal non-ideal solution, the Gibbs energy of the mixture is

graphic file with name srep00713-m2.jpg

and the chemical-potential difference is then

graphic file with name srep00713-m7.jpg

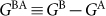where Inline graphic is the difference in Gibbs energy per molecule between pure configurations A and B, kB is Boltzmann's constant, and ω = ω(P) is the interaction parameter, which depends on pressure but not on temperature.

Considering x, the fraction of B, as the ‘reaction coordinate' or ‘extent of reaction'51, the condition of chemical reaction equilibrium,

graphic file with name srep00713-m9.jpg

yields the equilibrium constant K = K(T,P) of reaction (1) as

graphic file with name srep00713-m10.jpg

and defines the equilibrium fraction xe through

graphic file with name srep00713-m3.jpg

The expression (2) combined with the equilibrium condition x = xe is our equation of state for the two-state supercooled water. The non-ideality of the two-state mixture is entirely associated with the excess entropy of mixing SE = −ωx(1 − x), while the heat (enthalpy) of mixing is zero. The parameter ω determines the critical pressure through its pressure dependence, which we approximate as

graphic file with name srep00713-m11.jpg

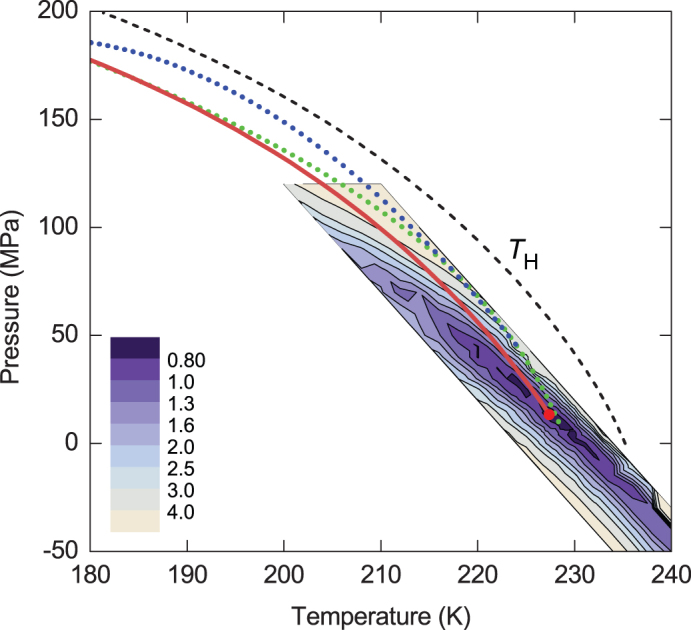
where 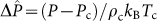Inline graphic with a subscript ‘c' denoting critical parameters. An alternative, regular-solution model would have a factor w/kBT in place of ω in equation (2), where the interaction parameter w would determine the critical temperature. For a regular solution, the excess entropy is zero, while the heat of mixing is HE = wx(1 − x), thus making phase separation purely energy driven.

The conditions for the critical point of liquid–liquid equilibrium,

graphic file with name srep00713-m13.jpg

yield in the case of the athermal-solution model the critical parameters xc = 1/2 and ω(Pc) = 2. At pressures below the critical pressure, ω < 2 and the Gibbs energy versus fraction x = xe shows a single minimum. Above the critical pressure, ω > 2 and there are one or two minima in the Gibbs energy, depending on the value of the equilibrium constant K(T,P). If there are two minima, the minimum with the lowest Gibbs energy represents stable equilibrium, and the other minimum corresponds to a metastable state. When lnK(T,P) = 0, both minima have the same Gibbs energy, representing two-phase equilibrium. The critical temperature Tc and the location of the liquid–liquid transition (LLT) curve in the P–T plane are thus determined by the dependence of the equilibrium constant K on temperature and pressure. Since the LLT curve is defined as an analytical function of temperature and pressure lnK(T,P) = 0, this function is to be obtained from the experimental data. In Supplementary Section 1 we explain how we match the LLT curve of the two-state model to the experimentally expected shape and location. The resulting expression for lnK is

graphic file with name srep00713-m14.jpg

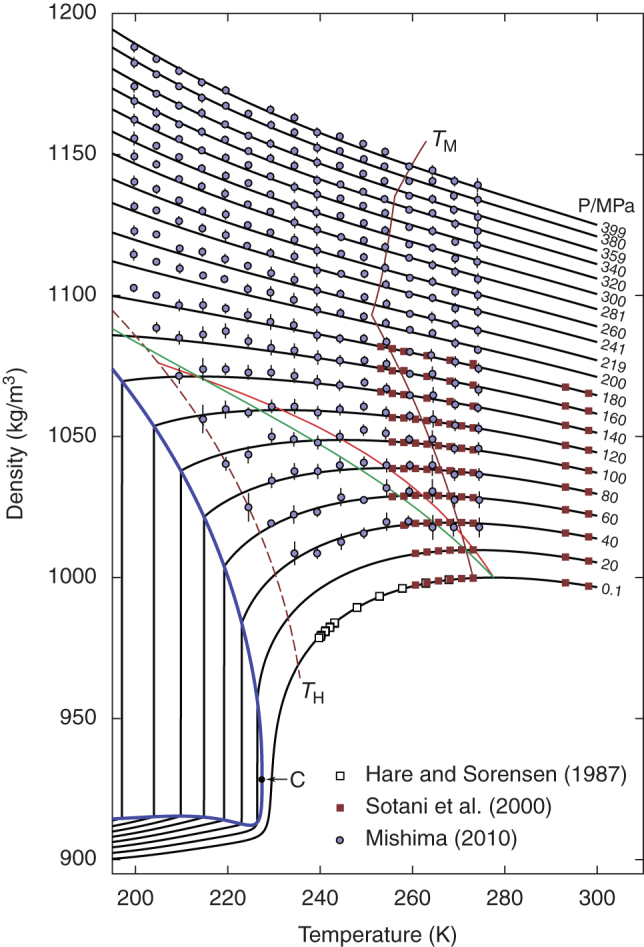
where 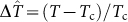Inline graphic. The parameter a = −ρckBdT/dP is the slope of the LLT curve at the critical point, and b determines the curvature. The parameter λ is proportional to the heat of reaction (1), while the product υ = λ a is proportional to the volume change of the reaction. Since λ/υ = ΔS/ρckBΔV = Q/TΔV, the heat of reaction is asymptotically related to the latent heat of phase separation through λΔx = Q/kBTc, while Δx = ΔS/kBλ = Q/λkBTc serves as the order parameter along the LLT.

The Gibbs energy GA of the pure structure A defines the background properties and is approximated as

graphic file with name srep00713-m4.jpg

where m (0 to 3) and n (0 to 5) are integers and cmn are adjustable coefficients. Expressions for thermodynamic properties which follow from our model are given in Supplementary Section 2.

Effects of critical fluctuations

Thermodynamics predicts the divergence of fluctuations at the critical point. Entropy fluctuations are proportional to the isobaric heat capacity CP, volume/density fluctuations are proportional to the isothermal compressibility κT , and cross entropy–volume fluctuations are proportional to the thermal expansion coefficient αP24. The two-state model described above is essentially mean-field, not affected by fluctuations. Being expanded near the critical point in powers of x − xc, equation (2) takes the form of a Landau expansion24. The procedure to include the effects of critical fluctuations is well developed and known as crossover theory47. This procedure is fully described in Supplementary Section 3. The variables x − xc and P − Pc are renormalized such that the behaviour close to the critical point agrees with the asymptotic critical behaviour48, and crosses over to mean-field behaviour given by the equation of state, (2) and (3), far away from the critical point.

Description of experimental data

We have fitted both the mean-field and the crossover formulation of our two-state model to experimental data, as described in Supplementary Section 4. We adopt the location of the liquid–liquid coexistence parallel to the homogeneous nucleation curve, which appears to be close to a suggestion of Mishima13,20 based on the shape of metastable melting curves of different ices, and a ‘singularity line' of Kanno and Angell7 based on the extrapolation of the compressibility anomalies. The optimum locations of the critical point form a narrow band in the P–T diagram. The best fit for the critical point is obtained at about 227 K and 13 MPa, with λ = 2.3 and ω0 = 0.35. The LLT curve was chosen to intersect the band of LLCP locations at the optimal value of the critical pressure (Fig. 2) where it has a dimensionless slope of 1/a = 15.3. This location of the critical point is about 10% of ρckBTc higher than that optimized by the mean-field approximation (see Supplementary Section 4A). This shift is induced by critical fluctuations, as follows from crossover theory.

Figure 2. Optimization of the LLCP location.

Figure 2

Open in a new tab

The coloured map shows the reduced sum of squared residuals. The solid red line is the hypothesized LLT curve. The dashed curve shows the temperature of homogeneous ice nucleation19 TH. The blue dotted curve is the LLT suggestion by Mishima13 and the green dotted curve is the ‘singularity' line suggested by Kanno and Angell7.

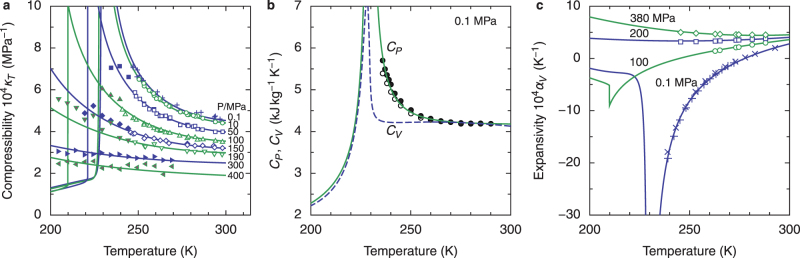
The description of the density and the response functions are shown in Figs. 3 and 4. A significant improvement compared to the previous works16,48,49 is that our equation of state does not show any sign of additional thermodynamic instability beyond the liquid–liquid separation. We now believe that the mechanical and thermal instability below the LLT, reported previously16,48,49, were associated with the asymptotic nature of the equation of state, which caused negative backgrounds of the compressibility. The number of adjustable background coefficients in equation (4) is now 14, to be compared with 1648,49 (see Supplementary Table S1). Another improvement is the agreement of the coexistence densities, shown in Fig. 5, with the experimental densities of lowdensity and high-density amorphous water. We also fitted our model to all available experimental data for supercooled D2O with the same quality as for H2O (see Supplementary Section 4B). As an alternative, we also tried to apply the two-state regular-solution model as previously suggested by Ponyatovsky et al.35 and Moynihan36. With the same number of adjustable parameters, a regular-solution two-state model fails (about ten times higher root-mean-square error) to describe experimental data on supercooled water.

Figure 3. Density of cold and supercooled water as a function of temperature and pressure.

Figure 3

Open in a new tab

Black curves are the predictions of the crossover two-state model. TM (dark red) indicates the melting temperature and TH indicates the homogeneous nucleation temperature. The thick blue line is the liquid–liquid equilibrium curve, with the critical point C. The red line is the line of maximum density, and the green line is the line of a constant LDL fraction of about 0.12. Symbols represent experimental data12,13,52. Mishima's data13 have been shifted by at most 0.3% to bring them into agreement with data for stable water, as described in Ref. 48.

Figure 4. Response functions as a function of temperature.

Figure 4

Open in a new tab

(a) Isothermal compressibility7,13,53. (b) Heat capacity at constant pressure CP (open circles: data from Archer and Carter10, closed circles: data from Angell et al.6) and at constant volume CV (calculated) at 0.1 MPa. See Supplementary Section 5 for more details. (c) Thermal expansivity11,12,54. In a, b, and c, the curves are the prediction of the crossover two-state model, and the symbols represent experimental data.

Figure 5. Density along the liquid–liquid transition curve.

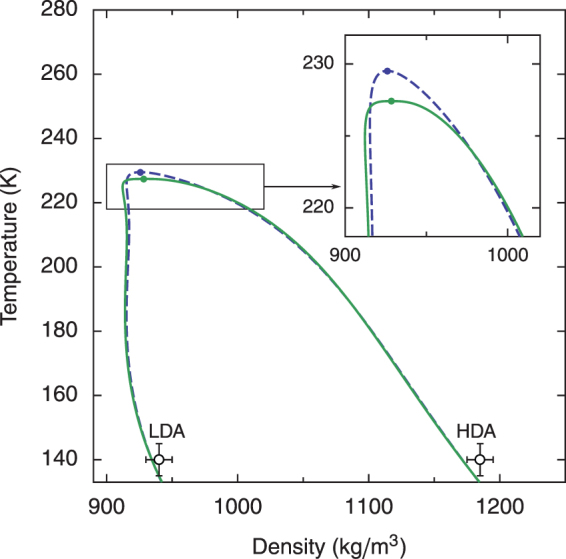
Figure 5

Open in a new tab

The dashed line represents the mean-field two-state model; the solid line represents the crossover two-state model. The open circles are the densities of the low-density amorphous (LDA) and high-density amorphous (HDA) phases of water at 200 MPa31. One can notice that the crossover LLT curve is flatter than the LLT curve in the mean-field approximation and that the actual position of the critical point is shifted to a lower temperature by critical fluctuations.

In Fig. 6, we compare the LDL fraction x predicted by our equation of state and that obtained in simulations of the mW model by Moore and Molinero45. Remarkably, both results show a similar temperature dependence. In contrast, this fraction for an ideal LDL/HDL solution would be almost a linear function of temperature. The experimental maximum density line is located approximately along the line of constant LDL fraction x = 0.12 as shown in Fig. 3.

Figure 6. Fraction of molecules in the low-density state.

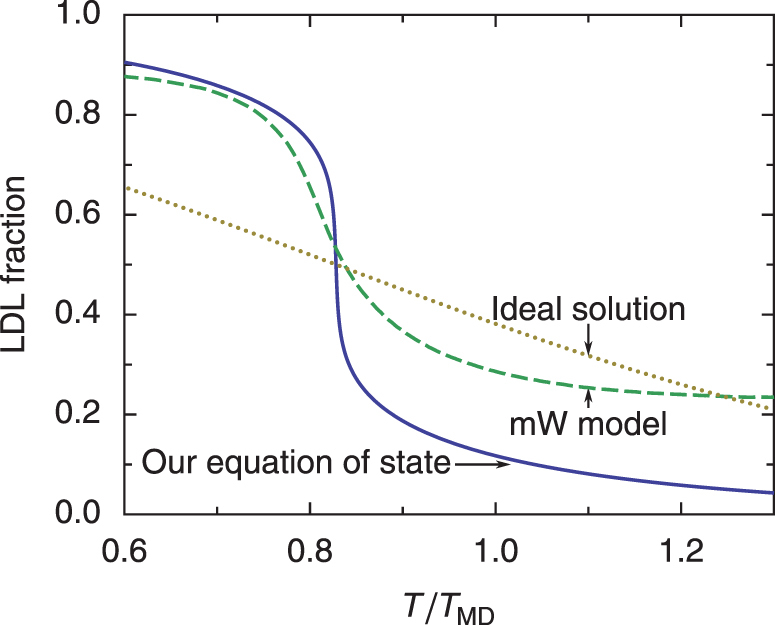
Figure 6

Open in a new tab

The fraction x is shown for the two-state model at 0.1 MPa, in the case of an athermal solution (solid) and an ideal solution (dotted). The dashed curve is the fraction of four-coordinated water molecules, i.e., the fraction of water molecules with four neighbours, for mW water simulations performed by Moore and Molinero45 (see Supplementary Section 6). The temperature is scaled by the temperature of maximum density TMD (250 K for the mW model and 277 K for real water).

Discussion

We confirm the previous finding15,16 of a critical pressure that is much lower than found in simulations39,40,41. We believe that the low critical pressure reflects the entropy-driven nature of liquid–liquid criticality in supercooled water. As shown by Stokely et al.30, the LLCP critical pressure is determined by the ratio of hydrogen-bond cooperativity and hydrogen-bond covalent strength. The higher the ratio, the lower the critical pressure.

The necessity to develop a microscopic model for water, which would be consistent with its athermal two-state character, and which would clarify the microscopic nature of the order parameter, (x − xc)/xc, is evident. Strong non-ideality caused by negative entropy of mixing is well known for some binary aqueous solutions of non-electrolytes where solute molecules form hydrogen bonds with water molecules55. Our equation of state, being purely phenomenological, does not provide information on the microscopic structure of molecular packing or structure. However, we may speculate that two different structures of water with different arrangements of hydrogen bonds could exhibit more configurations after being unmixed as a result of pressurizing.

Finally, the problem of the influence of the hypothesized liquid–liquid separation on homogeneous ice nucleation remains unresolved. The fact that the LLT curve is located just below the homogeneous nucleation curve and imitates its shape suggests that homogeneous ice nucleation may be caused by the entropy/structure fluctuations associated with the liquid–liquid transition. A connection between the change in the structure of liquid water and the crystallization rate of ice was shown for the mW model44. Whether the LLCP of simulated water-like models is in the metastable region or just projected to be in the unstable region, the liquid–liquid criticality still may be responsible for the observed anomalies in the accessible domain.

Author Contributions

M.A.A. conceived the project and formulated the two-state model. V.H. analysed the model and fitted it to experimental data. M.A.A. and V.H. wrote the manuscript.

Supplementary Material

Supplementary Information

Supplement

srep00713-s1.pdf (507.6KB, pdf)

Acknowledgments

We acknowledge collaboration with C.E. Bertrand, D.A. Fuentevilla, J. Kalová, J. Leys, and J.V. Sengers.We thank C.A. Angell, P.G. Debenedetti, O. Hellmuth, O. Mishima, V. Molinero, and H.E. Stanley for useful discussions. The research has been supported by the Division of Chemistry of the US National Science Foundation under Grant No. CHE-1012052. The research of V. Holten was also supported by the International Association for the Properties of Water and Steam.

References

  1. Franks F. Introduction–Water, the unique chemical. .In Franks F., (ed.) The Physics and Physical Chemistry of Water, vol. 1 of Water: A Comprehensive Treatise, chap. 1 (Plenum, 1972).
  2. Rosenfeld D. & Woodley W. L. Deep convective clouds with sustained supercooled liquid water down to −37.5°C. Nature 405, 440–442 (2000). [DOI] [PubMed] [Google Scholar]
  3. Heymsfield A. J. & Miloshevich L. M. Homogeneous ice nucleation and supercooled liquid water in orographic wave clouds. J. Atmos. Sci. 50, 2335–2353 (1993). [Google Scholar]
  4. Song Y., Sharp R., Lu F. & Hassan M. The future potential of cryopreservation for assisted reproduction. Cryobiology 60, S60–S65 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Poole P. H., Sciortino F., Essmann U. & Stanley H. E. Phase behaviour of metastable water. Nature (London) 360, 324–328 (1992). [Google Scholar]
  6. Angell C. A., Oguni M. & Sichina W. J. Heat capacity of water at extremes of supercooling and superheating. J. Phys. Chem. 86, 998–1002 (1982). [Google Scholar]
  7. Kanno H. & Angell C. A. Water: Anomalous compressibilities to 1.9 kbar and correlation with supercooling limits. J. Chem. Phys. 70, 4008–4016 (1979). [Google Scholar]
  8. Kanno H. & Angell C. A. Volumetric and derived thermal characteristics of liquid D2O at low temperatures and high pressures. J. Chem. Phys. 73, 1940–1947 (1980). [Google Scholar]
  9. Tombari E., Ferrari C. & Salvetti G. Heat capacity anomaly in a large sample of supercooled water. Chem. Phys. Lett. 300, 749–751 (1999). [Google Scholar]
  10. Archer D. G. & Carter R. W. Thermodynamic properties of the NaCl + H2O system. 4. Heat capacities of H2O and NaCl(aq) in cold-stable and supercooled states. J. Phys. Chem. B 104, 8563–8584 (2000). [Google Scholar]
  11. Hare D. E. & Sorensen C. M. Densities of supercooled H2O and D2O in 25 µ glass capillaries. J. Chem. Phys. 84, 5085–5089 (1986). [Google Scholar]
  12. Hare D. E. & Sorensen C. M. The density of supercooled water. II. Bulk samples cooled to the homogeneous nucleation limit. J. Chem. Phys. 87, 4840–4845 (1987). [Google Scholar]
  13. Mishima O. Volume of supercooled water under pressure and the liquid-liquid critical point. J. Chem. Phys. 133, 144503 (2010). [DOI] [PubMed] [Google Scholar]
  14. Xu L. et al. Relation between the Widom line and the dynamic crossover in systems with a liquid—liquid phase transition. Proc. Natl. Acad. Sci. U.S.A. 102, 16558–16562 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Fuentevilla D. A. & Anisimov M. A. Scaled equation of state for supercooled water near the liquid-liquid critical point. Phys. Rev. Lett. 97, 195702 (2006). Erratum ibid. 98, 149904 (2007). [DOI] [PubMed] [Google Scholar]
  16. Bertrand C. E. & Anisimov M. A. The peculiar thermodynamics of the second critical point in supercooled water. J. Phys. Chem. B 115, 14099–14111 (2011). [DOI] [PubMed] [Google Scholar]
  17. Wagner W., Riethmann T., Feistel R. & Harvey A. H. New equations for the sublimation pressure and melting pressure of H2O ice Ih. J. Phys. Chem. Ref. Data 40, 043103 (2011). [Google Scholar]
  18. Kanno H., Speedy R. J. & Angell C. A. Supercooling of water to −92°C under pressure. Science 189, 880–881 (1975). [DOI] [PubMed] [Google Scholar]
  19. Kanno H. & Miyata K. The location of the second critical point of water. Chem. Phys. Lett. 422, 507–512 (2006). [Google Scholar]
  20. Mishima O. Liquid-liquid critical point in heavy water. Phys. Rev. Lett. 85, 334–336 (2000). [DOI] [PubMed] [Google Scholar]
  21. Bridgman P. W. Water, in the liquid and five solid forms, under pressure. Proc. Am. Acad. Arts Sci. 47, 441–558 (1912). [Google Scholar]
  22. Kell G. S. & Whalley E. Equilibrium line between ice I and III. J. Chem. Phys. 48, 2359–2361 (1968). [Google Scholar]
  23. Lee T. D. & Yang C. N. Statistical theory of equations of state and phase transitions. II. Lattice gas and Ising model. Phys. Rev. 87, 410–419 (1952). [Google Scholar]
  24. Landau L. D. & Lifshitz E. M. Statistical Physics, vol. 5 of Course of Theoretical Physics (Pergamon, Oxford, 1980), 3 edn. [Google Scholar]
  25. Mishima O. & Stanley H. E. The relationship between liquid, supercooled and glassy water. Nature 396, 329–335 (1998). [Google Scholar]
  26. Tu Y., Buldyrev S. V., Liu Z., Fang H. & Stanley H. E. Different water scenarios for a primitive model with two types of hydrogen bonds. EPL 97, 56005 (2012). [Google Scholar]
  27. McMillan P. F. Polyamorphic transformations in liquids and glasses. J. Mater. Chem. 14, 1506–1512 (2004). [Google Scholar]
  28. Wilding M. C., Wilson M. & McMillan P. F. Structural studies and polymorphism in amorphous solids and liquids at high pressure. Chem. Soc. Rev. 35, 964–986 (2006). [DOI] [PubMed] [Google Scholar]
  29. Anisimov M. A., Agayan V. A. & Collings P. J. Nature of the Blue-Phase-III-isotropic critical point: An analogy with the liquid-gas transition. Phys. Rev. E 57, 582–595 (1998). [Google Scholar]
  30. Stokely K., Mazza M. G., Stanley H. E. & Franzese G. Effect of hydrogen bond cooperativity on the behavior of water. Proc. Natl. Acad. Sci. U.S.A. 107, 1301–1306 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Loerting T. et al. How many amorphous ices are there? Phys. Chem. Chem. Phys. 13, 8783–8794 (2011). [DOI] [PubMed] [Google Scholar]
  32. Whiting H. A new theory of cohesion applied to the thermodynamics of liquids and solids. Proc. Am. Acad. Arts Sci. 19, 353–431 (1884). [Google Scholar]
  33. Röntgen W. C. Ueber die Constitution des flüssigen Wassers. Ann. Phys. (Leipzig) 281, 91–97 (1892). [Google Scholar]
  34. Vedamuthu M., Singh S. & Robinson G. W. Properties of liquid water: Origin of the density anomalies. J. Phys. Chem. 98, 2222–2230 (1994). [Google Scholar]
  35. Ponyatovsky E. G., Sinitsyn V. V. & Pozdnyakova T. A. The metastable T–P phase diagram and anomalous thermodynamic properties of supercooled water. J. Chem. Phys. 109, 2413–2422 (1998). [Google Scholar]
  36. Moynihan C. T. Two species/nonideal solution model for amorphous/amorphous phase transition. Mat. Res. Soc. Symp. Proc. 455, 411–425 (1997). [Google Scholar]
  37. Zhang Y. et al. Density hysteresis of heavy water confined in a nanoporous silica matrix. Proc. Natl. Acad. Sci. U.S.A. 108, 12206–12211 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Nagoe A., Kanke Y., Oguni M. & Namba S. Findings of Cp maximum at 233 K for the water within silica nanopores and very weak dependence of the Tmax on the pore size. J. Phys. Chem. B 114, 13940–13943 (2010). [DOI] [PubMed] [Google Scholar]
  39. Liu Y., Panagiotopoulos A. Z. & Debenedetti P. G. Low-temperature fluid-phase behavior of ST2 water. J. Chem. Phys. 131, 104508 (2009). [Google Scholar]
  40. Sciortino F., Saika-Voivod I. & Poole P. H. Study of the ST2 model of water close to the liquid–liquid critical point. Phys. Chem. Chem. Phys. 13, 19759–19764 (2011). [DOI] [PubMed] [Google Scholar]
  41. Kesselring T. A., Franzese G., Buldyrev S. V., Herrmann H. J. & Stanley H. E. Nanoscale dynamics of phase flipping in water near its hypothesized liquid-liquid critical point. Sci. Rep. 2, 474 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Molinero V. & Moore E. B. Water modeled as an intermediate element between carbon and silicon. J. Phys. Chem. B 113, 4008–4016 (2009). [DOI] [PubMed] [Google Scholar]
  43. Limmer D. T. & Chandler D. The putative liquid-liquid transition is a liquid-solid transition in atomistic models of water. J. Chem. Phys. 135, 134503 (2011). [DOI] [PubMed] [Google Scholar]
  44. Moore E. B. & Molinero V. Structural transformation in supercooled water controls the crystallization rate of ice. Nature 479, 506–508 (2011). [DOI] [PubMed] [Google Scholar]
  45. Moore E. B. & Molinero V. Growing correlation length in supercooled water. J. Chem. Phys. 130, 244505 (2009). [DOI] [PubMed] [Google Scholar]
  46. Fisher M. E. Scaling, universality and renormalization group theory. .In Hahne F. J. W., (ed.) Critical Phenomena, Lecture Notes in Physics, vol. 186, 1–139 (Springer, Berlin, 1983).
  47. Behnejad H., Sengers J. V. & Anisimov M. A. Thermodynamic behavior of fluids near critical points. .In Goodwin A. R. H., , Sengers J. V., & Peters C. J. (eds.) Applied Thermodynamics of Fluids chap. 10, 321–367 (RSC Publishing, Cambridge, UK, 2010). [Google Scholar]
  48. Holten V., Bertrand C. E., Anisimov M. A. & Sengers J. V. Thermodynamics of supercooled water. J. Chem. Phys. 136, 094507 (2012). [DOI] [PubMed] [Google Scholar]
  49. Holten V., Kalová J., Anisimov M. A. & Sengers J. V. Thermodynamics of liquid–liquid criticality in supercooled water in a mean-field approximation. Int. J. Thermophys. 33, 758–773 (2012). [Google Scholar]
  50. Eisenberg D. & Kauzmann W. The Structure and Properties of Water, 256–267 (Oxford University Press, New York, 1969). [Google Scholar]
  51. Prigogine I. & Defay R. Chemical Thermodynamics (Longmans, Green & Co., London, 1954). [Google Scholar]
  52. Sotani T., Arabas J., Kubota H. & Kijima M. Volumetric behaviour of water under high pressure at subzero temperature. High Temp. High Pressures 32, 433–440 (2000). [Google Scholar]
  53. Speedy R. J. & Angell C. A. Isothermal compressibility of supercooled water and evidence for a thermodynamic singularity at −45°C. J. Chem. Phys. 65, 851–858 (1976). [Google Scholar]
  54. Ter Minassian L., Pruzan P. & Soulard A. Thermodynamic properties of water under pressure up to 5 kbar and between 28 and 120°C. Estimations in the supercooled region down to −40°C. J. Chem. Phys. 75, 3064–3072 (1981). [Google Scholar]
  55. Glew D. N., Mak H. D. & Rath N. S. Aqueous non-electrolyte solutions: Part VII – Water shell stabilization by interstitial nonelectrolytes. .In Covington A. K., & Jones P., (eds.) Hydrogen-bonded Solvent Systems 195–210 (Taylor & Francis, London, 1968). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplement

srep00713-s1.pdf (507.6KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES