Polymer scaling laws of unfolded and intrinsically disordered proteins quantified with single-molecule spectroscopy

Abstract

The dimensions of unfolded and intrinsically disordered proteins are highly dependent on their amino acid composition and solution conditions, especially salt and denaturant concentration. However, the quantitative implications of this behavior have remained unclear, largely because the effective theta-state, the central reference point for the underlying polymer collapse transition, has eluded experimental determination. Here, we used single-molecule fluorescence spectroscopy and two-focus correlation spectroscopy to determine the theta points for six different proteins. While the scaling exponents of all proteins converge to 0.62 ± 0.03 at high denaturant concentrations, as expected for a polymer in good solvent, the scaling regime in water strongly depends on sequence composition. The resulting average scaling exponent of 0.46 ± 0.05 for the four foldable protein sequences in our study suggests that the aqueous cellular milieu is close to effective theta conditions for unfolded proteins. In contrast, two intrinsically disordered proteins do not reach the Θ-point under any of our solvent conditions, which may reflect the optimization of their expanded state for the interactions with cellular partners. Sequence analyses based on our results imply that foldable sequences with more compact unfolded states are a more recent result of protein evolution.

It has become increasingly clear that the structure and dynamics of unfolded proteins are essential for understanding protein folding (1–3) and the functional properties of intrinsically disordered proteins (IDPs) (4–6). Theoretical concepts from polymer physics (7–9) have frequently been used to describe the properties of unfolded polypeptide chains (4, 10, 11) with the goal to establish the link between protein folding and collapse (12–15). However, the methodology to test many of these concepts experimentally has only become available rather recently (2, 16, 17). A considerable body of experimental and theoretical work suggests that the dimensions of unfolded proteins depend on parameters such as amino acid composition (4), temperature (18), and solvent quality (3, 10, 15, 19). The continuous collapse of polymers has been treated exhaustively by a number of theories (20–24) based on general principles that relate the dimensions and the length of a chain to its free energy. However, a prerequisite for the quantitative application of these theories and their comparison to experimental results is that the dimensions of the Θ-state are known, which serves as an essential reference state. At the Θ-point*, chain–chain and chain–solvent interactions balance such that the polymer is at a critical point, at which the thermodynamic phase boundaries disappear. As a result, the polypeptide chain obeys the same length scaling as an ideal chain without excluded volume and intrachain interactions. However, the Θ-conditions for protein chains are unknown. Besides its importance for obtaining the correct thermodynamic parameters of the chain, such as excluded volume and interaction energies, the Θ-state for proteins has been suggested to be of special biological relevance since folding is predicted to occur most efficiently when the Θ-point coincides with the transition midpoint for folding (9, 25, 26), while several previous results have been taken to suggest that unfolded proteins and folding intermediates are below the Θ-point under physiological conditions (27–30).

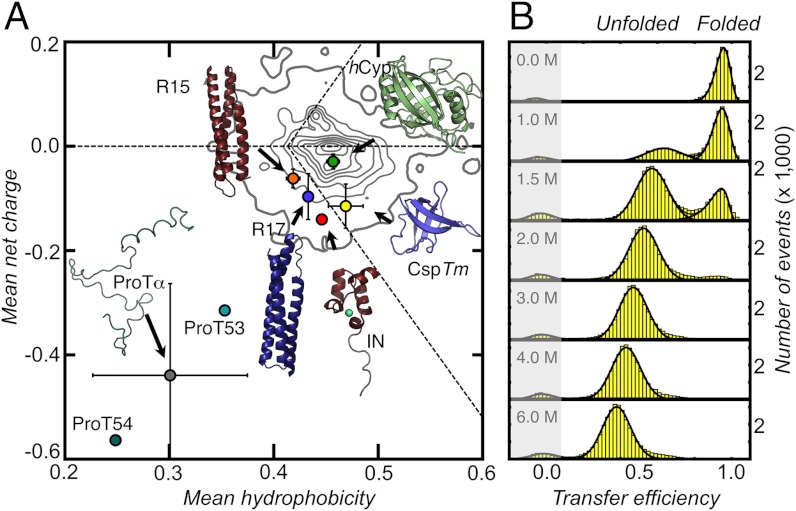
One way of obtaining this missing information is by means of scaling laws (20, 22) that relate the radius of gyration of the unfolded protein (R_G) to its length (N) via R_G ∝ N^ν. By determining the scaling exponent ν at different solvent conditions, the Θ-conditions are identified as the conditions for which ν = 1/2. Here we used single-molecule Förster resonance energy transfer (smFRET) to systematically determine the dimensions of seventeen chain segments with different lengths in six different unfolded proteins at a wide range of denaturant concentrations, resulting in a large data set (Fig. 1A and SI Appendix, Table S1). To investigate the sequence dependence of the Θ-conditions, we chose four foldable proteins [cold shock protein, CspTm (3); cyclophilinA, hCyp (31); spectrin domains R15 and R17 (32)] and two more highly charged IDPs (prothymosin α, ProTα, and the N-terminal domain of HIV Integrase, IN) (4) (Fig. 1A and SI Appendix, Table S1). Estimates for the scaling exponent ν, the Θ-conditions, and the free energy of solvation could be obtained for all six proteins.

Fig. 1.

Structures and amino acid compositions of the proteins used in this study (A) and single-molecule FRET efficiency histograms for CspTm (Csp66, SI Appendix, Table S1) at different concentrations of GdmCl (B). (A) Mean net charge, including the charges of the attached fluorophores, versus mean hydrophobicity per residue for hCyp, CspTm, R15, R17, IN, and ProTα (variants ProT53 and ProT54, SI Appendix) (circles). Error bars are standard deviations of mean net charge and mean hydrophobicity of the different variants of each protein. The density plot represents the distribution of 10,905 monomeric proteins with a sequence similarity ≤ 30% taken from the Protein Data Bank. The horizontal dashed line indicates a mean net charge of zero. Diagonal dashed lines indicate the separation line between intrinsically disordered and folded proteins suggested by Uversky et al. (48).

Results

To probe the dimensions of the unfolded states of the six proteins, we attached AlexaFluor 488 as a donor and AlexaFluor 594 as an acceptor chromophore at different positions within the polypeptide chains (SI Appendix, Table S1). The labeled proteins were investigated with confocal smFRET while freely diffusing in solution. In the resulting transfer efficiency histograms for each protein and variant, up to three peaks are observed: The peak at very high transfer efficiency (E) results from folded molecules, and the peak at E ≈ 0 results from molecules lacking an active acceptor dye (Fig. 1B and SI Appendix, Figs. S1–S3). We focus exclusively on the peak at intermediate transfer efficiencies, which results from unfolded molecules (Fig. 1B). The use of smFRET allows us to discriminate this population of unfolded molecules from folded molecules even in the virtual absence of denaturant (SI Appendix, Figs. S1–S3). With increasing concentration of the denaturant GdmCl, the transfer efficiency distributions of the unfolded subpopulations of all variants show a pronounced shift to lower E values, corresponding to an expansion of the polypeptide chains (Fig. 1B and SI Appendix, Figs. S1–S3), as observed previously for a broad range of proteins and peptides (3, 10, 15, 19, 33).

Chain dimensions from FRET efficiencies.

Quantitative information about the dimensions of the unfolded proteins can be obtained from the average values 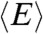of their transfer efficiency peaks. We used the coil-to-globule transition theory of Sanchez (21) to extract the chain dimensions from 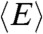. The advantage of this theory is its ability to describe the dimensions of a chain under all solvent conditions by explicitly taking into account effects such as excluded volume, intrachain interactions, and multibody interactions (10, 11, 21). The theory provides an expression for the probability density function of the radius of gyration r_G in the form of a Boltzmann-weighted Flory–Fisk distribution (11, 34):

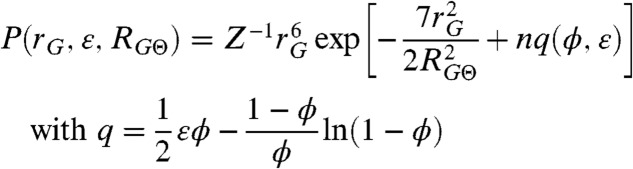[1]

Here, 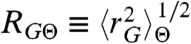is the root mean squared radius of gyration of the Θ-state; ε is the mean interaction energy between amino acids; ϕ is the volume fraction of the chain; n is the number of amino acids in the chain segment probed by FRET; Z is a normalization factor; and q is the excess free energy per monomer with respect to the ideal chain (11). An expression similar to Eq. 1 was also obtained in heteropolymer theories (12, 13), showing that Eq. 1 is not specific for homopolymers (SI Appendix). Note, however, that none of these descriptions take into account effects from sequence complexities; e.g., the patterning of residues.

In order to relate the distribution P(r_G,ε,R_GΘ) to a segment end-to-end distance distribution P(r,ε,R_GΘ), which is required to describe the transfer efficiencies of the polypeptide chains, we used the conditional probability density function P(r|r_G) suggested by Ziv and Haran (11) (SI Appendix, Eq. S1). The observed mean transfer efficiency 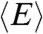is related to Eq. 1 by

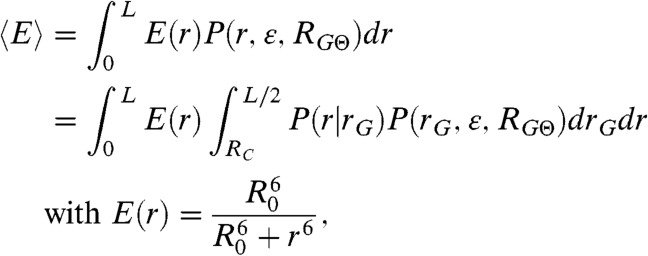[2]

where R₀ is the Förster radius (5.4 nm in our case) and L is the contour length of the protein segment probed. Importantly, the root mean squared radius of gyration of the chain segment, 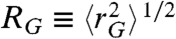, is largely independent of the specific value of R_GΘ (SI Appendix, Fig. S8), which allows us to determine R_G for every protein segment from its mean transfer efficiency, 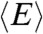. We then use the scaling of R_G with the number of peptide bonds in the unfolded protein segments, R_G ∝ N^ν, to determine R_GΘ from the conditions at which ν = 1/2. With the correct value of R_GΘ, we then determine ε exactly. P(r|r_G) (SI Appendix, Eq. S1) assumes unfolded proteins to be spherical in shape, which is an approximation (35–37), but we investigated the accuracy of Eq. 2 by simulation and found the error in R_G to be ≤ 6% (SI Appendix, Fig. S5).

The radius of gyration of polymers scales with the number of bonds (N) according to the power-law relation R_G = ρ₀N^ν. The specific value of ν depends on the dimensions of the chain, with a value of 3/5 for the expanded coil state (22), 1/2 for the Θ-state, and 1/3 for the most compact globule state (21, 35). In contrast, the value of the prefactor ρ₀ depends on the details of the monomer and the bond geometry. For a self-avoiding chain with scaling exponent ν, R_G is given by (38)

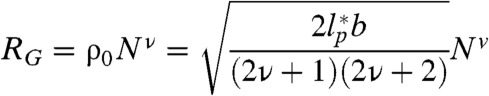[3]

(The derivation for a special case can also be found in ref. 34). Here, b = 0.38 nm (39) is the distance between two C_α-atoms, and 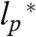is the persistence length (SI Appendix). Values for ρ₀ from experiments (0.19 ± 0.03 nm and 0.2 ± 0.1 nm) (40, 41) and simulations (0.22 ± 0.02 nm, 0.24 nm, 0.198 ± 0.037 nm, and 0.199 nm) (42–45) obtained under good solvent conditions (ν = 3/5) yield 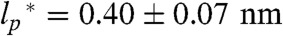, in agreement with persistence lengths from force spectroscopy experiments (39). Since the range of segment lengths accessible with smFRET is not broad enough to determine ρ₀ independently, we fixed 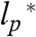(but not ρ₀) to this value of 0.40 nm. For comparison, a free fit of the length scaling of R_G for 10,905 folded proteins selected from the Protein Data Bank results in ν = 0.34 and a persistence length of 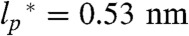(Fig. 2) (35), but even using this value for our analysis as an upper bound does not change our conclusions (SI Appendix).

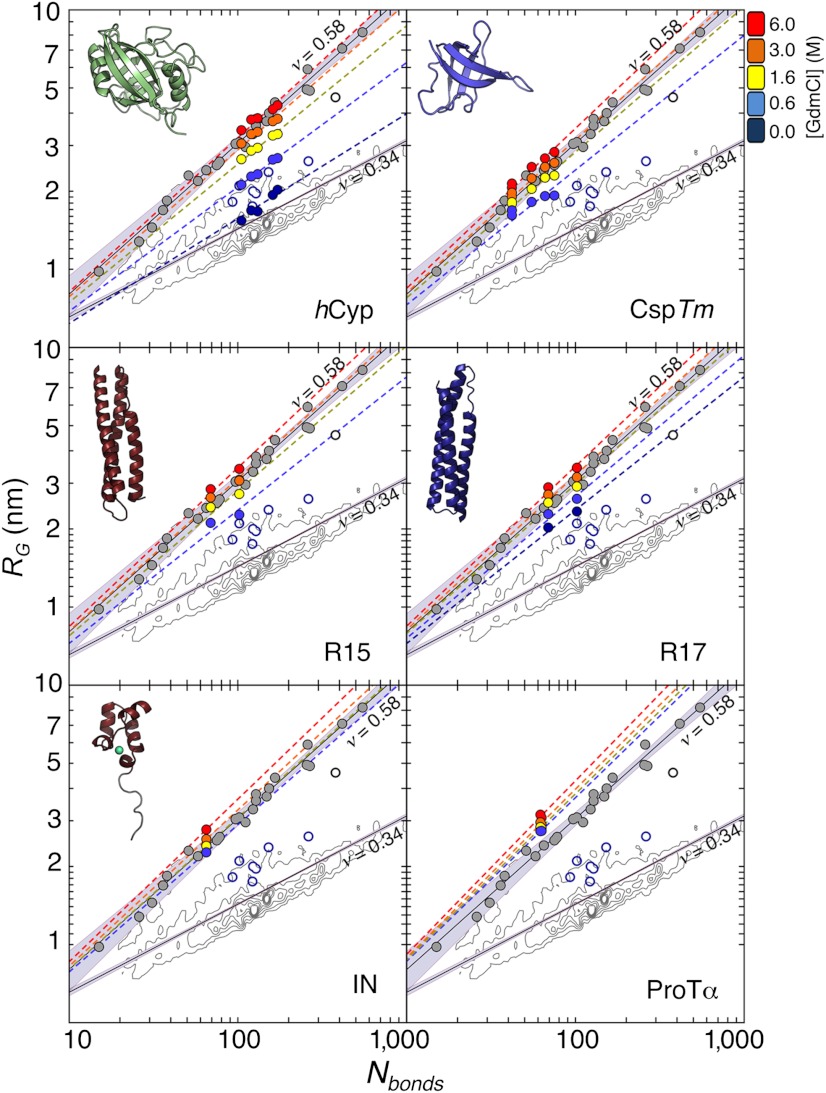
Fig. 2.

Radius of gyration, R_G, for all proteins and variants as a function of the number of bonds, N_bonds = N + l, at different GdmCl concentrations (see color scale). Each dye linker was estimated to be equivalent to 4.5 peptide bonds (l = 9) (61). Colored dashed lines are fits according to Eq. 3 with 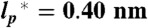. The contour plots represent the distribution of R_G values for the folded proteins shown in A. Gray circles are the R_G values determined for unfolded proteins via SAXS, taken from Kohn et al. (40). Open blue circles are R_G values of denatured proteins under native conditions determined with SAXS, taken from Uzawa et al. (30). Black solid lines are fits of the data taken from Kohn et al. (40) and of the 10,905 monomeric native proteins from the Protein Data Bank with Eq. 3. The resulting scaling exponents are indicated.

Identifying the Θ conditions from FRET and two-focus FCS.

Previous measurements of the scaling exponent ν for unfolded proteins at high concentrations of denaturant resulted in values between 0.50 and 0.67 (40, 41, 46, 47). In the most extensive study, R_G for 28 proteins was determined by SAXS in the presence of high concentrations of GdmCl or urea (40). From this data set, ν = 0.598 ± 0.028 was obtained, indistinguishable from the theoretical prediction of 3/5 for an excluded volume chain (22), which indicates that unfolded proteins are in the coil-state and in good solvent at high concentrations of denaturant (Fig. 2). Under comparable solvent conditions (6 M GmdCl), we found the R_G values from smFRET to be in remarkable agreement with R_G = 0.2 nm N^3/5, the scaling law obtained with SAXS (40) (Fig. 2). The scaling exponents we obtained at 6 M GdmCl range from 0.59 for hCyp to 0.63 for the hydrophilic IDP integrase. The high ν-value of prothymosin α (ν = 0.67), a highly negatively charged IDP (4, 48), points towards a specific interaction of the chain with the denaturant GdmCl (4), as previously suggested based on molecular dynamics simulations (49).

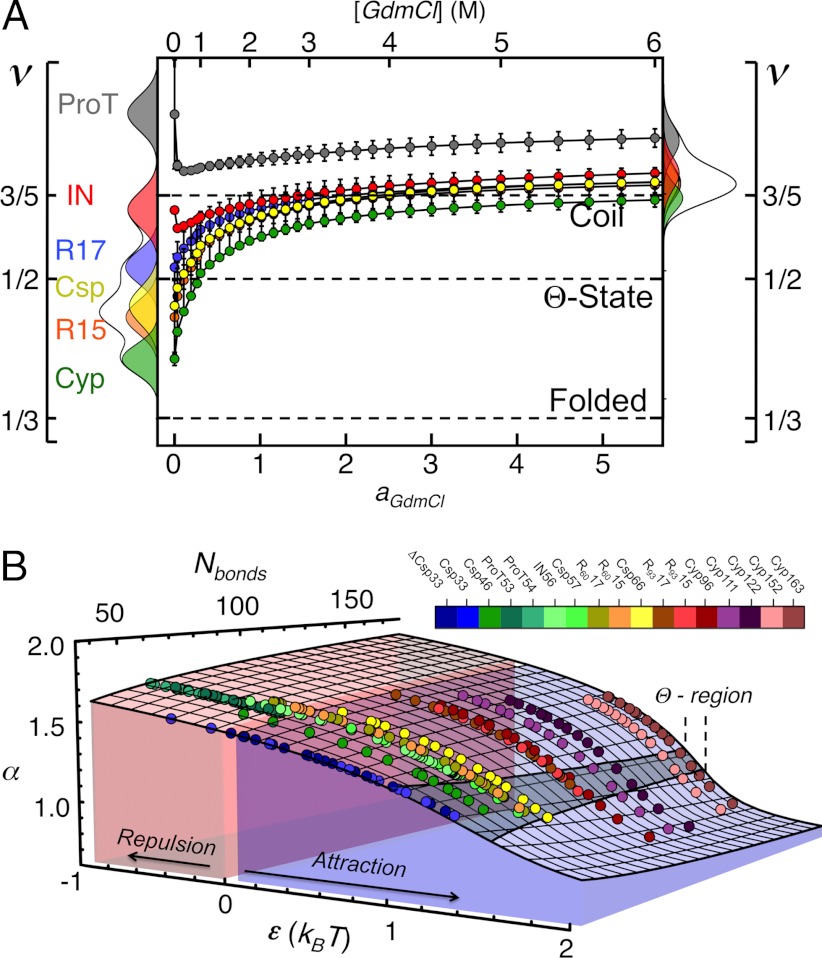
A decrease in the concentration of GdmCl leads to a compaction and to a corresponding decrease of ν for all six unfolded proteins (Figs. 2 and 3A). While the values of ν are close to 3/5 at high GdmCl concentrations for all proteins, they diverge with decreasing denaturant (Fig. 3A). Due to electrostatic repulsion at low ionic strength, the scaling exponents for the two charged IDPs, IN and ProTα, increase in water (4), reaching values of 0.58 for IN and 0.70 for ProTα. In contrast to the IDPs, the scaling exponents of the four foldable proteins decrease monotonically with decreasing solvent quality, but a substantial divergence of their scaling exponents is observed at the lowest denaturant concentrations, suggesting an increasing effect of sequence composition on the chain dimensions. The scaling exponents range from 0.40 for the most hydrophobic sequence (hCyp) to 0.51 for the most hydrophilic (R17), with a mean value of ν = 0.46 ± 0.05 in water—i.e., close to the Θ-regime.

Fig. 3.

Scaling exponents (A) and phase transition surface (B) for the unfolded proteins and variants of this study. (A) Error bars represent the uncertainties of the fits shown in Fig. 2, and the distributions in water (Left) and 6 M GdmCl (Right) reflect the changes in the scaling exponents upon variation of 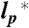by ± 10% around its estimated value of 0.40 nm. (B) Comparison between experimentally determined expansion factors α (filled circles) for all variants and proteins of this study and the numerically computed expansion factors α with our estimate for R_GΘ using Eq. 1. Shaded volumes indicate the regimes of attractive (ε > 0) and repulsive (ε < 0) intrachain interaction energies. The gray shaded region indicates the transition regime between α_c = 1, the critical value for infinitely long chains, and α_c = 1 + (19/22)ϕ₀, the approximation for finite chains as given by Sanchez (21). Here, ϕ₀ is the volume fraction of the Θ-state relative to the most compact state (SI Appendix).

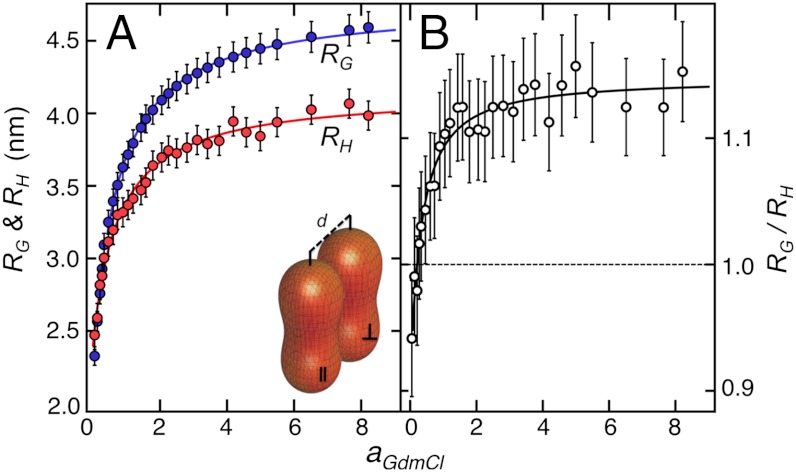
An independent experimental approach to probe the collapse transition and the resulting change in the scaling exponents of polymers is the comparison of R_G with the average hydrodynamic radius, R_H. While both R_G and R_H are measures of the dimensions of the chain, their relative magnitude depends on the scaling regime (20), and the ratio R_G/R_H has thus been used to locate the collapse transition (50). To determine R_H with sufficient precision, we used two-focus fluorescence correlation spectroscopy (2f-FCS) (51) (SI Appendix, Fig. S4), where the crosscorrelation between the fluorescence intensities from two partially overlapping foci is used to determine the diffusion time. The distance between the foci was determined to high accuracy by calibration with dynamic light scattering data (SI Appendix), resulting in very accurate translational diffusion coefficients and hydrodynamic radii. Fig. 4A shows the comparison of R_H from 2f-FCS with R_G determined from smFRET as a function of the GdmCl activity for singly labeled unfolded hCyp, the largest polypeptide chain of this study. As expected, R_H increases with increasing concentration of GdmCl, confirming the expansion of the unfolded protein observed with smFRET (Fig. 4A). As observed previously (10, 41), the ratio R_G/R_H does not approach the expected limit of 1.5 at high concentrations of GdmCl. This might be the result of residual intrachain interactions even at high GdmCl concentrations, or of a direct interaction of guanidinium ions with the unfolded polypeptide chain (49), leading to slower diffusion and higher apparent values for R_H. At low GdmCl activities, where the latter effect should be negligible, R_G/R_H decreases in a cooperative fashion, indicating a pronounced change in the scaling behavior and the scaling exponent of unfolded hCyp. The maximally compact state (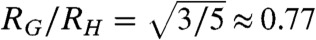) (20, 50), however, is not reached even at the lowest accessible GdmCl activities (a_GdmCl = 0.05; GdmCl = 0.25 M) (Fig. 4B), as suggested also by the scaling exponent of ν = 0.45 ± 0.03. These results support our estimates for the scaling exponents of unfolded hCyp from smFRET (Fig. 3A).

Fig. 4.

Comparison between the radii of gyration and the hydrodynamic radii for hCyp as a function of GdmCl activity. (A) Radius of gyration, R_G, (blue circles) for Cyp163 (SI Appendix, Table S1) rescaled to the full length sequence (N_bonds = 166 + 9) according to the scaling laws shown in Fig. 2, and hydrodynamic radius (R_H) determined from 2fFCS (red circles) for the donor-labeled variant CypV2C as a function of the denaturant activity, a_GdmCl. Error bars for R_G were estimated from the change in 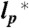by ± 10%. Error bars for R_H represent the standard deviation of ± 0.1 nm estimated from the calibration of the instrument (SI Appendix). Solid lines are fits according to y = y(0) + γa_GdmCl/(K + a_GdmCl), where y is R_G or R_H, respectively. Inset: Arrangement of the foci with parallel and vertical polarization in the 2f-FCS setup (51). (B) R_G/R_H as a function of the GdmCl activity. Error bars result from the error propagation of the uncertainties shown in A. The solid line is the ratio of the fits shown in A.

Interaction energies and the Tanford transfer model.

The determination of the scaling exponents (Fig. 3A) now allows us to compute the absolute values of the intrachain interaction energies ε for the six unfolded proteins from the measured transfer efficiencies using Eq. 2. The radius of gyration of the Θ-state, which we found to be 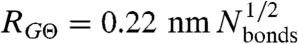(Eq. 3), the interaction energy ε, and the chain length N then fully determine the phase transition behavior of the unfolded chains within the framework of Sanchez theory (21). A comparison of the experimental data with a numerical evaluation of Eq. 1 in terms of the expansion factor α = R_G/R_GΘ shows how the cooperativity of the collapse transition increases with increasing chain length (Fig. 3B). Strictly speaking, a second-order phase transition of the Landau type is only obtained in the limit of N → ∞ (21). Hence, for the finite size of the proteins investigated here, with 33 ≤ N ≤ 163, the transitions are pseudo-second-order, resulting in a rounding of the transition (21, 52).

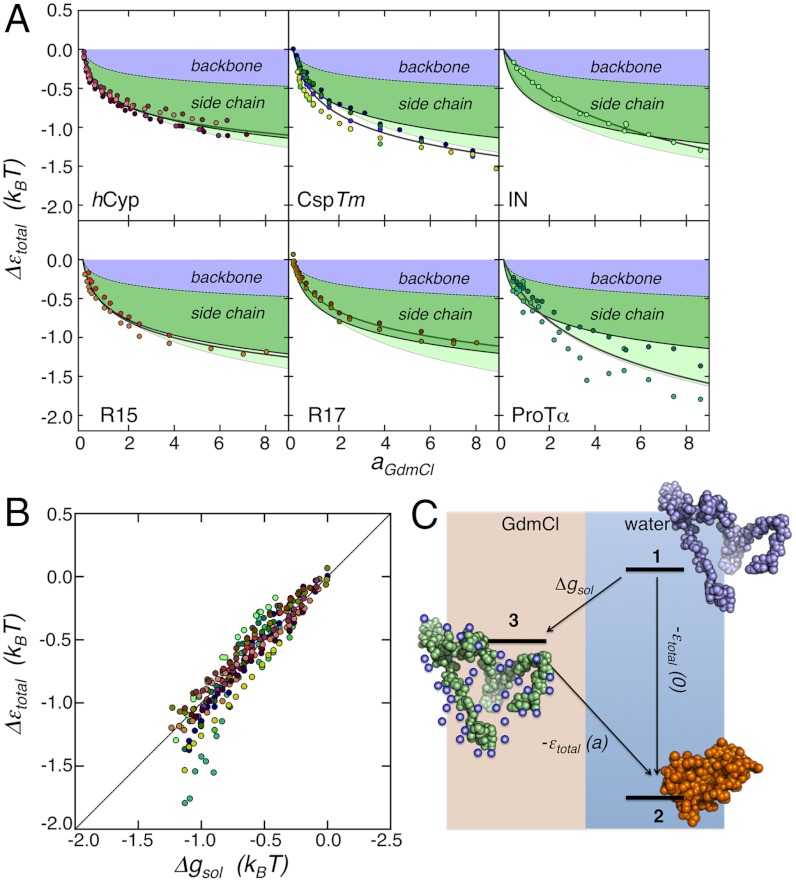
Since the absolute value of ε depends on specific numerical factors in the theory, it is instructive to investigate the difference between the interaction energies in water, ε(0), and GdmCl solution ε(a_GdmCl), respectively, Δε = ε(0) - ε(a_GdmCl). The values of Δε determined for the different interdye variants of length n_DA can then be rescaled to the full-length protein (n_total) according to Δε_total = Δε(n_DA/n_total)^1/2 (SI Appendix). Δε_total shows a pronounced dependence on the GdmCl activity for all six proteins (Fig. 5A). The effect of GdmCl on protein chains can be modeled as a preferential interaction of the denaturant with the polypeptide chain (49, 53). This weak-binding model describes the solvation free energy for the polypeptide chain as Δg_sol = -βγ log(1 + Ka_GdmCl), where γ corresponds to the effective number of binding sites for GdmCl molecules, K is the apparent equilibrium constant for binding, and β = (RT)^-1, where R is the ideal gas constant and T is the temperature. Fits with this model provide a good description of the change in Δε_total with GdmCl activity for all proteins investigated here (Fig. 5A). In addition, we find a remarkable agreement of the absolute values of Δε_total with the transfer free energies (Δg_sol) of the polypeptide chains from water into GdmCl solutions (54) calculated based on their amino acid sequences (Fig. 5 A and B and SI Appendix, Fig. S6). This accordance suggests that the expansion of unfolded proteins, at least for the proteins investigated here, can be explained quantitatively by the change in free energy upon interaction of GdmCl molecules with the chain, implying Δε_total = Δg_sol. This finding strongly supports the use of this equality in a heteropolymer theory of protein folding (13) and in the molecular transfer model, where it was employed to predict the dimensions of denatured proteins at varying concentrations of GdmCl (14). A simple thermodynamic cycle, in which the total intrachain interaction energy, -ε_total(0), is reduced by the free energy of transferring the amino acid sequence from water to GdmCl (Δg_sol), illustrates the effect of GdmCl on the intrachain interaction energy, -ε_total(a), and R_G (Fig. 5C). Finally, these results directly support the correlation between the m-value for folding and the free energy change of collapse predicted by Alonso and Dill (13) and found experimentally by Ziv and Haran (11) (SI Appendix).

Fig. 5.

Relative intrachain interaction energies, Δε_total, as a function of GdmCl activity, and comparison between Δε_total and Δg_sol. (A) Δε_total for the proteins of this study (circles, colors as in Fig. 3B) together with the fits according to the Schellman weak binding model (gray solid line), and, for comparison, the Tanford transfer free energies Δg_sol calculated for the full-length sequences (black line) according to ref. 54. Contributions from the backbone and side chains to Δg_sol are shaded in blue and green, respectively. The effect of the δg_sol-values estimated for Glu and Asp on Δg_sol is indicated as a light green shaded area. From the discrepancy between Δε_total and Δg_sol for ProTα, we obtained δg_sol for Glu and Asp at 6 M GdmCl to be -798 cal mol^-1 (SI Appendix, Eq. S14 and Table S2). (B) Correlation between Δε_total and Δg_sol and thermodynamic cycle (C) illustrating the effect of GdmCl on the chain energy as explained in the main text. State 1 is a hypothetical expanded unfolded state in water and state 3 is the same state in the presence of GdmCl. State 2 is the collapsed unfolded state in water.

Effect of sequence composition on the scaling exponent.

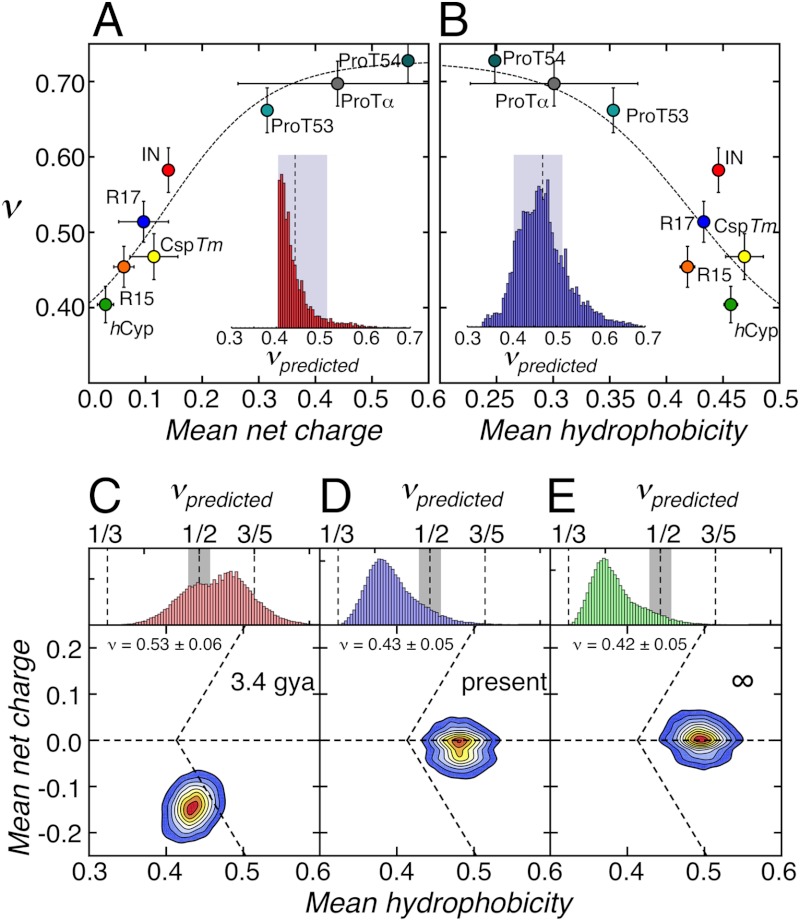
A detailed analysis of the effect of sequence composition on the scaling exponents of the six proteins in water reveals a pronounced positive correlation between ν and the net charge of the polypeptide (Fig. 6A), and a negative correlation between ν and sequence hydrophobicity (Fig. 6B). A similar correlation has recently been observed in molecular dynamics simulations of protamines, positively charged intrinsically disordered peptides (55). These correlations allow us to estimate the scaling exponents also for other proteins. Values of the scaling exponents predicted for the unfolded states of 10,905 monomeric proteins from the Protein Data Bank, based on the correlation between ν and net charge (Fig. 6A, Inset), and ν and hydrophobicity (Fig. 6B, Inset) indicate that the majority of these proteins fall into the range of the scaling exponents observed with the foldable proteins in this study. A value of 0.45 ± 0.03 is obtained as a mean value of the two distributions, remarkably close to the value expected for the Θ-state (ν = 1/2).

Fig. 6.

Scaling exponents, sequence composition, and evolutionary trends. (A) Correlation between the scaling exponents of the proteins and the net charges of their sequences at pH 7. (B) Correlation between the scaling exponents of the six proteins and the mean hydrophobicity of their sequences. Horizontal error bars are the standard deviations as shown in Fig. 1A; vertical error bars reflect the changes in the scaling exponents upon variation of 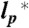by ± 10%. Dashed lines in A and B are global fits according to empirical equations chosen to give reasonable limits of ν (SI Appendix, Eq. S29). Insets: Frequency histograms of the predicted scaling exponents for the unfolded states of the proteins selected from the pdb shown in Fig. 1 A and B based on the fits in A (red) and B (blue), respectively. The shaded areas indicate the regime of scaling exponents between ν = 0.40 and ν = 0.51, which encompass 93% of proteins in A and 71% of proteins in B. (C–E) Distributions of predicted scaling exponents (Top) and mean net charge versus hydrophobicity (Bottom) for 50,000 amino acid sequences drawn randomly from the amino acid frequency distribution of the last universal ancestor (C), current proteins (D), and predicted for the distant future (E). The mean scaling exponents are indicated. See SI Appendix, Eqs. S29–S31 for calculation of the scaling exponents. Amino acid frequencies were taken from table 3 in ref. 60.

Discussion

In order to quantify the thermodynamics of unfolded proteins with polymer theory, information about the Θ-point of the unfolded protein is indispensable (11, 21). Using smFRET, we determined the effective Θ-point of unfolded polypeptide chains by extracting the scaling exponents for four foldable proteins (CspTm, hCyp, R15, R17) and two intrinsically disordered proteins (ProTα and IN). The R_G-values and scaling exponents obtained at high GdmCl are in quantitative agreement with values from SAXS (40) (Fig. 2) and SANS (41), indicating that smFRET is not only a precise but also an accurate method to determine the chain dimensions of unfolded proteins. With the ability to resolve subpopulations, smFRET allows us additionally to obtain the full range of scaling exponents down to physiological solvent conditions.

The higher net charge of the two intrinsically disordered proteins IN and ProTα (Fig. 1A) affects the scaling exponents and leads to an increase of ν at very low GdmCl concentrations (Fig. 3A). The resulting expanded conformations under physiological conditions might reflect an optimization of the sequences for the interaction with their cellular ligands, in keeping with suggestions from theory and simulations that binding kinetics can be accelerated in extended unfolded conformer ensembles (5). In contrast to the IDPs, the scaling exponents of the four foldable proteins decrease monotonically with decreasing solvent quality (Fig. 3A). However, with a mean scaling exponent of 0.46 ± 0.05 in water, they are still much more expanded than a dense globule, which would obey a scaling exponent of 1/3, as observed for folded globular proteins. Note that the scaling exponents of the two coexisting regimes, folded and unfolded, in water are significantly different (ν_folded = 0.34, ν_unfolded ≈ 0.46). Although theories for homopolymers predict a phase separation into compact globules (ν = 1/3) and expanded chains (ν = 1/2) in poor solvent at high concentrations of the polymer (23), these theories are insufficient to reconcile the two coexisting scaling regimes under our experimental conditions of almost infinite dilution.

In heteropolymer theory, the effective intrachain interaction energy can be approximated by the sum of two mean-field terms, one for backbone interactions (ε_bb) and one for side-chain interactions (ε_sc), ε = ε_bb + ε_sc. Simulations (29) and experiments (33, 56) suggest that backbone interactions of polypeptide chains are attractive in water, implying that water is a poor solvent for the polypeptide chain backbone with ε_bb > 1. Our mean scaling exponent of 0.46 ± 0.05 of unfolded proteins in water (i.e. ε ≈ 1) (Fig. 3 A and B) would then imply that ε_sc is on average repulsive, i.e. ε_sc < 0. Hence, backbone and side-chain interactions nearly compensate in water, leading to a chain close to its critical point. In case the cooperative formation of specific interactions in folded proteins exceeds the mean-field energy term ε, compact folded proteins with ν = 1/3 and expanded unfolded proteins with ν > 1/3 can coexist. This scenario is in accord with lattice simulations that suggest that the folding of proteins can occur without populating a dense unstructured globule (57).

What do our results imply for protein folding? Although a collapse to a very dense state (ν = 1/3 and R_G/R_H = 0.77) favors folding by reducing the conformational entropy, it could drastically slow down the dynamics of the chain (57) by processes such as internal friction, which have been shown to increase with increasing compaction of unfolded proteins (16, 17, 33, 58). However, especially during the early stages of the folding process, many interactions have to be sampled to find the correct contacts that incrementally decrease the energy of the protein. Simulations based on simple models predict that unfolded chains close to the Θ-regime can accomplish this optimization process more efficiently than chains that are in the completely collapsed globule regime (9, 25, 26). Our results for hCyp, CspTm, R15, and R17 (Figs. 2 and 3), and a comparison of their hydrophobicity and net charge with those of a large number of foldable protein sequences (Fig. 6) implies that natural sequences are indeed close to this regime, and only very few proteins are expected to reach the maximally compact regime with ν = 1/3 in their unfolded state (Fig. 6). However, not only extreme compaction, but also expansion caused by a high net charge of the polypeptide (4, 55) can impede folding, as exemplified by IDPs that are folding incompetent without their biological ligands (48). An intermediate regime of compaction as prevalent in current sequences (Fig. 6) therefore indeed seems most favorable for folding. Within this regime, however, topology-specific effects such as contact order (59) appear to play the dominant role in determining the folding rates of current foldable proteins.

The correlations among net charge, hydrophobicity, and scaling exponents (Fig. 6) finally also allow us to assess the change in average chain dimensions during protein evolution. Based on bioinformatics analyses (60), ancestral proteins are assumed to have consisted of only eight to ten different amino acids with high average hydrophilicity (Fig. 6 C–E). The resulting scaling exponent of 0.53 ± 0.06 for these ancestral proteins (SI Appendix, Eqs. S29–S31) is close to what we observe for current IDPs, implying that IDPs may be remnants of ancestral protein sequences, whereas foldable sequences with more compact unfolded states are a more recent result of protein evolution (Fig. 6 C–E).

Materials and Methods

Details of the expression, purification, and labeling of the protein variants and single-molecule measurements are described in detail in the SI Appendix.