Abstract
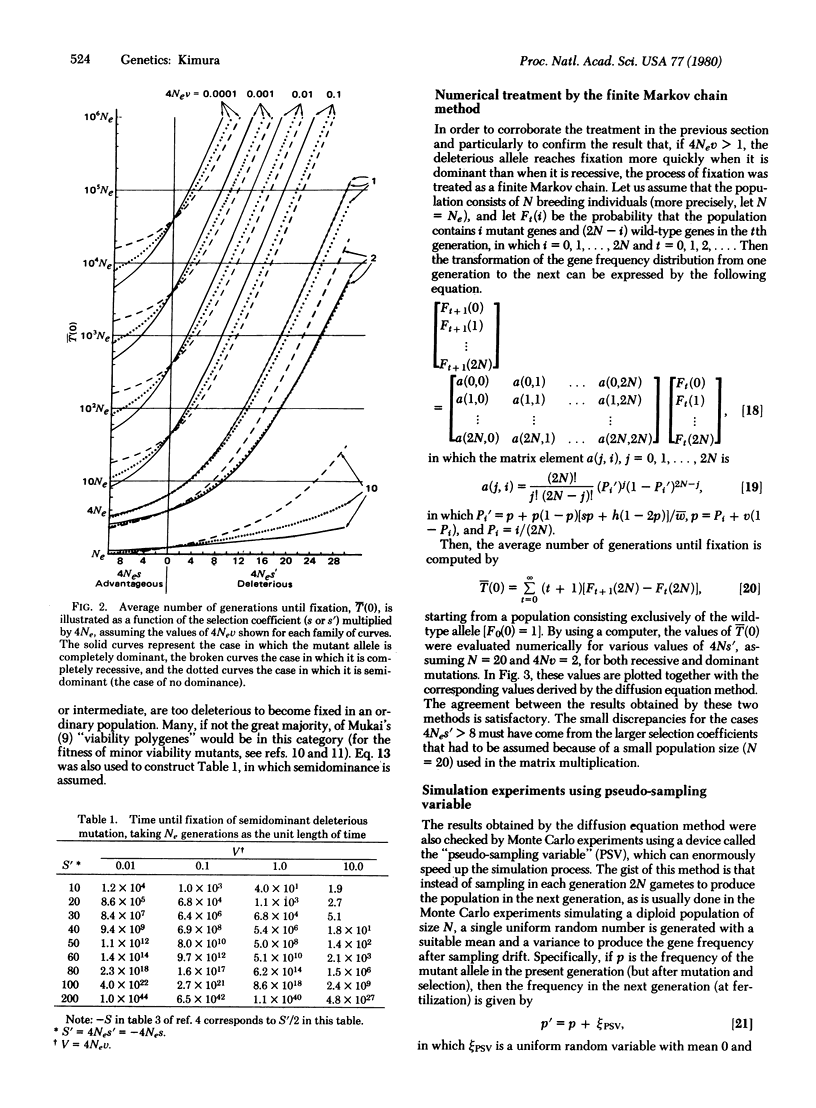
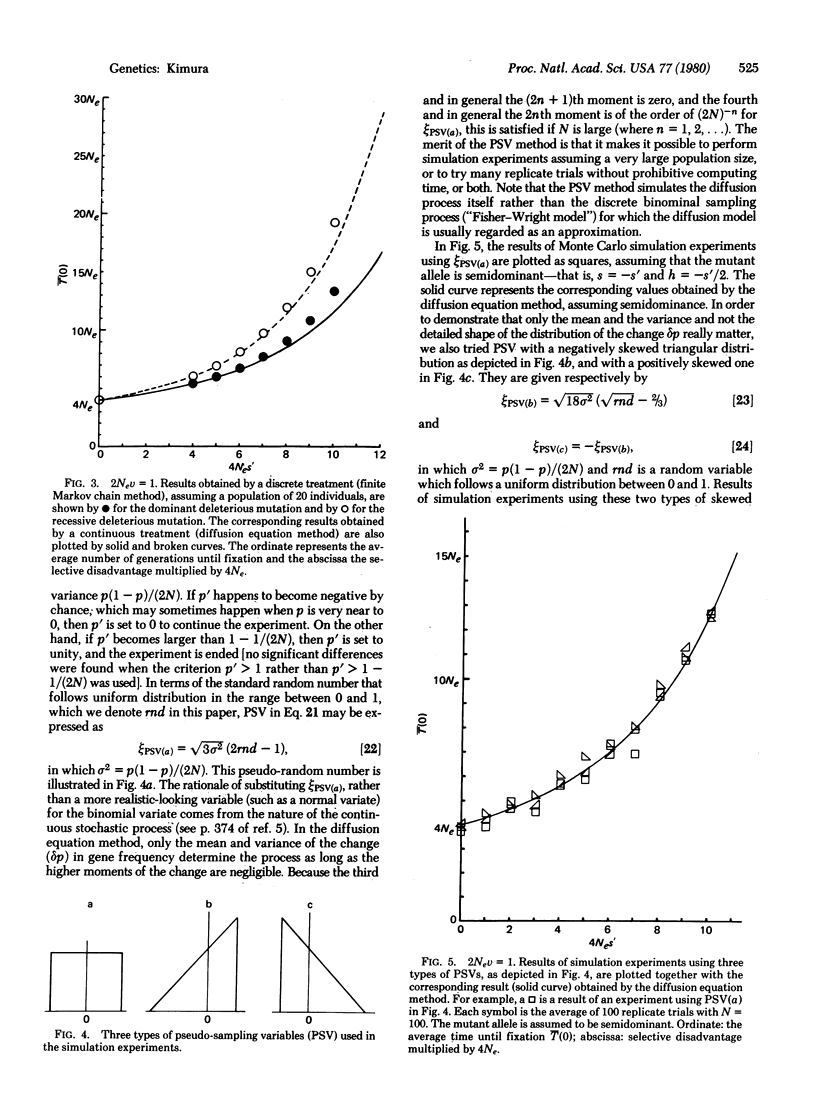
We consider a single locus, and denote by A the wild-type allele and by A′ the mutant allele that is produced irreversibly in each generation from A at the rate v. Let 1 + s, 1 + h, and 1 be, respectively, the relative fitnesses of mutant homozygote A′A′, mutant heterozygote A′A, and wild-type homozygote AA. Then, it is shown, on the basis of the diffusion equation method, that the average time until fixation of the mutant allele (A′) in a randomly mating population of effective size Ne, given that the initial frequency is p, is [Formula: see text] in which B(x) = (S/2)x2 + Hx(1 - x), S = 4Nes, H = 4Neh, and V = 4Nev. Of particular interest are the cases in which the mutant allele is deleterious (s = -s′, s′ > 0). Three cases are considered; the mutant is: (i) completely dominant s = h = -s′, (ii) completely recessive s = -s′, h = 0, and (iii) semidominant s = -s′, h = -s′/2, in which s′ is the selection coefficient against the mutant homozygote. It is shown that the average time until fixation is shorter when the deleterious mutant allele is dominant than when it is recessive if 4Nev is larger than 1. On the other hand, the situation is reversed if 4Nev is smaller than 1. It is also shown that for a mutant allele for which Nes′ > 10, it takes such a long time until fixation that we can practically ignore the occurrence of random fixation of a deleterious allele under continued mutation pressure. To supplement the analytical treatment, extensive simulation experiments were performed by using a device called the pseudo-sampling variable, which can enormously accelerate the process of simulation by a computer. This method simulates the diffusion process itself rather than the binominal sampling process (in population genetics the diffusion model is usually regarded as an approximation of the discrete binomial sampling process).
Keywords: population genetics, evolution, stochastic process, degeneration of character, Monte Carlo simulation
Full text
PDF


Selected References
These references are in PubMed. This may not be the complete list of references from this article.
- Crow J. F., Kimura M. Efficiency of truncation selection. Proc Natl Acad Sci U S A. 1979 Jan;76(1):396–399. doi: 10.1073/pnas.76.1.396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crow J. F. Minor viability mutants in Drosophila. Genetics. 1979 May;92(1 Pt 1 Suppl):s165–s172. [PubMed] [Google Scholar]
- Felsenstein J. The evolutionary advantage of recombination. Genetics. 1974 Oct;78(2):737–756. doi: 10.1093/genetics/78.2.737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haigh J. The accumulation of deleterious genes in a population--Muller's Ratchet. Theor Popul Biol. 1978 Oct;14(2):251–267. doi: 10.1016/0040-5809(78)90027-8. [DOI] [PubMed] [Google Scholar]
- Li W. H., Nei M. Persistence of common alleles in two related populations or species. Genetics. 1977 Aug;86(4):901–914. doi: 10.1093/genetics/86.4.901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MUKAI T. THE GENETIC STRUCTURE OF NATURAL POPULATIONS OF DROSOPHILA MELANOGASTER. I. SPONTANEOUS MUTATION RATE OF POLYGENES CONTROLLING VIABILITY. Genetics. 1964 Jul;50:1–19. doi: 10.1093/genetics/50.1.1. [DOI] [PMC free article] [PubMed] [Google Scholar]


