On the rules of integration of crowded orientation signals

Abstract

Crowding is related to an integration of feature signals over an inappropriately large area in the visual periphery. The rules of this integration are still not well understood. This study attempts to understand how the orientation signals from the target and flankers are combined. A target Gabor, together with 2, 4, or 6 flanking Gabors, was briefly presented in a peripheral location (4° eccentricity). The observer's task was to identify the orientation of the target (eight-alternative forced-choice). Performance was found to be nonmonotonically dependent on the target–flanker orientation difference (a drop at intermediate differences). For small target–flanker differences, a strong assimilation bias was observed. An effect of the number of flankers was found for heterogeneous flankers only. It appears that different rules of integration are used, dependent on some salient aspects (target pop-out, homogeneity–heterogeneity) of the stimulus pattern. The strategy of combining simple rules may be explained by the goal of the visual system to encode potentially important aspects of a stimulus with limited processing resources and using statistical regularities of the natural visual environment.

1. Introduction

At present, a majority of researchers seem to agree that crowding is related to the integration of feature signals over an inappropriately large area in the visual periphery (e.g., Levi, Hariharan, & Klein, 2002; Pelli, Palomares, & Majaj, 2004). However, the rules of this integration are far from being understood.

Most frequently, the integration of crowded features has been studied using orientation as an example of feature dimension. Parkes, Lund, Angelucci, Solomon, and Morgan (2001) asked observers to discriminate the target orientation (clockwise or anticlockwise from horizontal). The target was surrounded by different numbers of horizontal or tilted flankers. They found that a simple rule of averaging could explain their experimental data. Solomon, Felisberti, and Morgan (2004) used a similar task and varied systematically the orientations of flankers. They measured both sensitivity (reciprocal of orientation discrimination threshold) and bias (systematic error) as dependent on the orientation of flankers. They could not explain the results by any averaging model. Instead, they suggested a model with lateral inhibition and amplification. Baldassi, Megna, and Burr (2006) modified the clockwise–anticlockwise task to gain more information about the perceived orientations. Their observers had to estimate the perceived target orientation either by choosing one from 12 response probes or by rotating a response probe until it matched the target orientation. Gheri and Baldassi (2008) applied this method to traditional crowding stimuli. These studies also reject simple averaging and suggest that some combination of averaging and selection of an object, maximally different from the reference orientation, can explain their results.

In all these studies, orientation of the target varied around some natural reference value (horizontal or vertical), and the main task was to discriminate between the clockwise and anticlockwise tilt, relative to the reference. It is possible that the task and the set of stimuli play some role in the observed rules of integration. For example, a max rule may be optimal only when the target is the maximally tilted object among flankers.

Obviously, the averaging model should fail when the orientation differences between objects become large. Actually, there is no meaningful average for two orthogonal orientations (e.g., Mardia & Jupp, 2000). The crowding studies where objects with orthogonal orientations have been used are consistent with the notion of positional uncertainty or random selection of objects, with some preference for the target location (Põder, 2008; Põder & Wagemans, 2007). This is well in accordance with many studies that have used letters as stimuli (e.g., Huckauf & Heller, 2002; Nandy & Tjan, 2007). However, this account may be valid for orthogonal orientations only.

Recently, Greenwood, Bex, and Dakin (2009) attempted to discriminate averaging and substitution/random selection models experimenting with another visual feature—the relative position of line segments. Their analysis showed that the results were consistent with a weighted averaging of the target and flanker positions.

The purpose of this study was to examine the roles of simple mechanisms, such as averaging and random selection, in the integration of orientation signals. In this study, a novel design of experiment was used. I combined the target identification task (Baldassi et al., 2006) with the systematic variation of target–flanker difference (Solomon et al., 2004). To avoid any effects of a fixed reference orientation, the target and flanker orientations were chosen from a set of equally spaced orientations around the clock. I used relatively simple sets of flankers that should discriminate the elementary pooling mechanisms. In addition to the target–flanker orientation difference, the number of flankers was also varied.

2. Methods

The stimuli were presented on a 15-inch cathode ray tube (CRT) monitor with a resolution of 1,024 × 768 pixels. They were composed of Gabor patches—cosine gratings, windowed by a circular Gaussian. The sigma of the window was equal to half of the wavelength. The spatial frequency was approximately 6 cpd. The orientation of Gabors was selected from the eight possible orientations (from 0 to 157.5°, with steps of 22.5°). The stimuli were presented on a gray background (with a luminance of about 50 cd/m²). The contrast of the stimuli was 90%. The luminance function of the monitor was measured by a Hagner EC1 photometer and approximated by a power function. The inverse of this function was used for the gamma correction.

On each trial, a group of Gabor patches was presented for 60 ms, unpredictably either left or right from the fixation point. The Gabor positioned in the center of the group was the target. It was surrounded by two, four, or six flankers. The eccentricity of the target was 4°. The distance of the flankers from the target (measured from center to center) was 0.4° (0.1 E [E –is the eccentricity of the target]). The flankers were located in equal steps around the target; the angular position of the first flanker was selected randomly. The observer's task was to identify the orientation of the target and ignore the flankers. After exposure of a stimulus, the observer indicated his/her response by clicking a patch with closest to the perceived target orientation in the response panel. An example of stimuli and the response panel are shown in Figure 1(a) and (b). No feedback about the accuracy was provided. The orientation of the target, as well as the flankers, was random. There were two conditions of flankers' orientations (mixed within the blocks of trials). In the first condition, all flankers had the same orientation [varied independently of the target orientation; Figure 1(c)]. In the second condition, there were two orientations of flankers, symmetrical relative to the target orientation, and equal numbers of flankers with both orientations [e.g., two flankers tilted 45° clockwise and two other flankers 45° anticlockwise from the target orientation; Figure 1(d)]. The symmetry constraint creates a kind of statistical dependence between the target and two groups of flankers in this condition. However, it seems unlikely that the observers could use this regularity because the trials of different conditions were mixed, and naive observers had no idea how the flanker orientations were selected.

Figure 1.

Examples of stimuli used in this study. An example of stimulus display (a). Response panel (b). Examples of stimuli with homogeneous flankers (c), and with flankers, symmetrical relative to the target orientation (d).

Three observers took part in the experiment: the author and two other observers, who were uninformed about the theoretical background and the methods of stimulus selection. Each observer ran 1,200 trials. The experiment was run in blocks of 100 trials. The number of flankers was held constant within a block.

3. Results

The distributions of responses relative to target orientation (pooled across the absolute orientations) are given in Figures 2 and 3. Figure 2 depicts the results for three individual observers and Figure 3—for different numbers of flankers. The differences across observers seem to be modest and quite random. The effect of the number of flankers is more interesting. While the curves of different numbers of flankers virtually overlap for the homogeneous flankers, there is a clear decrease in correct (target) responses with increasing number of flankers for the condition with two symmetrical flanker orientations (see Figure 3). This effect is most salient for the condition with maximum flanker–flanker difference (±45° flankers).

Figure 2.

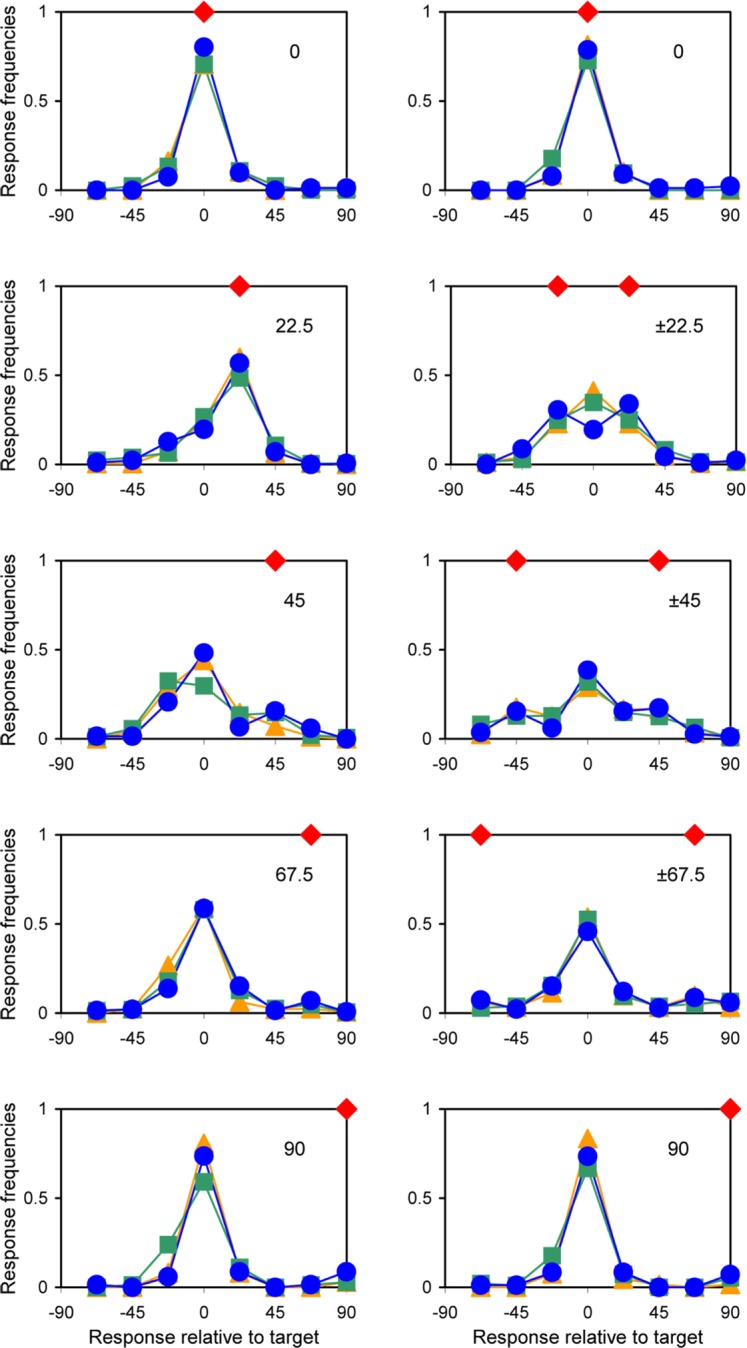
Distributions of responses relative to target orientation for different orientations of flankers. Homogeneous flankers (left), symmetrical flankers (right); orientations of flankers indicated by red diamonds. (orange triangles, observer EP; green squares, VA; blue circles, LP).

Figure 3.

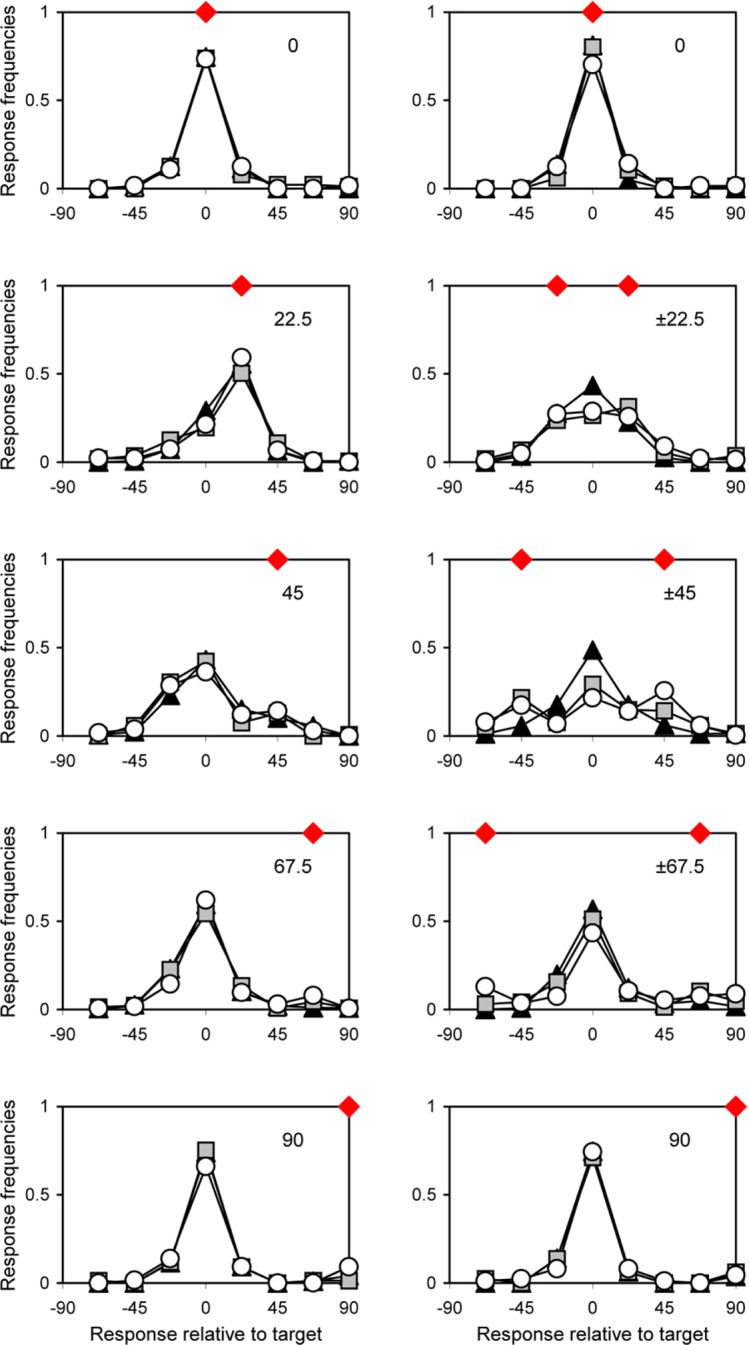
Distributions of responses relative to target orientation for different orientations and numbers of flankers. Homogeneous flankers (left), symmetrical flankers (right); orientations of flankers indicated by red diamonds. Black triangles, two flankers; gray squares, four flankers; white circles, six flankers.

Figures 4 and 5 show some general aspects of the data (pooled across the observers and the numbers of flankers). The systematic error (bias) and standard deviation (reciprocal of sensitivity), as dependent on target–flanker differences, are given in Figure 4. Bias was calculated as the mean of differences between response and target orientations using the equation for the mean of circular variables (see Appendix B). Standard deviation is the root mean square of the variation of responses about that mean. Figure 5 depicts the data from Figure 2 as a three-dimensional surface plot.

Figure 4.

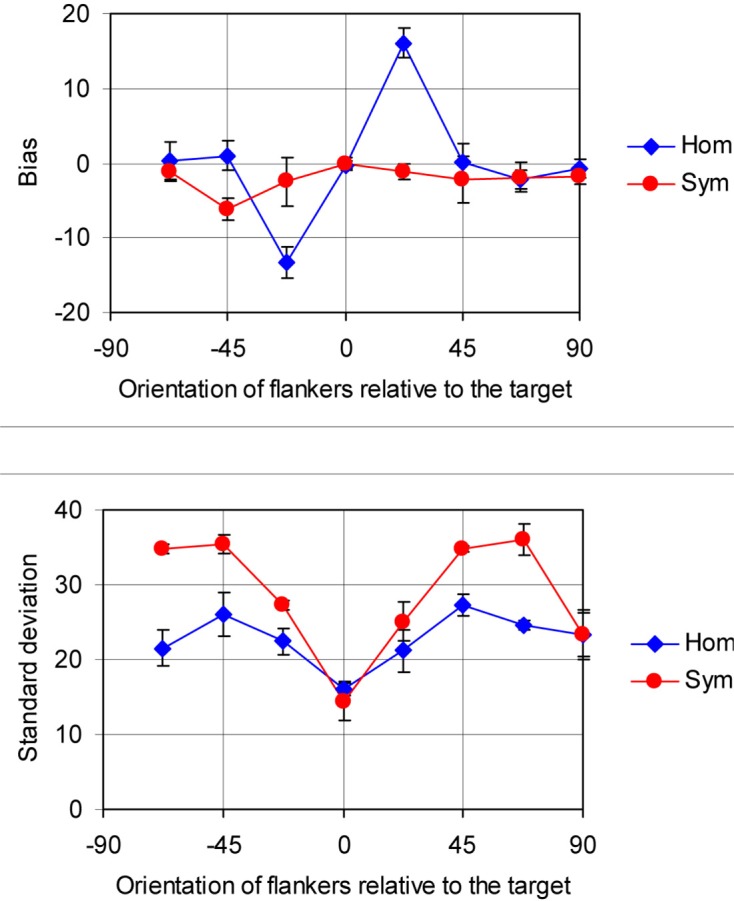
Bias and standard deviation of responses as dependent on orientation of flankers, relative to target, averaged across three observers. Blue diamonds, homogeneous flankers; red circles, symmetrical flankers. Error bars are standard errors of the mean.

Figure 5.

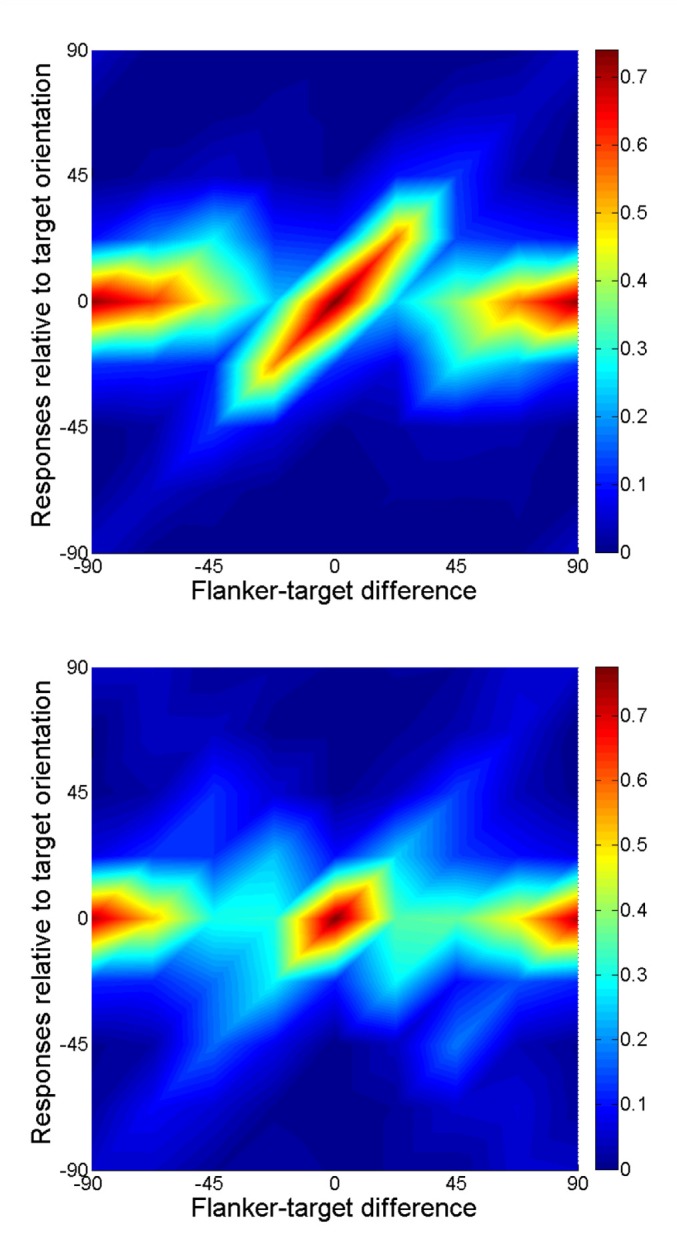
Response distributions (from Figure 2, pooled across three observers) presented as a three-dimensional plot. Homogeneous flankers (top), symmetrical flankers (bottom). Color codes the proportions of responses.

The condition with homogeneous flankers shows a very strong assimilation bias for small (22.5°) target–flanker differences (as if the orientation of flankers was reported instead of the target). Sensitivity is best when the target and flankers have the same orientation and slightly worse with orthogonal flankers. The lowest sensitivity (highest standard deviation) occurs at intermediate differences, about 45°. With two symmetrical flanker orientations, the standard deviation is much higher, especially for the 67.5° target–flanker difference. As one can expect, there were no systematic biases in the symmetrical condition.

The graphs in Figure 4 bear some resemblance to those from Solomon et al. (2004). However, the assimilation bias, which dominates in the present data, was tiny and restricted to very small target–flanker differences in the Solomon et al. (2004) data. Instead, repulsion from the flanker orientation (classical tilt illusion) was the dominant bias in that study. Standard deviations follow similar curves in both studies, but their absolute values are 5–10 times larger in this study. (In addition, there was no difference in standard deviation between the homogeneous and symmetrical flanker conditions in Solomon et al., 2004, results). By and large, the differences between the present results and the results of Solomon et al. (2004) can be explained by different tasks and different levels of stimulus uncertainty. Some interesting implications of these differences will be discussed later.

There are several interesting details that are lost when using the bias and sensitivity measures only. For relatively large target–flanker differences, there is evidence of multimodality of the distributions: consistent additional bumps at the orientations of flankers (see Figure 2). In addition to the strong assimilation bias at 22.5°, there seems to be a repulsion bias that pushes the main group of responses away from the flanker orientation at 45° and 67.5° target–flanker differences. Figure 5 shows that the data break naturally into two parts, probably reflecting an employment of two different mechanisms.

The likely candidate models (averaging and substitution/random selection) predict that the responses should be distributed according to either a single unimodal symmetrical error distribution (supposedly normal) or a mixture of several error distributions, corresponding to the target and flanker orientations. An attempt to fit the distributions in Figure 2 with a single Gaussian or double exponential (Laplace) distribution showed that this simplest account can be definitely rejected for the majority of conditions. Only the conditions with 0° and 22.5° target–flanker difference could be satisfactorily approximated by a single error distribution (although, p < 0.05 for one of three observers). However, all these distributions could be reasonably well fit by mixtures of two or three Laplace distributions. The fit of Laplace distribution as compared with Gaussian was found better for all three observers. This is somewhat surprising and may be related with the absolute identification task used in this study. Details of the approximation, optimal parameters, and goodness-of-fit are given in Appendix A.

Obviously, the full data set does not conform to the (simple or weighted) averaging model that predicts a unimodal distribution centered in some position between the target and flanker orientations. Neither are the results consistent with the simple spatial uncertainty (or random selection) model that predicts a fixed proportion of flanker-based responses independently of the target–flanker orientation difference. It is clear that spatial selectivity of the pooling mechanism depends on orientation differences between the target and flankers. When the target–flanker difference is small, the response is mostly determined by the orientation of flankers (this may be consistent with averaging, too). With large target–flanker differences, the responses are based mostly on the target orientation. This general effect is consistent with several earlier studies that have shown a decrease in crowding with increasing the target–flanker difference (e.g., Felisberti, Solomon, & Morgan, 2005; Kooi, Toet, Tripathy, & Levi, 1994). These data suggest that it is essentially the probability of flanker (or average)-based responses that goes down with increasing target–flanker difference.

4. Modeling

The results for the homogeneous flankers can be accounted for by a relatively simple functional model (a mathematical description is given in Appendix B, the main relationships in Figure 6). In essence, it is a simplified version of the Bayesian inference with competitive priors (e.g., Stocker & Simoncelli, 2008; Yuille & Bülthoff, 1996). I assume that visual system can easily detect some salient properties of stimulus (e.g., target pop-out) and selects a method of further calculations dependent on these properties.

Figure 6.

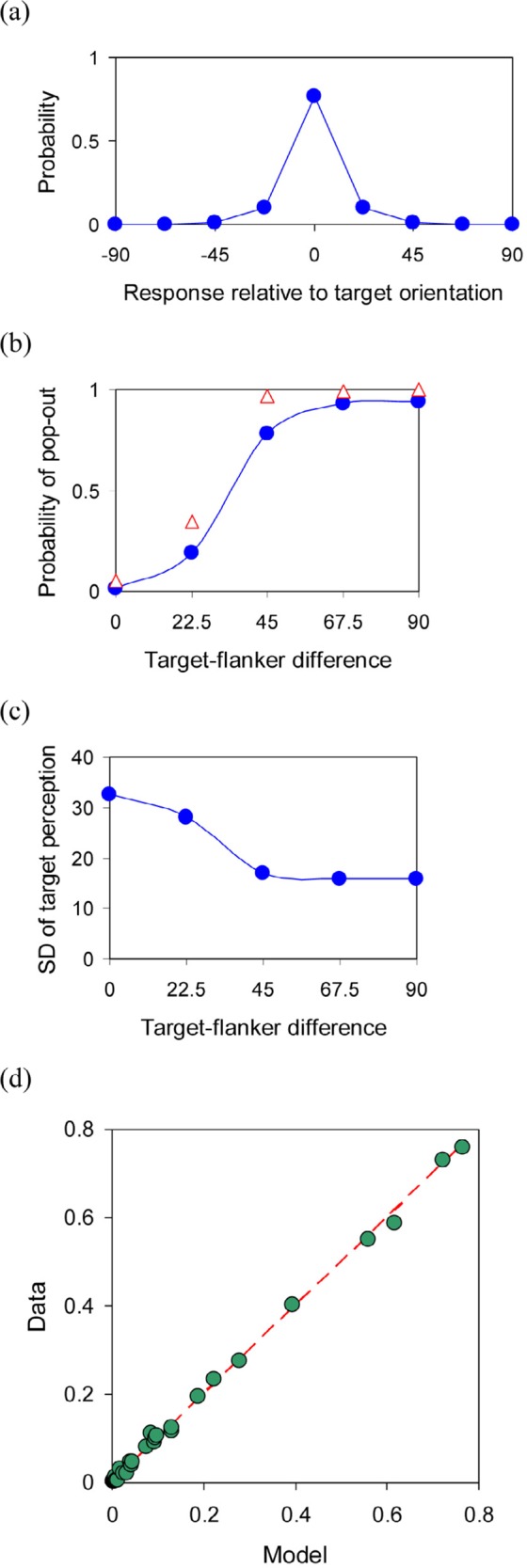
Main relationships and the fit of the model for the condition with homogeneous flankers. Response errors approximated by double exponential distribution (a). Estimated probability of target pop-out as dependent on target–flanker difference (red triangles are the results of the difference detection from control experiment; b). Function from the same curve used for standard deviation of perceived target orientation (c). Actual vs. predicted proportions (data pooled across three observers; d).

Thus, I suppose that a unique target among flankers is detected (pops out) with a probability that increases monotonically with target–flanker difference. [This function estimated from the data is given in Figure 6(b).] If the target pops out, its orientation is measured, with some random error, and combined with the information that it differs from the orientation of flankers. This results in repulsion from the flankers' orientation. A rigorous modeling of this effect would need additional assumptions and complex calculations. I used a simple assumption that the repulsion effect is proportional to the difference between the target and an assumed prior, centered orthogonally to the flankers. Thus, the repulsion effect (if present) increases with target–flanker similarity. But the probability of pop-out (and hence probability of repulsion) decreases with target–flanker similarity. The final result is a maximum repulsion bias at some intermediate target–flanker similarity. In the case of no pop-out, the average orientation of the objects, with a random error, is reported. (The same model, with the orientation of flankers instead of the average orientation, could account for the main aspects of the data, too, but gave a somewhat worse fit.)

The distributions of errors could be well approximated by a double exponential (Laplace) distribution [Figure 6(a)]. For the best fit, the standard error of the perceived target orientation has to increase for poorly detectable targets (for small target–flanker differences). The variability of the average orientation could be fixed.

To test the plausibility of the proposed role of target pop-out, a small control experiment was run where observer had to detect the presence of differently oriented target object among homogeneous flankers. The results are depicted in Figure 6(b) together with the estimated probabilities of pop-out from the main experiment. The curves are really quite similar. A somewhat higher detection rate in the control experiment can be reasonably explained by a focused attention to the detection task in that case.

For the two symmetrical flanker orientations, the probability of the target-based responses also increases with target–flanker difference. However, the assumption about global averaging is clearly wrong (at least for the target–flanker differences 45° and 67.5°). Instead, the orientation of either one or another group of flankers (or just an individual random flanker) is reported when the target orientation is not correctly identified. It looks like the averaging is vetoed by the perceived heterogeneity of flankers. Another difference between the conditions with heterogeneous and homogeneous flankers was a strong effect of the number of flankers for heterogeneous flankers. This is also consistent with the probabilistic selection of individual objects in the case of heterogeneous flankers. With homogeneous flankers, however, the target pop-out is the main determinant of performance, and because the pop-out is largely independent of (or even improves with increasing) the number of flankers, no effect of number of flankers is observed in that case. For the symmetrical flankers, it is still possible that with small differences between the two flanker orientations, the average orientation was used in a proportion of trials or the target could be grouped together with either one or another group of flankers and the observer could report the average of that group as a response. These data cannot unambiguously separate these possibilities.

5. Discussion

This study used a novel experimental design to examine the perception of orientation in conditions of visual crowding and revealed several new aspects of the integration of crowded orientation signals. It was shown that elementary integration rules (averaging, random selection) by themselves cannot explain the data. The selection of the elementary rules seems to be determined by a perceived pop-out of the target and homogeneity–heterogeneity of the flankers. This idea of probabilistic selection of processing routines dependent on salient properties of stimulus accounts well for these data and explains several apparently contradictive results from earlier studies.

The results with homogeneous flankers are well explained by a simple idea that detection of target–flanker difference (target pop-out) determines whether the target or average orientation is reported by observer. The probability of target pop-out naturally increases with the target–flanker difference. While the pop-out precludes averaging, there are other forms of interference that impair target perception in that case. Percept of the target is biased away from the flanker orientation and is much noisier as compared with a no-flankers condition. This model is consistent with findings that target–flanker dissimilarity can reduce the crowding effect (e.g., Felisberti et al., 2005; Kooi et al., 1994) and with studies that have shown a strong negative correlation between the target salience (as measured by visual search experiment) and crowding (Gheri, Morgan, & Solomon, 2007; Sayim, Westheimer, & Herzog, 2011). Also, Gheri et al. (2007) have concluded that there may be several mechanisms for crowding, dependent on target saliency. This study goes a step further suggesting a specific model for this dependency.

With strongly heterogeneous flankers, however, neither averaging nor pop-out plays an important role. The results are consistent with probabilistic selection of orientations within an integration field, assuming a somewhat higher probability for the target orientation.

In total, to explain this data set, three different rules of integration are combined: averaging for perceived homogeneity, repulsion bias for pop-out target, and probabilistic selection for heterogeneous (irregular) patterns. Obviously, this account is consistent with the previous reports of both averaging when flankers are homogeneous and similar to the target (Parkes et al., 2001) and random selection when flankers are strongly heterogeneous (Põder & Wagemans, 2007). Also, the idea of rule switching naturally explains the puzzling data from the last experiment of Parkes et al. (2001; the condition with flankers tilted in the opposite direction to the target) that could not be approximated by any monotonic psychometric function.

The present results seem to contradict the conclusions of Greenwood et al. (2009), based on a somewhat similar experiment with another visual feature—relative position of line segments. Their results were best fit by a weighted averaging model. It is possible that different visual features are combined according to different rules (note that relative position cannot be considered a typical simple feature, such as orientation, spatial frequency, or color). However, the interpretation of their results is also complicated by an additional reference repulsion mechanism, which itself is not well understood. The design of the present experiment avoids this kind of complication.

Also, note that the signed-max rule used by Gheri and Baldassi (2008) is not applicable to the present data. This rule assumes a search for an object, maximally different from a fixed reference orientation. There was no such reference in my experiment.

The present findings are in accordance with a general Bayesian view on vision. Quite similar ideas have been used for the explanation of different perceptual biases (e.g., Stocker & Simoncelli, 2008; Yu, Dayan, & Cohen, 2009; Zhaoping & Jingling, 2008. The visual system exploits the regularities of the natural visual world and tends to see things that are more probable in a given context. If you have no or very little information about the orientation of the target, the best guess is the orientation of adjacent objects (if you have perceived them), because the orientation at nearby positions is highly correlated in natural scenes (e.g., Felsen, Touryan, & Dan, 2005). But if you see that the target object looks different from its surroundings, you should select the orientation that is different enough to be consistent with this information. Note that the information from surrounding objects is useful only with nearly homogeneous or gradually changing orientation patterns. When the orientations of flankers are considerably different, their average is less informative (with very different orientations, calculation of the average itself becomes indefinite), and a probabilistic selection from the orientations within an integration field may be a better option. Because there are much less processing resources in the visual periphery (as compared with the fovea), it must rely more on the contextual information. At the same time, the limited resources should be devoted to the detection of the potentially most informative visual features in the natural visual environment. This study suggests that homogeneity–heterogeneity and singleton pop-out may be estimated obligatorily and control the perception of local features.

This kind of functional explanation does not contradict looking for relevant mechanisms at the neurobiological level. Actually, there must be some machinery that carries out these purposeful (and sometimes misleading) calculations in the form of neural interactions. The regularities observed in this study are probably determined at several levels of visual processing. While the calculation of a pop-out has been usually related with V1 (e.g., Li, 2000), the integration should occur at some higher level (possibly V4; e.g., Motter & Simoni, 2007). However, this integration should not be considered as a calculation of just one parameter (e.g., average) but as an attempt to select the best interpretation of the input pattern from a limited set of highly probable and potentially informative patterns. Interestingly, the multiplicative and divisive interactions between local population responses of neurons used in the models by Solomon et al. (2004) may actually implement a Bayesian combination of information from the target and flankers. According to this study, this should be complemented by a mechanism of competing interpretations.

The results of this study may shed some new light on the well-known tilt illusion (e.g., Gibson, 1937; Schwartz, Sejnowski, & Dayan, 2009; Solomon et al., 2004). When a similar stimulus (the target and homogeneous flankers) is presented in more favorable conditions (e.g., at the fixation point, with long exposure, without orientation and position uncertainty), a repulsion bias, the tilt illusion, is observed at the same orientation differences where the strong assimilation bias was found in this study. I suggest that the character of illusion may be determined by the perceived homogeneity of the pattern vs. pop-out of the target (perceived homogeneity implies assimilation and target pop-out implies repulsion). Note that the pop-out detection thresholds (8°–16°) from the work of Felisberti et al. (2005) predict very well the target–flanker differences where assimilation turns into repulsion in the experiments done by Solomon et al., 2004 (about 10°), with identical stimuli and presentation conditions. This hypothesis is also consistent with an increase of assimilation bias in the conditions with visual noise reported by Mareschal, Morgan, and Solomon (2010, because noise should impair the target pop-out. Earlier, I indicated that the standard deviations of responses in this study were about 5–10 times larger than in the results from the work of Solomon et al. (2004). Interestingly, the target–flanker orientation differences where assimilation turns into repulsion differ by a comparable factor (from approximately 10° in the work of Solomon et al., 2004, to 45° in this study). This makes sense if we assume that the accuracy of target perception and target pop-out are limited by the same internal orientation noise.

An obvious limitation of this study is an assumption that the effects of flankers are independent of their actual positions around the target. Several studies have shown that this is not true in general. Livne and Sagi (2007) demonstrated that crowding can be reduced considerably when the flankers are organized in a smooth circular configuration. May and Hess (2007 have argued that colinear Gabor patches (snakes) are less affected by crowding than parallel ones (ladders). It is improbable that the configuration effects played an important role in the findings of this study. Random selection of flankers' positions rarely produces exact “good” configurations, and their effects are cancelled by equally probable “bad” configurations. However, a theoretical account should not ignore the configuration effects. Interestingly, these effects fit well into the general idea of a description of peripheral image patches in terms of a few ecologically important properties. We just have to complement the already suggested homogeneity–heterogeneity and singleton pop-out with circularity and co-linearity. The neurobiological plausibility of this idea is supported by findings that neurons in cortical visual areas beyond V1 are often selective to similar kind of patterns (e.g., Hegde & Van Essen, 2003.

6. Conclusion

Simple models, such as averaging and random selection, on their own cannot account for the effects of flankers on the perception of target orientation. However, they may be used as building blocks of a more general model. The visual system combines information according to different rules dependent on salient properties of a stimulus, such as target pop-out and the perceived homogeneity–heterogeneity of flankers. The observed regularities of perception can be explained by an attempt to encode potentially important aspects of a stimulus using limited neural resources in the visual periphery and using contextual information to reconstruct unreliable or lost features.

Appendix A. Approximation of response distributions with mixtures of Laplace distributions

Distribution of responses for each target–flanker difference was approximated by a mixture of either two or three Laplace distributions,

$${\displaystyle f(\theta )=\sum _{i=1}^n{p}_{i}L(\theta ,\mu ,b_i),\sum _{i=1}^n{p}_i=1}$$

, where p_i is proportion of component distribution i, L(θ, μ_i, b_i) is Laplace distribution with mean μ_i and scale parameter b_i, and n is the number of distributions (two or three). Ordinary Laplace distribution is

$${\displaystyle L(\theta ,\mu ,b_i)=\frac{1}{2b}\exp \left(\frac{|\theta -\mu |}{b}\right)}$$

.

Because orientation is a circular variable with a period of 180°, the wrapped distributions ${\displaystyle L_w(\theta ,\mu ,b)=\sum _{k=-\infty }^{\infty }L(\theta +k\times 180°,\mu ,b)}$ must be used instead of L(θ, μ, b). I used the simplified approximations, wrapped over three periods (k = −1 to 1). Orientations θ and μ_i are measured relative to target orientation. Maximum likelihood fits were found using the Excel Solver add-in. Means (μ_i), scale parameters (b_i), and proportions (p_i) were adjusted to reproduce experimental data. For homogeneous flankers, the mixtures composed of two component distributions were used, and separate fits with equal and different scale parameters were found. For symmetric flankers, three component distributions were used, and the mixtures were constrained to be symmetrical about the target orientation. Because of less degrees of freedom, only the fit with equal scale parameters could be used for this condition. The optimal values of parameters and badness-of-fit are given in Table A1.

Table A1. Distributions of responses fit by the mixtures of Laplace distributions.

Target–flanker difference (deg)	Means (deg)		Scale parameters (deg)			Proportion p1	G-statistic
	μ1	μ2	b1	b2	b
0	0	90	–	–	10.8	0.99	5.3 ns
22.5	28.4	21.8	–	–	12.6	0.27	15.6∗∗
45	28.9	38.9	–	–	12.5	0.79	2.4 ns
67.5	24.0	67.5	–	–	12.5	0.94	3.1 ns
90	0	90	–	–	10.5	0.94	7.3∗
0	0	90	10.8	12.2	–	0.99	5.2∗
22.5	222.5	16.2	22.8	10.6	–	0.14	4.8 ns
45	29.1	38.6	11.9	13.9	–	0.78	1.9 ns
67.5	23.8	70.1	12.9	8.2	–	0.95	2.8 ns
90	0	90	10.6	10.1	–	0.94	7.2∗∗
±22.5	0	619.9	–	–	15.2	0.32	9.1∗∗
±45	0	641.0	–	–	15.7	0.50	1.8 ns
±67.5	0	673.4	–	–	14.7	0.80	1.3 ns

Note. The fit parameters (means, scale parameters, proportion of the first component distribution in the mixture) and badness-of-fit (G-statistic) are reported. Data were pooled across the observers and numbers of flankers. Statistical significance of differences between approximation and the data:

^∗∗p < 0.01

^∗p < 0.05, ns p > 0.05.

Appendix B. A model for the homogeneous flankers' condition

Distribution of responses is a mixture of two components—the distributions of responses to the target (f_T(θ)) and to the average orientation (f_A(θ)), in proportions determined by the probability of target pop-out (p_P)

$${\displaystyle f_R(\theta )=p_P\times f_T(\theta )+(1-p_P)\times f_A(\theta )}$$

.

Probability of the target pop-out increases monotonically with target–flanker differences

$${\displaystyle p_P=f_T\left(\right|{\theta }_F-{\theta }_T\left|\right)}$$

.

Both components are double exponential (Laplace) distributions

$${\displaystyle f_T(\theta )=\frac{1}{2b_T}\exp (-\frac{|\theta -({\theta }_T-{\theta }_C)|}{b_T})}$$

$${\displaystyle f_A(\theta )=\frac{1}{2b_A}\exp (-\frac{|\theta -{\theta }_A|}{b_A}),}$$

, where b_T and b_A are scale parameters (standard deviation σ = b√2), θ_c is context effect that pushes the perceived target away from the flankers' orientation.

θ_c = k_c × sgn (θ_F − θ_T) × (90° − |θ_F − θ_T|), except for |θ_F − θ_T| = 0, when a “hallucinated” pop-out target was assumed to be orthogonal to the flankers.

Average orientation was calculated using a method for averaging directional variables with doubling the angles (e.g., Mardia & Jupp, 2000):

$${\displaystyle Q_A=\left\{\begin{array}{cc}\frac{1}{2}\arctan \left(\frac{s}{c}\right)\hfill & c\ge 0\hfill \\ \frac{1}{2}\arctan \left(\frac{s}{c}\right)+90°\hfill & \hfill c\le 0\hfill \end{array}\right\}}$$

$${\displaystyle S=\frac{1}{n_o}\sum _i\sin (2{\theta }_{\mathit{oi}})}$$

$${\displaystyle S=\frac{1}{n_o}\sum _i\cos (2{\theta }_{\mathit{oi}})}$$

θ_oi is the orientation of object i and n_O is the number of objects (target plus flankers) in a display.

In the all calculations, the simple approximation of wrapped distribution

$${\displaystyle f_w(\theta )=\sum _{k=-1}^{1}f(\theta +k\times 180°)\mathrm{was}\mathrm{used}\mathrm{instead}\mathrm{of}f(\theta )}$$

.

I noticed that, for the best fit, the scale parameter b_T should increase for small target–flanker differences. I assumed that it has two independent parts: a constant and one induced by similar flankers. For simplicity, I related the last term to the pop-out probability because of a qualitatively similar behavior,

$${\displaystyle b_T=\sqrt{b_{T0}^2+b_{T1}^2\times {(1-p_P)}^2}}$$

.

To reduce the number of empty cells, I pooled the data across the observers and across the positive and negative (clockwise and anticlockwise) target–flanker differences. The final data set consists of 34 cells and has 29 degrees of freedom.

In the model reported here, nine free parameters were used: five pop-out probabilities p_P, scale parameters b_T0, b_T1, and b_A, and repulsion factor k_C. MS Excel Solver was used to find the parameters that minimized the log-likelihood ratio statistic G = 2 ΣO_ij ln(O_ij/E_ij), where O_ij is the observed and E_ij is the expected frequency in cell i, j.

The model fit the average data quite well (G = 35.3, df = 20, p = 0.02, R² = 0.998). It accounted perfectly for the individual data from two observers and somewhat worse for those from the third observer (G = 26.1, p > 0.05, G = 23.9, p > 0.05, G = 46.2, p < 0.01 for EP, VA, and LP, respectively). (However, the individual tests may be not reliable because of empty cells in the data.)

The main relationships of the optimal model and actual vs. predicted proportions for the averaged data are given in Figure 6(d). The optimal scale parameters b_T0 = 11.1° and b_A = 10.9° correspond to a standard deviation of about 16°. The additional (masking) noise term b_T1 = 20.4°, and the repulsion factor k_C = 0.21 (meaning that an estimated repulsion effect was about 9° for the 45° target–flanker difference).

When using the orientation of flankers instead of the average orientation in the case of no target pop-out, the fit was significantly worse for the average data (G = 55.0, df = 20, p < .001) and for two individual observers.

Applying the model separately for the conditions with different numbers of flankers revealed that the fit improved with increasing number of flankers (G = 37.9, p < 0.01; G = 32.6, p < 0.05; G = 21.5, p > 0.05 for two, four, and six flankers, respectively). Also, the additional noise parameter b_T1 dropped to zero for the two-flanker condition. These results suggest that some mechanisms may work differently with such a small number of flankers.