Abstract
We consider nonparametric regression of a scalar outcome on a covariate when the outcome is missing at random (MAR) given the covariate and other observed auxiliary variables. We propose a class of augmented inverse probability weighted (AIPW) kernel estimating equations for nonparametric regression under MAR. We show that AIPW kernel estimators are consistent when the probability that the outcome is observed, that is, the selection probability, is either known by design or estimated under a correctly specified model. In addition, we show that a specific AIPW kernel estimator in our class that employs the fitted values from a model for the conditional mean of the outcome given covariates and auxiliaries is double-robust, that is, it remains consistent if this model is correctly specified even if the selection probabilities are modeled or specified incorrectly. Furthermore, when both models happen to be right, this double-robust estimator attains the smallest possible asymptotic variance of all AIPW kernel estimators and maximally extracts the information in the auxiliary variables. We also describe a simple correction to the AIPW kernel estimating equations that while preserving double-robustness it ensures efficiency improvement over nonaugmented IPW estimation when the selection model is correctly specified regardless of the validity of the second model used in the augmentation term. We perform simulations to evaluate the finite sample performance of the proposed estimators, and apply the methods to the analysis of the AIDS Costs and Services Utilization Survey data. Technical proofs are available online.
Keywords: Asymptotics, Augmented kernel estimating equations, Double robustness, Efficiency, Inverse probability weighted kernel estimating equations, Kernel smoothing
1. INTRODUCTION
The existing missing data literature mainly focuses on estimation methods in parametric regression models, that is, models for the conditional mean of an outcome given covariates indexed by finite dimensional regression parameters. However, the functional form of the dependence of an outcome on a covariate is often unknown in advance and can be complicated (Hastie and Tibshirani 1990; Wand and Jones 1995). For example, Zhang, Lin, and Sowers (2000) found that the profile of progesterone level during a menstrual cycle follows a nonlinear pattern which is hard to fit using standard parametric models and is best fitted by nonparametric smoothing techniques. Likewise, Harezlak et al. (2007) found that the protein intensities from mass spectrometry are very complex and need to be fit using nonparametric smoothing methods. Limited literature is available for nonparametric regression in the presence of missing data.
Our work is motivated by the AIDS Costs and Services Utilization Survey (ACSUS) (Berk, Maffeo, and Schur 1993). The ACSUS sampled subjects with AIDS in 10 randomly selected United States cities with the highest AIDS rates. A question of interest in this study is how the risk of hospital admission one year after study enrollment is related to the baseline CD4 counts. Although it is known that a lower CD4 count is associated with a higher risk of hospitalization, the functional form of dependence is unknown and expected to be nonlinear with a potential threshold. We are hence interested in modeling this relationship nonparametrically. However, about 40% of the patients did not have the first-year hospital admission data available. As shown in Section 4, naive nonparametric regression using complete data could only yield an inconsistent estimator of the mean curve if the missing is not completely at random, a likely situation in this problem. It is therefore of interest to develop flexible nonparametric regression methods to estimate the effect of baseline CD4 counts on the risk of hospitalization that adequately adjust for outcomes missing at random (MAR), that is, missing depending on observed data (Little and Rubin 2002). In addition, because the fraction of missing outcomes is large, it is also important that the methodology maximally exploits the information in available auxiliary variables. The methods we develop in this paper are also useful for nonparametric regression estimation in two-stage studies (Pepe 1992), where the second-stage outcome is not observed for all study units and the probability of observing the outcome depends on the first-stage auxiliaries and covariates, but is independent of the outcome, that is, it is MAR.
Limited work has been done on nonparametric regression in the presence of missing data. Wang et al. (1998) considered estimation of a nonparametric regression curve with missing covariates. Liang et al. (2004) considered estimation of a partially linear model with missing covariates and described inverse probability weighted (IPW) estimation of the nonparametric component of the model. Chen et al. (2006) studied local quasi-likelihood estimation with missing outcomes when missingness depends only on the regression covariate. None of these articles considered, as we do here, the possibility that always observed auxiliaries are available, a case that arises often in practice. Our work differs in that we propose augmented inverse probability weighted (AIPW) kernel estimators that exploit the information in the auxiliary variables while at the same time allowing for the possibility that missingness may depend on them, thus making the MAR assumption more plausible.
In this paper we generalize kernel estimating equation methods (Wand and Jones 1995; Fan and Gibjels 1996; Carroll, Ruppert, and Welsh 1998) to accommodate outcomes missing at random in a similar spirit to IPW and AIPW methods for parametric regression (Robins, Rotnitzky, and Zhao 1994, 1995; Rotnitzky and Robins 1995; Rotnitzky, Holcroft, and Robins 1997; Robins 1999). After studying the properties of naive kernel estimating equations based on complete cases, we propose the IPW kernel estimating equations and a class of AIPW kernel estimating equations. We present the asymptotic properties of the solutions to these weighted kernel estimating equations and compare them in terms of asymptotic biases and variances. We argue that clever choices of the augmentation term can yield important efficiency gains over the IPW kernel estimators. The proposed IPW and AIPW kernel estimators are consistent under MAR if the missingness mechanism is known by design or can be parametrically modeled. Indeed, with one specific choice of the augmentation term, the AIPW kernel estimator confers some protection against model misspecification in that it remains consistent even if the model for the missingness probabilities is misspecified provided that a parametric model for the conditional mean of the outcome given the covariates and auxiliaries is correctly specified, a property known as double-robustness.
2. THE GENERALIZED NONPARAMETRIC MODEL WITH MISSING OUTCOMES
We consider a generalized nonparametric mean model when the outcome may be missing at random. Specifically, suppose the study design calls for a vector of variables (Yi, Zi, Ui) to be measured in each subject i of a random sample of n subjects from a population of interest. The variable Yi denotes the outcome which may not be observed in all subjects and the variable Zi denotes a scalar covariate that is always observed. We assume that the mean of Yi depends on Zi through a generalized nonparametric model
| (1) |
where g(·) is a known monotonic link function (McCullagh and Nelder 1989) with a continuous first derivative, μi = E(Yi|Zi), and θ(z) = g{E(Y|Z = z)} is an unknown smooth function of z that we wish to estimate. The variables Ui, which we assume are always observed, are recorded in the dataset for secondary analyses. However, for our purposes they are regarded as auxiliary variables as we are not interested in estimation of E(Yi|Zi, Ui), but rather in estimation of E(Yi|Zi). The covariates Ui are nevertheless useful in that they can both help explain the missing mechanism and improve the efficiency with which we estimate the nonparametric function θ(·).
We assume that outcomes are MAR (Little and Rubin 2002), which in our setting amounts to assuming that
| (2) |
where Ri = 1 if Yi is observed and Ri = 0 otherwise. That is, we assume the probability that the outcome is missing may depend on the observed data, that is, covariates and auxiliaries, but is independent of the outcome given the observed data. This assumption automatically holds in two stage sampling designs (Pepe 1992; Reilly and Pepe 1995) with covariates and auxiliaries measured at the first stage and outcomes measured on a subsample at the second stage. Using probabilities of selection into the second stage that depend on the variables collected at the first stage can help improve the efficiency with which one estimates the regression of Y on Z (Breslow and Cain 1988).
3. THE KERNEL ESTIMATING EQUATIONS FOR MISSING OUTCOMES AT RANDOM
In the absence of missing data, local polynomial kernel estimating equations have been proposed by Carroll, Ruppert, and Welsh (1998) as an extension of local likelihood estimation. When the data are not fully observed, one naive estimation approach is to simply solve the local polynomial kernel estimating equations using only completely observed units. However, as we show in Theorem 1 in Section 4, the resulting estimator θ̂naive(z) is generally inconsistent under MAR, except when: (a) the conditional mean of E(Y|Z, U) depends at most on Z or, (b) the selection probability Pr(R = 1|Z, U) depends at most on Z. This result is not surprising once we connect our inferential problem to causal inference objectives and relate it to well-known facts in causality. The MAR assumption (2) is equivalent to the assumption of no unmeasured confounding (Robins et al. 1999) or ignorability (Rubin 1976) for the potential outcome under treatment R = 1 in the subpopulation with Z = z. This assumption stipulates that, conditional on Z = z, U are the only variables that can simultaneously be (i) correlates of the outcome within treatment level and (ii) predictors of treatment R = 1. When (a) or (b) holds, either (i) or (ii) is violated. In such case, the effect of R = 1 on Y is unconfounded and consequently naive conventional, that is, unadjusted, estimators of the association of Y with R = 1 conditional on Z = z are consistent estimators of the causal estimand of interest. In fact, when (b) holds but (a) is false, the naive estimator will be consistent but inefficient because it fails to exploit the information about E(Y|Z = z) in the auxiliary variables U. Thus, even in such setting it is desirable to develop alternative, more efficient, estimation procedures. The Augmented Inverse Probability Weighted (AIPW) kernel estimators developed in this paper address this issue.
When the outcomes are missing at random, Robins, Rotnitzky, and Zhao (1995) and Rotnitzky and Robins (1995) proposed an inverse probability weighted (IPW) estimating equation for parametric regression, that is, when θ(·) is parametrically modeled as θ(·; ν) indexed by a finite dimensional parameter vector ν, where ν ∈ Rk. Robins and Rotnitzky (1995) showed that one can improve the efficiency of the IPW estimator by adding to the IPW estimating function a parametric augmentation term. We extend their idea and propose a class of AIPW kernel estimating equations for estimating the nonparametric function θ(·). We weight the units with complete data by either the inverse of the true selection probability πi0 = Pr(Ri = 1|Zi, Ui) (if known, for instance, as in two-stage sampling designs) or the inverse of an estimator of it, and add an adequately chosen augmentation term. We show that, just as for estimation of a parametric model for θ(·), inclusion of the augmentation term can lead to efficiency improvement for estimation of the nonparametric regression function θ(·). Unlike parametric regression, the augmentation term depends on a kernel function.
Specifically, let Kh(s) = h−1K(s/h), where K(·) is a mean-zero density function. Without loss of generality, we here focus on local linear kernel estimators. For any scalar x, define G(x) = (1, x)T and α = (α0, α1)T. For any target point z, the local linear kernel estimator approximates θ(Zi) in the neighborhood of z by a linear function G(Zi − z)T α. Let μ(·) = g−1(·). Suppose we postulate a working variance model var(Yi|Zi) = V[μ{ θ(Zi)}; ζ], where ζ ∈ Rr is an unknown finite dimensional parameter and V(·, ·) is a known working variance function. To estimate πi0 we postulate a parametric model
| (3) |
where π(Z, U; τ) is a known smooth function of an unknown finite dimensional parameter vector τ ∈ Rk. For example, we can assume a logistic model , where . We compute τ̂, the maximum likelihood estimator of τ under model (3) and then we estimate πi0 with π̂i = π (Zi, Ui; τ̂). Then we define the augmented inverse probability weighted (AIPW) kernel estimating equations as
| (4) |
where
| (5) |
with is the first derivative of μ(·) evaluated at G(Zi − z)T α, δ(Zi, Ui) is any arbitrary, user-specified, possibly data-dependent, function of Zi and Ui, and Vi = V[μ{G(Zi − z)Tα}; ζ]. As ζ is unknown in practice, we estimate it using the inverse probability weighted moment equations , where , and α̂j(ζ) = {α̂0,j(ζ), α̂1,j(ζ)}T solve (4) with z = Zj, j = 1, …, n. Denote the resulting estimator by ζ̂. The AIPW estimator of θ(z) is θ̂AIPW (z) = α̂0,AIPW(ζ̂) where α̂AIPW = {α̂0,AIPW(ζ̂), α̂1,AIPW(ζ̂)} solves (4) with Vi replaced by V[μ{G(Zi − z)T α}; ζ̂].
In the AIPW kernel estimating equations (4), the term UIPW,i(α) is zero for subjects with missing outcomes and for those with observed outcomes it is simply equal to their usual contribution to the local kernel regression estimating equations weighted by the inverse of their probability of observing the outcome given their auxiliaries and covariates. The term Ai(α), which is often referred to as an augmentation term, differs from that used in parametric regression [equations (38) and (39), Robins, Rotnitzky, and Zhao 1994] in that it additionally includes the kernel function Kh(·), and in that it approximates μ{θ(Zi)} = g−1{θ(Zi)} by the local polynomial μ{G(Zi − z)T α}.
Two key properties, formally proved in Section 4, make the AIPW kernel estimating equation methodology appealing, namely: (1) exploitation of the information in the auxiliary variables of subjects with missing outcomes and (2) double robustness.
Informally, property (1) is seen because both the subjects with complete data and those with missing outcomes in a local neighborhood of Z = z have a nonnegligible contribution to the AIPW kernel estimating equations. Consider the alternative IPW kernel estimator θ̂IPW(z), which is obtained by simply solving the IPW kernel estimating equations Σi UIPW,i(α) = 0, that is, ignoring the augmentation term in the estimating equations (4). Although θ̂IPW(z) depends on the auxiliary variables U of the units with missing outcomes through the estimators τ̂ that define the π̂i’s, this information is asymptotically negligible. Specifically, in Theorem 2, we show that when the support of Z is compact, under regularity conditions, the asymptotic distribution of θ̂IPW(z) as h → 0, n → ∞ and nh → ∞ is the same regardless of whether one uses the true πi0 (and hence do not use auxiliary data of incomplete units) or the fitted value π̂i computed under a correctly specified parametric model (3). This is different from inference under a parametric regression model for E(Y|Z) where, as noted by Robins, Rotnitzky, and Zhao (1994, 1995), estimation of the missingness probabilities helps improve the efficiency in estimation of regression coefficients. The reason is that the convergence of the ML estimator of πi0 under a parametric model is at the -rate while nonparametric estimation of θ(z) is at a slower rate. To see this note that only the O(nh) units that have values of Z in a neighborhood of z of width O(h) contribute to the IPW kernel estimating equations for E(Y|Z = z), so only the auxiliary variables of these units are relevant. However, as n → ∞, the data of these units could not enter into the IPW kernel estimating equations via the estimation of πi0 through the estimation of the finite dimensional parameter τ. This is so because for computing τ̂ parametrically all n units are used and the contribution of the O(nh) relevant units is asymptotically negligible. The above discussions suggest that compared to the IPW kernel estimator, the AIPW kernel estimator of θ(z) can better explore the information in the auxiliary variables of subjects with missing outcomes.
To construct AIPW estimators with property (2), the double-robustness, we specify a parametric model
| (6) |
where η is an unknown finite dimensional parameter vector, and we estimate η using the method of moments estimator η̂ based on data from completely observed units. Under the MAR assumption (2), η̂ is -consistent for η, provided model (6) is correctly specified (Little and Rubin 2002). We then compute θ̂AIPW(z) using δ(Zi, Ui) = δ(Zi, Ui; η̂). In Theorem 3 in Section 4, we show that such estimator θ̂AIPW(z) is doubly robust, that is, it is consistent when either model (3) for πi0 is correct or model (6) for E(Yi|Zi, Ui) is correct, but not necessarily both. The practical consequence of double-robustness is that it gives data analysts two opportunities of carrying out valid inference about θ(z), one for each of the possibly correctly specified models (6) or (3). In contrast, as shown in Theorem 1 in Section 4, consistency of the IPW kernel estimator θ̂IPW(z) requires that the selection probability model (3) for πi0 must be correctly specified. One may question the possibility that the fully parametric model (6) for E(Yi|Zi, Ui) is correct when in fact the model of scientific interest for E(Yi|Zi) is left fully nonparametric precisely because of the lack of knowledge about the dependence of the mean of Y on Z. This valid concern is dissipated when it is understood that model (6) is only a working model that simply serves to enhance the chances of getting nearly correct (and indeed, nearly efficient) inference. Aside from this, it should also be noted that it is possible that data analysts may have refined knowledge of the conditional dependence of Y on Z within level of U, but not marginally over U.
In addition, in Section 4 we show that the preceding double-robust estimator θ̂AIPW(z) has an additional desirable property. Specifically, if model (6) is correctly specified then the double-robust estimator θ̂AIPW(z) has the smallest asymptotic variance among all estimators solving AIPW kernel estimating equations with πi0 either known or estimated from a correctly specified parametric model (3). That is, the asymptotic variance of the resulting double-robust estimator θ̂AIPW(z) that uses δ(Zi, Ui) = δ(Zi, Ui; η̂) with η̂ a -consistent estimator of η under a correct model (6), is less than or equal to that of an AIPW kernel estimator using any other arbitrary function δ(Zi, Ui) when the selection probability model (3) is correct.
Remark 1
Our estimators θ̂AIPW(z) use the IPW method of moments estimator of the variance parameter ζ. Although one could construct an AIPW method of moments estimator of ζ, this is unnecessary because improving the efficiency in estimation of the parameters ζ does not help improve the efficiency in estimation of the nonparametric function θ(z). This is in accordance to estimation of parametric regression models for E(Y|Z), where it is well known that the efficiency of two-stage weighted least squares is unaffected by the choice of -consistent estimator of var(Y|Z) at the first stage. In fact, Theorem 3 in Section 4 asserts that the efficiency with which θ(z) is estimated is unaltered even if the working model for var(Y|Z) is incorrectly specified. This is in contrast to parametric regression models where incorrect modeling of var(Y|Z) results in inefficient estimators of the regression parameters. The reason is that nonparametric regression is local and variability in a diminishing neighbor of z is constant asymptotically.
4. ASYMPTOTIC PROPERTIES
4.1 Asymptotic Properties of the Proposed Estimators
In this section, we investigate the asymptotic properties of the AIPW local linear kernel estimator introduced in the preceding section and compare it with the naive and IPW nonparametric estimators. In our developments we make the following assumptions: (I) n → ∞, h → 0, and nh → ∞; (II) z is in the interior of the support of Z; and (III) the regularity conditions (i) and (ii) stated at the beginning of the web Appendix hold.
Denote by θ̃naive(z), θ̃IPW(z), θ̃AIPW(z) the asymptotic limits of θ̂naive(z), θ̂IPW(z), θ̂AIPW(z). The AIPW kernel estimator θ̂AIPW(z) solves (4). The IPW kernel estimator θ̂IPW(z) solves , where UIPW,i(α) is defined in (5). The naive estimator θ̂naive(z) is the standard kernel estimator using only the complete data and solves a kernel estimating equation similar to the IPW kernel estimating equation except that π̂i is set to be 1 for all units. Standard arguments on the convergence of solutions to kernel estimating equations imply that under assumptions (I)–(III) there should exist a sequence of solutions (α̂0,naive, α̂1,naive) of the naive kernel estimating equations at z such that as the sample size n → ∞, the sequence converges in probability to a vector (α̃0,naive, α̃1,naive) with the first component α̃0,naive, through-out denoted as θ̃naive(z), satisfying
| (7) |
where ζ̃ is the probability limit of ζ̂.
Likewise, the IPW kernel estimating equations should have a sequence of solutions (α̂0,IPW, α̂1,IPW) that converge in probability to a vector (α̃0,IPW, α̃1,IPW) with the first component α̃0,IPW, throughout denoted as θ̃IPW(z), satisfying
| (8) |
where π̃ = π(Z, U; τ̃), and τ̃ is the probability limit of τ̂.
Similarly, the AIPW kernel estimating Equations (4) should have a sequence of solutions (α̂0,AIPW, α̂1,AIPW) that converge in probability to a vector (α̃0,AIPW, α̃1,AIPW) with the first component α̃0,AIPW, throughout denoted as θ̃AIPW(z), satisfying
| (9) |
where δ̃(Z, U) = δ(Z, U; η̃), and η̃ is the probability limit of η̂.
Throughout we assume that such sequences exist. Theorem 1 exploits the form of (7), (8), and (9) to derive concise expressions for the probability limits of θ̂naive(z), θ̂IPW(z), and θ̂AIPW(z) under MAR.
Theorem 1
Under the MAR assumption (2), the following results hold:
The probability limit θ̃naive(z) of the naive kernel estimator defined in (7) satisfies θ̃naive(z) = μ−1[μ{ θ(z)} + cov(R, Y|Z = z)/E(R|Z = z)];
The probability limit θ̃IPW(z) of the IPW kernel estimator defined in (8) satisfies θ̃IPW(z) = θ(z) when π̂i is either computed under a correctly specified model (3) or is replaced by the true πi0 in the IPW kernel estimating function (5);
The probability limit θ̃AIPW(z) of the AIPW kernel estimator defined in (9) satisfies θ̃AIPW(z) = θ(z) when the AIPW kernel estimating equations (4) use either (i) the true πi0 or π̂i computed under a correctly specified model (3); or (ii) δ(Z, U) = E(Y|Z, U), or δ(Z, U) = δ(Z, U; η̂) with η̂ calculated under a correctly specified model (6).
The proof of Theorem 1 is given in web Appendix A.1. It follows from Theorem 1 that θ̂naive(z) is generally inconsistent for θ(z) except when R and Y are conditionally uncorrelated given Z. In particular, this implies that when missingness depends on variables U other than Z which further predict Y, θ̂naive(z) is inconsistent. However, if either of the following two conditions hold, then cov(R, Y|Z = z) = 0 and therefore θ̂naive(z) is consistent for θ(z). Specifically:
Condition a. The missing indicator R depends on the covariate Z but given Z it is conditionally independent of auxiliary variables U.
Condition b. The conditional mean of Y given Z and U depends only on Z.
Theorem 1, part (III) shows that the AIPW kernel estimator θ̂AIPW(z) has the remarkable double-robustness property alluded to in the preceding section: its consistency requires the correct specification of either a model for πi0 or a model for E(Y|Z, U), but not necessarily both.
In what follows, we study the asymptotic distributions of the proposed estimators. Theorem 2 and Theorem 3 provide the asymptotic bias and variance of θ̂IPW(z) and θ̂AIPW(z), respectively, under MAR. Corollaries following these theorems show that in the class of AIPW kernel estimating equations that use either the true πi0 or a consistent estimate of πi0, the optimal AIPW kernel estimating equation that yields a solution with the smallest asymptotic variance is obtained by setting δ(Zi, Ui) = E(Yi|Zi, Ui) or δ(Zi, Ui) = E(Yi|Zi, Ui; η̂) with η̂ a -consistent estimator of η computed under a correctly specified model (6). In addition, the solution of the optimal AIPW kernel estimating equations is at least as efficient as that of the IPW kernel estimating equations. A sketch of the proofs of Theorems 2 and 3 is given in web Appendix A.2 and web Appendix A.3, respectively. In what follows, fZ (·) stands for the density function of Z, bK (z) ≡ ∫K2(s) ds/[μ(1){θ(z)}]2fZ (z), c2(K) ≡ ∫s2K(s) ds, and π0(Z, U) denotes the true probability of R = 1 given (Z, U).
Theorem 2
Suppose π̂i is computed under a correctly specified model (3) or is replaced by its true value. Suppose Pr(R = 1|Z, U) > c > 0 for some constant c with probability 1 in a neighborhood of Z = z. Then, under the MAR assumption (2) and assumptions (I)–(III) above, we have that
| (10) |
where
Theorem 2 shows that the asymptotic bias of θ̂IPW(z) is of order O(h2), and the variance of θ̂IPW(z) is of order O(1/nh) and does not depend on the working variance V(·) in the IPW kernel estimating equations. This result indicates that, in contrast to parametric regression estimation, misspecification of the working variance V(·) of Y|Z does not affect the asymptotic variance of θ̂IPW(z). Theorem 2 also shows that to this order the bias and variance do not depend on whether the selection probabilities are known or estimated parametrically.
Theorem 3
Suppose that in the AIPW kernel estimating equations (4), (a) π̂i is computed under a model (3) or it is replaced by fixed probabilities and (b) δ(Z, U) is a fixed and known function or it is replaced by the function δ(Z, U; η̂) with η̂, a method of moments estimator of η under model (6) based on units with observed outcomes. Suppose Pr(R = 1|Z, U) > c > 0 for some constant c with probability 1 in a neighborhood of Z = z, and the MAR assumption (2) and assumptions (I)–(III) above hold. Consider additional conditions:
model (3) is correct or, π*(Z, U) = π0(Z, U) when is used instead of π̂i in (4), or
model (6) is correct when δ(Z, U; η̂) replaces δ(Z, U) in (4) or δ(Z, U) is equal to the true conditional expectation E(Y|Z, U) otherwise.
If either (i) or (ii) (but not necessarily both) hold, then
| (11) |
where
| (12) |
π̃ (Z, U) denotes π*(Z, U) if is used, or it denotes the probability limit of π̂(Z, U) if π̂i is used, and δ̃(Z, U) denotes δ(Z, U) if δ(Z, U) is used, or the probability limit of δ(Z, U; η̂) if δ(Z, U; η̂) is used.
Theorem 3 shows that the leading term of the asymptotic bias of θ̂AIPW(z) is the same as that of θ̂IPW(z) when the model for the selection probability is correctly specified. Furthermore, it remains the same even when the model for the selection probability is wrong, as long as the model for the conditional mean of the outcome given covariates and auxiliaries is correctly specified. Display (12) provides the general form of the asymptotic variance of θ̂AIPW(z) when either model (3) or model (6) is correctly specified. If model (6) is correctly specified, then (12) simplifies to bK (z)E[π0(Z, U)/π̃2(Z, U) var(Y|Z, U) + [E(Y|Z, U) − μ{ θ(Z)}]2|Z = z].
On the other hand, if model (3) for the selection probability is correctly specified, the following corollary explores the properties of WAIPW(z) and it establishes that among the AIPW kernel estimating equations, the one that uses δ(Zi, Ui) = δ(Zi, Ui; η̂) with η̂ estimated under a correctly specified model (6) has a solution with the smallest asymptotic variance.
Corollary 1
Under the assumptions of Theorem 3, if the selection probability model (3) is correctly specified, then
| (13) |
WAIPW(z) is minimized at δ̃(Z, U) = E(Y|Z, U). Consequently, when model (3) is correct, the estimator θ̂AIPW(z) that uses δ(Z, U) = δ(Z, U; η̂) from a correctly specified model for E(Y|Z, U), throughout denoted as θ̂opt,AIPW (z), has the smallest asymptotic variance among all AIPW estimators θ̂AIPW(z). The asymptotic variance of θ̂opt,AIPW(z) is equal to
Note that it follows from (13) that WAIPW(z) agrees with WIPW(z) when δ̃(Z, U) = μ{θ(Z)}. This implies that, under correct specification of the selection probability model, the AIPW estimators that use δ(Z, U) equal to the fitted value δ(Z; ω̂) from a parametric model δ(Z; ω) for E(Y|Z), rather than the fitted value from a parametric model for E(Y|Z, U), are asymptotically equivalent to IPW estimators.
A direct comparison of the asymptotic variance of θ̂opt,AIPW(z) to that of θ̂IPW(z) in Theorem 2 immediately gives that the optimal AIPW kernel estimator is always at least as efficient as the IPW kernel estimator when indeed model (6) is correctly specified, as the next corollary establishes.
Corollary 2
Suppose that θ̂opt,AIPW(z) and θ̂IPW(z) solve, respectively, the optimal AIPW and IPW kernel estimating equations that use the true πi0 or π̂i estimated under a correctly specified model (3). Then θ̂opt,AIPW(z) is at least as efficient as θ̂IPW(z) asymptotically, and the reduction in the asymptotic variance conferred by θ̂opt,AIPW(z) is
When Pr[π0(Z, U) < 1] > 0, the difference WIPW(z) −Wopt,AIPW(z) is 0 only when E(Y|Z = z, U) − E(Y|Z = z) = 0, that is, when U does not predict Y in addition to Z. When U predicts Y above and beyond Z, as is expected for covariates U usually recorded in epidemiological studies, WIPW(z) − Wopt,AIPW(z) is strictly positive. Thus θ̂opt,AIPW(z) is usually more efficient than θ̂IPW(z).
4.2 An Improved Estimator
A warning is appropriate at this stage. Our results show that using the optimal augmentation term we improve upon the efficiency of the IPW estimator. However, it is not guaranteed that any augmentation term in the AIPW kernel estimating equation leads to efficiency gains over the IPW method. In practice, one often does not know whether model (6) is correct, and hence is uncertain that θ̂AIPW(z) is more efficient than θ̂IPW(z). Nevertheless we can follow a strategy proposed by Tan (2006) for estimation of the marginal mean of an outcome and remedy this problem. Specifically, the following simple modification results in an AIPW kernel estimating function that yields double-robust estimators guaranteed to be at least as efficient as the IPW estimator θ̂IPW(z) and as the optimal AIPW estimator θ̂opt,AIPW(z) when model (3) holds for the selection probability. Let and . Let α̂mod = {α̂mod,0, α̂mod,1} solve
| (14) |
where is evaluated at ζ̂. The proposed modified estimator is θ̂mod(z) = α̂mod,0. Note that (14) is just like the AIPW equation (4) except that the contribution to the augmentation term of each subject is multiplied by the factor κ̂(α). Remarkably, this modification ensures that the new estimator θ̂mod(z) is at least as efficient as the IPW estimator θ̂IPW(z) and as the optimal AIPW estimator θ̂opt,AIPW(z) when model (3) holds and at the same time is double-robust. To see this, first note that multiplication by the factor κ̂(α) in the augmentation term implies that the solution θ̂mod(z) to the modified AIPW estimating equations converges in probability to the solution of a population equation just like (9) except that the second term in the left-hand side of that equation is multiplied by
When model (3) is correct, then π̃(Z, U) = π0(Z, U) and the second term of the left-hand side of (9) is zero, regardless of whether it is evaluated at the true θ(z) or not and regardless whether or not it is multiplied by the constant κ while the first term is unaffected by the modification and remains equal to zero when evaluated at θ(z). Thus θ̂mod(z) is consistent for θ(z) when model (3) is correctly specified. On the other hand, when model (6) is correct, then δ̃(Z, U) = E(Y|Z, U) and a straightforward calculation shows that κ = 1 regardless of whether or not π̃(Z, U) is equal to Pr(R = 1|Z, U), thus implying that θ̂mod(z) is consistent for θ(z) since, as we argued earlier, θ(z) solves Equation (9). This shows that θ̂mod(z) is double-robust. To show that θ̂mod(z) is at least as efficient as θ̂opt,AIPW(z) and as θ̂IPW(z) when model (3) is correctly specified, we can argue as in the proof of Theorem 3 and show that θ̂mod(z) has the same limiting distribution as θ̂AIPW(z), except that the asymptotic variance WAIPW(z) is replaced by
A straightforward calculation yields that the denominator of κ is equal to
Thus, Wmod(z) is equal to bK (z) times the residual variance from the population regression of Y* = R[Y − μ{θ(Z)}]/π0(Z, U) on X* = {R/π0(Z, U) − 1}[δ̃(Z, U) − μ{θ(Z)}]. Since the residual variance E[(Y* − κX*)2] minimizes the mean squared error E[(Y* − aX*)2] over all a ∈ R, then we conclude that Wmod(z) = bK (z)E[(Y* − κX*)2] is less than or equal to WIPW(z) = bK (z)E[Y*2] and to Wopt,AIPW(z) = bK (z)E[(Y* − X*)2], where δ̃(Z, U) = E(Y|Z, U). Consequently, θ̂mod(z) is at least as efficient as θ̂IPW(z) and as θ̂opt,AIPW(z) when π̂i is computed under a correctly specified model for the selection probabilities.
4.3 Bandwidth Selection
Choosing an appropriate bandwidth parameter h is important in nonparametric regression. From Theorems 2 and 3, the asymptotic optimal bandwidths hIPW,opt and hAIPW,opt can be chosen by minimizing the corresponding asymptotic weighted mean integrated squared errors, respectively. Specifically, the asymptotically optimal bandwidth for estimating θ̂IPW(z) is given by hIPW,opt = [{4 ∫WIPW(z) dz}/{c2(K)∫θ″(z) dz}]1/5n−1/5 and the asymptotically optimal bandwidth for estimating θ̂AIPW(z) is given by hAIPW,opt = [{4∫WAIPW(z) dz}/{c2(K)∫θ″(z)dz}]1/5n−1/5.
To choose h in practice, we can easily generalize the empirical bias bandwidth selection (EBBS) method of Ruppert (1997) to derive a data-driven bandwidth selection approach for non-parametric regression with missing data. Specifically, one calculates the empirical mean squared errors EMSE{z; h(z)} of θ̂(z), where , at a series of z and h(z) and chooses h(z) to minimize EMSE{z; h(z)}. Note h(z) is choosen to vary with z, and thus is local. Here is the empirical bias, and is the Sandwich variance estimator. For example, the Sandwich variance estimator of the IPW kernel estimator θ̂IPW(z) can be calculated as the (1, 1) element of the matrix (AIPW)−1BIPW(AIPW)−1, where
and
The Sandwich variance estimator of the naive kernel estimator θ̂naive(z), and of the AIPW kernel estimator θ̂AIPW(z) can be constructed in a similar way.
5. SIMULATIONS
In this section, we conduct simulation studies to evaluate the finite-sample performance of the AIPW kernel estimator θ̂AIPW(z), and compare it with the naive kernel estimator θ̂naive(z) and the IPW kernel estimator θ̂IPW(z). Our simulation mimics the observed data generating process of a two-stage study design, in which U and Z are measured at the first stage on all study subjects, but Y is measured at the second stage only on a subset of the study participants. The second-stage validation subset is selected with selection probabilities that may depend on the first stage variables. We consider two situations, where the outcome Y is either normal or binary, respectively. We generate a random sample of size n of (Z, U, Y, R) for each replication. Z is generated from a uniform(0, 1) distribution, U is generated from a uniform(0, 6) independently of Z, and the mean of the outcome Y has the general form
| (15) |
In case one, g(x) = x and the outcome Y is generated from a normal distribution with mean E(Y|Z, U) and variance σ2 = 3, where β1 = 1.3, m(x) = 2 · F8,8(x) and Fp,q(x) = Γ(p + q){Γ(p)Γ(q)}−1xp−1(1 − x)q−1, a unimodal function. In case two, g(x) = logit(x) where logit(x) = log{x/(1 + x)} and the outcome Y is generated from a Bernoulli distribution with mean E(Y|Z, U), where β1 = 0.32, and m(x) = 1.2 · Φ(8 × x − 4) + 0.4. In both situations, We generate R, the selection indicator, according to the probability model
| (16) |
where π(Zi, Ui) = Pr(Ri = 1|Zi, Ui) is the probability that subject i is selected to the second stage, a1 = 0.5 and a2 = 6. τ0 and τ1 are selected so that the Monte Carlo median missing percentage of the outcome Y is around 50% for the normal case and about 30% for the Bernoulli case. Since the selection probability depends on U only, the missing is at random.
Our primary interest lies in estimating the marginal mean curve of the outcome Y given the scalar covariate Z, that is, μ{θ(z)}, which is E(Y|Z) = E[E(Y|Z, U)|Z]. We generated 500 datasets with sample size n = 500 or 300. For each simulated dataset, we computed the naive, IPW and AIPW estimates of θ(z), in the first case under the model μi = θ(Zi) and in the second case under model logit(μi) = θ(Zi). We use the generalized EBBS method as described in Section 4.3 to choose the optimal local bandwidth.
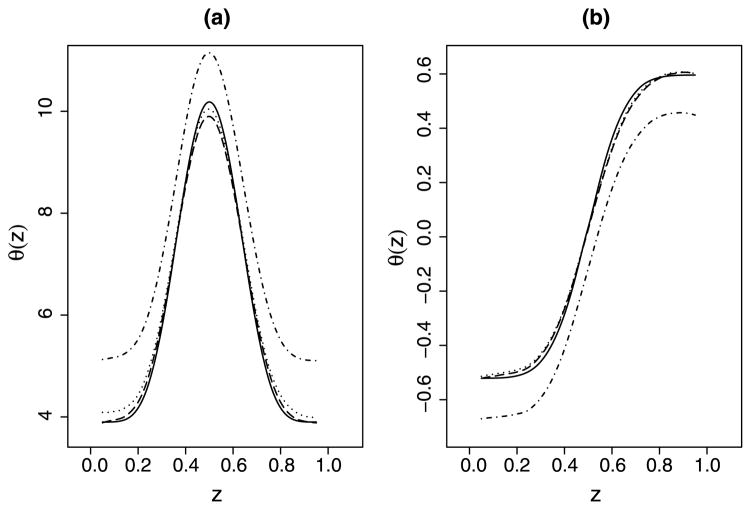
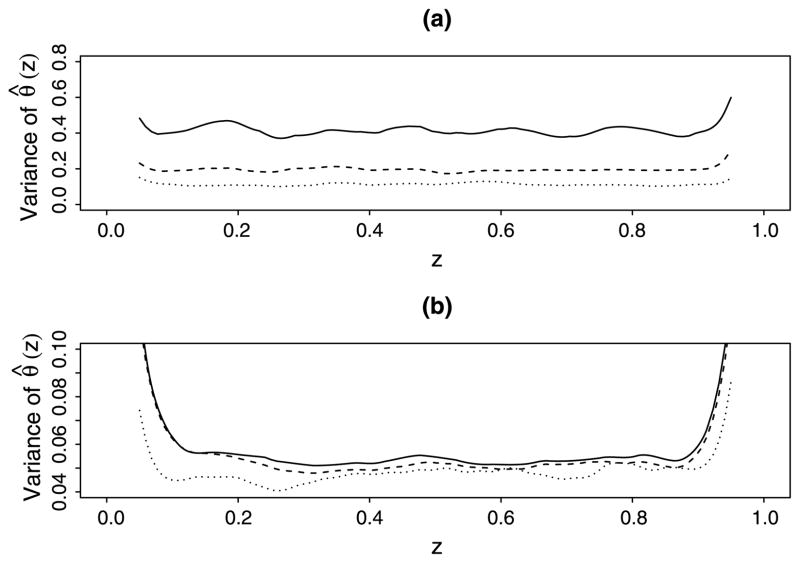
The empirical average of the estimated nonparametric curves θ̂(·) over the 500 replications, using the naive, IPW and AIPW estimators are displayed in Figure 1. The plot in the left panel shows the estimators of θ(z) in case 1 (identity link) and the plot in the right panel shows the estimators in case 2 (logit link). The same trend was observed for both plots. The IPW and AIPW kernel estimates are close to the true curve θ(·), while the naive approach yields a biased estimate. Figure 2 illustrates the empirical point-wise variances of θ̂IPW(·) and θ̂AIPW(·) when n = 500, the top panel for the identity link case and the bottom panel for the logit link case. The figure shows that the AIPW estimator has a smaller point-wise variance than the IPW estimator.
Figure 1.
Simulation results of the estimated nonparametric functions using naive, IPW, and AIPW kernel methods based on 500 replications with sample size n = 500. The left panel is for case 1 (identity link), while the right panel is for case 2 (logit link): —— true θ(z), – · – · the naive kernel estimator, · · · · the IPW kernel estimator, and – – – the AIPW kernel estimator.
Figure 2.
Empirical point-wise variances of the IPW and AIPW estimates of θ(·), based on 500 replications with sample size n = 500. The top panel is for case 1 (identity link), while the bottom panel is for case 2 (logit link): —— the IPW kernel estimate, – – – the AIPW kernel estimate, and · · · · · the kernel estimate when there is no missing data.
Table 1 summarizes the performance of each nonparametric estimate using the integrated relative bias, the integrated empirical standard error (SE), the integrated estimated SE, and the integrated empirical mean integrated squared error (MISE), over the support of Z. As predicted by theory, the naive kernel estimate has a much larger relative bias than the IPW and AIPW kernel estimates. Furthermore, the corresponding AIPW kernel estimate has a smaller variance and a smaller MISE than the IPW kernel estimate. For example in the identity link case, the AIPW kernel estimate has about 52% gain in MISE efficiency compared to the IPW kernel estimate when n = 500. In the logit link case, the MISE efficiency gain is about 7%. The increased efficiency gain of AIPW over IPW in case 1 (identity link) compared to case 2 (logit link) can be explained by the fact that in case 1 the auxiliary variable U is highly correlated with the outcome Y while in case 2, the correlation between U and Y is much lower.
Table 1.
Simulation results of relative biases, SEs and MISEs of the naive, IPW and AIPW estimates of θ(z) based on 500 replications (in parenthesis are the Monte Carlo SEs)
|
n = 500
|
n = 300
|
|||||||
|---|---|---|---|---|---|---|---|---|
| Relative bias1 | EMP SE2 | EST SE3 | EMP MISE4 | Relative bias | EMP SE | EST SE | EMP MISE | |
| Normal case (identity link) | ||||||||
| No missing | 0.017 (0.002) | 0.336 (0.011) | 0.326 (0.001) | 0.130 (0.008) | 0.017 (0.004) | 0.434 (0.005) | 0.431 (0.003) | 0.207 (0.011) |
| Naive | 0.234 (0.003) | 0.437 (0.014) | 0.431 (0.003) | 1.713 (0.032) | 0.233 (0.006) | 0.578 (0.020) | 0.573 (0.002) | 1.843 (0.079) |
| IPW | 0.034 (0.004) | 0.645 (0.013) | 0.642 (0.002) | 0.451 (0.020) | 0.044 (0.012) | 0.843 (0.017) | 0.839 (0.006) | 0.770 (0.043) |
| AIPW | 0.018 (0.003) | 0.443 (0.012) | 0.438 (0.004) | 0.215 (0.012) | 0.019 (0.005) | 0.579 (0.012) | 0.567 (0.005) | 0.356 (0.013) |
| Logistic case (logit link) | ||||||||
| No missing | 0.048 (0.024) | 0.220 (0.005) | 0.213 (0.001) | 0.049 (0.002) | 0.074 (0.016) | 0.254 (0.013) | 0.249 (0.001) | 0.067 (0.006) |
| Naive | 0.662 (0.048) | 0.229 (0.007) | 0.223 (0.001) | 0.075 (0.004) | 0.667 (0.051) | 0.267 (0.011) | 0.260 (0.001) | 0.099 (0.008) |
| IPW | 0.058 (0.021) | 0.239 (0.007) | 0.234 (0.001) | 0.058 (0.003) | 0.095 (0.022) | 0.283 (0.009) | 0.278 (0.001) | 0.084 (0.006) |
| AIPW | 0.054 (0.016) | 0.234 (0.096) | 0.231 (0.001) | 0.054 (0.003) | 0.099 (0.025) | 0.276 (0.007) | 0.270 (0.001) | 0.080 (0.005) |
Relative bias is defined as .
EMP SE is the empirical SE, defined as , where is the sampling SE of the replicated θ̂(z).
EST SE is the estimated SE, defined as , where is the sampling average of the replicated sandwich estimates .
EMP MISE is the empirical MISE, defined as ∫{θ̂(z) − θ(z)}2 dF(z).
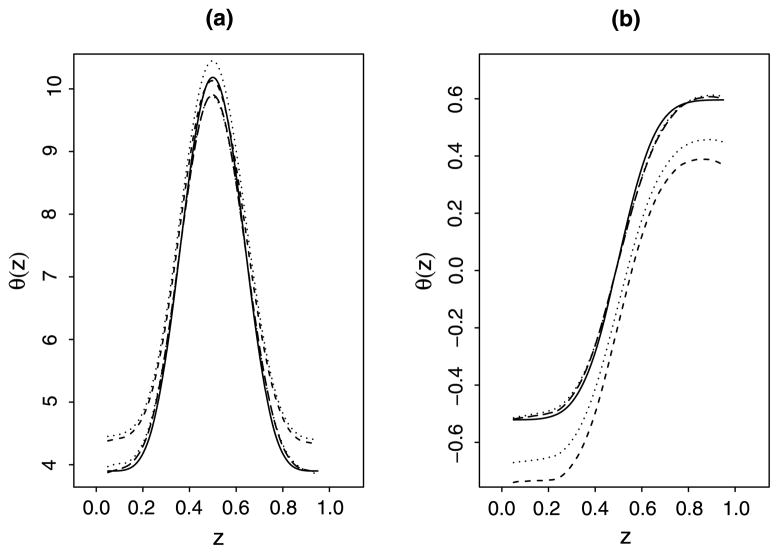
To check the double-robustness property of the AIPW estimator, we computed θ̂AIPW(·) using (i) estimates of πi0’s under an incorrectly specified model with Ui replaced by in the right-hand side of (16) but with δi0’s computed under a correctly specified model (15), (ii) δi0’s computed under an incorrectly specified model with Ui replaced by in the right-hand side of (15) but with estimates of πi0’s under the correctly specified model (16), and (iii) both π̂i and δi computed under incorrectly specified models, with Ui replaced by in the right-hand side of (16) and (15), respectively. The simulation results in Table 2 and Figure 3 show that the AIPW kernel estimate is still close to the true θ(z) when either the model of π(Z, U) or the model of E(Y|Z, U) is correctly specified. In contrast, the IPW estimate with a misspecified model of π(Z, U) is further away from the true θ(z), as well as the AIPW estimate when both the model of π(Z, U) and the model of E(Y|Z, U) are not correctly specified.
Table 2.
Simulation results of the relative biases, SEs and MISEs of the IPW and AIPW estimates of θ(·) using π̂ inconsistent for π0 and/or δ = Ê(Y|Z, U) inconsistent for E(Y|Z, U), based on 500 replications (in parenthesis are the Monte Carlo SEs)
|
n = 500
|
n = 300
|
|||||||
|---|---|---|---|---|---|---|---|---|
| Relative bias1 | EMP SE2 | EST SE3 | EMP MISE4 | Relative bias | EMP SE | EST SE | EMP MISE | |
| Normal case | ||||||||
| AIPW (π wrong) | 0.017 (0.004) | 0.481 (0.016) | 0.475 (0.002) | 0.251 (0.017) | 0.018 (0.005) | 0.635 (0.020) | 0.629 (0.008) | 0.423 (0.028) |
| AIPW (E[Y|Z, U] wrong) | 0.023 (0.004) | 0.640 (0.018) | 0.636 (0.007) | 0.442 (0.021) | 0.021 (0.010) | 0.832 (0.034) | 0.825 (0.019) | 0.728 (0.042) |
| AIPW (both wrong) | 0.068 (0.003) | 0.641 (0.012) | 0.638 (0.004) | 0.835 (0.019) | 0.066 (0.004) | 0.841 (0.022) | 0.837 (0.011) | 1.125 (0.065) |
| IPW (π wrong) | 0.105 (0.004) | 0.471 (0.011) | 0.462 (0.003) | 0.522 (0.027) | 0.108 (0.006) | 0.632 (0.021) | 0.629 (0.003) | 0.723 (0.044) |
| Logistic case | ||||||||
| AIPW (π wrong) | 0.052 (0.021) | 0.254 (0.007) | 0.251 (0.001) | 0.066 (0.003) | 0.102 (0.026) | 0.295 (0.012) | 0.289 (0.001) | 0.092 (0.008) |
| AIPW (E[Y|Z, U] wrong) | 0.056 (0.022) | 0.236 (0.006) | 0.233 (0.001) | 0.057 (0.003) | 0.095 (0.027) | 0.276 (0.007) | 0.271 (0.001) | 0.080 (0.005) |
| AIPW (both wrong) | 0.975 (0.058) | 0.249 (0.008) | 0.250 (0.001) | 0.111 (0.005) | 0.978 (0.064) | 0.286 (0.010) | 0.281 (0.001) | 0.136 (0.008) |
| IPW (π wrong) | 0.662 (0.047) | 0.229 (0.007) | 0.223 (0.001) | 0.075 (0.004) | 0.667 (0.051) | 0.267 (0.011) | 0.263 (0.001) | 0.099 (0.008) |
Relative bias is defined as .
EMP SE is the empirical SE, defined as , where is the sampling SE of the replicated θ̂(z).
EST SE is the estimated SE, defined as , where is the sampling average of the replicated sandwich estimates .
EMP MISE is the empirical MISE, defined as ∫{θ̂(z) − θ(z)}2 dF(z).
Figure 3.
Simulation results of the IPW and AIPW estimates of θ(·) using an incorrectly specified π model and/or an incorrectly specified δ = E(Y|Z, U) model, based on 500 replications with sample size n = 500. The left panel is for case 1 (identity link) and the right panel is for case 2 (logit link): —— the true θ(z), – – – the AIPW kernel estimator when the model for π(Z, U) is misspecified, – · – · the AIPW kernel estimator when the model for E[Y|Z, U] is misspecified, - - - the AIPW kernel estimator when both models are misspecified, and · · · · the IPW kernel estimator when the model for π(Z, U) is misspecified.
6. APPLICATION TO ACSUS DATA
We applied the IPW kernel estimating equation and the AIPW kernel estimating equation, as well as the naive kernel estimating equation, to analyze the ACSUS data described in Section 1. In this illustrative example, our main interest is to investigate the effect of the baseline CD4 counts on the risk of hospitalization during the first year since enrollment into the study. Since the risk of hospitalization depends on various covariates, such as HIV status, treatments, race, and gender, but we only consider a marginal nonparametric mean model of the risk of hospital admission on baseline CD4 counts, we restricted our analysis to a subset of homogeneous subjects for illustrative purpose. Specifically, we limited our analysis to 219 white patients, who were between 25 and 45 years old at entry. They were HIV infected or had AIDS and were treated with anti-retroviral drugs but not admitted to hospital at entry. The CD4 counts ranged from 4 to 1716 among this study cohort, with median equal to 186, and interquartile-range (70, 315). Health care records were used to determine hospitalization during the first year after study enrollment. Although lower CD4 counts are expected to be associated with a higher risk of hospitalization, the functional form of this association is unknown and might be nonlinear. As discussed in Section 1, about 40% of the patients did not have the first-year hospital admission data available. If missing outcomes induced selection bias, the patients who have the first-year hospitalization information may not represent the original study cohort and may lead to biased estimation.
Because the distribution of CD4 counts is highly skewed, we took a log transformation and define Z = log(baseline CD4 count). The missing data model was fit using a logistic regression with Z as well as the other covariates in Table 3, which are binary. The coefficient estimates and their SEs are shown in Table 3. Having insurance and help with transportation enhance the chance of remaining in the study, while use of other medical practitioners, psychological counseling, having help at home and lower CD4 count are significantly associated with a higher chance of dropping out.
Table 3.
Estimates of the logistic regression coefficients of the probability of being observed by the end of the first year in the ACSUS data
| Covariates | Estimate | SE | p-value |
|---|---|---|---|
| Intercept | −2.62 | 0.85 | 0.002 |
| Has help at home | −0.65 | 0.36 | 0.063 |
| Has private health insurance only | 0.53 | 0.45 | 0.241 |
| Has both private and public health insurance | 2.13 | 0.83 | 0.010 |
| Has public health insurance only | −0.11 | 0.47 | 0.819 |
| Use other medical practitioners | −0.95 | 0.49 | 0.053 |
| Use psychological counseling | −0.80 | 0.35 | 0.022 |
| Log CD4 count | 0.64 | 0.14 | <0.001 |
| Has help with transportation | 2.39 | 0.94 | 0.011 |
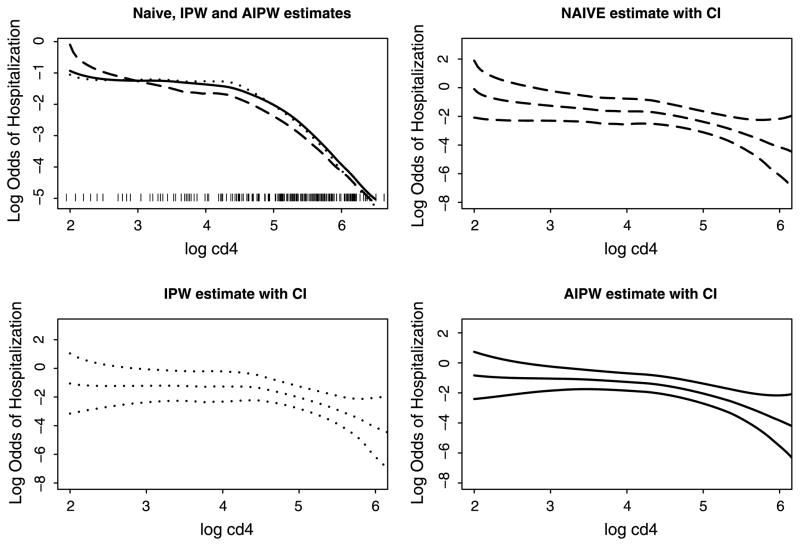
We fit the generalized nonparametric model (1) using logit(μi) = θ(Zi) to investigate the dependence pattern of the first-year risk of hospitalization on baseline CD4 counts. The bandwidth was selected using the generalized EBBS method described in Section 4.3. The estimates of the curve θ(z) using the naive kernel estimating equations, the IPW kernel estimating equations and the AIPW kernel estimating equations are shown in Figure 4. Point-wise Wald CIs centered at the naive, IPW, and AIPW kernel estimates and with standard error estimated using the Sandwich formulae described in Section 4.3, are also presented. For computing the AIPW estimate, we fit parametric models for δ. Exploration of the data shows that the regression function with a quadratic term in log CD4 and the other covariates in Table 3 fits the data well. Residual plot shows no patterns.
Figure 4.
The naive, IPW, and AIPW estimates of θ(log CD4 counts) on the log odds of one-year hospitalization in the ACSUS study. The upper left panel displays three estimates: – – – the naive kernel estimate, · · · · the IPW kernel estimate, —— the AIPW kernel estimate. Each vertical ticker along the x-axis stands for one observation. The other three panels display each estimate separately together with point-wise CIs.
Since only very few patients had log CD4 count lower than 3, the kernel estimates are not stable when log CD4 count is less than 3. We focus our discuss on the estimates of the curve when log CD4 count is greater than 3. The IPW and AIPW estimates are similar, while the naive one underestimates the risk of hospitalization for most of the range of CD4 in our study cohort. Since patients having help at home are more likely to drop out and these patients are likely to be sicker patients, the patients who have the first-year hospital admission information available are actually a biased sample of the whole study population. Therefore, the naive approach using the complete cases directly leads to a biased estimate of the nonparametric function θ(z) and underestimates the risk of hospitalization. Our analysis using the IPW and the AIPW kernel estimating equations indicates that the risk of hospitalization decreases nonlinearly as CD4 count increases with a change point. Specifically, when CD4 count is relatively low (CD4 count < 90), the risk of being admitted to hospitals remains fairly stable at about 25%. As the CD4 count exceeds this threshold, the risk of hospitalization decreases quickly as CD4 count goes up.
7. DISCUSSION
In this paper we proposed local polynomial kernel estimation methods for nonparametric regression when outcomes are missing at random. We showed that the naive local polynomial kernel estimator is generally inconsistent except for special cases. We proposed IPW and AIPW kernel estimating equations to correct for potential selection bias, with the ultimate goal of maximally exploiting the information in the observed data. Unlike parametric regression, the augmentation term in the AIPW kernel estimating equations incorporates a kernel function. We showed that both the IPW and AIPW kernel estimators are consistent when the selection probabilities are known by design or consistently estimated. When the model for the selection probabilities is misspecified, the IPW kernel estimating equation fails to yield a consistent estimator. However, the AIPW kernel estimator still yields consistent estimators of the regression function if a model for E(Y|Z, U) is correctly specified. This double robustness property of the AIPW approach provides the investigators two chances to make a valid inference. The AIPW kernel estimating equation also has the potential to enhance the efficiency with which we estimate the nonparametric regression function. We have shown that within the AIPW estimating equation family, the optimal estimator is obtained by using the true selection probability or its consistent estimates and the augmentation term estimated from a correctly specified model for E(Y|Z, U). It is of future research interest to study whether this estimator is optimal in a bigger class of estimators. Another interesting topic of future investigation is the possibility of enhancing the efficiency of the IPW estimator via estimation of the missingness probabilities at nonparametric rates, for example, under generalized additive models rather than under parametric models.
The IPW and AIPW kernel estimating equations provide consistent estimators when the selection probability model π is correctly specified and is bounded away from 0. In finite samples, when some π’s are close to 0, the IPW and AIPW estimators might not perform well. This is not surprising, as very large weights associated with these very small π’s dramatically inflate a few observations especially when the sample size is moderate, and cause results unstable. Special caution is hence needed when applying the proposed methods to studies when the selection probability is very small for some sample units.
We have focused in this paper on nonparametric regression on a single scalar covariate when the outcome is missing at random. The proposed method can be extended to semiparametric regression, where some covariates are modeled parametrically and some covariates are modeled nonparametrically. The proposed methods can also be easily generalized to higher order local polynomial kernel regression and nonparametric regression with multiple covariates, for example, using generalized additive models. Extension of our work to these settings will be reported in a separate paper.
Supplementary Material
Acknowledgments
Wang and Lin’s research is partially supported by a grant from the National Cancer Institute (R37-CA–76404). Rotnitzky’s research is partially supported by grants R01-GM48704 and R01-AI051164 from the National Institutes of Health.
Footnotes
Supplementary materials for this article are available online. Please click the JASA link at http://pubs.amstat.org.
Technical Proofs: Regularity conditions and proofs for Theorems 1, 2, and 3 in Section 4. (webappendix.pdf)
Contributor Information
Lu Wang, Email: luwang@umich.edu, Department of Biostatistics, University of Michigan, Ann Arbor, MI 48109.
Andrea Rotnitzky, Email: andrea@utdt.edu, Department of Economics, Di Tella University, Buenos Aires, 1425, Argentina and Adjunct Professor, Department of Biostatistics, Harvard School of Public Health, Boston, MA 02115.
Xihong Lin, Email: xlin@hsph.harvard.edu, Department of Biostatistics, Harvard School of Public Health, Boston, MA 02115.
References
- Berk M, Maffeo C, Schur C. AHCPR Publication No 93-0019. Agency for Health Care Policy and Research; Rockville, MD: 1993. Research Design and Analysis Objectives, AIDS Cost and Services Utilization Survey (ACSUS) Reports, No. 1. [PubMed] [Google Scholar]
- Breslow N, Cain K. Logistic Regression for Two-Stage Case-Control Data. Biometrika. 1988;75:11–20. [Google Scholar]
- Carroll RJ, Ruppert D, Welsh AH. Local Estimating Equations. Journal of the American Statistical Association. 1998;93:214–227. [Google Scholar]
- Chen J, Fan J, Li K-H, Zhou H. Local Quasi-Likelihood Estimation With Data Missing at Random. Statistica Sinica. 2006;16:1044–1070. [Google Scholar]
- Fan J, Gijbels I. Local Polynomial Modelling and Its Applications. London: Chapman & Hall; 1996. [Google Scholar]
- Harezlak J, Wang M, Christiani D, Lin X. Quantitative Quality-Assessment Techniques to Compare Fractionation and Depletion Methods in SELDI-TOF Mass Spectrometry Experiments. Bioinformatics. 2007;23:2441–2448. doi: 10.1093/bioinformatics/btm346. [DOI] [PubMed] [Google Scholar]
- Hastie T, Tibshirani R. Generalized Additive Models. Boca Raton, FL: Chapman & Hall/CRC; 1990. [Google Scholar]
- Liang H, Wang S, Robins JM, Carroll RJ. Estimation in Partially Linear Models With Missing Covariates. Journal of the American Statistical Association. 2004;99:357–367. [Google Scholar]
- Little RJA, Rubin DB. Statistical Analysis With Missing Data. 2. New York: Wiley; 2002. [Google Scholar]
- McCullagh P, Nelder J. Generalized Linear Models. London: Chapman & Hall; 1989. [Google Scholar]
- Pepe MS. Inference Using Surrogate Outcome Data and a Validation Sample. Biometrika. 1992;79:355–365. [Google Scholar]
- Reilly M, Pepe MS. A Mean Score Method for Missing and Auxiliary Covariate Data in Regression Models. Biometrika. 1995;82:299–314. [Google Scholar]
- Robins JM. Proceedings of the Section on Bayesian Statistical Science. Alexandria, VA: American Statistical Association; 1999. Robust Estimation in Sequentially Ignorable Missing Data and Causal Inference Models; pp. 6–10. [Google Scholar]
- Robins JM, Rotnitzky A. Semiparametric Efficiency in Multivariate Regresion Models With Missing Data. Journal of the American Statistical Association. 1995;90:122–129. [Google Scholar]
- Robins JM, Rotnitzky A, Zhao LP. Estimation of Regression Coefficients When Some Regressors Are Not Always Observed. Journal of the American Statistical Association. 1994;89:846–866. [Google Scholar]
- Robins JM, Rotnitzky A, Zhao LP. Analysis of Semiparametric Regression Models for Repeated Outcomes in the Presence of Missing Data. Journal of the American Statistical Association. 1995;90:106–121. [Google Scholar]
- Rotnitzky A, Robins J. Semiparametric Regression Estimation in the Presence of Dependent Censoring. Biometrika. 1995;82(4):805–820. [Google Scholar]
- Rotnitzky A, Holcroft C, Robins JM. Efficiency Comparisons in Multivariate Multiple Regression With Missing Outcomes. Journal of Multivariate Analysis. 1997;61:102–128. [Google Scholar]
- Rubin DB. Inference and Missing Data. Biometrika. 1976;63:581–592. [Google Scholar]
- Ruppert D. Empirical-Bias Bandwidths for Local Polynomial Non-parametric Regression and Density Estimation. Journal of the American Statistical Association. 1997;92:1049–1062. [Google Scholar]
- Tan Z. A Distributional Approach for Causal Inference Using Propensity Scores. Journal of the American Statistical Association. 2006;101:1619–1637. [Google Scholar]
- Wand M, Jones M. Kernel Smoothing. London: Chapman & Hall; 1995. [Google Scholar]
- Wang CY, Wang S, Gutierrez RG, Carroll RJ. Local Linear Regresion for Generalized Linear Models With Missing Data. The Annals of Statistics. 1998;26:1028–1050. [Google Scholar]
- Zhang D, Lin X, Sowers M. Semiparametric Regression for Periodic Longitudinal Hormone Data From Multiple Menstrual Cycles. Biometrics. 2000;56:31–39. doi: 10.1111/j.0006-341x.2000.00031.x. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.