Denaturant-dependent folding of GFP

Abstract

We use molecular simulations using a coarse-grained model to map the folding landscape of Green Fluorescent Protein (GFP), which is extensively used as a marker in cell biology and biotechnology. Thermal and Guanidinium chloride (GdmCl) induced unfolding of a variant of GFP, without the chromophore, occurs in an apparent two-state manner. The calculated midpoint of the equilibrium folding in GdmCl, taken into account using the Molecular Transfer Model (MTM), is in excellent agreement with the experiments. The melting temperatures decrease linearly as the concentrations of GdmCl and urea are increased. The structural features of rarely populated equilibrium intermediates, visible only in free energy profiles projected along a few order parameters, are remarkably similar to those identified in a number of ensemble experiments in GFP with the chromophore. The excellent agreement between simulations and experiments show that the equilibrium intermediates are stabilized by the chromophore. Folding kinetics, upon temperature quench, show that GFP first collapses and populates an ensemble of compact structures. Despite the seeming simplicity of the equilibrium folding, flux to the native state flows through multiple channels and can be described by the kinetic partitioning mechanism. Detailed analysis of the folding trajectories show that both equilibrium and several kinetic intermediates, including misfolded structures, are sampled during folding. Interestingly, the intermediates characterized in the simulations coincide with those identified in single molecule pulling experiments. Our predictions, amenable to experimental tests, show that MTM is a practical way to simulate the effect of denaturants on the folding of large proteins.

Our understanding of the folding mechanisms of small single domain proteins has advanced significantly over the last twenty years thanks to theoretical developments (1–7), simulations (8–13), and advances in experimental methods (14–19). Indeed, it can be justly stated that simulations of structure-based models are remarkably successful in predicting the folding mechanisms in the presence (20–22) and absence of denaturants (23–25). More refined questions, such as the relationship between pathway diversity and the symmetry of the underlying native structures (26), transition path times for crossing free energy barriers (27), the nature of the transition state ensemble (28–31) have also been addressed using theory and experiments. In contrast, much less is known about how large proteins with number, N, of amino acids exceeding ≈200 with complex β-sheet fold.

Folding mechanisms of Green Fluorescent Protein (GFP), with predominantly β-sheet native structures stabilized by contacts between residues that are well separated along the sequence, have been extensively investigated (32–40). However, the details of the folding kinetics including the structures in the states that are visited along the folding routes are unexplored. It has been difficult to describe quantitatively the folding of GFP because of the extraordinarily long equilibration times, which has made it non-trivial to obtain consistent values of even thermodynamic quantities using different experimental probes. For example, the number of intermediates and their stabilities, and the associated denaturant-dependent properties (m-values) are not unambiguously known for many of the variants of GFP. Because of the presence of a visual chromophore, that is shielded from water by the barrel structure (Fig. 1A), GFP has been used as a marker in a number of biotechnology and biophysical applications ranging from protein-protein interactions to gene expression (41). Consequently, it is important to map in detail the folding landscapes of FPs (32), which could aid in the development of new GFP tools for use in in vivo localization studies.

Fig. 1.

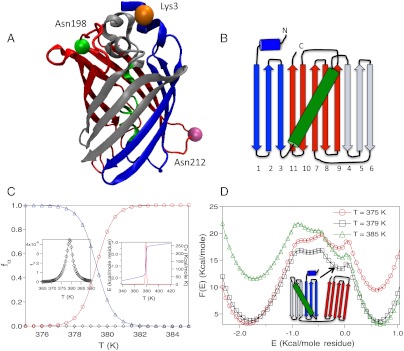
GFP structure and thermal folding. (A) Ribbon diagram of Citrine (Yellow version of GFP, PDB ID: 1HUY). Residues marked in orange, green and mauve are Lys3, Asn198, and Asn212, respectively. (B) Splay representation of GFP. The N-terminus β-strands are represented in blue, the kinked helix at the center of the β-strand barrel is in green, the three β-strands in the center, which form local contacts are in silver, and the C-terminus β-strands are in red. (C) Fraction of GFP in the NBA, INT, and UBA as a function of temperature, T, are shown in triangles, diamonds, and circles respectively. The left inset shows f_INT(T) as a function of T. The right inset shows energy, E, and the heat capacity, C_v as a function of T. (D) Free energy of GFP as a function of E for temperatures above and below the melting temperature (T = 379 K). The structure of one of the intermediates is shown in splay representation.

The folded structure of GFP has eleven β-strands that are closed to form the characteristic barrel structure (Figs. 1A and 1B). The chromophore, surrounded by the barrel and the capping helices, causes hysteresis (denaturant-induced equilibrium folding and unfolding do not coincide even on time scales that exceed hours) in the folding of a number of variants of GFP (34, 35). Mutants that inhibit chromophore formation fold without hysteresis, and could form the basis of describing the de novo folding of the complex barrel structure.

Here, we use simulations of a coarse-grained (CG) Self-Organized Polymer model (42) with side chains (SOP-SC) (21) of GFP, with N = 230. Our simulations are performed for a chromophore less variant of GFP, Citrine, which differs from the wild type sequence by point mutations at four locations, S65G/V68L/Q69M/S72A/T203Y (36). Thermal denaturation and unfolding induced by Guanidinium chloride (GdmCl) (simulated using the Molecular Transfer Model (MTM)) (20) show that equilibrium folding can be approximately described by a two-state model. Folding trajectories probing equilibrium fluctuations and free energy profiles point to the presence of intermediates. We show, in agreement with experiments (33, 38), using a variety of probes of the structures (distributions of the radius of gyration, R_g, solvent accessible surface area, and structural overlap function, χ) that in the intermediate, the N-terminus is folded whereas the C-terminus region comprising of strands β₇ to β₁₀ are flexible and disordered. Upon initiating folding the time-dependent decrease in , obtained using Brownian dynamics simulations (21, 43), shows that compaction occurs in at least two major stages. In accord with the predictions of the kinetic partitioning mechanism(KPM) (44) Citrine folds by at least four distinct routes. In the dominant pathway, folding commences from preformed local β-sheet structures and occurs in an almost all-or-none manner. Stable local structures associate by diffusion-collision mechanism (45) resulting in the folded state. Besides providing testable predictions, such as the linear decrease in the melting temperature as a function of GdmCl and urea concentrations, our work shows that the complexity of GFP folding can be fairly accurately captured using the SOP-SC model in conjunction with MTM.

Results

Thermal Denaturation:

We used multicanonical (MC) molecular dynamics simulations (46, 47) so that thermodynamic properties of Citrine can be computed accurately (see SI Text, and Movie S1 for details). Dependence of the total energy 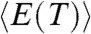as a function of temperature, T, and the associated heat capacity 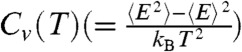both indicate that folding occurs cooperatively (inset in Fig. 1C). The melting temperature, corresponding to the peak in C_v(T) in the absence of denaturants is, T_m = 379 K (see right inset in Fig. 1C). The structural overlap function, χ, is used to distinguish between the Native Basin of Attraction (NBA), equilibrium intermediates (I_EQL), and UBA, the unfolded basin of attraction (Methods). The fraction of molecules in the Native Basin of Attraction, f_NBA(T), as a function of T shows that the folding transition is cooperative (Fig. 1C) suggesting that a two-state description is adequate. The value of T_m computed using P(T_m) = 0.5 yields T_m = 379 K, which coincides with the peak in the heat capacity (Fig. 1C). The T_m value obtained in our simulations are in very good agreement with calorimetry measurements (48, 49), thus validating the SOP-SC model.

The two state nature of thermal unfolding obtained from Fig. 1C hides the presence of equilibrium intermediates, which are evident in the MC folding trajectory (see Fig. S1 in the SI Text). The time dependent changes in E and χ in Fig. S1 show that at least two equilibrium states (hereafter referred collectively as I_EQL) are populated. The dips in the plots of free energy profiles, F(E) as a function of E, above and below T_m correspond to population of intermediates with χ values in the range specified in Methods (Fig. 1D). The inset in Fig. 1C shows that f_INT(T) is very small, which explains the apparent two-state folding of Citrine in the absence of the chromophore (see also (34)). The finding that I_EQL are populated during the folding process (see also Fig. 2) provides indirect support to the analysis used in experimental studies, which found that a three-state description provides a quantitative fit to denaturant unfolding of Citrine in the presence of chromophore. Thus, the intermediate is, in all likelihood, stabilized by the chromophore.

Fig. 2.

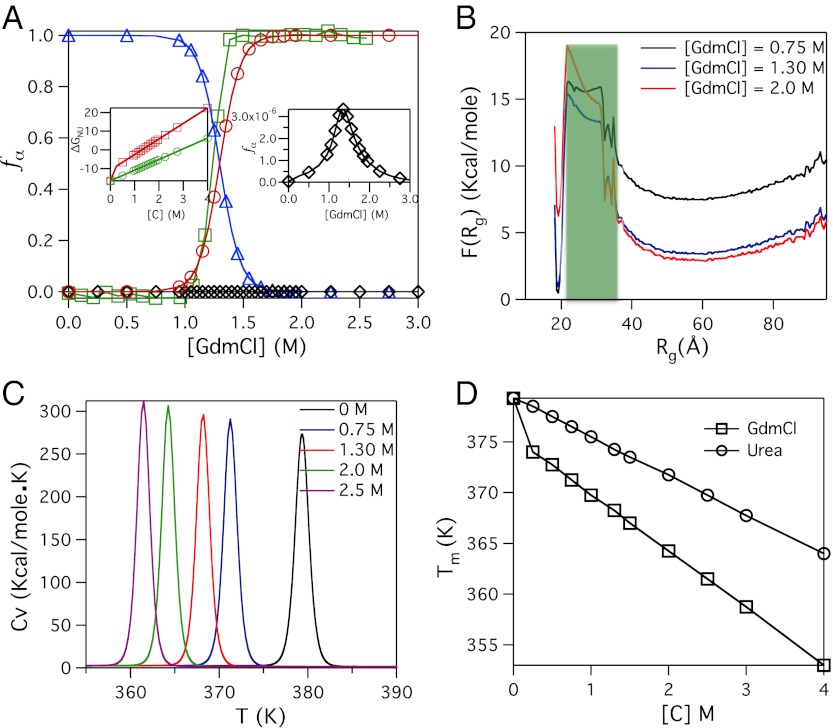
Denaturant effects on GFP: (A) Dependence of f_α([C]) (α = NBA, INT, and UBA) as a function of GdmCl concentration. Blue triangles, black diamond, and red circles are used for f_NBA([C]), f_INT([C]), and f_UBA([C]), respectively. The experimental data for fraction of protein in UBA as a function of [C] is shown in green squares. The right inset shows the low probability of populating the intermediate species. The left inset shows the linear variation of free energy difference between the NBA and UBA, ΔG_NU, as a function of denaturant concentrations. The data in red and green are for GdmCl and Urea, respectively. (B) Free Energy profiles, F(R_g), of GFP as a function of R_g show the population of a thermodynamic intermediate corresponding to the shaded green area. (C) Heat capacity as a function of GdmCl. (D) Variations in the melting temperature, corresponding to the peak in C_v(T), as a function of denaturant concentrations. The upper curve is for urea and the lower one corresponds to GdmCl.

Denaturant Induced Unfolding:

To make a direct comparison with ensemble experiments (33, 34) we simulated the effects of Guanidinium chloride (GdmCl) using the MTM (see Methods and SI Text for details). Following our previous work (21), we choose a simulation temperature, T_s, at which the free energy differences between the NBA and the unfolded state, ΔG_NU( = G_N(T_s) - G_U(T_s)) calculated from simulations agree with the measured value of 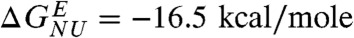for R96A mutant (34) at denaturant concentration, [C] = 0. We chose R96A as a reference GFP for fixing T_s because it exhibits a clear equilibrium two-state transition (34). Since the absolute values of the effective interaction energies in CG models cannot be determined, we used T_s as an adjustable parameter to get accurate estimate of ΔG_NU. The choice of T_s, which is the only parameter that is fixed in our simulations, amounts to choosing the overall free energy scale (21). The dependence of f_NBA[C] and f_UBA[C] on [C] at T_s = 368.2 K also shows that Citrine folds and unfolds reversibly in an apparent two state manner(Fig. 2A). However, the right inset in Fig. 2A shows signs for the presence of an intermediate.

The midpoint of the folding transition f([C_m]) = 0.5 yields C_m = 1.3 M. The simulated equilibrium titration curves can be fit using a two state model from which the dependence of ΔG_NU([C]) on [C] can be calculated using 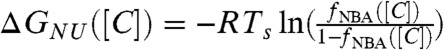. The linear fit, 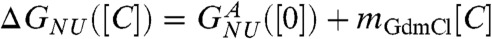, yields the apparent stability at [C] = 0, 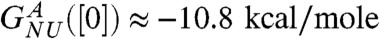and m_GdmCl ≈ 11.3 kcal/mole.M. We attribute the difference between 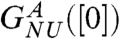and 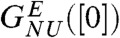to well established uncertainties in the measured transfer energies at low GdmCl concentration. For comparison we also show the experimental results on R96A. The left inset in Fig. 2A, which shows the dependence of ΔG_NU([C]) on [C] using the experimental data on R96A yields 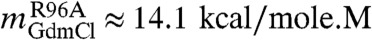and C_m ≈ 1.3 M. The m and C_m values obtained from simulations are in reasonable agreement with experiments.

To ensure that the source of discrepancy between 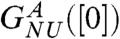and 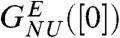is due to the problems associated with transfer free energy measurements involving GdmCl, we calculated the dependence of ΔG_NU([C]) on [C] for urea induced unfolding using the MTM theory (20). The left inset in Fig. 2A shows that ΔG_NU([C]) also decreases linearly as urea [C] increases. The calculated value of G_NU([0]) ≈ -16.4 kcal/mole is in excellent agreement with experiment (34). The MTM based theory predicts that m_urea ≈ 5.7 kcal/mole.M, which is considerably smaller than m_GdmCl. The predictions for urea induced unfolding of Citrine can be tested experimentally.

The apparent all or none transition in Fig. 2A gives no indication of the presence of I_EQL (see also Fig. 1C). However, the free energy profiles, F(R_g), as a function of R_g (Fig. 2B) shows that there are two high energy intermediates at all values of [C]. As is the case in thermal denaturation, the probability of observing these states is extremely small even though the signature of their presence is evident in the folding trajectories (Fig. S1 in SI Text). The free energy profiles projected along E and R_g both are similar implying that these states are structurally similar.

The heat capacity curves at various values of GdmCl concentrations show that the peaks corresponding to T_m([C]) decreases as [C] increases (Fig. 2C). The decrease in T_m([C]) is linear for both GdmCl and urea (Fig. 2D). The variations in T_m([C]) can be fit using T_m([C]) = T_m([0]) - α_i[C], where α_urea = 3.85 K/M and α_GdmCl = 5.7 K/M. Taken together, the simulations show that the global equilibrium folding of Citrine, without the chromophore, induced by temperature or denaturants is cooperative.

Structural Characteristics of I_EQL and Unfolded States:

From the multicanonical trajectories (Fig. S1) and the free energy profiles (Fig. 1D and Fig. 2B) we infer that there are two equilibrium intermediates. In one of the intermediates, interactions involving predominantly the C-terminal strands (β₇ - β₁₀) are disrupted. Almost all of the contacts in the C-terminal strands are broken in the second intermediate (Fig. 3A). In both the the intermediates, the N-terminal β strands are formed and undergo small fluctuations (Fig. 3A). Interestingly, H/D exchange experiments show that these regions have the largest exchange rates suggesting that in I_EQL the C-terminal region is flexible (33), whereas the N-terminal strands are more-or-less intact. Thus, the structural attributes of the equilibrium intermediates in our simulations are similar to those identified in experiments.

Fig. 3.

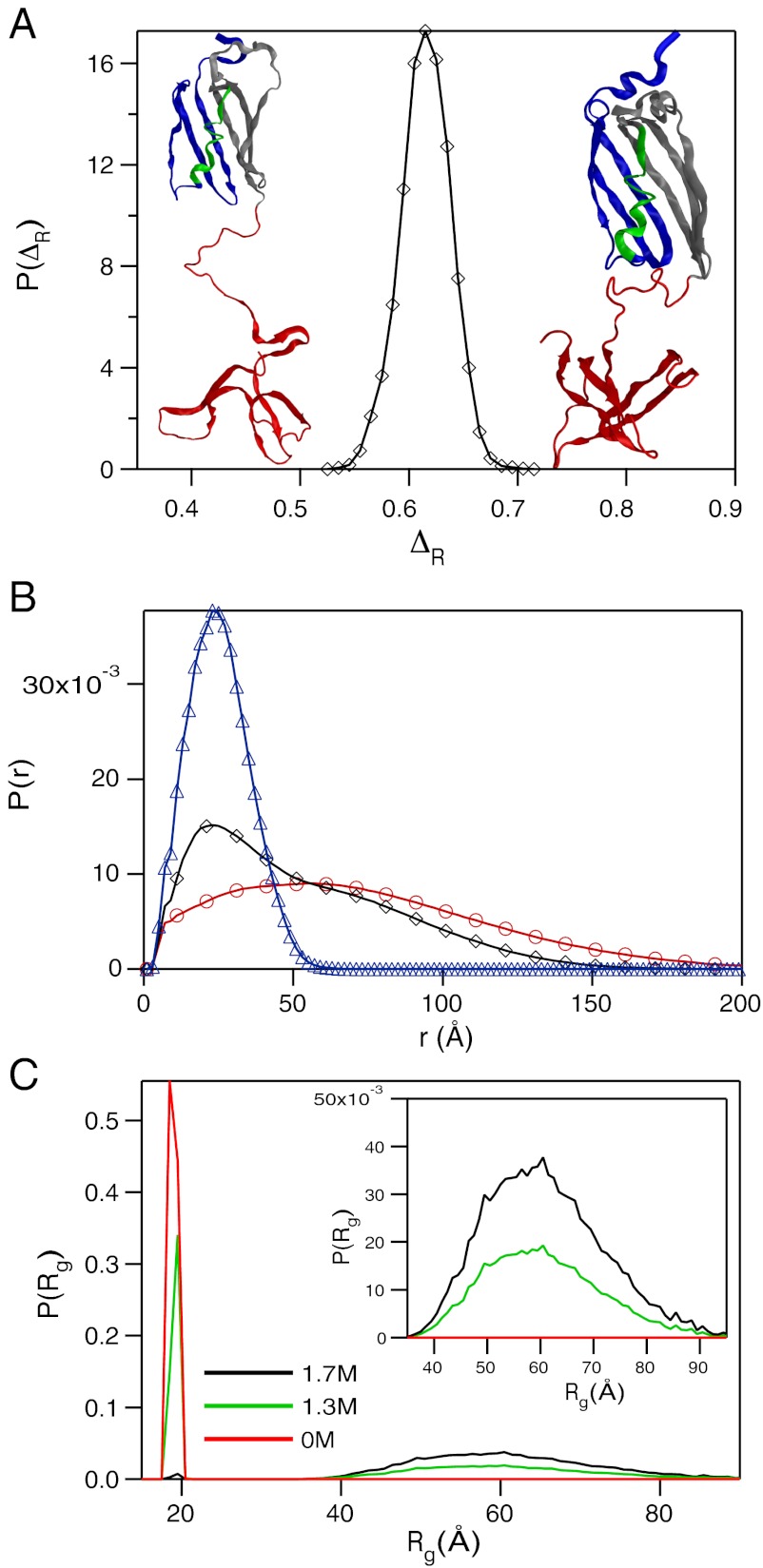
(A) Distribution of P(Δ_R) where Δ_R is the relative accessible surface area (see text for details) in one of the kinetic intermediates with attributes similar to that found under equilibrium. The typical structure sampled at equilibrium is on the left whereas the structure on the right represents a conformation obtained in the kinetic simulation in the EQL pathway. (B) Distribution, P(r), as a function of r, the distance between a pair of sites for NBA (triangles), INT (diamonds), and UBA (circles) computed using conformations sampled at equilibrium with [C] = 0. (C) Distribution of R_g as a function of GdmCl concentration. The midpoint of the transition is C_m = 1.3 M. The inset shows P(R_g) at large R_g.

To compare with the SAXS experiments, we also calculated the pair distance distribution P(r) for the folded, I_EQL, and the unfolded states by varying the GdmCl concentration (Fig. 3B). At low [C], we find that P(r) is peaked around 20 Å. The mean 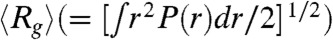≈20 Å compares well with the value obtained using 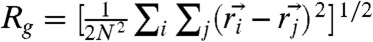where 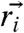and 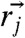are the positions of the ith and jth beads respectively from the X-ray structure. The P(r) for I_EQL is broader with a shoulder around 50 Å, which corresponds to structures with complete disruption of the C-terminal structure. The value of 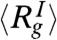for I_EQL ≈ 43.8 Å. The P(r) for the unfolded state at high GdmCl concentration is broad with a tail that extends to ≈200 Å. The calculated value of 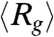for the unfolded state is 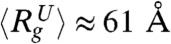. The features found in P(r) for the three states are in broad agreement with SAXS experiments (38) on a different variant of GFP in which unfolding is triggered by decreasing pH. However, the values of 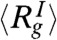and 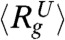obtained from simulations are considerably higher than the estimates from SAXS at pH = 4 and pH = 2.2, respectively. It is unclear if the greater compaction of I_EQL and the unfolded state at acidic pH compared to simulations is due to the different conditions (pH versus temperature), the restricted range of scattering vectors (38) or due to the short comings of the SOP-SC model. The distribution P(R_g) of R_g shows that as [C] increases GFP samples extended conformations with R_g exceeding 80^° (Fig. 3C).

Collapse and Folding Kinetics:

We used Brownian dynamics simulations to generate 80 folding trajectories starting from an initial ensemble of equilibrated structures at a high temperature (T_H > 420 K) and reducing the temperature to T = 300 K to initiate folding. From the distribution of first passage times, P_FP(s), we calculated the probability, 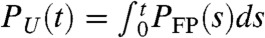, that Citrine has not folded at time, t (inset in Fig. 4A). The folding time obtained from the exponential decay of P_U(t) ≈ exp(-t/τ_F) is τ_F ≈ 5 ms. Although there is a wide range for τ_F reported in experiments the smallest value for τ_F for Citrine from recent experiments is ≈1 s (36). Thus, our estimate of τ_F is at least a hundred fold less than experimental values, which could arise from neglect of solvent and the coarse-grained representation of the proteins.

Fig. 4.

GFP folding kinetics. (A) Time (t) dependent decrease in 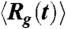. The solid line in green is a two exponential fit to the data. The inset shows the fraction of trajectories unfolded, P_u(t) as function of t, with the solid black line being an exponential fit. (B) Total energy E as a function of t for folding along four pathways. A representative trajectory for each pathway is shown. (C) Dynamic profiles generated using the folding trajectories in terms of χ and R_g for KIN1 and KIN2 in red and black respectively. The ribbon diagram of the kinetic intermediate in KIN2 shows that β₁ - β₃ sheets are not packed onto the rest of the GFP barrel structure. (D) Plot of χ as function of R_g for folding pathways KIN3 and EQL are in green and blue, respectively. Interactions involving the helix and β₁ - β₃ in the first intermediate sampled in KIN3 with the rest of the barrel are absent. The second intermediate in KIN3 is similar to the one observed for KIN2. In the intermediate populated in the EQL pathway, the C-terminal β-sheets do not interact with the ordered N-terminal strands β₁ - β₆.

The time-dependent changes in 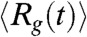during the folding process shows that collapse occurs in two stages (Fig. 4A). The decay of 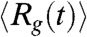can be fit using 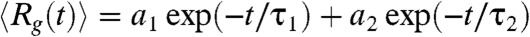, where a₁ = (23.4 ± 0.2) Å, a₂ = (22.5 ± 0.2) Å, τ₁ = 3.6 ms and τ₂ = 43.47 ms (Fig. 4A). The decrease in the value of R_g(t) in each stage is roughly the same (≈22 Å). However, there is a separation in the time scales in the two stages implying that distinctly different ensembles of structures are sampled in two stages. The structures reached at the end of the first stage correspond to minimum energy compact structures (50) that guide the folding of Citrine. The predicted multistage compaction of GFP, similar to that found in other proteins (51), can be tested using time-resolved SAXS experiments.

Parallel Pathways and Kinetic Intermediates:

By analyzing the 80 folding trajectories using E (see Methods) as the progress variable for the folding reaction (Fig. S2) we find that Citrine folds along four pathways. For reasons explained below, we classify the structures populated in three of the pathways as kinetic intermediates and the intermediate in the fourth has most of the hallmarks of I_EQL. Representative trajectories one from each pathway, displaying energy as a function of t, show that in each pathway folding occurs in stages (Fig. 4B). The nature of structures and their lifetimes vary greatly depending on the pathway. In the dominant pathway KIN1, through which ≈50% of the flux to the native state is channeled, Citrine folds in nearly a two state manner (Fig. 4B). In this pathway, β-strands at the N-terminus, the core of the protein, and the C-terminal strands form rapidly in a single step. The folding units in the long lived meta-stable states collide and consolidate (see Movie S1 in the SI Text) as envisioned in the diffusion-collision model (45).

In the second kinetic pathway, KIN2, representing ≈16% of the trajectories, folding occurs through an intermediate in which tertiary contacts between strands β₃ and β₁₁ and the interface between β₁ and β₆ are not formed (Fig. 4C). The structural properties of the intermediate in KIN2, such as the distributions of R_g and χ, differ from I_EQL, and hence we conclude that it is observed only during the process of folding. Similarly, in the third kinetic pathway, KIN3, through which about 10% of the flux to the native state flows, the intermediates shown in Fig. 4D are observed. The intermediate shown in Fig. 4D, has a kinked helix interacting with the N-terminal β-sheets. The splay diagram shows further that long-range interactions involving β₃ and β₁₁ as well as β₁ and β₆ are disrupted.

Equilibrium Folding Intermediate:

In about 15% of the trajectories an intermediate whose structural characteristics almost coincide with I_EQL is populated. The folding trajectory (Fig. 4B) and the [χ,R_g] plot in Fig. 4D show that the intermediate has a long lifetime. There are four lines for evidence which show that the kinetic and equilibrium intermediates are structurally similar. First, the 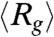obtained using the conformations sampled with folded N-terminal strands (the C-terminal strands are fluid-like) at equilibrium is ∼14 Å whereas those obtained from kinetic trajectories is ∼13 Å. Second, the typical conformations sampled at equilibrium and during the folding process are similar (compare the structures in Fig 3A). In both the structures the strands β₁ through β₆ are formed whereas the C-terminal is more flexible. Third, the values of χ for the conformations corresponding to the plateau in E as a function of t (purple line in Fig. 4B) is in the range 0.7 < χ ≤ 0.895, which coincides with the estimates obtained using equilibrium trajectories (see also the shaded green region in Fig. 2B). Fourth, we calculated the distribution, P(Δ_R), of 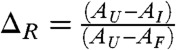, where A_U, A_I and A_N are the solvent accessible surface area (SASA) for the unfolded, I_EQL, and the native states respectively using the conformations sampled during the kinetic simulations (plateau region in the purple curve in Fig. 4B). From P(Δ_R) in Fig. 3A we find that the mean values 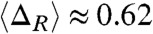, which compares well with the experimental value 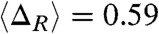estimated for the equilibrium intermediate in the Citrine folding (36). Thus, we surmise that the structures sampled along the EQL pathway (Fig. 4B) are similar to those observed under equilibrium conditions.

Relation Between Collapse, Secondary Structure Formation and Folding:

It has been shown that for efficient folding, collapse and folding occur nearly simultaneously (52), where as for larger complex proteins collapse precedes by folding. In Fig. 4C and 4D we show the conformations sampled in all the pathways. Each conformation is represented by χ and R_g. We conclude from the results in Figs. 4C and 4D that in all the four pathways Citrine undergoes compaction (reduction in R_g) before folding (decrease in χ). These findings show that the search for the NBA occurs among the ensemble of minimum energy compact structures (50). To explore the link between secondary structure formation and collapse we plot the fraction, f_ss, of secondary structure acquired as the polypeptide chain collapses. Fig. S3 shows that in all the pathways the value of f_ss is relatively small even after substantial collapse, which also implies that collapse generates a fluid-like globule. Consolidation of structure occurs only after reduction in chain dimension.

Topological Traps:

In 6 out the 80 folding trajectories topological traps (44) give rise to Citrine misfolding. In five of the trajectories, Citrine is kinetically trapped in a native-like structure in which the loop connecting β₉ and β₁₀ (Fig. 5B) is in an incorrect position, thus disrupting the interactions between β-strands 4 and 9. In the other misfolded structure (35), the helix is outside the barrel and hence does not pack in the center as observed in the native structure.

Fig. 5.

Topological traps and model for GFP folding. (A) The wild type GFP structure in blue is superimposed onto the misfolded structure in red. Misfolding of the loop connecting β₉ and β₁₀ causes a topological trap. The arrows show the correct (folded) and incorrect (misfolded) conformation of the loop. (B) In the second misfolded structure the barrel involving the 11 β-strands form with no contact between the central α-helix and rest of the structure. (C) Folding landscape and network of connected states based on simulations. The flux through the four channels and the routes from the UBA to the NBA are indicated by arrows. Because topological traps (structures in (A) and (B)) are dead ends in the folding process they do not reach the NBA on the time scale of our simulations. Thus, the total flux to the NBA from UBA is less than 100%. Representative structures sampled along the four pathways as well as an unfolded conformation are shown.

Discussion

Intermediates in GFP Folding:

Compelling evidence for postulating the presence of equilibrium intermediates is the non-coincidence of free energies extracted using fluorescence and NMR measurements even though visually the decrease in fluorescence as a function of GdmCl suggests that a two-state description is sufficient (33). More recently, single molecule fluorescence experiments have presented clear evidence for three state equilibrium folding of Citrine with the chromophore (36). The presence of high energy equilibrium intermediates in R96A is only evident in free energy profiles computed as a function of energy (Fig. 1D), radius of gyration (Fig. 2B), and the fraction of native contacts (Fig. S1B). The structural characteristics of I_EQL support the finding based on equilibrium H/D exchange experiments showing order in the N-terminus and flexibility in the C-terminal region spanning β₇ to β₁₀ (33). It is worth pointing out that one of the intermediates populated in single molecule pulling experiments corresponds to unfolding in the C-terminus domain with β₁ through β₆ remaining intact (53). Thus, both experiments and simulations point to the presence of I_EQL. The observation that I_EQL in our simulations is a high energy intermediate occurring with negligible probability whereas the ones characterized in experiments are stable suggests that the intermediates in GFP folding are stabilized by the chromophore.

Comparing Simulation and Experimental Folding Pathways:

We have found evidence for kinetic intermediates that direct folding to the native state. The range of kinetic intermediates observed in our simulations have previously been identified in single molecule pulling experiments and simulations (39, 40, 42, 53). When GFP is stretched by applying mechanical force, f, between residues 3 and 212 (Fig. 1), GFP unfolds along two routes. In the first one, unfolding is in an all-or-none process where as in the second pathway unfolding occurs by populating an intermediate (53). The increase in the contour length upon unfolding GFP from the folded to the intermediate state is consistent with formation of a structure in which strands (1–6) are intact and the rest are unfolded. Our simulations and previous ensemble experiments (33, 37, 38) have identified such an intermediate as occurring both in equilibrium and during the folding process.

When mechanical force is applied (53) to the residues 3 and 198, GFP unfolds by populating a different intermediate in which the 3 N-terminus β-strands (β₁, β₂, β₃) have ruptured away from the rest of the barrel. In addition, when f is applied to the ends of the molecule the dominant unfolding pathway also occurs through such an intermediate (40, 42). We showed (42) that upon initiating folding by reducing the mechanical force from a high value to f = 0, a long-lived metastable intermediate similar to that observed in KIN2 and KIN3 is populated before the barrel structure forms. We find here that in the process of refolding, upon temperature quench, the intermediate with loss of interactions between strands (1–3) and rest of the barrel is populated in pathways KIN2 and KIN3.

Single molecule fluorescence experiments have also shown that Citrine unfolds by parallel pathways. In one of the pathways, the folded state is reached directly, where as an intermediate with a low FRET is populated in the other (36). It is likely, that these low FRET states are an ensemble of conformations containing a mixture of equilibrium and kinetic intermediates. Taken together it is clear that folding GFP must occur through a number of distinct intermediates, which become visible only by using different techniques. By combining all the results from simulations and experiments, we propose a model (Fig. 5B) for GFP folding that involves a complex network of connected states through which the flux to the native flows. The resulting multiple pathways include equilibrium and kinetic intermediates as well as misfolded structures. Detailed comparison between our simulations and experiments show that a number of different experimental probes are needed to quantitatively map the folding landscape of GFP, and presumably other proteins with complex topology.

Collapse and Folding:

Since it was first demonstrated theoretically that folding and collapse transitions are intimately linked for proteins that reach the native state efficiently (54, 55) there has been considerable interest in validating this concept. For wild type GFP it is unmistakable that folding is preceded by populating compact intermediate species. Both SAXS experiments (38) as well our simulations show that a compact state, with 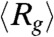intermediate between the values in the folded and unfolded states, is present and is likely to be on-pathway to the NBA. The kinetic folding trajectories clearly show (Fig. 4 C and D) that GFP first collapses before the formation of secondary and tertiary interactions. Our finding is strikingly similar to the order in which structure is acquired in monellin with β-sheet topology (51) as well as in GFP upon force quench (42).

Methods

SOP-Side Chain (SOP-SC) Model:

In the SOP-SC model, which uses residue-dependent interaction between SCs (56), each residue is represented by two interaction centers one for the backbone atoms and the other corresponds to the side chain atoms. The SOP-SC model is constructed using the crystal structure of Citrine, an improved yellow version of GFP (57), with the Protein Data Bank PDB ID: 1HUY. Citrine has 5 mutations compared to the wild type GFP (S65G, V68L, Q69M, S72A, T203Y). The residues labeled 0 and 1A in 1HUY are deleted. In Citrine the chromophore, labeled residue 66 in 1HUY, involves residues GLY65, TYR66, and GLY67. In our simulations the chromophore is disabled by eliminating the chemical reaction involving the three chromophore residues. The functional form of SOP-SC model and the parameters of the CG force field are given in Table S1 in the SI Text.

Molecular Transfer Model (MTM):

The energy of transferring a specific protein conformation from water to the denaturant solution at concentration [C] is written as 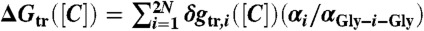where the summation includes both backbone and side chain atoms, δg_tr,i([C]) is the experimentally measured transfer free energy of i, α_i is the solvent accessible surface area (SASA) of the bead i, α_Gly-i-Gly is the solvent accessible surface area of the bead in the tripeptide Gly - i - Gly. The radii of amino acid backbone and sidechain are given in Table S2. The transfer free energies δg_tr,i([C]) for the backbone and side chains, taken from experiments (20, 22, 58), are listed in table S3 in ref. (21). The values for α_Gly-i-Gly are listed in table S4 in ref. (21). The thermodynamic properties of a protein at [C] ≠ 0 are obtained using the procedure described earlier (20, 22).

Data Analysis:

We use the structural overlap function (59) 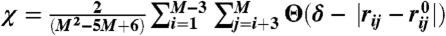to distinguish between the various populated states. Here, M = 2N = 460 is the number of interaction centers in the SOP-SC representation of GFP, r_ij is the distance between the beads i and j with 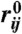being the corresponding distance in the folded state, Θ is the Heaviside step function, and δ = 2 Å. The conformation with 0 < χ ≤ 0.7 are folded, an intermediate state has 0.7 < χ ≤ 0.895, and conformations with χ > 0.895 are unfolded (Fig. S1 in the SI Text).