Separating the effects of internal friction and transition state energy to explain the slow, frustrated folding of spectrin domains

Abstract

The elongated three-helix bundle domains spectrin R16 and R17 fold some two to three orders of magnitude more slowly than their homologue R15. We have shown that this slow folding is due, at least in part, to roughness in the free-energy landscape of R16 and R17. We have proposed that this roughness is due to a frustrated search for the correct docking of partly preformed helices. However, this accounts for only a small part of the slowing of folding and unfolding. Five residues on the A helix of R15, when inserted together into R16 or R17, increase the folding rate constants, reduce landscape roughness, and alter the folding mechanism to one resembling R15. The effect of each of these mutations individually is investigated here. No one mutation causes the behavior seen for the five in combination. However, two mutations, E18F and K25V, significantly increase the folding and unfolding rates of both R16 and R17 but without a concomitant loss in landscape roughness. E18F has the greatest effect on the kinetics, and a Φ-value analysis of the C helix reveals that the folding mechanism is unchanged. For both E18F and K25V the removal of the charge and resultant transition state stabilization is the main origin of the faster folding. Consequently, the major cause of the unusually slow folding of R16 and R17 is the non-native burial of the two charged residues in the transition state. The slowing due to landscape roughness is only about fivefold.

The 15th, 16th, and 17th domains of chicken brain α-spectrin (R15, R16, and R17) have very similar structures, stabilities, and β-Tanford (β_T) values (which reflect the compactness of the transition state for folding and unfolding) (1–6). However, the folding of R15 differs from that of R16 and R17 in a number of respects. R15 folds and unfolds two orders of magnitude faster than R16 and three orders of magnitude faster than R17. R16 and R17 have two sequential transition states, and for both domains the first of these (TS1) shows significant landscape roughness (or “internal friction”) (7). This has not been seen for any other domain of comparable size and folding kinetics, although theory has long predicted the possibility of such landscape roughness (8–15). R15 has a broad transition state (characterized by “rollover” in the unfolding limb for some mutants and for wild type under some conditions), but due to the speed of folding and unfolding it is not known whether it has two sequential transition states (16). However, the early transition state of R15 (which corresponds to TS1 of R16 and R17 and will be referred to as such) has a smoother, less frustrated landscape (7).

Φ-value analysis shows that for all three domains the A and C helices are partially structured at TS1, whereas the B helix is relatively unstructured (16–18). R16 and R17 fold via a framework-like mechanism, with some tertiary contacts formed but more extensive secondary structure that extends throughout the A and C helices. In contrast, R15 folds via a nucleation-condensation mechanism with the interacting regions of the A and C helices forming the nucleus (Fig. S1).

We have shown, using a core-swap strategy, that is it possible to produce fast-folding variants of R16 and R17 that have a smoother energy landscape and have a folding mechanism that is more like that of R15 than their slow-folding parents (Fig. S1) (7). A number of core-swapped versions of R16 and R17 have been investigated. These have core residues from fast-folding R15 grafted into slow-folding R16 and R17 and some of these are described in Table 1. Essentially our results show that substitution of just five residues in the A helix—residues that constitute the folding nucleus in the A helix of R15 (see shaded area in Fig. S1A)—are sufficient to convert the slow folding proteins into fast folding versions.

Table 1.

Properties of wild-type (WT) spectrin domains and some core-swapped variants

Protein	Comment	kfs	ΔGD-N kcal mol-1	Internal friction (σ) cP
R15	WT	60,000 ± 13000	6.8 ± 0.2	0.26 ± 0.09
R16	WT	126 ± 2	6.4 ± 0.2	3.9 ± 0.8
R17	WT	30 ± 2	6.0 ± 0.2	6.4 ± 2.7
R16o15c	R16/R17 with the core of R15 (22/24 substitutions)	1,533 ± 35	5.5 ± 0.2	2.1 ± 0.2
R17o15c		141 ± 5	3.3 ± 0.2	0.63 ± 0.11
R16m5	R16 with 5 substitutions in helix A	4,300 ± 700	4.6 ± 0.1	ND
R17m5	R17 with 5 substitutions in helix A	120 ± 10	2.9 ± 0.1	ND

These data were determined using urea as the denaturant at 25 °C.

ND: not done.

Data compiled from refs. 6, 7, and 16.

Here we show, using a series of point mutations, that it is possible to dissect this behavior further. We show that it is possible to speed folding (and unfolding) significantly, without altering the folding mechanism and without affecting landscape frustration. Our results are consistent with the hypothesis that the landscape roughness originates from a frustrated search for the correct docking of partly preformed helices, and quantification of the frustration allows us to show that landscape roughness is responsible for slowing the folding by about fivefold.

Results

The Kinetics of the Five Mutations.

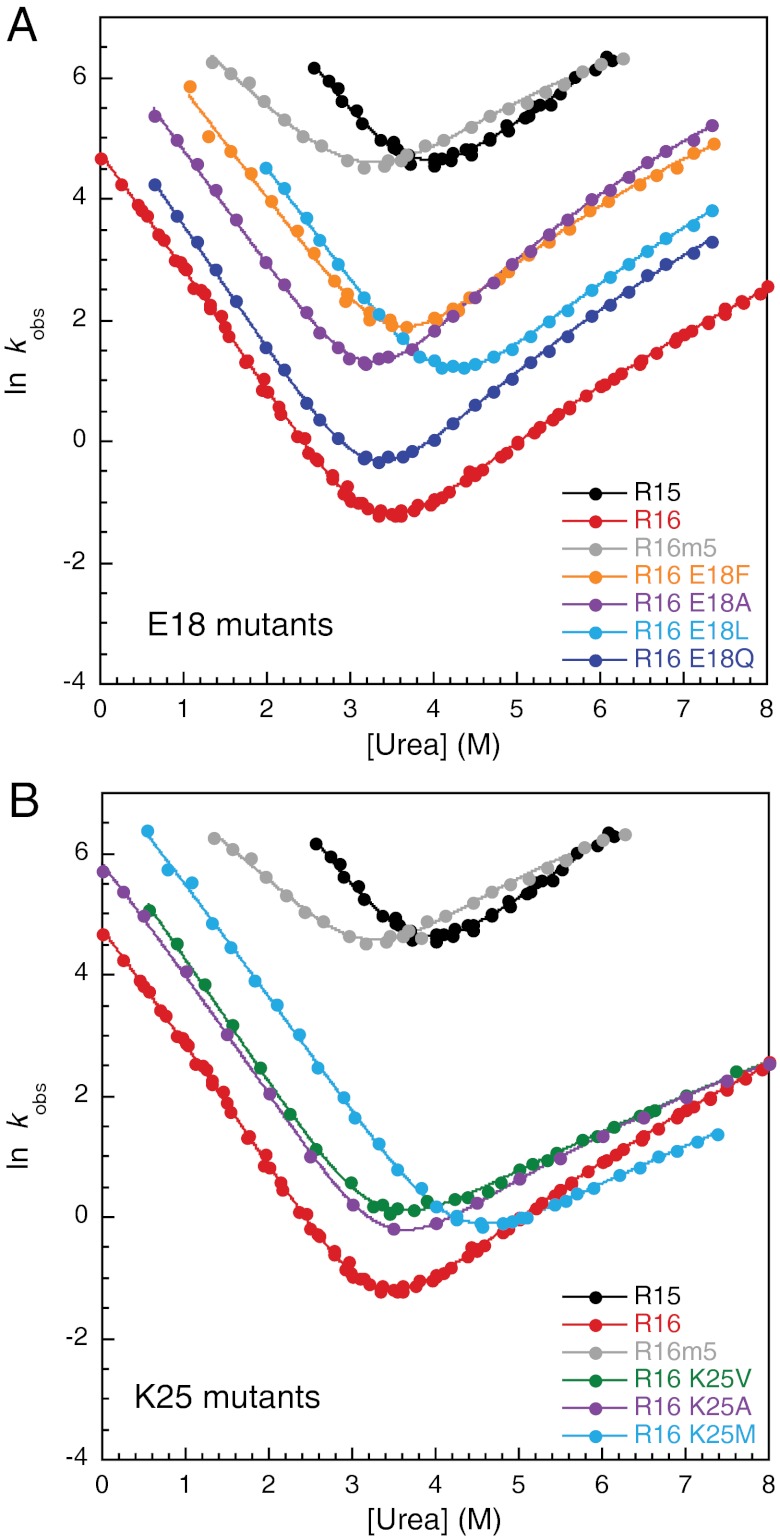
The five substitutions in the A-helix E18F, E19D, I22L, K25V, and V29L (Fig. 1) were introduced individually into R16, and the effect of each on the thermodynamics and kinetics of folding was investigated (Fig. 2 A and B and Table S1). The chevron plot of wild-type R16 displays a shift in the unfolding m value with concentration of denaturant, and this downward curvature in the unfolding arm is also observed for the five mutants reported here. The curvature is most pronounced for K25V but present for all mutants. A number of models have been used to fit such downward curvature; the model that has been shown to best fit R16, and its mutants, is a sequential transition state model with two obligatory, sequential transition states separated by a high-energy intermediate (17, 19–23).

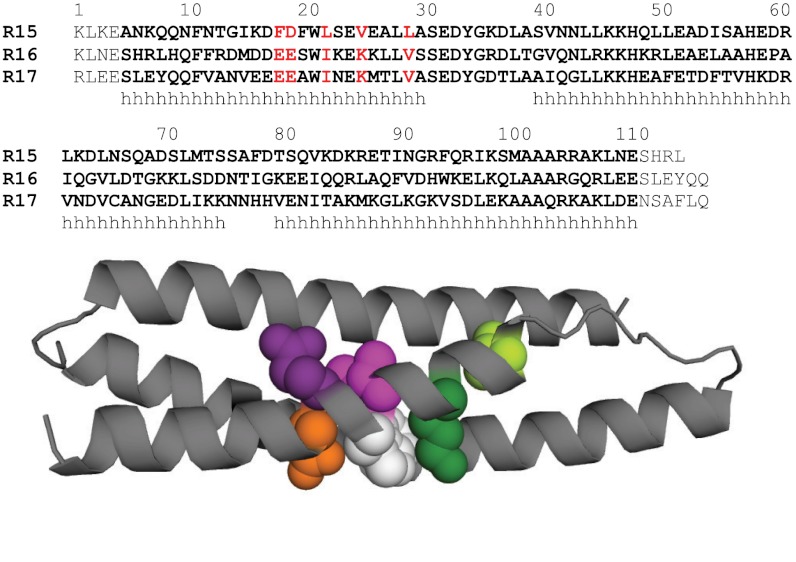
Fig. 1.

Locations of the mutations made in R16. (Top) Structural alignment of the sequences of R15, R16, and R17. The 106 residues in each domain are highlighted in bold. Each domain is extended by flanking residues. Helical regions indicated with h. The five core residues in Helix A described in this study are highlighted in red. (Bottom) R16 is shown as a cartoon with Glu18 shown in orange, Glu19 in purple, Ile22 in pink, Lys25 in dark green, and Val29 in pale green. Also shown is the conserved Trp21 in white.

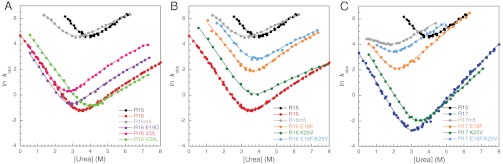
Fig. 2.

The effect of the five individual mutations on the kinetics of R16 and R17 compared to the wild-type proteins and core-swapped domains with all five substitutions. (A) Chevron plots of the conservative R16 mutants that have only a small effect on the kinetics. (B) Chevron plots of the two R16 mutants that have a more significant effect on the kinetics: E18F , K25V, and the double mutant E18F/K25V. (C) Chevron plots of the mutations made in B made in an R17 background. Wild-type data are taken from Scott et al. (6).

The most obvious difference between R16 and R16m5 (which contains all five of these substitutions) is the significant increase in both k_f and k_u. Three of the substitutions are fairly conservative (E19D, I22L, and V29L), and individually these have little effect on the folding or unfolding kinetics (with Φ-values estimated close to 0 or 1, from visual inspection of the chevron plots and calculation) (Fig. 2A). By contrast, the change in folding and unfolding rate constants of two nonconservative mutants (E18F and K25V) affect the kinetics in a nonstandard way, speeding both folding and unfolding. Furthermore, the effects are approximately additive so that the double mutant E18F/K25V folds and unfolds some 40–50 times faster than the parent R16, although at the midpoint, the rate constants are still significantly lower than that of R15m5 (Fig. 2B). Interestingly, neither of these two nonconservative mutations affects the stability of R16 appreciably.

These two individual mutations, E18F and K25V, were also made in R17, along with the double mutant E18F/K25V (Fig. 2C and Table S1). Equilibrium denaturation curves fitted well to a two-state transition. In urea, the kinetics of R17 fit well to a two-state model, so this minimal model was used to fit the R17 data (7, 18). The effect of these two mutations on the stability of R17 differs from that seen in R16. E18F significantly destabilizes R17, and K25V is slightly stabilizing. However, the effect on the kinetics is similar to that seen for R16: E18F speeds up both folding and unfolding considerably, and K25V has a similar, but much smaller, effect. The double mutant E18F/K25V shows the same additive behavior as in R16. A reduction is seen in m_kf in E18F/K25V, which is similar to that seen for R17m5 and other R17 core-swapped domains (7).

The Effect of Solvent Viscosity on the Folding of E18F and K25V.

For the core-swapped proteins, faster folding and unfolding kinetics have been accompanied by reduced landscape frustration (7). To probe whether E18F and V25K have an effect on the roughness of TS1 in R16 viscosity analyses were performed on these R16 mutants. The approach used was identical to that used to determine the dependence of the R16 wild-type kinetics on solvent viscosity. Kramers’ theory describes a reaction as a diffusive movement over an energy surface (15, 24). We used an empirically derived formulation by Ansari et al. (25),

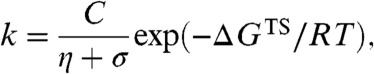[1]

where k is the folding or unfolding rate constant, C is a temperature and solvent independent term including all components of the pre-exponential factor except the friction terms, η is the solvent viscosity, σ the “internal friction” of the protein, and ΔG^TS the height of the energy barrier (7, 25, 26). This formulation is experimentally useful but does assume that solvent friction and internal friction are additive. By altering η at a constant ΔG^TS and temperature the effect of σ on k can be determined. When the barrier to folding or unfolding is smooth, σ will be negligible, thus k is inversely proportional to η and the slope of a relative rate constant vs. inverse of relative solvent viscosity plot should be close to unity. This has been seen for a number of small domains, including R15 (7–13). The folding and unfolding rate constants of R16 or R17 when TS1 is rate limiting, in contrast, show little dependence on solvent viscosity due to a substantial value of σ (Fig. 3 and Table 1). σ is determined from a plot of η against 1/k fitted with a rearranged version of [1]

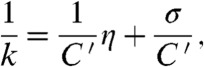[2]

where C^′ = C exp(-ΔG^TS/RT), thus maintaining the assumption that ΔG^TS is invariant with glucose concentration. Solvent viscosity is easily adjusted by the addition of small molecule viscogens such as glucose. In addition to its viscogenic properties glucose stabilizes proteins (27). Due to this stabilization these experiments are performed using the stronger denaturant, GdmCl. The stability of the transition state, ΔG^TS, cannot be determined and the isostability approach is widely applied to overcome this (8–13, 28). Such an approach has been criticized (29), but the strength of our experiments is the comparative nature of our study. (For a more complete discussion see the supporting information of Wensley et al. (7)).

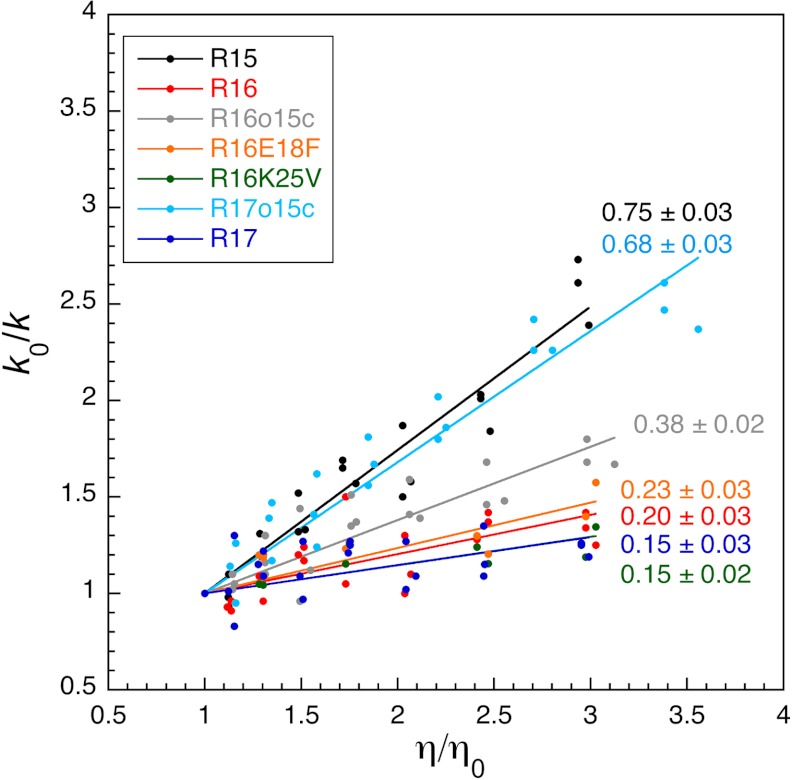
Fig. 3.

The mutation E18F has no effect on the internal friction seen at TS1 of R16. The dependence of the relative rate constants, k₀/k, on relative solvent viscosity, η/η₀ for a number of spectrin domains. Although the core-swapped proteins R17o15c and R16o15c all show an increase in solvent viscosity dependence over their parent R17 and R16 domains, R16E18F and R16K25V do not alter the solvent viscosity dependence. Data for wild-type domains and core-swapped domains taken from (7).

Chevron plots of R16, E18F, and K25V were collected at 0.00, 0.50, 1.00, 1.50, and 1.75 M glucose using GdmCl as the denaturant (Fig. S2). Downward curvature can again be seen in the unfolding arms of both of these mutants. The effect of glucose on the m values of E18F and K25V is the same as on wild-type R16, with m_kf reducing with increasing glucose concentrations.

From these fits, rate constants were calculated for the crossing of TS1, the transition state known to be frustrated in wild-type R16, and used to determine k_f at ΔG_D-N = 1.5 kcal mol^-1 and the rate constant (i.e., k_f = k_u) at ΔG_D-N = 0.0 kcal mol^-1 for each glucose concentration. Relative solvent viscosity vs relative rate constant plots are shown in Fig. 3, data in Table S2, and plots used to calculate σ shown in Fig. S2 B and D. The mean slopes in Fig. 3 for E18F and K25V are essentially the same as wild-type R16 (0.23 ± 0.03, 0.15 ± 0.02, and 0.20 ± 0.03, respectively) and significantly lower than the slopes for the core swap (R16o15c), which has reduced internal friction (slope of 0.38 ± 0.02). Likewise the internal friction values calculated from these data are the same for R16 and the single mutants (weighted average for σ is 3.8 ± 1.1 cP for E18F, 6.3 ± 1.5 cP for K25V compared with 3.9 ± 0.8 cP for wild-type R16) (Table S2). Thus, despite increasing the folding and unfolding kinetics of R16, by about 20-fold in the case of E18F, neither of these two mutations have reduced the landscape frustration experienced by R16 as it crosses TS1.

The Transition State Structure of R16 E18F.

R16 folds by a framework-like mechanism, manifested by significant secondary structure in the transition state (Ala-Gly Φ-values exceed the tertiary core-packing Φ-values) (17) (Fig. S1). By contrast R15 folds by an archetypal nucleation-condensation mechanism with concomitant formation of secondary structure and tertiary structure and regions of high phi values in interacting regions of helices A and C (16) (Fig. S1). In the core-swapped proteins, faster folding has not only been associated with a decrease in landscape roughness but also with a change in folding mechanism, from framework-like toward nucleation-like (7). Because the mutation E18F has the most significant effect on the folding and unfolding kinetics of the five individual mutations made, the effect of this mutation on the transition state structure of R16 was probed via Φ-value analysis of the C helix. This helix was selected because the differences in the Φ-value patterns between R15 and R16, from which we infer differences in folding mechanism, are the most clear in this helix (17). Because the purpose of this Φ-value analysis is comparative, the mutations chosen and the conditions used were identical to those used for the wild-type R16 Φ-value analysis. Two mutation types were made: (i) core mutations where a non-disruptive, deletion mutation was made to a core residue to probe tertiary structure formation and core packing at the transition state, and (ii) surface mutations where each position was mutated first to alanine then to glycine and the two compared to probe helix formation (Ala-Gly scanning) (30, 31).

The stability of each mutant was probed via equilibrium denaturation ( and 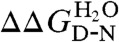values are shown in Table S3). Each mutant fitted well to a two-state transition, and the mean m_D-N-value was 1.9 kcal mol^-1 M^-1, the same as that seen in the wild-type R16 Φ-value analysis (17). Each mutated protein has the same loss of stability in the E18F background as in the wild-type background (Fig. S3), suggesting there has been no significant change in structure upon mutation. Chevron plots for all mutations are shown in Fig. S4, and these were fitted using the sequential transition state model (Methods). Φ-values were determined from folding data for TS1 (Fig. 4 and Table S3). Rather than determining Φ at 0 M denaturant, as was done for wild-type R16, Φ was determined at 2 M urea. This was because the faster folding of E18F meant data could not be collected at or close to 0 M urea. It should be noted that the pattern of Φ-values does not differ if the extrapolated 0 M values are used instead.

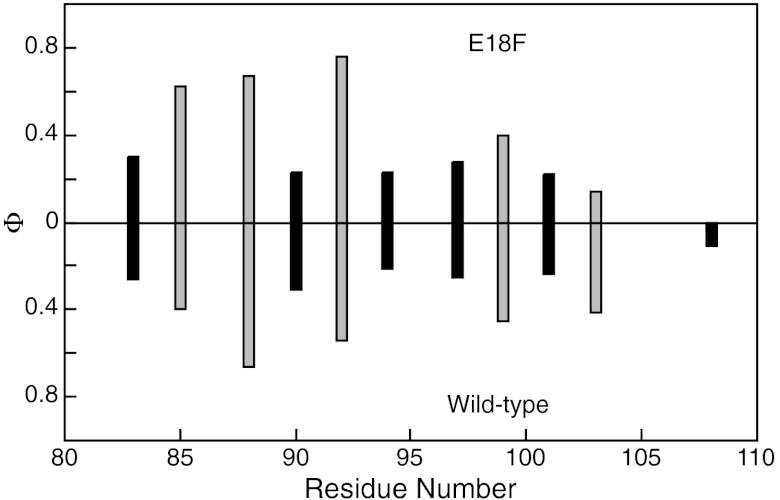
Fig. 4.

The Φ-values of the C helix of R16 are not altered by the mutation E18F. (A) Φ-values for TS1 of R16 for E18F (Upper) and wild-type (Lower) (17). Core mutations are shown in black, surface Ala-Gly scanning mutations shown in gray.

The C helix TS1 Φ-values of R16 E18F show a clear distinction between surface Φ-values, which probe helix formation, and core Φ-values that probe tertiary interactions (p = 0.02). The former are consistently larger, so the C helix has more secondary structure formed by TS1 than tertiary. This pattern of Φ-values is very similar to that seen for the C helix of wild-type R16 (Fig. 4), indicating that the mutation E18F in R16 has no effect on the structure of TS1. Indeed, the comparison of the Φ-values obtained at each position in the two cases shows that they are very well correlated (p = 0.002). Thus, E18F, despite altering the folding and unfolding kinetics significantly, does not alter the transition state structure or folding mechanism of R16.

The Removal of the Charged Residues E18 and K25.

Both E18F and K25V mutations result in substitution of a charged residue by a hydrophobic residue, leading naturally to this question: Is the effect on the rate of folding the result of removal of a charge or of introducing of hydrophobicity? Note that the Phe in E18F is likely to provide a large hydrophobic surface. Further mutations were made at these sites to address this question; E18Q, E18L, E18A and K25A, and K25M (Fig. 5 and Table S1). The mutational sequence Glu18-Gln18-Ala18 shows that the loss of the charge, then loss of the polar residue, is key to increasing both the folding and unfolding rate constants of R16. The addition of large hydrophobic groups, either leucine or phenylalanine, has a small effect, but it is minor relative to the effect of charge loss. The removal of the charged group at position 25 (K25A) is also key to the faster K25V kinetics; the alanine to valine mutation is silent. The addition of methionine, which is not β-branched, has only a small stabilizing effect. So at both positions it is the loss of the charged side chain, not the gain of hydrophobic residues, that is the origin of the faster folding and unfolding kinetics.

Fig. 5.

Substituting the charged residues Glu18 and Lys25 speeds the folding and unfolding of R16. (A) Chevron plots of mutations at position 18. (B) Chevron plots of mutations at position 25. Data for K25A taken from Scott et al. (17).

Discussion

Substitution of the charged residues E18 and K25 is sufficient to speed the folding of R16 significantly. Both E18 and K25 are considered to be “core residues” because they have less than 15% solvent exposed surface area. However, inspection of the structure reveals that the charged moieties of both the side chains are, in fact, largely solvent exposed. The β_T of R16 is approximately 0.6. This suggests that, although the transition state of R16 is more collapsed than the denatured state, it is still significantly less compact than the native state. Thus we infer that the charged portions of E18 and K25 are actually buried to some extent in the transition state, causing significant destabilization, which is relieved when the protein finally collapses to its compact native structure. Such nonnative burial of charged residues within the transition state has been observed before, for instance in CI2 and S6 (32, 33).

However, these fast-folding single- and double-mutant variants do not have the characteristics of the more extensively core-swapped R16 protein (or the fast folding R15): that is, reduced landscape roughness and an altered pattern of Φ-values (from which we infer a change in mechanism). Thus this study enables us to distinguish between two distinct effects, the energetic barrier and the landscape roughness. First, the slowing of folding that comes from the classical destabilization of the transition state by burial of the charge in the collapsed but not compact structure. Second, the internal friction that we have previously proposed to be due to a frustrated search for the correct docking of partly preformed helices. From the data presented here we calculate that the effects on ΔG^TS‡ of these two mutations account for about a 40-fold change in the folding and unfolding rate constants of R16 and that the effect of the viscosity dependent prefactor accounts for only approximately a fivefold change (Tables S1 and S2).

In this study we have seen that the correlation between folding mechanism and frustration is maintained for these spectrin domains, which is consistent with our misdocking hypothesis. The value for the internal friction reported in the spectrin domains is among the highest observed so far, and yet the depression in the rate of folding and unfolding is only a factor of five. This means that it is quite possible that such friction also exists in other protein systems. Unfortunately there are only two other proteins for which both viscosity measurements and Φ-value analyses have been performed. Both of these proteins, protein L and CspB, have been shown to fold via a nucleation mechanism, and neither displays significant internal friction (9, 10, 34, 35).

We would not have pursued the question of why R16 and R17 fold so slowly had we not seen such very large differences in folding and unfolding rate constants compared to R15. Although we made 72 variants of R15 and 84 variants of R16 in our Φ-value analyses, by chance we did not make any substitutions at position E18, which might have guided our eyes toward charge burial as being an important factor (note what a relatively small effect K25V has here). Perhaps this study emphasizes the importance of systematic and extensive comparative studies of the folding of homologous proteins. Without the very marked differences in behavior of the three spectrin domains, we would not have discovered the phenomenon of internal friction in protein domains that fold in the ms-s time scale, a phenomenon that had long been predicted but that remained unseen in experiment. However, spectrin R16 and R17 are the first, relatively slow (ms-s) folding proteins where landscape frustration has been identified and where such frustration has been shown to slow folding. Discovery of internal friction in R16 and R17 prompted us to carry out extensive protein engineering studies that have allowed us to suggest a mechanistic explanation for landscape frustration.

Methods

All mutagenesis, protein expression, purification, and biophysical data collection were performed as before (6, 16).

Equilibrium denaturation curves for both R16 and R17 mutants fitted well to a two-state transition (36). All R16 mutant chevron plots were fitted using the sequential transition state model (17, 19–23). In urea, the parameters (m₂ = -0.7 M^-1 and m_-2 = 0.5 M^-1), obtained from global fitting of R16 wild-type and its large set of Φ-value mutants (17), were used to constrain the fits of the data presented herein. Good agreement was seen between kinetic and thermodynamic parameters (Table S1). E18 mutants unfold considerably faster than other R16 mutants so some unfolding arms collected are very short due to the upper limit for accurate data collection on our stopped-flow apparatus (600 s^-1). Consequently, the second limiting slope could not be accurately fitted for L97A and A101G, so these were fitted to a two-state model with the unfolding m value fixed to 1.2 M^-1. In GdmCl, the set of R16 chevrons collected for the wild-type viscosity analysis were globally fitted sharing m₂ and m_-2, although the second slope did not become rate limiting within the range of data collected (7). These unfolding m values (m₂ = -2.0 M^-1 and m_-2 = 1.3 M^-1) were used to constrain the fits of the E18F dataset. However, the shallower gradient seen for K25V, which is due to a reduced difference in free energy between TS1 and TS2, results in many more data points on the second limiting slope, and this data set cannot be fitted with the wild-type unfolding m values. Consequently, the set of five chevrons was globally fitted with shared unfolding m values, resulting in m₂ = -1.6 M^-1 and m_-2 = 1.1 M^-1. These values were not used for E18F, because they were determined from a considerably smaller dataset than that used for wild-type R16. All R17 chevron plots were fitted using a two-state model (18). Viscosity analyses were performed as described (7).