Mixed-Effects State Space Models for Analysis of Longitudinal Dynamic Systems

Summary

The rapid development of new biotechnologies allows us to deeply understand biomedical dynamic systems in more detail and at a cellular level. Many of the subject-specific biomedical systems can be described by a set of differential or difference equations which are similar to engineering dynamic systems. In this paper, motivated by HIV dynamic studies, we propose a class of mixed-effects state space models based on the longitudinal feature of dynamic systems. State space models with mixed-effects components are very flexible in modelling the serial correlation of within-subject observations and between-subject variations. The Bayesian approach and the maximum likelihood method for standard mixed-effects models and state space models are modified and investigated for estimating unknown parameters in the proposed models. In the Bayesian approach, full conditional distributions are derived and the Gibbs sampler is constructed to explore the posterior distributions. For the maximum likelihood method we develop a Monte Carlo EM algorithm with a Gibbs sampler step to approximate the conditional expectations in the E-step. Simulation studies are conducted to compare the two proposed methods. We apply the mixed-effects state space model to a data set from an AIDS clinical trial to illustrate the proposed methodologies. The proposed models and methods may also have potential applications in other biomedical system analyses such as tumor dynamics in cancer research and genetic regulatory network modeling.

1. Introduction

State space modelling has been used mainly in time series data analysis. It has found application in many areas, such as economics, engineering, biology etc. A state space model consists of a state equation and an observation equation. The state equation models the process of the states while the observation equation links the observations to these underlying states. A standard linear state space model can be written as

$${\mathit{x}}_t={\mathit{F}}_t{\mathit{x}}_{t-1}+{\mathit{v}}_t,$$ (1)

$${\mathit{y}}_t={\mathit{G}}_t{\mathit{x}}_t+{\mathit{w}}_t,$$ (2)

where x_t is the state vector, y_t is the observation vector, F_t is the state transition matrix, and G_t is the observation matrix. It is assumed that vectors v_t and w_t are independent and identically distributed with v_t ~ N(0, Q) and w_t ~ N(0, R). The system matrices (F_t, G_t) and the covariance matrices (Q, R) may contain unknown parameters θ and ω, respectively.

In this paper, motivated by HIV dynamic studies, we propose a class of mixed-effects state space models (MESSM) based on the longitudinal feature of the dynamic systems. In the models, the system matrices contain random effects, and the dimension and structure of the system matrices are specified a priori and may be based on a system of differential/difference equations, which is often used in engineering applications. Two estimation methods for standard mixed-effects models and state space models, the Bayesian approach and the maximum likelihood method, are modified and investigated for estimating unknown parameters in the proposed MESSM. Simulation studies are carried out to assess the finite-sample performance of the two estimation methods, and the results indicate that both methods provide quite reasonable estimates for the parameters. The mixed-effects state space models are applied to a data set from an AIDS clinical trial to illustrate the proposed methodologies.

The primary interest of state space modelling is to estimate the state variables based upon the observations. If the parameters are known, the well-known Kalman filter (Kalman, 1960) yields, under the condition of linearity and normality, the optimal estimates of the states. For unknown parameters the maximum likelihood method provides efficient estimates under certain conditions (Schweppe, 1965; Pagan, 1980; Jensen and Petersen, 1999).

The state space model provides rich covariance structures for the observations y_t. It indeed covers the covariance structure of ARMA (Autoregressive Moving Average) models as the latter can be written into a state space form. Another interesting aspect of the state space model is its flexibility in modeling the underlying mechanism (state equation) and the observations (observation equation) separately.

A longitudinal study usually involves a large number of individuals with observations for each individual taken over a period of time. Variation among the observations consists of the between-subject variation and the within-subject variation. In the very popular linear random-effects models (Laird and Ware, 1982)

$${\mathit{y}}_i={\mathit{x}}_i\mathit{\beta }+{\mathit{Z}}_i{\mathit{b}}_i+{\mathit{e}}_i,{\mathit{b}}_i~\text{N}(\mathbf{0},\mathit{D}),{\mathit{e}}_i~\text{N}(\mathbf{0},{\mathbf{\Omega }}_i),$$

the random effects b_i and errors e_i = [e_i1, · · ·, e_ini]′ account for the between-subject and within-subject variation, respectively. Covariance matrix Ω_i may be diagonal or has a complicated structure (Jones, 1993; Diggle, Liang and Zeger, 1994). In particular, Jones (1993) considered the ARMA covariance structure for Ω_i. In this work ARMA models were transformed into state space forms, and the Kalman filter was used to compute the likelihood.

Stochastic models have been used to model longitudinal data. For example, Rahiala (1999) proposed a random-effects autoregressive (AR) model for a growth curve study in which the AR coefficients were treated as random effects. The state space approach was briefly discussed in Rahiala’s paper for the computation of the likelihood with missing data.

Instead of using the state space approach as a computational tool, we consider the state space modeling approach to directly model longitudinal dynamic systems in this paper. We introduce the random effects to the system matrices F_t and G_t in (1)–(2) to account for between-individual variations in longitudinal studies. It is a stochastic modeling approach, but is more flexible than the random-effects AR model and can easily handle irregularly spaced data and missing data. Such modeling approach inherits the modeling power of state space models for dynamic systems as well as the idea of random effects for longitudinal studies. Thus it is especially useful in dealing with mechanism-based longitudinal dynamic systems (Huang, Liu and Wu, 2006).

This paper is organized as follows. In Section 2, we introduce the MESSM, state some basic assumptions on the system matrices, and give an illustration example based on an HIV dynamic model. Section 3 presents estimation methods for both the individual and the population state variables. The Bayesian approach and the maximum likelihood (ML) method are proposed to estimate unknown parameters in the proposed models in Section 4. In Section 5 we present results from simulation studies and apply the MESSM to an AIDS clinical trial data. In Section 6 we summarize the results and discuss possible extensions of the MESSM and other related issues.

2. Model Specification

A linear MESSM can be written as

$${\mathit{x}}_{i,t+1}=\mathit{F}({\mathit{\theta }}_i){\mathit{x}}_{it}+{\mathit{v}}_{it},{\mathit{v}}_{it}~\text{N}(0,\mathit{Q}),$$ (3)

$${\mathit{y}}_{it}=\mathit{G}({\mathit{\theta }}_i){\mathit{x}}_{it}+{\mathit{w}}_{it},{\mathit{w}}_{it}~\text{N}(0,\mathit{R}),$$ (4)

where y_it is the q × 1 vector of observations for the ith (i = 1, …, m) subject at time t (t = 1, …, n_i), x_it is the p × 1 state vector, v_it is the p × 1 dynamic disturbance vector, and w_it is the q × 1 vector of the observation errors. {v_it} and {w_it} are assumed to be mutually independent within themselves and independent to each other. We assume that the initial values x_i0’s are independent and x_i0 ~ N(τ, A). This assumption is critical in deriving the population state in Section 3.2, but not important for the formulation of the parameter estimation methods in Section 4. The p × p transition matrix F(θ_i) and the q × p observation-system matrix G(θ_i) are parameterized with the r × 1 parameter vector θ_i, and the p × p matrix Q and the q × q matrix R with the d × 1 vector of parameters ω. Note that the parameters for F and G are not necessarily same. They may share some common parameters or may have different parameters. However, for presentation convenience, we use θ_i to denote all the unknown parameters in both F and G. Similar handling is applied for ω. Recognized as a vector of individual parameters, θ_i can be modelled as

$${\mathit{\theta }}_i=\mathit{\theta }+{\mathit{b}}_i,{\mathit{b}}_i~\text{N}(0,\mathit{D}),$$ (5)

where θ is the fixed effect or the population parameter vector (r × 1), and the vectors b_i are the random effects, which are assumed to be i.i.d. random vectors. Model (5) for the mixed effects can be generalized without much difficulty to more complicated linear or nonlinear models with covariates (Davidian and Giltinan, 1995; Vonesh and Chinchilli, 1996).

We give an illustration example for the proposed MESSM based on an HIV dynamic model proposed by Perelson et al. (1997). This model consists of three differential equations describing the interaction between the target cells and HIV infection. It was assumed that the antiviral therapy completely blocked the reproduction of infectious HIV virions, thus the newly produced virions were all noninfectious. The model was written as

$$\frac{{dT}^{\ast }}{dt}={kV}_{I}T-\delta T^{\ast },\frac{{dV}_I}{dt}=-{cV}_I,\frac{{dV}_{NI}}{dt}=N\delta T^{\ast }-{cV}_{NI},$$ (6)

where V_I, V_NI, T and T^* represented the plasma concentrations of infectious viruses, noninfectious viruses, uninfected T-cells, and productively infected T-cells, respectively. Wu, Ding, and DeGruttola (1998) and Wu and Ding (1999) introduced a mixed-effects model approach for HIV dynamics that was shown to improve the estimation of both the individual and the population parameters. Because in practice HIV dynamic data were collected at discrete times (days), difference equations may be considered to replace the differential equations (6). If the total plasma HIV concentration (V = V_NI + V_I) and T^* were observed, a mixed-effects state space model for system (6) could be formulated as

$${\mathit{x}}_{it}={\mathit{F}}_i{\mathit{x}}_{i,t-1}+{\mathit{v}}_{it},$$ (7)

$${\mathit{y}}_{it}={\mathit{Gx}}_{it}+{\mathit{w}}_{it},$$ (8)

where y_it is the observed (T^* V) for the ith patient at time t,

$${\mathit{x}}_{it}={(\begin{array}{ccc}{T}_{it}^{\ast }& V_{I_{it}}& V_{N{I}_{it}}\end{array})}^{\prime },{\mathit{F}}_i=\left[\begin{array}{ccc}1-{\delta }_i& k_i{T}_i& 0\\ 0& 1-c_i& 0\\ N_i{\delta }_i& 0& 1-c_i\end{array}\right],\mathit{G}=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 1\end{array}\right].$$

The mixed effects ${\mathit{\theta }}_i={(\begin{array}{cccc}1-{\delta }_i& k_i{T}_i& N_i{\delta }_i& 1-c_i\end{array})}^{\prime }$ are assumed to follow

$${\mathit{\theta }}_i=\mathit{\theta }+{\mathit{b}}_i,{\mathit{b}}_i={(\begin{array}{cccc}{b}_{i1}& b_{i2}& b_{i3}& b_{i4}\end{array})}^{\prime }~\text{N}(\mathbf{0},\mathit{D}),$$

where $\mathit{\theta }={(\begin{array}{cccc}1-\delta & kT& N\delta & 1-c\end{array})}^{\prime }={(\begin{array}{cccc}{\theta }_1& {\theta }_2& {\theta }_3& {\theta }_4\end{array})}^{\prime }$ are population parameters.

The proposed MESSM in this study is a hybrid of mixed-effects models and the state space models. It inherits the strengths of both types of models. The mixed effects link all subjects via the population structure, which establishes the concept of the population dynamics. The estimation of unknown parameters for individual subjects, especially for those with insufficient observations, can be improved by borrowing information from other subjects. State space modelling is especially valuable when the system dynamics can be described by mathematical models. Irregularly spaced data, common in longitudinal studies, could be handled easily by state space models. Moreover, state space models can flexibly incorporate various correlation structures for serially correlated longitudinal data.

3. Estimation of State Variables

In this section we consider the estimation of both individual state variables and population state variables in a mixed-effects state space model for given parameters θ and ω.

3.1 The Kalman filter and the estimation of individual states

The estimation of an individual state x_it can be classified into three types based on the amount of information that is available. The estimation of x_it is called a one-step-ahead prediction if {y_i1, · · ·, y_i,t−1} are observed; it is called a filtered estimation if {y_i1, · · ·, y_it} are observed; and a smoothed estimation if {y_i1, · · ·, y_ini(n_i > t)} are observed. If the parameters θ_i and ω are known in the linear MESSM (3) – (4), then the Kalman filter (Kalman, 1960) provides the basic solutions to the three types of estimation problems. The Kalman filter is a recursive algorithm which produces the linear estimators for the state variables. It is well-known that, under the assumption of normality, these estimators obtained from the Kalman filter are unbiased and minimize the mean squared error. We review the iterative algorithm of the Kalman filter in the following discussion. Details of the Kalman filter can be found in Harvey (1989), Brockwell and Davis (1991), and West and Harrison (1997).

Let x_it|k denote the estimation of the individual state x_it given the observations {y_i1, …, y_ik}. Let P_it|k be the covariance matrix of the estimation error x_it|k − x_it. Use F_i and G_i to represent F(θ_i) and G_i(θ_i), respectively. The Kalman recursion proceeds as follows,

$$\begin{array}{l}{\mathit{x}}_{it\mid t-1}={\mathit{F}}_i{\mathit{x}}_{i,t-1\mid t-1},{\mathit{P}}_{it\mid t-1}={\mathit{F}}_i{\mathit{P}}_{i,t-1\mid t-1}{\mathit{F}}_i^{\prime }+\mathit{Q},\\ {\mathit{f}}_{it}={\mathit{y}}_{it}-{\mathit{G}}_i{\mathit{x}}_{it\mid t-1},{\mathit{O}}_{it}={\mathit{G}}_i{\mathit{P}}_{it\mid t-1}{\mathit{G}}_i^{\prime }+\mathit{R},\\ {\mathit{x}}_{it\mid t}={\mathit{x}}_{it\mid t-1}+{\mathit{K}}_{it}{\mathit{f}}_{it},{\mathit{P}}_{it\mid t}={\mathit{P}}_{it\mid t-1}-{\mathit{K}}_{it}{\mathit{G}}_{it}{\mathit{P}}_{it\mid it-1},\end{array}$$

where ${\mathit{K}}_{it}={\mathit{P}}_{it\mid t-1}{\mathit{G}}_i^{\prime }{{\mathit{O}}_{it}}^{-1}$ is the Kalman gain matrix, f_it is the innovation with covariance matrix O_it. x_it|t−1 and x_it|t are the one-step-ahead prediction and the filtered estimation of x_it, respectively.

Let ${\mathit{P}}_{it,n}=E\{({\mathit{x}}_{it}-{\mathit{x}}_{it\mid t-1})({\mathit{x}}_{in}-{\mathit{x}}_{in\mid n-1}^{\prime })\},{\mathbf{\Theta }}_{in}={\mathit{F}}_i{\mathit{P}}_{in\mid n-1}{\mathit{G}}_i^{\prime }$, and ${\mathbf{\Delta }}_{in}={\mathit{G}}_i{\mathit{P}}_{in\mid n-1}{\mathit{G}}_i^{\prime }+\mathit{R}$. The fixed-point smoothing algorithm proceeds as follows:

$${\mathit{x}}_{it\mid n}={\mathit{x}}_{it\mid n-1}+{\mathit{P}}_{it,n}{\mathit{G}}_i^{\prime }{{\mathbf{\Delta }}_{in}}^{-1}{\mathit{f}}_{in},$$ (9)

$$\begin{array}{l}{\mathit{P}}_{it,n+1}={\mathit{P}}_{it,n}{({\mathit{F}}_i-{\mathbf{\Theta }}_{in}{{\mathbf{\Delta }}_{in}}^{-1}{\mathit{G}}_i)}^{\prime },\\ {\mathit{P}}_{it\mid n}={\mathit{P}}_{it\mid n-1}-{\mathit{P}}_{it,n}{\mathit{G}}_i^{\prime }{{\mathbf{\Delta }}_{in}}^{-1}{\mathit{G}}_i^{\prime }{\mathit{P}}_{it,n}^{\prime },\end{array}$$ (10)

with the initial condition, P_it,t = P_it|t−1.

Under the normality assumption, the Kalman estimator x_it|k is the mean of x_it conditional on the data {y_i1, …, y_ik}. If the normality assumption does not hold, the Kalman filter may not produce the conditional means of the states. The Bayesian approach provides an alternative method for the estimation of the state vectors (Section 4.1).

3.2 Population state variable and the EM algorithm enhanced smoothing

From (3), we can write x_it in terms of x_i0 and {v_is, s ≤ t}:

$${\mathit{x}}_{it}={{\mathit{F}}_i}^t{\mathit{x}}_{i0}+\sum _{k=0}^{t-1}{{\mathit{F}}_i}^k{\mathit{v}}_{i,t-k}.$$ (11)

Here F_i = F (θ_i) is a function of θ_i. Therefore, under the assumptions that the initial values x_i0’s are i.i.d. and θ_i’s are i.i.d., Equation (11) implies that x_it’s are i.i.d. at a given time point t. Thus the individual state variables x_it (i = 1, · · ·, m) follow a common mean process x_t plus a mean zero process, and can be modelled as

$${\mathit{x}}_{it}={\mathit{x}}_t+{\mathit{z}}_{it},{\mathit{z}}_{it}~(0,{\mathit{B}}_t).$$ (12)

We call x_t the population state variable at time t, which represents the mean response of all individuals at time t. Vector z_it represents the deviation of the individual state x_it from the population variable x_t with B_t being the covariance matrix.

If the x_it’s were observable, the maximum pseudo-likelihood estimation of x_t would then be the sample mean ${\sum }_{i=1}^m{\mathit{x}}_{it}/m$. However, because in practice the x_it’s are usually not directly observable, we instead use the Kalman smoothing estimate x_it|ni(t < n_i), denoted by x̃_it, to replace x_it in (12). Let ς_it = x̃_it − x_it be the estimation error of x̃_it, then ς_it has mean 0 and covariance matrix Σ_it = P_it|ni as defined in Section 3.1. One can establish a variance-components model for x̃_it

$${\stackrel{\sim }{\mathit{x}}}_{it}={\mathit{x}}_t+{\mathit{z}}_{it}+{\mathit{\varsigma }}_{it}.$$ (13)

Treating x̃_it as “data”, we maximize the pseudo-likelihood function to estimate the population state x_t and the covariance matrix B_t, that is, to maximize

$$l({\mathit{\sum }}_t,{\mathit{B}}_t\mid {\stackrel{\sim }{\mathit{x}}}_{it})=-\sum _{i=1}^m\{log\mid {\mathbf{\sum }}_i+{\mathit{B}}_t\mid +{({\stackrel{\sim }{\mathit{x}}}_{it}-{\mathit{x}}_t)}^{\prime }{({\mathbf{\sum }}_i+{\mathit{B}}_t)}^{-1}({\stackrel{\sim }{\mathit{x}}}_{it}-{\mathit{x}}_t)\}.$$

Note that if we assume normality in model (13), the resulting likelihood function is equivalent to the pseudo-likelihood function. Thus, the EM algorithm developed by Steimer, Mallet, Golmard and Boisvieux (1984) to maximize the likelihood function under the normality assumption can be adapted as follows to maximize the pseudo-likelihood function for the estimation of x_t and B_t:

1. Initialization: ${\widehat{\mathit{x}}}_t^{(0)}=m^{-1}{\sum }_{i=1}^m{\stackrel{\sim }{\mathit{x}}}_{it},{\widehat{\mathit{B}}}_t^{(0)}=m^{-1}{{\sum }_{i=1}^m({\stackrel{\sim }{\mathit{x}}}_{it}-{\widehat{\mathit{x}}}_t^{(0)})({\stackrel{\sim }{\mathit{x}}}_{it}-{\widehat{\mathit{x}}}_t^{(0)})}^{\prime }$

2. E-step: Update the individual estimates of state variables:

   $${\widehat{\mathit{x}}}_{it}^{(k+1)}={[{({\widehat{\mathit{B}}}_t^{(k)})}^{-1}+{\mathbf{\sum }}_{it}^{-1}]}^{-1}[{({\widehat{\mathit{B}}}_t^{(k)})}^{-1}{\widehat{\mathit{x}}}_t^{(k)}+{\mathbf{\sum }}_{it}^{-1}{\stackrel{\sim }{\mathit{x}}}_{it}].$$
3. M-step: Update the population estimates of state variable and parameters,

   $$\begin{array}{l}{\widehat{\mathit{x}}}_t^{(k+1)}=m^{-1}{\sum }_{i=1}^m{\widehat{\mathit{x}}}_{it}^{(k+1)},\\ {\widehat{\mathit{B}}}_t^{(k+1)}=m^{-1}\left\{{\sum }_{i=1}^m({\widehat{\mathit{x}}}_{it}^{(k+1)}-{\widehat{\mathit{x}}}_t^{(k+1)}){({\widehat{\mathit{x}}}_{it}^{(k+1)}-{\widehat{\mathit{x}}}_t^{(k+1)})}^{\prime }+{{\sum }_{i=1}^m({({\widehat{\mathit{B}}}_t^{(k)})}^{-1}+{\mathbf{\sum }}_{it}^{-1})}^{-1}\right\}.\end{array}$$

4. Repeat Steps 2 and 3 until convergence is reached. Estimates of both individual states and population states are collected at the final step.

We have proposed to estimate the population state variable based on the smoothing estimates of the individual state variables. In a similar way, the filtered or predicted individual state variables can be used to estimate the population state variable if the interested time point t is beyond the last time point of observations. Note that if the assumption that x_i0’s are i.i.d. does not hold, then the population state variable x_t is no longer the mean of x_it. In this case, the estimated x̂_t using the EM algorithm may be considered as an average of the estimated individual state variables after adjusting for the estimation errors.

4. Parameter Estimation

In this section we discuss parameter estimation in MESSM from both the Bayesian and the likelihood perspectives. The Bayesian approach and the ML method for mixed-effects models and the state space models have been well established (Harvey, 1989; Davidian and Giltinan, 1995; Vonesh and Chinchilli, 1996; West and Harrison, 1997). The proposed estimation methods for MESSM are combinations of these estimation methods.

4.1 Bayesian Approach

The Bayesian approach for state space models has been studied by many authors in recent years. Linear state space models have been presented in West and Harrison (1997). Nonlinear non-Gaussian state space models have been studied in, for example, Kitagawa (1987, 1996), Carlin, Polson, and Stoffer (1992), De Jong and Shephard (1995), and Chen and Liu (2000). Most of these studies focus on the estimation of state variables, while the estimation of unknown parameters in the models has not been paid enough attention. For MESSM we adopt the method proposed by Carlin, Polson and Stoffer (1992), in which the Gibbs sampler was used to draw samples from the full conditional distributions of state variables x_t and parameters conditional on the observations y_t. This approach is straightforward and easy to implement, and it has produced good results in our simulation studies. However, our method differs from Carlin et al. (1992) in that (1) independent individual subjects are involved in the MESSM; (2) we include one more hierarchical structure on the individual parameters; and (3) we emphasize both parameter estimation and state variable estimation. For the Bayesian approach, prior distributions are assigned to the parameters, and the inference is based upon the posterior distributions. Note that, if only one subject i is considered and the prior distribution N(θ, D) is assigned to θ_i, then conceptually θ and D are simply hyperprior parameters for a standard state space model. However, these hyperprior parameters represent the population parameters when all the subjects are considered, and thus have their own interpretations at the population level.

When the conjugate prior distributions are carefully chosen, the full conditional distributions have closed forms and are easy to sample from. The Gibbs sampler can then be used to explore the posterior distributions of the unknown parameters.

Let W(ϒ, ν) denote a Wishart distribution with the scale matrix ϒ and the degrees of freedom parameter ν. We use the following prior distributions:

$$\begin{array}{l}\mathit{\theta }~\text{N}(\mathit{\eta },\mathbf{\Delta }),{\mathit{D}}^{-1}~\text{W}({({\mathit{D}}^{\ast })}^{-1},\rho ),\\ {\mathit{Q}}^{-1}~\text{W}({\mathit{Q}}^{\ast -1},{\rho }_1),{\mathit{R}}^{-1}~\text{W}({\mathit{R}}^{\ast -1},{\rho }_2),{\mathit{x}}_{i0}~\text{N}(\mathit{\tau },\mathit{A}).\end{array}$$ (14)

As one of the referees pointed out, for dynamic systems, vague and proper priors may lead to improper posteriors. In order to avoid improper posterior densities, Bates and Watts (1988) suggested to put a locally uniform prior on the expectation surface to represent a non-informative prior, instead of putting a locally uniform prior on the parameter space. Under our model setting, it is possible that vague proper priors on the parameter space can be translated into informative priors in the state space and can lead to improper posteriors.

The full conditional distributions can be derived as follows:

1. The conditional distributions of the state vectors are

   $$p({\mathit{x}}_{it},\mid \mathit{y},{\mathit{x}}_{i,k\ne t},\mathit{\theta },\mathit{D},\mathbf{\Theta },\mathit{Q},\mathit{R})~\text{N}({\mathit{H}}_{it}^{-1}{\mathit{\lambda }}_{it},{{\mathit{H}}_{it}}^{-1}),$$ (15)
   where for t ≠ 0 or n_i

   $${\mathit{H}}_{it}={\mathit{Q}}^{-1}+{{\mathit{F}}_i}^{\prime }{\mathit{Q}}^{-1}{\mathit{F}}_i+{{\mathit{G}}_i}^{\prime }{\mathit{R}}^{-1}{\mathit{G}}_i,$$ (16)

   $${\mathit{\lambda }}_{it}={\mathit{Q}}^{-1}{\mathit{F}}_i{\mathit{x}}_{i,t-1}+{{\mathit{F}}_i}^{\prime }{\mathit{Q}}^{-1}{\mathit{x}}_{i,t+1}+{{\mathit{G}}_i}^{\prime }{\mathit{R}}^{-1}{\mathit{y}}_{it};$$ (17)

   for t = 0, H_i0 = F_i′Q⁻¹F_i + A⁻¹, λ_i0 = F_i′Q⁻¹x_i1 + A⁻¹τ; and for t = n_i, ${\mathit{H}}_{i{n}_i}={\mathit{Q}}^{-1}+{\mathit{G}}_i^{\prime }{\mathit{R}}^{-1}{\mathit{G}}_i$, λ_ini = Q⁻¹F_ix_i,ni−1 + G_i′R⁻¹ y _ini.

2. The conditional distributions of θ_i, θ, and D are

   $$p({\mathit{\theta }}_i\mid \mathit{x},\mathit{y},\mathit{\theta },\mathit{D},{\mathbf{\Theta }}_{-i},\mathit{Q},\mathit{R})~\text{N}({\mathit{J}}_i^{-1}{\mathit{\zeta }}_i,{\mathit{J}}_i^{-1}),$$ (18)

   $$\begin{array}{c}p(\mathit{\theta }\mid \mathit{x},\mathit{y},\mathit{D},\mathbf{\Theta },\mathit{Q},\mathit{R})~\text{N}\left\{{(m{\mathit{D}}^{-1}+{\mathbf{\Delta }}^{-1})}^{-1}({\sum }_i^m{\mathit{D}}^{-1}{\mathit{\theta }}_i+{\mathbf{\Delta }}^{-1}\mathit{\eta }),{(m{\mathit{D}}^{-1}+{\mathbf{\Delta }}^{-1})}^{-1}\right\},\\ p({\mathit{D}}^{-1}\mid \mathit{x},\mathit{y},\mathit{\theta },\mathbf{\Theta },\mathit{Q},\mathit{R})~\text{W}[{\{{\sum }_i^m({\mathit{\theta }}_i-\mathit{\theta }){({\mathit{\theta }}_i-\mathit{\theta })}^{\prime }+{\mathit{D}}^{\ast }\}}^{-1},m+\rho ],\end{array}$$ (19)
   where ${\mathit{J}}_i={\sum }_{t=1}^{n_i}({\mathit{T}}_{i,t-1}^{\prime }{\mathit{Q}}^{-1}{\mathit{T}}_{i,t-1}+{\mathit{L}}_{it}^{\prime }{\mathit{R}}^{-1}{\mathit{L}}_{it})+{\mathit{D}}^{-1}$,

   $$\begin{array}{l}{\mathit{\zeta }}_i=\sum _{t=1}^{n_i}\left\{{\mathit{T}}_{i,t-1}^{\prime }{\mathit{Q}}^{-1}({\mathit{x}}_{it}-\stackrel{\sim }{\mathit{F}}{\mathit{x}}_{i,t-1})+{{\mathit{L}}_{it}}^{\prime }{\mathit{R}}^{-1}({\mathit{y}}_{it}-\stackrel{\sim }{\mathit{G}}{\mathit{x}}_{it})\right\}+{\mathit{D}}^{-1}\mathit{\theta },\\ {\mathit{T}}_{i,t-1}=({\mathit{x}}_{i,t-1}^{\prime }\otimes {\mathit{I}}_p){\mathit{U}}_{\mathbf{1}},\text{and}{\mathit{L}}_{it}=({\mathit{X}}_{it}^{\prime }\otimes {\mathit{I}}_q){\mathit{U}}_{\mathbf{2}}.\end{array}$$

   ‘⊗’ stands for kronecker product. U₁ or U₂ has dimension of p² × r or q² × r (r is length of θ) and is defined as follows. Remember that each element of F_i or G_i can be represented by a linear combination of all elements in θ_i. If we strip out F_i or G_i by column and stack them, the formalized vector with length p² or q² which we denote as vec(F_i) or vec(G_i) can be represented by the product of U₁ or U₂ with θ_i, i.e., vec(F_i) = U₁θ_i and vec(G_i) = U₂θ_i.

3. The conditional distributions of the covariance matrices Q and R are

   $$p({\mathit{Q}}^{-1}\mid \mathit{x},\mathit{y},\mathit{\theta },\mathbf{\Theta },\mathit{Q},\mathit{D})~\text{W}[{\{{\mathit{Q}}^{\ast }+\frac{1}{2}\sum _{i=1}^m\sum _{t=1}^{n_i}{({\mathit{x}}_{it}-{\mathit{F}}_i{\mathit{x}}_{i,t-1})}^{\prime }({\mathit{x}}_{it}-{\mathit{F}}_i{\mathit{x}}_{i,t-1})\}}^{-1},s+{\rho }_1],$$ (20)

   $$p({\mathit{R}}^{-1}\mid \mathit{x},\mathit{y},\mathit{\theta },\mathbf{\Theta },\mathit{R},\mathit{D})~\text{W}[{\{{\mathit{R}}^{\ast }+\frac{1}{2}\sum _{i=1}^m\sum _{t=1}^{n_i}{({\mathit{y}}_{it}-{\mathit{G}}_i{\mathit{x}}_{it})}^{\prime }({\mathit{y}}_{it}-{\mathit{G}}_i{\mathit{x}}_{it})\}}^{-1},s+{\rho }_2],$$ (21)

   where $s={\sum }_{i=1}^m{n}_i$.

Note that irregularly spaced data can be treated as data with missing observations, and the full conditional distributions only need slight adjustments at the time points of missing data. For example, suppose y_it is missing, the conditional distribution p(x_it|y, x_i,k≠t, · · ·) in (15) depends only on x_i,t−1, x_i,t+1 and the parameters, but not on y_it. Thus, one needs to drop the terms G_i′R⁻¹G_i in (16) and G_i′R⁻¹y_it in (17), which are related to the observation. With the large number of missing data, the Bayesian approach ran reasonably fast. However, a large number of missing data can slow down the EM algorithm. It is well-known that the EM algorithm has a linear convergence rate, which is determined by the information ratio of the missing data to the complete data. For sparse data, a large amount of information, including the random effects, the state vectors and many observations, is missing, and therefore the convergence of the EM algorithm can be quite slow.

The construction of the Gibbs sampler is based on the full conditional distributions. Starting from an arbitrary set of initial values, samples are drawn from the conditional distributions sequentially. Let Φ be the collection of all the components involved in the full conditional distributions, i.e., Φ = (x₁₀, · · ·, x_1n1, · · ·, x_m0, · · ·, x_mnm, θ₁, · · ·, θ_m, θ, D, Q, R). Let Φ − {u} be the set of all the components except {u}. Here {u} can be any component or a set of components in Φ. Starting from the initial value Φ⁽⁰⁾, the Gibbs sampler draws a sample ${\mathit{x}}_{10}^{(1)}$ from p(x₁₀| {Φ − {x₁₀}}⁽⁰⁾, y), then draws ${\mathit{x}}_{11}^{(1)}$ from $p({\mathit{x}}_{11}\mid {\mathit{x}}_{10}^{(1)},{\{\mathbf{\Phi }-\{{\mathit{x}}_{10},{\mathit{x}}_{11}\}\}}^{(0)},\mathit{y})$, and so on up to R⁽¹⁾ from p(R| {Φ − {R}}⁽¹⁾, y). Suppose that the Jth iteration produces a sample Φ^(J). When J is large, Φ^(J) is a sample from the posterior distribution p(Φ|y) (Geman and Geman, 1984). The posterior distribution of the kth component of Φ can be approximated by (Carlin, Polson and Stoffer, 1992)

$$p({\mathrm{\Phi }}_k\mid \mathit{y})\approx \frac{1}{J}\sum _{j=1}^{J}p\{{\mathrm{\Phi }}_k\mid {(\mathbf{\Phi }-{\mathrm{\Phi }}_k)}^{(j)},\mathit{y}\}.$$ (22)

The posterior mean can be taken as the point estimate of a parameter if the Bayesian loss function is chosen to be the squared-error loss.

Assuming that the observations are available up to time n_i, the Gibbs sampler constructed above can produce samples from the posterior distribution p(x_it|y) for t ≤ n_i. For t < n_i this is a solution to the smoothing problem defined in Section 3.1. For t = n_i the posterior distribution p(x_ini|y) provides a solution for the filtering problem at time n_i. To solve the prediction problem, i.e. for t > n_i, one can treat {y_i,ni+1, y_i,ni+2, · · ·, y_it} as missing and derive the conditional distributions for the state vectors {x_i,ni+1, x_i,ni+2, · · ·, x_it}, then include these state vectors in the Gibbs sampler. Compared with the Kalman filter, the Gibbs sampler approach is more flexible and can be extended to nonlinear and non-Gaussian cases (Carlin, Polson and Stoffer, 1992), which also provides a unified framework for the state estimation and parameter estimation. However, the Gibbs sampler approach is computationally expensive, and does not provide online solutions to the estimation problems.

4.2 Estimation by the EM algorithm

For the standard Gaussian linear state space models, the ML method for the estimation of parameters has been well studied (Harvey, 1989). The idea of the ML method is to calculate the likelihood function via the prediction error decomposition (Schweppe, 1965) in which the Kalman filter is applied to obtain the innovations and their covariances. Due to the complexity of the likelihood function of the standard state space model, numerical methods, specifically the EM algorithm (Watson and Engle, 1983) and the Newton-Raphson algorithm (Engle and Watson, 1981), are often applied. We can extend the EM algorithm proposed by Watson and Engle (1983) to find the MLE of unknown parameters for the MESSM (3)–(5). The variance estimate can be obtained by inversing the observed Fisher information matrix, which can be used to get the interval estimates for the unknown parameters under a normal distribution assumption. To save space, we provide the details on implementation of EM algorithm in the Web Supplementary Appendix.

The EM algorithm proposed here is closely related to the Bayesian approach as both contain a Gibbs sampling scheme, and the full conditional distributions for the Gibbs sampler are very similar. The differences are also clear. The EM algorithm is developed for the likelihood approach, thus the parameters (θ, Q, R, D) are not treated as random and no prior distributions are needed. Computationally, in the Bayesian approach the parameters (θ, Q, R, D) are constantly updated by sampling from their conditional distributions, while in the EM algorithm they remain fixed during the sampling step, and are updated only in the M-step. Therefore, for one iteration of the EM algorithm, the sampling step is computationally less expensive than the Bayesian approach, but extra computational costs is needed in the M-step. From our experience, running one iteration of the EM algorithm is more time consuming than running the Gibbs sampler in the Bayesian approach, assuming equal number of Gibbs iterations. The convergence of the EM algorithm is also slow, usually more than 50 iterations are needed for convergence. Overall the computational cost for the EM algorithm is much higher. However, an alternative approach, the stochastic approximation EM (SAEM) approach (Delyon, Lavielle and Moulines 1999) is very efficient and generally applicable to obtain the maximum likelihood estimates for the unknown parameters in nonlinear mixed-effects models from longitudinal data, which is worthy more exploring for potential online estimation.

5. Numerical Examples

To illustrate the usefulness of the proposed MESSM and estimation methods, we carried out two simulations studies: one is a simple univariate MESSM and another is a more complicated bivariate MESSM. To save space, we only report the simulation results from the bivariate model in this section and report the results from the univariate MESSM in the Web Supplementary Appendix. We also applied the proposed MESSM and estimation methods to an AIDS clinical data set in this section.

Simulation Study

Consider a MESSM model (3)–(4) with p = 2, q = 1, r = 2, ${\mathit{F}}_i=\left(\begin{array}{cc}0.7& 0\\ {\theta }_{1i}& {\theta }_{2i}\end{array}\right)$ and $G=(\begin{array}{ll}1\hfill & 1\hfill \end{array})$. Let $\mathit{D}={\sigma }_D^2\mathit{I},\mathit{Q}={\sigma }_Q^2\mathit{I}$. Set $\mathit{\theta }=(\begin{array}{ll}{\theta }_1\hfill & {\theta }_2\hfill \end{array})=(\begin{array}{ll}0.3\hfill & 0.6\hfill \end{array}),{\sigma }_D^2=0.0064,{\sigma }_Q^2=1.44$, and R = 1. The variances Q and R were selected to make the Filter Input Signal to Noise Ratio (FISNR) (Anderson and Moore, 1979) close to 3:2. We assumed the following priors for the Bayesian approach

$${\sigma }_D^{-2}~\text{G}({\beta }_0,{\beta }_1),{\sigma }_Q^{-2}~\text{G}({\nu }_0,{\nu }_1),R^{-1}~\text{G}({\omega }_0,{\omega }_1),x_{i0}~\text{N}(\tau ,A).$$ (23)

Here G(., .) stands for the Gamma distribution. We specified the priors by setting β₀ = 0.5, β₁ = 0.0001, ν₀ = 0.5, ν₁ = 0.5, ω₀ = 0.5, ω₁ = 0.5, τ = 20, and A = 100. Note that the true value of ${\sigma }_D^2$ is very small (close to zero). If a prior for ${\sigma }_D^2$ is selected to be skewed toward zero such as the one we used in our simulation, it is easier to identify this variance parameter as suggested by one of the referees. Otherwise, the estimate of ${\sigma }_D^2$ is poor. We assumed a normal prior distribution N(η, Δ) for θ with η = (0.5, 0.5)′ and $\mathbf{\Delta }={\sigma }_{\mathrm{\Delta }}^2\mathit{I}=2\mathit{I}$. For this bivariate MESSM, $\stackrel{\sim }{\mathit{F}}=\left(\begin{array}{cc}0.7& 0\\ 0& 0\end{array}\right)$ contained the known parameters in the system matrix F_i. A simulation study of 50 replicates was carried out for m = 20 and n = 20. The Gibbs sampler was run for 20000 iterations for each replicate. The estimation results are shown in Table 1. In this table $RE=\sqrt{\mathit{MSE}}/(\mathit{True}\mathit{Parameter})$ represents the relative error. For both the Bayesian approach and the EM algorithm the estimates for θ₁ and θ₂ were close to the true values. The Bayesian estimates of ${\sigma }_Q^2$ and R were better than the EM estimates. However the EM algorithm provided better estimation for ${\sigma }_D^2$.

Table 1.

Parameter estimation for the bivariate MESSM model with 50 replicates, m = 20 and n = 20.

	θ̂1		θ̂2		${\widehat{\sigma }}_D^2$		${\widehat{\sigma }}_Q^2$		R̂
	B	EM	B	EM	B	EM	B	EM	B	EM
Mean	0.305	0.293	0.594	0.606	0.009	0.006	1.357	1.122	1.04	1.164
Bias	0.005	−0.007	−0.006	0.006	0.0026	−0.0004	−0.083	−0.318	0.04	0.164
MSE	0.0014	0.0012	0.0018	0.0014	7 × 10−6	3 × 10−6	0.142	0.345	0.09	0.215
RE	0.125	0.115	0.071	0.062	0.413	0.271	0.262	0.401	0.300	0.463

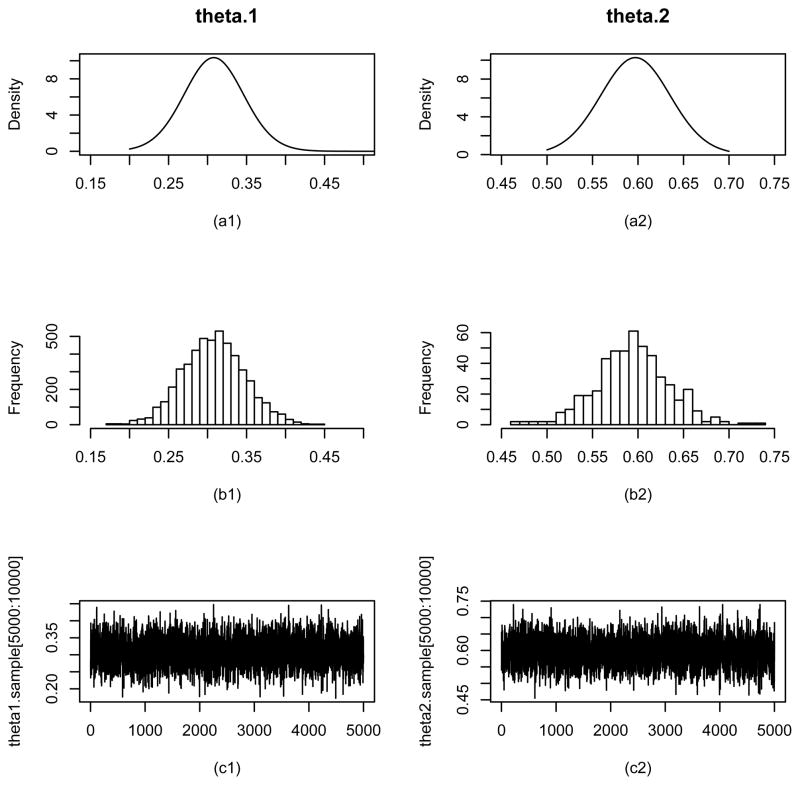
Figure 1 shows the histogram of the Gibbs samples for θ₁ and θ₂ and the estimated marginal posterior densities for both parameters. Considering θ₁, one notices that $p({\theta }_1\mid \{\mathbf{\Phi }-{\theta }_1\},\mathit{y})=p({\theta }_1\mid {\theta }_{11},\cdots ,{\theta }_{1m},{\sigma }_D^2)$ with Φ being the collection of all the parameters and the state variables. Using the formula (22) the estimated posterior density can be derived as

Figure 1.

Parameter estimation results for θ₁ and θ₂ from the Bayes method for the simulation study (the bivariate MESSM model). (a1) and (a2) are estimated posterior densities, (b1) and (b2) are histograms of the Gibbs sampler, and (c1) and (c2) are trace plots for the last 5000 samples for θ₁ and θ₂, respectively.

$$\widehat{p}({\theta }_1\mid \mathit{y})\approx \frac{1}{J}\sum _{j=1}^J\text{N}\left({\theta }_1\mid \frac{{\sigma }_{\mathrm{\Delta }}^2}{m{\sigma }_{\mathrm{\Delta }}^2+{\sigma }_D^{2(j)}}\sum _{i=1}^m{\theta }_{1i}^{(j)}+\frac{{\sigma }_D^{2(j)}}{m{\sigma }_{\mathrm{\Delta }}^2+{\sigma }_D^{2(j)}}{\eta }_1,\frac{{\sigma }_{\mathrm{\Delta }}^2{\sigma }_D^{2(j)}}{m{\sigma }_{\mathrm{\Delta }}^2+{\sigma }_D^{2(j)}}\right)$$

where η₁ is the first element of η, and N(θ₁|a, b) stands for the normal density with mean a and variance b. The histogram shows that the Gibbs samples for θ₁ are tightly centered around 0.3, and agrees very well with the estimated posterior density. The similar plots for θ₂ are also displayed in Figure 1. It can be seen that the Gibbs samples for θ₂ are concentrated around 0.6, the true parameter value of θ₂. To monitor the convergence of the Gibbs samples the trace plots for both parameters are also shown in Figure 1. The trace plots do not display any signs of patterns, suggesting the convergence to the stationary distribution. Similarly the Gibbs samples for the other parameters D, Q and R (not shown) also suggest the convergence of the Gibbs samplers.

HIV Dynamic Application

We applied the MESSM to a data set from the AIDS Clinical Trial Group (ACTG) Study 315 (Wu and Ding, 1999). In this trial, 53 HIV infected patients were treated with potent antiviral drugs (ritonavir, 3TC, and AZT). Among those 5 dropped out of the study. Treatments started on day 0 and the plasma concentration of HIV-1 RNA was repeatedly measured on days 0, 2, 7, 10, 14, 21, 28 and weeks 8, 12, 24, 48 after the initiation of the treatment. Perelson et al. (1997) suggested a two-phase clearance of viral load. The first phase featured a rapid drop in viral load due to the exponential death rate of the productively infected cells during the first four weeks of treatment. The decline of viral load was slower in the second phase due to the slow clearance rate of the long lived infected T-cells or latently infected T-cells. Here we considered a time-varying MESSM for the ACTG 315 data assuming the rate of clearance changed at the mid-point of week 4 (i.e. day 24). This model is closely related to the simple HIV dynamic model with a constant rate (Ho et al. 1995). The MESSM is written as

$$x_{it}={\theta }_{it}{x}_{i,t-1}+v_{it},\text{and}{y}_{it}=x_{it}+w_{it},$$

where y_it is the base 10 logarithm of the measured viral load from patient i at time t, and x_it represents the base 10 logarithm of the actual viral load. θ_it indicates the viral clearance rate for patient i at day $t({\theta }_{it}={\theta }_i^{(1)}\text{for}t\le 23;{\theta }_{it}={\theta }_i^{(2)}\text{for}t>23)$. Here ${\theta }_i^{(k)}~N({\theta }^{(k)},D_k)$ for k = 1, 2, and ${\theta }_i^{(k)}$ are independent. Note that we may use the log-transformation to guarantee θ_it to be positive. For other complicated constraints of parameters, there is no general method to deal with and we may need to deal with this problem case-by-case. Although this is an simplified HIV dynamic model, it serves to illustrate the proposed methodologies.

The similar prior distributions as in the simulation studies were utilized for the Bayesian approach (see the Web Supplementary Appendix). Table 2 gives the estimation values of both the population parameters and the individual parameters ${\theta }_i^{(k)}$ following the Bayesian approach. The EM estimation was similar and omitted.

Table 2.

Parameter estimation and forecasts of viral load for the HIV dynamic model. Confidence interval for population estimates are included in brackets.

Estimation of population parameters
θ̂ 1	θ̂2		D̂1	D̂2		Q̂	R̂
0.976(0.974,0.979)	0.994(0.991,0.997)		0.0052 (0.004,0.0075)	0.0046(0.003,0.0065)		0.119(0.104,0.134)	0.204(0.174,0.238)
Estimation of the individual parameters for 48 patients
${\theta }_i^{(1)}$
0.975753	0.972227	0.976278	0.975794	0.97177	0.976373	0.98232	0.976072
0.975554	0.979314	0.976282	0.978256	0.973686	0.98045	0.976808	0.976119
0.972679	0.976762	0.97706	0.974961	0.975959	0.974782	0.97605	0.977631
0.976737	0.977898	0.979602	0.978431	0.974501	0.975863	0.977751	0.976239
0.977426	0.977808	0.978213	0.976879	0.973311	0.979874	0.97188	0.978342
0.974063	0.972705	0.974047	0.975449	0.975593	0.976236	0.979845	0.9746
${\theta }_i^{(2)}$
0.994389	-	0.994317	0.993837	0.993597	0.996628	0.993837	-
-	0.994033	0.993657	0.994675	0.992734	0.994795	0.994546	0.994494
0.994527	0.994921	0.994156	0.993475	0.9951	0.994282	-	0.992501
0.994217	0.994472	0.991974	-	-	0.994325	0.993253	0.99328
-	0.993176	0.993242	0.993993	0.993556	0.994226	0.993714	0.9946
0.994275	0.993367	0.99472	0.994184	0.993569	0.996103	0.993211	0.994178

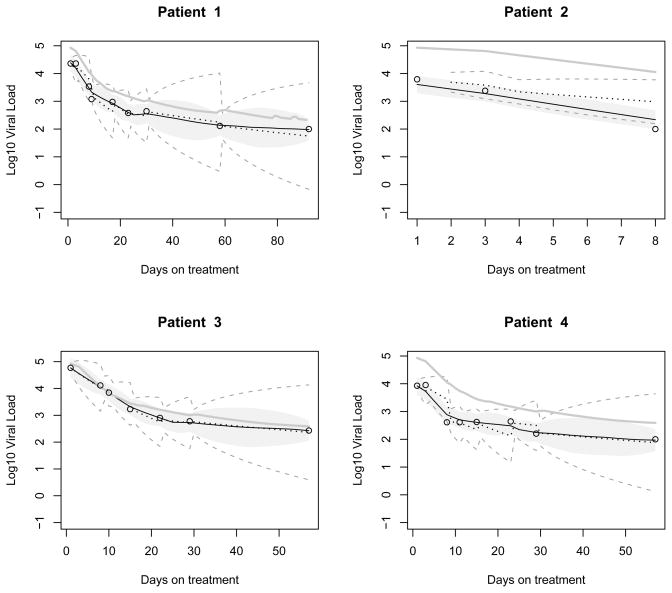
Figure 2 shows the one-step-ahead Kalman forecasts (dotted curves) of the individual states for the first four patients using the estimated individual parameters. The estimated posterior means for the individual states using the Gibbs sampler approach are also shown in solid curves. As expected the posterior mean curves are smooth and close to the observed values. A Kalman forecast jumps one day after the time point of an observation, indicating an adjustment based on the observation. The model checking results are shown in Figure S1 in the Web Supplementary Appendix. The fitted viral loads from both methods match the data quite well. The normal assumption on measurement errors is validated by QQ plots. The density estimates of individual parameters show that the normality assumption on random effects is satisfied for both methods.

Figure 2.

Estimation and prediction of viral load for four patients in the HIV dynamic study (four subjects with different number of measurements and different response patterns are selected for illustration). Base 10 logarithm of the viral loads are shown in circles. The smoothing estimates using the Gibbs sampler approach are shown in black solid curves, and the 95% error bounds are shown by the shaded grey region. The one-step-ahead Kalman forecasts are shown in black dotted curves, and the prediction error bounds are in grey dashed curves. The estimates of population state variable are shown as the gray solid curve.

6. Discussion

In many biomedical longitudinal studies, the underlying biological mechanisms are well studied and mathematical representations, usually a set of differential or difference equations, are available. In this paper, we have proposed a class of mixed-effects state space models for analysis of longitudinal dynamic systems that may arise from biomedical studies. With the intention of giving a comprehensive treatment of this subject, we investigated two methods for estimation of unknown parameters in the proposed models by borrowing ideas from standard mixed-effects models. The concept of population state was introduced, and the EM-enhanced smoothing was proposed. Filtering, smoothing and forecasting algorithms for estimation of individual states were also discussed based on the Kalman filter methods.

The MESSM may be further extended to nonlinear and non-Gaussian cases. It is well-known that, for nonlinear and non-Gaussian state space models, the Kalman estimates of states are not optimal in terms of unbiasedness and mean squared errors. Other filters, such as the extended Kalman filter (Anderson and Moore, 1979), usually involve linear approximation of the nonlinear functions. Although lacking optimality and often awkward when handling complicated models, these filters have been applied extensively simply because there were no other alternative methods. In the past decades, the Bayesian approach and the Gibbs sampler techniques have provided good solutions for smoothing problems in nonlinear non-Gaussian state space models (Carlin, Polson and Stoffer, 1992; Carter and Kohn, 1994 and 1996). Such approach could be adapted to nonlinear non-Gaussian MESSM. A major limitation for the Gibbs sampler approach lies in its incapability of online filtering. Recently sequential Monte Carlo methods (Liu and Chen, 1998), such as the particle filter (Gordon, 1993; Kitagawa 1996), have provided a general framework for online filtering for nonlinear and non-Gaussian state space models. However, when the particle filter approach is extended to MESSM, the extra layer of the mixed effects in the system matrices of MESSM adds significant computational difficulties that need to be overcome in practice.

In summary, we have introduced the MESSM which brings together the techniques of mathematical modelling, time series analysis, and longitudinal data analysis to deal with longitudinal dynamic systems with many potential applications in biomedical research, such as hepatitis virus dynamics (Nowak et al. 1996), tumor dynamics in cancer research (Swan, 1984; Martin and Teo, 1994), and genetic regulatory network modeling (Chen, He and Church, 1999; Holter et al. 2001). However, many theoretical and methodological problems for MESSM remain unsolved. We expect that our paper can attract more attention and stimulate more research in this promising research area.