Abstract
Classifying patients into different risk groups based on their genomic measurements can help clinicians design appropriate clinical treatment plans. To produce such a classification, gene expression data were collected on a cohort of burn patients, who were monitored across multiple time points. This led us to develop a new classification method using time-course gene expressions. Our results showed that making good use of time-course information of gene expression improved the performance of classification compared with using gene expression from individual time points only. Our method is implemented into an R-package: time-course prediction analysis using microarray.
Keywords: Classification, Gene expression, Longitudinal, Time-course
1. Introduction
Patients suffering from burn injuries face different risks of morbidity and mortality. Accurate classification of high-risk and low-risk patients plays an important role in their diagnosis, prognosis, and therapy. Existing research shows that severely burned patients undergo immune depression, increased risk of infections, and post-burn hypermetabolic response. As a first step, to more accurately identifying the molecular mechanisms after burn injury, time-course gene expression data were measured on a cohort of burn patients (www.gluegrant.org). However, in order to make good use of the time-course gene expression measurements, we need to build good genomic classifiers using the time-course gene expression data.
Some methods have been developed for the time-course gene expression. These methods focus on extracting temporal patterns of differential expression. Storey and others (2005) detected changes in expression over time using a spline-based approach. Yuan and Kendziorski (2006) and Yuan and others (2008) analyzed microarray time-course data under multiple biological conditions with hidden Markov models. Tai and Speed (2006) proposed a multivariate empirical Bayes statistic to detect differentially expressed genes. Ma and others (2009) used a functional ANOVA mixed-effect model to characterize time-course gene expression observations and detect differential expression. Zhou and others (2010) developed TANOVA to handle the factorial structure in time-course microarray data. Zhang and others (2010) developed a prediction model for the survival outcome using time-course gene expression. However, in the binary or categorical outcome scenario, classification problems using the time-course structure have not been solved.
In this paper, we proposed a novel classification method using time-course gene expression. We applied our method to predict the risk categories of burn patients and multiple sclerosis patients.
2. Methods
We assume that there are p features (e.g. genes) measured on N observations across T time points. Denote by X the p×T×N dimensioned variable with N observations xgti, where g∈{1,…,p}, t∈{1,…,T}, i∈{1,…,N}. Let Xg** denote the T×N matrix, which is the expression matrix of gene g across T time points. For simplification, we write Xg** as Xg. Let Y be an N-vector of outcome measurements. The outcome can be binary or categorial variables. To make use of the time-course information, we evaluate the gene response based on information pooled across time. We search for a direction in the T-dimensional time space that has the strongest response signal of interest, and extract predictors based on the projection on this direction, and we call this the “optimal direction”. This direction captures the gene response to the outcome, and then ordinary classification methods can be used. We order the paragraphs below as follows. We first introduce two types of estimation of “optimal direction”. Then we give the procedure of model selection and the extraction of final classifiers.
2.1. Estimating optimal direction
As addressed in Zhang and others (2010), the unknown optimal direction is gene-specific and dependent on the outcome variable of interest. In the binary or categorical outcome scenario, we need to define a new appropriate objective function to estimate the “optimal direction”. The objective function should capture the time-course structure of gene expression and variance of different classes. The projection should reflect the information of class labels.
Suppose that we have K classes, and let Ck be the indices of the Nk samples in class k. Given gene expression Xg for each gene g, we denote the between-class variance as SBg, which is the variance of class means of Xg. The within-class variance is denoted as SWg, which is the pooled variance about the means. We want to find the linear combination 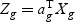 (ag is a T×1 vector), such that the between-class variance (
(ag is a T×1 vector), such that the between-class variance (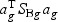 ) is maximized relative to the within-class variance (
) is maximized relative to the within-class variance (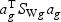 ), which is called the Fisher criterion. Let J(ag) denote the objective function, i.e.
), which is called the Fisher criterion. Let J(ag) denote the objective function, i.e. 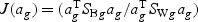 , where SBg=(…SBtg…)T, SWg=(…SWtg…) and for t∈{1,…,T},
, where SBg=(…SBtg…)T, SWg=(…SWtg…) and for t∈{1,…,T}, 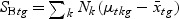
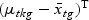 ,
, 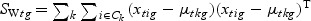 ,
, 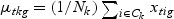 ,
, 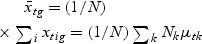 , and Nk is the number of cases in class Ck. The direction of projection is the largest eigenvalue of
, and Nk is the number of cases in class Ck. The direction of projection is the largest eigenvalue of 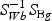 , by solving a generalized eigenvalue problem.
, by solving a generalized eigenvalue problem.
Fisher’s criteria provides a linear “optimal direction” of projection with the assumption that Σk(|g)=Σ(|g) for ∀k, where Σk(|g) is the covariance matrix for class k and gene g. If the covariance matrices for all classes do not equal each other, the “optimal direction” of projection will be non-linear. Biologically, this can happen due to the complex mechanisms of gene regulation, such as, auto-regulation. Let Mg be the column vector 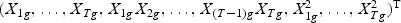 , which consists of the gene expression vector for every time point of gene g, together with items of the expansion of
, which consists of the gene expression vector for every time point of gene g, together with items of the expansion of 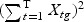 , respectively. Take gene expression from two time points as an example, and let X1g, X2g denote the gene expression from the first and the second time points, respectively. Then, Mg is a 5×N matrix
, respectively. Take gene expression from two time points as an example, and let X1g, X2g denote the gene expression from the first and the second time points, respectively. Then, Mg is a 5×N matrix 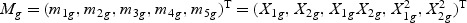 . The “optimal direction” bg is a column vector of length 5. The projected gene expression is
. The “optimal direction” bg is a column vector of length 5. The projected gene expression is 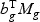 . The vector bg can be obtained by maximizing
. The vector bg can be obtained by maximizing 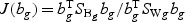 , where
, where 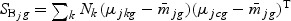 ,
, 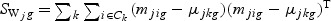 ,
, 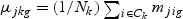 ,
, 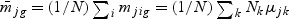 ,and Nk is the number of cases in class Ck. The direction of projection bg is the largest eigenvalue of
,and Nk is the number of cases in class Ck. The direction of projection bg is the largest eigenvalue of 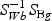 , by solving a generalized eigenvalue problem.
, by solving a generalized eigenvalue problem.
2.2. Classification
The weighted gene expression is obtained by projecting the gene expression of individual time points to the “optimal direction”. Here we use the centroid shrinkage method (PAM) to select the predictors Tibshirani and others (2002). Let zgi be the weighted expression for gene g and sample i. The modified t statistic for g, comparing class k with the overall centroid is defined as 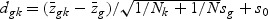 , where sg is the pooled within-class standard deviation for gene g with
, where sg is the pooled within-class standard deviation for gene g with 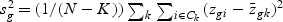 , and s0 is a positive constant with the same value for all genes. This is included to guard against the probability of large dgk values arising by chance from genes with low expression levels. We set s0 equal to the median value of the si over the set of genes.
, and s0 is a positive constant with the same value for all genes. This is included to guard against the probability of large dgk values arising by chance from genes with low expression levels. We set s0 equal to the median value of the si over the set of genes.
Each dgk is shrunken toward zero by soft thresholding dgk′=sign(dgk)(|dgk|−Δ)+. For gene g, if dgk is not shrunken to zero, then gene g is selected as one of the final predictors. The test sample is classified to the nearest shrunken centroid. Given a test sample with expression levels 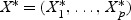 ,
, 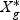 is a T×N matrix of expression for gene g of N subjects across T time points. If linear optimal projection is used, the weighted gene expression for gene g is calculated as
is a T×N matrix of expression for gene g of N subjects across T time points. If linear optimal projection is used, the weighted gene expression for gene g is calculated as 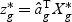 , where
, where 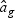 is the “optimal direction” obtained from the training data. If
is the “optimal direction” obtained from the training data. If
non-linear optimal projection is used, the weighted gene expression for gene g is calculated as 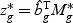 , where
, where 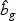 is the “optimal direction” obtained from the training data. The discriminant score for class k is defined as
is the “optimal direction” obtained from the training data. The discriminant score for class k is defined as
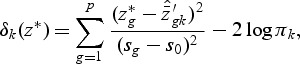 |
where 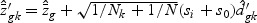 , and
, and 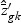 ,
, 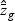 , and
, and 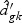 are obtained from the training data. If
are obtained from the training data. If 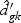 is shrunken to zero, then
is shrunken to zero, then 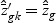 for ∀k. The classification rule is then C(X*)=C(z*)=ℓ, where
for ∀k. The classification rule is then C(X*)=C(z*)=ℓ, where 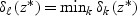 .
.
The tuning parameter Δ is chosen by 2-fold cross-validation. During the 2-fold cross-validation, the whole set training of data is split into two parts. We obtain the direction of projection for every gene and run the centroid-shrinking algorithm for each tuning parameter Δ on the weighted gene expression data using the first part data. Then we make predictions on the second part of the training data and record the prediction errors for each value of the tuning parameter Δ. This whole process is performed multiple times with random splits. The value for the tuning parameter is chosen as the one that produces the most sparse model with the minimum average prediction error adding one standard error. Of note about the cross-validation is that we need to recalculate the vector of projection direction during the cross-validation to select the tuning parameter. This is because the model must be completely retrained for each fold. For more details about the justification of the cross-validation technique, we refer the reader to Hastie and others (2009). For the underlying model for the time-course prediction analysis using microarray (TPAM) approach, we refer the reader to supplementary material available at Biostatistics online.
One can note that we seek this direction in a supervised way. Instead of using the supervised optimal direction, one may think of using an unsupervised direction, for example, using the first principal component of time-course gene expression as the direction of projection. The shortage of the unsupervised direction is that it does not consider the information of the outcome. Although the first principal component is the direction of the largest variance of the time-course gene expression, it is not the direction most related to the outcome automatically. We call this method PC-PAM, which uses the first principal component of time-course gene expression as the direction of projection at the first stage, and applies PAM on the weighted gene expression as the second stage. For comparison, we also apply the PC-PAM on the simulation and burn data.
2.3. Alternative methods
The procedures of the second stage in our approach are not limited to the centroid shrinkage method. Other variable selection methods in the classification scenario can be used at the second stage. Alternative methods can be LASSO in Tibshirani (1996), ELASTIC NET in Zou and Hastie (2005), and support vector machine (SVM) in Hastie and others (2009), etc. For a detailed description, we refer the reader to the corresponding original literatures. Here, we briefly describe each method.
For categorical response variable G with K>1 levels, the generalized model using binomial (K=2) or multinomial (K>2) regression is 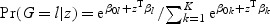 , where z is the explanatory variable.
, where z is the explanatory variable.
Let pl(zi)=Pr(G=l|zi), and let gi∈{1,2,…,K} be the ith response. We maximize the penalized log-likelihood
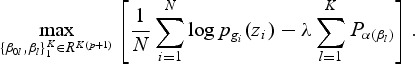 |
(2.1) |
Denote by Y the N×K indicator response matrix, with elements yil=I(gi=l). Then the log-likelihood part of (2.1) is the form of
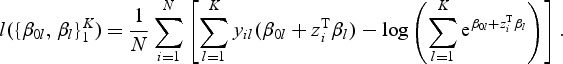 |
The penalty part of objective function (2.1) 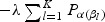 has the form of
has the form of 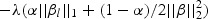 . The tuning parameter is λ. We chose α=1, which is the LASSO penalty, and α=0.5, which is the ELASTIC NET penalty. LASSO and ELASTIC NET have been implemented in the R-package named glmnet using coordinate descent algorithms described in Friedman and others (2010). If z has the values of weighted gene expression that were projected using the “optimal direction”, we call the corresponding method as TLASSO when α=1, or T-ELASTIC NET when α=0.5. When the projection was calculated by the first principal component, we call the corresponding method as PC-LASSO or PC-ELASTIC NET.
. The tuning parameter is λ. We chose α=1, which is the LASSO penalty, and α=0.5, which is the ELASTIC NET penalty. LASSO and ELASTIC NET have been implemented in the R-package named glmnet using coordinate descent algorithms described in Friedman and others (2010). If z has the values of weighted gene expression that were projected using the “optimal direction”, we call the corresponding method as TLASSO when α=1, or T-ELASTIC NET when α=0.5. When the projection was calculated by the first principal component, we call the corresponding method as PC-LASSO or PC-ELASTIC NET.
For SVM, one can minimize the error function 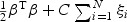 , subject to the constraints yi(βTϕ(zi)+b)≥1−ξi and ξi≥0, i={1,…,N}. Here ϕ is the kernel function, β is the vector of coefficients, b is a constant, ξi are parameters for handling non-separable training data, yi are the class labels , zi is the random variable for the weighted gene expression, and C is the tuning parameter. The SVM algorithm is implemented in the R-package called e1071. If z has the values of the weighted gene expression which were projected using the “optimal direction”, we call the corresponding method TSVM. If the projection was calculated by the first principal component, we call the corresponding method PC-SVM.
, subject to the constraints yi(βTϕ(zi)+b)≥1−ξi and ξi≥0, i={1,…,N}. Here ϕ is the kernel function, β is the vector of coefficients, b is a constant, ξi are parameters for handling non-separable training data, yi are the class labels , zi is the random variable for the weighted gene expression, and C is the tuning parameter. The SVM algorithm is implemented in the R-package called e1071. If z has the values of the weighted gene expression which were projected using the “optimal direction”, we call the corresponding method TSVM. If the projection was calculated by the first principal component, we call the corresponding method PC-SVM.
3. Results
We have performed four simulation studies to validate the performance of our methods. We refer the reader to the supplementary material available at Biostatistics online for details. Below, we applied our methods on two real data sets—one is for the burn patients and the other one is for the multiple sclerosis patients.
3.1. Classification of complicated and uncomplicated burn patients
Blood samples of burn patients are collected to measure the gene expression by the Affymetrix HU133 Plus 2.0 arrays. Each array consisted of about 50 000 probe sets. Patients are monitored according to time. According to the time of sampling, the longitudinal data can be divided into three stages—early stage (within 1 day to 10 days with 3 days of median time), middle stage (11 days to 49 days with 19 days of median time), and late stage (50 days to more than 1 year). Blood samples from healthy people are also collected for the control. In our classification study, we only use the data of burn patients from the early stage and the middle stage to build the genomic classifiers. Gene expression data are normalized by dChip (see Li and Wong, 2001) and further reduced to 7354 probe sets using the coefficient of variation (CV, standard deviation/mean) criterion (CV >0.8). We then log2-scale gene expression profiles and use gene expression from early and middle stages to build the predictors. For patients with several measurements during the early or middle stage, we take the median gene expression. According to the multiple-organ-failure scores (MOF) and the survival status, patients are divided into two classes— “complicated” and “uncomplicated”. If a patient has died or MOF ≥3, then this patient belongs to the “complicated group”, otherwise, the patient belongs to the “uncomplicated group”.
We randomly divided the 123 patients into a training set with a size of 62 and a test set with a size of 61. We use a linear optimal projection at the first stage of our method. Let 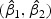 denote the weights of gene expression from early time points and middle time points. We first generated the weights using the training data based on the Fisher criterion. Then we performed the PAM analysis to build predictors based on the weighted gene expression data. We used the linear discriminant function and made the prediction on the test data. The weights of the early- and middle-stage expression of the selected 100 genes are shown in Figure 1. The amplitude of
denote the weights of gene expression from early time points and middle time points. We first generated the weights using the training data based on the Fisher criterion. Then we performed the PAM analysis to build predictors based on the weighted gene expression data. We used the linear discriminant function and made the prediction on the test data. The weights of the early- and middle-stage expression of the selected 100 genes are shown in Figure 1. The amplitude of 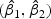 reflects the contribution of gene expression from each time point. The sign of
reflects the contribution of gene expression from each time point. The sign of 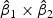 reflects the relationship between two time points. If the sign of
reflects the relationship between two time points. If the sign of 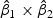 is positive, it means that the two time points have additive effects on the outcome. If the sign of
is positive, it means that the two time points have additive effects on the outcome. If the sign of 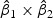 is negative, it suggests that the outcome is related to the trend of that gene across time. The histogram of the weights for the first time point is plotted on the top of the figure; the histogram of the weights for the second time point is plotted on the right side of the figure.
is negative, it suggests that the outcome is related to the trend of that gene across time. The histogram of the weights for the first time point is plotted on the top of the figure; the histogram of the weights for the second time point is plotted on the right side of the figure.
Fig. 1.
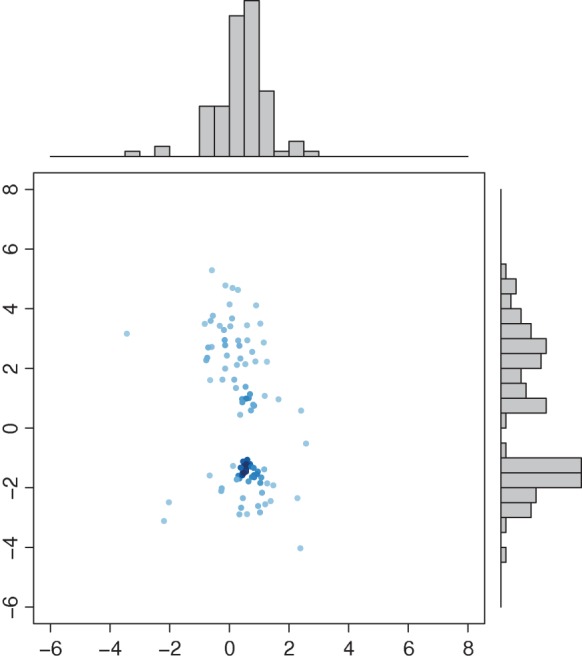
Weights of the early stage and the second stage for the projection. X-axis: weights of the early stage; Y -axis: weights of the middle stage. Top panel: histogram of the weights from the early stage; right panel: histogram of the weights from the second stage.
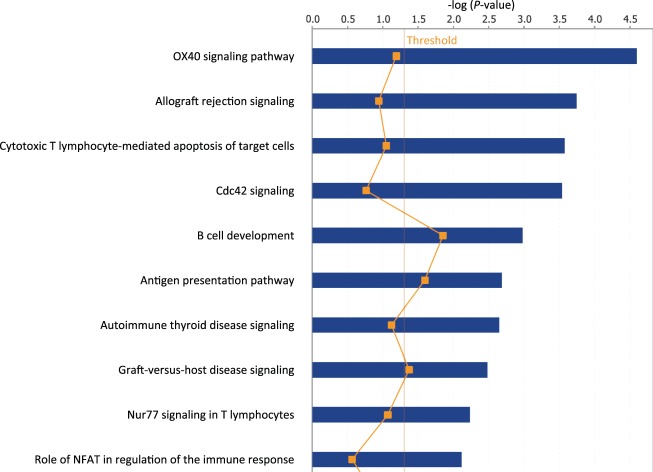
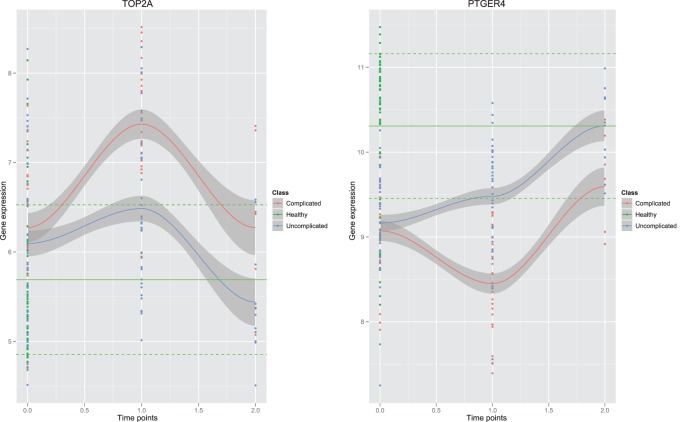
One can see that overall amplitudes from the second time point are larger than those from the first time point. This indicates that gene expression from the second time point carries more signals to separate patients into high-risk and low-risk groups. Patients in the test data set are divided into two groups—the complicated group and the uncomplicated group. The error rate on the test data set is 0.13. The gene set enrichment analysis of selected predictors shows that the final predictors are enriched in immune response pathways and signaling pathways, such as, OX40 signaling pathway, Cdc42 signaling T cell receptor signaling, etc. (Figure 2). Among these final predictors, some are known biomarkers which have been used for drug targets. Table 1 shows the names, types, and related drugs. Taking TOP2A as an example, it is an enzyme that is located in the nucleus. We plotted its time-course gene expression from the test data set. The red color indicates complicated patients after classification using the final selected classifiers. The blue color indicates uncomplicated patients (see the left panel of Figure 3).
Fig. 2.
Enriched pathways of gene classifiers in the burn patients’ data.
Table 1.
Known biomarkers within the final predictors
| Symbol | Type | Drug(s) |
|---|---|---|
| CSF1R | Kinase | Sunitinib, pazopanib |
| TOP2A | Enzyme | Novobiocin, etoposide, CPI-0004Na, etc. |
| PTGER4 | G-protein-coupled receptor | Misoprostol, prostaglandin E2, etc. |
| EGFR | Kinase | Cetuximab, AEE 788, panitumumab, etc. |
| CYP19A1 | Enzyme | Atamestane, anastrozole, etc. |
| CD52 | Other | Alemtuzumab |
Fig. 3.
TOP2A (left panel) and PTGER4 (right panel) gene expression trends on the test data. X-axis indicates time points. Y -axis is the gene expression. Green: control, red: complicated burn patients, blue: uncomplicated burn patients. The solid green line indicates the mean gene expression of healthy people the dotted green line indicates the mean ± standard deviation.
To see the whole trend of gene expression, we plotted gene expression from all the three time stages—early, middle, and late. The smooth-spline regression is applied to fit the curve of the time-course trend. To see how gene expression of burn patients deviated from the normal gene expression, we plotted in green the gene expression from the blood of healthy people. The solid green line shows the mean of gene expression from healthy people. The dotted green lines shows the mean ± standard deviation of the gene expression from healthy people. One can see that both complicated burn patients’ TOP2A gene expression and uncomplicated burn patients ’ TOP2A gene expression were activated at the middle stage compared with the gene expression at the early stage and control. Complicated TOP2A gene expression had larger activation compared with the uncomplicated TOP2A gene expression. Both the complicated TOP2A gene expression and uncomplicated TOP2A gene expression were decreased toward normal at the late stage. The uncomplicated TOP2A gene expression was nearer to the control gene expression than the complicated TOP2A gene expression. PTGER4 was another validated biomarker; it is a G-protein-coupled receptor, located at the plasma membrane. The trend of PTGER4 gene expression was opposite to the trend of TOP2A gene expression. Both the complicated group and the uncomplicated group of PTGER4 gene expression were decreased at the middle stage, and then increased toward normal at the late stage (see right panel of Figure 3). But the trends of the uncomplicated and the complicated group have different shapes. The PTGER4 gene expression of the uncomplicated group is nearer to the control compared with the complicated group at both the middle stage and the late stage.
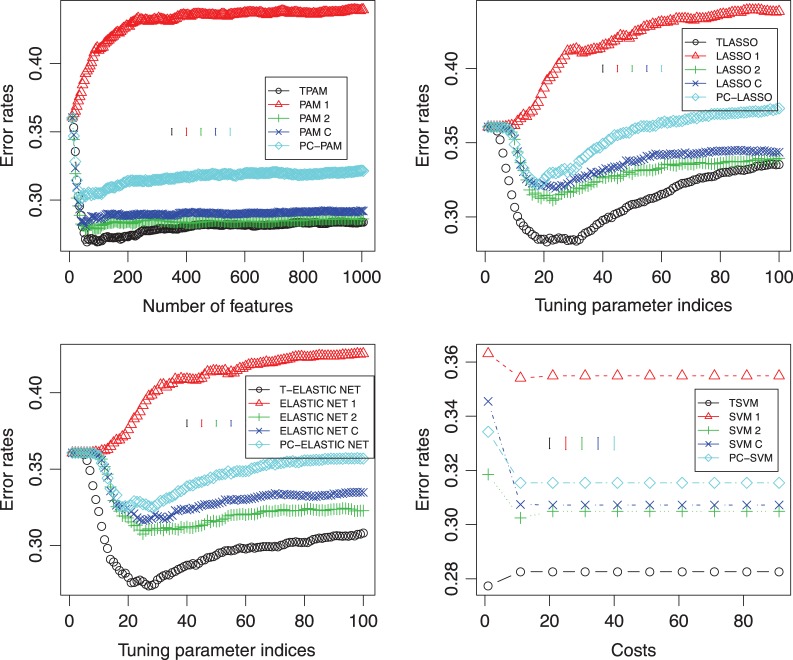
To check whether prediction using the longitudinal gene expression is better than using the individual time points, we repeated the prediction by randomly splitting samples into the training and test sets for 100 iterations. The averaged performance on the test data is shown in the top-left panel of Figure 4. Besides using PAM as the second stage of the method, we also tried LASSO, ELASTIC NET, and SVM. The results of comparison were showed in top-right, bottom-left, and bottom-right panels of Figure 4, respectively. One can see that our methods using the longitudinal gene expression have the better performance.
Fig. 4.
Classification performances using different methods at the second stage of our approach as well as using different methods directly on the burn patients’ data. Top-left: TPAM, PAM, and PC-PAM; top-right: TLASSO, LASSO, and PC-LASSO; bottom-left: T-ELASTIC NET, ELASTIC NET, and PC-ELASTIC NET; bottom-right: TSVM, SVM, and PC-SVM. ∘: using the Fisher criterion to obtain the direction of projection at the first stage; △: using the first time point; +: using the second time point; ×: combining the early and middle time points;  : using the first principal component as the direction of projection at the first stage. Y -axis is the error rate on the test data. The X-axis in the top-left panel is the number of features selected in the models. The X-axes in the top-right and bottom-left panels are the indices of the tuning parameter; each index i (i∈{0,…,99}) corresponds to λmax−i(λmax−λmin)/99; λmax is the maximum value of the tuning parameter λ calculated by default by R-package glmnet. λmin=λmaxλmin.ratio and λmin.ratio=0.01, which is the default value of glmnet. The axis in the bottom-right panel is the cost that corresponds to the parameter c in the R-package e1071.
: using the first principal component as the direction of projection at the first stage. Y -axis is the error rate on the test data. The X-axis in the top-left panel is the number of features selected in the models. The X-axes in the top-right and bottom-left panels are the indices of the tuning parameter; each index i (i∈{0,…,99}) corresponds to λmax−i(λmax−λmin)/99; λmax is the maximum value of the tuning parameter λ calculated by default by R-package glmnet. λmin=λmaxλmin.ratio and λmin.ratio=0.01, which is the default value of glmnet. The axis in the bottom-right panel is the cost that corresponds to the parameter c in the R-package e1071.
3.2. Classification of multiple sclerosis patients
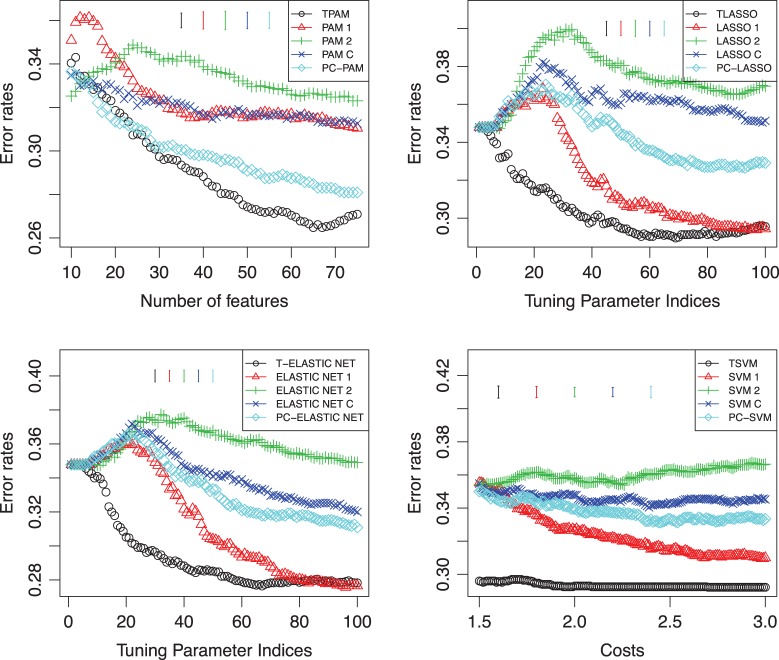
We also applied our methods on the problem of classification of multiple sclerosis patients with respect to their response to interferon-beta (IFNβ) treatment based on their gene expression profiles. IFNβ is considered as the treatment of multiple sclerosis. Baranzini and others (2005) monitors 52 multiple sclerosis patients after the initiation of IFNβ and measured their time-course gene expression profiles of 70 genes. The longitudinal 70-gene expression data set was generated by kinetic reverse-transcription PCR. These patients showed different clinical responses. Based on the clinical criteria such as relapse rate and disability status, the patients were divided into good and bad responders. Here we use the gene expression data measured in the first and the ninth month to investigate the classification problem. We applied our methods using the time-course gene expression data with four different methods (PAM, LASSO, ELASTIC NET, and SVM) at the second stage of our approaches, which were denoted as TPAM, TLASSO, T-ELASTIC NET, and TSVM, respectively. We also tried PAM, LASSO, ELASTIC NET, and SVM on individual time point gene expression as well as simply combining all gene expression data or using the principal component decomposition (PC-PAM, PC-LASSO, PC-ELASTIC NET, PC-SVM) to replace the fisher criterion as the direction of projection. We split patients into training and test evenly and performed 100 random splits. The average prediction errors on the test data with different tuning parameters are shown in Figure 5. The average standard error bars of each method are also plotted in Figure 5. For TPAM, PAM, and PC-PAM, we used the original gene expression data in Baranzini and others (2005). For the remaining methods, log-scaled gene expression data were used, which have better performance than using the raw gene expression. One can see that our methods using the time-course gene expression have better performance than the other methods.
Fig. 5.
Classification performances using different methods at the second stage of our approach as well as using different methods directly on the data of Multiple Sclerosis patients. Top-left: TPAM, PAM, and PC-PAM; top-right: TLASSO, LASSO, and PC-LASSO; bottom-left: T-ELASTIC NET, ELASTIC NET, and PC-ELASTIC NET; bottom-right: TSVM, SVM, and PC-SVM. °: using the Fisher criterion to obtain the direction of projection at the first stage; △: using the first time point; +: using the second time point; ×: combining the early and middle time points;  : using the first principal component as the direction of projection at the first stage. Y -axis is the error rate on the test data. The X-axis in the top-left panel is the number of features selected in the models. The X-axes in the top-right and bottom-left panels are the indices of the tuning parameter; each index i (i∈{0,…,99}) corresponds to λmax−i(λmax−λmin)/99; λmax is the maximum value of the tuning parameter λ calculated by default by R-package glmnet. λmin=λmaxλmin.ratio and λmin.ratio=0.01, which is the default value of glmnet. The axis in the bottom-right panel is the cost that corresponds to the parameter c in the R-package e1071.
: using the first principal component as the direction of projection at the first stage. Y -axis is the error rate on the test data. The X-axis in the top-left panel is the number of features selected in the models. The X-axes in the top-right and bottom-left panels are the indices of the tuning parameter; each index i (i∈{0,…,99}) corresponds to λmax−i(λmax−λmin)/99; λmax is the maximum value of the tuning parameter λ calculated by default by R-package glmnet. λmin=λmaxλmin.ratio and λmin.ratio=0.01, which is the default value of glmnet. The axis in the bottom-right panel is the cost that corresponds to the parameter c in the R-package e1071.
4. Discussion
We have proposed a new statistical classification method using the longitudinal gene expression. Our studies on the burn patients’ data and multiple sclerosis patients’ data showed that making good use of the longitudinal structure of gene expression can improve the predictive power. Some known biomarkers were recovered by our method. Their time-course gene expression showed reasonably different trends between the complicated group and uncomplicated group. The methods presented in our paper work better in a homogeneous data than a heterogeneous data scenario. This is because the weights for the projection of the test data are the same weights obtained from the training data. If the test data are too different from the training data, the estimated “optimal direction” from the training data will be very different from the one for the test data. The procedures of the second stage are not limited to the centroid shrinkage method. Other variable selection methods in the classification scenario, such as LASSO, ELASTIC NET, and SVM, can be used at the second stage. If in concurrence with genomic information, clinical and baseline covariate information is also available, this information can be integrated with the selected genomic predictors by a multivariate regression model. Incorporating clinical information might improve the performance of classification.
Gene selection is very important and can be of biological interest. In the framework of significance analysis, one can choose significance analysis of microarrays (SAM) in Tusher and others (2001) and calculate the modified t-statistic on the weighted gene expression. We can use the permutation analysis as proposed in SAM to address those significant genes. Of note about the permutation analysis is that we need to recalculate the direction of projection in each permutation and obtain a new weighted gene expression. Then the modified t-statistic is computed using the specific weighted gene expression for each permutation. Then potentially significant genes can be obtained using a scatter plot of the observed t-statistic vs. the expected t-statistic.
The false discover rate (FDR) for multiple testing can be calculated by the estimated number of falsely significant genes over the number of genes called significant from the original data. The estimated number of falsely significant genes was the average of the number of genes called significant from all permutations. For details of the FDR calculation, we refer the reader to the SAM in Tusher and others (2001).
Owing to the development of technology, more time-course data are emerging, and so our classification approach will have wide applications. In our study, the gene expressions are measured by a microarray. Recently, next-generation sequencing technologies have been developing very fast. Gene expression can be measured by one such technology, RNA-seq. Compared with the continuous intensity measurement of Microarry, the RNA-seq measures the gene expression in a discrete digital way. This brings new challenges for the classification methods based on the gene expression obtained from the RNA-seq.
The R-package TPAM is available on CRAN.
Supplementary material
Supplementary material is available at http://biostatistics.oxfordjournals.org.
Funding
This study was supported by P01HG000205 and NIH U54 GM-062119.
Supplementary Material
Acknowledgements
We wish to acknowledge the efforts of many individuals at participating institutions of the Glue Grant Program that generated the clinical and genomic data reported here. Conflict of Interest: None declared.
References
- Baranzini S. E., Mousavi P., Rio J., Caillier S. J., Stillman A., Villoslada P., Wyatt M. M., Comabella M., Greller L. D., Somogyi R. Transcription-based prediction of response to infbeta using supervised computational methods. PLoS Biology. 2005;3:e2. doi: 10.1371/journal.pbio.0030002. and others. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedman J., Hastie T., Tibshirani R. Regularized paths for generalized linear models via coordinate descent. Journal of Statistical Software. 2010;33:1–22. [PMC free article] [PubMed] [Google Scholar]
- Hastie T., Tibshirani R., Friedman J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. 2nd edition. New York: Springer; 2009. Springer Series in Statistics. [Google Scholar]
- Li C., Wong W. H. Model-based analysis of oligonucleotide arrays: expression index computation and outlier detection. Proceedings of the National Academy of Sciences of the United States of America. 2001;98:31–36. doi: 10.1073/pnas.011404098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma P., Zhong W., Liu J. S. Identifying differentially expressed genes in time course microarray data. Statistics in Biosciences. 2009;1:144–159. [Google Scholar]
- Storey J. D., Xiao W., Leek J., Tompkins R., Davis R. Significance analysis of time course microarray experiments. Proceedings of the National Academy of Sciences of the United States of America. 2005;102:12837–12842. doi: 10.1073/pnas.0504609102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tai Y. C., Speed T. A multivariate empirical bayes statistic for replicated microarray time course data. Annals of Statistics. 2006;34:2387–2412. [Google Scholar]
- Tibshirani R. Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society Series B-Methodological. 1996;58:267–288. [Google Scholar]
- Tibshirani R., Hastie T., Narasimhan B., Chu G. Diagnosis of multiple cancer types by shrunken centroids of gene expression. Proceedings of the National Academy of Sciences. 2002;99:6567. doi: 10.1073/pnas.082099299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tusher V. G., Tibshirani R., Chu G. Significance analysis of microarrays applied to the ionizing radiation response. Proceedings of the National Academy of Sciences. 2001;98:5116–5121. doi: 10.1073/pnas.091062498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan M., Kendziorski C. Hidden markov models for microarray time course data under multiple biological conditions (with discussion) Journal of the American Statistical Association. 2006;101:1323–1340. [Google Scholar]
- Yuan Y., Li C. T., Wilson R. Partial mixture model for tight clustering of gene expression time-course. BMC Bioinformatics. 2008;9:287. doi: 10.1186/1471-2105-9-287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y., Tibshirani R. J., Davis R. W. Predicting patient survival from longitudinal gene expression. Statistical Applications in Genetics and Molecular Biology. 2010;9 doi: 10.2202/1544-6115.1617. Article41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou B., Xu W., Herndon D., Tompkins R., Davis R., Xiao W., Wong W. H. Analysis of factorial time-course microarrays with application to a clinical study of burn injury. Proceedings of the National Academy of Sciences. 2010;107:9923. doi: 10.1073/pnas.1002757107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zou H., Hastie T. Regularization and variable selection via the elastic net. Journal of the Royal Statistical Society. Series B. 2005;67:301–320. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.