Bayesian Latent Factor Regression for Functional and Longitudinal Data

Summary

In studies involving functional data, it is commonly of interest to model the impact of predictors on the distribution of the curves, allowing flexible e ects on not only the mean curve but also the distribution about the mean. Characterizing the curve for each subject as a linear combination of a high-dimensional set of potential basis functions, we place a sparse latent factor regression model on the basis coe cients. We induce basis selection by choosing a shrinkage prior that allows many of the loadings to be close to zero. The number of latent factors is treated as unknown through a highly-e cient, adaptive-blocked Gibbs sampler. Predictors are included on the latent variables level, while allowing different predictors to impact different latent factors. This model induces a framework for functional response regression in which the distribution of the curves is allowed to change flexibly with predictors. The performance is assessed through simulation studies and the methods are applied to data on blood pressure trajectories during pregnancy.

1. Introduction

Many modern statistical analyses involve variables best represented as curves, surfaces or more general functions (Ramsey and Silverman, 2005). Examples include biomarker trajectories, images, videos, genetic codes and hurricane tracks. Data on such curves may come into two flavors, either measured on a dense, regular grid common to all observation units (subjects) or as measurements taken at irregular time points or locations that vary from subject to subject. Analyses of these two kinds of data are labeled, respectively, functional and longitudinal data analyses, abbreviated FDA and LDA; see Rice 2004. We explore the important issue of modeling and analyzing the relationship of such data with other covariate and outcome variables simultaneously measured on the same subjects.

Our work is motivated by the Healthy Pregnancy, Healthy Baby (HPHB) study, an ongoing prospective cohort study examining the effects of environmental, social, and host factors on racial disparities in pregnancy outcomes. Specifically, we want to characterize the trajectories in mean arterial blood pressure (MAP = 2/3 diastolic pressure + 1/3 systolic pressure) during pregnancy, while simultaneously addressing three main objectives: i) obtain a low dimensional representation of the individual curves; ii) incorporate covariate information (e.g., maternal age, maternal race, parity), thus allowing the distribution of the curves to change flexibly with predictors; and iii) link the clinical and functional predictors to subsequent health responses (e.g., gestational age at delivery, birth weight). Because functional data are infinite dimensional, their statistical analysis necessitates obtaining a low dimensional representation of the individual curves. Therefore, objective i) becomes absolutely crucial for building a hierarchical model where the curves are to be related to other covariates recorded on the same subjects.

To address these aims, we propose a new Bayesian latent factor model for functional data characterizing the curve for each subject as a linear combination of a high-dimensional set of basis functions, and place a sparse latent factor regression model on the basis coe cients. Within our framework, it is possible to study the dependence of the curve shapes on covariates incorporated through the distribution of the latent factors, and we can accommodate the joint modeling of functional predictors with scalar responses or multiple related functions.

The existing literature on FDA and LDA does not o er an encompassing framework that can address simultaneously the three aspects mentioned above, though there is a rich array of methods for each individual task. The most widely used tool to represent curves through a low dimensional vector is functional principal component analysis (FPCA; see Rice and Silverman, 1991; James, Hastie and Sugar, 2000; Yao, Müller and Wang, 2005; and references therein). In FPCA, a finite number of basis functions are derived by eigendecomposition of a smoothed version of the empirical covariance function of the observed curves. Each curve is then represented by a vector of eigen-scores with respect to the estimated basis. These scores are used to build a two-stage, plug-in model of how the curves a ect the response variable. Crainiceanu and Goldsmith (2009) propose a refinement where they plug-in only the FPCA basis functions at the second stage, while jointly modeling the eigen-scores with other variables of interest.

However, there is very little literature on how to perform FPCA when the curves may depend on additional covariates. Jian and Wang (2010) recently proposed an extremely flexible approach that accommodates covariates, but their method faces serious practical diffculties when the covariate dimension is not minuscule or when different covariates have a different degree of influence on the curve.

As an alternative to plugging-in FPCA bases and/or scores, which might underrepresent uncertainty, one can directly build models on the space of curves and then use discriminant analysis to perform functional classification. However, existing methods of this kind (e.g., De la Cruz-Mesia, Quintana and Müller, 2007, and Dunson, 2010 from a Bayesian standpoint) do not include covariate information to model the curves, and an extension along this line appears challenging in absence of a sparse representation of the curves. It is also possible to completely ignore modeling of the curves and just build regression models for scalar outputs based on functional and non-functional covariates (e.g., Reiss, Huang and Mennes, 2010; Zhu, Vannucci and Cox, 2010). Such approaches face diffculties when predictions are to be made with the functional covariates only partially and sporadically observed, such as when predicting the possibility of a low birth weight delivery given 5 MAP measurements until the 30th week of pregnancy. Additional references on functional regression in a Bayesian context include Behseta, Kass and Wallstrom (2005), Ray and Mallick (2006), Dunson (2009), Petrone, Guindani and Gelfand (2009), Rodriguez, Dunson and Gelfand (2009), and Bigelow and Dunson (2009).

In very different approaches, Nagin (1999) and Jones, Nagin, and Roeder (2001) adopt a mixture model representation to characterize curves through latent classes and let covariates impact on the class probabilities. However, they consider the curves only as response variables and do not discuss models where the curves play the role of functional predictors. Potentially, their method can be extended to an encompassing framework like ours by letting the latent class impact the distribution of the response variable, but this extension was not addressed by the authors. Secondly, by representing each curve by a vector of scores (instead of a single group label), we allow other variables to influence or depend on the curves in a local way. Alternatively, James and Sugar (2003) propose a model for clustering sparsely sampled functions assuming either a classification or mixture likelihood, but no attempt is made to build response models.

We avoid two-stage procedures by building a framework that simultaneously accommodates function-on-scalar and vector-on-function regression. Also, our model preserves the modeling goal of FPCA, that is, identifying a common basis and assigning low dimensional scores to individuals with respect to this basis. Along the same lines, we could easily accommodate the joint modeling of multiple related functions (function-on-function regression), but our emphasis was on developing methods motivated by the application to the study of blood pressure and pregnancy outcomes.

The rest of the paper is organized as follows: Section 2 outlines the functional latent factor regression model (LFRM). Section 3 extends the LFRM to allow joint modeling of a functional response and additional outcomes. Section 4 describes the application of our methodology to the blood pressure data. Conclusions are presented in Section 5. A simulation study and further discussions are reported in the Supplementary Materials.

2. Functional latent factor regression model

Let n denote the number of subjects in the study. We suppose that functional data on subject i are available as noisy measurements of an underlying smooth curve f_i(t) at n_i time points t_ij, j = 1, ··· , n_i. We denote these measurements as y_ij and model

$$y_{ij}=f_i\left(t_{ij}\right)+{∊}_{ij},$$ (1)

with ε_ij ~ N(0, φ²), independently across i and j. In our application, y_ij denotes the blood pressure (BP) measurement of the i-th woman at her j-th visit to the clinic during pregnancy, with t_ij denoting time (in weeks) from the onset of pregnancy.

To ensure smoothness, f₁(t), ··· , f_n(t) are assumed to belong to the linear span of a smooth finite basis {b₁(t), ··· , b_p(t)}:

$$f_i\left(t\right)=\sum _{i=1}^p{\theta }_{il}{b}_l\left(t\right).$$ (2)

It is important to use a sufficiently large p and to choose locally concentrated basis elements so that a rich variety of shapes for f_i(t) are entertained. In particular, after standardizing the time domain to [0, 1], we use Gaussian kernels

$$b_1\left(t\right)=1,\text{and}{b}_{l+1}\left(t\right)=\text{exp}(-\nu {\Vert t-{\psi }_l\Vert }^2),l=1,\cdots ,p-1$$ (3)

with equally spaced kernel locations ψ₁, ··· , ψ_p–1 and a bandwidth parameter ν to be specified later. By denoting the functional data vector of subject i by y_i, we can write

$${\mathbf{y}}_i={\mathbf{B}}_i{\theta }_i+{∊}_i,{∊}_i\sim {\mathrm{N}}_{n_i}(0,{\phi }^2\mathbf{I})$$ (4)

where B_i is the n_i × p matrix with rows {b₁(t_ij), ··· , b_p(t_ij)}, j = 1, ··· , n_i and θ_i = (θ_i1, ··· , θ_ip)′.

The coefficient vectors θ₁, ··· , θ_n capture all subject-to-subject variations in the functional data. But these vectors are non-sparse. They have a large dimension p and have highly correlated neighboring elements unless f₁(t), ··· , f_n(t) are sparse in the basis {b_l}. The latter is unlikely to hold for a pre-specified local basis such as ours. The non-sparsity of θ₁, ··· , θ_n makes them unfit to be included in a joint model with other observations of interest.

We obtain an attractive low dimensional representation of the curves by placing a sparse latent factor model on the basis coefficients

$${\theta }_i=\Lambda {\eta }_i+{\zeta }_i,\text{with}{\zeta }_i\sim {\mathrm{N}}_p(0,\Sigma )$$ (5)

where Λ = ((λ_lm)) is a p × k factor loading matrix with k << p, η_i = (η_i1, ··· , η_ik)′ is a vector of latent factors for subject i and ζ_i = (ζ_i1, ··· , ζ_ip)′ is a residual vector that is independent with the other variables in the model and is normally distributed with mean zero and a diagonal covariance matrix $\Sigma =\text{diag}({\sigma }_1^2,\cdots ,{\sigma }_p^2)$.

The low dimensional vectors θ₁, ··· , θ_n are used in all subsequent parts of our model where we seek to link the curves f₁(t), ··· , f_n(t) with other variables of interest. Like θ_i, the vector η_i can also be interpreted as a coe cient vector for subject i because we can write

$$f_i\left(t\right)=\sum _{m=1}^k{\eta }_{im}{\tilde{\varphi }}_m\left(t\right)+r_i\left(t\right)$$ (6)

where ${\tilde{\varphi }}_m\left(t\right)={\sum }_{l=1}^p{\lambda }_{lm}{b}_l\left(t\right),m=1,\cdots ,k$ form an unknown non-local basis to be learned from data and $r_i\left(t\right)={\sum }_{l=1}^p{\zeta }_{il}{b}_l\left(t\right)$ is a function-valued random intercept. This decomposition, without r_i(t), is analogous to an FPCA representation of f_i(t), except that the latter requires the basis functions ${\tilde{\varphi }}_1\left(t\right),\cdots ,{\tilde{\varphi }}_k\left(t\right)$ to be mutually orthogonal eigenfunctions. Although orthogonality enhances interpretability of the elements in the decomposition, this is not a primary concern in our application since we view the latent factorization only as a vehicle to link functional observations with other variables. To highlight this difference with FPCA, we refer to $\left\{{\tilde{\varphi }}_m\right\}$ as a dictionary.

The size k and the elements of the dictionary $\left\{{\tilde{\varphi }}_m\right\}$ depend on how Λ is modeled. We assign Λ a multiplicative, gamma process shrinkage (MGPS; Bhattacharya and Dunson, 2011) prior which favors an unknown but small dictionary size k (refer to Section 2.1 for details on the MGPS prior).

Given the sparsity of the data, it becomes mandatory to borrow information across the population of curves to improve inferences and predictions. Specifically, the LFRM model allows borrowing strength across the different subjects in estimating their functions in that the low dimensional dictionary functions $\left\{{\tilde{\varphi }}_m\right\}$, their number, and the random intercept r_i(t) are learnt by pooling information from all subjects.

The score vectors θ₁, ··· , θ_n can be put in any flexible joint model with other variables of interest. For example, information from a covariate x_i can be incorporated through a simple linear model

$${\eta }_i={\beta }^{\prime }{\mathbf{x}}_i+{\Delta }_i,{\Delta }_i\sim {\mathrm{N}}_k(0,\mathbf{I})$$ (7)

where β is a r × k matrix of unknown coefficients, and with r denoting the dimension of x_i. With a semi-conjugate model on β, this specification leads to very efficient posterior computation via Gibbs updating, as we describe in the next sub-section. Despite the simplicity of this linear model, the resulting model on f₁(t), ··· , f_n(t) allows a very flexible accommodation of the covariate information. Conditionally on $({\left\{b_l\right\}}_{l=1}^p,\Lambda ,\Sigma ,\beta ,{\left\{{\mathbf{x}}_i\right\}}_{i=1}^n)$, these curves are independent (finite rank) Gaussian processes with covariate dependent mean functions $\mathbb{E}\left[f_i\left(t\right)\right]={\sum }_{m=1}^k{\beta }_m^{\prime }{\mathbf{x}}_i{\tilde{\varphi }}_m\left(t\right)$ and a common covariance function $\mathbb{C}\mathrm{ov}\{f_i\left(t\right),f_i\left(s\right)\}={\sum }_{m=1}^k{\tilde{\varphi }}_k\left(t\right){\tilde{\varphi }}_m\left(s\right)+{\sum }_{l=1}^p{\sigma }_l^2{b}_l\left(t\right)b_l\left(s\right)$, where β_m denotes the m-th column of β.

2.1 Bayesian formulation, prior elicitation and posterior computation

A Bayesian formulation of our sparse LFRM is completed with priors for the parameters in (1)-(7). Given the dimensionality, it is practically important to choose conditionally conjugate priors that lead to efficient posterior computation via blocked Gibbs sampling. Typical priors for factor analysis constrain Λ to be lower triangular with positive diagonal entries using normal and truncated normal priors for the free elements of Λ and gamma priors for the residual precisions (Arminger, 1998; Lopes and West, 2004). However, following Bhattacharya and Dunson (2011) we note that such constraints are unnecessary and unappealing in leading to order dependence and computational inefficiencies. Hence, we follow their lead in using a MGPS prior for the loadings as follows:

$${\lambda }_{jh}\mid {\varphi }_{jh},{\tau }_h\sim \mathrm{N}(0,{\varphi }_{jh}^{-1}{\tau }_h^{-1}),{\varphi }_{jh}\sim \text{Gamma}(v∕2,v∕2),{\tau }_h=\prod _{l=1}^h{\delta }_l$$ (8)

$${\delta }_1\sim \text{Gamma}(a_1,1),{\delta }_l\sim \text{Gamma}(a_2,1),l\ge 2$$ (9)

j = 1, . . . , p, h = 1, . . . , k, δ_l, l ≥ 1, are independent, τ_h is a global shrinkage parameter for the hth column and ϕ_jh's are local shrinkage parameters for the elements in the hth column. Under a choice a₂ > 1, the τ_h's are stochastically increasing favoring more shrinkage as the column index increases. The choice of this shrinkage prior allows many of the loadings to be close to zero while avoiding factor splitting, thus inducing effective basis selection. The number of latent factors, k, is treated as unknown and tuned as the sampler progresses. Refer to Web Appendix A for a detailed discussion on the adaptive choice of k.

The prior structure under our model is completed by

$${\sigma }_j^{-2}\sim \text{Gamma}(a_{\sigma },b_{\sigma }),\text{and}{\phi }^{-2}\sim \text{Gamma}(a_{\phi },b_{\phi })$$ (10)

with j = 1, . . . , p. Furthermore, consider ${\eta }_{\cdot j}^{\prime }\sim \mathrm{N}({\tilde{\mathbf{X}}}^{\prime }{\beta }_j,{\mathrm{I}}_n)$, where ${\eta }_{\cdot j}^{\prime }$ denotes the j-th column of the n × k transpose of the matrix of latent factors η, β_j denotes the j-th column of the r × k matrix of coefficients β and X̃′ denotes the transpose of the matrix of predictors X̃. Each row i, i = 1, . . . , n, of X̃′ corresponds to the vector of predictors for subject i, ${\mathit{x}}_i^{\prime }=(x_{i1},\dots ,x_{ir})$. A Cauchy prior is induced on the matrix of coefficients β as follows

$${\beta }_j\sim \mathrm{N}(0,\text{Diag}\left({\omega }_{lj}^{-1}\right)),{\omega }_{lj}\sim \text{Gamma}(1∕2,1∕2),j=1,\dots ,k,l=1,\dots ,r.$$ (11)

The posterior computation proceeds via a straightforward Gibbs sampler, and is similar to the Markov Chain Monte Carlo (MCMC) algorithm for the sparse Bayesian infinite factor model in Bhattacharya and Dunson (2011). Details are provided in Web Appendix B.

A crucial aspect of our research is to ensure computational tractability to scale well in dimension and sample size. Our model builds more parametric (mostly linear) relationships between the different components, and the basis expansion chosen to represent the functions f_i induces posterior computation which involves the update of single, low dimensional component pieces. Thus, our structure leads to an efficient Gibbs sampler having block updating steps, while avoiding the need to invert large matrices. For example, the HPHB study contains data for 1,027 women with an average number of 10 measurements per subject (range = [1, 25]), for a total of N = 10, 290 observations, and with 12 clinical predictors collected for each woman. The posterior update took 71 seconds per hundred iterations in Matlab on an Intel(R) Core(TM)2 Duo machine. Our approach scales well both in the number of subjects and number of measurements, with simulation experiments showing that cases with n ≈ 4, 000 and N ≈ 40, 000 can be accommodated (a few minutes required per hundred iterations), while larger experiments face serious time and memory constraints.

Preliminary sensitivity analyses will be required to adjust the priors and other model parameters to provide the best fit to the data. To save on computing time, it might be preferable to run the preliminary analyses on a randomly chosen subset of subjects and proceed to the analysis of the complete data set when one is satisfied with the choice of the hyperparameters and other parameter values. This choice is discussed in Web Appendix C.

3. Joint modeling extension for the HPHB study

It is of interest to extend our LFRM to allow joint modeling of a functional predictor with scalar responses. For example, there is substantial interest in relating the BP trajectories to gestational age (GA) at delivery, birth weight (BW), and preeclampsia (hypertension and proteinuria at time of delivery).

We start with a simple probit extension of our model to predict premature delivery. A bivariate probit model for preeclampsia and low birth weight (LBW = weight under 2500 grams) is outlined in Section 3.2, and a joint model for BW, GA and MAP is presented in Section 3.3. These extensions involve straightforward modifications of the MCMC algorithm for the LFRM (Web Appendix B), which includes additional steps to sample from the full conditional posterior distributions of the new model parameters.

3.1 Probit model for risk of preterm birth

Preterm birth refers to the birth of a baby of less than 37 weeks GA. Let $z_i^{pb}=1$ if preterm birth and $z_i^{pb}=0$ if full-term birth. We let $\mathrm{P}(z_i^{pb}=1\mid \alpha ,\gamma ,{\eta }_i)=\Phi (\alpha +{\gamma }^{\prime }{\eta }_i)$, where Φ(·) denotes the standard normal distribution function. α is an intercept with a N(Φ^–1(0.123), 0.25) prior, where the hyperprior mean is chosen to correspond to the national average of 12.3% in 2008 (Hamilton et al., 2010), η_i are the latent factors for subject i, and γ is a vector of unknown regression coefficients with prior distribution γ ~ N_k(μ_γ, Σ_γ).

The full conditional posterior distributions needed for Gibbs sampling are not automatically available, but we can rely on the data augmentation algorithm of Albert and Chib (1993) to facilitate the computation:

$$z_i^{pb}=1(W_i>0)\text{with}{W}_i\sim \mathrm{N}(\alpha +{\gamma }^{\prime }{\eta }_i,1)$$

so that $\mathrm{P}(z_i^{pb}=1\mid \alpha ,\gamma ,{\eta }_i)=\Phi (\alpha +{\gamma }^{\prime }{\eta }_i)$ by marginalizing out W_i. Therefore, the same set of latent factors impacts on the functional predictor via the basis coefficients θ_i and on the response variables via the probability of preterm birth.

3.2 Bivariate probit model for preeclampsia and low birth weight

We develop a bivariate probit model to study the relationship between preeclampsia, LBW and gestational MAP. The sample proportion of LBW is 12%, thus slightly higher than the corresponding national rate of 8.2% in 2008 (Hamilton et al., 2010), whereas the sample proportion of preeclamptic women is 16%, far above the incidence of preeclampsia which typically affects 5-8% of all pregnancies (Cunningham et al., 2001).

Let us denote the outcome variables for preeclampsia and LBW as $z_p^i$ and $z_{lbw}^i$, respectively. In particular, $z_p^i$ is an indicator variable equal to 1 if woman i develops preeclampsia, and $z_{lbw}^i$ is an indicator variable equal to 1 if woman i delivers a LBW infant.

We adopt a data augmentation approach and introduce two underlying normal variables, $W_p^i$ and $W_{lbw}^i$, such that $z_p^i=1(W_p^i>0)$ and $z_{lbw}^i=1(W_{lbw}^i>0)$, with ${(W_p^i,W_{lbw}^i)}^{\prime }\sim \mathrm{N}(\mu ,\tilde{\Sigma })$, and $\mu ={({\alpha }_1+{\gamma }_1^{\prime }{\eta }_i,{\alpha }_2+{\gamma }_2^{\prime }{\eta }_i)}^{\prime }$ and $\tilde{\Sigma }=\left(\begin{array}{cc}\hfill 1\hfill & \hfill \rho \hfill \\ \hfill \rho \hfill & \hfill 1\hfill \end{array}\right)$, with ρ controlling the dependence between $z_p^i$ and $z_{lbw}^i$. The joint probability of preeclampsia and LBW is obtained by double integration of the bivariate normal distribution of the latent variables $W_p^i$ and $W_{lbw}^i$

$$\mathrm{Pr}(z_p^i=1,z_{lbw}^i=1)={\int }_0^{\infty }{\int }_0^{\infty }{\mathrm{N}}_2(W_p^i,W_{lbw}^i;\mu ,\tilde{\Sigma })d{W}_p^i,d{W}_{lbw}^i$$

Analogously, we can compute the marginal probability of observing preeclampsia and the marginal probability of LBW.

The Bayesian specification of the bivariate probit model is completed by choosing conditionally conjugate (normal and multivariate normal) prior distributions for the additional parameters. This choice is discussed in Web Appendix C.

Heterogeneity across subjects and dependence between the smooth function, f_i, and the outcomes, $z_p^i$ and $z_{lbw}^i$, is accommodated through the latent factors, η_i, which impact on the MAP measurements via the basis coefficients θ_i and on the probabilities of preeclampsia and LBW via the latent normal variables $W_p^i$ and $W_{lbw}^i$.

Our goal is to compare sequential predictions of the probability of preeclampsia and LBW for a test sample of women at different times during gestation, say at weeks 20, 25, and so on. Predictions are expected to improve over time, and we aim to assess whether we can make a detection with some certainty sufficiently early during gestation or if it is necessary to wait until close to delivery to make an accurate prediction.

3.3 Joint model of birth weight, gestational age at delivery and blood pressure

Let z_i denote the outcome for subject i, z_i = (z_ib, z_ig), with z_ib denoting the BW and z_ig the GA at delivery. To flexibly joint model GA at delivery and BW, we consider a two-component mixture-model of bivariate normal distributions

$$(z_{ig},z_{ib})\sim \sum _{h=0}^1{\pi }_{ih}\mathrm{N}({\mu }_h,{\Sigma }_h)$$ (12)

This model can be equivalently specified as

$$(z_{ig},z_{ib})\sim \mathrm{N}({\mu }_{T_i},{\Sigma }_{T_i})\text{with}{T}_i=1(W_i>0)$$ (13)

where T_i ∈ {0, 1} is a latent variable indicating which class (z_ig, z_ib) belong to, and π_ih = P(T_i = h). We now let the W_i's have independent t-distributions using a scale mixture of normals construction:

$$W_i\sim \mathrm{N}\left(\alpha +{\gamma }^{\prime }{\eta }_i,{\tilde{\sigma }}^2{\widehat{\varphi }}_i^{-1}\right),\text{with}{\widehat{\varphi }}_i\sim \text{Gamma}(\tilde{\nu }∕2,\tilde{\nu }∕2)$$ (14)

where γ a k × 1 vector of unknown regression coefficients with normal prior distribution, $\gamma \sim {\mathrm{N}}_k({\mu }_{\gamma }^{\ast },{\Sigma }_{\gamma }^{\ast })$, η_i are the latent factors for subject i and α ~ N(Φ^–1(0.1), 0.25). Note that (14) constitutes a t approximation to a logit link function on the mixing weights π_ih, and to ensure a good approximation to the univariate logistic distribution we set ${\tilde{\sigma }}^2\equiv {\pi }^2(\tilde{\nu }-2)∕3\tilde{\nu },\tilde{\nu }\equiv 7.3$ (O'Brien and Dunson, 2004). In addition, this approximation ensures conjugacy of the full conditional distributions, thus allowing efficient posterior update. To complete our Bayesian specification, we chose an inverse-Wishart (I-W) distribution for the covariance matrix, ${\Sigma }_h\sim \mathrm{I}\text{-}{\mathrm{W}}_2({\nu }_h^{\ast },{\mathbf{V}}_h)$, and a bivariate normal distribution for the mean μ_h, ${\mu }_h\sim {\mathrm{N}}_2({\mu }_0^h,{\Sigma }_{\mu 0}^h)$. The choice of the hypeparameter values is discussed in Web appendix C.

Therefore, the common set of latent factors impacts both on the functional predictor f_i and on the outcomes z_i = (z_ig, z_ib) via the class membership probability of the pregnancy outcomes, ${\pi }_{i1}\left({\eta }_i\right)=\mathrm{P}(T_i=1)=\Phi \left(\frac{\alpha +{\gamma }^{\prime }{\eta }_i}{\sqrt{{\tilde{\sigma }}^2{\widehat{\varphi }}_i^{-1}}}\right)$.

4. Application to the Healthy Pregnancy, Healthy Baby Study

The HPHB study is part of the US EPA-funded Southern Center on Environmentally Driven Disparities in Birth Outcomes and enrolls pregnant women from the Duke Obstetrics Clinic and the Durham County Health Department Prenatal Clinic. Our focus is on the investigation of gestational MAP. It is well known that hypertensive women are more likely to experience complications during pregnancy than normotensive women (Cunningham et al., 2001). In particular, gestational hypertension is associated with LBW and early delivery, and in the most serious cases the mother develops preeclampsia. In normotensive women, BP typically declines steadily until mid-gestation and then rises until delivery. In contrast, preeclamptic women typically experience no early decline in BP, with BP remaining stable during the first half of pregnancy and then rising until delivery. Also, primiparous, older, and non-Hispanic black women are more likely than other demographic groups to experience hypertensive disorders during pregnancy. Monitoring the gestational BP can help identify women at risk of adverse birth outcomes, and point to appropriate treatments.

Data were available for 1,027 English-literate women at least 18 years old, for a total of 10,290 measurements. Women with twin gestation or with known congenital anomalies were not included in our analysis. Women with pre-gestational chronic hypertension were also excluded since their BP was artificially lowered by medical treatment. Moreover, we only considered non-Hispanic black and non-Hispanic white women due to the limited number of Hispanics and other ethnic groups in the study.

The sampler described in Web Appendix B was run for 25,000 iterations, with the first 5,000 samples discarded as a burn-in and collecting every fifth sample to thin the chain. The sampler appeared to converge rapidly and mix efficiently based on the examination of traceplots of function estimates f_i(t_ij) at a variety of time locations and for different subjects. The estimated number of factors was 11, with a 95% credible interval of [9, 13].

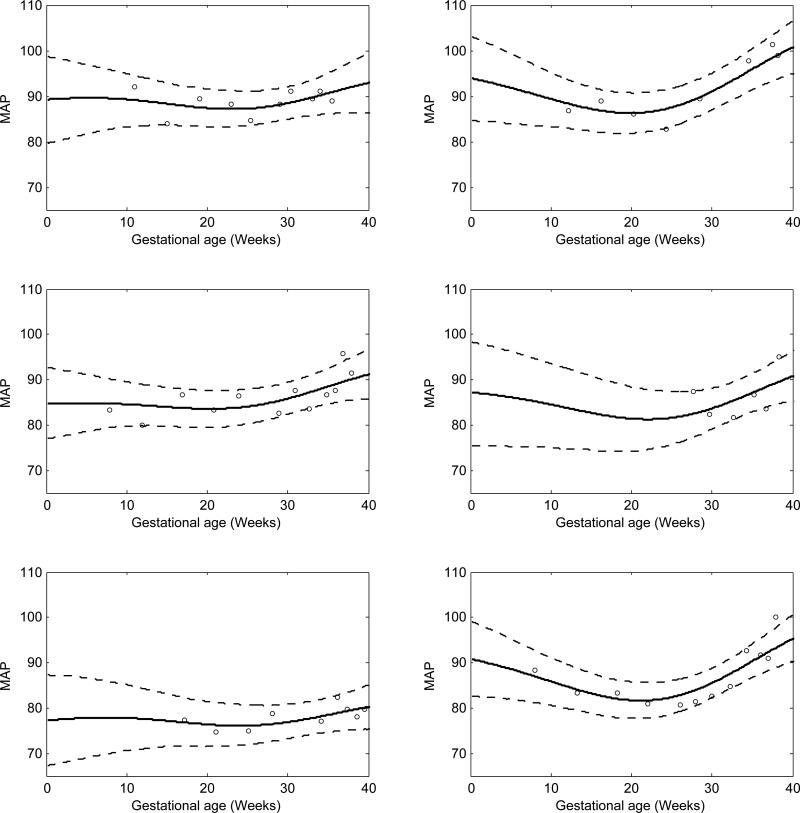
Figure 1 shows the results for 6 randomly selected women, with the MAP estimates following the typical U-shaped trajectory.

Figure 1.

MAP function estimates for 6 randomly selected women in the Healthy Pregnancy, Healthy Baby Study. The posterior means are solid lines and dashed lines are 95% pointwise credible intervals. The x-axis scale is time in weeks starting at the estimated day of ovulation.

Repeating the analysis for the two-stage FPCA approach (Web Figure 1), we observe accurate estimates at locations close to data points, but the estimates are inferior when no or few measurements are recorded. The use of a pre-specified, over-complete set of basis functions with no shrinkage on (and hence no basis selection) leads to overly-spiky curves.

To assess the predictive performance, we held out and predicted the MAP measurements collected after the 30–th week for 300 randomly selected women with at least one measurement in the first 30 weeks. We then compared our approach with “baseline” LFRM and two-stage FPCA with no covariates by setting η_i ~ N(0, I_k). Results are reported in Table 1. The high prediction errors were expected since there were many hard-to-predict outliers in the MAP measurements. Predictions improved with the LFRM, although the inclusion of covariate information did not significantly decrease the prediction errors.

Table 1.

Mean square predictive error (MSPE), predictive average absolute bias (PAAB) and predictive maximum absolute bias (PMAB) for the HPHB study with the LFRM and the two-stage FPCA approach fitted with and without covariates, respectively.

	LFRM		two-stage FPCA
	Covariates	No Covariates	Covariates	No Covariate
MSPE	88.36	89.91	92.16	92.22
PAAB	7.44	7.51	7.52	7.52
PMAB	43.50	43.29	49.51	49.62

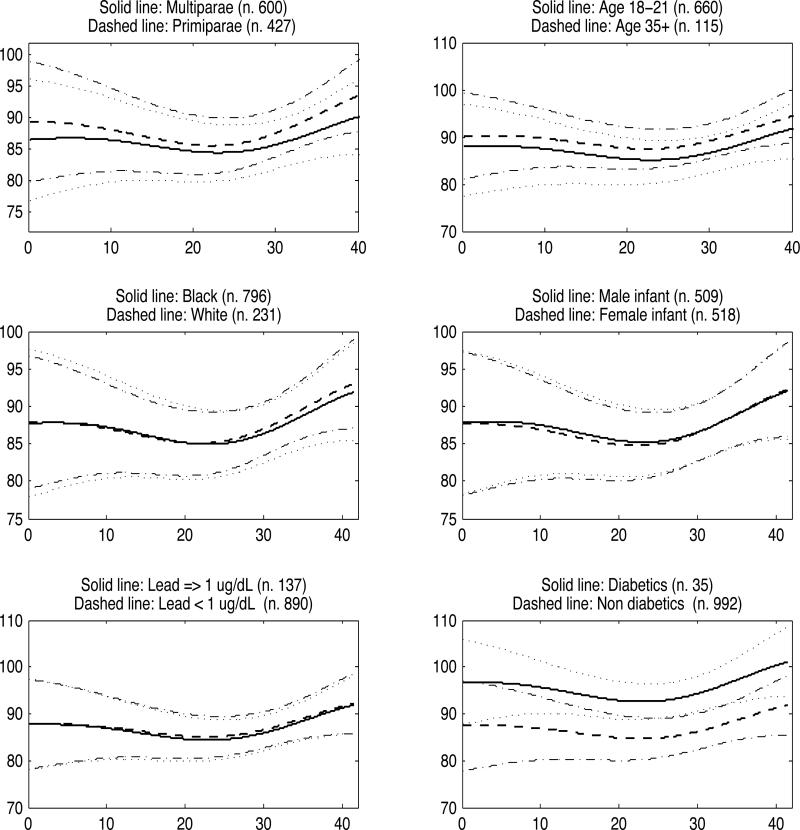
Figure 2, which shows how average MAP trajectories change across six different covariate groups, confirms previous findings on gestational BP, with older and primiparous women having higher BP, although discrepancies are small. Diabetic women have higher gestational BP than healthy women, with non-overlapping 95% credible intervals between mid-gestation and the 35th week. There were no differences among the remaining covariate groups.

Figure 2.

MAP function estimates for 6 representative covariate groups. Dotted lines represent 95% pointwise credible intervals and refer to the solid lines, and dash-dot lines are the 95% pointwise credible intervals referring to the dashed lines.

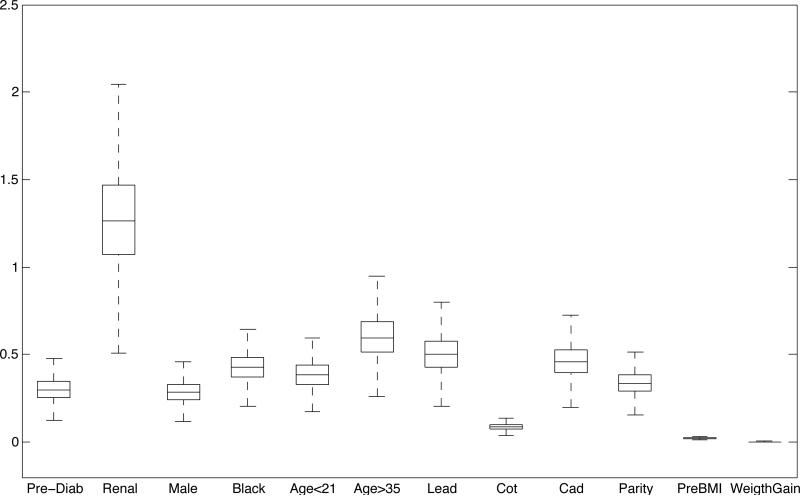
To assess the relative importance of the j-th covariate, we look at the j-th column of the k × r matrix β′, which contains the vector of coefficients associated with covariate j. The norms of the columns of β′ indicate whether the covariates have any impact on the latent factors. The magnitude of the elements within each column determines the load of the covariate on each latent factor. If $\Vert {\beta }_{\cdot j}^{\prime }\Vert =0$, covariate j does not impact on the estimate of any of the latent factors for any subject. Figure 3 shows side-by-side boxplots of the norms of the posterior estimates of the columns of β′. Greater relative impact is attributed to the indicators for renal disease and (age > 35), followed by lead and cadmium concentration in ng/mL and maternal race. Similarly, one can look at the norms of the columns of Λ to assess the relative impact of Λη_i on θ_i (Web Figure 2).

Figure 3.

Side-by-side boxplots of the norms of the posterior estimates of the columns of β.

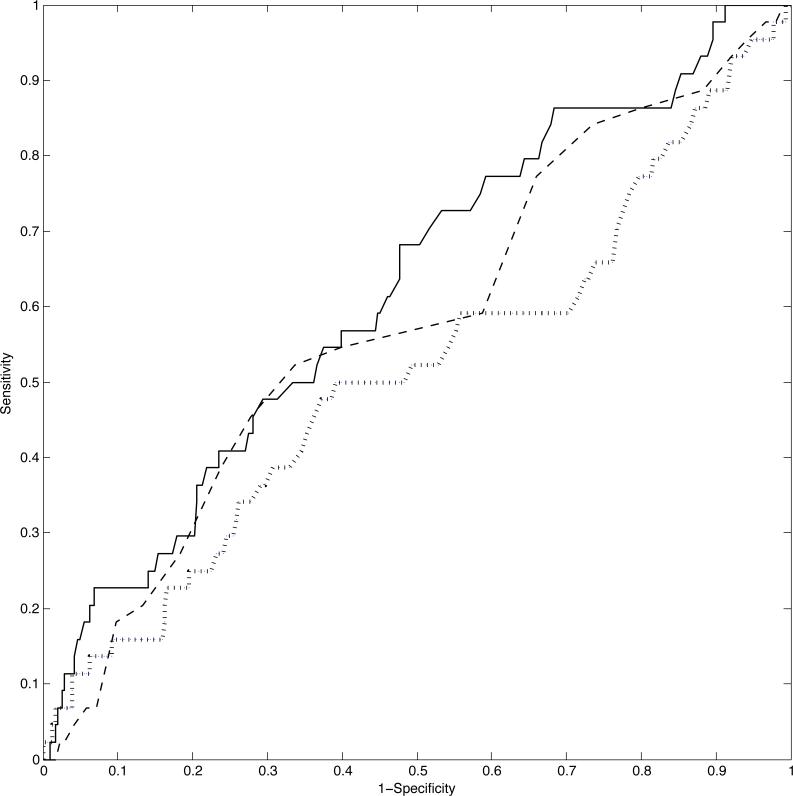
In terms of joint modeling, we report the results of a probit extension used to predict LBW. For this analysis, we randomly split the data into a training set of 677 women and a test set of 350 women. The complete data was retained for the training set whereas the test set was entirely held out, that is, neither the MAP measurements nor the final outcome were included. We compared the LFRM with the Dependent Dirichlet process (DDP) in De la Cruz-Mesia, Quintana and Müller (2007), the Kernel partition process (KPP) in Dunson (2010), and with two-stage FPCA. The ROC plot in Figure 4 shows that the LFRM outperforms the two-stage FPCA approach, and it is equally good as KPP in guaranteeing high sensitivity. However, the LFRM's classification performance could be potentially improved over the KPP (which does not include covariates) by letting the predictors directly impact on the probability of LBW, while currently only an indirect impact via the η_i's is accommodated. The DDP had worse performance than our approach, so the ROC curve was omitted for simplicity of exposition.

Figure 4.

ROC plot for the correct classification of LBW in the HPHB study: the solid line refers to the LFRM, the dashed line to the KPP, and the dotted line to two-stage FPCA.

Table 2 reports the posterior mean estimates of the marginal probabilities of preeclampsia and LBW (with Monte Carlo standard errors) computed at the 20th, 25th, 30th and 35th week of gestation for four randomly selected women in the test set. The final outcome information was included for women in the training set only, while the BP measurements at time of delivery were available for none of the women. Women in the test set had at least one MAP measurement before the 20th week, and at least one measurement after the 35th week. As early as 20 weeks of gestation, the LFRM estimated probabilities of preeclampsia and LBW were up to three times higher than the national rates for women who in fact experienced preeclampsia and/or LBW, with one exception being the probability of preeclampsia for woman 2, which was initially high but then dropped to 11.41% at the 35th week. By looking at Web Figure 3, it is evident that the curve and the BP measurements for woman 2 were similar to those of normotensive woman 4. Thus, it is possible that woman 2 had normal BP during the prenatal visits, but was still preeclamptic because she had very high BP (and proteinuria) at delivery.

Table 2.

Posterior mean estimates of the probabilities of preeclampsia and LBW (with Monte Carlo standard errors). $z_p^i$ and $z_{lbw}^i$ are indicator variables equal to 1 if woman i developed preeclampsia and delivered a LBW infant, respectively. Woman 1: $z_p^1=1$, $z_{lbw}^1=1$; Woman 2: $z_p^2=1$, $z_{lbw}^2=0$; Woman 3: $z_p^3=0$, $z_{lbw}^3=1$; Woman 4: $z_p^4=0$, $z_{lbw}^4=0$.

	Subjects
$\mathrm{Pr}(z_p^i=1)$	1	2	3	4
20th week	0.2545 (0.0037)	0.2085 (0.0034)	0.0711 (0.0019)	0.1179 (0.0025)
25th week	0.2819 (0.0047)	0.1314 (0.0031)	0.1148 (0.0038)	0.1046 (0.0027)
30th week	0.3640 (0.0044)	0.1960 (0.0035)	0.0855 (0.0023)	0.0985 (0.0023)
35th week	0.4185 (0.0042)	0.1141 (0.0023)	0.1128 (0.0024)	0.0983 (0.0021)
$\mathrm{Pr}(z_{lbw}^i=1)$	1	2	3	4
20th week	0.2582 (0.0054)	0.0858 (0.0032)	0.2544 (0.0053)	0.1144 (0.0037)
25th week	0.2391 (0.0056)	0.0644 (0.0030)	0.3166 (0.0062)	0.0981 (0.0038)
30th week	0.3193 (0.0058)	0.0986 (0.0035)	0.2865 (0.0057)	0.1056 (0.0036)
35th week	0.3462 (0.0058)	0.0608 (0.0027)	0.3462 (0.0058)	0.0997 (0.0034)

These findings suggest that, as early as the 20th week of gestation, the LFRM identifies women at high risk for adverse birth outcomes, with predictions getting more accurate around the 30th to 35th week of gestation. However, the LFRM may fail to identify the risk of preeclampsia in women who only register a sharp increase in MAP at delivery since the normotensive gestational BP would not be enough to detect the risk of the adverse outcome.

5. Discussion

The article has proposed a Bayesian latent factor regression model for functional data. The basic formulation generalizes the sparse Bayesian infinite factor model of Bhattacharya and Dunson (2011), which was developed for estimation of high-dimensional covariance matrices for vector data, to the functional data case. This allows one to include a high-dimensional set of pre-specified basis functions, while allowing automatic shrinkage and effective removal of basis coefficients not needed to characterize any of the curves under study. In addition, we consider several generalizations allowing predictors to impact on the latent factor scores and accommodating joint modeling of functional predictors with scalar responses that are modeled parametrically or via mixture models. Along the same lines, we can consider joint modeling of multiple related functions easily within the proposed framework, but our emphasis was on developing methods motivated by the application to the study of blood pressure and pregnancy outcomes.

The proposed framework has the advantage of straightforward computation via a simple Gibbs sampler and easy modifications for joint modeling of disparate data of many different types. In particular, the θ_i vector of basis coefficients in the functional data model can instead be replaced with concatenated coefficients within component models for different types of objects, including not only time trajectories but also images, movies, text, etc. This leads to a general shared latent factor framework for modeling high-dimensional mixed domain data that should have broad utility to be explored in future research. An interesting modification would be a semiparametric case that allows the latent variables densities to be unknown via nonparametric Bayes priors.