Abstract
Unraveling the nature of genetic interactions is crucial to obtaining a more complete picture of complex diseases. It is thought that gene-gene interactions play an important role in the etiology of cancer, cardiovascular and immune-mediated disease. Interactions among genes are defined as phenotypic effects that differ from those observed for independent contributions of each gene, usually detected by univariate logistic regression methods. Using a multivariate extension of linkage disequilibrium, we have developed a new method, based on distances between sample covariance matrices for groups of SNPs, to test for interaction effects of two groups of genes associated with a disease phenotype. Since a disease-associated interacting locus will often be in linkage disequilibrium with more than one marker in the region, a method that examines a set of markers in a region collectively can offer greater power than traditional methods. Our method effectively identifies interaction effects in simulated data, as well as in data on the genetic contributions to the risk for graft-versus-host disease following hematopoietic cell transplantation.
Keywords: genetic association studies, epistasis, multivariate analysis
INTRODUCTION
Many complex diseases are influenced by both genetic and environmental factors. Determining the underlying genetic etiology can be difficult, as it may involve single genes as well as interactions between two or more genes. While initial and ongoing efforts have centered on disease associations with single genes (a single nucleotide polymorphism (SNP) or haplotypes/diplotypes of multiple SNPs from single genes or regions), recent interest has expanded to include examination of gene-gene interactions regardless of their location within the genome [Cordell, 2009; Chatterjee et al., 2006; Zhao et al., 2006].
The effect of two genes on a disease outcome is considered an interaction if the effect on the phenotype of one gene depends on the other gene. The scale that is used to model the genetic effects on the phenotype may sometimes determine whether there is an interaction [Wang et al., 2010]. For example, a multiplicative interaction in a logistic model may be no longer an interaction when effects are modeled on an additive scale (see, for example, the example in section 2 of Kooperberg et al. [2009]). In practice, a gene-gene interaction is detected by testing for phenotypic effects that differ from those observed when each gene contributes independently, e.g. departure from additivity in a logistic regression model. Identifying gene-gene interactions does not just help to explain part of the heritability of a phenotype, it also points to pathways involving multiple genes, and therefore increases our understanding of the biology underlying the phenotype. In this paper we present an example from allogeneic hematopoietic stem cell transplantation (HCT), where an interaction between two genes in two genomes, the IL10 gene in the recipient and the IL10RB gene in the donor, have an interaction effect on Graft Versus Host Disease (GVHD), a well-known complication of HCT transplantation. This interaction suggests that pathways involving these two genes are important in understanding GVHD as a complication of HCT.
In most genetic association studies the “causal” SNP is not genotyped, but rather inference about a functional variant is made indirectly because a SNP that is in linkage disequilibrium (LD) with the causal SNP will show association with a phenotype. When the causal SNP is part of an LD group, multiple nearby SNPs may show an association [e.g. Dickson et al., 2010]. Similarly, we may expect that if there is an interaction effect on a disease of two causal SNPs, pairs of SNPs in the LD group adjacent to either of the two causal SNPs may show some association. In a traditional logistic regression analysis, this adjacent LD is not used as each pair of SNPs is tested separately for possible interactions, so we expect to lose power if nearby SNPs are not considered. Here we propose to test for interaction effects between blocks of SNPs, thereby possibly gaining power. In particular, our test can identify interactions between two genes, where in each gene the “causal” SNP may not be genotyped, but several other genes are genotyped.
Chatterjee et al. [2006] developed a procedure to identify main effects and interactions of groups of SNPs simultaneously using the Tukey one degree of freedom test. However, the goal of [Chatterjee et al., 2006] was to increase the power to identify SNPs that have a marginal effect using interactions, rather than to identify the interactions themselves. The same problem was addressed by Wang et al. [2009], who developed a Partial Least-Squares solution to this problem. Zaykin et al. [2006] studied the related problem of finding association between a group of SNPs and a phenotype. Similar to what we are proposing in the current paper, their approach compares the LD between cases and controls, but their approach is not geared towards identifying interactions. Crosslin et al. [2010] compares the approaches of Wang et al. [2009] and Zaykin et al. [2006]. Zhao et al. [2006] introduced a test for the interaction between two unlinked loci and defined interaction as deviation from penetrance. The disadvantage of this method is that the haplotype cannot be determined with certainty.
Cordell [2009] contains a comprehensive discussion of methods for identifying gene-gene interactions. Several approaches using data mining methods have been proposed [e.g. Ritchie et al., 2003; Ruczinski et al., 2002], as well as methods that first screen marginal associations to identify the most promising variants or genes to test for interactions [e.g. Kooperberg and LeBlanc, 2008; Wu et al., 2010; Millstein et al., 2006]. Other approaches focus on computational efficiency in light of the large number of possible interactions in GWAS [e.g. Zhang et al., 2010], and some approaches use penalized regression techniques such as the lasso [e.g. D’Angelo et al., 2009]. Clearly many methods have been used to identify gene-gene interactions, but it is beyond the scope of this paper to provide a comprehensive review here.
In this paper we propose a test for identifying gene-gene interactions, where the effect comes from a group (block) of genotyped variants, for example, all genotyped variants within a gene. The blocks need not be the same size. Li et al. [2009] attempted to use principle components of blocks of variants to identify gene-gene interactions. To the best of our knowledge, no other approach in the literature is designed for this particular problem.
It is easy to see that if the joint distribution of genotype markers depends on disease status, the disease status is associated with these markers [Millstein et al., 2006]. As a consequence, if the covariance matrix of a group of SNPs is different between cases and controls, the group of SNPs is associated with case-control status. While the reverse is not always true, it is true, for example, for a single SNP that is in Hardy-Weinberg equilibrium separately among cases and controls when the minor allele frequency in both groups is smaller than 0.5. In that situation, if the variances for a SNP are the same then the minor allele frequencies are the same, and there is no association. We cannot use a similar argument for the correlation matrix.
We can take this argument one level further: if the distribution of two (groups of) SNPs is each the same among cases and controls, neither of these (groups of) SNP(s) is by itself associated with disease status. If at the same time the joint distribution of these two (groups of) SNPs is associated with the disease status, the two (groups of) SNPs together are associated with the disease status. If neither of these (groups of) SNPs is by itself associated with disease status, this means that there is an interaction effect of these two (groups of) SNPs on disease status. This motivates our approach: if the off-diagonal part of a covariance matrix corresponding to the covariance between two (groups of) SNPs differs between cases and controls, we conclude that there is an interaction.
To exploit this in our method, we summarize and contrast the difference in LD between cases and controls. To measure the LD we use the composite LD (CLD), which is advantageous because it is not necessary to phase the genotype data. There are many measures to quantify LD. We show that there is a direct relation between CLD and the covariance matrix of a set of markers. Therefore, if the CLD patterns are different between cases and controls, we conclude that there is an interaction, making this particular measure of LD ideal for our purpose. A disease-associated interacting locus will often be in LD with more than one genotyped marker in the region. Therefore methods like ours that examine a set of markers in a region collectively can potentially offer greater power than the traditional method of examining 2-way or 3-way interactions in univariate logistic regression models.
METHODS
LINKAGE DISEQUILIBRIUM AND COMPOSITE LINKAGE DISEQUILIBRIUM
Linkage disequilibrium indicates that particular alleles at nearby sites co-occur on the same haplotype more often than is expected by chance. Lewontin [1964] defined the gametic LD coefficient as DAB = pAB−pApB, or the simple difference between the haplotype probability and the product of the allele frequencies, when data are collected on haplotypes for diallelic loci. Weir [1996] and Weir & Cockerham [1989] defined the non-gametic digenic disequilibrium coefficient DA/B = pA/B −pApB, where the slash indicates that the two alleles occur on different chromosomes. For the phase-unknown situation where random mating cannot be assumed, these papers introduce the composite linkage disequilibrium (CLD)
In the context of association mapping, Nielsen et al. [2004] presented a direct LD comparison approach involving two bi-allelic loci and noted that a test that directly compares the LD between the case and control groups can be a powerful alternative to either haplotype-based or single marker approaches. They considered only the case of unambiguous haplotype phase. When the haplotype phase is unknown, computational algorithms can be used to infer frequencies of haplotypes and, ultimately, to assess LD. Typically this requires the assumption of Hardy-Weinberg equilibrium (HWE) for the haplotypes. Schaid [2004] and Zaykin [2004] showed that LD estimation with use of the composite linkage disequilibrium approach provides results similar to the haplotype reconstruction method under HWE, is computationally simpler, and avoids the assumption of HWE for the haplotypes. Therefore we use CLD rather than LD to characterize the relation between SNPs.
Following Weir et al. [2004] we show the relationship between LD and CLD as follows. Let m and n be the number of cases and controls, respectively. Let xijk = 1 if the kth, k = 1, 2, haplotype in the jth, j = 1, 2, …, p, SNP for case i = 1, 2, …, m, carries major allele A and 0 if it carries minor allele a. The LD between SNPs j and j′ is the covariance of xijk and xij′k whereas the CLD between SNPs j and j′ is the covariance of
The quantities Xij and Xij′ are the proportions of the alleles a subject in the case group carries at SNP j and j′. Let X denote the m × p matrix {Xij}. Similarly, define yijk, Yijk, and Y for the control group, where Y is n × p. Thus, for genotype data we can estimate the CLD by the sample covariance between the genotypes (Xij, Xij′) without using phase information. Note that CLD does not require HWE to hold, but when HWE holds, CLD is equal to LD [Schaid, 2004; Weir et al., 2004, Zaykin 2004]. The CLD does not distinguish between the two possible phases of the double heterozygotes, so CLD can be defined for SNPs within the same chromosome (in cis) or between chromosomes (in trans).
TESTS FOR EQUALITY OF BLOCK INTERACTIONS
In order to compare CLDs between two groups of SNPs in cases and controls, rather than only between single pairs of SNPs, we propose two multivariate statistics that measure differences between blocks of pairwise CLDs in cases and controls. Let group 1 have p1 SNPs and group 2 have p2 SNPs, where p1 + p2 = p, and let S and T be the (p1 + p2) × (p1 + p2) sample covariance matrices for the two groups of SNPs for (m) cases and (n) controls, based on X and Y respectively. Partition S as
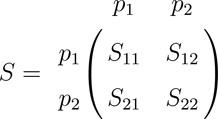 |
(1) |
and partition T similarly. Here S11 and S22 are the sample intra-group covariance matrices for group 1 and for group 2 respectively, and is the inter-group sample covariance matrix. Denote the corresponding quantities for the controls as T11, T22, and . Note that if p1 = p2 = 1, then S12 and T12 both reduce to CLD as defined above.
Let Σ (cases) and Ω (controls) be the population covariance matrices that correspond to S and T respectively, partitioned according to (1). We propose to test whether the interaction effects (= covariances) between the two groups of SNPs are different for cases than for controls, that is, to test equality of the block interactions, i.e., test
, rather than testing for differences between single pairs of corresponding elements in Σ12 and Ω12.
Let W = (mS + nT)/(m + n) be the pooled estimate of the covariance matrix, and W is partitioned similarly to S and T (1). We propose a method that is based on the Nagao [1973] normalized quadratic distance (NQD) and is defined as
applied to S̃ and T̃, where
| (2) |
Details can be found in Appendix 1. We believe that δ2 is a reasonable statistic for detecting departure from the null hypothesis H12. Because the distribution of δ2 under the null hypothesis is not known, we establish the significance levels of this statistics using permutation tests.
RESULTS
SIMULATION STUDY
We compared our proposed test to tests based on logistic regression (described below) in a simulation study. Because we wish to test whether multiple SNPs in two genetic regions have a non-null interaction effect on a phenotype, the univariate logistic regression approaches discussed in the Introduction are not applicable.
To generate our simulated data we created an artificial population using genotype data obtained from the HapMap project Caucasian population [The International HapMap Consortium, 2005]. We used PHASE [Stephens et al., 2001] to estimate haplotypes for SNPs rs7130285, rs2074040, rs3740878, rs7935586, and rs6485533 (denoted A1, …, A5) from the EXT2 gene and rs2713813, rs7951391, rs7480010, rs906625, and rs6485316 (denoted B1, …, B5) from the intergenic region of the LRRC4CX2 gene (the haplotypes and their frequencies are listed in Table I). Randomly paired haplotypes were used to create our population, so that our data has the same frequencies as in Table I.
TABLE I.
Haplotype frequencies for the simulation study.
| Block 1 | Block 2 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Haplotype | Frequency | Haplotype | Frequency | ||||||||
| 0 | 0 | 0 | 0 | 1 | 0.0544 | 0 | 0 | 1 | 1 | 0 | 0.0151 |
| 0 | 0 | 0 | 1 | 1 | 0.0163 | 0 | 0 | 1 | 1 | 1 | 0.0288 |
| 0 | 0 | 1 | 0 | 1 | 0.0239 | 0 | 1 | 0 | 0 | 0 | 0.0123 |
| 0 | 0 | 1 | 1 | 0 | 0.0258 | 0 | 1 | 0 | 1 | 0 | 0.0082 |
| 0 | 0 | 1 | 1 | 1 | 0.1645 | 0 | 1 | 0 | 1 | 1 | 0.0360 |
| 0 | 1 | 0 | 0 | 1 | 0.0066 | 0 | 1 | 1 | 0 | 0 | 0.0191 |
| 0 | 1 | 1 | 1 | 0 | 0.0118 | 0 | 1 | 1 | 1 | 1 | 0.0379 |
| 1 | 0 | 0 | 1 | 1 | 0.0413 | 1 | 0 | 1 | 0 | 0 | 0.0679 |
| 1 | 0 | 1 | 1 | 0 | 0.0061 | 1 | 0 | 1 | 0 | 1 | 0.0315 |
| 1 | 0 | 1 | 1 | 1 | 0.0328 | 1 | 0 | 1 | 1 | 1 | 0.0645 |
| 1 | 1 | 0 | 0 | 1 | 0.0589 | 1 | 1 | 0 | 0 | 1 | 0.0713 |
| 1 | 1 | 0 | 1 | 0 | 0.0252 | 1 | 1 | 0 | 1 | 0 | 0.1074 |
| 1 | 1 | 0 | 1 | 1 | 0.0276 | 1 | 1 | 0 | 1 | 1 | 0.0737 |
| 1 | 1 | 1 | 0 | 1 | 0.2832 | 1 | 1 | 1 | 0 | 0 | 0.0302 |
| 1 | 1 | 1 | 1 | 0 | 0.0379 | 1 | 1 | 1 | 0 | 1 | 0.1104 |
| 1 | 1 | 1 | 1 | 1 | 0.1837 | 1 | 1 | 1 | 1 | 0 | 0.0994 |
| 1 | 1 | 1 | 1 | 1 | 0.1862 | ||||||
We used interaction models developed by Marchini et al. [2005] to assign case and control status. We denote the models IM1 (for Interaction Model 1), IM2, and IM3. IM1 has main effects, but no interaction, IM2 has a multiplicative interaction and no main effect, and IM3 has a threshold interaction where the risk is increased if both SNPs have at least one copy of the minor allele. In each of the two genes we will designate one variant as the causal variant. Let g1 and g2 be the number of copies of the variant allele for the causal variant in the two genes. Note that we can write the probability of being a case (D = 1) for each of these three models in a logistic regression form:
Here β*,0, β0,* quantify the additive effects, β*,* measures the interactions between two loci, and β0,0 defines the intercept. The three interaction models are obtained by
IM1: β0,2 = 2β1,0 = β2,0 = 2β0,1, β1,1 = β1,2 = β2,1 = β2,2 = 0
IM2: β0,1 = β1,0 = β0,2 = β2,0 = 0, 4β1,1 = 2β1,2 = 2β2,1 = β2,2
IM3: β0,1 = β1,0, = β0,2 = β2,0 = 0, β1,1 = β1,2 = β2,1 = β2,2.
In our simulations for IM1 we take eβ0,0 = 0.01 in all models, so that each model only has one parameter β. Note that eβ0,0 = 0.01 corresponds to a moderately rare disease. We show results for a sample size of 1000 cases and 1000 controls. We examined smaller sample sizes, and found the results qualitatively similar. In our simulations, we used SNPs A3 and B3 as the casual SNPs. The minor allele frequencies of A3 and B3 are 0.2303 and 0.3090, respectively. In our simulations we consider three scenarios.
Case 1: Only A3 and B3 are observed. This is a standard scenario investigated in the literature, where the SNPs that are interacting are assumed to be observed.
Case 2: We observe A1, …, A5 and B1, …, B5. This is the scenario in which we observe blocks of SNPs, including the SNPs that we generated, to be causal. In this scenario we expect some power increase because the additional SNPs are in LD with A3 and B3, which may be offset by some decrease in power because of multiple comparisons.
Case 3: We observe A1, A2, A4, A5 and B1, B2, B4, B5. We believe that this is the most interesting scenario, as we do not observe the causal SNP, but observe the interaction through multiple SNPs that are in LD with the casual SNP. Our methods are specifically designed with this situation in mind.
We compare three testing methods: the quadratic distance-based statistic (δ2), and statistics arising from two logistic models (LM1, LM2) in which all SNPs that are considered are present in the model, coded additively. For LM1 we consider all pairwise interactions simultaneously, testing them using a likelihood ratio test, and for LM2 we consider each of the pairwise interactions separately, selecting the most significant one. We ran each simulation scenario 1, 000 times. For all three methods, significance levels are determined using 10, 000 permutations of case-control status, separately for each simulation.
The power results for Case 1, when the matrix size is 2 × 2 and equality of a single off-diagonal covariance pair is tested, are shown in Table II. Note that for this situation the two logistic regression statistics, LM1 and LM2, are identical. For IM1, where there are additive effects, but there is no interaction, we note that all approaches maintain the correct Type 1 error of 5%. It is important to note that this is the case, even if β01 ≠ 0, as formally a permutation test like the one we use tests whether there is any association between the genes and the disease. However, our test statistic is designed to only show an effect when there is an interaction effect, and not when individual genes have an effect on the phenotype.
TABLE II.
Power of the proposed test statistics for Case 1. Here p1 = p2 = 1 and we test for equality of the single elements of Σ12 and Ω12. IM1, multiplicative within and between loci – no interaction; IM2, multiplicative model and no main effects; IM3, the threshold model. For this set of simulations, 1000 cases and 1000 controls were sampled for each of 1000 simulation runs. We completed 10000 permutations for each data set, and controlled the significance level at α = 0.05.
| Parameter β in the model | |||||||
|---|---|---|---|---|---|---|---|
| 0 | 0.1 | 0.5 | 1 | 2 | 4 | ||
| IM1 | δ2 | 0.047 | 0.048 | 0.049 | 0.050 | 0.053 | 0.052 |
| LM1 = LM2 | 0.048 | 0.049 | 0.051 | 0.051 | 0.050 | 0.053 | |
| IM2 | δ2 | 0.053 | 0.068 | 0.106 | 0.184 | 0.653 | 1.000 |
| LM1 = LM2 | 0.049 | 0.061 | 0.102 | 0.176 | 0.615 | 1.000 | |
| IM3 | δ2 | 0.051 | 0.057 | 0.084 | 0.120 | 0.559 | 0.953 |
| LM1 = LM2 | 0.050 | 0.055 | 0.080 | 0.112 | 0.547 | 0.935 | |
For IM2, where there is a multiplicative interaction, and IM3, where there is an interaction with threshold (dominant × dominant) effects, all approaches have approximately the same power, which, for Case 1, is according to our expectation. After all, this is the situation in which the “blocks” consist of a single SNP, and the logistic regression is correct.
The power results for Case 2, when the matrix size is 10 × 10 and we test equality of the two off-diagonal 5 × 5 sub-matrices, are shown in Table III. As in Case 1, all approaches maintain the correct Type 1 error. For this case we note that for both IM2 and IM3, our proposed test statistic, δ2, has considerably more power than both logistic regression statistics, which have approximately the same power. Compared to Case 1 we notice that both logistic regression statistics have less power because of the larger multiple comparisons penalty (note that we correct using a permutation approach, and not using a Bonferoni correction, which would have led to even more loss of power for logistic regression). On the other hand, the power of δ2 increases from Case 1 to Case 2, because this statistic exploits the CLD among entire block of SNPs. This suggests that even if the causal SNP is genotyped (or imputed) it is still beneficial to include neighboring SNPs, as long as they have some LD, in testing for interactions. Each of the neighboring SNPs carries some signal, as they are weakly correlated with the causal SNP.a Our statistic δ2 “adds” those weak signals to the signal of the causal SNP to strengthen that signal somewhat, as there is no multiple comparisons penalty with a single test.
TABLE III.
Power of the proposed test statistics for Case 2. Here p1 = p2 = 5 and we test for equality of the two 5 × 5 blocks Σ12 and Ω12. IM1, multiplicative within and between loci – no interaction; IM2, multiplicative model and no main effects; IM3, the threshold model. For this set of simulations, 1000 cases and 1000 controls were sampled for each of 1000 simulation runs. We completed 10000 permutations for each data set, and controlled the significance level at α = 0.05.
| Parameter β in the model | |||||||
|---|---|---|---|---|---|---|---|
| 0 | 0.1 | 0.5 | 1 | 2 | 4 | ||
| IM1 | δ2 | 0.048 | 0.047 | 0.049 | 0.051 | 0.052 | 0.053 |
| LM1 | 0.049 | 0.050 | 0.051 | 0.052 | 0.053 | 0.052 | |
| LM2 | 0.048 | 0.049 | 0.051 | 0.052 | 0.051 | 0.052 | |
| IM2 | δ2 | 0.049 | 0.072 | 0.134 | 0.225 | 0.821 | 1.000 |
| LM1 | 0.051 | 0.059 | 0.089 | 0.154 | 0.521 | 1.000 | |
| LM2 | 0.050 | 0.062 | 0.095 | 0.169 | 0.558 | 1.000 | |
| IM3 | δ2 | 0.051 | 0.065 | 0.104 | 0.195 | 0.701 | 1.000 |
| LM1 | 0.050 | 0.056 | 0.072 | 0.104 | 0.468 | 0.990 | |
| LM2 | 0.050 | 0.057 | 0.080 | 0.119 | 0.468 | 1.000 | |
The power results for Case 3, when the matrix size is 8 × 8 and equality of the two off-diagonal 4 × 4 sub-matrices is tested, are shown in Table IV. For this case the causal SNPs are not part of the data that are analyzed. As a result, the logistic regression methods lose almost all the power they had in Case 2, as each of the individual SNPs that are tested are only weakly correlated with the causal SNPs. Our proposed statistic δ2 also loses power but the loss is much smaller, and this test still maintains reasonable power, especially for IM2, where the power is not much lower than in Case 1. This is the goal of our method, as in most real situations the causal SNP is not genotyped, and any signal that we are seeing is because of correlation with nearby (tag-)SNPs. We repreated the simulation for Case 3 (Table IV) with data sets of 3000 cases and controls (results not shown). Naturally the power of all approaches is better, but the general pattern that δ2 substantially outperforms logistic regression remains the same.
TABLE IV.
Power of the proposed test statistics for Case 3. Here p1 = p2 = 4 (the interaction SNPs have been eliminated for the analysis) and we test for equality of the two 4 × 4 blocks Σ12 and Ω12. IM1, multiplicative within and between loci – no interaction; IM2, multiplicative model and no main effects; IM3, the threshold model. For this set of simulations, 1000 cases and 1000 controls were sampled for each of 1000 simulation runs. We completed 10000 permutations for each data set, and controlled the significance level at α = 0.05.
| Parameter β in the model | |||||||
|---|---|---|---|---|---|---|---|
| 0 | 0.1 | 0.5 | 1 | 2 | 4 | ||
| IM1 | δ2 | 0.048 | 0.049 | 0.050 | 0.051 | 0.052 | 0.052 |
| LM1 | 0.047 | 0.049 | 0.049 | 0.051 | 0.052 | 0.052 | |
| LM2 | 0.048 | 0.048 | 0.051 | 0.050 | 0.051 | 0.053 | |
| IM2 | δ2 | 0.047 | 0.061 | 0.089 | 0.155 | 0.465 | 1.000 |
| LM1 | 0.049 | 0.054 | 0.060 | 0.084 | 0.226 | 0.685 | |
| LM2 | 0.049 | 0.055 | 0.065 | 0.099 | 0.242 | 0.721 | |
| IM3 | δ2 | 0.049 | 0.059 | 0.068 | 0.105 | 0.235 | 0.611 |
| LM1 | 0.049 | 0.050 | 0.054 | 0.061 | 0.067 | 0.128 | |
| LM2 | 0.049 | 0.050 | 0.055 | 0.069 | 0.076 | 0.141 | |
To examine whether the results observed for Case 3 depend on either the LD among the markers or the block length we carried out an additional simulation study. For this simulation we selected blocks of length 5, length 7 and length 21 out of the real data on Graft Versus Host Disease, which is used in the next section, so that the average CLD (r) between each of the pairs of SNPs has a pre-specified value of 0.2, 0.3, …, 0.8 (for the blocks of length 20 we only found situations with average LD ≤ 0.5). For those blocks we reconstruct the haplotypes, and then generate a population and an interaction signal using IM2 with the interaction β = 2 using the middle SNP of two blocks of the same length and the same average CLD identical to the other simulations. As in Case 3 we then remove this SNP from our analysis. Thus we have simulations with p1 = p2 = 4, with p1 = p2 = 6, and with p1 = p2 = 20. As before we generate 1000 cases and 1000 controls for each of 1000 simulation runs and base the P-values on 10,000 permutations. The results are shown in Table V.
TABLE V.
Power of the proposed test statistics for Case 3 and IM2 with the interaction β = 2, for different sizes of the blocks (p1 and p2) and different amounts of LD within the block (measured using |CLD| = |r|). For this set of simulations, 1000 cases and 1000 controls were sampled for each of 1000 simulation runs. We completed 10000 permutations for each data set, and controlled the significance level at α = 0.05.
| CLD | ||||||||
|---|---|---|---|---|---|---|---|---|
| 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | ||
| p1 = p2 = 4 | δ2 | 0.303 | 0.321 | 0.364 | 0.425 | 0.481 | 0.291 | 0.211 |
| LM1 | 0.175 | 0.186 | 0.204 | 0.212 | 0.228 | 0.240 | 0.181 | |
| LM2 | 0.184 | 0.205 | 0.211 | 0.228 | 0.249 | 0.251 | 0.190 | |
| p1 = p2 = 6 | δ2 | 0.349 | 0.381 | 0.405 | 0.483 | 0.511 | 0.544 | 0.460 |
| LM1 | 0.146 | 0.153 | 0.158 | 0.165 | 0.180 | 0.198 | 0.163 | |
| LM2 | 0.151 | 0.163 | 0.169 | 0.188 | 0.195 | 0.213 | 0.186 | |
| p1 = p2 = 20 | δ2 | 0.381 | 0.431 | 0.485 | 0.558 | |||
| LM1 | 0.091 | 0.108 | 0.114 | 0.121 | ||||
| LM2 | 0.096 | 0.115 | 0.120 | 0.125 | ||||
We note that the results in Table V confirm those in Table IV: δ2 is much more powerful than the logistic regression approaches. The gain is present for all values of r and all block sizes. The gains are the strongest for the larger block size, which is to be expected as δ2 is better able to exploit the additional variants. The apparent irregularity in this table with respect to the correlation r is caused by the fact that we only fixed the average correlation, and that minor allele frequencies differed between blocks with one value of the correlation and blocks with another value of the correlation. We repeated these simulations also using model IM3 and different values of β. The conclusions are identical (results not shown).
AN APPLICATION TO DATA ON GRAFT VERSUS HOST DISEASE
The IL10 and IL10RB genes are involved in immune regulation and suppression. A genetic polymorphism in the promoter region of IL10 has a significant association with the risk of graft versus host disease (GVHD) after allogeneic hematopoietic stem cell transplantation (HCT) with human leukocyte antigen (HLA) identical sibling donors. In a previous study of SNPs among 953 HLA-identical sibling transplants [Lin et al., 2005], the presence of the IL10 /-592*A allele in the patient or the IL10RB*G allele in the donor was significantly associated with lower risk of severe acute GVHD and non-relapse mortality. It is thought that IL10 may facilitate immune tolerance after allogeneic transplantation. Higher IL10 production by ex-vivo stimulated recipient cells before transplantation is associated with reduced risk of acute GVHD and non-relapse mortality [Holler et al., 2000]. In this example our goal was to see whether an interaction between IL10 and IL10RB has a synergistic effect on the risk for GVHD. We tested this hypothesis using a dataset with two groups, one of which developed GVHD (case) while the other did not (control), with a sample size of 350 for each group. These data originated from a study investigating how genetic diversity among patients and donors contributes to differences in individual responses to tissue injury, inflammation, and severity of acute GVHD. For IL10 five SNPs (rs4845140, rs3024505, rs4844553, rs4311892, and rs1554286) were genotyped in the patients and for IL10RB, five SNPs (rs2248118, rs2244305, rs2834173, rs2850001, and rs1058867) were genotyped in the donors; thus (p1 = p2 = 5) and the corresponding covariance matrix is 10 × 10. Note that the SNPs that were genotyped do not include the same as those studied in [Lin et al., 2005], but all SNPs are in the same haplotype blocks. In the combined data each of the pairwise correlations between an IL10 and an IL10RB is smaller than 0.1.
We applied our proposed statistics δ2 and the two logistic regression methods, LM1 and LM2 for testing whether there is an interaction effect of IL10 and IL10RB on GVHD. The statistic δ2 results in off-diagonal blocks that are statistically significantly different between cases and controls with p = 0.0264. The results for LM1 and LM2 are barely statistically significant, with p = 0.0483 and p = 0.0465 respectively. Thus, our approach gives stronger evidence that there is an interaction with likely biological significance.
DISCUSSION
Classical methods for identifying disease-susceptibility genes focus on one genomic area or locus at a time. They have worked well for Mendelian disorders but appear insufficient for complex traits because of the presumed multiplicity of genes involved. To facilitate the search for sets of SNPs jointly associated with a disease phenotype, we have developed a new statistic for testing for interaction effects between two blocks of SNPs—two genes—based on defining a distance between sample covariance matrices.
A test for equality of the off-diagonal block corresponding to the covariance between the two genes of the two matrices becomes a test of an interaction effect between the two genes on case-control status. Our proposed method avoids the need for a multiple comparisons correction as we have a single test for interaction. We believe that avoiding multiple comparisons is a main reason why our test offers greater power than the traditional method of individual pairwise testing of SNPs.
Simulation results reveal that our method is more powerful than traditional logistic regression-based methods. For the matrix size 2 × 2, where the SNPs that are interacting are observed, the power results for the proposed statistic δ2 and logistic regression behave approximately equally. When we consider multiple SNPs in a gene, and assume that the true causal interacting SNPs are among them, the power is higher for δ2 than for logistic regression (Table III). The scenario in Table IV is the most interesting one, as we eliminate the interaction SNPs for the analysis. Again, here we see that power is much larger for δ2 than logistic regression. In this case we do not observe the causal SNP, but rather the interaction through multiple SNPs that are in LD.
We can easily apply our proposed methods to explore interactions between two loci, where there is gene-gene independence in the controls (in a population with a rare disease), as we would simply set the off-diagonal sub-matrix for the controls equal to zero. Initial simulations suggest this significantly improves power. We are currently working on an extension of our methods that will allow us to test whether many genes—a network of SNPs—associate with a phenotype by comparing two complete covariance matrices. We note here that for all our simulations we generated the interaction effect using a logistic model. The logistic model was, however, not used for identification of the interaction, suggesting some robustness of our approach for the model of the interaction.
As we argued in the introduction, if the covariances between gene 1 and gene 2 are different between cases and controls, there must be an interaction effect of genes 1 and 2 on the disease outcome. An advantage of logistic regression for the situation when both genes have a single marker is that the coefficient in the logistic model is the log of the odds ratio. There is naturally a relation between the difference in the covariances and the magnitude of the odds ratio. See the Appendix 2 for details. We note, however, that for the situation where the genes have multiple markers that are in LD with each other, the multiple estimates of interaction parameters in the logistic model have a higher variance, and may be hard to interpret. Of course if an interaction effect is identified, a follow-up study may be warranted to characterize such an interaction.
To evaluate performance for detection of interactions between two loci, the proposed δ2 statistic was applied to data from hematopoietic cell transplantation (HCT) patients and donors. In this example we wished to distinguish between groups of patients, for example those who developed GVHD and those who did not. Our study population, consisting of paired patients and donors, provided a unique opportunity to assess genome-genome interaction between recipient and donor genomes [Spilianakis et al., 2005]. Using our methods, we confirmed a statistical interaction between these two unlinked loci, a beautiful example of two different chromosomes showing a statistical interaction that aligns with a known biological interaction between different cells, in this case, from two different individuals. This suggests that the pathway involving both the IL10 and IL10RB genes is likely an important player in GVHD.
While computing test statistics for many blocks of SNPs is computationally intensive, it is reasonably achievable by spreading computations over clusters of computers. In practice we would test for interactions between a limited number of blocks of interest, either because there is biological interest (as was the case for our IL10 example), or because these blocks suggest the strongest marginal effects (using a similar approach as Kooperberg and LeBlanc [2008]). Each of these limited numbers of blocks could then be compared with the complete genome in a sliding window fashion. A computationally intense approach would be to carry out permutation tests separately for each possible interaction. Rather than separate permutation tests, we would first “rank” all tests, and only carry out the tests for interactions with the largest statistics, for example using the Holm step down procedure [Drton and Perlman, 2008]. The Box approximation for normally distributed data can be applied to obtain the asymptotic null distribution [Anderson, 2003]. Software implementing our methods will be made available in an R-package.
Our methods can be extended to test for gene-environment interactions. Here, instead of comparing the covariance between two blocks of SNPs, we compare the covariance between a block of SNPs and a block of environmental variables. We can then apply δ2 to detect interaction differences between cases and controls. An advantage of this approach is that multi-level categorical environmental variables (e.g. smoking, which is often coded using two levels, current and former, compared to a reference level of none) can be considered as a block of environmental variables, just like a block of SNPs in one gene is considered jointly. We can also for environmental, non-genetic, variables (or additive components to control stratification, e.g. Price et al. [2006]) as is typically done in traditional regression models. We consider the following approach. Before applying our method, we first regress each of the SNPs considered for the tests, separately on all environmental variables. Then we apply our methods to compare the covariance matrices of the residuals from these regressions. Another possible extension of our approach is to extend the methods to interactions involving three or more blocks of SNPs by replacing S̃ and T̃ in equation (2) by a partition involving multiple blocks. A limitation of our approach is that it does not easily generalize to continuous phenotypes. Another limitation is that, unlike for logistic regression, it does not easily generalize to third and higher order interactions. However, we note that the power to identify higher order interactions is very limited, and in fact, we are not aware of any higher order interactions that have been successfully replicated in other studies.
It is now common practice to impute untyped variants in genome-wide studies. If an untyped variant that is imputed well is in fact the single causal variant in a gene contributing to an interaction, testing this variant may be a powerful approach to identify the interaction. However, as we saw in Case 2 of our simulation study, including additional variants that are in LD with the causal variant improves the power of a study. In addition, not all variants can be imputed well (e.g. variants with low minor allele frequency), and our approach is also applicable to smaller (candidate gene) studies, where there may not be enough typed variants to carry out an imputation.
Novel genomic tools and computational methods have led to a dramatic increase in the rate of discovery of disease genes. While traditional association studies have sought single marker or single gene associations, phenotypes result from complex interactions among large numbers of genes. Extensions of the statistical methods we have proposed will allow the investigation of relationships among groups of SNPs in many genes and can discriminate between the genetic signatures of distinct groups of subjects. By identifying interactions among networks of genes, we may further our understanding of how the collective behavior of genes gives rise to phenotypes as well as our ability to predict disease outcome. Detecting interactions among disease associated SNPs may reveal basic biological mechanisms that are critical to understanding development and progression of a disease state [Hartwell et al., 2006], and in this way provide a powerful and promising foundation for the development of novel diagnostics and therapeutic strategies.
ACKNOWLEDGMENTS
We thank Lindsey Muir for discussion and critical reading of the manuscript.
Contact Grant Sponsors: National Institutes of Health.
Contact grant numbers: T32 CA80416, K25 DK08279, R01 HG006164, P01 CA53996, R01 CA90998.
APPENDIX 1
DERIVATION OF THE TEST STATISTIC
The Nagao [1973] normalized quadratic distance (NQD) is modified as follows:
applied to S̃ and T̃, where
where W = (mS + nT)/(m + n). Here W11 (respectively W22) is the pooled estimate of Σ11 (Σ22) if Σ11 = Ω11 (Σ22 = Ω22) based on S11 and T11 (S22 and T22). To ensure that W is nonsingular with probability 1, it is only required that m + n ≥ p1 + p2 ≕ p. Note too that W = (mS̃ + nT̃)/(m + n).
In general, neither S̃ nor T̃ need be positive definite. Nonetheless, δ2 is a valid measure of distance between S12 and T12 if Σ11 = Ω11 and Σ22 = Ω22 because
Thus δ2 = 0 iff S12 = T12. Furthermore we have the equivalent expressions
where, using symmetric matrix square roots,
Note that L is a symmetric matrix and that
where l1 ≥ ⋯ ≥ lp are the ordered eigenvalues of L, equivalently, the ordered eigenvalues of
APPENDIX 2
AN ADDITIONAL SIMULATION
This is a small simulation to demonstrate the relation between the differences in the covariance and the log-odds parameters in a logistic regression model.
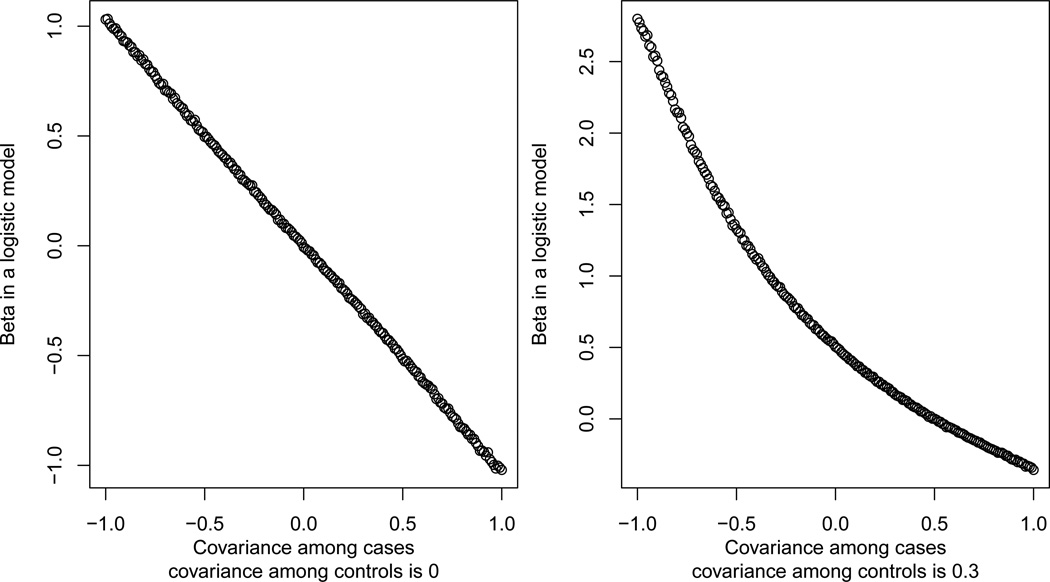
Consider the 2 × 2 covariance matrix . We generated bivariate predictors for 100,000 controls from a multivariate normal distribution with mean 0 and covariance matrix C(0) and for 100,000 cases from a multivariate normal distribution with mean 0 and covariance matrix C(σ), for −1 < σ < 1. We then carried out a logistic regression of case-control status against the two predictors and their interaction. We repeated this calculation with control covariance matrix of C(0.3). In Figure I we show the relation between σ and β in these logistic models. We note that there is a clear relation between these two parameters, which may or may not appear linear.
Fig 1.
Relation between the difference in the covariance and a logistic regression parameter.
REFERENCES
- Anderson TW. An Introduction to Multivariate Statistical Analysis. New York: Wiley; 2003. [Google Scholar]
- Chatterjee N, Kalaylioglu Z, Moslehi R, Peters U, Wacholder S. Powerful Multilocus Tests of Genetic Association in the Presence of Gene-Gene and Gene-Environment Interactions. Am J Hum Genet. 2006;79:1002–1016. doi: 10.1086/509704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chaudhuri S, Perlman MD. Two step-down tests for equality of covariance matrices. Linear Algebra and its Applications. 2006;417:42–63. [Google Scholar]
- Cordell HJ. Detecting gene-gene interactions that underlie human diseases. Nat Rev Genet. 2009;10:392–404. doi: 10.1038/nrg2579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crosslin DR, Qin X, Hauser ER. Assessment of LD matrix measures for the analysis of biological pathway association. Stat Appl Gen Mol Biol. 2010;9:35. doi: 10.2202/1544-6115.1561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- D’Angelo G, Rao D, Gu CC. Combining least absolute shrinkage and selection operator (LASSO) and principal-components analysis for detection of gene-gene interactions in genome-wide association studies. BMC Proceedings. 2009;3(Suppl 7):S62. doi: 10.1186/1753-6561-3-s7-s62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dickson SP, Wang K, Hakornarson H, Goldstein DB. Rare variants create synthetic genome-wide associations. PLoS Biology. 2010;8 doi: 10.1371/journal.pbio.1000294. e1000294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drton M, Perlman M. T Multiple testing and error control in Gaussian graphical model selection. J Statist. Sci. 2007;22:430–449. [Google Scholar]
- Hartwell L, Hood L, Goldberg M, Reynolds N, Silver L, Veres R. Genetics: from genes to genomes. Columbus: McGraw-Hill; 2006. [Google Scholar]
- Holler E, Roncarolo MG, Hintermeier-Knabe R, Eissner G, Ertl B, Schulz U, Knabe H, Kolb HJ, Andreesen R, Wilmanns W. Prognostic significance of increased IL-10 production in patients prior to allogeneic bone marrow transplantation. Bone marrow transplantation. 2000;25:237–241. doi: 10.1038/sj.bmt.1702126. [DOI] [PubMed] [Google Scholar]
- Kooperberg C, LeBlanc M. Increasing the power of identifying gene × gene interactions in genome-wide association studies. Genet Epidemiol. 2008;32:255–263. doi: 10.1002/gepi.20300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kooperberg C, LeBlanc M, Dai JY, Rajapakse I. Structures and assumptions: Strategies to harness gene × gene and gene × environment interactions in GWAS. Stat Science. 2009;24:472–488. doi: 10.1214/09-sts287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewontin RC. The Interaction of Selection and Linkage. I. General Considerations; Heterotic Models. Genetics. 1964;49:49–67. doi: 10.1093/genetics/49.1.49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li J, Tang R, Biernacka JM, de Andrade M. Identification of gene-gene interactions using principal components. BMC Proc. 2009;3:S78. doi: 10.1186/1753-6561-3-s7-s78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin M-T, Storer B, Martin PJ, Tseng L-H, Grogan B, Chen P-J, Zhao LP, Hansen JA. Genetic variation in the IL-10 pathway modulates severity of acute graft-versus-host disease following hematopoietic cell transplantation: synergism between IL-10 genotype of patient and IL-10 receptor {beta} genotype of donor. Blood. 2005;106:3995–4001. doi: 10.1182/blood-2004-11-4338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marchini J, Donnelly P, Cardon LR. Genome-wide strategies for detecting multiple loci that influence complex diseases. Nat Genet. 2005;37:413–417. doi: 10.1038/ng1537. [DOI] [PubMed] [Google Scholar]
- Millstein J, Conti DV, Gilliland FD, Gauderman WJ. A Testing Framework for Identifying Susceptibility Genes in the Presence of Epistasis. Am J Hum Genet. 2006;78:15–27. doi: 10.1086/498850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagao H. On Some Test Criteria for Covariance Matrix. The Annals of Statistics. 1973;1:700–709. [Google Scholar]
- Nielsen DM, Ehm MG, Zaykin DV, Weir BS. Effect of Two- and Three-Locus Linkage Disequilibrium on the Power to Detect Marker/Phenotype Associations. Genetics. 2004;168:1029–1040. doi: 10.1534/genetics.103.022335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price AL, Patterson NJ, Plenge RM, Weinblatt ME, Shadick NA, Reich D. Principal components analysis corrects for stratification in genome-wide association studies. Nat Genet. 2006;38:904–909. doi: 10.1038/ng1847. [DOI] [PubMed] [Google Scholar]
- Ritchie MD, Hahn LW, Roodi N, Bailey LR, Dupont WD, Parl FF, Moore JH. Multifactor-dimensionality reduction reveals high-order interactions among estrogen-metabolism genes in sporadic breast cancer. Am J Hum Genet. 2001;69:138–147. doi: 10.1086/321276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruczinski I, Kooperberg C, LeBlanc M. Logic Regression. J Comp and Grap Stat. 2003;12:475–511. [Google Scholar]
- Schaid DJ. Linkage Disequilibrium Testing When Linkage Phase Is Unknown. Genetics. 2004;166:505–512. doi: 10.1534/genetics.166.1.505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spilianakis CG, Lalioti MD, Town T, Lee GR, Flavell RA. Interchromosomal associations between alternatively expressed loci. Nature. 2005;435:637–645. doi: 10.1038/nature03574. [DOI] [PubMed] [Google Scholar]
- Stephens M, Smith NJ, Donnelly P. A New Statistical Method for Haplotype Reconstruction from Population Data. Am J Hum Genet. 2001;68:978–989. doi: 10.1086/319501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The International HapMap Consortium. A haplotype map of the human genome. Nature. 2005;437:1299–1320. doi: 10.1038/nature04226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang T, Ho G, Ye K, Strickler H, Elston RC. A partial least-square approach for modeling gene-gene and gene-environment interactions when multiple markers are genotyped. Genet Epidemiol. 2009;33:6–15. doi: 10.1002/gepi.20351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X, Elston RC, Zhu X. The meaning of interaction. Hum Hered. 2010;70:269–277. doi: 10.1159/000321967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weir BS. Genetic data analysis II. Sunderland, MA: Sinauer Associates; 1996. [Google Scholar]
- Weir BS, Cockerham CC. Complete characterization of disequilibrium at two loci. In: W.Feldman M, editor. Mathematical Evolutionary Theory. Princeton University Press; 1989. pp. 86–110. [Google Scholar]
- Weir BS, Hill WG, Cardon LR. Allelic association patterns for a dense SNP map. Genet Epidemiol. 2004;27:442–450. doi: 10.1002/gepi.20038. [DOI] [PubMed] [Google Scholar]
- Wu J, Devlin B, Ringquist S, Trucco M, Roeder K. Screen and clean: a tool for identifying interactions in genome-wide association studies. Genet Epidemiol. 2010;34:275–285. doi: 10.1002/gepi.20459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zaykin DV. Bounds and normalization of the composite linkage disequilibrium coefficient. Genet Epidemiol. 2004;27:252–257. doi: 10.1002/gepi.20015. [DOI] [PubMed] [Google Scholar]
- Zaykin DV, Meng Z, Ehm MG. Contrasting linkage-disequilibrium patterns between cases and controls as a nove association-mapping methods. m J Hum Genet. 2006;78:737–746. doi: 10.1086/503710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang X, Pan F, Xie Y, Zou F, Wang W. COE: A General Approach for Efficient Genome-Wide Two-Locus Epistasis Test in Disease Association Study. J Comp Bio. 2010;17:401–415. doi: 10.1089/cmb.2009.0155. [DOI] [PubMed] [Google Scholar]
- Zhao J, Jin L, Xiong M. Test for Interaction between Two Unlinked Loci. Am J Hum Genet. 2006;79:831–845. doi: 10.1086/508571. [DOI] [PMC free article] [PubMed] [Google Scholar]