DRIFT PROMOTES SPECIATION BY SEXUAL SELECTION

Abstract

Quantitative genetic models of sexual selection have generally failed to provide a direct connection to speciation and to explore the consequences of finite population size. The connection to speciation has been indirect because the models have treated only the evolution of male and female traits and have stopped short of modeling the evolution of sexual isolation. In this article we extend Lande’s (1981) model of sexual selection to quantify predictions about the evolution of sexual isolation and speciation. Our results, based on computer simulations, support and extend Lande’s claim that drift along a line of equilibria can rapidly lead to sexual isolation and speciation. Furthermore, we show that rapid speciation can occur by drift in populations of appreciable size (N_e ≥ 1000). These results are in sharp contrast to the opinion of many researchers and textbook writers who have argued that drift does not play an important role in speciation. We argue that drift may be a powerful amplifier of speciation under a wide variety of modeling assumptions, even when selection acts directly on female mating preferences.

Although quantitative genetic models of sexual selection have illuminated many evolutionary phenomena, they have generally failed to make explicit predictions about speciation. The list of illuminated phenomena includes runaway dynamics (Lande 1981), the “sexy son” hypothesis (Kirkpatrick 1985; Pomiankowski et al. 1991), good genes (Schluter and Price 1993; Kirkpatrick 1996; Iwasa and Pomiankowski 1999), and sexual conflict (Gavrilets 2000; Gavrilets et al. 2001, Gavrilets and Hayashi 2005). The fact that rapid evolution of sexual signals occurs under some conditions in most models in this family implies a strong connection to speciation. Furthermore, the existence of equilibrium lines or cycles in some models carries the implication that pairs of replicate populations could speciate as a consequence of equilibrium differences in sexual signals (Mead and Arnold 2004). Despite the apparent clarity of these implications about speciation, the models in question stop short of actually modeling the approach to speciation. In particular, most quantitative genetic models have provided only speculations about the extent of speciation because they have failed to make explicit the connection to sexual isolation.

The reason for the disconnect between quantitative genetic models of sexual selection and speciation is that the models have primarily considered evolution within single populations, and they have failed to specify the relationship between trait evolution and sexual isolation among populations. To successfully make the needed connection, a model must sample pairs of evolving populations and assess their sexual isolation. The primary, novel aim of this article is to make explicit statements about the evolution of sexual isolation by combining a model for evolution by sexual selection (Lande 1981) with a model for sexual isolation (Arnold et al. 1996). As a result, we can quantitatively describe the conditions that can lead to speciation by sexual isolation in terms of estimable parameters of selection, inheritance, and population size.

Translating the output of models of sexual selection into the currency of speciation (the extent of reproductive isolation) is important for three reasons. First, by explicitly modeling the time course of evolving sexual isolation, we will show that drift can help promote speciation in only a thousand generations. Furthermore, histories in which periods of increasing isolation alternate with periods of decreasing isolation are common in our simulations. This pattern, in which isolation waxes and wanes, has far-reaching implications but is seldom discussed in the speciation literature. Second, the needed translation connects the literature on sexual selection models (Mead & Arnold 2004) with an extensive empirical literature on sexual isolation. By modeling the evolution of sexual isolation—and not just divergence in sexually selected traits—we can compare our theoretical results with patterns of sexual isolation observed in major empirical surveys (Tilley et al. 1990; Coyne and Orr 1997). In particular, we show that under realistic values of inheritance, selection, and population size, drift could have played an important role in producing the patterns of sexual isolation (and hence speciation) that have been observed in radiations of plethodontid salamanders and Drosophila. Third, the approach we outline promises a solution to the long-standing, notorious problem of constructing discriminating tests among the many alternative models of sexual selection (Bradbury and Andersson 1987). By establishing a new model-data connection, we should be able to test sexual selection models using the predictions they make about patterns of sexual isolation, a possibility that we will explore in a later article.

A surprising limitation of most quantitative genetic models of sexual selection is that they fail to explore the evolutionary stochasticity that arises from finite population size. By assuming infinite population size, most models make predictions about the expected evolutionary behavior of the average population, while ignoring variation about that expectation. This limitation characterizes virtually all of the 30 models of sexual selection reviewed by Mead and Arnold (2004). The problem is that by ignoring such stochastic variation we may miss the essential message of the model. For example, although the deterministic equilibrium for a model may be a point in phenotypic trait space, stochasticity (i.e., genetic drift) may produce a considerable cloud of variable outcomes about that point. A focus on the cloud is important because, as we will show, stochasticity can amplify the opportunity for sexual isolation and speciation. Consequently, our secondary aim is to explore the implications of finite population size for the evolution of sexual isolation and speciation. Lande (1981) provided a foundation for this exploration in the form of equations for the variance expected among evolving replicate populations in sexual signals and preferences. Nevertheless, Lande (1981) did not explore the stochastic evolution of sexual isolation. We use computer simulations to assess the validity of some of Lande’s approximations, as well as to make detailed portrayals of the stochastic evolution of sexual isolation. Although we focus our combined analytical and simulation approach on a single evolutionary model (Lande 1981), we argue that this approach could be profitably applied to any of the 30 quantitative genetic models of sexual selection that have been constructed so far (Mead and Arnold 2004).

Theoretical Background

We used a model developed by Lande (1981) to simulate the evolution of behavioral isolation by sexual selection in finite populations. According to this model, evolution of a male ornamental trait is driven by natural and sexual selection. Female mating preferences for that male trait evolve as a correlated response. The male ornament, z, and female preference, y, are normally distributed, sex-limited quantitative traits with phenotypic means z̄ and ȳ and variances σ² and τ². Likewise, the additive genetic (breeding) values of the two traits are normally distributed. The additive genetic variances of both the male ornament (G) and female preference (H) are assumed to be in mutation–selection balance and to remain approximately constant (Lande 1976). Additive genetic covariance between the male ornament and female preference (B) is created by linkage disequilibrium that arises from mate choice and sexual selection and is likewise assumed to remain approximately constant in mutation–selection balance (Lande 1980, 1981). Males do not protect or provision mates. Every female is inseminated each generation, and hence there is no fecundity selection on female preference nor is there any direct viability selection on preference. The male ornament experiences weak natural (viability) selection, described by a Gaussian curve with an intermediate optimum θ and width ω. Following viability selection, the male trait distribution experiences sexual selection arising from female mate choice. The sexual preference of each female is described by a Gaussian curve with an intermediate optimum y and width ν. In other words, a female’s preference is absolute in the sense that she most prefers to mate with a male with ornament value y, and her tendency to mate falls off as the ornament of a prospective mate deviates in either direction from that value. The overall selection gradient on the male trait (β) is therefore generated by natural selection towards an optimal male phenotype and sexual selection generated by Gaussian mating preference functions

$$\beta =\frac{S}{{\sigma }^2}=\frac{\overline{y}/\alpha -(1+1/\alpha )\overline{z}+\theta }{{\omega }^2},$$

where S is the total shift in the male trait mean caused by selection within a generation (the overall selection differential) and α = ν²/ω². Because there is no direct selection on the female preference trait y, it evolves by genetic drift and as a correlated response to selection on the male trait. At equilibrium the forces of natural and sexual selection balance (β = 0) yielding a line of equilibrium given by the equation

$$\overline{y}=(\alpha +1)\overline{z}+\alpha \theta .$$

The per generation deterministic change in the means of the male ornament and the female preference is given by the equations

$$\Delta \overline{z}=\frac{1}{2}G\beta ,$$ (1a)

$$\Delta \overline{y}=\frac{1}{2}B\beta .$$ (1b)

Away from the line of equilibrium, populations evolve in response to selection along lines with a slope given by the genetic regression B/G. Populations evolving in response to selection either walk-towards a line of stable equilibrium (when B/G < α + 1) or runaway from a line of unstable equilibrium (when B/G > α+ 1). In this article we explore the stable (walk-towards) case, the most likely outcome in many natural systems (Mead and Arnold 2004). Selection ceases once a population reaches the stable line of equilibrium, but the population may drift along the line and will be driven back to the line by selection if it drifts away from the line.

Lande (1981) also characterized the process of population differentiation by drift along the line of equilibrium. Let the population mean phenotype be a column vector, (z̄ ȳ)^T, where T denotes transpose. Each generation sampling in a finite population of effective size N_e will produce variance among a set of replicate populations in this vector that is given by the variance–covariance matrix

$$V=\frac{1}{N_e}\left(\begin{array}{cc}G\hfill & B\hfill \\ B\hfill & H\hfill \end{array}\right).$$ (2)

At any generation t, the probability distribution of mean phenotypes is bivariate Gaussian. Using a diffusion approximation, Lande (1981) found that the variance–covariance matrix for this distribution at generation t converges to approximately

$$\mathbf{D}(t)=\frac{H(1-r_g^2)t}{N_e{(\alpha +1-B/G)}^2}\left(\begin{array}{cc}1\hfill & \alpha +1\hfill \\ \alpha +1\hfill & {(\alpha +1)}^2\hfill \end{array}\right),$$ (3)

where $r_g=B/\sqrt{\mathit{\text{GH}}}$ is the additive genetic correlation between the male ornament and female mating preference. The diagonal elements in this matrix are the among-replicate variances in trait means (male ornament and female preference). The off-diagonal element is the among-replicate covariance between male and female trait means. Note that the correlation in the matrix on the right-hand side of equation (3) is 1, so the evolutionary dynamics are equivalent to univariate evolution along the line of equilibrium. Consequently, one issue that we can resolve with simulation is the question of how much additional variance might be contributed by drift away from, and response to selection back towards, the line of equilibrium. As we will see, the contribution is negligible. In the next section we extend the Lande (1981) model so that it makes explicit predictions about sexual isolation.

A pair of replicate populations, A and B, can diverge in average phenotype and hence become sexually isolated as their mean male and female trait values are shuffled towards and along a line of equilibrium by selection and drift. In any given generation, sexual isolation can be assessed by calculating the average probability of mating within and between populations A and B given the means and variances for male ornaments and female preferences in the two populations. Formulas are derived in Arnold et al. (1996) under Lande’s (1981) assumptions for the case of absolute mating preferences. In extending Lande’s (1981) model to make predictions about sexual isolation, we assume that either just two traits, z and y, account for sexual isolation, or that z and y represent linear combinations of many male and female traits that jointly account for sexual isolation. Under the second interpretation, we assume that the coefficients of the linear combinations do not evolve.

The probability that a randomly chosen female will mate with a male of phenotype z, ψ (z), is a key female variable in this formulation. Averaging this probability over the phenotypic distribution of males yields the average probability of mating, π, given an encounter between a male randomly chosen from one population and a female randomly chosen from the same or a different population. This conditional probability, π, coincides with the probability of mating that is commonly assessed in studies of sexual isolation (e.g., Malogolowkin-Cohen et al. 1965), thereby providing a direct connection between sexual selection models and empirical data on sexual isolation. This overall probability of mating, π, reaches a maximum value when the mean of the male trait, z̄, coincides with mean value of mates most preferred by females, ȳ, and falls off as a Gaussian curve as the male mean deviates in either direction from the female mean. More exactly, the average probability of mating when the female is drawn from population i and the male from population j is

$${\pi }_{\mathit{\text{ij}}}=c_{\mathit{\text{ij}}}\text{exp}(-d_{\mathit{\text{ij}}}^2/2{\mathrm{\Sigma }}^2),$$ (4)

where 0 ≤ c_ij ≤ 1 is the distance between the mean of the most preferred mate of females in population i and the mean of the male trait in population j, d_ij = ȳ_i − z̄_j, and Σ² = τ² + υ² + σ². Thus, this expression can be used to calculate the average probabilities of mating in encounters within and between populations. The constant c_ij can be thought of as the probability of mating between partners when the male and female means coincide. For simplicity, we assume that c_ij = 1 for all combinations of population encounters. Note that the probability given in equation (4) is the overall probability of mating given an encounter between potential partners drawn randomly from populations i and j, and not necessarily the frequency of matings within and between populations over a generation.

Total sexual (joint) isolation between populations A and B can be calculated as

$$\mathit{\text{JI}}={\pi }_{\mathit{\text{AA}}}+{\pi }_{\mathit{\text{BB}}}-{\pi }_{\mathit{\text{AB}}}-{\pi }_{\mathit{\text{BA}}}.$$ (5)

JI is a conventional measure of sexual isolation that effectively ranges from zero (when all within and between population encounters are equally successful) to two (when all within population encounters are successful but all between populations encounters are not) (Bateman 1949; Merrell 1950; Malogolowkin-Cohen et al. 1965). Because JI does not involve ratios of variables, it has smaller standard errors than some other measures of isolation. A more complete illustration of the dynamics of Lande’s (1981) model and its relationship to JI in our simulation model is available at the website http://oregonstate.edu/%uyedaj/sexualselection.html.

We can also obtain an expression for the expected value of JI under Lande’s (1981) assumptions. Because the difference between z̄ and ȳ within populations is expected to be negligible compared to the corresponding difference between populations, we can make the simplifying assumption that d_AA = d_BB = 0. This simplification yields π_AA = π_BB = 1 and π_AB = π_BA. Thus, the key probability affecting the distribution of JI is the distribution of interpopulation mating probabilities (π_AB and π_BA). The distributions of these probabilities are identical and simply a function of the distribution of male phenotype among replicate populations at generation t, which can in turn be obtained using Lande’s dispersion matrix equation (3). Using the distribution function method, we can derive the probability density function (PDF) of π_AB at generation t (Appendix), so that the probability that π_AB takes the value x at generation t is

$$f{\pi }_{\mathit{\text{AB}}}(x)=\frac{{\mathrm{\Sigma }}^2{x}^{{\mathrm{\Sigma }}^2/2D_z(t)}}{x\sqrt{-2\pi D_z(t){\mathrm{\Sigma }}^2\text{ln}(x)}},\text{for}0\le x\le 1,$$ (6)

where D_z(t) is the variance of z̄ among replicate populations at generation t as approximated by the first element of Lande’s dispersion matrix D(t) (eq. 3). Although this density function in equation (6) is not well characterized, it can be evaluated numerically. Assuming that the within population mating probabilities are close to 1, the expected value of JI at generation t is 2(1 − E[π_AB(t)]), where E[π_AB(t)] is the expected value of π_AB at generation t, which is obtained from equation (6).

Methods

THE SIMULATION MODEL

We simulated the evolution of trait means in 10,000 independent replicate population pairs for 1000–10,000 generations for each of 324 parameter combinations in a fully factorial design. Each replicate consisted of a pair of populations that started at the same point on the line of equilibrium, the natural selection optimum for the male trait (z̄ = ȳ = θ). For convenience and without loss of generality, we scaled z so θ = 0. Note that this scaling convention does not imply that there is an absence of the male ornament at the optimum, θ. Each generation, we calculated the total deterministic response to selection in each population using equation (1). Following selection, the per generation change due to drift was sampled from a bivariate normal distribution with zero means and a variance–covariance matrix given by equation (2) and added to the selection response. After 1,000 and 10,000 generations, we calculated JI for each population pair to generate a distribution of 10,000 replicate values of JI. The mean and variance of JI and the proportion (P_i) of JI values greater than 1.6 (see below) were obtained from this distribution. All simulations and analyses were performed in R (R Development Core Team 2007).

Wherever possible we made benign and/or biologically realistic choices of parameter values. We standardized the phenotypic variances of the two traits before selection, so that σ² = τ² = 1. We simulated all combinations of cases in which natural selection was relatively weak (ω² = 25, 50, and 100) and sexual selection was relatively strong (ν² = 5, 10, and 20), so that α = ν²/ω² ranged from 0.05 to 0.8. The values of ω² that we used correspond to the weak end of a distribution of values for stabilizing selection estimated in natural populations (Kingsolver et al. 2001; Estes and Arnold 2007). Stinchcombe et al. (2008) have pointed out a common error in the estimation of coefficients of stabilizing/disruptive selection (γ). The range of ω² values that we used corresponds to a γ range of −0.04 to −0.01, assuming no directional selection (β = 0), which is well within the span of true values of γ reported by Stinchcombe et al. (2008) and, indeed, at the commonly observed, weak end of the stabilizing selection distribution. (See Estes and Arnold (2007) for the formula we used to convert between γ and ω².) Measurements of female preference functions are rarer than estimates of stabilizing selection, but nevertheless, studies of acoustic insects and amphibians (Gerhardt and Huber 2002) suggest that when preference functions are unimodal, curvature is weak compared with the distribution of male trait values (i.e., ν² > σ²). We varied G and H so that the genetic correlation between ornament and preference was in the moderate-to-high range $(r_g=B/\sqrt{\mathit{\text{GH}}}=0.6-0.9)$. Parameter values in this range are consistent with selection experiments in which a substantial correlated response in female preferences was detected after just a few generations of selection on male ornaments (Bakker 1993; Houde 1994; Wilkinson and Reillo 1994; Hollocher et al. 1997; Blows 1999; Gray and Cade 2000;Wagner et al. 2001). Finally, we used moderate to relatively large effective sizes (N_e = 500, 1000, 5000) to be consistent with empirical estimates (Estes and Arnold 2007) and to satisfy the assumption that genetic variances and covariances would be maintained by mutation–selection balance (Lande 1976, 1981).

In evaluating our results, we used a value of JI > 1.6 as a criterion for substantial sexual isolation. In a survey of sexual isolation in Drosophila, Coyne and Orr (1997) used one minus the ratio of the frequencies of heterospecific to homospecific matings as a measure of sexual isolation and found that in a strong majority of sympatric species the value of this index was 0.8 or higher. Assuming that π_AA = π_BB = 1, a value of 0.8 for their index corresponds to JI = 1.6. Likewise, in a survey of sexual isolation among 31 allopatric pairs of populations of salamanders in the Desmognathus ochrophaeus complex, JI ranged from 0.20±0.16 to 1.50 ± 0.12 (Arnold et al. 1996), again suggesting that JI = 1.6 is an appropriate criterion for substantial isolation.

In addition to the full simulation model, we used Lande’s diffusion approximation (Lande 1981, eq. 3) and the PDF of π_AB, equation (6), to generate distributions of JI for the same set of parameter combinations. These distributions were compared to the full simulation model to verify the accuracy of the simplifying assumptions used to derive equations (3) and (6). Methods are described in more detail in Supporting Appendix S1.

Results

SIMULATED EVOLUTION OF SEXUAL ISOLATION

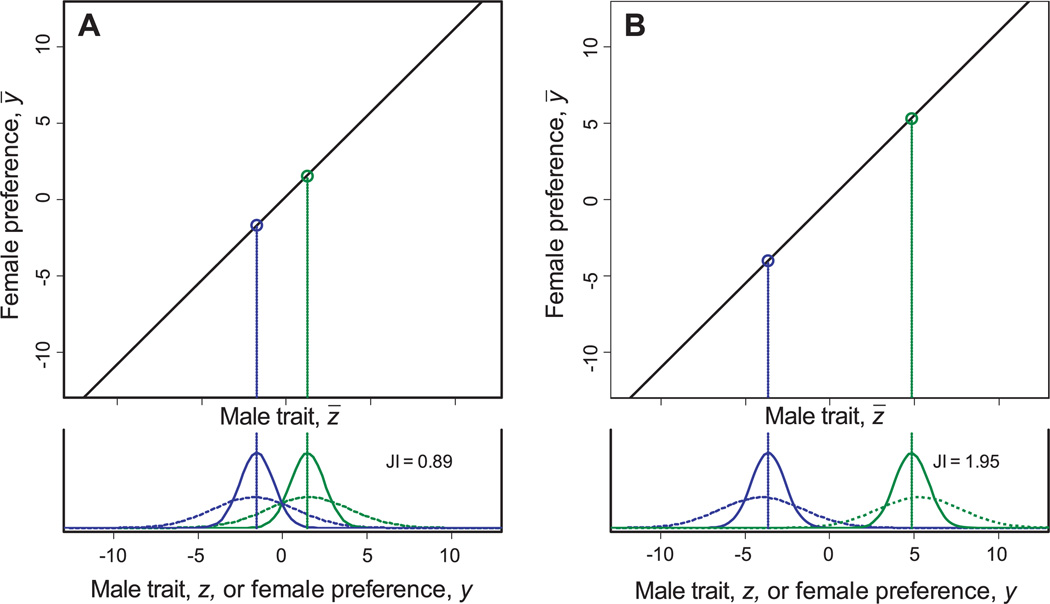
Simulations of the evolution of a male trait and female preference based on Lande’s (1981) model show that drift promotes rapid divergence in sexually selected traits. The model predicts a line of neutral equilibrium for the population means of the male trait, z̄, and female preference, ȳ, along which the forces of natural and sexual selection on the male trait exactly balance (Fig. 1). This equilibrium line is either stable or unstable, depending on parameters of genetic variance in the two traits and the strength of natural and sexual selection (Lande 1981). Here we consider only biologically realistic parameter values for which the line of equilibrium is stable; that is, populations that drift away from the line evolve back towards it. Independent populations evolve along the line by genetic drift, so that two populations may diverge from each other along the line of equilibrium. As the male trait distribution in one population diverges from the female preference in the other population, the probability of mating between populations decreases. We estimate the degree of sexual isolation between two populations by the joint isolation index (JI). Figure 1 illustrates an instance of modest isolation (Fig. 1A, JI = 0.89) and an instance of profound isolation (Fig. 1B, JI = 1.95). The time course for evolution of isolation in a sample run can be viewed at http://oregonstate.edu/~uyedaj/sexualselection.html.

Figure 1.

Sexual isolation between populations that have diverged along the line of equilibrium. The axes represent population means for a male trait and female preference. The upper portion of each graph shows the line of equilibrium predicted by the model. The lower portion of each graph shows the distributions in two independent populations of the male trait (solid lines) and the population-level average female preference (dashed lines). The scale in both portions is in units of within population phenotypic standard deviation of the male trait. (A) Two populations that have experienced modest divergence lie relatively close to each other on the line of equilibrium, resulting in a modest level of sexual isolation (JI = 0.89). (B) The two populations have experienced appreciable divergence, resulting in almost maximal sexual selection (JI = 1.95). Parameter values for this example are: σ² = 1, τ² = 1, and ν² = 5.

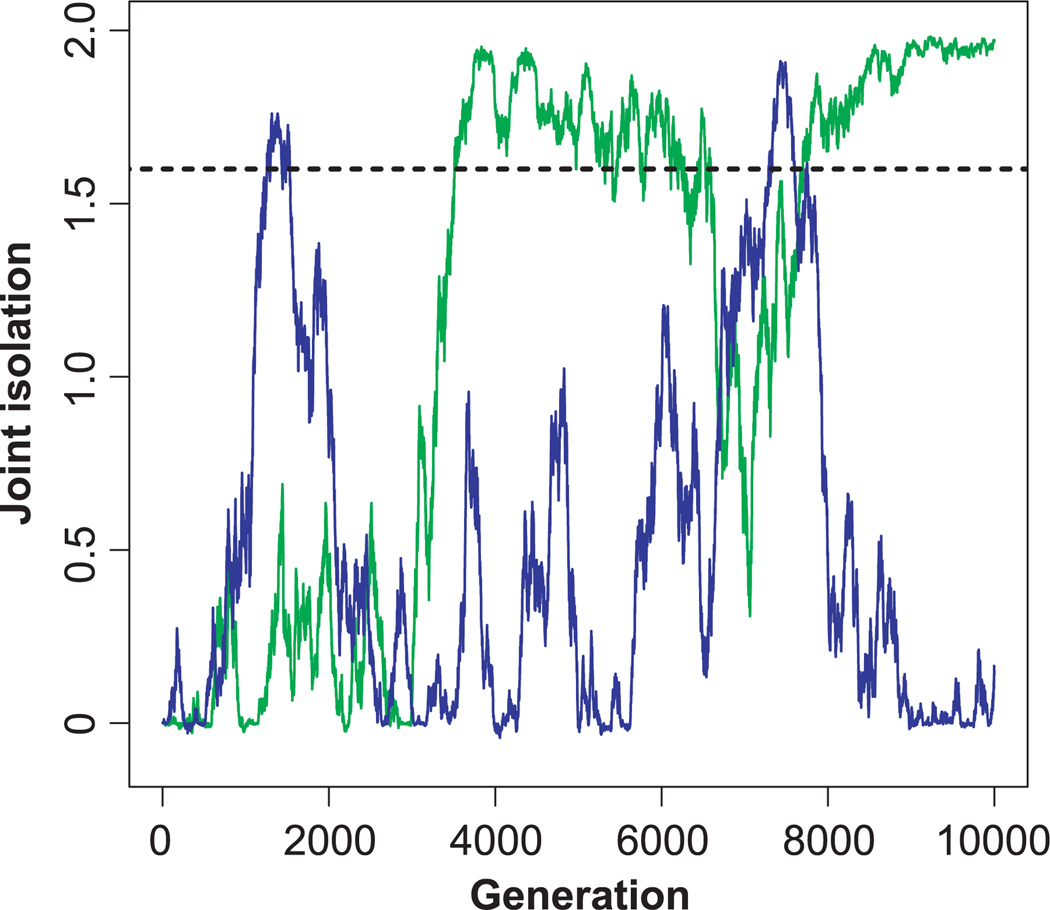
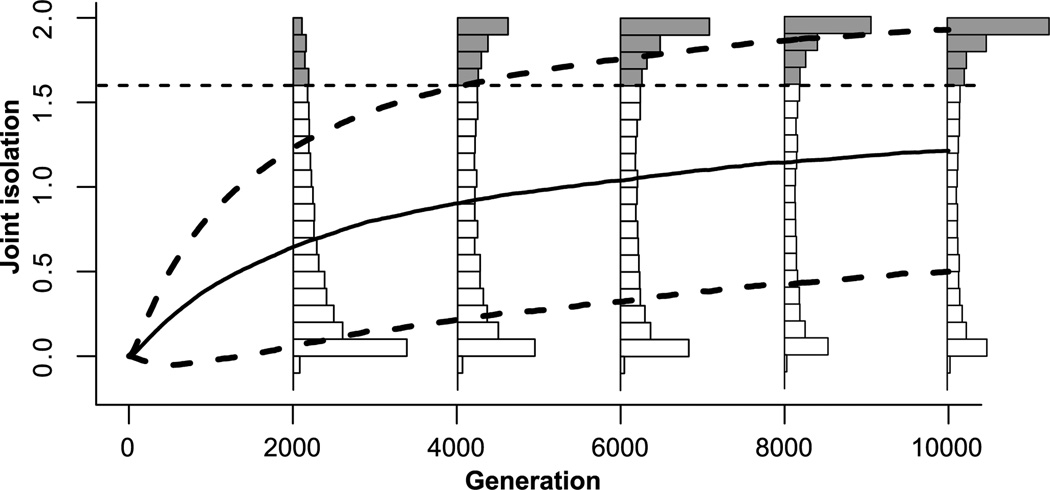
Because drift along the line of equilibrium is a random walk process, the trajectories of population pairs usually do not show a monotonic increase in sexual isolation. Instead, simulated pairs of populations may experience temporary periods of substantial sexual isolation (i.e., JI > 1.6) and then return to a level of isolation that in sympatry would allow interbreeding (Fig. 2). Nonetheless, the variance of trait values among independently evolving populations increases with time (eq. 3). As a result, both the mean value of JI across a large number of simulated population pairs and the proportion of pairs of populations at sexual isolation (JI > 1.6) increase monotonically under biologically realistic parameter values, as shown in Figure 3. The change from a unimodal to a bimodal distribution of JI, apparent in Figure 3, is characteristic of simulations under realistic parameter values resulting from the fact that JI is bounded at 2. Given enough time, the proportion of pairs of populations at complete isolation (i.e., π_AB = π_BA = 0, JI ≈ 2) asymptotically approaches 1 for all parameter values for which D > 0.

Figure 2.

Two examples of simulated evolutionary trajectories for sexual isolation. Joint isolation index (JI) is shown as a function of time for two pairs of populations (shown in blue and green). JI waxes and wanes as the populations drift away from or towards each other along the line of equilibrium. The horizontal dotted line corresponds to JI = 1.6, which may be considered a substantial level of sexual isolation (see text). Parameter values are: G = H = 0.6, γ = 0.7, N_e = 1000, ω² = 50, ν² = 5 (see text for explanation of parameters).

Figure 3.

Distribution of joint isolation (JI) in 10,000 independent pairs of populations over 10,000 generations of simulated evolution, showing mean isolation (solid line) and standard deviation (dashed lines). Histograms show the distribution of JI at 2000-generation intervals, with shaded bars indicating substantial sexual isolation (JI > 1.6). Note that JI ranges from 0 to 2 and is bimodally distributed at and beyond generation 4000. The proportion of replicates with JI > 1.6 increased from 9.1% in generation 2000, to 44.5% at generation 10,000. Parameter values as in Figure 2.

EFFECTS OF POPULATION SIZE, INHERITANCE, AND SELECTION ON THE EVOLUTION OF SEXUAL ISOLATION

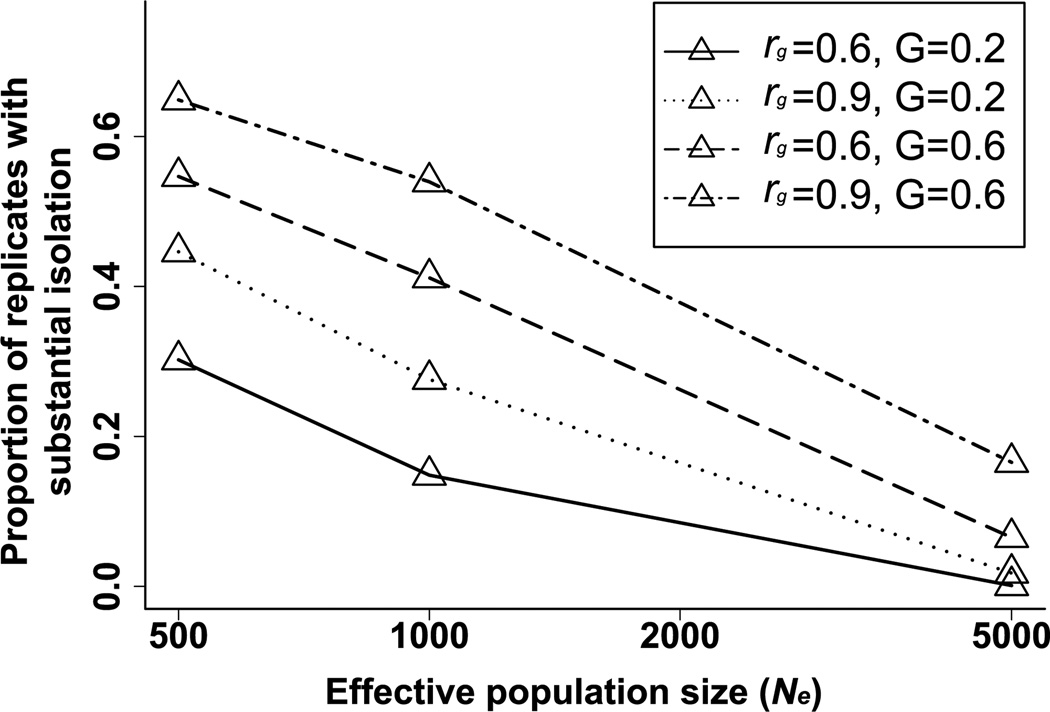
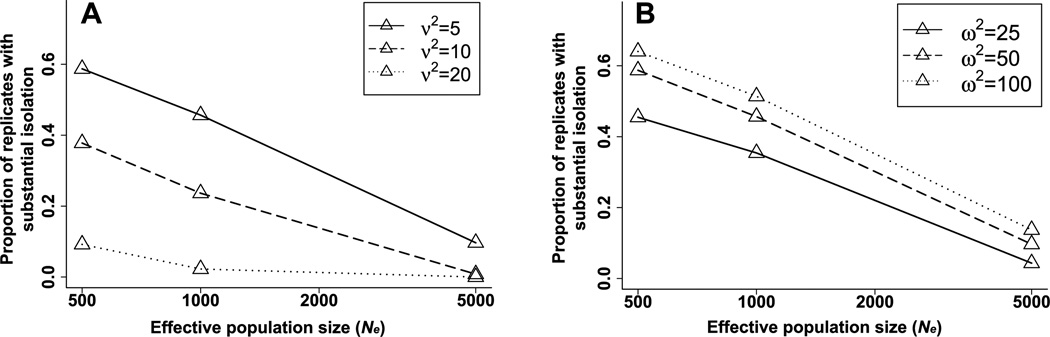
The evolution of sexual isolation depends on parameters of inheritance, population size, and selection, and we will consider their effects in that order. In light of the fact that the distribution of JI is often bimodal (Fig. 3), we used the proportion of replicate pairs that achieved a substantial level of isolation (JI > 1.6) as a summary measure of isolation for a set of replicate runs. In the discussions that follow, note that because we have standardized phenotypic variance of the male and female traits to 1, their additive genetic variances, G and H, are equivalent to heritabilities. In our simulations, evolution of sexual isolation by drift increased as either the genetic variance of the male trait, G, or the genetic correlation between the male and female trait, r_g, increased (Fig. 4). Not surprisingly, because genetic drift depends on effective population size, sexual isolation by drift decreased with increasing effective population size for all parameter combinations. As a result, at large population sizes the effect of inheritance parameters was reduced because relatively few population pairs evolved substantial isolation.

Figure 4.

Effect of inheritance and population size on the evolution of sexual isolation. The proportion of simulated pairs of populations with substantial isolation (JI > 1.6) is shown as a function of effective populations size (N_e) for different values of additive genetic variance of the male trait (G) and genetic correlation between the male trait and female preference (γ). The results are for 10,000 replicate pairs after 10,000 generations of evolution by drift. Values of other parameters: H = G, γ² = 50, ν² = 5.

Evolution of sexual isolation also depends on the strength of both natural and sexual selection on the male trait. Stronger natural selection on the male trait (lower values of ω²) reduces the evolution of sexual isolation by reducing the rate of drift along the line of equilibrium (Fig. 5A), as predicted by equation (3). In contrast, stronger sexual selection (lower values of ν²) increases the evolution of sexual isolation by drift (Fig. 5B) for two reasons. First, stronger sexual selection increases the variance among populations caused by drift along the line of equilibrium, as predicted by equation (3). Second, stronger sexual selection reduces the probability of mating between two populations, equation (4), given a particular difference in their male trait means.

Figure 5.

Effects of population size and selection on the evolution of sexual isolation. The proportion of simulated pairs of populations with substantial isolation (JI > 1.6) is shown as a function of effective populations size (N_e) for (A) different strengths of natural selection on the male trait (ω²; larger values indicate weaker selection) and (B) different strengths of sexual selection on the male trait (ν²; larger values indicate weaker selection). The results are for 10,000 replicate pairs after 10,000 generations of evolution by drift. Other parameter values as in Figure 2.

These effects of inheritance, selection, and population size on the evolution of sexual isolation are shown in greater detail in Table 1. Note that substantial sexual isolation can evolve by drift even in very large populations in only 1000 generations. In an especially favorable case (r_g = 0.9, ω² = 100, ν² = 5, α = 0.05), 11% of population pairs of effective size 1000 evolved substantial isolation after only 1000 generations, and after 10,000 generations 64% had achieved substantial isolation. Such very rapid evolution is exceptional, however, and in general substantial isolation commonly evolves only after 5000 or more generations.

Table 1.

The percentage of replicate population pairs evolving substantial isolation by drift as a function of population size, inheritance, and selection in simulations of Lande’s (1981) model. The proportion of replicate pairs of populations with substantial isolation (JI>1.6) shown in each cell represent the summary of 10,000 pairs of replicate populations after 1000 or 10,000 generations of evolution See text for explanation of parameters and justification for choices of parameter values.

				After 1000 generations						After 10,000 generations
				G=H=0.2			G=H=0.6			G=H=0.2			G=H=0.6
				Ne			Ne			Ne			Ne
rg	ω2	ν2	α	5000	1000	500	5000	1000	500	5000	1000	500	5000	1000	500
0.6	25	20	0.8	0	0	0	0	0	0	0	0	0	0	0	0
0.6	50	20	0.4	0	0	0	0	0	0	0	0	0.58	0	2.26	9.28
0.6	25	10	0.4	0	0	0	0	0	0.01	0	0.49	3.45	0.01	8.39	17
0.6	100	20	0.2	0	0	0	0	0	0.01	0	0.22	3.28	0.01	8.84	21.6
0.6	50	10	0.2	0	0	0	0	0	0.48	0	2.55	11.7	0.36	20.2	34.6
0.6	25	5	0.2	0	0	0.02	0	0.2	2.6	0.01	9.37	22.9	3.2	32.3	45
0.6	100	10	0.1	0	0	0	0	0.02	1.34	0	5.79	17.4	1.71	26.9	43.6
0.6	50	5	0.1	0	0	0.08	0	0.67	5.94	0.11	14.8	30.2	6.52	41.2	54.7
0.6	100	5	0.05	0	0	0.15	0	1.49	8.35	0.34	19.3	35.2	9.7	44.6	58.7
0.7	25	20	0.8	0	0	0	0	0	0	0	0	0	0	0	0
0.7	50	20	0.4	0	0	0	0	0	0	0	0	0.58	0	2.26	9.2
0.7	25	10	0.4	0	0	0	0	0	0.01	0	0.47	3.8	0.01	9.19	16.8
0.7	100	20	0.2	0	0	0	0	0	0	0	0.55	4.41	0.01	11.3	25.1
0.7	50	10	0.2	0	0	0	0	0	0.64	0	3.75	13.7	0.81	23.6	37.8
0.7	25	5	0.2	0	0	0.01	0	0.37	4.21	0.08	11.4	26.6	4.33	35.4	45.5
0.7	100	10	0.1	0	0	0	0	0.23	2.26	0.01	9.09	22.7	3.17	33.1	48.8
0.7	50	5	0.1	0	0	0.16	0	1.9	8.88	0.39	19.6	35.9	9.66	45.7	58.7
0.7	100	5	0.05	0	0.01	0.44	0	3.21	13.1	0.85	25.2	40.7	13.7	51.4	64
0.9	25	20	0.8	0	0	0	0	0	0	0	0	0	0	0	0
0.9	50	20	0.4	0	0	0	0	0	0	0	0	0.16	0	0.97	5.84
0.9	25	10	0.4	0	0	0	0	0	0	0	0.08	1.78	0	4.84	14.6
0.9	100	20	0.2	0	0	0	0	0	0	0	0.33	4.42	0.07	11.3	26.1
0.9	50	10	0.2	0	0	0	0	0	0.54	0	3.86	14.6	0.9	24.5	38.8
0.9	25	5	0.2	0	0	0.02	0	0.37	3.96	0.06	11.8	26.9	5	35	45.9
0.9	100	10	0.1	0	0	0	0	0.47	4.24	0.12	15	30.4	6.75	41.3	56.5
0.9	50	5	0.1	0	0	0.38	0	4.41	14.4	1.77	27.6	44.6	16.5	54	64.9
0.9	100	5	0.05	0	0.09	1.79	0.07	11.4	26.2	6.71	41.4	55.7	29.5	63.6	73.6

We compared the simulation results (Table 1) to results using both a diffusion approximation and a PDF (Supporting Table S1 and S2, Supporting Appendix S1). All three methods yielded very similar results for realistic parameter values, indicating that the simplifying assumptions used to derive equations (3) and (6) are good approximations.

In summary, using all three methods, the incidence of sexual isolation increased with time, with additive genetic variance in the male trait and female preference, with genetic correlation between the traits, and with strength of female preference. Evolution of sexual isolation decreased with stronger natural selection on the male trait and with larger effective population size.

Discussion

TEMPO AND PATTERN IN THE EVOLUTION OF SEXUAL ISOLATION

The novel contribution of this article is to describe the time course for the evolution of sexual isolation—not just the evolution of sexually selected traits under assumptions of quantitative inheritance. Our simulations indicate that sexual isolation is promoted by drift, even in populations of appreciable size. Instances of substantial isolation can evolve rapidly, in as few as 1000 generations, under favorable circumstances (strong genetic correlation between the sexes, weak natural selection on the male trait, strong female mating preferences), even when N_e is in the range 1000–5000. Thus, drift due to finite population size is a mechanism that could account for the moderate degrees of sexual isolation (JI < 1.0) that have been observed among allopatric populations in surveys of Drosophila and plethodontid salamanders (Coyne and Orr 1989, 1997; Tilley et al. 1990; Arnold et al. 1996).

Our simulations also suggest that the evolutionary history of sexual isolation is likely to be one in which isolation waxes and wanes. As a pair of populations evolves in allopatry, periods of divergence in male ornaments may alternate with periods of convergence, resulting in fluctuations in the degree of sexual isolation (Fig. 2). Of course, because the average trajectory across a large sample of population pairs shows a monotonic increase in isolation (Fig. 3), some individual trajectories may likewise be characterized by ever-increasing isolation. Waxing and waning of isolation is especially pronounced in our model because drift dominates evolutionary dynamics once populations reach the line of equilibrium. Even in models with more selective constraint, however, finite population size should result in temporary reversals in evolutionary trajectory and hence in some degree of waxing and waning.

The prospect of stochasticity in the evolution of reproductive isolation has often been ignored or dismissed in discussions of speciation. Coyne and Orr (2004), for example, argued that sexual isolation would evolve so slowly by drift that this route to speciation can be disregarded. If populations maintain effective sizes in excess of 5000, the role of drift may indeed be insubstantial (Table 1). In vertebrates and many other groups in which N_e is commonly in the range 500–1000, stochasticity may however play a large role in the divergence of mating preferences and hence in the evolution of isolation and speciation. In such groups, finite population size might promote both the rapid evolution of isolation and repeated evolutionary reversals that we have observed in our simulations. Furthermore, these conclusions do not require a strong assumption about the selective neutrality of preferences.

While we argue that drift that will increase the potential for sexual isolation, an earlier simulation study of Lande’s (1981) model arrived at the opposite conclusion (Nichols and Butlin 1989). The authors were concerned with the unstable runaway case and argued on the basis of their simulations that genetic variance and covariance will not be maintained in finite populations and so will limit divergence. They argued that this loss of variation will be exacerbated by a decrease in effective population size as the male trait distribution diverges from the viability optimum, causing fewer males to obtain the majority of the matings. Unfortunately, their simulations were apparently limited to very small population sizes and strong selection parameters (ω² = υ² ≈ σ² = τ²), and on that basis it is not surprising that little genetic variance and covariance was maintained in their simulation runs. In other words, Nichols and Butlin (1989) explored a small region of the parameter space with limited biological relevance (unstable case, very small population size, strong selection parameters), and consequently their results have little bearing on our conclusions. In another study that explored the consequences of finite population size, Wu (1985) simulated evolution by sexual selection in a genetic system with two haploid loci, each with multiple alleles. Although selection and population size were parameterized in a way that makes comparisons to natural populations or quantitative genetic models difficult, Wu (1985) found that the Fisher–Lande process worked synergistically to accelerate the evolution of sexual isolation, a result in line with ours.

THE ASSUMPTION OF SELECTIVELY NEUTRAL PREFERENCES

The assumption of the present model that female mating preferences are selectively neutral may seem untenable to readers familiar with the last 25 years of work on quantitative genetic models of sexual selection. Since 1981, nearly all such models have allowed for stabilizing or other modes of selection on preferences, that is direct costs (Mead and Arnold 2004). The inclusion of such costs can cause Lande’s (1981) line of equilibrium to collapse to a single, stable point of equilibrium (e.g., Pomiankowski et al. 1991). Because this collapse seems to erase the possibility of diversification of male ornaments and speciation, model builders have focused on alternative scenarios (such as cubic selection on preference or plateau selection on the male trait) that promote diversification by creating multiple points or stable limit cycles (reviewed in Mead and Arnold 2004). While exploring these scenarios, focus has been restricted to the deterministic behavior of the models (i.e., only populations of infinite size have been explored). Our exploration of stochastic behavior suggests that dismissal of stable equilibrium points, arising from direct costs to preferences, has been too hasty.

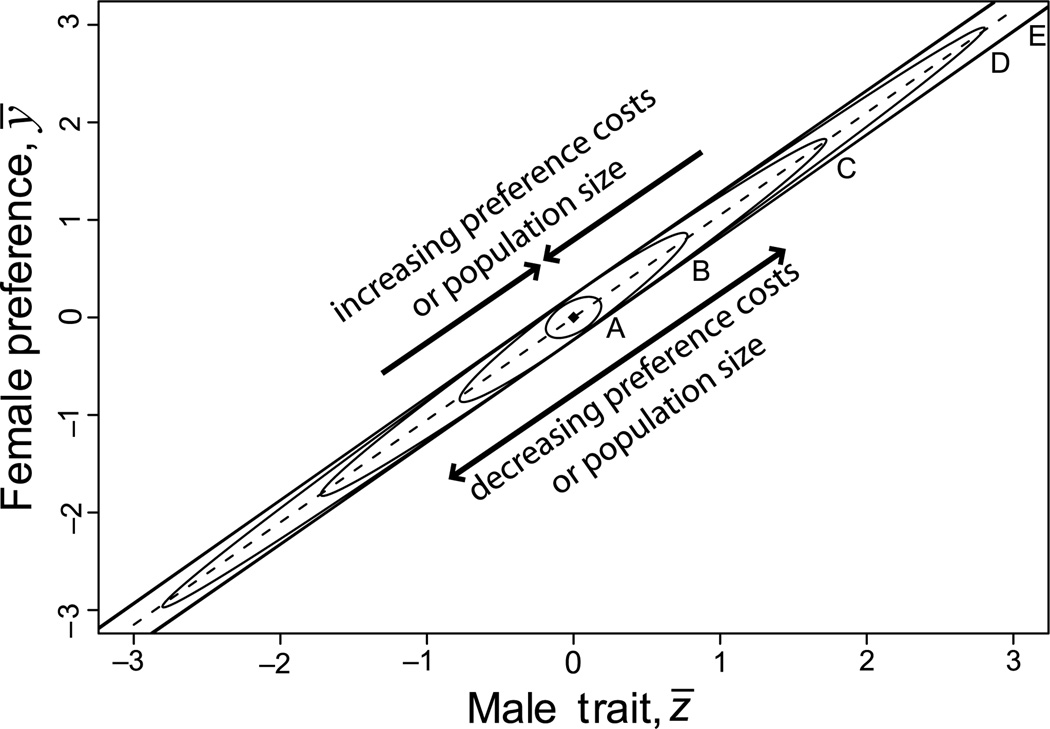
Adding a cost to preferences may restrict—but does not eliminate—the possibility of ornament diversification and speciation. Obviously a continuum exists between no costs and substantial costs to mating preferences, and many actual mating systems probably lie along this continuum. By including finite population size in models, one can readily show that along this continuum, the equilibrium changes from a line to a linear cloud to a point. This equilibrium continuum is shown in Figure 6. In a model with selection on preferences in a finite population, a balance is achieved between drift, which tends to disperse populations away from the equilibrium point that characterizes populations of infinite size, and selection, which drives populations towards that point. The resulting equilibrium cloud is large if populations are small and/or the cost of preferences is weak. As shown in Figure 6D, the equilibrium cloud can be of substantial size even in large populations if the cost of preferences is sufficiently small. Notice that in this particular case, mean ornamental values of populations may differ by nearly six phenotypic standard deviations. Thus, even when selection acts on preferences, both substantial ornament diversification and sexual isolation can occur.

Figure 6.

The effect of preference costs and population size on evolutionary equilibria. Adding direct costs to female preference results in a single equilibrium point in a population of infinite size (e.g., Pomiankowski and Iwasa 1993). We conducted simulations using the dynamic equations of Pomiankowski and Iwasa (1993, eq. 4) but allowed finite population size. This stochastic version of their model, which we will describe elsewhere, yields linear elliptical clouds at equilibrium. The size of the cloud depends on the magnitude of the preference costs and population size. Simulations were run for 10,000 generations for 2000 replicate populations with Ne = 1,000. The ellipses shown here are the 95% confidence ellipses at equilibrium. The scales on both axes are in units of within-population phenotypic standard deviation. Parameter values for Pomiankowski and Iwasa’s preference cost (B) for each ellipse are: (A) b = 0.1 (B) b = 0.01 (C) b = 0.0025 (D) b = 0.001 (E) b = 0 (i.e., no preference cost). Other parameter values are: γ = 0.7, G = H = 0.6, ω² = 50 and ν² = 5.

CLOUDS RATHER THAN POINTS OF STABLE EQUILIBRIUM

Our exploration of the stochastic behavior of Lande’s (1981) model highlights the need to explore stochastic versions of other models of sexual selection. A trend in the theoretical literature since 1981 has been to focus on equilibrium conditions in populations of infinite size, sometimes dropping genetic covariances from the model on the grounds that they do not affect the equilibrium (e.g., Kokko 2005). Our analysis of Lande’s (1981) model highlights the importance of both inheritance and selection during stochastic evolution. In particular, the size and configuration of the equilibrium cloud is affected both by population size and the genetic covariance between ornament and preference, equation (3). Because the Fisher–Lande process that relies on the genetic correlation between the sexes is embedded in virtually all of the 30 models derived from Lande (1981), stochastic versions of those models probably possess equilibrium clouds with similar properties. The implication of this result, which needs to be confirmed by more theoretical work, is that the last couple of decades of modeling have underestimated the potential for speciation by sexual selection.

BRIDGING FROM SEXUAL SELECTION TO SEXUAL ISOLATION AND SPECIATION

Our results establish the feasibility of explicitly modeling the evolution of sexual isolation and hence the path to speciation. An explicit connection to isolation and speciation is missing in most quantitative genetic models of sexual selection because modeling ends with a specification of ornament and preference evolution. The essential, often missing step is to extend existing models so that they treat the sampling properties of pairs of diverging populations. A second, missing step is to evaluate the degree of sexual isolation that is achieved by any given amount of divergence in ornaments and preferences. We used a particular model of sexual isolation (Arnold et al. 1996) to accomplish this second step, although sometimes it can be achieved directly from the model (Gavrilets and Hayashi 2005). In any case, specifying the degree of isolation in the currency of one of the standard measures of sexual isolation (e.g., JI) is especially useful. By using one of the standard currencies, the results of the model can be related directly to the extensive empirical literature on sexual isolation.

One problem in making a connection between sexual selection models and empirical measures of sexual isolation is the necessity of specifying a particular functional form for mating preferences. In the present case, we used just one (Gaussian-shaped, absolute) of many possible forms for mating preferences. An important goal for the future will be to establish whether conclusions about the evolution of sexual isolation depend tightly on assumptions about mode of preferences. Although general conclusions about the evolution of ornaments do not seem much affected by alternative assumptions about preference functions (Lande 1981), they might affect the rate at which isolation evolves.

Appendix

Probability density function for π_AB

Probability density function for π_AB

Let z̄_A be the mean male trait value from population A and z̄_B be the mean male trait value from population B. Approximating evolutionary divergence from an ancestor as a Gaussian diffusion process, the male trait means at generation t are normally distributed with mean of zero and a time-dependent variance equal to the first element in the dispersion matrix, equation (3),

$$\mathit{\text{Dz}}(t)=\frac{H(1-r_g^2)t}{N_e{(\alpha +1-B/G)}^2}.$$

Consequently, Z = z̄_A − z̄_B is normally distributed with a mean of zero and a variance approximately equal to 2D_z(t). If we assume that the differences between male and female trait values within a population are negligible compared to between populations (d_AA = d_BB = 0), then equation (4) becomes,

$${\pi }_{\mathit{\text{AA}}}=c_{\mathit{\text{AA}}}$$

$${\pi }_{\mathit{\text{BB}}}=c_{\mathit{\text{BB}}}$$

$${\pi }_{\mathit{\text{BA}}}=c_{\mathit{\text{BA}}}\text{exp}(-Z^2/(2{\mathrm{\Sigma }}^2))$$

$${\pi }_{\mathit{\text{AB}}}=c_{\mathit{\text{AB}}}\text{exp}(-Z^2/(2{\mathrm{\Sigma }}^2))$$

Thus, we can derive a formula for the cumulative distribution function of π_AB (and consequently of π_BA as well) by solving for the cumulative distribution function,

$$F_{{\pi }_{\mathit{\text{AB}}}}(x)=P[\text{exp}(-Z^2/(2{\mathrm{\Sigma }}^2))\le x]=P[Z\ge \sqrt{-2{\mathrm{\Sigma }}^2\text{ln}(x)}].$$

Substituting the cumulative distribution function for Z yields,

$$F_{{\pi }_{\mathit{\text{AB}}}}(x)=1-F_z\left[\sqrt{-2{\mathrm{\Sigma }}^2\text{ln}(x)}\right],$$

where F_Z is the cumulative distribution function of the random variable Z. Taking the derivative of both sides with respect to x and substituting in the probability density function (PDF) of Z yields the PDF for π_AB at generation t,

$$f_{{\pi }_{\mathit{\text{AB}}}}(x)=\frac{{\mathrm{\Sigma }}^2{x}^{{\mathrm{\Sigma }}^2/2D_z(t)}}{x\sqrt{-2\pi D_z(t){\mathrm{\Sigma }}^2\text{ln}(x)}},\text{for}0\le x\le 1,\text{and}0\text{elsewhere}.$$

The expected value of π_AB at generation t can be determined by integrating x fπ_AB (x) over x,

$$E[{\pi }_{\mathit{\text{AB}}}]=\underset{0}{\overset{1}{\int }}\frac{{\mathrm{\Sigma }}^2{x}^{{\mathrm{\Sigma }}^2/2D_z(t)}}{\sqrt{-2\pi D_z(t){\mathrm{\Sigma }}^2\text{ln}(x)}}\mathit{\text{dx}}.$$

Note that this probability of inter-population mating depends on two variances, D_z(t) and Σ². The first variance represents the dispersion among replicate populations in mean male trait value at generation t. The second variance is Σ² = τ² + υ² + σ², a constant (Arnold et al. 1996). Assuming that π_AB = π_BA and π_AA = π_BB = 1, then the expected value of JI at generation t is E (JI (t)) = 2(1 − E (π_AB(t))).