Abstract
The spatiotemporal dynamics of elementary Ca2+ release events, such as “blips” and “puffs” shapes the hierarchal Ca2+ signaling in many cell types. Despite being the building blocks of Ca2+ patterning, the mechanism responsible for the observed properties of puffs, especially their termination is incompletely understood. In this paper, we employ a data-driven approach to gain insights into the complex dynamics of blips and puffs. We use a model of inositol 1,4,5-trisphosphate (IP3) receptor (IP3R) derived directly from single channel patch clamp data taken at 10μM concentration of IP3 to simulate calcium puffs. We first reproduce recent observations regarding puffs and blips and then investigate the mechanism of puff termination. Our model suggests that during a puff, IP3Rs proceed around a loop through kinetic states from “rest” to “open” to “inhibited” and back to “rest”. A puff terminates because of self-inhibition. Based on our simulations, we rule out the endoplasmic reticulum (ER) Ca2+ depletion as a possible cause for puff termination. The data-driven approach also enables us to estimate the current through a single IP3R and the peak Ca2+ concentration near the channel pore.
Keywords: ion channel, IP3R, puffs, blips, Ca2+ signaling, puff termination
1 Introduction
Calcium (Ca2+) is a highly specific universal second messenger. The means by which a single ion can be both highly specific and universal is believed to lie in its spatiotemporal dynamics which are mediated by ion channels, pumps, and Ca2+ buffers [1]. One of the more intriguing aspects of the Ca2+ signaling toolkit are puffs which are brief (~ few tens of milliseconds) releases of Ca2+ through IP3Rs from the ER store. The IP3Rs are believed to be distributed in clusters [2-4]. Puffs result from the coordinated activity of multiple IP3Rs in the cluster [5-7]. Ca2+ puffs and blips (Ca2+ release events due to single open IP3R) are the building blocks of the increasingly complex spatiotemporal Ca2+ signaling patterns observed in several cell lines. Thus it has proved necessary to build models that can explain puff data [8-16]. Despite all these valuable efforts, certain aspects of puff dynamics such as their termination, remain incompletely understood. The goal of this work is to use a data-driven approach to; (1) reproduce recent observations about Ca2+ puffs, (2) investigate the mechanism of puff termination, and (3) give a reasonable estimate for the current through single IP3R and the maximum Ca2+ concentration near the channel pore.
Recently one of us (Parker) reported observations in which the change in a Ca2+ fluorescent indicator in SH-SY5Y cells that are thought to reflect the openings or closings of individual channels is observed [5, 17]. By measuring the step changes in fluorescence that reflect openings or closings of individual channels during a Ca2+ puff, we found that at most 10-20 channels are simultaneously open. More often, about 6-10 channels open simultaneously. In this paper, we assume that the maximum amplitude (or number of simultaneously open channels) ever observed at a given puff site represents the number of channels within the cluster. Experimental observations suggest a typical cluster diameter of 0.3 – 0.8 μm [2, 5, 18]. This implies that the mean distance between nearest neighbor channels is about 100 – 150 nm depending on the size and number of channels within a cluster. Previous studies concluded that a single IP3R channel releases a current I of about 0.025 – 0.5 pA [18-20]. Throughout this paper we will use a standard single-channel current of 0.075 pA. Based on the comparison between the model results and puff observations, we will argue that this is a reasonable value for the single channel current.
The IP3R is a Ca2+- sensitive Ca2+ channel. Single-channel measurements reveal that the equilibrium open probability (PO) of IP3R is bell-shaped with respect to Ca2+ [21, 22]. It is more probable for the channel to be open in the presence of 2 μM Ca2+ on the cytosolic side of the membrane than it is for it to open at 0.1 μM Ca2+ or 100 μM Ca2+. We use this property of IP3R along with kinetic data from the ligand concentration jump experiments [23] to develop a model for single-channel gating on which we build our puff model. Although several models for IP3R exist in literature (e.g. [22, 24, 25]), it seems more appropriate to use a data-driven single channel model for puff simulation in order to better assess our predictions.
We construct a model for puffs based on fairly coarse properties of the IP3R. The properties that we base our model on are (i) a simplified four-state Markov chain for the single-channel gating kinetics that we will argue is relevant to gating during puffs, (ii) the presumptive spatial distribution of channels, and (iii) the diffusion of Ca2+ from channel to channel in the presence of buffers. The model can account for the gross features of Ca2+ puffs with a single set of parameters. The model indicates that channels open because of cross-activation (in which channel A releases Ca2+ which then diffuses and causes nearest-neighboring channel B to experience near optimal Ca2+≈ 2 μM). The model further indicates that puffs terminate because of self-inhibition (in which channel A becomes inhibited after sensing high Ca2+> 100 μM near its own channel pore). We rule out the possibility of ER depletion as the reason for puff termination. With the mean transition times between various states of the IP3R constrained by the patch-clamp data and other parameters for Ca2+ and buffers kinetics available in the literature, we constrain the single channel current and Ca2+ concentration near the channel pore based on model comparison with the puffs data.
2 Single Channel Model
The gating of IP3R depends on both Ca2+ (C) and IP3 (I) concentrations. First, we will develop a seven state model that explains both the C and I dependence of the PO of a single IP3R channel. Once we have the seven state model, we will determine a simple four state model that reproduces the IP3R PO at fixed I = 10μM with the same accuracy as the full seven state model. We will build our puff model on the four state model.
The derivation of seven state model that explicitly treats IP3 binding is shown in Supplemental Methods section 1.1. The scheme for the seven state model is shown in Fig. 1S and the model fit to the PO of IP3R in Xenopus laevis oocytes is shown by the lines in Fig. 2S.
Next we will derive the four state model that explains the gating of IP3R under fixed I = 10μM and varying C. The PO of IP3R as a function of C at fixed I = 10μM is shown by the circles in Fig. 1. Each circle in Fig. 1 is the mean of multiple patch clamp experiments at given C value and the error bars are the standard errors of the mean. Using the information criterion [26] in the same manner as done for the seven state model, we find that the best fit to the PO data at I = 10μM is obtained by using the following function in C only. Note that the “best fit” here refers to the fit to the PO data at fixed I = 10μM and varying C unlike the seven state model that involves both Ca2+ and IP3 dependence.
| (1) |
| (2) |
Similar to the constant KXij in case of seven state model, the constants KA, KO, and KI will be associated with forward equilibrium constants below. To simplify the notation, we have dropped the indices ij representing the number of Ca2+ and IP3 bound to the channel. The fit to the PO data at fixed I = 10μM given by equation (1) is shown with solid line in Fig. 1. Like the seven state model, at least one state can be associated with each distinct monomial in the PO. The monomials here are: 1, KAC2, KOC2, and KIC5. Thus we have four states: R, A, O, and I. 1, KAC2, KOC2, and KIC5 in Z are the occupancies of R, A, O, and I states respectively with respect to R state. As will become clear below, in each state, the channel has four IP3 molecules bound. So, the occupancy of each state is multiplied by I4, where I is the IP3 concentration. For example, the occupancy of A state is KAC2I4 etc. However, I4 cancels out from the PO equation.
Fig. 1.
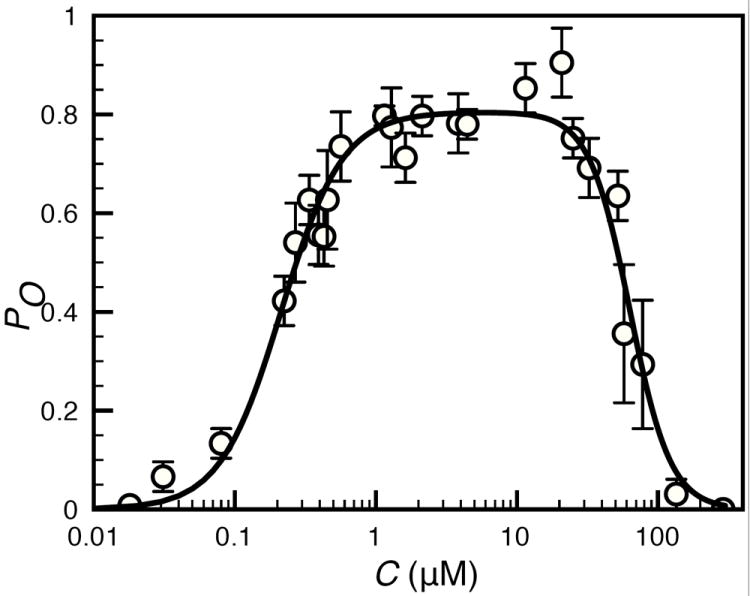
Equilibrium open probability of the single IP3R channel as a function of C at IP3 concentration of 10 μM. The solid line and circles represent the model fit and the mean PO from patch clamp experiments on Xenopus Laevis occytes [21] respectively. Error bars represent standard errors of the mean.
The equilibrium occupancies of R, A, and I states are given by:
| (3) |
| (4) |
| (5) |
The constants , , and are products of forward equilibrium constants along any path connecting the R state to the A, O, and I states respectively.
Thus we represent a single IP3R by a four-state model shown in Fig. 2. The model is consistent with the single-channel kinetics under conditions of 10μM IP3 concentration and with rapid perfusion experiments [23]. The four state model has a rest state (R) with no Ca2+ ions bound, an active closed state (A) with 2 Ca2+ bound, an open state (O) with 2 Ca2+ bound, and an inhibited state (I) with 5 Ca2+ bound. We take 5 Ca2+ to be bound in the inhibited state as that provides the best fit for the PO observed in Xenopus laevis oocytes. Under optimal1 conditions (C = 2μM and I = 10μM) the most probable behavior of the channel is that it flickers on and off between the open and active closed states. Our analysis indicates that 4 is the minimum number of states with four IP3 molecules bound to the receptor in order to account for the equilibrium PO of IP3R channels under 10μM IP3. We calculate the mean transition times from the PO data obtained from Xenopus laevis oocytes and rapid perfusion experiments [23] as described below.
Fig. 2.
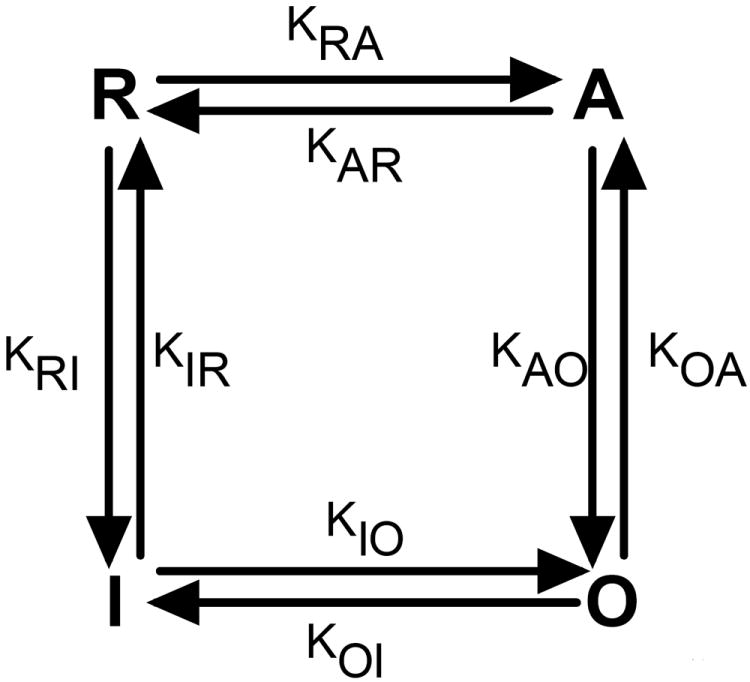
Schematic of the four state model for single IP3R channel. Kij represents the transition rate from state i to j where i, j =R, A, O, I.
Comparison of the four state model to the seven state model reveals that states R, A, O, and I in the four state model are the same as the four states in the top loop of the seven state model where they are represented by R04, A24, O24, and I54. Thus the IP3 dependence adds three more states (R00, A20, and I50) to the model. It is worth noticing that for the seven state model we took R00 as the reference state (hence KR00 = 1) while for the four state model we take R (represented by R04 in the seven state model) as the reference state. That is why we get different values for the occupancies of states R04, A24, O24, and I54 as compared to R, A, O, and I in the four state model. If we take R04 as the reference state, the occupancies of four states in the top loop of the seven state model are almost the same as the occupancies in the four state model. For the seven state model, the occupancy of state A24 relative to R04 = KA24 C2 I4/KR04 I4 = (C/CA24)2 where CA24 = (KR04/KA24)1/2 = 0.52μM. The occupancy of state O24 relative to R04 = KO24C2I4/KR04I4 = (C/CO24)2, CO24 = (KR04/KO24)1/2 = 0.26μM. Similarly, the occupancy of I54 state relative to R04 = KI54 C5 I4/KR04 I4 = (C/CI54)5, CI54 = (KR04/KI54)1/5 = 6.7μM. CA24, CO24, and CI54 in the seven state model have the same meanings as CA, CO, and CI in the four state model respectively. The values obtained here for the seven state model are very close to those for the four state model (Table 2S).
As clear from Fig. 2S, the PO at 10μM IP3 concentration given by the seven state model is exactly the same as given by the four state model. Thus for the remaining of this paper we will use the four state model to explore the behavior of puffs as both models behave in the same manner under 10μM IP3 concentration.
In principle the network can be learned completely from the ligand-dependent steady state dwell–time distributions but we have not yet done that. Rather, we turn to some of the coarser features of kinetic data that we have reported previously [23].
The kinetic data suggests that there is a direct link between O and I and that there is no direct link between R and O. We performed kinetic measurements on Sf9 cells [23] in which we measured the response of the channel to rapid jumps in the concentrations of both IP3 and Ca2+. The distribution of “inhibition latencies” fi(ti) (the distribution of times for the channel to go from actively gating to inhibited) is of particular interest. To measure the inhibition latency we jumped C from optimal (C ≈ 2μM where the PO is maximal or near maximal) to inhibiting (C ≈ 300μM where PO is near zero) at fixed IP3 concentration of 10 μM. If the channel had needed to traverse some sequence of states to get from the open state to the inhibited state (or states) there would have been no short inhibition latencies: fi(0) would have been zero or near zero. At least with the resolution afforded by our experiments there appear to be no states intermediate to O and I. We therefore conclude that the open state is directly connected to the inhibited state. Similarly the distribution of times to recover from inhibition (after dropping C from 300 μM to 2 μM), fir(tir), is nonzero at tir = 0 which is further evidence in support of a direct link between O and I. In the case of Xenopus laevis oocytes it seems unlikely that the doubly liganded open state is directly connected to the inhibited state which has 5 Ca2+ bound but the intermediate states have low occupancy. We have not performed kinetic measurements on Xenopus but we believe that the connectivity will be similar to that of the Sf9 cells. We believe that any states that are intermediate to the open and the inhibited states are traversed so rapidly that transition times as short as 0.1ms should be common. There appears to be nothing in the data that demands a link between A and I. We did report a deficit of short activation latencies when we jumped C from < 10nM to optimal. This implies that R is not directly connected to O. In another set of experiments, we jumped C from near 0 (C < 10 nM) to inhibiting value of 300 μM and found that 9 out of 103 experiments failed to cause channel bursts. Similarly, in experiments where we jumped C from 300 μM to < 10 nM, 88 out of 94 times the channel deactivated without bursting. Both these observations suggest a direct link between R and I states.
Thus the kinetic data for the Xenopus Leavis cell appears to be consistent with a network topology shown in Fig. 2. Note that we are interested in making a quantitive comparison to the puffs observed in SH-SY5Y cells. There are no single channel data available on the IP3R kinetics in SH-SY5Y cells. We assume that the network topology is consistent with the network illustrated in Fig. 2.
The only states we are including here have 0, 2, 2, and 5 Ca2+ bound. Clearly there is a “missing state” with one Ca2+ bound that mediates the transition between the rest state R which has no Ca2+ bound, and the active state A, which has two Ca2+ bound. We denote this missing low occupancy state by A1. Similarly, there are two low occupancy states between O and I and 4 low-occupancy states between I and R. The PO data are not adequate to provide accurate estimates of the occupancy of these states save that their occupancy is always low relative to that of the four primary states: R, A, O, I. Note that this does not imply that the occupancy of A1 is less than the occupancy of R for all C. Rather, it means that the occupancy of A1 is negligible compared to at least one of the four main states. Applying Occam’s razor, we set the occupancy of all the required low occupancy transition states to zero. Although these states have low occupancy, they impact the kinetic behaviors of the channel, serving as “speed bumps” for the probability flux between high occupancy states. The occupancy of transition states is low because the rates out of these states are high and this results in a finite probability flux. We introduce constants which we call “flux parameters” because they give the equilibrium probability flux between states. For example, is the flux of probability from A1 which has one Ca2+ ion bound to A which has two Ca2+ ions bound. We present the explicit derivation of the mean times between the four primary states under the assumption that they are separated by low occupancy transition states in Supplemental Methods sections 1.2 and 1.3. The transition rates are the inverses of the mean transition times.
3 Stochastic Simulations of the IP3R Cluster and Diffusion of Cytosolic Ca2+ and Buffers
We consider a cluster of 10 IP3R channels arranged in a two dimensional array with an inter-channel spacing of 120 nm. The gating of each channel is given by the four state model described in the previous section. Details of the stochastic scheme and diffusion of Ca2+ and buffers are given in Supplemental Methods sections 1.4 and 1.5 respectively.
Our evolution equations (Eqs. 37S-40S) neglect the consumption of buffers in the vicinity of the jth channel due to Ca2+ released by the ith channel (with i ≠ j) as the buffer consumed by a channel near its own pore is much higher than the buffer consumed by the same channel at the location of its neighbor. This would be an exact approximation if the channels were infinitely apart. The fact that channels in the cluster are at finite distance from each other makes this a crude approximation but not as crude as others made in the field [12, 27, 28]. The propagation of Ca2+ and buffers is simulated throughout a 3D cytosolic space. Considering the spherical symmetry around the channel, the Laplacian of Ca2+ and buffers in spherical coordinates is given as
| (6) |
where X = c, bm, bd.
We solve the set of differential equations (Eqs. 37S-40S) implicitly on a hemispherical volume of radius 5 μm with a spatial grid size of 5 nm for each channel and sum the contribution of all channels for the instantaneous Ca2+ concentration at a given point in space. The idea is that we are simulating the dynamics of a puff-site that is far from the plasma membrane, in essence a single puff-site in a semi-infinite medium. Under the simulated conditions the Ca2+ concentration at 5 μm does not change significantly. Thus we use 5 μm as the radius of the simulated volume. Increasing the radius of the simulated volume does not make an appreciable difference. The assumption that each channel has its own reservoir of buffers converts the 3D problem into N 1D problems, where N is the total number of channels. In this case, we solve 10 1D problems each with 1000 grid points. Solving this problem numerically with similar resolution in cartesian coordinates, for example, would require about a billion grid points, a very demanding computational job where thousands of puffs have to be simulated to extract statistics. The details of computational scheme are given in Supplemental Methods section 1.6.
Finally, Ca2+ concentration at the location of each channel is updated by adding the contributions from other channels in the cluster
| (7) |
Where rji is the distance between channels i and j, and cj is the Ca2+ concentration at a given point in space and time due to channel j.
This method is similar in spirit to the quasi-static approximation made by Nguyen, et al. [27] where local Ca2+ experienced by channel i due to other channels was calculated as . Here Ij, r, λ, and D is the source amplitude of channel j, distance of channel j from channel i, buffer space constant, and effective diffusion coefficient of Ca2+ respectively. Ij = 0 when the channel j is closed (see also [28]). The approximation made by [27, 28] is binary; an open channel contributes while a closed channel makes no contribution to the overall Ca2+ profile. We relax the binary static approximation made in these two studies. When a channel first opens the contribution to the overall Ca2+ profile is approximately . The contribution to the profile continues to evolve on a slow time-scale. When an open channel first closes, its contribution to the overall profile rapidly drops to a low but nonzero level and then decays slowly to zero. Furthermore, when the first channel opens, the quasi-static approximation made by Nguyen et al [27] fixes the first channel’s contribution to the Ca2+ concentration at the second channel. In reality, the first channel’s contribution to the Ca2+ concentration at the second channel will continue to increase as long as the first channel is open. Our approximation tracks these time-dependent contributions of the channels to the Ca2+ profile.
We estimate the fluorescence signal from total internal reflection fluorescence (TIRF) microscopy by the procedure outlined in [19] which is described in Supplemental Methods section 1.7. Details of experimental protocol are given in Supplemental Methods section 1.8.
4 Results
4.1 Puffs Statistics
The stochastic scheme described above allowed us to simulate Ca2+ puffs produced by a single cluster of 10 IP3Rs and blips due to a single channel inside the cluster. The simulation results are shown in Figs. 3, 4. Fig. 3 shows a representative time series of random Ca2+ puffs caused by cooperative openings of multiple channels. The modeled fluorescence changes in response to channel openings and closings in units of average fluorescence change during blips are shown in panel (A). That is, we measured the fluorescence changes during thousands of blips and used the average of these measurements as a unit for fluorescence changes during puffs and blips. The corresponding number of open channels during puffs and blips are shown in panel (B). One can clearly see step level changes in the fluorescence in response to channel openings and closings. The time series also show examples of Ca2+ blips caused by single channel openings (Fig. 3B). An expanded view of a single puff reveals that the changes in fluorescence are slower than the time-scale in which the channels open and close (insets in Fig. 3A, B). In the example shown in the insets, there is a single-channel event right before the puff in the open channels trace that cannot be detected in the fluorescence trace. Thus it is not possible to detect very brief channel openings and closings during the puff from fluorescence measurements. Furthermore, the amplitude of the fluorescence does not necessarily represent the actual number of open channels. In the insets, the numbers 1 and 2 correspond to four and three open channels, respectively (Fig. 3B inset). However, in the fluorescence, the peak corresponding to four open channels (1 in the inset) is lower than that corresponding to three open channels (2 in the inset) because three channels were open longer. This point will be further elaborated in Fig. 5 below. The distribution of all peak and step level amplitudes obtained from the simulated fluorescence data (see Fig. 3 for examples) is shown in Fig. 4 in units of blip amplitude. That is, we detected all step level changes in fluorescence due to channel openings and quantified them in unit of averaged fluorescence change during a blip. Peaks at integral values of amplitude similar to those from experimental observations can be clearly discerned (Fig. 4A of [5]).
Fig. 3.
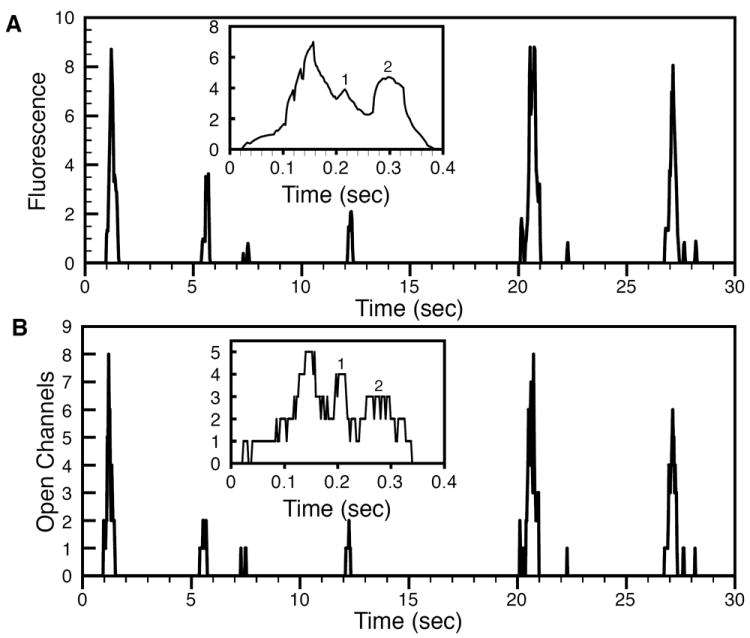
Random blips as openings of single channels and puffs as cooperative openings of multiple channels. Change in modeled fluorescence as a result of channel openings and closings in unit of average fluorescence change due to single channel events (i.e. fluorescence changes during thousands of blips were averaged and used as unit for the fluorescence change during puffs) (A) and the corresponding number of channel openings during puffs (B). The insets in (A) and (B) show an expanded view of the same puff.
Fig. 4.
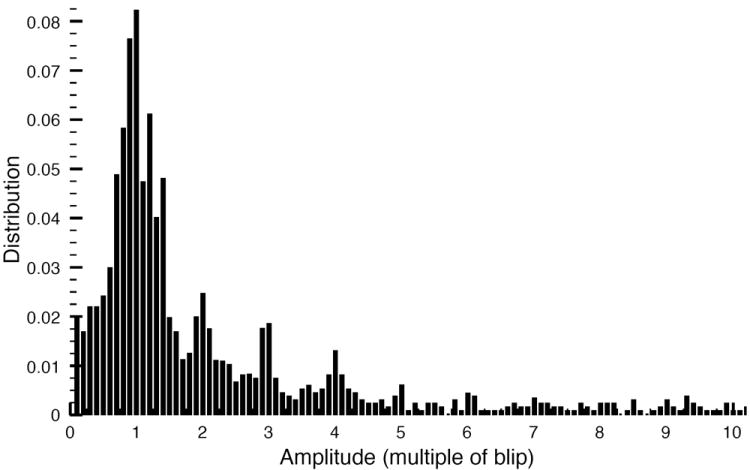
Distribution of simulated fluorescence changes due to channel openings during the puff in units of unitary Ca2+ events (averaged fluorescence change during blips).
Fig. 5.
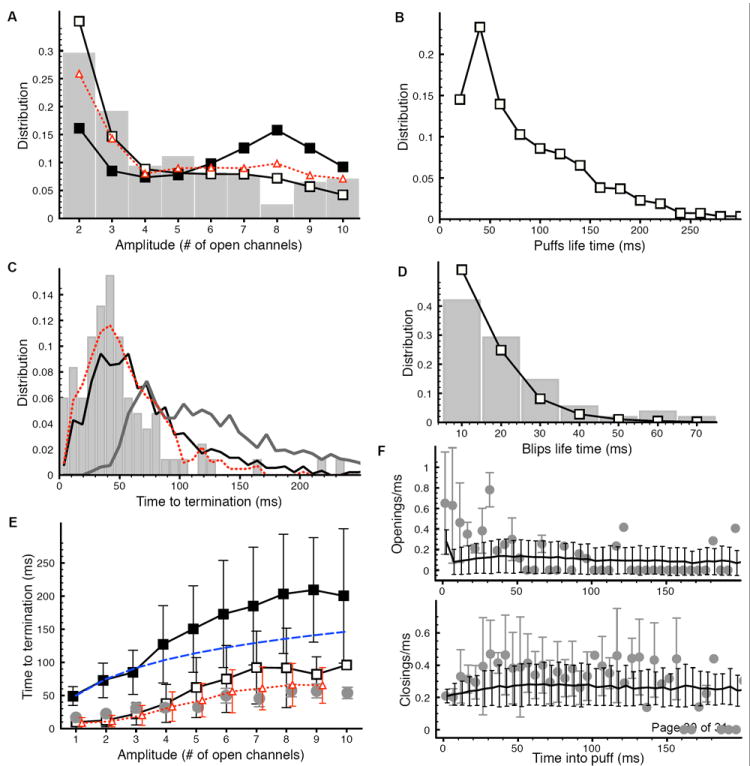
Statistics of Ca2+ puffs and blips: (A) Distribution of puff peak amplitude obtained from open channels (solid line with open squares), modeled fluorescence (solid line with filled squares), and experimental data (gray bars). The dotted line with triangles is the distribution obtained from modeled fluorescence when mean time for O to I and I to O transitions is decreased from 290 ms to 230 ms and 2.4 s to 1.92 s respectively. (B) Puff life time distribution. (C) Distribution of puff termination time obtained from open channels (black line), modeled fluorescence (dark gray line), and experimental data (gray bars). The dotted line represents the distribution obtained from the modeled fluorescence when mean times of 230 ms and 1.92 s are used for O to I and I to O transitions respectively. (D) Life time distribution for blips from simulations (solid line with squares) and experiment (gray bars). (E) Mean termination time of puffs as a function of amplitude estimated from open channels (solid line with open squares) and modeled fluorescence (solid line with filled squares). The light gray bullets are the experimental data and dashed line is harmonic series with n = 10 and τ = 50 ms. The dotted line with triangles is the model result when mean times of 230 ms and 1.92 s are used for O to I and I to O transitions respectively. (F) The number of openings/ms (upper panel) and closings/ms (lower panel) per puff as a function of time into puff given by the model. In (F) the gray bullets represent the experimentally observed openings/ms (upper panel) and closings/ms (lower panel). Experimental data reproduced from [5] with permission.
The distributions of various statistical properties calculated for several thousand puffs and blips are shown in Fig. 5. The distribution of puff amplitudes (maximum number of open channels during a puff) compares reasonably well with the experimental data from SH-SY5Y cells shown by the gray bars (Fig. 5A). The experimental data is modified from [5] by considering the puffs with maximum number of channels ≤ 10 and computing the distribution over this range in order to be consistent with a cluster size of 10 channels. Fig. 5A clearly shows that there are significant differences in the amplitude distributions obtained from modeled fluorescence and open channel count. The distribution obtained from modeled open channel counts has more small events and fewer big events compared to the distribution obtained from modeled fluorescence. As we will discuss below, the discrepancy between the distributions from modeled fluorescence and experiment decreases as we increase the transition rates between states O and I.
The distribution of puff life-times is shown in Fig. 5B. Our simulation generates puffs with shorter durations than earlier experimental observations [7]. However, the new improved imaging technique reveal shorter puff durations [5]. Furthermore, as we will show below the durations of puffs estimated from fluorescence measurements can be slightly longer than those estimated from the number of open channels.
The puff termination time (time from the peak of the puff to the base-line Ca2+) follows an exponential decay with a peak around 40 ms for the distribution obtained from the open channel count which is the same as the peak of distribution from TIRF experiments (Fig. 5C). All the distributions in Fig. 5C are based on puffs with 5 to 10 open channels. The distribution obtained from modeled fluorescence peaks around 70 ms. The distribution of puff termination time obtained from modeled fluorescence is shifted to the right when compared to the distribution from open channel count. This result indicates that the puffs actually have shorter termination time and duration than that estimated by fluorescence microscopy. We will discuss the discrepancy between the distributions from the model and experiment below.
The model is in good agreement with the distribution of Ca2+ blip life-times from single-channel events (Fig. 5D).
The modeled mean time to puff termination as a function of puff amplitude estimated from both the number of open channels and fluorescence is shown in Fig. 5E. The mean termination time versus amplitude of the puff estimated from number of open channels (solid line with open squares) is well in the range of experimentally observed values (light gray bullets). While the mean termination time estimated from modeled fluorescence (solid line with filled squares) shows longer puffs consistent with Fig. 5C. The mean termination time versus amplitude nearly follows a harmonic series as shown by the dashed line. We will discuss the significance of this behavior in the final section.
Fig. 5F shows the rate of channel openings (upper panel) and closings (lower panel) per puff as a function of time after puff initiation. The rate of channel openings and closings were calculated by counting the total number of channels that opened or closed during consecutive time windows of 5 ms and averaging the result over all puffs for that time window. For example, the average openings during the time 0 – 5 ms is calculated by counting the total number of channels that opened during the first 5ms of each individual puff and then averaging the result for all puffs. Finally, the average was divided by 5 ms. The open rate drops from high to low value rapidly in the initial phase of the puff. Channel opening and closing rates both agree with experimentally observed values (gray bullets in Fig. 5F). For the simulation shown in Fig. 5, the average statistics of puffs are: amplitude, 3.57 channels; duration, 37.40 ms; openings/ms, 0.44; closings/ms, 0.49; frequency 0.46puffs/sec; and duration of blips, 10 ms. Interestingly, we find that the stationary buffer and EGTA do not significantly effect the statistics of elementary Ca2+ release events (Fig. 3S).
The major discrepancy of our model is its prediction of longer termination time for bigger puffs as compared to the experimental data (Fig. 5C, E). There are two possible explanations for this discrepancy. First, the experimental distribution in Fig. 5C is based only on those puffs with no channel re-openings during the falling phase. That is, puffs where channels re-opened during the termination phase were not considered in the analysis. The second source of discrepancy comes from the mean times for the transitions between O and I states. As we will discuss further in the final section, the higher number of channel re-openings during the falling phase of the puff is the major contributor to the longer puff termination time. The number of re-openings decreases as we increase the transition rates between O and I states. We estimated the transition rates from the ligand jump experiments performed on IP3R in Sf9 cells [23]. It is possible that the mean transition times between O and I states of IP3R in SH-SY5Y cells are shorter than that for IP3R in Sf9 cells, thereby giving rise to higher transition rates between states O and I. Indeed, the termination time for bigger puffs decreases as we decrease the mean time for the transitions between O and I states (Fig. 5E, dotted line with triangles), shifting the termination time distribution to the left (Fig. 5C, dotted line). Decreasing the mean transition times between O and I states also improves the fit to the amplitude distribution (Fig. 5A, dotted line with triangles). Thus our modeled fluorescence signal suggests that the larger number of channel re-openings causes the number of larger amplitude puffs to increase (Fig. 5A, solid line with filled squares). Note that the higher transition rates between O and I states used here to improve the fits only point to a possibility in SH-SY5Y cells and are not based on single-channel observations. Since we do not have single channel estimates of transition rates in SH-SY5Y cells, we use the values obtained from Sf9 cells in the remainder of the paper.
Baylor and Hollingworth demonstrated that treating ATP as a buffer is important for Ca2+ spread within a half sarcomere of a frog skeletal muscle fiber activated by an action potential [29]. They showed that high concentration of ATP elongates the time course of SR Ca2+ release transients. In order to quantify the role of ATP buffering in puff dynamics, we repeated our simulation in the presence of ATP as Ca2+ buffer. We found that moderate ATP concentration doesn’t affect the statistics of elementary Ca2+ release events significantly (Fig. 4S). In the Baylor and Hollingworth’s model, the peak Ca2+ concentration was less than 20 μM. In our case, Ca2+ concentration at the channel throat rises as high as 300 μM [30]. We believe that the role of ATP buffering in modulating channel gating kinetics in our model is insignificant due to the high Ca2+ concentration at the channel location.
4.2 Puff Termination
Our hypothesis is that puffs terminate because of the self-inhibition of IP3R channels. To test this hypothesis, we reduced the probability of IP3R to go inhibited by increasing the mean transition time from state O to I by a factor f. We changed the reverse mean time by the same factor in order to maintain detailed balance. As we increase the mean transition times between O and I states the termination times distribution of puffs with 5 ≤ amplitude ≤ 10 shifts to the right showing that reducing the probability of the channel to go inhibited indeed delays the puff termination (Fig. 6A).
Fig. 6.
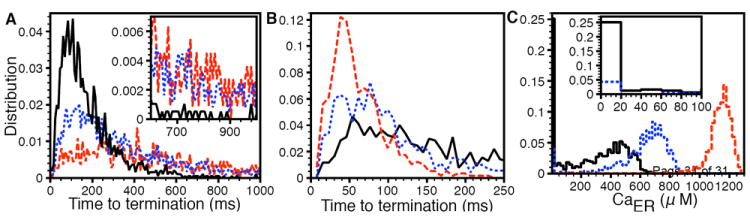
Puffs are terminated by IP3R inhibition not local ER depletion. (A) Distribution of time to termination of puffs for f = 2.5, 5, and 10 (solid, dotted, and dashed line respectively). The inset is an expanded view from 600 ms to 1000 ms. (B) Termination time distribution for , 900 μM, and 1300 μM (solid, dotted, and dashed line respectively). (C) Local ER Ca2+ concentration for simulations in (B). Different line patterns correspond to the same values as in (B). The inset is an expanded view from 0 to 100 μM.
There is considerable evidence in cardiac muscles that the local depletion of Sarcoplasmic Reticulum (SR) is the dominant mechanism for sparks termination (see for example [31], and [32] for review). To investigate the ER local Ca2+ depletion as a possible source for puff termination, we modified the equation for flux through the channel (Jj, see Supplemental Methods) so that it is proportional to the Ca2+ gradient across the ER membrane, i.e.
| (8) |
We used flux velocity, Vf = 1.75 × 104/(μMms), so that the current through the channel under optimal conditions (C = 2 μM) is 0.075 pA.
We computed the instantaneous value of CaER during the puff by translating the flux through the cluster into the Ca2+ concentration loss in a hemisphere of 700 nm radius in ER under the cluster. We considered the extreme situation where there is no replenishing of the ER micro-domain through Ca2+ diffusion or pump. A single channel having current I = X pA releases Ni = 3125 × X ions/ms. So the total number of ions, Nt, released by the cluster during time Δt is Nt = Ni × NO × Δt, where NO is the number of open channels in the cluster at a given time. We integrated Nt from 0 to t for the total number of ions released by the cluster at time t during the puff which started at time 0. One Ca2+ ion is equivalent to 1.66 × 106 μM × nm3. Ca2+ concentration lost by the hemisphere having volume δVER in the ER during time Δt is . Thus the instantaneous Ca2+ concentration in the ER micro-domain is . Where is the Ca2+ concentration in the ER at rest.
In Fig. 6B, we show the distribution of puff termination times for three different values. We consider puffs with 5 ≤ amplitude ≤ 10 because bigger puffs are more likely to deplete the ER as compared to the smaller puffs with amplitude < 5 (see Fig. 5S). In line with the observations in Fig. 5S, the probability of ER depletion increases as the number of channels in the cluster increases (Fig. 6S). This happens because bigger clusters having more than 10 channels produce larger puffs (amplitude > 10). The total number of puffs with amplitude ≥ 5 also increases as the number of channels per cluster increases. It is interesting to note that the distribution shifts to the left as we increase although the probability of local ER depletion decreases. For , one fourth of events cause local ER depletion (Fig. 6C, solid line) but the distribution has smaller number of short and larger number of long termination times as compared to where there are no local depletions. Based on this result we rule out local ER depletion as a reason for puff termination. Previous experimental observations support our conclusion. First, it is possible to evoke a second puff almost immediately after the first one. The amplitude of the second puff is not correlated with that of the first and on average is no smaller (Fig. 6 of [33]). Second, the stepwise decrements of Ca2+ fluorescence as individual channels close during a puff do not get progressively smaller and larger puffs do not terminate faster than smaller puffs [5]. Third, we recently found some instances where puffs fail to terminate. After producing several normal puffs, a puff at a site just keeps going, with a sustained fluorescence amplitude that declines little over several seconds (unpublished data). This last observation is in accord with our result. Had we allowed slow replenishing of ER by pump, diffusion, and buffers in case of , the CER would have a sustained smaller value causing a smaller flux through the channel. The smaller flux would have caused delayed channel inhibition and hence elongated puffs.
5 Discussion
Ca2+ ions encode information through their spatiotemporal patters. Puffs and blips are the building blocks of Ca2+ patterning. The dynamics of puffs, especially their termination mechanism remain incompletely understood. Here we used data-driven modeling to unveil one mechanism of puff termination. We first developed a single channel model for IP3R. We assumed that the channel gating kinetics as observed in patch clamp recordings obey the laws of mass action and detailed balance. These two laws together imply that the equilibrium open probability is given by a rational function in terms of the concentrations of the ligands that bind to the channel. Some of the key patch clamp measurements were taken at IP3= 10μM.
We constrained the model based on key experimental observations regarding single channel gating rather than using existing models. Our model suggests that during a puff, IP3R channels in a cluster proceed along a one-way trip around a loop through kinetic states from “rest” to “active and open” to “inhibited” and back to “rest” (Fig. 7S). The channels can switch back and forth between active and open states during the puff. However, the puff is terminated by channels entering the inhibited state. There are no channels in the active state immediately after a puff is terminated. In line with experimental observations, we ruled out local ER Ca2+ depletion as a reason for puff termination unlike Ca2+ sparks in cardiac muscles where local SR depletion is the dominant mechanism for spark termination [31, 32]. In the following, we argue further that puffs are terminated by self-inhibition of IP3Rs.
The problem of understanding puff dynamics is fundamentally a problem of analyzing the various space and time scales in light of the various reaction rates. From the open probability data we note that the occupancy probability for the inhibited state, PI, occurs only at Ca2+ concentrations above 10 μM [21]. For the SF9 cells, PI reaches the ten percent level at Ca2+ = 3.5 μM [23] while for Xenopus Laevis oocytes the ten percent level is reached only at Ca2+ = 36 μM [21]. A key question is whether an open channel can inhibit its neighbor. If we neglect buffers for the moment, and treat an IP3R as an ideal point source located in a planar membrane, an open channel contributes I/[2πrD] to the Ca2+ concentration a distance r away where D is the diffusion coefficient of free Ca2+ and is in the range of D ≈ .2 – .3 μm2/ms. With a mean spacing to nearest neighbor of about 120 nm and I = 0.075 pA, this corresponds to a contribution of about 1.3 – 2.0 μM to the Ca2+ that a channel experiences because a neighbor is open. The presence of buffers reduces the contribution so that an open channel contributes I exp(−r/λ)/2πr D to Ca2+ concentration a distance r away, where λ accounts for the decrease in Ca2+ due to Ca2+ buffers. [34]. With total buffer concentration BT ≈ 100 μM [35] and an on-rate, of about .2 μM−1 ms−1 [36], it is interesting to note that λ ≈ 120nm, the same as the nearest neighbor spacing. Under such buffering conditions, an open channel contributes 0.5–0.7 μM to the concentration that its average nearest neighbor experiences. PO for both Xenopus Laevis and SF9 is above the 90% level at 0.7 μM. PI is zero at 0.7 μM for both Xenopus and Sf9. Thus, open channels cannot raise the Ca2+ concentration experienced by their neighbors enough to result in significant PI. If channels are to reach the inhibited state, then it must be because they are sensing their own self-contribution to Ca2+.
The IP3R “outer radius” is about 10nm from the pore. The self-contribution to the concentration at the outer radius is 20 – 40 μM for an open channel and near zero when the channel is closed. Note that when a channel opens or closes, the initial change in concentration very close to the pore is instantaneous. Even at the nearest neighbor distance (~ 120 nm), the time for the concentration field to approach its quasi steady value is about 50 μs, which is very short relative to the channel gating times that are on the order of milliseconds or longer. Upon closing, a channel’s self-contribution to the Ca2+ concentration it senses at the outer radius drops from 20 – 40 μM to a very small value, depending on buffer, in times of about a microsecond. It follows that the only time that the inhibiting binding site is exposed to concentrations high enough to raise PI is when the channel is open. Thus, the channel must be open in order to become inhibited. Inhibition means self-inhibition. We conclude that the only way for a channel to sense inhibiting levels of Ca2+ is if the channel is open, unlike the 9 state model in [37] in which the channel cannot inhibit itself. Thus, puffs terminate because of self-inhibition causing finite puff lifetimes of a few hundred milliseconds.
If we consider n open channels at the peak of the puff that go inhibited independently of each other with τ the mean time to inhibition of a single channel, then the mean time taken by nth, (n − 1)th, …. , 2nd last, last open channel to close would be τ/n, τ/(n − 1), …., τ/2, τ/1. The total termination time for the puff is τ (1/n+1/(n−1)+……+1/2+1). As shown in Fig. 5E, the observed mean termination time versus the amplitude of puff nearly follows a harmonic series. The mean termination time for puffs with bigger amplitude given by the model moves away from the harmonic series. After analyzing individual puffs, we noticed that the longer puffs have more re-openings during the falling phase which elongates their termination time. This analysis leads to two conclusions. First, by fitting the puff termination time vs amplitude obtained from experimental data to the harmonic series one can estimate the mean open time of a single channel in a physiological environment. Second, the number of re-openings during the falling phase of the puff increases as we decrease the current through a single channel and vice versa. By using a single-channel Ca2+ current I = 0.02 pA, we estimated that the channel experience about 75 μM Ca2+ when open and the mean termination time for bigger puffs was about 4 times longer than the experimental values. Furthermore, the increased termination time was due to the increased number of re-openings during the falling phase of the puff. To get close to the experimentally observed termination time, we had to increase the channel current to 0.075 pA. Second, the number of re-openings also decreases as we increase the transition rate from state O to I. Since the mean transition times are constrained by the patch clamp data, we changed the channel current. Thus by fitting the model to the experimental termination time vs amplitude, the current through a single channel can be estimated. A single channel current of 0.075 pA gave us a reasonable fit to the data. This value is well within the observed limits [18-20]. The same practice also enabled us to estimate the Ca2+ concentration experienced by the channel due to its opening. Our model predicts that the Ca2+ concentration near an open channel can reach 300 μM [30].
We have assumed fixed IP3 concentration for the puff simulations in this paper. The goal was to understand key observations about puffs in terms of Ca2+ dependence only and to investigate the puff termination mechanism. Previous observations indicate that some key characteristics of puffs such as their amplitude are relatively insensitive to IP3 concentration [38, 39]. Further, we noticed that at 10 μM IP3 the four state single channel model used for puffs behaves in the same manner as the seven state model that considers explicit IP3 binding (Supplemental Methods section 1.1). We believe that our conclusion regarding self-inhibition as the mechanism for puff termination remains unchanged even if IP3 binding is taken into account. The effects of IP3 binding on IP3R gating have not been experimentally explored sufficiently to draw firm data-driven conclusions. We are currently investigating the effects of IP3 binding on the IP3R channel gating and will report our results in the future.
Supplementary Material
Acknowledgments
This material is based upon work supported by NIH under grant 5RO1GM065830-08.
Footnotes
We use the term “optimal” loosely to indicate a condition under which the IP3R has a fairly high PO.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Cheng H, Lederer WJ. Ca2+ Sparks. Physiol Rev. 2008;88:1491–1545. doi: 10.1152/physrev.00030.2007. [DOI] [PubMed] [Google Scholar]
- 2.Shuai J, Rose H, Parker I. The number and spatial distribution of IP3Rs underlying Ca2+ puffs in Xenopus oocytes. Biophys J. 2006;91:4033–4044. doi: 10.1529/biophysj.106.088880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Smith I, Wiltgen S, Shuai J, Parker I. Ca2+ puffs originate from pre-established stable clusters of IP3Rs. Sci Signaling. 2009;2:1–8. doi: 10.1126/scisignal.2000466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Rahman T, Skupin A, Falcke M, Taylor C. Clustering of IP3Rs by IP3 retunes their regulation by IP3 and Ca2+ Nature. 2009;458:655–659. doi: 10.1038/nature07763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Smith IF, Parker I. Imaging the quantal substructure of single IP3R channel activity during Ca2+ puffs in intact mammalian cells. Proc Natl Acad Sci USA. 2009;106:6404–6409. doi: 10.1073/pnas.0810799106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Callamaras N, Marchant J, Sun X, Parker I. Activation and co-ordination of IP3-mediated elementary Ca2+ events during global Ca2+ signals in Xenopus oocytes. J Physiol. 1998;509:81–91. doi: 10.1111/j.1469-7793.1998.081bo.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Sun X, Callamaras N, Marchant J, Parker I. A continuum of IP3-mediated elementary Ca2+ signalling events in Xenopus oocytes. J Physiol. 1998;509:67–80. doi: 10.1111/j.1469-7793.1998.067bo.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Shuai J, Jung P. Stochastic properties of Ca2+ release of IP3R clusters. Biophys J. 2002;83:87–97. doi: 10.1016/S0006-3495(02)75151-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ullah G, Jung P. Modeling the statistics of elementary Ca2+ release events. Biophys J. 2006;90:3485–3495. doi: 10.1529/biophysj.105.073460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Shuai J, Pearson J, Parker I. Modeling Ca2+ feedback on a single IP3R and its modulation by Ca2+ buffers. Biophys J. 2008;95:3738–3752. doi: 10.1529/biophysj.108.137182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Swaminathan D, Ullah G, Jung P. A simple sequential-binding model for Ca2+ puffs. Chaos. 2009;19:037109. doi: 10.1063/1.3152227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Rüdiger S, Shuai JW, Sokolov IM. Law of Mass Action, Detailed Balance, and the Modeling of Ca2+ Puffs. Phys Rev Lett. 2010;105:048103. doi: 10.1103/PhysRevLett.105.048103. [DOI] [PubMed] [Google Scholar]
- 13.Ullah G, Jung P, Machaca K. Modeling Ca2+ signaling differentiation during oocyte maturation. Cell Calcium. 2007;42:556–564. doi: 10.1016/j.ceca.2007.01.010. [DOI] [PubMed] [Google Scholar]
- 14.Dawson A, Lea E, Irvine R. Kinetic model of the IP3R that shows both steady-state and quantal patterns of Ca2+ release from intracellular stores. Biochem J. 2003;370:621. doi: 10.1042/BJ20021289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Solovey G, Dawson S, Chirico G. Intra-cluster percolation of Ca2+ signals. PloS one. 2010;5:e8997. doi: 10.1371/journal.pone.0008997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Swillens S, Dupont G, Combettes L, Champeil P. From Ca2+ blips to Ca2+ puffs: theoretical analysis of the requirements for interchannel communication. Proc Natl Acad Sci USA. 1999;96:13750–13755. doi: 10.1073/pnas.96.24.13750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Parker I, Smith I. Recording single-channel activity of IP3Rs in intact cells with a microscope, not a patch clamp. J Gen Physiol. 2010;136:119–127. doi: 10.1085/jgp.200910390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bruno L, Solovey G, Ventura A, Dargan S, Dawson S. Quantifying Ca2+ fluxes underlying Ca2+ puffs in xenopus laevis oocytes. Cell Calcium. 2010;47:273–286. doi: 10.1016/j.ceca.2009.12.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Shuai J, Parker I. Optical single-channel recording by imaging Ca2+ flux through individual ion channels: theoretical considerations and limits to resolution. Cell Calcium. 2005;37:283–299. doi: 10.1016/j.ceca.2004.10.008. [DOI] [PubMed] [Google Scholar]
- 20.Vais H, Foskett KJ, Mak DOD. Unitary Ca2+ current through recombinant type 3 IP3 receptor channels under physiological ionic conditions. 2010;136:687–700. doi: 10.1085/jgp.201010513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Mak DOD, McBride S, Foskett KJ. IP3 activation of IP3R Ca2+ channel by ligand tuning of Ca2+ inhibition. Proc Natl Acad Sci USA. 1998;95:15821–15825. doi: 10.1073/pnas.95.26.15821. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Mak DOD, McBride S, Foskett KJ. Spontaneous channel activity of the IP3R. Application of allosteric modeling to Ca2+ and IP3 regulation of IP3R single-channel gating. J Gen Physiol. 2003;122:583–603. doi: 10.1085/jgp.200308809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Mak DOD, Pearson JE, Cheung KH, Datta S, Fernandez-Mongil M, Foskett KJ. Rapid ligand-regulated gating kinetics of single IP3R Ca2+ release channels. EMBO Reports. 2007;8:1044–1051. doi: 10.1038/sj.embor.7401087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Sneyd J, Dufour J. A dynamic model of the type-2 IP3R. Proc Natl Acad Sci USA. 2002;99:2398. doi: 10.1073/pnas.032281999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.De Young G, Keizer J. A single-pool IP3R-based model for agonist-stimulated oscillations in Ca2+ concentration. Proc Natl Acad Sci USA. 1992;89:9895. doi: 10.1073/pnas.89.20.9895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Schwarz G. Estimating the dimension of a model. The Annals of Statistics. 1978;6:461–464. [Google Scholar]
- 27.Nguyen V, Mathias R, Smith G. A stochastic automata network descriptor for Markov chain models of instantaneously coupled intracellular Ca2+ channels. Bull Math Biol. 2005;67:393–432. doi: 10.1016/j.bulm.2004.08.010. [DOI] [PubMed] [Google Scholar]
- 28.Neher E. Vesicle pools and Ca2+ microdomains: New tools for understanding their roles in neurotransmitter release. Neuron. 1998;20:389–399. doi: 10.1016/s0896-6273(00)80983-6. [DOI] [PubMed] [Google Scholar]
- 29.Baylor S, Hollingworth S. Model of sarcomeric Ca2+ movements, including ATP Ca2+ binding and diffusion, during activation of frog skeletal muscle. J Gen Physiol. 1998;112:297. doi: 10.1085/jgp.112.3.297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Thul R, Falcke M. Release currents of IP3 receptor channel clusters and concentration profiles. Biophys J. 2004;86:2660–2673. doi: 10.1016/S0006-3495(04)74322-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Zima A, Picht E, Bers D, Blatter L. Termination of cardiac Ca2+ sparks: role of intra-SR Ca2+, release flux, and intra-SR Ca2+ diffusion. Circulation Res. 2008;103:e105. doi: 10.1161/CIRCRESAHA.107.183236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Rios E, Launikonis B, Royer L, Brum G, Zhou J. The elusive role of store depletion in the control of intracellular Ca2+ release. J Muscle Res Cell Motility. 2006;27:337–350. doi: 10.1007/s10974-006-9082-5. [DOI] [PubMed] [Google Scholar]
- 33.Callamaras N, Parker I. Phasic characteristic of elementary Ca2+ release sites underlies quantal responses to IP3. The EMBO J. 2000;19:3608–3617. doi: 10.1093/emboj/19.14.3608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Smith G. Analytical steady-state solution to the rapid buffering approximation near an open Ca2+ channel. Biophys J. 1996;71:3064–3072. doi: 10.1016/S0006-3495(96)79500-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Falcke M. Reading the patterns in living cells-the physics of Ca2+ signaling. Adv Phy. 2004;53:255–440. [Google Scholar]
- 36.Neher E, Augustine G. Ca2+ gradients and buffers in bovine chromaffin cells. J Physiol. 1992;450:273–301. doi: 10.1113/jphysiol.1992.sp019127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Shuai J, Pearson J, Foskett KJ, Mak DOD, Parker I. A kinetic model of single and clustered IP3 receptors in the absence of Ca2+ feedback. Biophys J. 2007;93:1151–1162. doi: 10.1529/biophysj.107.108795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Smith I, Wiltgen S, Parker I. Localization of puff sites adjacent to the plasma membrane: functional and spatial characterization of Ca2+ signaling in SH-SY5Y cells utilizing membrane-permeant caged IP3. Cell Calcium. 2009;45:65–76. doi: 10.1016/j.ceca.2008.06.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Yao Y, Choi J, Parker I. Quantal puffs of intracellular Ca2+ evoked by IP3 in Xenopus oocytes. J Physiol. 1995;482:533. doi: 10.1113/jphysiol.1995.sp020538. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


