Anisotropic Isolation by Distance: The Main Orientations of Human Genetic Differentiation

Abstract

Genetic differentiation among human populations is greatly influenced by geography due to the accumulation of local allele frequency differences. However, little is known about the possibly different increment of genetic differentiation along the different geographical axes (north–south, east–west, etc.). Here, we provide new methods to examine the asymmetrical patterns of genetic differentiation. We analyzed genome-wide polymorphism data from populations in Africa (n = 29), Asia (n = 26), America (n = 9), and Europe (n = 38), and we found that the major orientations of genetic differentiation are north–south in Europe and Africa, and east–west in Asia, but no preferential orientation was found in the Americas. Additionally, we showed that the localization of the individual geographic origins based on single nucleotide polymorphism data was not equally precise along all orientations. Confirming our findings, we obtained that, in each continent, the orientation along which the precision is maximal corresponds to the orientation of maximum differentiation. Our results have implications for interpreting human genetic variation in terms of isolation by distance and spatial range expansion processes. In Europe, for instance, the precise northnorthwest–southsoutheast axis of main European differentiation cannot be explained by a simple Neolithic demic diffusion model without admixture with the local populations because in that case the orientation of greatest differentiation should be perpendicular to the direction of expansion. In addition to humans, anisotropic analyses can guide the description of genetic differentiation for other organisms and provide information on expansions of invasive species or the processes of plant dispersal.

Introduction

The theory of isolation by distance (IBD), which was introduced by Wright (1943), describes the accumulation of local genetic differences under the assumption of local spatial dispersal (Slatkin 1993). Under IBD, pairwise measures of genetic differentiation are expected to increase with increasing geographical distance. For human populations, this correlation is evident at different geographical scales, including the worldwide scale (Ramachandran et al. 2005), the continental scale (Lao et al. 2008; Novembre et al. 2008; Tishkoff et al. 2009), as well as finer scales (Helgason et al. 2004; Salmela et al. 2008). Spatial analysis of genetic data can additionally provide the orientation at which the accumulation of genetic differentiation is the greatest (Oden and Sokal 1986; Rosenberg 2000). However, since the original work of Falsetti and Sokal (1993) who found orientational genetic clines in the human genetic structure of the British isles, such orientational analyses have been mainly restricted to plant species (Dutech et al. 2005; Austerlitz et al. 2007; Born et al. 2012). A notable exception is the work of Ramachandran and Rosenberg (2011) who investigated an original approach where they rotated population locations around poles different from the north pole to find orientations that provide stronger genetic clines than the north–south or east–west axis. Here, we provide the first comprehensive description of the orientations of main human genetic differentiation in four continents: Africa, America, Europe, and Asia. The analysis is based on single nucleotide polymorphism (SNP) data containing 2,599 individuals drawn from 101 populations consisting of n = 29 African populations, n = 26 Asiatic populations, n = 9 Native American populations, and n = 38 European populations (table 1).

Table 1.

Sample Information for the SNP and Microsatellite Data Sets.

Continent	Markers	Sample Size	Population No.	Population Name (Population Sample Size)	References
Africa	55,098 SNPs	587	29	Algeria (19), Bamoun (18), Biaka Pygmy (22), Brong (8), Bulala (15), Egypt (19), Fang (15), Fulani (12), Hadza (17), Hausa (12), Igbo (15), Kaba (17), Kongo (9), Libya (17), Luhya (36), Maasai (30), Mada (12), Mandenka (22), Mbuti Pygmy (13), Morocco N (18), Morocco S (16), Mozabite (29), Sahara OCC (18), San NB (17), San SA (31), Sandawe (28), Tunisia (18), Xhosa (11), Yoruba (47)	Henn et al. (2011)
America	439,046 SNPs	118	9	Aymara (24), Colombian (5), Guerrero (14), Karitiana (5), Maya (18), Yucatan (4), Pima (5), Quechua (24), Surui (5)	Bigham et al. (2010)
Asia	656,995 SNPs	428	26	Balochi (24), Brahui (25), Burusho (25), Cambodian (10), Dai (10), Daur (9), Han (44), Hazara (22), Hezhen (9), Japanese (28), Kalash (23), Lahu (8), Makrani (25), Miaozu (10), Mongola (10), Naxi (8), Oroqen (9), Pathan (22), She (10), Sindhi (24), Tu (10), Tujia (10), Uygur (10), Xibo (9), Yakut (25), Yizu (10)	Li et al. (2008)
Europe	279,344 SNPs	1,466	38	Netherlands (17), Norway (3), Albania (3), Austria (14), Belgium (43), Bosnia (9), Bulgaria (2), Croatia (8), Cyprus (4), Czech (11), Denmark (1), Finland (41), France (89), Germany (71), Greece (8), Hungary (19), Ireland (61), Italy (219), Kosovo (2), Latvia (1), LSFIN (41), Macedonia, (4), Poland (22), Portugal (128), Romania (14), Russian (6), Scotland (5), Serbia (44), Slovakia (1), Slovenia (2), Spain (136), Sweden (10), Swiss-French (125), Swiss-German (84), Swiss-Italian (13), Turkey (4), Ukraine (1), United Kingdom (200)	Nelson et al. (2008) and Surakka et al. (2010)
America	678 Micro	530	29	Ache (19), Arhuaco (17), Aymara (18), Cabecar (20), Chipewyan (29), Cree (18), Embera (11), Guarani (10), Guaymi (18), Huilliche (20), Inga (17), Kaingang (7), Kaqchikel (12), Karitiana (24), Kogi (17), Maya (25), Mixe (20), Mixtec (20), Ojibwa (20), Piapoco (13), Pima (25), Quechua (20), Surui (21), TicunaArara (17), TicunaTarapaca (18), Waunana (20), Wayuu (17), Zapotec (19), Zenu (18)	Wang et al. (2007)

A consequence of IBD patterns is that genome-wide SNP data convey information on the geographic origin of individuals such as their continent of origin (Allocco et al. 2007) or much more precise origin (Heath et al. 2008; Novembre et al. 2008; Drineas et al. 2010; O’Dushlaine et al. 2010; Hoggart et al. 2012; Yang et al. 2012). For example, Novembre et al. (2008) found that they can place 90% of a sample of European individuals within 700 km of their origin. The fact that genetic differentiation can increase at different rates in different geographic directions should affect the localization of geographic origin from genome-wide SNP data as localization should be more reliable for the orientation of maximum differentiation. In the different continents, we compared the localization errors along north–south (N–S) and east–west (E–W) orientations and checked whether the comparisons are compatible with the orientations of maximum differentiation.

Results

Multidimensional Scaling

To study the orientations of maximum genetic differentiation, we first applied multidimensional scaling (MDS) based on the pairwise F_ST matrices of the African, American, European, and Asiatic samples. For each continent, we projected the first component of MDS on a map using spatial interpolation (fig. 1; the two-dimensional MDS plots are displayed in supplementary fig. S1, Supplementary Material online). Visually, we found that the nondirectional orientation of the gradient of the first component of MDS is N–S in Europe and Africa, E–W in Asia, and NW–SE in America. However, in America, the interpolated map is a poor predictor of the values obtained with MDS because the R² measure between the interpolated and actual MDS values is 22%, whereas it is larger than 80% in the three other continents. As an alternative to MDS, we also considered principal component analysis (PCA) of the SNP data and found the same orientations when looking at the spatial projections of the first principal component (supplementary fig. S2, Supplementary Material online). However, because multivariate methods such as PCA can produce directional clines even under isotropic IBD model (Novembre and Stephens 2008), the synthetic maps (Cavalli-Sforza et al. 1994) of figure 1 and supplementary figure S2, Supplementary Material online, are not sufficient evidence for anisotropy.

Fig. 1.

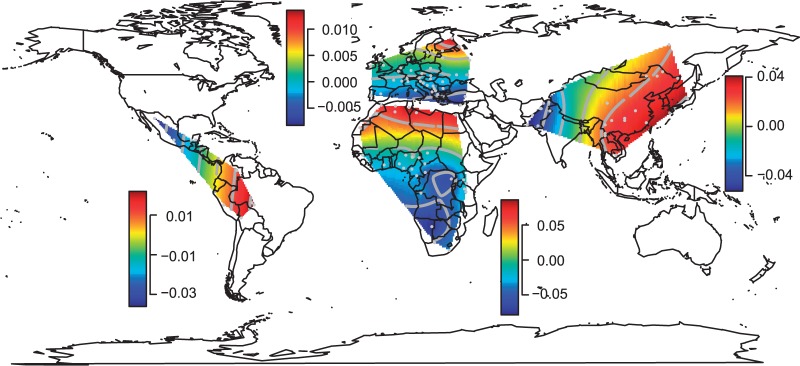
Spatial interpolation of the first component of MDS. MDS was applied separately in each continent using the pairwise intracontinetal F_ST matrix as dissimilarity matrix. Spatial interpolation was performed using the Krig function of the R fields package by considering a trend surface of degree 2. The gray dots represent the locations of the sampled populations. For each continent, the colored bar gives the scale of the first component of MDS. The MDS values are not on the same scale for the four continents reflecting the different levels of genetic differentiation within continents.

Accounting for Anisotropy in IBD Models

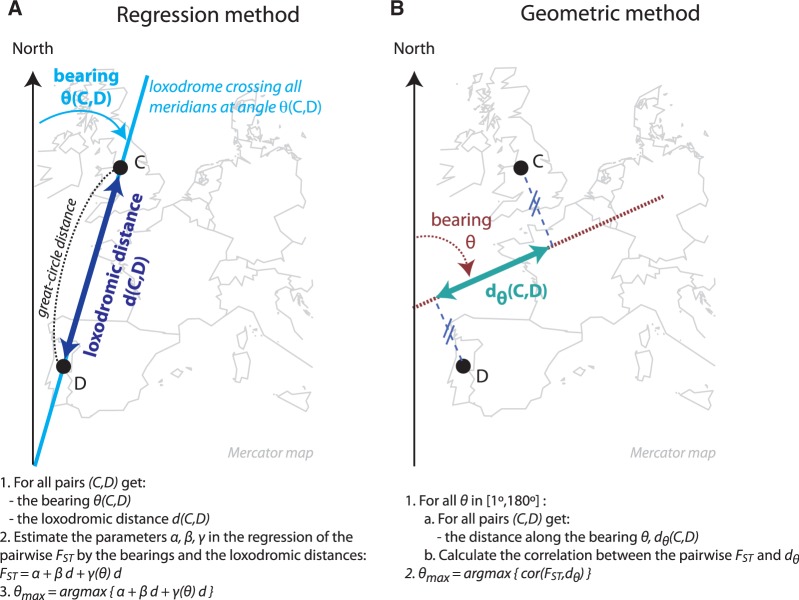
We developed two original methods that explicitly account for anisotropic patterns of IBD where anisotropy is defined as the property of being directionally dependent. One method is based on the following regression equation:

(1)

where θ is the bearing between two populations when following a line of fixed direction (a rhumb line or loxodrome, fig. 2) between the two populations, d is the distance along this line of fixed direction, and γ is a periodic parametric function (eq. 2) that should be maximum for the orientation of maximum differentiation. Equation (1) provides the geographic direction at which F_ST increases the fastest. The second method, we developed is based on geometric arguments. We computed, for each angle θ (), the linear correlation between F_ST and an orientational distance d_θ that corresponds to the distance between two populations when their coordinates are projected to a line of bearing θ (fig. 2). We computed the angle θ^max that maximizes the correlation between the pairwise population matrix of d_θ and the pairwise population matrix of F_ST values.

Fig. 2.

Schematic description of the regression and geometric approaches used for providing the angle of maximal differentiation.

We investigated the directions provided by both the regression (eq. 1) and geometric methods. In all continents but the Americas, both methods gave almost the same orientation of maximum differentiation: north–south (N–S) in Africa, eastsoutheast–westnorthwest in Asia, and northnorthwest–southsoutheast (NNW–SSE) in Europe (table 2 and supplementary fig. S3, Supplementary Material online, for a schematic description of the different orientations). For native American populations, the orientations found with the regression and the geometric methods were between 67° and 92° (measured clockwise from the N–S orientation). However, the bearing-dependent term γ(θ) in equation (1) was not significant in the Americas (partial Mantel test P = 0.33) in contrast to the other 3 three continents (P < 0.02). For Europe, Asia, and Africa, the orientations of maximum differentiation changed by at most 9° when we replaced F_ST in equation (1) by 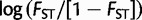and by at most 13° when additionally replacing d with 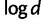(Slatkin 1993) (supplementary table S1, Supplementary Material online). We also investigated to what extent the results are changed when perturbing the geographical sampling locations of the sampled populations. We perturbed coordinates by moving each population on a different rhumb line of 500 km length and each angle was chosen uniformly between 0° and 360°. In Africa and Asia, the orientations changed by at most 12°. In Europe, the orientations of maximum differentiation after perturbation changed by at most 24° lying in between the NW–SE and N–S orientations (supplementary table S2, Supplementary Material online). In the Americas, the orientations changed by up to 56° confirming the lack of a robust axis of main Native American genetic differentiation.

Table 2.

Orientations of Maximum Differentiation.

	Africa	America	Asia	Europe
Regression method	9*** (160–33)	92 (22–167)	102*** (84–121)	167* (140–14)
Geometric method	6 (164–26)	67 (10–118)	102 (80–124)	167 (138–14)

Note.—All orientations are measured in degree clockwise from the N–S orientation (1°–180°). The 95% confidence intervals given in parenthesis should be read clockwise. The test for anisotropy in equation (1) was assessed with a partial Mantel test using 10,000 permutations. P value: *** < 0.001, * < 0.05.

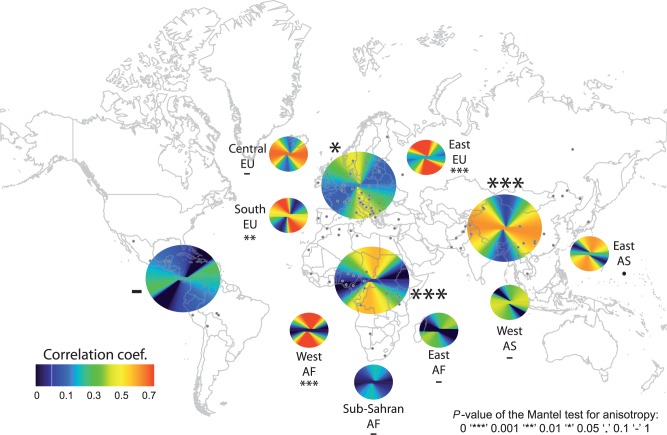
We also investigated the main orientations of genetic differentiation for regions within the different continents. For all continents and all regions with more than 10 sampled populations, figure 3 shows how the correlation between F_ST and the distance along the bearing θ, d_θ, changes as a function of θ (supplementary fig. S4, Supplementary Material online). In Sub-Saharan Africa, although the correlation between F_ST and N–S distances (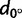) was larger than the correlation between F_ST and E–W distances (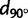), the strength of the correlation was considerably reduced compared with the full African sample (maximum R² of 0.09 for Sub-Saharan Africa vs. a maximum R² of 0.39 for all African populations). This was also reflected in the regression method of equation (1) applied to the Sub-Saharan populations because the bearing-dependent term γ(θ) was not significant (P = 0.35, supplementary table S3, Supplementary Material online) in contrast to the analysis of the entire African sample (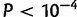). Furthermore, no significant anisotropy was found in Central Europe, East Asia, West Asia, and in East Africa (P > 0.05, fig. 3 and supplementary table S3, Supplementary Material online). By contrast, the regions within continent where the bearing term was significant (P < 0.05) were as follows: Eastern Europe and Southern Europe with a major NNE–SSW direction of differentiation as for the whole European sample, and Western Africa with a major N–S direction of differentiation as for the whole African sample (fig. 3 and supplementary tables S5–S7, Supplementary Material online, for the different subdivisions of the continents).

Fig. 3.

Correlation between FST and orientational distances computed along the different bearing lines. Results are shown for the four continents and for several subregions within Africa, Asia, and Europe. The symbols next to each circle indicate the significance of the test for anisotropy. The P values have been obtained using a partial Mantel test in equation (1). The gray dots represent the locations of the sampled populations. The large circles correspond to the continental analyses, whereas the smaller circles correspond to the analyses of regions within continent.

Because of the large number of populations available in the European data set (n = 38), we conducted an intensive robustness analysis for this continent. First, we removed all populations with only one or two sampled individuals as well as the late settlement Finnish isolate (LSFIN) resulting in a total of n = 30 populations with 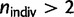. We found the same NNW–SSE orientation of maximum differentiation with a greater correlation between 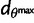and F_ST going from R² = 26% for the complete sample with n = 38 populations to R² = 53% for the sample with n = 30 populations. Second, we investigated to what extent the results obtained with n = 30 populations (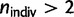) were robust with regard to the removal of the particularly large number of Southeastern populations present in POPRES. If Cyprus and Turkey, the two most Southeastern populations, were removed, the axis of maximum differentiation shifted from a NNW–SSE orientation toward an N–S orientation with the bearing-dependent slope in equation (1) still being significant (supplementary table S3, Supplementary Material online). If all other Southeastern populations (supplementary table S5, Supplementary Material online, for the list of populations) were removed, the orientation of maximum differentiation hardly changed, going from 167° to 161°. However, if Cyprus, Turkey, and all other Southeastern populations were excluded the anisotropic terms ceased to be significant (supplementary table S3, Supplementary Material online). Third, we found that the major orientation of genetic differentiation remained unchanged if we removed the Fennoscandian populations (supplementary table S3, Supplementary Material online). Finally, we also performed SNP pruning based on a linkage disequilibrium statistic. We considered a sliding window approach where we removed one of a pair SNPs when the r² pairwise statistic was larger than 0.5 (window size of 50 SNPs and step size of 5 SNPs). Using this procedure, we removed one-half of the SNPs, but we found the same NNW–SSE orientation of maximum differentiation. Similarly, the NNW–SSE orientation was consistently found when rare variants (minor allele frequency smaller than 20%) were removed.

Finally, because the sampling in Europe is particularly unbalanced—with sample sizes ranging from 1 individual (e.g., in Ukraine) to 200 individuals (in UK)—we investigated whether the results are influenced by the sampling scheme. We removed all populations with sample sizes smaller than 10 individuals and chose at random 10 individuals in each of the other populations. Performing 10 random replicates of this resampling approach, we found that the angles that provide the direction of maximum differentiation were always between 165° and 176° for both the geometric and the regression method. Using a threshold of 5 individuals instead of 10 provided similar results with angles between 164° and 178°. The fact that the directions are slightly shifted toward the N–S orientation results from the removal of the Cyprus and Turkey samples, which contain four individuals each (supplementary table S3, Supplementary Material online). This additional analysis confirms that the direction of maximum differentiation in Europe is not an artifact caused by the unbalanced sampling scheme of POPRES.

Comparison of the Continental Levels of Genetic Differentiation

In addition to investigating the orientations of maximum genetic differentiation, we compared the extent of genetic differentiation across continents. Using the fitted regressions of equation (1), we computed the expected F_ST between two putative populations that are located at the same place and between two populations separated by a distance of 1,000 km along the orientation of maximum differentiation (fig. 4 and supplementary fig. S5, Supplementary Material online). When comparing two nearby populations, Europe was found to be the continent with the smallest genetic differentiation (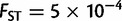) followed by Asia (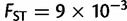), Africa (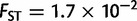), and America (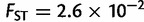). When comparing two populations separated by 1,000 km along the axis of main differentiation, the ranking stays the same: Europe (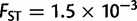) followed by Asia (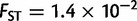), Africa (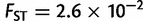), and America (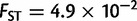). The genetic differentiation between two European populations separated by 1,000 km remained at least one order of magnitude smaller than two nearby African, American, or Asiatic populations. Although these findings may reflect the different pattern of genetic differentiation, they may also reflect the different sampling strategies of POPRES and the HGDP, with the POPRES individuals mainly coming from urban locations, and the HGDP focusing on more isolated populations which form tighter genetic clusters than the POPRES populations (Auton et al. 2009).

Fig. 4.

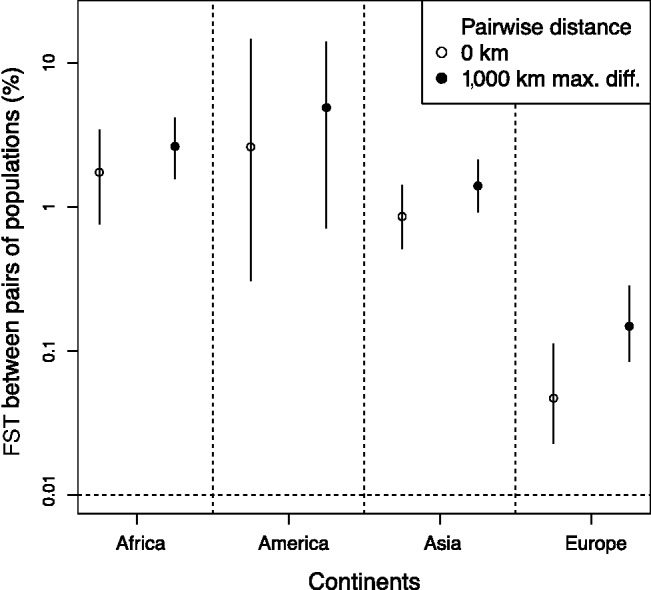
Prediction of average F_ST for pairs of populations separated by 0 and by 1,000 km along the axis of maximum differentiation. The logit-transformed F_ST was regressed with equation (1) to constrain the predicted F_ST to lie between 0 and 1.

Anisotropic Simulations

To check whether MDS, the geometric method, and the regression method accurately provided the orientation of main genetic differentiation, we carried out simulations under an IBD model with different short-range migration rates along N–S and E–W orientations. We performed simulations on a grid that mimicked Europe (supplementary fig. S6, Supplementary Material online), and we considered four sampling schemes to pick n = 38 populations containing 10 sampled individuals each: a uniform sampling over the whole grid (including water), a sampling similar to the European data, a sampling on a narrow N–S band, and a sampling on the narrow N–S band where we sampled only the populations at the upper ends of the band (clustered sampling, supplementary fig. S6, Supplementary Material online). When the axis of main differentiation was N–S, all three methods with all four sampling schemes captured the true orientation (supplementary fig. S7, Supplementary Material online). If the main orientation of genetic differentiation was E–W, all three methods performed well when sampling the populations over the whole grid or when mimicking the actual sampling of the European data. However, if the sampling was performed on a narrow N–S band, the geometric method failed because of the peculiar sampling scheme. For the case of a narrow N–S band with sampling at the upper ends of the N–S band, both MDS and the geometric method returned an N–S orientation instead of the actual E–W orientation (supplementary fig. S7, Supplementary Material online). The regression method of equation (1) appeared much more robust to the sampling scheme though it was slightly biased (for the clustered sampling scheme the mean value of the estimates was 97° instead of 90°).

Geographic Localization Based on SNPs

We applied a regression method to localize an individual’s origin based on his genotype, and we compared the localization errors in the N–S and E–W orientations. We regressed the latitude and the longitude using the scores of the PCA on the SNP data as dependent variables (eq. 3). Compared with Novembre et al. (2008) who considered the first two principal components PC₁ and PC₂ (as well as 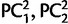, and PC₁ × PC₂) in the linear regressions, we chose the optimal number of PCs with a 5-fold cross validation routine.

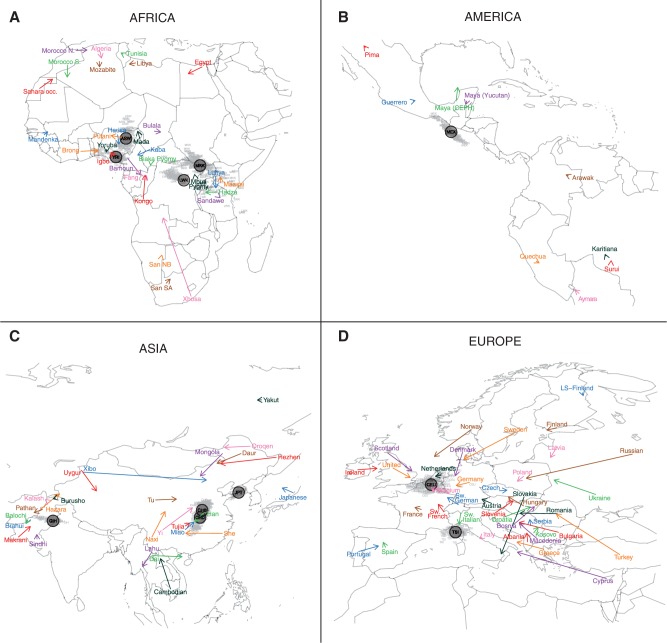
The origin of each individual was predicted using a regression model that was trained without the given individual. Figure 5 shows a map of the different continents where the true locations and the predicted locations averaged over individuals from the same population are displayed. We found that the median individual error varied considerably across continents: 250 km in America, 280 km in Europe, 430 km in Africa, and 510 km in Asia (table 3). For SNP data, considering an optimal number of principal components instead of two components decreased the median localization errors by 40–63% depending on continent (supplementary table S4, Supplementary Material online). The localization errors varied substantially between populations (supplementary fig. S8, Supplementary Material online) with two populations especially poorly localized: the Xhosa in Africa and the Xibo in Asia. That these populations were poorly localized actually reflects migration: the Xibo population originated in northeastern China, but migrated to northwestern China in the 18th century (Powell et al. 2007) and the Xhosa is a Bantu group that migrated from Central to East Africa and then to South Africa between AD 1000 and 1200 (Huffman 2006). In Europe, the populations for which the predictions were the worst are Russia, Turkey, and Cyprus, which are populations with sample size<6 and located at the border of the training set. Moreover, in Africa and Europe, we found a positive correlation (P < 0.01) between the localization errors and the individual distances to the centroid of the population samples. In all continents, the PC-regression implied some shrinkage toward the centroid of the populations because the projected values were closer to the centroid than the original data points (table 3).

Fig. 5.

Prediction of geographic origin based on SNP data. One arrow is plotted for each population. The origin of an arrow corresponds to the true location, and the arrow points to the predicted location averaged over all individuals in the population.

Table 3.

Median Errors of Geographic Localization Based on SNP Data.

	Africa	America	Asia	Europe
Optimal number of PCs	52	17	34	17
Error (km)	430	250	510	280
Relative error	0.15	0.10	0.17	0.24
Shrinkage	0.91	0.94	0.95	0.92

Note.—The relative errors are computed with respect to a naive localizer which assigns each individual to a population that is chosen at random among the sampled populations. The shrinkage is computed as the ratio of the mean distance between the predicted locations and the continental centroid and the mean distance between the true locations and the same centroid.

As a proof of concept, we investigated the localization of HapMap 3 individuals (The International HapMap 3 Consortium 2010). The individuals were neither included for learning the axes of the PCA (PC loadings) nor for the training of the regression equations. Although there were some discrepancies between the actual and predicted origins, the individuals were relatively well-assigned geographically. Utah residents with Northern and Western European ancestry (CEU) are placed in the Benelux region; Tuscans (TSI) near the French–Italian Riviera, Han Chinese from Beijing (CHB) and Chinese from Denver (CHD) are placed next to the Han populations, Japanese (JPT) are placed in Korea rather than in Japan, the Gujarati Indians from Houston (GIH) are placed a little north compared with the original Gujarat region, Massai (MKK) and Luhya (LWK) are placed eastward of the sampling location, and Yoruba are located close to the sampling area. American individuals with African ancestry (ASW) are placed north of the gulf of Guinea confirming the largely West African ancestry of present day African Americans (Bryc et al. 2010) (fig. 5). Despite of the aforementioned discrepancies, the overall localization of the HapMap 3 individuals showed the potential of the localization method.

The localization method should be sensitive to the orientation of main genetic differentiation and be more accurate in that orientation. This was true for the European data for which the median E–W error of 190 km was significantly larger than the median N–S error of 140 km (two-sided Wilcoxon test 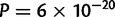, fig. 6). In Africa, the difference was not significant (P = 0.051) and both N–S and E–W errors were approximately 250 km. In America, the median E–W error of 140 km was significantly smaller than the N–S error of 180 km (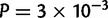). In contrast to what was expected based on the Asiatic E–W main orientation of differentiation, the median E–W error of 350 km was significantly larger than the N–S error of 200 km in Asia (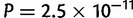). However, the sampling is more widespread along the E–W axis than along the N–S axis in Asia, and we did not account for that when comparing the median error distances in the two directions. To investigate this sampling effect, we divided each individual distance by the distance obtained with a naive localizer that picked one population in the continent at random to assign geographical coordinates to an individual. The rationale being that the error distance should be compared with the error obtained with a naive localizer to account for the possibly different difficulties of geographic localization in the two orthogonal spatial directions. After rescaling, we find the expected pattern in Africa, Asia, and Europe (errors smaller in N–S, E–W, and N–S orientations, respectively, with P = 0.034, 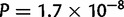, and ) and the difference in the two orthogonal orientations were not significant in the Americas (P = 0.81, fig. 6). The same results were found when considering the mean error instead of the median error (supplementary fig. S9, Supplementary Material online).

Fig. 6.

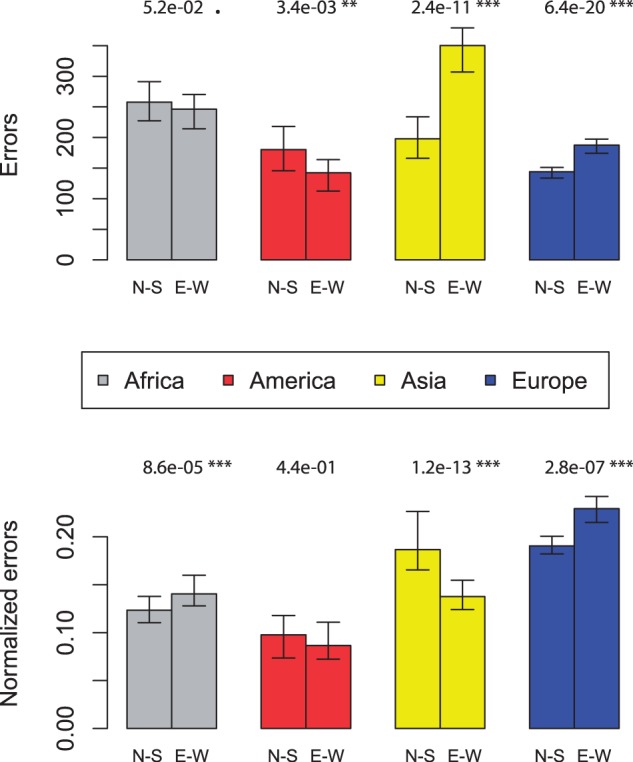
Median error of the localization method in N–S and E–W orientation. The upper panel shows the errors in km and the lower panel shows the relative error when the individual errors have been standardized by the errors obtained with a naive localizer that picks one population in the continent at random. Confidence intervals were estimated with bootstrap and P values were obtained with a two-sided Wilcoxon test.

Discussion

Continental Barriers to Gene Flow

In the “cline versus clusters” debate about the representation of human genetic diversity (Rosenberg et al. 2005), a consensus model has emerged in which most of the differentiation between human populations can be explained by continuous variations with some discontinuities arising from barriers to dispersal (Handley et al. 2007). We posit that these barriers to dispersal generate part of the anisotropy we detected. The Sahara barrier causes the N–S major orientation of African genetic differentiation since no anisotropic patterns were detected when restricting the analysis to the north or to the south of the Sahara desert (fig. 3 and supplementary table S3, Supplementary Material online). In Sub-Sahara, the absence of correlation between F_ST and geographical distances (supplementary table S3 and fig. S10, Supplementary Material online) can be explained by the presence of strongly diverged populations (e.g., San and Bantu speaking populations in southern Africa) sampled in nearby areas, and the relatively sparse population-sampling [we note that Schlebusch et al. (2012) recently provided a denser sample of sub-Saharan populations and a correlation was in fact detected]. A second important geographic barrier that has been suggested to be a barrier to gene flow is the Himalaya mountain range (Rosenberg et al. 2005; Gayden et al. 2007; Wang et al. 2012). However, the paucity of the HGDP populations around the Himalayas makes it difficult to investigate the role of the Himalayas in shaping the pattern of Asiatic genetic differentiation. Reassuringly, the E–W pattern of Asiatic genetic differentiation fits well with the major division of Asia into an Eastern and Western Asiatic genetic clusters (Rosenberg et al. 2002) with the restriction that both conclusions are drawn from the same HGDP populations, which are biased toward population isolates and are not representative of the present day population density (Cavalli-Sforza 2005).

Spatial Range Expansion in Europe

In addition to the continental barriers to gene flow, spatial range expansion can generate anisotropic patterns of genetic differentiation. Using computer simulations of spatial expansion scenarios, François et al. (2010) showed that genetic distances increased significantly faster with geographic distances along the transect perpendicular to the expansion than along the orientation of the expansion (see also Arenas et al. 2012). A spatial range expansion model that has been thoroughly investigated is the European “demic diffusion” model. This model posits that Neolithic farmers migrated into Europe in a SE to NW expansion from the near east and replaced Paleolithic populations of hunter–gatherers with little or no admixture (Ammerman and Cavalli-Sforza 1984; Chikhi et al. 2002). Because the orientation of greatest differentiation should be perpendicular to the orientation of expansion, the NNW–SSE axis of main European differentiation (Seldin et al. 2006; Bauchet et al. 2007; Tian et al. 2008; McEvoy et al. 2009) is not explained by the Neolithic demic diffusion model. Nonetheless, if Neolithic farmers admixed with the local Paleolithic populations and if the proportion of Paleolithic genes in the current gene pool is as large as 80%, the orientation of main differentiation is not necessarily orthogonal to the Neolithic expansion and depends on the starting point of the Paleolithic expansion (François et al. 2010). This admixture scenario received support from Skoglund et al. (2012) who demonstrated that Northern European Neolithic farmers originated from Mediterranean populations and that they eventually admixed with local hunter–gatherers to form the present day Northern European gene pool. Another evolutionary scenario that is compatible with the NNW–SSE axis of main European differentiation would be a northeastward spatial expansion from the Iberian refugium after the last glaciation (Bocquet-Appel et al. 2005; Pereira et al. 2005; Soares et al. 2010).

Orientation of Continental Axes and Patterns of Gene Flow

Diamond (1997) proposed that because populations at the same latitude experience the same climate, technological diffusion was more easy and rapid in the E–W direction than in the N–S direction. If the spread of technology accompanied the spread of people as assumed by the demic diffusion models (Diamond and Bellwood 2003), the level of genetic differentiation should then be the greatest along the N–S orientation. In Africa and in Europe, we show that Diamond’s prediction holds, but we found the opposite pattern in Asia. In addition, America was found to be the sole continent to lack an anisotropic pattern of genetic differentiation and it lacks an isolation-by-distance pattern at all. Because of the small number of populations in the Americas (n = 9), we additionally considered microsatellite data obtained for 29 Native American populations (Wang et al. 2007). The analysis of these data confirmed the absence of a pattern of IBD at the continental scale in the Americas (Mantel test P = 0.93, supplementary table S3, Supplementary Material online) and no orientation provided a positive correlation between genetic distance and orientational distances d_θ with a coefficient of determination R² larger than 2% (supplementary fig. S11, Supplementary Material online). The strong isolation experienced by some populations after divergence might have obscured the global signal of isolation-by-distance. For instance, the F_ST between Ache and Guarani populations is relatively large although the populations are very close geographically.

Diamond (1997) also hypothesized that the E–W axis of orientation of the Eurasian landmass explains the relatively faster spread of technology on this continent compared with the Americas which is oriented along the N–S axis. If technologies followed human migrations, then genetic differentiation should increase more rapidly along meridians in America than along parallels in Eurasia. Ramachandran and Rosenberg (2011) explicitly tested Diamond’s hypothesis and found that genetic differentiation increases per geographic unit more rapidly along meridians in the Americas than along parallels in Eurasia. Because the level of genetic differentiation differs by 1–2 order(s) of magnitude when comparing Native American F_STs with European or Asiatic F_STs (fig. 4), such comparisons are nevertheless quite difficult; F_ST-related measures such as the rate of increase of F_ST along a given direction, are likely to be larger in Native Americans than in any other group of populations because of the difference of scale. In addition, the lack of correlation between genetic and geographic distances in the Americas stresses the difficulty of quantifying the—longitudinal or latitudinal—rate at which genetic differentiation increases for Native American populations.

Limit of the Anisotropic and Localization Methods

Providing the orientation of main genetic differentiation is a descriptive tool to investigate the pattern of genetic differentiation. As with other descriptive techniques, such as PCA, deciphering the evolutionary processes that produced the observed pattern is of interest when studying human evolution. However, there is no one-to-one correspondence between evolutionary processes and statistical summaries of the data and it has been shown that different evolutionary scenarios can produce the same PCA configuration (McVean 2009). Since there are strong relationships between F_ST and PCA, it is conceivable that the same restrictions apply to the F_ST-based anisotropic methods presented here. For instance, we cannot determine whether the European anisotropic pattern is explained by a nonequilibrium range expansion model (François et al. 2010) or by an equilibrium isolation-by-distance model, which assumes long-term unequal migration rates in the two orthogonal spatial dimensions (Wilkinson-Herbots and Ettridge 2004; Novembre and Slatkin 2009). A second limitation of the anisotropic methods presented here concerns their sensitivity to the sampling scheme. Although the regression method of equation (1) was robust with respect to the sampling scheme (supplementary fig. S7, Supplementary Material online), the patterns of anisotropy found with MDS and the geometric method were influenced by the sampling scheme. Sensitivity to the sampling scheme is a common feature when investigating patterns of population differentiation. For instance clustered sampling schemes affect the ascertainment of population structure with clustering techniques (Schwartz and McKelvey 2009) and the axis of greatest variation in PCA can be either parallel or perpendicular to the axis of spatial expansion depending on the sampling scheme (DeGiorgio and Rosenberg 2012). However, by contrast to PCA, which is strongly influenced by uneven sampling schemes (McVean 2009), the regression, geometric, and MDS methods are population-based rather than individual-based and should be less sensitive to uneven sampling schemes (different number of individuals per population). Regarding the sampling of the investigated data, the HGDP data set, which provided the Asiatic and African populations samples and some of the American samples we analyzed, is biased toward isolated populations of anthropological interest. The HGDP collection of populations additionally suffers from discontinuities in geographical distribution of populations such as the gap of 20° of longitude that exists in Asia around the meridian of longitude 90° (Cavalli-Sforza 2005). The POPRES sampling in Europe is not biased toward population isolates as in the HGDP and covers all Europe although Western European populations have been more intensively sampled (n ≥ 100 for Italy, UK, Spain, Portugal, and Switzerland). A final issue concerns the localization approach based on PCA-regression, which weakly shrinks the predicted locations toward the centroid of the data. Shrinkage was detected also for the HapMap 3 individuals that did not contribute to the construction of the PC loadings (eigenvectors). The CEU sample from HapMap 3 was for instance located in the Benelux, whereas it is generally claimed to be of more Northern origin (He et al. 2009) as found using nearest neighbor regression instead of PCA-regression (Drineas et al. 2010). The Tuscany sample was similarly shrunk and pushed toward the French–Italian Riviera with PCA-regression, whereas it was better located using nearest neighbor regression (Drineas et al. 2010).

Conclusion

In summary, we have shown that the rate at which genetic differentiation increases differs according to orientations in Africa, Asia, and Europe, but not in the Americas. Confirming Jared Diamond’s predictions, genetic differentiation increases more rapidly along the N–S axis in Africa and Europe. However, the E–W axis of main genetic differentiation in Asia is at odds with Diamond’s prediction, but the current sampling of the HGDP populations is not satisfactory because it is not representative of the present day population density in Asia. Interestingly, the N–S orientation of anisotropy in East Asia is different from the overall Asiatic E–W orientation although the test for anisotropy did not reach the 5% significance threshold in East Asia (fig. 3 and supplementary table S3, Supplementary Material online). More generally, the current effort of sampling in different places of the world will provide a more detailed picture of the pattern of anisotropic differentiation. A future objective will be to move from coarse-grain anisotropic continental patterns to much more finer scales. In addition to humans, such anisotropic analyses can add to the description of genetic differentiation for many species with prevalent patterns of IBD and can help to investigate the expansions of invasive species or the processes of plant dispersal.

Materials and Methods

Genetic Data

We assembled data from 2,599 individuals drawn from 101 populations genotyped at hundreds of thousands of SNPs (table 1). In Europe, this included 1,466 individuals from 37 European populations of the Population Reference Sample (POPRES) (Nelson et al. 2008). The geographic location assigned to each European population was the central point of the geographic area of the country with some exceptions (provided by Novembre et al. 2008). We extended the POPRES data by adding 40 individuals from the Finnish capital area (Surakka et al. 2010) to the Finnish sample of POPRES (FIN), which originally consisted of a single individual. We additionally added a sample from the LSFIN of Northeastern Finland (Surakka et al. 2010). In total, there were 38 European populations. In Asia, we considered the 428 individuals from the 26 Asiatic populations of the HGDP-CEPH sample (Li et al. 2008). In Africa, we considered the data set compiled by Henn et al. (2011), which consists of 587 individuals from 29 populations. The Native American sample was compiled by Bigham et al. (2010) and contains 118 individuals from 9 populations. We additionally considered 678 microsatellite markers typed for 29 Native American populations (Wang et al. 2007). The geographic locations associated with the Asiatic, Native American, and African populations were provided by the aforementioned references. The number of SNPs available varied across continents with approximately 55,000 SNPs available in Africa, 440,000 SNPs in America, 660,000 SNPs in Asia, and 280,000 SNPs in Europe (table 1). We additionally predicted the geographic origin of 1,397 individuals from 10 populations of the third phase of the International Haplotype Map Project (The International HapMap 3 Consortium 2010).

When merging data from different SNP-chip versions, strand identification can be ambiguous leading to potential problems of identifying alleles for A/T and G/C SNPs. During the quality control, all A/T and G/C SNPs were removed for the European data (by us) and for the African data (by Henn et al. 2011). The Asian data were generated by the same SNP-chip version (Li et al. 2008). Quality control was performed for the American data although A/T and G/C SNPs were not removed (Bigham et al. 2010). To allow direct comparisons with the study of Bigham et al. (2010), we did not perform additional quality control with their data; however, we searched for potential allele mis-identifications among A/T and G/C SNPs, and found that the differences in minor allele frequencies between two Maya populations (typed by two different SNP-chip versions) were very similar for all SNP types. Being conservative and excluding the few SNPs identified as being potentially flipped did not impact the results of PCA, and are not expected to affect other analyses.

Multivariate Methods for Data Exploration

We first applied MDS and PCA to provide a geographic visualization of genetic clines. The pairwise F_ST values were computed with the formula of Weir and Cockerham (1984). Classical MDS of the pairwise F_ST data matrix was performed with the cmdscale R function (R Development Core Team 2011). PCA of the SNP data was performed using smartpca, part of the EIGENSOFT 3.0 package (Patterson et al. 2006).

Regression and Geometric Methods for Characterizing Anisotropy

To find the orientations of maximum differentiation and to formally test for anisotropy, we considered two different methods. These methods are based on extensions of the regression model for IBD that relates F_ST measures of genetic differentiation to geographic distances (Slatkin 1993; Rousset 1997).

The first method is based on the regression equation (1) that provides the rate of increase of F_ST for different geographical directions. In equation (1), the distance d along a line of fixed direction—that crosses all meridians at the same angle—is called the loxodromic distance (fig. 2) and differs from the great-circle distance although the differences are small at the continental scale (e.g., less than 3% for all pairs of populations in Asia). We consider the first order Fourier expansion for the rate β + γ (θ) at which genetic distances increase with spatial distances such that

(2)

Equation (2) defines a π-periodic function because the directions we are considering are not oriented, for example, there is no distinction between the N–S and S–N orientation. The orientation of main orientation is given by the angle θ for which 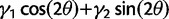is maximal.

The test for anisotropy assesses if both regression coefficients γ₁ and γ₂ are significantly different from 0. To provide a P value, we first regressed the pairwise F_ST with the distance d to obtain a matrix of residuals. We then regressed the residuals on cos(2θ)d and sin(2θ)d, and we used the R² as the test statistic. To find the distribution of the test statistic under the null hypothesis of isotropy, we considered a partial Mantel test procedure in which we randomly permuted the rows and columns of the matrix of residuals (Legendre 2000).

In the second extension of the IBD model, the geometric method, we computed, for each angle θ, the linear correlation between F_ST and an orientational distance d_θ that corresponds to the distance between two populations when their coordinates are projected to a line of bearing θ (fig. 2). For instance, for two populations located on the same meridian, as it is approximately the case for Oslo and Florence, the distance along a bearing of 90° (E–W orientation), 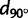, is null, whereas the distance along a bearing of 0° (N–S orientation), 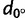, is approximately equal to the loxodromic distance between the two populations. To perform the computations of d_θ, we considered the Mercator projection because a loxodrome is a straight line in the Mercator projection. We then considered the coordinates of the projected populations (x₁, y₁) and (x₂, y₂) in a new system of coordinates where the first axis is a straight line of orientation θ (with respect to the meridian) and the second axis is orthogonal to the first one. The distance d_θ is given by the loxodromic distance between the points of coordinates 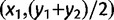and 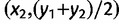(fig. 2). The angle θ^max maximizes the correlation between the pairwise values of d_θ and the pairwise F_ST values.

All the quantities related to spherical trigonometry (bearing, loxodromic distance, Mercator projection) were computed with the dedicated functions of the R geosphere package. For both the regression and the geometric method, the confidence intervals of the orientation of maximum differentiation were obtained with nonparametric bootstrap. The quantiles used to define the limits of the confidence intervals were computed using the circular R package that is dedicated to angular data. For the simulations of anisotropic isolation-by-distance patterns, the framework of the geometric method was also used to provide the orientation under which the first component of MDS varies the most. For each angle θ, we computed the correlation between the pairwise distances d_θ and the pairwise differences (in absolute value) of the first component of MDS and we returned the angle of maximum correlation.

Source codes in R for the regression and geometric methods are available at (http://membres-timc.imag.fr/Michael.Blum/Software.html; last accessed November 28, 2012).

Simulations of Anisotropic Patterns

To test the different methods that account for anisotropy, we simulated anisotropic IBD patterns with ms (Hudson 2002) using a 20 (N–S) × 24 (E–W) grid. Neighboring demes that are on the same meridian or the same parallel were separated by the same loxodromic distance (supplementary fig. S6, Supplementary Material online). The total N–S and E–W distance of the grid is 2,850 and 3,420 km, respectively and it covers all Europe (supplementary fig. S6, Supplementary Material online). The simulations with a major E–W orientation of differentiation assume that 4Nm = 5 for neighboring demes on the N–S axis whereas 4Nm = 1 between E–W neighboring demes. The parameter N denotes the local effective population size and m denotes the migration rate between neighboring demes. The two migration rates were swapped for simulating a major N–S orientation of differentiation.

Localization Methods

We predicted the latitude and the longitude of a given individual using the PCA-regression equation (Jolliffe 2002)

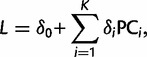(3)

where L denotes either latitude or longitude, PC_i denotes the score for the ith principal component computed from SNP data, and K denotes a given number of PCs to use. PCA was applied once for all individuals and the two regressions of equation (3) were trained five times on different overlapping subsets of individuals to perform 5-fold cross validation. We chose the optimal value of K by minimizing the mean great-circle distance between predicted and actual locations. For the HapMap 3 individuals, the individuals were projected onto the PC axis after the learning of the PC loadings (eigenvectors). To compute the E–W distances d_EW and N–S distances d_NS, we considered the equirectangular projection, which computes and 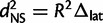where R is the radius of the earth, Δ_long and Δ_lat are the differences of longitude and latitude between the two points and cos(lat) is the cosine of the average latitude.

Supplementary Material

Supplementary tables S1–S7 and figures S1–S11 are available at Molecular Biology and Evolution online (http://www.mbe.oxfordjournals.org/).