Skip to main content
PMC home page
Genetics logoLink to Genetics
. 2013 Feb;193(2):453–465. doi: 10.1534/genetics.112.147199

Minimal Effect of Gene Clustering on Expression in Escherichia coli

Lusha W Liang 1,1, Razika Hussein 1,1, Dena H S Block 1, Han N Lim 1,2
PMCID: PMC3567736  PMID: 23222655

Abstract

Genes that interact or function together are often clustered in bacterial genomes, and it has been proposed that this clustering may affect gene expression. In this study, we directly compared gene expression in nonclustered arrangements and in three common clustered arrangements (codirectional, divergent, and operon) using synthetic circuits in Escherichia coli. We found that gene clustering had minimal effects on gene expression. Specifically, gene clustering did not alter constitutive expression levels or stochastic fluctuations in expression (“expression noise”). Remarkably, the expression of two genes that share the same chromosome position with the same promoter (operon) or with separate promoters (codirectional and divergent arrangements) was not significantly more correlated than genes at different chromosome positions (nonclustered arrangements). The only observed effect of clustering was increased transcription factor binding in codirectional and divergent gene arrangements due to DNA looping, but this is not a specific feature of clustering. In summary, we demonstrate that gene clustering is not a general modulator of gene expression, and therefore any effects of clustering are likely to occur only with specific genes or under certain conditions.

Keywords: gene colocalization, gene clustering, gene expression noise, genome organization, chromosome position effect

BACTERIAL genes that have products that interact or function within a common pathway are often adjacent to one another on the chromosome (i.e., the genes are “clustered”) (reviewed in Rocha 2008). Genes that are commonly clustered include those that encode proteins in a metabolic pathway or proteins in multi-protein complexes. Regulatory genes that encode transcription factors are also commonly located next to their target genes. Common arrangements of clustered genes are (1) codirectional (→→, genes on the same DNA strand with separate promoters); (2) divergent (←→, genes on opposite DNA strands with separate promoters); and (3) operons (→, genes on the same DNA strand with a shared promoter) (Korbel et al. 2004). Clustered genes that are located on opposite DNA strands with convergent transcription (→←) are less common.

A common functional explanation for gene clustering is that it results in more correlated gene expression. That is, genes that are next to each other on the chromosome are more likely to be affected in the same way by DNA compaction and supercoiling (Jeong et al. 2004; Kepes 2004; Peter et al. 2004; Allen et al. 2006; Mathelier and Carbone 2010), gene dosage (Cooper and Helmstetter 1968; Chandler and Pritchard 1975; Schmid and Roth 1987; Sousa et al. 1997), and neighboring sequences (De and Babu 2010). Therefore, the expression of clustered genes is expected to be more likely to increase and decrease in synchrony (due to variation in these local chromosome position effects), resulting in more correlated expression than occurs with nonclustered genes. It has been proposed that more correlated gene expression helps maintain the optimal stoichiometry of the gene products, thereby increasing efficiency and/or decreasing the concentration of toxic intermediates in metabolic pathways (Iber 2006).

While the hypothesis that bacterial gene clustering leads to more correlated expression is appealing, there is no clear evidence to support it. This hypothesis cannot be easily evaluated by comparing the expression patterns of native genes that are clustered and nonclustered because genes in clusters often share the same regulators (Hershberg et al. 2005) and/or regulate each other (Korbel et al. 2004). As a consequence, it is unclear whether a higher correlation in clustered genes compared to nonclustered genes (Korbel et al. 2004) is actually an effect of clustering itself or because their regulation is more likely to be coupled. In yeast, synthetic circuits have shown that neighboring genes are more correlated due to local chromosome position effects (Becskei et al. 2005). However, it is uncertain how applicable these findings are to bacteria, given their different mechanisms of transcription and translation. Furthermore, bacteria have different chromosome structures (Rocha 2008) and lack histones, which are largely responsible for position effects on gene silencing (Brand et al. 1985) and gene expression noise in eukaryotes (Batenchuk et al. 2011).

Given that gene clustering is common, any effect it has on gene expression could have a major impact on analyses of gene regulation and the construction of synthetic gene circuits. Therefore, we sought to directly test whether gene clustering increases correlations in expression and whether it affects other fundamental properties of gene expression. We performed the study using synthetic nonclustered and clustered arrangements consisting of two fluorescent reporter genes (cfp and yfp) that allow the measurement of gene expression in single cells. The clustered gene arrangements were assembled at two independent loci, and both coregulated (i.e., genes regulated by identical promoters) and noncoregulated (i.e., genes regulated by different promoters) arrangements were created. Gene expression in these synthetic clustered and nonclustered arrangements can be directly compared because they have identical genes and their output and regulation is decoupled from a cell’s physiology and feedback mechanisms. The first part of the study quantified maximum and minimum expression levels, cooperativity, and the inducer concentration needed for half-maximal expression in clustered and nonclustered gene arrangements. The second part of the study assessed the impact of gene clustering on stochastic fluctuations and correlations in gene expression.

Materials and Methods

Plasmids and strains

Details of the plasmids, strains, and oligonucleotides are provided in Supporting Information, Table S1, Table S2, and Table S3. The plasmids were constructed with cfp and yfp reporters under the control of the PLlacO-1 and PLtetO-1 promoters amplified from the pZ system of plasmids (Lutz and Bujard 1997). Monomeric forms of cfp and yfp were PCR-amplified from plasmids provided by R. Tsien (University of California at San Diego) (Zacharias et al. 2002; Shaner et al. 2004). We used the highly efficient ribosome binding sequence (RBS) (T7 10 5′ UTR sequence) from the pET-11a plasmid (Stratagene) to enable single chromosomal copies of the genes to be easily visualized. Plasmids were constructed as templates for PCR amplification, and the PCR product consisting of the promoter, fluorescent gene, and/or terminator was inserted into the chromosome using the lambda Red system (Datsenko and Wanner 2000).

Nonclustered gene arrangements were created by two sequential chromosome integrations. Codirectional gene arrangements were constructed by inserting one gene into the genome followed by integration of a second gene downstream of the first gene. Divergent genes were constructed by inserting the second gene on the opposite strand and upstream of the first integration. Operons were created by removing the promoter and terminator sequences separating the two genes in codirectional arrangements, resulting in a “scar” sequence of ∼82 nucleotides separating the first and second genes. Terminators were included in the gene arrangements to prevent transcription out of the fluorescent reporter genes. We found no evidence of transcription readthrough into the gene arrangements or transcriptional collisions between genes in the arrangements and neighboring sequences (see Results). All strains were verified by DNA sequencing.

Measurement of gene expression

Single colonies grown overnight in LB media were diluted 1/25,000 into fresh LB media with the appropriate IPTG concentration and grown for a further 3.75 hr at 37° and 200 rpm. The samples were harvested and placed on ice. Immediately prior to microscopy, 1.5 mL of culture was concentrated by centrifugation at 16,100 relative centrifugal force (rcf) for 1 min and resuspended in LB, and 3 μl was placed on a glass slide with a cover slip (Corning Company). Approximately five images were captured per slide using a Pixus 1024 CCD camera (Princeton Instruments) on a Nikon TE2000E inverted microscope with an X-cite 120PC lamp (Exfo) as previously described (Lim et al. 2011). Single cells were identified in each image, and their average fluorescence was measured using software (Metamorph 7.0, Molecular Devices). There were ∼360 identified cells per slide. We measured the background fluorescence levels in a control strain without fluorescent genes, which were subtracted from the above measurements.

Messenger RNA measurements

The protocol and probes used for the Northern blots were identical to that previously reported (Lim et al. 2011). Total RNA was extracted from two separate cultures for each strain at OD600 = 0.1–0.5 using the RNeasy mini kit and RNase free, DNase I (Qiagen). The membranes were probed with a 127-bp PCR product that is complementary to the 5′ end of cfp and yfp or with a 115-bp PCR product that is complementary to 16S ribosomal RNA (loading control). The probes were labeled using the DIG High Prime DNA Labeling kit (Roche) and detected with the Detection Starter Kit II (Roche) and radiographic film (Amersham Hyperfilm ECL, GE Healthcare). Digital images were captured on a Gel Doc XR imaging system (Bio-Rad) by transillumination of the film and band intensity was quantified on nonsaturated exposures with Quantity One Analysis software (Bio-Rad).

Models and simulations

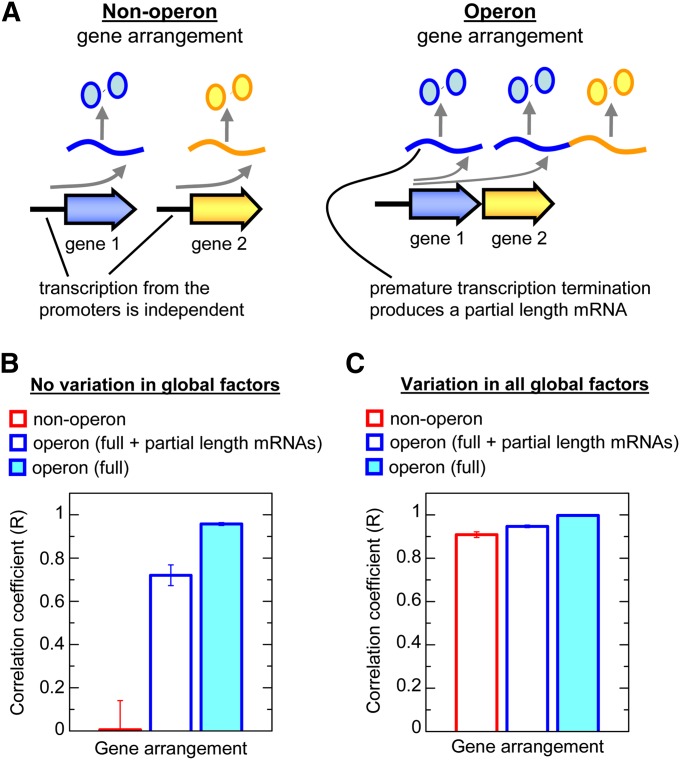
Simplified models of non-operon (nonclustered, codirectional, and divergent) and operon gene arrangements were constructed as shown in Figure 7A. Our experiments showed no convincing evidence that nonclustered, codirectional, and divergent genes had different constitutive expression or correlation coefficients; therefore, they are described by the same model—that is, two genes regulated by independent promoters (“non-operon”). The operon has a single promoter that can produce a full-length messenger RNA (mRNA) containing the sequence of two genes or a partial-length mRNA containing all the coding sequence of the first gene but not the second gene due to premature termination. Premature termination occurs randomly for 50% of transcription events.

Figure 7 .

Figure 7 

Open in a new tab

Correlation coefficients from stochastic simulations of non-operon and operon arrangements. (A) Simplified schemes for non-operon and operon gene arrangements as described in the main text. (B) Correlation coefficients of non-operon and operon gene arrangements generated by stochastic simulations in the absence of variation in global factors of gene regulation. (C) Correlation coefficients of non-operon and operon gene arrangements generated by stochastic simulations with global fluctuations (±50% of the mean) in transcription, mRNA degradation, translation, and protein degradation.

Constitutive expression by the different gene arrangement models was simulated to support the proposed bases for the findings in Figure 6. An mRNA is produced at an average rate of 0.3 mRNA molecules/min and degraded at a rate proportional to the mRNA concentration and the rate constant k−m (0.15/min). The mRNA degradation rate constant was based on a typical half-life of 5 min [i.e. ln(2)/5 min] (Bernstein et al. 2002), and this was used to calculate the production rate based on a relatively high steady-state mRNA concentration of two molecules per cell due to the strong promoter (Taniguchi et al. 2010). Protein is generated at a rate determined by the product of the mRNA concentration and the translation rate constant kp (4.0 proteins/mRNA molecule/min) and degraded at a rate proportional to the protein concentration and the rate constant kd (0.03/min). The protein degradation rate constant was determined by the growth rate as previously reported (Block et al. 2012), and this was used to calculate the translation rate constant, assuming the protein concentrations (267 proteins/cell) are higher than average (Taniguchi et al. 2010) due to high mRNA concentrations and the efficient RBS from the T7 10 gene (Olins and Rangwala 1989). It should be noted that the experimental values for the mRNA and protein concentrations may be higher than our simulated values; therefore, the simulated contribution of “intrinsic” noise to gene expression and the effect of operon arrangements on the correlation coefficient should be considered to be an upper bound.

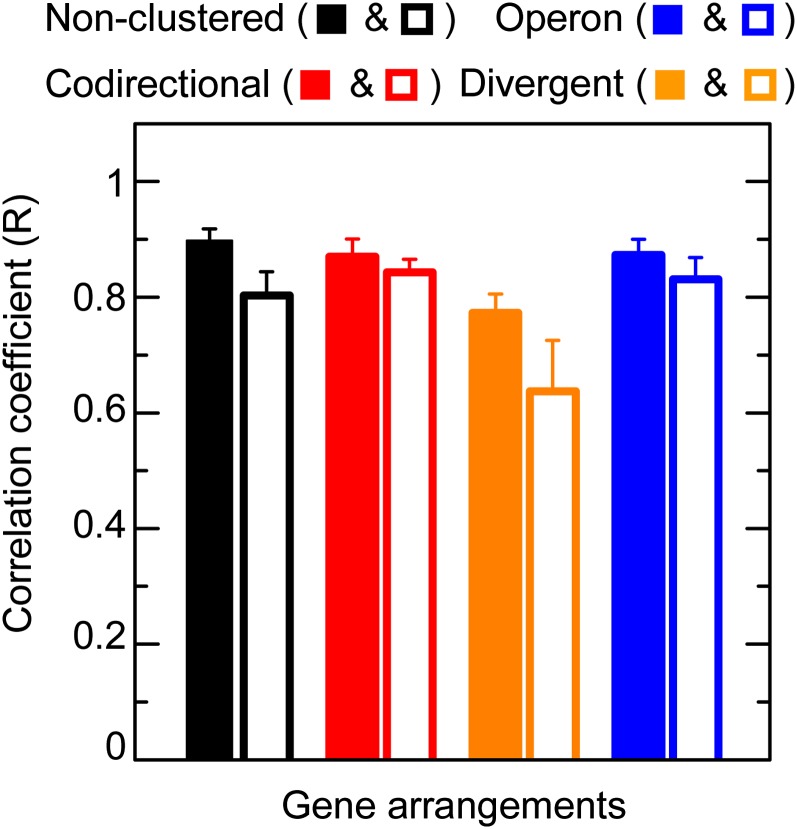
Figure 6 .

Figure 6 

Open in a new tab

Correlation coefficient of gene expression in clustered and nonclustered gene arrangements with lacI deleted. Data symbols indicate the gene arrangements shown in Figure 1A. Error bars indicate SEM of five to seven replicate measurements. Correlation coefficients are calculated from all cells. An analysis with only the cells within 2 SD of the mean expression is shown in Figure S9.

Variation in global factors such as RNA polymerase, RNase E, ribosomes, and cell growth were included in the simulations by assuming that the rate constants randomly varied from cell to cell by up to ±50% of the mean. These random differences in the global factors that alter the rate constants for the different reaction steps (transcription, mRNA degradation, translation, and protein clearance) were fixed over the time course of the simulations based on reported observations (Rosenfeld et al. 2005) and uniformly distributed over the range. The simulations were performed with Gillespie’s algorithm (Gillespie 1977) using Matlab R2008a (The Mathworks).

Results

Experimental system

Clustered and nonclustered gene arrangements were constructed using the cfp and yfp genes encoding monomeric CFP and YFP, respectively (Zacharias et al. 2002; Shaner et al. 2004) (Figures 1A and 3A; Figure S1; Figure S2). The nonclustered genes were placed at separate chromosome locations (intS and galK) approximately equidistant from the origin of replication to minimize differences in gene dosage (Cooper and Helmstetter 1968; Sousa et al. 1997). For the clustered group, three common gene arrangements were examined: (1) codirectional, (2) divergent, and (3) operon. The clustered gene arrangements were constructed at both the intS and galK sites (Elowitz et al. 2002), and the order of cfp and yfp was swapped at the two sites so we could distinguish general effects from effects that are limited to a particular locus or gene order. For simplicity, we refer to gene arrangements as being at “intS” if cfp or yfp is located at intS or the adjacent gtrAB genes and at “galK” if cfp or yfp is located at galK or the adjacent galM gene. CFP and YFP expression were measured by fluorescence microscopy (Materials and Methods).

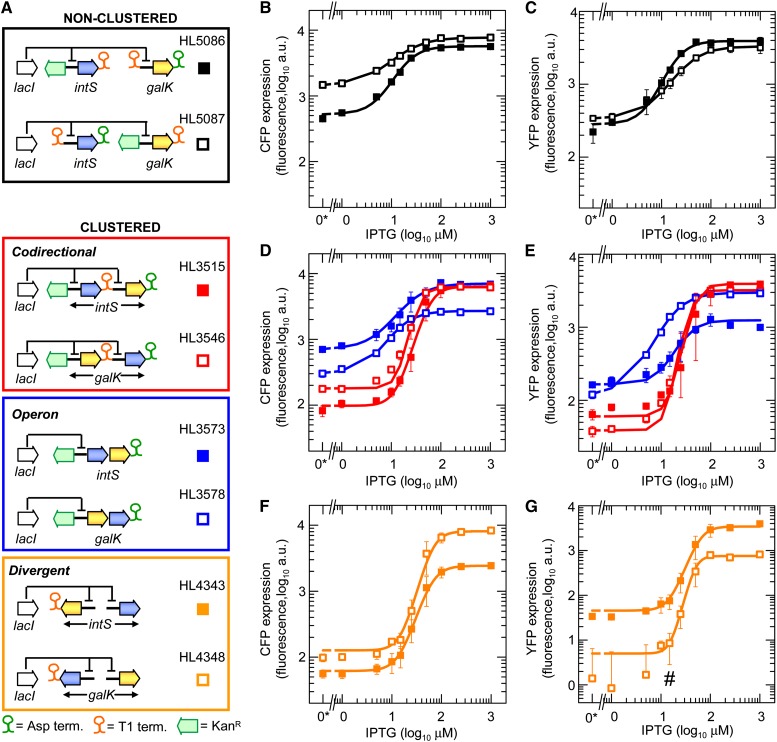
Figure 1 .

Figure 1 

Open in a new tab

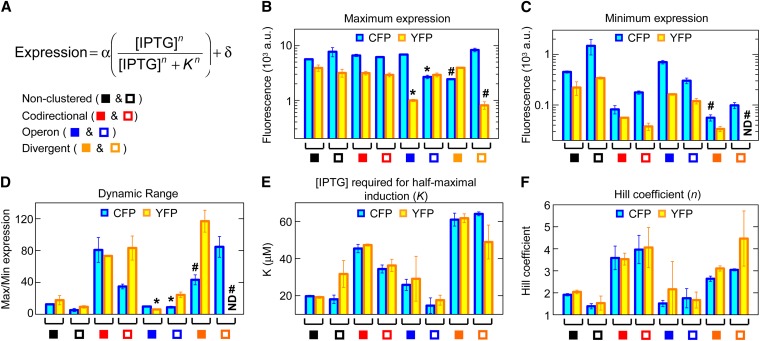
Induction curves for coregulated genes. Error bars indicate the SEM of duplicate (HL5087), triplicate (HL3546, HL3573, HL3578, HL4343, and HL4348), and quadruplicate (HL3515 and HL5086) measurements. (A) Diagram showing the arrangements of coregulated genes where LacI regulates both genes. (B–G) CFP and YFP expression at different IPTG concentrations. Data symbols indicate gene arrangements shown in A, and lines are fits obtained with the Hill function. The number sign (#) indicates expression values for HL4348 at low IPTG concentrations after background subtraction were ≤0; therefore, a small offset (5 a.u.) was added to the expression simply to enable visualization of the data on logarithmic plots. “0*” indicates an actual value of zero, not 10°.

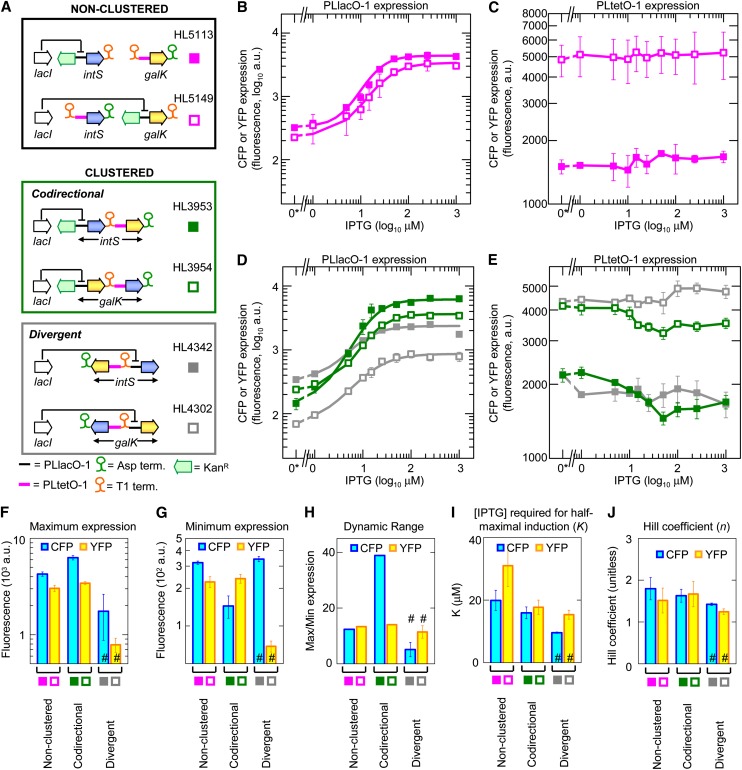
Figure 3 .

Figure 3 

Open in a new tab

Induction curves for noncoregulated genes. Error bars indicate the SEM of duplicate (HL5113 and HL5149) and triplicate (HL3953, HL3954, HL4302, and HL4342) measurements. (A) Diagram showing the noncoregulated gene arrangements where one gene has the PLlacO-1 promoter and the other has the PLtetO-1 promoter. (B–E) Induction curves for CFP and YFP expression at different IPTG concentrations. Data symbols indicate gene arrangements shown in A. Lines are fits to the Hill function in B and D. Lines in C and E are a guide to the eye. “0*” indicates an actual value of zero, not 10°. (F–J) Maximum expression, minimum expression, dynamic range, IPTG concentration required for half-maximal induction, and Hill coefficient for the different gene arrangements shown in A. A number sign (#) indicates measurements of cfp and yfp genes without terminators.

We were unable to insert the different gene arrangements into the chromosome in a single step so they were assembled piece by piece. As a consequence, in some cases the kanamycin antibiotic resistance gene (KanR) had to be left in situ to prevent loss of the inserted genes due to flanking FRT sites, and in other cases KanR was removed to permit the insertion of a second fluorescent gene. Therefore, some genes had KanR upstream of the promoter and others had a terminator upstream (Figure 1A). We made two different nonclustered gene arrangements (HL5086 and HL5087) with the upstream sequences of cfp and yfp swapped so that we could account for the effect of the different upstream sequences on gene expression. Terminators were located downstream of each gene except for one of the two genes in each divergent arrangement (for reasons that are unclear, these arrangements could not be constructed when both genes had a terminator). There was no decrease in gene expression or the correlation coefficient of nonclustered genes that would indicate that transcriptional collisions and readthrough were occurring and affecting gene expression (see sections below).

We confirmed the expected transcript lengths with Northern blots using a 127-bp cfp probe complementary to the 5′ end of cfp and yfp (100% and >99% nucleotide identity, respectively) (Figure S3). The blots showed that the transcription terminators function as expected and that there is no transcription readthrough from native flanking sequences into the gene arrangements. The blots also indicated that operons generated partial-length mRNAs as well as full-length mRNAs. Partial-length operon mRNAs are not uncommon (Nilsson and Uhlin 1991; Yarchuk et al. 1992; Patel and Dunn 1995; Khemici and Carpousis 2004). In these arrangements, the partial-length mRNAs contain the 5′ sequence and are about the length of the first gene; therefore, they are probably due to premature transcription termination at the “scar” sequence, which can form a hairpin loop between the first and second genes.

Gene clustering does not alter constitutive expression levels

In the first set of experiments, we measured the “induction curves,” which specify the steady-state gene expression at various IPTG concentrations (Figure 1, B–G), in arrangements where both cfp and yfp were transcribed from the PLlacO-1 promoter (termed “coregulated”). Expression from PLlacO-1 was varied by adding IPTG to the media, which prevents the inhibition of transcription by LacI repressor expressed from the native lacI gene. For each induction curve, we determined the maximum and minimum expression [α and δ, respectively; both expressed in arbitrary units (a.u.) of fluorescence], the IPTG concentration required for half-maximal induction (K, expressed in micromolar units), and the Hill coefficient (n, unitless) by fitting the induction curves to a Hill-type function (Figure 2A). K is a measure of transcription factor-binding affinity, and n specifies the amount of cooperativity and steepness of the induction curves.

Figure 2 .

Figure 2 

Open in a new tab

Effects of gene clustering on coregulated gene expression. Error bars indicate the SEM (number of replicates is stated in Figure 1 legend). (A) Hill function and its parameters (defined in main text). (B–F) Maximum expression, minimum expression, dynamic range, IPTG concentration required for half-maximal induction, and Hill coefficient for the different gene arrangements. Data symbols indicate the gene arrangements in A. An asterisk (*) indicates low maximum expression of cfp and yfp in the second position of the operons; a number sign (#) indicates cfp or yfp without a terminator; ND: not displayed because the values were ≤0 after background subtraction.

Maximum expression, which is a measure of constitutive expression, was similar among clustered and nonclustered gene arrangements except for genes in the second position of operons and genes lacking terminators (Figure 2B and Table S4). The reduced expression of the second gene in operons is probably due to premature transcription termination (see above), and the reduced expression of genes without terminators may be due to differences in the 3′ mRNA sequence altering its folding and translation or its degradation rate. The important point from these measurements is that highly expressed genes can be clustered without affecting each other’s constitutive expression.

The minimum expression, dynamic range (ratio of maximum to minimum expression), IPTG concentration required for half-maximal induction (K), and Hill coefficient (n), which are all measures of transcription factor binding, varied among the arrangements (Figure 2, C–F; Table S4). Nonclustered and operon gene arrangements had very similar values for all these properties. In contrast, codirectional and divergent gene arrangements had reduced minimum expression and increased dynamic range, Hill coefficient, and IPTG concentration required for half-maximal induction; together, these changes indicate increased transcription factor binding. The increased transcription factor binding is probably due to DNA looping (Oehler et al. 1990, 1994), which allows LacI bound at neighboring promoters to interact.

We next examined gene regulation in a set of noncoregulated gene arrangements where one PLlacO-1 promoter in each arrangement was replaced by the constitutively transcribed PLtetO-1 promoter (Figure 3A). Gene expression was again measured at varying IPTG concentrations (Figure 3, B–E), and the induction curves for the PLlacO-1 promoter were fitted to the Hill function. Most of the noncoregulated, codirectional, and divergent gene arrangements had similar values as nonclustered genes (excluding genes that lack a terminator) for minimum expression, dynamic range, IPTG concentration for half-maximal induction, and Hill coefficient (Figure 3, F–J; Table S4). That is, the codirectional and divergent gene arrangements no longer had increased transcription factor activity and cooperativity without the second copy of the PLlacO-1 promoter to enable LacI binding and DNA looping between neighboring promoters.

Gene clustering has minimal impact on gene expression noise

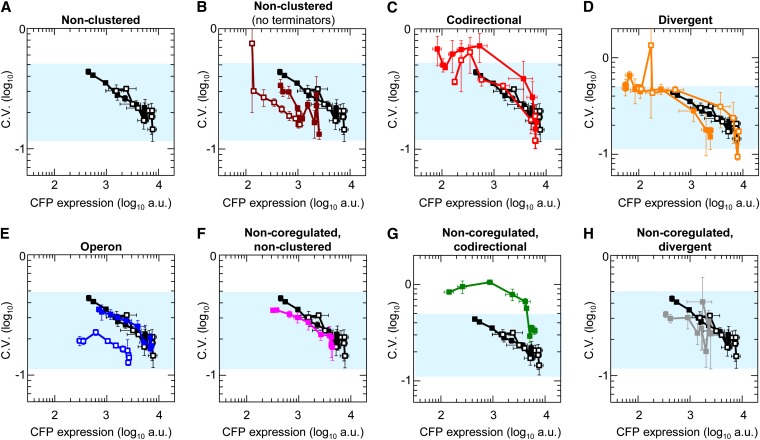
We characterized the impact of gene clustering and gene arrangements on stochastic fluctuations in expression (i.e., gene expression noise). Gene expression noise was quantified by the coefficient of variation (C.V.), which is simply the standard deviation of the expression divided by the mean. The C.V. was determined for all strains as well as an additional set of nonclustered genes without downstream terminators (configuration shown in Figure S2). The latter serve as controls for the divergent gene arrangements to determine whether any difference in expression noise is due to the arrangement itself or due to one of the genes lacking a terminator.

Our analysis showed that gene expression noise generally decreased as the mean expression increased in agreement with previous models (Paulsson 2004) and experiments (Elowitz et al. 2002; So et al. 2011) (Figure 4, A–H). We found no consistent difference in this relationship between expression noise and mean expression in clustered and nonclustered arrangements. That is, the “curve” did not move up or down in the different arrangements (with the exception of the coregulated, codirectional arrangements), which would have indicated increased or decreased expression noise for a given mean expression. The coregulated, codirectional gene arrangements displayed increased gene expression noise for both CFP (Figure 4C) and YFP at intermediate IPTG concentrations (Figure S4C). The increased gene expression noise in codirectional arrangements is likely to be due to very high levels of cooperativity (Figure 2F) and the steep induction curves (Paulsson 2004; Pedraza and van Oudenaarden 2005). An increased level of gene expression noise is observed with CFP in the noncoregulated, codirectional arrangement (Figure 4G) but YFP in the same arrangement does not show increased gene expression noise (Figure S4G).

Figure 4 .

Figure 4 

Open in a new tab

Gene expression noise for CFP in nonclustered and clustered gene arrangements. YFP expression noise is shown in Figure S4. (A–H) Each panel shows the C.V. for a different gene arrangement. The nonclustered gene arrangement with terminators serves as a reference in all plots (blue shading indicates the range of the C.V. for this arrangement). Data symbols indicate gene arrangements shown in Figure 1A and Figure 3A. In addition, we include nonclustered genes without terminators (brown symbols, B). An analysis that has only cells within 2 SD of the mean is shown in Figure S5. Error bars indicate the SEM (number of replicates is stated in the legends of Figures 1 and 3).

Nonclustered genes without terminators (Figure 4B; Figure S4B; Figure S5B) had much lower mean expression than nonclustered genes with terminators, but the maximum and minimum levels of expression noise are almost the same (resulting in the curve shifting left as opposed to up or down). That is, the free LacI concentration at 0 and 1000 μM IPTG produces the same amount of gene expression noise in nonclustered genes with and without terminators even though their mean expression is different. Therefore, the amount of gene expression noise is not primarily determined by the mean expression itself but rather by the free LacI concentration and thus the activity of the transcription factor. This finding is consistent with our previous study (Block et al. 2012) and other reports in bacteria and yeast (Elowitz et al. 2002; Pedraza and van Oudenaarden 2005; Rosenfeld et al. 2005; Skupsky et al. 2010). In summary, our measurements show that gene clustering and arrangements do not directly influence gene expression noise but can indirectly modulate it by altering transcription factor binding.

The correlation coefficient is modulated by transcription factor binding

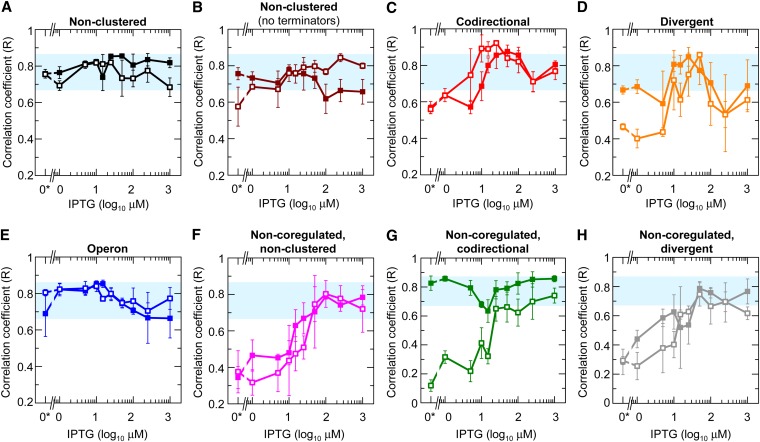
It has been proposed that stochastic fluctuations in gene expression will be more correlated for clustered genes (particularly for operons) compared to nonclustered genes (Swain 2004; van Hoek and Hogeweg 2007; Rocha 2008). To investigate this, we calculated the correlation coefficient (R), which is a scale independent metric for assessing the linear dependence of CFP and YFP expression (Taylor 1997) (Figure S6), for all gene arrangements (Figure 5). R varies from 1 (completely correlated) to 0 (completely uncorrelated) to −1 (completely anti-correlated).

Figure 5 .

Figure 5 

Open in a new tab

Correlation coefficient as a function of IPTG concentration for clustered and nonclustered gene arrangements. (A–H) Each panel shows the correlation coefficient for a different gene arrangement. Data symbols indicate the gene arrangements shown in Figures 1A and 3A. In addition, we include nonclustered genes without terminators (brown symbols, B). Analyses including only cells within 2 SD of the mean expression are shown in Figure S7. The correlation coefficients are plotted as a function of mean expression in Figure S8. “0*” indicates an actual value of zero, not 10°. Blue-shaded regions show the approximate upper and lower bounds of the nonclustered gene arrangements with terminators. Error bars indicate the SEM (number of replicates is stated in the legends of Figures 1 and 3).

Because the correlation coefficient can be sensitive to outliers, we repeated the analyses with only those cells within 2 SD of the mean expression and we obtained similar results (Figure S7). In our system, CFP and YFP do not have equivalent intensity distributions; therefore, the “intrinsic” (uncorrelated variation in expression) and “extrinsic” (correlated variation in expression) components of the gene expression noise could not be calculated (Elowitz et al. 2002; Paulsson 2005). However, a positive correlation coefficient typically indicates the presence of extrinsic noise, and, as the extrinsic noise increases, the correlation coefficient approaches a value of 1.

The correlation coefficient for coregulated, nonclustered genes showed little change with increasing IPTG (Figure 5, A and B). Therefore the LacI concentration (and consequently its activity) appears to have little effect on the correlation coefficients of nonclustered genes in contrast to its effects on gene expression noise. The high correlation at maximum induction when LacI is unable to bind suggests that fluctuations in global factors [including RNA polymerases, ribosomes, and the growth rates of individual cells (Elowitz et al. 2002; Strovas et al. 2007; Tsuru et al. 2009)] cause the constitutive expression of the nonclustered genes to increase and decrease together.

The correlation coefficients for codirectional and divergent gene arrangements were reduced at low and high IPTG concentrations and elevated at intermediate IPTG concentrations (Figure 5, C and D). Therefore, in contrast to nonclustered genes, codirectional and divergent gene arrangements are modulated by LacI activity. At low IPTG concentrations, the correlation coefficient may be reduced for several reasons (see further explanation in the Discussion): (1) there is strong repression resulting in decreased mean expression and increased intrinsic noise; (2) the induction curve is “flat” at low-IPTG concentrations in these arrangements (Figure 1), making it less sensitive to fluctuations in the LacI concentration; and (3) bursts of expression may occur from only one gene due to DNA looping and partial dissociation of the bound LacI complexes (Choi et al. 2008). At intermediate IPTG concentrations, DNA looping may cause coordinated switching of the two genes between the repressed and unrepressed states. These correlated switching events plus the variation in global factors explain the slightly higher correlation in the expression of genes in the codirectional arrangement compared to the nonclustered arrangement (compare the average of the peaks in Figure 5C and Figure S7C with Figure 5, A and B, and Figure S7, A and B, respectively). At high-IPTG concentrations, LacI binding cannot occur so there is no coordinated switching of gene expression and the correlation coefficient is less than at intermediate-IPTG concentrations but still relatively high due to fluctuations in global factors.

In operons, the correlation coefficients at most IPTG concentrations were relatively constant and similar to the nonclustered arrangements (compare Figure 5E with Figure 5A). While this result was initially surprising, it is completely consistent with all our other findings. The nonclustered genes showed that most of the correlations in gene expression arise from fluctuations in global factors (i.e., extrinsic noise) and that stochastic gene-to-gene variation (i.e., intrinsic noise), which contributes to anti-correlated expression, is relatively low. Therefore, further reducing the latter by transcribing genes in the same mRNA to eliminate anti-correlated transcription events has minimal effect on the correlation coefficient (see supporting models below).

The correlation coefficient for most of the noncoregulated genes in clustered and nonclustered arrangements generally increased with the IPTG concentration (Figure 5, F–H). The exception appeared to be the noncoregulated, codirectional arrangement (HL3953, Figure 5G), but this was primarily due to a small number of outliers (Figure S7G). The general increase in the correlation coefficients can be explained by fluctuations in the global factors having opposing effects on PLtetO-1 and PLlacO-1. Global factors that cause gene expression from PLtetO-1 and PLlacO-1 to increase will also increase LacI production and thus act to repress some of the expression from PLlacO-1. The net result is a decrease or a smaller increase in PLlacO-1 expression compared to PLtetO-1 and thus a reduced correlation for the noncoregulated genes. At high-IPTG concentrations, LacI cannot bind, and therefore PLlacO-1 expression is not constrained and is free to increase and decrease in synchrony with PLtetO-1 expression in response to fluctuations in global factors, resulting in a higher correlation coefficient.

In summary, gene clustering by itself does not appear to directly modulate the amount of correlation in gene expression, but certain arrangements can do so indirectly via DNA looping and/or highly cooperative transcription factor binding.

Constitutive gene expression is highly correlated

The above experiments at saturating IPTG concentrations strongly suggested that variation in global factors causes highly correlated constitutive expression. We deleted the lacI gene in strains with nonclustered and clustered gene arrangements to eliminate the possibility that LacI might have influenced the correlation coefficients even at saturating concentrations of IPTG. We found that, with lacI deleted, the correlation coefficient for constitutive expression was still very high and that it was similar in both nonclustered and clustered gene arrangements (Figure 6). In particular, we again observed that the correlation coefficient was not significantly higher in operons than in other gene arrangements. The correlation coefficient for the divergent arrangements was slightly lower than other arrangements, and the significance and basis of this is unclear.

It has been shown theoretically that the constitutive expression of genes in operons should be more correlated than the expression of genes in non-operon arrangements (i.e., nonclustered, codirectional, and divergent arrangements) (Swain 2004; Sneppen et al. 2010). A likely reason that this was not experimentally observed is because these models did not include variation in global factors, which minimizes the contribution of gene-to-gene variation to the total gene expression noise and the correlation coefficient. To demonstrate this point, we created models of non-operon and operon gene expression (i.e., any arrangement where two genes are transcribed in separate mRNAs and an arrangement where two genes share a single mRNA, respectively). There were two models for the operon; in one, a single promoter produced only full-length mRNAs and in the other a single promoter produced equal amounts of full-length and partial-length mRNAs as was observed experimentally (the partial-length mRNA only has the complete sequence for the first gene due to premature transcription termination).

We simulated the two models with each reaction step (transcription, mRNA degradation, translation, and protein degradation) occurring stochastically (Figure 7A and Materials and Methods). These simulations without variation in global factors showed that the expression of genes in operons was highly correlated compared to non-operon arrangements because each stochastic transcription and degradation event caused the mRNA for both genes to be created and destroyed at the same time. In contrast, the creation and destruction of the separate mRNAs for each gene in non-operon arrangements was independent, and therefore constitutive expression was less correlated. In addition, the simulations under these conditions showed that premature transcription termination has a small effect on the correlation coefficient of operon genes (Figure 7B).

We repeated the simulations with the inclusion of variation in global factors such as the concentrations of RNA polymerases, RNA degradosomes and ribosomes, and the growth rate that determines the clearance rate of stable proteins such as CFP and YFP. Variation in global factors caused the constitutive expression of genes in non-operon and operon arrangements to become more highly correlated (Figure 7C and Figure S10). However, the relative increase in the correlation coefficient was greater for non-operon arrangements, and consequently the difference in the correlation coefficients between operon and non-operon arrangements was much smaller with variation in global factors just as we observed experimentally.

In summary, the experiments and simulations demonstrate that fluctuations in global factors cause highly correlated constitutive expression in our system. As a consequence, gene clustering and the organization of genes into operons has relatively little impact on the correlation of constitutive gene expression.

Discussion

In this study, we systematically assessed the general effects of clustering and common gene arrangements on expression using synthetic circuits in Escherichia coli that allowed expression between nonclustered and clustered genes to be directly compared at identical loci and without feedback control. It would have been very difficult to characterize the effects of clustering and gene arrangements by analyzing the expression of native genes because there are too many confounding factors. Our system also enabled the assessment of multiple facets of gene expression, including constitutive expression, transcription factor activity, gene expression noise, and correlations in gene expression.

Our results showed that gene clustering and arrangements generally have minimal effects on expression. Gene clustering did not directly alter constitutive expression, gene expression noise, or correlations in gene expression. However, some clustered arrangements (e.g., codirectional and divergent) have the potential to alter transcription factor binding via DNA looping and this can indirectly alter the noise and correlations in gene expression. It must be stressed that DNA looping is not specific to clustering and can be achieved by simply having multiple transcription factor-binding sites in the vicinity of the gene (Oehler et al. 1990, 1994; Geanacopoulos et al. 2001; Schleif 2010; Lewis et al. 2011). The absence of direct effects of clustering on gene expression is very informative; as we further discuss below, it indicates that spatial differences within bacteria and along the chromosome generally have minimal impact on gene expression.

Our demonstration that gene clustering does not alter constitutive expression indicates that there is no significant competition or local recruitment of global factors even with highly expressed genes (otherwise the maximum expression of clustered genes would have been lower or higher than nonclustered genes). Therefore, there must be an excess of the global factors required for gene expression and rapid diffusion of these factors in the cell under our experimental conditions (i.e., exponential growth in rich media at 37° with vigorous mixing and aeration). However, this may not be the case during stress when cellular processes compete for ribosomes (Scott et al. 2010).

We found that the total gene expression noise in our system was not directly altered by gene clustering. However, in codirectional arrangements, an indirect increase in gene expression noise does occur at intermediate-IPTG concentrations due to their more switch-like response curves. The minimal impact of clustering and arrangements on gene expression noise is consistent with our recent finding that altering chromosome position (and thus altering local factors such as DNA supercoiling and neighboring DNA sequences) does not affect gene expression noise (Block et al. 2012).

Our measurements showed that the two major contributors to gene expression noise in our system are the transcription factor (LacI) and the global factors. Global factors may affect any aspect of gene expression, including transcription, translation, mRNA degradation, and protein degradation (Maheshri and O’Shea 2007; Shahrezaei et al. 2008). Other studies using fluorescent reporter genes have also shown that global factors are important contributors to the total gene expression noise (Elowitz et al. 2002; Pedraza and van Oudenaarden 2005; Raser and O’Shea 2005; Taniguchi et al. 2010). Fluctuations in global factors also affect LacI production and/or degradation, causing its concentration to fluctuate. Therefore, stochastic variation in global factors can both directly and indirectly (via LacI) contribute to total gene expression noise. Global factors tend to fluctuate over long timescales, resulting in cell-to-cell variation in expression (i.e., extrinsic noise) rather than gene-to-gene variation in expression within a cell (i.e., intrinsic noise) (Maheshri and O’Shea 2007; Shahrezaei et al. 2008).

Intrinsic noise arises from stochasticity in the production and degradation of mRNAs and proteins, and it generally increases as their concentrations decrease (i.e., intrinsic noise increases as the mean expression decreases) (Elowitz et al. 2002; Paulsson 2004). We were unable to directly estimate the contribution of intrinsic noise to the total gene expression noise because the reporter genes did not have equivalent intensity distributions (Elowitz et al. 2002; Paulsson 2005). However, we can get some sense of the impact of intrinsic noise from the correlation coefficient because it contributes to anti-correlated expression as well as to correlated expression whereas extrinsic noise contributes only to correlated expression. That is, if there is a significant amount of intrinsic noise, we would expect anti-correlated expression to increase (and therefore the correlation coefficient to decrease) as the mean expression decreases (Elowitz et al. 2002; Paulsson 2004).

In nonclustered and operon arrangements, the correlation coefficient was high at all expression levels (Figure 5, A and E), which suggests that the intrinsic noise is relatively small in these arrangements. In contrast, the correlation coefficient in codirectional and divergent gene arrangements was reduced at low mean-expression levels. The decreased correlation coefficient could be due to potent repression causing very low mean expression and therefore a greater amount of intrinsic noise (i.e. increased anti-correlated expression noise). However, it may also be due to other effects of DNA looping and cooperativity including a “flat” induction curve at low-IPTG concentrations (i.e. less correlated expression noise because fluctuations in the LacI concentration have less effect on the target gene) and partial dissociation of LacI complexes causing bursts of expression from only one gene (i.e. increased anti-correlated expression noise) (Choi et al. 2008).

It has been predicted that the expression of genes in operons should be much more correlated than in nonclustered genes (Swain 2004; Sneppen et al. 2010). However, our experiments and simulations show that the actual difference in the correlation in expression of nonclustered and operon genes will be relatively small when global factors are important contributors to the total gene expression noise. The expression of genes in operons will be substantially more correlated than in other arrangements only if the variation in global factors is much smaller than we observed; the transcription rate is very low so the intrinsic noise is greater (Elowitz et al. 2002; Paulsson 2005); fluctuations in the concentration and activity of the transcription factor are not causing correlated fluctuations in coregulated gene expression; and, to a lesser extent, there is minimal premature transcription termination. Fluctuations in global factors depend on the environment (reviewed in Maheshri and O’Shea 2007), so it is possible that genes in clusters and operons could have measurably higher correlations under some conditions. It is unclear how common the regulatory and environmental requirements needed to produce more correlated expression for genes in native operons occur physiologically.

While we have found no evidence that gene clustering has general functional effects on gene expression, clustering may have specific functional effects for particular regulatory mechanisms and pathways. It has been proposed that clustering may aid the coordinated folding of proteins within multi-protein complexes because translation can occur at the site of transcription (Pal and Hurst 2004). The close proximity of clustered genes also enables transcription factors at their promoters to interact and modulate their activity as we observed in the codirectional and divergent gene arrangements. Native divergent genes often have overlapping promoters (Korbel et al. 2004; Warren and ten Wolde 2004b; Bendtsen et al. 2012) that can result in the binding of a transcription factor (or RNA polymerase) at one promoter, excluding transcription factor (or RNA polymerase) binding at the other (Hershberger et al. 1993; Choy et al. 1995; Wang et al. 1998). These overlapping promoters may generate anti-correlated expression and enhance the stability of genetic switches (Warren and ten Wolde 2004a; Bendtsen et al. 2012). The arrangement of genes in operons may facilitate a “just-in-time” synthesis of components in pathways, thereby ensuring that proteins are made as they are needed to maximize efficiency (Zaslaver et al. 2004, 2006). Operons may also aid the evolvability of gene regulation because it is easier to evolve complex programs at a single promoter regulating multiple genes than at multiple promoters each regulating a single gene (Price et al. 2005).

Gene clustering may have arisen due to the many specific functional advantages that it provides for gene regulation as we describe above. However, an alternative explanation is that clustering occurs because it increases the probability that multiple genes needed to acquire and regulate a new trait (e.g., genes in a metabolic pathway) are inherited in a single horizontal gene transfer event due to their close genetic linkage, as proposed in the “selfish operon hypothesis” (Lawrence and Roth 1996). Genetic linkage and functional explanations for the origin of gene clustering and gene arrangements are not mutually exclusive and both may be important.

Our study has practical applications for the engineering of synthetic circuits, which often require several functionally related genes to generate a compound or achieve a specific function (de Lorenzo 2008; Lee et al. 2008; medema et al. 2011). It was previously unknown whether the output of synthetic gene circuits could be improved by replicating the common arrangements that occur in the genome. We have shown that clustering by itself should not be a goal or a constraint on the design of gene circuits, at least under conditions of exponential growth and high expression, which are common conditions for the use of many synthetic systems. However, in cases where genes are regulated by the same transcription factor and greater transcription factor activity and cooperativity is desired, it could be beneficial to have the genes in codirectional or divergent arrangements (at the cost of a reduced correlation in gene expression at low levels of induction). Conversely, if a graded response is required, then genes should be placed within an operon or nonclustered arrangement.

Gene clustering is a common feature of genome organization, but its impact on bacterial gene expression had not been comprehensively and systematically studied in an experimental system; this study represents an important step forward in addressing this knowledge gap. We found no difference in the constitutive expression levels, expression noise, and correlations in expression of three common clustered arrangements compared to nonclustered arrangements. While our data appear to exclude general effects of clustering on gene expression, it is possible that there may be specific genes and/or environmental conditions where clustering does modulate expression.

Supplementary Material

Supporting Information
supp_193_2_453__index.html (3.6KB, html)

Acknowledgments

We thank David Adamson for helpful discussions and comments on the manuscript, Emily Chang for assistance with fluorescence microscopy measurements, and Bernadett Gaal for constructing some of the plasmids that were used as templates for the PCR products that were integrated into the chromosome. This work was supported by start-up funds and a Committee On Research Faculty Research Grant from the University of California, Berkeley. The authors state there are no conflicts of interest. L.W.L., R.H., and D.H.S.B. made the strains and performed the measurements. H.N.L. designed the experiments, performed the analyses and simulations, and wrote the paper.

Footnotes

Communicating editor: A. Hochschild

Literature Cited

  1. Allen T. E., Price N. D., Joyce A. R., Palsson B. O., 2006.  Long-range periodic patterns in microbial genomes indicate significant multi-scale chromosomal organization. PLOS Comput. Biol. 2: e2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Batenchuk C., St-Pierre S., Tepliakova L., Adiga S., Szuto A., et al. , 2011.  Chromosomal position effects are linked to sir2-mediated variation in transcriptional burst size. Biophys. J. 100: L56–L58 [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Becskei A., Kaufmann B. B., van Oudenaarden A., 2005.  Contributions of low molecule number and chromosomal positioning to stochastic gene expression. Nat. Genet. 37: 937–944 [DOI] [PubMed] [Google Scholar]
  4. Bendtsen K. M., Erdossy J., Csiszovszki Z., Svenningsen S. L., Sneppen K., et al. , 2012.  Direct and indirect effects in the regulation of overlapping promoters. Nucleic Acids Res. 39: 6879–6885 [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Bernstein J. A., Khodursky A. B., Lin P. H., Lin-Chao S., Cohen S. N., 2002.  Global analysis of mRNA decay and abundance in Escherichia coli at single-gene resolution using two-color fluorescent DNA microarrays. Proc. Natl. Acad. Sci. USA 99: 9697–9702 [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Block D. H., Hussein R., Liang L. W., Lim H. N., 2012.  Regulatory consequences of gene translocation in bacteria. Nucleic Acids Res. 40: 8979–8992 [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Brand A. H., Breeden L., Abraham J., Sternglanz R., Nasmyth K., 1985.  Characterization of a “silencer” in yeast: a DNA sequence with properties opposite to those of a transcriptional enhancer. Cell 41: 41–48 [DOI] [PubMed] [Google Scholar]
  8. Chandler M. G., Pritchard R. H., 1975.  The effect of gene concentration and relative gene dosage on gene output in Escherichia coli. Mol. Gen. Genet. 138: 127–141 [DOI] [PubMed] [Google Scholar]
  9. Choi P. J., Cai L., Frieda K., Xie X. S., 2008.  A stochastic single-molecule event triggers phenotype switching of a bacterial cell. Science 322: 442–446 [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Choy H. E., Park S. W., Aki T., Parrack P., Fujita N., et al. , 1995.  Repression and activation of transcription by Gal and Lac repressors: involvement of alpha subunit of RNA polymerase. EMBO J. 14: 4523–4529 [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Cooper S., Helmstetter C. E., 1968.  Chromosome replication and the division cycle of Escherichia coli B/r. J. Mol. Biol. 31: 519–540 [DOI] [PubMed] [Google Scholar]
  12. Datsenko K. A., Wanner B. L., 2000.  One-step inactivation of chromosomal genes in Escherichia coli K-12 using PCR products. Proc. Natl. Acad. Sci. USA 97: 6640–6645 [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. De S., Babu M. M., 2010.  Genomic neighbourhood and the regulation of gene expression. Curr. Opin. Cell Biol. 22: 326–333 [DOI] [PubMed] [Google Scholar]
  14. de Lorenzo V., 2008.  Systems biology approaches to bioremediation. Curr. Opin. Biotechnol. 19: 579–589 [DOI] [PubMed] [Google Scholar]
  15. Elowitz M. B., Levine A. J., Siggia E. D., Swain P. S., 2002.  Stochastic gene expression in a single cell. Science 297: 1183–1186 [DOI] [PubMed] [Google Scholar]
  16. Geanacopoulos M., Vasmatzis G., Zhurkin V. B., Adhya S., 2001.  Gal repressosome contains an antiparallel DNA loop. Nat. Struct. Biol. 8: 432–436 [DOI] [PubMed] [Google Scholar]
  17. Gillespie D. T., 1977.  Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 81: 2340–2361 [Google Scholar]
  18. Hershberg R., Yeger-Lotem E., Margalit H., 2005.  Chromosomal organization is shaped by the transcription regulatory network. Trends Genet. 21: 138–142 [DOI] [PubMed] [Google Scholar]
  19. Hershberger P. A., Mita B. C., Tripatara A., deHaseth P. L., 1993.  Interference by PR-bound RNA polymerase with PRM function in vitro. Modulation by the bacteriophage lambda cI protein. J. Biol. Chem. 268: 8943–8948 [PubMed] [Google Scholar]
  20. Iber D., 2006.  A quantitative study of the benefits of co-regulation using the spoIIA operon as an example. Mol. Syst. Biol. 2: 43. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Jeong K. S., Ahn J., Khodursky A. B., 2004.  Spatial patterns of transcriptional activity in the chromosome of Escherichia coli. Genome Biol. 5: R86. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Kepes F., 2004.  Periodic transcriptional organization of the E. coli genome. J. Mol. Biol. 340: 957–964 [DOI] [PubMed] [Google Scholar]
  23. Khemici V., Carpousis A. J., 2004.  The RNA degradosome and poly(A) polymerase of Escherichia coli are required in vivo for the degradation of small mRNA decay intermediates containing REP-stabilizers. Mol. Microbiol. 51: 777–790 [DOI] [PubMed] [Google Scholar]
  24. Korbel J. O., Jensen L. J., von Mering C., Bork P., 2004.  Analysis of genomic context: prediction of functional associations from conserved bidirectionally transcribed gene pairs. Nat. Biotechnol. 22: 911–917 [DOI] [PubMed] [Google Scholar]
  25. Lawrence J. G., Roth J. R., 1996.  Selfish operons: horizontal transfer may drive the evolution of gene clusters. Genetics 143: 1843–1860 [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Lee S. K., Chou H., Ham T. S., Lee T. S., Keasling J. D., 2008.  Metabolic engineering of microorganisms for biofuels production: from bugs to synthetic biology to fuels. Curr. Opin. Biotechnol. 19: 556–563 [DOI] [PubMed] [Google Scholar]
  27. Lewis D., Le P., Zurla C., Finzi L., Adhya S., 2011.  Multilevel autoregulation of lambda repressor protein CI by DNA looping in vitro. Proc. Natl. Acad. Sci. USA 108: 14807–14812 [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Lim H. N., Lee Y., Hussein R., 2011.  Fundamental relationship between operon organization and gene expression. Proc. Natl. Acad. Sci. USA 108: 10626–10631 [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Lutz R., Bujard H., 1997.  Independent and tight regulation of transcriptional units in Escherichia coli via the LacR/O, the TetR/O and AraC/I1–I2 regulatory elements. Nucleic Acids Res. 25: 1203–1210 [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Maheshri N., O’Shea E. K., 2007.  Living with noisy genes: how cells function reliably with inherent variability in gene expression. Annu. Rev. Biophys. Biomol. Struct. 36: 413–434 [DOI] [PubMed] [Google Scholar]
  31. Mathelier A., Carbone A., 2010.  Chromosomal periodicity and positional networks of genes in Escherichia coli. Mol. Syst. Biol. 6: 366. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Medema M. H., Breitling R., Bovenberg R., Takano E., 2011.  Exploiting plug-and-play synthetic biology for drug discovery and production in microorganisms. Nat. Rev. Microbiol. 9: 131–137 [DOI] [PubMed] [Google Scholar]
  33. Nilsson P., Uhlin B. E., 1991.  Differential decay of a polycistronic Escherichia coli transcript is initiated by RNaseE-dependent endonucleolytic processing. Mol. Microbiol. 5: 1791–1799 [DOI] [PubMed] [Google Scholar]
  34. Oehler S., Eismann E. R., Kramer H., Muller-Hill B., 1990.  The three operators of the lac operon cooperate in repression. EMBO J. 9: 973–979 [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Oehler S., Amouyal M., Kolkhof P., von Wilcken-Bergmann B., Muller-Hill B., 1994.  Quality and position of the three lac operators of E. coli define efficiency of repression. EMBO J. 13: 3348–3355 [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Olins P. O., Rangwala S. H., 1989.  A novel sequence element derived from bacteriophage T7 mRNA acts as an enhancer of translation of the lacZ gene in Escherichia coli. J. Biol. Chem. 264: 16973–16976 [PubMed] [Google Scholar]
  37. Pal C., Hurst L. D., 2004.  Evidence against the selfish operon theory. Trends Genet. 20: 232–234 [DOI] [PubMed] [Google Scholar]
  38. Patel A. M., Dunn S. D., 1995.  Degradation of Escherichia coli uncB mRNA by multiple endonucleolytic cleavages. J. Bacteriol. 177: 3917–3922 [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Paulsson J., 2004.  Summing up the noise in gene networks. Nature 427: 415–418 [DOI] [PubMed] [Google Scholar]
  40. Paulsson J., 2005.  Prime movers of noisy gene expression. Nat. Genet. 37: 925–926 [DOI] [PubMed] [Google Scholar]
  41. Pedraza J. M., van Oudenaarden A., 2005.  Noise propagation in gene networks. Science 307: 1965–1969 [DOI] [PubMed] [Google Scholar]
  42. Peter B. J., Arsuaga J., Breier A. M., Khodursky A. B., Brown P. O., et al. , 2004.  Genomic transcriptional response to loss of chromosomal supercoiling in Escherichia coli. Genome Biol. 5: R87. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Price M. N., Huang K. H., Arkin A. P., Alm E. J., 2005.  Operon formation is driven by co-regulation and not by horizontal gene transfer. Genome Res. 15: 809–819 [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Raser J. M., O’Shea E. K., 2005.  Noise in gene expression: origins, consequences, and control. Science 309: 2010–2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Rocha E. P., 2008.  The organization of the bacterial genome. Annu. Rev. Genet. 42: 211–233 [DOI] [PubMed] [Google Scholar]
  46. Rosenfeld N., Young J. W., Alon U., Swain P. S., Elowitz M. B., 2005.  Gene regulation at the single-cell level. Science 307: 1962–1965 [DOI] [PubMed] [Google Scholar]
  47. Schleif R., 2010.  AraC protein, regulation of the l-arabinose operon in Escherichia coli, and the light switch mechanism of AraC action. FEMS Microbiol. Rev. 34: 779–796 [DOI] [PubMed] [Google Scholar]
  48. Schmid M. B., Roth J. R., 1987.  Gene location affects expression level in Salmonella typhimurium. J. Bacteriol. 169: 2872–2875 [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Scott M., Gunderson C. W., Mateescu E. M., Zhang Z., Hwa T., 2010.  Interdependence of cell growth and gene expression: origins and consequences. Science 330: 1099–1102 [DOI] [PubMed] [Google Scholar]
  50. Shahrezaei V., Ollivier J. F., Swain P. S., 2008.  Colored extrinsic fluctuations and stochastic gene expression. Mol. Syst. Biol. 4: 196. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Shaner N. C., Campbell R. E., Steinbach P. A., Giepmans B. N., Palmer A. E., et al. , 2004.  Improved monomeric red, orange and yellow fluorescent proteins derived from Discosoma sp. red fluorescent protein. Nat. Biotechnol. 22: 1567–1572 [DOI] [PubMed] [Google Scholar]
  52. Skupsky R., Burnett J. C., Foley J. E., Schaffer D. V., Arkin A. P., 2010.  HIV promoter integration site primarily modulates transcriptional burst size rather than frequency. PLOS Comput. Biol. 6: e1000952. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Sneppen K., Pedersen S., Krishna S., Dodd I., Semsey S., 2010.  Economy of operon formation: cotranscription minimizes shortfall in protein complexes. mBio. 1(4): e00177-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. So L. H., Ghosh A., Zong C., Sepulveda L. A., Segev R., et al. , 2011.  General properties of transcriptional time series in Escherichia coli. Nat. Genet. 43: 554–560 [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Sousa C., de Lorenzo V., Cebolla A., 1997.  Modulation of gene expression through chromosomal positioning in Escherichia coli. Microbiology 143(Pt. 6): 2071–2078 [DOI] [PubMed] [Google Scholar]
  56. Strovas T. J., Sauter L. M., Guo X., Lidstrom M. E., 2007.  Cell-to-cell heterogeneity in growth rate and gene expression in Methylobacterium extorquens AM1. J. Bacteriol. 189: 7127–7133 [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Swain P. S., 2004.  Efficient attenuation of stochasticity in gene expression through post-transcriptional control. J. Mol. Biol. 344: 965–976 [DOI] [PubMed] [Google Scholar]
  58. Taniguchi Y., Choi P. J., Li G. W., Chen H., Babu M., et al. , 2010.  Quantifying E. coli proteome and transcriptome with single-molecule sensitivity in single cells. Science 329: 533–538 [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Taylor J. R., 1997.  An Introduction to Error Analysis: The Uncertainties of Physical Measurement, pp. 327 University Science Books, Sausalito, CA [Google Scholar]
  60. Tsuru S., Ichinose J., Kashiwagi A., Ying B. W., Kaneko K., et al. , 2009.  Noisy cell growth rate leads to fluctuating protein concentration in bacteria. Phys. Biol. 6: 036015. [DOI] [PubMed] [Google Scholar]
  61. van Hoek M., Hogeweg P., 2007.  The effect of stochasticity on the lac operon: an evolutionary perspective. PLOS Comput. Biol. 3: 1071–1082 [DOI] [PMC free article] [PubMed] [Google Scholar]
  62. Wang P., Yang J., Ishihama A., Pittard A. J., 1998.  Demonstration that the TyrR protein and RNA polymerase complex formed at the divergent P3 promoter inhibits binding of RNA polymerase to the major promoter, P1, of the aroP gene of Escherichia coli. J. Bacteriol. 180: 5466–5472 [DOI] [PMC free article] [PubMed] [Google Scholar]
  63. Warren P. B., ten Wolde P. R., 2004a.  Enhancement of the stability of genetic switches by overlapping upstream regulatory domains. Phys. Rev. Lett. 92: 128101. [DOI] [PubMed] [Google Scholar]
  64. Warren P. B., ten Wolde P. R., 2004b.  Statistical analysis of the spatial distribution of operons in the transcriptional regulation network of Escherichia coli. J. Mol. Biol. 342: 1379–1390 [DOI] [PubMed] [Google Scholar]
  65. Yarchuk O., Jacques N., Guillerez J., Dreyfus M., 1992.  Interdependence of translation, transcription and mRNA degradation in the lacZ gene. J. Mol. Biol. 226: 581–596 [DOI] [PubMed] [Google Scholar]
  66. Zacharias D. A., Violin J. D., Newton A. C., Tsien R. Y., 2002.  Partitioning of lipid-modified monomeric GFPs into membrane microdomains of live cells. Science 296: 913–916 [DOI] [PubMed] [Google Scholar]
  67. Zaslaver A., Mayo A. E., Rosenberg R., Bashkin P., Sberro H., et al. , 2004.  Just-in-time transcription program in metabolic pathways. Nat. Genet. 36: 486–491 [DOI] [PubMed] [Google Scholar]
  68. Zaslaver A., Mayo A., Ronen M., Alon U., 2006.  Optimal gene partition into operons correlates with gene functional order. Phys. Biol. 3: 183–189 [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supporting Information
supp_193_2_453__index.html (3.6KB, html)
6974a71c93ab80883cad305df885b2f1_genetics.112.147199-12.pdf (872.2KB, pdf)
1267efc8857722f5dc282ea45d20687b_genetics.112.147199-4.pdf (172.3KB, pdf)
da6e7e19899bcfece8d52a1232ffb20a_genetics.112.147199-9.pdf (167KB, pdf)
eb0059eaa5224c28f728ba95cd21c3de_genetics.112.147199-1.pdf (111.9KB, pdf)
67554930daf2c9d951fdc72bd0f00396_genetics.112.147199-7.pdf (138.7KB, pdf)
9513dd363bdf85f2bb81afdf0861a5c9_genetics.112.147199-14.pdf (138KB, pdf)
b663533dcb0da0bebe779b150d2a48b1_genetics.112.147199-5.pdf (118.4KB, pdf)
c10405828560485cd32f07d0dc539aa9_genetics.112.147199-11.pdf (125.9KB, pdf)
1212ad9d8850f0f307b410de3bb80756_genetics.112.147199-2.pdf (133KB, pdf)
1368169e65211397f5173e7c8a4c808d_genetics.112.147199-10.pdf (96.5KB, pdf)
2ab2f390c4401064403b76b75b38d827_genetics.112.147199-3.pdf (95.6KB, pdf)
f2e83c5b309b5bd74306325f08f096d8_genetics.112.147199-8.pdf (83KB, pdf)
422720f649b32931ab30191553cd2e30_genetics.112.147199-15.pdf (60.3KB, pdf)
ceabc565c1275d00405e67fd48690264_genetics.112.147199-6.pdf (62.6KB, pdf)
cfc0f69c8e9f71e289e182635ca4419a_genetics.112.147199-13.pdf (89.3KB, pdf)

Articles from Genetics are provided here courtesy of Oxford University Press

RESOURCES