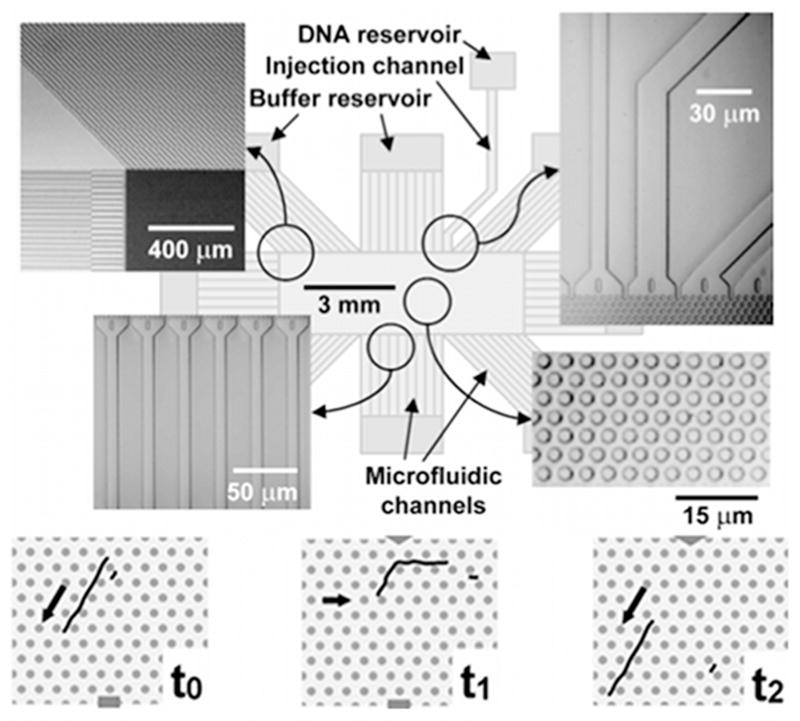
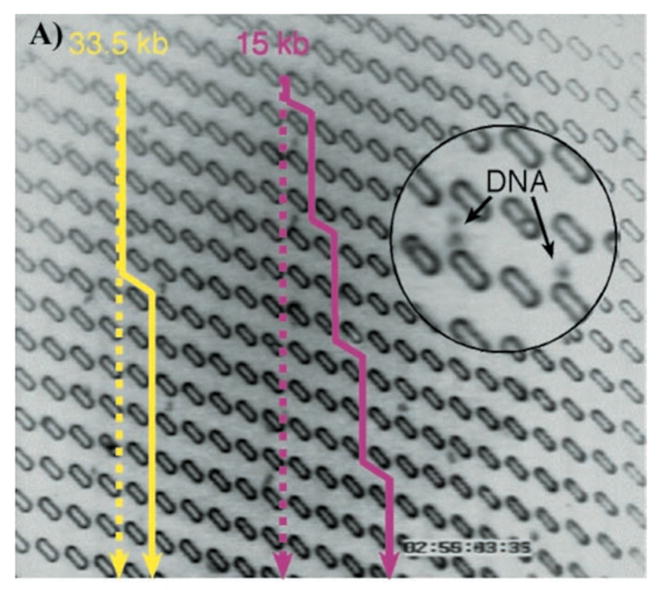
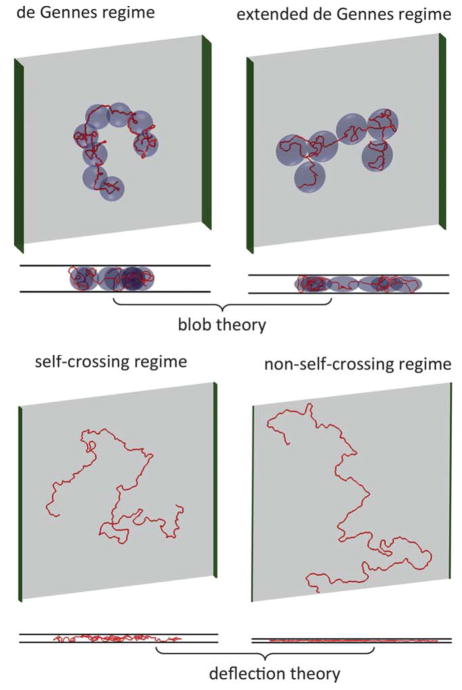
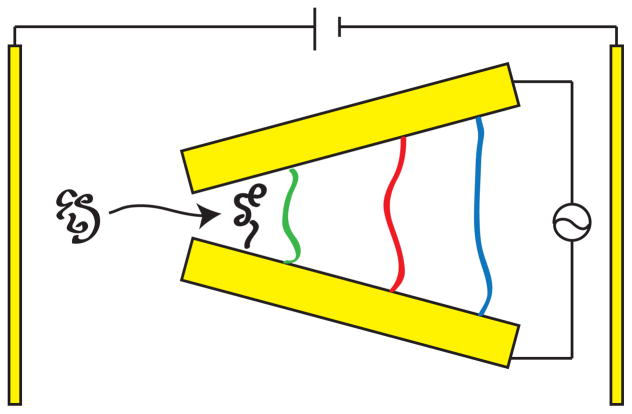
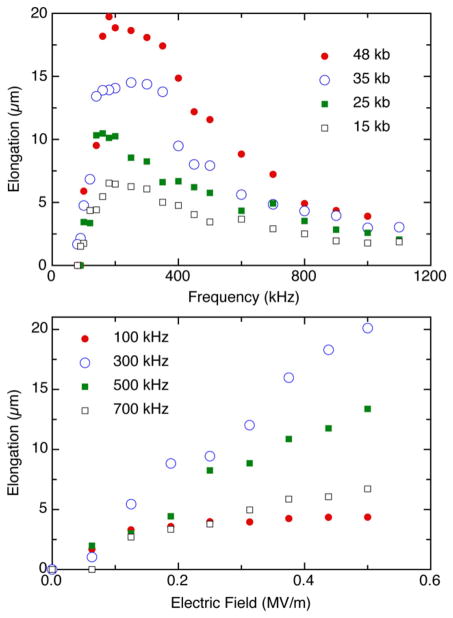
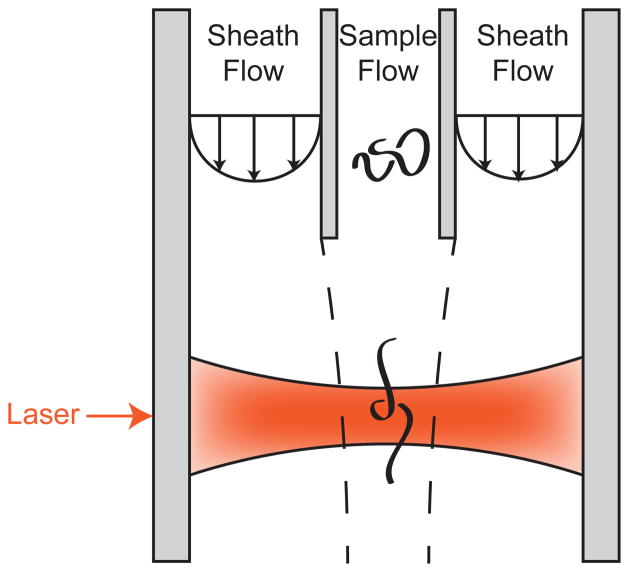
1 Introduction
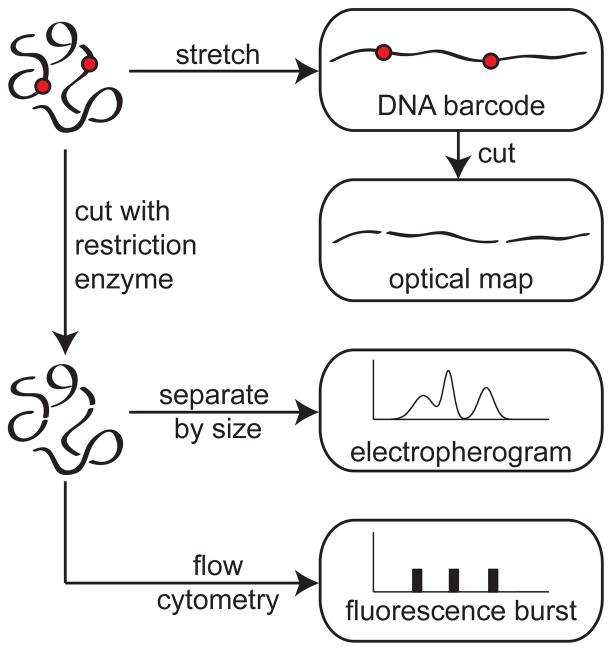
This review addresses methods for obtaining sequence information directly from unamplified genomic length DNA. Our generic starting point is a large piece of DNA that contains many thousands of base pairs (kilobase pairs, kbp) or even millions of base pairs (megabase pairs, Mbp). We would like to determine the genomic distance between two repeats of a given sequence, indicated by the red dots on the coiled DNA molecule in Figure 1. This type of large scale genomic mapping is an important complement to sequencing.1 For example, consider the challenges in obtaining “medical grade” human genome2 that contains a complete diploid genome sequence for a patient with accurate structural variation information, such as copy number polymorphism and gene rearrangements. Ideally, every patient genome should be de novo assembled independently, especially in a cancer genome with highly scrambled structural rearrangements. Unfortunately, even though sequencing costs are decreasing, high-throughput sequencing still suffers from limitations3,4 such as (i) limited read lengths, which hinders de novo genome assembly and hampers detection of large inversions,5 and (ii) difficulty with tandem repeats and telomeric regions.5–7 Even if emerging sequencing technologies deliver on their promises8–10 and enable long, accurate sequencing reads, a sequencing approach to the medical grade genome would still suffer from the “data deluge” problem of trying to store, annotate, and compare vast numbers of genomes.11 Moreover, it is not at all obvious that we need to compare every base to make a useful diagnosis. Indeed, many large genomic rearrangements in the kilobase to megabase pair range are important determinants of phenotype and disease states.12
Figure 1.
Schematic illustration of different approaches to obtain genomic information. The typical resolution of these methods is 1 kilobase pair (kbp). The red dots are meant to depict the location of restriction sites (when the DNA is cut at these location) or the location of some probe molecule (for DNA barcoding).
In this context, genome mapping is a key tool for detecting such large scale rearrangements, and we will see methods here that operate with high-throughput on single molecules of DNA. Of the many applications of genome mapping that we will discuss in Section 3, a particularly notable example is detecting copy number variants.13 These are easily seen as changes in the distance between red dots in Figure 1 but very hard to obtain from short sequencing reads. The connection between mapping and sequencing is analogous to exploring Google Maps with the zoom in/out functions. While the very localized street view (i.e., short reads from next generation sequencing) is useful, one would get lost without any contextual location information, especially when the houses look alike (i.e., copy number amplifications and repeats obtained from genome mapping).
Mapping has a long history in genomics. Let us consider the classic case where the sequences that we are trying to map are restriction sites, which can be selectively cut using proteins known as restriction enzymes. For decades, gel electrophoresis served as the standard approach for determining the sizes of restriction fragments, with pulsed field gel electrophoresis being the workhorse method when the fragments are longer than tens of kilobase pairs. While the electrophoretic mobility of DNA in free-solution depends on molecular weight only for very short DNA, typically less than around 100 base pairs (bp),14 there is a strong dependence of electrophoretic mobility on molecular weight when the DNA is forced to move through a porous medium due to the interactions between the DNA and the fibers of the gel. Agarose gels are the medium of choice for double-stranded DNA, with pore sizes in the hundreds of nanometers range.15 The sizes of the fragments are obtained by comparing their electrophoretic mobilities to known standards (often called a “ladder” with reference to the appearance of regularly spaced bands in a gel) and using theory15 to interpolating the sizes of DNA fragments in the sample with electrophoretic mobilities that are between the bands in the ladder.
The main appeal of gel electrophoresis is the minimal cost of the gel and the easy protocol. Moreover, it is simple to recover the DNA from a gel by cutting out the bands at the end of the process. Gel electrophoresis thus serves both an analytical purpose (determining the sizes of the DNA fragments) and a preparative purpose (recovery of the fractionated sample). The generic downsides of gel electrophoresis are its semi-quantitative nature, the relatively long time for analysis, and the challenges in automating the process. As an extreme example, pulsed field gel electrophoresis of megabase DNA (e.g., yeast chromosomes) can require hours to days.
Electrophoretic separations can be accelerated using DNA capillary electrophoresis in entangled polymers, especially with automated systems.16,17 The capillary electrophoresis experiment is somewhat more complicated that its gel electrophoresis counterpart, since it requires a high voltage power supply and laser-induced fluorescence (LIF) detection. However, the latter expenses are more than offset by the improved speed of the separation, the increased sensitivity of LIF, and the facile automation of the process.18,19 The physics of DNA electrophoresis in entangled polymers are quite similar to gel electrophoresis,15,20,21 although there are some subtle differences.22 Indeed, even pulsed field gel electrophoresis methods can be adapted to capillaries,23,24 albeit only in the field inversion mode. An important advance in capillary electrophoresis was the development of intercalating cyanine dyes such as YOYO and TOTO,25 which are very bright and permit the observation of single DNA molecules. These dyes play a critical role in many of the techniques that we will encounter here.
In this review, we will discuss the various approaches highlighted in Figure 1 that obtain the same information (and sometimes even more information) as pulsed field gel electrophoresis in a fraction of the total time using only a handful of DNA molecules. Indeed, a number of these methods are able to interrogate single molecules of DNA, which opens the door to understanding genomic diversity in a given species in a facile manner.26 We will consider three classes of analysis methods:
Class 1: Microfluidic separation methods. These approaches separate long DNA with higher resolution or higher speed than pulsed field gel electrophoresis. As is the case in gel electrophoresis, the size of the unknown DNA is determined by comparing its electrophoretic mobility to the electrophoretic mobilities of a known standard or a calibration curve.
Class 2: DNA stretching. In these methods, the DNA is extended from its bulk equilibrium conformation and imaged using a sensitive camera. For large genomic DNA, this method facilitates the assembly of the data, as explained in Section 4.2.
Class 3: Fluorescence burst measurements. These methods are essentially flow cytometry experiments using dyed DNA, where the size of each DNA fragment is inferred from the number of photons emitted as it passes by a detector.
The development of each of these methods started in the early 1990s, and we will review the progress of each class from its origin to the present day.
We begin our review with some requisite background information. In Section 2, we cover the physical properties of double-stranded DNA. The physics and chemistry of polymers,27,28 in particular DNA,29,30 are covered in a number of excellent textbooks and monographs. Therefore, we will restrict ourselves to those properties that are necessary to understand the physical mechanisms underlying these new classes of methods. We then continue in Section 3 by discussing the different types of sequence specific data that are obtained by the techniques covered in this review, beginning with the generic problems of restriction mapping and DNA fingerprinting (which have their origins in gel electrophoresis) and move onto the newer techniques of optical mapping and DNA barcoding (which require single molecule measurements.)
We conclude our introductory material with a discussion of how one obtains sizing data in Section 4. We begin with ensembles of molecules, which draws heavily from the excellent text on separation sciences by Giddings.31 We anticipate that the audience for this review paper may be rather diverse, since much of the seminal work in the emerging methods discussed later in our review arose from laboratories in physics and electrical engineering. Our review of the principles of separations science will not only benefit newcomers to the field, but also readers well versed in separations science who may not have noticed some of the subtleties arising in microfluidic separations. We conclude the introductory material with a discussion of what one can measure from a single molecule experiment, highlighting the relative advantages of DNA stretching and fluorescence burst analysis.
We then proceed to discuss the various methods for solving the problem outlined in Figure 1. We begin in Section 5 with a review of the classical methods in gel and capillary electrophoresis. We do not aim to have a comprehensive review of gel electrophoresis but rather want to motivate the subsequent sections. We are relatively brief and refer the reader to a number of previous reviews of DNA electrophoresis15,17,32–34 for additional details. We then move sequentially and in substantial depth through the different classes of methods in Section 6 (microfluidic separation methods), Section 7 (DNA stretching), and Section 8 (fluorescence burst measurements). At the end of Section 8, we also cover instances where several of these methods have been combined.
One of our overarching goals in this review is to discuss these three different classes of mapping technologies in a coherent way. Indeed, the first reports of all of the methods covered in Section 6 to Section 8 appeared in the early 1990s but their relative merits are rarely discussed. Thus, we will conclude our review in Section 9 with our opinion on this subject. For the moment, none of these approaches “beyond gel electrophoresis” has replaced gel electrophoresis or capillary electrophoresis as a standard method in routine use. However, several of these methods have reached a level of maturity (and, in some cases, commercialization) where they are poised to have an impact outside of the analytical chemistry community.
2 Properties of DNA
DNA is one of the most important biomolecules and the extensive work on characterizing its physical properties should not come as a surprise. There are several excellent textbooks on the subject,29,30 and we will cover only those elements that are needed to understand the material in the remainder of this review. DNA is a polyelectrolyte, so we will need to consider both its polymeric properties and its electrostatic properties.
2.1 Polymer Properties
Let us begin with a description of the polymeric properties of DNA. For the most part, we will be considering the sizing of double-stranded DNA (dsDNA) in this review. As a result, our references to “DNA” will refer to double-stranded DNA unless otherwise noted. In the canonical B-form of double-stranded DNA, the two strands of the DNA are wrapped around one another in the famous double-helix form35 with a rise of 0.34 nm/bp. Note that the latter length scale is for naked B-DNA, and insertion of intercalating dyes, such as YOYO or TOTO, increases the extension by a factor of almost 30%.36–38 For our purposes, the double helix conformation leads to two important physical properties. First, the base pairs are shielded from the external environment. Thus, to a reasonable first approximation, we can treat the DNA as a homopolymer independent of its sequence of base pairs. This model is clearly an approximation and it fails at smaller length scales, for example, when there is an A-tract that leads to a kink in the DNA39,40 or other sequences that change the bending stiffness.41 Second, the double helical conformation is very stiff relative to the 2 nm bare width of the backbone. The stiffness is characterized by the persistence length, lp, of the polymer. The persistence length is the characteristic length scale over which the correlations in the backbone tangent vector decay. A somewhat more accessible (although qualitative) definition of the persistence length is the length scale over which the polymer can be bent by thermal energy of the strength kBT, where kB is Boltzmann’s constant and T is the absolute temperature. A reasonable value for the persistence length of double-stranded DNA in a high ionic strength buffer is 53 nm,42 although we will see in Section 2.2 that the persistence length of a polyelectrolyte like DNA is a function of the ionic strength of the medium. While double-stranded DNA is not as stiff as some other biopolymers, such as actin, it is considerably stiffer than most synthetic polymers, such as polyethylene.27,28 By contrast, single-stranded DNA (ssDNA) is a much more flexible polymer. The experimental data for the persistence length of ssDNA do not lead to a clear picture, with the reported values between 0.75 nm and 5.2 nm.39,43–48 Since the bases of single-stranded DNA are not shielded from the solvent, the persistence length of ssDNA should depend more strongly on its sequence and the environment around the DNA than is the case for dsDNA.
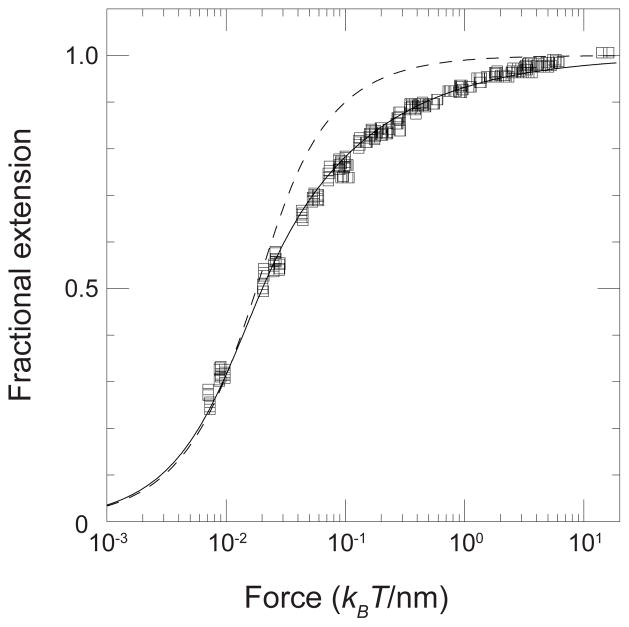
A polymer such as DNA maximizes its configurational entropy by adopting a random coil conformation in free solution. One thus needs to do work on the polymer to deform it from a random coil, for example, by pulling from the ends of the chain.51 Many of the DNA sizing methods we will explore in this review rely upon DNA deformation, so it is worthwhile to briefly discuss the topic here. The force-extension relationship is often referred to as the elasticity of the polymer. As seen in Figure 2, the entropic elasticity of DNA is well described by the exact solution to the wormlike chain model. Marko and Siggia42,50 also proposed a convenient interpolation formula to describe the force extension behavior of a wormlike chain,
Figure 2.
Fit of the wormlike chain model to the experimental force-extension behavior for a 97 kbp DNA.49 The solid symbols are experimental data. The solid line is the numerical solution of the wormlike chain model using a persistence length of lp = 53 nm and a contour length L = 32.8 μm. The dashed curve is the prediction of a freely jointed model with a segment length b = 100 nm. Reprinted with permission from Ref.50 Copyright 1995 American Chemical Society.
| (1) |
where Re is the extension (end-to-end distance) of the chain. In light of the widespread application of Eq. (1), it is not uncommon for the force-extension relationship for DNA referred to as the “Marko-Siggia” force.
Figure 2 only shows the force-extension behavior for double-stranded DNA under moderate forces, which exhibits a plateau at the contour length of the chain, L. Note that the latter parameter is obtained by fitting the experimental data, rather than assuming a rise of 0.34 nm per base pair (which would lead to a contour length of 32.64 μm in Figure 2). While the deformations that we will see in this review can be quite strong, we will still be in the regime of entropic elasticity governed by the wormlike chain model. However, we should point out that DNA overextends when the applied force exceeds around 70 pN43,52 due to structural changes in the double helix. The latter behavior contrasts with synthetic polymers, which can only be extended out to their contour length L.
The size of the DNA molecule in free solution can be described by the root-mean-squared (rms) end-to-end distance, Re. As the molecule’s conformation is a random walk, the averaged end-to-end distance is zero, but the rms value is well defined. For a wormlike chain (sometimes called the Kratky-Porod model), the equilibrium end-to-end distance in the absence of an applied force is given by28
| (2) |
When the chain is short compared to the persistence length, L ≪ lp, the DNA is essentially a rod-like molecule whose extension is Re ≈ L. In contrast, long wormlike chains where L ≫ lp lead to the end-to-end distance
| (3) |
In the polymer physics literature,27,28 one often refers to a statistical segment length, b. The latter length scale allows us to describe a large number of different polymer models (e.g., the freely jointed chain) in terms of a single length scale. The idea of the statistical segment length b has its origin in the scaling for the end-to-end distance of a random walk,
| (4) |
Comparing Eq. (3) and Eq. (4) leads to b = 2lp for the wormlike chain, which is also known as the Kuhn length. The number of segments in the random walk of a wormlike chain is the number of Kuhn segments, Nk ≡ L/b. Note that the number of Kuhn segments can be a non-integer number, since it is simply a definition.
The derivation of Eq. (2) neglected the influence of excluded volume interactions. When the chain is very long, it becomes more likely that distal segments along the chain interact. Flory53 provided the original derivation for the size of a polymer coil in the presence of excluded volume interactions
| (5) |
with ν = 3/5 being the Flory exponent. The modern value of the Flory exponent,54 ν = 0.5877, is remarkably close to the original result from Flory.
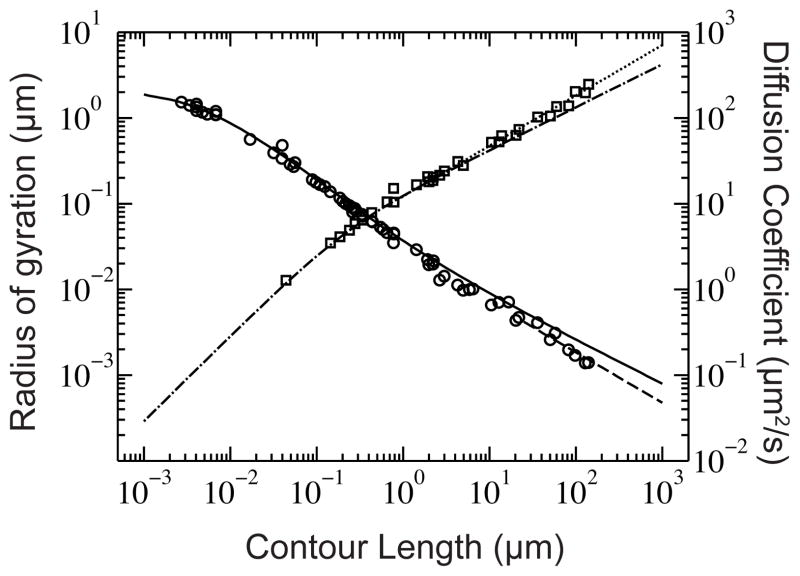
While Re is a useful theoretical construct, the radius of gyration, Rg, is the more prevalent size scale since it can be measured from a number of experimental methods.27 The radius of gyration quantifies the rms distance between parts of the molecule and its center of mass. Figure 3 presents a compilation of experimental data for the radius of gyration as a function of the contour length of dsDNA for a wide range of experimental conditions.55–81 As was the case for the force-extension behavior in Figure 2, the wormlike chain model is an excellent description for the radius of gyration. We can also clearly see the different regimes of DNA size in this figure. For short chains, the radius of gyration increases linearly with the contour length. For moderate values of the contour length, the chain is an ideal random walk with the scaling in Eq. (4). At the largest contour lengths, the radius of gyration breaks away from the ideal chain scaling and begins to follow the self-avoiding random walk scaling in Eq. (5). The experimental data in Figure 3 also highlight the stiffness of dsDNA — the excluded volume interactions only start to manifest around a contour length of 10 μm, i.e. near the size of λ DNA (48.5 kbp), the “hydrogen atom” for modeling and experiments on DNA.
Figure 3.
Radius of gyration (squares) and diffusion coefficient (circles) of DNA for a wide range of experimental conditions found in literature.55–82 The solid line represents the diffusion coefficient of a wormlike chain, according to the theory of Yamakawa83 with a bead hydrodynamic radius of 1.14 nm; the dashed line indicates diffusive scaling like N−ν. The dash-dot line is Eq. (2) and the dotted line shows the Nν scaling for the radius of gyration. Table S1 lists of each experimental data point and the corresponding value of the ionic strength. As we will discuss in Section 2.2, the different ionic strengths change the persistence length of the DNA, which can be a source of the scatter in the data.
In free solution, the DNA is small enough to experience substantial Brownian motion and will thus diffuse under the influence of thermal fluctuations. In the absence of any hydrodynamic interactions between the segments of the chain, the diffusion coefficient will obey the Rouse model84
| (6) |
where η is the solvent viscosity. The Rouse model is valid when the hydrodynamic screening is strong, for example, in an entangled polymer melt or in a gel.28 There is no hydrodynamic screening in free solution, whereupon the diffusion coefficient follows the Zimm model85
| (7) |
The Rouse model and Zimm model are often referred to as “free draining” and “non-draining”, respectively. These terms refer to the model of the fluid moving with the polymer coil during the latter’s diffusive motion. In the free draining (Rouse) case, the fluid acts independently on each segment of the polymer and thus easily “drains” from the interior of the coil. The resulting friction is proportional to the number of segments in the chain, which is reflected in the denominator of Eq. (6). In contrast, the non-draining (Zimm) coil “carries” the fluid with it during its diffusive motion. The fluid is not literally trapped inside the polymer coil for all time, but the hydrodynamics make the chain appear like a solid object that cannot “drain” the fluid in its interior.86,87 The friction is thus proportional to the size of the coil, as seen in the denominator of Eq. (7).
Figure 3 also includes a collection of experimental data for the diffusion coefficient of dsDNA obtained in a range of experimental conditions and using various experimental techniques.55–81 As is the case with both the force-extension relationship and the radius of gyration, the diffusion coefficient for a wormlike chain83 describes the DNA experimental data very well. The limiting cases for free-solution behavior of the chain are apparent here as well. For short, stiff chains, the diffusive behavior is like a free-solution rod
| (8) |
where a is the hydrodynamic radius of the rod. The diffusivity of long chains obeys Eq. (7), which includes excluded volume behavior when the chain is sufficiently long.62 Indeed, with the advent of bright intercalating dyes for DNA and sensitive cameras, it is now routine to infer the radius of gyration of a long DNA coil by measuring its diffusion coefficient by videomicroscopy.62
2.2 Electrostatic Properties
In addition to its polymeric properties, we will also need to be concerned with the electrostatic properties of DNA. Figure 4 schematically depicts the local ionic environment near the DNA backbone. DNA is an acid and thus adopts a negative charge when it is dissolved in solution. The charge density on DNA is very high, and some of the counterions undergo Manning condensation88 to reduce the charge density along the backbone such that the negative charges are nominally spaced by the Bjerrum length,
Figure 4.
Schematic illustration of the local electrostatics near a DNA coil in free solution.
| (9) |
where e is the charge of an electron, ε0 is the permittivity of free space and εb is the bulk permittivity of the medium. Immediately proximate to the DNA chain is a region of adsorbed counterions, called the Stern layer. Near the backbone is a layer of diffuse charges whose distribution is a balance between their electrostatic interaction with the negatively charged DNA backbone and their diffusion. The characteristic length scale describing the decay of the electrostatic potential away from the chain is the Debye length,
| (10) |
where
| (11) |
is the ionic strength of a medium containing a concentration ci of species with valence zi. Figure 5 shows how the Debye length changes as a function of the ionic strength of the medium, which is an easily controlled experimental parameter. The combination of the Stern layer and the Debye layer is often called the double layer. Outside of the double layer, the fluid is electrically neutral everywhere.
Figure 5.
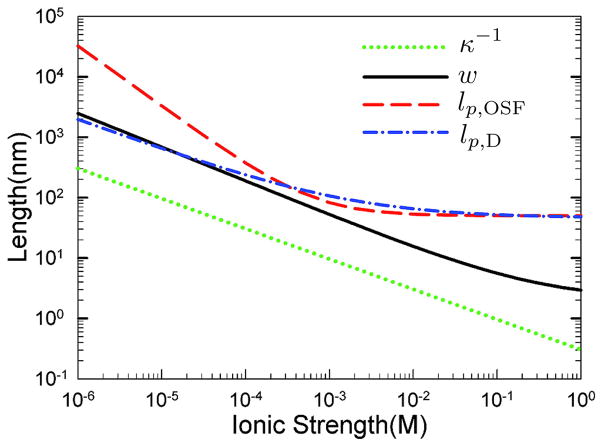
Calculation of the Debye length, effective width, and persistence length as a function of ionic strength using two different models for the persistence length. The persistence length lp;OSF is computed from the Odijk-Skolnick-Fixman theory in Eq. (12) and alternate value, lp,D, is computed using the theory from Dobrynin90 in Eq. (13). The effective width, w, is obtained from Stigter’s theory.89,91 Adapted with permission from Ref.92 Copyright 2008 American Chemical Society.
While the electrostatic environment proximate to the DNA is often described in terms of a Debye layer, the charge density on DNA (even in the presence of Manning condensation) is still very high. As a result, one should not treat the electrical potential using the linearized form of the Poisson-Boltzmann equation. Rather, the electrostatics should be treated using the nonlinear form of the Poisson-Boltzmann equation, which is called the Gouy model.89 In either case, the characteristic length scale arising from the model is still given by Eq. (10).
At equilibrium, there are two important effects of ionic strength. First, the persistence length increases with decreasing ionic strength due to electrostatic repulsion between the unshielded phosphate groups on the backbone of the chain. The classical model for the persistence length of a polyelectrolyte is the Odijk-Skolnick-Fixman (OSF) theory,93,94 which can be cast in the useful form for DNA92
| (12) |
where is the bare persistence length of the chain. Recently, Dobrynin90,95 called into question the OSF theory and proposed an alternate model from regression of experimental data.96,97 For DNA, this alternate model has the useful form92
| (13) |
Figure 5 shows how the models for the persistence length in Eq. (12) and Eq. (13) depend on the ionic strength of the medium. For the relatively high ionic strengths that characterize most of the experiments that we will see here, the two theories give very similar predictions since the ionic strength correction vanishes for high ionic strengths. The theories give substantially different predictions at low ionic strengths, which will become important for some of the DNA stretching applications in Section 7.
The second important effect of electrostatic interactions is the change in the effective width w of the DNA backbone. A naïve approximation for the width of the DNA backbone is 2 nm, which is the bare width of the double helix. When two DNA segments are nearby, their double layers overlap and the resulting electrostatic repulsion makes them appear to be thicker than the bare width. Stigter89,91 developed a widely used theory to describe the effective width of the DNA in solution. The effective width in his theory arises from comparing the osmotic pressure one would expect to see in a collection of short DNA rods to that for a solution of neutral rods of width w.91 The challenge in applying this theory is that the osmotic pressure calculations are only valid for the Debye model for the double layer, but the DNA is very highly charged so we need to use the Gouy model. Stigter89 showed how to map the electrostatic distribution from the Gouy model onto an equivalent Debye model through a numerical shooting procedure. The outcome of these calculations is seen in Figure 5. The results92 presented in Figure 5 are particularly useful since they extend to much lower ionic strengths than Stigter’s original interpolation table.89 As we can see, the electrostatic interactions can lead to an effective width that is much larger than the bare backbone width of the DNA. Even in the high ionic strength buffers common in electrophoresis, the effective width is around 10 nm.
The Stigter model for the effective width is only valid when the DNA segments are far enough apart that the approximation of the equivalent Debye model is valid.91 Moreover, the theory was developed for modeling short DNA in solution, which we have already seen from Eq. (2) are rodlike. One might question the model’s accuracy for segment-segment interactions, although it is reasonable to assume that nearby segments are rod-like on a local length scale.
3 Obtaining Sequence Specific Data
Having covered the basic physical properties of DNA, we now discuss the applications of the methods described in our review. We begin in Section 3.1 with restriction mapping, which is the classic approach for obtaining large scale sequence information. We also consider the closely related protocol of DNA fingerprinting, which is essentially an unsorted restriction map obtained using a rare cutting enzyme. Both of these protocols are amenable to gel electrophoresis, and many of the new separation devices we will visit in Section 6 and the flow cytometry methods in Section 8 were intended for restriction mapping or DNA fingerprinting. In Section 3.2, we discuss optical mapping and DNA barcoding. Note that, in some contexts, the terms “optical mapping” and “DNA bar-coding” can have commercial connotations, referring to a particular company’s technique. Here, we chose to use these terms generically to describe optical reading of restriction digests or the labeling of internal parts of the chain, respectively. Both of these methods require interrogating single molecules of DNA, but the extra experimental effort described in Section 7 is rewarded by increased information density. In contrast to restriction mapping and DNA fingerprinting, separations cannot be used for this second group of methods. After we review the overall approaches in the present section, we will continue in Section 4 with an explanation of how one actually goes about the DNA sizing tasks required to construct these maps.
In what follows, we will refer to both the contour length and the genomic length of a DNA molecule. By contour length, we mean the physical distance (e.g., in microns) of a segment of the chain. By genomic length, we mean the number of base pairs contained in a segment of the chain. Both terms are used in the literature, with contour length being prevalent in the physics literature and genomic length (or genomic distance) being prevalent in the biology literature.
3.1 Restriction Mapping and DNA Fingerprinting
The principle behind restriction mapping is illustrated schematically in Figure 6. Beginning with the genomic DNA isolated from a collection of cells, for example, from a bacterial culture or a collection of virus particles, the genomic DNA are incubated with a restriction enzyme, which cuts the DNA at sequence specific locations. For example, we will frequently encounter the HindIII restriction enzyme, which cleaves DNA by recognizing the sequence 5′-AAGCTT-3′. For the genome of the λ bacteriophage (a 48.5 kbp DNA that is ubiquitous in the papers discussed in this review), the HindIII enzyme makes seven cuts in the DNA that yields fragments between 2 kbp and 23 kbp. New England Biolabs maintains a useful online resource98 for restriction enzyme data. The DNA fragments in the resulting mixture are then separated as a function of their molecular weight, which allows us to determine the distance between the recognition sequences for the enzyme. If we repeat the procedure again with a different restriction enzyme, the corresponding set of fragment sizes will give the genomic distance between the recognition site of the second enzyme. These data can then be assembled into a restriction map, which gives global information about the location of particular sequences along the DNA.
Figure 6.
Schematic illustration of restriction mapping. Typical restriction maps of genomes include the locations of numerous restriction sites; the map produced by the example shown here would only correspond to two restriction enzymes (the red ellipses and green rectangles) with seven total restriction sites.
We will also consider a related task known as DNA fingerprinting. While one might regard the location of the restriction sites in Figure 6 as a fingerprint, a DNA fingerprint is normally generated by using a single rare-cutting restriction enzyme (such as SmaI or NotI) and large, chromosomal DNA, for example, in the work99,100 that we will see in Section 8.1. The analogies with human fingerprint analysis are straightforward. First, by using a rare restriction enzyme, the sizes of the corresponding fragments, which can be in the hundreds of kbp range, make up a distinctive “fingerprint” for the genome of the DNA. Figure 7 shows one such fingerprint obtained by pulsed field gel electrophoresis and the flow cytometry methods we will discuss in Section 8.1. We can think of the DNA fingerprint as an unassembled restriction map, since one does not try to sort the fragments to obtain the locations of the restriction sites along the original genome.
Figure 7.
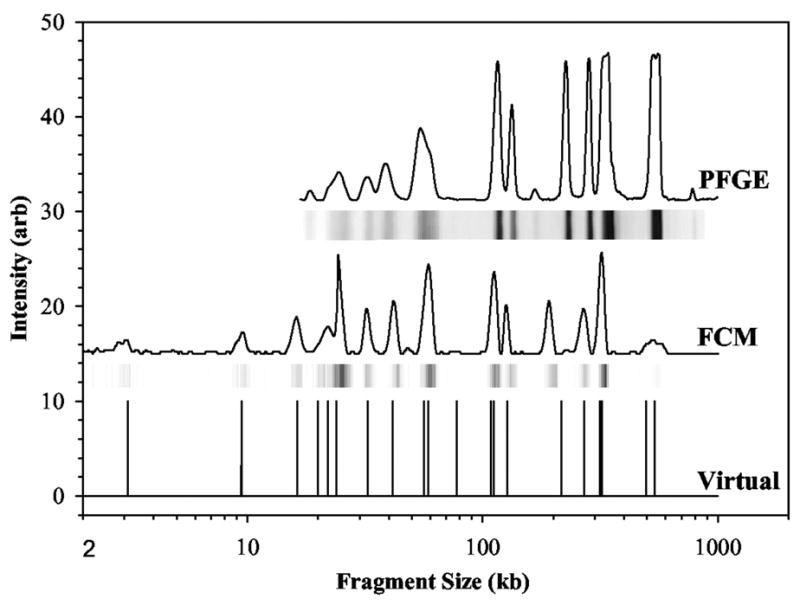
Comparison of pulsed field gel electrophoresis (PFGE) electropherograms and flow cytometry (FCM) for SmaI digested S. aureus Mu50. The raw PFGE data are the bands, which have been converted into a set of peaks, and the raw FCM data are the peaks, which have been converted into bands. The virtual digest is the expected location of the peaks based on the sequence of this strain. Reprinted with permission from Ref.100 Copyright 2004 American Society for Microbiology.
DNA fingerprinting is a quick method for identifying strains of microorganisms. If the sequence of a particular microorganism is known, it is also possible to work in reverse and make a plot of the expected locations of the restriction fragments. This is the case in Figure 7, where the DNA fingerprint aligns closely with the expected location for the restriction fragments. A common approach to strain identification is to compare its DNA fingerprint to a database of known organismal fingerprints. The Centers for Disease Control (CDC) in the United States maintains one such database, known as Pulsenet,101 for pathogenic microorganisms. This database is invaluable for identifying foodborne disease-causing bacteria, such as E. coli O157:H7, when there is an outbreak. (The latter strain was responsible for an outbreak of diseased spinach from California in 2006.)
3.2 Optical Mapping and DNA Barcoding
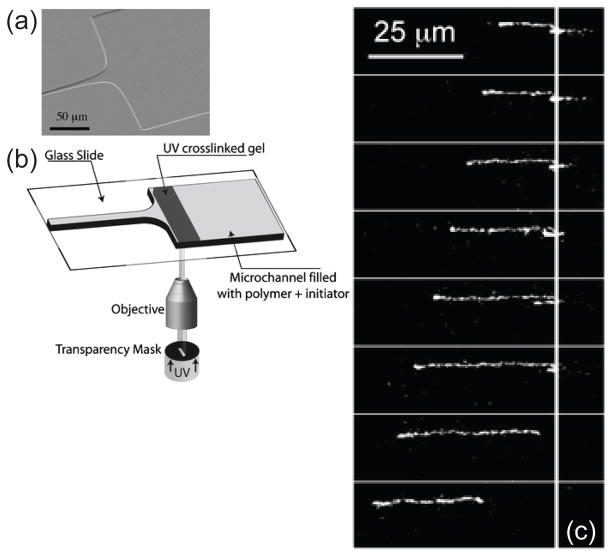
One of the challenges in analyzing a restriction digest, as illustrated in Figure 6, is the assembly of the fragments into a restriction map. (The problem is alleviated in the context of DNA fingerprinting, since one simply compares the fingerprints rather than determining the original location of the cuts.) At a single molecule level, a more direct approach to obtaining a restriction map is to reverse the order of operations in the analysis by first stretching the DNA and then doing the restriction reaction. The advantage of this approach is clear from Figure 8. In these experiments,102 the DNA stretched in a flow of molten agarose that included the restriction enzyme. When the gel cools, the DNA is fixed in the elongated form (top panel of Figure 8) and, presumably, the restriction enzyme is bound to its recognition site. When the enzyme cofactor Mg2+ is added to the gel, the restriction enzyme is activated and cleaves the DNA. The advantage of stretching first and then cleaving is that we can obtained ordered information about the location of the restriction fragments. For example, we can see that there are two restriction sites on the stretched DNA in Figure 8, and the distance between them can be obtained from the images. This technique is named “optical mapping”102 to make the analogy to restriction mapping, where the location of the restriction sites is obtained from an optical image. Assembling the optical maps into a global restriction map is much easier than is the case for data obtained from a separation experiment, since each optical map preserves the local ordering of the restriction fragments along the sequence. In addition to identifying the location of restriction sites, one can use the RecA-assisted endonuclease technique103 to identify the sites of methylation.
Figure 8.
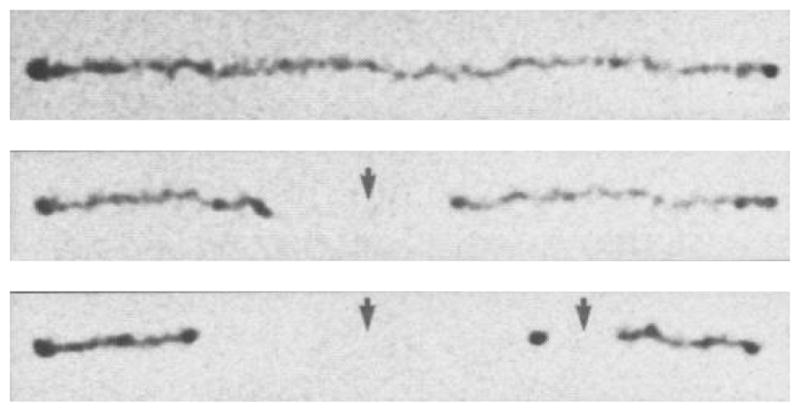
Time elapsed fluorescence micrograph of a stretched DNA molecule in molten agarose (image color inverted from the original). The arrows mark sites for CspI restriction endonuclease cleavage. Adapted with permission from Ref.102 Copyright 1993 American Association for the Advancement of Science.
The pioneering experiments102 used a gel to fix the DNA. As we can easily see in Figure 8, the fixation is weak and the molecule is allowed to relax, presumably as it disentangles from fibers in the agarose network. Thus, a major focus of our discussion in Section 7 are methods to create strong stretching of the DNA to avoid the relaxation present in Figure 8. Molecular combing,104,105 which we will discuss in more detail in Section 7.1, was a major breakthrough in the field and is now the most well developed method for stretching DNA.
An important part of optical mapping is the origin of the DNA sample used to create the map. In an early study,106 entire yeast genomes were stretched by molecular combing prior to analysis. An alternate approach is the optical PCR method.107 Here, long-range PCR is performed on the genomic DNA and the subsequent PCR products are combed. By choosing appropriate primers, one does not need to separate the genomic DNA and it is possible to obtain a sufficient amount of DNA to map. It should be noted that specific knowledge of primers is necessary, but once these are obtained, no more sequence information is needed. Ultimately, a shotgun technique has proven to be the most useful approach for handling large, high-throughput projects.108,109 In the shotgun technique, genomic DNA is extracted and randomly sheared by gentle pipetting. While simple enough, random shearing leads to a distribution of large fragment sizes that are individually sized, but then need to be assembled to get a whole genome map. Assembly is facilitated by an algorithm110 specifically designed for restriction map assembly.
Motivated by the need to process larger genome sets, algorithms for optical map assembly have matured.111,112 The computational problem is inherently difficult because measurements are made on individual molecules, which is not the case in sequencing assembly. Previous algorithms110 relied on a Bayesian method that was not scalable to large, shotgun mapped genomes. However, an algorithm developed by Valouev et al.111,112 solved this problem with a novel implementation of an “overlap-layout-consensus” strategy — a common technique in sequencing assembly.
The power of DNA stretching increased with the use of site-specific labels, instead of the site-specific restriction cuts that had been used previously. The term “DNA barcoding” is broadly applied to such site specific labeling methods, although it has also been termed single molecule linear analysis,113 genome mapping,114 direct linear analysis,115 or genome sequence scanning116 in different commercial applications. Advantages to DNA barcoding over restriction mapping include the possibility to increase resolution by using point-spread functions to locate probe positions below the diffraction resolution limit.117,118 In addition, since the DNA chain is not cut, we avoid the need to do biochemical reactions on a surface. Perhaps the earliest example of DNA barcoding is the use of surface hybridization probes to examine microdeletions in the tuberculosis sclerosis 2 gene on human DNA.106 In the latter experiments, the DNA were first stretched onto the surface, followed by hybridization with the probes.
There are now a number of ways to barcode the chain.120 One option121 is to replace the restriction enzymes with nicking enzymes. In this case, specific sequences are removed from a single strand instead of severing the entire chain. The excised nucleotides are then replaced by fluorescent ones, which are reincorporated using a DNA polymerase. Figure 9 shows a chain specifically labeled in this way, where the backbone is labeled with YOYO.119
Figure 9.
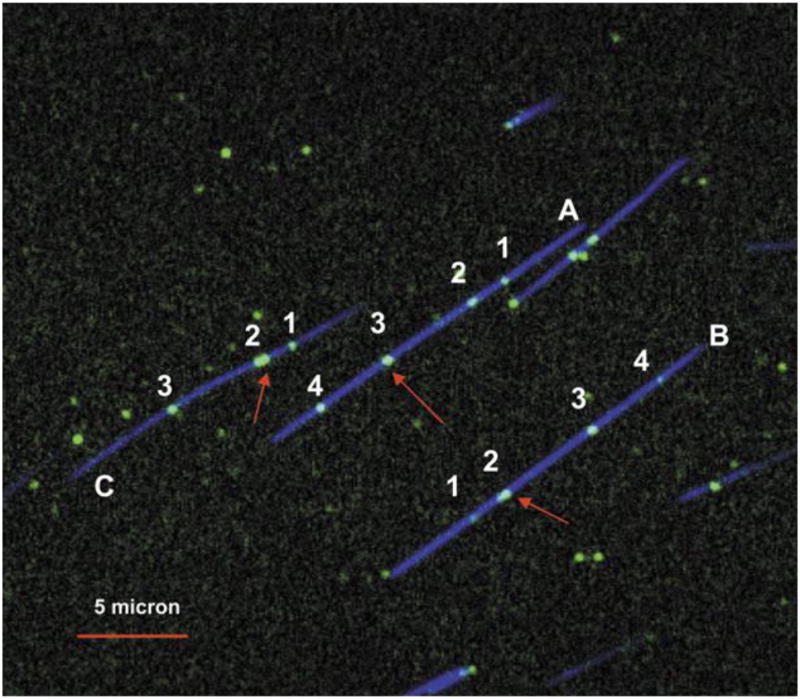
DNA barcoding using nicking enzymes and fluorescent nucleotides. The blue color corresponds to a YOYO labeled backbone and the green color corresponds to nicking enzyme sites. Each labeled fragment (A, B, and C) contains seven nicking sites, but only four (numbered 1–4) are distinguishable — due to diffraction — on molecules A and B and only three are distinguishable on fragment C. Red arrows indicate clustered nicking labels (for 2 which has three nicking sites and for 3 which has two). Adapted with permission from Ref.119 Copyright 2007 Oxford University Press.
In addition to nick-based labeling, quantum dots have been used to label DNA chains.122 Quantum dots have high photostability and, to some extent, have a smaller effect on the physical and chemical properties of the labeled DNA than is the case with fluorescent labels. Thus, it is hoped that quantum dots will allow for longer observation times and more accurate detection of DNA-protein interactions.
To provide a more dense labeling of the chain, Neely et al.13 used a “methyltransferase-directed activated group” method to incorporate fluorescent labels at methylated sites. By choosing the number of bases in the methyltransferase, one can tailor the density of the barcode along the DNA chain. With a four-base methyltransferase (M.HhaI), 215 target sites on λ DNA were labeled with a claimed resolution of about 660 bp for a single molecule. In addition, this method is purported to be able to label chains to a resolution as low as 20 bp.13
Finally, we conclude this section by highlighting the role that optical mapping has assumed in modern genomic analysis. Specifically, optical mapping has played an important role in sequence finishing efforts and analyzing genomic structural variation. Key accomplishments of optical mapping include (i) verifying123,126,129,131 or identifying mistakes131,136 in genome assembly, (ii) aiding in sequence finishing efforts,129,130,132,135 (iii) clarifying regions that are hard to determine from second-generation sequencing, such as tandem repeats and telomeric sequences,5,6 (iv) detecting methylation sites,7,134 (v) identifying individual pathogen genomes in a mixture of microorganisms,133 (vi) locating the origin of the 2006 California spinach poisoning outbreak,127,128 and (vii) analyzing genomic structural variation such as translocations, insertions, deletions, inversions and copy number variants in a range of pathogenic and human genomes.5,13,26,124,125,137,138 Notable examples of the genomes studied to date are listed in Table 1 and include pathogens, agricultural products and the human genome. It is also worth remarking that the state of the art optical mapping approach has been commercialized by OpGen. In general, their devices are able to process data sets on larger and more complex genomes than were previously possible, including many of the most recent examples listed in Table 1. The broad use of optical mapping reveals its place as a genomics mainstay and a modern complement to next generation sequencing.
Table 1.
Notable genomes characterized by optical mapping.
| Organism | Reference(s) |
|---|---|
| Plasmodium falciparum | 123 |
| Escherichia coli | 7,124,125 |
| Escherichia coli O157:H7 | 126–128 |
| Yersinia pestsis | 125,129 |
| Rhodobacter sphaeroides | 130 |
| Leishmania major | 131 |
| Shigella flexneri | 125 |
| Rhodospirillum rubrum | 132 |
| Adenovirus | 133 |
| T4 Bacteriophage | 133 |
| λ Bacteriophage | 13,133,134 |
| Xenorhabdus nematophila | 5 |
| Xenorhabdus bovienii | 5 |
| Oryza sativa | 6 |
| Zea mays ssp. mays L | 135 |
| Mycobacterium avium ssp. paratuberculosis | 136 |
| Staphylococcus aureus | 137 |
| Homo sapien | 26,124,138 |
4 Principles of DNA Sizing
Both the biological origins of DNA and the routine use of DNA sizing in molecular biology make the task of determining the molecular weight of DNA in a mixture qualitatively different than, say, determining the polydispersivity index (PDI) of a synthetic polymer. The molecular weight of the chains in a mixture of synthetic polymers are typically distributed around some average molecular weight, as seen in Figure 10a. Such a molecular weight distribution arises from variations in the initiation, chain extension, and termination reactions during the synthesis of the chains.27 In contrast, most DNA analysis scenarios involve mixtures of DNA that contain a well defined set of molecular weights. While one can technically define a PDI for a mixture of DNA, one should really think of the molecular weight distribution as the series of delta functions seen in Figure 10b. Since the various species in a mixture of DNA are widely separated in molecular weight with no variance about each peak, determining their sizes requires a method to resolve these delta functions.
Figure 10.
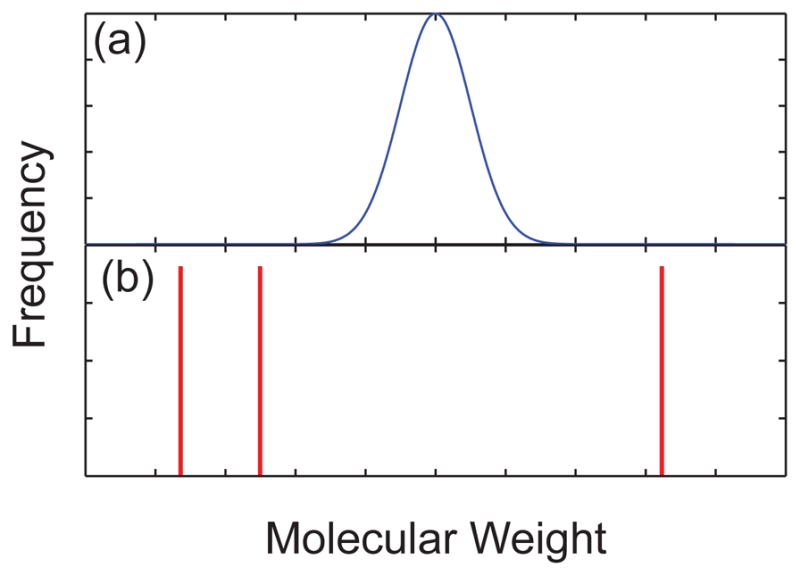
Schematic illustration of the molecular weight distribution for (a) a synthetic polymer and (b) a mixture of different sized DNA.
There are, in general, two approaches to determining the size of DNA molecules. The classical approach is based on an ensemble of molecules. The unknown sample is separated as a function of molecular weight, for example, by gel electrophoresis, and the relative speeds of the unknowns are compared to the speeds of known molecular weight DNA. The reference standard is often referred to as a DNA “ladder” due to their appearance in gel electrophoresis. In contrast to size exclusion chromatography of a polydisperse polymer mixture, the width of the bands (or peaks) in such a DNA separation only contains information about the fluctuations in the separation process, rather than any additional information about the polydispersivity of the sample. This is a standard task in analytical chemistry and forms the basis for much of separation science.31 We will provide a primer on the subject in Section 4.1. The other approach is to interrogate individual molecules of DNA. The latter is a relatively new approach that arose with the introduction of bright intercalating dyes.25 There are a number of different quantities that one obtains from observing the fluorescence of individual molecules of DNA, which are covered in Section 4.2.
4.1 Sizing Many DNA Molecules
Let us begin our discussion by reviewing some of the standard concepts in separation sciences, paying particular attention to the concepts and terminology that we will use to compare different devices and methods. Some of the material covered in this section is standard, and we will not include detailed references. The reasons for this primer are twofold. First, as the topic of DNA separations has permeated a number of disciplines outside of chemistry, we anticipate that some readers may not have formal training in separation science. Indeed, a substantial amount of the groundbreaking work described in this review was performed by physicists and electrical engineers. We suspect that readers new to the field will benefit from the definitions of the various jargon, such as theoretical plates and separation resolution, that will appear in later parts of the review. Second, the standard equations in separation science, such as Eq. (37), involve a number of non-trivial assumptions. While these assumptions are often valid in classical separation methods such as capillary electrophoresis and chromatography, this is not always the case for DNA electrophoresis in microfabricated devices. Where appropriate, we will highlight assumptions that need to be used with care in the analysis of experimental data. For the reader looking for more details on separation science, by far the most lucid text on this topic is the classic work by Giddings.31 The monograph by Brenner139 is an additional reference for understanding the generic connection between microscopic transport processes and macroscopically observable behavior that we will discuss next.
4.1.1 Transport Parameters
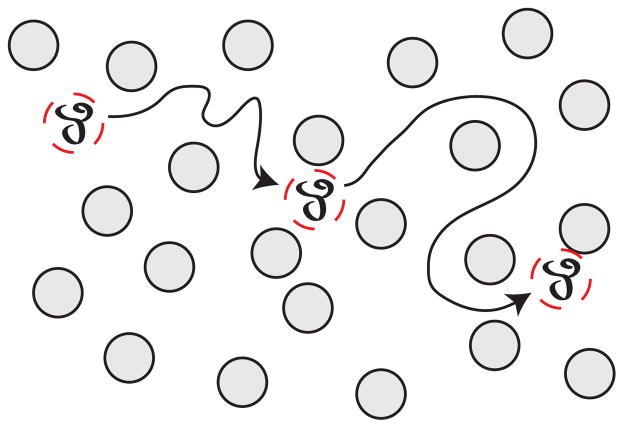
A given separation process can be viewed at either of the length scales illustrated in Figure 11. Figure 11a depicts the reptation of a long DNA molecule through a relatively tight array of cylindrical obstacles,140–142 which we will discuss in more detail in Section 5.1 and Section 6.1. At the microscopic scale, each molecule undertakes a stochastic trajectory as it wends its way through the separation medium. In principle, we can define a trajectory ri(t) describing the three-dimensional position r of the center of mass of each molecule i as a function of time t. Viewed at this small length scale, the separation process can appear quite complicated. It is generally challenging to develop a realistic model for the distribution of ri(t).
Figure 11.
Schematic illustration of the difference between (a) the microscopic details of DNA migration in a microfabricated separation device and (b) the macroscopic viewpoint used to analyze the separation. The microchannel in (b) contains many obstacles, and the schematic shows two different sized DNA that have been separated due to their different migration speeds through the matrix. Note the different length scales in (a) and (b).
However, from an operational viewpoint, the microscopic details of the DNA motion are only relevant inasmuch as they produce an averaged behavior that depends on molecular weight. This viewpoint is emphasized by the schematic in Figure 11b, where the details of the motion of the individual DNA molecules are averaged out into a concentration field inside the column. Although much of our subsequent discussion will focus on the analysis of a single “band” of DNA in the device, one ultimately wants to separate the mixture into different bands that correspond to different molecular weights. For example, Figure 11b illustrates a separation of DNA with two different molecular weights the post array. The schematic also clarifies why we are often interested in the macroscopic viewpoint; while advances in fluorescence microscopy and camera technologies now permit one to visualize the dynamics of long DNA, for the purposes of separations it is much more convenient to simply measure this concentration field.
For a given DNA molecular weight, there are two key macroscopic transport parameters: (i) the mean velocity vector
| (14) |
and (ii) the effective diffusion tensor,
| (15) |
which is also referred to as a dispersion tensor in the fluid mechanics literature.139 In the latter, the angular brackets 〈···〉i refer to an ensemble average over all of the molecules in the ensemble that possess the same molecular weight. In many circumstances, the separation proceeds along the direction of a (time-averaged) electric field vector, although we will discuss several counterexamples in the context of continuous separations in Section 6.6. For example, the system in Figure 11b requires an electric field E oriented along the axial direction in the microchannel to move the DNA. Quite often, we only require the components of the mean velocity vector and dispersion tensor along the direction of net motion. If we define the electric field magnitude E ≡ |E|, then we can define
| (16) |
and
| (17) |
As a matter of convention, velocities are frequently expressed as an electrophoretic mobility,
| (18) |
The electric field is normally expressed in units of V/cm. While these are not the SI units (and there are papers that use V/m), there are sensible reasons why V/cm is the common unit for the electric field in gel electrophoresis. First, most gels are several centimeters in size, so centimeters are a natural unit for length. Second, the typical electric fields for DNA gel electrophoresis are tens of V/cm or less, so the choice of V/cm leads to O(1) values for the electric field. The electrophoretic mobility then has units of cm2/Vs, with a typical value for DNA in free solution143 of 10−4cm2/Vs. However, the characteristic length scale for microfluidic devices is, by definition, micrometers. While it may seem odd to express the electrophoretic mobility in units of μm × cm/Vs, these turn out to be quite convenient for microfluidic devices; the electrophoretic mobility is O(1) and multiplying by the electric field (in V/cm) leads to the DNA velocity in μm/s, which is the relevant speed for videomicroscopy experiments.
A common but rarely stated assumption in the context of DNA electrophoresis is that the moments defined by Eq. (14) and Eq. (15) converge. We will proceed here making the same assumption, but we should point out that there is evidence that the dispersion coefficient may not converge even for gel electrophoresis.144 Moreover, as the separation times become faster and faster, it is not obvious that the residence time inside the device is sufficient to reach the long-time limit.145 The case where there is a well defined mean velocity but a diverging second moment arises quite frequently in the theory of continuous-time random walks, which have a long history in chromatography theory in the context of the two-state model.146–148
If the moments describing the mean velocity and dispersivity converge, then we can write an averaged convection-diffusion equation describing the concentration field at long times.139 Since we are primarily concerned with transport in the direction of the electric field, we can write this equation as
| (19) |
where the direction of net motion is defined to be the x-direction. To solve this equation, we need an initial condition and appropriate boundary conditions. It is simplest to consider the fundamental solution to the equation in an unbounded domain,
| (20) |
which is the normal (or Gaussian) distribution. Physically, Eq. (20) describes the evolution of the concentration field in position and time from an initial condition of a unit mass injected as a delta function at the origin. The advantage of working with the fundamental solution, aside from its pedagogical utility, is that we can easily determine the concentration field corresponding to a more realistic initial condition by convolving Eq. (20) with the actual initial condition in the device.
Our analysis thus far only considered the broadening of the peak caused by interactions with the separation medium, which is captured by the dispersion coefficient D̄. The corresponding variance in the peak width in space as a function of time is
| (21) |
In general, there are many additional sources of band broadening due to the injection process, the detection, and non-uniformities in the column, say due to Joule heating or a non-uniform surface potential that causes a non-uniform electroosmotic flow.149 These additional sources of band broadening are normally assumed to be additive31 so that the total variance of the peak in space is
| (22) |
The total variance is time dependent, since it includes the dispersion contribution in Eq. (21), but some contributions may be independent of time. Thus, it sometimes proves convenient to describe the concentration field in Eq. (20) by a more generic form of the Gaussian distribution
| (23) |
that accounts for all of the sources of band broadening. In the latter, x̄ = Ūt is the average position of the band at a time t. Since σ includes time dependent and time independent terms, one should use caution when introducing Eq. (21) into Eq. (23) if the non-diffusive contributions to the band broadening are substantial. When this is the case, one can account for these sources by noting that total variance, σ2, is the sum of the variances of each contribution – the standard deviation is, however, not additive.
Although the velocity and dispersion coefficient are fairly easy to understand at a conceptual level, separation data are often reported as the number of theoretical plates. The concept of a theoretical plate is often confusing to newcomers in separations science, although it quickly becomes apparent that the goal is to have the largest number of these plates. The confusion is further increased in the context of many microfabricated separation systems, where one often creates a periodic array of features. It is tempting to assume that each one of these features, such as a single entropic trap,150 corresponds to a theoretical plate. While there is no fundamental reason one cannot define a theoretical plate as a unit cell of a repeating pattern, the concept of a plate height in separations science is generally defined at the macroscopic level (Figure 11b) rather than the microscopic level (Figure 11a).
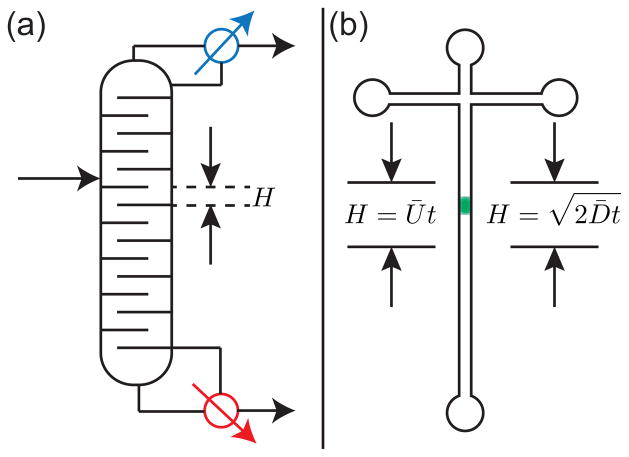
The concept of a theoretical plate has its origin in staged equilibrium separations,151 such as the distillation column illustrated in Figure 12a. In staged distillation, there are literally plates (also known as trays) where there is mass transfer between a liquid phase flowing down the column and a vapor phase flowing up the column. In an ideal column, the liquid and vapor leaving a given tray (in opposite directions) are in thermodynamic phase equilibrium. For given specifications for the top and bottom product, one can then calculate the required number of theoretical plates, Np, based on this equilibrium assumption. Since the column literally contains plates, their physical properties and fluid mechanical issues require that the plates be separated by some distance H inside the column, which is the plate height. This classical chemical engineering calculation enables one to estimate the required height of the distillation column, L = NpH. Since real columns do not achieve equilibrium on each plate, there is normally an efficiency, ηp < 1, associated with the mass transfer limitations, whereupon the real column size is the larger value L = NpH/ηp.
Figure 12.
(a) Standard definition of a theoretical plate in distillation, an example of an equilibrium-based separation process. (b) Extension of the concept of theoretical plate heights in the context of a non-equilibrium separation. In a separation, the theoretical plate height H is a mathematical definition and not associated with a physical region of the device or the location of the band.
The connection to non-equilibrium separations in a microchannel can only be obtained at a macroscopic level. Using the definitions of the mean velocity in Eq. (16) and dispersivity in Eq. (17), one can define a time scale at which the convection and diffusion are balanced over a corresponding distance H. Note that this definition has no connection to the microstructure of the separation column (e.g., the array of posts in Figure 11) and is thus valid even in the absence of any sieving medium, as is the case in classical capillary electrophoresis. As indicated in Figure 12b, the convective time scale is t = H/Ū and the diffusive time scale is t = H2/2D̄. Setting these two values equal furnishes the normal definition for the theoretical plate height,
| (24) |
The prefactor of 2 is retained in the definition commonly used in separation science,31 although this is a custom rather than something with a strong physical basis. [Indeed, one could just as well use the first-passage time152 for diffusion in a region of size H, which would change the prefactor in Eq. (24).] Our quick derivation readily furnishes the physical interpretation for a theoretical plate height; at a macroscopic level, the plate height is a characteristic region over which the analyte diffuses at the same rate as it is convected, which is akin to “equilibration” in a non-equilibrium system. Naturally, it is desirable to have the smallest plate height possible since this is equivalent to minimizing the band broadening in the device.
One often sees the data reported in terms of the number of plates in a separation rather than a plate height. For a column of length L, the number of theoretical plates is
| (25) |
The analogy with intensive and extensive properties then becomes apparent; the plate height is an intensive property of the separation medium and the number of plates is an extensive property. In the context of separations, the extensive property has meaning since one can often relate the quality of the separation to the number of plates. Moreover, in the case of microfabricated systems, it is not always trivial to lengthen the column to increase the number of plates for a fixed plate height H. For example, adding serpentine turns to a separation channel can increase the dispersion.153–156
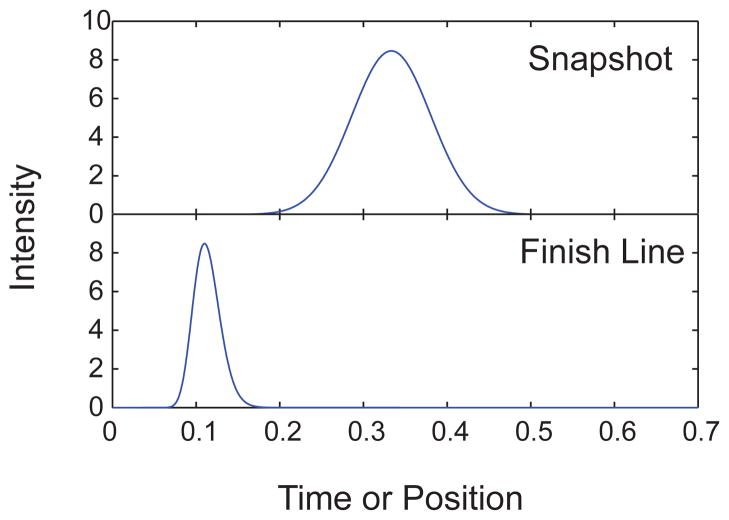
4.1.2 “Snapshot” versus “Finish Line” Detection
If we have a “normal” separation process that evolves in space and time according to Eq. (20) [or, more generally, Eq. (23)], there are two methods to measure the progress of the separation, snapshot and finish line. In snapshot detection, one makes a measurement of the concentration field in space at some fixed point in time. The separation is performed for a known amount of time, after which the gel is stained and photographed to measure the location of the bands. This is the standard method in gel electrophoresis. In finish line detection, one measures the distribution of times required to reach some fixed point in space. There is an open window in the capillary at some point downstream, and the analytes are detected as they pass through this window by laser-induced fluorescence or UV adsorption. This is the standard method in capillary electrophoresis.
Many of the microfabricated devices that we will encounter in our review use finish line detection because it is easily implemented and, as we will see shortly, can reduce the apparent band broadening. The device is mounted on an epifluorescence microscope, and the location of the objective is fixed at a particular location along the microchannel. It is straightforward to move the detector after the bands have passed to make a subsequent measurement,157,158 provided that the bands are reasonably close together in space and narrow. This series of measurements permits an estimate of the mean velocity and dispersivity inside the channel. It is somewhat more difficult to implement a snapshot detection, since one needs to automate the microscope stage and rapidly scan through the channel at a fixed point in time.159,160 If the DNA rapidly move through the device, then the scanning can lead to artifacts as one is not really obtaining a snapshot of the separation at a given point in time. Alternatively, one can use a low magnification objective and take an image of a large region of the separation channel at a fixed point in time. This second method only works if the signal is very strong.
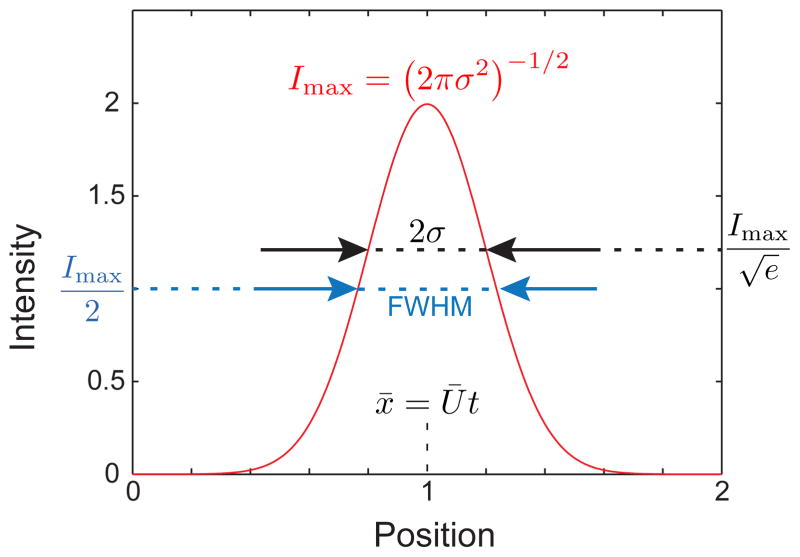
Let us consider first the snapshot method, which is conceptually simpler than the finish line method. Although it makes sense to refer to an overall concentration field c(x,t), for detection purposes we will refer to an intensity I that would be measured at the detector. (As is the convention in experiments, we will ignore the units on I, since the typical measurement is a voltage that is proportional to the number of photons collected by a photomultiplier tube.) Let us consider the case where the variance is solely caused by the motion through the device. If we make the measurement at a time t = τ, then the measured intensity will be
| (26) |
The maximum value of the peak, Imax = (4πD̄τ)−1/2, occurs at the mean position of the band, x̄ = Ūτ. The variance of the peak, , is located by finding the position at which or, more accurately, fitting the intensity with Eq. (26) and extracting the variance as a fitting parameter. For Gaussian peaks, the fitting procedure is straightforward. However, it is sometimes difficult to fit experimental data to a Gaussian because the signal-to-noise ratio in the tails affects the fit. This problem is exacerbated in microfluidic systems because the number of molecules passing the detector at a given time is sometimes small. Indeed, one can work at low enough concentrations that the individual pulses caused by single molecules become apparent.161 In the case where a Gaussian peak is difficult to obtain, it is common to use the full width at half maximum (FWHM) as a measure of the band broadening. If we have reason to believe the peak should be a Gaussian, the measure of the FWHM is easily converted to the variance by multiplying the FWHM by the conversion factor, . While we have focused on the case where σ2 = 2D̄t, the analysis of snapshot data readily accommodates other forms of band broadening through Eq. (23).
The analysis of finish line data is somewhat more complicated for DNA electrophoresis, in particular in microfabricated systems. The classical model in separations science31 assumes each band rapidly passes by the detector. In this limiting case, the band width stays relatively constant during the detection and the finish line detection can be thought of as a series of snapshots taken at different times τ = tr for each one of the bands, where tr = L/Ū is the residence time of a given band. If these assumptions hold, as is often the case in free-solution capillary electrophoresis of small molecules, the analysis of the finish line detection simplifies tremendously.31 Unfortunately, many of the DNA separation devices discussed in this review involve fairly broad bands that have a considerable residence time at the detector. Indeed, some of our own work,162 which reported fairly high resolution finish line separations of long DNA, involved bands that spend over 1 minute passing the detector. Since these long residence time bands appear frequently in the context of DNA electrophoresis in microfabricated devices, it behooves us to spend some time carefully considering the effect of the band spreading as it passes the detector.
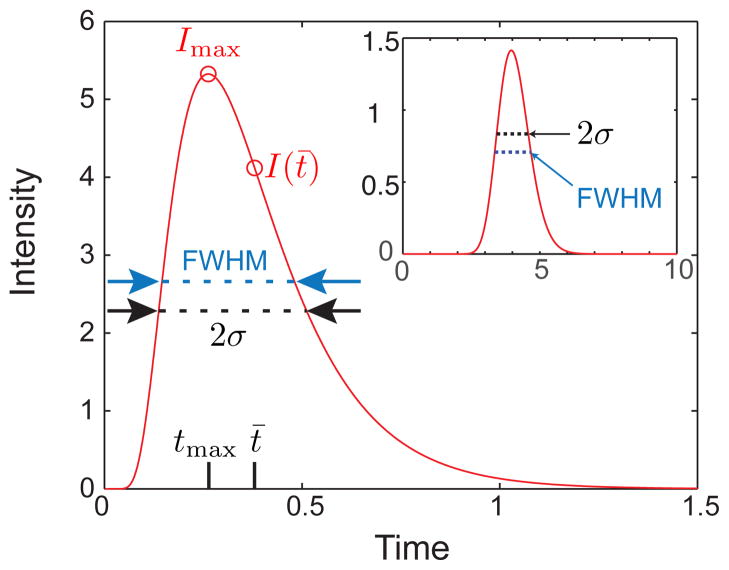
In Figure 14, we show a finish line result for the same mean velocity and dispersion coefficient used to produce Figure 13. The difference between the two detection methods is apparent. When we take a measurement at a fixed position x = L, the corresponding intensity distribution,
Figure 14.
Finish line detection of a Gaussian function with unit mass, Ū = 0.5, and D̄ = 0.01 at position L = 0.15. The velocity and dispersion coefficient are identical to Figure 13. The maximum value of the concentration, Imax, the variance, σ, the full width half maximum (FWHM), and the location of the concentration at the mean elution time, I(t̄), are indicated. The inset shows the same Gaussian peak measured at L = 2.
Figure 13.
Snapshot of a Gaussian function with unit mass, Ū = 0.5, and D̄ = 0.01 at time τ = 2. The maximum value of the intensity, Imax, the variance in intensity, σ, the full width half maximum (FWHM), and the location of the maximum value of the intensity, x = Ūt, are indicated.
| (27) |
is not a Gaussian in time. For the purposes of understanding the system, it is useful to define a dimensionless time, t̃ = t/tr, and a Péclet number, Pe = ŪL/D̄, for a given detector distance L. Since there is no possibility for anything to pass by the detector before t = 0, the peak is asymmetric with a tail towards larger values of time. A consequence of the asymmetry is that the peak of the distribution, Imax, occurs at a time,
| (28) |
that is not equal to the average dimensionless time for the DNA to pass the detector,
| (29) |
Although we cannot easily invert Eq. (27), we can compute the full width at half maximum numerically. The variance in dimensionless time,
| (30) |
can be obtained from the normalized, second centered moment of Eq. (27). Note that the simple relationship between σ and FWHM we obtained for snapshot detection no longer holds for finish line detection. Indeed, as we see in the inset of Figure 14, the relative magnitude of these two quantities changes with the distance from the injection.
We selected the particular values in Figure 14 to highlight the asymmetric nature of the peaks at short distances, which is often neglected. The reason for this neglect is that, as the residence time increases, the peak becomes more symmetric. The relevant limit is Pe → ∞. Converting back to dimensional notation, for very long columns we have
| (31) |
and
| (32) |
In the inset of Figure 14, which corresponds to Pe = 100, the values of tmax and t̄ only differ by 3%.
We cast Eq. (32) in a form that highlights the advantages of the finish line detection in reducing the apparent band broadening in a separation. Let us consider a snapshot detection at some time tr and the equivalent finish line detection at the corresponding position L = Ūtr for a large value of the Péclet number. The variance of the bands in space is given by σ2 = 2D̄tr whereas the variance of the bands in time is given by Eq. (32). As we can see in Figure 15, the same nominal residence time leads to a much sharper peak in a finish line detection. However, this advantage only holds true for the analysis of a single band. In a separation, there will be many bands that need to be resolved. The disadvantage of the finish line separation is the need to wait for all of the species to pass the detector.159 Not only does this increase the time for the separation, since the lagging species may spend considerable time moving through the separation matrix, but it also leads to band broadening of these slow moving species. There are separation processes where the species are quickly resolved in space due to a severe retardation of some of the species, in which case a snapshot detection can be much more effective.
Figure 15.
Comparison of the snapshot and finish line detection of a Gaussian function with unit mass, Ū = 3, and D̄ = 0.01 for Pe = 100. The choice of Péclet number fixes the equivalence between the length of the separation for the finish line, L = Pe(D/U), and thus the residence time, tr = L/U, for the snapshot detection.
4.1.3 Separation Resolution
Regardless of the detection method, the figure of merit for a given separation is the separation resolution. In light of the different detection methods, the independent variable for the detector, ξ, can be either the position, x, or the time, t. We will assume it is possible to deconvolve the total intensity at the detector, I(ξ), into the sum of intensity contributions from each of the n species,
| (33) |
Likewise, for each of the intensity distributions, we will assume that the first two (centered) moments of ξ are finite. Under these rather modest assumptions, the separation resolution is defined as
| (34) |
where ξ̄j is the first moment of ξj and is the second centered moment of ξj. The resolution is clearly a dimensionless number and valid for both finish line and snapshot detection.
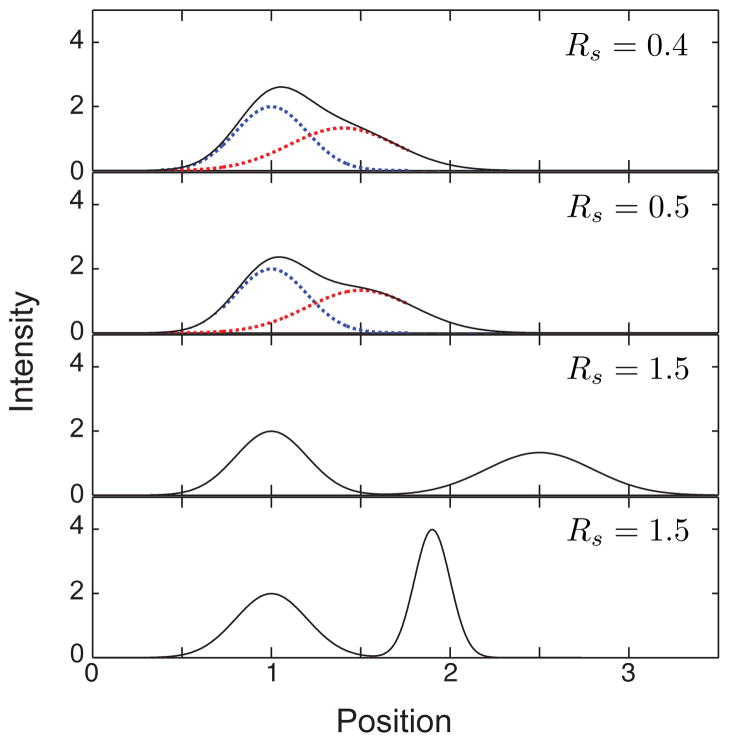
Figure 16 illustrates the concept of the separation resolution for a snapshot detection of Gaussian peaks, where the intensity profile is given by Eq. (26). At the relatively low value of Rs = 0.4, one would be hard-pressed to identify two distinct peaks from the black curve. As a matter of convention, one takes the value Rs = 0.5 as the limit of detection for two peaks.31 In Figure 16, we can clearly see the formation of the shoulder in the electropherogram due to the red curve at Rs = 0.5. The widespread use of Sanger sequencing, which requires discriminating between nearby peaks in an electropherogram, led to substantial improvements in the ability of computer algorithms to distinguish almost overlapping peaks. Automated peak resolution algorithms (normally referred to as “base calling” software in the sequencing literature) can distinguish between peaks for values as small as Rs ≈ 0.25.163 Once we reach a resolution Rs = 1.5, the peaks are considered to be “baseline resolved.” As indicated in Figure 16, baseline resolution can be achieved by increasing the spacing between the peaks or reducing the band broadening.
Figure 16.
Illustration of different values of the resolution, Rs, for the case ξ = x. The solid black line corresponds to the total intensity at the detector. The dashed blue lines correspond to a peak with x̄ = 1 and σ = 0.3. The dashed red lines correspond to a second peak that produces the desired resolution. In the top three panels, the red curve has σ = 0.3. In the bottom panel, the red curve has σ = 0.1. Since the peaks are base line resolved for Rs = 1.5, only to the total intensity is shown.
For snapshot detection, we can derive a commonly invoked formula that relates the separation resolution to the number of theoretical plates.31 As we will see, this derivation involves a number of assumptions that are questionable in the context of DNA electrophoresis in microfabricated devices. Since Eq. (37) is often used in the DNA electrophoresis literature without confirming that its assumptions are valid, it is worthwhile to recall its origin. For a snapshot detection of two species at some time τ, we know that ξ̄j = Ūjτ and . Substituting the latter in Eq. (34) yields
| (35) |
Eq. (35) immediately highlights the commonly stated property that the separation resolution increases with the square root of the time for the separation. To make further progress, one needs to assume that D̄1 ≈ D̄2 and define a single dispersion coefficient, D̄. We also need to define an effective length for the separation, Leff = 〈Ū〉 τ, where we introduced the average of the two species mean velocities, 〈Ū〉 ≡(Ū1 +Ū2)/2. Using the latter in Eq. (35) yields
| (36) |
where we introduced another notational simplification, ΔŪ = |Ū1 −Ū2|. This result can be simplified by combining Eq. (24) and Eq. (25) to produce the standard result
| (37) |
where Np is now some nominal number of theoretical plates based on the average of the species velocities, 〈Ū〉, and the assumption that D̄1 ≈ D̄2 ≡D̄.
There is an appealing aspect to Eq. (37), since the resolution is decomposed into one factor that depends on the relative difference in speed between the two species and a second multiplicative factor that captures the band broadening in a dimensionless form that is connected to the plate height and the length of the separation column. Thus, Eq. (37) makes a useful connection between the somewhat abstract concept of a theoretical plate and the much more practical concept of separation resolution. While we have found Eq. (37) useful sometimes to analyze separation data,164 especially when models exist for computing Ū and D̄, one should always keep in mind the assumptions required to make the leap from Eq. (34) to Eq. (37).
4.2 Sizing Single DNA Molecules
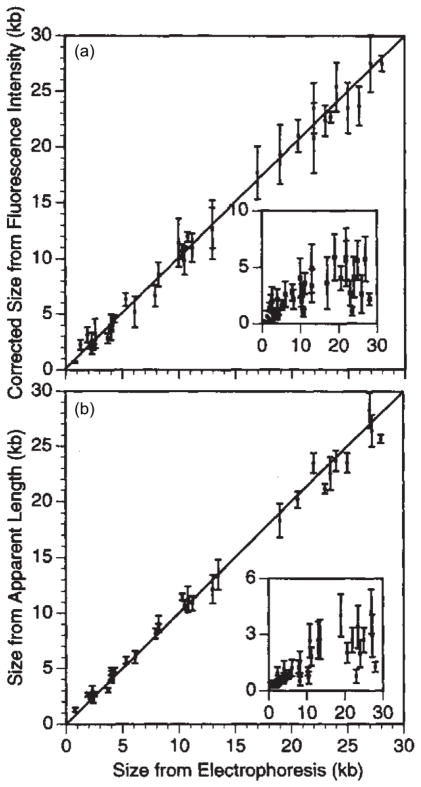
Having covered the basic concepts in DNA separations, let us now turn our attention to measurements of single DNA molecules. As we discussed in the context of optical mapping and DNA barcoding in Section 3.2, we can also determine the size of DNA fragments by stretching them out. The idea for single molecule sizing of DNA appears to have first been proposed by Guo, Huff and Schwartz165 while looking at fluorescence microscopy images of hooking collisions in tight agarose gels during electrophoresis. The key to this brief paper (and to all subsequent stretch-sizing techniques) is the relationship between the fluorescence intensity in a microscope image and the contour length of the molecule. The goal is to obtain a calibration curve similar to the one in Figure 17, which shows a linear relationship between the size measured from DNA stretching and the size measured from electrophoresis. This figure nicely illustrates the correspondence between the methods we will discuss in the present section and those reviewed in the previous one.
Figure 17.
Calibration of (a) integrated fluorescence intensity and (b) apparent extension, which are measures of the chain size versus size measured from electrophoresis. The insets are estimations of the standard deviations of the population. Adapted with permission from Ref.166 Copyright 1995 Nature Publishing Group.
To date, three metrics have been used to obtain a DNA length from a fluorescence intensity map: a probe-probe distance, an extension, and the integrated fluorescence intensity. As shown in Figure 18, these metrics can be related to the intensity profile of the probe or dye attached to the chain. Each method of obtaining the genomic length is obtained by different principles of polymer physics.
Figure 18.
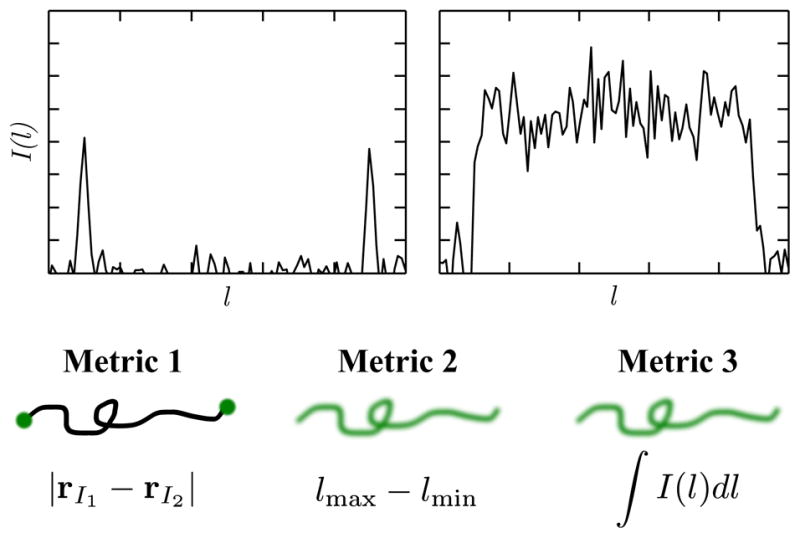
Three different methods to obtain a measure of genomic length using fluorescence microscopy: (1) Probe-probe distance, (2) extension, (3) integrated intensity. Plots show simulated fluorescence profiles for probes (left) and for intercalating dyes (right). The area under the curve on the right gives the total fluorescence intensity.
The probe-probe distance is obtained from the distance between the two peaks in fluorescence intensity corresponding to the labels. In this case one usually accounts for the diffraction limit by fitting the peaks to a Gaussian point spread function to obtain a more precise location of the probes.117 The probe-probe distance is the experimental analogue to the “end-to-end” distance measure commonly evoked in theoretical polymer physics literature [see Eq. (2)]. The probe-probe distance R is often proportional to the genomic distance L, R = k1L. However, there is another subtlety associated with a probe-probe distance measure because the distance between probes cannot be measured unless it exceeds the diffraction limit, which is around 200 nm for the wavelengths used in these experiments. Thus, the ability to resolve two probes is a strong function of the chain stretching.167 However, once the distance between the probes exceeds the diffraction limit, their distance can be measured with a precision much better than the diffraction limit by fitting the fluorescence data and looking for the peak. The state-of-the-art in sub-diffraction imaging is below one nanometer,168 and it is relatively easy to get below 10 nm if the background noise is suppressed. In addition, even if the probes are spaced far enough apart so that they are resolvable on a fully stretched chain, when the chain is able to coil and fold (e.g. in a dynamic measurement), one loses the ability to distinguish the orientation of the probes.
If intercalating dyes or fluorescent nucleotides are used, one may instead directly calculate the extension of the chain. The extension is defined as the total linear distance from the beginning of the chain to the end of the chain, also known as the mean span. This quantity can be calculated using a simple cutoff or more precisely by fitting a 1D step function convolved with a Gaussian to account for the diffraction limited optics.169 The apparent extension, X, is proportional to the genomic distance, X = k2L, in most cases of interest. A notable exception is in quasi-2D confinement, which we will consider in more detail in Section 7.3. The sensitivity of the extension measurement, summarized by the constant of proportionality, k2, is related to the degree of stretching. In cases where the stretching is the strongest, we would expect k2 to approach unity. Given that the diffraction limit for fluorescent detection is approximately 200 nm, a naïve estimate of the limit of resolution for a fully stretched chain is about 600 bp.
The most straightforward metric to understand is the integrated intensity, which is simply the sum of the total fluorescence, or the area under the curve in Figure 18. To make such a measurement, we assume that an intercalating dye or fluorescent nucleotides are evenly distributed along the contour of the chain such that the integrated intensity, Itot, is proportional to the contour length of the molecule, Itot = k3L. It is important to realize that the sensitivity of the measurement is determined by this constant of proportionality. To see this, consider a case when k3 is small; here, a large change in the actual contour length of the molecule δL results in a small change in the intensity measured δItot, and thus a low sensitivity. For the integrated intensity metric, the constant of proportionality is determined by the average intensity per length of chain, or more specifically the number of photons collected per length of chain. An important consequence of this property is that the sensitivity of the measure (i.e. constant of proportionality) does not rely on chain stretching. High throughput sizing methods solely exploiting this third metric, namely fluorescence burst analysis, are discussed in Section 8.
Of course, all three metrics which rely on the fluorescence intensity can only give a relative measure of the length of a chain. To obtain an absolute length, a calibration curve or a quantitatively accurate theory is necessary. However, we will see that many of the techniques are repeatable such that a calibration is relatively straightforward. This contrasts with gel electrophoresis (where a standard needs to be run for each sizing) and many of the separation devices we will explore in Section 6 (where absolute calibration is a challenge). Finally, we note that the three metrics in Figure 18 are not mutually exclusive and that multiple measures can be used in a multi-color fluorescence technique.
5 State of the Art: Gel and Capillary Electrophoresis
With our overall objectives stated, we now turn our attention to the classical methods for DNA separations, namely gel and capillary electrophoresis. While we briefly touched on these subjects in Section 1, we will spend somewhat more time covering the regimes of Ogston sieving, entropic trapping and biased reptation here in Section 5.1. We will also survey the basic concepts in pulsed field gel electrophoresis in Section 5.2, as well as capillary electrophoresis in Section 5.3. As we will devote a substantial portion of the review to microfluidic methods, we discuss the generic advantages of microchip electrophoresis in Section 5.4. We conclude in Section 5.5 with the rationale for moving away from gel electrophoresis.
5.1 Regimes of DNA Electrophoresis in a DC Field
We begin with the standard method for sizing DNA, namely DNA gel electrophoresis in a dc electric field. Our aim in this section is to provide a sufficient overview so that the remainder of our review can be understood in the context of this standard method. For more detailed overviews of DNA electrophoresis, the reader is referred to the seminal review paper on the physics of DNA gel electrophoresis15 and a series of expert reviews on DNA electrophoresis17,33,34 celebrating the 30th anniversary of the journal Electrophoresis.
There are two standard media for gel electrophoresis, agarose and polyacrylamide. Agarose forms a physical gel; there are no chemical cross-links between the agarose fibers, but the forces between the fibers are so strong that the gel needs to be boiled to return it to a liquid state. The pore sizes in agarose are hundreds of nanometers,15 depending on the concentration of the agarose. The preparation of agarose gels is simple and inexpensive, and they are widely used. Agarose gels are also available in precast forms that can increase the reproducibility of the separation. Poly-acrylamide gels are chemically cross-linked and have very small pore sizes, on the order of tens of nanometers.15 Polyacrylamide gels are considerably more challenging to cast than agarose gels, and one needs to use care since the acrylamide monomers are neurotoxins. Precast polyacrylamide gels are also readily available. In general, agarose gels are used to separate longer DNA whereas polyacrylamide gels are used to separate short double-stranded DNA and single-stranded DNA. For the latter, one normally adds a chemical denaturant such as urea to eliminate the base-base interactions.
The particular mechanism of separation in a gel depends on the ratio Rg/a, where Rg is the radius of gyration of the DNA and a is the nominal pore size in the gel. The regime Rg/a ≪ 1, illustrated schematically in Figure 19, is normally referred to as Ogston sieving. Although we have drawn the DNA in this figure as a small random coil, the Ogston sieving regime for double-stranded DNA usually involves rigid rod-like DNA because the pore size of the gel is commensurate with the Kuhn length of the DNA. In either case, the effective volume occupied by the DNA is small compared to the pore size and excluded volume interactions between the fibers and the DNA are more important than any deformation of the DNA itself. The theory for the transport in this regime (which applies beyond DNA to globular molecules such as proteins) was developed by Ogston,170 Morris171 and Rodbard and Chrambach,172 and the theory is sometimes called the OMRC model. The basis of this model is that the electrophoretic mobility decays exponentially with the free volume available to the particle. If the migration indeed follows the OMRC model, then a semilog plot of the mobility versus the gel concentration will yield a straight line, since the free volume itself is a function of the density of gel fibers. The latter method of analyzing the data is known as a Ferguson plot.173 The Ferguson plot is only linear for very weak electric fields, since the OMRC model is a quasi-equilibrium model that requires that the DNA be able to completely sample its configurational and translational degrees of freedom in the pore space. One of the challenges in modeling DNA with the ORMC model is that the latter treats the DNA as a rigid particle, whereas the DNA can deform to enter the pore spaces. The validity of the OMRC model for deformable particles has been addressed using an exactly solvable version of Ogston sieving.174
Figure 19.
Schematic illustration of Ogston sieving. The DNA is small compared to the pore size in the gel so it can move freely through the interstices without deformation. Note that the pore spacing in the “gels” in Figure 20 and Figure 21 is identical to this figure, but the DNA is longer.
Now consider the case where the DNA molecular weight increases such that Rg ≈ a, illustrated in Figure 20. In a gel, the distribution of pores sizes implies there are some pores with Rg < a and others with Rg > a. We thus expect some of the pores in a disordered gel will be large enough for the DNA to reside inside them in its equilibrium coil shape, whereas transport through other pores requires substantial DNA deformation. The dynamics in this case were first described theoretically175–177 and only later observed in experiments.178,179 This regime is known as entropic trapping, since the DNA must pay an entropic penalty to hop between the larger pores inside the gel. The details of the motion through a random medium that contains entropic traps are complicated, since one needs to know the microstructure of the medium to characterize the traps. We will see in Section 6.1.2 and Section 6.1.3 that microfabricated devices can be designed specifically to exploit entropic trapping150,180–185 in a well defined geometry. For polyacrylamide gels, there now exists a quantitative theory for the electrophoretic mobility186 that incorporates the details of the pore structure in the gel, which can be obtained from independent measurements.187
Figure 20.
Schematic illustration of entropic trapping. Some of the pores are large enough for the DNA to fit inside without any deformation. To move between the trapping sites, the DNA needs to deform from its equilibrium coil to squeeze through the narrower constrictions. The dashed lines show the volume occupied by the DNA.
As the molecular weight of the DNA increases further such that Rg ≫ a, the DNA simultaneously occupies multiple pores, as illustrated in Figure 21. Each one of the pores contains a subchain of the DNA. Since we saw in Figure 3 that short chains of DNA are ideal random walks, it is reasonable to model the chain overall as a series of subchains (“blobs”) containing (a/lk)2 Kuhn segments. The gel plays the role of a reptation tube,51 and the DNA moves like a snake through this reptation tube in a curvilinear motion. Under the influence of the electric field, this reptative motion is biased towards the positive electrode. For weak electric fields, the corresponding mobility in the biased reptation model has the scaling189–191
Figure 21.
Schematic illustration of biased reptation. The chain is confined by the fibers of the gel to a reptation tube (dashed, red line). The arrows indicate possible directions for the chain to move along the tube. In the biased reptation model, the probability of moving in one of these two directions is biased by the electric field. A key assumption in the reptation theory is that the chain is confined inside the tube and cannot form hernias.188
| (38) |
where N is the molecular weight of the DNA and E is the strength of the electric field. The inverse scaling with molecular weight is the key to the separation of modest sized DNA (kilobase sizes) in agarose gels. It also explains why the bands of a ladder of equispaced molecular weights are compressed towards the entry of the gel.
Two problems occur when the electric field is increased in the biased reptation regime. First, it is possible for the chains to become trapped in long-lived U-shaped conformations due to backwards motion in the reptation tube.192 The probability of forming these long-lived states is a function of the chain length and thus leads to a mobility minimum as a function of molecular weight.192 As one might imagine, the presence of such a mobility minimum makes it difficult to assign the bands in a gel to different molecular weights since they are now “scrambled.” Second, as the field increases the DNA reptation tube tends to become oriented in the direction of the electric field. The proper description of the mobility in this so-called “biased reptation with orientation” regime requires a rather sophisticated treatment of the chain dynamics to account for fluctuations in the length of the reptation tube.193–195 Under weak electric fields, the mobility predicted by the biased reptation with fluctuations theory in the unoriented regime is the same as Eq. (38). Under strong electric fields, the biased reptation with fluctuations theory predicts the mobility in the oriented regime is193
| (39) |
The latter predictions are in excellent agreement with systematic experiments in agarose gels, some of which took many days to complete.196 Moreover, comparing Eq. (38) and Eq. (39), we can infer that for a given value of the electric field strength there exists a critical molecular weight
| (40) |
above which the DNA can no longer be separated in a dc field by biased reptation. Eq. (40) implies that one could continue to reduce the electric field as the molecular weight of the DNA increases and still achieve a separation, since there must exist a particular value of the electric field where even a very large chain remains in the unoriented regime. However, there are two problems with this strategy. First, the time to complete the experiment increases as the magnitude of the electric field decreases. In addition, long running times introduce problems in maintaining the stability of the system (e.g., the buffer composition).196 Second, and perhaps more important, at low electric fields the diffusion of the DNA in the gel197 begins to compete with the electrophoretic mobility. The plate height [Eq. (24)]increases and the resolution [Eq. (37)] decreases.
Once the biased reptation mechanism breaks down at even higher electric fields, a number of other modes of migration are postulated for DNA electrophoresis. One such idea is geometration,198–200 where the chain moves like an inchworm through the gel. This qualitative picture agrees with the dynamics observed in early single molecule experiments of DNA electrophoresis in agarose gels.201,202 We will see in Section 6.1.1 that the geometration mechanism can be exploited in microfabricated post arrays to separate DNA by size by greatly increasing the pore size to a regime a > Rg while using DNA with many Kuhn segments. In contrast, in the tight pores of a gel, geometration leads to a mobility that is independent of molecular weight. There are also theories of herniation203,204 that aim to describe the motion of megabase pair DNA in a high field. Similar to geometration, the herniation theory of DNA electrophoresis in a high field also leads to a mobility that is independent of molecular weight.
5.2 Pulsed Field Gel Electrophoresis
It is clear from the previous section that long DNA cannot be separated in a gel under a constant electric field. In order to achieve a sensible migration velocity, we need a strong electric field. However, strong electric fields lead to size-independent electrophoretic mobilities. While the exact mechanism giving rise to this behavior (biased reptation with orientation, geometration, herniation, etc.) depends on the magnitude of the electric field, all of the mechanisms share two important features: (i) the chain becomes oriented in the direction of the electric field; and (ii) the motion is steady, at least in a time-averaged sense, where fluctuations in the chain conformation can be described by a time-independent ensemble average or by a repetitive cycle. The key to separating long DNA in a gel is using an unsteady electric field, where the field direction (and, possibly, the field magnitude) periodically changes. Recall that, in the molecular-weight independent regime, the mobility in Eq. (39) scales linearly with the electric field. The resulting chain velocity, v ~ E2, is thus nonlinear in the electric field, introducing the possibility of resonance. Furthermore, although the mobility of long chains is independent of molecular weight when averaged over long times, the approach to the steady state regime depends on the molecular weight, with longer chains requiring more time to become fully oriented.
Viovy205 proposed a qualitative phase diagram for pulsed field electrophoresis, based on the biased reptation model, that partitions the phase space of time and molecular weight into four regions:
Short chains (N < N*): These sizes, which are readily separated in continuous electric fields, have short reorientation times and a linear relationship v ~ E. As such, they are essentially unaffected by any of the new phenomena introduced by pulsed electric fields (except for the trivial effect of changing migration direction).
Macroscopic regime: For very long pulse times, the fraction of time spent reorienting is small. Thus, long chains spend most of their time undergoing oriented motion along either the first or the second electric field direction. The resulting migration is then simply the average of the motion along each directions, and experiments clearly show that the mobility in this regime reaches an asymptotic value.206,207
Effective-field regime: For very short pulse times, the molecules are never able to reorient themselves. The head of the chain is thus oriented in the average direction of the two electric fields.
Intermediate regime: Here the pulse time is commensurate with the reorientation time, so the relationship between the mobility and the field is nontrivial. We will focus on this regime, as it is the most interesting for separations.
The literature on pulsed field electrophoresis is vast — and rather qualitative. Many early experimental studies of PFGE were parametric in nature, trying to identify the optimal electric field strength, pulse switch time, and field angle for a given separation. Such information is essential in the lab because each separation requires somewhere between 4 to 72 hours,208 and failed separations are a serious issue. Moreover, given the number of possible parameter combinations, a scattershot, heuristic optimization is very time consuming and unlikely to succeed.
To guide our discussion, we will divide the numerous variants of pulsed field electrophoresis into two broad classes, based upon their underlying molecular mechanisms. In the first class, crossed-field gel electrophoresis (CFGE), the electric field periodically switches between two directions with the angle φ between them being 0° < φ < 180°. In the second class, field inversion gel electrophoresis (FIGE), the phase of the electric field is reversed, i.e. φ = 180°. We will not spend a great deal of time discussing the practice of pulsed field electrophoresis, as numerous references already exist, including the book by Birren and Lai209 and various review articles.15,208,210–214 Pulsed field gel electrophoresis has matured to the point where sophisticated commercial apparatuses are now available to implement any of the protocols described below.
Let us first address the role of the orientation of the two electric fields. The original idea215 for crossed-field gel electrophoresis is depicted in Figure 22a. The two electric fields are orthogonal to one another, and the potential during a given pulse is applied from a single electrode to a row of grounded electrodes, resulting in an inhomogeneous electric field. This configuration was very successful — it can separate yeast chromosomal DNA up to 2000 kbp, a 40-fold improvement over the 50 kbp limit of continuous field electrophoresis. However, the inhomogeneous electric field curves the migration paths, and the exact path taken by the band depends on the location of the loading well. As a result, the migration distance varies from lane to lane, which complicates sizing the bands. However, it was initially believed that the inhomogeneous electric field was essential for the separation, and the technique was called “pulsed-gradient gel electrophoresis”.215
Figure 22.
Schematic of (a) an inhomogeneous pulsed field215 setup with φ = 90° and (b) a homogeneous φ =120° (hexagonal) CHEF configuration.216
By cleverly applying different potentials to an array of electrodes, it is possible to impose homogeneous electric fields at different angles, giving straight migration paths.216,217 One such system, called Contour-clamped Homogeneous Electric Field (CHEF) electrophoresis, is depicted schematically in Figure 22b. Homogeneous electric fields are not very successful when φ ≤ 90°. However, when the angle is obtuse, the separation quality is markedly improved.216 It turns out that the particular value of the angle is not very important, so long as it is obtuse; the mobility of the bands is essentially independent of the field angle for 105° ≤ φ ≤ 165° 206 and the mobility decrease is approximately linear with molecular weight.218,219 Interestingly, the resolution can be increased by a factor of two by using a three-field program that alternates between two crossed fields and a field inversion step.217
The success of the obtuse angle is related to the time for the DNA to reorient itself when the electric field changes direction. This basic idea was confirmed by early single molecule observations,201,202 as well as linear dichroism experiments220 that showed shorter DNA having both a lower degree of orientation and faster rate of reorientation. The orthogonal inhomogeneous setup in Figure 22a was probably successful because the effective angle between the electric fields increases towards the bottom of the gel.
Subsequent modeling efforts205,222–228 and experiments221,226,227 ultimately produced a quantitative understanding of how the reorientation process depends on the angle of the electric field and the molecular weight of the DNA. There are two critical features that came out of these studies. First, for short chains, the so-called “switchback” model222 provides a good description of the chain dynamics. When the field switches directions, the head and tail exchange roles and the DNA needs to “turn the corner” to begin moving in the new field direction. The switchback time is a function of molecular weight. We will see in Section 6.6 that a suitable modification229 of the switchback mechanism also provides a useful description of the dynamics of longer chains in artificial gels, which have much larger pore spacing than agarose gels. For larger chains in agarose gels, part of the path is retraced when the molecule turns around, further increasing the slow-down effect of the reorientation with increasing molecular weight.226 Moreover, the DNA are in narrow conformations and immobile during reorientation in a 120° field.226 Second, the formation of hernias such as the ones in Figure 23 play a critical role. While long chains can form hernias at many points,224 short chains tend to reorient from their ends.228 Thus, the qualitative features of the reorientation depend on molecular weight.
Figure 23.
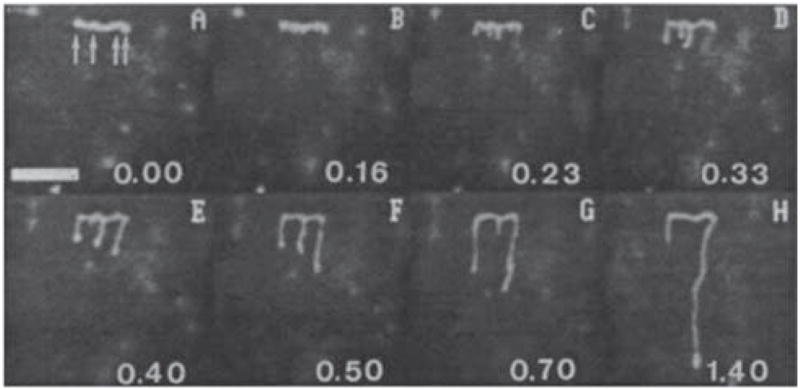
Reorientation of T2 DNA during pulsed field gel electrophoresis. Image (A) was taken a few seconds after the electric field in the horizontal direction was turned off and immediately before the electric field of 20 V/cm in the vertical direction was turned on. The scale bar is 8 μm. Reprinted with permission from Ref.221 Copyright 1990 American Chemical Society.
Like its continuous field counterpart, CFGE exhibits a mobility minimum under certain conditions.220,230 Simulations indicate that when the FIGE operates at a frequency corresponding to a mobility minimum, the corresponding DNA tends to spend most of its time moving backwards during reorientation, rather than being immobile.231 This contrasts with what we saw in continuous fields, where the mobility minimum is caused by infrequent (but long-lived), low mobility U-shaped conformations.
Depending on the ratio of the pulse time to the reorientation time, CFGE also exhibits band inversion. The inversion is easy to see during an experiment, since the inverted band tends to spread laterally.230 During band inversion, nothing new happens to the shorter chain. During each pulse, it completely reorients itself and then migrates in the new field direction. On the other hand, under these conditions the pulse time is too short for the longer chain to reorient itself. It will either remain oriented along one of the pulse directions230 or occasionally be trapped in a metastable state that is broken by fluctuations.205 In either case, the mobility of the longer chain is much higher than its shorter counterpart because the longer chain tends to spend a significant amount of time undergoing fast, oriented movement along one of the electric field directions, rather than stopping and reorienting each time the electric field direction changes. This model also explains the lateral band spreading, since the longer chains spend much of their time moving along the direction of one of the field pulses (without preference for a particular direction), rather than moving along the average direction of the electric fields.
The equipment required for a CFGE separation is relatively complicated and expensive, especially when compared to the conventional equipment used for gel electrophoresis in continuous electric fields. One possible approach to reduce the complexity of the experiment is to periodically turn off the electric field and let the oriented DNA relax toward their equilibrium coiled conformations.232,233 In principle, this is a way to separate the DNA, since both the relaxation time and the reorientation time (when the field is turned on again) depend on molecular weight. Unfortunately, the relaxation time of long DNA in a gel is very slow. Under thermal relaxation, theory205,234 predicts an ordinary two day pulsed field separation would last close to one month! Indeed, it would be better to make two pulses in the same direction, but reduce the magnitude of the second pulse.205
Another option is to periodically change the direction of the electric field, but make the time (or the field strength) greater in one direction so that the net motion is biased, a protocol called field-inversion gel electrophoresis (FIGE).235 Based on our understanding from biased reptation, we might suspect that FIGE will not work. When the electric field is inverted, biased reptation says that the chain will simply move backwards through its tube, without significant rearrangement. Nevertheless, long DNA can indeed be separated by FIGE. The key to the separation mechanism is the coupling of the internal modes of the polymer (or fluctuations in the tube, in the reptation lingo) to the changing electric field direction. For example, in simulations using a generalized reptation model with internal modes, the chain backbone is under asymmetric tension during the oriented motion.236 When the electric field polarity is inverted, the direction of the asymmetry also needs to be inverted. The asymmetry is steeper for larger chains and takes longer to reverse, giving rise to the separation. Reorientation in FIGE is thus related to rearranging the internal conformation of the chain, rather than forcing the chain to point along a new electric field direction, as was the case in CFGE. Similar molecular weight-dependent reorientation effects arise in simulations using Brownian dynamics,224 reptons,237 lakes-straits238,239 and non-local Monte Carlo225,231 simulations. Overall, the dynamics of a particular field inversion event are strongly dependent on the instantaneous chain conformation when the electric field is inverted.237
The key experimental variable for tuning a pulsed field separation (for a constant electric field strength) is the pulse ratio Tp, i.e. the ratio between the forward and reverse pulse durations. In the two limiting cases, the separation is poor: (i) If Tp is too large, then the reverse pulse will have little effect, and the motion should resemble that in a continuous field. Based on non-local Monte Carlo simulations, the return to continuous electric field behavior occurs around a pulse ratio of Tp = 5.225 (ii) In contrast, if Tp is too close to one, then net motion will be very slow. From experimental data,240 it appears a pulse ratio Tp = 3 is optimal and gives a good linear regime for the mobility.
It would seem that FIGE offers significant practical advantages over CFGE, since the experimental setup is simpler and the migration paths are always straight. However, FIGE is plagued by a severe mobility minimum.207,235,240,241 Moreover, in contrast to CFGE, the FIGE mobility minimum is not accompanied by lateral band broadening, making it more difficult to identify. The mobility minimum occurs at intermediate values of the pulse time,207 indicating that it is related to a resonance between the reorientation of the molecule and the changing field.224,225,231,236,237,239
In addition to DNA separations by molecular weight, pulsed electric fields can also be used to concentrate DNA using a protocol known as synchronous coefficient of drag alteration (SCODA).242–244 The method relies on a nonlinear relationship between the velocity and electric field. As we saw in Eq. (39), such a relationship exists in the biased reptation with orientation regime. [Note that, in the experiments supporting the SCODA method,242,244 the electrophoretic mobility is best fit with a two parameter model, μ = a + bE, rather than Eq. (39).] In the SCODA protocol, one simultaneously applies a rotating uniform electric field with an frequency ω and a rotating quadrupolar electric field with frequency 2ω. The time averaged velocity of the DNA points towards the center of these rotating electric fields,242 resulting in concentration of the DNA at the center of the gel. In contrast, other charged moieties with electrophoretic mobilities μ ≠ μ(E) will simply move in circles under the zero time-averaged electric field.
The aforementioned protocol acts as a DNA concentrator, moving the DNA towards the center of the gel. In practice, there are several other steps that can improve the DNA purification via SCODA. For example, the DNA can be injected into the gel electrokinetically,244 thereby rejecting any positively charged species in the sample. Moreover, by applying a small dc bias on top of the rotating electric fields, species that are not strongly trapped by the SCODA method will elute from the gel.244 With the latter strategies, SCODA can be used to isolate DNA from humid acid,244 extract DNA from challenging tar sand samples,244 or remove DNA from other PCR contaminants for forensic applications.243
The basic theory underlying the SCODA concentration effect requires that the DNA velocity depend nonlinearly on the electric field. As a result, DNA cannot be concentrated in the biased reptation without orientation regime, since the mobility in Eq. (38) is independent of the electric field. From a practical standpoint, this is an advantageous feature of SCODA since very high electric fields can be used. Moreover, the SCODA method requires that the DNA relax each time the electric fields change direction, such that most of the migration occurs in the biased reptation with orientation regime. The latter feature opens the opportunity to operate in a filtration mode; if the rotation rate exceeds the reorientation time of the DNA, then these DNA will not be concentrated at the center of the gel.244 Since the reorientation time depends on the molecular weight of the DNA, SCODA frequencies in the hundreds of millisecond range can reject large DNA.244
5.3 Capillary Electrophoresis
The idea that DNA can be separated in a polymer solution should not be particularly shocking at this point — even a reversible gel like agarose is essentially a polymer solution, except that the interactions between the agarose chains at room temperature are so strong that the solution needs practically to be boiled to separate the chains.245 Polymer solutions only became popular with the advent of Capillary Electrophoresis (CE). In contrast to slab gels, capillaries allow for significantly higher applied voltages (and concomitantly shorter separation times) because the large surface to volume ratio of a capillary efficiently dissipates Joule heat and suppresses convection. In the first attempts at capillary electrophoresis, the gels were polymerized in situ, but this led to a number of critical problems:245 (i) volume changes during polymerization led to cracks in the gel; (ii) the gel sometimes broke during manipulation due to differences in the compressibility moduli of the gel and water; (iii) the gels suffered from hydrolysis at alkaline pH; and (iv) the entrance of the gels sometimes became clogged after repeated use. These problems were alleviated by using entangled polymer solutions, although such solutions introduce some new technical problems of their own.
An enormous amount of effort has been expended in the search for optimal polymers for capillary electrophoresis. In general, polymers are chosen based on their resolving power, speed of separation, solution viscosity and their ability to suppress electroosmotic flow.246 A low solution viscosity is important for injecting the polymer solution into the capillary, and the suppression of electroosmotic flow allows for more reproducible separations (and quicker elution times if, as is usually the case, the electroosmotic flow opposes the electrophoretic motion).
Table 2 lists the most common polymers used in CE. Each polymer brings with it certain advantages and disadvantages. Moreover, polymers which work very well in one lab sometimes are less effective in others, due to differences in preparation.248,249 Perhaps the biggest issue in polymer solutions is their extremely high zero-shear viscosity, which makes injection into narrow capillaries difficult. The viscosity problem is even more pronounced for CE on a chip — unlike capillaries, most chips can only withstand a moderate amount of pressure before cracking.250 Fortunately, many polymers such as LPA are shear-thinning;251 their viscosity decreases as the velocity gradient increases. This results in significant improvements in polymer loading, provided the flow can be started in the first place.
Table 2.
| Polymer | Abbreviation | Polymer | Abbreviation |
|---|---|---|---|
| poly(acrylamide) | PA | linear poly(acrylamide) | LPA |
| methylcellulose | MC | hydroxyethylcellulose | HEC |
| hydroxypropylcellulose | HPC | hydroxypropylmethylcellulose | HPMC |
| glucomannan | none | poly(ethylene glycol) | PEG |
| poly(n,n-dimethylacrylamide) | PDMA | poly(ethylene oxide) | PEO |
A variety of strategies have been proposed to avoid the high pressure needed to inject high molecular weight polymer solutions, including using a mixture of high and low molecular weight polymers252 and drawing the polymer into the capillary concurrent with the DNA.253 The most promising (and certainly the most innovative) approach to the viscosity problem is to use polymers with switchable viscosities that can be converted from low viscosity liquids to high viscosity associating networks by changing the temperature.250 Since most commercial capillary electrophoresis equipment already includes temperature control, such matrices are simple to incorporate into the existing infrastructure. Thermoresponsive polymers also present the opportunity to control the mesh size of the network (i.e., the spacing between entangled polymers) through the temperature.254,255
Although the data are scattered, several key trends have become apparent. First, stiffer networks appear to be better for separations.246,247,256,257 It is hypothesized that the resolving power increases because stiff networks are more resilient and not deformed by the motion of the poly-electrolytes258 or because the reptation time of the polymers constituting the network is dramatically reduced.163 This hypothesis is reinforced by the quality of separations in very deformation-resistant media, such as interpenetrating networks,259 polymer blends260 and grafted copolymers.261 Indeed, an interpenetrating network259 was the first polymer solution able to resolve all 22 fragments in the benchmark φBR322/HaeIII digest in a single run, including two fragments differing in length by one base pair. Similarly, ultrahigh molecular weight LPA is a good option for sequencing. It has been used to sequence well over 1000 bp,163,262,263 compared to the ca. 550 bp possible with the commercially available “performance optimized polymer” (POP).246 Unfortunately, stiffer networks typically possess high viscosities264 and are thus difficult to inject into the capillary.
At a given solution viscosity, the optimal polymer to employ depends on the flexibility of the polyelectrolyte being separated. In general, long DNA are better resolved with a low concentration of a high molecular weight polymer, because the lower concentration delays the onset of orientation19 by increasing the blob size. In contrast, small DNA are better resolved in a high concentration of moderate molecular weight polymer, in order to reduce the blob size.249,264 The latter pair of observations accord well with a report that the optimal separation matrix has a reptation time on the order of the renewal time of the DNA being separated.257 However, this general trend runs counter to successful Sanger sequencing in high molecular weight LPA. This may not be a fair comparison, since the length-of-read (LOR) depends not only on the polymer solution, but also on the choice of base pair dyes and the data analysis software.163
Although capillary electrophoresis is generally performed in entangled polymer mixtures, an alternate approach known as End-Labeled Free-Solution Electrophoresis (ELFSE), or drag-tag electrophoresis, is also available.265 The idea behind ELFSE is to break the equal scaling of electric charge and friction with the number of monomers during free solution electrophoresis. The first approach266 was to attach a low-charge molecule to the ends of the DNA chains. Biotin and dimethoxytrityl, both with sizes similar to a single nucleotide, were initially used as drag tags to separate single-stranded DNA266 and a streptavidin/biotin drag tag was used to separate double-stranded DNA.267 Early experiments using ELFSE for sequencing268 required purifying the streptavidin prior to bonding and moving to a smaller capillary inner diameter to reduce the electroosmotic flow.
Theoretical modeling269 suggested the streptavidin-ssDNA complex may suffer from entanglement during low-field electrophoresis, as the size of the streptavidin molecule is similar to the persistence length of the DNA. From this starting point, three key properties of the drag tag were identified: The drag tag should (i) have low net electric charge; (ii) have high hydrodynamic friction; and (iii) be monodisperse. These insights motivated the development of engineered peptide drag tags with branched chains,270,271 recombinant proteins272 and very long drag tags273,274 that led to substantial improvements in the separation power.
A novel contribution to ELFSE is using peptide nucleic acid amphiphiles (PNAA), which function as synthetic, sequence-specific DNA binding partners.275 They also have the ability to form PNAA micelles when an aliphatic tail is added. The mobility of both the PNAA micelles and the DNA/PNAA hybrids reveals that the complementary DNA strands have a higher mobility than dissimilar DNA sequences in the presence of the PNAA micelles.275 This work implied that micellar electrokinetic chromatography could separate DNA fragments tagged with PNAA strands, which was demonstrated experimentally.276 Micelles offer some advantages over typical drag tags. Since the partitioning behavior by its nature samples many thousands of micelles, the exact monodispersivity in micelle size is not as critical as that for the fixed drag tag chains and globules used in other free solution electrophoresis techniques.276 Tagging of PNAA at both ends of the ssDNA complexes allows for drag coefficients277 on par with the results from the genetically engineered drag tags.273
5.4 Microchip Electrophoresis
Many of the early, seminal papers on lab-on-a-chip ideas dealt directly with electrophoretic separations278–281 and there now exist highly integrated chips with miniaturized DNA electrophoresis as a key step in the process282–287 and massively parallel DNA electrophoresis separations on chip.288 These devices are already making inroads into real applications, such as forensics,289 and commercial systems are now available from Caliper and Shimadzu. Capillary electrophoresis is readily downsized to a microchip,255 although one needs to be concerned with the pressures during loading. Conventional slab gel electrophoresis techniques have also been converted to microchip formats, although this is considerable easier with a chemically cross-linked gel such as polyacrylamide,290,291 especially if the polymerization is done with photo initiation.292,293 The improvements in separations using microchips have been very impressive, such as a 600 bp sequencing read length in only 6.5 minutes.294
The physics of separations in microchips and conventional gel/capillary electrophoresis are identical. Moreover, the heat dissipation in microchip electrophoresis is comparable to capillary electrophoresis, and many of the key parameters for analytical separations scale favorably as the system size is decreased.295 For example, ELFSE benefits from an increased electric field.267 Moving to a microchip platform296 allowed the use of fields up to 700 V/cm and extremely long sequencing reads. For most purposes, the primary advantage of microchip electrophoresis will be the ability to make precise, small-volume injection of the sample using valve-less techniques.278,297 These injections reduce the band broadening of the initial plug and thus lead to sharper separations. Since many of the separation devices we will encounter in Section 6 use these same type of injection methods, it is worthwhile to review the most common forms of injection here.
Figure 24 illustrates the two simplest modes of injection, both of which use a single intersection.298 In a floating injection (Figure 24a), a voltage is applied to the analyte reservoir and the analyte waste reservoir is grounded. The potentials in the other reservoirs are allowed to float, which causes some leakage of the sample into the buffer and separation channels. In the dispensing step, the voltages are switched to pump from the buffer reservoir into all of the other reservoirs. This drives the plug into the separation channel and causes a “pull-back” flow of sample into the analyte and analyte waste channels. In a pinched injection (Figure 24b), a small potential is applied to the waste and buffer reservoirs during the injection step. The flows arriving from the side channels “focus,” or sharpen, the sample plug. The dispensing step is the same as in a floating injection. Pinched injections provide better temporal stability and plug lengths than their floating counterparts.
Figure 24.
Injection and dispensing steps for (a) a floating injection and (b) a pinched injection.298 The arrows indicate the direction of the analyte transport in the different channels. For the case of a negatively charged species such as DNA, the arrows correspond to the direction opposite to the electric field.
One downside of the injection schemes in Figure 24 is that the sample volume is dictated primarily by the channel size, although it is also influenced somewhat by leakage into the side channels (for floating injections) or the degree of focusing (for pinched injections). Gated injection, shown in Figure 25a, is a simple technique that allows for a variable sample size.299 In this technique, the analyte is pumped around a right-hand turn and then diverted into the separation channel during the dispensing step. The amount of sample injected depends on the duration of the dispensing step. Another advantage of this technique is that there is always a flow in the separation channel towards the detector, allowing for higher throughput.
Figure 25.
Loading, dispensing, and reloading of a gated injection.299 The arrows indicate the direction of the analyte transport in the different channels. For the case of a negatively charged species such as DNA, the arrows correspond to the direction opposite to the electric field.
In all of the above injection techniques, the dispensing step is accompanied by a “pull-back” of some of the plug into the analyte and analyte waste reservoirs. The pull-back step is important for achieving precise injections. For tightly focused flows, however, this step needs to be carefully controlled to retain sufficient signal strength at the detector.299
A single intersection is the simplest possible geometry for valveless sample injection. Channels constructed with multiple crosses, such as the ones shown in Figure 26, allow a wider variety of options. For example, in the double-T (aka shifted-T) configuration279 shown in Figure 26a, the sample is first loaded from the analyte reservoir into a short, straight section that connects the latter to the analyte waste. Upon switching the voltages, the plug of sample in the main channel is injected into the separation channel and the other arms are pulled back. This method allows for very precise and reproducible injection volumes,279,301,302 with the amount of sample injected controlled by the channel geometry. Numerical and experimental results suggest that double-T injection schemes also reduce the leakage into the channel when compared to single intersection methods, thereby maintaining the baseline fluorescence in the separation channel.300 We have generally used double-T injections in all of our work. The basic double-T injection can be extended to the “double injection” technique depicted in Figure 26b, where the first cross focuses the stream and the second cross injects the narrowed sample.303,304 This strategy can be further generalized to multiple ports303.
Figure 26.
Loading and dispensing steps for (a) double-T279 and (b) multi-cross injections.300 The arrows indicate the direction of the analyte transport in the different channels. For the case of a negatively charged species such as DNA, the arrows correspond to the direction opposite to the electric field.
It is also possible to use a combination of electrokinetic and pressure driven flows to perform the injection.305 In this protocol, a pressure gradient drives the sample into the intersection while an electric field focuses it. The field is then turned off to allow some of the sample to flow into the separation channel. In a final step, the field is reapplied to inject the sample. In principle, this injection scheme eliminates the mobility bias in electrokinetic injection techniques (since the latter tend to inject a greater amount of the more electrically mobile species). However, efficient application of this protocol requires precise control over the pressures in the different reservoirs, which can be difficult to do without automated control.301
Sample injection is a well defined physical problem, and there have been many numerical studies of different injection processes.299,303,304,306,307 By far the most comprehensive of these studies is the series by Fu et al.,303,304,306 which involved finding the unsteady numerical solutions of the Poisson equation for the electric field, the Nernst-Planck equation for the ion distribution, and the Navier-Stokes equations for the fluid flow. The resulting predictions are in almost exact agreement with experiments. Moreover, this type of detailed numerical scheme provides guidelines for optimizing the applied voltages for various injection schemes. From an engineering standpoint, though, it is not clear that this level of numerical sophistication is necessary. Although it is useful to include the entrance effects,303,304,306 excellent results have been achieved using steady state equations in a much simpler computational model,308 which is valid when the relaxation time for the injection is fast compared to the total injection time and the injection point is far from the reservoir.
5.5 Why Consider Alternative Approaches?
Given that there already exists an inexpensive, simple option (gel electrophoresis) and a more involved, sensitive approach (capillary electrophoresis), one might wonder why a large number of groups have pursued the non-conventional approaches described in this review. There are three apparent technological motivations:
Electrophoresis in a dc field fails to separate DNA above a critical molecular weight. The exact cutoff depends on the electric field strength and the pore size in the gel,194 but it is normally in the tens of kilobase pair range. Although long DNA can be separated and thus sized by periodically changing the direction of the electric field via pulsed field gel electrophoresis,215,217,235 these separations require hours to days to size DNA in the hundreds of kilobase to megabase range. Thus, rapid separations of long DNA in artificial gels will be a major focus of our discussion in Section 6.
The most challenging task in DNA sizing is determining the molecular weight of a single long molecule of DNA. We will discuss the substantial efforts to adopt fluorescence burst analyses, in particular in conjunction with flow cytometry, as a single DNA detection strategy in Section 8. Likewise, we will also consider the emerging single-molecule techniques based on stretching the DNA and simply measuring its length by microscopy in Section 7.
Finally, the rise of lab-on-a-chip technologies provides a strong motivation to integrate DNA sizing methods with other analytical techniques. While there are already excellent examples of downsizing standard DNA electrophoresis separations as part of these devices,282–285 some of the monolithic separation media that we will see later in this review should be even easier to integrate into lab-on-a-chip devices.
While technological needs certainly motivated the development of the unconventional sizing methods discussed in this review, we cannot ignore the role of intellectual curiosity. To a large extent, most of these new sizing methods take advantage of microfabrication and nanofabrication techniques pioneered by the semiconductor industry. Whereas gels and entangled polymers typically only allow one to control the average pore size of the matrix, microfabrication permits exquisite control over the features in a given device. Moreover, it is relatively straightforward to create perfectly periodic systems using step-and-repeat patterns, thereby removing the heterogeneity of disordered systems such as gels. In addition to the creative new device designs produced by microfabrication, the experimental data obtained in these devices raised a number of intriguing scientific questions whose answers have greatly enhanced our understanding of the basic physics of DNA transport and confined DNA.32
6 Microfluidic Separation Methods
In this section, we discuss microfluidic approaches for determining the size of DNA based on their electrophoretic mobilities. By and large, these systems attempt to circumvent the limitations of gel electrophoresis described in Section 5.1, in particular for long DNA. As we proceed through these various devices, it is useful to keep several figures of merit in mind. First, the typical upper limit for a separation by conventional dc gel electrophoresis is around 10–20 kbp. This separation requires several hours in a typical electrophoresis buffer, but the rate can be accelerated by using buffers that reduce the Joule heating.309–311 Second, while pulsed field gel electrophoresis permits separations into the megabase pair range, the separations take many hours to days to achieve baseline resolution. Third, although gel electrophoresis separations take considerable time, the amount of DNA processed in a given gel electrophoresis experiment is large (on a laboratory scale) and easily recovered by cutting out the bands.
We begin our discussion with so-called artificial gels in Section 6.1. These systems are not literally gel-like materials, since they are fabricated in hard materials such as silicon or glass or replica molded into polymers such as polydimethylsiloxane (PDMS). Rather, the moniker “artificial gel” refers to the connection between the physics of DNA transport in these devices and the principles of gel electrophoresis we discussed in Section 5.1. Indeed, it was recognized immediately that artificial gels could not only be used as new separation media but also serve as a model platform for studying the physics of DNA electrophoresis.312
We then move on to methods that do not have direct parallels to gel electrophoresis. In Section 6.2, we discuss applications of dielectrophoresis to DNA separations. Dielectrophoresis involves the motion of a polarizable particle in a nonuniform electric field, and thus has a direct analogy with magnetism. We then consider cases where DNA can be separated in the absence of any structural features in Section 6.3. DNA can also be separated through transient interactions with the surface, a mechanism known as surface electrophoresis that forms the subject of Section 6.4, or through interactions with a lipid bilayer, which is the subject of Section 6.5.
All of the methods listed above provide improvements over gel and capillary electrophoresis in terms of the speed of the separation. However, recall that gel electrophoresis permits one to separate relatively large amounts of DNA at the laboratory scale and recover the fragments if the bands are baseline resolved. If one only wants to determine the molecular weight of the sample, then the microfluidic methods in Section 6.1 to Section 6.4 reduce the separation time from many hours to around 30 minutes. However, if one wants to recover the fractionated samples as well, these microfluidic methods are less appealing. There are relatively straightforward methods for recovering the bands in a microchip separation313,314 that have some similarities with capillary electrophoresis. Even if the bands are recovered successfully, the amount of material per band is still quite small. Indeed, if we think carefully about the electrokinetic injection methods described in Figure 24 to Figure 26, we immediately realize that (i) the amount of sample injected is quite small and (ii) the most popular injection methods, such as the double-T, send most of the sample to the waste during the loading step.
In Section 6.6, we will describe a host of microfluidic methods that allow for a continuous separation of the injected DNA. Some of the methods exploit variants on the artificial gel approaches for post arrays and entropic traps, while others are based on entirely new physical mechanisms that have not been realized in gels. In these systems, the DNA move at different angles as a function of their molecular weight. (The DNA may move at different speeds too, but the velocity of the DNA is irrelevant to the separation process after the initial startup period.) The DNA can thus be continuously injected into the device and different bands can be collected at exit ports on the opposite side. Such devices are probably the most exciting advance in this field, but we need to understand the basic mechanisms behind the analytical separations before moving onto these preparative separation methods.
Finally, we conclude our discussion of separation methods in Section 6.7 with a suite of methods that use hydrodynamic flows, rather than electrophoresis, to separate DNA by size. We will pay particular attention to hydrodynamic chromatography in sub-micron capillaries, which is emerging as a rather simple and effective method to size DNA up to the 100 kbp range.
6.1 Artificial Gels
We begin our discussion of separation based methods with artificial gels because these systems bear the closest resemblance to gel electrophoresis. Two key concepts became apparent in our discussion of gel electrophoresis in Section 5.1. First, as illustrated succinctly in Figure 20, the fibers of a gel can be envisioned as a disorder array of obstacles. While it is sometimes desirable to create such a disordered array of obstacles by microfabrication315 or self-assembly,302,316,317 most artificial gels consist of ordered pore structures. Ordered systems greatly simplify the modeling of the separation process, almost to the point where we can construct tractable models that describe much of the underlying physics.32 From a separations standpoint, ordered systems also reduce the band broadening caused by fluctuations in the microstructure of the separation medium. This advantage has been well highlighted in the chromatography literature.318–321 Second, the biased reptation mechanism arises when the nominal pore size of the gel is small compared to the radius of gyration of the DNA. For agarose gels with pore sizes on the order of hundreds of nanometers, only DNA shorter than about 10–20 kbp by size can be separated by a dc electric field before reaching the electric field cutoff described by Eq. (40).196 While the DNA longer than 10 kbp can be separated in a gel using an electric field with periodically changing direction, we saw in Section 5.2 that these pulsed field gel electrophoretic separations require hours to days to separate DNA. In principle, one can continue to dilute the agarose to further increase the pore size. Indeed, ultradilute agarose gels322,323 are capable of separating DNA in the hundreds of kilobase pair range. Unfortunately, these ultradilute gels are fragile and difficult to handle. The situation is reversed in microfabricated systems; creating large pore spaces is easy but fabricating length scales commensurate with agarose or polyacrylamide gels is very hard. Thus, separating long DNA is a major focus for artificial gels.
We will consider three different types of artificial gels. In Section 6.1.1, we will discuss the large number of studies on DNA electrophoresis in post arrays. While schematics such as the one in Figure 21 are meant to illustrate the basic principle behind gel electrophoresis, post arrays actually consist of a two dimensional array of obstacles. In Section 6.1.2, we will consider an alternate motif consisting of a periodic array of slits and wells. For long DNA, this device architecture provides a systematic way to exploit the entropic trapping phenomenon illustrated in Figure 20. For short DNA, the slit-well motif provides a simple, one-dimensional chromatographic separation. Both post arrays and entropic trapping have been the subject of extensive physical modeling. The relevant models were discussed in a recent review,32 so we will be brief in the present publication. Finally, in Section 6.1.3, we will cover DNA separations in colloidal crystals. In contrast to post arrays and slit-well motifs, colloidal crystals form a three dimensional porous matrix. However, if the colloids are monodisperse, the porous matrix possess a long range order that cannot be achieved in a gel.
6.1.1 Post Arrays
Microfabricated post arrays contain many posts with diameters in the micron or hundreds of nanometer range. A typical videomicroscopy image of DNA collisions in a post array from our own work using micron sized posts324 is shown in Figure 27. While moving through the post array, the DNA molecules collide with a post, unravel, and disengage by a rope-over-pulley mechanism in a time that depends on the length of the molecule.325,326 An electric field strength of around 10 V/cm is required to significantly stretch the DNA molecule to form a hooking collision,38,327 and the nature of the collision depends strongly on the relative distance between the center of mass of the DNA and the post (the impact parameter).327–330 Since the electric field dominates diffusive motion, unhooking from the post is effectively a deterministic process even when the lengths of the two arms of the chain extending from the post are relatively similar.331 During a collision DNA forms the four types of collisions (U, J, X, W) observed in Figure 28.332,333 These only represent the types of collisions with a single isolated obstacle; a veritable alphabet soup of shapes are observed in the collision with multiple obstacles.334–336
Figure 27.

Epifluorescence microscopy image of dyed λ DNA molecules interacting with a hexagonal array of 1 μm diameter oxidized silicon posts. The electrophoretic motion at 10 V/cm is from left-to-right. The inset shows an SEM image of the oxidized post array. This previously unpublished figure was produced in the course of the research leading to Ref.324 The details of the experimental system are described in the latter reference.
Figure 28.
Examples of (a) U, (b) J, (c) X, (d) W collisions of T4-DNA (166 kbp) with an isolated 1.6 μm diameter post during Brownian dynamics simulations. The numbers on the left side of the images correspond to the dimensionless time between two successive snapshots. Reprinted with permission from Ref.333 Copyright 2007 American Chemical Society.
The DNA-post collisions are the basic unit of the electrophoretic separation in post arrays, and many collisions are required to yield a separation.326 There are two ways to quantify the time that the DNA interacts with the post, the first of which is the unhooking time. From a modeling standpoint, the unhooking time is a convenient quantity. Indeed, most of the data for the collisions in Figure 28 (except for the W collisions) collapses onto a simple model expressed in terms of the length of the short arm during the collision.332,337 However, the unhooking time overestimates the contribution of a collision to the separation because it fails to account for the translation of the center of mass of the molecule during the collision.332 Rather, the relevant parameter for separations is the hold-up time, defined as the delay in the center of mass motion due to a post collision.338
The electrophoretic mobility of DNA in a post array depends on the frequency of collisions and the hold-up time of the collisions. Since the collision frequency is independent of the electric field339 and the hold-up time is inversely proportional to electric field,332 the mobility is independent of electric field.339 The holdup time itself depends on the molecular weight,325,326 which is the mechanism behind the separation.32 In contrast to these hooking collisions, roll-off collisions resulting in little DNA deformation do not significantly contribute to a sized based separation.338
The protocols for making post array devices have matured through the years, with Figure 29 showing the evolution of nanopost array technology from the first device312 in 1992 to a very impressive high aspect ratio device341 in 2006. In the devices used for separations, the channel widths are typically around 25 to 50 μm, with depths in the 4 to 10 μm range. The array itself extends along the axis of the channel. When electron beam lithography is used to pattern the array, which is common for densely packed nanoposts,142,340,342–345 the array of posts with diameters in the hundreds of nanometers range typically spans a millimeter in length. Moreover, electron beam lithography allows the posts to be patterned with very small gaps between them. These lengths can be reduced to such a small scale that nanopost arrays have also been used to filter out large DNA by a simple filtration process.346 While the gel fibers of an agarose gel are much smaller that the nanoposts used in these arrays, the pore size in the device can be tuned to match the pore size of agarose gels. Indeed, the first post array device highlighted the potential for these systems to act as models for gel electrophoresis.312 In contrast to the random, disordered fiber placement of a gel, nanopost arrays are highly ordered sieving matrices.
Figure 29.
SEM images of microfabricated post arrays showing improvements in the fabrication process. (A) 1 μm diameter, 150 nm tall posts appearing in 1992;312 (B) 200 nm diameter, 600 nm tall posts appearing in 2004;340 and (C) 300 nm diameter, 15 μm tall posts appearing in 2006.341 Reprinted with permission from Refs.312,340,341 Copyright 1992 Nature Publishing Group;312 2004 American Chemical Society;340 2006 Institute of Physics Publishing.341
Note that electron beam lithography is not the only method for creating nanopost arrays. It is also possible to create densely spaced posts using nanosphere lithography, where a colloidal crystal serves as the etch mask,347 or soft UV nano-imprint lithography.345 Yet another technique involves the removal of a sacrificial layer resulting in an insulating silicon nitride device.140 Zinc oxide nanowires also create a dense array of very thin nanoposts.329 While these nanowires are easily grown via solution chemistry and are much thinner than the silicon-based posts, the arrays are not ordered. Moreover, the experiments need to be performed at a pH near the isoelectric point of ZnO to avoid charging of the wires.329 Although ZnO nanowires have been used successfully to study the physics of DNA collisions with isolated small posts,329 they have not yet been used as a separation medium.
Arrays created by conventional photolithography techniques, which can pattern micron sized posts37,158,312,324,325,348,349 as well as sub-micron posts,160,162,341,350 are capable of producing centimeter-long separation channels. Moreover, projection lithography permits access to sub-micron sized posts while maintaining a reasonably large area pattern.160,341,350 If one desires a wafer-scale pattern of sparse nanoposts, it is possible to first pattern an array of micron sized posts in photoresist and then thin the post diameter down to several hundred nanometers using an oxygen plasma.162,330 Sparse arrays of very small posts have also been fabricated using phase shift lithography.351,352
The final device must be electrically insulating to allow electrophoretic motion of DNA through the channel. Fabricating the device in quartz340,343 or fused silica345 provides a uniform insulating surface. An alternate approach is to build the channel geometry in silicon, and then grow an insulating layer on the silicon using thermal oxidation.341 The growth of an oxide layer significantly increases the post diameter; however, Figure 29c shows posts with a final diameter of 300 nm fabricated with this technique.341 It is important to remember that the device fabrication often includes an undercut of the mask during reactive ion etching,160 so the diameter of the bare silicon posts pattern prior to etching is smaller than the original mask.
An alternative technique to produce sparse post arrays relies on the self-assembly of super-paramagnetic bead suspensions.164,302,316,339 In this approach, a solution containing super-paramagnetic beads with size around 600 nm is pumped into a PDMS microchannel. After the hydrodynamic flow is stopped, an external magnetic field of approximately 10 mT is applied with a magnetic coil, trapping the beads into a metastable quasi-hexagonal array of columns. Different array structures can be formed by washing the beads with different surfactants.339 Due to aggregation of the columns as they form, the resulting array has micron sized posts with several microns between the posts. These arrays are considered only quasi-ordered due to this aggregation effect as well as defects introduced by the shape of the channel boundaries.353,354 The order of the magnetic bead array can be increased by placing nickel dots on a glass substrate that act as seed points for magnetic bead self assembly.355
Table 3 summarizes the separation data obtained in the various devices described above. Several trends are immediately clear from these results. First, the bands in the devices are usually resolved, but not always baseline resolved, in several minutes. (See Figure 16 for representative plots of the separation resolution to compare with the data in Table 3.) Since the resolution should increase with the separation time from Eq. (35), it should be possible to increase the resolution simply by increasing the size of the post arrays. However, as we noted earlier, the lithographic techniques used to pattern the arrays have limited spatial extent. While it is possible to increase the separation channel length with the same device footprint by introducing serpentine turns in the channel, these turns can give additional dispersion.153–156 Moreover, as the separation time increases, the signal-to-noise ratio deteriorates due to the band broadening. Recall that the depth of the channels (several microns) is commensurate with the radius of gyration of long DNA, so the number of DNA per unit volume is not very high. It is our experience that post arrays that include a serpentine channel to increase the separation channel length do not lead to the expected increase in separation resolution for these reasons. Second, most of the experiments reported in the literature only use a few DNA species per experiment. Indeed, the most common experiments are separations of λ DNA (48.5 kbp) and its dimer, or between λ DNA and T4 DNA (168.9 kbp) or some other binary mixture. The reason for choosing these binary mixtures is the ready availability of these DNA and the inability for dc gel electrophoresis to resolve such long chains. Based on the available data in the literature, it appears that the band capacity (i.e., the number of species that can be resolved) for these devices is relatively low. While two species can be readily resolved in a manner of minutes, it remains to be seen whether a more complicated mixture of long DNA can be resolved in a single electrophoretic run. Based on our own work, we are not optimistic that the band capacity can be increased much beyond the separation data reported in the literature without increasing the depth of the channels, which is a technological challenge that has only been met in rare cases341 like Figure 29c.
Table 3.
Experimentally realized separation resolutions in post array devices. The classifications highlight the different class of devices. For the magnetic beads, the post size is a nominal value since the aggregation of the beads and polydispersivity in the bead sizes lead to many post sizes near this nominal value. The resolution data correspond to either results directly reported in the relevant reference or values computed from the published electropherograms.
| Classification | Post Size | E (V/cm) | DNA sizes (kbp) | Time (s) | Resolution | Ref. |
|---|---|---|---|---|---|---|
|
| ||||||
| Nanoposts | 500 nm | 10 | 1 and 10.1 | 130 | 1.45 | 340 |
| 500 nm | 10 | 10.1 and 38.4 | 170 | 2.69 | 340 | |
| 500 nm | 10 | 4.4 and 6.6 | 520 | 1.08 | 340 | |
| 500 nm | 10 | 6.6 and 9.4 | 520 | 1.04 | 340 | |
| 500 nm | 10 | 9.4 and 23 | 680 | 2.39 | 340 | |
| 300 nm | 500 | 48.5 and 166 (T4) | 120 | 1.0 | 345 | |
| 150 nm | 30 | 2 and 5 | 60 | 1.43 | 142 | |
| 150 nm | 30 | 5 and 10 | 75 | 1.56 | 142 | |
| < 1 μm | 35 | 21 and 165 | 121 | 0.8 | 341 | |
|
| ||||||
| Sparse Posts | 1 μm | 20 | 2.7 and 48.5 | 500 | 0.96 | 349 |
| 360 nm | 10 | 15 and 33.5 | 1150 | 1.66 | 162 | |
| 360 nm | 10 | 33.5 and 48.5 | 1250 | 1.22 | 162 | |
|
| ||||||
| Nanofence | 600 nm | 10 | 15 and 48.5 | 400 | 1.8 | 160 |
| 600 nm | 10 | 33.5 and 48.5 | 400 | 0.91 | 160 | |
|
| ||||||
| Magnetic Beads | n/a | 3.2 | 48.5 and 97 | 2000 | 2.0 | 316 |
| n/a | 3.2 | 48.5 and 145.5 | 2300 | 1.3 | 316 | |
| n/a | 7 | 15 and 48.5 | 800 | 2.6 | 316 | |
| n/a | 7 | 33.5 and 48.5 | 800 | 1.0 | 316 | |
| 1.3 μm | 20.3 | 48.5 and 97 | 275 | 1.27 | 302 | |
| 1.3 μm | 20.3 | 97 and 168.9 | 275 | 1.16 | 302 | |
| 1.4 μm | 18.8 | 48.5 and 97 | 250 | 1.84 | 302 | |
|
| ||||||
| Pulsed Fields | 2 μm | 224 | 48.5 and 168.9 | 660 | 17.96 | 348 |
| 2 μm | 224 | 48.5 and 168.9 | 10 | 1.0 | 348 | |
While the particular arrays highlighted in Figure 29 feature relatively dense arrays of posts, they require sophisticated fabrication techniques. We have wondered whether similar quality separations are possible using sparse, ordered arrays. Sparse ordered post arrays are easily fabricated using step-and-repeat masks and conventional photolithography, and these ordered devices have large spaces (relative to the DNA radius of gyration) between neighboring posts. If the array is very sparse,349 the DNA molecules tend to move in the interstices between posts and rarely collide with the posts of the array. This effect is known as channeling.158 Brownian dynamics simulations have suggested that the long range orientational order in a post array leads to channeling.356 Another simulation study showed that hairpin formation (or collision) is more frequent in disordered arrays, and that random post positions are essential for separations.357 However, these simulations neglected the deflection of the electric field lines around the insulating posts. Later Brownian dynamics simulations that accounted for the non-uniform electric field showed that DNA collides frequently in an ordered array and that this agrees with experiments in an array of 1 μm posts with 3 μm center-to-center spacing.158 The curved electric field lines drive the DNA molecule across the channel, as shown in Figure 30, resulting in more frequent collisions. The predictions of these later Brownian dynamics simulations agree very well with experimental data for λ DNA electrophoresis in an array of 1 μm posts with a 3 μm center-to-center distance.158 Thus, it is reasonable to expect that relatively sparse post arrays fabricated using simple step-and-repeat patterns should lead to good separations of long DNA.
Figure 30.
Sparse array of posts with diameter d and center-to-center spacing a. During electrophoretic transport the DNA molecules follow the dashed electric field lines. The extensional electrophoretic flow in the extensional zone leads to a deformation of the DNA327 that increases the probability of collision. The focusing zone after the post has electric field lines that tend to drive the DNA into a position that favors collisions with the next post. Reprinted with permission from Ref.158 Copyright 2009 The American Physical Society.158
The conclusions drawn from these fundamental experiments and simulations158 have been confirmed in subsequent separation work. For example, experiments have demonstrated separations in sparse arrays of 1 μm diameter posts and 360 nm diameter posts, with the separation resolution between 15 kbp to 48.5 kbp DNA improving as the post size decreases.162 Further Brownian dynamics simulations of DNA electrophoresis in 1 μm post with 3 μm center-to-center spacing predicted that λ DNA and T4 DNA will have baseline resolution after 15 mm at E = 30 V/cm,336 which should require around 7 minutes. This separation resolution is higher for low electric field strengths,336 which also has been our experience in experiments in this type of post array.
Thus far, we have focused on “crystalline” post arrays where the posts are arranged in a regularly repeating hexagonal or square pattern. It is not obvious a priori that a crystalline arrangement is the optimal way to arrange a post array, although virtually all of the post arrays constructed via microfabrication feature regular arrays. To test this hypothesis, we recently compared the mobility and band broadening in ordered and disordered arrays.315 The devices were fabricated in silicon dioxide and contain arrays of 1 μ m diameter posts with an average post density corresponding to a hexagonal array of posts with a 5 μ m center to center spacing, either in an ordered hexagonal array or an array which has a disorder that is similar to that realized in magnetic bead arrays.302,339 These experiments315 revealed that the band broadening is greater in the disordered array, while the electrophoretic mobility does not depend on the array order. We can thus conclude, at least for this post density, that ordered arrays yield superior separation performance due to a reduction in band broadening.315
It also appears that providing large open regions can enhance the separation in a post array. The “nanofence” array160 consists of a repeating pattern of two rows of 600 nm diameter posts separated by a 20 μm post-free region. The device was fabricated by projection lithography in silicon. Although the number of posts in this device is much lower than any of the arrays we have discussed thus far, we see in Table 3 that the resolution of the prototype device is comparable to existing arrays of regularly spaced posts. Surprisingly, the high resolving power of the device is due to enhanced stretching of the DNA molecule in the post-free region160 rather than an expected reduction in the band broadening due to the regularly spaced collisions with the nanofences.358
The development of models for the separation and their application to experiments has taken a tortuous but ultimately successful path. As a historical aside, we should point out that extrapolations from simulation data and models for collisions with isolated, single posts,326,328 made a few years after the development of the first post array312 in 1992, predicted that post arrays would not be able to separate long DNA due to the dispersion caused by the collision326 or the distance between posts required to realize single post collision statistics.328 As we have seen in our review of the various devices produced since 2002, there is ample experimental evidence to the contrary. It behooves us to briefly review how realistic models must incorporate both the statistics for the collisions with the posts and the transport in the array. A natural starting point would be the geometration models from gel electrophoresis,198–200 which already acknowledge the potential for DNA to undergo rope-over-pulley collisions under modest electric fields. It is readily apparent that the geometration models for a gel lack predictive power for transport in post arrays, since they predict that the mobility is independent of molecular weight.200 Thus, more sophisticated models of DNA transport were developed with the goal of predicting how the macrotransport properties such as electrophoretic mobility and band broadening depend on the DNA-scale physics. One early attempt was a semi-phenomenological lattice Monte Carlo model359 that estimates the mobility and band broadening of the DNA as a function of the average collision time and the collision probability, both of which can be obtained from separate single molecule experiments339 or a microscale physical model. However, when the relevant experiments were performed,302,339 it became apparent that while many of the underlying assumptions of this model are qualitatively correct, the model fails to quantitatively predict the dispersivity during electrophoresis.339
Further improvements in models for DNA transport relied on continuous-time random walk (CTRW) theory, in particular the Scher-Lax CTRW.360 Originally developed by Scher and Lax to describe electron transport in disordered solids, the Scher-Lax CTRW model consists of a repetitive sequence of steps where the particle exhibits both a random waiting time at a trapping site and a random distance traversed between these trapping sites. Building on the geometration model for gel electrophoresis,200 the CTRW model for DNA electrophoresis in a post array consists of: (i) collision with post and extension into two arms, (ii) electric-field-driven unhooking from the post, and (iii) uniform translation until the next collision.164,361,362 The configuration of the DNA molecule at the beginning of the collision determines the hold-up time of the collision. The first CTRW model applied to post arrays164 assumed the chain was completely extended during the collision. To achieve accurate results in CTRW models, we must account for incomplete chain extension361,362 as well as the relaxation time and for interactions with multiple posts.336,358 Incomplete extension of the molecule does not strongly affect the electrophoretic velocity, but increases the dispersivity.361 These CTRW models164,361,362 treat successive collisions as uncorrelated events, an assumption that has been experimentally verified.324 One of the shortcomings of these models is that they estimate collision probabilities and hold-up times based on microscale models which are not adequately accurate.324 A more recent CTRW model relies on measurements of the hold-up time of a collision and the distance between collisions to make predictions of macrotransport properties.358 The latter model, which builds on the continuous-time random walk theory for a two state system with converging moments,147 readily reduces to the previous Scher-Lax CTRW models164,361,362 as limiting cases.358 Combined with a simulation method that reproduced experimentally measured hold-up times and collision probabilities,158,324 this model predicted separation parameters over a wide range of DNA sizes and electric field strengths.358
Post arrays can also be operated under a pulsed field, analogous to the pulsed field gel electrophoresis separations we saw in Section 5.2. The fabrication methods are identical to the fabrication methods for dc field separations, and the origin for the advantages of using a post array are the same. The major limitation in pulsed field gel electrophoresis is the extraordinarily long time required for the DNA to reorient itself in the direction of the new electric field in the small pores of a gel. By increasing the pore sizes to the micron scale in a post array, the DNA can readily reorient themselves in the new field direction.229 Pulsed field operation of a post array device allows linear fractionation of long DNA,229 and using an entropic trap at the injection point (see Section 6.1.2) permits the injection of a relatively narrow band of long DNA. Using the aforementioned properties of microfabricated post arrays, Austin and coworkers348 demonstrated that very long DNA (100 kbp) can be separated in 10 seconds in a pulsed field. The increase in separation resolution from this mode of operation seems to offset the increased difficulty of applying a pulsed electric field to the device. Indeed, we will see that the methods of applying pulsed fields in a microfluidic device are critical to the very promising methods we will explore in Section 6.6. The separation time during pulsed field electrophoresis in the post array device is a substantial improvement over the separation time required in PFGE.
Another approach to using pulsed fields for DNA separations is the entropic recoil mechanism.141,363 When the posts are very densely spaced, the DNA needs to pay an entropic penalty when it unravels and begins to reptate through the post array. If the electric field is turned off and the DNA is only partially inserted into the post array, it will recoil back to the entrance of the array to maximize its configurational entropy.141 Since the time to completely unravel and enter the post array is a function of molecular weight, gradually increasing the duration of the “on” pulse of the electric field should produce a separation as a function of molecular weight.363 During the shorter pulses, the short DNA will be injected into the array and thus not feel the entropic recoil effect. As the pulse time increases, the short DNA will continue to move through the array but the long DNA will still remain outside the array until the pulse time is sufficient for complete injection. While the entropic recoil effect does lead to a separation as a function of molecular weight via this mechanism,363 the bands are very broad due to the stochastic nature of the injection process. Moreover, DNA that enter the array in a hairpin formation are injected at a different time than the same sized DNA that enter the array head-first. Given the additional challenges inherent in fabricating a very dense array of posts,141 the entropic recoil mechanism has not received much further attention as a separation mechanism.
Anisotropic post arrays have also been used to separated DNA in a electrophoretic size exclusion chromatography mode.142 As illustrated in Figure 31a and Figure 31b, these posts are very anisotropic and one would not observe the rope-over-pulley separations we saw thus far, especially since the potential drop is in the vertical direction in the figure. Indeed, the electric field in the narrow gap between the posts is very weak. As the DNA are convected down the large channels between the posts, they can sometimes diffuse and enter the small gaps between the posts. The probability for entering these small gaps is a function of the size of the DNA, with the smaller DNA having a greater partitioning into the space between the posts. As a result, the larger DNA elute first in Figure 31c, as we would expect in a size exclusion chromatography separation. Although the separation here appears quite promising, size exclusion chromatography has not been explored in great detail.
Figure 31.
Size exclusion chromatography separation of DNA in a post array. (a) Principle of the size exclusion process. (b) SEM image of the post array. (c) Electropherogram for a separation voltage of 40 V and a separation length of 4 mm. Reprinted with permission from Ref.142 Copyright 2003 American Institute of Physics.
Overall, DNA separation in post arrays drastically decreases the separation time of long DNA compared to PFGE. However, the complex apparatuses necessary for fabrication, operation and detection have thus far prevented widespread adoption of post array devices for long DNA separation.
6.1.2 Entropic Traps and Nanofilters
In the previous section, we saw how microfabricated post arrays could break the biased reptation mechanism in gel electrophoresis by increasing the pore size into the regime of mechanical instability for agarose gels,322,323 thereby extending the range of DNA that can be separated in a dc field into the hundreds of kilobase pair range (see Table 3). We also noted in the context of Figure 29 that microfabricated post arrays can remove the inherent disorder of gels through the use of step-and-repeat patterns. In addition to simplifying the modeling of the system,312 it appears that these more regularly spaced posts reduce the band broadening315 and thus produce sharper separations.
We now turn our attention to how microfabricated devices enhance separations in the other regimes of DNA electrophoresis covered in Section 5.1, namely Ogston sieving (Figure 19) and entropic trapping (Figure 20). Recall that Ogston sieving refers to the case where the radius of gyration of the DNA is smaller than the pore size, and the separation is due to the molecular weight dependence of the free volume available to the DNA as it migrates through the gel in the absence of substantial deformation.170–172 In contrast, the entropic trapping regime refers to the case where the nominal pore size in the gel is commensurate with the radius of gyration of the DNA. The relevant transport mechanism in entropic trapping involves hopping between cavities separated by an energy barrier associated with a temporary loss of configurational entropy.175–177 One particular challenge for entropic trapping in gels is the variance in the pore sizes in the gel,187 which leads to a distribution in energy barriers during entropic trapping186 and concomitant band broadening. One also experiences similar problems in the Ogston sieving regime of gel electrophoresis, since the local free volume available to the DNA in a heterogeneous gel fluctuates (in the Lagrangian sense, where we follow the particle) and thus leads to band broadening. Microfabricated devices should be able to minimize the latter issues, since we have already seen that it is straightforward to produce periodic sieving matrices by microfabrication.
In principle, we can imagine making post arrays that directly reflect the length scales in Figure 19 and Figure 20, thereby creating two-dimensional versions of both Ogston sieving and entropic trapping. We could also tailor the exact location of the posts to either create a spatially homogeneous free volume for the DNA (in Ogston sieving) or regularly space the large pores (for entropic trapping). Measuring the DNA transport in such a device would be an intriguing direct experimental test of the exactly solvable, two dimensional lattice models for Ogston sieving developed by Slater and coworkers,174,364–367 in particular the role of non-conducting fibers368 and designed dead-end pores.369,370 However, constructing a post array at these length scales is technologically challenging. Interesting physics would likely result from such experiments, but it is unlikely that the separations would be a substantial improvement over the other methods discussed in this review.
Rather, the regimes of Ogston sieving and entropic trapping have been exploited primarily using the device designs illustrated in Figure 32. When the device is used for separating long DNA, it is referred to as an entropic trap.150,181–183 When the device is used for separating short DNA, it is referred to as a nanofilter.184,185,371,372 In both cases, the device is an array of repeating thick and thin regions. The lateral patterning of the device is done by optical lithography, so the typical length of a thick or thin region is in the micron regime and the channel is around 25 μm wide. The thick regions are about 300 nm to 3 μm deep and the thin slits are usually between 20 and 90 nm, with smaller lengths scales prevalent for the nanofilter and the longer length scales prevalent for entropic trapping. Recently, the nanofilter geometry was turned on its side and called a “nanowall” array.373 The latter device consists of 5 μm high and 215 μm long walls separated by a gap of 200 nm. The device contains 20 nanowall regions before the detector, where each wall region is separated by a 35 μm gap. The periodicity of the nanowall device is much larger than the schematic in Figure 32, and features much fewer periods than the standard entropic trapping system.150
Figure 32.
Slit-well motifs for exploiting (a) the entropic trapping regime using long DNA and (b) the Ogston sieving regime using short DNA. (c) The devices are patterned by two etching steps. As we see from the side view of the device (90° rotation of the other schematics), the optical lithography patterning of the devices leads to similar periodicities and channel sizes in both types of devices. The direction of the DNA motion is the same in panels (a) and (b).
The DNA can be driven though the array with an electric field150,181–185,371,372 or by a pressure driven flow.374 We will devote most of our time in this section to discuss the separations achieved in entropic trapping and nanofilter configurations. However, the slit-well motif32 is not the only way to exploit the physics of these regimes. Thus, we will also devote some time to consider alternative designs that are amenable to soft lithography375,376 and a rather novel idea of using oil slugs to create entropic traps in large microchannels.377,378
The basis for separations using the system in Figure 32a was the subject of considerable interest. The original device182 consisted of alternating thick regions, about 1 μm deep, and thin regions, 90 nm deep, and was only used for observing single molecules of long DNA as they moved through the traps under the influence of an electric field. Remarkably, the experiments revealed that the large molecules travel faster than the smaller molecules. This result was unexpected, since the configurational entropy lost by entering the slit should increase with molecular weight. The explanation181 is that the larger molecules have a higher escape attempt frequency, which is more important than their larger free energy barrier.150,181 These experiments also spurred a great deal of theoretical work to understand the details of the process. We recently reviewed the theoretical literature elsewhere.32
In the present review, we would like to focus on the applications of the entropic trapping device rather than the underlying physics. In addition to verifying that the single molecule dynamics in previous work181,182 indeed lead to a separation, the seminal experiments on entropic trap separations150 introduced two practical innovations. The first innovation was the method for loading the DNA. Escaping an entropic trap requires overcoming the energy barrier in a thermally activated escape process. The electric field tilts the potential energy landscape, so the effective barrier height decreases with increasing electric field strength.181 Indeed, for a sufficiently high electric field, there will be no trapping since the DNA can easily overcome the barrier when the favorable change in enthalpy caused by moving in the potential gradient dominates the entropic penalty for entering the slit. In contrast, at very low electric fields, the probability of jumping over the barrier by thermal energy is exponentially small. As a result, the DNA can be pressed against the first trap using a weak electric field. When the electric field is increased to the separation voltage, the DNA hop over the first barrier as a narrow injection band. While this type of injection was first proposed in the entropic trapping separation,150 it was critically important in the ultrafast separations of long DNA via pulsed field electrophoresis in a post array a few years later.348 The second innovation was the multilane separation device illustrated in Figure 33, which mimics the typical setup in gel electrophoresis. One of the challenges in the separation devices we discussed in Section 6.1.1 is the calibration. The experimental data presented in Table 3 always involved separating known sizes of DNA. These are the sensible experiments to validate the operation of a device. However, if we want to identify the size of unknown bands, we need to compare their speeds to a calibrated standard. One of the major (and rarely discussed) shortcomings in many microfluidic separation devices is the reproducibility of the absolute mobility. Since these devices have extremely high surface area to volume ratios and very small amounts of sample, the combination of experiment-to-experiment fluctuations in the surface properties and the relatively low signal-to-noise ratio makes an absolute calibration challenging in prototype devices. The device architecture in Figure 33 minimizes these issues.
Figure 33.
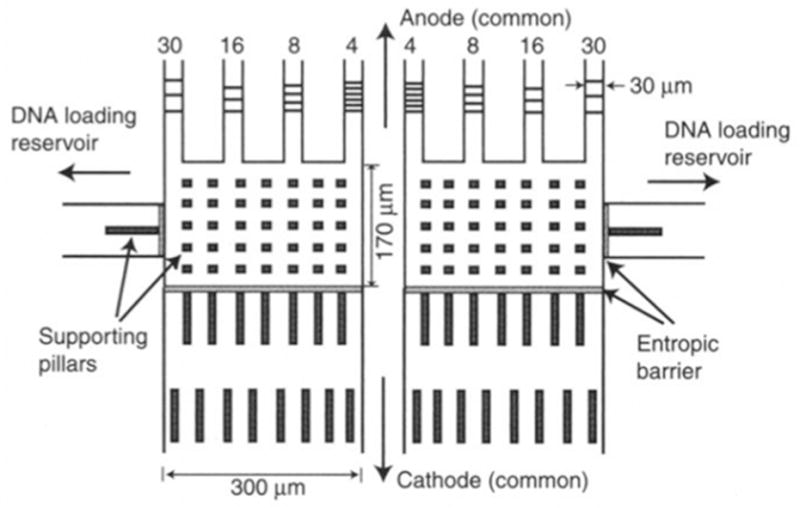
Schematic of the multilane separation device for entropic trapping. All eight channels are connected to a common anode and cathode. Each set of four arrays is connected to their own DNA loading zone. This allows for two different mixtures to be separated simultaneously, similar to a submarine gel electrophoresis setup. Reprinted with permission from Ref.150 Copyright 2000 American Association for the Advancement of Science.
The key variables for the separation are the electric field strength and the pitch of the array.150,183 A smaller pitch leads to better separations since it can increase the number of traps for a given length. However, the use of optical lithography limited the original pitch to 2 μm.150 The current pitch limitation is just under 1 μm without using expensive and slow direct write lithography systems. Note that a strongly confined chain and a short pitch could lead to the DNA spanning multiple traps, a subject we will discuss in the context of nanopit arrays379,380 in Section 7.3. Higher electric fields decrease the elution time, but lower the resolution since the barrier for escaping the trap is lowered. The resolution also decreased with DNA length. This requires longer DNA molecules to be run at lower field and for a longer time,183 analogous to gel electrophoresis. The entropic trap can resolve DNA in the hundreds of kilobase pair range in around 30 minutes, which is comparable to the performance in post arrays. The band capacity of the entropic trap appears to be superior to the post arrays, with almost complete baseline of a 5 kbp DNA ladder (7 bands).150,183
In the standard entropic trapping device,150,181–183 illustrated schematically in Figure 32, the deep region of the device has a volume that is large compared to the nominal volume of the DNA coil. As we show in Figure 32, the DNA can thus coil freely in the deep region. If the length scales are decreased further, then the DNA will be deformed in both the slit and the well region. A device of this type374 was named the “nanogroove array.” Here, the well is only 150 nm deep and varies in width from 75 to 600 nm. We will discuss the conformation of DNA at these length scales in depth in Section 7, but for the moment we will simply state that the DNA in the well is in a de Gennes regime. The slits are 50 nm deep and the periodicity of the device is between 1 μm and 2.6 μm. For these experiments,374 the λ DNA, T4 DNA and 42.2 kbp circular DNA were animated by a pressure driven flow instead of an electric field. At low flow rates, the DNA falls into the 150 nm grooves and is extended along the width of the device in the de Gennes regime, but is not able to escape the groove. By increasing the flow velocity, the DNA will exit the groove and travel to the next groove in a “sidewinder” type motion. The sidewinder motion is independent of DNA size. Increasing the velocity further causes herniation into the slit, which leads to a “tumbleweed” conformation. The molecule can transition between the two states with the “tumbleweed” state being faster. Also, longer molecules are more likely to exhibit the “tumbleweed” state so this leads to sized based separation.374
At the very highest flow velocities, only the “tumbleweed” conformation is seen and separation no longer occurs. The transition between the two states is also different for linear and circular DNA, so this device can also separate DNA based on topology and not just size.374 All the above studies150,181–183,374 used long DNA (greater than 5 kbp). The radii of gyration of these DNA are always on the order of or larger than the slit depth. The DNA must deform from their free solution configuration in order to escape the entropic trap, and the long molecules elute first due to an increased probability to escape the trap. Let us now consider the opposite limit where we work with relatively short DNA molecules in the 100 bp range. Recall from Eq. (2) that there is a crossover from coiled configurations to rod-like configurations as the contour length of the DNA, L, decreases to the Kuhn length (i.e., twice the persistence length). The persistence length of DNA is around 53 nm, corresponding to 300 bp per Kuhn length. Thus, these short DNA are expected to be fairly rigid molecules. When the depths of the slit and the well are decreased somewhat, as illustrated schematically in Figure 32, the device becomes appropriate for separating short DNA in a manner akin to Ogston sieving.184,185 Small DNA fragments, 50 bp to 1600 bp, and slits between 55 and 80 nm were used to satisfy the requirements of the Ogston regime. In this regime, the smaller fragments eluted first. These are exactly the physics one would expect from the Ogston model, since the free volume available to the DNA in the slits decreases with molecular weight. While the model bears some similarities to Ogston sieving, it is probably more appropriate to think of the device as a one-dimensional chromatographic separation based on the partitioning between the slits and the wells.185,381
Note that such an equilibrium model is only valid for very weak electric fields where the DNA have sufficient time to sample their configurational space in the well and the slit via rotational diffusion. At higher electric fields, scaling analysis and simulations382 predict that the device would operate in a band inverted mode, where the larger rod-like DNA would elute first. These predictions were eventually realized in experiments372 using a fused silica device that could support the very high electric fields (circa 500 V/cm) required to reach the band inversion regime.
As we might expect, there is also a band inversion185 that must occur as a function of molecular weight as the transport transitions between the Ogston regime, where the smaller DNA elute first, and entropic trapping regime, where the larger DNA elute first. Figure 34 shows this transition from a decreasing to an increasing mobility as a function of DNA fragment size, independent of electric field.185 The transition occurs when the radius of gyration is about the same size as the slit. In this case the slit was 73 nm and the radius of gyration for the DNA at the crossover point was 80 nm.185
Figure 34.
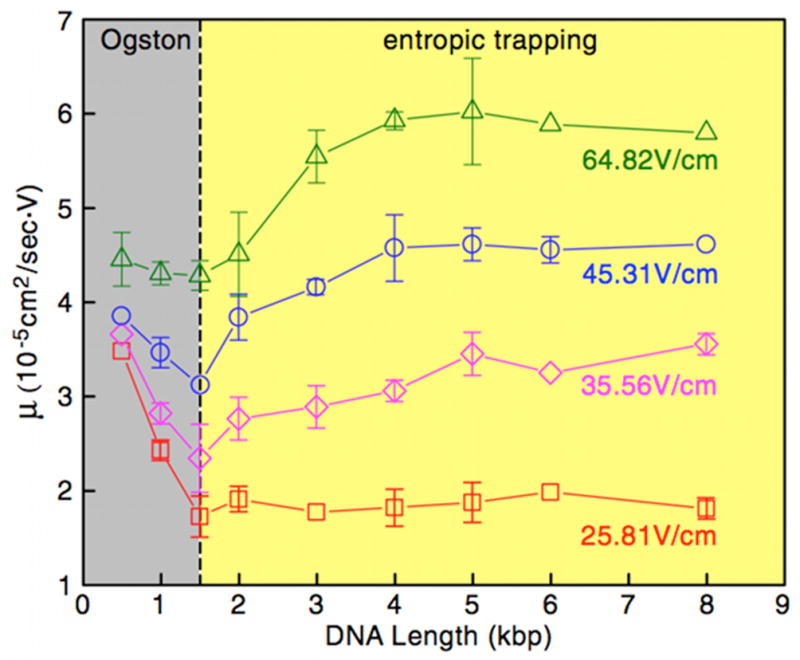
Mobility as a function of DNA length at several electric fields in the DNA nanofilter.185 This figure illustrates the transition from the Ogston regime, where the mobility decreases with length, to the entropic trapping regime, where the mobility increases with molecular weight. Reprinted with permission from Ref.185 Copyright 2006 American Physical Society.
While steric interactions are sufficient to provide confinement, the slit size needs to be very small (tens of nanometers) to see a partitioning effect for small DNA. Recall from Figure 4 that any charged surface is associated with a Debye layer of counterions whose characteristic length scale is given by Eq. (10). The devices we have consider thus far are fabricated in silicon, followed by thermal oxidation, or fabricated in fused silica. In either case, the surface adopts a negative charge in the basic pH buffers used for electrophoresis. As a result, the DNA is repelled from the surface by electrostatic interactions. Lowering the ionic strength increases the electrostatic repulsion between the DNA and the walls, leading to an increase in the size of the region where the double-layers overlap between the DNA and the walls. Since the nanofilter mode of the device operates through a standard chromatographic mechanism185 based on the partitioning of the rigid, short DNA molecules between the slit and the well,381 the effect of the electrostatic interactions is equivalent to reducing the physical size of the slit. As we might expect, the selectivity and resolution are enhanced at low ionic strength.371
The slit-well motif in Figure 32 is not the only artificial gel that operates in the Ogston sieving and entropic trapping regimes. Figure 35 shows two particular examples fabricated in PDMS. Note that entropic trapping via thin slits is unlikely to be successful in a soft material like PDMS, since they would collapse. The upper panels of Figure 35 show a post array with 15 μm posts with 1 μm spacing at the thinnest point.376 These posts are much too large to be useful for the separations discussed in Section 6.1.1, since the post sizes are almost an order of magnitude larger than the DNA coil. For the same reason, this post array is not the same as the systems studied using the exactly solvable lattice models for DNA electrophoresis.174,364–370 Rather, the device operates in an entropic trapping mode because the interstitial space between the post, where the DNA travels, has larger pockets connected by thin gaps, shown as the lighter grey area in Figure 35. These gaps act as entropic traps. This device features a sized based separation of molecules that have a radius of gyration on the order of the gap.376 The lower panel of Figure 35 shows a device with a uniform depth but wavelike structures along the walls.375 One can think of this system as the slit-well motif turned on its side, albeit at a slightly larger length scale where the features are commensurate with the radius of gyration of the DNA rather than its persistence length. Two different systems are shown in Figure 35, one with the wavelike structures on both walls and one with the wavelike structure on a single wall.375 Videomicroscopy experiments375 of T2 and λ DNA electrophoresis in these systems showed that the DNA interacts with and is stretched by the features on the wall. The interaction between the DNA and the wall was stronger for the longer DNA and this led to a smaller velocity when traveling through the channel.375 Both of the devices in Figure 35 have gaps that are about the size as the radius of gyration of the molecules they are separating, where the longer molecule has to squeeze a little more than the smaller one. So the larger molecule travels slower,375,376 as opposed to the case in the early entropic traps where the gap was much smaller than the radius of gyration and the larger molecules traveled faster.182
Figure 35.
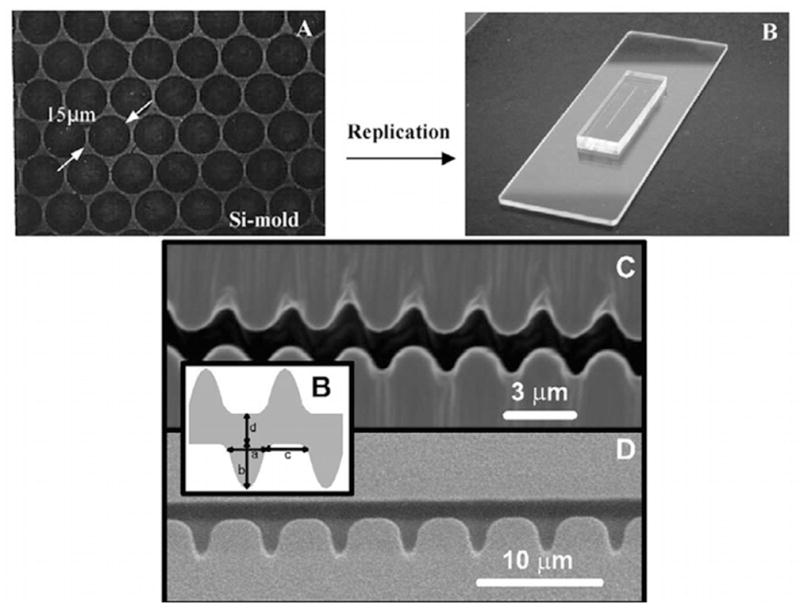
Images of the PDMS devices for entropic trapping. The top two images are a post array device,376 where (A) is an SEM of the silicon mold and (B) is a photograph of the final device. Reprinted with permission from Ref.376 Copyright 2003 Elsevier Science B.V. The bottom panel are SEM images of structured channels, with the inset defining the dimensions of the structures. Reprinted with permission from Ref.375 Copyright 2003 Elsevier Science B.V.
An alternate approach to entropic trapping is to use the thin film formed between an oil slug and the wall of a channel,377 shown in Figure 36. This thin region produces a nanoslit and the transition from the large channel to the slit serves as an entropic trap. When the DNA is driven through the channel it encounters the slug and slowly stretches as the bulk of the coil slowly unravels to fit into the thin region. Once most of the molecule enters the thin area it quickly transverses the gap and exits due to the intensified electric field in the gap. While one should, in principle, be able to construct an entropic trapping device out of a series of oil slugs in a channel, this setup has only been used thus far to stretch DNA377 to about 50% of its contour length.377 The DNA can also be combed to the surface using a surfactant for the surface coating and high electric fields.378 We will discuss DNA stretching and molecular combing in more detail in Section 7. Both the stretching and combing were achieved in cheap and easy to fabricate PDMS channels at very tractable dimensions between 100 and 200 μ m.377,378
Figure 36.
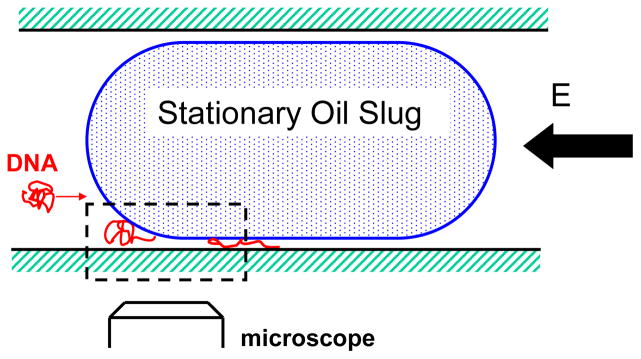
Schematic of the oil slug in the microchannel. The region between the wall of the channel and the oil slug creates a nanoslit. The interface between the channel and the nanoslit causes the DNA molecule to stretch. Reprinted with permission from Ref.377 Copyright 2008 American Institute of Physics.
Overall, the entropic trapping geometry seems quite promising, since the speed of the separation is comparable (but somewhat slower) than the other methods discussed in this review and the band capacity seems very good. There are some minor technical challenges relative to the post arrays but they are easily overcome. For example, the device fabrication requires two etching steps to create the slit and the well, but the patterning is all done using conventional photolithography. Likewise, the injection method requires multiple field strengths, but this is easily implemented using a programmable power supply. The limiting issue is the band inversion as a function of electric field and molecular weight. Care needs to be taken when performing separations as the order of elution can be reversed if the molecule is about the same size as the slit size.185
6.1.3 Colloidal Crystals and Self Assembly
Many of the artificial gels discussed above involve top-down microfabricated patterns, with the exception of the oil slug entropic trap. Such devices exploit the ease of fabricating periodic patterns such as post arrays and entropic traps using techniques pioneered by the semiconductor industry. Colloidal crystals are instead formed by the self-assembly of colloids into a close-packed arrangement, creating a three-dimensional network with periodic characteristics. This method of fabrication is considered bottom-up, and exploits the driving forces behind crystallization in confinement383–386 to form close-packed periodic separation matrices. A key difference between these bottom-up devices and their top-down counterparts is the three-dimensional nature of the colloidal crystal. Colloidal crystals have inherent length scales based on the size of the colloids, which can be fabricated anywhere from the nanoscale to the microscale.
The three-dimensional network brought about by colloidal crystallization can be thought of as an ordered analog of an agarose gel. In a regular, close-packed colloidal crystal, the interstitial spaces are connected by narrow constrictions. The space available to DNA molecules is shown in Figure 37. The similarity between the pore space of a colloidal crystal and that of an agarose gel naturally leads us to apply the theories of DNA mobility discussed in Section 5.1, such as biased reptation or Ogston sieving, to colloidal crystal DNA electrophoresis. Both regimes rely on the interplay between the size of the space available to the DNA and the size of the DNA molecule itself.
Figure 37.
(a) The space available to a DNA molecule in a close-packed plane (purple) when one attempts to fit a solid sphere (green) into the interstitial space. (b) The space actually available to a DNA molecule in a random conformation. The actual three-dimensional network available to the molecule is much more complex than illustrated in this two dimensional projection.
Unlike a gel matrix, a colloidal crystal by definition is periodically ordered. Therefore many assumptions based on the random nature of gels may not be true in colloidal crystals. For example, the theories of biased reptation and Ogston sieving both assume that the molecule will experience an ensemble average of conformations and angles with the applied electric field. This assumption is valid in a gel since the sieving matrix is inherently random; there is a distribution of pore sizes, which are distributed randomly throughout the gel. In contrast, a model of DNA electrophoresis in colloidal crystals must account for the discrete nature of the pore connectivity.387 It is also possible to have dead-ends in a gel, where the DNA has difficulty moving in the direction of the field and becomes temporarily trapped. The biased reptation and Ogston sieving models predict aggregate behavior, and as such work well in these fully random networks. Colloidal crystals, on the other hand, are not fully random networks. Their close-packed arrangement possess order over lengths much longer than the molecules being analyzed. This order calls in to question the assumption that a DNA molecule will be able to experience a full range of orientations with respect to the electric field, as well as a wide variety of pore sizes. For the moment our comments are speculative, but it is already known321 that order improves separations during protein chromatography in colloidal crystals. We are confident that systematic studies of the order of the colloids will show whether the order of a colloidal crystal has a significant impact on the quality of the separation in these devices when compared to the usual gels.
There are two common ways to integrate colloidal crystals into a separation channel: sedimentation of the colloids and convective self-assembly. Sedimentation involves adding a colloidal suspension to a fabricated device (either a capillary or microchannel) and allowing the colloids to settle against a barrier.383 In most applications, this barrier would be a physical frit or weir that allows fluid to pass through, but blocks the passing of colloids. It could also be an interface, such as an air-liquid interface. The sedimentation process requires that the colloids settle under gravitational forces. For small colloids (with diameters below around 1 μm) this sedimentation process can take days. Sedimented colloids are also weakly bonded by van der Waals forces when they pack, as they have only been brought in to contact by the weaker gravitational forces. However, the long assembly time can lead to a better packing, as a settling particle conceivably has more time to find a close-packed site and therefore is more likely to pack well.
Convective self-assembly (CSA) is an active process that greatly accelerates the crystallization process.388 In CSA, the colloids are carried through the suspension and brought to a nucleation site, either a frit or an air-liquid interface (as discussed above). The convection can be brought about either through a pressure head or solvent evaporation. Most often, one uses a combination of both driving forces. This method does not rely on the slow gravitational forces to settle the particles, but instead carries them directly to the crystal growth plane. In contrast to sedimentation, the crystal is grown quickly. This would imply that the packing would be less efficient, as an individual particle would have less dwell time to find an ideal site. However, the evaporative forces in CSA through the established crystal focus the motion of the colloid into a correct close-packed arrangement.389
Monodisperse colloids are available in a wide range of materials. Most devices in literature are made from either silica or polystyrene particles.180,390–395 The polydispersivity of the colloids is a key factor in determining the quality of the resulting crystal. Colloidal crystallization requires a low standard deviation from the average diameter – less than 1% is desirable.396 However, procedures for creating tightly-distributed colloids from both silica and polystyrene allow for their rather inexpensive use en masse, as they are commercially available at a reasonable cost. Since the separation mechanism depends on the 3D pore network and not any surface characteristics, the choice of colloid material is irrelevant to the separation performance provided that the DNA do not adsorb to the colloids.
The earliest work on DNA electrophoresis in colloidal crystals focused on examining the mobility of single molecular weights of DNA.390,391 In the pioneering experiments,390 the mobility was measured in bulk crystals using a fluorescent fringe technique in a colloidal crystal formed by sedimentation. Later videomicroscopy experiments391 examined the dynamics of long DNA in a colloidal crystal. While these experiments showed the potential to separate DNA in a colloidal crystal, a functioning separation device also requires integrating the colloidal crystal inside of a device that allows for DNA injection. The first such device392 used a molded PDMS slab for the channel, which was bonded to a clean glass microscope slide after punching out access holes in the PDMS to act as fluid reservoirs. These devices could be easily fabricated in a reproducible manner, although one needs to be particularly careful with the cleanliness of the glass substrate for colloidal crystal assembly. The permeability of the PDMS was overcome by presoaking the devices in running buffer overnight.
The assembly of stable, ordered colloids in the device requires some care in the experimental protocol (as we have learned the hard way through our own experiments in this area), so we would like to point out a few key experimental steps when the colloids are integrated into the separation channel using CSA. In the prototype devices,392 one of the reservoir holes in the PDMS was punched through the end of the separation channel. This easily-overlooked detail is critical for proper and rapid assembly of the colloidal crystal. The relatively hydrophobic PDMS surface coupled with the open area of the reservoir leads to the creation of an air-liquid-glass-PDMS evaporation interface that is pinned at the outflow of the device.392 The colloidal crystal then grows directly from this interface. If this interface is allowed to expand into a patterned reservoir, then one can end up with a large (relative to the channel cross-section) initial volume to crystallize, which will take much longer to do so. Also, the expanded interfacial area leads to a decrease in the convective driving force, slowing colloidal motion down the channel. After the growing crystal fills the separation arm, crystallization is stopped by replacing the colloidal suspension in the source reservoirs with deionized water.392 After all of the remaining colloids are incorporated into the crystal, the deionized water is replaced with running buffer and allowed to equilibrate. Afterwards, the device is pre-run until the current stabilizes. This pre-run step is important to help ensure crystal stability. In the case of silica particles, the surfaces are left unmodified and contain unbound charges. These have the potential to both become mobile in the presence of an electric field as well as create large amounts of electroosmotic flow. Electroosmotic flow can be suppressed by using a high ionic strength buffer or by adding a dynamic coating such as PVP.392
Colloidal crystals are indeed able to rapidly separate DNA using the basic physical principles of gel electrophoresis. The prototype separation devices392 were able to separate a DNA ladder of 100–2000 bp fragments in under two minutes in less than a millimeter of separation matrix. The separation experiment is also remarkably stable; the absolute mobility of the separated species changed by less than 2% over five hours of experimentation and the crystals were stable under fields up to 60 V/cm, with only minor disruption of the bed at the channel ends.392 In addition to the separations of the short DNA, it is also possible to separate larger DNA such as T4 GT7 (166 kbp) and λ (48.5 kbp) DNA in 1.53 μm diameter silica colloids in 3 minutes in only 1.5 mm of crystal.392
The analogy to agarose gels qualitatively describes the relationship between DNA size and colloid diameter. Agarose separations of larger molecules (> 10 kbp) typically require lower concentration gels, creating larger average pore sizes. In a colloidal crystal, the pore size is geometrically related to the diameter of the colloids forming the crystal. Zeng and Harrison392 used the size of the largest circle that can fit between three close-packed colloids (i.e. 15% of the colloid diameter) as an estimate of the available volume for the DNA. Figure 37 shows that the actual space available to a DNA chain is much harder to quantify, especially since the DNA would need to deform on length scales smaller than the persistence length to utilize the full void volume. Using the former estimate of the available pore space shows that the colloids used in the experiments are similar to agarose gels (in the 2–3% range for the larger colloids) and smaller colloids form something akin to the pore spaces in a tighter polyacrylamide gel.392
An alternative approach to achieve bottom-up creation of gel analogs is to create an inverse opal. The opal gemstone is essentially a close-packed arrangement of silica spheres of diameter comparable to the wavelength of visible light. An inverse opal is the negative of that three-dimensional structure: pores become walls and the colloids becomes the pores. The primary route to fabricate an inverse opal structure is to first create a colloidal crystal in the desired region of the microfluidic device. Then one replaces the suspension fluid with a polymerizable material, such as SU-8 or polyacrylamide.180,393 Due to incomplete wetting of the colloids by the polymer precursors, there are narrow holes connecting the pores in an inverse opal after polymerization.397 To complete the inverse opal fabrication, the colloidal template must be removed, taking care to use a method that does not damage the rest of the device. In the case of polystyrene spheres, toluene can be used to dissolve the colloids.393 Silica can be removed using hydrofluoric acid (commonly diluted in a buffered oxide etch).397 The rate of colloid removal can be greatly enhanced by having exposed colloids at the surface of an open device,393 as the distance to etch will be less perpendicular to the channel than in-line with the channel.
In the polymerization step, it is essential that the crystal is completely infiltrated by the liquid phase. Any gaps will result in cavities, which in turn will significantly contribute to band broadening. Also, it is crucial that the polymerized network be adequately rigid. It cannot collapse under pressurized flow (pumping is a common wetting and cleaning procedure) or its own weight. Finally, the material should be capable of being rewetted. For example, the process used by Kuo et al.347 requires multiple drying steps in the fabrication procedure, but the rewetting process is not included. From our experience, native SU-8 is difficult to wet spontaneously, and as such requires the addition of a pressure head.
The resulting structure of an inverse opal, shown in Figure 38a and Figure 38b, is easily compared to an agarose gel, as one can readily visualize the space available to the DNA molecules. As we might expect, the separations readily mimic agarose gels, as shown in the side-by-side comparison between a gel lane and the microfluidic device shown in Figure 38c and Figure 38d. In these experiments, all nine of the species in the ladder from 500 bp to 10 kbp were baseline resolved in less than 10 minutes in a field of 20 V/cm at an elution distance of 2.5 mm, which is faster than gel electrophoresis with similar resolution.393 In addition to these separation experiments, inverse opals have also been used for basic physical studies of DNA.180,394,395 Perhaps the most famous of these experiments was the demonstration of entropic trapping (in the absence of an electric field) as the DNA jumps between pores of the inverse opal network through the narrow constrictions between them.180
Figure 38.

(a) A side-on SEM of the inverse opal, fabricated from SU-8. This image shows three parallel channels. These are not the channels used for the separations. (b) Close-up of the porous structure, which is analogous to an agarose gel network. The scale bar in (a) and (b) is 400 nm. (c) Bands from electrophoresis of a 1 kbp ladder in an agarose gel. (d) Bands from electrophoresis of a 1kbp ladder in an inverse opal. The dashed lines represent the walls of the microchannel. The scale bar in (c) and (d) is 1 cm. Figure reproduced with permission from Ref.393 Copyright 2007 Elsevier B.V.
We have focused thus far on separations that rely in some way on the ordered packing of colloidal particles, but there are also a number of studies that have used micelle-forming block polymers such as pluronics,398–404 liquid crystals,405–407 and core-shell nanospheres408 to create alternatives to agarose gels that exhibit useful properties (such as thermoswtichable viscosities) along with packings that are similar to colloidal crystals. We focus here on the DNA separations in nanospheres.408 The particles in these experiments408 were formed by polymerization of the hydrophobic core of the block copolymer poly(ethylene glycol) and poly(lactic acid) with a methacryloyl group capping the PLA end, leaving flexible PEG on the surface. The microchannel was a simple cross injection and completely filled with the nanosphere solution at a 1% concentration.408 Unlike the previous colloidal crystal separations, the solution of nanospheres is present in the entire channel and does not require any localization of the separation matrix. A dyed DNA mixture is then injected using a two-step pressurization process.408 In the first step, the DNA flows through the cross arm of the injection region until a steady-state flow is achieved. In the second step, the pressure is switched to flow down the separation arm for a few seconds prior to turning on the electric fields in the separation arm and cutting off the pressure driven flow. This novel injection mechanism permits the separation of DNA across the 100–1000 bp and 1–15 kbp ranges.408
There were three interesting findings that came out of these nanosphere experiments. First, turning on the electric field after the pressure injection initially focuses the injected band.408 The band width would decrease from approximately 1 mm to 50 μm, and then the bands become separated by the matrix. This focusing mechanism is a unique property of using the nanospheres, as it cannot be reproduced in gels, free solution, or entangled polymer solutions.408 Second, accurate injections cannot be obtained without using the primary pressurization technique.408 Since the nanospheres are not packed like a colloidal crystal, it is possible that the pressurization step is critical to achieve a robust sieving matrix. Third, the separation is only possible using the electric field and no separation is observed under pressurized flow.408 This third feature explains the success of the injection mechanism. If there was also a separation in the pressure driven flow, then it would be necessary to isolate the nanospheres in the separation channel, akin to the experiments we described in colloidal crystals.392 Otherwise, the nanosphere separations would encounter the same issues with the pressurized injection method as one has with the electrokinetic injection; namely that the sieving matrix is present everywhere.
The exact nature of the separation mechanism in nanospheres remains a bit mysterious. The DNA chains retain a configuration similar to free solution. This behavior is unlike the motion in an agarose gel, where the chain would deform and tends to elongate in the direction of the field. A possible mechanism behind the size-based separation is a transient partitioning of the DNA chain in the unbounded PEG chains on the surfaces of the nanospheres.408
There are several attractive features of nanospheres for microchip separations.408 First, the separation solution has a low viscosity and can be easily prepared. Additionally, the separable range can be tuned by altering the injection pressures. Also, the separation device can be flushed and cleaned for repeated uses. The downside is that any future processing of the molecules would first need to compensate for the fact that the DNA is present in a mixture with nanospheres, which would likely need to be separated. As the nanospheres have a diameter on par with the persistence length of dsDNA, this process would likely be cumbersome.
The data in the literature for DNA separations in the three types of colloidal-based methods described above (colloidal crystals, inverse opals, and nanospheres) indicate that they all have similar levels of performance. The DNA sizes separated range from between 100 bp up to 100 kbp throughout several experiments.392,393,408 In terms of fabrication, the nanosphere suspension requires only a knowledge of polymer chemistry in order to fabricate nanospheres of high uniformity, a task that Tabuchi et al. claim is facile.408 After doing so, one can use the suspension in prefabricated separation devices, taking some of the precautions mentioned above. The inverse colloidal crystal, on the other hand, requires the greatest amount of fabrication expertise, as it utilizes all the methods of colloidal crystal engineering with the addition of careful photopatterning, developing and etching. An upside to both the colloidal crystal techniques is that they can be better integrated into larger lab-on-a-chip analytical devices as they present localized separation media. Through the use of weirs or localized deposition, colloidal crystals can be grown at assigned locations in a fabricated channel. Once formed, regular colloidal crystals also have a rigid structure, which can facilitate long-term crystal stability.
6.2 Dielectrophoresis
Dielectrophoresis was originally discovered by H.A. Pohl,409,410 and is described at length in his book.411 Interestingly, although Pohl performed much of his pioneering work on dielectrophoresis at the Naval Research Lab in 1943, it did not appear in the open literature until significantly after the end of World War II. The dielectrophoretic force arises from the inherent polarizability of some materials. Simply put, dielectrophoresis is the electrical equivalent of the magnetic force that drives iron filings to the poles of a magnet.412 Many of the key features of dielectrophoresis are illustrated by analyzing the simple problem of a dielectric polarizable particle with a polarizability p placed in an electric field E. The polarizability of the particle leads to a dielectrophoretic potential413
| (41) |
where εp is the dielectric constant of the particle. The force per unit volume acting on the particle is the gradient of this potential
| (42) |
Eq. (42) immediately demonstrates two generic features that distinguish dielectrophoresis from electrophoresis. First, the particle only experiences a dielectrophoretic force in an inhomogeneous field, i.e. where ∇E2 ≠ 0. Second, the dielectrophoretic force varies with the square of the electric field. Consequently, the direction of dielectrophoresis does not change when the direction of the field is reversed, so dielectrophoresis operates in both ac and dc fields. For a charged particle, ac fields are often preferably to avoid the presence of simultaneous electrophoretic forces as well as the formation of bubbles.
In a polarizable fluid such as water, both the particle and the fluid are affected by the dielectrophoretic force. Consequently, the net dielectrophoretic force per unit volume acting on the particle is the difference between these dielectrophoretic forces,
| (43) |
and depends on the difference in dielectric constants between the particle and fluid. Eq. (43) tells us the basic features of dielectrophoretic motion. First, whether the particle moves towards regions of stronger or weaker electric field intensity depends on its polarizability relative to the fluid. In positive dielectrophoresis (which is the case for DNA), the particle is more polarizable than the fluid, so that it moves towards regions of increasing field intensity. Negative dielectrophoresis is the converse. Second, if there is a point where there the gradient vanishes, then the particle experiences no dielectrophoretic force there.
The argument leading to Eq. (43) assumes a perfectly polarizable particle and fluid that can be characterized by a constant permittivity ε. As we illustrate in Figure 39, this is certainly not the case for DNA. While the backbone charges in DNA are fixed on the chain, the nearby counterions are mobile. Figure 39 illustrates the basic principle behind DNA polarization. Since the DNA and its counterions move in opposite directions in an electric field, the system consisting of DNA and its counterions can become polarized upon the application of an electric field. Note that the polarization of DNA is a transient phenomena, since the flux of counterions will relax the polarization. Thus, the most common way to polarize the DNA is to use an alternating current (ac) field with a frequency that is fast compared to the diffusion time for the counterions.
Figure 39.

Schematic illustration of the polarization of a DNA/counterion system. In the absence of the electric field, the system in the dashed lines is electroneutral and unpolarized. For clarity, only the DNA (negatively charged) and the counterions (positively charged) are shown. Immediately after the application of an electric field, the counterions move in the direction of the electric field and the DNA moves in the opposite direction. The system in the dashed lines is still electroneutral but it is now polarized. The polarization only exists on a time scale that is short compared to the relaxation time of the counterions. After longer times, the flux of counterions from left-to-right replenishes the lost counterions on the left hand side while maintaining electroneutrality. Thus, in a steady uniform electric field, the DNA/counterion cloud is unpolarized and the motion is due to electrophoresis.
Since there is the possibility for relaxation phenomena, a correct description of the dielectrophoresis of DNA requires knowledge of the complex permittivity of the DNA particle, , as well as the possibility of a complex polarizability of the fluid, . If we convert into a body force, it is common to express the dielectrophoretic force as414
| (44) |
where R is the size of the particle, εm is the relative permittivity of the suspending medium415 and the dipolar Clausius-Mosotti factor is given by412
| (45) |
Since the force is real, only the real part of fCM affects the DNA.
The polarizability of the DNA/counterion system drawn in Figure 39 remains a controversial topic and much of the recent literature was reviewed by Holzel.414 In the context of DNA sizing, there is a bit of a “chicken-and-the-egg” issue here. While dielectric relaxation measurements are one way to measure the polarizability of DNA,414,416 one can also infer the polarizability of DNA from models of the separation process, for example, the trapping method we will discuss here.417 Moreover, the role of hydrodynamics remains an relatively unexplored issue.418 Even the scaling of the dielectrophoretic force with the radius of gyration of the DNA is not clear. For polarizable colloidal particles, the dielectrophoretic force scales with the volume of the particle by Eq. (44). However, experiments on DNA suggest that the polarizability of DNA is almost linearly proportional to the radius of gyration.417 Moreover, the polarizability of DNA is likely a function of its conformation, especially for supercoiled DNA.417
Eq. (44) highlights one of the critical issues for dielectrophoretic manipulation of small molecules such as DNA. The body force is proportional to the volume of the particle, and the radius of gyration for DNA is typically in the sub-micron range.62 As a result, we require very large values of ∇E2 so that the dielectrophoretic force becomes comparable to the random thermal force. Microfabrication thus becomes essential for dielectrophoresis of DNA. Figure 40 illustrates the two approaches to creating strong electric field gradients in a microfabricated device. The earliest devices416,420–426 used microfabricated electrodes to generate the electric field. For example, electron-beam lithography was used to pattern very small gaps (300 nm) between electrodes used for DNA dielectrophoresis,427 and it is easy to reach electric fields around 10,000 V/cm in the narrow gap between the electrodes using only a modest applied voltage (e.g., 150 V peak-to-peak). The shape of the electrodes also plays a role in the dielectrophoretic force by sculpting the shape of ∇E2. However, even simple planar electrodes420 can generate a dielectrophoretic force if the electrodes are thin. While the electric field in the plane of the surface is uniform (neglecting the end effects), the electric field in the bulk of the solution is nonuniform. This concept is illustrated in Figure 40B.
Figure 40.
Schematic illustration of (A) the electric field produced by a constriction in an insulator and (B) the electric field proximate to an electrode. Reprinted with permission from Ref.419 Copyright 2011 Wiley-VCH.
Microfabrication is by far the most common approach to create the electrodes. However, it is not the only possible approach. A particularly intriguing method428 is to deposit a thin film of amorphous hydrogenated silicon with optically transparent ZnO as the back contact. When a laser illuminates a region of the thin film, the exposed part of the film becomes conductive an opens up an electronic path between the back contact and the fluid. Thus, the illuminated region of the film acts as an “electrode.” Moreover, one can move the “electrode” to different locations simply by moving the location of the laser spot.
An alternate approach to create strong electric field gradients is to create a constriction of the type in Figure 40A.413,429,430 Since virtually all of the materials used for microfluidics, such as fused silica and PDMS, are electrically insulating, the electric field lines are always parallel with the surface of the insulating walls. In a constriction, the electric field lines are compressed to create a strong electric field gradient. While Figure 40A shows a system consisting of a single constriction, the more common approach to creating an “electrodeless dielectrophoresis” system is a pattern of posts such as the one in Figure 41.413 The size of the gap between the posts is dictated by the requisite strength of the electric field. The trapezoidal posts in Figure 41 have a 1 μm wide by 1.25 μm deep constriction at the narrowest point,413 and gaps on the micron scale are typical for DNA manipulation.417,431–433 The advantage of the electrodeless system lies in its operation, since there is no need to address or fabricate individual electrodes. Naturally, the tradeoff is a loss in the flexibility of the device operation, since there is no way to selectively turn on/off the field gradient in an individual constriction. While we have focused here on arrays of constrictions, any system that generates a strong electric field gradient is sufficient. For example, the small (~ 100 nm) aperture at the end of a nanopipette is sufficient for DNA trapping.434,435
Figure 41.

Dielectrophoretic trapping of 386 bp DNA using a voltage of 1 kV (5 V peak-to-peak across each unit cell) with applied frequencies of (a) 200 Hz, (b) 400 Hz, (c) 800 Hz, and (d) 1000 Hz. The frame size is 80 × 80 μ m. The vertical line in (d) refers to a later figure in Ref.413 Reprinted with permission from Ref.413 Copyright 2002 Biophysical Society.
Provided that one can create a sufficiently strong electric field gradient, either using electrodes425,426,436–439 or an electrodeless system,413,417,431–433,440–442 then it is possible to trap the DNA by dielectrophoresis. Virtually every paper has reported that DNA undergoes positive dielectrophoresis (i.e., motion towards the maximum in the electric field gradient), with but one exception426 that was explained as the result of high solution conductivity. As the Clausius-Mosotti factor in Eq. (45) depends on the complex permittivity of the DNA, one would expect the trapping to depend on the frequency of the electric field. Figure 41 illustrates this phenomenon in the context of an electrodeless system. At low frequencies (200 Hz), no DNA are trapped in the constrictions. As the frequency of the ac electric field increases, the trapping efficiency continues to increase. Note that the potential drop across a unit cell of this device (5 V) is quite small. However, due to the very narrow gap between the posts, the electric field gradients are large. Indeed, it is important to keep in mind that the relevant quantity for the trapping is (∇E)·E, i.e., the product of the field strength and the field gradient.413
Although our general focus here is on ways to size DNA, we should point out that there are a number of applications that rely on simply trapping DNA by dielectrophoresis. For example, dielectrophoresis is a facile method to purify DNA from a solution433 or to enhance the local concentration for a DNA hybridization assay.442 Indeed, one of the most promising aspects of dielectrophoresis is the potential for on-chip integration,432 even up to the possibility of performing most of the sample-in, answer-out operations via a sequence of dielectrophoretic manipulations.441 Since the dielectrophoretic force increases with the size of the DNA molecule, it becomes increasingly easier to trap the DNA as its size increases. For example, entire E. coli chromosomes can be readily captured in a dielectrophoretic trap at a constriction.440 When the traps are created by addressable electrodes, applying a dc pulse between electrodes allows one to readily move the DNA around the system.425 Although most of the work on DNA trapping by dielectrophoresis involves double-stranded DNA, dielectrophoresis has also been used to concentrate single-stranded DNA. In principle, trapping short single-stranded DNA is challenging since the DNA is very flexible and thus its radius of gyration is small compared to the equivalent contour length of double-stranded DNA. However, in the presence of an electroosmotic flow, it is possible to concentrate 20 nucleotide single-stranded DNA in a dielectrophoretic trap.437 While we have been very brief in our review of DNA trapping, a wide variety of these applications have been reviewed elsewhere.415
Concurrent with the earliest reports on dielectrophoresis of DNA,420 Ajdari and Prost443 proposed that dielectrophoresis could be used to enhance separations by conventional DNA electrophoresis. The basic argument behind the separation process is straightforward. In free-solution, we know that the electrophoretic mobility of the DNA is independent of molecular weight for sufficiently long DNA. However, we know that the force causing the DNA to be trapped by dielectrophoresis increases with the size of the DNA. In the presence of an ac electric field (to produce the dielectrophoretic trapping) and a superimposed dc electric field (to provide the electrophoretic motion), the DNA is transported in a tilted potential that has some qualitative similarities with the explanation of entropic trapping we saw in Section 6.1.2. The probability of hopping out of a dielectrophoretic trap increases as the molecular weight decreases, leading to a separation. Using some plausible numbers for the parameters in this model, Ajdari and Prost443 predicted the dielectrophoretic separation would be two orders of magnitude faster than separations by pulsed field gel electrophoresis for long DNA.
The promise of dielectrophoretic separation was realized by Ros and coworkers417,431,432 almost 15 years after its theoretical prediction.443 However, the protocol used in the dielectrophoretic separation varies somewhat from the original idea of hopping in a tilted potential. In the separation device,432 the DNA are injected into an array of posts using a pinched injection. At the start of the separation, the dc field dominates and the ac field is a weak perturbation. As a result, none of the DNA are trapped by dielectrophoresis and they proceed down the post array via electrophoresis. Over time, the ac field strength is increased in a stepwise manner. At some point, the ac field becomes strong enough to immobilize the largest DNA at a constriction while the smaller DNA are still mobile. The critical ac field strength for trapping is a function of the size of the DNA. Thus, the smallest DNA become trapped at the furthest distance down the channel. At the end of the process, the ac field is so strong that all of the DNA are trapped at constrictions in the post array. The dc field is then turned off and the channel is scanned using a motorized microscope stage432 to produce electropherograms like the ones in Figure 42. Since there exists a critical field for trapping, we can also imagine operating these devices in a chromatographic mode where the DNA are eluted as a function of size.422,431
Figure 42.
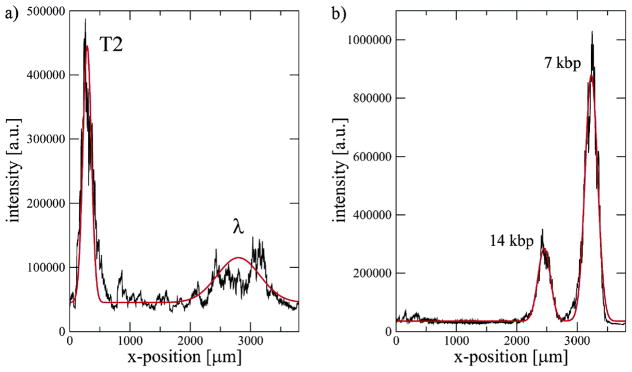
Electropherograms for the dielectrophoretic separation of DNA using a gradual increase in the strength of the ac electric field. The black lines are the raw data and the red lines are fits. In both cases, a steady field with a 12 V drop across the channel provides the dc electrophoretic motion and the ac field has a frequency of 60 Hz. (a) Separation of λ DNA (48.5 kbp) and T2 DNA (164 kbp). The ac field increases from 150 V in 0.6 V increments every 3 seconds until reaching 189 V. (b) Separation of a 7 kbp closed circular plasmid and its 14 kbp dimer. The ac field increases from 198 V in 6 V increments every 30 seconds until reaching 240 V. Reprinted with permission from Ref.432 Copyright 2007 American Chemical Society.
The dielectrophoretic separation of λ DNA and T2 DNA in Figure 42a is comparable to the separations we have seen in other methods — a resolution of 2.95 (based on the red fitting curve in the figure) is achieved after 200 seconds.432 However, the electropherogram in Figure 42a indicates that the λ DNA seems to be trapped over a fairly wide number of traps, and the electropherogram overall is somewhat noisier than the fitted function. In contrast, Figure 42b shows a very sharp separation of the circular plasmid DNA in a similar time frame (240 seconds).432 Note that the separation times do not include the 6 minutes required to scan the channel, so the overall time for the separation is quite similar to the methods reported in Section 6.1. The dielectrophoretic trapping depends on both the length of the DNA and its conformation, so this method was also able to resolve a linear 12.2 kbp DNA from its closed circular counterpart.417
While the trapping method417,431,432 seems to be the most efficient approach to separate DNA by size via dielectrophoresis, it is not the only possibility. If the electrodes are patterned on the surface of the channel and one imposes a fluid flow, the DNA should be attracted via dielectrophoresis to the slow moving streamlines near the surface. Since the distribution of DNA across the streamlines will depend on molecular weight, this approach has the potential for a field flow fractionation.444 Unfortunately, the prototype device for field flow fractionation via dielectrophoresis did not yield a high resolution.445 For the relatively easy separation of pUC17 (2.7 kbp) and λ DNA, the resolution is only around 0.4. Other approaches for DNA separations by dielectrophoresis have been proposed,446,447 but the experimental evidence for their effectiveness is not convincing.
6.3 Electrophoresis in (Extreme) Confinement
Most of the DNA separation methods we have seen thus far rely on a confining geometry to deform the DNA, which then results in an electrophoretic mobility that depends on molecular weight. Indeed, even gel electrophoresis operates on this principle in the biased reptation regime.15 Microfabricated systems permit an exquisite control over the degree of confinement and thus present the opportunity to explore whether DNA can be separated by size solely due to the confinement effect. At the outset, we have reason to be skeptical of this hypothesis. For example, in the development of the DNA nanofilter, which is one of the most strongly confining systems that we have encountered thus far, Fu et al.184 controlled for their proposed separation mechanism by performing the same experiments using a constant 60 nm slit height. Since the DNA in these experiments are longer than the typical cutoff (≈ 400 bp) for the weak dependence of electrophoretic mobility on molecular weight,14 it is unsurprising that there was no separation in the unpatterned 60 nm nanoslit.184
While the constant free-solution mobility observed in capillary electrophoresis14,448 holds down to at least 60 nm,184,449 this behavior seems to break down for nanoslits in the 20 nm range.449,450 The first experiments449 were performed in a fused silica nanoslit using 5× TBE buffer and showed clear separations between DNA in the 2 kbp to 10 kbp range using an electric field of 25 V/cm. The Debye length for this high ionic strength buffer is so small that one should question the applicability of a continuum theory. At the minimum, it is reasonable to assume that the electrostatic interactions between the DNA and the walls are screened even though the DNA is very strongly confined. The experiments also used 2% (w/w) of polyvinylpyrrolidone (PVP, MW = 10,000) to suppress the electroosmotic flow. The latter additive is critical to the experimental protocol, since the electroosmotic flow is so strong in the absence of PVP that the DNA cannot enter the nanoslit.449 While these experiments449 used longer DNA and a smaller slit height than the previous control experiments for the nanofilter,184 it is clear that the molecular weight dependent electrophoretic mobility is caused by the channel size; experiments using the same DNA in a 70 nm slit height led to no separation.449
This anomalous mobility still holds for electric fields (60 V/cm to 2000 V/cm) that are more commonly encountered in capillary electrophoresis.450 Moreover, a set of systematic experiments using λ DNA indicated a strong change in the DNA dynamics as a function of the electric field strength.450 Explicitly, the motion appears to be smooth below 300 V/cm, but exhibits trapping behavior at higher electric fields. Moreover, these long-lived trapping events occur at preferred locations in the chip.451 There is thus a sharp drop off in the electrophoretic mobility by almost a factor of 10 from its peak value at 500 V/cm.450 These observations of the DNA dynamics are only qualitative (“smooth” or “trapped”) since the corresponding DNA velocities are much too fast to obtain detailed trajectory information.
The origin for the molecular weight-dependent mobility449,450 and the apparent dependence of the electrophoretic mobility on electric field strength450 remains controversial. The electrophoretic mobility appears to be described by the functional form449
| (46) |
where μ0 and A are fitting parameters and N is the number of base pairs. In principle, the quantity μ0 should be the free solution mobility in the absence of any confinement. Cross et al.449 proposed that this functional form can be explained by frictional contacts with the walls of the nanoslit, where the scaling N1/2 comes from the amount of DNA that should be in contact with the walls. Although the functional form of Eq. (46) is an empirical description of the data, the evidence for this frictional model would be best if it came from an analysis of the DNA trajectories. However, the experiments used to obtain the fitting parameters449 were measurements of the mobilities obtained from electropherograms. Moreover, similar experiments with λ DNA using videomicroscopy450,451 indicate that the DNA motion is smooth for the electric fields used to develop Eq. (46).449 One can have continuous friction effects, but is seems more likely that a frictional model would lead to velocity fluctuations that are directly related to the frequency of near surface contacts. In addition, in our experience, PVP provides an excellent coating for preventing DNA adsorption to surfaces. In the absence of the PVP coating or a poorly applied coating, we have observed numerous sticking events to microposts.
A second possibility for the molecular weight-dependent mobility is the change in the DNA conformation due to stretching in the nanoslit. Theoretically, the constant free solution mobility observed in unconfined geometries results from the configurational averaging of the hydrodynamic interactions between different parts of the chain.452 If the chain is able to sample its equilibrium configurational space in free solution, the configurational averages cancel out the molecular weight dependent terms.452 Recent experiments453 using converging channels to stretch the DNA (c.f. Section 7.4) provided strong support for this theory because the corresponding electrophoretic mobility depends on the stretching of the DNA. Moreover, simulations453 of the experimental data in this converging channel showed the origin of the behavior is indeed a loss of hydrodynamic screening, as we might expect from the basic theoretical arguments.452 The mobility of DNA in the magnetic bead array in Section 6.1.1 also appears to have a dependence on the DNA configuration, with the nominal DNA velocity before a collision being slower than that after the collision.339
While the hydrodynamic screening argument is attractive, especially since the DNA certainly cannot sample its free solution configuration space inside a small nanoslit, it also has some deficiencies. First, under such strong confinement, we would also expect to have significant screening of the hydrodynamics between segments of the chain due to the presence of the walls. As a result, the straightforward arguments about free solution electrophoresis452 are no longer valid. Second, we would expect to observe similar effects in a ≈ 50 nm slit height since the latter channels are still close to the persistence length of double-stranded DNA42,96 and much smaller than the radius of gyration for kilobase pair sized DNA. Since the electrophoretic mobility is independent of size in 60 nm184 and 70 nm449 nanoslits, changes in hydrodynamic screening are also insufficient to explain the molecular weight dependent electrophoretic mobility in very thin nanoslits.
A particularly intriguing possibility is the presence of nonlinear electrophoretic effects due to the surface roughness450 or the presence of the highly charged DNA in a narrow channel.454 The latter scenario implies the possibility of concentration polarization around the DNA molecule. Concentration polarization may be an important factor in DNA translocation through nanochannels, where the DNA is unconfined in one dimension. DNA in a nanoslit is unconfined in two dimensions, so the one-dimensional model used to describe concentration polarization breaks down.454 The surface roughness mechanism seems, at first glance, a likely candidate to explain the data. We already saw in Section 6.2 that large electric field gradients can lead to polarization of the DNA and a trapping effect that is a function of molecular weight. While the nanometer scale roughness of the substrate is not particularly important if one is creating micron scale features, roughness can play a critical role when the channel height is reduced. Figure 43 shows an atomic force microscope (AFM) image of the surface of the fused silica substrate used to create the 20 nm nanoslits used by Salieb-Beugelaar et al.450 for the high electric field DNA electrophoresis experiments we mentioned previously. Although the root-mean-squared (rms) roughness of the surface is only around 1 nm, similar to that reported in the other nanoslit experiment by Cross et al.,449 there are occasional pits in the substrate that extend down to almost 8 nm. These pits are not the result of the etching process, being present in the original substrate.450 The sharp surface features could lead to electric field gradients that could polarize the DNA and lead to dielectrophoretic trapping. It is not apparent whether such pits were present in the device used by Cross et al.,449 since they presented similar results for the rms roughness but did not provide evidence in support or against the presence of large defects in the surface.
Figure 43.
Atomic force microscope (AFM) image of the surface of the channels used in 20 nm nanoslit DNA electrophoresis experiments measured using a 2 nm radius tip. The rms roughness is between 0.8 to 1.1 nm but the maximum hole depth is 8 nm. Reprinted with permission from Ref.450 Copyright 2008 American Chemical Society.
Dielectrophoretic trapping seems to be a plausible mechanism because the strong confinement of the channel forces the DNA to remain proximate to the electric field gradients caused by the surface roughness. However, a series of experiments451 using 1 kHz alternating current electric fields superimposed on the driving dc field demonstrated that the superimposed ac field does not lead to increased trapping. Since we have already seen in Section 6.2 that ac fields lead to polarization of the DNA, their negligible effect on the DNA trapping rules out the possibility of dielectrophoresis as the origin for the molecular weight-dependent electrophoretic mobility.
The most likely reason that the electrophoretic mobility depends on molecular weight in very narrow channels is the presence of the low molecular weight PVP coating.451 There are some reasonable arguments against the influence of the PVP coating,449 since it is much lower in molecular weight than the PVP used as an entangled sieving matrix in capillary electrophoresis of DNA455 and, as a surface coating, it is probably lying flat on the surface.449 However, the surface coating is dynamic and the interactions between the PVP and the surface should be fluctuating.451 A nominal PVP thickness of 4 nm on each wall,451 which would be negligible in a typical 50 μm diameter capillary, means that the PVP occupies 40% of the width of a 20 nm slit. It is possible that the DNA becomes transiently entangled with the PVP coating. Although this separation has been referred to as a “nanogel”,451 one should not confuse the mechanism of the separation with the ultra-thin-layer agarose gel electrophoresis456,457 since (i) to be strict about the nomenclature, the PVP in a nanoslit is not a gel (since there are no physical or chemical crosslinks) and (ii) the length scales are quite different, with the nanoslit containing ≈ 4 nm thick polymer brush whereas ultra-thin-agarose gels are still several hundred microns thick.456 Rather, the separation mechanism for DNA moving between two proximate polymer brushes most closely resembles the constraint release mechanism proposed for capillary electrophoresis in entangled polymer solutions.20,21 In contrast to an entangled polymer solution, where the reptation of the sieving matrix releases the constraint on the DNA motion, the PVP is in dynamic equilibrium with the surface. As a result, the time scales for the constraint release are much different. Moreover, if the DNA can also pull the PVP off the surface and drag it through the solution, then there is also an element of the transient entanglement coupling mechanism that occurs during DNA electrophoresis in ultra-dilute polymer solutions.458
Clearly, the underlying physical mechanism for the molecular weight-dependent electrophoretic mobility in a nanoslit remains an open question, although we feel that the entanglement with the dynamic wall coating seems to be the most reasonable explanation. It is not apparent that there is an experiment that will unambiguously determine the underlying physical mechanism. We are reasonably optimistic that the molecular dynamics simulations that have proven very useful at elucidating the mechanisms for electroosmotic flow suppression by surface adsorbed polymers459–462 and, in particular, entanglement with a single neutral polymer,463 could shed light on this question. In particular, the length scales of the nanoslits are quite small so an explicit representation of the polymers, fluid, and the counterions should be feasible and reasonably mimic the experimental system.
We previously noted that the PVP coating was critical to the experiments449 in nanoslits because the electroosmotic flow would otherwise prevent the DNA from entering the nanoslit. In principle, one should be able to suppress the electroosmotic flow by switching to a pH that is closer to the isoelectric point of the silica surface (e.g., pH = 4). Unfortunately, the DNA electrophoretic mobility is also suppressed at such a low pH.451 However, it is possible to inject the DNA in the absence of a polymer coating if we switch to a larger silica slit or capillary.464,465 In the presence of electroosmotic flow from a silica surface, the DNA will move towards the negative electrode since the electroosmotic flow velocity (which opposes the DNA electrophoresis) is faster than the DNA electrophoretic velocity. In such a system, it appears465 that the net velocity of T2 DNA (164 kbp) is substantially higher than the net velocity of λ DNA for rather small electric fields (≈2 to 8 V/cm) and slit heights between 0.5 μm and 4 μm, with an abrupt switch to a molecular weight-independent mobility above slit heights of 4 μm. The latter experiments were not actually separations (i.e., they did not include any injection of a band of DNA) and the mobilities were obtained from videomicroscopy.465 There is also a report of separations of DNA in a 21 μm diameter capillary in the presence of electroosmotic flow under an electric field of 200 V/cm.464 The latter study, which included a systematic set of control experiments, clearly indicated the importance of the electroosmotic flow; the separation vanishes when the capillary is coated (as we would have expected from similar experiments with electroosmotic flow suppression14,448) and the separation resolution depends strongly on the ionic strength of the buffer (which affects the electroosmotic flow).
The electrophoretic mobilities in both of these experiments464,465 were explained by an excess positive charge in the diffuse layer that presumably shields the DNA. However, this explanation is questionable since the Debye layer is only around 10–30 nm. A more likely explanation is the additional contribution due to hydrodynamic flows. Before the electric field is turned on, the system is at hydrodynamic equilibrium. As a result, there will be no convective motion of the DNA in the absence of the electric field, which is indeed the case in experiments.465 However, in the presence of a strong electroosmotic flow, fluid with a pH greater than the isoelectric point of silica is continuously pumped. At some point, the additional hydrostatic head will be sufficient to drive a sensible hydrodynamic flow against the electroosmosis. The point at which this hydrodynamic flow matters depends on the particular design of the experimental system, such as the length of the channel between the electrodes, the smallest channel dimension, and the aspect ratio of the reservoirs. Nevertheless, there must be some hydrodynamic flow opposing the electroosmotic flow in a system connecting two reservoirs unless the gas pressure above the reservoirs is dynamically controlled to prevent any hydrodynamic back flow. (In microfluidic systems, there are many opportunities for anomalous hydrodynamic flows to develop and cause band broadening during DNA electrophoresis. There now exists an automated system for dynamically controlling the pressure301 that has since been commercialized.) Although there are not sufficient data to draw a definitive conclusion,464,465 we suspect that hydrodynamic flows may play an important role in the experimental observations.
Our discussion thus far has indicated that, for practical purposes, DNA cannot be separated by size solely due to confinement. However, it is apparent that confinement can enhance classical separation mechanisms. For example, we know from capillary electrophoresis experiments14 that DNA below around 400 bp move with a molecular weight-dependent electrophoretic mobility. The difference in free solution electrophoretic mobilities of these small oligonucleotides is enhanced when they are confined in a 100 nm slit.466 Indeed, these DNA cannot be resolved using the same experimental buffers when the slit height is increased to 1.56 μm,466 presumably due to the band broadening caused by the injection and the diffusion of the DNA. The enhanced separation is attributed to the effect of the electric double layers, which occupy up to 20% of the channel width in some of the experiments.466 Indeed, experiments using a very thick double layer (1 mM salt) exhibited a band inversion phenomenon where the largest DNA eluted first.466
The enhanced separation of oligonucleotides in nanoslits also provides an efficient approach towards electrophoretic detection of DNA hybridization.467 In this assay, one of the strands of the DNA is labeled with Alexa-488. In the absence of the complementary strand, only one DNA band appears in the electropherogram. The solution includes fluorescein as a fluorescent tracer dye, which makes it easy to compare the relative mobilities between different experiments. In the presence of the complementary (but unlabeled) strand, two DNA peaks appear in the electropherogram. The baseline resolution between the hybridized and unhybridized DNA in a nanoslit467 is very impressive since previous capillary electrophoresis experiments14 indicate that 27-mers would only have a 4% difference in electrophoretic mobility between the single-stranded and double-stranded form.467 Although we have only highlighted the ability to detect complete hybridization, this assay is particularly useful for elucidating the role of single mismatches (single nucleotide polymorphisms or SNPs) by comparing the area under the curves in the electropherograms.467 In the latter mode of operation, the fluorescein plays an important role in the analysis by providing a reference standard for the detected fluorescence intensity.
6.4 Surface Electrophoresis
In the previous section, we saw that free solution electrophoresis of long DNA only appears to lead to a separation when the DNA interact strongly with the surface, although the particular mechanism (surface friction449 versus constraint release451) remains controversial. It is also possible to effect the electrophoretic separation of long DNA by initially depositing the DNA on a weakly adsorbing surface in a method aptly termed “surface electrophoresis.”468 In the initial approach towards this technique,468 the DNA were first adsorbed to a cleaned silicon strip by drying a drop of DNA-laden buffer at one edge of the strip. As the droplet dries, the DNA are adsorbed onto the surface through the weak attraction between DNA and the (presumably) oxidized silicon on the surface. The affinity for the DNA to a silicon dioxide surface is a strong function of pH and any functional groups that might be present on the surface, a physicochemical interaction that has been nicely demonstrated in single molecule studies469–472 and familiar to anyone who has used a chromatography column to extract DNA from solution. The strip is then inserted into a groove in a standard submarine gel electrophoresis apparatus with the edge containing the adsorbed DNA on the cathodic side of the groove. The remainder of the process is the same as in submarine agarose gel electrophoresis; the substrate is covered by a normal electrophoresis buffer (e.g., TBE) and the electric field is applied.
The initial experiments using bare Si wafers468 were very promising, with a 1 kbp DNA ladder baseline resolved using an electric field of 4.5 V/cm after approximately 80 minutes. While the magnitude of the mobility, 10−5cm2/Vs, is similar to agarose gel electrophoresis, the scaling of the mobility with molecular weight, μ ~N−0.22, is considerably weaker than the scaling for biased reptation in a gel,15,189,190 μ ~ N−1. However, the surface electrophoresis apparatus maintains its favorable scaling to a much higher molecular weight than agarose gel electrophoresis. Under a dc electric field, the mobility dependence in an agarose gel disappears by the time we reach a molecular weight around λ DNA (48.5 kbp).196 Later surface electrophoresis experiments473 showed that a scaling similar to the one in the original experiments,468 μ ~ N−0.25±0.02, extends out to T2 DNA (164 kbp). Another particularly appealing feature of surface electrophoresis is the weak band broadening observed in experiments with λ DNA.474 Although there are only experimental data for two electric fields (5 V/cm and 11.6 V/cm), it appears that the band broadening decreases with increasing electric field.474 This behavior contrasts with the typical results in agarose gel electrophoresis,197 where the band broadening depends on the regime and, for most regimes, increases with electric field.
When the surface is coated with a silane layer, the scaling for the mobility improves to μ ~ N−0.87, which is still not quite as good as agarose gel electrophoresis. Interestingly, the paper describing the original experiments468 is the only publication reporting the use of a silane layer for surface electrophoresis, and many of the other papers475,476 we will encounter in this section use the bare Si surface as the baseline for comparison. We did not find any subsequent papers exploring the silane surface in more depth.
One of the most important aspects of this separation mechanism is the fairly narrow “injection” band produced by the drying DNA droplet used for the loading.473 When the droplet dries, the DNA are convected towards the pinned contact line in a manner analogous to the formation of coffee rings.477 Provided the DNA concentration in the droplet is chosen properly,478 the DNA will tend to adsorb only in the ring along the outer edge. If the droplet is large but the detection is only made from DNA from one side of the ring, it still corresponds to a very narrow initial band width. Alternatively, when the initial droplet is very small (e.g., 100 to 200 nL468), the radius of the droplet itself is quite small. In either case, the narrowness of the band of DNA produced from the drying mechanism is a critical component of the success of surface electrophoresis. It is also important that the detector only counts the fluorescence contributed by the DNA on the surface. When the electric field is applied, confocal microscopy reveals the presence of a plume of DNA that desorbs immediately at the start of the experiment.473 These DNA will move towards the positive electrode at the free solution mobility and would thus represent a spurious peak if they were included in the analysis. Moreover, since there is substantial convection from the free solution electrophoresis of these DNA, their band may be very broad and could potentially impede the detection of the peaks from the surface adsorbed DNA. As a historical note, we recall that gel electrophoresis was initially developed by Tiselus479 to avoid exactly this problem of convection during the electrophoresis of colloidal particles and mixtures of proteins.
The proposed separation method,468 supported by molecular dynamics simulations,480 is that the adsorbed DNA forms a series of loops and trains. The loops increase the entropy of the DNA, since there are many configurations available to these unadsorbed segments of the chain, whereas the trains along the surface benefit from favorable enthalpic interactions. This simulation model,480 used extensively to rationalize some of the experimental data468,474,475,481 but called into question by some of the work reviewed below,482 provides a qualitative understanding of the process as a function of the adsorption strength. We refer to these conclusions as qualitative since there is no obvious way to map the complicated chemical interactions between DNA (in an electrolyte) and the surface to a single parameter. The distribution of loops and trains is also a function of the molecular weight of the DNA,468 so the extent of the surface interactions will be a function of molecular weight. The separation should be possible for moderate surface affinity, where the loops can be driven downstream by the electric field and reattach to the surface. However, if the surface is very strongly attractive, the DNA are completely adsorbed and there are no loops to move the chains.
An alternate (but qualitatively similar) model arose from later Brownian dynamics simulations of two-dimensional DNA electrophoresis with trapping sites either randomly distributed on the surface483 or patterned on the surface.484 In either case, the DNA is purported to move through the medium by trapping in these sites and then extension towards another trapping site. The molecular weight dependence arises from the number of segments that can be present inside a site and the ability for the DNA to depin itself from a trap; smaller DNA have a weak electrophoretic driving force allowing them to escape from a trap and thus exhibit a lower mobility than their larger counterparts.483 The model for periodic patterns484 also predicts periodic oscillations in the mobility versus molecular weight that are not observed in experiments. The particular model of DNA used in the corresponding simulations484 is not a realistic depiction of the physics of a long DNA molecule, which is a likely source of this discrepancy.
It is extremely difficult to confirm these dynamical models on a bare Si surface operating in a submarine electrophoresis mode,468,473 since there is no easy way to use a high numerical aperture objective to obtain single-molecule dynamics data. However, if we replace the Si surface with bare silica, we can now see through the transparent surface from below. To observe the DNA dynamics on the surface, Jing et al.482 used total internal reflection (TIRF) microscopy. The evanescent wave in their setup probes the first 160 nm above the silica/water interface, which is appropriate for imaging the DNA surface dynamics. In contrast to the picture developed from molecular dynamics simulations,468,480 the experiments on silica surfaces indicate that the DNA frequently completely desorb from the surface (and thus leave the depth of focus for TIRF) and readsorb to the surface at a later point downstream.482 The contacts with the surface still play the dominant role in determining the electrophoretic mobility, but the mechanism is not due to the migration of loops of the DNA along the surface.468,480
There are also data482 for the dynamics of DNA surface electrophoresis with different surface treatments for the silica. Treatment in ozone followed by piranha solution led to surfaces with a large number of silanol groups. Further treatment with silanes led to self-assembled monolayers containing either amino or methyl groups, whereas condensation reactions of surfaces rich in amino groups with acetic acid led to amino groups on the surface. There are also data482 for a coating with polyvinyl amide, which could potentially entangle the DNA in a manner similar to the one proposed for the anomalous mobility in very thin nanoslits, discussed in Section 6.3.451 The ordering of the mobility, seen in Table 4, is consistent with the affinity of the DNA towards the surface. In this respect, the data agree with loop-train molecular dynamics simulations468,480 that predict that the mobility should depend on the energy of adsorption for the DNA to the surface. Remarkably, the most hydrophobic surface (methyl) has the lowest electrophoretic mobility. It is likely that this result is an artifact of using λ DNA in the experiment, which has 12 base overhangs on either side of the DNA.482 These hydrophobic end groups would be strongly attracted to the hydrophobic surface.
In addition to the surface treatments listed in Table 4, Lee and Kuo485 studied a large number of other possible surfaces for DNA electrophoresis. For the most part, many of the surfaces exhibited such strong adsorption of the DNA that it was impossible to obtain any mobility data. The best results were obtained using a glass surface that was previously exposed to an oxidizing environment, which led to a scaling μ ~ N−0.491 for the EcoRI digest of λ DNA. There are also hints that one can enhance the surface electrophoresis process at the interface existing along the corner of a microchannel,486 but the data for the bands is not convincing.
Table 4.
Mobility of λ DNA on different surfaces. PVAm stands for polyvinyl amide. Data reproduced from Ref.482
| Type of Surface | Mobility (10−4cm2/Vs) |
|---|---|
| SiOH | 7.4 ± 0.5 |
| Amide | 5.3 ± 0.5 |
| PVAm | 3.7 ± 0.5 |
| Amino | 2.2 ± 0.2 |
| Methyl | 2.1 ± 0.4 |
Thus far, we have focused exclusively on DNA separations using bare surfaces with different surface treatments. However, there are numerous approaches (such as microcontact printing487) that can pattern these surfaces with features on the length scales of the DNA. In the context of surface electrophoresis, Rafailovich and coworkers475,481 have pursued a block copolymer patterning method to lay down metal dots with a center-to-center distance commensurate with several times the persistence length of the DNA. Figure 44 shows one such pattern of Au dots on a Si surface. While the block copolymer patterning method is an efficient approach to create a quasi-ordered array of very small dots (e.g., for next generation magnetically patterned media488) without any direct write nanopatterning, it still requires significantly more processing than the bare silicon wafer used in the early experiments.468,473 For example, although the small scale pattern in Figure 44 was formed using block polymer assembly, creating the gold dots required focused ion beam milling of a gold film.481 Thus, we should view the results obtained in these systems in light of the additional difficulty in their fabrication.
Figure 44.
(A) Scanning electron microscopy (SEM) image of gold nanodots on a Si surface. (B) Atomic force microscope image of the same system. (C) Energy dispersion analysis of the bare Si and the Si/Au regions, respectively. Reprinted with permission from Ref.481 Copyright 2006 American Chemical Society.
The surface pattern was used to obtain mobility data for a supercoiled DNA ladder from 2067 to 16210 bp, with the mobility scaling improving through the presence of the gold nanodots.481 Figure 45 shows the most impressive results obtained to date using a surface electrophoresis apparatus.475 These experiments used a nanopatterned surface of Ni dots, rather than Au, but with a similar distribution to Figure 44a. Although these experiments475 used linear DNA and a different metal on the surface, the scaling for the electrophoretic mobility is essentially unchanged when compared to the gold nanodot pattern.481 However, we should note the impressive 5 decades of molecular weights in this figure, which includes data obtained from the HindIII digest of λ DNA, λ DNA, T2 DNA, and three different chromosomal DNA from S. Pombe containing 3.5, 4.7 and 5.7 megabase pairs (Mbp). The figure is a compilation of data obtained from separate experiments, as the agarose plugs used for the chromosomal DNA standards make it difficult to mix the S. Pombe DNA with the samples containing smaller DNA.475 These experiments used an electric field of 5 V/cm and detection from 5 to 10 mm from the injection point. The inset of Figure 45 shows the data for the separation of the S. Pombe chromosomal DNA. The total time for the separation is around 3 hours and 20 minutes, which is a substantial improvement over pulsed field gel electrophoresis for such large DNA.
Figure 45.
Mobility as a function of DNA size for surface electrophoresis on silicon with a hexagonal pattern of nickel spots. The dashed line at the top is the free solution mobility. The inset shows the separation of three chromosomes from S. Pombe (1 =3.5 Mbp 2 = 4.7 Mbp 3 = 57 Mbp). Adapted with permission from Ref.475 Copyright 2004 American Chemical Society.
One possible explanation for the improved separation using the nanodot pattern in Figure 44 is the presence of the large electric field gradients proximate to the metal/Si interface, which could be sufficient to lead to dielectrophoretic trapping.481 We have already explored a number of separations using dielectrophoresis in Section 6.2. Inset b in Figure 46 shows a simpler surface electrophoresis geometry that should also lead to dielectrophoretic trapping on the surface. This system still uses gold but now has equally spaced strips with a micron-scale periodicity.476 The latter length scale is accessible using conventional lithographic patterning techniques for metal surfaces. The DNA in this system jump between the strips. If the DNA is long enough, then it is possible for it to span multiple strips during its electrophoresis. The system illustrated in Figure 46 is actually a more accurate representation of the hopping method proposed by Ajdari and Prost443 than the insulator based dielectrophoresis devices417,431,432 we saw in Section 6.2.
Figure 46.
Mobility versus molecular weight for surface electrophoresis on an Au striped surface with a spacing of 3 μ m. The dashed curve is a prediction for a parameter β that is related to the stretching of the DNA from a simple model described in Ref.476 Inset (a) is an electropherogram for the λ DNA MonoCut mix. Inset (b) is an image of DNA trapped on the surface pattern with an 8 μ m spacing. Reprinted with permission from Ref.476 Copyright 2007 American Physical Society.
As seen in Figure 46, the electrophoretic mobility on such a surface consists of three regimes. Very small DNA do not experience substantial dielectrophoretic trapping by the gold strips and move in a manner analogous to the surface electrophoresis separations we saw previously using a bare Si surface.468,473 Presumably, the adsorption to the Si and Au surfaces are different, which could explain the somewhat lower slope in the mobility for the untrapped DNA in Figure 46. When the DNA experience both dielectrophoretic trapping and surface electrophoresis, the mobility scaling improves. Indeed, the scaling exhibited in this system, μ ~ N−0.87, is identical to the scaling we saw previously for a silane coated surface.468 It is not obvious which system is easier to operate, since the silane coated wafer requires less clean room fabrication but more care in the treatment of the surface. One advantage of the uniform surface electrophoresis is that its mobility scaling appears to extend to relatively high molecular weights.473 In contrast, large DNA in the dielectrophoretic trapping surface can span multiple traps. The mobility scaling in this regime, μ ~ N−0.08, is clearly insufficient to effect a separation.
Before we leave the subject of separations based on DNA-surface interactions, we should mention an alternative approach based on DNA hybridization to the surface.489 In this approach, the DNA that needs to be sized is hybridized to surface probes. When an electric field is applied perpendicular to the surface, the now tethered DNA are pulled in the vertical direction by the electric field. There is a critical electric field for dehybridization from the surface, and the magnitude of this critical electric field decreases with the size of the DNA. By gradually increasing the electric field strength and looking for the surface desorption, one can in principle determine the size of the DNA that was previously hybridized to the surface.489 This surface tethering method has been used to separate human genomic DNA (> 100 kbp) from λ DNA,489 as well as to separate single-stranded DNA in the 100 bp range.490 It remains to be seen whether this method can be used as a more general sizing tool.
6.5 Lipid Bilayers
In the surface electrophoresis methods discussed in the previous section, the DNA are trapped by a chemical affinity for the surface. Although the technique has been dubbed surface electrophoresis, the DNA still spans a three dimensional space. We now turn our attention to an approach that produces two dimensional electrophoresis by adsorbing the DNA to a cationic lipid bilayer. The lipid bilayer is formed on a glass substrate, which permits a facile analysis by conventional epifluorescence microscopy. Since the DNA are adsorbed to the bilayer, the problems with additional DNA in the solution proximate to the surface (which necessitated using TIRF microscopy482 for a silica surface) are no longer an issue. Videomicroscopy of DNA on a lipid bilayer has contributed substantially to our understanding of polymers in two dimensions, in particular confirming the scaling exponent for the radius of gyration of a self-avoiding chain in two dimensions.491 The lipid bi-layer provides substantial hydrodynamic screening for the DNA motion, whereupon the diffusion coefficient exhibits Rouse scaling,492 D ~ N−1.
If an electric field is applied in the plane of the lipid bilayer, then the DNA can undergo electrophoresis in two dimensions. The initial experiments for DNA electrophoresis in a lipid bilayer493 indicated that the DNA dynamics are similar to what we observed in the post arrays in Section 6.1.1. As we can see in Figure 47, the DNA can become hooked around obstacles and exhibit the same U-shaped collisions that we observed for a collision with a microfabricated post.325,326 Based on observations such as the one in Figure 47, Olson et al. 493 concluded that DNA electrophoresis in a lipid bilayer is analogous to 2D electrophoresis in a system of dilute obstacles, and that the number of hooking events can be used to estimate the density of lipids in the bilayer. The latter observation led to one of the seminal computational studies of DNA electrophoresis in a post array,357 whose results have proven extremely useful in understanding transport in arrays of posts.32
Figure 47.
Sequence of images of λ DNA hooking on lipids during electrophoresis in a lipid bilayer at E = 3.3 V/cm. The scale bar is 10 μ m and the times for each image are listed in seconds. Reprinted with permission from Ref.493 Copyright 2001 American Chemical Society.
However, a subsequent study of DNA electrophoresis in a lipid bilayer494 called into question the interpretation of the system as a dilute array of obstacles.493 If we examine Figure 47 closely, it appears that the pivot point for the DNA hooking does not move during a collision. A lipid bilayer is a fluid system, so if the DNA were hooked on the lipids in the bilayer then we would expect that the pivot point would be dragged downstream while the DNA unhooks.494 The situation here is analogous to capillary electrophoresis in an ultra-dilute polymer solution, where the hooked DNA molecule drags the neutral polymer chain during the unhooking process.458,463 Since preparation of the lipid bilayer requires exquisite care in the cleanliness of the surface, it is possible that the immobile hooking points leading to collisions such as the one in Figure 47 are not collisions with the lipid obstacles but rather with impurities.
Figure 48 shows one of the most stunning results from the experiments494 supporting biased reptation as the migration mechanism in a lipid bilayer. At low electric fields, the DNA appears to undergo a weak biased reptation and the superimposition of the series of images looks like a blob moving, in general, in the direction of the electric field. At higher electric fields, the chain appears to be exploring the different possible pore spaces inside the bilayer. The summation of the images at a higher electric field bear a remarkable resemblance to the images from simulations of megabase pair DNA194,225 that ultimately led to the development of the biased reptation with fluctuations theory for gel electrophoresis.193–195 Although there are only data for four different molecular weights of DNA, the mobility also appears to follow the biased reptation scaling law, μ̃ ~ N−1. The normalized mobility
Figure 48.
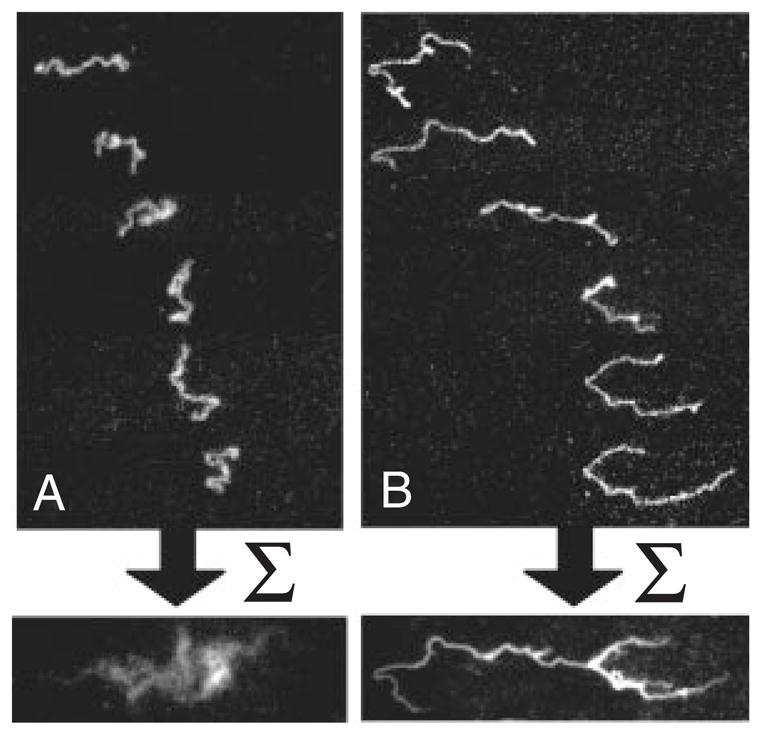
Videomicroscopy images of DNA electrophoresis on a cationic lipid bilayer. The snapshots in (A) correspond to an electric field of 0.2 V/cm and the snapshots in (B) correspond to an electric field of 10 V/cm. The image at the bottom is the time average of each series. Reprinted with permission from Ref.494 Copyright 2009 Wiley-VCH.
| (47) |
is the electrophoretic mobility observed in the experiment, μ, divided by the product of the molecular weight of the DNA and its diffusion coefficient. The latter parameter can be obtained from a measurement of the DNA dynamics in the absence of an electric field. Since the diffusivity obeys Rouse dynamics,492 D ~ N−1, then a mobility of the form of Eq. (47) should still produce the correct scaling with molecular weight. The additional normalization with ND corrects for variations in the preparation of the lipid membrane.494 In addition to demonstrating that DNA electrophoresis in the lipid membrane follows biased reptation, these experiments494 also demonstrated the existence of hooking events on both mobile and immobile obstacles.
Overall, the experiments by Kahl et al.494 provide convincing evidence that a lipid bilayer can provide a confining environment similar to a gel. Although imperfections in the bilayer can lead to hooking events similar to a post array,493 the dominant mode of migration on a very well prepared lipid bilayer is biased reptation. The lipids thus form an obstacle-dense medium through their aggregation near the DNA chain, which leads to the formation of the reptation tube.494
In addition to data for double-stranded DNA, there are also data for the electrophoresis of short single-stranded DNA on a lipid bilayer.495 Unfortunately, the electrophoretic mobility of these short DNA on the bilayer is independent of molecular weight. Since their diffusivity still appears to be Rouse-like, with D ~ N−0.89, it might be possible to separate them using the geometric ratchet methods496 that we will explore in Section 6.6.
Although there are certainly molecular weight-dependent interactions between DNA and a lipid bilayer, at least for double-stranded DNA, it is not clear that a lipid bilayer is a desirable medium for sizing DNA. First, there are challenges with defining the initial band since the DNA need to first adsorb onto the bilayer. Second, the preparation of a quality bilayer is very challenging,494 especially when we compare it to the easy preparation of an agarose gel. Third, a cationic lipid membrane itself is charged, so the electric field needs to be periodically reversed (e.g., at 0.01 Hz) to avoid demixing of the charged membrane.494 With these limitations in mind, it seems that the power of using a lipid bilayer lies in examining the properties of polymers in two dimensions491,492 rather than exploiting its confining abilities to separate DNA by size.
6.6 Continuous Separations
The separation devices we have discussed so far all operate in a batch mode, analogous to gel electrophoresis and capillary electrophoresis. Batch separations are appropriate for analytical scale separations, where a small amount of DNA are analyzed to determine their molecular weight distribution. The small amount of sample certainly has some advantages, for example, when the sample is rare and only a small amount of material is available for the separation. In many cases, it is desirable to separate the DNA and collect the fractionated products, which is normally referred to as a preparative separation. At a laboratory scale, agarose gel electrophoresis is sufficient for preparative purposes, since fairly large amounts of DNA can be processed in a single run and the bands are readily extracted from the gel with a scalpel.
In principle, batch microfluidic separations could be run in a massively parallel fashion to process enough DNA for preparative purposes. However, there are several critical issues with such an approach. First, the number of channels required for the separation is enormous; if a single microfluidic injection of the type in Figure 24 to Figure 26 analyzes a few nanoliters of fluid, we would need thousands of channels to reach the throughput of gel electrophoresis. Second, while the injection methods we covered in Section 5.4 are effective at creating a narrow injection band for an analytical separation, they waste a large amount of material in the loading process. In contrast, gel electrophoresis makes efficient use of most of the starting material. Third, collecting the bands from a batch separation is a challenging task. While there are several approaches appearing in the literature,313,314 it is not obvious that the bands in a complicated and unknown mixture of DNA can be efficiently collected at the end of the microchannel.
If one desires a throughput appropriate for preparative separations, it is better to switch to a continuous separation process. As we will see in this section, continuous separations have been developed as extensions of some of the methods we discussed in Section 6.1, such as pulsed field electrophoresis in a post array498,499 and entropic traps/nanofilters.500,501 Other methods, such as ratchet based separations496,497,502–507 and deterministic lateral displacement,508 rely on physical principles that have not yet been covered in our review. The advantage of a continuous separation is easily seen in Figure 49, which reproduces data from an optimized version of a tilted Brownian ratchet separation.497 Different sized DNA fragments travel at different angles from the initial injection stream. By the end of the device the DNA has separated into different bands which can be shunted off into different channels for collection and further analysis. These devices can be run for hours and sometimes for days,498,506 which allows for throughput that is currently impossible in batch microfluidic devices. Also, continuous devices simplify the injection procedure. All continuous devices need is a thin initial stream, which can be created by using a thin channel before the DNA enters the device as opposed to more complicated batch injection procedures discussed in Section 5.4. These advantages make continuous separation devices ideal for integration into larger lab-on-a-chip type devices509,510 that require DNA (or protein) separations as one of the preparatory steps of the device.
Figure 49.
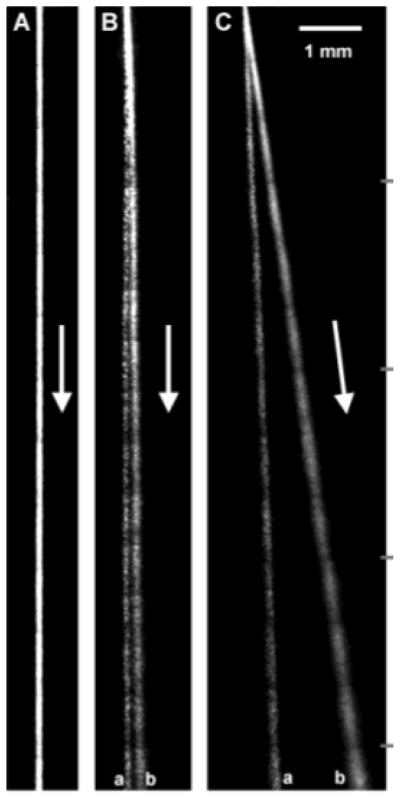
A separation of two different sized DNA molecules performed in a continuous separation device. The band with the larger defection angle is the smaller DNA. (A) No tilt, high speed. (B) No tilt, low speed. (C) Tilted, low speed. Species (a) is 164 kbp and species (b) is 48.5 kbp. Adapted with permission from Ref.497 Copyright 2003 American Chemical Society.
One of the earliest working continuous separation devices was the DNA prism,498 seen in Figure 50. The working principle behind the DNA prism is a clever extension of the pulsed field post array system348 we discussed at the end of Section 6.1.1. In conventional pulsed field gel electrophoresis, the electric field strength remains constant but the direction of the electric field changes. As a result, DNA of different sizes move at different speeds but all of the DNA move in the same net direction.229 As we can see in Figure 50, the DNA prism operates using two different field directions and two different electric field strengths.498 Following the standard practice in pulsed field gel electrophoresis, the fields are oriented at 120° from each other. The DNA initially travels in the direction of the stronger field. The field is then switched to the weaker field direction. Since the electric field is not very strong, the longer DNA molecules are unable to reorient with the field. This means that on average the longer DNA travels in the direction of the stronger field. The shorter DNA molecules are able to reorient and travel in the new field direction until the stronger pulse is applied again. This means the shorter DNA tends to travel in the average field direction to varying degrees that depend on the DNA length. Note that the relevant parameter for the separation is the amount of time the DNA have to reorient when the direction of the field changes. Thus, although the initial work used a square wave of different electric field strengths,498 one can effect the same separation by using long and short pulses of electric fields with the same magnitude.
Figure 50.
Top: Schematic of the DNA prism. The SEM images in the insets highlight different regions of the device. Bottom: Illustration of the separation mechanism. At t0 both the long and short fragment travel in the strong field direction. At t1 the field is switched to the weak field in a new direction. The long DNA molecule cannot get all the way around the corner, but the smaller molecule can. At t2 the field is switched back to the strong field and the long DNA travel down the same channel while the shorter DNA is now in a new channel. Reprinted with permission from Ref.498 Copyright 2002 Nature Publishing Group.
The first DNA prism device498 was constructed using photolithography as a 3 mm by 9 mm hexagonal array of posts. The post are 2 μm in diameter, spacing, and height. As we can see in Figure 50, the array is surrounded by several bundles of microfluidic channels that lead to large buffer reservoirs. The channels serve two purposes. First, they create uniform and tunable electric fields within the large post array by the current injection method, where the high resistance channels act as current injectors.511 Second, the microfluidic channels can also be used to selectively capture the separated DNA fragments. The location of these outlet channels can be designed so that desired fragments can be collected for further analysis while the other fragments are sent to separate stream for separate analysis or to the waste. Note that the current injection method511 is a robust way to apply the pulsed fields, but it still requires at least four, and up to eight, electrodes to work.
More recently, the DNA prism technology was recreated in colloidal crystals.499 We have already discussed the methods for creating the colloidal crystal arrays in Section 6.1.3, so this device can be seen as a straightforward combination of the colloidal crystal separation device392 and the DNA prism technology.507 The major challenge is creating a large crack-free self assembled colloidal crystal, which benefits from the fact that the current injection microchannels also create more evaporation fronts for convective self assembly.499 These later devices317,499,512 also carefully considered the role of pore spacing and the frequency of the electric field. At very low and very high frequencies, there is no separation.499 Neither result is particularly surprising in light of the regimes of pulsed field gel electrophoresis covered in Section 5.2, since the low frequency regime minimizes the effect of the reorientation time (which is the origin of the separation498), and the high frequency regime does not provide sufficient time for any of the DNA to reorient. Since one must get a separation in the DNA prism for some frequency range, there is a peak in the deflection angle at moderate frequencies between 1 and 30 Hz, with the exact location of the peak depending on the electric field499 and vanishing when the colloids are very small.512 In moderate sized colloids (330 nm and 900 nm), the optimal separation frequency is higher for higher fields, with the smaller colloids (330 nm) producing better separations than the larger (900 nm) colloids.499 Similar to what we saw in the discussion of post arrays315 in Section 6.1.1, the colloidal crystal separation benefits from having an ordered array of pore spacing.317
The DNA prism has also been integrated into lab-on-a-chip devices for sample preparation.509,510 We will discuss these devices in the context of their integrated functionality in Section 8.4.
The entropic traps and nanofilters we saw in Section 6.1.2 have also been integrated into a continuous separation format in the so-called anisotropic nanofilter array (ANA)500,501,513 illustrated in Figure 51. This device works by superimposing two perpendicular electric fields, using the current injection method to create the electric fields.511 One field drives the DNA through a deep channel while the other field drives it towards a parallel deep channel. Separating the two deep channels is a narrow space that constitutes the entropic trap or nanofilter. As was the case in the batch devices we discussed in Section 6.1.2, the probability of the DNA crossing through the thin gap depends on the size of the DNA, which leads to different sized fragments traveling at different angles.500 If the thin slits act as entropic traps,150,181–183 then the larger DNA are most likely to cross through the trap and have a larger deflection angle. Conversely, if the thin slits act as nanofilters,184,185 then the smaller DNA have a higher hopping frequency and thus a larger deflection angle.
Figure 51.
Schematic illustration of the anisotropic nanofilter array (ANA). (a) For the Ogston sieving regime, where the radius of gyration is smaller than the gap, the smaller molecule has a higher rate of crossing the gap. (b) For the entropic trapping regime, where the radius of gyration is larger than the gap, the larger molecule has a higher rate of crossing the gap. This image is for the planar ANA device, but the same idea holds for the vertical device. Adapted with permission from Ref.500 Copyright 2007 Nature Publishing Group.
There are two generic ways to create the anisotropic nanofilter array. Recall from Section 6.1.2 that the entropic traps and nanofilters were originally fabricated using two etch steps to create a multiple-depth device, with the narrow slit having a thickness in the tens of nanometer range. In the planar device ANA device, the same strategy is employed in the continuous separation device, where the distance between the etched silicon and the glass ceiling creates the thin slit.500 It is also possible to create an array of high aspect ratio pillars that span the channel height with very narrow gaps between them, where the gap between the pillars creates the thin slit (which is now turned on its side).501 The latter vertical device is much harder to fabricate, since it requires making highly anisotropic etches and backfilling to produce the narrow gap.501 However, the vertical device has a much higher throughput, 1000 nl/h,501 when compared to the 1 nl/h throughput for the planar device.500 While the two devices have not been directly compared, the separation mechanisms are the same so their performance should be very similar, aside from the increased throughput for the vertical device. In applications, one should carefully consider the balance between throughput and cost of the fabrication.
The devices described so far (DNA prism and ANA) are continuous versions of the post arrays and entropic traps we saw in previous sections. Let us now consider ratchet methods, which permit continuous separations of DNA without using any of the physical principles we explored in Section 6.1. We will focus our attention on ratchet systems rather than the emerging methods using deterministic lateral displacement,508 which seem to have found their niche in the separation of colloidal particles and cells514–516 rather than their limited applications to DNA.508 Brownian ratchets have a rich history in physics.517 The idea behind a Brownian ratchet is to “rectify” the random Brownian motion in order to achieve directional transport. The rectification requires doing work on the particles, which for DNA usually occurs in the form of an electric field. There are two different ways to rectify the motion — a flashing ratchet, where the electric field changes in time, and a Brownian ratchet, where the geometry of the device produces the separation under a constant electric field.
The flashing ratchet518 has been used to separate DNA by size.502,504,505 In a flashing ratchet, an asymmetric potential field turns on and off periodically. When the potential is on, the DNA are localized at the minima of the potential field. When the field is turned off, the DNA travel randomly under Brownian motion. The typical choice of potential is a sawtooth. Since the potential is asymmetric in space, it is more likely that the DNA will diffuse to the “short” side of the sawtooth rather than the “long” side in the absence of the field. Thus, when the potential field turns back on, the random motion is rectified into directional motion as the DNA fall into the local minima of the sawtooth potential field. In the context of DNA, the flashing sawtooth potential was created502,504,505 using an interdigitated electrode array. As predicted by theory,518 the DNA travel up the array in a size dependent manner that depends on the frequency and duration of the on/off pulses.502,504,505
As we saw for dielectrophoresis in Section 6.2, it is sometimes preferable to try to use a passive post array over interdigitated electrodes, since the passive system simplifies the device operation. Theoretical analysis519,520 suggested that an array of obstacles tilted with respect to the electric field can separate DNA by size in a continuous manner. The experimental realization503 of this idea appears in Figure 52. (Note that a similar principle was also realized using charged lipids moving in a patterned lipid bilayer.496) The obstacles are arranged in such a way so that, as the DNA moves downward through the array, the diffusion path to the next channel on the right is shorter than to the left. Smaller molecules diffuse much quicker than larger molecules, so the smaller molecules are more likely to travel to the right, while the larger DNA molecules tend to travel in the field direction, as shown in Figure 52. There are some questionable assumptions in the original theories,519,520 in particular related to the neglect of the curved field lines caused by the insulating obstacles.32,521,522 However, as the results for the optimized ratchet device in Figure 49 show, one can certainly separate DNA by size using a Brownian ratchet.
Figure 52.
A image of the Brownian ratchet. For the molecule to travel from the gap it is in to the adjacent gap to the right, it needs to move from the gap to the start of the next tilted obstacle, about 1.5 μm. To move to the left gap the molecule needs to travel the entire distance of the obstacle, about 5 μm, or be shunted back to the gap it started at by the obstacle. It also has less time to diffuse left before colliding with the obstacle. Practically, no molecules travel to the left. Reprinted with permission from Ref.503 Copyright 1999 National Academy of Sciences of the U.S.A.
The progress from the prototype in Figure 52 to the optimal result in Figure 49 was an interesting one, so it is worthwhile to recount the key steps along the way. The first device was a large array of asymmetric obstacles set at 45° from the applied field, created to test a theoretical idea that DNA molecules could be separated based on their size dependent diffusion.503 Single molecule experiments,503 shown in Figure 52, demonstrated that different sized molecules travelled at different angles. However, the original device503 was not used for a separation since it was incapable of injecting a thin steam of the DNA.503 The next step taken to improve the device was to add an injection port.506 This second generation device featured a laser micromachined hole in the back of the device, usually 10–30 μm in diameter, that now allowed the device to be used for separations.506 While the latter experiments did show that the separations occurred in the expected range519 for the electric field strength, they revealed that the models519,520 of the process did not accurately capture the separation due to the deflection of the electric field lines by the insulating obstacles and the finite size of the DNA. Realizing the optimal separations497 required tilting the obstacles 18.4° from horizontal and tilting the entire array away from the vertical.507 This second change led to a smaller distance between the center of a channel and the distance needed to diffuse in order to be in the next channel, allowing for faster separations and ultimately producing the results seen in Figure 49.497
6.7 Hydrodynamic Methods
Having completed our review of electrophoretic separations, we conclude this section on separation methods with some comments on hydrodynamic approaches. We consider three cases: post arrays, simultaneous hydrodynamic and electrophoretic motion in capillaries, and hydrodynamic chromatography in confinement.
We saw in Section 6.1.1 that DNA can be separated by electrophoresis in relatively sparse arrays of posts. These results also extend to hydrodynamic separations of DNA in similarly sparse arrays. An applied electric field acts on a tethered polyelectrolyte equivalent to a hydrodynamic flow,37,523–525 resulting in similar dynamics during electrophoresis and during pressure driven flow.526 Thus, the dynamics that lead to a separation in electrophoretic collisions with a post should also prevail during hydrodynamic collisions, although there is the possibility for additional hydrodynamic interactions between the extending arms of the chain.463,527 Using a sparse array of 70 nm posts created by a multi-exposure phase shift lithography approach,352 hydrodynamic flows led to a resolution of 2.3 in 2 minutes between 16 and 33 kbp DNA.351 When we compare the latter data to the electrophoretic separation data in Table 3, we see that pressure driven flow and electrophoresis through sparse nanopost arrays lead to similar resolutions.
While hydrodynamic flows are generally deleterious to electrophoretic separations, Zheng and Yeung528 proposed a novel approach where the hydrodynamic flow during capillary electrophoresis enhances the separation. The fundamental basis behind their method is the radial migration of DNA during simultaneous electrophoresis, electroosmosis and hydrodynamic flow.529,530 The direction of the migration depends on the relative direction of the hydrodynamic flow and the electrical actuation; the DNA tend to migrate towards the wall when the two flows are in opposite directions, whereas the DNA tend to migrate towards the center of the capillary when the two flows are coincident.528 Moreover, the rate of the focusing is a function of the molecular weight, with the larger DNA orienting more quickly. (The migration of deformable particles such as bubbles and droplets across streamlines is a classic problem in hydrodynamics.) These properties can be used to separate two species with widely different values of the focusing time. The idea528 is to periodically reverse the direction of the hydrodynamic flow by changing the height of the cathode reservoir with a time constant that is between the reorientation times for the two species. Neglecting diffusion, the smaller DNA (with the faster reorientation time) will tend to oscillate in the flow but their net velocity will be zero. In contrast, the larger DNA (with the slower reorientation time) will spend half of their time in the slow streamlines near the walls and the other half of their time in the fast streamlines in the center of the channel. Since the mean velocity of the hydrodynamic flow is not equal to half the maximum velocity, the larger DNA should exhibit a net velocity. While the actual transport process is considerably more complicated, mostly due to Taylor-Aris dispersion in the oscillating flow,139 this mechanism produced a baseline separation between λ DNA and linearized φX174 (5,386 bp).528 Although this is a very clever separation mechanism, the oscillating hydrodynamic flow has limited utility since the switching frequency needs to lie between the focusing time of two species. The mechanism should be able to act as a filter by separating DNA around some cutoff, but it is not obvious how to tune the frequency of the flow reversal to separate a more complicated mixture of molecular weights.
DNA confinement has also proved to be a useful enhancement to hydrodynamic chromatography of DNA. The separation mechanism here relies on the exclusion of the larger DNA from the streamlines near the walls, which results in the larger molecules exiting the column first.31 One needs to take care when hydrodynamic chromatography is performed in very narrow channels. Figure 53a depicts experimental data for the relative velocities of three different DNA molecules as a function of the slit height, h.531 When h > Rg, as illustrated schematically in Figure 53b, the DNA follow the normal hydrodynamic chromatography mechanism with the largest DNA moving at the highest velocity due to the excluded slow streamlines near the wall. The radius of gyration for λ DNA (48.5 kbp) is 0.73 μm,62 so we might expect the hydrodynamic chromatography mechanism to be manifest for channels that are larger than a few microns in height. As we can see in Figure 53a, the hydrodynamic chromatography effect is indeed present for these larger channels. Using a random flight model for the DNA chain, Stein et al.531 also developed predictions for the density of DNA segments as a function of the narrow direction in the channel. Figure 53c clearly shows the origin for the hydrodynamic chromatography, where the smallest DNA (the blue curve) is able to explore the full range of fluid velocities. In contrast, the small slit height h < Rg depicted in Figure 53d leads to compression of the DNA into a pancake conformation.532 The predicted density of the DNA segments in Figure 53e is independent of the size of the chain. The latter prediction is consistent with the relative velocities of the chains, which are independent of molecular weight in Figure 53a for the smallest channel heights. It is unfortunate that the velocities become independent of molecular weight in this regime, since these experiments531 indicate a strong suppression of Taylor-Aris dispersion in the narrowest slits and one would thus expect sharp bands. However, the results in Figure 53 indicate that all of these bands would overlap, negating any benefits of their sharpness.
Figure 53.
(a) Relative velocity as a function of nanoslit height, h. (b) Schematic illustration of hydrodynamic chromatography for h ≫ Rg. (c) Prediction from a random flight model for the density of DNA segments as a function of molecular weight. The color coding is the same as in (a). (d) Schematic illustration of the DNA configurations for h = 3.81 μm. (e) Prediction from a random flight model for the density of DNA segments as a function of molecular weight for h = 500 nm. The color coding is the same as in (a). In (c) and (e), the fluid profile is indicated in gray. Modified with permission from Ref.531 Copyright 2006 The National Academy of Sciences of the U.S.A.
The picture of DNA hydrodynamic chromatography developed from the fundamental experiments531 described in Figure 53 goes a long way towards explaining the analytical results obtained in very long, narrow capillaries.533–537 The earliest experiments534 used a 500 nm capillary and were limited to separating relatively short DNA; excellent results were obtained with a 1 kbp ladder and the largest DNA separation was between a 10 kbp and 20 kbp fragment. Considerably higher quality results were obtained by increasing the capillary diameter.533 For example, Figure 54 shows a hydrodynamic chromatography separation of a wide range of DNA from 75 bp to 106 kbp in a single run of around 2.5 hours.533 However, DNA from 106 kbp to 1.9 Mbp cannot be separated by hydrodynamic chromatography in a 750 nm capillary537 since the molecules now need to deform to move through the capillary. The capillary diameter used here is approximately twice the radius of gyration of the largest DNA in the sample. As a result, we would not expect any of these DNA to be in the regime of Figure 53d, and they should all be affected by the hydrodynamic chromatography mechanism.
Figure 54.
Hydrodynamic chromatography of DNA in a 2.5 μm inner diameter, 445 cm long capillary under a pressure of 360 psi in a 10 mM Tris, 1 mM EDTA buffer. Reprinted with permission from Ref.533 Copyright 2010 American Chemical Society.
We suspect that there is considerable room for further improvement in hydrodynamic chromatography of long DNA in narrow capillaries. The narrow bore capillaries are obtained from a commercial manufacturer533–536 and these materials are not very easy to produce with a uniform inner diameter. For example, Liu et al.536 observed resolutions between 1.1 to 3.4 for the separation of 2027 bp and 2322 bp fragments when they used different segments of a 50 m long capillary. Any breakthroughs that permit the production of long, uniform capillaries are sure to improve the reproducibility of this method. Perhaps more importantly, a constant capillary diameter will eliminate any axial gradients in the flow and the corresponding band broadening caused by Taylor-Aris dispersion in a slowly varying channel.538,539
7 DNA Stretching
Unlike separation based methods, which rely on a molecular-weight dependent mobility to isolate and size ensembles of DNA, stretching methods rely on visualizing single elongated molecules. Consequently, in stretching techniques the genomic length is measured directly rather than inferred from the electrophoretic mobility. To be more specific, intercalating dyes, fluorescent nucleotides and probes and other techniques of labeling the chain give rise to a fluorescence intensity map that is a function of space and time. We then infer the length from the intensity map, as discussed in Section 4.2.
In order to produce the most accurate measurement, it is important that the DNA be strongly stretched. In this section, we discuss the different approaches to stretching DNA, either through its attachment to a surface (Section 7.1), by confinement (Section 7.2 and Section 7.3), flow (Section 7.4 and Section 7.5) or by dielectrophoresis (Section 7.6). We focus primarily on methods for DNA stretching that do not require previous functionalization of the DNA molecules. With but one exception,540 we are going to exclude the stretching of end-tethered DNA by flows,541–544 including the impressive work using DNA curtains,545,546 permanent immobilization of DNA between electrodes by dielectrophoresis,414,415 and various tweezer-based methods.547–549 Such systems have found great utility for studying DNA/enzyme interactions on stretched DNA. However, they are not particularly useful for sizing DNA since the throughput is low.
7.1 Surface Stretching
As we mentioned in the context of Figure 8, agarose was the original medium for stretching and fixing DNA.102,165 However, gel-based stretching suffers from major drawbacks. For example, because the gel is three-dimensional, the stretched molecule is not guaranteed to be in the focal plane — a problem that leads to measurement errors, especially for longer fragments. Although one can handle the focusing problem using scanning confocal microscopy,550 it is preferable to use simpler fluorescence microscopy techniques. In addition, as we saw in Figure 8, a loose network of agarose fibers allows significant relaxation of the polymer chain upon cleavage with a restriction enzyme. This limits the resolution to about 20 kbp.551 The key accomplishment of this early work was establishing that a molecule of DNA could actually be extended and sized using fluorescence microscopy.102,165
Another option for stretching DNA is to attach it to a functionalized surface. For example, DNA will adsorb to aminopropyltriethoxysilane (APTES)551 and polylysine166 surfaces, and it can be stretched out in a flow. Compared to molten agarose, these surfaces improve the fractional extension from around 0.3 in agarose to 0.5 on glass, solve the depth of field problem, and increase resolution to around 1 kbp. However, these particular surface chemistries also add complexity because DNA is not the only object that absorbs to the surface. As a result, the coatings need to be carefully controlled to reach optimal levels of total absorbed DNA, strength of adsorption, and DNA stretching. In addition, the surface chemistry interferes with biochemical reactions in some conditions.
The key breakthrough in surface stretching was the idea of molecular combing.104,105 Figure 55, which shows an example of molecular combing, illustrates how this process takes advantage of two phenomena: selective attachment and contact line stretching. First, a glass coverslip is treated with a monolayer of silane molecules with an exposed vinyl group. When a DNA solution is applied, the silanized surface selectively attaches to the ends of the DNA, specifically to the 5′ end. This selective attachment is the first key to molecular combing and is a major step beyond what was achieved previously. The surface does not attract other molecules in solution, leading to a clean experiment. Second, since the DNA is adsorbed at its terminus, the rest of the DNA can be stretched by the flow. Explicitly, a receding contact line leads to stretching by forces at the air-water interface, causing the DNA to extend and remain on the surface. We already saw this basic idea in the surface electrophoresis experiments in Section 6.4, since it is the approach used to load the DNA onto the surface. Importantly, these hydrodynamic forces are strong enough to overcome the entropic resistance to molecular extension, but not strong enough to break covalent bonds.
Figure 55.
Schematic of molecular combing process. The silanized surface of the glass selectively attaches the 5′ end of the DNA, and the moving air-water contact line stretches and fixes the DNA molecule to the surface. DNA is represented in the figure as free-solution (f), bound (b), combed (c) and looped (lo) — when both ends bind to the surface. The scale bar is 25 μm. Adapted with permission from Ref.106 Copyright 1997 American Association for the Advancement of Science.
Molecular combing offered significant advantages over the previous methods used to stretch and fix DNA. The receding contact line leads to almost full extension and improves the amount of DNA attached to the surface. One should also not overlook the increase in sensitivity that molecular combing provides. Since the molecules are fixed on a surface, extremely small amounts of DNA (attomoles) are required to get a signal.104 However, the single molecule nature of these methods is a mixed blessing; they provide a very sensitive measure, but the need for high-throughput is ever present in order to get statistical accuracy.
With the breakthrough in molecular combing and the proof-of-principle experiments on mapping whole chromosomes,106 the focus switched towards increasing throughput and automation552 with the goal of providing a complimentary technique to DNA sequencing.553 The next key step was to ensure that the stretched molecules are aligned, which permits mechanized and computerized operation of optical sizing. One option used the previously discussed “coffee ring” effect477 in arrays of tiny of droplets of DNA solution on an APTES-treated glass surface,554 as shown in Figure 56. Here, a moving contact line stretches and fixes the DNA, similar to the mechanism for molecular combing on a dipped glass slide. These “fluid fixed” molecules are aligned radially as the drop evaporates, which is also shown in Figure 56C and Figure 56D. Using the fluid fixing technique and capitalizing on the regular alignment of DNA allows for automatic image acquisition, which was a major step towards high throughput applications.
Figure 56.
Fluid fixing of DNA on APTES-treated glass surfaces. The drying process produces a high degree of alignment within the spot. Spotting these droplets with an automated process facilitates automated image analysis of fragment sizes. Scale bars represent 20 μm in (A–C) and 5 μm in (D–F). Adapted with permission from Ref.554 Copyright 1998 National Academy of Sciences of the U.S.A.
The coffee ring effect is not the only option for creating aligned stretching. One can also use a motor driven, droplet spreading tool on an APTES-treated glass surface,555 drag a micropipette tip across the surface556 or incline the glass slide to produce a gravitational flow.557 Other methods of fixation include DNA adsorption to hydrophobic SU-8 in nanochannels558 and investigations of molecular combing of oligonucleotides.559
All of these bulk combing methods lead to good stretching of the DNA in the general direction of the flow, but due to random positioning and variance in orientation, stretched DNA often overlap. This overlap is easily seen in Figure 55 and, to a lesser extent, in Figure 56D. Machine vision processes that size individual molecules based on their total fluorescence intensity become extremely difficult to implement when the DNA overlap. Indeed, this was the motivation behind using small DNA droplets.554 While the DNA droplets work well for smaller clone fragments, they are insufficient for large fragments of genomic DNA. Since optical map assembly simplifies as the size of the DNA increases, analogous to the ease of genome assembly with long sequencing read lengths, it is worthwhile to develop a method for stretching very long DNA molecules without overlap.
The key to handling very large DNA is to use microfluidic channels to comb the DNA. DNA molecules align perpendicular to the dynamic contact line of an air-water interface.561 This effect can be exploited by using a set of microchannels in PDMS that are bonded to a “molecular combing” surface of silanized glass.560 By filling the DNA by capillary action, DNA near the glass surface attach and they are stretched by a mechanism similar to molecular combing. Figure 57 illustrates the power of this method using a variety of different sized DNA molecules. Importantly, this process allows much longer strands of DNA, including large genomic DNA, to be aligned and sized without overlapping.
Figure 57.
Surface stretching via microfluidic channels yields highly aligned DNA on the surface. (a) PDMS microchannel. (b–e) Montages of stretched DNA using adenovirus DNA (b), λ DNA 9c), RS281 DNA (d) and T2 DNA (e). (f–i) Magnification of small segments of images (b)–(e). Reprinted with permission from Ref.560 Copyright 2004 American Chemical Society.
We have focused so far on optical methods for measuring the length of the DNA on the surface because they are the fastest analysis methods. However, we should point out that a number of other approaches can be used to interrogate surface stretched DNA with higher spatial resolution than fluorescence microscopy. For example, molecular combing on mica permits DNA imaging by atomic force microscopy (AFM).562 Using fluid fixing methods, AFM images demonstrate extensions close to 95% of the full contour length of λ DNA without the influence of intercalating dyes.563 AFM imaging has also been used to evaluate the effects of surface derivatization,564 indicating that variations in silane deposition during surface silanization is the main cause for variability in biochemical activity on combed DNA. Surface stretched DNA can also be analyzed using secondary ion mass spectrometry.565 By bombarding the surface of combed DNA with a high energy Cs+ ion and collecting the sputtered fragments in a mass spectrometer, DNA can be imaged with a 50 nm resolution — well below the diffraction limit imposed by fluorescence microscopy.
The applications of single molecule DNA sizing on surfaces is proceeding at a rapid pace. Already work is being done on using barcoding-like methods on surfaces to study DNA methylation,566 analysis of DNA-RNA complexes to study transcription,567,568 and lab-on-a-chip devices for complete cell trapping, DNA extraction and molecular combing.569 We should also point out that surface stretching of DNA has moved beyond the problem of DNA sizing into methods that use DNA as a one-dimensional nanostructured template.570–573
7.2 Nanochannels
An alternative approach to stretching DNA by molecular combing is to confine the molecule in a channel whose characteristic size, D, is smaller than the bulk radius of gyration, Rg, of the chain. Unlike flow- or surface-stretching, no external forces are required for DNA to extend in such a channel; the molecule is stretched in its equilibrium conformation. Due to this stretching in confinement an appropriate measure of size is the fractional extension, 〈X/L〉, which we define here as the mean span of the DNA along the channel axis relative to its contour length. Because the molecule is in equilibrium, one can in principle make a continuous measurement of the genomic length of a single molecule as a function of time. In theory, this can lead to an arbitrarily precise measure of genomic length as the molecule can be repeatedly measured as it fluctuates due to Brownian motion about its equilibrium stretch.574 Of course, the time required to make such measurements depends on the fluctuations and their influence on the end-to-end distance correlation function, as well as the limits of photobleaching and the desired throughput of the device.
This technique for DNA sizing was first explored in the seminal paper by Austin and coworkers,575 where they fabricated 100 nm nanochannels using nanoimprint lithography and successfully measured the extension of a ladder of concatemers of λ DNA. Using de Gennes’ theory for confined polymers,51 which we will discuss shortly, they argued that the decorrelation (i.e. relaxation) time of the extension of λ DNA is on the order of one second. By employing this principle and making 20 measurements over the course of a minute, their fractional extension measurement of 〈X/L〉 = 0.38 has a resolution of about 150 nm (400 bp). Subsequent experiments576 explored DNA extension for a number of channel sizes, achieving larger fractional extensions (up to 0.75) with smaller channels and providing measurements of the end-to-end distance relaxation times as a function of channel size. However, the experimental results seemed to disagree with de Gennes’ scaling predictions.51
These apparent discrepancies between theory and experiment now appear to be resolved.577,578 In order to better understand the analysis that follows, we will briefly review the current understanding of the behavior of semiflexible polymers such as DNA confined in a tube. As we begin, we should disclose that the physics of confined DNA remains a very active area of research at the time of this review, and anything we say here on the cutting edge of the field will undoubtedly be dated well before the review is published. We also note that our viewpoint of confined semiflexible chains is certainly biased by our recent work in this field.578,579
Figure 58 shows our current understanding of the regimes of extension for a confined, semiflexible chain, such as DNA, based on Monte Carlo simulation results for DNA in nanochannels.578 In the weakest confinement (i.e., the largest channel size), the chain does not feel any effect from the walls and remains in its equilibrium, coiled conformation. For a self-avoiding chain, the size of the coil is Rg ≅ L3/5(wlp)1/5, where lp is the persistence length of the chain and w is the effective width of the chain. The former quantity reflects the length scale over which thermal energy can bend the chain, whereas the latter quantity captures the excluded volume interactions. As DNA is a charged molecule, the excluded volume interactions include the electrostatic contribution we discussed in Section 2.2, as well as a steric contribution. It is important to note that, in the context of confinement, we need to think about the flexibility of the chain as the ratio of its persistence length to effective width, lp/w. Since DNA has a ratio lp/w = O(10), it is semiflexible, which adds a layer of complexity to the analysis.579,580
Figure 58.
Qualitative sketch of the regimes of extension for a DNA chain as a function of the channel size D. The schematics show the qualitative models for the configurations of a confined chain. Adapted with permission from Ref.578 Copyright 2011 American Chemical Society.
The fractional extension in free solution, like other measures of polymer size, is a function of the chain length,
| (48) |
so the asymptotic value at infinite channel size in Figure 58 depends on the size of the chain. The schematic in Figure 58 is a generic result for a very long chain; if the DNA is too short, then it is possible to transition into the bulk behavior without experiencing all of the possible regimes of confinement.578
As the channel size decreases further, the chain begins to be squeezed by the presence of the nearby walls and thus its fractional extension begins to increase. The case of weak confinement was described over 30 years ago by de Gennes and coworkers,51,581 and this regime is commonly referred to as the “de Gennes” regime. Here, the chain is envisioned as a series of blobs of size D where the chain is self-avoiding within the blob. The corresponding fractional extension has the form
| (49) |
The particular scaling with the channel size D comes from using the Flory exponent for the excluded volume, ν = 3/5. If we use a more accurate result for the Flory exponent,54 ν = 0.5877, the scaling578 becomes 〈X〉 ~ D−0.7015.
In the opposite limit of very strong confinement, where D ≪ lp, Odijk582 envisioned the chain as a series of deflection segments. While we are focusing here exclusively on DNA, it is worthwhile to mention recent stunning videomicroscopy images of actin filaments583 that conclusively demonstrate the existence of this “Odijk” regime. Actin has a very large persistence length, so one can obtain a strongly confined chain using micron-sized channels. Odijk582 determined that the fractional extension has the non-power law form
| (50) |
where α is a prefactor. Gommper and colleagues584,585 have computed the parameter α (as well as the prefactor describing the fluctuations about the mean extension) to very high precision for both circular tubes and rectangular channels. We have found these calculations to be extremely useful in analyzing simulation data in the Odijk regime.167,578
For flexible chains, that is chains with lp/w = O(1), the Odijk and de Gennes regimes appear to be a sufficient description of the extension of the chain. However, as previously stated DNA is a semiflexible polymer. Monte Carlo simulations578 of DNA suggest the presence of two additional regimes between the de Gennes regime and Odijk regime when DNA is confined in a nanochannel. As the channel size decreases past the edge of the de Gennes regime, we enter a so-called “extended de Gennes” regime where the chain now looks like a series of cylindrical blobs that exist at the border between ideal and excluded volume subchains.586 The corresponding extension is the same as in the de Gennes regime,577,586
| (51) |
hence the moniker “extended” de Gennes. The predicted free energy in the extended de Gennes regime differs from the de Gennes regime,578 so we might expect to observe different dynamics in these two regimes even if the scaling law for the extension remains fixed.578
Between the Odijk and extended de Gennes regime, there exists yet another regime where it appears that the scaling for the chain extension follows the behavior578,587,588
| (52) |
The details surrounding this regime are not well understood, and we simply refer to it as a “transition” regime between the Odijk and extended de Gennes regime. Indeed, it is not even clear at this time whether the extended de Gennes and transition regimes are, in fact, regimes in the universal sense. To provide specific numbers, we summarize the fractional extension scaling regimes as well as the currently understood regime limits for a “long” piece of DNA in a high ionic strength buffer in Table 5.
Table 5.
Channel sizes of regimes of confinement for DNA in a high ionic strength buffer. The values in this table are based on 5 × TBE buffer (165 mM), with the persistence length lp = 50nm and an effective width w = 4.7nm.92 For λ DNA, the radius of gyration is Rg = 0.73 μm.62
| Regime | 〈X/L〉 | Channel Size |
|---|---|---|
| Bulk | L−2/5 | D > Rg |
| de Gennes | D−0.701 | 530nm < D < Rg |
| Extended de Gennes | D−0.701 | 100nm < D < 530nm |
| Transition | D−1 | 50nm < D < 100nm |
| Odijk | Eq. (50) | D < 50nm |
From the analysis of the physics of confined DNA, it is clear that we would like to be in the Odijk regime in order to maximize stretching and obtain the most sensitive measure of genomic length. Stretching in the Odijk regime will also insure that we have no hairpin folds and that we are able to resolve site-specific probes with maximum accuracy.167 If we are in the Odijk regime, theory and empirical evidence suggest that the maximum resolution of a single measure is on the order of 1 kilobase pair.167,574
This means, of course, that we would like to have the smallest channels possible, which was exactly the course that was initially pursued. There are however two engineering challenges that needed to be overcome in order to put DNA into channels in the Odijk regime. First, nanochannels that are sufficiently small must be fabricated, and second, DNA must somehow be loaded into these channels. These engineering hurdles were solved589,590 using the device design illustrated in Figure 59. Channel sizes down to 10 or 20 nm (see Figure 59a) were created by nanoimprint lithography and subsequent non-uniform depositions by electron-beam deposition and sputtering techniques. In order to load DNA, the steep entropy gradient at the interface of the nanochannel needs to be smoothed. This was accomplished by rows of increasingly dense posts at the interface of the channel (see Figure 59b). In addition, by using diffraction gradient lithography, the floor of the microchannel is gradually raised to meet the nanochannel’s reduced height.
Figure 59.
Device design for loading DNA into channels in the Odijk regime. (a) SEM micrograph of 85 nm nanochannels made by nanoimprint lithography that are subsequently thinned to channels on the order of 10 nm. The scale bar is 500 nm. Also included is the diffraction gradient lithography schematic (right), showing the gradual slope change approaching the nanochannels. (b) Schematic of microchannel-nanochannel interface (top), and fluorescence micrograph of the loading process. Adapted with permission from Ref.589,590 Copyright 2002 American Institute of Physics.
To date, the nanofabrication challenge to make channels smaller than 50nm — and thus in the Odijk regime — has been met by a number of methods. Many of the techniques use direct-write nanolithography methods such as electron-beam lithography591–593 or focused ion-beam milling594–599 to pattern the nanochannel lines. Direct write techniques are inherently serial and relatively expensive, so they are limited in the number and lengths of channels they can produce. However when combined with nanoimprint lithography for pattern transfer, only a single master needs to be produced. Nanoimprint lithography has thus become a powerful and popular method to replicate nanochannels,590,592,593,599–604 and in one case, even to seal them.605 These direct-write techniques are also sometimes coupled with sacrificial materials,591,603 which obviates the need for bonding to seal the channels. If one is fortunate enough to have some discretion in the exact size and number of channels, there are even some commercially available (e.g. LightSmyth, NILT) stamps that may be used as a master for nanoimprint lithography.
Nanometer resolution direct-write methods are not the only available methods for pattern creation. A popular alternative are nanoscale sacrificial materials that can be subsequently etched away to form the nanochannels. Examples include electrospun polymer fibers,606,607 silica nanowires608 and even molecular combed DNA.609 In addition to clever implementations of sacrificial materials, micromachining610,611 and side-etching of SiGe612 have also produced nanometer scale channels. Another broad class of techniques uses stress-induced deformation to reach nanometer lengths. This has been done by heating and applying tensile forces to polycarbonate microchannels,613 and laser-assisted pulling of silica capillaries.614,615 There also exist a variety of methods based on creating nanometer scale cracks616–618 or folds619 on the surface of an elastomeric material (e.g. PDMS or polystyrene). One variant on this theme capitalizes on the collapse of larger PDMS slits to obtain nanometer scale channels,620 while another uses the nanoscale space between a PDMS sheet and a hard step.621 On top of the flexibility in the fabrication aspects, elastomeric materials have also shown unique properties as nanochannels. For instance, Huh et al.616 demonstrated the ability to dynamically tune the size of nanochannels by stress-induced deformation leading to altered transport properties.
In addition to the widespread use of nanoimprint, sacrificial materials, pulling, and surface defect techniques, there are a number of less widely used techniques of obtaining nanoscale channels. These include interferometric lithography,352,590,622 injection molding,623 inorganic nan-otubes,624 porous alumina membranes625 and some unconventional combinations of lithography techniques.601,626 There are also techniques that shrink larger channels by deposition or oxidation.590,602,627
While it is now possible to fabricate and seal very small channels, one still needs to load the DNA for the stretching experiment. In our review of the literature, we identified two groups that have managed to produce channels smaller than 10 nm,598,602 but neither group reports loading DNA into channels of that size. However, several studies successfully report loading DNA into channels smaller than 50 nm,114,576,601,602 but doing so remains a non-trivial task.
The Odijk regime582 is defined by a channel size that is small compared to the persistence length of the chain, D ≪ lp. If one increases the persistence length of the DNA, then it should be possible to work with even larger channels. The key here is to exploit the ionic strength dependence of the physical properties of DNA608,628–630 that were discussed in Section 2.2. In particular, we recall from Figure 5 that the persistence length increases dramatically as the ionic strength decreases due to unshielding of electric charges along the DNA backbone.90,93–95 If we consider a low ionic strength buffer such as 0.02× TBE, as shown in Table 6, we see that channel sizes on the order of 100 nm are in the Odijk regime. It is also interesting to note that when the ionic strength is raised, the effective width increases significantly and the local monomer anisotropy (lp/w) decreases. This decrease in anisotropy leads to the decrease or disappearance of transition regimes between the Odijk and de Gennes regimes.
Table 6.
Channel sizes of regimes of confinement for DNA in a low ionic strength buffer. This table corresponds to 0.02 × TBE buffer (ionic strength = 0.57 mM),92 where the persistence length is lp = 107 nm and the effective width is w = 73 nm.
| Regime | Channel Size |
|---|---|
| Bulk | D > Rg |
| de Gennes | 157nm < D < Rg |
| Odijk | D < 107nm |
The low ionic strength approach led to much higher fractional extensions, up to 0.82 ± 0.03 in 50 nm channels and 0.46 ± 0.02 in 200 nm channels.628 One of the challenges is that the anti-photobleaching agents contribute to the ionic strength of the buffer.92 Removing these agents permits ionic strengths as low as 0.05 mM and fractional extensions as high as 0.86 ± 0.087 in 250nm × 250nm PDMS nanochannels.630
Along these same lines, the addition of inert crowding agents, such as the polysaccharide dextran, have also shown to affect the extension of DNA in nanochannels.631,632 This is interpreted as a depletion interaction, where the effective size of the channel is reduced due to the volume fraction of the dextran molecules. However, the over-extension behavior only continues until a threshold concentration is reached, after which the DNA molecule condenses into a globule. Crowding has produced fractional extensions of approximately 0.5 for a 150 nm × 300 nm channel.631 However, the details of these interactions are not well understood, and practical devices for measuring genomic distance have not employed the molecular crowding technique.
Given that we can fabricate channels and successfully load DNA, we are still left the question of how to actually do the sizing. In Section 7.1, we remarked that a key advantage of optical mapping is the measurement of ordered restriction fragments of single molecules. However, because optical mapping relies on molecules statically fixed to a surface, an ensemble of molecules must still be used to reduce the measurement error and to account for inhomogeneous stretching and strand breaks.574 Nanochannel confinement attempts to go one step further by providing a method to make multiple measurements of the same molecule.
The first attempt to do this applied the most straightforward idea — cut the restriction fragments in the channel and measure the size of each fragment,574 analogous to the gel-based method102 that we saw in Figure 8. The main challenge of this method is to separate the stretching and cutting steps. In the gel system, the approach is straightforward since the Mg2+ can be added at any time. In the microfluidic system, this was accomplished by separating the DNA/restriction enzyme solution from the cofactor Mg2+ by establishing a Mg2+ gradient across the nanochannel using the device in Figure 60a. Here, a microchannel (a) is loaded with the Mg2+-rich buffer and the other microchannel (b) is loaded with DNA and the restriction enzyme. The Mg2+ gradient is thus set up across the nanochannels (c). DNA molecules, pre-decorated with bound enzyme, enter the channels, where they are stretched and subsequently react when exposed to sufficient concentrations of cofactor. Upon reaction the DNA molecule is cleaved and the two fragments are free to diffuse independently as seen in Figure 60b.
Figure 60.
(a) Schematic of nanochannel device for ordered restriction mapping. Note the separate locations for loading the DNA and loading the restriction enzyme co-factor Mg2+. (b) Time-resolved restriction maps of single PacI cut of a 61 kbp DNA PAC insert. Adapted with permission from Ref.574 Copyright 2005 National Academy of Sciences of the U.S.A.
Restriction mapping in this way suffers from the need to do the restriction chemistry in the nanochannel, which adds significant complexity. As we mentioned in Section 3.2, it is much simpler if sequence-specific markers are incorporated to the backbone of the DNA molecule prior to loading. Additionally, increased resolution can in principle be realized by the ability to do sub-diffraction-limit positioning of fluorescent labels.13,117 However, the resolution is still limited by the ability to minimally resolve the individual labels.167 This group of methods, collectively named DNA barcoding, has been performed (not necessarily in conjunction with nanochannels) using a variety of labels including peptide nucleic acid probes,115 nicking/fluorochrome-labelled nucleotides,629,633 quantum dots,634 nick-flap probes113 and a methyltransferase directed method.13 These labels can be applied using standard techniques prior to the introduction of the polymer into the channel.
Instead of labeling the polymer backbone before loading, Reisner et al.635,636 capitalized on the fact that local DNA denaturation is sequence dependent and that the fluorescence intensity of intercalating dyes is highly dependent on the double-stranded state of DNA. Thus by addition of formamide and gentle heating, they obtain sequence-dependent barcodes without the addition of probes. Moreover, they can capture the structure of the experimental barcodes by statistical mechanical calculations using the local melting probabilities and optical point-spread functions. Examples of the intensity profiles of both melt-mapping and barcoding are shown in Figure 61.
Figure 61.
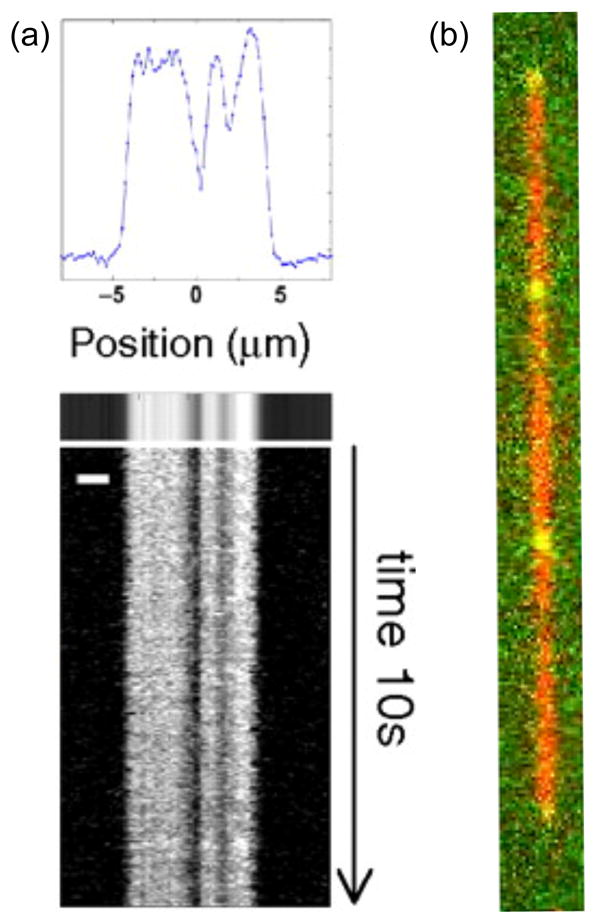
(a) Local melting maps (scale bar is 2 μm) for λ DNA at 28°C. Adapted with permission from Ref.635 Copyright 2010 National Academy of Sciences of the U.S.A. (b) DNA barcoding showing two colors, one for the backbone dye and a second for the internal probes. Adapted with permission from Ref.633 Copyright 2011 Su et al. and subject to the Creative Commons Attribution License.
We conclude our discussion of nanochannel stretching with a brief overview of ongoing work in the field. It appears that much of the basic knowledge for nanochannel stretching has been developed, including basic fabrication techniques, equilibrium behavior, and proof of principle devices. That being said, there are still some major gaps in our understanding — transition regimes in nanochannels being a notable example.578,633 However, the platform now exists for further fundamental research exploring dynamics and the effects of external fields on compression and extension of DNA in a nanochannel by an external electric field,637 as well as the relaxation of DNA in channels638 and near channel entrances.639 We will also explore highly non-equilibrium process for sizing by fluorescence burst analysis640 in Section 8.4. The role of entropic elasticity in confining geometries and under external fields is of central interest in this analysis, which has also held the attention of theorists.641,642
In addition to fundamental research, the field is also open to a second generation of devices. Tapered nanochannels643,644 offer one such example. Here, a slowly varying channel size is used as a type of “confinement spectroscopy” to study the effect of the entropic force on the extension of DNA. The use of tapered nanochannels has allowed a facile replication of the pioneering experiments on the extension of DNA.576 Other new devices are widening the scope of the technology to include a broader range of biological applications, such as epigenetic analysis.134,645 In this vein, Lim et al.134 studied a DNA methylation technique with concatemers of λ DNA. Methylated and non-methylated strands of λ phage DNA were annealed and placed in a nanochannel with a fluorophore-tagged methyl-CpG-binding domain protein fragment. This creates a barcode of methylation sites and the methylation profile can be obtained by fluorescence microscopy with a resolution of approximately 10 kbp.
7.3 Nanoslits
In the last section, we focused on quasi-1D confinement, i.e. nanochannels. By relaxing the constraint of nanoscale size in one dimension we get quasi-2D confinement, i.e. nanoslits. In the literature the somewhat arbitrary distinction between a nanoslit and a nanochannel is hazy and often the term “nanochannel” is used for any slit or groove with one dimension less than a micron in size. However, a nanoslit is most often referred to as a channel with a large aspect ratio (width to height), of the order of 10:1. While this colloquial definition is adequate for organizational purposes, we believe a more technical definition is appropriate. For a polymer chain to be in true quasi-2D confinement, we need the slit walls to be wide enough so that the polymer is not confined in the plane of the nanoslit. This is best illustrated by Figure 62, where we see three different channels of varying width W and the same depth (out of the page). The true quasi-2D confinement is illustrated on the right with the polymer chain manifesting an in-plane radius of gyration, R|| < W. At some critical width, the slit becomes narrow enough that W = R||. For slits below this confinement, the polymer is confined in a high-aspect ratio nanochannel.
Figure 62.
Polymer confinement in a nanochannel (left), high-aspect ratio nanochannel at the critical point where the slit width, W, equals the in plane radius of gyration (center), and a slit with true quasi-2D confinement (right). In this image, the chain is strongly confined in the direction perpendicular to the page.
Nanoslit research had a more nebulous beginning than nanochannel research, possibly due to the relative simplicity of fabrication. One of the earliest papers on nanoslits37 looked at DNA unhooking times as a function of slit height to test the electrohydrodynamic equivalence principle.523 As part of this study, they observed that relaxation time of T4 DNA changes in slit heights ranging from 5 μm to 90 nm. We have also seen the utility of slits for separations in the entropic trapping device150,181–183 in Section 6.1.2 and extreme confinement449–451 in Section 6.3, and we will see work on DNA stretching in slits combined with fluorescence burst analysis115 in Section 8.4. By the mid-2000’s, DNA stretching in nanofluidic devices had become a problem of interest, and work on slits in this vein began more earnestly. Much of the work in nanoslits initially focused on fundamental polymer physics, perhaps because it was not initially clear how slits could be effectively used to stretch DNA for genomic applications.
Two problems in particular have occupied fundamental studies of the polymer physics in nanoslits, namely the thermodynamic problem (i.e. the equilibrium extension of the polymer with or without external fields and forces), and the dynamic problem (i.e. diffusive behavior and relaxation times). Just as is the case with nanochannels, the physics of DNA in nanoslits is important for our understanding of the current applications for DNA sizing. Accordingly we will briefly review the current understanding of these systems. In particular we will review the equilibrium case with no external fields, however when we need more detail for a specific method or device, we will elaborate further.
Unlike the case with nanochannels, where a pioneering experiment challenged the existing scaling theory, the investigation of the polymer physics of slits mostly confirmed the blob theory of de Gennes.577,646–648 In this regime, the chain is compressed by the walls into compression blobs on the order of the slit height, H, and the blobs form a two-dimensional self-avoiding walk that gives rise to an in-plane fractional extension92
| (53) |
Note that a qualitative difference arises in slits due to the fact that an increase of chain length decreases the local volume fraction of the chain.649 Thus, the fractional extension decreases with increasing chain length, 〈X〉/L ~ L−1/4. The latter scaling contrasts sharply with the case for nanochannels, where the extension is linear in the contour length, i.e., 〈X〉/L ~ L0. This fact, which has been verified by experiment,650 has at least two practical implications for stretching DNA in slits. The first, and more obvious fact, is that slits will not stretch as well as channels for a given minimum confinement dimension. The second is that since the extension does not scale linearly with the polymer size, DNA apparent length is a less useful measure of genomic distance. This does not preclude the use of integrated fluorescence intensity to measure the size of a segment of the chain. This is the method of choice in a slit,629 since the total integrated intensity does not change if the chain backfolds on itself. In the case of slits, stretching enables the use of barcode markers, which can then be used to assemble ordered maps by measuring the genomic distance between markers by cumulative fluorescence intensity.
Let us now consider the equilibrium regimes of nanoslit extension. By decreasing the slit height, the amount of chain per blob decreases. At some point, the chain can no longer form isometric blobs. The nature of this transition was studied by a pair of conflicting experimental studies by Bonthuis et al.651 and Tang et al.169 The former study suggested that the transition was sharp, and that the chain behavior quickly entered an Odijk regime. The latter study instead observed a broad transition over a large range of chain extensions, but did not observe an Odijk regime.
By coupling this information with several simulation studies,578,652,653 Dai et al.648 provided a comprehensive look at the equilibrium behavior of DNA in nanoslits that seems to resolve the controversy. These simulations648 showed a broad transition, due to an additional blob regime, as well as two distinct deflection regimes. For slits slightly smaller than the minimum value required for the de Gennes regime, excluded volume interactions cause the chain to swell axially. The confined chain thus forms “pancake blobs” with an in-plane diameter larger than the slit height. This is the “extended de Gennes” regime in a nanoslit, analogous to its counterpart in nanochannels.578 In the extended de Gennes regime, the polymer exhibits the fractional extension given in Eq. (53).
Decreasing the slit height further so that blobs can no longer be formed (strong confinement) provides the onset of the lesser confined of two Odijk regimes.577,648 In this “self-crossing regime,” the DNA molecule has enough space to experience excluded volume interactions. Below a critical slit height, the molecule can no longer cross itself and enters the strong confinement limit in a “non-self-crossing” Odijk regime. In the non-self-crossing regime the fractional extension is
| (54) |
where f is a complicated dimensionless function of the slit height and the effective width.648 A summary of the four regimes of quasi-2D confinement is shown in Figure 63.
Figure 63.
Four regimes of confinement in a nanoslit648 that appear to explain the existence of a broad transition169 in slit extension from the classical de Gennes regime to the Odijk regime. Adapted with permission from Ref.648 Copyright 2012 Royal Society of Chemistry.
Given that we understand the basic physics of DNA confinement in nanoslits, we are ready to examine devices for DNA stretching. Since slits do a relatively poor job of stretching polymers because of the dimensionality of the geometry, something must be done to enhance stretching. As we discussed in the context of nanochannels,628 one can increase the stretching in a nanoslit629 by decreasing the ionic strength of the system, and thereby increasing the persistence length of the polymer. By using a 100 nm × 1 μm slit, Jo et al.629 obtained a fractional extension of around 0.6 for λ and T4 DNA. As mentioned previously, the genomic distance was obtained using the integrated fluorescence intensity. By nicking and fluorochrome labeling specific sites, they629 also obtained ordered maps similar to the DNA barcodes we saw in Figure 9.
Note that while nominally a slit, the latter device is better characterized as a high-aspect ratio (10:1) nanochannel for the reasons discussed earlier. Indeed, in addition to the DNA mapping applications, this study629 included the derivation of an expression for the fractional extension of a long chain in strong confinement (Odijk regime),
| (55) |
where H is the slit height, and W is the slit width. It is worth remarking that the fractional extension is not a function of the polymer length [compare to Eq. (54)], revealing the fact that we are not in quasi-2D confinement.
One of the main advantages of the 100 nm × 1 μm slits is that they can be made in PDMS,629 something that is not often possible when working with such small scale devices. When attempting to make nanoscale features in PDMS, large aspect ratio structures often collapse. If we want to realize the scaling for quasi-2D confinement behavior in Eq. (54) in a PDMS channel, slit collapse may become a significant problem. To some extent, the problem of channel collapse is reduced by adding a glass support to the back of the PDMS,654 which allows the use of much wider slits (on the order of 100 μm).
The choice of slit material brings up the question of different methods of fabrication of nanoslit devices, for which various techniques exist. The most conventional is through the use of a shallow etching step followed by fusion bonding or anodic bonding for glass or silicon devices.655 Using bonding techniques, one can routinely get sub-100 nm slit heights and even down to an impressively small 2 nm slit.656 There is also work on integrating electrodes into the nanoslit.657 Other techniques beyond “etch and bond” have also been explored, including photolithography with sacrificial materials,658 high-precision micromilling and thermoplastics,659 microcontact printing660 and a novel “nanoglassblowing” technique.661
Nanofluidic devices feature very high surface to volume ratios. As a result, it is possible to enhance the stretching of the DNA through adsorption to the surface. For example, DNA was attracted to the corners of the device and subsequently assumed highly elongated conformations (〈X〉/L ≈ 1) in 0.35 mM Tris HCl.662,663 The stretching was mostly independent of slit height below a threshold size (100 nm), but the fractional extension increased dramatically upon lowering the ionic strength. This is a strange observation, considering that both the walls of the device and the DNA are negatively charged. While direct evidence is sparse concerning the exact mechanism of adsorption, it seems that dielectrophoresis may play a role; the DNA is animated in the device by electric fields, which may exhibit strong gradients due to the small radius of curvature of the walls at the slit corners. Lin et al.664 have verified this stretching behavior and noted a definite transition from quasi-2D to quasi-1D chain conformation statistics, but were unable to further explain the mechanism of adsorption or stretching. This study664 also reported DNA adsorption to posts in regular post arrays such as those discussed in Section 6.1.1. Owing to the post attraction, electrophoretic dynamics are also qualitatively different from the more common hooking collision dynamics. That being said, given the state of understanding of DNA adsorption phenomena, it appears that more fundamental work is needed before a useful device can be made.
Slits have also been combined with indentations (pits or groves) where the trapping occurs by simple electrostatic attraction and repulsion665 or by entropy,379 as shown in Figure 64. Here, due to the free energy landscape dictated by entropic and excluded volume interactions, DNA is attracted to the nanopits and single-pit or multi-pit occupancies can be stable equilibrium states depending on the nanopit array geometry parameters.379 In addition, by exerting forces such as a pressure driven flow, one can obtain long-lived metastable states where the molecule remains stretched across two pits for several minutes.379 In some cases, λ and T4 DNA stretch between two pits with fractional extensions similar to that in a 100 nm × 100 nm channel.379,576
Figure 64.
Schematic of the (a) chip design and microchannels and (b) nanoslit and nanopit array for a nanopit entropic trap. Adapted with permission from Ref.666 Copyright 2012 American Chemical Society.
DNA exhibits complicated dynamics during the transport in nanopit arrays.374,380,666 For instance, pressure driven DNA transport proceeds by thermally activated hopping, similar to entropic trapping (Section 6.1.2) when the polymer occupies a single pit in equilibrium.380 However, when the polymer occupies multiple pits at equilibrium, its transport is characterized by a “spooling” behavior due to the lack of a free-energy barrier for pit-to-pit transport. Properly quantifying the dynamics of DNA in nanopits requires an accurate accounting for the hydrodynamic interactions.667 Brownian dynamics simulations combined with a General Geometry Ewald-like Method for the polymer hydrodynamics in confinement667 suggest that two types of regimes exist: a stochastic low-Péclet number regime and a deterministic high-Péclet number regime.
In the absence of an electric field or pressure driven flow, the DNA trapped in the pit can still undergo diffusive behavior.666 From a physical standpoint, this motion requires thermal activation to an excited state above the ground state, which involves transfer of contour length between pits, before relaxing back to the ground state of equilibrium pit occupancy. Interestingly, the diffusion shows a non-monotonic dependence on the pit spacing due to the quantized nature of the pits.666 In other words, the diffusion has a local minimum when the average occupancy of DNA in a nanopit is near an integer number because the polymer can assume a more stable ground state. In the nanopit systems, it appears that even though stable or metastable stretched states are possible, practical devices implementing these ideas for measuring a genomic length have not yet been made.
A substantial amount of work has been done to understand the physics of DNA in nanoslits. Yet, very few nanoslit devices seem able to produce the high-throughput type of stretching needed for efficient DNA sizing. Indeed the most practical device, made by the Schwartz group,629 is not truly quasi-2D confinement, but rather a high-aspect ratio nanochannel in a low-ionic strength buffer. It appears that a quasi-2D geometry is simply not amenable to strongly stretching long DNA chains.
7.4 Steady Flows and DC Electric Fields
We now turn our attention to non-equilibrium stretching of DNA in flows. The deformation of polymers in flow fields has a long history in the context of non-Newtonian rheology.251 At the outset, we will focus on the extension of a single DNA molecule in a planar elongation flow, which has the velocity field251
| (56) |
where ij is the unit vector in direction j. The quantity ε̇ is the elongation rate, which has units of inverse time. With our particular choice of coordinate system, this flow features compression along the x-axis and extension along the y-axis, as illustrated in the inset of Figure 65. The key kinematical feature of an extensional flow is that the distance l between two nearby fluid particles on the y-axis separated by some initial displacement l0 grows exponentially in time, l = l0eε̇Δt.
Figure 65.
Fluorescence microscopy images of λ DNA stretching in an extensional flow with an extensional rate ε̇ = 0.86 s−1. The images are spaced at 0.13 s intervals. The dynamics of the stretching depend strongly on the initial conformation of the chain, which is sketched at the left hand side of the image. The inset is a schematic image of the extensional flow in a cross-slot channel. Reprinted with permission from Ref.668 Copyright 1997 American Association for the Advancement of Science.
In fluid mechanics, one standard approach to create a planar extensional flow is to use the cross-slot geometry in Figure 65 where the fluid flow enters from the two sides and exits to the top and bottom. At the center of the cross slot (i.e., x = 0 and y = 0), there is a stagnation point with zero velocity. The idea behind DNA stretching in extensional flows is to trap the DNA at the stagnation point and then observe its extension in the y direction. One of the challenges in the experiment is maneuvering the molecule to the stagnation point and then correcting for any drift of the chain during the experiment.669 A particularly clever solution to the problem uses a two-layer PDMS device with a so-called “Quake” valve670 to control the fluidic resistance of one of the outlet channels.671,672 Schroeder and coworkers671,672 have developed an automated videomicroscopy protocol to dynamically trap particles at the stagnation point by controlling the valve pressure in response to the particle position.
The relevant dimensionless number for describing the extension of the DNA in an elongational flow is the Deborah number,251
| (57) |
where τ is the longest relaxation time of the chain. The relaxation time depends on a number of factors, most notably the molecular weight of the chain.673 For short chains, where hydrodynamic interactions are negligible, the relaxation time is predicted from the Rouse model to have the scaling τ ~ L2. In longer chains, the hydrodynamic interactions between different segments of the chain affect its relaxation, leading to a scaling τ ~ L3ν, where ν is the Flory exponent. In some of the systems we will encounter, the chain will be confined inside a small enough channel where we cannot neglect the hydrodynamic screening caused by the walls (which reduces the hydrodynamic interactions between segments of the chain) or the additional friction due to the presence of these walls. The relaxation time is often measured in a separate experiment to determine the Deborah number in the flow. We should also note that there appear to be two separate time scales characterizing the relaxation of a highly extended chain in a slit.674 The first relaxation time is related to the formation of blobs, followed by a second one related to the relaxation of the chain of blobs.
Much of the work in this subsection is motivated by a series of seminal papers from Chu and coworkers36,668,669,675 and the corresponding simulations676–679 that helped flesh out the details of these experiments. To a large extent, the goal of these experiments was to use fluorescently labeled DNA as a model polymer for testing the theories of polymer deformation in a shear flow, as opposed to using the extensional flow as a method to size the DNA. As we will see shortly, it did not take long for others to recognize the potential of extensional flows for DNA sizing.
Figure 65 shows a classic image of the dynamics of DNA extension in a cross-slot flow as a function of time. The DNA is trapped at the stagnation point (red dot in the inset) and, under the flow, the DNA is extended in the y-direction. Recently, a similar cross-slot flow device was used to stretch designer sequences of single-stranded DNA that act similar to flexible polymers.680 Single-stranded DNA is considerably more flexible than double-stranded DNA, so its persistence length to effective width ratio should be lp/w ≈ 1. As a result, it is reasonable to expect that single-stranded DNA stretching experiments will correspond more closely with the predictions for flexible chains,580 such as the classic theories by de Gennes.51 Likewise, by comparing the data for single-stranded DNA to data for double-stranded DNA, the role of the semiflexibility should become apparent. While these single-stranded DNA experiments are in the early stages, we expect that they will shed considerable light on the impact of the semiflexible nature of double-stranded DNA.
The initial condition of the chain plays an important role in the eventual extension. Since it is difficult to discern the details of the configurations from the experimental data, due to the diffraction limited optics, simulations676–679 can play an important role. In the context of the data in Figure 65, simulations676 of the same system showed that the critical feature is the location of the center of mass of the chain relative to the ends of the chain; when the center of mass is upstream from both ends of the chain, it leads to folding 94% of the time. de Gennes681 described the dependence of the chain dynamics on the initial configuration as “molecular individualism.” From a DNA sizing standpoint, the existence of this individualistic behavior is a critical problem since the measured length of the chain would seem to depend on its initial configuration unless one waits a long enough time to remove all of the folds. In Section 8.4, we will explore the numerous approaches that have been proposed to suppress molecular individualism through “preconditioning” of the chain prior to the extensional flow.
If the Deborah number is large, it means that the rate of extension by the flow exceeds the rate at which the DNA relaxes due to thermal motion. In order for the DNA to be extended in the flow, the elongation rate needs to exceed some critical threshold, which is referred to as the coil-stretch transition.51 One of the major successes of the original series of experiments by Chu and coworkers36,668,669,675 was the proof of the hysteresis in this coil-stretch transition.669 These were Herculean experiments, requiring enormous DNA molecules (yeast genomes, 1.3 to 1.7 mm in contour length) and extraordinarily long residence times at the stagnation point (hours) to ensure that the DNA accumulates sufficient strain to actually become extended.
There are a pair of proof-of-principle examples where a cross-slot flow is used for restriction mapping. In the first example,682 the DNA was mixed with fluorescently labeled EcoRI restriction enzymes in the absence of Mg2+, so that the enzyme does not have cleavage activity. A decorated DNA molecule is then trapped at the stagnation point; at De = 3.9, the DNA extends to 88% of its contour length and the location of the restriction fragments can be measured to within 5 kbp accuracy. While this proof-of-principle experiment is encouraging, creating a library of fluorescently labeled restriction fragments is a technical challenge. In the subsequent example,683 the decorated DNA arrived through one of the entry channels and a stream containing the Mg2+ arrived through the other entry channel. When the DNA is immobilized at the interface by the stagnation point, it stretches in the flow. The presence of the Mg2+ leads to cleavage of the DNA, and the location of the cleavage point is measured by fluorescence microscopy. In many respects, this experiment is analogous to the original optical mapping papers in molten agarose102 that we saw in Figure 8 and the pioneering nanochannel restriction experiment574 in Figure 60. In principle, one should be able to use dynamic control of the flow, e.g. the device from Schroeder and coworkers,672 to capture one of the cleaved segments and observe the next reaction.683 It remains to be seen whether restriction mapping in a cross-slot is a viable method for routine use. For the moment, its main advantages lie in studying the kinetics of an enzymatic reaction683 or DNA compaction684 rather than as a high-throughput sizing method.
Fluid flow in a cross-slot is a classical approach to creating an extensional flow in rheology, and thus can stretch neutral polymers and polyelectrolytes such as DNA. Since DNA is charged, it is also possible to stretch it using an extensional electric field, which we can think of as an electrophoretic “flow” field with velocity v = μE. Indeed, the idea of thinking about an electrophoretic velocity field proved extremely useful in understanding the role of the finite size of a post on the collision processes governing sizing in the post array.38,327
Perhaps the most straightforward approach to create a stagnation point in an electric field is the T-junction setup in Figure 66.685 The location of the stagnation point is controlled by the electric potentials at the three arms of the microchannel; by grounding the inlet arm, the extent of the flow into the outlet arms is easily controlled by a pair of power supplies. Indeed, Tang and Doyle reported that the DNA is easily trapped within the stagnation point simply by manual control of the potentials.685 The stretching here is substantial, reaching around 70% at De = 3.0. The extensional flow only exists near the channel junctions, since the electric field lines must be straight far from the junction. Nevertheless, it is clear that one can obtain substantial stretching using an electrophoretic flow field. For example, Figure 66 shows the 94% fractional extension of a concatemer of ten λ DNA molecules. The rate of the stretching is also reasonably quick, with the sequence of images corresponding to 4 seconds of video.
Figure 66.

Images of the stretching of a 10-λ concatemer (485 kbp) in an extensional electric field created at a T-junction. The images are separated by 0.33 seconds. The inset is a schematic of the T-junction, with the stagnation point indicated by the circle. Modified with permission from Ref.685 Copyright 2007 American Institute of Physics.
We can also take advantage of the confinement effects discussed in Section 7.3 to further enhance the stretching.686 Using a 300 nm nanoslit, the fractional extension of the chain at a cross-slot reaches almost 50% at De = 1.0. There is clear evidence that the confinement leads to improved stretching of the chain (at the equivalent Deborah number) when compared to the 2 μm slit used in Figure 66,685 with the ability to reach around 70% extension at fairly low strain rates. The enhanced stretching due to confinement can be explained entirely by the existence of a longer relaxation time in the confined channel.674 DNA relaxation in nanoslits has also been directly studied in some detail, including both experiments37,169,651,674,687,688 and simulations.689–691 However, the details surrounding the longer relaxation time in a slit remain a subject of some debate. While examining the coil-stretch transition in cross-slot devices, Tang et al.688 suggested that the source of the two distinct relaxation times may come from the way in which DNA force-extension behavior is modified by slit confinement. A recent simulation study692 has suggested however that a simple generalization (using the equilibrium stretch at zero force) of the Marko-Siggia interpolation formula in Eq. (1) describes the polymer behavior well. Another simulation of relaxation times suggests further that the inclusion of excluded volume interactions is essential in order to qualitatively reproduce the two-relaxation-time feature that characterizes DNA relaxation in slits.691 On top of this, the diffusion behavior of DNA in slits is not completely understood and has yet to be comprehensively explained. Both the effects of hydrodynamics on the diffusion and relaxation of DNA in slits and the role of confinement in the force-extension behavior of DNA remain active areas of research.692–694
Thermophoresis is another possible approach for stretching DNA by flow.695 Thermophoretic flows are driven by temperature gradients in a fluid. When a laser locally heats the fluid near a DNA molecule, the chain stretches around 35% to 45%. While DNA manipulation by thermophoresis is an emerging area,696–698 including in the context of separations,699 thermophoretic stretching has not been explored in much detail.
All of the methods that we have discussed so far have a relatively low throughput. For example, the electrophoretic stretching in a T-junction685 has an apparent throughput of around 100 kbp/s. Moreover, in methods requiring a stagnation point, there are many molecules that pass through the junction without being trapped at the intersection. Indeed, even when one molecule is trapped at the stagnation point, there may be other molecules that pass through the junction while the first molecule is being observed. From an analytical standpoint, it would be desirable to (i) analyze every molecule as it passes through the stretching region and (ii) do so in a high-throughput, automated manner. We will revisit this topic in Section 8.4, when we review combinations of DNA stretching with fluorescence burst analysis.
7.5 Unsteady Flows and AC Electric Fields
Steady extensional flows are not the only way to enhance DNA stretching in flow. It is also possible to achieve reasonable stretching by using an oscillating, pressure driven flow field.700,701 The pressure driven flow in a channel leads to shear, which can produce tumbling of the DNA molecules as well as extension. One of the most interesting features of polymer solutions in a shear flow is the tendency for the chains to migrate away from the walls and toward the center of the channel,702 which is now understood from theory to be an effect of hydrodynamic interactions between the chain and the wall.703 In the context of DNA stretching, the drift towards the center of the channel simplifies the imaging in a relatively wide channel by removing the challenge imposed by the limited focal depth of the high numerical aperture objectives normally used to visualize DNA.700 However, the high shear rate required for stretching blurs the DNA.701 If the pressure driven flow is driven by a syringe pump, the pumping mechanism and the compliance of the microchannel/tubing provide a clever solution to the blurring of the image in flow. When the flow is reversed, the screw driving the piston needs to reverse and there is a brief period (around 50 ms) when the flow in the channel ceases. Using fairly large microchannels with a 40 μm × 40 μm cross section, it is possible to observe fractional extension around 50% during the brief flow cessation.
Let us now turn our attention to unsteady “flows” created by ac electric fields. Remarkably, strong DNA stretching has been observed in ac electric fields generated in simple channel geometries containing entangled polymers. At first glance, this behavior may be surprising since, in typical gel or capillary electrophoresis, there are no electric field gradients because gels and entangled polymer solutions allow the ions to move freely through the system. As a result, there is no extensional component of the electrophoretic “flow.” Nevertheless, DNA can be highly extended in an ac electric field when the DNA are immersed in an entangled network of high molecular weight linear polyacrylamide (700,000 to 1,000,000 Da).704–706 The mesh size of an entangled linear polyacrylamide solution is estimated to be around 2 nm,704 which is similar to the DNA backbone width and much less than the persistence length. The DNA is thus very strongly confined in this system, but the confinement itself is dynamic.27
The DNA stretching in this system is divided into four different regimes705 as a function of the frequency of the ac electric field. At low frequencies (< 0.4 Hz), the DNA are somewhat extended. The center of mass position oscillates back and forth in response to the oscillating field. At slightly higher frequencies (0.4 to 2 Hz), there is an anti-resonance regime where the DNA fluctuates between a coiled and elongated state. At again higher frequencies (2 Hz to 75 Hz), the chain becomes highly elongated and its center of mass position remains steady. At the highest frequencies (> 75 Hz), the DNA is pointed in the direction of the electric field but its extension decreases. If the DNA starts in a relaxed conformation, it is also important to condition the DNA using a low frequency field to pull out the hairpins.
Most of the data obtained in earlier publications used 7 wt% solutions of linear polyacrylamide, as these concentrations were optimal for the separation of large DNA using capillary electrophoresis.707,708 The typical fractional stretching achieved in 7 wt% linear polyacrylamide solutions is around 60%, with reports of λ DNA extension to 10 μm706 and 1.1 Mbp DNA extended out to around 200 μm.705 In the latter case, it is possible that the DNA was sheared,705 although a component of the extension out of the plane of focus is also a possible reason why the measured extension for the 1.1 Mbp seems low relative to the result for λ DNA.
The fractional extension is a strong function of the frequency of the electric field and the concentration of the polymer. For example, T4 DNA was extended almost completely using 7 wt% linear polyacrylamide and a frequency of 6 Hz.704 A nearly complete extension of λ DNA was obtained using 3.75 wt% linear polyacrylamide, a strong electric field of 3000 V/cm, and a much higher frequency of 1 MHz.709 In the latter system, the fractional extension exhibits a non-monotonic dependence on the concentration of the polymer.709
The mechanism behind the DNA stretching in ac electric fields remains unresolved.705,709 Indeed, there are similarly mysterious results surrounding the dc electrophoresis of long DNA in high molecular weight linear polyacrylamide solutions. In Section 5.1, we saw that DNA separations are only possible in the unoriented regime, where the reptation tube represents a random walk of blobs. While there is no separation in the biased reptation with orientation regime, the chain can become stretched in this regime. The stretching in an agarose gel is modest,710 due to the relatively large pore spacing, but the most sophisticated theory of biased reptation with fluctuations195 predicts a regime for tight gels where the chain stretching should be substantial. Indeed, videomicroscopy measurements of long DNA electrophoresis in entangled solutions of high molecular weight linear polyacrylamide (700,000 to 1,000,000 Da) show that the DNA tends to migrate head-on in a configuration that is oriented with the electric field.707,708 At lower concentrations (3 wt%), the chains form U-shaped configurations708 reminiscent of Figure 28. However, at higher concentrations (7 wt%), the chains move persistently in an elongated, I-shaped configuration.708 The extension is not complete, but it appears that the DNA mobility for very long DNA is a function of molecular weight. Indeed, chromosomal sized DNA were separated in 5 minutes using 7 wt% linear polyacrylamide solutions.708 The existence of such a separation contradicts the theory of biased reptation with fluctuations,193,195 but the large electric field used in these experiments708 (400 V/cm) violates a key assumption of the biased reptation theory, namely that the electric field is low enough to avoid reptation tube leakage. As the simpler dc electrophoretic behavior is not described by theory, it is unsurprising that the ac stretching problem is also poorly understood.
The absence of a mechanism for the DNA stretching has not impeded applications of this technology. For example, linear polyacrylamide solutions were used for a DNA barcoding application with fluorescently labeled EcoRI in the absence of Mg2+, similar to what we saw in Section 7.4 with extensional flows.682,683 There also exists a device for sizing single DNA molecules following restriction.711 Here, the DNA are confined to femtoliter chambers with a single DNA molecule per chamber. After the restriction digest, the DNA fragments are extended using an ac electric field applied by titanium microelectrodes. Fractional extensions around 80% were achieved using 1200 V/cm fields at a frequency of 1.5 kHz and 7 wt% linear polyacrylamide.711 However, it is challenging to handle complicated restriction digests in this device due to the overlap between fragments in the small chambers. Moreover, the circular chambers are not ideally suited for DNA stretching. Since the electric field is applied in a Cartesian direction, most of the DNA do not have a full diameter available for extension.
7.6 Dielectrophoresis
In Section 6.2, we considered separations where the DNA becomes trapped in a strong electric field gradient created near an electrode patterned on the bottom surface or by the compression of electric field lines at an insulating constriction (see Figure 40). For the electrodeless dielectrophoresis devices,413,429,430 the characteristic length scale for the minimum in the dielectrophoretic potential in Eq. (41) is commensurate with the radius of gyration of the DNA. Thus, the dielectrophoretic force is used to trap the DNA. As we saw in Section 6.2, this trapping force can be used to separate DNA as a function of molecular weight.417,431,432,443 For metal electrodes, the gradient in the electric field is localized near the metal-fluid interface. In general, the length scale for the minimum of the dielectrophoretic potential is small compared to the size of a large DNA molecule. The DNA are thus trapped along the edges of the electrodes425,436 or localized by using a quadrupolar electrode configuration.439
If two electrodes are proximate to one another, it is also possible to have the DNA stretch between the minima near each electrode. Naturally, such stretching would require the two electrodes be no further apart than the contour length of the DNA. In the earliest paper on DNA dielectrophoresis, Washizu and Kurosawa420 proposed using a system akin to the one in Figure 67 for DNA sizing. The DNA are introduced by flow into the region between two slanted electrodes. If an ac field is applied between the two electrodes, the DNA will tend to stretch between them. As the DNA flow from left to the right, either by electrophoresis or a hydrodynamic flow, they will reach a point where their ends become trapped by the electrodes and cannot extend any further. The prediction420 is that bands will form along the electrodes corresponding to different size DNA, similar to what one would observe from gel electrophoresis.
Figure 67.
Principle behind a dielectrophoresis sizing device.420 Two electrodes are placed at an angle to one another to create local maxima in the electric field gradient near each of the electrodes. An ac field is applied between these two electrodes, so that any DNA molecules between the electrodes tends to be stretched between them. The DNA enter the gap between these electrodes by dc electrophoresis or a fluid flow.
Unfortunately, the sizing device in Figure 67 remains at the thought experiment stage and we do not know what factors need to be controlled to realize its potential. The closest experiment is the systematic single molecule apparatus in Figure 68.712 Here, the DNA are fed through the access channel under a dc electric field. The microchannels are only 1 μ m wide and 4 μ m deep, so the DNA tend to get held up briefly at the entrance to the microchannels. Moreover, since the electric field is much stronger in the microchannels, the DNA are rapidly convected to the stretching region. Once a DNA molecule exits the microchannel region, the dc field between pads A and B is turned off and the ac field between pads C and D is turned on. The metal islands between the edges of electrode C and electrode D lead to strong electric field gradients that can stretch the DNA. The purpose of this device is to illustrate the ability to lay down DNA “wires” between electrodes, which can then be metallized as part of a molecular electronics device.713 Since the fluidic channels are made in PDMS, one could remove the fluidic system after wiring the interconnects between the metal islands. Indeed, such electrical engineering applications seem to motivate other dielectrophoretic stretching devices of this type.714 Nevertheless, we can easily see how the fluidic system712 in Figure 68 could be combined with the electrode configuration420 in Figure 67 to realize a dielectrophoretic sizing device.
Figure 68.
Device for single molecule insertion and stretching of DNA molecules by dielectrophoresis. (a) Photograph of the overall device. The dc electric field is applied between pads A and B, and the ac electric field is applied between pads C and D. (b) View of the active region of the device. The access channel is 300 μ m wide and the microchannels are 1 μ m wide. The channels are 4 μ m deep. (c) DNA stretching region. The voltage is applied between electrode C and D, and the DNA are stretched between the isolated metal spots on the surface. Reprinted with permission from Ref.712 Copyright 2007 Wiley-VCH.
The ability for the DNA to extend between the two electrodes depends both on the frequency and the electric field strength. Figure 69 shows data for the extension of different sized DNA between two parallel electrodes separated by a 40 μ m gap.540 In these experiments, the DNA were tethered to one of the electrodes. While we have excluded these types of tethered DNA experiments from our discussion of sizing, since the throughput is low, tethered DNA experiments are ideal for systematically examining the extension under dielectrophoresis. The top panel of Figure 69 indicates that the extension of the DNA is non-monotonic as a function of frequency, with the optimal stretching occurring around 250 kHz. Note that the extension at the peak frequency is close to complete.540 Unsurprisingly, the bottom panel of Figure 69 shows that the DNA stretching increases with the strength of the electric field.540 The dielectrophoretic stretching is also a strong function of the pH of the buffer, with strong stretching at a pH of 8 and no stretching at a pH of 4 or 10.715
Figure 69.
Elongation of DNA by dielectrophoresis in a 40 μ m wide gap between two electrodes. Top: Extension as a function of frequency for different molecular weights. Bottom: Extension of λ DNA as a function of electric field strength for different frequencies. Reprinted with permission from Ref.540 Copyright 2006 IOP Publishing Ltd.
One might question whether the DNA stretching by parallel electrode devices is actually due to dielectrophoresis. A device with parallel electrodes on a glass surface, such as the one540 used to generate the data in Figure 69, possesses an inhomogeneous zeta potential on the surface. Inhomogeneously charged surfaces can give rise to convection rolls,716 which could stretch a DNA molecule tethered to one of the surfaces. In typical microscopy experiments, one only sees the projection of the chain and it is quite challenging to connect the dynamics of the projection to a three-dimensional motion.541 However, confocal microscopy provides access to the “side view” of the extending DNA chain. Confocal microscopy experiments,717 combined with calculations of the electric field around the electrodes, clearly indicate that the DNA is extending along the electric field gradient.
8 Fluorescence Burst Analysis
We now turn our attention to the second class of single molecule sizing, fluorescence burst analysis. The basic difference between DNA sizing by electrophoresis versus fluorescence burst analysis is illustrated in Figure 1. In a separation, the sizes of the DNA molecules are inferred from the electrophoretic mobility of the different bands. We also need a model to calculate the sizes of DNA whose electrophoretic mobilities lie between the electrophoretic mobilities of the standards in the DNA ladder, since most methods do not produce a linear dependence of the electrophoretic mobility on molecular weight. In fluorescence burst analysis, one obtains a histogram of the frequency of different fluorescence intensities as the DNA molecules flow one-by-one past a detector. If there is a linear relationship between fluorescence and the DNA size, we can readily infer the sizes of the unknown DNA by comparison with a (linear) calibration curve. The distinct advantage of fluorescence burst analysis is that we no longer need to sort the DNA to obtain the histogram. Thus, the problem boils down to ensuring that (i) data are obtained from single DNA molecules, (ii) the data correspond to intact molecules with uniform residence times in the detector and (iii) the calibration curve is indeed linear.
We begin in Section 8.1 by covering the exploitation of flow cytometry to size DNA. Flow cytometry is a standard method for detecting and sorting particles and cells, and it has been applied successfully to sizing long DNA to obtain fingerprints from restriction digests of genomic DNA. The term “cytometry” generally refers to counting of cells, but we will retain it here for measuring DNA sizes as well. Figure 70 illustrates the basic principle behind flow cytometry, using DNA as the analyte. The geometric setup in this figure consists of a larger, outer cuvette and a smaller, inner capillary that is partially inserted into the outer cuvette. A very dilute solution of dyed DNA is injected into the system under pressure driven flow through the central capillary. The sample stream is “focused” by the flow in the larger capillary, which is known as a sheath flow. The sample then passes by a laser beam that is focused a short distance away from the exit of the smaller capillary. The sample needs to be sufficiently dilute so that the probability of more than one DNA molecule being in the excitation volume at the same time is vanishingly small. For the purpose of DNA sizing, one then obtains the intensity of the emitted fluorescence as a function of time. Many commercial flow cytometers also include the ability to obtain fluorescence data from multiple laser beams in the detection region and the ability to sort the samples based on the results of the fluorescence assay.
Figure 70.
Schematic illustration of the principle of flow cytometry for sizing DNA. The sheath flow focuses the sample stream as it flows towards the laser excitation. Dashed lines demarcating the boundary between fluid elements in the sheath flow and the sample flow are included to illustrate the flow focusing concept. The laser induced fluorescence detection is normally performed at a 90° angle with respect to the excitation.
In this section, we will also discuss devices for miniaturized cytometry measurements in Section 8.2 that use electric fields, rather than a hydrodynamic flow, to animate the DNA. Electric fields are often desirable in small scale systems, since the pressure drop rapidly increases as the size of the channels decrease.
Fluorescence burst analysis has also been used in conjunction with the separation methods we covered in Section 6 and the DNA stretching protocols that we discussed in Section 7. We will consider the use of fluorescence burst analysis to analyze the output of capillary electrophoresis and hydrodynamic chromatography separations in Section 8.3. Finally, in Section 8.4, we will see how DNA stretching and fluorescence burst analysis can be combined into a high throughput method for reading DNA barcodes.
8.1 Flow Cytometry
Devices for performing flow cytometry measurements of DNA, using a strategy analogous to Figure 70, were reported independently by two different groups at Los Alamos National Laboratories in 1993.718,719 In both cases, the sample flow was focused to a width around 20 μm for detection, with a residence time in the beam ranging from 20 ms in the first device718 to 0.87 ms in the second one,719 which correspond to flow velocities of 0.7 mm/s and 50 mm/s, respectively. These prototype devices, while promising, were limited to analyzing DNA in the 10 to 50 kbp range.
The original flow cytometry devices718,719 and many subsequent designs used orthogonal excitation, where the emitted light is collected by a detector that is orthogonal to the plane illustrated in Figure 70. In this configuration, the output is insensitive to the polarization of the dye molecules along the DNA. However, if the detector is not orthogonal to the excitation, then the intensity of the emitted light is sensitive to the optical polarization of the dyes on the DNA720 and thus to the DNA elongation. Measurements using λ DNA and non-orthogonal excitation indicate that the molecule is almost completely stretched in the flow,720 as we have tried to illustrate in Figure 70. Based on what we saw in Section 7.4, the stretching of DNA in a flow is unsurprising.
Initially, obtaining data for small DNA molecules using flow cytometry represented a substantial challenge due to the relatively low signal-to-noise ratio for small molecules. The signal from the smaller DNA is readily increased by increasing the residence time in the laser beam, and thus the number of times the molecule can be excited.721 One needs to take care with such a scheme, since photobleaching can degrade the measurement, but residence times up to 5 ms do not seem to be impacted by photobleaching.721 However, even if the residence time is increased, the signal from the small restriction fragments may still be overwhelmed by a background of fluorescence from randomly sized, small fragments in the sample stream. These contaminants presumably result from shearing of the large DNA during the sample preparation.722 One effective solution is to electroelute the DNA out of an agarose plug and then use spermine and spermidine to bind the long DNA and stabilize it,723 which not only allows one to analyze long DNA but also unmasks the signal from the shorter DNA. Obviously, the signal-to-noise ratio is also increased by reducing the noise. A critical step in this direction was thinning the shell of the outer cuvette down to 100 μm to reduce scattering721 and replacing the photomultiplier tube used for detection with a single-photon sensing avalanche photodiode,724 which leads to a 200% to 300% increase in the count rate.725 There are also reports of increased sensitivity by changing the illumination to epifluorescence,726 two-photon detection,727 or confocal detection,530 albeit at a cost of more complicated optics.
Many of the issues related to resolving smaller DNA in the sample appear to have been solved in the most advanced DNA flow cytometer reported in the literature.724 This device can detect restriction fragments from 125 bp to 500 kbp. The sheath flow is established by gravity, which provides a smooth, steady flow rate. However, there are issues related to bubble formation when the sample flow is also introduced by gravity; the bubbles are compressible and thus perturb the flow of DNA across the laser beam.723 Advanced devices724 use nitrogen gas pressure to inject the sample stream723 and taper the inlet capillary by wet etching.724
The throughput of these devices, using a 2 ms residence time in the laser, is around 100 fragments/s.728 While this may appear to be a relatively slow rate of analysis, simulations suggest that one could obtain a result within one standard deviation of the mean with only 5 measurements, although in practice one needs closer to 100 measurements to obtain an accurate value.729 The requisite throughput is thus quite small; in principle, a fingerprint containing 40 restriction fragments could be sized in less than a minute. In practice the analysis time is somewhat longer (e.g., 30 minutes100), which is still much faster than pulsed field gel electrophoresis if one skips the electroelution step723 and instead dissolves the gel using GELase.100 It is possible to increase the throughput of the measurement to 2000 fragments/s by using a planar sheet of laser light and imaging the DNA passing through the laser sheet using a CCD camera.728 While it is certainly desirable to increase the throughput of the measurement, the CCD imaging method is prone to numerous artifacts due to the limited readout time from the camera and the different flow velocities at different points inside the illuminated region.728 As a result, laser spot illumination with avalanche photodiode detection is the preferred approach.
The most attractive feature of sizing DNA by the fluorescence bursts in flow cytometry is that the detected fluorescence intensity should be linear in the molecular weight if the dye is stoichiometrically bound to the DNA. Note that this linearity is only valid for orthogonal excitation. As we mentioned earlier, in non-orthogonal excitation, the polarization changes the burst size as a function of stretching of the DNA.720 Since the extension of the DNA will depend on the relaxation time of the DNA (and thus its molecular weight), the burst size in non-orthogonal detection depends non-linearly on the size of the DNA.720,730 For the typical case of orthogonal excitation, Keller and coworkers have frequently cited this linearity as a strong advantage of flow cytometry. In addition to the linear dependence on molecular weight, the burst intensity does not seem to depend on the topology of the DNA.722 As a result, supercoiled DNA can be analyzed by flow cytometry without linearizing the DNA prior to analysis. This characteristic contrasts sharply with pulsed field gel electrophoresis, where the electrophoretic mobility strongly depends on the DNA topology.
To make the linearity transparent, Figure 71a shows data obtained for λ DNA concatemers.723 As seen in the raw data, the fluorescence intensity is not a sum of delta functions (as one might have hoped in an analogy to Figure 10). Rather, the intensity corresponding to a given size of DNA is well described by a Gaussian function, whereupon the overall distribution can be described by a sum of such Gaussians. As seen in Figure 71b, the mean value for each Gaussian is linearly related to the molecular weight of the DNA. These data also highlighted the importance of using spermine and spermidine to stabilize the long DNA molecules; in the absence of the proteins, peaks were only obtained for λ and 2-lambda; DNA.
Figure 71.
Linear response of fluorescence burst analysis in flow cytometry with the size of the DNA. (a) Histogram of the burst sizes (in bins of 10 photoelectrons, pe) for concatemers of λ DNA (48.5 kbp) up to 7-λ (339.5 kbp). The dark line is the raw data; the white line is the sum of seven Gaussian functions fit to the data. The frequency of large concatemers is very low. (b) Linearity of the response in the burst size with respect to the size of the DNA fragments. The correlation coefficient is 0.99998. Reproduced from Ref.723 with permission. Copyright 1999 Wiley-Liss, Inc.
Flow cytometry has proven to be a very effective method for obtaining DNA fingerprints for different bacterial strains, analogous to the restriction fragment length polymorphism (RFLP) analysis typically performed using pulsed field gel electrophoresis.731 Figure 72 shows one particular example of fingerprints obtained from three different species of bacteria using the rare cutting restriction enzyme Not I. Similar to Figure 71, the output from the flow cytometry is fit with a sum of Gaussian functions to estimate the size of the restriction fragments. With such a large (and, for a new strain or species, unknown) number of possible restriction fragments, it would seem that fitting the fluorescence burst data with a sum of Gaussians might introduce substantial errors, particularly for the larger fragments that (i) have a very long residence time in the beam and (ii) are present in low numbers. From the standpoint of DNA fingerprinting, such errors are not particularly troublesome since one can clearly distinguish between different output signals in data such as Figure 72 even if the number of fragments may not be correct. Indeed, one runs into similar issues analyzing the gels from pulsed field gel electrophoresis, since low quantity bands may be too faint to detect and poorly resolved bands might be interpreted as a single, broad band. If we make the reasonable assumption that the Gaussian fits in Figure 72 correspond to the location of the restriction sites in these organisms, then the two largest fragments for E. coli and B. globigii are missing from the output, presumably due to shear cleavage.
Figure 72.
Flow cytometry burst histograms for the NotI fingerprints of three different organisms. The black lines are the raw data and the white lines are the sum of Gaussian fits to the data. Adapted with permission from Ref.99 Copyright 1999 Wiley-Liss, Inc.
One of the challenges in using fluorescence bursts to size the DNA is the conversion from the burst intensity in Figure 71a to a molecular weight in Figure 71b. A simple option is to spike the unknown sample with some small DNA as an internal size standard.722 This approach is most effective if the unknown DNA have a higher molecular weight than the internal standard,722 since the linearity in Figure 71 allows one to readily extrapolate the line for the standards to the range of molecular weights for the unknown sample. In general, it is not always obvious what DNA to use for the internal standards since their peaks (which are, by necessity, relatively strong) may obscure fluorescence bursts obtained from similar sized DNA in the unknown sample. Moreover, an abundance of DNA in the sample that are slightly different in molecular weight than the standard could inadvertently shift the location of the peak for the standard and thus lead to an incorrect calibration.
A second challenge is correctly balancing the dye to DNA ratio in the experiment. For proof-of-principle experiments, this ratio is not a major issue since one can systematically explore a range of ratios and select the one that provides the optimal experimental result. For an unknown sample, in particular a rare sample, the challenge becomes manifest since one can only perform a limited number of experiments. Moreover, the recovery of DNA from a bacterial sample is not perfect and, for new organisms, we do not know the size of the chromosome. As a result, even if the cell density is known, the amount of genomic DNA used for the flow cytometry experiment is still unknown. Most of the early work in flow cytometry used an air-cooled Ar ion laser (488 nm) and frequently used TOTO-1 or POPO-3 dyes, which fluoresce very strongly when bound to the DNA backbone. Unfortunately, the fluorescence of these dyes depends strongly on the dye to DNA ratio. Moreover, the fluorescence is quenched in the presence of a large excess of unbound dye.732 From an exhaustive study of different dyes that are excited with 488 nm light, it appears that PicoGreen at a concentration of 0.8 μM is the optimal choice since the corresponding fluorescence intensity is the least sensitive to DNA concentration in the relevant range of 5 to 2000 ng/mL.732 This dye proved especially useful in the fingerprinting of 5 strains of E. coli and 6 strains of S. arueus using flow cytometry.731
As laser technology continued to advance during the development of these flow cytometry devices, it became clear that less expensive, diode-pumped solid state lasers724 would be preferable to the air-cooled Ar ion laser used in the earlier systems.733 These solid state lasers are also available at slightly higher wavelengths (532 nm) and offered the opportunity to explore new dyes. In an approach analogous to the one that led to the selection of PicoGreen for 488 nm excitation, the SYTOX Orange dye appears to be the optimal choice for 532 nm excitation over a range of DNA concentrations.
Given the extensive amount of engineering that has gone into the flow cytometry method, it is useful to compare the most recent results in this system to the comparable data for pulsed field gel electrophoresis.100 Figure 7, which we presented in Section 3.1, compares data obtained by both methods for the SmaI digest of S. aureus Mu50. To convert the flow cytometry data to molecular weights, the sample was spiked with 17.4, 48.5 and 165.6 kbp standards.100 The sequence of this organism is known, so one can also produce the “virtual” digest in Figure 7 by searching the genome for SmaI recognition sites. As we can see in the figure, flow cytometry continues to have some challenges in identifying the largest DNA fragments, but otherwise the flow cytometry data are in excellent agreement with the virtual digest and similar in accuracy (4% ± 4%) to the corresponding data for pulsed field gel electrophoresis (5% ± 2%). The uncertainty estimates for the accuracy of the fragment sizing were obtained from 45 replicates, which is a much larger data set than many studies that we have encountered in this review. We should also point out that the accuracy of these electrophoresis experiments100 is much better than the rule of thumb value of 10%. While the precision and accuracy of the two methods were similar, the flow cytometry only took 30 minutes compared to 24 hours for pulsed field gel electrophoresis and required much less sample than in electrophoresis. These advantages need to be balanced against the easy parallelization of gel electrophoresis, where many lanes can be run simultaneously and the time per lane is much less than 24 hours.100 Moreover, pulsed field gel electrophoresis is ubiquitously used in laboratories (for a reasonable one-time cost to purchase the equipment). The flow cytometer used in this study is one of a kind100 but the flow cytometer is available to external users through the National Flow Cytometry Resource at Los Alamos Laboratory.734
In addition to measuring the size of the DNA, it is also possible to detect the presence of sequence specific probes using the flow cytometry method.736 Figure 73 illustrates the basic principle in the context of one of the electrophoretic cytometry devices that will be discussed in Section 8.2. In the two color experiment, one needs to make a cross correlation analysis736 between the channel detecting the presence of the DNA (e.g., the green channel) and the presence of the probe (e.g., the red channel). If a burst appears on both channels at the same time, it indicates the presence of DNA with the bound probe. An advantage of this method is that it does not require cleaning up the sample prior to analysis since bursts on the probe channel in the absence of a burst on the DNA channel are simply the passage of unbound probes. In the earliest work of this type,736 which analyzed intact maize genomic DNA, the probes were peptide nucleic acids (PNA) and bound to the chains in a hybridization assay. In a later flow cytometry experiment,720 Cy5-streptavidin probes were bound to the ends of biotinylated DNA. When the DNA is digested, the end fragments are easily detected by the simultaneous bursts on the DNA channel and the Cy5 channel.
Figure 73.
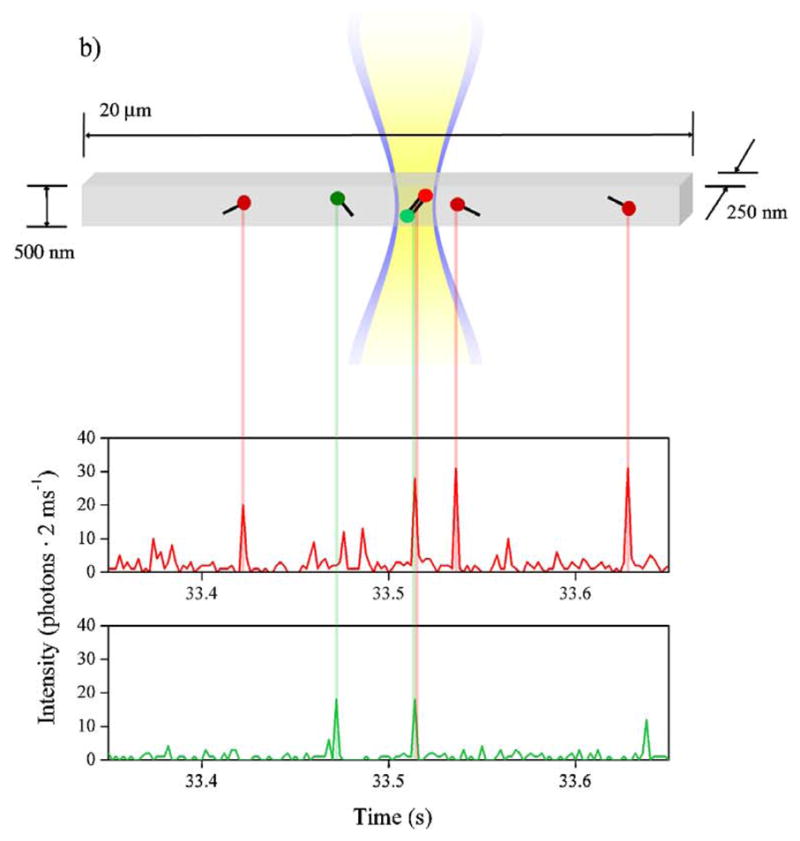
Illustration of the principle of two color analysis of DNA in cytometry device. These particular experiments were performed in a submicron channel using electrophoretic cytometry, which is discussed in more detail in Section 8.2. Reprinted with permission from Ref.735 Copyright 2007 American Institute of Physics.
8.2 Electrophoretic Cytometry
In addition to shot noise and scattering from the glass walls, the major sources of noise in flow cytometry measurements using a setup such as Figure 70 are (i) the scattering from the fluid and (ii) additional noise from any fluorescence impurities. A straightforward approach to reduce the noise is to reduce the volume of fluid illuminated by the laser spot. While confocal imagining offers an optical approach,530 the microfluidic methods we have seen in previous sections of this review present a simpler alternative. Instead of using a sheath flow to focus the sample stream, one simply uses a small channel volume to reduce the amount of sample in the excitation region. Figure 74 shows the first such device for DNA measurements.737 While the device geometry in Figure 74 may seem very simplistic compared to the devices we encountered in the sections on separation devices and on nanochannels, we should bear in mind that (i) this device appeared shortly after the seminal paper from Whitesides on soft lithography281 and (ii) the simplest approach is frequently the best approach. Here, the channels narrow down to a 5 μm by 3 μm cross section for the detection region. The corresponding detection volume of 375 fL is an order of magnitude smaller than in the sheath flow devices. Since the channel sizes are small, it is much simpler to use electrophoretic actuation instead of a hydrodynamic flow, hence our moniker of “electrophoretic cytometry.” Although only a prototype, the sizing data for the HindIII digest of λ DNA obtained in this device is comparable to data obtained in sheath flow cytometry devices737 and proved useful for examining double strand breaks due to radiation damage.738 The prototype was also used to analyze DNA up to 400 kbp, but the linearity of the response737 is not as good as we saw in Figure 71. It is not clear whether the deviation from the linear response is a result of the small sample volume or a deficiency that could be addressed if this microfluidic flow cytometer received the same amount of engineering as its sheath flow counterpart. The two outlets from the detection region also permit a binary sorting of the DNA based on their fluorescence into the left or right arm,737 which has also been used for the so-called microfabricated fluorescence-activated cell sorter (μFACS).739
Figure 74.
Microfluidic flow cytometer for DNA fabricated in PDMS. The inset is a magnified image of the intersection of the channels. The large channels are 100 μm wide and narrow to 5 μm at the junction. The channels are 3 μm deep. The pillars in the wide channels support the ceiling of the channel. Reprinted with permission from Ref.737 Copyright 2009 National Academy of Sciences of the U.S.A.
Further reducing the detection volume increases the signal-to-noise ratio.740,741 Channel dimensions down to 500 nm wide are accessible using projection photolithography,742 which permits a large number of analysis channels on a given chip, and a depth of 250 nm is equally easy to achieve using reactive ion etching. The detection volume in these devices drops another three orders of magnitude down to 0.16 fL.742 Moreover, when the channel size drops below the wavelength of the laser used for excitation, the focal volume can be treated as a region of uniform intensity.735 As a result, each molecule that passes through the laser light should be excited equally. An early example740 using a 1 μm wide, 270 nm deep nanoslit demonstrated the basics of this principle by sizing the HindIII digest of λ DNA. A subsequent experiment735 used the two color scheme in Figure 73 to analyze the products from a quantitative PCR reaction as a function of the cycle number in the reaction. The primers were labeled with either the green or red dye, whereupon a simultaneous burst on both color channels indicates the presence of amplified DNA rather than unused primers. This detection system led to a marked increase in sensitivity, with the breakthrough occurring around 15 to 20 cycles instead of the 35 cycles required, for example, in laser induced fluorescence from a continuous flow microfluidic quantitative PCR device.743 The two color excitation scheme has also proven useful for methylation analysis using TOTO-3 for the DNA dye and histones that have been modified with GFP.742
As the size of the channels decreases, we eventually reach a regime where the DNA is confined in a manner similar to what we saw in Section 7.2. An obvious opportunity here is to use the burst intensity to size the DNA rather than using an image of its length.640 Indeed, the data thus obtained for the HindIII digest of λ DNA in a 250 nm wide, 100 nm deep channel are comparable to similar data obtained from flow cytometry experiments.640 Moreover, there are no difficulties distinguishing the 125 bp and 564 bp fragments above the noise in the nanochannel device, although the linearity in the intensity versus molecular weight is not very good at the lower molecular weights.640
8.3 Fluorescence Burst Analysis of Ultralow Concentration Separations
So far, we have only considered fluorescence burst methods that start from some random mixture of DNA molecules. The output of the sizing data thus consists of an unordered listing of burst sizes versus time. To produce data similar to Figure 71 or Figure 72, these data need to be binned and converted into a histogram of the burst frequencies. We might imagine that the data analysis process might be simplified by fractionating the DNA by molecular weight before the burst analysis. Alternatively, we can also imagine using the burst analysis at the end of a separation to (i) increase the sensitivity of the detection and (ii) provide a second measurement of the DNA size.
The main body of work in this area consists of combining fluorescence burst analysis with capillary electrophoresis of the DNA in hydroxyethylcellulose (HEC).161,725 Here, the goal is to detect the separations of DNA with as few as 50 to 100 molecules per band. Similar to what we saw in the electrophoretic cytometry section, the 18 fL probe volume in these experiments is much smaller than what can be achieved in a sheath flow such as Figure 70. As a result, the signal-to-noise ratio is very good in the capillary electrophoresis separations. DNA as small as 100 bp were detected in the capillary electrophoresis experiments725 years before similar detection was reported for sheath flows.724 Achieving this sensitivity required a systematic optimization of the parameters, including the processing of the fluorescence burst data.725 The detection was further improved by moving from a capillary to microchip electrophoresis in 3% linear polyacrylamide.744 The microchip system also included a focusing current to improve the sample detection.
The hydrodynamic chromatography methods we discussed in Section 6.3 have also been combined with fluorescence burst analysis to detect below 100 molecules per band.536 Similar to the results in capillary electrophoresis, the 100 bp fragments are easily detected above the baseline. The limit of detection in these experiments is 2 to 3 orders of magnitude lower than previous hydrodynamic separations.534
8.4 DNA Stretching and Fluorescence Burst Analysis
We can also try to add DNA stretching to further enhance the analytical capabilities of flow cytometry-based devices. One such approach is known as Direct Linear Analysis (DLA), which was introduced by US Genomics.115 They have recently re-branded their approach as “genome sequence scanning.” In the context of the methods in this review, we can think of these devices as DNA barcoding in an extension flow using a particular set of genomic tags.115 In the device illustrated schematically in Figure 75, the DNA molecules are decorated with these fluorescent tags and the DNA are pushed by a pressure driven flow through a post array, which is intended to “precondition” the DNA and hopefully remove the molecular individualism.668,681 The DNA then enter a hyperbolic constriction, which provides the extensional flow to stretch the DNA. The remainder of the device is similar to a flow cytometer, where multiple laser beams detect the fluorescence bursts as the DNA move through the detection region.
Figure 75.
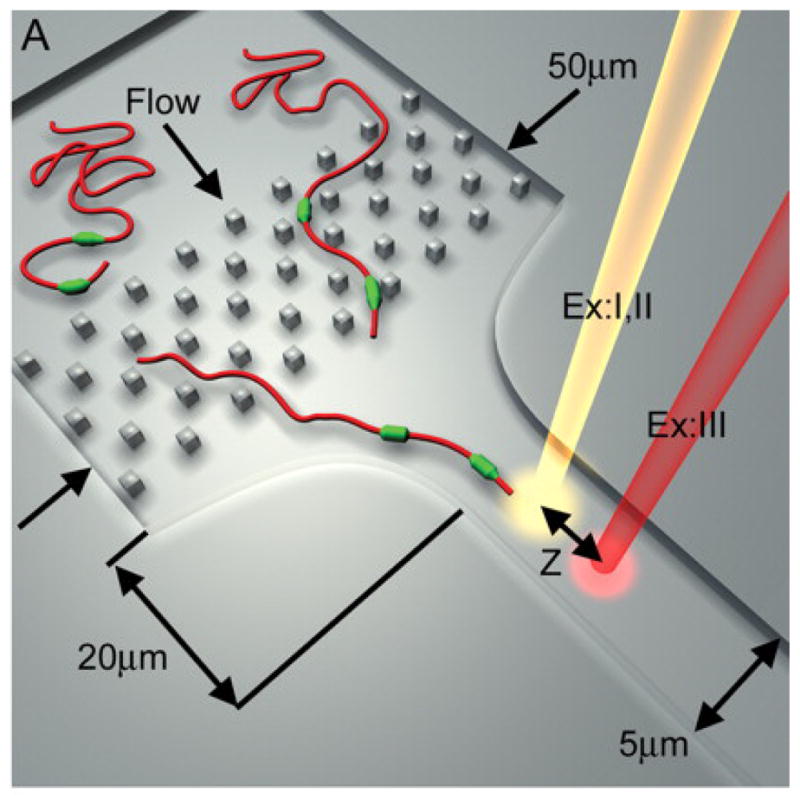
Artistic rendition of direct linear analysis device from US Genomics. Reprinted with permission from Ref.115 Copyright 2004 Creative Commons License.
In the original report of this device,115 more than half of the DNA molecules that entered the hyperbolic constriction were stretched to at least 90% of the full contour length. The minimum distance between the fluorescent tags required to resolve them is around 5 kbp, which is greater than the ≈ 1 kbp limit for reading DNA barcodes in the Odijk regime of a nanochannel.167 If the tags are sufficiently far apart, the DLA experiment identified the location to within 2 kbp, which is somewhat better than the 5 kbp resolution obtained in videomicroscopy measurements of a different tag in a cross-slot flow.682
In addition to measuring the location of the fluorescent tags, one can also obtain a measure of the DNA length by labeling the backbone. While the DNA length can be measured by the total fluorescence burst intensity when it moves through the spot, akin to flow cytometry, it is also possible to make a second measurement based on the residence time in the spot if the DNA is well stretched. Similar to what we saw in flow cytometry, the accuracy of the measurement increases with the residence time in the detector. Since the hydrodynamic force stretching the DNA is proportional to the product of the fluid viscosity and the flow rate, the resolution of the measurement of the length for a given stretching force improves in higher viscosity buffers (and concomitantly lower velocity).745 Naturally, this strategy entails a tradeoff between the resolution and throughput of the device.
The design of the funnel geometry also plays a key role in the efficiency of the stretching.745 Explicitly, the distribution of DNA extensions observed at the end of the funnel depends on how the strain rate evolves through the contraction. A funnel design where the strain rate increases as the DNA passes through the funnel leads to a narrower distribution of fractional extensions (with a peak near full extension) than funnel designs with constant strain, a sudden increase in strain at the inlet, or a sudden increase in strain at the outlet.745 In the “increasing strain rate” design, one even observes overstretched DNA at high linear velocities.745
This mapping technology has advanced significantly since its original introduction in 2004, in part due to the improvements in the design of the stretching flow.745 In a recent mapping report,746 the throughput of the device is up to 15 to 30 Mb/s using a flow rate of 12 μm/ms and 20 kHz data acquisition, which appear to be the optimal settings to stretch and analyze 100 to 250 kbp DNA. The throughput is markedly higher than the 0.1 Mb/s obtained by electrophoretic flow stretching. With such high throughput, the data for a typical bacterial strain requires around 20 to 40 minutes to analyze, with more complicated mixtures of organisms requiring around 4 hours, although the initial sample preparation requires an additional 4.5 hours. This second generation method746 also integrates an automated sample preparation for extracting the DNA and two color mapping to increase the data density.
The DLA device also continues to evolve as a lab-on-a-chip apparatus, with its most recent incarnation510 reproduced in Figure 76. The device now includes a pair of pre-concentration steps and a DNA prism device (see Section 6.6) to remove the smaller DNA from the large molecules before the stretching analysis. Interestingly, the technology has also led to a system for multiplexed detection of proteins using the so-called “digital” DNA technology,509 where the binding to specifically designed recombinant DNA serves as the multiplexing platform. The device in Figure 76 was used to detect airborne pathogens, and this new focus of the technology is reflected by the fact that, in 2010, US Genomics changed their name to PathoGenetix.
Figure 76.
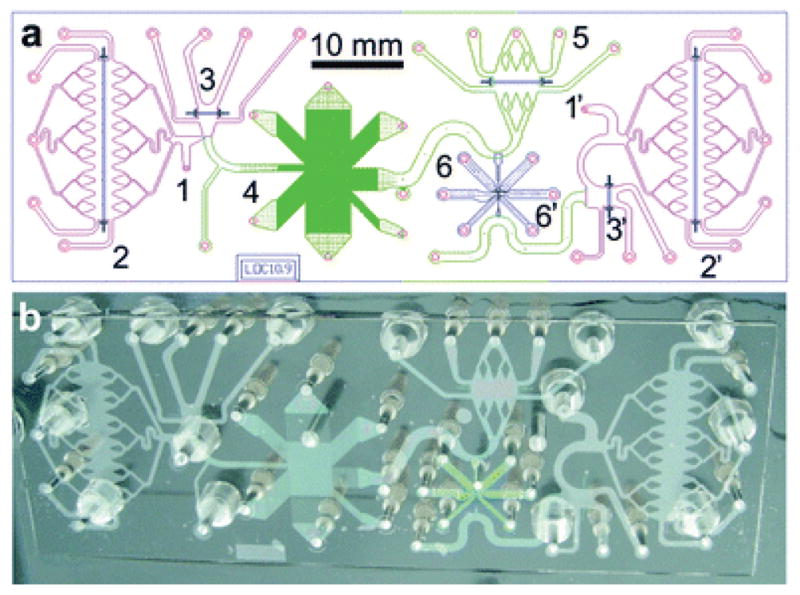
Highly integrated device that combines separations, DNA stretching, and fluorescence burst analysis. (a) Schematic illustration of the device. (b) Actual device. The various numbered components of the device are described in the original reference.510 Note that component 4 is a DNA prism. Reprinted with permission from Ref.510 Copyright 2011 Royal Society of Chemistry.
While the DLA device uses a pressure driven flow, we saw previously in Section 7.4 that one can obtain equally good stretching by replacing the hydrodynamic flow field with an equivalent electrophoretic “flow” field.747 Interestingly, although the electric field does not feature any vorticity, the DNA chain can still rotate during its approach to the hyperbolic constriction by non-local electrophoretic effects that arise when the DNA coil is large compared to the length scale of the electric field gradients.748 While the DNA certainly extend within the hyperbolic constriction, the agreement between experiments and simulations is not very good.749 Although previous experimental work686 suggested that nonlinear electrokinetic effects, such as dielectrophoresis, do not play a role in the electrophoretic extension, a careful subsequent analysis demonstrated that |(∇E) · E| approaches 1.4 × 107 V2/cm3, which is close to the values used to trap DNA in the dielectrophoresis experiments we discussed in Section 6.2. If nonlinear electrokinetics are indeed present, they present an opportunity for further enhancing the stretching through the design of the channel shape and the concomitant electric field gradients.
Initially, it was believed that one of the key components of the device in Figure 75 is the post array at the entrance to the hyperbolic constriction. One consequence of the post array is to partially extend the DNA prior to entering the constriction, which then reduces the amount of strain that needs to be introduced by the hyperbolic constriction. However, if the goal is to reduce the necessary strain, this particular post array does not appear to be the optimal approach. The device in Figure 75 consists of square posts with 1 μm sides with a 2.5 μm spacing between posts.115 We would expect that a gradient in post sizes would provide even more efficient stretching before the entrance to the constriction, which is an approach used in nanochannels.575,589 Rather, the main impetus for the post array is to counter the problem of molecular individualism.681
In principle, the molecular individualism can be attenuated by the collisions with the posts. Remarkably, it seems that only 3 rows of posts are required to achieve the typical stretching by hydrodynamic flow through the array since the DNA tends to relax quickly after the collisions,526 analogous to the process occurring during transport through the post arrays used for DNA electrophoresis in Section 6.1.1. The latter data were obtained for pressure driven flow through a somewhat different system featuring a hexagonal array of posts with similar size (1.22 μm × 1.38 μm) but with a much deeper channel (14.2 μm).526 The array was also much longer than 3 rows, and the typical stretching after 12 rows is around 15%–20%. There is also a rather broad distribution of extensions inside the array, with a tail extending up to a fractional extension of around 50%.
Naturally, if we can use an electric field to stretch the DNA in the contraction, we can also use electrophoresis through a post array to precondition the DNA before the contraction.750 The most desirable collisions are the U/J type collisions in Figure 28, which lead to strong extension of the chain. Unfortunately, the X collisions332,337 shown in Figure 28 occur very frequently during the collision with a post.160,330,332,333 Nevertheless, the post array increases the average stretching in the contraction by removing the initial configurations that lead to slower stretching. For large De, the post array has a negligible impact on the final extension since the constriction generates a very strong stretching flow. A key conclusion of the study of prestretching in the post array750 is that making the post spacing small compared to the DNA molecule increases the stretching. We observed a similar effect in the separations in the nanofence array160 discussed in Section 6.1.1.
While a post array appears to be a robust method to assist in the preconditioning of the chain, one can also envision placing a single large post at the inlet of the channel,751 with the goal of achieving the strong deformation caused by the collision with a large, insulating obstacle.38 The challenges here are primarily in the fabrication of such a device with a narrow gap between the post and the entrance to the contraction.
Remarkably, subsequent work showed that the posts used in devices similar to the one in Figure 75 are superfluous.745 While the posts are critical to achieving extension in a deep channel,526 the device in Figure 75 is etched to a uniform depth of 1 μm. Such a geometry corresponds to a weakly confining slit for the typical DNA (≈ 100 kbp) used in the analysis. As the flow rate increases, the combination of the velocity gradient between the floor and the ceiling of the device, the confinement-induced stretching, and the long relaxation time of these DNA leads to substantial fractional extensions prior to the entry to the funnel.745 Indeed, in a 1 μm deep slit, an inlet velocity of 2 μm/ms leads to an average fractional extension of 30% at the funnel inlet.745 Overall, the inclusion of the post arrays only increase the fraction of stretched molecules by 5% to 10%.752
An oscillating force field is another possible approach to precondition the DNA. To date, the work in this area has been entirely simulation-based. Larson677 predicted that an oscillating, planar extensional flow can precondition the DNA such that the number of folded conformations is reduced when the DNA is finally subjected to a steady extensional flow. Such an oscillating flow can be added to the device in Figure 75 by adding cross channels before the hyperbolic contraction that apply the oscillating transverse electric field. Unfortunately, Brownian dynamics simulations of such a device do not indicate that this DNA “massage” approach leads to an increase in stretching at the hyperbolic contraction.748 One possible explanation for the failure of the design strategy are the time scales in the process. In order to separate the various unit operations of the device, the cross channels need to be located some distance away from the hyperbolic constriction. (Most likely, fabrication constraints would set the minimum distance between unit operations.) If the DNA are slowly convected through the system, then there is sufficient time for relaxation after the oscillating electric field region, thereby undoing any preconditioning of the chain configuration. Conversely, if the DNA are rapidly convected through the system, then there may not be sufficient residence time in the oscillating field region to achieve sufficient strain.748 As the simulation procedure appears to be robust, we are cautiously optimistic that these design hurdles can be surmounted in the near future.
One of the most intriguing ideas to precondition the DNA before the contraction is to use a gel/fluid interface to stretch the DNA.747,753 As see in Figure 77, the gel is created near the inlet of the hyperbolic contraction by UV cross linking from a microscope objective. Under an electric field, the DNA reptate through the gel. At the exit of the gel, the DNA experience a step change in electrophoretic mobility as they are transiently tethered at the edge of the gel. The ensuing extension at the hyperbolic constriction is very good, with a peak in the distribution of the extension close to 90% extension for De = 14.747 Unfortunately, it seems that the gel is not an ideal material to use in practice since it is hard to fabricate, requires rinsing of the channel, and leads to sticking of the DNA.750 As a result, it is difficult to reuse the channels.
Figure 77.
(a) Hyperbolic contraction similar to the system in Figure 75. (b) Illustration of the experimental protocol for creating a gel near the entrance to the hyperbolic contraction. (c) Images of the DNA extension as it crosses from the gel into the fluid before the hyperbolic contraction. The solid line indicates the location of the gel/fluid interface. Reprinted with permission from Ref.747 Copyright 2006 Royal Society of Chemistry.
Combining nanochannel confinement with electrophoretic cytometry also introduces the possibility of obtaining high-throughput data on the configurations and dynamics of confined DNA. As seen in Figure 78a, this system involves the entry of the DNA from a nanoslit to the nanochannel, wherein the DNA move past two nearby laser spots under the influence of the electric field. Figure 78b shows a typical response from the DNA moving through a laser spot.640 Reccius et al. observed a wide range of responses of this type, which they were able to classify into eight types of folded structures consisting of one, two or three folds of the DNA.640 Remarkably, the DNA also appear to be more strongly extended during their electrophoresis through the nanochannel than they would be at equilibrium and that the extent of stretching depends on the electric field strength.640 By comparing the time to cross the two beams, one can also obtain a measurement of the DNA speed in a method dubbed “single molecule electrophoresis”.754 Although we would expect the DNA electrophoretic mobility to be independent of molecular weight in this channel, based on our discussion in Section 6.3, the data indicate that the electrophoretic mobility of the DNA depends on the number of folds in the DNA.640 We suspect that the mobility differences are manifestations of the electrohydrodynamic equivalence principle,523 since the chain cannot sample the equilibrium set of configurations.452 However, a complete understanding of the various dynamics observed in these experiments requires considerably more work.
Figure 78.
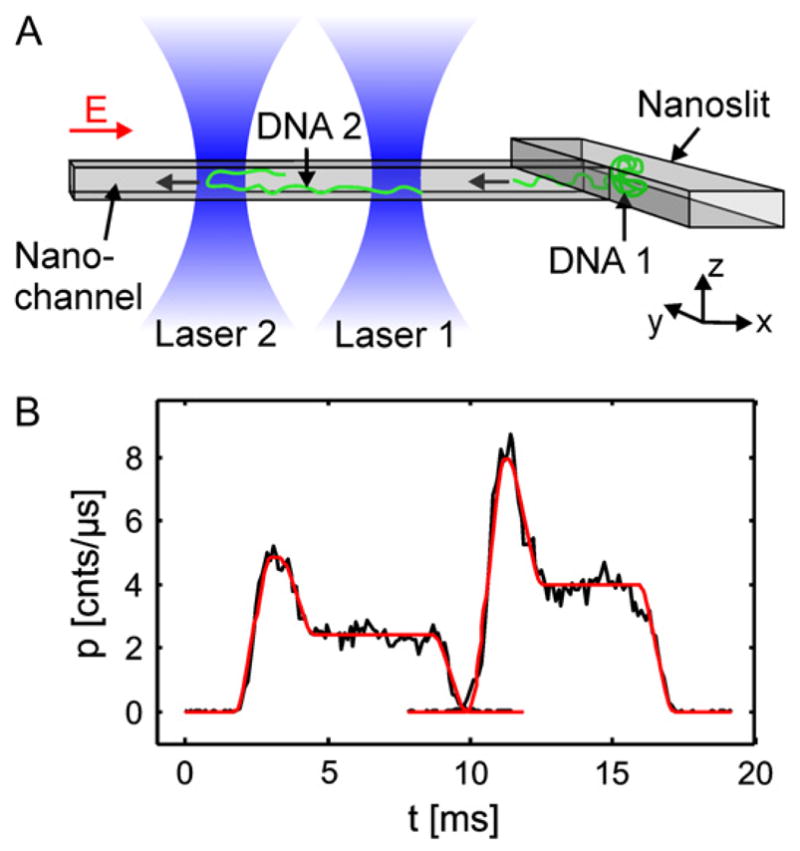
(a) Schematic illustration of the two laser-spot device for DNA electrophoretic cytometry in a nanochannel. (b) Trace of the intensity output through the laser spots for a folded DNA molecule. Reprinted with permission from Ref.640 Copyright 2008 Biophysical Society.
9 Perspectives
Having completed our review of the field, we would like to conclude here with our opinions about the relative merits of the different methods and their potential to impact the genomic applications discussed in Section 3. One of the first things that should be apparent from our review is that none of these techniques are easily implemented in a standard biology lab in their prototype formats. The best microfabricated devices require sophisticated clean room fabrication techniques, the flow cytometry approaches require optics for sensitive detection and a very stable fluid flow, and DNA stretching requires a camera that is sensitive enough to image single DNA molecules. Moreover, implementing some of the techniques, such as nanochannel mapping and direct linear analysis, requires a combination of these skills. The leap from preparing and running agarose gels to any of the methods in this review is quite large. Thus, it is not surprising that the methods discussed in this review did not quickly spread through typical biology laboratories. Indeed, the only methods that we covered here that can be readily implemented in existing gel or capillary electrophoresis equipment are surface electrophoresis on a bare silicon surface468,473 and hydrodynamic chromatography in thin capillaries,533–537 although the detection step for the former method is more challenging than imaging a gel.
However, we should also keep in mind that the bioanalytical community are strong adopters of new technologies that demonstrate a clear advantage over existing techniques. The best example in the context of our review was the emergence of automated capillary electrophoresis systems for separating single stranded DNA.16,17 These systems offer substantial benefits in throughput compared to running conventional agarose gels, but they required substantial engineering to automate the sample handling, optics, and data analysis. One can now readily purchase a capillary electrophoresis machine and be up and running in a short period of time. A similar circumstance surrounded the development of pulsed field gel electrophoresis. While field inversion gel electrophoresis235 can be implemented with a conventional submarine gel electrophoresis apparatus and a minor change in the power supply, the more powerful CHEF methods216 illustrated in Figure 22b requires substantially more engineering. Again, commercialization of the apparatus led to widespread use in laboratories. Both the automated capillary electrophoresis machines and pulsed field gel electrophoresis setups are relatively expensive, but the cost is offset by the performance of the device.
We should thus expect that those systems closest to commercialization would produce the best results. Of the systems that we reviewed here, the most mature methods in terms of their operation are flow cytometry and optical mapping by surface stretching. This should be apparent by the number of important biological studies appearing in the optical mapping literature (Table 1) and the comprehensive DNA fingerprints obtained by flow cytometry (Figure 7 and Figure 72). The flow cytometer is available for use as part of the National Flow Cytometry Resource at Los Alamos National Laboratory, which limits its widespread use but does provide researchers in the field with a shared resource. In contrast, optical mapping by surface stretching is available in a commercial device called Argus (OpGen), and a nanochannel mapping device is coming to market (BioNano Genomics). The commercialization of benchtop devices follows in the tradition of the capillary electrophoresis machines, promising “sample-in, answer-out” capabilities in a highly automated device. From our review, it is not clear which of these two mapping technologies will prove to be the most powerful in the end. The surface stretching techniques were introduced104 almost a decade before the first successful experiments involving nanochannel stretching.575 As we saw in Table 1, there are already impressive biological results emerging from surface stretching. It remains to be seen whether the advantages of measuring near equilibrium in nanochannels will lead to equally important applications in biology. In any event, the presence of two competing technologies in the market should benefit the field as a whole.
What about the separation devices? We did see several examples where separation devices were integrated with devices for DNA stretching and fluorescence burst analysis, such as the post array for conditioning DNA prior to extension in a contraction115 and the use of the DNA prism to purify DNA samples prior to stretching analysis.510 The fact that these technologies were employed in commercial devices gives us hope that the separation devices discussed in this review will have some impact as a component of integrated lab-on-a-chip devices. Although most integrated analysis devices that use separations282–287 employ conventional electrophoretic separations, there are advantages to moving to monolithic separation matrices that can be easily incorporated into the device. However, these monolithic separation media need to perform as well or better than the state-of-the-art polymers for capillary electrophoresis.294 To date, this is not the case.
In the context of restriction mapping and DNA fingerprinting, our review indicates that separation-based methods are not yet competitive with flow cytometry. However, it is not entirely clear to us whether the reason for this difference is an intrinsic problem with the idea of using separations versus fluorescence burst analysis or the way in which the two different approaches were pursued over the past 20 years. The ideas for both methods appeared almost simultaneously, with the first post array312 appearing in 1992 and the seminal papers on flow cytometry718,719 appearing the next year. The flow cytometry approaches were immediately pursued by a team of researchers at Los Alamos who worked diligently to develop the technology for more than a decade. The publications that we discussed in Section 8.1 illustrate a steady progress from the proof-of-principle718,719 to the optimal device,724 with eventual application to real biological problems.100 This approach parallels the work done in optical mapping by Schwartz and coworkers that led to the OpGen technology. In contrast, we saw a wide variety of separation devices in Section 6 that were pursued by a number of different research groups. Moreover, the first separations in a post array142,316,340 appeared almost a decade after the idea was proposed. While the work on microfabricated separation devices has provided a wealth of information about the physics of DNA electrophoresis,32 this research area did not benefit from the systematic approach to the development of the technology that we saw in optical mapping or flow cytometry. As the first commercial microchip electrophoresis systems for miniaturized capillary electrophoresis are now becoming available (Caliper, Shimadzu), there is still time for the separation devices to show their utility. However, from the standpoint of mapping long DNA, it seems that both fluorescence burst analysis and optical mapping have a large and potentially insurmountable lead.
Let us conclude with a brief look towards the future. The writing of this review coincided with the news report10 of the imminent availability of a nanopore sequencer (Oxford Nanopore) that costs $900, can sequence almost 45 kbp per second, and can decode an entire, intact bacterial genome. While these stunning results have not yet been subjected to peer review, they point towards another leap forward in sequencing technology. At the same time, the existing high-throughput sequencing technologies are becoming increasingly affordable for individual users as benchtop apparatuses.4 Is there any need for mapping technologies? With the current state of sequencing technology, we believe the answer is yes. First, high-throughput sequencers still have trouble decoding certain sequences, such as tandem repeats, and we have already seen in Table 1 a number of genome assemblies that were only finished with the help of optical mapping. Moreover, the availability of a large scale map greatly facilitates the assembly of unknown genomes and the analysis of highly scrambled genomes, such as occurs in cancer, that are not easily assembled from high-throughput sequencing. That being said, even if genome sequencing finally realizes the ability to read, with minimal errors, entire genomes in a single shot, it is not obvious whether such a data deluge11 is necessary for many genomic screening tasks.12
Supplementary Material
Acknowledgments
The original versions of Section 5.2, Section 5.3, Section 5.4, and a portion of Section 6.2 were written by KDD in 2005 while he was at Institut Curie. The latter work was part of a collaboration with Gary W. Slater (University of Ottawa) and Jean-Louis Viovy (Institut Curie). We thank both collaborators for their comments on earlier versions of these sections and their permission to include the text in the present review paper. We also thank Han Cao (BioNano Genomics) for illuminating discussions on the importance of genome mapping. Some of the discussion of basic concepts in polymer physics was inspired by a graduate course on the subject taught by Prof. David C. Morse in 2012. Michel Gauthier (University of Ottawa) drew the original versions of Figure 4, Figure 22, Figure 24, Figure 25 and Figure 26. Barry Badeau computed the ionic strengths appearing in Table S1. Our work in this area during the preparation of this review was supported by the NIH (R01-HG005216 and R21-GM103409), NSF (CBET-0642794 and DMR-1206045), DARPA Young Investigator Award N66001-09-1-2103, the David and Lucille Packard Foundation, and a Teacher-Scholar Award from the Dreyfus Foundation.
Footnotes
Supporting Information Available
Experimental conditions for Figure 3. This material is available free of charge via the Internet at http://pubs.acs.org/.
References
- 1.Niedringhaus TP, Milanova D, Kerby MB, Snyder MP, Barron AE. Anal Chem. 2011;83:4327. doi: 10.1021/ac2010857. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.van der Straaten T, Guchelaar H-J, Swen JJ. Pharmacogenetics. 2012;13:369–372. doi: 10.2217/pgs.12.6. [DOI] [PubMed] [Google Scholar]
- 3.Mardis ER. Nature. 2011;470:198. doi: 10.1038/nature09796. [DOI] [PubMed] [Google Scholar]
- 4.Loman NJ, Misra RV, Dallman TJ, Constantinidou C, Gharbia SE, Wain J, Pallen MJ. Nat Biotechnol. 2012;30:434. doi: 10.1038/nbt.2198. [DOI] [PubMed] [Google Scholar]
- 5.Latreille P, Norton S, Goldman BS, Henkhaus J, Miller N, Barbazuk B, Bode HB, Darby C, Du Z, Forst S, Gaudriault S, Goodner B, Goodrich-Blair H, Slater S. BMC Genomics. 2007;8:321. doi: 10.1186/1471-2164-8-321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Zhou S, Bechner MC, Place M, Churas CP, Pape L, Leong SA, Runnheim R, Forrest DK, Goldstein S, Livny M, Schwartz DC. BMC Genomics. 2007;8:278. doi: 10.1186/1471-2164-8-278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ananiev GE, Goldstein S, Runnheim R, Forrest DK, Zhou S, Potamousis K, Churas CP, Bergendahl V, Thomson JA, Schwartz DC. BMC Mol Biol. 2008;9:68. doi: 10.1186/1471-2199-9-68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Eid J, Fehr A, Gray J, Luong K, Lyle J, Otto G, Peluso P, Rank D, Baybayan P, Bettman B, Bibillo A, Bjornson K, Chaudhuri B, Christians F, Cicero R, Clark S, Dalal R, Dewinter A, Dixon J, Foquet M, Gaertner A, Hardenbol P, Heiner C, Hester K, Holden D, Kearns G, Kong X, Kuse R, Lacroix Y, Lin S, Lundquist P, Ma C, Marks P, Maxham M, Murphy D, Park I, Pham T, Phillips M, Roy J, Sebra R, Shen G, Sorenson J, Tomaney A, Travers K, Trulson M, Vieceli J, Wegener J, Wu D, Yang A, Zaccarin D, Zhao P, Zhong F, Korlach J, Turner S. Science. 2009;323:133. doi: 10.1126/science.1162986. [DOI] [PubMed] [Google Scholar]
- 9.Koren S, Schatz MC, Walenz BP, Martin J, Howard JT, Ganapathy G, Wang Z, Rasko DA, McCombie WR, Jarvis ED, Phillippy AM. Nat Biotechnol. 2012;30:693. doi: 10.1038/nbt.2280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Pennisi E. Science. 2012;336:534. doi: 10.1126/science.336.6081.534. [DOI] [PubMed] [Google Scholar]
- 11.Pollack A. New York Times. Nov 30, 2011. DNA Sequencing Caught in a Deluge of Data. [Google Scholar]
- 12.Feuk L, Carson AR, Scherer SW. Nat Rev Genet. 2006;7:85. doi: 10.1038/nrg1767. [DOI] [PubMed] [Google Scholar]
- 13.Neely RK, Dedecker P, Hotta J-i, Urbanaviciute G, Klimasauskas S, Hofkens J. Chem Sci. 2010;1:453. [Google Scholar]
- 14.Stellwagen NC, Gelfi C, Righetti PG. Biopolymers. 1997;42:687. doi: 10.1002/(SICI)1097-0282(199711)42:6<687::AID-BIP7>3.0.CO;2-Q. [DOI] [PubMed] [Google Scholar]
- 15.Viovy J-L. Rev Mod Phys. 2000;72:813. [Google Scholar]
- 16.Heller C. Electrophoresis. 2001;22:629. doi: 10.1002/1522-2683(200102)22:4<629::AID-ELPS629>3.0.CO;2-S. [DOI] [PubMed] [Google Scholar]
- 17.Karger BL, Guttman A. Electrophoresis. 2009;30:S196. doi: 10.1002/elps.200900218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Heller C. Electrophoresis. 1999;20:1962. doi: 10.1002/(SICI)1522-2683(19990701)20:10<1962::AID-ELPS1962>3.0.CO;2-H. [DOI] [PubMed] [Google Scholar]
- 19.Heller C. Electrophoresis. 1999;20:1978. doi: 10.1002/(SICI)1522-2683(19990701)20:10<1978::AID-ELPS1978>3.0.CO;2-G. [DOI] [PubMed] [Google Scholar]
- 20.Viovy J-L, Duke TAJ. Electrophoresis. 1993;14:322. doi: 10.1002/elps.1150140155. [DOI] [PubMed] [Google Scholar]
- 21.Duke T, Viovy J-L. Phys Rev E. 1994;49:2408. doi: 10.1103/physreve.49.2408. [DOI] [PubMed] [Google Scholar]
- 22.Forster RE, Hert DG, Chiesl TN, Fredlake CP, Barron AE. Electrophoresis. 2009;30:2014. doi: 10.1002/elps.200900264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Kim YS, Morris MD. Anal Chem. 1995;67:784. doi: 10.1021/ac00101a002. [DOI] [PubMed] [Google Scholar]
- 24.Shi X, Hammond RW, Morris MD. Anal Chem. 1995;67:3219. doi: 10.1021/ac00114a018. [DOI] [PubMed] [Google Scholar]
- 25.Rye HS, Yue S, Wemmer DE, Quesada MA, Haugland RP, Mathies RA, Glazer AN. Nucleic Acids Res. 1992;20:2803. doi: 10.1093/nar/20.11.2803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Teague B, Waterman MS, Goldstein S, Potamousis K, Zhou S, Reslewic S, Sarkar D, Valouev A, Churas C, Kidd JM, Kohn S, Runnheim R, Lamers C, Forrest D, Newton MA, Eichler EE, Kent-First M, Surti U, Livny M, Schwartz DC. Proc Natl Acad Sci USA. 2010;107:10848. doi: 10.1073/pnas.0914638107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Hiemenz PC, Lodge TP. Polymer Chemistry: Second Edition. CRC Press; Boca Raton: 2007. [Google Scholar]
- 28.Rubinstein M, Colby RH. Polymer Physics. Oxford University Press; New York: 2003. [Google Scholar]
- 29.Calladine CR, Drew HR. Understanding DNA. Academic Press; San Diego: 1997. [Google Scholar]
- 30.Bloomfield VA, Crothers DM, Tinioco I., Jr . Nucleic Acids: Structures, Properties and Functions. University Science Books; Sausalito, CA: 2000. [Google Scholar]
- 31.Giddings JC. Unified separation science. John Wiley & Sons; New York: 1991. [Google Scholar]
- 32.Dorfman KD. Rev Mod Phys. 2010;82:2903. [Google Scholar]
- 33.Slater GW. Electrophoresis. 2009;30:S181. doi: 10.1002/elps.200900154. [DOI] [PubMed] [Google Scholar]
- 34.Stellwagen NC. Electrophoresis. 2009;30:S188. doi: 10.1002/elps.200900052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Watson JD, Crick FHC. Nature. 1953;171:737. doi: 10.1038/171737a0. [DOI] [PubMed] [Google Scholar]
- 36.Perkins, Smith DE, Larson RG, Chu S. Science. 1995;268:83. doi: 10.1126/science.7701345. [DOI] [PubMed] [Google Scholar]
- 37.Bakajin OB, Duke TAJ, Chou CF, Chan SS, Austin RH, Cox EC. Phys Rev Lett. 1998;80:2737. [Google Scholar]
- 38.Randall GC, Doyle PS. Macromolecules. 2005;38:2410. [Google Scholar]
- 39.Rivetti C, Walker C, Bustamante C. J Mol Biol. 1998;280:41. doi: 10.1006/jmbi.1998.1830. [DOI] [PubMed] [Google Scholar]
- 40.Lu Y, Weers BD, Stellwagen NC. Biopolymers. 2003;70:270. doi: 10.1002/bip.10458. [DOI] [PubMed] [Google Scholar]
- 41.Ortiz V, de Pablo JJ. Phys Rev Lett. 2011;106:238107. doi: 10.1103/PhysRevLett.106.238107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Bustamante C, Marko JF, Siggia ED, Smith S. Science. 1994;265:1599. doi: 10.1126/science.8079175. [DOI] [PubMed] [Google Scholar]
- 43.Smith SB, Cui YJ, Bustamante C. Science. 1996;271:795. doi: 10.1126/science.271.5250.795. [DOI] [PubMed] [Google Scholar]
- 44.Kuznetsov SV, Shen YQ, Benight AS, Ansari A. Biophys J. 2001;81:2864. doi: 10.1016/S0006-3495(01)75927-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Achter EK, Felsenfeld G. Biopolymers. 1971;10:1625. doi: 10.1002/bip.360100916. [DOI] [PubMed] [Google Scholar]
- 46.Murphy MC, Rasnik I, Cheng W, Lohman TM, Ha TJ. Biophys J. 2004;86:2530. doi: 10.1016/S0006-3495(04)74308-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Mills JB, Vacano E, Hagerman PJ. J Mol Biol. 1999;285:245. doi: 10.1006/jmbi.1998.2287. [DOI] [PubMed] [Google Scholar]
- 48.Tinland B, Pluen A, Sturm J, Weill G. Macromolecules. 1997;30:5763. [Google Scholar]
- 49.Smith SB, Finzi L, Bustamante C. Science. 1992;258:1122. doi: 10.1126/science.1439819. [DOI] [PubMed] [Google Scholar]
- 50.Marko JF, Siggia ED. Macromolecules. 1995;28:8759. [Google Scholar]
- 51.de Gennes PG. Scaling Concepts in Polymer Physics. Cornell University Press; Ithaca, NY: 1979. [Google Scholar]
- 52.Cluzel P, Lebrun A, Heller C, Lavery R, Viovy J-L, Chatenay D, Caron F. Science. 1996;271:792. doi: 10.1126/science.271.5250.792. [DOI] [PubMed] [Google Scholar]
- 53.Flory PJ. Principles of Polymer Chemistry. Cornell University Press; Ithaca, NY: 1953. [Google Scholar]
- 54.Li B, Madras N, Sokal AD. J Stat Phys. 1995;80:661. [Google Scholar]
- 55.Gray HB, Jr, Hearst JE. J Mol Biol. 1968;35:111. doi: 10.1016/s0022-2836(68)80041-5. [DOI] [PubMed] [Google Scholar]
- 56.Soda K, Wada A. Biophys Chem. 1984;20:185. doi: 10.1016/0301-4622(84)87023-4. [DOI] [PubMed] [Google Scholar]
- 57.Godfrey JE, Eisenberg H. Biophys Chem. 1976;5:301. doi: 10.1016/0301-4622(76)80042-7. [DOI] [PubMed] [Google Scholar]
- 58.Kam Z, Borochov N, Eisenberg H. Biopolymers. 1981;20:2671. doi: 10.1002/bip.1981.360201213. [DOI] [PubMed] [Google Scholar]
- 59.Lukacs GL, Haggie P, Seksek O, Lechardeur D, Freedman N, Verkman AS. J Biol Chem. 2000;275:1625. doi: 10.1074/jbc.275.3.1625. [DOI] [PubMed] [Google Scholar]
- 60.Voordouw G, Kam Z, Borochov N, Eisenberg H. Biophys Chem. 1978;8:171. doi: 10.1016/0301-4622(78)80008-8. [DOI] [PubMed] [Google Scholar]
- 61.Godfrey JE. Biophys Chem. 1976;5:285. doi: 10.1016/0301-4622(76)80041-5. [DOI] [PubMed] [Google Scholar]
- 62.Smith DE, Perkins TT, Chu S. Macromolecules. 1996;29:1372. [Google Scholar]
- 63.Mansfield ML, Douglas JF. Macromolecules. 2008;41:5412. [Google Scholar]
- 64.Wilcoxon J, Schurr JM. Biopolymers. 1983;22:2273. doi: 10.1002/bip.360221011. [DOI] [PubMed] [Google Scholar]
- 65.Robertson RM, Laib S, Smith DE. Proc Natl Acad Sci USA. 2006;103:7310. doi: 10.1073/pnas.0601903103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Sorlie SS, Pecora R. Macromolecules. 1988;21:1437. [Google Scholar]
- 67.Nicolai T, Mandel M. Macromolecules. 1989;22:2348. [Google Scholar]
- 68.Harpst JA, Dawson JR. Biophys J. 1989;55:1237. doi: 10.1016/S0006-3495(89)82919-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Eimer W, Williamson JR, Boxer SG, Pecora R. Biochemistry. 1990;29:799. doi: 10.1021/bi00455a030. [DOI] [PubMed] [Google Scholar]
- 70.Bonifacio GF, Brown T, Conn GL, Lane AN. Biophys J. 1997;73:1532. doi: 10.1016/S0006-3495(97)78185-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Krasna AI. J Colloid Interface Sci. 1972;39:632. [Google Scholar]
- 72.Allison SA, Sorlie SS, Pecora R. Macromolecules. 1990;23:1110. [Google Scholar]
- 73.Pecora R. Science. 1991;251:893. doi: 10.1126/science.2000490. [DOI] [PubMed] [Google Scholar]
- 74.Eimer W, Pecora R. J Chem Phys. 1991;94:2324. [Google Scholar]
- 75.Fukudome K, Yamaoka K, Ochiai H. Polymer J. 1987;19:1385. [Google Scholar]
- 76.Lederer H, May RP, Kjems JK, Baer G, Heumann H. Eur J Biochem. 1986;161:191. doi: 10.1111/j.1432-1033.1986.tb10141.x. [DOI] [PubMed] [Google Scholar]
- 77.Seils J, Dorfmüller T. Biopolymers. 1991;31:813. doi: 10.1002/bip.360310702. [DOI] [PubMed] [Google Scholar]
- 78.Kovacic RT, Van Holde KE. Biochemistry. 1977;16:1490. doi: 10.1021/bi00626a038. [DOI] [PubMed] [Google Scholar]
- 79.Schmid CW, Rinehart FP, Hearst JE. Biopolymers. 1971;10:883. doi: 10.1002/bip.360100511. [DOI] [PubMed] [Google Scholar]
- 80.Jolly D, Eisenberg H. Biopolymers. 1976;15:61. doi: 10.1002/bip.1976.360150107. [DOI] [PubMed] [Google Scholar]
- 81.Sorlie SS, Pecora R. Macromolecules. 1990;23:487. [Google Scholar]
- 82.Stellwagen NC, Magnusdottir S, Gelfi C, Righetti PG. Biopolymers. 2001;58:390. doi: 10.1002/1097-0282(20010405)58:4<390::AID-BIP1015>3.0.CO;2-K. [DOI] [PubMed] [Google Scholar]
- 83.Yamakawa H, Fujii M. Macromolecules. 1973;6:407. [Google Scholar]
- 84.Rouse PE. J Chem Phys. 1953;21:1272. [Google Scholar]
- 85.Zimm BH. J Chem Phys. 1956;24:269. [Google Scholar]
- 86.Ottinger HC. Rheol Acta. 1996;35:134. [Google Scholar]
- 87.Kenward M, Slater GW. Eur Phys J E. 2004;14:55. doi: 10.1140/epje/i2004-10006-4. [DOI] [PubMed] [Google Scholar]
- 88.Manning GS. Quat Rev Biophys. 1978;11:179. doi: 10.1017/s0033583500002031. [DOI] [PubMed] [Google Scholar]
- 89.Stigter D. J Colloid Interface Sci. 1975;53:296. [Google Scholar]
- 90.Dobrynin AV. Macromolecules. 2006;39:9519. [Google Scholar]
- 91.Stigter D. Biopolymers. 1977;16:1435. doi: 10.1002/bip.1977.360160705. [DOI] [PubMed] [Google Scholar]
- 92.Hsieh CC, Balducci A, Doyle PS. Nano Lett. 2008;8:1683. doi: 10.1021/nl080605+. [DOI] [PubMed] [Google Scholar]
- 93.Odijk T. J Polymer Sci B. 1977;15:477. [Google Scholar]
- 94.Skolnick J, Fixman M. Macromolecules. 1977;10:944. [Google Scholar]
- 95.Dobrynin AV. Macromolecules. 2005;38:9304. [Google Scholar]
- 96.Baumann CG, Smith SB, Bloomfield VA, Bustamante C. Proc Natl Acad Sci USA. 1997;94:6185. doi: 10.1073/pnas.94.12.6185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Porschke D. Biophys Chem. 1991;40:169. doi: 10.1016/0301-4622(91)87006-q. [DOI] [PubMed] [Google Scholar]
- 98.http://www.neb.com.
- 99.Kim YS, Jett JH, Larson EJ, Penttila JR, Marrone BL, Keller RA. Cytometry. 1999;36:324. doi: 10.1002/(sici)1097-0320(19990801)36:4<324::aid-cyto7>3.0.co;2-k. [DOI] [PubMed] [Google Scholar]
- 100.Ferris MM, Yan X, Habbersett RC, Shou Y, Lemanski CL, Jett JH, Yoshida TM, Marrone BL. J Clin Microbiol. 2004;42:1965. doi: 10.1128/JCM.42.5.1965-1976.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.http://www.cdc.gov/pulsenet.
- 102.Schwartz DC, Li X, Hernandez LI, Ramnarain SP, Huff EJ, Wang Y-K. Science. 1993;262:110. doi: 10.1126/science.8211116. [DOI] [PubMed] [Google Scholar]
- 103.Wang YK, Huff EJ, Schwartz DC. Proc Natl Acad Sci USA. 1995;92:165. doi: 10.1073/pnas.92.1.165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Bensimon A, Simon A, Chiffaudel A, Croquette V, Heslot F, Bensimon D. Science. 1994;265:2096. doi: 10.1126/science.7522347. [DOI] [PubMed] [Google Scholar]
- 105.Bensimon D, Simon AJ, Croquette V, Bensimon A. Phys Rev Lett. 1995;74:4754. doi: 10.1103/PhysRevLett.74.4754. [DOI] [PubMed] [Google Scholar]
- 106.Michalet X, Ekong R, Fougerousse F, Rousseaux S, Schurra C, Hornigold N, van Slegtenhorst M, Wolfe J, Povey S, Beckmann JS, Bensimon A. Science. 1997;277:1518. doi: 10.1126/science.277.5331.1518. [DOI] [PubMed] [Google Scholar]
- 107.Skiadas J, Aston C, Samad A, Anantharaman TS, Mishra B, Schwartz DC. Mamm Genome. 1999;10:1005. doi: 10.1007/s003359901148. [DOI] [PubMed] [Google Scholar]
- 108.Lin J, Qi R, Aston C, Jing J, Anantharaman TS, Mishra B, White O, Daly MJ, Minton KW, Venter JC, Schwartz DC. Science. 1999;285:1558. doi: 10.1126/science.285.5433.1558. [DOI] [PubMed] [Google Scholar]
- 109.Lai Z, Jing J, Aston C, Clarke V, Apodaca J, Dimalanta ET, Carucci DJ, Gardner MJ, Mishra B, Anantharaman TS, Paxia S, Hoffman SL, Venter JC, Huff EJ, Schwartz DC. Nat Genet. 1999;23:309. doi: 10.1038/15484. [DOI] [PubMed] [Google Scholar]
- 110.Anantharaman TS, Mishra B, Schwartz DC. J Comput Biol. 1997;4:91. doi: 10.1089/cmb.1997.4.91. [DOI] [PubMed] [Google Scholar]
- 111.Valouev A, Li L, Liu Y-C, Schwartz DC, Yang Y, Zhang Y, Waterman MS. J Comput Biol. 2006;13:442. doi: 10.1089/cmb.2006.13.442. [DOI] [PubMed] [Google Scholar]
- 112.Valouev A, Schwartz DC, Zhou S, Waterman MS. Proc Natl Acad Sci USA. 2006;103:15770. doi: 10.1073/pnas.0604040103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113.Das SK, Austin MD, Akana MC, Deshpande P, Cao H, Xiao M. Nucleic Acids Res. 2010;38:e177. doi: 10.1093/nar/gkq673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114.Lam ET, Hastie A, Lin C, Ehrlich D, Das SK, Austin MD, Deshpande P, Cao H, Nagarajan N, Xiao M, Kwok PY. Nat Biotechnol. 2012;30:771–776. doi: 10.1038/nbt.2303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115.Chan EY, Goncalves NM, Haeusler RA, Hatch AJ, Larson JW, Maletta AM, Yantz GR, Carstea ED, Fuchs M, Wong GG, Gullans SR, Gilmanshin R. Genome Res. 2004;14:1137. doi: 10.1101/gr.1635204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116.http://www.usgenomics.com.
- 117.Qu X, Wu D, Mets L, Scherer NF. Proc Natl Acad Sci USA. 2004;101:11298. doi: 10.1073/pnas.0402155101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118.Gordon MP, Ha T, Selvin PR. Proc Natl Acad Sci USA. 2004;101:6462. doi: 10.1073/pnas.0401638101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119.Xiao M, Phong A, Ha C, Chan TF, Cai D, Leung L, Wan E, Kistler AL, DeRisi JL, Selvin PR, Kwok PY. Nucleic Acids Res. 2007;35:e16. doi: 10.1093/nar/gkl1044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 120.Neely RK, Deen J, Hofkens J. Biopolymers. 2011;95:298. doi: 10.1002/bip.21579. [DOI] [PubMed] [Google Scholar]
- 121.Hu X, Aston C, Schwartz DC. Biochem Bioph Res Co. 1999;254:466. doi: 10.1006/bbrc.1998.9971. [DOI] [PubMed] [Google Scholar]
- 122.Crut A, Géron-Landre B, Bonnet I, Bonneau S, Desbiolles P, Escudé C. Nucleic Acids Res. 2005;33:e98. doi: 10.1093/nar/gni097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 123.Jing J, Lai Z, Aston C, Lin J, Carucci DJ, Gardner MJ, Mishra B, Anantharaman TS, Tettelin H, Cummings LM, Hoffman SL, Venter JC, Schwartz DC. Genome Res. 1999;9:175. [PMC free article] [PubMed] [Google Scholar]
- 124.Herrick J, Michalet X, Conti C, Schurra C, Bensimon A. Proc Natl Acad Sci USA. 2000;97:222. doi: 10.1073/pnas.97.1.222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125.Zhou S, Kile A, Bechner M, Place M, Kvikstad E, Deng W, Wei J, Severin J, Runnheim R, Churas C, Forrest D, Dimalanta ET, Lamers C, Burland V, Blattner FR, Schwartz DC. J Bacteriol. 2004;186:7773. doi: 10.1128/JB.186.22.7773-7782.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 126.Lim A, Dimalanta ET, Potamousis KD, Yen G, Apodoca J, Tao CH, Lin JY, Qi R, Skiadas J, Ramanathan A, Perna NT, Plunkett G, Burland V, Mau B, Hackett J, Blattner FR, Anantharaman TS, Mishra B, Schwartz DC. Genome Res. 2001;11:1584. doi: 10.1101/gr.172101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 127.Kotewicz ML, Jackson SA, LeClerc JE, Cebula TA. Microbiology. 2007;153:1720. doi: 10.1099/mic.0.2006/004507-0. [DOI] [PubMed] [Google Scholar]
- 128.Kotewicz ML, Mammel MK, LeClerc JE, Cebula TA. Microbiology. 2008;154:3518. doi: 10.1099/mic.0.2008/019026-0. [DOI] [PubMed] [Google Scholar]
- 129.Zhou S, Deng W, Anantharaman TS, Lim A, Dimalanta ET, Wang J, Wu T, Chunhong T, Creighton R, Kile A, Kvikstad E, Bechner M, Yen G, Garic-Stankovic A, Severin J, Forrest D, Runnheim R, Churas C, Lamers C, Perna NT, Burland V, Blattner FR, Mishra B, Schwartz DC. Appl Environ Microbiol. 2002;68:6321. doi: 10.1128/AEM.68.12.6321-6331.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 130.Zhou S, Kvikstad E, Kile A, Severin J, Forrest D, Runnheim R, Churas C, Hickman JW, Mackenzie C, Choudhary M, Donohue T, Kaplan S, Schwartz DC. Genome Res. 2003;13:2142. doi: 10.1101/gr.1128803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 131.Zhou S, Kile A, Kvikstad E, Bechner M, Severin J, Forrest D, Runnheim R, Churas C, Anantharaman TS, Myler P, Vogt C, Ivens A, Stuart K, Schwartz DC. Mol Biochem Parasit. 2004;138:97. doi: 10.1016/j.molbiopara.2004.08.002. [DOI] [PubMed] [Google Scholar]
- 132.Reslewic S, Zhou S, Place M, Zhang Y, Briska A, Goldstein S, Churas C, Runnheim R, Forrest D, Lim A, Lapidus A, Han CS, Roberts GP, Schwartz DC. Appl Environ Microbiol. 2005;71:5511. doi: 10.1128/AEM.71.9.5511-5522.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 133.Ferris MM, Yoshida TM, Marrone BL, Keller RA. Anal Biochem. 2005;337:278. doi: 10.1016/j.ab.2004.10.050. [DOI] [PubMed] [Google Scholar]
- 134.Lim SF, Karpusenko A, Sakon JJ, Hook JA, Lamar TA, Riehn R. Biomicrofluidics. 2011;5:034106. doi: 10.1063/1.3613671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 135.Zhou S, Wei F, Nguyen J, Bechner M, Potamousis K, Goldstein S, Pape L, Mehan MR, Churas C, Pasternak S, Forrest DK, Wise R, Ware D, Wing RA, Waterman MS, Livny M, Schwartz DC. PLOS Genet. 2009;5:e1000711. doi: 10.1371/journal.pgen.1000711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 136.Wu C-W, Schramm TM, Zhou S, Schwartz DC, Talaat AM. BMC Genomics. 2009;10:25. doi: 10.1186/1471-2164-10-25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 137.Shukla SK, Kislow J, Briska A, Henkhaus J, Dykes C. J Bacteriol. 2009;191:5717. doi: 10.1128/JB.00325-09. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 138.Giacalone J, Delobette S, Gibaja V, Ni L, Skiadas Y, Qi R, Edington J, Lai Z, Gebauer D, Zhao H, Anantharaman T, Mishra B, Brown LG, Saxena R, Page DC, Schwartz DC. Genome Res. 2000;10:1421. doi: 10.1101/gr.112100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 139.Brenner H, Edwards DA. Macrotransport Processes. Butterworth-Heinemann; Boston: 1993. [Google Scholar]
- 140.Turner SW, Perez AM, Lopez A, Craighead HG. J Vac Sci Technol B. 1998;16:3835. [Google Scholar]
- 141.Turner SWP, Cabodi M, Craighead HG. Phys Rev Lett. 2002;88:128103. doi: 10.1103/PhysRevLett.88.128103. [DOI] [PubMed] [Google Scholar]
- 142.Baba M, Sano T, Iguchi N, Iida K, Sakamoto T, Kawaura H. Appl Phys Lett. 2003;83:1468. [Google Scholar]
- 143.Olivera BM, Baine P, Davidson N. Biopolymers. 1964;2:245. [Google Scholar]
- 144.Yarmola E, Calabrese PP, Chrambach A, Weiss GH. J Phys Chem B. 1997;101:2381. [Google Scholar]
- 145.Dorfman KD, Brenner H. J Appl Phys. 2001;90:6553. [Google Scholar]
- 146.Giddings JC, Eyring H. J Phys Chem. 1955;59:416. [Google Scholar]
- 147.Weiss GH. J Stat Phys. 1976;15:157. [Google Scholar]
- 148.Weiss GH, Rubin RJ. Adv Chem Phys. 1983;52:363. [Google Scholar]
- 149.Long D, Stone HA, Ajdari A. J Colloid Interface Sci. 1999;212:338. doi: 10.1006/jcis.1998.6015. [DOI] [PubMed] [Google Scholar]
- 150.Han J, Craighead HG. Science. 2000;288:1026. doi: 10.1126/science.288.5468.1026. [DOI] [PubMed] [Google Scholar]
- 151.Cussler EL. Diffusion: Mass Transfer in Fluid Systems. Cambridge University Press; 1997. [Google Scholar]
- 152.Redner A. Guide to First-Passage Processes. Cambridge University Press; Cambridge: 2001. [Google Scholar]
- 153.Culbertson CT, Jacobson SC, Ramsey JM. Anal Chem. 1998;70:3781. [Google Scholar]
- 154.Molho JI, Herr AE, Mosier BP, Santiago JG, Kenny TW, Brennen RA, Gordon GB, Mohammadi B. Anal Chem. 2001;73:1350. [Google Scholar]
- 155.Rush BM, Dorfman KD, Brenner H, Kim S. Ind Eng Chem Res. 2002;41:4652. [Google Scholar]
- 156.Yariv E, Brenner H, Kim S. SIAM J Appl Math. 2004;64:1099. [Google Scholar]
- 157.Culbertson CT, Jacobson SC, Ramsey JM. Talanta. 2002;56:365. doi: 10.1016/s0039-9140(01)00602-6. [DOI] [PubMed] [Google Scholar]
- 158.Ou J, Cho J, Olson DW, Dorfman KD. Phys Rev E. 2009;79:061904. doi: 10.1103/PhysRevE.79.061904. [DOI] [PubMed] [Google Scholar]
- 159.Lo RC, Ugaz VM. Lab Chip. 2008;8:2135. doi: 10.1039/b811033f. [DOI] [PubMed] [Google Scholar]
- 160.Park S-G, Olson DW, Dorfman KD. Lab Chip. 2012;12:1463. doi: 10.1039/c2lc00016d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 161.Haab BB, Mathies RA. Anal Chem. 1995;67:3253. doi: 10.1021/ac00114a023. [DOI] [PubMed] [Google Scholar]
- 162.Ou J, Joswiak MN, Carpenter SJ, Dorfman KD. J Vac Sci Technol A. 2011;29:011025. [Google Scholar]
- 163.Zhou H, Miller AW, Sosic Z, Buchholz B, Barron AE, Kotler L, Karger BL. Anal Chem. 2000;72:1045. doi: 10.1021/ac991117c. [DOI] [PubMed] [Google Scholar]
- 164.Minc N, Viovy J-L, Dorfman KD. Phys Rev Lett. 2005;94:198105. doi: 10.1103/PhysRevLett.94.198105. [DOI] [PubMed] [Google Scholar]
- 165.Guo X-H, Huff EJ, Schwartz DC. Nature. 1992;359:783. doi: 10.1038/359783a0. [DOI] [PubMed] [Google Scholar]
- 166.Meng X, Benson K, Chada K, Huff EJ, Schwartz DC. Nat Genet. 1995;9:432. doi: 10.1038/ng0495-432. [DOI] [PubMed] [Google Scholar]
- 167.Wang Y, Reinhart WF, Tree DR, Dorfman KD. Biomicrofluidics. 2012;6:014101. doi: 10.1063/1.3672691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 168.Pertsinidis A, Zhang Y, Chu S. Nature. 2010;466:647. doi: 10.1038/nature09163. [DOI] [PubMed] [Google Scholar]
- 169.Tang J, Levy SL, Trahan DW, Jones JJ, Craighead HG, Doyle PS. Macromolecules. 2010;43:7368. [Google Scholar]
- 170.Ogston AG. Trans Faraday Soc. 1958;54:1754. [Google Scholar]
- 171.Morris CJOR. Protides of the Biological Fluids. 1966;14:543. [Google Scholar]
- 172.Rodbard D, Chrambach A. Proc Natl Acad Sci USA. 1970;65:970. doi: 10.1073/pnas.65.4.970. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 173.Ferguson KA. Metabolism. 1964;13:985. doi: 10.1016/s0026-0495(64)80018-4. [DOI] [PubMed] [Google Scholar]
- 174.Boileau J, Slater GW. Electrophoresis. 2001;22:673. doi: 10.1002/1522-2683(200102)22:4<673::AID-ELPS673>3.0.CO;2-W. [DOI] [PubMed] [Google Scholar]
- 175.Baumgartner A, Muthukumar M. J Chem Phys. 1987;87:3082. [Google Scholar]
- 176.Muthukumar M, Baumgartner A. Macromolecules. 1989;22:1937. [Google Scholar]
- 177.Muthukumar M, Baumgartner A. Macromolecules. 1989;22:1941. [Google Scholar]
- 178.Smisek DL, Hoagland DA. Science. 1990;248:1221. doi: 10.1126/science.2349481. [DOI] [PubMed] [Google Scholar]
- 179.Rousseau J, Drouin G, Slater GW. Phys Rev Lett. 1997;79:1945. [Google Scholar]
- 180.Nykypanchuk D, Strey HH, Hoagland DA. Science. 2002;297:987. doi: 10.1126/science.1073277. [DOI] [PubMed] [Google Scholar]
- 181.Han J, Turner SW, Craighead HG. Phys Rev Lett. 1999;83:1688. [Google Scholar]
- 182.Han J, Craighead HG. J Vac Sci Technol A. 1999;17:2142. [Google Scholar]
- 183.Han J, Craighead HG. Anal Chem. 2002;74:394. doi: 10.1021/ac0107002. [DOI] [PubMed] [Google Scholar]
- 184.Fu J, Mao P, Han J. Appl Phys Lett. 2005;87:263902. doi: 10.1063/1.2149979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 185.Fu J, Yoo J, Han J. Phys Rev Lett. 2006;97:018103. doi: 10.1103/PhysRevLett.97.018103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 186.Shi N, Ugaz V. Phys Rev Lett. 2010;105:108101. doi: 10.1103/PhysRevLett.105.108101. [DOI] [PubMed] [Google Scholar]
- 187.Wang J, Gonzalez AD, Ugaz VM. Adv Mater. 2008;20:4482. [Google Scholar]
- 188.Semenov AN, Joanny J-F. Phys Rev E. 1997;55:789. [Google Scholar]
- 189.Lerman L, Frisch H. Biopolymers. 1982;21:995. doi: 10.1002/bip.360210511. [DOI] [PubMed] [Google Scholar]
- 190.Lumpkin O, Zimm BH. Biopolymers. 1982;21:2315. doi: 10.1002/bip.360211116. [DOI] [PubMed] [Google Scholar]
- 191.Slater GW, Noolandi J. Phys Rev Lett. 1985;55:1579. doi: 10.1103/PhysRevLett.55.1579. [DOI] [PubMed] [Google Scholar]
- 192.Noolandi J, Rousseau J, Slater GW, Turmel C, Lalande M. Phys Rev Lett. 1987;58:2428. doi: 10.1103/PhysRevLett.58.2428. [DOI] [PubMed] [Google Scholar]
- 193.Duke TAJ, Semenov AN, Viovy J-L. Phys Rev Lett. 1992;69:3260. doi: 10.1103/PhysRevLett.69.3260. [DOI] [PubMed] [Google Scholar]
- 194.Duke T, Viovy J-L, Semenov AN. Biopolymers. 1994;34:239. [Google Scholar]
- 195.Semenov AN, Duke TAJ, Viovy J-L. Phys Rev E. 1995;51:1520. doi: 10.1103/physreve.51.1520. [DOI] [PubMed] [Google Scholar]
- 196.Heller C, Duke TAJ, Viovy J-L. Biopolymers. 1994;34:249. [Google Scholar]
- 197.Slater GW. Electrophoresis. 1993;14:1. doi: 10.1002/elps.1150140102. [DOI] [PubMed] [Google Scholar]
- 198.Deutsch JM. Science. 1988;240:922. doi: 10.1126/science.3363374. [DOI] [PubMed] [Google Scholar]
- 199.Deutsch JM, Madden TL. J Chem Phys. 1989;90:2476. [Google Scholar]
- 200.Popelka S, Kabatek Z, Viovy J-L, Gas B. J Chromatogr A. 1999;838:45. [Google Scholar]
- 201.Schwartz DC, Koval M. Nature. 1989;338:520. doi: 10.1038/338520a0. [DOI] [PubMed] [Google Scholar]
- 202.Smith SB, Aldridge PK, Callis JB. Science. 1989;243:203. doi: 10.1126/science.2911733. [DOI] [PubMed] [Google Scholar]
- 203.Obukhov SP, Rubinstein M. J Phys II. 1993;3:1455. [Google Scholar]
- 204.Lee N, Obukhov S, Rubinstein Electrophoresis. 1996;17:1011. doi: 10.1002/elps.1150170608. [DOI] [PubMed] [Google Scholar]
- 205.Viovy J-L. Electrophoresis. 1989;10:429. doi: 10.1002/elps.1150100521. [DOI] [PubMed] [Google Scholar]
- 206.Birren BW, Lai E, Clark SM, Hood L, Simon MI. Nucleic Acids Res. 1988;16:7563. doi: 10.1093/nar/16.15.7563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 207.Crater GD, Gregg MR, Holzwarth G. Electrophoresis. 1989;10:310. doi: 10.1002/elps.1150100507. [DOI] [PubMed] [Google Scholar]
- 208.Smith CL, Cantor CR. Methods Enzymol. 1987;155:449. doi: 10.1016/0076-6879(87)55030-3. [DOI] [PubMed] [Google Scholar]
- 209.Birren B, Lai E. Pulsed field gel electrophoresis: A practical guide. Academic Press; San Diego, CA: 1993. [Google Scholar]
- 210.Anand R. Trends Gen. 1986;2:278. [Google Scholar]
- 211.Smith CL, Cantor CR. Nature. 1986;319:701. [Google Scholar]
- 212.Olson MV. J Chromatogr. 1989;470:377. doi: 10.1016/s0021-9673(01)83565-2. [DOI] [PubMed] [Google Scholar]
- 213.Gardiner K. Anal Chem. 1991;63:658. doi: 10.1021/ac00007a003. [DOI] [PubMed] [Google Scholar]
- 214.Sor F. Methods Mol Cell Biol. 1992;3:65. [Google Scholar]
- 215.Schwartz DC, Cantor CR. Cell. 1984;37:67. doi: 10.1016/0092-8674(84)90301-5. [DOI] [PubMed] [Google Scholar]
- 216.Chu G, Vollrath D, Davis RW. Science. 1986;234:1582. doi: 10.1126/science.3538420. [DOI] [PubMed] [Google Scholar]
- 217.Clark SM, Lai E, Birren BW, Hood L. Science. 1988;241:1203. doi: 10.1126/science.3045968. [DOI] [PubMed] [Google Scholar]
- 218.Vollrath D, Davis RW. Nucleic Acids Res. 1987;15:7865. doi: 10.1093/nar/15.19.7865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 219.Mathew MK, Smith CL, Cantor CR. Biochemistry. 1988;27:9210. doi: 10.1021/bi00426a020. [DOI] [PubMed] [Google Scholar]
- 220.Akerman B, Jonsson M. J Phys Chem. 1990;94:3828. [Google Scholar]
- 221.Gurrieri S, Rizzarelli E, Beach D, Bustamante C. Biochemistry. 1990;29:3396. doi: 10.1021/bi00465a036. [DOI] [PubMed] [Google Scholar]
- 222.Southern EM, Anand R, Brown WRA, Fletcher DS. Nucleic Acids Res. 1987;15:5925. doi: 10.1093/nar/15.15.5925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 223.Slater GW, Noolandi J. Electrophoresis. 1989;10:413. doi: 10.1002/elps.1150100520. [DOI] [PubMed] [Google Scholar]
- 224.Deutsch JM. J Chem Phys. 1989;90:7436. [Google Scholar]
- 225.Duke TAJ, Viovy J-L. J Chem Phys. 1992;96:8552. [Google Scholar]
- 226.Hutson MS, Holzwarth G, Duke T, Viovy J-L. Biopolymers. 1995;35:297. [Google Scholar]
- 227.Neitzey LM, Holzwarth G, Duke T, Viovy J-L. Biopolymers. 1995;35:307. [Google Scholar]
- 228.Long D, Viovy J-L. Phys Rev E. 1996;53:803. doi: 10.1103/physreve.53.803. [DOI] [PubMed] [Google Scholar]
- 229.Duke TAJ, Austin RH, Cox EC, Chan SS. Electrophoresis. 1996;17:1075. doi: 10.1002/elps.1150170616. [DOI] [PubMed] [Google Scholar]
- 230.Gunderson K, Chu G. Mol Cell Biol. 1991;11:3348. doi: 10.1128/mcb.11.6.3348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 231.Duke TAJ, Viovy J-L. Phys Rev Lett. 1992;68:542. doi: 10.1103/PhysRevLett.68.542. [DOI] [PubMed] [Google Scholar]
- 232.Slater GW, Noolandi J. Biopolymers. 1985;24:2181. [Google Scholar]
- 233.Fesjian S, Frisch HL, Jamil T. Biopolymers. 1986;25:1179. doi: 10.1002/bip.360250702. [DOI] [PubMed] [Google Scholar]
- 234.Viovy J-L. Biopolymers. 1987;26:1929. [Google Scholar]
- 235.Carle GF, Frank M, Olson MV. Science. 1986;232:65. doi: 10.1126/science.3952500. [DOI] [PubMed] [Google Scholar]
- 236.Noolandi J, Slater GW, Lim HA, Viovy J-L. Science. 1989;243:1456. doi: 10.1126/science.2928779. [DOI] [PubMed] [Google Scholar]
- 237.Duke TAJ. J Chem Phys. 1990;93:9055. [Google Scholar]
- 238.Zimm BH. Phys Rev Lett. 1988;61:2965. doi: 10.1103/PhysRevLett.61.2965. [DOI] [PubMed] [Google Scholar]
- 239.Zimm BH. J Chem Phys. 1991;94:2187. [Google Scholar]
- 240.Heller C, Pohl FM. Nucleic Acids Res. 1990;18:6299. doi: 10.1093/nar/18.21.6299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 241.Kobayashi T, Doi M, Makino Y, Ogawa M. Macromolecules. 1990;23:4480. [Google Scholar]
- 242.Marziali A, Pel J, Bizzotto D, Whitehead LA. Electrophoresis. 2005;26:82. doi: 10.1002/elps.200406140. [DOI] [PubMed] [Google Scholar]
- 243.Broemeling D, Pel J, Gunn D, Mai L, Thompson J, Poon H, Marziali A. JALA. 2008;13:40. doi: 10.1016/j.jala.2007.10.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 244.Pel J, Broemeling D, Mai L, Poon H, Tropini G, Warren R, Holt R, Marziali A. Proc Natl Acad Sci USA. 2009;106:14796. doi: 10.1073/pnas.0907402106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 245.Viovy J-L, Heller C. In: Capillary Electrophoresis: An Analytical Tool in Biotechnology (Analytical Biotechnology series) Righetti PG, editor. CRC Press; Boca Raton: 1996. p. 477. Chapter Principles of size-based separations in polymer solutions. [Google Scholar]
- 246.Albarghouthi MN, Barron AE. Electrophoresis. 2000;21:4096. doi: 10.1002/1522-2683(200012)21:18<4096::AID-ELPS4096>3.0.CO;2-W. [DOI] [PubMed] [Google Scholar]
- 247.Quesada MA. Curr Opin Biotech. 1997;8:82. doi: 10.1016/s0958-1669(97)80162-0. [DOI] [PubMed] [Google Scholar]
- 248.Dovichi NJ. Electrophoresis. 1997;18:2393. doi: 10.1002/elps.1150181229. [DOI] [PubMed] [Google Scholar]
- 249.Albarghouthi MN, Buchholz BA, Doherty EAS, Bogdan FM, Zhou HH, Barron AE. Electrophoresis. 2001;22:737. doi: 10.1002/1522-2683(200102)22:4<737::AID-ELPS737>3.0.CO;2-S. [DOI] [PubMed] [Google Scholar]
- 250.Buchholz BA, Shi W, Barron AE. Electrophoresis. 2002;23:1398. doi: 10.1002/1522-2683(200205)23:10<1398::AID-ELPS1398>3.0.CO;2-8. [DOI] [PubMed] [Google Scholar]
- 251.Bird RB, Armstrong RC, Hassager O. Dynamics of Polymeric Liquids Volume 1: Fluid Mechanics. John Wiley & Sons; New York: 1987. [Google Scholar]
- 252.Cottet H, Gareil P. Electrophoresis. 2002;23:2788. doi: 10.1002/1522-2683(200208)23:16<2788::AID-ELPS2788>3.0.CO;2-C. [DOI] [PubMed] [Google Scholar]
- 253.Chen H-S, Chang H-T. Anal Chem. 1999;71:2033. doi: 10.1021/ac981356k. [DOI] [PubMed] [Google Scholar]
- 254.Kan CW, Barron AE. Electrophoresis. 2003;24:55. doi: 10.1002/elps.200390031. [DOI] [PubMed] [Google Scholar]
- 255.Kan CW, Doherty EAS, Buchholz BA, Barron AE. Electrophoresis. 2004;25:1007. doi: 10.1002/elps.200305785. [DOI] [PubMed] [Google Scholar]
- 256.Mitnik L, Salome L, Viovy J-L, Heller C. J Chromatogr A. 1995;710:309. doi: 10.1016/0021-9673(95)00500-5. [DOI] [PubMed] [Google Scholar]
- 257.Cottet H, Gareil P, Viovy J-L. Electrophoresis. 1998;19:2151. doi: 10.1002/elps.1150191219. [DOI] [PubMed] [Google Scholar]
- 258.Wu CH, Quesada MA, Schneider DK, Farinato R, Studier FW, Chu B. Electrophoresis. 1996;17:1103. doi: 10.1002/elps.1150170620. [DOI] [PubMed] [Google Scholar]
- 259.Song LG, Liu TB, Liang DH, Fang DF, Chu B. Electrophoresis. 2001;22:3688. doi: 10.1002/1522-2683(200109)22:17<3688::AID-ELPS3688>3.0.CO;2-I. [DOI] [PubMed] [Google Scholar]
- 260.Sun M, Lin JS, Barron AE. Electrophoresis. 2011;32:3233. doi: 10.1002/elps.201100260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 261.Liang D, Song L, Zhou S, Zaitsev VS, Chu B. Electrophoresis. 1999;20:2856. doi: 10.1002/(SICI)1522-2683(19991001)20:14<2856::AID-ELPS2856>3.0.CO;2-#. [DOI] [PubMed] [Google Scholar]
- 262.Carrilho E, Ruiz-Martinez MC, Berka J, Smirnov I, Goetzinger W, Miller AW, Brady D, Karger BL. Anal Chem. 1996;68:3305. doi: 10.1021/ac960411r. [DOI] [PubMed] [Google Scholar]
- 263.Goetzinger W, Kotler L, Carrilho E, Ruiz-Martinez MC, Salas-Solano O, Karger BL. Electrophoresis. 1998;19:242. doi: 10.1002/elps.1150190217. [DOI] [PubMed] [Google Scholar]
- 264.Sartori A, Barbier V, Viovy J-L. Electrophoresis. 2003;24:421. doi: 10.1002/elps.200390052. [DOI] [PubMed] [Google Scholar]
- 265.Noolandi J. Electrophoresis. 1993;14:680. doi: 10.1002/elps.11501401108. [DOI] [PubMed] [Google Scholar]
- 266.Völkel AR, Noolandi J. Macromolecules. 1995;28:8182. [Google Scholar]
- 267.Heller C, Slater GWW, Mayer P, Dovichi N, Pinto D, Viovy J-L, Drouin G. J Chromatogr A. 1998;806:113. [Google Scholar]
- 268.Ren H, Karger AE, Oaks F, Menchen S, Slater GW, Drouin G. Electrophoresis. 1999;20:2501. doi: 10.1002/(SICI)1522-2683(19990801)20:12<2501::AID-ELPS2501>3.0.CO;2-H. [DOI] [PubMed] [Google Scholar]
- 269.Desruisseaux C, Long D, Drouin G, Slater GW. Macromolecules. 2001;34:44. [Google Scholar]
- 270.Haynes RD, Meagher RJ, Won J-I, Bogdan FM, Barron AE. Bioconjugate Chem. 2005;16:929. doi: 10.1021/bc0496915. [DOI] [PubMed] [Google Scholar]
- 271.Haynes RD, Meagher RJ, Barron AE. Biopolymers. 2011;96:702. doi: 10.1002/bip.21627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 272.Meagher RJ, Won J-I, Coyne JA, Lin J, Barron AE. Anal Chem. 2008;80:2842. doi: 10.1021/ac702591t. [DOI] [PubMed] [Google Scholar]
- 273.Albrecht JC, Lin JS, Barron AE. Anal Chem. 2011;83:509. doi: 10.1021/ac102188p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 274.Lin JS, Albrecht JC, Meagher RJ, Wang X, Barron AE. Biomacromolecules. 2011;12:2275. doi: 10.1021/bm200358r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 275.Lau C, Bitton R, Bianco-Peled H, Schultz DG, Cookson DJ, Grosser ST, Schneider JW. J Phys Chem B. 2006;110:9027. doi: 10.1021/jp057049h. [DOI] [PubMed] [Google Scholar]
- 276.Grosser ST, Savard JM, Schneider JW. Anal Chem. 2007;79:9513. doi: 10.1021/ac7016376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 277.Savard JM, Grosser ST, Schneider JW. Electrophoresis. 2008;29:2779. doi: 10.1002/elps.200700580. [DOI] [PubMed] [Google Scholar]
- 278.Manz A, Harrison DJ, Verpoorte EMJ, Fettinger JC, Paulus A, Ludi H, Widmer HM. J Chromatogr. 1992;593:253. [Google Scholar]
- 279.Effenhauser CS, Manz A, Widmer HM. Anal Chem. 1993;65:2637. [Google Scholar]
- 280.Harrison DJ, Fluri K, Seiler K, Fan Z, Effenhauser CS, Manz A. Science. 1993;261:895. doi: 10.1126/science.261.5123.895. [DOI] [PubMed] [Google Scholar]
- 281.Duffy DC, McDonald JC, Schueller OJA, Whitesides GM. Anal Chem. 1998;70:4974. doi: 10.1021/ac980656z. [DOI] [PubMed] [Google Scholar]
- 282.Burns MA, Johnson BN, Brahmasandra SN, Handique K, Webster JR, Krishnan M, Sammarco TS, Man PM, Jones D, Heldsinger D, Mastrangelo CH, Burke DT. Science. 1998;282:484. doi: 10.1126/science.282.5388.484. [DOI] [PubMed] [Google Scholar]
- 283.Lagally ET, Mednitz I, Mathies RA. Anal Chem. 2001;73:565. doi: 10.1021/ac001026b. [DOI] [PubMed] [Google Scholar]
- 284.Pal R, Yang M, Lin R, Johnson BN, Srivastava N, Razzacki SZ, Chomistek KJ, Heldsinger DC, Haque RM, Ugaz VM, Thwar PK, Chen Z, Alfano K, Yim MB, Krishnan M, Fuller AO, Larson RG, Burke DT, Burns MA. Lab Chip. 2005;5:1024. doi: 10.1039/b505994a. [DOI] [PubMed] [Google Scholar]
- 285.Easley CJ, Karlinsey JM, Bienvenue JM, Legendre LA, Roper MG, Feldman SH, Hughes MA, Hewlett EL, Merkel TJ, Ferrance JP, Landers JP. Proc Natl Acad Sci USA. 2006;103:19272. doi: 10.1073/pnas.0604663103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 286.Thaitrong N, Liu P, Briese T, Lipkin WI, Chiesl TN, Higa Y, Mathies RA. Anal Chem. 2010;82:10102. doi: 10.1021/ac1020744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 287.Liu P, Li X, Greenspoon SA, Scherer JR, Mathies RA. Lab Chip. 2011;11:1041. doi: 10.1039/c0lc00533a. [DOI] [PubMed] [Google Scholar]
- 288.Emrich CA, Tian H, Medintz IL, Mathies RA. Anal Chem. 2002;74:5076. doi: 10.1021/ac020236g. [DOI] [PubMed] [Google Scholar]
- 289.Greenspoon SA, Yeung SHI, Johnson KR, Chu WK, Rhee HN, McGuckian AB, Crouse CA, Chiesl TN, Barron AE, Scherer JR, Ban JD, Mathies RA. J Forensic Sci. 2008;53:828. doi: 10.1111/j.1556-4029.2008.00750.x. [DOI] [PubMed] [Google Scholar]
- 290.Woolley AT, Mathies RA. Proc Natl Acad Sci USA. 1994;91:11348. doi: 10.1073/pnas.91.24.11348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 291.Woolley AT, Mathies RA. Anal Chem. 1995;67:3676. doi: 10.1021/ac00116a010. [DOI] [PubMed] [Google Scholar]
- 292.Brahmasandra SN, Ugaz VM, Burke DT, Mastrangelo CH, Burns MA. Electrophoresis. 2001;22:300. doi: 10.1002/1522-2683(200101)22:2<300::AID-ELPS300>3.0.CO;2-F. [DOI] [PubMed] [Google Scholar]
- 293.Ugaz VM, Brahmasandra SN, Burke DT, Burns MA. Electrophoresis. 2002;23:1450. doi: 10.1002/1522-2683(200205)23:10<1450::AID-ELPS1450>3.0.CO;2-L. [DOI] [PubMed] [Google Scholar]
- 294.Fredlake CP, Hert DG, Kan CW, Chiesl TN, Root BE, Forster RE, Barron AE. Proc Natl Acad Sci USA. 2008;105:476. doi: 10.1073/pnas.0705093105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 295.Manz A, Graber N, Widmer HM. Sensors Actuators B. 1990;1:244. [Google Scholar]
- 296.Albrecht JC, Kerby MB, Niedringhaus TP, Lin JS, Wang XX, Barron AE. Electrophoresis. 2011;32:1201. doi: 10.1002/elps.201000574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 297.Harrison DJ, Manz A, Fan Z, Ludi H, Widmer HM. Anal Chem. 1992;64:1926. [Google Scholar]
- 298.Jacobson SC, Hergenroder R, Koutny LB, Warmak RJ, Ramsey JM. Anal Chem. 1994;66:1107. [Google Scholar]
- 299.Ermakov SV, Jacobson SC, Ramsey JM. Anal Chem. 2000;72:3512. doi: 10.1021/ac991474n. [DOI] [PubMed] [Google Scholar]
- 300.Lin C-H, Yang R-J, Tai C-H, Lee C-Y, Fu L-M. J Micromech Microeng. 2004;14:639. [Google Scholar]
- 301.Futterer C, Minc N, Bormuth V, Codarbox J-H, Laval P, Rossier J, Viovy J-L. Lab Chip. 2004;4:351. doi: 10.1039/b316729a. [DOI] [PubMed] [Google Scholar]
- 302.Minc N, Futterer C, Dorfman KD, Bancaud A, Gosse C, Goubault C, Viovy J-L. Anal Chem. 2004;76:3770. doi: 10.1021/ac035246b. [DOI] [PubMed] [Google Scholar]
- 303.Fu L-M, Yang R-J, Lee G-B, Pan Y-J. Electrophoresis. 2003;24:3026. doi: 10.1002/elps.200305528. [DOI] [PubMed] [Google Scholar]
- 304.Fu L-M, Yang R-J, Lee G-B. Anal Chem. 2003;75:1905. doi: 10.1021/ac020741d. [DOI] [PubMed] [Google Scholar]
- 305.Gai HW, Yu LF, Dai ZP, Ma YF, Lin BC. Electrophoresis. 2004;25:1888. doi: 10.1002/elps.200305835. [DOI] [PubMed] [Google Scholar]
- 306.Fu L-M, Yang R-J, Lee G-B, Liu H-H. Anal Chem. 2002;74:5084. doi: 10.1021/ac025821w. [DOI] [PubMed] [Google Scholar]
- 307.Ren L, Sinton D, Li D. J Micromech Microeng. 2003;13:739. [Google Scholar]
- 308.Sinton D, Ren LQ, Li DQ. J Colloid Interface Sci. 2003;260:431. doi: 10.1016/s0021-9797(02)00181-9. [DOI] [PubMed] [Google Scholar]
- 309.Brody JR, Kern SE. BioTechniques. 2004;36:214. doi: 10.2144/04362BM02. [DOI] [PubMed] [Google Scholar]
- 310.Brody JR, Calhoun ES, Gallmeier E, Creavalle TD, Kern SE. BioTechniques. 2004;37:598. doi: 10.2144/04374ST04. [DOI] [PubMed] [Google Scholar]
- 311.Brody JR, Kern SE. Anal Biochem. 2004;333:1. doi: 10.1016/j.ab.2004.05.054. [DOI] [PubMed] [Google Scholar]
- 312.Volkmuth WD, Austin RH. Nature. 1992;358:600. doi: 10.1038/358600a0. [DOI] [PubMed] [Google Scholar]
- 313.Mohanty SK, Kim D, Beebe DJ. Electrophoresis. 2006;27:3772. doi: 10.1002/elps.200600238. [DOI] [PubMed] [Google Scholar]
- 314.Sun K, Li Z, Ueno K, Juodkazis S, Noji S, Misawa H. Electrophoresis. 2007;28:1572. doi: 10.1002/elps.200600685. [DOI] [PubMed] [Google Scholar]
- 315.Olson DW, Dorfman KD. Phys Rev E. (submitted) [Google Scholar]
- 316.Doyle PS, Bibette J, Bancaud A, Viovy J-L. Science. 2002;295:2237. doi: 10.1126/science.1068420. [DOI] [PubMed] [Google Scholar]
- 317.Nazemifard N, Wang L, Ye W, Bhattacharjee S, Masliyah JH, Harrison DJ. Lab Chip. 2012;12:146. doi: 10.1039/c1lc20855a. [DOI] [PubMed] [Google Scholar]
- 318.Regnier FE. J High Resol Chromatogr. 2000;23:19. [Google Scholar]
- 319.Billen J, Gzil P, Vervoort N, Baron GV, Desmet G. J Chromatogr A. 2005;1073:53. doi: 10.1016/j.chroma.2004.10.042. [DOI] [PubMed] [Google Scholar]
- 320.De Pra M, Kok WT, Gardeniers JGE, Desmet G, Eeltink S, van Nieuwkasteele JW, Schoenmakers PJ. Anal Chem. 2006;78:6519. doi: 10.1021/ac060915h. [DOI] [PubMed] [Google Scholar]
- 321.Malkin DS, Wei B, Fogiel AJ, Staats SL, Wirth MJ. Anal Chem. 2010;82:2175. doi: 10.1021/ac100062t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 322.Fangman WL. Nucleic Acids Res. 1978;5:653. doi: 10.1093/nar/5.3.653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 323.Serwer P. Anal Biochem. 1981;112:351. doi: 10.1016/0003-2697(81)90304-3. [DOI] [PubMed] [Google Scholar]
- 324.Olson DW, Ou J, Tian M, Dorfman KD. Electrophoresis. 2011;32:573. doi: 10.1002/elps.201000466. [DOI] [PubMed] [Google Scholar]
- 325.Volkmuth WD, Duke T, Wu MC, Austin RH, Szabo A. Phys Rev Lett. 1994;72:2117. doi: 10.1103/PhysRevLett.72.2117. [DOI] [PubMed] [Google Scholar]
- 326.Nixon GI, Slater GW. Phys Rev E. 1994;50:5033. doi: 10.1103/physreve.50.5033. [DOI] [PubMed] [Google Scholar]
- 327.Randall GC, Doyle PS. Phys Rev Lett. 2004;93:058102. doi: 10.1103/PhysRevLett.93.058102. [DOI] [PubMed] [Google Scholar]
- 328.Sevick EM, Williams DRM. Phys Rev Lett. 1996;76:2595. doi: 10.1103/PhysRevLett.76.2595. [DOI] [PubMed] [Google Scholar]
- 329.Araki N, Aydil ES, Dorfman KD. Electrophoresis. 2010;31:3675. doi: 10.1002/elps.201000331. [DOI] [PubMed] [Google Scholar]
- 330.Joswiak MN, Ou J, Dorfman KD. Electrophoresis. 2012;33:1013. doi: 10.1002/elps.201100471. [DOI] [PubMed] [Google Scholar]
- 331.Laachi N, Cho J, Dorfman KD. Phys Rev E. 2009;79:031928. doi: 10.1103/PhysRevE.79.031928. [DOI] [PubMed] [Google Scholar]
- 332.Randall GC, Doyle PS. Macromolecules. 2006;39:7734. [Google Scholar]
- 333.Kim JM, Doyle PS. Macromolecules. 2007;40:9151. [Google Scholar]
- 334.Volkmuth WD, Duke TAJ, Austin RH, Cox EC. Proc Natl Acad Sci USA. 1995;92:6887. doi: 10.1073/pnas.92.15.6887. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 335.Sevick EM, Williams DRM. Europhys Lett. 2001;56:529. [Google Scholar]
- 336.Cho J, Dorfman KD. J Chromatogr A. 2010;1217:5522. doi: 10.1016/j.chroma.2010.06.057. [DOI] [PubMed] [Google Scholar]
- 337.Masubuchi Y, Oana H, Akiyama T, Matsumoto M, Doi M. J Phys Soc Japan. 1995;64:1412. [Google Scholar]
- 338.Saville PM, Sevick EM. Macromolecules. 1999;32:892. [Google Scholar]
- 339.Minc N, Bokov P, Zeldovich KB, Futterer C, Viovy J-L, Dorfman KD. Electrophoresis. 2005;26:362. doi: 10.1002/elps.200410115. [DOI] [PubMed] [Google Scholar]
- 340.Kaji N, Tezuka Y, Takamura Y, Ueda M, Nishimoto T, Nakanishi H, Horiike Y, Baba Y. Anal Chem. 2004;76:15. doi: 10.1021/ac030303m. [DOI] [PubMed] [Google Scholar]
- 341.Chan YC, Lee Y-K, Zohar Y. J Micromech Microeng. 2006;16:699. [Google Scholar]
- 342.Ogawa R, Ogawa H, Oki A, Hashioka S, Horiike Y. Thin Solid Films. 2007;515:5167. [Google Scholar]
- 343.Ogawa R, Kaji N, Hashioka S, Baba Y, Horiike Y. Jpn J Appl Phys. 2007;46:2771. [Google Scholar]
- 344.Kaji N, Oki A, Ogawa R, Takamura Y, Nishimoto T, Nakanishi H, Horiike Y, Tokeshi M, Baba Y. Isr J Chem. 2007;47:161. [Google Scholar]
- 345.Shi J, Fang AP, Malaquin L, Pepin A, Decanini D, Viovy J-L, Chen Y. Appl Phys Lett. 2007;91:153114. [Google Scholar]
- 346.Hattori W, Someya H, Baba M, Kawaura H. J Chromatogr A. 2004;1051:141. [PubMed] [Google Scholar]
- 347.Kuo C-W, Wei KH, Lin C-H, Shiu J-Y, Chen P. Electrophoresis. 2008;29:2931. doi: 10.1002/elps.200700943. [DOI] [PubMed] [Google Scholar]
- 348.Bakajin O, Duke TAJ, Tegenfeldt J, Chou C-F, Chan SS, Austin RH, Cox EC. Anal Chem. 2001;73:6053. doi: 10.1021/ac015527o. [DOI] [PubMed] [Google Scholar]
- 349.Ou J, Carpenter SJ, Dorfman KD. Biomicrofluidics. 2010;4:013203. doi: 10.1063/1.3283903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 350.Chan YC, Zohar Y, Lee Y-K. Electrophoresis. 2009;30:3242. doi: 10.1002/elps.200900127. [DOI] [PubMed] [Google Scholar]
- 351.Viero Y, He Q, Bancaud A. Small. 2011;7:3508. doi: 10.1002/smll.201101345. [DOI] [PubMed] [Google Scholar]
- 352.Viero Y, He Q, Mazenq L, Ranchon H, Fourniols JY, Bancaud A. Microfluid Nanofluid. 2011;12:465. [Google Scholar]
- 353.Haghgooie R, Li C, Doyle PS. Langmuir. 2006;22:3601. doi: 10.1021/la0601051. [DOI] [PubMed] [Google Scholar]
- 354.Haghgooie R, Doyle PS. Soft Matter. 2009;5:1192. [Google Scholar]
- 355.Saliba AE, Gosse C, Minc N, Roblin C, Dorfman KD, Viovy J-L. In: Kitamori T, Fujita H, Hasebe S, editors. Society for Chemistry and Micro-Nano Systems; Proceedings of the 10th International Conference on Miniaturized Systems for Chemistry and Life Sciences; Tokyo, Japan. Nov. 5–6, 2006; 2006. pp. 386–388. [Google Scholar]
- 356.Mohan A, Doyle PS. Phys Rev E. 2007;76:040903(R). doi: 10.1103/PhysRevE.76.040903. [DOI] [PubMed] [Google Scholar]
- 357.Patel PD, Shaqfeh ESG. J Chem Phys. 2003;118:2941. [Google Scholar]
- 358.Olson DW, Dutta S, Laachi N, Tian M, Dorfman KD. Electrophoresis. 2011;32:581. doi: 10.1002/elps.201000467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 359.Dorfman KD, Viovy J-L. Phys Rev E. 2004;69:011901. doi: 10.1103/PhysRevE.69.011901. [DOI] [PubMed] [Google Scholar]
- 360.Scher H, Lax M. Phys Rev B. 1973;7:4491. [Google Scholar]
- 361.Dorfman KD. Phys Rev E. 2006;73:061922. doi: 10.1103/PhysRevE.73.061922. [DOI] [PubMed] [Google Scholar]
- 362.Mohan A, Doyle PS. Macromolecules. 2007;40:8794. [Google Scholar]
- 363.Cabodi M, Turner SWP, Craighead HG. Anal Chem. 2002;74:5169. doi: 10.1021/ac025879a. [DOI] [PubMed] [Google Scholar]
- 364.Slater GW, Guo HL. Electrophoresis. 1996;17:977. doi: 10.1002/elps.1150170604. [DOI] [PubMed] [Google Scholar]
- 365.Slater GW, Guo HL. Electrophoresis. 1996;17:1407. doi: 10.1002/elps.1150170903. [DOI] [PubMed] [Google Scholar]
- 366.Slater GW, Treurniet JR. J Chromatogr A. 1997;772:39. [Google Scholar]
- 367.Mercier J-F, Slater GW. Macromolecules. 2001;34:3437. [Google Scholar]
- 368.Mercier J-F, Tessier F, Slater GW. Electrophoresis. 2001;22:2631. doi: 10.1002/1522-2683(200108)22:13<2631::AID-ELPS2631>3.0.CO;2-3. [DOI] [PubMed] [Google Scholar]
- 369.Gauthier MG, Slater GW. J Chem Phys. 2002;117:6745. [Google Scholar]
- 370.Gauthier MG, Slater GW, Dorfman KD. Eur Phys J E. 2004;15:71. doi: 10.1140/epje/i2004-10037-9. [DOI] [PubMed] [Google Scholar]
- 371.Bow H, Fu J, Han J. Electrophoresis. 2008;29:4646. doi: 10.1002/elps.200800256. [DOI] [PubMed] [Google Scholar]
- 372.Strychalski EA, Lau HW, Archer LA. J Appl Phys. 2009;106:024915. doi: 10.1063/1.3183953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 373.Yasui T, Kaji N, Ogawa R, Hashioka S, Tokeshi M, Horiike Y, Baba Y. Anal Chem. 2011;83:6635. doi: 10.1021/ac201184t. [DOI] [PubMed] [Google Scholar]
- 374.Mikkelsen MB, Reisner W, Flyvbjerg H, Kristensen A. Nano Lett. 2011;11:1598. doi: 10.1021/nl1044764. [DOI] [PubMed] [Google Scholar]
- 375.Duong TT, Kim G, Ros R, Streek M, Schmid F, Brugger J, Anselmetti D, Ros A. Microelectron Eng. 2003;67–68:905. [Google Scholar]
- 376.Inatomi K, Izuo S, Lee S, Ohji H, Shiono S. Microelectron Eng. 2003;70:13. [Google Scholar]
- 377.Hsieh SF, Chang CP, Juang YJ, Wei HH. Appl Phys Lett. 2008;93:084103. [Google Scholar]
- 378.Hsieh SF, Wei HH. Phys Rev E. 2009;79:021901. doi: 10.1103/PhysRevE.79.021901. [DOI] [PubMed] [Google Scholar]
- 379.Reisner W, Larsen NB, Flyvbjerg H, Tegenfeldt JO, Kristensen A. Proc Natl Acad Sci USA. 2009;106:79. doi: 10.1073/pnas.0811468106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 380.Bonis-O’Donnell JTD, Reisner W, Stein D. New J Phys. 2009;11:075032. [Google Scholar]
- 381.Giddings JC, Kucera E, Russell CP, Myers MN. J Phys Chem. 1968;72:4397. [Google Scholar]
- 382.Laachi N, Declet C, Matson C, Dorfman KD. Phys Rev Lett. 2007;98:098106. doi: 10.1103/PhysRevLett.98.098106. [DOI] [PubMed] [Google Scholar]
- 383.Park SH, Xia Y. Chem Mater. 1998;10:1745. [Google Scholar]
- 384.Yang SM, Ozin GA. Chem Commun. 2000;24:2507. [Google Scholar]
- 385.Prevo BG, Velev OD. Langmuir. 2004;20:2099. doi: 10.1021/la035295j. [DOI] [PubMed] [Google Scholar]
- 386.Kim MH, Im SH, Park OO. Adv Funct Mater. 2005;15:1329. [Google Scholar]
- 387.Laachi N, Dorfman KD. J Chem Phys. 2010;133:234104. doi: 10.1063/1.3516176. [DOI] [PubMed] [Google Scholar]
- 388.Kim E, Xia Y, Whitesides GM. J Am Chem Soc. 1996;118:5722. [Google Scholar]
- 389.Norris DJ, Arlinghaus EG, Meng L, Heiny R, Scriven LE. Adv Mater. 2004;16:1393. [Google Scholar]
- 390.Meistermann L, Tinland B. Phys Rev E. 2000;62:4014. doi: 10.1103/physreve.62.4014. [DOI] [PubMed] [Google Scholar]
- 391.Zhang H, Wirth MJ. Anal Chem. 2005;77:1237. doi: 10.1021/ac0488964. [DOI] [PubMed] [Google Scholar]
- 392.Zeng Y, Harrison DJ. Anal Chem. 2007;79:2289. doi: 10.1021/ac061931h. [DOI] [PubMed] [Google Scholar]
- 393.Kuo CW, Shiu JY, Wei KH, Chen P. J Chromatogr A. 2007;1162:175. doi: 10.1016/j.chroma.2007.06.037. [DOI] [PubMed] [Google Scholar]
- 394.Zeng Y, Harrison DJ. Electrophoresis. 2006;27:3747. doi: 10.1002/elps.200600233. [DOI] [PubMed] [Google Scholar]
- 395.Shiu J-Y, Whang W-T, Chen P. J Chromatogr A. 2008;1206:72. doi: 10.1016/j.chroma.2008.07.012. [DOI] [PubMed] [Google Scholar]
- 396.Pieranski P. Contemp Phys. 1983;24:25. [Google Scholar]
- 397.Jiang P, Hwang KS, Mittleman DM, Bertone JF, Colvin VL. J Am Chem Soc. 1999;121:11630. [Google Scholar]
- 398.Rill RL, Locke BR, Liu Y, Van Winkle DH. Proc Natl Acad Sci USA. 1998;95:1534. doi: 10.1073/pnas.95.4.1534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 399.Rill RL, Liu Y, Van Winkle DH, Locke BR. J Chromatogr A. 1998;817:287. doi: 10.1016/s0021-9673(98)00522-6. [DOI] [PubMed] [Google Scholar]
- 400.Wu CH, Liu TB, Chu B. J Non-Crystalline Solids. 1998;235:605. [Google Scholar]
- 401.Svingen R, Alexandridis P, Akerman B. Langmuir. 2002;18:8616. [Google Scholar]
- 402.Ugaz VM, Lin RS, Srivastava N, Burke DT, Burns MA. Electrophoresis. 2003;24:151. doi: 10.1002/elps.200390007. [DOI] [PubMed] [Google Scholar]
- 403.Svingen R, Akerman B. J Phys Chem B. 2004;108:2735. [Google Scholar]
- 404.Zhang J, Gassmann M, He WD, Wan F, Chu B. Lab Chip. 2006;6:526. doi: 10.1039/b515557f. [DOI] [PubMed] [Google Scholar]
- 405.Carlsson N, Winge A-S, Engström S, Akerman B. J Phys Chem B. 2005;109:18628. doi: 10.1021/jp0516893. [DOI] [PubMed] [Google Scholar]
- 406.Carlsson N, Sanandaji N, Voinova M, Akerman B. Langmuir. 2006;22:4408. doi: 10.1021/la052086l. [DOI] [PubMed] [Google Scholar]
- 407.Sanandaji N, Carlsson N, Voinova M, Akerman B. Electrophoresis. 2006;27:3007. doi: 10.1002/elps.200500812. [DOI] [PubMed] [Google Scholar]
- 408.Tabuchi M, Ueda M, Kaji N, Yamasaki Y, Nagasaki Y, Yoshikawa K, Kataoka K, Baba Y. Nat Biotechnol. 2004;22:337. doi: 10.1038/nbt939. [DOI] [PubMed] [Google Scholar]
- 409.Pohl HA. J Appl Phys. 1951;22:869. [Google Scholar]
- 410.Pohl HA. J Appl Phys. 1958;29:1182. [Google Scholar]
- 411.Pohl HA. Dielectrophoresis. Cambridge University Press; New York: 1978. [Google Scholar]
- 412.Gascoyne PRC, Vykoukal J. Electrophoresis. 2002;23:1973. doi: 10.1002/1522-2683(200207)23:13<1973::AID-ELPS1973>3.0.CO;2-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 413.Chou CF, Tegenfeldt JO, Bakajin O, Chan SS, Cox EC, Darnton N, Duke TAJ, Austin RH. Biophys J. 2002;83:2170. doi: 10.1016/S0006-3495(02)73977-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 414.Holzel R. IET Nanobiotechnol. 2009;3:28. doi: 10.1049/iet-nbt.2008.0014. [DOI] [PubMed] [Google Scholar]
- 415.Lapizco-Encinas BH, Rito-Palomares M. Electrophoresis. 2007;28:4521. doi: 10.1002/elps.200700303. [DOI] [PubMed] [Google Scholar]
- 416.Bakewell DJ, Ermolina I, Morgan H, Milner J, Feldman Y. Biochim Biophys Acta. 2000;1493:151. doi: 10.1016/s0167-4781(00)00176-7. [DOI] [PubMed] [Google Scholar]
- 417.Regtmeier J, Eichhorn R, Bogunovic L, Ros A, Anselmetti D. Anal Chem. 2010;82:7141. doi: 10.1021/ac1005475. [DOI] [PubMed] [Google Scholar]
- 418.Zhao H. Phys Rev E. 2011;84:021910. doi: 10.1103/PhysRevE.84.021910. [DOI] [PubMed] [Google Scholar]
- 419.Regtmeier J, Eichhorn R, Viefhues M, Bogunovic L, Anselmetti D. Electrophoresis. 2011;32:2253. doi: 10.1002/elps.201100055. [DOI] [PubMed] [Google Scholar]
- 420.Washizu M, Kurosawa O. IEEE Trans Ind Appl. 1990;26:1165. [Google Scholar]
- 421.Kabata H, Kurosawa O, Arai I, Washizu M, Margarson SA, Glass RE, Shimamoto N. Science. 1993;262:1561. doi: 10.1126/science.8248804. [DOI] [PubMed] [Google Scholar]
- 422.Washizu M, Suzuki S, Kurosawa O, Nishikaza T, Shinohara T. IEEE Trans Ind Appl. 1994;30:835. [Google Scholar]
- 423.Washizu M, Kurosawa O, Arai I, Suzuki S, Shimamoto N. IEEE Trans Ind Appl. 1995;31:447. [Google Scholar]
- 424.Suzuki S, Yamanashi T, Tazawa S, Kurosawa O, Washizu M. IEEE Trans Ind Appl. 1998;34:75. [Google Scholar]
- 425.Asbury CL, van den Engh G. Biophys J. 1998;74:1024. doi: 10.1016/s0006-3495(98)74027-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 426.Bakewell DJG, Hughes MP, Milner JJ, Morgan H. Proc 20th Int Conf IEEE Med Biol Soc. 1998;2:1079. [Google Scholar]
- 427.Dewarrat F, Calame M, Schonenberger C. Single Mol. 2002;3:189. [Google Scholar]
- 428.Hoeb M, Raedler JO, Klein S, Stutzmann M, Brandt MS. Biophys J. 2007;93:1032. doi: 10.1529/biophysj.106.101188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 429.Cummings EB, Singh AK. Proc SPIE. 2000;4177:151. [Google Scholar]
- 430.Cummings EB, Singh AK. Anal Chem. 2003;75:4724. doi: 10.1021/ac0340612. [DOI] [PubMed] [Google Scholar]
- 431.Ros A, Hellmich W, Regtmeier J, Duong TT, Anselmetti D. Electrophoresis. 2006;27:2651. doi: 10.1002/elps.200500923. [DOI] [PubMed] [Google Scholar]
- 432.Regtmeier J, Duong TT, Eichhorn R, Anselmetti D, Ros A. Anal Chem. 2007;79:3925. doi: 10.1021/ac062431r. [DOI] [PubMed] [Google Scholar]
- 433.Gallo-Villanueava RC, Rodriguez-Lopez CE, Diaz-de-la Garza RI, Reyes-Betanzo C, Lapizco-Encinas BH. Electrophoresis. 2009;30:4195. doi: 10.1002/elps.200900355. [DOI] [PubMed] [Google Scholar]
- 434.Ying LM, White SS, Bruckbauer A, Meadows L, Korchev YE, Klenerman D. Biophys J. 2004;86:1018. doi: 10.1016/S0006-3495(04)74177-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 435.Clarke RW, Piper JD, Ying L, Klenerman D. Phys Rev Lett. 2007;98:198102. doi: 10.1103/PhysRevLett.98.198102. [DOI] [PubMed] [Google Scholar]
- 436.Asbury CL, Diercks AH, van den Engh G. Electrophoresis. 2002;23:2658. doi: 10.1002/1522-2683(200208)23:16<2658::AID-ELPS2658>3.0.CO;2-O. [DOI] [PubMed] [Google Scholar]
- 437.Wong PK, Chen C-Y, Wang T-H, Ho C-M. Anal Chem. 2004;76:6908. doi: 10.1021/ac049479u. [DOI] [PubMed] [Google Scholar]
- 438.Bakewell DJ, Morgan H. IEEE Trans Nanobiosci. 2006;5:139. [PubMed] [Google Scholar]
- 439.Du J-R, Juang Y-J, Wu J-T, Wei H-H. Biomicrofluidics. 2008;2:044103. doi: 10.1063/1.3037326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 440.Prinz C, Tegenfeldt JO, Austin RH, Cox EC, Sturm JC. Lab Chip. 2002;2:207. doi: 10.1039/b208010a. [DOI] [PubMed] [Google Scholar]
- 441.Chou CF, Zenhausern F. IEEE Eng Med Biol. 2003;22:62. doi: 10.1109/memb.2003.1266048. [DOI] [PubMed] [Google Scholar]
- 442.Swami N, Chou C-F, Ramamurthy V, Chaurey V. Lab Chip. 2009;9:3212. doi: 10.1039/b910598k. [DOI] [PubMed] [Google Scholar]
- 443.Ajdari A, Prost J. Proc Natl Acad Sci USA. 1991;88:4468. doi: 10.1073/pnas.88.10.4468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 444.Giddings JC. Science. 1993;260:1456. doi: 10.1126/science.8502990. [DOI] [PubMed] [Google Scholar]
- 445.Lao AIK, Hsing I-M. Lab Chip. 2005;5:687. doi: 10.1039/b503729h. [DOI] [PubMed] [Google Scholar]
- 446.Parikesit GOF, Markesteijn AP, Piciu OM, Bossche A, Westerweel J, Young IT, Garini Y. Biomicrofluidics. 2008;2:024103. doi: 10.1063/1.2930817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 447.Nedelcu S, Watson JHP. J Phys D. 2004;37:2197. [Google Scholar]
- 448.Nkodo AE, Garnier JM, Tinland B, Ren H, Desruisseaux C, McCormick LC, Drouin G, Slater GW. Electrophoresis. 2001;22:2424. doi: 10.1002/1522-2683(200107)22:12<2424::AID-ELPS2424>3.0.CO;2-1. [DOI] [PubMed] [Google Scholar]
- 449.Cross JD, Strychalski EA, Craighead HG. J Appl Phys. 2007;102:024701. [Google Scholar]
- 450.Salieb-Beugelaar GB, Teapal J, van Nieuwkasteele J, Wijnperlé D, Tegenfeldt JO, Lisdat F, van den Berg A, Eijkel JCT. Nano Lett. 2008;8:1785. doi: 10.1021/nl080300v. [DOI] [PubMed] [Google Scholar]
- 451.Castillo-Fernandez O, Salieb-Beugelaar GB, Van Nieuwkasteele JW, Bomer JG, Arundell M, Samitier J, van den Berg A, Eijkel JCT. Electrophoresis. 2011;32:2402. doi: 10.1002/elps.201100278. [DOI] [PubMed] [Google Scholar]
- 452.Long D, Ajdari A. Eur Phys J E. 2001;4:29. [Google Scholar]
- 453.Liao W-C, Watari N, Wang S, Hu X, Larson RG, Lee LJ. Electrophoresis. 2010;31:2813. doi: 10.1002/elps.201000081. [DOI] [PubMed] [Google Scholar]
- 454.Das S, Dubsky P, van den Berg A, Eijkel JCT. Phys Rev Lett. 2012;108:138101. doi: 10.1103/PhysRevLett.108.138101. [DOI] [PubMed] [Google Scholar]
- 455.Gao QF, Yeung ES. Anal Chem. 1998;70:1382. doi: 10.1021/ac970999h. [DOI] [PubMed] [Google Scholar]
- 456.Szoke M, Sasvari-Szekely M, Guttman A. J Chromatogr A. 1999;830:465. doi: 10.1016/s0021-9673(98)00878-4. [DOI] [PubMed] [Google Scholar]
- 457.Guttman A, Lengyel T, Szoke M, Sasvari-Szekely M. J Chromatogr A. 2000;871:289. doi: 10.1016/s0021-9673(99)00958-9. [DOI] [PubMed] [Google Scholar]
- 458.Barron AE, Blanch HW, Soane DS. Electrophoresis. 1994;15:597. doi: 10.1002/elps.1150150184. [DOI] [PubMed] [Google Scholar]
- 459.Tessier F, Slater GW. Macromolecules. 2005;38:6752. [Google Scholar]
- 460.Tessier F, Slater GW. Macromolecules. 2006;39:1250. [Google Scholar]
- 461.Hickey OA, Harden JL, Slater GW. Phys Rev Lett. 2009;102:108304. doi: 10.1103/PhysRevLett.102.108304. [DOI] [PubMed] [Google Scholar]
- 462.Hickey OA, Holm C, Harden JL, Slater GW. Macromolecules. 2011;44:9455. [Google Scholar]
- 463.Kenward M, Slater GW. Eur Phys J E. 2006;20:125. doi: 10.1140/epje/i2006-10008-2. [DOI] [PubMed] [Google Scholar]
- 464.Iki N, Kim Y, Yeung ES. Anal Chem. 1996;68:4321. [Google Scholar]
- 465.Mathe J, di Meglio J-M, Tinland B. J Colloid Interface Sci. 2007;316:831. doi: 10.1016/j.jcis.2007.07.063. [DOI] [PubMed] [Google Scholar]
- 466.Pennathur S, Baldessari F, Santiago JG, Kattah MG, Steinman JB, Utz PJ. Anal Chem. 2007;79:8316. doi: 10.1021/ac0710580. [DOI] [PubMed] [Google Scholar]
- 467.Huber DE, Markel ML, Pennathur S, Patel KD. Lab Chip. 2009;9:2933. doi: 10.1039/b901739a. [DOI] [PubMed] [Google Scholar]
- 468.Pernodet N, Samuilov V, Shin K, Sokolov J, Rafailovich MH, Gersappe D, Chu B. Phys Rev Lett. 2000;85:5651. doi: 10.1103/PhysRevLett.85.5651. [DOI] [PubMed] [Google Scholar]
- 469.Kang SH, Shortreed MR, Yeung ES. Anal Chem. 2001;73:1091. doi: 10.1021/ac0013599. [DOI] [PubMed] [Google Scholar]
- 470.Li H-W, Park H-Y, Porter MD, Yeung ES. Anal Chem. 2005;77:3256. doi: 10.1021/ac048143h. [DOI] [PubMed] [Google Scholar]
- 471.Isailovic S, Li H-W, Yeung ES. J Chromatogr A. 2007;1150:259. doi: 10.1016/j.chroma.2006.09.093. [DOI] [PubMed] [Google Scholar]
- 472.Liu X, Wu Z, Nie H, Liu Z, He Y, Yeung ES. Anal Chim Acta. 2007;602:229. doi: 10.1016/j.aca.2007.09.020. [DOI] [PubMed] [Google Scholar]
- 473.Seo YS, Samuilov VA, Sokolov J, Rafailovich M, Tinland B, Kim J, Chu B. Electrophoresis. 2002;23:2618. doi: 10.1002/1522-2683(200208)23:16<2618::AID-ELPS2618>3.0.CO;2-W. [DOI] [PubMed] [Google Scholar]
- 474.Li B, Fang X, Luo H, Petersen E, Seo Y-S, Samuilov V, Rafailovich M, Sokolov J, Gersappe D, Chu B. Electrophoresis. 2006;27:1312. doi: 10.1002/elps.200500444. [DOI] [PubMed] [Google Scholar]
- 475.Seo Y, Luo H, Samuilov VA, Rafailovich M, Sokolov J, Gersappe D, Chu B. Nano Lett. 2004;4:659. [Google Scholar]
- 476.Petersen E, Li B, Fang X, Luo H, Samuilov V, Gersappe D, Sokolov J, Chu B, Rafailovich M. Phys Rev Lett. 2007;98:088102. doi: 10.1103/PhysRevLett.98.088102. [DOI] [PubMed] [Google Scholar]
- 477.Deegan RD, Bakajin O, Dupont TF, Huber G, Nagel SR, Witten TA. Nature. 1997;389:827. doi: 10.1103/physreve.62.756. [DOI] [PubMed] [Google Scholar]
- 478.Fan X, Li B, Petersen E, Seo Y-S, Samuilov VA, Chen Y, Sokolov JC, Shew C-Y, Rafailovich MH. Langmuir. 2006;22:6308. doi: 10.1021/la060479u. [DOI] [PubMed] [Google Scholar]
- 479.Tiselus A. Trans Faraday Soc. 1937;33:524. [Google Scholar]
- 480.Luo HB, Gersappe D. Electrophoresis. 2002;23:2690. doi: 10.1002/1522-2683(200208)23:16<2690::AID-ELPS2690>3.0.CO;2-R. [DOI] [PubMed] [Google Scholar]
- 481.Li B, Fang X, Luo H, Seo Y-S, Petersen E, Ji Y, Rafailovich M, Sokolov J, Gersappe D, Chu B. Anal Chem. 2006;78:4743. doi: 10.1021/ac060686z. [DOI] [PubMed] [Google Scholar]
- 482.Jing B, Yang Q, Zhu Y, Zhao J. J Polymer Sci B. 2009;47:2541. [Google Scholar]
- 483.Reichhardt CJO, Reichhardt C. Phys Rev E. 2006;74:051908. [Google Scholar]
- 484.Braiman A, Thundat T, Rudakov F. Appl Phys Lett. 2010;97:033703. [Google Scholar]
- 485.Lee HH, Kuo Y. Jpn J Appl Phys. 2008;47:2300. [Google Scholar]
- 486.Ghosh A, Patra TK, Kant R, Singh RK, Singh JK, Bhattacharya S. Appl Phys Lett. 2011;98:164102. [Google Scholar]
- 487.Xia Y, Whitesides GM. Annu Rev Mat Sci. 1998;28:153. [Google Scholar]
- 488.Baruth A, Rodwogin MD, Shankar A, Erickson MJ, Hillmyer MA, Leighton C. ACS Appl Mat Interfaces. 2011;3:3472. doi: 10.1021/am200693x. [DOI] [PubMed] [Google Scholar]
- 489.Gao L, Wu J, Gao D, Wu J. Appl Phys Lett. 2007;91:113902. [Google Scholar]
- 490.Wu J, Zhao S-L, Gao L, Wu J, Gao D. Lab Chip. 2011;11:4036. doi: 10.1039/c1lc20600a. [DOI] [PubMed] [Google Scholar]
- 491.Maier B, Radler JO. Phys Rev Lett. 1999;82:1911. [Google Scholar]
- 492.Maier B, Radler JO. Macromolecules. 2000;33:7185. [Google Scholar]
- 493.Olson DJ, Johnson JM, Patel PD, Shaqfeh ESG, Boxer SG, Fuller GG. Langmuir. 2001;17:7396. [Google Scholar]
- 494.Kahl V, Hennig M, Maier B, Rädler JO. Electrophoresis. 2009;30:1276. doi: 10.1002/elps.200800430. [DOI] [PubMed] [Google Scholar]
- 495.Athmakuri K, Rohovie M, Padala C, Cole R, Kane RS. Langmuir. 2010;26:13393. doi: 10.1021/la101679n. [DOI] [PubMed] [Google Scholar]
- 496.van Oudenaarden A, Boxer SG. Science. 1999;285:1046. doi: 10.1126/science.285.5430.1046. [DOI] [PubMed] [Google Scholar]
- 497.Huang LR, Cox EC, Austin RH, Sturm JC. Anal Chem. 2003;75:6963. doi: 10.1021/ac0348524. [DOI] [PubMed] [Google Scholar]
- 498.Huang LR, Tegenfeldt JO, Kraeft JJ, Sturm JC, Austin RH, Cox EC. Nat Biotechnol. 2002;20:1048. doi: 10.1038/nbt733. [DOI] [PubMed] [Google Scholar]
- 499.Zeng Y, He M, Harrison DJ. Angew Chem Int Edit. 2008;47:6388. doi: 10.1002/anie.200800816. [DOI] [PubMed] [Google Scholar]
- 500.Fu J, Schoch RB, Stevens AL, Tannenbaum SR, Han J. Nat Nanotechnol. 2007;2:121. doi: 10.1038/nnano.2006.206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 501.Mao P, Han J. Lab Chip. 2009;9:586. doi: 10.1039/b809370a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 502.Bader JS, Hammond RW, Henck SA, Deem MW, McDermott GA, Bustillo JM, Simpson JW, Mulhern GT, Rothberg JM. Proc Natl Acad Sci USA. 1999;96:13165. doi: 10.1073/pnas.96.23.13165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 503.Chou CF, Bakajin O, Turner SWP, Duke TAJ, Chan SS, Cox EC, Craig-head HG, Austin RH. Proc Natl Acad Sci USA. 1999;96:13762. doi: 10.1073/pnas.96.24.13762. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 504.Hammond RW, Bader JS, Henck SA, Deem MW, McDermott GA, Bustillo JM, Rothberg JM. Electrophoresis. 2000;21:74. doi: 10.1002/(SICI)1522-2683(20000101)21:1<74::AID-ELPS74>3.0.CO;2-K. [DOI] [PubMed] [Google Scholar]
- 505.Bader JS, Deem MW, Hammond RW, Henck SA, Simpson JW, Rothberg JM. Appl Phys A. 2002;75:275. [Google Scholar]
- 506.Cabodi M, Chen YF, Turner SWP, Craighead HG, Austin RH. Electrophoresis. 2002;23:3496. doi: 10.1002/1522-2683(200210)23:20<3496::AID-ELPS3496>3.0.CO;2-9. [DOI] [PubMed] [Google Scholar]
- 507.Huang LR, Silberzan P, Tegenfeldt JO, Cox EC, Sturm JC, Austin RH, Craighead HG. Phys Rev Lett. 2002;89:178301. doi: 10.1103/PhysRevLett.89.178301. [DOI] [PubMed] [Google Scholar]
- 508.Huang LR, Cox EC, Austin RH, Sturm JC. Science. 2004;304:987. doi: 10.1126/science.1094567. [DOI] [PubMed] [Google Scholar]
- 509.Burton RE, White EJ, Foss TR, Phillips KM, Meltzer RH, Kojanian N, Kwok LW, Lim A, Pellerin NL, Mamaeva NV, Gilmanshin R. Lab Chip. 2010;10:843. doi: 10.1039/b922106a. [DOI] [PubMed] [Google Scholar]
- 510.Meltzer RH, Krogmeier JR, Kwok LW, Allen R, Crane B, Griffis JW, Knaian L, Kojanian N, Malkin G, Nahas MK, Papkov V, Shaikh S, Vyavahare K, Zhong Q, Zhou Y, Larson JW, Gilmanshin R. Lab Chip. 2011;11:863. doi: 10.1039/c0lc00477d. [DOI] [PubMed] [Google Scholar]
- 511.Huang LR, Tegenfeldt JO, Kraeft JJ, Sturm JC, Austin RH, Cox EC. Generation of large-area tunable uniform electric fields in microfluidic arrays for rapid DNA separation. Electron Devices Meeting; IEDM Technical Digest. International; IEEE. 2001; 2001. pp. 363–366. [Google Scholar]
- 512.Nazemifard N, Bhattacharjee S, Masliyah JH, Harrison DJ. Angew Chem Int Edit. 2010;49:3326. doi: 10.1002/anie.200906343. [DOI] [PubMed] [Google Scholar]
- 513.Fu J, Mao P, Han J. Nat Protoc. 2009;4:1681. doi: 10.1038/nprot.2009.176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 514.Morton KJ, Loutherback K, Inglis DW, Tsui OK, Sturm JC, Chou SY, Austin RH. Proc Natl Acad Sci USA. 2008;105:7434. doi: 10.1073/pnas.0712398105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 515.Morton KJ, Loutherback K, Inglis DW, Tsui OK, Sturm JC, Chou SY, Austin RH. Lab Chip. 2008;8:1448. doi: 10.1039/b805614e. [DOI] [PubMed] [Google Scholar]
- 516.Beech JP, Tegenfeldt JO. Lab Chip. 2008;8:657. doi: 10.1039/b719449h. [DOI] [PubMed] [Google Scholar]
- 517.Reimann P. Phys Rep. 2002;361:57. [Google Scholar]
- 518.Astumian RD. Science. 1997;276:917. doi: 10.1126/science.276.5314.917. [DOI] [PubMed] [Google Scholar]
- 519.Duke TAJ, Austin RH. Phys Rev Lett. 1998;80:1552. [Google Scholar]
- 520.Ertas D. Phys Rev Lett. 1998;80:1548. [Google Scholar]
- 521.Austin RH, Darnton N, Huang R, Sturm J, Bakajin O, Duke T. Appl Phys A. 2002;75:279. [Google Scholar]
- 522.Li Z, Drazer G. Phys Rev Lett. 2007;98:050602. doi: 10.1103/PhysRevLett.98.050602. [DOI] [PubMed] [Google Scholar]
- 523.Long D, Viovy J-L, Ajdari A. Phys Rev Lett. 1996;76:3858. doi: 10.1103/PhysRevLett.76.3858. [DOI] [PubMed] [Google Scholar]
- 524.Long D, Viovy J-L, Ajdari A. J Phys Cond Matt. 1996;8:9471. [Google Scholar]
- 525.Shendruk TN, Hickey OA, Slater GW, Harden JL. Curr Opin Colloid Interface Sci. 2012;17:74. [Google Scholar]
- 526.Teclemariam NP, Beck VA, Shaqfeh ESG, Muller SJ. Macromolecules. 2007;40:3848. [Google Scholar]
- 527.André P, Long D, Ajdari A. Eur Phys J B. 1998;4:307. [Google Scholar]
- 528.Zheng JJ, Yeung ES. Anal Chem. 2003;75:3675. doi: 10.1021/ac034430u. [DOI] [PubMed] [Google Scholar]
- 529.Zheng JJ, Yeung ES. Anal Chem. 2002;74:4536. doi: 10.1021/ac0257344. [DOI] [PubMed] [Google Scholar]
- 530.Zheng JJ, Yeung ES. Aust J Chem. 2003;56:149. [Google Scholar]
- 531.Stein D, van der Heyden FHJ, Koopmans WJA, Dekker C. Proc Natl Acad Sci USA. 2006;103:15853. doi: 10.1073/pnas.0605900103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 532.Brochard F. J Phys Paris. 1977;38:1285. [Google Scholar]
- 533.Wang X, Veerappan V, Cheng C, Jiang X, Allen RD, Dasgupta PK, Liu S. J Am Chem Soc. 2010;132:40. doi: 10.1021/ja909233n. [DOI] [PubMed] [Google Scholar]
- 534.Wang X, Wang S, Veerappan V, Byun CK, Nguyen H, Gendhar B, Allen RD, Liu S. Anal Chem. 2008;80:5583. doi: 10.1021/ac800549k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 535.Wang X, Kang J, Wang S, Lu JJ, Liu S. J Chromatogr A. 2008;1200:108. doi: 10.1016/j.chroma.2008.05.088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 536.Liu KJ, Rane TD, Zhang Y, Wang T-H. J Am Chem Soc. 2011;133:6898. doi: 10.1021/ja200279y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 537.Wang X, Liu L, Pu Q, Zhu Z, Guo G, Zhong H, Liu S. J Am Chem Soc. 2012;134:7400. doi: 10.1021/ja302621v. [DOI] [PubMed] [Google Scholar]
- 538.Hoagland DA, Prudhomme RK. AIChE J. 1985;31:236. [Google Scholar]
- 539.Dorfman KD. Chem Eng Commun. 2010;197:39. [Google Scholar]
- 540.Wälti C, Germishuizen WA, Tosch P, Kaminski CF, Davies AG. J Phys D. 2006;40:114. [Google Scholar]
- 541.Doyle PS, Ladoux B, Viovy J-L. Phys Rev Lett. 2000;84:4769. doi: 10.1103/PhysRevLett.84.4769. [DOI] [PubMed] [Google Scholar]
- 542.van Oijen AM, Blainey PC, Crampton DJ, Richardson CC, Ellenberger T, Xie XS. Science. 2003;301:1235. doi: 10.1126/science.1084387. [DOI] [PubMed] [Google Scholar]
- 543.Kim S, Blainey PC, Schroeder CM, Xie XS. Nat Methods. 2007;4:397. doi: 10.1038/nmeth1037. [DOI] [PubMed] [Google Scholar]
- 544.van Oijen AM. Biopolymers. 2007;85:144. doi: 10.1002/bip.20624. [DOI] [PubMed] [Google Scholar]
- 545.Granéli A, Yeykal CC, Robertson RB, Greene EC. Proc Natl Acad Sci USA. 2006;103:1221. doi: 10.1073/pnas.0508366103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 546.Granéli A, Yeykal CC, Prasad TK, Greene EC. Langmuir. 2006;22:292. doi: 10.1021/la051944a. [DOI] [PubMed] [Google Scholar]
- 547.Bustamante C, Macosko JC, Wuite GJL. Nat Rev Mol Cell Biol. 2000;1:130. doi: 10.1038/35040072. [DOI] [PubMed] [Google Scholar]
- 548.Moffitt JR, Chemla YR, Smith SB, Bustamante C. Annu Rev Biochem. 2008;77:205. doi: 10.1146/annurev.biochem.77.043007.090225. [DOI] [PubMed] [Google Scholar]
- 549.Strick TR, Dessinges M-N, Charvin G, Dekker NH, Allemand J-F, Bensimon D, Croquette V. Rep Prog Phys. 2003;66:1. [Google Scholar]
- 550.Laib S, Rankl M, Ruckstuhl T, Seeger S. Nucleic Acids Res. 2003;31:e138. doi: 10.1093/nar/gng138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 551.Cai WW, Aburatani H, Stanton VP, Housman DE, Wang YK, Schwartz DC. Proc Natl Acad Sci USA. 1995;92:5164. doi: 10.1073/pnas.92.11.5164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 552.Cai WW, Jing JP, Irvin B, Ohler L, Rose E, Shizuya H, Kim UJ, Simon M, Anantharaman T, Mishra B, Schwartz DC. Proc Natl Acad Sci USA. 1998:3390. doi: 10.1073/pnas.95.7.3390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 553.Aston C, Mishra B, Schwartz DC. Trends Biotechnol. 1999;17:297. doi: 10.1016/s0167-7799(99)01326-8. [DOI] [PubMed] [Google Scholar]
- 554.Jing J, Reed J, Huang J, Hu X, Clarke V, Edington J, Housman D, Anantharaman TS, Huff EJ, Mishra B, Porter B, Shenker A, Wolfson E, Hiort C, Kantor R, Aston C, Schwartz DC. Proc Natl Acad Sci USA. 1998;95:8046. doi: 10.1073/pnas.95.14.8046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 555.Yokota H, Johnson F, Lu HB, Robinson RM, Belu AM, Garrison MD, Ratner BD, Trask BJ, Miller DL. Nucleic Acids Res. 1997;25:1064. doi: 10.1093/nar/25.5.1064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 556.Otobe K, Ohtani T. Nucleic Acids Res. 2001;29:e109. doi: 10.1093/nar/29.22.e109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 557.Oshige M, Yamaguchi K, Matsuura S-i, Kurita H, Mizuno A, Katsura S. Anal Biochem. 2010;400:145. doi: 10.1016/j.ab.2010.01.021. [DOI] [PubMed] [Google Scholar]
- 558.Yang B, Dukkipati VR, Li D, Cardozo BL, Pang SW. J Vac Sci Technol B. 2007;25:2352. [Google Scholar]
- 559.Chan TF, Ha C, Phong A, Cai DM, Wan E, Leung L, Kwok PY, Xiao M. Nucleic Acids Res. 2006;34:e113. doi: 10.1093/nar/gkl593. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 560.Dimalanta ET, Lim A, Runnheim R, Lamers C, Churas C, Forrest DK, de Pablo JJ, Graham MD, Coppersmith SN, Goldstein S, Schwartz DC. Anal Chem. 2004;76:5293. doi: 10.1021/ac0496401. [DOI] [PubMed] [Google Scholar]
- 561.Petit CAP, Carbeck JD. Nano Lett. 2003;3:1141. [Google Scholar]
- 562.Hu J, Wang M, Weier H-UG, Frantz P, Kolbe W, Ogletree DF, Salmeron M. Langmuir. 1996;12:1697. [Google Scholar]
- 563.Wang W, Lin J, Schwartz DC. Biophys J. 1998;75:513. doi: 10.1016/S0006-3495(98)77540-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 564.Reed J, Singer E, Kresbach G, Schwartz DC. Anal Biochem. 1998;259:80. doi: 10.1006/abio.1998.2640. [DOI] [PubMed] [Google Scholar]
- 565.Cabin-Flaman A, Monnier A-F, Coffinier Y, Audinot J-N, Gibouin D, Wirtz T, Boukherroub R, Migeon H-N, Bensimon A, Jannière L, Ripoll C, Norris V. Anal Chem. 2011;83:6940. doi: 10.1021/ac201685t. [DOI] [PubMed] [Google Scholar]
- 566.Cerf A, Cipriany BR, Benítez JJ, Craighead HG. Anal Chem. 2011;83:8073. doi: 10.1021/ac202506j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 567.Wu T, Schwartz DC. Anal Biochem. 2007;361:31. doi: 10.1016/j.ab.2006.10.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 568.Yu H, Schwartz DC. Anal Biochem. 2008;380:111. doi: 10.1016/j.ab.2008.05.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 569.Cinque L, Yamada A, Ghomchi Y, Baigl D, Chen Y. Microelectronic Eng. 2011;88:1733. [Google Scholar]
- 570.Klein DCG, Gurevich L, Janssen JW, Kouwenhoven LP, Carbeck JD, Sohn LL. Appl Phys Lett. 2001;78:2396. [Google Scholar]
- 571.Nyamjav D, Ivanisevic A. Adv Mater. 2003;15:1805. [Google Scholar]
- 572.Zhang J, Ma Y, Stachura S, He H. Langmuir. 2005;21:4180. doi: 10.1021/la050129s. [DOI] [PubMed] [Google Scholar]
- 573.Guan J, Lee LJ. Proc Natl Acad Sci USA. 2005;102:18321. doi: 10.1073/pnas.0506902102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 574.Riehn R, Lu M, Wang Y-M, Lim SF, Cox EC, Austin RH. Proc Natl Acad Sci USA. 2005;102:10012. doi: 10.1073/pnas.0503809102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 575.Tegenfeldt JO, Prinz C, Cao H, Chou S, Reisner WW, Riehn R, Wang YM, Cox EC, Sturm JC, Silberzan P, Austin RH. Proc Natl Acad Sci USA. 2004;101:10979. doi: 10.1073/pnas.0403849101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 576.Reisner W, Morton KJ, Riehn R, Wang YM, Yu Z, Rosen M, Sturm JC, Chou SY, Frey E, Austin RH. Phys Rev Lett. 2005;94:196101. doi: 10.1103/PhysRevLett.94.196101. [DOI] [PubMed] [Google Scholar]
- 577.Odijk T. Phys Rev E. 2008;77:060901(R). doi: 10.1103/PhysRevE.77.060901. [DOI] [PubMed] [Google Scholar]
- 578.Wang Y, Tree DR, Dorfman KD. Macromolecules. 2011;44:6594. doi: 10.1021/ma201277e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 579.Tree DR, Wang Y, Dorfman KD. Phys Rev Lett. 2012;108:228105. doi: 10.1103/PhysRevLett.108.228105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 580.Latinwo F, Schroeder CM. Soft Matter. 2011;7:7907. doi: 10.1039/c1sm05298e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 581.Daoud M, de Gennes PG. J Phys Paris. 1977;38:85. [Google Scholar]
- 582.Odijk T. Macromolecules. 1983;16:1340. [Google Scholar]
- 583.Noding B, Koster S. Phys Rev Lett. 2012;108:088101. doi: 10.1103/PhysRevLett.108.088101. [DOI] [PubMed] [Google Scholar]
- 584.Yang Y, Burkhardt TW, Gompper G. Phys Rev E. 2007;76:011804. doi: 10.1103/PhysRevE.76.011804. [DOI] [PubMed] [Google Scholar]
- 585.Burkhardt TW, Yang Y, Gompper G. Phys Rev E. 2010;82:041801. doi: 10.1103/PhysRevE.82.041801. [DOI] [PubMed] [Google Scholar]
- 586.Brochard-Wyart F, Tanaka T, Borghi N, de Gennes PG. Langmuir. 2005;21:4144. doi: 10.1021/la0474114. [DOI] [PubMed] [Google Scholar]
- 587.Cifra P, Benkova Z, Bleha T. J Phys Chem B. 2009;113:1843. doi: 10.1021/jp806126r. [DOI] [PubMed] [Google Scholar]
- 588.Cifra P. J Chem Phys. 2012;136:024902. doi: 10.1063/1.3674304. [DOI] [PubMed] [Google Scholar]
- 589.Cao H, Tegenfeldt JO, Austin RH, Chou SY. Appl Phys Lett. 2002;81:3058. [Google Scholar]
- 590.Cao H, Yu ZN, Wang J, Tegenfeldt JO, Austin RH, Chen E, Wu W, Chou SY. Appl Phys Lett. 2002;81:174. [Google Scholar]
- 591.Harnett CK, Coates GW, Craighead HG. J Vac Sci Technol B. 2001;19:2842. [Google Scholar]
- 592.Thamdrup LH, Klukowska A, Kristensen A. Nanotechnology. 2008;19:125301. doi: 10.1088/0957-4484/19/12/125301. [DOI] [PubMed] [Google Scholar]
- 593.Kim SH, Cui Y, Lee MJ, Nam S-W, Oh D, Kang SH, Kim YS, Park S. Lab Chip. 2011;11:348. doi: 10.1039/c0lc00015a. [DOI] [PubMed] [Google Scholar]
- 594.Campbell LC, Wilkinson MJ, Manz A, Camilleri P, Humphreys CJ. Lab Chip. 2004;4:225. doi: 10.1039/b312592k. [DOI] [PubMed] [Google Scholar]
- 595.Wang KG, Yue SL, Wang L, Jin AZ, Gu CZ, Wang PY, Feng YC, Wang YC, Niu HB. Microfluid Nanofluid. 2006;2:85. [Google Scholar]
- 596.Maleki T, Mohammadi S, Ziaie B. Nanotechnology. 2009;20:105302. doi: 10.1088/0957-4484/20/10/105302. [DOI] [PubMed] [Google Scholar]
- 597.Fanzio P, Mussi V, Manneschi C, Angeli E, Firpo G, Repetto L, Valbusa U. Lab Chip. 2011;11:2961. doi: 10.1039/c1lc20243j. [DOI] [PubMed] [Google Scholar]
- 598.Menard LD, Ramsey JM. Nano Lett. 2011;11:512. doi: 10.1021/nl103369g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 599.Wu J, Chantiwas R, Amirsadeghi A, Soper SA, Park S. Lab Chip. 2011;11:2984. doi: 10.1039/c1lc20294d. [DOI] [PubMed] [Google Scholar]
- 600.Dumond JJ, Low HY, Rodriguez I. Nanotechnology. 2006;17:1975. [Google Scholar]
- 601.Liang X, Morton KJ, Austin RH, Chou SY. Nano Lett. 2007;7:3774. doi: 10.1021/nl072253x. [DOI] [PubMed] [Google Scholar]
- 602.Xia Q, Morton KJ, Austin RH, Chou SY. Nano Lett. 2008;8:3830. doi: 10.1021/nl802219b. [DOI] [PubMed] [Google Scholar]
- 603.Li WL, Tegenfeldt JO, Chen L, Austin RH, Chou SY, Kohl PA, Krotine J, Sturm JC. Nanotechnology. 2003;14:578. [Google Scholar]
- 604.Abad E, Juarros A, Retolaza A, Merino S, Marie R, Kristensen A. Microelectron Eng. 2011;88:300. [Google Scholar]
- 605.Guo LJ, Cheng X, Chou CF. Nano Lett. 2004;4:69. [Google Scholar]
- 606.Verbridge SS, Edel JB, Stavis SM, Moran-Mirabal JM, Allen SD, Coates G, Craighead HG. J Appl Phys. 2005;97:124317. [Google Scholar]
- 607.Bellan LM, Strychalski EA, Craighead HG. J Vac Sci Technol B. 2008;26:1728. [Google Scholar]
- 608.Zhang C, Zhang F, van Kan JA, van der Maarel JRC. J Chem Phys. 2008;128:225109. doi: 10.1063/1.2937441. [DOI] [PubMed] [Google Scholar]
- 609.Guan J, Boukany PE, Hemminger O, Chiou N-R, Zha W, Cavanaugh M, Lee LJ. Adv Mater. 2010;22:3997. doi: 10.1002/adma.201000136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 610.Han AP, de Rooij NF, Staufer U. Nanotechnology. 2006;17:2498. doi: 10.1088/0957-4484/17/10/010. [DOI] [PubMed] [Google Scholar]
- 611.Hoang HT, Segers-Nolten IM, Berenschot JW, de Boer MJ, Tas NR, Haneveld J, Elwenspoek MC. J Micromech Microeng. 2009;19:065017. [Google Scholar]
- 612.Sordan R, Miranda A, Traversi F, Colombo D, Chrastina D, Isella G, Masserini M, Miglio L, Kern K, Balasubramanian K. Lab Chip. 2009;9:1556. doi: 10.1039/b819520j. [DOI] [PubMed] [Google Scholar]
- 613.Sivanesan P, Okamoto K, English D, Lee CS, DeVoe DL. Anal Chem. 2005;77:2252. doi: 10.1021/ac048923q. [DOI] [PubMed] [Google Scholar]
- 614.Zhang B, Wood M, Lee H. Anal Chem. 2009;81:5541. doi: 10.1021/ac9009148. [DOI] [PubMed] [Google Scholar]
- 615.Steinbock LJ, Otto O, Chimerel C, Gornall J, Keyser UF. Nano Lett. 2010;10:2493. doi: 10.1021/nl100997s. [DOI] [PubMed] [Google Scholar]
- 616.Huh D, Mills KL, Zhu X, Burns MA, Thouless MD, Takayama S. Nat Mater. 2007;6:424. doi: 10.1038/nmat1907. [DOI] [PubMed] [Google Scholar]
- 617.Mills KL, Huh D, Takayama S, Thouless MD. Lab Chip. 2010;10:1627. doi: 10.1039/c000863j. [DOI] [PubMed] [Google Scholar]
- 618.Xu B-Y, Xu J-J, Xia X-H, Chen H-Y. Lab Chip. 2010;10:2894. doi: 10.1039/c005245k. [DOI] [PubMed] [Google Scholar]
- 619.Chung S, Lee JH, Moon M-W, Han J, Kamm RD. Adv Mater. 2008;20:3011. [Google Scholar]
- 620.Park S-M, Huh YS, Craighead HG, Erickson D. Proc Natl Acad Sci USA. 2009;106:15549. doi: 10.1073/pnas.0904004106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 621.Park KD, Lee SW, Takama N, Fujii T, Kim BJ. Microelectron Eng. 2009;86:1385. [Google Scholar]
- 622.O’Brien MJ, Bisong P, Ista LK, Rabinovich EM, Garcia AL, Sibbett SS, Lopez GP, Brueck SRJ. J Vac Sci Technol B. 2003;21:2941. [Google Scholar]
- 623.Utko P, Persson F, Kristensen A, Larsen NB. Lab Chip. 2011;11:303. doi: 10.1039/c0lc00260g. [DOI] [PubMed] [Google Scholar]
- 624.Fan R, Karnik R, Yue M, Li DY, Majumdar A, Yang PD. Nano Lett. 2005;5:1633. doi: 10.1021/nl0509677. [DOI] [PubMed] [Google Scholar]
- 625.Ma C, Yeung ES. Anal Chem. 2010;82:654. doi: 10.1021/ac902109g. [DOI] [PubMed] [Google Scholar]
- 626.Cho YH, Lee SW, Fuji T, Kim BJ. Microelectron Eng. 2008;85:1275. [Google Scholar]
- 627.Wong CC, Agarwal A, Balasubramanian N, Kwong DL. Nanotechnology. 2007;18:135304. doi: 10.1088/0957-4484/18/13/135304. [DOI] [PubMed] [Google Scholar]
- 628.Reisner W, Beech JP, Larsen NB, Flyvbjerg H, Kristensen A, Tegenfeldt JO. Phys Rev Lett. 2007;99:058302. doi: 10.1103/PhysRevLett.99.058302. [DOI] [PubMed] [Google Scholar]
- 629.Jo K, Dhingra DM, Odijk T, de Pablo JJ, Graham MD, Runnheim R, Forrest D, Schwartz DC. Proc Natl Acad Sci USA. 2007;104:2673. doi: 10.1073/pnas.0611151104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 630.Kim Y, Kim KS, Kounovsky KL, Chang R, Jung GY, de Pablo JJ, Jo K, Schwartz DC. Lab Chip. 2011;11:1721. doi: 10.1039/c0lc00680g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 631.Zhang C, Shao PG, van Kan JA, van der Maarel JRC. Proc Natl Acad Sci USA. 2009;106:16651. doi: 10.1073/pnas.0904741106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 632.Jones JJ, van derMaarel JRC, Doyle PS. Nano Lett. 2011;11:5047. doi: 10.1021/nl203114f. [DOI] [PubMed] [Google Scholar]
- 633.Su T, Das SK, Xiao M, Purohit PK. PLoS ONE. 2011;6:e16890. doi: 10.1371/journal.pone.0016890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 634.Ebenstein Y, Gassman N, Kim S, Antelman J, Kim Y, Ho S, Samuel R, Michalet X, Weiss S. Nano Lett. 2009;9:1598. doi: 10.1021/nl803820b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 635.Reisner W, Larsen NB, Silahtaroglu A, Kristensen A, Tommerup N, Tegenfeldt JO, Flyvbjerg H. Proc Natl Acad Sci USA. 2010;107:13294. doi: 10.1073/pnas.1007081107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 636.Welch RL, Sladek R, Dewar K, Reisner WW. Lab Chip. 2012;12:3314. doi: 10.1039/c2lc40504k. [DOI] [PubMed] [Google Scholar]
- 637.Reccius CH, Mannion JT, Cross JD, Craighead HG. Phys Rev Lett. 2005;95:268101. doi: 10.1103/PhysRevLett.95.268101. [DOI] [PubMed] [Google Scholar]
- 638.Levy SL, Mannion JT, Cheng J, Reccius CH, Craighead HG. Nano Lett. 2008;8:3839. doi: 10.1021/nl802256s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 639.Mannion JT, Reccius CH, Cross JD, Craighead HG. Biophys J. 2006;90:4538. doi: 10.1529/biophysj.105.074732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 640.Reccius CH, Stavis SM, Mannion JT, Walker LP, Craighead HG. Biophys J. 2008;95:273. doi: 10.1529/biophysj.107.121020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 641.Arnold A, Bozorgui B, Frenkel D, Ha B-Y, Jun S. J Chem Phys. 2007;127:164903. doi: 10.1063/1.2799513. [DOI] [PubMed] [Google Scholar]
- 642.Jun S, Thirumalai D, Ha B-Y. Phys Rev Lett. 2008;101:138101. doi: 10.1103/PhysRevLett.101.138101. [DOI] [PubMed] [Google Scholar]
- 643.Persson F, Utko P, Reisner W, Larsen NB, Kristensen A. Nano Lett. 2009;9:1382. doi: 10.1021/nl803030e. [DOI] [PubMed] [Google Scholar]
- 644.Westerlund F, Persson F, Kristensen A, Tegenfeldt JO. Lab Chip. 2010;10:2049. doi: 10.1039/c004878j. [DOI] [PubMed] [Google Scholar]
- 645.Streng DE, Lim SF, Pan J, Karpusenka A, Riehn R. Lab Chip. 2009;9:2772. doi: 10.1039/b909217j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 646.Brochard F, de Gennes PG. J Chem Phys. 1977;67:52. [Google Scholar]
- 647.Chen Y-L, Graham MD, de Pablo JJ, Randall GC, Gupta M, Doyle PS. Phys Rev E. 2004;70:060901(R). doi: 10.1103/PhysRevE.70.060901. [DOI] [PubMed] [Google Scholar]
- 648.Dai L, Jones JJ, van der Maarel JRC, Doyle PS. Soft Matter. 2012;8:2972. [Google Scholar]
- 649.Sakaue T, Raphaël E. Macromolecules. 2006;39:2621. [Google Scholar]
- 650.Lin P-K, Fu CC, Chen YL, Chen YR, Wei PK, Kuan CH, Fann WS. Phys Rev E. 2007;76:011806. doi: 10.1103/PhysRevE.76.011806. [DOI] [PubMed] [Google Scholar]
- 651.Bonthuis DJ, Meyer C, Stein D, Dekker C. Phys Rev Lett. 2008;101:108303. doi: 10.1103/PhysRevLett.101.108303. [DOI] [PubMed] [Google Scholar]
- 652.Cifra P, Benkova Z, Bleha T. Faraday Discuss. 2008;139:377. doi: 10.1039/b716546c. [DOI] [PubMed] [Google Scholar]
- 653.Cifra P, Benkova Z, Bleha T. J Phys Chem B. 2008;112:1367. doi: 10.1021/jp076355n. [DOI] [PubMed] [Google Scholar]
- 654.Lee J, Yun Y-K, Kim Y, Jo K. Bull Korean Chem Soc. 2009;30:1793. [Google Scholar]
- 655.Mao P, Han J. Lab Chip. 2005;5:834. doi: 10.1039/b502809d. [DOI] [PubMed] [Google Scholar]
- 656.Chuanhua D, Arun M. Nat Nanotechnol. 2010;5:848. [Google Scholar]
- 657.Mokkapati VRSS, Di Virgilio V, Shen C, Mollinger J, Bastemeijer J, Bossche A. Lab Chip. 2011;11:2711. doi: 10.1039/c1lc20075e. [DOI] [PubMed] [Google Scholar]
- 658.Cheng GJ, Pirzada D, Dutta P. J Microlith Microfab Microsyst. 2005;4:013009. [Google Scholar]
- 659.Chantiwas R, Hupert ML, Pullagurla SR, Balamurugan S, Tamarit-Lopez J, Park S, Datta P, Goettert J, Cho Y-K, Soper SA. Lab Chip. 2010;10:3255. doi: 10.1039/c0lc00096e. [DOI] [PubMed] [Google Scholar]
- 660.Kim C-B, Chun H, Chung J, Lee KH, Lee JH, Song K-B, Lee S-H. Anal Chem. 2011;83:7221. doi: 10.1021/ac200859b. [DOI] [PubMed] [Google Scholar]
- 661.Strychalski EA, Stavis SM, Craighead HG. Nanotechnology. 2008;19:315301. doi: 10.1088/0957-4484/19/31/315301. [DOI] [PubMed] [Google Scholar]
- 662.Krishnan M, Mönch I, Schwille P. Nano Lett. 2007;7:1270. doi: 10.1021/nl0701861. [DOI] [PubMed] [Google Scholar]
- 663.Krishnan M, Petrasek Z, Moench I, Schwille P. Small. 2008;4:1900. doi: 10.1002/smll.200800227. [DOI] [PubMed] [Google Scholar]
- 664.Lin P-K, Lin K-h, Fu C-C, Lee KC, Wei P-K, Pai W-W, Tsao P-H, Chen YL, Fann WS. Macromolecules. 2009;42:1770. [Google Scholar]
- 665.Krishnan M, Mojarad N, Kukura P, Sandoghdar V. Nature. 2010;467:692. doi: 10.1038/nature09404. [DOI] [PubMed] [Google Scholar]
- 666.Klotz AR, Brandao HB, Reisner WW. Macromolecules. 2012;45:2122. [Google Scholar]
- 667.Zhang Y, de Pablo JJ, Graham MD. J Chem Phys. 2012;136:014901. doi: 10.1063/1.3672103. [DOI] [PubMed] [Google Scholar]
- 668.Perkins TT, Smith DE, Chu S. Science. 1997;276:2016. doi: 10.1126/science.276.5321.2016. [DOI] [PubMed] [Google Scholar]
- 669.Schroeder CM, Babcock HP, Shaqfeh ESG, Chu S. Science. 2003;301:1515. doi: 10.1126/science.1086070. [DOI] [PubMed] [Google Scholar]
- 670.Unger MA, Chou HP, Thorsen T, Scherer A, Quake SR. Science. 2000;288:113. doi: 10.1126/science.288.5463.113. [DOI] [PubMed] [Google Scholar]
- 671.Tanyeri M, Johnson-Chavarria EM, Schroeder CM. Appl Phys Lett. 2010;96:224101. doi: 10.1063/1.3431664. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 672.Tanyeri M, Ranka M, Sittipolkul N, Schroeder CM. Lab Chip. 2011;11:1786. doi: 10.1039/c0lc00709a. [DOI] [PubMed] [Google Scholar]
- 673.Doi M. Introduction to Polymer Physics. Clarendon Press; Oxford: 1996. [Google Scholar]
- 674.Balducci A, Hsieh C-C, Doyle PS. Phys Rev Lett. 2007;99:238102. doi: 10.1103/PhysRevLett.99.238102. [DOI] [PubMed] [Google Scholar]
- 675.Smith DE, Chu S. Science. 1998;281:1335. doi: 10.1126/science.281.5381.1335. [DOI] [PubMed] [Google Scholar]
- 676.Larson RG, Hu H, Smith DE, Chu S. J Rheol. 1999;43:267. [Google Scholar]
- 677.Larson RG. J Non-Newtonian Fluid Mech. 2000;94:37. [Google Scholar]
- 678.Schroeder CM, Shaqfeh ESG, Chu S. Macromolecules. 2004;37:9242. [Google Scholar]
- 679.Shaqfeh ESG. J Non-Newtonian Fluid Mech. 2005;130:1. [Google Scholar]
- 680.Brockman C, Kim SJ, Schroeder CM. Soft Matter. 2011;7:8005. doi: 10.1039/C1SM05297G. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 681.de Gennes PG. Science. 1997;276:1999. doi: 10.1126/science.276.5321.1999. [DOI] [PubMed] [Google Scholar]
- 682.Dylla-Spears R, Townsend JE, Jen-Jacobson L, Sohn LL, Muller SJ. Lab Chip. 2010;10:1543. doi: 10.1039/b926847b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 683.Xu W, Muller SJ. Lab Chip. 2011;11:435. doi: 10.1039/c0lc00176g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 684.Xu W, Muller SJ. Lab Chip. 2012;12:647. doi: 10.1039/c2lc20880f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 685.Tang J, Doyle PS. Appl Phys Lett. 2007;90:224103. [Google Scholar]
- 686.Balducci AG, Tang J, Doyle PS. Macromolecules. 2008;41:9914. [Google Scholar]
- 687.Hsieh C-C, Balducci A, Doyle PS. Macromolecules. 2007;40:5196. [Google Scholar]
- 688.Tang J, Trahan DW, Doyle PS. Macromolecules. 2010;43:3081. doi: 10.1021/ma902689c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 689.Stigter D. Biophys Chem. 2002;101:447. doi: 10.1016/s0301-4622(02)00166-7. [DOI] [PubMed] [Google Scholar]
- 690.Woo NJ, Shaqfeh ESG, Khomami B. J Rheol. 2004;48:281. [Google Scholar]
- 691.Trahan DW, Doyle PS. Macromolecules. 2011;44:383. [Google Scholar]
- 692.Chen Y-L, Lin P-K, Chou C-F. Macromolecules. 2010;43:10204. [Google Scholar]
- 693.Lin PK, Chang JF, Wei CH, Tsao PH, Fann WS, Chen YL. Phys Rev E. 2011;84:031917. doi: 10.1103/PhysRevE.84.031917. [DOI] [PubMed] [Google Scholar]
- 694.Yeh J-W, Taloni A, Chen Y-L, Chou C-F. Nano Lett. 2012;12:1597. doi: 10.1021/nl2045292. [DOI] [PubMed] [Google Scholar]
- 695.Ichikawa M, Ichikawa H, Yoshikawa K, Kimura Y. Phys Rev Lett. 2007;99:148104. doi: 10.1103/PhysRevLett.99.148104. [DOI] [PubMed] [Google Scholar]
- 696.Duhr S, Arduini S, Braun D. Eur Phys J E. 2004;15:277. doi: 10.1140/epje/i2004-10073-5. [DOI] [PubMed] [Google Scholar]
- 697.Reineck P, Wienken CJ, Braun D. Electrophoresis. 2010;31:279. doi: 10.1002/elps.200900505. [DOI] [PubMed] [Google Scholar]
- 698.Thamdrup LH, Larsen NB, Kristensen A. Nano Lett. 2010;10:826. doi: 10.1021/nl903190q. [DOI] [PubMed] [Google Scholar]
- 699.Maeda Y, Buguin A, Libchaber A. Phys Rev Lett. 2011;107:038301. doi: 10.1103/PhysRevLett.107.038301. [DOI] [PubMed] [Google Scholar]
- 700.Chen YL, Graham MD, de Pablo JJ, Jo K, Schwartz DC. Macromolecules. 2005;38:6680. doi: 10.1021/ma050238d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 701.Jo K, Chen Y-L, de Pablo JJ, Schwartz DC. Lab Chip. 2009;9:2348. doi: 10.1039/b902292a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 702.Agarwal US, Dutta A, Mashelkar RA. Chem Eng Sci. 1994;49:1693. [Google Scholar]
- 703.Ma H, Graham MD. Phys Fluids. 2005;17:083103. [Google Scholar]
- 704.Ueda M, Yoshikawa K, Doi M. Polymer J. 1997;29:1040. [Google Scholar]
- 705.Ueda M, Yoshikawa K, Doi M. Polymer J. 1999;31:637. [Google Scholar]
- 706.Oana H, Ueda M, Washizu M. Biochem Biophys Res Commun. 1999;265:140. doi: 10.1006/bbrc.1999.1614. [DOI] [PubMed] [Google Scholar]
- 707.Ueda M, Baba Y. Anal Sci. 1997;13:109. [Google Scholar]
- 708.Ueda M, Oana H, Baba Y, Doi M, Yoshikawa K. Biophys Chem. 1998;71:113. doi: 10.1016/s0301-4622(98)00093-3. [DOI] [PubMed] [Google Scholar]
- 709.Namasivayam V, Larson RG, Burke DT, Burns MA. Anal Chem. 2002;74:3378. doi: 10.1021/ac025551h. [DOI] [PubMed] [Google Scholar]
- 710.Slater GW, Rousseau J, Noolandi J. Biopolymers. 1987;26:863. doi: 10.1002/bip.360260607. [DOI] [PubMed] [Google Scholar]
- 711.Lam L, Sakakihara S, Ishizuka K, Takeuchi S, Noji H. Lab Chip. 2007;7:1738. doi: 10.1039/b711826k. [DOI] [PubMed] [Google Scholar]
- 712.Kumemura M, Collard D, Yamahata C, Sakaki N, Hashiguchi G, Fujita H. ChemPhysChem. 2007;8:1875. doi: 10.1002/cphc.200700268. [DOI] [PubMed] [Google Scholar]
- 713.Braun E, Keren K. Adv Phys. 2004;53:441. [Google Scholar]
- 714.Hölzel R, Gajovic-Eichelmann N, Bier FF. Biosensors Bioelectronics. 2003;18:555. doi: 10.1016/s0956-5663(03)00024-1. [DOI] [PubMed] [Google Scholar]
- 715.Sung KE, Burns MA. Anal Chem. 2006;78:2939. doi: 10.1021/ac051662f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 716.Ajdari A. Phys Rev Lett. 1995;75:755. doi: 10.1103/PhysRevLett.75.755. [DOI] [PubMed] [Google Scholar]
- 717.Wälti C, Tosch P, Davies AG, Germishuizen WA, Kaminski CF. Appl Phys Lett. 2006;88:153901. [Google Scholar]
- 718.Castro A, Fairfield FR, Shera EB. Anal Chem. 1993;65:849. [Google Scholar]
- 719.Goodwin PM, Johnson ME, Martin JC, Ambrose WP, Marrone BL, Jett JH, Keller RA. Nucleic Acids Res. 1993;21:803. doi: 10.1093/nar/21.4.803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 720.Agronskaia A, Schins JM, de Grooth BG, Greve J. Anal Chem. 1999;71:4684. [Google Scholar]
- 721.Petty JT, Johnson ME, Goodwin PM, Martin JC, Jett JH, Keller RA. Anal Chem. 1995;67:1755. [Google Scholar]
- 722.Huang ZP, Petty JT, O’Quinn B, Longmire JL, Brown NC, Jett JH, Keller RA. Nucleic Acids Res. 1996;24:4202. doi: 10.1093/nar/24.21.4202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 723.Huang ZP, Jett JH, Keller RA. Cytometry. 1999;35:169. doi: 10.1002/(sici)1097-0320(19990201)35:2<169::aid-cyto9>3.3.co;2-b. [DOI] [PubMed] [Google Scholar]
- 724.Habbersett RC, Jett JH. Cytometry. 2004;60A:125. doi: 10.1002/cyto.a.20042. [DOI] [PubMed] [Google Scholar]
- 725.Haab BB, Mathies RA. Appl Spectrosc. 1997;51:1579. [Google Scholar]
- 726.Schins JM, Agronskaya A, de Grooth BG, Greve J. Cytometry. 1998;32:132. doi: 10.1002/(sici)1097-0320(19980601)32:2<132::aid-cyto8>3.0.co;2-n. [DOI] [PubMed] [Google Scholar]
- 727.van Orden A, Cai H, Goodwin PM, Keller RA. Anal Chem. 1999;71:2108. doi: 10.1021/ac9811221. [DOI] [PubMed] [Google Scholar]
- 728.Van Orden A, Keller RA, Ambrose WP. Anal Chem. 2000;72:37. doi: 10.1021/ac990782i. [DOI] [PubMed] [Google Scholar]
- 729.Ferris MM, Habbersett RC, Wolinsky M, Jett JH, Yoshida TM, Keller RA. Cytometry. 2004;60A:41. doi: 10.1002/cyto.a.20000. [DOI] [PubMed] [Google Scholar]
- 730.Werner JH, Larson EJ, Goodwin PM, Ambrose WP, Keller RA. Appl Optics. 2000;39:2831. doi: 10.1364/ao.39.002831. [DOI] [PubMed] [Google Scholar]
- 731.Larson EJ, Hakovirta JR, Cai H, Jett JH, Burde S, Keller RA, Marrone BL. Cytometry. 2000;41:203. doi: 10.1002/1097-0320(20001101)41:3<203::aid-cyto7>3.0.co;2-2. [DOI] [PubMed] [Google Scholar]
- 732.Yan X, Grace WK, Yoshida TM, Habbersett RC, Velappan N, Jett JH, Keller RA, Marrone BL. Anal Chem. 1999;71:5470. doi: 10.1021/ac990780y. [DOI] [PubMed] [Google Scholar]
- 733.Yan XM, Habbersett RC, Cordek JM, Nolan JP, Yoshida TM, Jett JH, Marrone BL. Anal Biochem. 2000;286:138. doi: 10.1006/abio.2000.4789. [DOI] [PubMed] [Google Scholar]
- 734.http://nfcr.lanl.gov/instruments.html.
- 735.Stavis SM, Corgie SC, Cipriany BR, Craighead HG, Walker LP. Biomicrofluidics. 2007;1:034105. doi: 10.1063/1.2789565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 736.Castro A, Williams JGK. Anal Chem. 1997;69:3915. doi: 10.1021/ac970389h. [DOI] [PubMed] [Google Scholar]
- 737.Chou HP, Spence C, Scherer A, Quake S. Proc Natl Acad Sci USA. 1999;96:11. doi: 10.1073/pnas.96.1.11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 738.Filippova EM, Monteleone DC, Trunk JG, Sutherland BM, Quake SR, Sutherland JC. Biophys J. 2003;84:1281. doi: 10.1016/S0006-3495(03)74943-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 739.Fu AY, Spence C, Scherer A, Arnold FH, Quake SR. Nat Biotechnol. 1999;17:1109. doi: 10.1038/15095. [DOI] [PubMed] [Google Scholar]
- 740.Foquet M, Korlach J, Zipfel W, Webb WW, Craighead HG. Anal Chem. 2002;74:1415. doi: 10.1021/ac011076w. [DOI] [PubMed] [Google Scholar]
- 741.Stavis SM, Edel JB, Li YG, Samiee KT, Luo D, Craighead HG. Nanotechnology. 2005;16:S314. doi: 10.1088/0957-4484/16/7/002. [DOI] [PubMed] [Google Scholar]
- 742.Cipriany BR, Zhao R, Murphy PJ, Levy SL, Tan CP, Craighead HG, Soloway PD. Anal Chem. 2010;82:2480. doi: 10.1021/ac9028642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 743.Chabert M, Dorfman KD, de Cremoux P, Roeraade J, Viovy J-L. Anal Chem. 2006;78:7722. doi: 10.1021/ac061205e. [DOI] [PubMed] [Google Scholar]
- 744.Haab BB, Mathies RA. Anal Chem. 1999;71:5137. doi: 10.1021/ac990644t. [DOI] [PubMed] [Google Scholar]
- 745.Larson JW, Yantz GR, Zhong Q, Charnas R, Antoni DCM, Gallo MV, Gillis KA, Neely LA, Phillips KM, Wong GG, Gullans SR, Gilmanshin R. Lab Chip. 2006;6:1187. doi: 10.1039/b602845d. [DOI] [PubMed] [Google Scholar]
- 746.Protozanova E, Zhang M, White EJ, Mollova ET, Ten Broeck D, Fridrikh SV, Cameron DB, Gilmanshin R. Anal Biochem. 2010;402:83. doi: 10.1016/j.ab.2010.03.024. [DOI] [PubMed] [Google Scholar]
- 747.Randall GC, Schultz KM, Doyle PS. Lab Chip. 2006;6:516. doi: 10.1039/b515326c. [DOI] [PubMed] [Google Scholar]
- 748.Hsieh C-C, Lin T-H. Biomicrofluidics. 2011;5:044106. doi: 10.1063/1.3655565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 749.Trahan DW, Doyle PS. Biomicrofluidics. 2009;3:012803. doi: 10.1063/1.3055275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 750.Balducci A, Doyle PS. Macromolecules. 2008;41:5485. [Google Scholar]
- 751.Chuncheng Z, Feng J, Qianqian C. Polymer. 2009;50:5326. [Google Scholar]
- 752.Phillips KM, Larson JW, Yantz GR, D’Antoni CM, Gallo MV, Gillis KA, Goncalves NM, Neely LA, Gullans SR, Gilmanshin R. Nucleic Acids Res. 2005;33:5829. doi: 10.1093/nar/gki895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 753.Underhill PT, Doyle PS. Phys Rev E. 2007;76:011805. doi: 10.1103/PhysRevE.76.011805. [DOI] [PubMed] [Google Scholar]
- 754.Castro A, Shera EB. Anal Chem. 1995;67:3181. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.