A computational study of water and CO migration sites and channels inside myoglobin

Abstract

Pathways are computed for transport of H₂O and CO in myoglobin (Mb), using the single sweep and zero-temperature string methods in a fully atomistic, explicitly solvated model system. Our predictions of sites and barriers in the pathways for CO transport agree with previous studies. For H₂O, we predict a binding site in the distal pocket (DP), in agreement with crystallographic observations, and another one close to Leu 29 which explains the importance of this residue in controlling the pocket’s hydrophobicity, as well as disordered minima in the largely apolar xenon cavities. In particular, H₂O can occupy and transition among the xenon cavities, Xe4, Xe2, and Xe3. Our results support the hypothesis that the thermodynamically most favorable entry/exit portal for H₂O is the so-called histidine gate (HG), the same as for CO. This result, along with the observation of water occupation of both DP and apolar Xe cavities, suggest that water and small gas molecules like CO compete for access to the protein interior, and therefore models of gas molecule transport within proteins should also explicitly consider water transport.

Introduction

Diffusion of small molecules inside proteins is essential for many biological processes. Many proteins are targets of small compounds that through binding modulate their biological activity. Many such proteins function as carriers, binding to ligands with high affinity and selectivity, and consequently are able to release them in a controlled manner. A better understanding of the process of diffusion of a small molecule from the solvent to interior pockets of a protein would contribute to our understanding of the function of these proteins. Calculation of free energy changes associated with diffusion processes remains a significant challenge, and it can be directed for example to improve structure-based design of ligands with potential to diffuse and bind with enhanced selectivity and affinity to the protein target.

Myoglobin (Mb), an intracellular oxygen storage protein, has been the center of attention for many years in the study of diffusion pathways and mechanisms of ligand binding. Numerous experimental and computational techniques have been used to study diffusion of small ligands inside Mb.^1–17 X-ray structures and spectroscopic studies conducted at a variety of temperatures and pressures have shown the existence of hydrophobic cavities with a volume ranging from 30 to 100 ų inside Mb, where CO, NO, and O₂ can migrate.^14,18 Cavities in Mb (Figure 1) include the so-called distal pocket (DP) and four distinct apolar xenon sites, termed Xe1, Xe2, Xe3, and Xe4.^12,19–24 Crystal structures provide evidence of water in DP.²⁵ When no ligand is bound to the heme iron cation, H₂O can enter DP and compete with CO in rebinding to the heme group, possibly causing CO to be trapped in Xe1 with H₂O forming non-covalent interactions with the imidiazole ring of His 64.¹² The competition of CO with H₂O in DP implies that H₂O displacement is required for CO binding to the heme.²⁶ Complementing experimental studies were several computational studies which focused on diffusion of CO inside Mb.^{5–8,10,13,16,27,28} Those studies addressed the diffusion of CO entry and exit from Mb focusing only on CO, but do not consider the role of H₂O, which is known to affect the association rate constant of CO.²⁶ In particular, changes in distal water occupancy can critically influence the kinetics of binding of CO, and mutations of E7 introducing apolar residues in DP can shift the water DP-to-solvent equilibrium.²⁵ Recent work has been done to develop a fingerprint of Mb solvation sites, both external and internal, although the free energy changes associated with water migration in Mb were not calculated.²⁹

Figure 1.

Representation of Mb with distal His 64 of E7 (stick), heme group (stick) and Xenon adsorption sites (yellow spheres) located in the interior of the protein (ribbon).

Standard MD techniques have the potential to shed light on ligand migration, but even long MD simulations face difficulties collecting good statistics due to undersampling transitions between minima in some reasonable free energy landscape.³⁰ This is because diffusion of ligand molecules in and out of protein cavities can be excessively slow due to energetic barriers associated with the motion of Mb residues. Recently, Maragliano et al.¹⁰ used the single sweep method to compute the free energy associated with CO in Mb, and further used the string method on the free energy hypersurface to compute pathways of minimum free energy connecting low energy sites. In this work, we employ the single-sweep/string method protocol to study the diffusion of water in Mb.

We find here that the free energy for H₂O has many local minima on the surface of Mb, in DP and in internal cavities. Our findings also support the notion that water and CO preferentially migrate from the DP to the solvent through the HG site. We note that by comparison to the CO free energy, water and CO migrate to different sites and have quite different networks of interconnecting pathways.

Theory and Methods

Single-sweep PMF reconstruction and pathway characterization

The single-sweep method is used to map free energy landscapes in collective variables (CVs). Briefly, single-sweep uses temperature-accelerated MD (TAMD)^31,32 to rapidly explore the chosen CV space, and samples in that space are harvested and used as locations where mean forces are accumulated for later reconstruction into an approximate free energy. In TAMD, the system is extended to include z-variables that act as anchor-points for CVs, whose mapping functions are θ(x):

$$U_k(x,z)=V(x)+\frac{1}{2}k{\mid \theta (x)-z\mid }^2$$ (1)

where k > 0 is an adjustable parameter.

The extended system evolves according to the following dynamics:

$$m_x\ddot{x}=-{\nabla }_{x}V(x)-k\sum _{\alpha =1}^N({\theta }_{\alpha }(x)-z_{\alpha }){\nabla }_x{\theta }_{\alpha }(x)+\text{thermostat}\text{terms}\text{at}{\beta }^{-1}$$ (2)

$$\overline{\gamma }\stackrel{.}{z}=k(\theta (x)-z)+\sqrt{2\gamma {\overline{\beta }}^{-1}}\eta (t)$$ (3)

where m_x is the mass and η(t) is a Gaussian process with mean 0 and covariance 〈η_α(t)η_α′(t′)〉 = δ_αα′δ(t − t′). γ̄ is a friction coefficient, and 1/β̄ is an artificial temperature. By taking 1/β̄ > 1/β, the system is able to cross barriers along the trajectory of z(t) and visit relevant regions of CV space which are not accessible at the physical temperature 1/β on typical MD timescales.

Centers for mean force calculations are harvested from a collection of TAMD simulations, or “sweeps”, to cover all the relevant regions of the PMF. The only criterion for allowing a sampled configuration to be a center is that it has to be no closer than some chosen threshold distance from any other center in CV space. The mean force f_k is computed at each center z_k, by running TAMD while fixing z(t) = z_k:

$$f_k=\frac{1}{T}{\int }_0^{T}k(\theta (x(t))-z_k)dt$$ (4)

After the mean forces f₁, …, f_K are calculated the 3D-PMF is reconstructed using a radial basis function (RBF) representation of A(z) for the centers z₁, …, z_K.

$$A(z)=\sum _{\alpha =1}^N{a}_k{\varphi }_{\sigma }(\mid z-z_k\mid )+C$$ (5)

The arbitrary origin of A(z) is adjusted using the constant C. Euclidean norm is indicated as |…| in R^N, and ϕ_σ(u) is an RBF with length-scale parameter σ; we used ϕ_σ(u) = exp(−u²/2σ²), where σ can be adjusted manually to provide a best-fit of the free energy gradients, and the optimal values are determined using a procedure as described previously.¹⁰ Briefly, a gradient error estimate E is used to find optimal parameters a_k

$$E(a,\sigma )=\sum _{k=1}^K{\left|\sum _{k^{\prime }=1}^K{a}_{k^{\prime }}{\nabla }_z{\varphi }_{\sigma }(\mid z_k-z_{k^{\prime }}\mid )+f_k\right|}^2$$

The minimization procedure involved solving a linear system in which coefficients can be obtained explicitly and it has been described in details in previous work.³² The second step of the approach is to compute minimal free energy pathways (MFEP’s) connecting local minima using the zero-temperature string method (ZTS).^33–36

Protocol

The initial structure of Mb with CO was retrieved from the PDB (PDB ID 2MB5). The starting structure for Mb with H₂O was obtained from Mb with CO by mutating the CO into H₂O and retaining the original oxygen atom coordinates. The crystallographic water molecules located outside the protein matrix, and ions, were removed. Ionization states were assigned considering neutral pH, histidines were not protonated and necessary hydrogen atoms were added. The centers of mass of residues 10, 100 and 150 were restrained near their original coordinates using an isotropic quadratic function with force constant k_f = 1.0 kcal/mol/Ų to fix the orientation of the protein during the simulations. A rectilinear box with explicit water was built to solvate the protein. The system included 2533 protein atoms, 18515 water molecules for solvation, 1 ion, and 3 atoms or 2 atoms of the small ligand. The MD simulations were carried out using NAMD v. 2.8³⁷ using the CHARMM27 force field³⁸ with TIP3P water³⁹. Periodic boundary conditions were used and long-range electrostatics were computed using particle-mesh Ewald summation with grid spacing of 1 Å. Van der Waals interactions were cut off beyond a distance of 9 Å and covalent bonds were kept fixed by using the SHAKE algorithm. A Langevin thermostat was used to control the temperature at 310 K with a coupling constant of 5 ps⁻¹, and the integration time step was 2 fs. The system was equilibrated for 2 ns at constant pressure (P = 1.01 bar) and temperature (T = 310 K) by using a Langevin Nosé-Hoover piston with a coupling constant of 1 ps for the thermostat and 0.5 ps for the barostat. The box dimensions were 65 × 60 × 60 ų (21049 atoms) for equilibration and production runs. For the simulations in which we recompute the CO pathways, we model the CO dissociated state and the system is not allowed to bind the Fe and switch to the associated state (C-Fe). The parameters of the potential to describe the dissociated state are retrieved from previous work.⁴⁰ During pre-single-sweep MD equilibration the ligand was always located inside DP for both cases of CO and H₂O. TAMD simulations started after the equilibration.

We selected 3 CVs for both CO and H₂O: the Cartesian coordinates of the center of mass of the ligand molecule. We assumed that the diffusion of the small molecule can be analyzed using a small number of CVs, and the choice of those variables is based on the capability of mapping the resulting PMF on the initial structure and the relative ease in tracking the small molecule to detect when it has exited the protein to the solvent. Orientational and translational displacement of the protein was avoided using harmonic restrains described above. The exploration of the unknown free energy landscape is performed using 10 independent TAMD simulations, in each of which the CO or H₂O after sampling interior cavities of Mb escaped to the solvent. We have used as parameters for all TAMD simulations κ = 200 kcal/(mol Ų), β̄⁻¹ = 5 kcal/mol, γ̄ = 50 ps⁻¹, and a time step of 2 fs. We tried also to run simulations with β̄⁻¹ = 10 kcal/mol and β̄⁻¹ = 20 kcal/mol keeping the other parameters fixed, but CO and H₂O then exited the protein too rapidly without sampling the cavities or locations between them.

All the TAMD trajectory frames were combined together to obtain a single sweep of the center of mass coordinates. This trajectory is used to select the centers in CV space, where the mean forces were calculated to reconstruct the PMF. We selected the centers starting from z₁and depositing a center along the trajectory such that no two centers are closer than 2.5 Å from each other. At the end we deposited 250 centers for CO and 130 for H₂O, respectively (Figure 2).

Figure 2.

130 centers for H₂O (top) and 250 for CO (bottom) as blue spheres (H₂O) or red spheres (CO) located inside Mb. The protein backbone is shown in cyan ribbon, the heme group as bonds.

We compute the mean forces at the centers with a simulation in which we set z(t) = z_k, and k = 200 kcal/(mol Ų) described in the Eq. 4. The mean forces were accumulated for 500 ps in order to insure convergence of the mean force. These calculations were distributed in parallel since they are independent from each other. Gaussian RBFs were used for the reconstruction of the PMF with an optimal value of σ = 3 Å and we obtained a relative residual error of 0.6. VMD was used to produce the protein graphical representations.⁴¹

Results

H₂O and CO PMF Maps in Mb

We determined 3-D PMF’s in two separate sets of single sweep calculations for CO and H₂O. Both CO and H₂O cross the protein interior in 1 ns timescale to reach the solvent from the initial configuration in DP in all TAMD simulations launched. At the beginning of the simulations H₂O was confined by residues Leu 29, Phe 43, His 64, Val 68, and Ile 107. Energetic barriers arise from the side chains orientation of key residues like Leu 29, Leu 32, Phe 33, Arg 45, His 64, Ile 107, and Ile 111 in DP that limit the motion of small molecules among cavities inside the protein in unbiased simulations. Overall, we observe that our TAMD simulations are successful in overcoming the energetic barriers and sampling relevant regions of the 3D-PMF going from DP to the apolar cavities and to reach the solvent.

Free energy minima on the 3D-PMF in the case of H₂O represent locations of hydration sites in the protein. Free energy minima for water are found on the surface of the protein, and also inside the core of the protein matrix in Xe2, Xe3, Xe4 and DP (Table 1). We found a deep minimum on the surface of the protein next to Glu 109, which is a conserved residue and located on the surface (Figure 3), and it represents the global minimum. Free energy minima are located in close proximity to His 64 in DP with free energy −7.9 kcal/mol, and close to His 24 in Xe4 with free energy −5.9 kcal/mol, relative to the unbound ligand state. Water evidently forms polar interactions with those specific residues. Free energy local minima of water inside DP are shown in Figure 4. The 3D-PMF for H₂O clearly indicates the presence of hydration sites inside the DP pocket. One local free energy minimum is found in proximity of Nε of His 64 in E7, and it is compatible with the hydration site shown in the crystal structure of Mb with water located in DP.²⁵ A second minimum can be found in the interior of the protein on the other side of the side chain of Leu 29 from the His 64 minimum. The shape of the 3D-PMF (Figure 4) in the DP shows that water in DP can exchange positions within the pocket even if it occupies on average the site close to Nε of His 64.

Table 1.

Local minima sites for water identified using single-sweep.

Site	Energy(kcal/mol)	Residues
1	−8.0	Glu109
2	−7.9	His64
3	−7.0	Glu105
4	−6.5	Lys79
5	−5.9	His24
6	−5.7	Arg45
7	−5.7	Phe33
8	−5.6	Gln26
9	−5.4	Arg139
10	−5.2	Glu18
11	−4.8	Arg139
12	−4.4	Glu85
13	−4.3	His24

Figure 3.

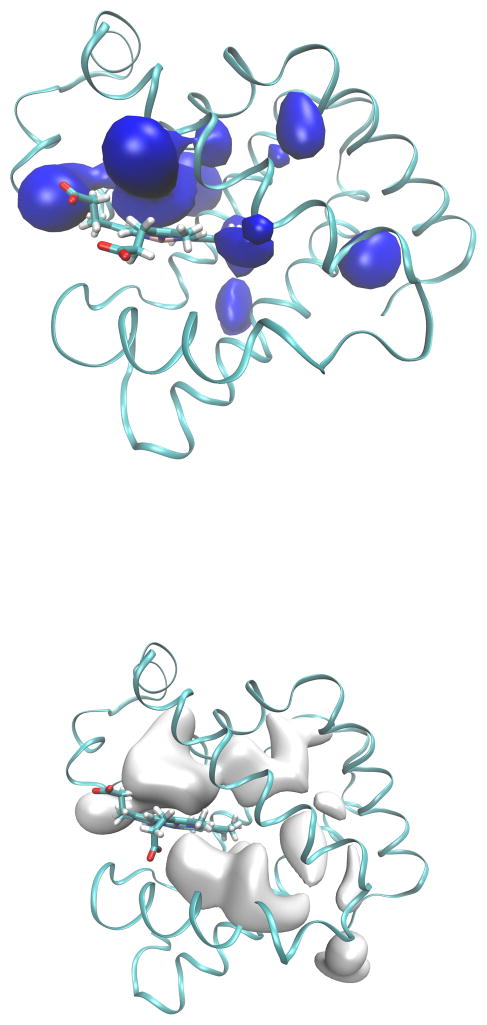
Isosurfaces of the 3D-PMF of Mb for H₂O (top) and CO (bottom). Surfaces are represented at 7 kcal/mol with respect to their global energy minima. The global minimum for water is in proximity of Glu 109 on the surface of Mb, and the global minimum for CO is in Xe4.

Figure 4.

Close up view of local free energy minima of the PMF for H₂O close to DP of Mb. One local free energy minima is found in proximity of Nε of His 64 in E7. The isosurface of the PMF is shown as a mesh, while the heme group, His 64 and Leu 29 are represented as sticks, and the protein in ribbon. The isosurface is 8 kcal/mol from the global minimum. The two minima are labeled with a number inside the mesh.

The 3D-PMF surface is also calculated for CO (Figure 3). We perform those calculations to assess the quality of our PMF reconstruction with respect to a previous study,¹⁰ and to compare the H₂O PMF with that of CO produced using the same methods and simulation codes. One minimum is found in DP which is extended, with another minimum in Xe4 pocket. Our findings reveal here that local structure of the free energy in DP differs for CO and H₂O (Figure 3), and H₂O has a minimum towards the interior of Mb facing Xe4 that may signify its easy displacement in that direction. The minimum located in Xe2 is shifted slightly by 1 Å comparing the Xe2 site determined in the crystal structures. Finally, the Xe3 cavity also has a minimum. Thus, the minima for CO included all the known apolar cavities where CO was found: DP, Xe1, Xe2, Xe3, and Xe4. In particular, the shape of local free energy minima reasonably correlates with experimental defined internal Xe sites to which CO can migrate. The 3D-PMF shows the deepest free energy minima in Xe4. Overall, the minima are located in the apolar cavities and DP, and they reproduce the locations found by experiments on CO diffusion.⁴² These results are in agreement with many computational studies directed to map the diffusion of CO inside Mb.^{4–8,10,13,28}

Diffusion pathways

After locating the free energy minima, we focus our attention on the diffusion pathways and entry/exit portals for H₂O and CO. We first make the reasonable assumption that in diffusing through protein channels, ligands will roughly follow pathways of minimal free energy, so identifying diffusion routes is the same as finding MFEP’s on the PMF’s. The small molecule in the initial configuration is located in the DP, and the pathway to allow migration to the solvent covers a distance of 30–40 Å. From the local free energy minima we search for the dominant pathways for H₂O and CO on their respective 3D-PMF’s using the ZTS method as described above (Theory and Methods). MFEPs for H₂O show energetic barriers and dominant pathways as well free energy difference between a pair of Xe sites can be summed up for each barrier to determine the relative total energy barrier considering all the minima in the MFEPs (Table 2). Figure 5 shows free-energy profiles along MFEP’s for water connecting solvent with Mb internal cavities. Figure 6 shows the dominant pathways as red curves connecting DP to HG, Xe4, Xe2, Xe1, and Xe3. The isosurface of the 3D-PMF is shown (gray, 7 kcal/mol with respect to Xe4) with gray spheres indicating the local minima. Figure 7 shows the dominant pathways for water in a similar format as the CO pathways. The dominant pathways for CO computed in this study start in DP and go to HG, Xe4, Xe2, and Xe3 with local minima in blue spheres. For water the red tubes connecting the internal cavities are organized differently with respect to CO indicating two distinct networks for the two molecules.

Table 2.

Total free energy barriers calculated for local minima sites in Mb.

Ligand	DP-HGa	DP-Xe4a	Xe4-Xe2a	Xe2-Xe1a	Xe2-Xe3a
ΔAH2O	7.2	4.9	7.5	-	5.5
ΔACO	7.0	7.0	8.5	1.2	3.6

^ain kcal/mol.

Figure 5.

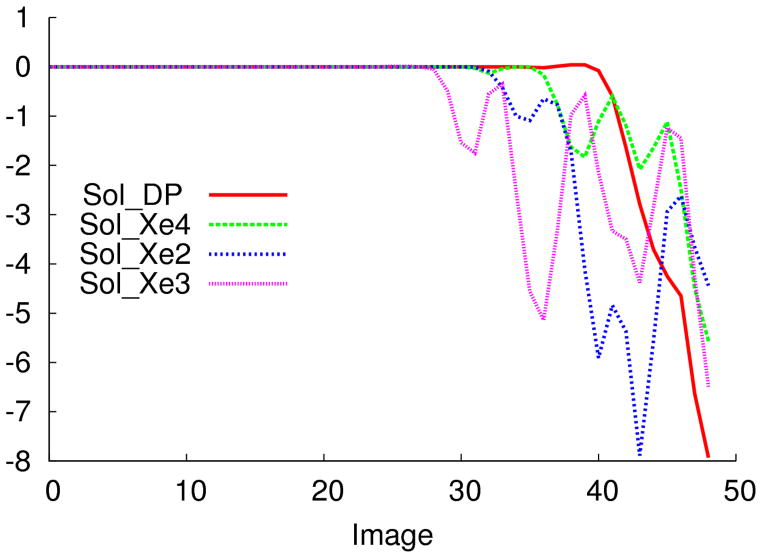
Free-energy profiles along MFEPs for water migration from the solvent to internal cavities. The difference is calculated with 50 images using the string method. Solvent-DP(red), solvent-Xe4 (green), solvent-Xe3 (purple), and solvent-Xe2 (blue) are represented.

Figure 6.

MFEPs for CO from DP-HG, DP-Xe4, Xe4-Xe2, and Xe2-Xe3. Local minima along the pathways (red) are presented as spheres (gray). The isosurface is drawn considering an energy level of 7 kcal/mol from the global minimum in Xe 4.

Figure 7.

MFEPs for water from DP-HG, DP-Xe4, Xe4-Xe2, and Xe2-Xe3. Local minima are blue spheres and pathways are red tubes. The isosurfaces are drawn with an energy level of 7 kcal/mol from the global minimum at Glu 109.

For water the difference in free energy from solvent to DP through HG is 8.0 kcal/mol (Figure 5), and there is a small barrier to enter the protein. Water to enter Xe4 has to overcome a barrier of 2.1 kcal/mol. In contrast, the entrance from Xe2 has three barriers, the first two are about 0.5 kcal/mol, and the third one is of 5.0 kcal/mol. Migration of water inside the protein from Xe3 is unlikely due to many high barriers that need to be overcome to enter the protein matrix. We can establish that the most likely route from entry of water inside Mb is from HG to DP.

Surprisingly, however, we found that H₂O traverses a high barrier prior even to entering the DP compared with the barriers of internal apolar sites. The barriers we computed suggest that H₂O exits the binding pocket more easily to enter other cavities than it does to exit the protein. DP-Xe4 migration shows a barrier of 4.9 kcal/mol compared with 8.0 kcal/mol for H₂O to leave through HG. Water can shuttle to other internal cavities from Xe4. The local pathway from Xe4 to Xe2 has a barrier of 7.5 kcal/mol. Xe2-Xe3 migration has a barrier of 5.5 kcal/mol.

We measure a barrier of 7.0 kcal/mol from HG to DP for CO. In contrast, the energy barrier for migration from DP to Xe4 has two minima with a difference of 5.0 kcal/mol for the first one, and 2.0 kcal/mol for the second one. The Xe4-Xe2 migration crosses two barriers, 4.2 kcal/mol and 4.3 kcal/mol which together constitute the largest energetic barrier in pathways of diffusion. From Xe2 to Xe1 the barrier is 1.2 kcal/mol. Free energy barriers from Xe2 to Xe3 is of 1.3 kcal/mol and 2.3 kcal/mol, respectively. In a recent work, Bossa et al.²⁷ measured PMF barrier of ~2.6 kcal/mol from Xe4 to DP for CO, computed from a long umbrella sampling simulation with a flat umbrella potential of which about 3 ns is spent by CO at the barrier. Those results were reproduced by Cohen et al.⁷ with a different technique. These methodologies are based on a different approach, in the first work PMF is calculated using umbrella sampling²⁷, in the second one implicit ligand sampling is used,⁷ but overall our results are similar to theirs.

Also, we can construct channels of migration inside the protein matrix for CO and H₂O inter-connecting DP, Xe4, Xe2, Xe1, and Xe3 (Figure 6 and Figure 7). Differences between CO and H₂O are shown; in general we can say that CO follows different dominant routes of migration inside Mb than does water, and the Xe1 pocket is not visited by water.

Discussion

The computational method presented here provides free energies and small ligand diffusion pathways in Mb. Overall, the free energy minima for CO in DP, Xe4, Xe2, Xe1, and Xe3 are located in similar sites to other studies^7,13,27 and agree with crystallographic and spectroscopic evidence of wild type structures and mutants of Mb in the apolar cavities.^2,42–46 The PMF calculation for H₂O adds a critical missing piece in the general picture of CO diffusion. H₂O free energy local minima are located in DP, suggesting that water has an important role in DP both in controlling the HG entry of CO and in creating competition for CO binding to His 64 in the pocket. The presence of a minimum for water close to Leu 29 can explain how the displacement of water can take place in DP to allow the rebinding of CO ligand to the heme. Indeed, the replacement of Leu 29 with a less hydrophobic residue leads to the invasion of water in DP due to the decrease of hydrophobicity.⁴⁷ Leu 29 forms a separation barrier between the two energy minima in DP, and the presence of this barrier allows us to conclude that wetting/dewetting transitions with high water mobility likely exist in Mb. Although the hydration sites cannot be correlated with residence time of water⁴⁸ DP contains hydrophobic side chains capable to increase the residence time for water.⁴⁸ The hydration water sites detected by X-ray diffraction experiments²⁵ systematically overlap onto calculated high-density regions within the approximations of Debye–Waller factors generally used in crystallographic refinement, which assume fully harmonic oscillations of small molecules in crystals. The presence of free energy minima for H₂O in the DP of Mb matched qualitatively previous experimental work,²⁶ confirming hydration properties of unliganded DP pocket, and the high occupancy of water that agrees with H₂O hydrogen bonding to Nε of His 64.^25,49 Furthermore, our results argue that water can be present in the Xe2 of Mb even if it is not seen in the crystal structures, suggesting further that waters in these cavities are more disordered with shorter residence times compared with water in DP.⁴⁸ The presence of minima located in Xe4 and Xe3 can be understood by the polar side chains of His 24, and His 82 that may form hydrogen bonds with the water molecule. The 3D-PMF is different for CO and H₂O, in that the minima for CO are deep inside the apolar cavities due to the hydrophobic nature of residues in the protein matrix. Findings of local minima for H₂O support the general model drawn by the Brunori and Gibson scheme in which water binding to His 64 is an intermediate state,²¹ but also the DP can be characterized by dry and wet regions. Our prediction that water has an ordered behavior in DP, and is instead disordered in the other cavities (Xe4, and Xe2, and Xe3) is important because it implies that water in cavities needs to be modeled in high resolution structures.^50,51

Considering all the pathways and barriers we can speculate that the entry portal for H₂O is the HG, but then the migration to other internal cavities like Xe4 and Xe2 is possible. MFEPs show a low free energy barrier for H₂O from DP to Xe4 which suggests that when CO returns to DP to bind the heme, water can be displaced in the DP-Xe4 direction and then exit the protein. On the other side, the migration of H₂O from Xe4 to Xe2 seems to be unlikely due to a high free energy penalty, and instead the transition from DP to Xe2 and then from Xe1 and to the solvent is likely to be one dominant pathway. CO binding is thermodynamically favored in DP compared with H₂O which can be also captured transiently. Indeed, an apolar gas like CO is favored entropically to move out of the water solvent, but the gain is compensated in the transfer to a closed internal cavity inside a protein. Once the CO moves to apolar cavities H₂O binding to His 64 is possible. If CO returns to DP to rebind or exit the protein matrix the water needs to be displaced, and it is possible for this displacement to carry water into disordered internal sites.

It is not yet possible to experimentally map the free energy of ligands inside proteins at ambient conditions, so we cannot compare our CO and H₂O free energies directly to experiment. However, as pointed out by Elber,⁹ we can make approximations of the escape time CO from DP through the HG route using simple transition-state theory; with a frequency of 2 ps⁻¹, our DP-to-HG barrier for CO implies an escape time of about 200 ns, and that for water is about 300 ns. Kinetics of geminate rebinding^15,52 suggest the CO escape time is a bit lower, about 100 ns. However, we stress that a more robust comparison of kinetics can be made by forgoing TST in favor of simulation methods such as milestoning,⁵³ an avenue we are currently pursuing.

Finally, we briefly discuss our choice of CV’s. We followed the example of Maragliano et al.¹⁰ in choosing as CV’s the cartesian coordinates of the ligand center of mass. Within the context of any CV-based enhanced sampling method, this of course means that there might be other slow variables that are missed, and in particular, one might be concerned here with transitions among side-chain rotameric states which may influence transport pathways.^5,54 It is possible to include such variables in a single-sweep analysis, but adding a fourth dimension to CV space would increase the number of mean-force computations by a large factor, making it somewhat challenging. Alternative approaches to detecting and handing hidden barriers once one has made an obvious choice for CV’s should be pursued. At this stage, because single-sweep evidently does well at identifying key sites, these results provide a baseline against with more sophisticated methods that include additional slow variables could be compared.

Conclusions

We used the single-sweep/string method to compute diffusion pathways for water and CO in Mb. Local free energy minima for water are located in DP and agree with experimental results, and local minima are observed in Xe4, Xe2, and Xe3, which are regions in which water was not resolved in the crystal structures. From the PMF maps of water and CO we can assume the presence of competition for the apolar sites inside Mb. Given this, it is likely that transport of water and CO inside Mb are interconnected and experimental diffusion rates are also reciprocally affected by the presence of those two molecules. This motivates future work in which the direct dependency of diffusion rates of CO on the presence of water inside the protein can be addressed.