Abstract
The ability to accurately determine the elastic modulus of each layer of the human cornea is a crucial step in the design of better corneal prosthetics. In addition, knowledge of the elastic modulus will allow design of substrates with relevant mechanical properties for in vitro investigations of cellular behavior. Previously, we have reported elastic modulus values for the anterior basement membrane and Descemet’s membrane of the human cornea, the surfaces in contact with the epithelial and endothelial cells, respectively. We have completed the compliance profile of the stromal elements of the human cornea by obtaining elastic modulus values for Bowman’s layer and the anterior stroma. Atomic force microscopy (AFM) was used to determine the elastic modulus, which is a measure of the tissue stiffness and is inversely proportional to the compliance. The elastic response of the tissue allows analysis with the Hertz equation, a model that provides a relationship between the indentation force and depth and is a function of the tip radius and the modulus of the substrate. The elastic modulus values for each layer of the cornea are: 7.5 ± 4.2 kPa (anterior basement membrane), 109.8 ± 13.2 kPa (Bowman’s layer), 33.1 ± 6.1 kPa (anterior stroma), and 50 ± 17.8 kPa (Descemet’s membrane). These results indicate that the biophysical properties, including elastic modulus, of each layer of the human cornea are unique and may play a role in the maintenance of homeostasis as well as in the response to therapeutic agents and disease states. The data will also inform the design and fabrication of improved corneal prosthetics.
1. Introduction
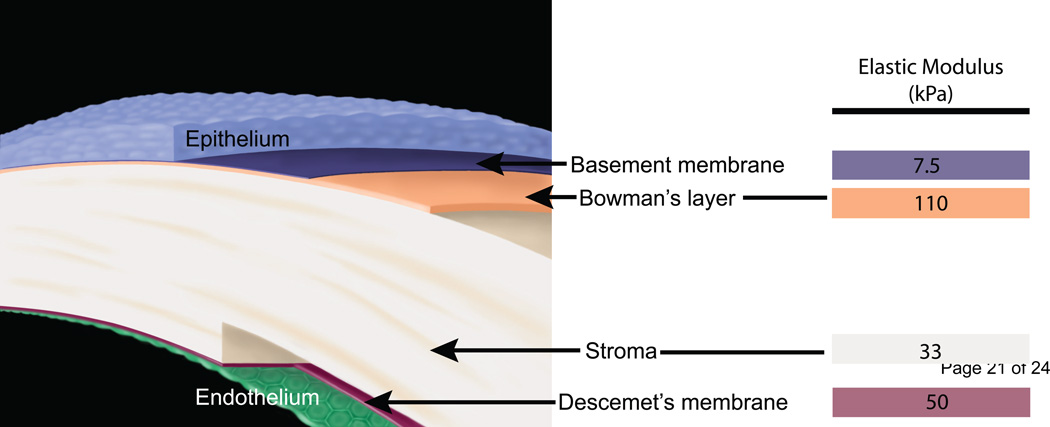
The cornea provides a protective barrier to maintain ocular integrity while simultaneously acting as the most powerful refractive surface in the eye responsible for transmitting and focusing light onto the retina. The human cornea is comprised of distinct layers including the epithelium, anterior basement membrane, Bowman’s layer, the stroma, Descemet’s membrane (posterior basement membrane) and the endothelium as seen in Fig. 1 (Klyce and Beuerman, 1988). The structure of each of these layers is unique. The native corneal stroma constitutes approximately 90% of the corneal thickness and thus is important in maintaining its mechanical shape and structure. The stroma is a rich topographically patterned environment comprising sheet-like transparent fibrillar parallel bundles of collagen, with a sparse population of keratocytes located between the lamellae. In contrast, the collagen fibril arrangement of Bowman’s layer is more random in organization compared to the largely parallel arrangement found within lamellae of the stoma. The corneal basement membranes are specializations of extracellular matrix through which the epithelial and endothelial cells attach to the underlying or overlying stroma, respectively. Basement membrane topography is complex, consisting of a network of fibers, pores and bumps with feature sizes in the submicron to nanoscale range (Abrams et al., 2000). The average pore size of Descemet’s membrane is smaller than that of the anterior basement membrane, creating a more compact structure (Abrams et al., 2000).While each layer has a distinct structure, the mechanical properties of the cornea are typically reported only for the composite structure.
Fig. 1.
A schematic depicting the layers of the human cornea and the corresponding elastic modulus values obtained from atomic force microscopy: the epithelium, the anterior basement membrane (7.5 kPa), Bowman’s layer (110 kPa), the stroma (33 kPa), Descemet’s membrane (50 kPa) and the endothelium. Illustration (without elastic modulus values) reprinted with permission from (Last et al., 2009).
Several different methods have been used to determine the bulk elastic modulus of the cornea (a value that integrates all layers of the cornea), and a wide range of values has been published (0.01 – 11.1 MPa) (Elsheikh et al., 2007; Hjortdal, 1996; Hoeltzel et al., 1992; Jayasuriya et al., 2003a; Jayasuriya et al., 2003b; Jue and Maurice, 1986; Liu and Roberts, 2005; Nash et al., 1982; Nyquist, 1968; Wollensak and Iomdina, 2009; Wollensak et al., 2003; Zeng et al., 2001). Two common testing methods that have been used are tensile testing, which involves pulling on a strip of the cornea,(Hoeltzel et al., 1992) and bulge testing (Elsheikh et al., 2007), which involves pressure being applied behind the cornea and measuring the deflection of the cornea as a function of pressure (Elsheikh et al., 2007). The latter method has the added advantage of relating the applied pressure to the intraocular pressure (IOP) and the elastic modulus can then be determined as a function of the IOP. Neither of these techniques is applicable for determining the specific elastic modulus of each discrete corneal layer. In addition, it is difficult to isolate each layer for testing and tensile testing require a mechanical grip to hold and pull the material, which would be difficult for the thin Bowman’s layer (~8–12 µm).
Atomic force microcopy (AFM) has proven to be a useful technique for the imaging and characterization of soft, biological materials and there are many reviews that describe the uses and advantages of AFM for biological materials, including applications in high resolution imaging, real time imaging in physiological conditions, indentation experiments and single molecule force measurements.(Alessandrini and Facci, 2005; Cohen and Bitler, 2008; Costa, 2003; Deniz et al., 2008; Ebner et al., 2008; Franz and Puech, 2008; Frederix et al., 2009; Gadegaard, 2006; Goksu et al., 2009; Haupt et al., 2006; Ikai, 2008; Kasas and Dietler, 2008; Morris et al., 1999; Muller, 2008; Muller and Dufrene, 2008; Noy, 2006; Parot et al., 2007; Radmacher, 2007; Ritort, 2006; Santos and Castanho, 2004; Seantier et al., 2008; Veerapandian and Yun, 2009; Withers and Aston, 2006; Wright and Armstrong, 2006; Zhu and Sun, 2006)
The AFM has several advantages in the study of biological materials over electron microscopy, including the ability to image in liquid with minimal sample preparation (no labeling, fixing or coating). The AFM is also able to exert and measure forces on the order of pico-Newtons, enabling the indentation of cells or tissues at small indentation depths and low forces. AFM has been successfully used for determining the mechanical properties of many tissues and cells.(Alessandrini and Facci, 2005; Bowen et al., 2000; Canetta and Adya, 2005; Costa, 2003; Docheva et al., 2008; Hsieh et al., 2008; Jandt, 2001; Kasas and Dietler, 2008; Li et al., 2008; Mathur et al., 2001; Rabinovich et al., 2005; Radmacher, 2007; Rico et al., 2005; Sirghi et al., 2008; Wagh et al., 2008) AFM nanoindentation allows for a determination of the local, elastic modulus of each of the corneal layers. Our laboratory recently determined the elastic modulus of anterior basement membrane and Descemet’s membrane of the human cornea to be 7.5 ± 4.2 and 50 ± 17.8 kPa, respectively (Last et al., 2009). The purpose of this study was to determine the elastic modulus of Bowman’s layer and the anterior stroma of the human cornea and compare these results to the elastic modulus values obtained previously for the anterior basement membrane and Descemet’s membrane.
2. Methods
2.1 Sample Preparation
Human corneas determined unsuitable for transplantation were obtained from the Missouri Lions Eye Bank (Columbia, MO). The ages of the cornea donors ranged from 19 to 73 years, with a median age of 61 years for Bowman’s layer and 62 years for the stroma. The corneas were stored in Optisol (Chiron Ophthalmics, Irvine, California) at 4° C. The epithelial and endothelial cells were removed to reveal the anterior basement membrane and Descemet’s membrane, respectively, using previously reported procedures (Abrams et al., 2000). The epithelial cells were removed by placing the corneas in 2.5 mM ethylenediamine tetraaceticacid (EDTA) in HEPES buffer (pH = 7.2) for 2 hours at 37° C (Abrams et al., 2000). The endothelium was removed by placing the corneas in the EDTA solution for 30 minutes at 37° C followed by sonication (Crest Ultrasonic Cleaner, WI, USA) in PBS at 2 amps for 3 minutes. Prior to laser ablation any remaining epithelial cells were removed with a 69 beaver blade. A VISX Star S4 IR Excimer Laser (Abbott Medical Optics Inc, Abbott Park, IL) was used to photoablate the superficial elements of the cornea to either partially enter into Bowman’s layer (6 mm diameter, 6 Hz, 8 pulses = 2 µm) or ablate through Bowman’s layer into the anterior stroma (6 mm diameter, 6 Hz, 84 pulses = 20 µm). Histologic examination of photoablated specimens not used in AFM analysis was performed to confirm that the layer of interest was intact and exposed for AFM analysis. The edges of the photoablated area were marked with a 69 Beaver blade using the surgical microscope of the Visx laser blade. Samples were prepared for AFM by dissection of a piece of tissue from within the photoablated area. The tissue was adhered with cyanoacrylate glue (Loctite Super Glue Gel, Henkel Corporation) in the center of a 5 mm diameter well, created with a nylon washer, on a stainless steel disk. The samples were stored in Optisol for a minimum of 30 minutes after preparation and AFM analysis was performed within 12 hours in 1x phosphate buffered saline (PBS).
2.2. Instrumentation
Force curves were acquired with a Nanoscope IIIa Multimode scanning probe microscope (Bruker, Santa Barbara, CA). The samples were transferred to the AFM without drying and placed in a commercially available liquid cell (Bruker, Santa Barbara, CA). Silicon nitride cantilevers with a borosilicate sphere as the tip (1 µm radius, Novascan Technologies, Inc. Ames, IA) were used. The nominal spring constant of the cantilevers was 0.06 N/m. Force curves were obtained on at least 10 different locations on the sample surface. Each force curve was taken at a rate of 2 µm/sec. Data was collected from the Bowman’s layer of 6 different human donor corneas and the anterior stroma of 5 different human donor corneas.
2.3 Data Analysis
The force curves were analyzed using the Hertz model for a sphere in contact with a flat surface as previously described (Domke and Radmacher, 1998; Last et al., 2009). The applicability of this method of data analysis to soft biological materials has been previously discussed.(Cappella and Dietler, 1999; Lin and Horkay, 2008; McKee et al., 2011; Radmacher, 2007) The optical sensitivity and the spring constant of each cantilever were determined for accurate measurement of the elastic modulus. Optical sensitivity was measured as the slope of the force curve, taken in PBS, when the tip was in contact with a rigid surface. The optical sensitivity was used to convert cantilever deflection in volts to deflection in nanometers (x). Spring constants (k) were measured using Sader’s method(Sader, 1995). The Hertz model provides a relationship between the loading force and the indentation, which for a spherical indenter is:
| (1) |
where F is the loading force in Newtons, ν is Poisson’s ratio (assumed to be 0.5), δ is the indentation depth (= (z-zo)-(d-do)), E is the elastic modulus in Pascals and R is the radius of the tip. The values obtained from the force curve are z, zo, d and do, where z is the piezo displacement, d is the cantilever deflection, and zo and do are the values at initial contact of the tip with the sample. Using this equation with F = k(d-do) gives an expression for E:
| (2) |
3. Results and Discussion
3.1. Bowman’s layer and the stroma
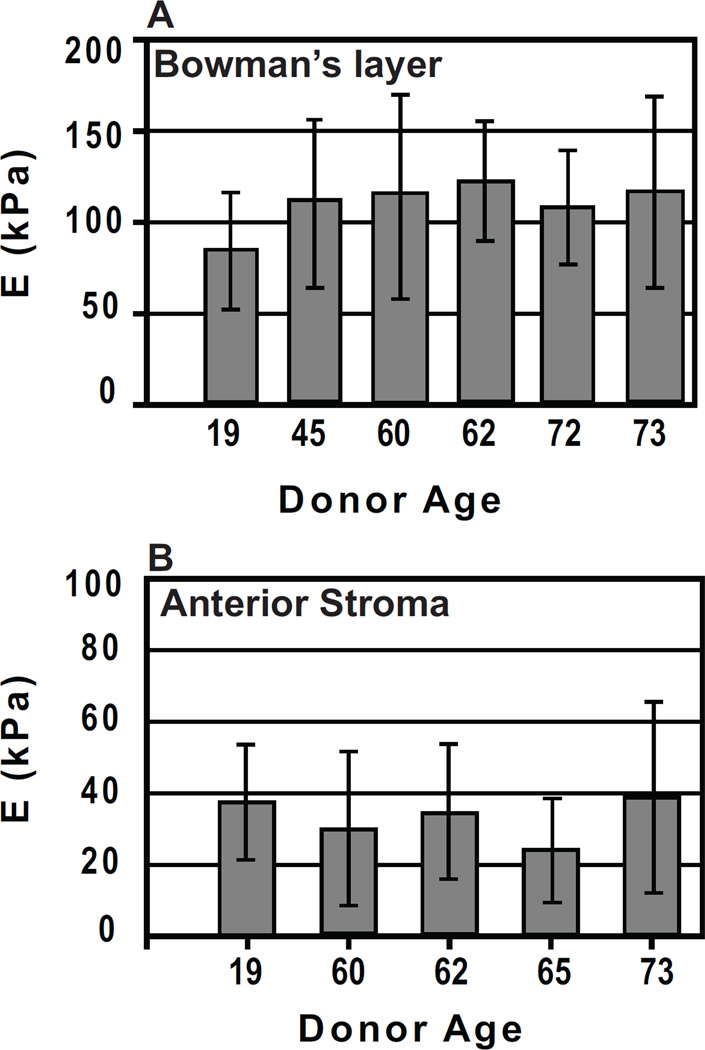
Force curves were obtained after photoablation to determine the compliance of Bowman’s layer or the stroma. Force curves acquired for Bowman’s layer were typical of an elastic material, generally consisting of a straight line approach when the tip is not in contact with the substrate and having no jump-to-contact as the tip approaches the surface, indicating minimal interactions of the tip with the surface (Fig. 2A). The approach and retract curves overlap, indicating an absence of viscoelastic effects at the indentation rate used (2 µm/sec). In approximately 20% of the force curves, a small adhesion (an average of less than 1nN) of the tip to the surface upon retraction, which increased with increasing indentation depth, was observed. In such cases, the indentation depth was decreased to minimize the adhesion. The mean elastic modulus values on the six samples ranged from 84 – 123 kPa, with an overall mean of 109.8 ± 13.2 kPa (Fig. 3A).
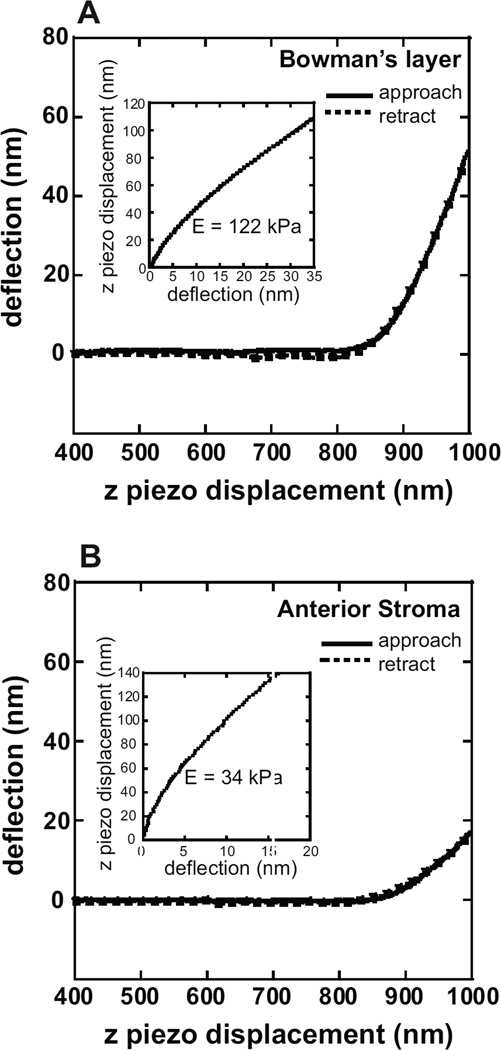
Fig. 2.
Typical force curves obtained from (A) Bowman’s layer and (B) the anterior stroma. The solid line represents the cantilever deflection as the cantilever approaches the surface. The dashed line represents the cantilever deflection upon retraction from the surface. The approach and retract curves overlap, indicating elastic behavior at the indentation rate used (2 μm/sec). Values for the initial contact point of the tip with the sample and the cantilever deflection and z piezo position are obtained from the force curve and used in the Hertz analysis to determine the elastic modulus. Insets: Curve fit of the experimental data (dotted lines) with the Hertz equation (solid line) to determine the elastic modulus.
Fig. 3.
(A) Elastic modulus results for Bowman’s layer obtained from 6 human donor corneas. A minimum of 10 measurements is included in the calculation of the mean elastic modulus and standard deviation for each donor. The average of the means is E = 109.8 ± 13.2 with a range of 84–123 kPa. (B) Elastic modulus results for the anterior stroma from 5 human donor corneas. A minimum of 10 measurements is included in the calculation of the mean elastic modulus and standard deviation for each donor. The average of the means is E = 33.1 ± 6.1 kPa, with a range of 24–39 kPa.
Force curves obtained for the anterior stroma also typically were consistent with those of a soft, elastic material (Fig. 2B). The mean elastic modulus on the five anterior stroma samples ranged from 24 – 39 kPa, with an overall mean of 33.1 ± 6.1 kPa (Fig. 3B). In the stroma samples, tip – sample adhesion was observed in 30% of the force curves, an increase from Bowman’s layer. In addition, a large hysteresis in the approach and retract force curves was often observed and these force curves were not used in the analysis. The topography of the corneal surface before and after photoablation has been characterized, revealing an increase in the surface roughness (Nogradi et al., 2000). In particular, it was found that photoablation to Bowman’s layer resulted in a surface that remained smooth. After photoablation to the anterior stroma, however, there was an increase in the surface roughness. It is therefore likely that this increase in roughness of the stromal surface is a contributing cause of the increased difficulty in obtaining force curves for analysis for the anterior stroma.
3.2. The anterior basement membrane and Descemet’s membrane
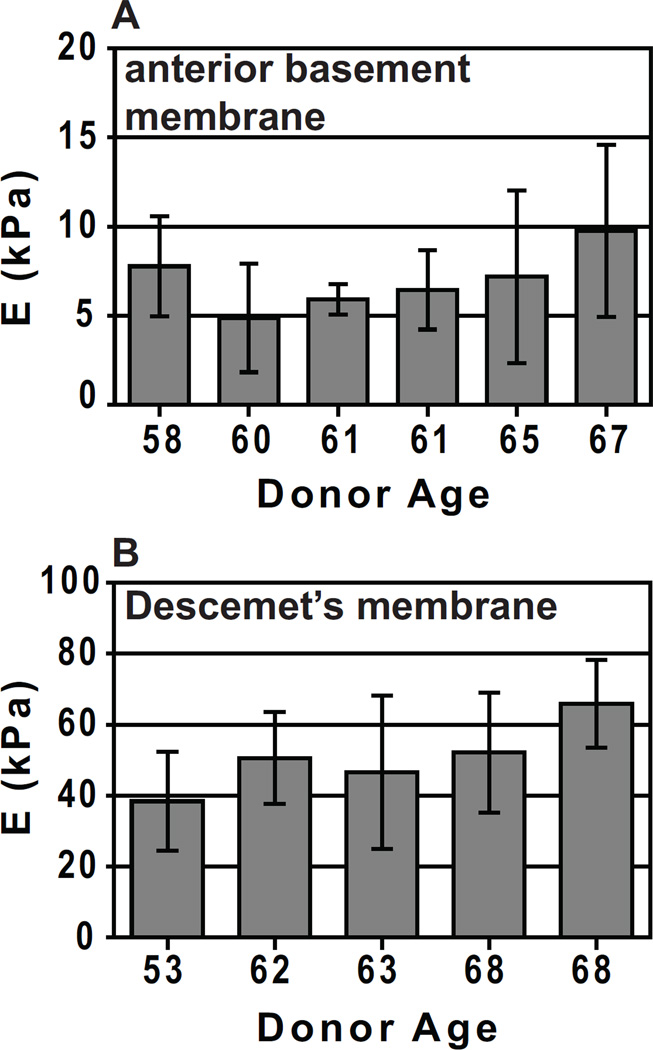
Previously, our laboratory has reported mean elastic modulus values for the human corneal basement membranes (Last et al., 2009). The anterior basement membrane and Descemet’s membrane are the surfaces directly in contact with the epithelial and endothelial cell layers, respectively. The value obtained for the modulus of the anterior basement membrane was 7.5 ± 4.2 kPa, while the modulus obtained for Descemet’s membrane was 47.6 ± 16.5 kPa (Fig. 4) (Last et al., 2009). The topography of Descemet’s membrane is similar to that of the anterior basement membrane but has a more compact organization, with smaller pore dimensions in Descemet’s membrane. This important structural difference is consistent with the observed differences in elastic modulus.
Fig. 4.
(A) Elastic modulus results for the anterior basement membrane from 6 human donor corneas. A minimum of 10 measurements is included in the calculation of the mean elastic modulus and standard deviation for each donor. The average of the means is E = 7.5 ± 4.2 kPa with a range of 2 kPa – 15 kPa. (B) Elastic modulus results for Descemet’s membrane of 5 human donor corneas. A minimum of 10 measurements is included in the calculation of the mean elastic modulus and standard deviation for each donor. The average of the means is E = 50 ± 17.8 kPa with a range of 20 kPa – 80 kPa. Reprinted with permission from (Last et al., 2009).
3.3. Discussion of values
This study utilized AFM nanoindentation to measure the local compliance of Bowman’s layer and the anterior stroma of the human cornea. Similar to our previous study on corneal membranes (Last et al., 2009), a spherical AFM tip (nominal radius of 1 µm) was selected for several reasons. A spherical tip was chosen because typical conical AFM tips (nominal radius of 10 nm) create a larger strain field than spherical tips during indentation which may impact the measured modulus of these soft biological materials and because the topographic features of the collagen fibers are of approximately the same size as the conical AFM tip radius with a fiber size of 30 nm (Edelhauser and Udels, 2003).
Similar to the previous study characterizing corneal basement membranes (Last et al., 2009), inter-individual variability in elastic modulus was observed at both corneal locations. This variation in the modulus among corneas is not surprising due to the inherent differences between human donors. The age, sex, and differences in stromal thickness of the corneas may impact the measured elastic modulus. It is known that many human tissues stiffen with age, including the human cornea and lens (Elsheikh et al., 2007; Fisher, 1987; Hollman et al., 2007). In addition, aging has been associated with increased microdots or dysgenic cellular remnants in the anterior stroma and folds in the posterior stroma, which could also alter local compliance (Hillenaar et al., 2011). It is also possible that an undisclosed underlying disease state of an individual donor impacted the elastic modulus as has been shown for normal versus osteoarthritic chondrocytes and normal and malignant breast tissue (Hsieh et al., 2008; Samani et al., 2007).
Interestingly, Bowman’s layer had an approximately 3-fold greater greater elastic modulus in comparison to the anterior stroma. A recent study investigating the three dimensional arrangement of collagen fibers within the cornea found “bow spring-like structures” attached to Bowman’s layer and deeper layers of the anterior stroma which would serve to reinforce and thus stiffen Bowman’s layer similar to load-bearing elements of girders and bridges (Winkler et al., 2011). Other differences between Bowman’s layer and the anterior stroma that could explain the disparity in elastic modulus include collagen fiber composition, collagen fiber diameter and proteoglycan composition. The more randomly oriented, smaller diameter collagen fibrils of Bowman’s layer results in a denser collagen arrangement and likely contributes to the increase in stiffness in comparison to the lamellar arrangement of larger collagen fibrils within the anterior stroma. These results mirror the previous study from our laboratory which showed that more densely packed Descemet’s membrane had a greater elastic modulus than the anterior basement membrane (Last et al., 2009).
The elastic modulus for the anterior stroma found in the present study was approximately 20 fold greater than what has been recently reported (Winkler et al., 2011). There are several reasons that could account for these differences. First, the depth of measurement of the stroma was more anterior in the present study (less than 20 µm) in comparison to the previous study (140 µm). Second-harmonic imaging has revealed a higher degree of lamellar interconnectivity in the anterior cornea(Morishige N, 2007). In addition, a study by Winkler and colleagues demonstrated that an 8 fold greater elastic modulus in the anterior stroma in comparison to the posterior stroma (Winkler et al., 2011). Thus, it is likely that the increased fiber interconnectivity present within the anterior stroma just underlying Bowman’s layer is responsible for the greater elastic modulus in the present study. Second, atomic force microscopy and indentation testing were used in the present and previous studies, respectively, to determine the elastic modulus of the anterior stroma. The probe tip used in indentation testing was much larger in comparison to the tip used in atomic force microscopy and this could dramatically alter the measurement of local compliance (McKee et al., 2011). Finally, corneal preservation techniques differed between the two studies. In the present study, the corneal buttons unsuitable for transplantation were stored in Optisol then incubated in PBS for a minimum of 30 minutes prior to measurement. In contrast, corneas tested in the previous study were obtained as whole eyes and first infused with PBS under pressure then treated with dextran to decrease post-mortem corneal edema following epithelial removal (Winkler et al., 2011). It is possible that the differences in hydration states between the corneal samples in the present and previous study resulted in different elastic modulus measurements for the anterior stroma.
Another recent study measuring the elastic modulus of the anterior stroma as measured by AFM reported values ranging from 1.14 – 2.63 MPa, several orders of magnitude greater than that reported by Winkler, et al or described here.(Lombardo et al., 2012) There are many experimental differences that may contribute to this large discrepancy including tip size, scan rates and indentation depths. Lombardo et al. used a conical tip for indentation with a radius of curvature of 10 nm. This tip size is smaller than the average diameter of an individual collagen fiber (30 nm) and it is possible that the larger elastic modulus value reflects the modulus of the fiber. In addition, slower scan rates (2 μm/sec vs. 3 – 95 μm/sec), and lower loads (1 nN vs. 0.25 – 2.5 μN) were used in the present study, eliminating hysteresis in the force curves. It should also be noted that in the present study we are photoablating the sample 20 μm through the anterior basement membrane and Bowman’s layer to expose the anterior stroma. Lombardo et al. are indenting up to 2.7 μm from the top of the anterior basement membrane. Since the central Bowman’s layer has been reported to have a thickness of 17.7 ± 1.7 μm, it is likely that this measurement is from Bowman’s layer and not the anterior stroma.(Tao A, 2011)
4. Conclusions
We have determined the mechanical properties for several corneal layers and found that the mechanical properties vary between the layers. Knowledge of the mechanical properties of each layer is a crucial step in the design of improved prosthetics.
Highlights.
We have completed the compliance profile of the stromal elements of the human cornea by obtaining elastic modulus values for Bowman’s layer and the anterior stroma
Atomic force microscopy (AFM) was used to determine the elastic modulus
The elastic modulus values for each layer of the cornea are: 7.5 ± 4.2 kPa (anterior basement membrane), 109.8 ± 13.2 kPa (Bowman’s layer), 33.1 ± 6.1 kPa (anterior stroma), and 50 ± 17.8 kPa (Descemet’s membrane)
Acknowledgments
The authors thank Prof. Nicholas Abbott for use of the AFM. This work was funded by the National Institutes of Health National Eye Institute 1R01EY019745 (PR), 5R01EY016134 (CJM), 1KO8EY021142 (SMT), 1R01CA133567-01 (CJM) and an unrestricted gift from Research to Prevent Blindness (UC, Davis).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Abrams GA, Schaus SS, Goodman SL, Nealey PF, Murphy CJ. Nanoscale topography of the corneal epithelial basement membrane and Descemet's membrane of the human. Cornea. 2000;19:57–64. doi: 10.1097/00003226-200001000-00012. [DOI] [PubMed] [Google Scholar]
- Alessandrini A, Facci P. AFM: a versatile tool in biophysics. Measurement Science & Technology. 2005;16:R65–R92. [Google Scholar]
- Bowen WR, Lovitt RW, Wright CJ. Application of atomic force microscopy to the study of micromechanical properties of biological materials. Biotechnology Letters. 2000;22:893–903. [Google Scholar]
- Canetta E, Adya AK. Atomic force microscopy : applications to nanobiotechnology. Journal of the Indian Chemical Society. 2005;82:1147–1172. [Google Scholar]
- Cappella B, Dietler G. Force-distance curves by atomic force microscopy. Surf. Sci. Rep. 1999;34:1. [Google Scholar]
- Cohen SR, Bitler A. Use of AFM in bio-related systems. Current Opinion in Colloid & Interface Science. 2008;13:316–325. [Google Scholar]
- Costa KD. Single-cell elastography: Probing for disease with the atomic force microscope. Disease Markers. 2003;19:139–154. doi: 10.1155/2004/482680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deniz AA, Mukhopadhyay S, Lemke EA. Single-molecule biophysics: at the interface of biology, physics and chemistry. Journal of the Royal Society Interface. 2008;5:15–45. doi: 10.1098/rsif.2007.1021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Docheva D, Padula D, Popov C, Mutschler W, Clausen-Schaumann H, Schieker M. Researching into the cellular shape, volume and elasticity of mesenchymal stem cells, osteoblasts and osteosarcoma cells by atomic force microscopy. J Cell Mol Med. 2008;12:537–552. doi: 10.1111/j.1582-4934.2007.00138.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Domke J, Radmacher M. Measuring the elastic properties of thin polymer films with the atomic force microscope. Langmuir. 1998;14:3320–3325. [Google Scholar]
- Ebner A, Wildling L, Zhu R, Rankl C, Haselgrubler T, Hinterdorfer P, Gruber HJ. Functionalization of probe tips and supports for single-molecule recognition force Microscopy. Top. Curr. Chem. 2008;285:29–76. doi: 10.1007/128_2007_24. [DOI] [PubMed] [Google Scholar]
- Edelhauser HF, Udels JL. The cornea and the sclera. In: Kaufman PL, Alm A, editors. Adler's Physiology of the Eye. St. Louis: Mosby; 2003. [Google Scholar]
- Elsheikh A, Wang DF, Pye D. Determination of the modulus of elasticity of the human cornea. Journal of Refractive Surgery. 2007;23:808–818. doi: 10.3928/1081-597X-20071001-11. [DOI] [PubMed] [Google Scholar]
- Fisher RF. The Influence of Age on Some Ocular Basement-Membranes. Eye-Transactions of the Ophthalmological Societies of the United Kingdom. 1987;1:184–189. doi: 10.1038/eye.1987.35. [DOI] [PubMed] [Google Scholar]
- Franz CM, Puech PH. Atomic Force Microscopy: A Versatile Tool for Studying Cell Morphology, Adhesion and Mechanics. Cellular and Molecular Bioengineering. 2008;1:289–300. [Google Scholar]
- Frederix P, Bosshart PD, Engel A. Atomic Force Microscopy of Biological Membranes. Biophysical Journal. 2009;96:329–338. doi: 10.1016/j.bpj.2008.09.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gadegaard N. Atomic force microscopy in biology: technology and techniques. Biotechnic & Histochemistry. 2006;81:87–97. doi: 10.1080/10520290600783143. [DOI] [PubMed] [Google Scholar]
- Goksu EI, Vanegas JM, Blanchette CD, Lin WC, Longo ML. AFM for structure and dynamics of biomembranes. Biochimica Et Biophysica Acta- Biomembranes. 2009;1788:254–266. doi: 10.1016/j.bbamem.2008.08.021. [DOI] [PubMed] [Google Scholar]
- Haupt BJ, Pelling AE, Horton MA. Integrated confocal and scanning probe microscopy for biomedical research. Thescientificworldjournal. 2006;6:1609–1618. doi: 10.1100/tsw.2006.269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hillenaar T, van Cleynenbreugel H, Remeijer L. How Normal Is the Transparent Cornea? Effects of Aging on Corneal Morphology. Ophthalmology. 2011 doi: 10.1016/j.ophtha.2011.07.041. [DOI] [PubMed] [Google Scholar]
- Hjortdal JO. Regional elastic performance of the human cornea. J Biomech. 1996;29:931–942. doi: 10.1016/0021-9290(95)00152-2. [DOI] [PubMed] [Google Scholar]
- Hoeltzel DA, Altman P, Buzard K, Choe KI. Strip Extensiometry for Comparison of the Mechanical Response of Bovine, Rabbit, and Human Corneas. Journal of Biomechanical Engineering-Transactions of the Asme. 1992;114:202–215. doi: 10.1115/1.2891373. [DOI] [PubMed] [Google Scholar]
- Hollman KW, O'Donnell M, Erpelding TN. Mapping elasticity in human lenses using bubble-based acoustic radiation force. Experimental Eye Research. 2007;85:890–893. doi: 10.1016/j.exer.2007.09.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hsieh CH, Lin YH, Lin S, Tsai-Wu JJ, Herbert Wu CH, Jiang CC. Surface ultrastructure and mechanical property of human chondrocyte revealed by atomic force microscopy. Osteoarthritis and Cartilage. 2008;16:480–488. doi: 10.1016/j.joca.2007.08.004. [DOI] [PubMed] [Google Scholar]
- Ikai A. Nanobiomechanics of proteins and biomembrane. Philos Trans R Soc Lond B Biol Sci. 2008;363:2163–2171. doi: 10.1098/rstb.2008.2269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jandt KD. Atomic force microscopy of biomaterials surfaces and interfaces. Surface Science. 2001;491:303–332. [Google Scholar]
- Jayasuriya AC, Ghosh S, Scheinbeim JI, Lubkin V, Bennett G, Kramer P. A study of piezoelectric and mechanical anisotropies of the human cornea. Biosens Bioelectron. 2003a;18:381–387. doi: 10.1016/s0956-5663(02)00144-6. [DOI] [PubMed] [Google Scholar]
- Jayasuriya AC, Scheinbeim JI, Lubkin V, Bennett G, Kramer P. Piezoelectric and mechanical properties in bovine cornea. J Biomed Mater Res A. 2003b;66:260–265. doi: 10.1002/jbm.a.10536. [DOI] [PubMed] [Google Scholar]
- Jue B, Maurice DM. The Mechanical-Properties of the Rabbit and Human Cornea. Journal of Biomechanics. 1986;19:847–853. doi: 10.1016/0021-9290(86)90135-1. [DOI] [PubMed] [Google Scholar]
- Kasas S, Dietler G. Probing nanomechanical properties from biomolecules to living cells. Pflugers Archiv-European Journal of Physiology. 2008;456:13–27. doi: 10.1007/s00424-008-0448-y. [DOI] [PubMed] [Google Scholar]
- Klyce SD, Beuerman RW. Structure and Function of the Cornea. In: Kaufman HE, B B, McDonald MB, editors. The Cornea. New York: Churchill Livingstone; 1988. [Google Scholar]
- Last JA, Liliensiek SJ, Nealey PF, Murphy CJ. Determining the mechanical properties of human corneal basement membranes with atomic force microscopy. Journal of Structural Biology. 2009;167:19–24. doi: 10.1016/j.jsb.2009.03.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li QS, Lee GY, Ong CN, Lim CT. AFM indentation study of breast cancer cells. Biochem Biophys Res Commun. 2008;374:609–613. doi: 10.1016/j.bbrc.2008.07.078. [DOI] [PubMed] [Google Scholar]
- Lin DC, Horkay F. Nanomechanics of polymer gels and biological tissues: A critical review of analytical approaches in the Hertzian regime and beyond. Soft Matter. 2008;4:669–682. doi: 10.1039/b714637j. [DOI] [PubMed] [Google Scholar]
- Liu J, Roberts CJ. Influence of corneal biomechanical properties on intraocular pressure measurement - Quantitative analysis. Journal of Cataract and Refractive Surgery. 2005;31:146–155. doi: 10.1016/j.jcrs.2004.09.031. [DOI] [PubMed] [Google Scholar]
- Lombardo M, Lombardo G, Carbone G, De Santo MP, Barberi R, Serrao S. Biomechanics of the anterior human corneal tissue investigated with Atomic Force Microscopy. Invest Ophthalmol Vis Sci. 2012 doi: 10.1167/iovs.11-8720. [DOI] [PubMed] [Google Scholar]
- Mathur AB, Collinsworth AM, Reichert WM, Kraus WE, Truskey GA. Endothelial, cardiac muscle and skeletal muscle exhibit different viscous and elastic properties as determined by atomic force microscopy. J Biomech. 2001;34:1545–1553. doi: 10.1016/s0021-9290(01)00149-x. [DOI] [PubMed] [Google Scholar]
- McKee CT, Last JA, Russell P, Murphy CJ. Indentation versus tensile measurements of Young's modulus for soft biological tissues. Tissue Eng Part B Rev. 2011;17:155–164. doi: 10.1089/ten.teb.2010.0520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morishige N WA, Kenney MC, Brown DJ, Kawamoto K, Chikama T, Nishida T, Jester JV. Second-harmonic imaging microscopy of normal human and keratoconus cornea. Invest Ophthalmol Vis Sci. 2007;48:1087–1094. doi: 10.1167/iovs.06-1177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morris V, Kirby A, Gunning A. Atomic Force Microscopy for Biologists. London: Imperial College Press; 1999. [Google Scholar]
- Muller DJ. AFM: a nanotool in membrane biology. Biochemistry. 2008;47:7986–7998. doi: 10.1021/bi800753x. [DOI] [PubMed] [Google Scholar]
- Muller DJ, Dufrene YF. Atomic force microscopy as a multifunctional molecular toolbox in nanobiotechnology. Nature Nanotechnology. 2008;3:261–269. doi: 10.1038/nnano.2008.100. [DOI] [PubMed] [Google Scholar]
- Nash IS, Greene PR, Foster CS. Comparison of Mechanical-Properties of Keratoconus and Normal Corneas. Experimental Eye Research. 1982;35:413–424. doi: 10.1016/0014-4835(82)90040-9. [DOI] [PubMed] [Google Scholar]
- Nogradi A, Hopp B, Revesz K, Szabo G, Bor Z, Kolozsvari L. Atomic force microscopic study of the human cornea following excimer laser keratectomy. Exp Eye Res. 2000;70:363–368. doi: 10.1006/exer.1999.0795. [DOI] [PubMed] [Google Scholar]
- Noy A. Chemical force microscopy of chemical and biological interactions. Surface and Interface Analysis. 2006;38:1429–1441. [Google Scholar]
- Nyquist GW. Rheology of Cornea - Experimental Techniques and Results. Experimental Eye Research. 1968;7:183. doi: 10.1016/s0014-4835(68)80064-8. [DOI] [PubMed] [Google Scholar]
- Parot P, Dufrene YF, Hinterdorfer P, Le Grimellee C, Navajas D, Pellequer JL, Scheuring S. Past, present and future of atomic force microscopy in life sciences and medicine. Journal of Molecular Recognition. 2007;20:418–431. doi: 10.1002/jmr.857. [DOI] [PubMed] [Google Scholar]
- Rabinovich Y, Esayanur M, Daosukho S, Byer K, El-Shall H, Khan S. Atomic force microscopy measurement of the elastic properties of the kidney epithelial cells. J Colloid Interface Sci. 2005;285:125–135. doi: 10.1016/j.jcis.2004.11.041. [DOI] [PubMed] [Google Scholar]
- Radmacher M. Studying the mechanics of cellular processes by atomic force microscopy. Cell Mechanics. 2007:347–372. doi: 10.1016/S0091-679X(07)83015-9. [DOI] [PubMed] [Google Scholar]
- Rico F, Roca-Cusachs P, Gavara N, Farre R, Rotger M, Navajas D. Probing mechanical properties of living cells by atomic force microscopy with blunted pyramidal cantilever tips. Phys Rev E Stat Nonlin Soft Matter Phys. 2005;72:021914. doi: 10.1103/PhysRevE.72.021914. [DOI] [PubMed] [Google Scholar]
- Ritort F. Single-molecule experiments in biological physics: methods and applications. Journal of Physics-Condensed Matter. 2006;18:R531–R583. doi: 10.1088/0953-8984/18/32/R01. [DOI] [PubMed] [Google Scholar]
- Sader JE. Parallel Beam Approximation for V-Shaped Atomic-Force Microscope Cantilevers. Review of Scientific Instruments. 1995;66:4583–4587. [Google Scholar]
- Samani A, Zubovits J, Plewes D. Elastic moduli of normal and pathological human breast tissues: an inversion-technique-based investigation of 169 samples. Physics in Medicine and Biologym. 2007;6:1565. doi: 10.1088/0031-9155/52/6/002. [DOI] [PubMed] [Google Scholar]
- Santos NC, Castanho M. An overview of the biophysical applications of atomic force microscopy. Biophysical Chemistry. 2004;107:133–149. doi: 10.1016/j.bpc.2003.09.001. [DOI] [PubMed] [Google Scholar]
- Seantier B, Giocondi MC, Le Grimellec C, Milhiet PE. Probing supported model and native membranes using AFM. Current Opinion in Colloid & Interface Science. 2008;13:326–337. [Google Scholar]
- Sirghi L, Ponti J, Broggi F, Rossi F. Probing elasticity and adhesion of live cells by atomic force microscopy indentation. Eur Biophys J. 2008;37:935–945. doi: 10.1007/s00249-008-0311-2. [DOI] [PubMed] [Google Scholar]
- Tao A WJ, Chen Q, Shen M, Lu F, Dubovy SR, Shousha MA. Topographic thickness of Bowman's layer determined by ultra-high resolution spectral domain-optical coherence tomography. Invest Ophthalmol Vis Sci. 2011;52:3901–3907. doi: 10.1167/iovs.09-4748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Veerapandian M, Yun K. Study of Atomic Force Microscopy in Pharmaceutical and Biopharmaceutical Interactions - A Mini Review. Current Pharmaceutical Analysis. 2009;5:256–268. [Google Scholar]
- Wagh AA, Roan E, Chapman KE, Desai LP, Rendon DA, Eckstein EC, Waters CM. Localized elasticity measured in epithelial cells migrating at a wound edge using atomic force microscopy. Am J Physiol Lung Cell Mol Physiol. 2008;295:L54–L60. doi: 10.1152/ajplung.00475.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winkler M, Chai D, Kriling S, Nien CJ, Brown DJ, Jester B, Juhasz T, Jester JV. Non-Linear Optical Macroscopic Assessment of 3-D Corneal Collagen Organization and Axial Biomechanics. Invest Ophthalmol Vis Sci. 2011;52:8818–8827. doi: 10.1167/iovs.11-8070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Withers JR, Aston DE. Nanomechanical measurements with AFM in the elastic limit. Advances in Colloid and Interface Science. 2006;120:57–67. doi: 10.1016/j.cis.2006.03.002. [DOI] [PubMed] [Google Scholar]
- Wollensak G, Iomdina E. Long-term biomechanical properties of rabbit cornea after photodynamic collagen crosslinking. Acta Ophthalmol. 2009;87:48–51. doi: 10.1111/j.1755-3768.2008.01190.x. [DOI] [PubMed] [Google Scholar]
- Wollensak G, Spoerl E, Seiler T. Stress-strain measurements of human and porcine corneas after riboflavin-ultraviolet-A-induced cross-linking. J Cataract Refract Surg. 2003;29:1780–1785. doi: 10.1016/s0886-3350(03)00407-3. [DOI] [PubMed] [Google Scholar]
- Wright CJ, Armstrong I. The application of atomic force microscopy force measurements to the characterisation of microbial surfaces. Surface and Interface Analysis. 2006;38:1419–1428. [Google Scholar]
- Zeng YJ, Yang J, Huang K, Lee ZH, Lee XY. A comparison of biomechanical properties between human and porcine cornea. Journal of Biomechanics. 2001;34:533–537. doi: 10.1016/s0021-9290(00)00219-0. [DOI] [PubMed] [Google Scholar]
- Zhu J, Sun RG. Applications of atomic force microscopy to the structures and functions of single protein molecule. Chinese Journal of Analytical Chemistry. 2006;34:735–740. [Google Scholar]