Analysing bivariate survival data with interval sampling and application to cancer epidemiology

Abstract

In biomedical studies, ordered bivariate survival data are frequently encountered when bivariate failure events are used as outcomes to identify the progression of a disease. In cancer studies, interest could be focused on bivariate failure times, for example, time from birth to cancer onset and time from cancer onset to death. This paper considers a sampling scheme, termed interval sampling, in which the first failure event is identified within a calendar time interval, the time of the initiating event can be retrospectively confirmed and the occurrence of the second failure event is observed subject to right censoring. In a cancer data application, the initiating, first and second events could correspond to birth, cancer onset and death. The fact that the data are collected conditional on the first failure event occurring within a time interval induces bias. Interval sampling is widely used for collection of disease registry data by governments and medical institutions, though the interval sampling bias is frequently overlooked by researchers. This paper develops statistical methods for analysing such data. Semiparametric methods are proposed under semi-stationarity and stationarity. Numerical studies demonstrate that the proposed estimation approaches perform well with moderate sample sizes. We apply the proposed methods to ovarian cancer registry data.

1. Introduction

Ordered bivariate survival data arise frequently in biomedical studies when bivariate failure events are considered to be the major outcomes to identify the progression of a disease. In cancer studies, for example, it is of interest to understand the process from birth to cancer onset, and then to death. Disease registry or surveillance systems commonly collect data with incidence of disease occurring within a calendar time interval. This is referred to as interval sampling, and we consider the induced sampling bias problems in this paper.

Consider a case population where two failure events occur in chronological order following the occurrence of the initiating event, and a case refers to the presence of the first failure event. Denote the calendar time of the initiating event by T, the time from the initiating event to the first failure event by Y and the time from the first event to the second event by Z. The variables Y and Z are expected to be correlated because they come from the same subject. Bivariate failure times (Y, Z) are the outcome variables of interest in this paper. Wang & Wells (1998), Lin et al. (1999) and Schaubel & Cai (2004) proposed estimation methods for bivariate or multivariate survival data subject to right censoring. This paper focuses on developing estimation approaches for analysing survival data collected under the interval sampling scheme.

In this paper, the case population under interval sampling is made up of subjects whose first failure event occurs within a calendar time interval [0, t₀], which is described by the constraint −T ⩽ Y ⩽ t₀ − T. Thus, Y is observed subject to double truncation and individuals with the first failure event occurring before time 0 or after time t₀ are excluded. The observation of Z is subject to right censoring because of loss to follow-up or end-of-study, and the induced sampling bias due to its correlation with the first failure time Y. Then, if the second failure event occurs before calendar time of censoring C ⩽ t₀, it is uncensored and Z is observed subject to the further constraint Y + Z ⩽ C − T, and otherwise it is censored with censoring time C − (T + Y). Figure 1 shows the schema for bivariate survival data with interval sampling with constant C = t₀.

Fig. 1.

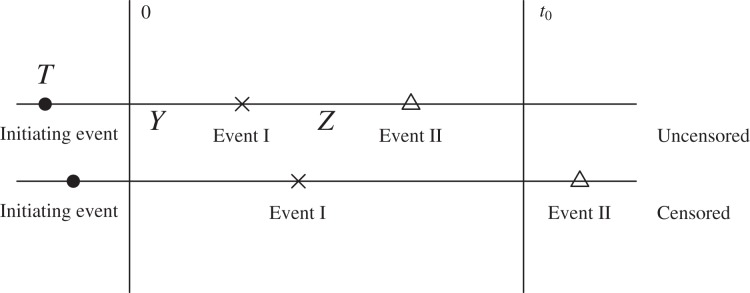
The interval sampling cohort with event I occurring within time interval [0, t₀], T is the calendar time of the initiating event (T ⩽ t₀) and (Y, Z) are the bivariate failure times of interest.

The research is motivated by statistical problems arising in analysis of cancer registry data. In this application, T is the calendar time of birth of an ovarian cancer patient, and Y and Z are, respectively, age of cancer onset and residual lifetime after cancer onset. Using age as the scale, the cancer event occurs at age Y and death occurs at age Y + Z. Due to interval sampling, Y is observed subject to double truncation and Z is subject to possibly dependent right censoring. With long survival times, sampling bias is nonnegligible, especially in the natural history of cancers. It is also important to develop methods to study the joint survival distribution for bivariate survival data. For example, the survival function of one failure time conditional on the other, such as the conditional probability of surviving more than five years given disease onset at age 50 years or older, is often of interest in practice. A joint survival function estimator can be used to produce an estimator for such a conditional survival function, and it enables one to compare the failure time distributions between two or more groups.

The inference procedures are developed for the case population experiencing the first failure event within the calendar time interval [0, t₀]. Assume that the initiating events occur over calendar time with rate function λ (t) for t ⩽ t₀, which is the average number of events in unit time at t or an unconditional probability function defined for a point process:

$$\lambda (t)=\underset{\mathrm{\Delta }\to 0^{+}}{\text{lim}}\hspace{0.17em}\frac{\text{pr}\{N(t+\mathrm{\Delta })-N(t)>0\}}{\mathrm{\Delta }},$$

where N(t) is the total number of events prior to time t. For instance, λ (t) is the unconditional birth rate over calendar time for the study population. For the case population, let f_Y,Z (y, z), f_Y (y) and f_Z (z) denote the population joint density function of (Y, Z) and the marginal densities of Y and Z, respectively. Let F_Y (y) and F_Z(z) denote the corresponding population distribution functions of Y and Z, where y₋ = inf{y : F_Y (y) > 0}, y₊ = sup{y : F_Y (y) < 1}, z₋ = inf{z : F_Z (z) > 0}, z₊ = sup{z : F_Z (z) < 1} and t₋ = inf{t : λ (t) > 0}. To reduce mathematical complexity in our discussion, assume that the failure time Y has finite support, that is, y₊ < ∞. Here we use this as a technical condition under which the density function of T and the joint density functions of (T, Y), (T, Y, Z) can be defined. The constraint y₊ < ∞ is not required for the inferential results of (Y, Z), but does make the likelihood discussion much easier. In this paper, we focus on the case population, so all the subjects under study experience the disease within the calendar time interval, which explains why the constraint y₊ < ∞ is reasonable. Let g(t) denote the population density function of T in the interval [−y₊, t₀ − y₋], for instance, the population density of birth times. It is derived as a normalized rate function from λ (t),

$$g(t)=\lambda (t)I(-y_{+}⩽t⩽t_0-y_{-})/{\int }_{-y_{+}}^{t_0-y_{-}}\lambda (u)\hspace{0.17em}\text{d}u,$$ (1)

and the corresponding population distribution function is denoted by G(t). Assume (T₁, Y₁, Z₁), …, (T_n, Y_n, Z_n) are independent and identically distributed. Consider the following assumptions.

Assumption 1. The disease process is independent of when the initiating event occurs, that is, (Y, Z) is independent of T.

Assumption 2. The initiating event occurs at a constant rate over calendar time, that is, λ (t) is constant for −y₊ ⩽ t ⩽ t₀ − y₋, so that G(·) is uniform(−y₊, t₀ − y₋).

The two assumptions are fundamental for studying the probability structures of the primary outcomes in this paper. We say that the model is semi-stationary if only Assumption 1 is satisfied, stationary if both Assumptions 1 and 2 are satisfied and nonstationary if neither Assumption 1 nor 2 is assumed. The discussion here is focused on the semi-stationary and stationary conditions. However, Assumptions 1 and/or 2 could be violated when, for instance, an improved screening strategy was developed and it might lead to earlier disease detection. In this article, we propose a statistical framework to properly analyse the bivariate survival time with interval sampling under semi-stationarity and stationarity, and study inference on the joint distribution and dependence structure of bivariate survival data.

2. Semiparametric Estimation under Semi-stationarity

2.1. Estimation of θ

In this section, we consider a general situation when only Assumption 1 holds, and focus on a semi-stationary model to estimate the joint survival function on the basis of observed biased data. For simplicity, we consider constant censoring, where the observation of death ends at calendar time t₀. This can be replaced by random censoring. Specifically, we consider a joint model for T and (Y, Z), and parameterize the distribution function of T by G(t; θ), where θ ∈ Θ and Θ is an open set in R^k. For example, in cancer studies, G describes the birth rate for cancer patients. Particular interest is focused on estimation of the parameter θ in G(t; θ) and the joint survival function of (Y, Z).

The estimation of θ is complicated by the bias from interval sampling. We explore the sampling bias on the distribution of T. For the interval sampling cohort, the calendar time of the initiating event, T, is observable subject to the constraint −Y ⩽ T ⩽ t₀ − Y. The joint density of observed (t, y) can be written as

$$\begin{array}{ll}{p}_{T,Y}(t,y)\hfill & =\frac{g(t)f_Y(y)I(-y⩽t⩽t_0-y)}{\text{pr}(-T⩽Y⩽t_0-T)}\hfill \\ \hfill & =\frac{f_Y(y)I(-y⩽t⩽t_0-y)}{S_Y(t_0-t)-S_Y(-t)}\times \frac{\{S_Y(t_0-t)-S_Y(-t)\}g(t)}{\int \{S_Y(t_0-s)-S_Y(-s)\}g(s)\text{d}s}\hfill \\ \hfill & =p_{Y|T}(y|t)\times p_T(t),\hfill \end{array}$$

where g(t) is the population density function of T. Thus, the sampling density of T, p_T (t), is proportional to its population density g(t),

$$p_T(t)=\frac{\{S_Y(t_0-t)-S_Y(-t)\}g(t)}{\int \{S_Y(t_0-s)-S_Y(-s)\}g(s)\text{d}s},$$

and is generally biased under either stationarity or semi-stationarity, which implies systematic bias when using the ordinary empirical distribution to estimate the so-called birth rate of diseased patients for cancer registry data.

The conditional likelihood approach is used to estimate parameter θ. When Assumption 1 is assumed, the joint density of uncensored (t, y, z) can be derived as the density of (T, Y, Z) conditional on −T ⩽ Y ⩽ t₀ − T and Y + Z ⩽ t₀ − T :

$$\begin{array}{ll}{p}_{T,Y,Z}(t,y,z)\hfill & =\frac{g(t)f_{Y,Z}(y,z)I(-y⩽t⩽t_0-y-z)}{\text{pr}(-Y⩽T⩽t_0-Y-Z)}\hfill \\ \hfill & =\frac{g(t)I(-y⩽t⩽t_0-y-z)}{G(t_0-y-z)-G(-y)}\times \frac{\{G(t_0-y-z)-G(-y)\}{f}_{Y,Z}(y,z)}{\int \{G(t_0-u-\upsilon )-G(-u)\}{f}_{Y,Z}(u,\upsilon )\text{d}u\hspace{0.17em}\text{d}\upsilon }\hfill \\ \hfill & =p_{T|Y,Z}(t|y,z)\times p_{Y,Z}(y,z).\hfill \end{array}$$ (2)

The first bracketed term above, denoted by p_{T | Y,Z}(t | y, z), specifies the conditional density of observed t given observed uncensored (y, z); the second bracketed term, denoted by p_Y,Z(y, z) is the joint density of uncensored (y, z). Thus, the conditional likelihood function of observed t given observed (y, z) is

$$L_{\text{c}}(\theta )=\prod _{i=1}^n{p}_{T|Y,Z}(t_i|y_i,z_i,\theta )=\prod _{i=1}^n\frac{g(t_i;\theta )}{G(t_0-y_i-z_i;\theta )-G(-y_i;\theta )}.$$

The target parameter θ is the only parameter involved in the conditional likelihood, since the nuisance parameter f_Y,Z (·, ·) is eliminated by conditioning. The conditional maximum likelihood estimator of θ, denoted by θ̂, can be derived by maximizing L_c(θ) for θ ∈ Θ. Large sample properties of θ̂ are obtained using techniques similar to those of Andersen (1970). Under regularity conditions and as n → ∞, θ̂ converges in probability to θ, and n^1/2(θ̂ − θ) converges weakly to a mean zero multivariate normal distribution with variance-covariance matrix $I_{\text{c}}^{-1}$, where I_c = E[{∂ log p_T|Y,Z (T_i | Y_i, Z_i)/∂θ}{∂ log p_{T | Y,Z} (T_i | Y_i, Z_i)/∂θ}^T] is the Fisher information matrix for the conditional likelihood function L_c(θ).

2.2. Estimation of joint survival function S_Y,Z(y, z)

In many situations, the maximum likelihood approach produces efficient estimators. In our case, the full likelihood function L can be expressed as the product of the conditional likelihood and the marginal likelihood: L{θ, f_Y,Z(·, ·)} = L_c(θ) × L_Y,Z {θ, f_Y,Z(·, ·)}, where L_c involves only θ. In this section, we show that the semiparametric maximum likelihood estimator of S_Y,Z(y, z) can be derived by a two-step procedure.

First consider the case when θ is known. As shown in (2), the joint density function p_Y,Z(y, z) of uncensored (y, z) can be written as

$$p_{Y,Z}(y,z)=\frac{\{G(t_0-y-z;\theta )-G(-y;\theta )\}{f}_{Y,Z}(y,z)}{\int \int \{G(t_0-u-\upsilon ;\theta )-G(-u;\theta )\}{f}_{Y,Z}(u,\upsilon )\text{d}u\hspace{0.17em}\text{d}\upsilon }.$$ (3)

Define a weight function h(y, z) = G(t₀ − y − z) − G(−y), which describes the selection bias of observing (y, z). Its value coincides with the probability that initiating events occur within the window (−y, t₀ − y − z]. The sampling density p_Y,Z(y, z) is generally biased and proportional to the population density f_Y,Z(y, z), and the direction of bias is determined by h(y, z). Thus, an estimator of the joint survival function of (Y, Z) is

$${\widehat{S}}_{Y,Z}(y,z,\theta )=\frac{{\sum }_{i=1}^n{\{G(t_0-Y_i-Z_i;\theta )-G(-Y_i;\theta )\}}^{-1}I(Y_i>y,Z_i>z)}{{\sum }_{i=1}^n{\{G(t_0-Y_i-Z_i;\theta )-G(-Y_i;\theta )\}}^{-1}}.$$

If θ is known, Ŝ_Y,Z (y, z, θ) can be proved to be the nonparametric maximum likelihood estimator of S_Y,Z (y, z), a special case of Vardi (1985). As n → ∞, Ŝ_Y,Z (y, z, θ) is consistent, and the process n^1/2{Ŝ_Y,Z (y, z, θ) − S_Y,Z (y, z)} converges weakly to a bivariate zero-mean Gaussian process with covariance function

$$\begin{array}{ll}{\sigma }^2\hfill & =H_{-1}\hspace{0.17em}H\hspace{0.17em}(\frac{{\int }_y^{\infty }{\int }_z^{\infty }{\{G(t_0-u-\upsilon ;\theta )-G(-u;\theta )\}}^{-1}\hspace{0.17em}{f}_{Y,Z}(u,\upsilon )\text{d}u\hspace{0.17em}\text{d}\upsilon }{H_{-1}}\{1-S_{Y,Z}(y^{\prime },z^{\prime })\}\hfill \\ \hfill & +S_{Y,Z}(y,z)\hspace{0.17em}\left[S_{Y,Z}(y^{\prime },z^{\prime })-\frac{{\int }_{y^{\prime }}^{\infty }{\int }_{z^{\prime }}^{\infty }{\{G(t_0-u-\upsilon ;\theta )-G(-u;\theta )\}}^{-1}\hspace{0.17em}{f}_{Y,Z}(u,\upsilon )\text{d}u\hspace{0.17em}\text{d}\upsilon }{H_{-1}}\right]),\hfill \end{array}$$

where H = ∫ ∫{G(t₀ − u − υ; θ) − G(−u; θ)} f_Y,Z (u, υ) du dυ, and H₋₁ = ∫ ∫{G(t₀ − u − υ; θ) − G(−u; θ)}⁻¹ f_Y,Z(u, υ) du dυ. A consistent variance estimator σ̂² can be obtained by replacing H and H₋₁ by empirical distribution functions, and S_Y,Z (y, z) by Ŝ_Y,Z (y, z, θ).

Now suppose θ is unknown. We replace θ in Ŝ_Y,Z (y, z, θ) by the conditional maximum likelihood estimator θ̂ and derive an estimator of S_Y,Z (y, z) as Ŝ_Y,Z (y, z, θ̂). This can be proved to be the semiparametric maximum likelihood estimator using an argument similar to that in Wang (1989). The error of Ŝ_Y,Z (y, z, θ̂) can be decomposed into two terms,

$${\widehat{S}}_{Y,Z}(y,z,\widehat{\theta })-S_{Y,Z}(y,z)=\{{\widehat{S}}_{Y,Z}(y,z,\theta )-S_{Y,Z}(y,z,)\}+\{{\widehat{S}}_{Y,Z}(y,z,\widehat{\theta })-{\widehat{S}}_{Y,Z}(y,z,\theta )\},$$

where the first error term is determined by σ². The error in the second term is generated by the use of θ̂ to estimate θ. The distributions of the two terms can be proved to be asymptotically orthogonal to each other because θ in the second term is estimated by the conditional likelihood estimator. This property will be used in the proof of Theorem 1 in the Appendix.

Therefore, the joint survival function can be estimated by

$${\widehat{S}}_{Y,Z}(y,z,\widehat{\theta })=\frac{{\sum }_{i=1}^n{\{G(t_0-Y_i-Z_i;\widehat{\theta })-G(-Y_i;\widehat{\theta })\}}^{-1}\hspace{0.17em}I(Y_i>y,Z_i>z)}{{\sum }_{i=1}^n{\{G(t_0-Y_i-Z_i;\widehat{\theta })-G(-Y_i;\widehat{\theta })\}}^{-1}},$$

where (Y_i, Z_i) are the uncensored bivariate failure times, Ŝ_Y,Z (y, z, θ̂) is a weighted empirical estimator and S_Y,Z(y, z) is identifiable on the domain {(y, z) : y + z ⩽ t₀ − t₋}. The estimator Ŝ_Y,Z(y, z, θ̂) has the following properties.

Theorem 1. The estimator Ŝ_Y,Z (y, z, θ̂) is consistent, and as n → ∞, the process n^1/2{Ŝ_Y,Z (y, z, θ̂) − S_Y,Z (y, z,)} converges weakly to a bivariate zero-mean Gaussian process with covariance function Σ = ∇_θŜ_Y,Z (y, z, θ)^T $I_{\text{c}}^{-1}$ ∇_θŜ_Y,Z (y′, z′, θ) + σ².

The proof can be found in the Appendix. Vector notation for the gradient ∇_θ is used since θ ∈ R^k. A consistent estimator of Σ is Σ̂ = ∇_θ Ŝ_Y,Z (y, z, θ̂)^T $I_{\text{c}}^{-1}$ ∇_θ Ŝ_Y,Z (y′, z′, θ̂) + σ̂².

The above joint survival function estimate can be used to produce an estimator Ŝ_Y (y, 0, θ̂) for the marginal survival function. The same approach of modelling (T, Y, Z) could be applied to (T, Y) and a more efficient estimator of S_Y (y) is

$${\widehat{S}}_Y(y,{\widehat{\theta }}_{*})=\frac{{\sum }_{i=1}^n{\{G(t_0-{\tilde{Y}}_i;{\widehat{\theta }}_{*})-G(-{\tilde{Y}}_i;{\widehat{\theta }}_{*})\}}^{-1}\hspace{0.17em}I({\tilde{Y}}_i>y)}{{\sum }_{i=1}^n{\{G(t_0-{\tilde{Y}}_i;{\widehat{\theta }}_{*})-G(-{\tilde{Y}}_i;{\widehat{\theta }}_{*})\}}^{-1}},$$

where Ỹ_i is the observed first failure time and θ̂_* is obtained by maximizing the conditional likelihood function of the observed {t} given the observed {y}. Compared with the {Y_i}, which are from uncensored bivariate failure times (Y_i, Z_i), the {Ỹ_i} contain more data points. Also, Ŝ_Y (y, θ̂_*) can be proved to be a semiparametric maximum likelihood estimator of S_Y (y).

The marginal survival function of Z is not in general easily estimated under semi-stationarity due to induced sampling bias and dependent censoring; however, it is possible to estimate the conditional probability function pr_Z|Y(Z > z | y₁ < Y ⩽ y₂) = {S_Y,Z (y₁, z) − S_Y,Z (y₂, z)}/{S_Y (y₁) − S_Y (y₂)} as long as y + z ⩽ t₀ − t₋. In fact, this conditional probability may be of interest even when S_Z is estimable. An estimator of pr_Z|Y (Z > z | y₁ < Y ⩽ y₂) is

$${\widehat{\text{pr}}}_{Z|Y}(Z>z|y_1<Y⩽y_2)=\frac{{\widehat{S}}_{Y,Z}(y_1,z,\widehat{\theta })-{\widehat{S}}_{Y,Z}(y_2,z,\widehat{\theta })}{{\widehat{S}}_Y(y_1,{\widehat{\theta }}_{*})-{\widehat{S}}_Y(y_2,{\widehat{\theta }}_{*})}.$$

Estimation of such a conditional survival function can be used in exploratory analysis to detect possible correlation between Y and Z, as shown in the Supplementary Material.

The stationary condition when both Assumptions 1 and 2 hold is often of interest both in practice and theory. We have proposed a stationary model, assuming G is uniform, to estimate the joint survival function, which is a special case of the semi-stationary model and the method discussed in this section. The details of the stationary model are provided in the Supplementary Material. When G is totally unknown, the development of a nonparametric approach to estimate the joint survival function is possible. Using our notation, the conditional density of observed y given t is

$$p_{Y|T}(y|t)=\frac{f_Y(y)I(-y⩽t⩽t_0-y)}{S_Y(t_0-t)-S_Y(-t)},$$

from which the nonparametric maximum likelihood estimator of S_Y (y) can be obtained by a conditional likelihood approach developed by Efron & Petrosian (1999) for doubly truncated data. The semiparametric model is generally a compromise between the nonparametric model and the stationary model, and is designed to incorporate the parametric information from the distribution function G. Moreover, the semiparametric estimator Ŝ_Y (y, θ̂) has an explicit form and manageable asymptotic expressions for development of large sample properties, while the Efron–Petrosian estimator must be computed using an iterative algorithm. Although it is interesting to extend the nonparametric estimation technique to the bivariate case, we will not pursue this here.

It is important to check the validity of the parametric distribution assumption H₀ : T ∼ G(t; θ). This can be done by plotting the nonparametric maximum likelihood estimate Ĝ_n(t) against Ĝ(t, θ̂). Since T is also doubly truncated subject to the constraint −Y ⩽ T ⩽ t₀ − Y, estimating G is essentially dual to estimating S_Y. Shen (2008) provided an algorithm to jointly compute the nonparametric maximum likelihood estimators of both G and S_Y. The plot is used to examine the adequacy of the fit of the parametric distribution of T.

The above method uses only uncensored data. However, most disease registry data involve a large number of subjects over a long time period, and many observations are uncensored. In general, the proportion of uncensored data would be typically sufficient, or more than sufficient, for use of the proposed method. Nevertheless, with a slightly stronger model assumption in § 3, we have developed a method to analyse the bivariate survival data based on both uncensored and censored observations. Another possible solution is to utilize the information from censored observations in estimating θ in G(t; θ). We could model (T, Y) to obtain a conditional maximum likelihood estimator θ̂_* based on observed first failure time {Ỹ_i}, instead of modelling (T, Y, Z) using only uncensored bivariate failure times {Y_i, Z_i}. In general, θ̂_* is expected to be more efficient than θ̂, and accordingly, a new weight {G(t₀ − Y_i − Z_i; θ̂_*) − G(−Y_i ; θ̂_*)} could be used to replace {G(t₀ − Y_i − Z_i ; θ̂) − G(−Y_i ; θ̂)} in constructing the weighted empirical joint survival function estimator. In this way, we may take advantage of some information from censored observations, at least for the first failure time. The properties of the resulting joint survival function estimator with the new weight, as well as its efficiency gain, are under investigation.

3. Semiparametric Copula Model under Stationarity

3.1. Failure time distributions

The estimation method proposed in § 2 only uses uncensored data and particularly focuses on adjusting for the sampling bias from double truncation. In this section, we estimate the bivariate survival function based on both censored and uncensored observations. With a slightly stronger assumption on the dependence structure of the bivariate distribution, a semiparametric copula model under stationarity is used, which allows one to model and estimate the margins and dependence separately. We investigate the semiparametric copula model by a two-stage estimation approach similar to those of Genest et al. (1995) and Shih & Louis (1995). We first explore the probability structure for each failure time marginally and obtain the nonparametric consistent estimators for marginal survival functions under stationarity, ignoring the dependence. Then these estimators are substituted into a conditional likelihood for the association parameter, yielding a pseudo likelihood (Gong & Samaniego, 1981). The association parameter is then estimated by solving the estimating equation derived from the pseudo conditional likelihood.

First, we consider the first failure time Y, which is sampled given −T ⩽ Y ⩽ t₀ − T. The joint density of observed (t, y) can be written as

$$\begin{array}{ll}{p}_{T,Y}(t,y)\hfill & =\frac{g(t)f_Y(y)I(-y⩽t⩽t_0-y)}{\text{pr}(-Y⩽T⩽t_0-Y)}\hfill \\ \hfill & =\frac{g(t)I(-y⩽t⩽t_0-y)}{G(t_0-y)-G(-y)}\times \frac{\{G(t_0-y)-G(-y)\}{f}_Y(y)}{\int \{G(t_0-u)-G(-u)\}\hspace{0.17em}{f}_Y(u)\hspace{0.17em}\text{d}u}\hfill \\ \hfill & =p_{T|Y}(t|y)\times p_Y(y).\hfill \end{array}$$

Under stationarity when T is uniformly distributed, the marginal density of observed y, p_Y (y), becomes f_Y (y), so the sampling density of y coincides with its population density and double truncation from interval sampling does not result in bias on Y. Therefore, the nonparametric estimator of S_Y (y) is simply the empirical survival function ${\widehat{S}}_Y\hspace{0.17em}(y)={\sum }_{i=1}^n\hspace{0.17em}I\hspace{0.17em}({\tilde{Y}}_i>y)$, where Ỹ_i is the observed first failure time. The nonparametric maximum likelihood estimator of S_Y (y), Ŝ_Y (y), is consistent.

For the second failure time Z, we investigate its probability structure under stationarity. Specifically, we show that the sampling distribution of Z is the same as the target population distribution. Let W = T + Y denote the calendar time when the first failure event occurs. With sampling window [0, t₀], only those cases satisfying 0 ⩽ W ⩽ t₀ are included in the sampling population. The stationary condition implies that f_{Y,Z | T} (y, z | t) = f_Y,Z (y, z) and λ (t) = λ₀ for −y⁺ < t ⩽ t₀ − y₋. The occurrence rate of the first failure event at W = w over the calendar time window [0, t₀] can then be derived as

$$\varphi (w)={\int }_{-\infty }^w{f}_{Y|T}(w-t|t)\lambda (t)\text{d}t={\lambda }_0{\int }_{-\infty }^w{f}_Y(w-t)\text{d}t={\lambda }_0{\int }_0^{\infty }{f}_Y(y)\text{d}y={\lambda }_0.$$ (4)

That is, the occurrence rate of the first failure event is the same as that of the initiating event. Also, the joint rate function of (Z, W) is

$$\varphi (w)\hspace{0.17em}{f}_{Z|W}(z|w)={\int }_{-\infty }^w{f}_{Y,Z|T}(w-t,z|t)\lambda (t)\text{d}t={\lambda }_0{\int }_0^{\infty }{f}_{Y,Z}(y,z)\text{d}y={\lambda }_0{f}_Z(z).$$ (5)

From (4) and (5), we conclude that f_Z (z) = f_{Z | W} (z | w) almost surely for all (w, z), so Z is independent of W. The censoring time for observing Z is C − W, where C is the calendar time of censoring. If C is a constant, for example, the calendar time of the end of study, the independence of Z and W implies the independence of Z and C − W. This independent censoring also extends to the situation when C is not a constant, simply by imposing independence between Z and C, as commonly employed in a survival model. Therefore, survival data {{min(z_i, c_i − w_i), I (z_i ⩽ c_i − w_i)} : c_i ⩾ w_i} can be treated as right-censored for obtaining the Kaplan–Meier estimator of the marginal survival function S_Z (z).

3.2. Copula model and two-stage semiparametric estimation

Suppose the bivariate failure times (Y, Z) come from the C_α copula for some association parameter α, where C_α is a distribution function with density c_α on [0, 1]². Then the joint survival function and density function of (Y, Z) are

$$S_{Y,Z}(y,z)=C_{\alpha }\{S_Y(y),S_Z(z)\},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{f}_{Y,Z}(y,z)=c_{\alpha }\{S_Y(y),S_Z(z)\}{f}_Y(y)f_Z(z),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}y,z⩾0.$$

A two-stage estimation strategy is used to estimate the association parameter α. For observed data (t, y, x, δ) where x = min(z, c − t − y) and δ = I (z ⩽ c − t − y), the conditional likelihood function of {(y_i, x_i, δ_i)} given {t_i} is

$$L_c(\alpha )=\prod _{i=1}^n\frac{f_{Y,Z}{(y_i,x_i)}^{{\delta }_i}{\{\partial S_{Y,Z}(y_i,x_i)/\partial y_i\}}^{1-{\delta }_i}}{S_Y(c_i-t_i)-S_Y(-t_i)}.$$

In derivation of L_c(α), the distribution of T is eliminated by conditioning. Under stationarity, however, T follows a uniform distribution, and the conditional and unconditional likelihoods contain the same information on α. Here we use the conditional likelihood only for simplicity. The two margins S_Y (y) and S_Z (z) are estimated by the empirical survival function Ŝ_Y (y) and the Kaplan–Meier estimator Ŝ_Z (z), respectively. Denote {S_Y (y_i), S_Z (x_i)} by (u_i, υ_i) for i = 1, …, n. The conditional likelihood of α is

$$L_{\text{c}}(\alpha )\propto \prod _{i=1}^n{f}_{Y,Z}{(y_i,x_i)}^{{\delta }_i}\hspace{0.17em}{\left\{\frac{\partial S_{Y,Z}(y_i,x_i)}{\partial y_i}\right\}}^{1-{\delta }_i}=\prod _{i=1}^n{c}_{\alpha }{(u_i,{\upsilon }_i)}^{{\delta }_i}\hspace{0.17em}{\left\{\frac{\partial C_{\alpha }(u_i,{\upsilon }_i)}{\partial u_i}\right\}}^{1-{\delta }_i}.$$ (6)

Since the denominator of L_c(α) is a function of S_Y that does not involve α, it is appropriate to estimate α by maximizing (6). Let

$$l(\alpha ,u,\upsilon )=c_{\alpha }{(u,\upsilon )}^{\delta }\hspace{0.17em}{\left\{\frac{\partial C_{\alpha }(u,\upsilon )}{\partial u}\right\}}^{1-\delta },\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{U}_{\alpha }^{(c)}(\alpha ,S_Y,S_Z)=\frac{\partial }{\partial \alpha }\sum _{i=1}^n\hspace{0.17em}\text{log}\hspace{0.17em}l(\alpha ,S_Y,S_Z).$$

The semiparametric estimator α̂ for α is the solution to the pseudo score function derived from the pseudo conditional likelihood

$$\begin{array}{ll}{U}_{\alpha }^{(p)}(\alpha ,{\widehat{S}}_Y,{\widehat{S}}_Z)\hfill & =\frac{\partial }{\partial \alpha }\hspace{0.17em}\left(\sum _{i=1}^n{\delta }_i\hspace{0.17em}\text{log}[c_{\alpha }\{{\widehat{S}}_Y(y_i),{\widehat{S}}_Z(x_i)\}]+(1-{\delta }_i)\hspace{0.17em}\text{log}\hspace{0.17em}\left[\frac{\partial C_{\alpha }\{{\widehat{S}}_Y(y_i),{\widehat{S}}_Z(x_i)\}}{\partial u_i}\right]\right)\hfill \\ \hfill & =0.\hfill \end{array}$$

The following conditions are assumed to develop large sample properties for α̂.

Condition 1. The standard regularity conditions for the maximum likelihood estimator hold.

Condition 2. The functions W_α {α, S_Y (y), S_Z (z)}, V_α {α, S_Y (y), S_Z (z)}, V_α,1{α, S_Y (y), S_Z (z)} and V_α,2{α, S_Y (y), S_Z (z)} are continuous and bounded for (y, z) ∈ 𝒜 = [y₋, y₊] × [z₋, z₊], where

$$\begin{array}{ll}{W}_{\alpha }\{\alpha ,S_Y(y),S_Z(z)\}=\frac{\partial \hspace{0.17em}\text{log}\hspace{0.17em}l(\alpha ,u,\upsilon )}{\partial \alpha },\hfill & V_{\alpha }\{\alpha ,S_Y(y),S_Z(z)\}=\frac{{\partial }^2\hspace{0.17em}\text{log}\hspace{0.17em}l(\alpha ,u,\upsilon )}{\partial {\alpha }^2},\hfill \\ V_{\alpha ,1}\{\alpha ,S_Y(y),S_Z(z)\}=\frac{{\partial }^2\hspace{0.17em}\text{log}\hspace{0.17em}l(\alpha ,u,\upsilon )}{\partial \alpha \partial u},\hfill & V_{\alpha ,2}\{\alpha ,S_Y(y),S_Z(z)\}=\frac{{\partial }^2\hspace{0.17em}\text{log}\hspace{0.17em}l(\alpha ,u,\upsilon )}{\partial \alpha \partial u}.\hfill \end{array}$$

The asymptotic properties of α̂ are summarized as follows.

Theorem 2. The estimator α̂ is consistent, and as n → ∞, n^1/2(α̂ − α₀) converges weakly to the normal distribution with mean zero and variance ${\rho }^2=({\rho }_1^2+{\rho }_2^2)/{\rho }_1^4$.

A consistent estimator of ρ² is obtained as ${\widehat{\rho }}^2=({\widehat{\rho }}_1^2+{\widehat{\rho }}_2^2)/{\widehat{\rho }}_1^4$. The precise definitions of ${\rho }_1^2$ and ${\rho }_2^2$ together with the details of the proof can be found in the Supplementary Material.

For the bivariate survival function, a natural estimator is then obtained by replacing the unknown quantities in the copula model S_Y,Z (y, z) = C_α {S_Y (y), S_Z (z)} by appropriate estimators. Specifically, the margins S_Y (y) and S_Z (z) are replaced by their nonparametric estimators, the empirical survival function for Y and the Kaplan–Meier estimator for Z, and α is replaced by the two-stage association estimator α̂. The asymptotic properties of Ŝ_Y,Z (y, z) are summarized in Theorem 3, with the proof provided in the Supplementary Material.

Theorem 3. The estimator Ŝ_Y,Z (y, z) is consistent, and as n → ∞, the process n^1/2{Ŝ_Y,Z (y, z) − S_Y,Z (y, z)} converges weakly to a bivariate zero-mean Gaussian process with covariance function [∂C{α, S_Y (y), S_Z (z)}/∂α]² ρ² + ω²(y, z).

4. Simulation Studies

4.1. Joint survival function estimation under semi-stationarity

We evaluate the finite-sample performance of the semiparametric estimator Ŝ_Y,Z (y, z, θ̂) under semi-stationarity by simulation. Data {(t₁, y₁, z₁), …, (t_n, y_n, z_n)} with interval sampling are generated for the semi-stationary model. Define T = −3K + 10, where K ∼ exp(θ), and let the bivariate failure times (Y, Z) be generated from Clayton’s (1978) copula, S_Y,Z (y, z) = {S_Y (y)^−α + S_Z (z)^−α − 1}^−1/α, with unit exponential margins and association parameter α = 2. An observation (t, y, z) is included in the dataset if and only if 0 ⩽ t + y ⩽ 10 and is censored if t + y + z ⩾ 10. The proportion of uncensored observations is around 0.6. We generate 1000 simulated samples with n = 400.

Table 1 summarizes the empirical bias, average model-based standard error of θ̂ and Ŝ_Y,Z (y, z, θ̂), empirical standard error and 95% coverage probability of Ŝ_Y,Z (y, z, θ̂) at nine time-points (y, z), where y and z take values 0.22, 0.51 and 0.92, corresponding to marginal survival probabilities of 0.8, 0.6 and 0.4. The confidence interval is constructed based on the estimated asymptotic variance, and the empirical 95% coverage probability is based on the 1000 confidence intervals. The estimators are approximately unbiased and the model-based variance estimators work well, with coverage probabilities close to 95% at most time-points. As θ increases, the biases and standard errors increase.

Table 1.

Simulation summary statistics for Ŝ_Y,Z under semi-stationarity

θ	Bias(θ̂)	SE(θ̂)	y	z	SY,Z	Bias(ŜY,Z)	SEe(ŜY,Z)	SEm(ŜY,Z)	CP(ŜY,Z)
0.5	0.6	7.9	0.22	0.22	0.686	−0.1	3.2	3.2	96
				0.51	0.547	−0.3	3.7	3.6	96
				0.92	0.383	−0.2	4.1	3.9	96
			0.51	0.22	0.547	0.1	3.7	3.6	96
				0.51	0.469	−0.1	3.9	3.7	95
				0.92	0.353	−0.1	3.9	3.9	95
			0.92	0.22	0.383	−0.2	4.1	3.8	94
				0.51	0.353	−0.2	4.1	3.9	95
				0.92	0.295	−0.1	4.1	3.9	95
1.0	0.8	9.0	0.22	0.22	0.686	−0.1	3.7	3.6	95
				0.51	0.547	−0.1	4.5	4.6	96
				0.92	0.383	−0.2	5.2	5.1	95
			0.51	0.22	0.547	−0.2	4.4	4.3	95
				0.51	0.469	−0.2	4.8	4.7	94
				0.92	0.353	−0.1	5.2	5.2	94
			0.92	0.22	0.383	−0.2	5.2	5.2	95
				0.51	0.353	−0.2	5.4	5.3	95
				0.92	0.295	−0.3	5.5	5.3	95
2.0	1.0	16.7	0.22	0.22	0.686	−0.7	5.7	5.6	96
				0.51	0.547	−0.9	7.7	7.6	98
				0.92	0.383	−1.4	9.6	9.5	97
			0.51	0.22	0.547	−0.9	7.7	7.6	96
				0.51	0.469	−1.1	8.7	8.5	96
				0.92	0.353	−1.2	10.0	9.5	95
			0.92	0.22	0.383	−1.0	9.4	8.9	94
				0.51	0.353	−1.1	9.8	9.2	95
				0.92	0.295	−1.4	10.3	9.7	95

Bias(θ̂), empirical bias (×10²) of θ̂; SE(θ̂), average model-based standard error (×10²) of θ̂; Bias(Ŝ_Y,Z), empirical bias (×10²) of Ŝ_Y,Z; SE_e(Ŝ_Y,Z), empirical standard error (×10²) of Ŝ_Y,Z; SE_m(Ŝ_Y,Z), average model-based standard error (×10²) of Ŝ_Y,Z; CP(Ŝ_Y,Z), nominal 95% coverage probability of Ŝ_Y,Z.

4.2. Semiparametric copula model under stationarity

The performances of the two-stage estimator α̂ and joint survival function estimator Ŝ_Y,Z (y, z) in the semiparametric copula model under stationarity are examined by simulation. Two sampling schemes are explored: random sampling and interval sampling. A set of data {(t₁, y₁, z₁), …, (t_n, y_n, z_n)} is generated with interval sampling: define T = −13K + 9, where K ∼ U(0, 1), and generate bivariate failure times (Y, Z) from three Archimedean copula models: Clayton’s family, a positive stable copula and Frank’s family, whose explicit expressions are given in the Supplementary Material. For each copula, we use unit exponential margins, and choose three values of α in order to accommodate different levels of dependence between Y and Z. An observation (t, y, z) is included in the dataset if and only if 0 ⩽ t + y ⩽ 10 and is censored if t + y + z ⩾ 10. For each value of α we generate 1000 simulated samples with n = 400.

Table 2 presents simulation results for α̂ and Ŝ_Y,Z (y, z) = C{α̂, Ŝ_Y (y), Ŝ_Z (z)}. The estimated joint survival probability is reported at two time-points, (y, z) = (0.22, 0.22) and (0.22, 0.51), and is there denoted by S₁ and S₂. For the three copula models, the proposed method performs quite well with both sampling plans. The biases of α̂, Ŝ₁ and Ŝ₂ are fairly small. For the association parameter, the empirical standard error and average model-based standard error are generally close, which may imply that inference about α is reasonably good. The empirical coverage probabilities are all quite close to 95%. The stronger the dependence of (Y, Z), indicated by a larger absolute value of α, the bigger the bias and standard error for α̂. However, no such phenomenon is observed for Ŝ₁ and Ŝ₂.

Table 2.

Simulation summary statistics for α̂ and Ŝ_Y,Z under different sampling schemes for samples from Clayton’s family, positive stable frailties and Frank’s family

Model	α	Sampling	Bias(α̂)	SEe(α̂)	SEm(α̂)	CP(α̂)	Bias(Ŝ1)	SEe(Ŝ1)	CP(Ŝ1)	Bias(Ŝ2)	SEe(Ŝ2)	CP(Ŝ2)
Clayton	0.50	Random	1.2	9.3	7.8	97	0.5	2.3	97	0.3	2.3	95
		Interval	2.0	10.8	9.2	96	0.3	2.5	94	0.2	3.0	94
	1.33	Random	1.4	14.9	12.7	98	0.4	2.4	97	0.2	2.5	94
		Interval	4.7	17.9	16.3	97	0.4	2.8	96	0.5	3.2	94
	3.00	Random	5.4	26.1	24.3	98	0.3	2.1	97	0.1	2.4	96
		Interval	10.2	30.4	28.5	97	−0.4	3.0	95	−0.7	3.3	94
Positive Stable	1.25	Random	0.1	2.6	1.8	94	0.3	2.7	98	0.1	2.6	96
		Interval	0.6	5.8	4.9	94	0.3	2.5	98	0.3	2.8	96
	1.67	Random	0.3	6.7	5.2	94	0.1	2.2	96	0.2	2.7	94
		Interval	0.7	9.5	7.8	94	−0.2	2.9	96	−0.2	3.1	96
	2.50	Random	1.3	10.3	8.3	95	0.3	2.1	94	−0.2	2.6	96
		Interval	2.2	15.5	13.7	94	0.3	3.0	96	0.2	2.8	94
Frank	2.00	Random	1.4	32.8	31.2	96	0.3	2.1	97	−0.2	2.2	96
		Interval	1.4	35.7	34.3	96	0.4	2.3	96	0.3	2.5	95
	−1.00	Random	0.6	28.0	26.7	95	0.6	2.3	94	0.4	2.3	94
		Interval	1.0	34.7	32.9	95	0.5	2.5	94	0.4	2.8	94
	−2.00	Random	2.3	32.0	30.8	95	0.3	2.4	95	0.4	2.3	94
		Interval	1.6	37.2	35.5	95	0.4	2.6	95	0.5	3.0	94

Bias(α̂), empirical bias (×10²) of α̂; SE_e(α̂), empirical standard error (×10²) of α̂; SE_m(α̂), average model-based standard error (×10²) of α̂; CP(α̂), 95% coverage probability of α̂; Bias(Ŝ₁), empirical bias (×10²) of Ŝ₁ with S₁ = S_Y,Z (0.22, 0.22); SE_e(Ŝ₁), empirical standard error (×10²) of Ŝ₁; CP(Ŝ₁), 95% coverage probability of Ŝ₁; Bias(Ŝ₂), empirical bias (×10²) of Ŝ₂ with S₂ = S_Y,Z (0.22, 0.51); SE_e(Ŝ₂), empirical standard error (×10²) of Ŝ₂; CP(Ŝ₂), nominal 95% coverage probability of Ŝ₂.

5. Application to SEER cancer registry data

5.1. Analysis under semi-stationarity

This section presents an analysis of ovarian cancer data collected by the Surveillance, Epidemiology and End-Results programme to address statistical issues arising from interval sampling and to study the natural history of ovarian cancer. The programme is an epidemiological surveillance system consisting of population-based cancer registries designed to track cancer incidence and survival in the U.S.A. Collection of the data began from 1 January 1973 (Ries et al., 2005). The registries routinely collect information on newly diagnosed cancer patients residing in geographically defined areas representing 26 percent of the U.S. population. Information is available on each person’s birth date, cancer diagnosis date, death date, type of cancer, sex, race, state of residence, etc. The cohort of interest consists of 36 728 ovarian cancer patients diagnosed from 1973 to 2002 under interval sampling, among whom 24 236 died before 31 December 2002, and others were censored. In the analysis, the initiating time is birth time, T, and the bivariate failure times are age of cancer onset, Y and residual lifetime, Z.

In analysis of the data from this study, residual lifetime after cancer onset was typically analysed by regression methods such as the proportional hazards model, conditioning on age of cancer onset. These analyses treat age-onset as a conditional variable and therefore should be interpreted conditionally. Our focus here is unconditional analysis of disease natural history, that is, it is unconditional on age of cancer onset. Nevertheless, all the models considered in this paper have a certain conditional component, since the data are observed conditioning on the fact the subjects were diagnosed with cancer within the study time interval. The age of cancer onset distribution was typically empirically estimated and the median age of cancer onset was reported in Altekruse et al. (2010). However, such a statistical analysis is biased because the marginal distribution of age of cancer onset from the sampling population is subject to bias due to interval sampling, and the joint distribution of age of cancer onset and residual lifetime is also sampling-biased. Existing analyses have commonly ignored these biases.

We apply the method developed under semi-stationarity to the ovarian cancer data, assuming that (Y, Z) is independent of T. All the variables are analysed on a scale in years. As discussed in § 2.1, the sampling density of T is generally biased and it is not appropriate to use the empirical method to estimate the birth rate. To estimate the distribution of T, we use two polynomial models for the rate function λ (t) in (1): a linear model λ (t) = c₀ + θ₁t, and a quadratic polynomial model λ (t) = c₀ + θ₁t + θ₂t², where c₀ is a positive-valued constant.

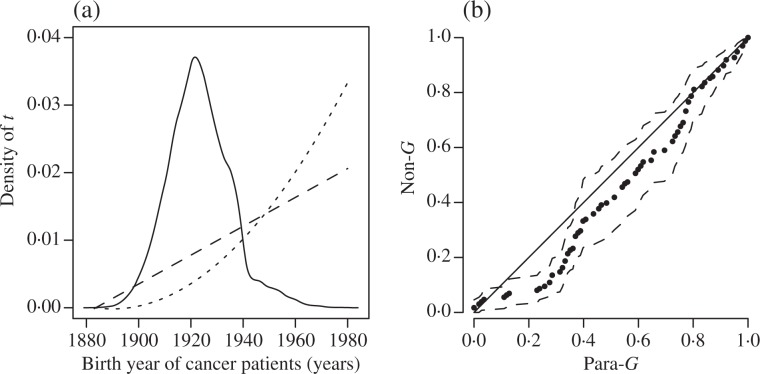
The density plots in Fig. 2(a) show that the difference between linear and quadratic models is small. The figure also demonstrates the huge bias in estimating the birth density by the empirical method. An increasing trend in birth rate for the case cohort over the calendar time is found in both models. Such a trend could be explained by the post-World War II baby boom or the improvement of ovarian cancer screening techniques. Given the similarity of the two polynomial models, the linear model is chosen as the birth density in analysis. With λ (t) = c₀ + θt, we have θ̂ = 3.914 (0.030). The validity of this parametric model was assessed by plotting the nonparametric maximum likelihood estimator Ĝ_n(t) (Shen, 2008) against Ĝ(t, θ̂) for the distribution function of T in Fig. 2(b), which suggests the assumption of linear birth rate is approximately correct.

Fig. 2.

Birth density plots and scatter-plot of Ĝ_n(t) against Ĝ(t, θ̂). (a) Birth density plots: the biased empirical estimate (solid), the linear model estimate (dash) and the quadratic model estimate (dot). (b) Scatter-plot of Ĝ_n(t) against Ĝ(t, θ̂) with 95% pointwise confidence bands based on bootstrap (dash). The diagonal line y = x is shown as a reference. Non-G, nonparametric estimator Ĝ_n(t); Para-G, parametric estimator Ĝ(t, θ̂).

The joint survival probability estimators are calculated using both empirical and proposed methods. To obtain the standard errors of estimated joint survival probabilities, we adopt a non-parametric bootstrap method, resampling subjects with replacement from the dataset. The resampling procedure is repeated 500 times for the overall cancer patients, white patients and nonwhite patients, respectively. While the asymptotic variance of Ŝ_Y,Z (y, z, θ̂) has a rather complicated form, the ordinary bootstrap method would provide a direct and robust way to estimate the standard error. Table 3 summarizes the results at nine bivariate time-points, with y = 62.2, 69.8, 77.5 years and z = 0.25, 1.58, 4.58 years, corresponding to the quartiles of observed age of cancer onset and residual lifetime. The table provides the empirical and proposed estimated joint survival probabilities with bootstrap standard errors, and shows clear differences between the empirical and proposed estimates. As indicated by (3), the empirical estimate is generally biased since it does not account for interval sampling. The analytical result suggests that the empirical method may underestimate the joint survival probabilities, given our model specification on the distribution of T. Table 3 also provides estimated joint survival probabilities by race. It is shown that white patients are likely to be diagnosed at older ages and survive longer than nonwhite patients, consistent with the literature (Ries et al., 2005). The impact of age of cancer onset on residual lifetime, explored in the Supplementary Material, suggests negative association between age of onset and residual lifetime.

Table 3.

Estimated joint survival probabilities at quartiles of observed age of cancer onset and residual lifetime

		All			White			Nonwhite
y	z	Ŝemp	Ŝprop	SE	Ŝemp	Ŝprop	SE	Ŝemp	Ŝprop	SE
62.2	0.25	62.2	62.3	4.0	63.1	62.9	4.2	56.9	57.3	1.0
	1.58	36.7	40.2	2.6	37.5	40.7	2.7	30.7	34.4	1.0
	4.58	16.0	22.2	1.5	16.3	22.7	1.7	12.1	17.5	0.8
69.8	0.25	41.2	45.1	2.9	42.0	45.7	3.0	34.8	39.1	1.1
	1.58	22.0	26.8	1.8	22.7	27.3	1.9	17.3	21.9	1.1
	4.58	9.3	13.9	0.9	9.3	14.3	1.2	6.4	10.5	0.7
77.5	0.25	18.9	24.3	1.6	19.2	24.8	1.8	14.4	19.6	1.0
	1.58	8.6	12.8	0.9	8.9	13.0	1.0	6.4	10.0	0.7
	4.58	3.4	6.2	0.5	3.4	6.3	0.6	2.2	4.5	0.5

y, age of cancer onset; z, residual lifetime; Ŝ_emp, empirical estimate of joint survival probability (×10²); Ŝ_prop, proposed estimate of joint survival probability (×10²); SE, bootstrap standard error (×10²) based on 500 replications.

5.2. Example of the copula model under stationarity

We now illustrate the copula model under stationarity considered in § 3. The analysis in § 5.1 shows that in general the birth rate of the ovarian cancer patients increases over time. To apply the semiparametric copula model proposed under stationarity, we restrict the study population to 12 363 ovarian cancer patients who were born between 1920 and 1930, and assume a constant birth rate for this sub-cohort. The constant birth rate assumption is checked by plotting the nonparametric estimator of birth distribution against its parametric estimator. Figure 2 of the Supplementary Material suggests that this assumption is fairly reasonable.

A negative association between age of ovarian cancer onset and residual lifetime is found in § 5.1. Hence, we choose a Frank copula model to fit the dependence structure. Under stationarity, the marginal survival functions of age of onset and residual lifetime are consistently estimated by the empirical survival function and the Kaplan–Meier estimator. For the overall sub-cohort of 12 363 patients, the estimated association parameter α̂ = −3.69 with 95% confidence interval (−3.97, −3.40) and bootstrap percentile confidence interval (−3.92, −3.42). The first interval is constructed based on the asymptotic normality, in which the standard error of α̂ is computed using 500 bootstrap resamples. The corresponding estimated rank correlation coefficient τ̂ = −0.36 with 95% confidence interval (−0.39, −0.34) and bootstrap percentile confidence interval (−0.38, −0.34). For white patients, α̂ = −3.73 with 95% confidence interval (−4.06, −3.39) and bootstrap percentile confidence interval (−4.16, −3.47). For nonwhite patients, α̂ = −3.39 with 95% confidence interval (−4.31, −2.47) and bootstrap percentile confidence interval (−4.27, −2.49). There is a significant negative association between age of cancer onset and residual lifetime, for all the three groups, though the magnitude of the association is slightly different between white and nonwhite patients and the confidence intervals are wider for the nonwhite group due to its smaller size.

6. Concluding remarks

Under regularity conditions, we develop large sample properties for the association parameter estimator α̂ in copula model. In particular, we assume boundedness of the score function and its partial derivatives. This assumption was also adopted by Shih & Louis (1995) and many others in the derivation of large sample properties for their two-stage estimator of α in a copula model. However, some popular copula functions, such as the positive stable copula, are equivalent to the independence copula when the association parameter takes its value on the boundary of the parameter space. In this case, the score function and its partial derivatives may be unbounded. The violation was discussed by Chen et al. (2010), who extended the asymptotic results allowing for copulas with unbounded score function and partial derivatives. While this is not the major focus of this paper, we rely on the boundedness assumption to derive the large sample properties. The likelihood theory cannot easily be developed when this assumption is invalid, which makes testing independence of bivariate survival data possibly problematic using the copula model. Therefore, a nonparametric test of independence between bivariate survival times with interval sampling needs to be developed.

The assessment of risk factors or treatments is always crucial in biomedical studies, and an appropriate Cox regression model would allow for multiple risk factors. While our current method focuses on the natural history of disease progression, another interesting extension is to develop efficient estimating methods of the regression model for bivariate survival data with interval sampling. In some applications, information about time-dependent variables becomes available only after a certain time. For example, the treatment information of the ovarian cancer patients under study is provided by SEER-Medicare Link Data (Warren et al., 2002), which were collected from 1986. Therefore, a prevalent sample is involved and this further complicates the analysis. In such settings, methods need to be developed to address the problems and bias arising from both interval and prevalent sampling. The copula model approach could be extended to accommodate covariates with a regression model in studying the association.

Appendix.

Proof of Theorem 1. We study the consistency and asymptotic normality of Ŝ_Y,Z (y, z, θ̂). If θ is known, the properties of Ŝ_Y,Z (y, z, θ) follow from Vardi (1985) with a weight function involving θ, and thus Ŝ_Y,Z (y, z, θ) − S_Y,Z (y, z) converges to 0 in probability. Since θ̂ → θ in probability and Ŝ_Y,Z (y, z, θ) is continuous, Ŝ_Y,Z (y, z, θ̂) − Ŝ_Y,Z (y, z, θ) converges to 0 in probability. Therefore, Ŝ_Y,Z (y, z, θ̂) − S_Y,Z (y, z) = {Ŝ_Y,Z (y, z, θ) − S_Y,Z (y, z)} + {Ŝ_Y,Z (y, z, θ̂) − Ŝ_Y,Z (y, z, θ)} converges to 0 in probability. This completes the proof of consistency of Ŝ_Y,Z (y, z, θ̂).

Observe that

$$\begin{array}{lll}{n}^{1/2}\{{\widehat{S}}_{Y,Z}(y,z,\widehat{\theta })-S_{Y,Z}(y,z)\}\hfill & =\hfill & n^{1/2}\{{\widehat{S}}_{Y,Z}(y,z,\theta )-S_{Y,Z}(y,z)\}\hfill \\ \hfill & \hfill & +n^{1/2}\{{\widehat{S}}_{Y,Z}(y,z,\widehat{\theta })-{\widehat{S}}_{Y,Z}(y,z,\theta )\}.\hfill \end{array}$$ (A1)

As identified in § 2.2, the process n^1/2{Ŝ_Y,Z (y, z, θ) − S_Y,Z (y, z)} converges weakly to a bivariate zero-mean Gaussian process with covariance function σ². By counting process methodology (van der Vaart, 1998), the first term in (A1) can be approximated by

$$n^{1/2}\{{\widehat{S}}_{Y,Z}(y,z,\theta )-S_{Y,Z}(y,z)\}=n^{-1/2}\sum _{i=1}^n\varphi (\theta ,Y_i,Z_i,y,z)+o_p(1),$$ (A2)

where E{ϕ(θ, Y_i, Z_i, y, z)} = 0 for each θ.

To develop an asymptotic result for the second term in (A1), the additional variation due to estimating θ by θ̂ needs to be handled. Empirical process and semiparametric inference techniques are employed for the asymptotic properties of the second term in (A1). Note that Ŝ_Y,Z (y, z, θ) can be re-expressed as the empirical process ${\widehat{S}}_{Y,Z}(y,z,\theta )=n^{-1}\hspace{0.17em}{\sum }_{i=1}^n\hspace{0.17em}I(Y_i>y,Z_i>z)r(Y_i,Z_i,\theta )$, where $r(Y_i,Z_i,\theta )={\{G(t_0-Y_i-Z_i;\theta )-G(-Y_i;\theta )\}}^{-1}/{\sum }_{i=1}^n{\{G(t_0-Y_i-Z_i;\theta )-G(-Y_i;\theta )\}}^{-1}$. In § 2.1, it has been shown that n^1/2(θ̂ − θ) converges in distribution to a mean zero multivariate normal distribution with variance-covariance matrix $I_{\text{c}}^{-1}$, where θ̂ is the maximum likelihood estimator from the conditional likelihood function L_c(θ). Therefore, by functional delta method for the empirical process (Kosorok, 2008), we get that n^1/2{Ŝ_Y,Z (y, z, θ̂) − Ŝ_Y,Z (y, z, θ)} → N{0, ∇_θŜ_Y,Z (y, z, θ)^T $I_{\text{c}}^{-1}$ ∇_θ Ŝ_Y,Z (y, z, θ)} in distribution. Thus, the second term in (A1) can be approximated by

$$\begin{array}{lll}{n}^{1/2}\{{\widehat{S}}_{Y,Z}(y,z,\widehat{\theta })-{\widehat{S}}_{Y,Z}(y,z,\theta )\}\hfill & =\hfill & n^{-1/2}{\nabla }_{\theta }{\widehat{S}}_{Y,Z}{(y,z,\theta )}^T\hspace{0.17em}{I}_{\text{c}}^{-1}\hspace{0.17em}\sum _{i=1}^n\frac{\partial }{\partial \theta }\hspace{0.17em}\text{log}\hspace{0.17em}{p}_{T|Y,Z}(T_i|Y_i,Z_i)+o_p(1)\hfill \\ \hfill & =\hfill & n^{-1/2}{\nabla }_{\theta }\{{\widehat{S}}_{Y,Z}{(y,z,\theta )}^T\hspace{0.17em}{I}_{\text{c}}^{-1}\hspace{0.17em}\sum _{i=1}^n\phi (T_i,Y_i,Z_i)+o_p(1),\hfill \end{array}$$ (A3)

where E{φ(T_i, Y_i, Z_i)} = E{∂ log p_{T | Y,Z} (T_i | Y_i, Z_i)/∂θ} = 0. Combining (A2) and (A3), we get

$$\begin{array}{lll}{n}^{1/2}\{{\widehat{S}}_{Y,Z}(y,z,\widehat{\theta })-S_{Y,Z}(y,z)\}\hfill & \cong \hfill & n^{1/2}\sum _{i=1}^n\varphi (\theta ,Y_i,Z_i,y,z)\hfill \\ \hfill & \hfill & +n^{-1/2}{\nabla }_{\theta }\{{\widehat{S}}_{Y,Z}{(y,z,\theta )}^T\hspace{0.17em}{I}_{\text{c}}^{-1}\hspace{0.17em}\sum _{i=1}^n\phi (T_i,Y_i,Z_i).\hfill \end{array}$$ (A4)

Also the corresponding distributions of these two terms are asymptotically orthogonal to each other, since

$$E\{\varphi (\theta ,Y_i,Z_i,y,z)\phi (T_i,Y_i,Z_i)\}=E\hspace{0.17em}\left[\varphi (\theta ,Y_i,Z_i,y,z)E\hspace{0.17em}\left\{\frac{\partial }{\partial \theta }\hspace{0.17em}\text{log}\hspace{0.17em}{p}_{T|Y,Z}(T_i|Y_i,Z_i)|Y_i,Z_i\right\}\right]=0.$$ (A5)

Therefore, (A4) and (A5) imply that n^1/2{Ŝ_Y,Z (y, z, θ̂) − S_Y,Z (y, z)} converges weakly to a bivariate zero-mean Gaussian process with covariance function Σ, specified as ∇_θ Ŝ_Y,Z (y, z, θ)^T $I_{\text{c}}^{-1}$ ∇_θ Ŝ_Y,Z (y′, z′, θ) + σ². It is natural to estimate Σ by Σ̂ =∇_θ Ŝ_Y,Z (y, z, θ̂)^T $I_{\text{c}}^{-1}$ ∇_θ Ŝ_Y,Z (y′, z′, θ̂) + σ̂². The consistency of Ŝ_Y,Z (y, z, θ̂), Ŝ_Y,Z (y′, z′, θ̂), Î_c and σ̂² implies that Σ̂ is a consistent estimator of Σ.

Supplementary Material

Supplementary material available at Biometrika online includes joint survival function estimation under stationarity and the corresponding simulation, a description of Archimedean copula models used in simulation, supplementary figures and table for the analysis in § 5, and detailed proofs of Theorems 2 and 3.