Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2013 May 30;3:1898. doi: 10.1038/srep01898

Information dissipation as an early-warning signal for the Lehman Brothers collapse in financial time series

Rick Quax 1, Drona Kandhai 1,2, Peter M A Sloot 1,3,4,a
PMCID: PMC3667490  PMID: 23719567

Abstract

In financial markets, participants locally optimize their profit which can result in a globally unstable state leading to a catastrophic change. The largest crash in the past decades is the bankruptcy of Lehman Brothers which was followed by a trust-based crisis between banks due to high-risk trading in complex products. We introduce information dissipation length (IDL) as a leading indicator of global instability of dynamical systems based on the transmission of Shannon information, and apply it to the time series of USD and EUR interest rate swaps (IRS). We find in both markets that the IDL steadily increases toward the bankruptcy, then peaks at the time of bankruptcy, and decreases afterwards. Previously introduced indicators such as ‘critical slowing down' do not provide a clear leading indicator. Our results suggest that the IDL may be used as an early-warning signal for critical transitions even in the absence of a predictive model.

A system consisting of coupled units can self-organize into a critical transition if a majority of the units suddenly and synchronously change state1,2,3. For example, in sociology, the actions of a few can induce a collective tipping point of behavior of the larger society4,5,6,7,8,9,10,11. Epileptic seizures are characterized by the onset of synchronous activity of a large neuronal network12,13,14,15,16,17,18. In financial markets the participants slowly build up an ever densifying web of mutual dependencies through investments and transactions to hedge risks, which can create unstable ‘bubbles'19,20,21,22,23. Detecting the onset of critical transitions in these complex dynamical systems is difficult because we lack the mechanistic insight to create models with predictive power24,25,26,27.

A characteristic of self-organized critical transitions is that the network of interactions among the units leads to long-range correlations in the system, or in other words, every unit ‘feels' the state of every other unit to some extent.

Here we measure this self-organized correlation in terms of the transmission of information among units. Shannon's information theory quantifies the number of bits that is needed to determine the state of a unit (i.e. Shannon entropy), as well as the fraction of these bits that is contributed by the state of any other unit (mutual information)28. We introduce the information dissipation length (IDL) as a measure of the characteristic distance of the decay of mutual information in the system. As such it can be used to detect the onset of long-range correlations in the system that precede critical transitions.

We apply the IDL indicator to unique time series of interbank risk trading in the USD and EUR currency and find evidence that it indeed detects the onset of instability of the markets several months before the Lehman Brothers bankruptcy. In contrast, we find that the critical slowing down indicator and other early warning signals used in the literature do not provide a clear warning. Our results suggest that the Lehman Brothers bankruptcy was a self-organized critical transition and that the IDL could have served as a leading indicator.

As a system's unit influences the state of another unit it transfers information28 about its own state to the other unit29,30,31,32,33,34. For instance, each particle in an isolated gas ‘knows' something about the momenta of neighboring particles due to the transfer of momentum during collisions. That is, the momentum of a particle is the result of its recent collisions with other particles. This information is in turn transferred to other particles in subsequent collisions, and so on. At each interaction the information is only partially transferred due to stochasticity and ambiguity29,31,35,36, so information about the state of one particle can only reach a certain distance (IDL) before it is lost.

The IDL measures to what extent the state of one unit influences the states of other units. As the state of one unit depends on another unit, a fraction of the bits of information that determine its state becomes a reflection of the other unit's state. This creates a certain amount of mutual information among them. A unit can then influence other units in turn, propagating these ‘transmitted' bits further into the network. This generates a decaying amount of mutual information between distant units that eventually settles at a constant. The higher the IDL of a system, the larger the distance over which a unit can influence other units, and the better the units are capable of a collective transition to a different state. Because of this we can measure the IDL of systems of coupled units and detect their propensity to a catastrophic change, even in the absence of a predictive model. See Sections S1 and S2 in the SI for a more detailed explanation and how it differs from existing indicators.

We measure the IDL of risk-trading among banks by calculating the IDL of the returns of interest-rate swaps (IRS) across maturities. The rationale is that the dependencies between banks are expected to be reflected in the dependencies of swap rates across maturities, as we explain next. Each financial institute is typically exposed to a significant amount of risk of changes in short-term and long-term interest rates, and buys corresponding IRSs to cancel out or ‘hedge' these risks. If an institute has difficulties in financing its short-term interest rate hedges and consequently has a higher chance of default, then each long-term IRS that it holds becomes less valuable (and vice versa). The corresponding buyers of these long-term (short-term) IRSs must buy additional long-term (short-term) IRSs on the market to compensate, increasing the demand. An increased dependence between institutes can therefore lead to an increased dependence of the prices of IRSs of different maturities. A significant increase of this approximated IDL may indicate the onset of a critical event. We consider it to be a warning if a threshold of two times the 3-year standard deviation above the mean is exceeded. This generates clusters of warnings about once in three years, which is a tradeoff between medium (twin) crises and the most severe (triple) crises; see Section S7 for the derivation.

The IDL of the IRS market at time t is estimated as follows. The swap prices form a one-dimensional system because, for instance, a 3-year IRS logically consists of a 2-year IRS and a prediction of the value of a 1-year IRS that starts two years in prospect. That is, that the price of the ith maturity depends on the price of a maturity i − 1 and a (stochastic) prediction component. We therefore assume that the stochastic interaction between the IRS prices of maturities i and i + 1 is equal for all i37, which leads to an exponential decay of information across the maturities (see Section S1 in the SI). The IDL at time t is thus calculated as the halftime of the mutual information between maturity 1 and i for increasing i. We estimate the mutual information between two maturities at time t using the 300 most recent return values, using the equiprobable binning procedure; see Methods for details.

The market of interest rate swaps (IRS) is the largest financial derivatives market today38 with more than 504 thousand billion USD notional amounts outstanding, or almost 80% of the total market. The buyer of an IRS pays a fixed premium to the seller, while the seller pays the variable LIBOR or EURIBOR interest rate to the buyer. In effect, the seller insures the buyer against unexpected fluctuations in LIBOR or EURIBOR in return for the expected net value of the IRS. Swap prices can significantly influence the funding rates of financial institutions and therefore play a key role in the profit-and-loss and risk of financial institutions such as banks, insurance companies and pension funds.

Our data is provided by the ING Bank and consists of the daily prices of IRSs in the USD and EUR currency for the maturities of 1 (USD only), 2, …, 10, 12, 15, 20, 25, and 30 years. The data spans more than twelve years: the EUR data from 12/01/1998 to 12/08/2011 and the USD data from 04/29/1999 to 06/06/2011. The prices of IRSs are based on LIBOR and EURIBOR, respectively, which are the average interbank interest rates at which banks lend money to each other. Our data correspond to IRSs with yearly fixed payments in exchange of quarterly variable payments because these swaps are the most liquidly traded across a wide range of maturities. The data is made available in the SI online.

Results

Evidence of IDL as an indicator of instability

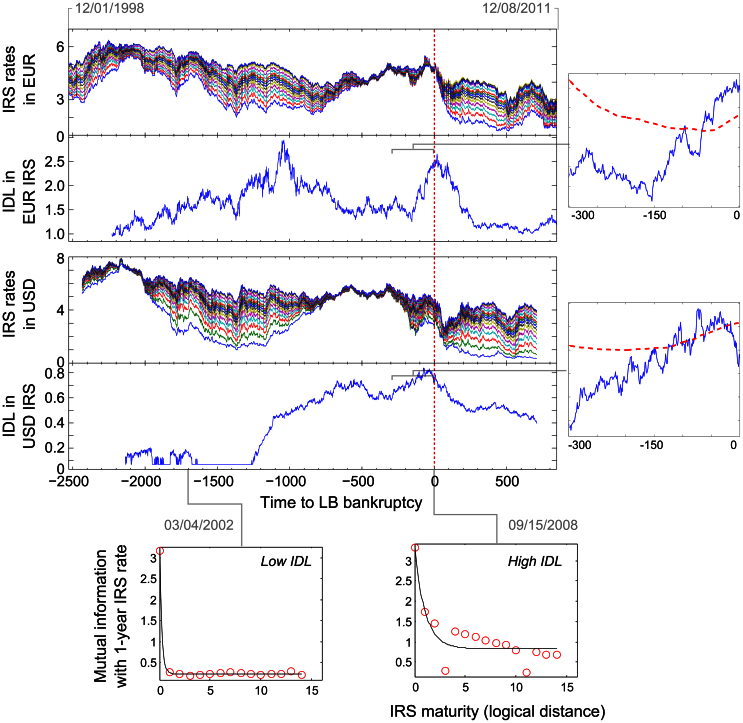
In Figure 1 we show the original time series of IRS rates with the corresponding values of IDL. In both markets, the day of the Lehman Brothers bankruptcy is preceded by a significant increase of IDL and a decrease afterwards. This is consistent with our hypothesis that a self-organized transition requires that information about the state of a unit can travel a large distance through the system. The decrease of IDL following the bankruptcy is consistent with interpreting a critical phenomenon as the release of built-up stress1, similar to the way that an earth quake releases the built-up tension between tectonic plates. These two observations together suggest that the Lehman Brothers bankruptcy was a self-organized critical transition and that the IDL indicator is capable of detecting it. We verify experimentally that the IDL indicator indeed detects serial correlations between maturities and is not prone to false alarms by computing the IDL for randomly generated time series with a known period of serially correlated time series; see Section S6 in the SI for details.

Figure 1. The original time series of the IRS rates for different maturities and the corresponding IDL indicators for the EUR and USD markets.

Figure 1

Open in a new tab

The IDL at time t is calculated using the 300 most recent returns up to time t. Inset: the IDL indicator and a warning threshold during the 300 trade days preceding the LB bankruptcy. We set the warning threshold at two times standard deviations above the mean IDL of a sliding window of 750 trade days. Bottom: the mutual information between the rates of the 1-year maturity IRS and all other maturities (red circles) at two different trade days. The fitted exponential decay is used to estimate the IDL of the IRS rates across maturities for that specific trade day.

Although in both markets the IDL indicator peaks near the Lehman Brothers bankruptcy, the two curves differ significantly in shape. Finding the underlying causes is highly speculative, nevertheless it is important to evaluate the plausibility that the IDL detected an increased instability of the financial market. Next we discuss the behavior of the IDL curves and their potential relations with significant economic phenomena.

In the USD market, a long-term build-up of stress starts in the beginning of 2004 and continues for more than four years, eventually peaking shortly before the bankruptcy. This is consistent with the common belief that markets create ‘bubbles'20, which grow slowly over time and may ‘burst', leading to sudden regime shifts triggered by a catalyzing event. In the U.S. financial market, the performance of subprime mortgage loans is considered a major cause of the current global financial crisis39,40. The subprime share of the mortgage market increased from about 8% in 2001 to 20% in 2006. Demyanyk and van Hemert40 show in this context that the quality of loans deteriorated for six consecutive years before the crisis, and suggest that the market followed a classic lending ‘boom-bust' scenario which was masked by a prevailing high house price appreciation. This latter phenomenon, termed the ‘house price bubble'41, went hand-in-hand with the surge of subprime mortgage loans. The U.S. season-adjusted house-price index had been growing at an increasing rate from 1991 to 200642, which stimulated the sale of low-rate mortgages based on the premise that the house prices would keep growing. Around the year-end of 2005, however, the growth rate stopped increasing and in March 2006 the growth rate had its largest-ever drop to below zero, after which the prices continued to decrease. As a result, home owners were less capable of financing the loan and the underlying security decreased in value, which further deteriorated the quality of the loans and destabilized the lending banks.

The EUR market, on the other hand, appears to have played a more submissive role. The IDL indicator rises distinctly for about half a year before the Lehman Brothers bankruptcy and diminishes in about the same amount of time. One plausible explanation is that the ever-growing instability in the USD market at some point ‘infected' the EUR market, i.e., the EUR market may have become increasingly unstable as a consequence of the high instability of the USD market. This explanation is consistent with the observation that the financial crisis initiated in the U.S., whereas Europe responded to the U.S. crisis rather than initiating its own. The ‘infection' occurs due to the intimate relation between the EUR and USD markets.

Evidence of IDL as an early warning signal

We find that the IDL indicator could have served as an early-warning signal for the Lehman Brothers bankruptcy. We define the earliest time at which a warning could be given as the point where the IDL increases beyond a predefined warning threshold (see the inset of Figure 1). In the USD market data we find that the earliest clear warning precedes the bankruptcy by 118 trade days and lasts for 8 days, followed immediately by a warning that lasts for 7 days. In the EUR market the warning is much more pronounced, but also more concentrated near the bankruptcy. A clear warning starts 67 trade days in advance and lasts for 117 trade days.

Comparison to critical slowing down and other indicators

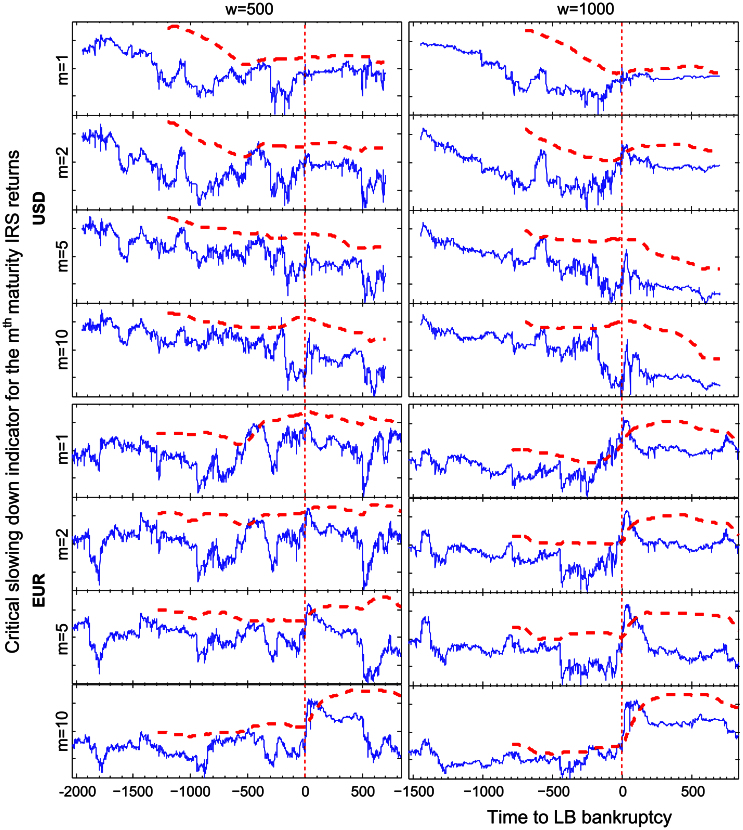
The most well-known leading indicator of critical transitions is the increase of the autocorrelation of fluctuations of the system state2,43,44,45,46. The intuition is that if an unstable system is perturbed it returns more slowly to its natural state compared to a stable system. The more stable the system, the stronger the tendency to return to its natural state, so the more quickly it responds to transient perturbations.

We compute the first-order autoregression coefficient of the fluctuations of each maturity IRS time series for all possible window sizes and show a representative set of results in Figure 2; see the Methods section for details. We find indeed signs of critical slowing down around the Lehman Brothers bankruptcy for certain window sizes. However, it is difficult to find parameter values that provide a sustained advance warning, that is, where the indicator crosses the warning threshold for more than a few days before the bankruptcy. Only in the EUR data for the 1-year maturity and a sliding window size of around 1000 trade days we find a significant early warning, which disappears for a sliding window larger than 1250 trade days (see Section S5.1 in the SI).

Figure 2. The solid blue line is the coefficient of the first-order autoregression of the detrended time series, which is a measure of critical slowing down.

Figure 2

Open in a new tab

The dashed red line is the warning threshold of two standard deviations above the mean of a sliding window of 750 trade days, as in Figure 1. The coefficient is computed of a sliding window of 500 (left) and 1000 (right) trade days which is detrended using a Gaussian smoothing kernel with a standard deviation of 5 trade days. We show the critical slowing down indicator for the first, second, fifth, and tenth maturity in the USD and EUR markets.

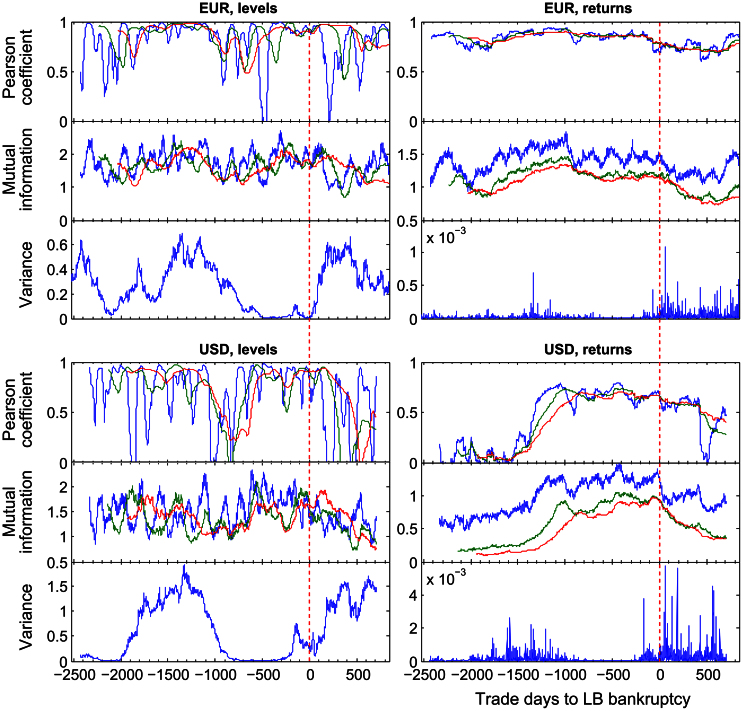
Another type of generic leading indicators used in the literature are the spatial correlation and spatial variance of the signals of the units of a system3,47,48,49,50,51,52. See Figure 3. In our data, the dimension of maturities can be taken as the ‘spatial' dimension. The traditional correlation function used is the linear Pearson correlation, shown in the top panels of Figure 3. We also compute the correlations using the mutual information function, shown in the middle panels, since this function can capture non-linear relationships as well. In finance, correlations are often calculated using the relative differences (returns) of time series instead of the absolute values (19), so we repeat the calculations on the returns shown in the right half of Figure 3.

Figure 3. Alternative leading indicators for the IRS time series in both markets, in levels and in returns.

Figure 3

Open in a new tab

We computed the average cross-maturity Pearson correlations for sliding window sizes of 100 days (blue line), 300 days (green line), and 500 days (red line) between the 1-year IRS and all other maturities. The variance at time t is computed of the levels (returns) of all maturities of the single trade day t. Time point 0 on the horizontal axis corresponds to the day of the Lehman Brothers bankruptcy.

We find that in our time series these indicators do not show a distinctive change of behavior around the time of the bankruptcy in both markets. One possible explanation is that all IRS prices correlate strongly with external financial indices (such as the home-price index), which may dominate the observed correlations in the IRS prices across the maturities. In this scenario the IDL is still capable to be a leading indicator because it ignores the correlation that is shared among all IRS prices. That is, the information in the IRS prices of different maturities decays as a + b·(ft)1−i where a is the information (or correlation) shared among all IRS prices, and the estimated rate of decay ft is independent of a.

More traditional indicators used for financial time series are the magnitude or spread of interest rates53. However, Figure 1 as well as the variances in the level data in Figure 3 show that neither measure provide a clear warning: a high (USD) and low-spread period (EUR) occurred more than a year before the bankruptcy and was returning to normal at the time of the bankruptcy.

Lastly, the same swap with a different variable payment frequency (e.g., monthly, quarterly, semi-annually) were quoted at the same price in the market before 2007. During the recent crisis, a significant price difference across frequencies emerged54. Although this has a major impact on the valuation and risk management of derivatives, this so-called ‘basis' does not provide a clear early warning (see Section S5.2 in the SI).

Discussion

From an optimistic viewpoint, the IDL indicator may improve the stability of the financial derivatives market. Our observation that previously introduced leading indicators did not provide an early warning for the Lehman Brothers bankruptcy, and the crisis that followed, is consistent with the hypothesis that leading indicators lose their predictive power in financial markets55. A plausible explanation is that an increase of a known leading indicator could be directly followed by preemptive policy by central banks56, a change of behavior of the market participants, or both, until the indicator returns to its normal level. This would imply that the financial system is capable of avoiding the type of critical transitions for which it has leading indicators: it changes behavior as it approaches such a transition, while it remains vulnerable to other critical transitions for which it has no indicators. The fact that the IDL indicator provides an early warning signal suggests that it is capable of detecting a type of transition for which the financial system had no indicators at the time. Therefore, from this viewpoint the IDL indicator potentially makes the financial system more resilient because it improves its capability of avoiding catastrophic changes.

From a pessimistic viewpoint, on the other hand, the IDL indicator may actually decrease the stability of the financial system. Upon an increase of IDL, participants may respond in a manner that increases the IDL further, reinforcing the participants' response, and so on, propelling the financial system towards a crisis. This is a general dichotomy for all early warning indicators in finance57. In the absence of a mechanistic model of the financial derivatives market it is difficult to predict the effect of a warning indicator.

Our results are a marked step forward in the analysis of complex dynamical systems. The IDL is a generic indicator that may apply to any self-organizing system of coupled units. For many such systems we lack the mechanistic insight necessary to build models with sufficient predictive power. Remarkably, we find evidence that the percolation of information can provide a tell-tale of self-organized critical phenomena even in the absence of a descriptive model. Although we study the financial derivatives market here, it seems reasonable to expect that it is true for a wide range of systems such as the forming of opinions in social networks5,6,7,8,9,10,11, the extinction of species in ecosystems3,44,45,49,58,59,60,61, phase transitions and spontaneous magnetization in physics47,62,63,64, robustness in biological systems65,66, and self-organization of populations of cells67 and even software components68.

Methods

Calculating the IDL in the IRS time series

Because the IRS price levels are not stationary within the sliding window sizes we use relative differences (returns) instead. Let 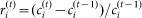Inline graphic denote the return of an IRS with maturity i = 1,…,15 at time t, where 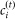Inline graphic denotes the corresponding price level. We fit the exponential decay 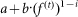Inline graphic to the measured Shannon information 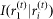Inline graphic as function of i, where a is the mutual information that all IRS rates have in common, b is the normalizing factor 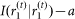Inline graphic, and f(t) is the rate of decay of the mutual information between the IRS rates across maturities. We define the IDL as the corresponding halftime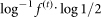Inline graphic. 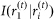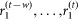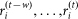The mutual information Inline graphic is estimated by constructing an adaptive69 contingency table of the two vectors Inline graphic and Inline graphic, which are the 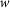Inline graphic most recently observed returns in the market at time t. To construct this table we divide the range of values of each vector into h bins of variable size such that each bin contains about the same number of samples. Two observed pairs of returns are considered equal if they fall into the same bin. 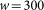Our results are robust against choosing the parameters Inline graphic and h; see Section S4 in the SI for more details. The results in Figure 1 were produced with a window of Inline graphic trade days and binning the return values into h = 10 bins.

Calculating the first-order autoregression coefficient of fluctuations

Calculating this coefficient of a given time series requires two parameters: the standard deviation of the Gaussian smoothing kernel g, which de-trends the signal, and the number of most recent IRS prices 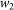Inline graphic which are used to compute the autoregression. The procedure is identical for each maturity. First we use the smoothing kernel to compute a running weighted average of the time series, where each IRS price level becomes the weighted average of its neighbors. Then we subtract it from the original time series to obtain the de-trended signal, i.e., the short-term fluctuations. Of these fluctuations we calculate the first-order autoregression coefficient at time t using the 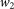Inline graphic preceding prices. The autoregressive model used is the Yule-Walker model70. The results in Figure 2 were produced with a kernel of size g = 5 and a sliding window of 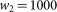Inline graphic price levels. This procedure can be calculated for the price levels regardless of non-stationarity since it contains a de-trending step. 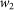See Sections S5.1 and S5.4 in the SI for more details as well as results for different values of g and Inline graphic.

Calculating the spatial correlation and variance

At each time point we calculate the spatial correlation coefficient at time t as Inline graphic, using the preceding 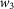Inline graphic IRS rates of maturity 1 and maturities i, i = 1,2,…,15. Here, Fcorr is either the standard Pearson correlation for the upper plots in Figure 3, or the mutual information function for the middle plots; 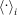Inline graphic denotes the arithmetic average of the correlation values for the different maturities, and 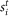Inline graphic denotes the price of an IRS of maturity i at time t. The results in Figure 3 were produced using sliding windows of sizes 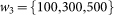Inline graphic. The spatial variance is computed at each time point t as 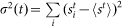Inline graphic. 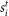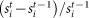We repeat the calculations after replacing each original level Inline graphic by its relative difference (returns) Inline graphic.

Author Contributions

R.Q. and P.M.A.S. conceived the project; D.K. gathered the data, R.Q. analyzed the data; R.Q., D.K. and P.M.A.S. wrote the paper. The opinions expressed in this work are solely those of the authors and do not represent in any way those of their current and past employers.

Supplementary Material

Supplementary Information

Supporting INformation on Information dissipation as an early-warning signal for the Lehman Brothers collapse in financial time series

srep01898-s1.pdf (2.9MB, pdf)

Acknowledgments

We thank Prof. Cars H. Hommes for his insightful comments. We acknowledge the financial support of the Future and Emerging Technologies (FET) programme within the Seventh Framework Programme (FP7) for Research of the European Commission, under the FET-Proactive grant agreement TOPDRIM, number FP7-ICT-318121, as well as under the FET-Open grant agreement DynaNets, number FP7-ICT-233847. Peter Sloot acknowledges the NTU Complexity Program in Singapore as well as the Leading Scientist Program' of the Government of the Russian Federation, under contract 11.G34.31.0019.

References

  1. Bak P. How nature works: the science of self-organized criticality. (Copernicus Press, 1996). [Google Scholar]
  2. Scheffer M. et al. Early-warning signals for critical transitions. Nature 461, 53–59 (2009). [DOI] [PubMed] [Google Scholar]
  3. Dakos V., van Nes E., Donangelo R., Fort H. & Scheffer M. Spatial correlation as leading indicator of catastrophic shifts. Theoretical Ecology 3, 163–174 (2010). [Google Scholar]
  4. Grodzins M. The metropolitan area as a racial problem. (University of Pittsburgh Press, 1958). [Google Scholar]
  5. Granovetter M. Threshold Models of Collective Behavior. American Journal of Sociology 83, 1420–1443 (1978). [Google Scholar]
  6. Klemm K., Eguiluz V. M., Toral R. & Miguel M. S. Nonequilibrium transitions in complex networks: a model of social interaction. Phys. Rev. E 67, 026120 (2003). [DOI] [PubMed] [Google Scholar]
  7. Holme P. & Newman M. E. J. Nonequilibrium phase transition in the coevolution of networks and opinions. Phys. Rev. E 74, 056108 (2006). [DOI] [PubMed] [Google Scholar]
  8. Castellano C., Fortunato S. & Loreto V. Statistical physics of social dynamics. Rev. Mod. Phys. 81, 591–646 (2009). [Google Scholar]
  9. Barthélemy M., Nadal J.-P. & Berestycki H. Disentangling collective trends from local dynamics. Proc. Natl. Acad. Sci. U.S.A. 107, 7629–7634 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Xie J. et al. Social consensus through the influence of committed minorities. Phys. Rev. E 84, 011130 (2011). [DOI] [PubMed] [Google Scholar]
  11. Durrett R. et al. Graph fission in an evolving voter model. Proc. Natl. Acad. Sci. U.S.A. (2012). 10.1073/pnas.1200709109 [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Mormann F., Andrzejak R. G., Elger C. E. & Lehnertz K. Seizure prediction: the long and winding road. Brain 130, 314–333 (2007). [DOI] [PubMed] [Google Scholar]
  13. Jefferys J. G. R., Curtis M. de & Avoli, M. Neuronal network synchronization and limbic seizures. Epilepsia 51, 19 (2010). [Google Scholar]
  14. Cymerblit-Sabba A. & Schiller Y. Network Dynamics during Development of Pharmacologically Induced Epileptic Seizures in Rats In Vivo. J. Neurosci 30, 1619–1630 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Koehling R. & Staley K. Network mechanisms for fast ripple activity in epileptic tissue. Epilepsy Res. 97, 318–323 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Meisel C. & Kuehn C. Scaling Effects and Spatio-Temporal Multilevel Dynamics in Epileptic Seizures. PLoS ONE 7, e30371 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Cymerblit-Sabba A. & Schiller Y. Development of hypersynchrony in the cortical network during chemoconvulsant-induced epileptic seizures in vivo. J. Neurophysiol 107, 1718–1730 (2012). [DOI] [PubMed] [Google Scholar]
  18. Litt B. & Echauz J. Prediction of epileptic seizures. Lancet Neurol. 1, 22–30 (2002). [DOI] [PubMed] [Google Scholar]
  19. Johnson N. F., Jefferies P. & Hui P. M. Financial Market Complexity. (Oxford University Press, 2003). [Google Scholar]
  20. Sornette D. Why Stock Markets Crash: Critical Events in Complex Financial Systems. (Princeton University Press, 2004). [Google Scholar]
  21. Kirou A., Ruszczycki B., Walser M. & Johnson N. Computational Modeling of Collective Human Behavior: The Example of Financial Markets. in Computational Science (Bubak, M., van Albada, G.,Dongarra, J.& Sloot, P.) 5101, 33–41 (Springer Berlin/Heidelberg, 2008). [Google Scholar]
  22. May R. M. & Arinaminpathy N. Systemic risk: the dynamics of model banking systems. J. R. Soc. Interface 7, 823–838 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Haldane A. G. & May R. M. Systemic risk in banking ecosystems. Nature 469, 351–355 (2011). [DOI] [PubMed] [Google Scholar]
  24. Sornette D. Predictability of catastrophic events: Material rupture, earthquakes, turbulence, financial crashes, and human birth. Proc. Natl. Acad. Sci. U.S.A. 99, 2522–2529 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Turcotte D. L. & Rundle J. B. Self-organized complexity in the physical, biological, and social sciences. Proc. Natl. Acad. Sci. U.S.A. 99, 2463–2465 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Hallerberg S. Predictability of extreme events in time series. (2008). [Google Scholar]
  27. Su R.-Q., Ni X., Wang W.-X. & Lai Y.-C. Forecasting synchronizability of complex networks from data. Phys. Rev. E 85, 056220 (2012). [DOI] [PubMed] [Google Scholar]
  28. Cover T. M. & Thomas J. A. Elements of information theory. 6, (Wiley-Interscience, 1991). [Google Scholar]
  29. Crutchfield J. P. & Feldman D. P. Statistical complexity of simple one-dimensional spin systems. Phys. Rev. E 55, R1239–R1242 (1997). [Google Scholar]
  30. Wheeler J. A. in (Hey, A. J. G.) 309–336 (Perseus Books, 1999). [Google Scholar]
  31. Crutchfield J. P., Ellison C. J. & Mahoney J. R. Time's Barbed Arrow: Irreversibility, Crypticity, and Stored Information. Phys. Rev. Lett. 103, 094101 (2009). [DOI] [PubMed] [Google Scholar]
  32. Feldman D. P., McTague C. S. & Crutchfield J. P. The organization of intrinsic computation: Complexity-entropy diagrams and the diversity of natural information processing. Chaos 18, 043106 (2008). [DOI] [PubMed] [Google Scholar]
  33. Lloyd S. Programming the Universe: A Quantum Computer Scientist Takes on the Cosmos. (Knopf, 2006). [Google Scholar]
  34. Wiesner K. Nature computes: Information processing in quantum dynamical systems. Chaos 20, 037114 (2010). [DOI] [PubMed] [Google Scholar]
  35. Ellison C., Mahoney J. & Crutchfield J. Prediction, Retrodiction, and the Amount of Information Stored in the Present. Journal of Statistical Physics 136, 1005–1034 (2009). [Google Scholar]
  36. James R. G., Ellison C. J. & Crutchfield J. P. Anatomy of a Bit: Information in a Time Series Observation. Chaos 21, 15 (2011). [DOI] [PubMed] [Google Scholar]
  37. Riccardo Rebonato. Volatility and Correlation: The Perfect Hedger and the Fox. (Wiley, 2004). [Google Scholar]
  38. Semiannual OTC derivatives statistics at end-December 2011. (Bank for International Settlements, 2012). at <http://www.bis.org/statistics/derstats.htm> accessed April 29, 2013. [Google Scholar]
  39. Hellwig M. F. Systemic Risk in the Financial Sector: An Analysis of the Subprime-Mortgage Financial Crisis. De Economist 157, 129–207 (2009). [Google Scholar]
  40. Demyanyk Y. & Van Hemert O. Understanding the Subprime Mortgage Crisis. Review of Financial Studies 24, 1848–1880 (2011). [Google Scholar]
  41. Clark S. P. & Coggin T. D. Was there a U.S. house price bubble? An econometric analysis using national and regional panel data. Q Rev Econ Finance 51, 189–200 (2011). [Google Scholar]
  42. Monthly House Price Indexes for Census Divisions and U. S. January 1991 to Latest. (Federal Housing Finance Agency, 2012). at <http://www.fhfa.gov>, accessed April 29, 2013. [Google Scholar]
  43. Wissel C. A universal law of the characteristic return time near thresholds. Oecologia 65, 101–107 (1984). [DOI] [PubMed] [Google Scholar]
  44. Dakos V. et al. Slowing down as an early warning signal for abrupt climate change. Proc. Natl. Acad. Sci. U.S.A. 105, 14308–14312 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Carpenter S. R. et al. Early Warnings of Regime Shifts: A Whole-Ecosystem Experiment. Science 332, 1079–1082 (2011). [DOI] [PubMed] [Google Scholar]
  46. Lenton T. M., Livina V. N., Dakos V., van Nes E. H. & Scheffer M. Early warning of climate tipping points from critical slowing down: comparing methods to improve robustness. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 370, 1185 –1204 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Bloch I., Hansch T. W. & Esslinger T. Measurement of the spatial coherence of a trapped Bose gas at the phase transition. Nature 403, 166–170 (2000). [DOI] [PubMed] [Google Scholar]
  48. Guttal V. & Jayaprakash C. Spatial variance and spatial skewness: leading indicators of regime shifts in spatial ecological systems. Theoretical Ecology 2, 3–12 (2009). [Google Scholar]
  49. Drake J. M. & Griffen B. D. Early warning signals of extinction in deteriorating environments. Nature 467, 456–459 (2010). [DOI] [PubMed] [Google Scholar]
  50. Donangelo R., Fort H., Dakos V., Scheffer M. & van Nes E. H. Early warnings for catastrophic shifts in ecosystems: comparison between spatial and temporal indicators. Int. J. Bifurcation Chaos 20, 315–321 (2010). [Google Scholar]
  51. Bailey R. M. Spatial and temporal signatures of fragility and threshold proximity in modelled semi-arid vegetation. Proceedings of the Royal Society B: Biological Sciences 278, 1064 –1071 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Dakos V., Kéfi S., Rietkerk M., Nes E. H. van & Scheffer, M. Slowing Down in Spatially Patterned Ecosystems at the Brink of Collapse. The American Naturalist 177, E153–E166 (2011). [DOI] [PubMed] [Google Scholar]
  53. Estrella A. & Mishkin F. S. Predicting U.S. Recessions: Financial Variables as Leading Indicators. Rev. Econ. Stat. 80, 45–61 (1998). [Google Scholar]
  54. Whittall C. The price is wrong. Risk (2010). at <http://www.risk.net/risk-magazine/feature/1594823/the-price-wrong>, accessed April 29, 2013. [Google Scholar]
  55. MacKenzie D. An Engine, Not a Camera. (MIT Press, 2008). [Google Scholar]
  56. Davis E. P. & Karim D. Comparing early warning systems for banking crises. Journal of Financial Stability 4, 89–120 (2008). [Google Scholar]
  57. Morris, Carmen & Graciela Assessing Financial Vulnerability: An Early Warning System for Emerging Markets. (Institute for International Economics, 2000). [Google Scholar]
  58. Biggs R., Carpenter S. R. & Brock W. A. Turning back from the brink: Detecting an impending regime shift in time to avert it. Proc. Natl. Acad. Sci. U.S.A. 106, 826–831 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Chen L., Liu R., Liu Z.-P., Li M. & Aihara K. Detecting early-warning signals for sudden deterioration of complex diseases by dynamical network biomarkers. Sci. Rep. 2 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Dai L., Vorselen D., Korolev K. S. & Gore J. Generic Indicators for Loss of Resilience Before a Tipping Point Leading to Population Collapse. Science 336, 1175–1177 (2012). [DOI] [PubMed] [Google Scholar]
  61. Barnosky A. D. et al. Approaching a state shift in Earth's biosphere. Nature 486, 52–58 (2012). [DOI] [PubMed] [Google Scholar]
  62. Sadler L. E., Higbie J. M., Leslie S. R., Vengalattore M. & Stamper-Kurn D. M. Spontaneous symmetry breaking in a quenched ferromagnetic spinor Bose-Einstein condensate. Nature 443, 312–315 (2006). [DOI] [PubMed] [Google Scholar]
  63. Xu S.-Y. et al. Topological Phase Transition and Texture Inversion in a Tunable Topological Insulator. Science 332, 560–564 (2011). [DOI] [PubMed] [Google Scholar]
  64. Gong M., Tewari S. & Zhang C. BCS-BEC Crossover and Topological Phase Transition in 3D Spin-Orbit Coupled Degenerate Fermi Gases. Phys. Rev. Lett. 107, 195303 (2011). [DOI] [PubMed] [Google Scholar]
  65. Kitano H. Biological robustness. Nat Rev Genet 5, 826–837 (2004). [DOI] [PubMed] [Google Scholar]
  66. MacNeil L. T. & Walhout A. J. M. Gene regulatory networks and the role of robustness and stochasticity in the control of gene expression. Genome Research 21, 645–657 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  67. Gregor T., Fujimoto K., Masaki N. & Sawai S. The Onset of Collective Behavior in Social Amoebae. Science 328, 1021–1025 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  68. Sloot P. M. A., Overeinder B. J. & Schoneveld A. Self-organized criticality in simulated correlated systems. Computer Physics Communications 142, 76–81 (2001). [Google Scholar]
  69. Cellucci C. J., Albano A. M. & Rapp P. E. Statistical validation of mutual information calculations: Comparison of alternative numerical algorithms. Phys. Rev. E 71, 066208 (2005). [DOI] [PubMed] [Google Scholar]
  70. Monson H. Statistical digital signal processing and modeling. (John Wiley & Sons, 1996). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supporting INformation on Information dissipation as an early-warning signal for the Lehman Brothers collapse in financial time series

srep01898-s1.pdf (2.9MB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES