Skip to main content
PMC home page
Bioinformatics logoLink to Bioinformatics
. 2013 Jun 19;29(13):i335–i343. doi: 10.1093/bioinformatics/btt220

A graph kernel approach for alignment-free domain–peptide interaction prediction with an application to human SH3 domains

Kousik Kundu 1,2,†, Fabrizio Costa 1,†, Rolf Backofen 1,2,3,4,*
PMCID: PMC3694653  PMID: 23813002

Abstract

Motivation: State-of-the-art experimental data for determining binding specificities of peptide recognition modules (PRMs) is obtained by high-throughput approaches like peptide arrays. Most prediction tools applicable to this kind of data are based on an initial multiple alignment of the peptide ligands. Building an initial alignment can be error-prone, especially in the case of the proline-rich peptides bound by the SH3 domains.

Results: Here, we present a machine-learning approach based on an efficient graph-kernel technique to predict the specificity of a large set of 70 human SH3 domains, which are an important class of PRMs. The graph-kernel strategy allows us to (i) integrate several types of physico-chemical information for each amino acid, (ii) consider high-order correlations between these features and (iii) eliminate the need for an initial peptide alignment. We build specialized models for each human SH3 domain and achieve competitive predictive performance of 0.73 area under precision-recall curve, compared with 0.27 area under precision-recall curve for state-of-the-art methods based on position weight matrices.

We show that better models can be obtained when we use information on the noninteracting peptides (negative examples), which is currently not used by the state-of-the art approaches based on position weight matrices. To this end, we analyze two strategies to identify subsets of high confidence negative data.

The techniques introduced here are more general and hence can also be used for any other protein domains, which interact with short peptides (i.e. other PRMs).

Availability: The program with the predictive models can be found at http://www.bioinf.uni-freiburg.de/Software/SH3PepInt/SH3PepInt.tar.gz. We also provide a genome-wide prediction for all 70 human SH3 domains, which can be found under http://www.bioinf.uni-freiburg.de/Software/SH3PepInt/Genome-Wide-Predictions.tar.gz.

Contact: backofen@informatik.uni-freiburg.de

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

SH3 domains are an important class of peptide recognition module and probably the most widespread protein domain found in protein databases (Cesareni et al., 2002). Thus, SH3 domains are involved in many cellular processes such as signaling, cell-communication, growth and differentiation. Furthermore, the SH3 complexity corresponds with the complexity of the genome (Carducci et al., 2012). These domains specifically recognize short linear proline-rich peptide sequences (Lim et al., 1994; Mayer, 2001; Musacchio et al., 1992). SH3 domains have a conserved 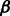Inline graphic-barrel fold, which is formed by five or six 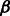Inline graphic strands arranged in two anti-parallel 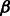Inline graphic sheets. SH3 domains are ∼60 amino acids in length and mainly found in intra-cellular proteins.

Approximately 300 SH3 domains are known in the human proteome (Karkkainen et al., 2006). As 25% of human proteins contain proline-rich regions (Li, 2005), and SH3 domains recognize proline-rich peptides, it is an open challenge to understand how the hundreds of SH3 domains achieve a high specificity in selecting their physiological partners to regulate specific biological functions.

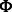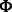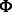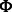The canonical proline-rich peptide motifs recognized by most of the human SH3 domains have a PxxP core and are classified in two major groups: class I and class II. The consensus sequences for these two groups are denoted as +xInline graphicPxInline graphicP (class I) and Inline graphicPxInline graphicPx+ (class II), where x represents any naturally occurring amino acid, 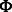Inline graphic represents a hydrophobic amino acid and + represents as a positively charged amino acid (normally arginine and lysine). Structural studies of the SH3–peptide complexes with class I and class II motif suggest that these two types of peptide ligands bind to an SH3 domains in opposite orientations (Lim et al., 1994; Yu et al., 1994). Previous studies reveled that the positively charged residues in the peptide sequence, such as arginine and lysine, play an important role in the binding with the respective SH3 domain (Feng et al., 1994, 1995). Based on the characteristics of the binding site, the SH3 domains prefer either one or the other pepitde motif. Peptide motifs can be further classified into subgroups depending on the tolerance for the substitution of the lysine residue with the arginine residue (Carducci et al., 2012).

Although most human SH3 domains bind with class I and/or class II motifs, a subset of SH3 domains have the ability to recognize noncanonical or atypical peptide motifs. For example, NCK1 SH3 domains and the SH3 domains from EPS8 family are able to bind with a PxxDY motif (Kesti et al., 2007; Mongiovi et al., 1999). EPS8 and its SH3 domain have an important role in mitogenetic signaling. Overexpression of EPS8 increased epidermal growth factor-dependent transformation and mitogenic responsiveness to epidermal growth factor (Fazioli et al., 1993; Matoskova et al., 1995). The RxxK motif was also found to interact with SH3 domains of the STAM2 (Kato et al., 2000), SLP-76, GRAP2-C proteins (Liu et al., 2003). Peptides that are sufficiently similar to class I or class II motifs are also recognized by several SH3 domains. For instance, the motif RxxPxxxP (similar to class I) and the motif PxxxPR (similar to class II) bind with the SH3 domain in CTTN (Tian et al., 2006) and CIN85/SH3KBP1 proteins (Moncalian et al., 2006), respectively.

Enormous amount of data are generated by various high-throughput experiments designed to address the binding specificity of SH3 domains, such as phage display (Tonikian et al., 2007), SPOT synthesis (Landgraf et al., 2004) or peptide array screening (Wu et al., 2007). Current associated computational methods, however, are usually based on the popular position weight matrices (PWMs) (Brannetti et al., 2000; Kim et al., 2011). There are two major drawbacks of PWMs. First, they are essentially linear models and thus ignore the correlation between the various positions in the peptide ligand (Liu et al., 2010). This also implies that they cannot differentiate between peptide classes. For that reason, few approaches are proposed recently, which use multi-PWM models for addressing the problem of multiple peptide classes (Gfeller et al., 2011; Kim et al., 2011). Second, they are based on a multiple alignment of the peptide ligands, which is a hard task for proline-rich SH3-bound peptides. Even minor alignment errors typically introduce significant noise in PWMs estimate. Other tools rely on resolved 3D domain–peptide structures, which are, however, known only for a few cases. Thus, they typically cannot directly make use of the available high-throughput data. These include the structure-based energy model by Hou et al. (2006) and the neural network model by Ferraro et al. (2006).

Here, we present a machine-learning approach to overcome the aforementioned drawbacks. Our method is based on a graph-kernel technique that, differently from the PWMs, does not require an initial peptide multiple alignment. Furthermore by virtue of its nonlinearity assumptions, it can adequately capture all types of peptide classes. We build specialized models for each of 70 human SH3 domains achieving competitive predictive performance compared with the state-of-the-art method (Kim et al., 2011). Furthermore, we show how we can leverage the information contained in related domains by building a single comprehensive model for a set of six SH3 domains further improving the predictive performance. Although high throughput datasets are available to train statistical-based learning approaches, we note that the presence of spurious interactions in the experimental data (either false negative or false positive) can severely affect the quality of the induced model. To tackle this problem, we use several approaches to identify a subset of high confidence negative interaction data. These instances are then used to train a model in a setting with reduced noise-to-signal ratio.

2 METHODS

We present an effective machine-learning method for the prediction of protein domain-peptide interactions. The method is based on a graph-kernel approach, which, in contrast to the majority of other approaches, does not require the peptide sequences to be aligned and can, at the same time, exploit high-order correlations between amino acid residues. Finally, we show how to build a model that takes in input both the peptide information and the (aligned) domain amino acid sequence. By doing so, we can exploit information from related SH3 domains and enhance the overall prediction performance.

2.1 Dataset

In our study, we use the large-scale human SH3–peptide interaction data from the high density peptide array experiment (Carducci et al., 2012). A total of 9192 peptides of length 15 were used in the CHIP experiment. The SH3–peptide interactions that gave a positive signal in peptide CHIP experiment have been stored in the newly developed interaction database PepspotDB. From PepspotDB, we have retrieved 16 032 nonredundant interactions for 70 human SH3 domains and 2802 peptides. Among them, a total of 478 interactions were also supported by the literature as reported by the MINT database (Licata et al., 2012) (see Table 1 for details).

Table 1.

Summary of the whole data for 70 human SH3 domains

No. of Positive No. of Negative No. of Unknown
Peptides 2802 9188 9188
Interactions 16 032 (478) 262 883 627 177
Open in a new tab

Note: Data available from the high density peptide array experiment of Carducci et al. (2012). In brackets are the interactions evidence available in MINT (Licata et al., 2012).

2.2 Feature encoding

2.2.1 Single domain modeling

For some protein domains, it is possible to identify a key amino acid necessary for a successful binding of a peptide (e.g. the phospho-tyrosine for the SH2 domain). This pivotal amino acid can then be used to identify an absolute reference system that allows to represent the peptide as a fixed size vector, i.e. each amino acid is identified as having position + i or − i starting from the pivotal amino acid. For SH3 domains, the situation is, however, more complex, as the key amino acid (proline) is abundant throughout the peptide sequence. A unique reference system based on proline cannot therefore be easily identified. Commonly, an initial alignment of the peptide sequences is performed in a preprocessing step. Errors in this phase can lead to a bad estimate of the model’s parameters and ultimately to bad predictive performances.

Here, we propose a kernel approach defined independently of an absolute reference for amino acid positions. In this way, we can move from a fixed-size vector type of encoding to a variable length sequence type encoding while still preserving a high discriminative power. The shift from a vector-based to a sequence-based approach can be extended further: if we move from sequences to graphs, we can then encode any other ancillary information on specific amino acids. To do so, we have to move from string kernel to efficient graph kernels. To ensure low run-times, we resort to the recently introduced (Costa and Grave, 2010) Neighborhood Subgraph Pairwise Distance Kernel (NSPDK) (see Supplementary Information for more details).

In more detail, to encode the peptide information, we proceed as follows. Given the experimental CHIP design constraints in peptide array library, we can only use peptide sequences of exactly 15 residues in length. We enrich the information available on each amino acid with their average physico-chemical properties, i.e. charge and hydrophobicity. As the graph-kernel approach can deal only with discrete labels, we discretize all properties. More specifically, as for charge, we have divided all common 20 amino acids into three groups as basic (R, K, H), acidic (D, E) and neutral (the remaining amino acids); as for hydrophobicity, we have identified four groups (very low, low, high and very high) based on their hydrophobicity scales following Kyte and Doolittle (1982), obtaining I, L, V as very high hydrophobic residues; A, M, C, F as high hydrophobic residues; G, T, S, W, Y, P as low hydrophobic residues; and rest of the amino acids (i.e. R, K, H, D, E, Q, N) are considered as very low hydrophobic residues.

The peptide is then modeled as a chain of unlabeled vertices: one per amino acid. Each vertex is then connected with a side-chain graph that encodes the ancillary properties, namely, of proximity: the charge, the hydrophobicity and the amino acid code (see Fig. 1, left). To generate features that are discriminative of the sequence direction, we model the peptide as a directed graph.

Fig. 1.

Fig. 1.

Open in a new tab

Graph encoding for peptide sequences (left) and for domain sequences (right). The encoding is enriched with charge, hydrophobicity and amino acid-type information. Peptide amino acid positions do not have an absolute reference, whereas domain amino acid positions receive an absolute positional reference according to a consensus alignment. Gaps receive a special encoding

2.2.2 Multiple domains modeling

When developing models for single domains, the input encodes only the information for the peptide sequence. However, when we want to induce a general model for a subset of related domains, the input should include also information on how a specific domain relates to the other ones so that useful knowledge can be transferred from interactions on similar domains. To do so, we model the domain amino acid sequence information in a similar fashion to the peptide encoding, with one important difference: as the position of specific amino acids is relevant to determine the specificity of the domain–peptide interaction, we additionally encode the information of an absolute positional reference. To do so, we align the related domains with the MUSCLE (Edgar, 2004) alignment software. In contrast to the peptide alignment, the SH3 domain alignment is highly reliable, mainly the alignment of n-SRC-loop and RT-loop in SH3 domains. Each domain-specific sequence is then projected onto the alignment, and the necessary gaps are finally introduced (see Fig. 1, right). The input for the multi-domain model therefore comprises two disconnected components, one for the peptide and one for the domain. To eliminate ambiguity issues, we distinguish the label alphabet for the peptide sequence from that of the domain sequence by means of appropriate prefixes.

3 RESULTS

3.1 Modeling with graph kernel features

Our approach is based on a graph encoding that allows to model relations between specific amino acids as well as different amino acid abstractions. This graph is then processed by a fast graph-kernel technique called NSPDK, recently introduced by Costa and Grave (2010), which extracts as explicit features, the occurrence counts of all the possible pairs of near small neighborhood subgraphs. The subgraph pairs are characterized by a radius and by a topological distance parameter (for details, see in Supplementary Information). The final classification task is then performed by a Support Vector Machine (SVM) based on the NSPDK graph kernel. By using an explicit vector encoding, we gain efficiency, as we avoid computing and storing the pairwise similarity matrix.

3.1.1 Single domain modeling

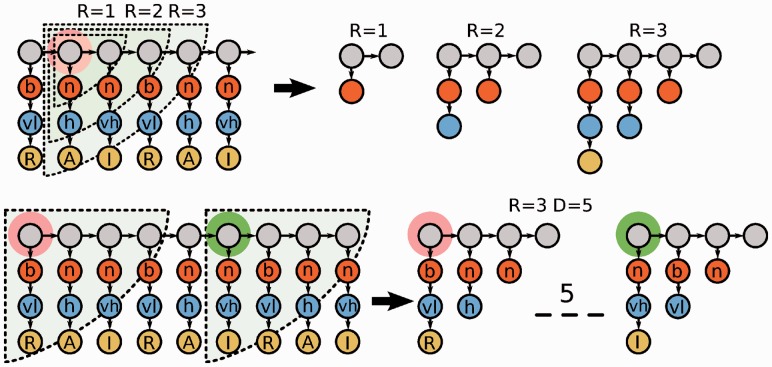
When developing models for each specific domain, we need only encode information on the candidate peptide sequence as described in Section 2.2. Different values for the radius parameter give rise to the parts illustrated in Figure 2.

Fig. 2.

Fig. 2.

Open in a new tab

Top: NSPDK features for Distance (D) = 0 and Radius (R) = 1, 2, 3 relative to a given root vertex highlighted in orange. The directedness property of the graph allows to induce features that can differentiate strand directions. Bottom: Ex. of feature for R = 3 and D = 5 capable to capture the correlation of two amino acid at relative distance 5. The sequence information that is not contained in the neighborhoods is ignored; the effect is equivalent to a don’t care pattern

Given the directed nature of the encoding graph, each neighborhood subgraph includes only amino acids that are downstream with respect to the current root node. With radius 1 and distance 0, each labeled vertex is considered independently: the corresponding feature representation encodes the frequency of each physico-chemical property (either the charge, the hydrophobicity or the amino acid type) in the single peptide; radius 2 allows properties of adjacent residues (e.g. hydrophobicity and adjacent charge information) to be modeled; radius 3 allows all properties for a single residue to be taken into account jointly. Even larger radius values can capture the joint information for adjacent pairs, triplets, etc., of residues. When pairs of neighborhood subgraphs at different distances are used, the composition of the subsequence between the two root vertices is ignored allowing a don’t care or soft type of feature matching. The order in which the properties are encoded is chosen to avoid generating features that subsume each other (i.e. given a neutrally charged amino acid, one can have multiple values for the hydrophobicity, but not the other way around). The final descriptors for each peptide contain all features with radii ranging from 0 up to 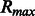Inline graphic and distances in 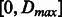Inline graphic. The optimal ranges are determined experimentally via cross-validation techniques. Finally, the training phase allows the determination of the weight distribution on all feature types (general and specific) to obtain optimal predictive performance

3.1.2 Multiple domains modeling

Several SH3 domains in the human genome bind strongly with class I and/or class II peptides. SH3 domains for FYN, BTK, HCK, FGR, SRC and LYN proteins are among them. The intuition underlying the multiple domains approach is that, if we are able to exploit the similarities across these domains, we can then increase the predictive performances for each specific domain. In practice, we would be performing a form of transfer-learning (Caruana, 1997) from one protein domain to another so that the examples used to induce a model on one domain would also contribute to form the bias of related models, increasing the effective number of available training instances.

To do so, we proceed by coupling the peptide information with the encoding for the domain in a joint feature space; more specifically, we encode the domain amino acid sequence information via its projection with respect to the domain consensus alignment. Here, the backbone vertex labels encode the specific position of the amino acid within the reference alignment. By introducing these absolute reference ids, all features (those describing physico-chemical properties and those describing the amino acid composition) become position specific. This absolute reference creates a joint feature space that ultimately allows information about interactions with different domains to be shared.

We are not trying to model the exact pairs of interacting amino acid residues (one in the peptide and one in the domain), as done in Ferraro et al. (2006). To do so would imply resorting to resolved protein complexes information, which is not available in large-scale. Rather, we represent the candidate interacting peptide and domain as a pair of disconnected graphs. The NSPDK procedure alone does not instantiate features that can directly express the relationship between parts of the peptide and of the domain sequences. However, we can take full advantage of the kernel trick and use nonlinear (i.e. polynomial or Gaussian) kernels. By doing so, the peptide-domain complex is implicitly represented by features that express combinations of the original features. We then rely on the statistical analysis of high-throughput experiments to infer the importance of each position specific features in the domain combined with nonposition specific features of the peptide sequence.

3.2 Dealing with false negatives

Traditional methods for peptide characterization rely on generative approaches where the probability of the model (often represented as a motif) is estimated from positive data alone. A typical approach is represented by PWMs (Kim et al., 2011) where the multinomial probability distribution for each position in the sequence is estimated independently via frequency counts. In the Machine Learning community, it is known that discriminative models have an advantage over generative ones, as they can rely on both positive and negative data; this allows them to better identify the decision boundary for the relevant region of the data space. Although generative methods often require less training examples, they do not achieve the same performance (Ng and Jordan, 2001). However, when negative data are assumed to be severely affected by noise, or even when the negative data is overly represented, one-class models can exhibit an advantage over discriminative ones. A typical scenario is when dealing with high-throughput experimental results such as phage display (Tonikian et al., 2007), SPOT synthesis (Landgraf et al., 2004) or peptide array screening (Wu et al., 2007). Here, to increase the confidence on the measurements, the experimental protocol makes use of stringent thresholds (e.g. requiring the agreement on several replicated experiments). In these cases, a large part of what would be labeled as lack of interaction (negative example) is just a weaker true interaction (positive example). To deal with these cases, we developed two approaches. The first one is a generative approach that makes use of multiple PWMs to model each peptide class. We then select a subset of instances that are not recognized by any specialized PWMs and use those are reliable negative instances to train a binary classifier. The second approach is based on a combination of a one-class and a semi-supervised method.

3.2.1 False negatives refinement

The key idea here is to use a generative approach to model each peptide class and select a subset of instances that are not recognized by any specialized model. We take an approach similar to Hui and Bader (2010) and select confident negative interactions using profile-based models (i.e. PWMs). To better represent the binding specificity of each domain, instead of using a single model, we resort to multiple PWMs, namely, one for each motif class for each SH3 domain.

In more detail, we first used the fuzzpro pattern search program from the EMBOSS package (Rice et al., 2000) to cluster the peptides into eight groups, one for each known motif class. We found that the majority of the peptides belong to the canonical motifs of class I and/or class II, whereas the rest belong to atypical motifs, mainly PxRP, PxxxPR, PxxDY and RxxKP motifs (see Supplementary Table S1).

Afterward, we used the popular EM-based MEME (Bailey and Elkan, 1995) algorithm to generate a PWM for each group.

Finally, we used MAST (Bailey and Gribskov, 1998), a sequence homology search algorithm, to identify the peptides matching the various PWMs. MAST ranks the input sequences according to an E-value type of score. We consider the peptides with high E-value (i.e. those that are not recognized with confidence by the model) as negatives. The cutoff score was set to the maximum E-value calculated for the known positive instances. Finally, for each domain, we select those peptides that are not recognized by any of the class specific PWMs. By doing so, we identify a total of Inline graphic200 K (262 883) negative interactions for the whole set of 70 human SH3 domains (see Table 1). Peptides considered as negative but that are close to the cutoff score are structurally similar to positive peptides.

Training and testing a model using only high confidence negative interactions can in principle induce a bias. To rule out such a case, we perform an additional experiment (see Section 3.4 later in the text) where we do not filter in any way the negative data.

3.2.2 One class semi-supervised model

The key idea here is to use the SVM one-class approach, pioneered by Schölkopf et al., 2001, to warm-start the self-training method for semi-supervised learning (Culp and Michailidis, 2007), restricting the prediction to negative instances only. In Schölkopf et al., 2001, it is shown how, to identify a region that contains with high probability most of the positive data, one can formulate the classic SVM optimization problem for binary classification using the origin of the feature space as the only negative instance. In case of normalized kernels, this boils down to using negative instances that are just the symmetric counterparts of the available positive instances. Here, we follow this latter way, given that we can produce the explicit sparse encoding and can therefore efficiently invert each instance.

The self-training approach to semi-supervised learning (Culp and Michailidis, 2007) is a wrapper method that iteratively uses the class predictions over the unlabeled data as true labels for a successive training phase until convergence to a stable state is reached. Here, we use the one-class model to initially induce the class information on the unsupervised instances, but, rather than using both positive and negative predictions, we accept only negative predictions. We select those instances that are predicted with the highest confidence (i.e. that are further away from the class boundary hyperplane) and use them to iteratively train the SVM model. For simplicity, we fix the fraction of the accepted negatives to 50% of the total number of unsupervised instances.

3.3 Performance of single domain model with filtered negatives

As detailed in Section 3.2.1, we induced PWMs to model several known classes of binding peptides for each SH3 domain. We used these models to select and filter away all peptides that were experimentally identified as noninteracting but that are recognized by the PWMs as belonging to one of the known classes of binding peptides. In this way, we obtain a total of 262 883 confident negative interactions for all 70 SH3 domains (the full list of positive and negative interaction data along with the class balance is given in Supplementary Table S2). We encode the peptide sequences as described in Section 2.2 and induce an SVM model for each SH3 domain based on the graph kernel. Even if here we use a linear SVM, we are inducing a nonlinear model with respect to the sequence of amino acid residues, i.e. the linear model is aware of higher order features that capture the correlation between pairs, triplets, etc., of amino acids.

We used a 10-fold stratified cross-validation to evaluate the predictive performance of each model. The hyper-parameters of the method were optimized in each fold by using a 5-fold cross-validation over the training set. Specifically, we optimized the radius parameter 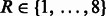Inline graphic and the distance parameter 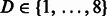Inline graphic for the graph kernel. The linear SVM model is induced using the Stochastic Gradient Descent approach championed by Bottou and Bousquet, 2008. 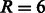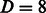The optimal values are achieved at Inline graphic and Inline graphic for most of the domains.

In Supplementary Table S3, we report the following quantities: 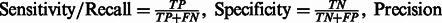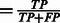Inline graphic Inline graphic, the area under the precision-recall curve (AUC PR) and the Area Under the Curve for the Receiver Operating Characteristic (AUC ROC). On average, we obtain a remarkable 0.73 AUC PR and 0.94 AUC ROC.

As for run times, as the NSPDK has essentially a linear complexity when dealing with bounded degree graphs, we report the estimated average time per instance: 0.07 s/instance on an ordinary 2.33 GHz Intel Core2 Duo CPU. This time includes the file upload in main memory, the graph feature generation and the parameters fitting of the model via the Stochastic Gradient Descent. In practice, this means that we can generate a model, given 1 K peptides in 1 min, or equivalently, a model for a proteome-scale 100 K peptides dataset in <2 h on a desktop machine.

We note that at times, we suffer from the high imbalance problem. For certain domains (e.g. CSK, DLG1, FISH, GRAP2-1, RUSC1, STAM2, etc.), the ratio between the available information for positive interactions and negative interactions is above 1–100. It is known in the Machine Learning literature that severely imbalanced class distribution negatively affects the performance of adaptive predictors (He and Garcia, 2009), as the tuning algorithms are generally biased toward the majority class. In our case, the majority class is the negative class, which implies a low sensitivity (true positive rate).

3.3.1 Comparison with state-of-the-art PWM approach

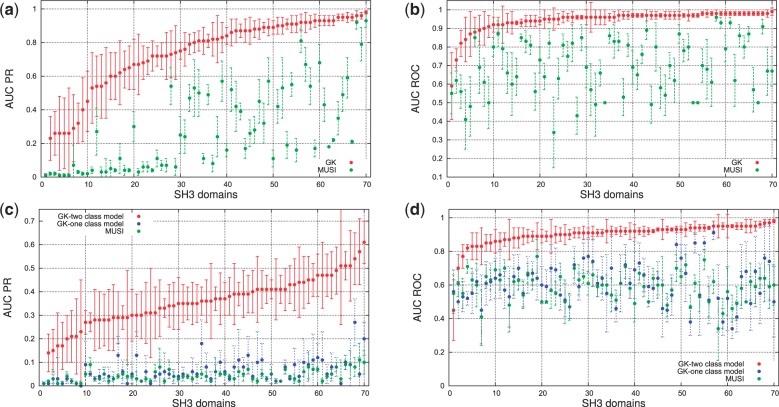
We have compared our results with a recently developed tool (Kim et al., 2011) based on PWMs called Multiple Specificity Identifier (MUSI). Even if the tool tries to increase the modeling complexity by replacing a single PWM with multiple PWMs, it remains in essence a linear model and therefore still suffers from the issues detailed in the Section 1, namely, the inability to model features correlation and the fact that it requires an initial error-prone peptide alignment phase. We have used exactly the same experimental setup as in our approach. In Figure 3, we report the comparative results with respect to AUC PR and AUC ROC performance measures for all 70 human SH3 domains. On average MUSI achieves a noncompetitive 0.27 AUC PR and 0.69 AUC ROC.

Fig. 3.

Fig. 3.

Open in a new tab

A 10-fold cross-validation performance. (a) + (b) comparison when using filtered negative interactions for Graph Kernel (GK) and MUSI. (c) + (d) comparison with nonfiltered negative interactions for binary class Graph Kernel (GK), one-class Graph Kernel and MUSI. The error bars represent respective standard deviation. The domains are sorted by increasing average performance for the Graph Kernel method

We were curious to see how our method performs on the same experimental dataset as done in Kim et al., 2011. To do so, we collected the interaction data used in the article by Kim et al., 2011. A total number of 2457 unique positive interactions were available for the SH3 domain from SRC protein. As the interaction peptides were identified by the phage display experiment, we could only get the positive interaction data. For preparing the negative interaction data, we took three different strategies. First, we consider the filtered negative data used in our study. Second, we prepare random negatives automatically generated by 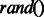Inline graphic function in Perl and third, we prepare the random negatives generated by the same strategy as described earlier in the text with 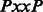Inline graphic core. Finally, we have performed stratified 10-fold cross-validation, using same parameter ranges for optimization and report AUC PR and AUC ROC performance measures for all these three datasets. Our approach shows much higher performance than MUSI tool. This would add another layer of confidence to the performance of our models. We also compare the performances of our graph-kernel approach and MUSI on our original dataset with these three datasets (see details in Supplementary Fig. S4).

The problem of generating the initial alignment was also tackled in a recent publication by (Andreatta et al., 2013). They identify multiple specificities in peptide data by performing two essential tasks simultaneously, alignment and clustering, and therefore find biologically relevant binding motifs that cannot be described well with a single PWM. Our approach sidesteps these issues altogether, as we just make a model based on all available peptide features (achieving at the same time a speed up of several orders of magnitude in run times).

3.4 Performance of single domain model with unfiltered negatives

Training and testing systems using only high confidence negative interactions can in principle induce a bias that alters the comparison between methods. To rule out such a case, we perform an additional experiment where we do not filter in any way the negative data. We use the same setup as in previous experiments (i.e. stratified 10-fold cross-validation), using the same parameters ranges for optimization. In Figure 3, we report the comparative results with respect to AUC PR and AUC ROC performance measures for all 70 human SH3 domains. The graph-kernel approach achieves an average AUC PR 0.35 and 0.90 AUC ROC. In the same conditions, MUSI achieves a noncompetitive AUC PR 0.04 and AUC ROC 0.58. This result confirm the advantages of the proposed discriminative graph-based method. The large difference in the performance with respect to the filtered case is due to (i) the imbalanced class distribution (up to 1:100) and (ii) the presence of a possibly large portion of false negatives.

3.5 Test on single domain model with one-class and semi-supervised filtered negatives

To test how important the precise information on true negatives (i.e. peptides that do not interact with the domain) is, we used the one-class and semi-supervised technique described in Section 3.2.2. The key idea here is to make use of information based primarily on the positive interactions to characterize the binding peptides; instances that are not well recognized by the model are then assumed to be negative. Once again, we operate in the same setup as for the unfiltered negatives experiment. In Figure 3, we report the comparative results with respect to AUC PR and AUC ROC performance measures for all 70 human SH3 domains. The one-class approach achieves an average AUC PR 0.063 and 0.61 AUC ROC. Although this result is statistically significant (according to a Wilcoxon Matched-Pairs Signed-Ranks Test, with P = 0.0003), the magnitude of the result let us conclude that using a generative approach to model protein–peptide interactions is noncompetitive with respect to discriminative approaches.

3.6 Multi-domain model

We aligned six domains (SH3 domains for FYN, BTK, HCK, FGR, SRC and LYN proteins) with the MUSCLE tool (Edgar, 2004). We used the SVM 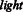Inline graphic (Joachims, 1999) software to train a Gaussian SVM over the explicit sparse feature encoding of peptide and domain sequence pairs. We evaluated the predictive performance using a 10-fold cross-validation over the six domain set using the filtered negatives as specified in Section 3.2.1. 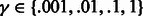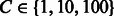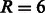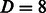The value for the Gaussian width was optimized on an internal 20% validation set over the range Inline graphic and the trade-off parameter Inline graphic, whereas the values of R and D for the graph kernel were fixed at the optimal value obtained in the previous experiments of Inline graphic and Inline graphic. As a baseline, we trained (and evaluated in an analogous setting) the six models independently on each domain, both using a linear kernel and a Gaussian compounded kernel. In Figure 4, we report the AUC PR and the AUC ROC for each SH3 domain and MUSI performance. In Supplementary Fig. S5, we report the sensitivity and the specificity, respectively. The experimental result confirms our intuitions: sharing information across related domains increases the predictive performance, mainly owing to an increase in sensitivity. We also note that the difference between models trained over single domains when using the linear kernel or the Gaussian one is nonstatistically significant. This result is also in line with our expectations, as the correlation between features is fully captured by the pairwise neighborhood subgraphs features, leaving no margin of improvement to the nonlinearity implemented by the kernel trick. With radius 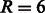Inline graphic and distance 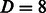Inline graphic, the kernel generates features spanning the whole sequence. Finally, we report the performance of the joint model when trained over the six domains, but tested over a novel albeit related LCK dataset. In this experiment, we are asking to predict the specificity for a novel domain, given only the information about the alignment of this domain to the overall consensus alignment. The model achieves an average AUC PR 0.85 and AUC ROC 0.96, with a high sensitivity 0.91 and specificity 0.96. The interesting finding is that the results are better than those obtained by training a model on the LCK protein alone; in this case, we obtain an average AUC PR 0.86 and AUC ROC 0.94, with a low sensitivity 0.55 and a high specificity 0.99. To understand the result, in the case of the LCK domain, we have experimental evidence only for 150 positive interactions, whereas the dataset for the six domains has a total of 910 nonredundant peptides involved in positive interactions. The experimental results support therefore the hypothesis that, at least in the LCK case, the domain alignment is sufficient to characterize the peptides binding model and to achieve therefore a higher overall sensitivity.

Fig. 4.

Fig. 4.

Open in a new tab

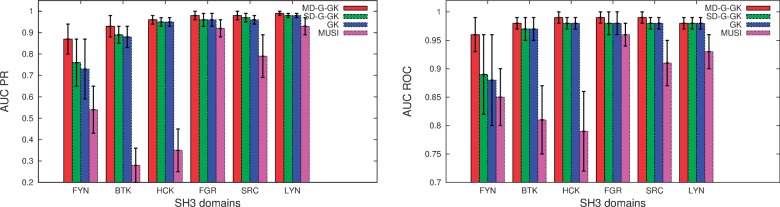
Precision-recall curves and AUC ROC curves for the Multi-Domain Gaussian Graph Kernel (MD-G-GK), the Single Domain Gaussian Graph Kernel (SD-G-GK), the Single Domain Linear Graph kernel (GK) and the MUSI tool for six related SH3 domains. The error bars represent respective standard deviation

3.7 Genome-wide analysis

We have performed a genome-wide analysis of SH3 domain-mediated interactions. Our aim was to identify the novel interactions that have important biological roles. We used UniProtKB/Swiss-Prot database (Magrane and UniProt Consortium, 2011), which is a manually curated and reviewed database. We retrieved 20 225 human proteins from UniProtKB/Swiss-Prot database, release 2012-06. For retrieving the peptide sequences, we scan all the available proteins with a window size of 15 and step size of 5. In this way, we have extracted a total number of Inline graphic2 M (2 209 474) peptide sequences.

In this analysis, we implemented co-cellular localization filter to avoid unlikely interactions, considering the term relative to the subcellular localization hierarchy in the controlled vocabulary of the Gene Ontology database (Ashburner et al., 2000). More clearly, the mature protein that contains the peptide and the protein that expresses the domains should share the same subcellular localization. In case of multiple cellular localization (e.g. GRB2 protein can be found in nucleus, cytoplasm, endosome and golgi apparatus), we consider a peptide eligible for binding only if it shares at least one of the localization term with the domain-containing proteins.

After filtering the eligible peptides, we scored them by the trained models and ranked according to the SVM scores. Finally, we report the top 50 predictions by each SH3 domain (see Supplementary File S1). Among the predictions, we observed a peptide (CKKLSPPPLPPRASI, position 151–165) from Phosphatidylinositol 4-phosphate 3-kinase C2 domain-containing subunit beta (Uniprot-id: O00750) was targeted by many SH3 domains (21 domains) that also share the same cellular compartment as annotated in Gene Ontology term database. There are also two evidence of interactions between PIK3C2B with GBR2 and PLCInline graphic-1 reported in STRING database (Franceschini et al., 2013). In addition, we took 478 real interactions reported in the MINT database (Licata et al., 2012), discarded them from our training set and could recover 397 (i.e. a recall 0.83).

In addition, we performed an analysis on these top 50 predictions for each SH3 domain to uncover the novel interaction functionalities using DAVID tool (Huang et al., 2009). The tool allows the possibility to perform a term-centric enrichment analysis on >40 different annotation categories. DAVID functional annotation chart, which identify enriched annotation terms associated with predicted proteins are reported. The smaller P-values indicate higher enrichment (see Supplementary File S2).

Applying the term-centric analysis, we have observed some biological meaningful interactions. For example, (i) SH3 domains from human P85-Inline graphic binds with a potential group of proteins (Uniprot-id: P21854, Q08209, Q07890, O00459, Q6ZUJ8) that play important role in B cell receptor signaling pathway. (ii) Among the top prediction by the SH3 domain from Human BTK protein, >50% proteins take a vital role in alternative splicing.

4 DISCUSSION

SH3 domain is probably the most widespread class of protein recognition modules. The interactions mediated by SH3 domains constitute an important class of protein interactions, involved in many cellular process. We presented a computational approach to predict domain–peptide interactions, using available high-throughput data. The method is an alignment-free approach based on an efficient graph kernel. Although, here, we present an application to SH3 domains, the method is general and can thus be trained to predict any protein–peptide interaction for which high-throughput data exists.

Current methods for protein–peptide interaction require often an initial multiple alignment of the bound peptides. As this is an error-prone process (especially in the case of SH3-domains, where peptides are proline-rich), one risks to introduce a significant amount of noise and obtain under performing models. In addition, current methods are often linear models (e.g. PWMs) and are therefore not able to represent high-order correlations between amino acid residues. Nonlinear method exist but have to deal with the high model complexity resulting from exponential number of high-order correlations achievable even for relatively short peptide sequences. If one uses the full alphabet of 20 amino acids, it becomes hard to gain sufficient data for a correct estimation of these complex models. One common solution is to use a reduced alphabet where each letter represents an entire amino acid class. This strategy, however, leads to inferior performance, especially when specific amino acids are preferred at specific positions. An alternative approach is to determine important interaction first by using resolved 3D domain–peptide structures. The major obstacle for the widespread application of this approach, however, is the limited availability of such structural data.

In this article, we use a different approach. We consider an alignment-free approach based on a graph representation of the peptide sequence where different abstraction levels are available in a unified way. By applying an efficient graph-kernel method, we were able to model high-order correlations that span different abstraction levels (e.g. a feature could represent a specific residue that has to be three positions to the right of a hydrophobic residue). The regularization provided by the SVM optimization scheme finally ensures that the model complexity is appropriately controlled and that only the features relevant for the task at hand are selected. Discarding the abstraction information (experiments not shown), i.e. using only the amino acid code information, leads to statistically significantly lower sensitivity. This confirms the intuition that using physico-chemical properties in the feature definition can adequately model cases that would otherwise be poorly covered by a sufficient number of sequences. It was also important to optimize the encoding order; therefore, we performed an experiment with different encoding order and proposed the best order to represent our graph (see Supplementary Fig. S6). Interestingly, the experimentally cross-validated optimal parameters value (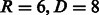Inline graphic) suggests that high-order amino acid correlations are required to obtain the best predictive performance, and that therefore linear models are inadequate.

Although we have previously used the NSPDK graph-kernel approach for clustering RNA structures (Heyne et al., 2012), here, differently from the RNA or molecular case, we do not have an obvious and natural way to encode information as a graph. The guiding principle, behind the choice of the proposed feature encoding, is to add ‘abstract information’ (like charge or hydrophobicity) in a somewhat ‘soft’ and incremental way. Rather than using an extended alphabet and maintaining a sequence encoding, the proposed graph encoding allows us to obtain features that are increasingly specialized. We have experimental evidence (see Supplementary Fig. S6) that a different choice in the ordering of the abstract information would yield suboptimal results, which become evident in the presence of imbalanced data. Additionally, we have investigated the performance of a string kernel (the k-mer kernel) along with other types of kernels, applied to the pure amino-acid sequences (i.e. without any additional information). Also, in this case, there is an evident drop in performance (see Section ‘Comparison with other predictive methods’ and Supplementary Fig. S7 in the Supplementary Information).

This confirms the intuition that using physico-chemical properties in the feature definition can adequately model cases that would otherwise be poorly covered by a sufficient number of sequences. Interestingly, we experimentally observed that high-order amino acid correlations are required to obtain the best predictive performance, suggesting that linear models are inadequate for this application.

Another common practice is to use generative models, i.e. models that try to capture the density distribution of the interacting peptides only. We showed that using one-class approaches is sub-optimal, even when considering models more expressive than the commonly used linear PWMs. The average predictive performance of a graph-kernel-based domain-specific model that is trained in a discriminative fashion is 0.35 AUC PR compared with 0.06 AUC PR when trained in a one-class way.

We tried to address the problem of selecting high-quality negative data. The issue is known in literature (see Ben-Hur and Noble, 2006 and Lo et al., 2005). In the application domain of protein–peptide interaction, it has been shown (Lo et al., 2005) that the common practice of generating negative instances by randomly shuffling peptide sequences simply leads to decreased predicted performance, as these instances do not resemble real biological sequences and are not therefore useful to determine useful class boundaries. We note, however, decreasing performance proportional to the level of class imbalance. When the ratio of negative instances versus positive ones is within 10-fold, we maintain an AUC PR 0.8, but for ratios greater than 100, performance drops to AUC PR 0.4 and lower (see Supplementary Figs S8 and S9).

We showed how the flexible graph-kernel approach allows the induction of multi-domain models. These models can leverage experimentally verified binding interactions on related domains and achieve high predictive performance even on domains for which no training material was available.

Finally, we performed a genome-wide prediction of human SH3–peptide interactions. All the learned models as well as all the genome-wide prediction interactions are available in http://www.bioinf.uni-freiburg.de//Software/SH3PepInt.

Our approach is general enough and can easily be applicable to other similar domains like SH2, PDZ and so forth. As for future work, given the computational efficiency of these models (a single-domain model can be trained on 100 K sequences in <2 h), we plan to provide a comprehensive set of predictors for all protein domains for which high-throughput data are available.

Supplementary Material

Supplementary Data
supp_29_13_i335__index.html (949B, html)

ACKNOWLEDGEMENTS

The authors thank David Gfeller and TaeHyung Kim for their help with the MUSI tool.

Funding: This work was funded by Centre for Biological Signalling Studies (BIOSS), University of Freiburg, Germany and the Excellence Initiative of the German Federal and State Governments (EXC 294 to R.B.). R.B. and F.C. were partially supported by the German Research Foundation (BA 2168/3-1 and BA 2168/4-2 SPP 1395 InKoMBio to R.B.).

Conflict of Interest: none declared.

REFERENCES

  1. Andreatta M, et al. Simultaneous alignment and clustering of peptide data using a Gibbs sampling approach. Bioinformatics. 2013;29:8–14. doi: 10.1093/bioinformatics/bts621. [DOI] [PubMed] [Google Scholar]
  2. Ashburner M, et al. Gene ontology: tool for the unification of biology. The gene ontology consortium. Nat. Genet. 2000;25:25–29. doi: 10.1038/75556. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Bailey T, Elkan C. The value of prior knowledge in discovering motifs with meme. Proc. Int. Conf. Intell. Syst. Mol. Biol. 1995;3:21–29. [PubMed] [Google Scholar]
  4. Bailey TL, Gribskov M. Combining evidence using P-values: application to sequence homology searches. Bioinformatics. 1998;14:48–54. doi: 10.1093/bioinformatics/14.1.48. [DOI] [PubMed] [Google Scholar]
  5. Ben-Hur A, Noble WS. Choosing negative examples for the prediction of protein-protein interactions. BMC Bioinformatics. 2006;7(Suppl. 1):S2. doi: 10.1186/1471-2105-7-S1-S2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Bottou L, Bousquet O. The tradeoffs of large scale learning. In: Platt J, et al., editors. Advances in Neural Information Processing Systems. Vol. 20. Cambridge, MA: NIPS Foundation. MIT Press; 2008. pp. 161–168. [Google Scholar]
  7. Brannetti B, et al. SH3-SPOT: an algorithm to predict preferred ligands to different members of the SH3 gene family. J. Mol. Biol. 2000;298:313–328. doi: 10.1006/jmbi.2000.3670. [DOI] [PubMed] [Google Scholar]
  8. Carducci M, et al. The protein interaction network mediated by human SH3 domains. Biotechnol. Adv. 2012;30:4–15. doi: 10.1016/j.biotechadv.2011.06.012. [DOI] [PubMed] [Google Scholar]
  9. Caruana R. Multitask learning. Mach. Learn. 1997;28:41–75. [Google Scholar]
  10. Cesareni G, et al. Can we infer peptide recognition specificity mediated by SH3 domains? FEBS Lett. 2002;513:38–44. doi: 10.1016/s0014-5793(01)03307-5. [DOI] [PubMed] [Google Scholar]
  11. Costa F, Grave KD. Proceedings of the 26 th International Conference on Machine Learning. Haifa, Israel: Omnipress; 2010. Fast neighborhood subgraph pairwise distance kernel; pp. 255–262. [Google Scholar]
  12. Culp M, Michailidis G. The 2007 Joint Statistical Meetings (JSM) Alexandria, VA: American Statistical Association; 2007. An iterative algorithm for extending learners to a semisupervised setting. [Google Scholar]
  13. Edgar RC. MUSCLE: multiple sequence alignment with high accuracy and high throughput. Nucleic Acids Res. 2004;32:1792–1797. doi: 10.1093/nar/gkh340. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Fazioli F, et al. Eps8, a substrate for the epidermal growth factor receptor kinase, enhances EGF-dependent mitogenic signals. EMBO J. 1993;12:3799–3808. doi: 10.1002/j.1460-2075.1993.tb06058.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Feng S, et al. Two binding orientations for peptides to the Src SH3 domain: development of a general model for SH3-ligand interactions. Science. 1994;266:1241–1247. doi: 10.1126/science.7526465. [DOI] [PubMed] [Google Scholar]
  16. Feng S, et al. Specific interactions outside the proline-rich core of two classes of Src homology 3 ligands. Proc. Natl Acad. Sci. USA. 1995;92:12408–12415. doi: 10.1073/pnas.92.26.12408. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Ferraro E, et al. A novel structure-based encoding for machine-learning applied to the inference of SH3 domain specificity. Bioinformatics. 2006;22:2333–2339. doi: 10.1093/bioinformatics/btl403. [DOI] [PubMed] [Google Scholar]
  18. Franceschini A, et al. STRING v9.1: protein-protein interaction networks, with increased coverage and integration. Nucleic Acids Res. 2013;41:D808–D815. doi: 10.1093/nar/gks1094. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Gfeller D, et al. The multiple-specificity landscape of modular peptide recognition domains. Mol. Syst. Biol. 2011;7:484. doi: 10.1038/msb.2011.18. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. He H, Garcia EA. Learning from imbalanced data. IEEE Trans. Knowl. Data Eng. 2009;21:1263–1284. [Google Scholar]
  21. Heyne S, et al. GraphClust: alignment-free structural clustering of local RNA secondary structures. Bioinformatics. 2012;28:i224–i232. doi: 10.1093/bioinformatics/bts224. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Hou T, et al. Computational analysis and prediction of the binding motif and protein interacting partners of the Abl SH3 domain. PLoS Comput. Biol. 2006;2:e1. doi: 10.1371/journal.pcbi.0020001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Huang DW, et al. Bioinformatics enrichment tools: paths toward the comprehensive functional analysis of large gene lists. Nucleic Acids Res. 2009;37:1–13. doi: 10.1093/nar/gkn923. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Hui S, Bader GD. Proteome scanning to predict PDZ domain interactions using support vector machines. BMC Bioinformatics. 2010;11:507. doi: 10.1186/1471-2105-11-507. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Joachims T. Making large-scale SVM learning practical. In: Schölkopf B, et al., editors. Advances in Kernel Methods-Support Vector Learning. Cambridge, MA, USA: MIT Press; 1999. pp. 169–184. [Google Scholar]
  26. Karkkainen S, et al. Identification of preferred protein interactions by phage-display of the human Src homology-3 proteome. EMBO Rep. 2006;7:186–91. doi: 10.1038/sj.embor.7400596. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Kato M, et al. A deubiquitinating enzyme UBPY interacts with the Src homology 3 domain of Hrs-binding protein via a novel binding motif PX(V/I)(D/N)RXXKP. J. Biol. Chemi. 2000;275:37481–37487. doi: 10.1074/jbc.M007251200. [DOI] [PubMed] [Google Scholar]
  28. Kesti T, et al. Reciprocal regulation of SH3 and SH2 domain binding via tyrosine phosphorylation of a common site in CD3epsilon. J. Immunol. 2007;179:878–885. doi: 10.4049/jimmunol.179.2.878. [DOI] [PubMed] [Google Scholar]
  29. Kim T, et al. MUSI: an integrated system for identifying multiple specificity from very large peptide or nucleic acid data sets. Nucleic Acids Res. 2011;40:e47. doi: 10.1093/nar/gkr1294. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Kyte J, Doolittle RF. A simple method for displaying the hydropathic character of a protein. J. Mol. Biol. 1982;157:105–132. doi: 10.1016/0022-2836(82)90515-0. [DOI] [PubMed] [Google Scholar]
  31. Landgraf C, et al. Protein interaction networks by proteome peptide scanning. PLoS Biol. 2004;2:E14. doi: 10.1371/journal.pbio.0020014. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Li SS. Specificity and versatility of SH3 and other proline-recognition domains: structural basis and implications for cellular signal transduction. Biochem. J. 2005;390:641–653. doi: 10.1042/BJ20050411. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Licata L, et al. MINT, the molecular interaction database: 2012 update. Nucleic Acids Res. 2012;40:D857–D861. doi: 10.1093/nar/gkr930. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Lim WA, et al. Structural determinants of peptide-binding orientation and of sequence specificity in SH3 domains. Nature. 1994;372:375–379. doi: 10.1038/372375a0. [DOI] [PubMed] [Google Scholar]
  35. Liu BA, et al. SH2 domains recognize contextual peptide sequence information to determine selectivity. Mol. Cell Pro. 2010;9:2391–2404. doi: 10.1074/mcp.M110.001586. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Liu Q, et al. Structural basis for specific binding of the Gads SH3 domain to an RxxK motif-containing SLP-76 peptide: a novel mode of peptide recognition. Mol. Cell. 2003;11:471–481. doi: 10.1016/s1097-2765(03)00046-7. [DOI] [PubMed] [Google Scholar]
  37. Lo SL, et al. Effect of training datasets on support vector machine prediction of protein-protein interactions. Proteomics. 2005;5:876–884. doi: 10.1002/pmic.200401118. [DOI] [PubMed] [Google Scholar]
  38. Magrane M UniProt Consortium. UniProt Knowledgebase: a hub of integrated protein data. Database (Oxford) 2011;2011:bar009. doi: 10.1093/database/bar009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Matoskova B, et al. Constitutive phosphorylation of eps8 in tumor cell lines: relevance to malignant transformation. Mol. Cell Biol. 1995;15:3805–3812. doi: 10.1128/mcb.15.7.3805. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Mayer BJ. SH3 domains: complexity in moderation. J. Cell Sci. 2001;114:1253–1263. doi: 10.1242/jcs.114.7.1253. [DOI] [PubMed] [Google Scholar]
  41. Moncalian G, et al. Atypical polyproline recognition by the CMS N-terminal Src homology 3 domain. J. Biol. Chem. 2006;281:38845–38853. doi: 10.1074/jbc.M606411200. [DOI] [PubMed] [Google Scholar]
  42. Mongiovi AM, et al. A novel peptide-SH3 interaction. EMBO J. 1999;18:5300–5309. doi: 10.1093/emboj/18.19.5300. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Musacchio A, et al. Crystal structure of a Src-homology 3 (SH3) domain. Nature. 1992;359:851–855. doi: 10.1038/359851a0. [DOI] [PubMed] [Google Scholar]
  44. Ng AY, Jordan MI. NIPS. MIT Press; 2001. On discriminative vs. generative classifiers: a comparison of logistic regression and naive bayes; pp. 841–848. [Google Scholar]
  45. Rice P, et al. EMBOSS: the European molecular biology open software suite. Trends Genet. 2000;16:276–277. doi: 10.1016/s0168-9525(00)02024-2. [DOI] [PubMed] [Google Scholar]
  46. Schölkopf B, et al. Estimating the support of a high-dimensional distribution. Neural Comput. 2001;13:1443–1471. doi: 10.1162/089976601750264965. [DOI] [PubMed] [Google Scholar]
  47. Tian L, et al. A noncanonical SH3 domain binding motif links BK channels to the actin cytoskeleton via the SH3 adapter cortactin. FASEB J. 2006;20:2588–2590. doi: 10.1096/fj.06-6152fje. [DOI] [PubMed] [Google Scholar]
  48. Tonikian R, et al. Identifying specificity profiles for peptide recognition modules from phage-displayed peptide libraries. Nat. Protoc. 2007;2:1368–1386. doi: 10.1038/nprot.2007.151. [DOI] [PubMed] [Google Scholar]
  49. Wu C, et al. Systematic identification of SH3 domain-mediated human protein-protein interactions by peptide array target screening. Proteomics. 2007;7:1775–1785. doi: 10.1002/pmic.200601006. [DOI] [PubMed] [Google Scholar]
  50. Yu H, et al. Structural basis for the binding of proline-rich peptides to SH3 domains. Cell. 1994;76:933–945. doi: 10.1016/0092-8674(94)90367-0. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Data
supp_29_13_i335__index.html (949B, html)
supp_btt220_Backofen_340_sup_1.pdf (1.1MB, pdf)
supp_btt220_Backofen_340_sup_S2.xlsx (52.7KB, xlsx)
supp_btt220_Backofen_340_sup_S1.xlsx (157.1KB, xlsx)

Articles from Bioinformatics are provided here courtesy of Oxford University Press

RESOURCES