Extensions of criteria for evaluating risk prediction models for public health applications

Abstract

We recently proposed two novel criteria to assess the usefulness of risk prediction models for public health applications. The proportion of cases followed, PCF(p), is the proportion of individuals who will develop disease who are included in the proportion p of individuals in the population at highest risk. The proportion needed to follow-up, PNF(q), is the proportion of the general population at highest risk that one needs to follow in order that a proportion q of those destined to become cases will be followed (Pfeiffer, R.M. and Gail, M.H., 2011. Two criteria for evaluating risk prediction models. Biometrics 67, 1057–1065). Here, we extend these criteria in two ways. First, we introduce two new criteria by integrating PCF and PNF over a range of values of q or p to obtain iPCF, the integrated PCF, and iPNF, the integrated PNF. A key assumption in the previous work was that the risk model is well calibrated. This assumption also underlies novel estimates of iPCF and iPNF based on observed risks in a population alone. The second extension is to propose and study estimates of PCF, PNF, iPCF, and iPNF that are consistent even if the risk models are not well calibrated. These new estimates are obtained from case–control data when the outcome prevalence in the population is known, and from cohort data, with baseline covariates and observed health outcomes. We study the efficiency of the various estimates and propose and compare tests for comparing two risk models, both of which were evaluated in the same validation data.

1. Introduction

Statistical models that predict disease incidence (Freedman and others, 2009), disease recurrence (Stephenson and others, 2006), mortality following disease onset (Albertsen and others, 2005), or response to treatment (O'Brien and others, 2011) are used in clinical practice and decision making, for example, to inform choices for a prevention or treatment with serious side effects. These models also have public health applications. They can be used to target preventive interventions to those with high enough risks to justify an intervention that has adverse effects and to identify high-risk individuals for intensive screening for early detection of disease.

We recently proposed two measures of concentration of risk that are directly relevant to public health decisions. We defined the “proportion of cases followed”, PCF(p), as the proportion of cases that would be followed in a program that followed the proportion p of the population at highest risk. We also proposed a complementary criterion, the “proportion needed to follow-up”, PNF(q), namely the proportion of the general population at highest risk that one needs to follow in order that a proportion q of those destined to become cases will be followed. We also derived tests for comparing PCF and PNF for two risk models evaluated in the same validation data (Pfeiffer and Gail, 2011).

Here, we extend these criteria in two ways. In the previous work, p or q were prespecified and fixed numbers. First, we introduce two new criteria by integrating PCF and PNF over a range of values of p or q to obtain iPCF, the integrated PCF, and iPNF, the integrated PNF (Section3). When integrating over the whole range of p and when the disease is rare, iPCF is similar to the area under the curve (AUC), the area under the receiver operating characteristic (ROC) curve (Pepe, 2003, p. 67). While the AUC is based on comparing ranks of the estimated risks in cases to those in non-cases, iPCF compares the risk in cases to risks in the whole population, which is a mixture of cases and non-cases. The AUC is ideal for measuring the discrimination accuracy in diagnostic applications, where one wants to distinguish cases from controls. For screening a general population, however, iPCF is more useful because it measures how different risks are in those destined to develop disease (or to have prevalent disease) from the population to be screened.

A key assumption in Pfeiffer and Gail (2011) was that the risk model is well calibrated. This assumption is also needed for novel estimates of iPCF and iPNF based on observed risks in a population alone (Section4.1). The second extension is to propose and study estimates of PCF, PNF, iPCF, and iPNF that are consistent even if the risk model is not well calibrated. These new estimates are obtained from case–control data when the outcome prevalence in the population is known, and from cohort data, with baseline covariates and observed health outcomes (Sections4.2 and4.3). We propose testing differences between two risk models evaluated on the same dataset using iPCF and iPNF (Section5). We then study the efficiency of the various estimates for these criteria and compare their performance for testing differences between two risk models evaluated on the same dataset in simulations (Section6). A data example is presented in Section7 before we close with a discussion (Section8).

2. Notation and background

We are interested in predicting the probability of a binary event, Y =1 or Y =0. This event could denote the incidence of a particular disease over a given time period, for example, 5 years, or of dying before the end of a defined time interval after disease onset. The event could also refer to the response to a treatment in a population with a particular disease. Given a set of baseline predictors X, a risk prediction model R(x)=P(Y =1 | X=x) is a mapping from the set Ω of possible values of X to [0,1]. In a specific population, the distribution of the covariates F_X(x) induces the distribution F of risk R that has support on [0,1] through

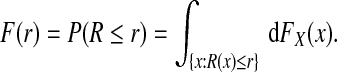(2.1)

We let G be the distribution of risk in those who experience the event (cases, Y =1),

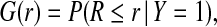and K be the distribution of risk in non-cases, or controls (Y =0),

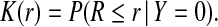We denote risk realizations from F by r^F, and risk realizations from cases and non-cases by r^G and r^K, respectively.

3. Criteria to assess model performance and their estimation

3.1. Review of the definition of PCF and PNF

We recently proposed and studied two criteria to assess the usefulness of models that predict the risk of disease incidence for screening and prevention, or the usefulness of prognostic models for management following disease diagnosis (Pfeiffer and Gail, 2011). The first criterion, the proportion of cases followed, PCF(p) is the proportion of cases who are included in the proportion p of individuals in the population at highest risk, given by

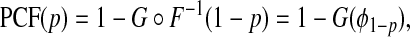(3.1)

where G∘F(x)=G{F(x)} is the composition of G with F and ϕ_1−p=F⁻¹(1−p) denotes the 1−pth quantile of F. The second criterion is the proportion needed to follow-up PNF(q) namely the proportion of the general population at highest risk that one needs to follow in order that a proportion q of cases will be followed, defined as

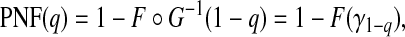(3.2)

where γ_1−q=G⁻¹(1−q) denotes the 1−qth quantile of the distribution of risk in cases, G.

If risk is concentrated in a small proportion of the population at highest risk, then PCF(p) will be high, even for small p and PNF(q) will be small, even for large q.

3.2. New criteria: iPCF and iPNF

While PCF(p) and PNF(q) are useful criteria for model evaluation, they require the specification of thresholds p and q. To lessen the dependency of these criteria on the given thresholds, we define the iPCF as

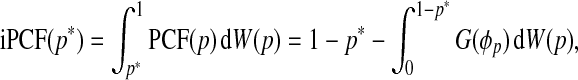(3.3)

where W is a probability measure on the unit interval. The iPNF is

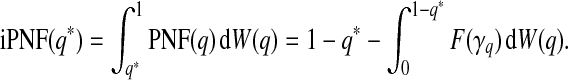(3.4)

In what follows, we assume dW(p)=dp. In that case, using a change of variables, we obtain

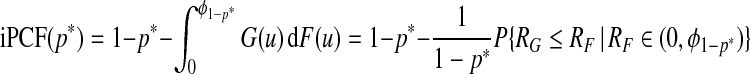(3.5)

and

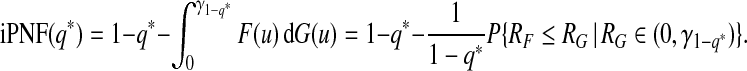(3.6)

For the special case of p*=q*=0, iPCF(0)=1−P(R_G≤R_F)=P(R_F<R_G) and iPNF(0)=1−P(R_F≤R_G)=P(R_F>R_G). We note that iPCF(0) is similar to the AUC, which can also be expressed as the probability that a randomly selected case has a higher projected risk than a randomly selected control, i.e. AUC=P(R_G>R_K). While the AUC is based on comparing ranks of the estimated risks in cases to those in non-cases, iPCF(0) compares risk in cases to risks in the whole population, which is a mixture of cases and non-cases. However, for a rare disease K≈F, and the values of the AUC and iPCF(0) will be close. Figure1 shows a PCF curve when the population distribution of risk F is a beta distribution with parameters α=1.5, β=28.5, with μ≡P(Y =1)=0.05. The area under this curve is iPCF(0)=0.71.

Fig. 1.

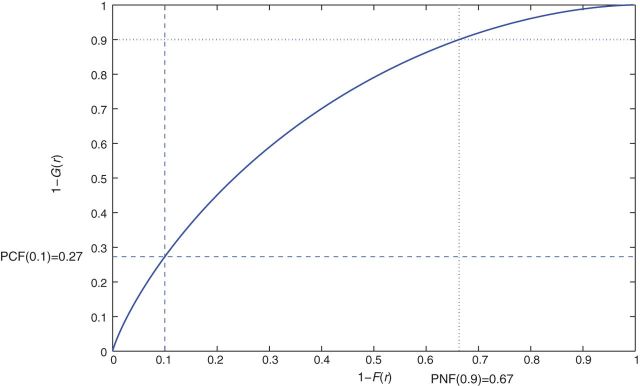
PCF curve when the distribution F of risk is a beta distribution with parameters α=1.5, β=28.5, with μ=0.05, corresponding to iPCF(0)=0.71.

Equations(3.5) and (3.6) resemble expressions for the partial area under the ROC curve (pAUC; McGlish 1989) that focuses on the region of the ROC curve with a low false positive rate, which is often of prime interest for diagnostic tests. Likewise, iPCF(p*) and iPNF(q*) can be used to focus on the high-risk portion of the population to be screened. However, (3.5) and (3.6) again use F as the reference population instead of K.

4. Estimation of PCF(p), PNF(q), iPCF and iPNF

We now study estimates of PCF, PNF, and their integrated versions, iPCF and iPNF, for three types of data and derive their asymptotic distributions. First, we assume that the risk model is well calibrated, and a random sample of risk estimates 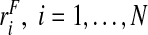, is observed. We first review the estimators of PCF and PNF used in Pfeiffer and Gail (2011) for this setting and propose novel estimators for iPCF and iPNF. We then estimate PCF, PNF, iPCF, and iPNF non-parameterically using random samples of risks in cases, 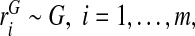and controls, 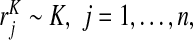assuming the event probability μ≡P(Y =1) in the population is known from external sources. We also study the corresponding estimates when a random sample of risks in the population and the associated binary outcomes 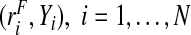, are available.

4.1. Estimation using observed risks in a population

If the risk model R is well calibrated, that is, P(Y =1 | r)=r, i.e. among individuals with risk r the fraction of events is r, then 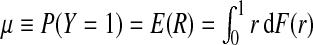, and the distributions G and K of risk in cases and non-cases, respectively, can be derived from the population distribution F as

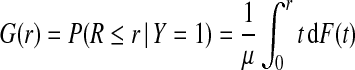(4.1)

and

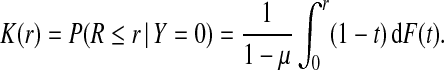(4.2)

In this setting, using (4.1),

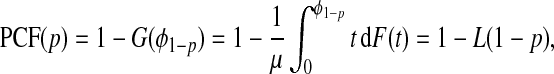(4.3)

where the L denotes the Lorenz curve of F (Goldie, 1977), and

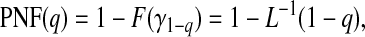(4.4)

where L⁻¹ is the inverse of the Lorenz curve, also called the concentration curve (Goldie, 1977).

Thus, if the risk model is well calibrated, PCF and PNF can be estimated from a random sample 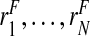of risks from the continuous distribution F in a given population. To briefly summarize earlier work (Pfeiffer and Gail, 2011), let 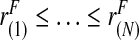denote the order statistics of the estimated risks, and [x] be the largest integer less than or equal to x. Following Goldie (1977), and letting 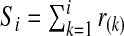, an estimate of the Lorenz curve and thus PCF is

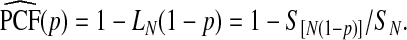(4.5)

Using the result of Goldie (1977) for the inverse function of the Lorenz curve, 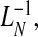for a fixed value of 1−q, the PNF is estimated as

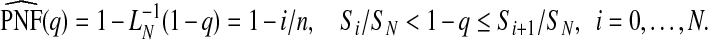(4.6)

By drawing on the distribution theory for the Lorenz cure and its inverse, we derived the asymptotic normality of the estimates in (4.5) and (4.6) and obtained their asymptotic variances using an influence function-based approach (Pfeiffer and Gail, 2011).

If the model is well calibrated, iPCF and iPNF also relate to the Lorenz curve and its inverse through

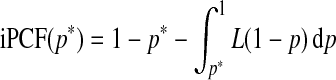and

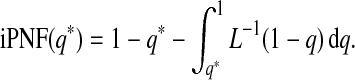It is easy to see that a popular summary measure of the Lorenz curve, the Gini index (Gini, 1912), defined as 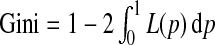, which is commonly used to measure income inequality in economics, is related to iPCF(0) through Gini=2iPCF(0)−1.

Using ordered risk estimates 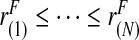in the population, a non-parametric estimate of iPCF based on (4.5) is thus obtained by interpolation as

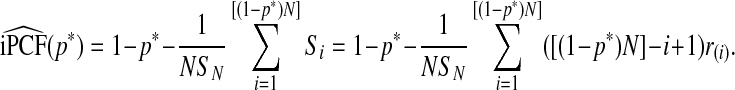(4.7)

For p*=0, this expression reduces to .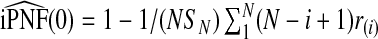

Similarly, we estimate iPNF using simple geometric arguments as

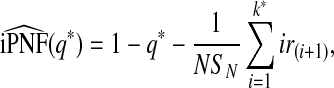(4.8)

where k* satisfies S_k*/S_N<q*≤S_k*+1/S_N.

In addition to being consistent, 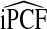and 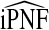also have asymptotically normal distributions. This follows directly from the fact that they are linear functionals of estimates of the Lorenz curve and its inverse, which are Gaussian stochastic processes (Goldie, 1977). The asymptotic variance estimates of 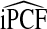and 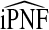are given in Appendix A, see supplementary material available at Biostatistics online.

4.2. Estimation using risks in a case–control sample when μ=P(Y =1) is known

We assume that risks 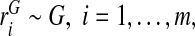from a random sample of cases and risks 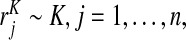from a random sample of non-cases from a population are available, and that the event probability μ=P(Y =1) in that population is known. We express the distribution of risk in the general population as F=μG+(1−μ)K, and estimate F using the empirical distribution functions

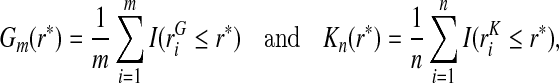as

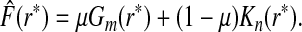Plugging G_m and 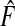into (3.1) yields

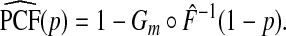(4.9)

The expression for PNF in (3.2) simplifies to PNF(q)=1−μ(1−q)−(1−μ)K∘G⁻¹(1−q) and thus

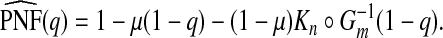(4.10)

Using F=μG+(1−μ)K in (3.5), we express iPCF as

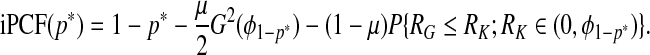(4.11)

We estimate iPCF using the empirical distribution functions G_m and K_n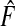, and and 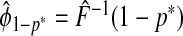as

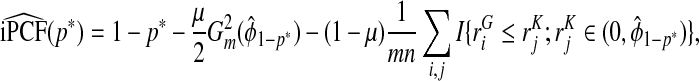(4.12)

where I(A) denotes the indicator function that is one if A is true and zero otherwise.

Similarly, iPNF given in (3.6) can be expressed as

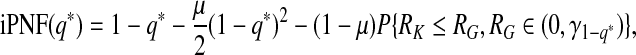(4.13)

and thus an estimate is given by

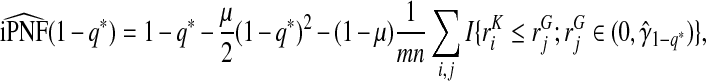(4.14)

where .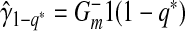

Consistency of 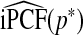and 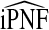follows immediately from the consistency of G_m and 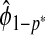, 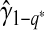and the fact that 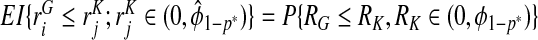and .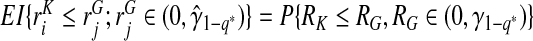

PCF, PNF, iPCF, and iPNF are functionals of the two distribution functions G and K that are estimated based on independent samples. We derive their asymptotic properties using a bivariate influence function approach (Pires and Branco, 2002) in Appendix B, see supplementary material available at Biostatistics online.

4.3. Estimation using risks and outcomes in a population

Here, a random sample of risks and the corresponding event outcomes in a population are available, that is, we observe the i.i.d. samples 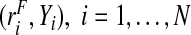. For a model that predicts disease incidence, these data would be comprised of risk estimates at baseline and observed outcomes at the end of the follow-up period, and for a model that predicts the prevalence of a disease, the risks and outcomes could be based on a cross-sectional sample.

We estimate PCF and PNF by plugging estimates of F, G and the corresponding quantiles ϕ and γ into the expressions (3.1) and (3.2), respectively. The distribution of risk in the general population, F, is estimated using the empirical distribution function in the whole population,

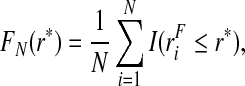and G is estimated using the empirical distribution function among cases,

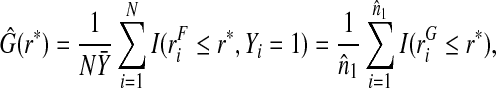where 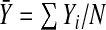denotes the empirical mean of Y and 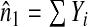. Estimates of iPCF and iPNF are obtained in a similar way as

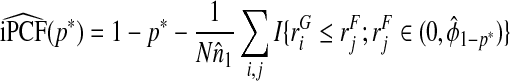(4.15)

and

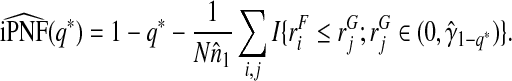(4.16)

The asymptotic distributions of the estimators for PCF, PNF, iPCF, and iPNF based on risks and outcomes in a cohort differ from the asymptotic distributions of the estimators (4.9)–(4.11) and (4.14) based on the case–control data in the previous section, as they use different estimates of F, and also incorporate the variation arising from estimating the disease prevalence and the number of cases, 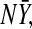in the population. In Appendix C (see supplementary material available at Biostatistics online), we derive their asymptotic distributions by treating F and G as functions of the bivariate distribution function of (r^F,Y).

5. Comparing two risk models

We previously proposed test statistics based on PCF and PNF for two risk models, R¹ and R², both of which were applied to the same population. To test whether, for fixed p, PCF¹=PCF², or for a fixed q, PNF¹=PNF², we use the statistics

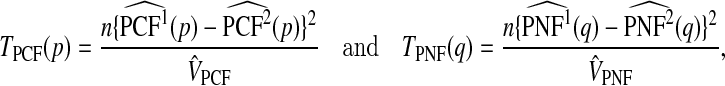(5.1)

where 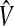are consistent estimates of the variance of the difference of the estimates.

Two new test statistics based on iPCF and iPNF to compare two models using correlated risk estimates (r¹,r²) are

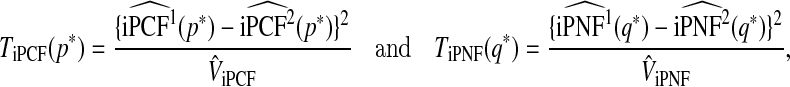(5.2)

where iPNF and iPCF for both models are evaluated at the same value p* or q*, respectively.

Asymptotically all test statistics, T_PCF,T_PNF, T_iPCF, and T_iPNF have a central 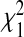distribution under H₀. Under the alternative, the non-centrality parameters for the test statistics are δ_PCF=n(PCF¹−PCF²)²/V _PCF, δ_PNF=n(PNF¹−PNF²)²/V _PNF, δ_iPCF=n(iPCF¹−iPCF²)²/V _iPCF, δ_iPNF=n(iPNF¹−iPNF²)²/V _iPNF, respectively. The variances for all test statistics can be computed based on the respective influence functions ψ^R₁ and ψ^R₂ for models 1 and 2 as V =Var(ψ^R₁−ψ^R₂), or alternatively, using a bootstrap variance estimate. In the simulations, we use the bootstrap variances in the formulas of the test statistics.

6. Simulations

6.1. Efficiency of estimates of PCF, PNF, iPCF, and iPNF

We use simulations to investigate the properties of the non-parametric estimates of PCF, PNF, iPCF, and iPNF defined in Sections4.1–4.3 and to compare their efficiency. We assume that the population distribution of risk is a beta distribution with parameters α and β, F(r)=B(r,α,β)/B(α,β), where 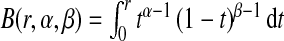and B(α,β)=B(1,α,β). In this setting, the distributions of risk in cases and non-cases are also beta distributions, given by G(r)=B(r,α+1,β)/B(α+1,β) and K(r)=B(r,α,β+1)/B(α,β+1). The subscript R refers to estimates based on the population risks only, the subscript CC is used for estimates based on risks observed for a case–control sample with known disease prevalence μ, and the subscript (R,Y) refers to estimates based on risks and observed outcomes in a population. The efficiency of the various estimates is compared using their asymptotic relative efficiencies (AREs), computed as the ratios of the influence function-based variances given in the Appendices (see supplementary material available at Biostatistics online).

To create data for each of the study designs, we first simulated risk estimates 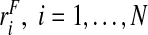, and then generated the binary outcomes Y _i from a binomial distribution with probability r_i, Y _i∼binom(1,r_i),i=1,…,N. For the estimates using the population-based risks and the risks and outcomes, we used all the observations of 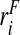or 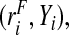respectively. To create a case–control study, we split the population into cases and non-cases and used the risk estimates from all the cases and all the non-cases together, with the true value of the disease prevalence μ. Thus, all estimates in a given simulation are based on the same observations.

Table1 gives results for 500 simulations each based on a random sample of size N=10 000 for a rare disease. The beta distribution parameters were α=6.55,1, and 0.3 with corresponding β=124.45,19.0, and 5.7 and expected risk μ=E(R)=0.05 for each (α,β) pair. The AUC values for these parameter choices are 0.63,0.79, and 0.98, respectively, corresponding to models with moderate to very high discriminatory ability. The mean estimates of PCF and PNF were very close to the theoretical values for all estimators. However, the estimates based on case–control data and cohort data with outcomes were much less precise than the corresponding estimates 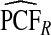and 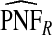. The AREs of 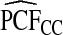compared with 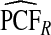ranged from 22.86 to 387.2, with more loss of efficiency for parameter values corresponding to smaller AUCs. For example, for p=0.20, ARE=367.45 for (α,β)=(6.55,124.45) and ARE=22.86 for (α,β)=(0.3,5.7). The AREs for the estimates based on risks and outcomes and based on case–control data were close to 1.00 in all cases. Estimates of PNF behaved very similarly to estimates of PCF in terms of efficiency (Table1). Again, 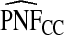and 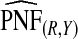were much less efficient than 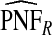for all settings.

Table 1.

Mean values of PCF and PNF estimated using observed risks R in a population, assuming that the model is well calibrated; risk estimates in a case–control sampling when the disease prevalence μ is known, and based on observations of (R,Y) in the population

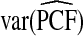								ARE
p	PCF true	R	CC	(R,Y)	R	CC	(R,Y)	CC/R	(R,Y)/R	(R,Y)/CC
α=6.55,β=124.45†
0.10	0.18	0.18	0.18	0.18	0.01	2.67	2.67	386.71	387.23	1.00
0.20	0.32	0.32	0.31	0.31	0.01	4.03	4.03	367.45	368.10	1.00
0.30	0.44	0.44	0.44	0.44	0.01	4.63	4.65	362.90	363.84	1.00
0.40	0.55	0.55	0.55	0.55	0.01	4.70	4.68	369.90	368.69	1.00
α=1,β=19‡
0.10	0.32	0.32	0.32	0.32	0.06	3.80	3.81	59.41	59.64	1.00
0.20	0.51	0.51	0.51	0.51	0.08	4.60	4.61	59.27	59.39	1.00
0.30	0.65	0.65	0.65	0.65	0.07	4.30	4.31	62.52	62.70	1.00
0.40	0.76	0.76	0.76	0.76	0.05	3.53	3.53	68.18	68.19	1.00
α=0.3,β=5.7§
0.10	0.51	0.51	0.51	0.51	0.22	4.23	4.32	19.07	19.48	1.02
0.20	0.73	0.73	0.73	0.73	0.16	3.65	3.71	22.48	22.86	1.02
0.30	0.86	0.86	0.86	0.86	0.08	2.35	2.38	28.20	28.46	1.01
0.40	0.93	0.93	0.93	0.93	0.03	1.28	1.29	38.74	38.98	1.01
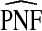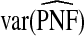								ARE
q	PNF true	R	CC	(R,Y)	R	CC	(R,Y)	CC/R	(R,Y)/R	(R,Y)/CC
α=6.55,β=124.45†
0.90	0.60	0.60	0.60	0.60	0.07	6.11	6.15	92.04	92.64	1.01
0.80	0.45	0.45	0.45	0.45	0.06	4.52	4.51	73.59	73.40	1.00
0.70	0.34	0.34	0.34	0.34	0.05	3.34	3.34	66.08	66.02	1.00
0.60	0.26	0.26	0.26	0.26	0.04	2.42	2.42	60.15	60.15	1.00
α=1,β=19.0‡
0.90	0.60	0.60	0.60	0.60	0.06	6.11	6.07	95.58	94.83	0.99
0.80	0.45	0.45	0.45	0.45	0.06	4.52	4.54	74.24	74.62	1.01
0.70	0.34	0.34	0.35	0.35	0.05	3.34	3.36	62.44	62.80	1.01
0.60	0.26	0.26	0.26	0.26	0.04	2.42	2.43	59.11	59.46	1.01
α=0.3,β=5.7§
0.90	0.35	0.35	0.38	0.38	0.11	3.58	3.65	32.19	32.81	1.02
0.80	0.25	0.25	0.26	0.26	0.08	1.89	1.93	24.23	24.75	1.02
0.70	0.18	0.18	0.19	0.19	0.05	1.14	1.14	21.79	21.79	1.00
0.60	0.13	0.13	0.14	0.14	0.04	0.71	0.72	20.15	20.33	1.01

Results are based on 500 simulations for each set of parameters (α,β) for the beta distribution and values of q and p. Each simulation has N=10 000 samples with μ=0.05.

AREs are computed as the ratio of the influence function-based variances.ARE=asymptotic relative efficiency, the ratio of the influence functions-based variances CC/R=var(T_CC)/var(T_R), (R,Y)/R=var(T_(R,Y))/var(T_R), (R,Y)/CC=var(T_(R,Y))/var(T_CC), where T=PCF or T=PNF, respectively.

^†AUC=0.63.

^‡AUC=0.79.

^§AUC=0.92.

Supplementary material available at Biostatistics online, Table S1, gives results for a common disease, μ=0.30 with α=6.55,1, and 0.3 and corresponding β=15.28,2.33, and 0.7, leading to the same AUC values as in Table1. The patterns were very similar to those seen in Table1, but the loss in efficiency for the case–control based estimates and for cohort data with outcome-based estimates was less pronounced than for a rare disease. 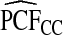and 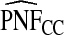were somewhat more efficient than 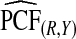and 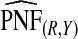for parameters resulting in larger AUC values. For example, for p=0.10, the variance ratio of 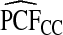compared with 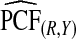was ARE=3.43 for (α,β)=(0.3,0.7).

Table2 gives results for iPCF and iPNF for 500 simulations, each based on a random sample of size N=10 000 for the same simulation settings as in Table1. Again, all methods had mean estimates that were very close to the theoretical values of iPCF and iPNF. Similar to PCF and PNF the estimates of iPCF and iPNF based on case–control data and (R,Y) were much less precise than corresponding estimates 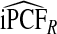and . 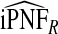For 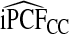compared with 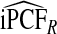, the AREs ranged from 316.73 to 46.58 and were lower for parameter values corresponding to larger AUCs. For example, for p=0.20, ARE=311.36 for (α,β)=(6.55,124.45) and ARE=59.61 for (α,β)=(1,2.33). Estimates of iPNF_CC and iPNF_(R,Y) were also less efficient than 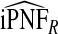, but the loss of efficiency was less pronounced than for iPCF. 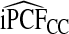and 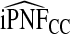were slightly more efficient than estimated based on the cohort with outcomes. Results for iPCF and iPNF for a common disease are given in Table S2, see supplementary material available at Biostatistics online.

Table 2.

Mean values of iPCF and iPNF estimated using: the population risk distribution F(R) assuming that the model is well calibrated; risks in a case–control study and known disease prevalence μ; observations of (R,Y) in the population

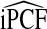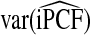								ARE
p†	iPCF true	R	CC	(R,Y)	R	CC	(R,Y)	CC/R	(R,Y)/R	(R,Y)/CC
α=6.55,β=124.45†
0.10	0.60	0.60	0.60	0.60	0	1.26	1.26	279.48	278.91	1.00
0.20	0.57	0.57	0.57	0.57	0	1.20	1.20	311.36	311.83	1.00
0.30	0.53	0.53	0.53	0.53	0	0.84	0.84	316.73	316.32	1.00
0.40	0.48	0.48	0.48	0.48	0	0.49	0.49	271.95	271.77	1.00
α=1,β=2.33‡
0.10	0.73	0.73	0.73	0.73	0.02	0.81	0.81	46.58	46.54	1.00
0.20	0.68	0.68	0.68	0.68	0.01	0.59	0.59	59.61	59.52	1.00
0.30	0.63	0.63	0.63	0.63	0.01	0.39	0.39	68.36	68.90	1.01
0.40	0.55	0.55	0.55	0.55	0	0.24	0.25	69.42	69.52	1.00
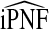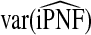								ARE
q†	iPNF true	R	CC	(R,Y)	R	CC	(R,Y)	CC/R	(R,Y)/R	(R,Y)/CC
α=6.55,β=124.45†
0.60	0.27	0.27	0.27	0.27	0.0014	0.44	0.44	311.04	310.85	1.00
0.70	0.22	0.22	0.22	0.22	0.0006	0.23	0.23	358.61	358.83	1.00
0.80	0.16	0.16	0.16	0.16	0.0003	0.10	0.10	353.88	353.58	1.00
0.90	0.09	0.09	0.09	0.09	0	0.02	0.02	506.42	506.83	1.00
α=1,β=19.0‡
0.60	0.19	0.19	0.19	0.19	0.01	0.49	0.49	58.48	58.39	1.00
0.70	0.16	0.16	0.16	0.16	0.01	0.27	0.27	53.43	53.46	1.00
0.80	0.12	0.12	0.12	0.12	0.0002	0.15	0.15	77.24	77.47	1.00
0.90	0.07	0.07	0.07	0.07	0	0.05	0.05	91.55	91.58	1.00
α=0.3,β=5.7‡
0.50	0.12	0.12	0.12	0.12	0.01	0.29	0.30	20.92	21.71	1.04
0.60	0.11	0.11	0.11	0.11	0.01	0.23	0.23	19.70	20.19	1.02
0.70	0.10	0.10	0.10	0.10	0.01	0.19	0.19	26.88	26.77	1.00
0.80	0.08	0.08	0.08	0.08	0	0.11	0.11	27.62	27.53	1.00
0.90	0.05	0.05	0.05	0.05	0	0.05	0.05	46.03	45.81	1.00

Results are based on 500 simulations for each set of parameters (α,β) for the beta distribution and values of q and p. Each simulation has N=10 000 samples with μ=0.05. AREs are computed as the ratio of the influence function-based variances.

ARE = asymptotic relative efficiency, the ratio of the influence functions-based variances CC/R=var(T_CC)/var(T_R), (R,Y)/R=var(T_(R,Y))/var(T_R), (R,Y)/CC=var(T_(R,Y))/var(T_CC), where T=PCF or T=PNF respectively.

^†AUC=0.63.

^‡AUC=0.79.

^§AUC=0.92.

6.2. Comparing two risk models using PCF, PNF, and iPCF and iPNF

We examined the size and power of the tests (5.1) and (5.2) for comparing risk models 1 and 2 when PCF, PNF, iPCF, and iPNF are estimated from observed bivariate risks 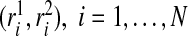, and risks and outcomes in a population. To simulate bivariate risks with outcome data, we first drew a random number m of cases (Y =1) in a population of size N from a binomial distribution with parameter μ, and assigned the remaining n=N−m individuals to be controls (Y =0). To obtain risk estimates from each model that have a marginal beta distribution and are correlated, we first generated bivariate normal random variables (X_i1,X_i2)∼MV N((0,0),Σ)i=1,…,N, where Σ₁₁=Σ₂₂=1 and Σ₁₂=Σ₂₁=ρ. 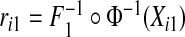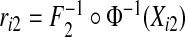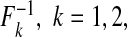We then separately computed risks for the n cases and m controls from and where denotes the inverse of the beta distribution function with parameters (α_k+1,β_k) for cases and parameters (α_k,β_k+1) for controls, and Φ⁻¹ is the inverse of the standard normal distribution.

Based on the random sample (r_i1,r_i2,Y _i),i=1,…,N, we computed the non-parametric estimates of T_PCF, T_PNF, T_iPCF, and T_iPNF using observed risks only as well as risks and outcome data in the population, with the bootstrap variance estimates based on B=500 bootstrap samples. A standard way to assess the discriminatory ability of two models is to compare their AUC or partial area under the curve (pAUC) values. When the test statistics were estimated from risks and outcome data, we computed non-parametric estimates of pAUC,

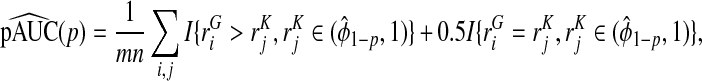and also used the test statistic

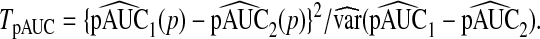Estimates of size and power were based on 100 simulations for each choice of parameter values. Each simulation is based on a random sample of N=1000 bivariate risks. We show results for ρ=0.2 and a common disease, μ=0.3, as other choices resulted in similar conclusions.

Tests based on PCF, iPCF, PNF, or iPNF had better power than T_pAUC for all settings in Table3. Table3 highlights again that estimates computed under the assumption of a well-calibrated model have better power than those relying on risks and outcome data. For example, for (α₁,β₁)=(1,2.3) and (α₂,β₂)=(1.2,2.8) the power ranged from 0.77 to 0.81 for iPCF_R, but was lower than 0.21 for iPCF_(R,Y) for all values of p, and from 0.79 to 0.82 for iPNF_R, and from 0.29 to 0.77 for iPNF_(R,Y); the power was lower for smaller values of q. Tests based on iPCF_R and iPNF_R had somewhat better power than tests based on PCF_R and PNF_R.

Table 3.

Power of the tests T_pAUC, T_PCF, T_PNF, T_iPCF, and T_iPNF for two beta-distributed risk models under the assumption of well-calibrated models, R₁ with parameters (α₁,β₁) and R₂ with parameters (α₂,β₂) for q=0.1 for sample size N=1000, with μ=0.3 and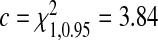

							Power for test based on
	pAUC	PCF	PNF	iPCF	iPNF		PCF	iPCF		PNF	iPNF
p,q	1,2	1,2	1,2	1,2	1,2	pAUC	R	R	(R,Y)	R	R	(R,Y)
(α1,β1)=(0.3,0.7),(α2,β2)=(0.5,1.17)
0.1, 0.9	0.06, 0.04	0.31, 0.29	0.44, 0.53	0.88, 0.84	0.95, 0.96	0.86	0.89	1.00	0.94	1.00	1.00	1.00
0.2, 0.8	0.14, 0.11	0.56, 0.51	0.34, 0.40	0.93, 0.90	0.89, 0.91	0.92	0.99	1.00	0.97	1.00	1.00	0.99
0.3, 0.7	0.23, 0.19	0.75, 0.67	0.27, 0.32	0.97, 0.94	0.82, 0.85	0.90	1.00	1.00	0.91	1.00	1.00	0.96
0.4, 0.6	0.32, 0.28	0.87, 0.80	0.22, 0.25	0.98, 0.97	0.75, 0.77	0.90	1.00	1.00	0.80	1.00	1.00	0.92
(α1,β1)=(6.55,15.3),(α2,β2)=(4.55,10.62)
0.1, 0.9	0.01, 0.01	0.16, 0.17	0.82, 0.80	0.68, 0.70	0.99, 0.99	0.10	0.98	1.00	0.28	1.00	0.99	0.90
0.2, 0.8	0.04, 0.04	0.29, 0.31	0.69, 0.67	0.76, 0.77	0.97, 0.96	0.12	1.00	1.00	0.13	1.00	1.00	0.68
0.3, 0.7	0.08, 0.09	0.42, 0.44	0.58, 0.55	0.82, 0.84	0.93, 0.92	0.24	1.00	1.00	0.27	1.00	1.00	0.61
0.4, 0.6	0.13, 0.15	0.53, 0.55	0.47, 0.45	0.88, 0.89	0.88, 0.87	0.16	1.00	1.00	0.18	1.00	1.00	0.34
(α1,β1)=(6.55,15.3),(α2,β2)=(8.55,19.95)
0.1, 0.9	0.01, 0.01	0.16, 0.15	0.82, 0.83	0.68, 0.67	0.99, 0.99	0.03	0.86	0.98	0.08	0.94	0.91	0.88
0.2, 0.8	0.04, 0.04	0.29, 0.28	0.69, 0.71	0.76, 0.75	0.97, 0.97	0.10	0.96	0.99	0.10	0.97	0.93	0.69
0.3, 0.7	0.08, 0.08	0.42, 0.40	0.58, 0.59	0.82, 0.82	0.93, 0.93	0.11	0.94	0.97	0.14	0.96	0.95	0.46
0.4, 0.6	0.13, 0.13	0.53, 0.51	0.47, 0.49	0.88, 0.87	0.88, 0.89	0.10	0.98	0.99	0.09	0.99	0.99	0.21
(α1,β1)=(1,2.3),(α2,β2)=(1.2,2.8)
0.1, 0.9	0.03, 0.03	0.25, 0.24	0.64, 0.67	0.79, 0.78	0.98, 0.98	0.09	0.41	0.77	0.16	0.81	0.81	0.77
0.2, 0.8	0.08, 0.07	0.43, 0.41	0.50, 0.52	0.86, 0.85	0.93, 0.94	0.12	0.57	0.81	0.21	0.78	0.80	0.59
0.3, 0.7	0.15, 0.14	0.58, 0.56	0.40, 0.42	0.91, 0.90	0.88, 0.88	0.13	0.61	0.78	0.13	0.63	0.79	0.31
0.4, 0.6	0.23, 0.22	0.70, 0.68	0.31, 0.33	0.94, 0.94	0.81, 0.82	0.19	0.70	0.81	0.16	0.66	0.82	0.29
(α1,β1)=(1,2.3),(α2,β2)=(1.3,3.03)
0.1, 0.9	0.03, 0.02	0.25, 0.23	0.64, 0.68	0.79, 0.77	0.98, 0.98	0.24	0.81	0.99	0.31	0.99	0.98	0.89
0.2, 0.8	0.08, 0.07	0.43, 0.41	0.50, 0.54	0.86, 0.84	0.93, 0.94	0.25	0.84	1.00	0.25	1.00	1.00	0.71
0.3, 0.7	0.15, 0.14	0.58, 0.55	0.40, 0.43	0.91, 0.89	0.88, 0.89	0.24	0.89	0.96	0.33	0.93	0.98	0.54
0.4, 0.6	0.23, 0.21	0.70, 0.67	0.31, 0.34	0.94, 0.93	0.81, 0.83	0.30	0.96	0.97	0.25	0.93	0.98	0.42

Estimates are based on 100 simulations for each set of parameter values. Bootstrap variances were based on B=500 replicates.

7. Data example

To illustrate the various estimates of PCF, PNF, iPCF, and iPNF, we used data from a validation study of a colorectal cancer (CRC) risk prediction model (Freedman and others, 2009) that was developed to aid decision making for colorectal cancer screening. The risk model R estimates the probability, or absolute risk (also called cumulative incidence), of the binary event defined as “developing CRC during the age interval (a,b], given that one is alive and free of CRC at age a”. Letting T denote the failure time, the absolute CRC risk R is

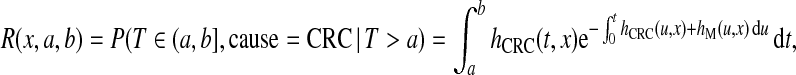where x denotes individual covariates, h_CRC(t,x) is the cause-specific hazard for CRC, and h_M(t,x) denotes the competing mortality hazard.

The validation data were from an independent sample of 108 057 women from a prospective cohort, the National Institutes of Health (NIH)-AARP Diet and Health Study (Park and others, 2009). For the ith woman in the validation cohort the starting age a_i of the prediction was her age at entry into the cohort, and the end of the prediction interval, b_i, the age the woman had at the sooner of the end of study or loss to follow-up. Note that b_i does not depend on whether the woman died or developed CRC. These events are accounted for in the calculation of absolute risk R. For the validation, we thus define the event as Y _i=1 if woman i develops CRC in (a_i,b_i] and Y _i=0 otherwise. The mean follow-up time was 6.9 years, and 965 women were diagnosed with CRC during follow-up. For estimates of PCF, PNF, iPCF, and iPNF based on case–control data, the disease prevalence μ was the observed incidence of CRC in the validation cohort.

Based on risk predictions for all 108 057 women in the study, R had 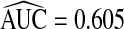. Estimates 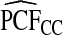and 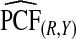were basically identical, but the latter had slightly wider confidence intervals as the uncertainty from estimating μ is also accommodated (Table4). For example, for p=0.10, 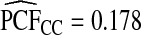with 95% CI (0.155,0.202) and 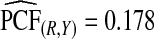(0.152,0.205); thus, 17.8% of the cases were in the 10% of women at highest risk. However, for p=0.10, 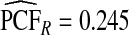(0.244,0.246), which noticeably overestimated the observed PCF=0.178. For PNF, a fraction 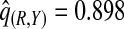of cases was found in the fraction 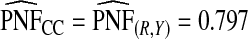of the population with the highest risk when q=0.90, showing an unbiased estimation of PNF. However, only a fraction 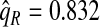of cases was found in the fraction 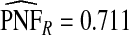of the population with highest risk when q=0.90. Thus, only 83.2% of cases instead of the desired 90% had risks in the highest 71.1% of the population, reflecting poor calibration. 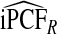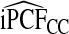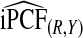Similarly, estimates were higher than and , and 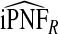were lower than estimates 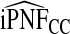and 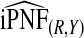(Table4).

Table 4.

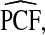
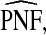
Estimates 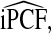and 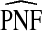(with 95% bootstrap confidence intervals in parenthesis) based on the observed distribution of risks R and outcome data for CRC in AARP women

p	PCF*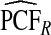
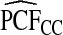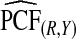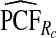0.10	0.178	0.245 (0.244, 0.246)	0.178 (0.155, 0.202)	0.178 (0.152, 0.205)	0.179
0.20	0.313	0.415 (0.413, 0.416)	0.313 (0.284, 0.342)	0.311 (0.277, 0.345)	0.307
0.30	0.423	0.551 (0.549, 0.552)	0.420 (0.387, 0.452)	0.420 (0.377, 0.462)	0.418
0.40	0.549	0.663 (0.662, 0.664)	0.547 (0.515, 0.579)	0.547 (0.500, 0.594)	0.518
q		,		,	,
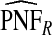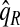
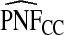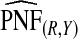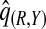
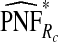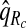
0.90		0.711 (0.710, 0.712), 0.832	0.797 (0.784, 0.810)	0.797 (0.737, 0.858), 0.898	0.857, 0.927
0.80		0.556 (0.555, 0.557), 0.704	0.660 (0.641, 0.679)	0.661 (0.600, 0.723), 0.800	0.725, 0.839
0.70		0.438 (0.437, 0.439), 0.585	0.543 (0.518, 0.569)	0.545 (0.490, 0.599), 0.691	0.602, 0.751
0.60		0.342 (0.341, 0.343), 0.473	0.446 (0.418, 0.473)	0.447 (0.393, 0.501), 0.597	0.488, 0.635
p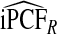
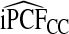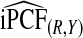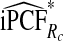0.10		0.667 (0.666, 0.668)	0.592 (0.589, 0.596)	0.592 (0.575, 0.609)	0.572
0.20		0.634 (0.633, 0.634)	0.568 (0.565, 0.572)	0.567 (0.552, 0.582)	0.547
0.30		0.585 (0.585, 0.586)	0.530 (0.527, 0.533)	0.530 (0.517, 0.543)	0.511
0.40		0.524 (0.524, 0.525)	0.482 (0.479, 0.486)	0.483 (0.472, 0.493)	0.464
q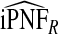
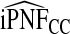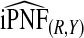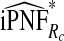0.90		0.083 (0.082, 0.083)	0.086 (0.084, 0.089)	0.086 (0.084, 0.089)	0.093
0.80		0.145 (0.145, 0.146)	0.160 (0.154, 0.165)	0.160 (0.154, 0.165)	0.172
0.70		0.195 (0.195, 0.195)	0.216 (0.207, 0.224)	0.216 (0.208, 0.225)	0.238
0.60		0.234 (0.233, 0.234)	0.268 (0.258, 0.278)	0.269 (0.259, 0.279)	0.293

The corresponding observed proportion of cases PCF* found among the fraction q of the AARP population at highest risk and the proportions p_R and p_CC of cases found among the fractions 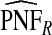and 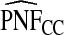of the AARP population at highest risk are also shown. 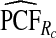and 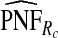are based means over five test sets of the model after recalibration using 5-fold cross-validation.

To illustrate the importance of good calibration for estimates of PCF, PNF, and iPCF and iPNF based on observed risks alone, we recalibrated the model and recalculated these estimates using 5-fold cross-validation. That is, we split the AARP cohort randomly into five equal-sized datasets, and used four of them to recalibrate the model by fitting a logistic regression model to observed CRC outcomes with the risk estimate r as the independent variable (Cox, 1958). This simple recalibration requires estimating only two parameters, the logistic intercept β₀ and slope β₁. We then used logit(r_c)=β₀+β₁r to predict CRC outcomes for women in the remaining fifth of the data, the test set, to estimate the criteria with the recalibrated model. The last column of Table4 shows averages of estimates of PCF, PNF, iPCF, and iPNF over the five test sets. After recalibration 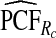was less biased, e.g. 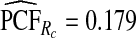for p=0.10. Similarly, a fraction 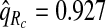of cases was found in the fraction 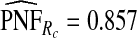of women at highest risk when q=0.90, reflecting improved calibration of R_c. Estimates and 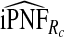were also noticeably closer to 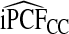and .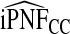

8. Discussion

We proposed two new criteria for model evaluation, iPCF and iPNF, respectively, which lessen the dependency of earlier criteria, PCF and PNF, on prespecified thresholds. PCF(p)=1−G∘F⁻¹(1−p) resembles the ROC value, which can be expressed as ROC(p)=1−G∘K⁻¹(1−p) (Huang and Pepe, 2009). Similarly, iPCF that also is based on comparing the distribution of risk in cases to the distribution of risk in the whole population instead of in non-cases, relates to the AUC, the partial area under the ROC curve, pAUC, or more generally, to the weighted area under the ROC curve (Li and Fine, 2010). For rare diseases, they tend to be very similar, but derivations of the asymptotic properties for criteria based on PCF and PNF are more involved, as unlike the estimates of the ROC curve and the (partial) AUC, the risks in the population and in cases are not independent. The comparison of risk in cases to non-cases is appropriate for diagnostic tests that are applied in a clinical setting. However, for risk models that may be used to identify high-risk individuals for screening or for assessing the impact of a screening program in a population, criteria based on comparing the risk of cases to the risk in the whole population are more relevant (Pharoah and others, 2002).

While decision making based on risk models for public health applications ultimately needs to incorporate cost considerations, the proposed criteria can aid in the initial assessment of the feasibility of a screening or intervention program. For example, assume that one can only afford to screen 10% of a population. If a particular model has a low PCF or high PNF, targeting those at highest risk based on that model will have limited preventive impact. In contrast, if a model has a high PCF or a low PNF, then a targeted screening program may identify a large proportion of the disease and reduce costs and the burden of screening. A more complete understanding is provided by iPCF and iPNF, which display the proportion of disease accounted for by cumulative proportions of individuals in the population ranked from the lowest to highest risk.

The new criteria are also useful for comparing two risk models evaluated on the same dataset. A test for comparing two models based on PCF had comparable power to a test based on pAUC. However, a test for model comparison based on iPCF had significantly better power than a test based on PCF, while the tests based on PNF and iPNF had similar power.

We also studied estimates of PCF, PNF, iPCF, and iPNF when either risk estimates alone, or risk estimates and outcomes in a case–control study with known prevalence or in a cohort study are available. Estimates that also used outcome data were less efficient than estimates that were based on only observed risks and the assumption that the model was well calibrated. The efficiency gain comes from the fact that, for a well-calibrated model, knowing F implies knowing G, the distribution of risk in the cases. All the observed risks in a population are thus used to estimate G. When one estimates G from the risks in observed cases in a cohort, i.e. based on (R,Y), the effective sample size is much reduced, leading to substantial losses in efficiency. However, as also highlighted by our real example, estimates of PCF, PNF, iPCF, and iPNF based on R alone are biased when the model is not well calibrated, and model comparisons can be misleading. In practice, if outcome data are not available, one is forced to use estimates such as 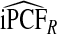. If outcome data are available, one can compute 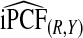. If there are large discrepancies, one must suspect miscalibration and rely on 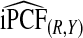. We thus recommend using estimates of the criteria based on R alone, but comparing them to estimates that also use Y to check unbiasedness.

Supplementary material

Supplementary material is available at http://biostatistics.oxfordjournals.org.

Funding

Intramural Research Program of the Division of Cancer Epidemiology and Genetics, National Cancer Institute.