Rotational Mobility of Single Molecules Affects Localization Accuracy in Super-Resolution Fluorescence Microscopy

Abstract

The asymmetric nature of single-molecule (SM) dipole emission patterns limits the accuracy of position determination in localization-based super-resolution fluorescence microscopy. The degree of mislocalization depends highly on the rotational mobility of SMs; only for SMs rotating within a cone half angle α > 60° can mislocalization errors be bounded to ≤ 10 nm. Simulations demonstrate how low or high rotational mobility can cause resolution degradation or distortion in super-resolution reconstructions.

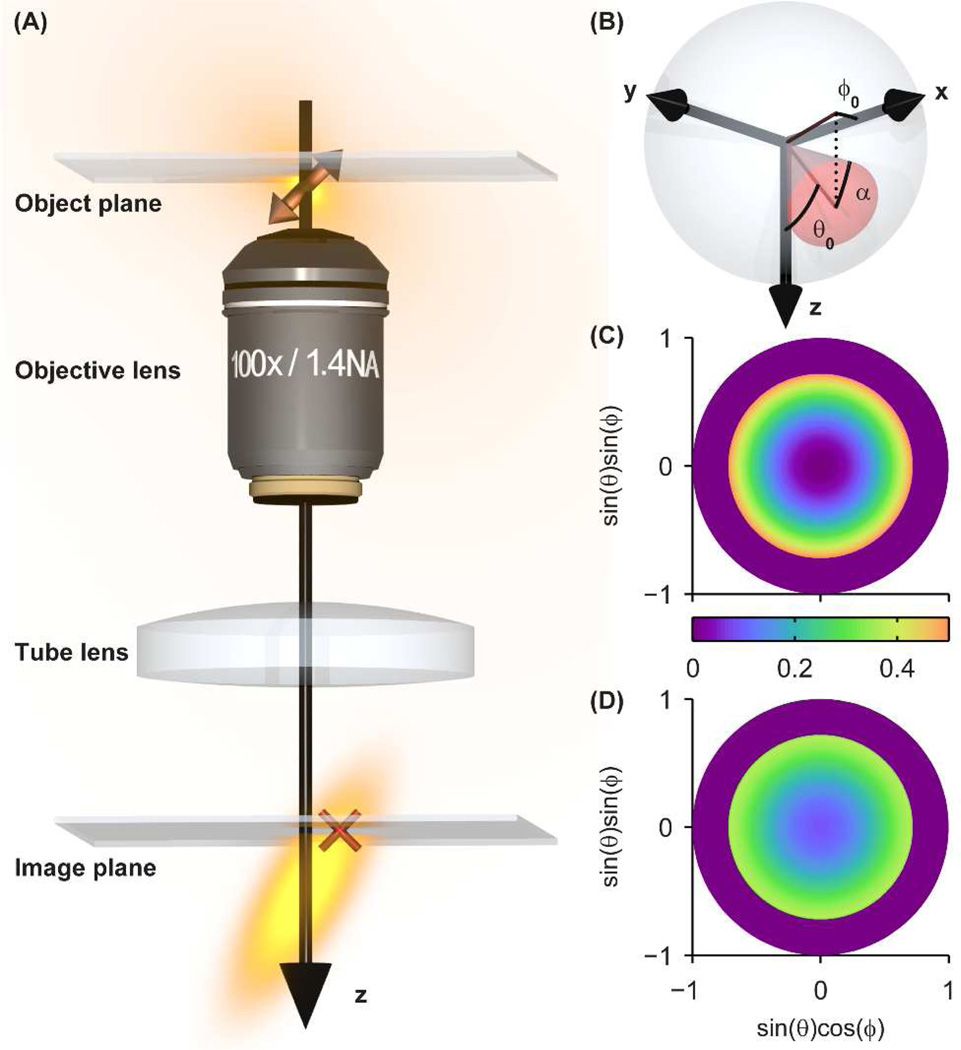
The advent of super-resolution far-field fluorescence microscopy has enabled non-invasive imaging of biological specimens at resolution well beyond the optical diffraction limit.^{1, 2} Of these techniques, a large class including (f)PALM^{3, 4} and STORM⁵ obtains this resolution improvement by 1) using active control of the emitting concentration in each frame to temporally separate the emission signals of single molecules (SMs) that label a structure, 2) extracting the position of each SM by finding the center of its photon distribution to precision on the order of tens of nanometers, and 3) reconstructing a pointillist image of the structure in post-processing. This class of techniques is known collectively as Single-Molecule Active Control Microscopy (SMACM). A key assumption underlying most SMACM analysis techniques is that the center of the photon distribution emitted by a SM corresponds to its true position. While this assumption holds for an isotropic point emitter, SMs are known to exhibit asymmetric dipole emission patterns that depend highly on the orientation of the molecular dipole relative to the imaging system,⁶ which results in an effective tilting of the three-dimensional (3D) point spread function (PSF) as depicted in Figure 1A. This tilted PSF means that for a molecule exactly at the focal plane, the peak of its photon distribution coincides closely with its true position, but if the molecule is above or below the focal plane, the peak of the distribution is laterally displaced from the molecule’s true position. Previous reports have noted that failing to account for this asymmetry can lead to significant localization errors (up to ~ 100–200 nm at modest defocus) when employing typical estimators of the molecular position from a detected image such as centroid calculation or fitting to a two-dimensional (2D) Gaussian function.^7–10 These studies address the worst case, i.e., molecules that are fixed in orientation on the timescale of imaging. If, on the other hand, molecules are free to sample a range of orientations during a single imaging frame, the recorded photon distribution is a superposition of images of SMs at various fixed orientations. In the limit that an emitting molecule is sufficiently rotationally mobile such that it uniformly samples all possible orientations during an image acquisition, the resulting photon distribution will again be symmetric about the true position of the molecule and thus no systematic localization error will be incurred. If a molecule has intermediate rotational mobility, then the mislocalization will be only partially mitigated. The effect of rotational mobility on single-molecule localization error has not, to the best of our knowledge, been quantitatively explored previously. In this report we provide a full theoretical treatment of the reduction of systematic dipole-induced localization inaccuracy due to rotational mobility and quantitate the effects on resolution and distortion of biologically inspired simulated images.

Figure 1.

Overview of SM dipole emission and rotational diffusion. (A) The emission pattern of a fixed SM in the object space of a microscope, consisting of an objective lens and tube lens, creates an asymmetric elongated 3D PSF in the image space. Slight defocus (here illustrated with the emitter below the focal plane) causes the lateral (x,y) photon distribution in the image plane to be shifted (red cross) relative to the true molecular position in the object plane. (B) Our model of rotationally diffusing SMs involves confinement to a hard-edged cone of orientation (θ₀, ϕ₀) and half angle α in spherical orientation space. The (C) photon absorption probability density and (D) image weighting factor η(θ, ϕ) for a cone of orientation (θ₀, ϕ₀) = (0°,0°) pointing toward the viewer and half angle α = 45° are plotted in two-dimensional orientation space with definitions given by the axis labels.

In a typical SM-based super-resolution experiment either small-molecule fluorophores or fluorescent proteins are attached to the structure of interest via linker molecules. While the linker precludes each molecule from translating freely, a fluorophore may still be able to rotate during imaging in certain conditions. The degree of rotational mobility is a function of a number of factors, including linker length and local environment.¹¹ While the effects of 3D rotations on single-molecule fluorescence images has been treated for applications to molecular motors in the regimes of slow and fast wobble previously,^{12, 13} here we seek to consider the more general case because the rotational relaxation times of some small dyes and fluorescent proteins are on the same order as their fluorescence lifetimes (~1–10 ns). We invoke a model for describing constrained rotational diffusion of molecules in which they rotate freely within a hard-edged cone of fixed half angle α (Figure 1B). Since the imaging times are on the order of 1 ms (and thus much larger than the fluorescence lifetime or rotational correlation time), we assume a molecule samples its allowed cone uniformly and continuously. This model has been used previously in the contexts of bulk anisotropy,¹⁴ NMR,¹⁵ and FRET^16–18 measurements. The theory described below is a 3D extension of previous work describing in-plane single-molecule rotational mobility.¹⁹

Within the cone angle model, the recorded image Ī of a SM will be a weighted integral over the images I(θ, ϕ) corresponding to each emission orientation (θ, ϕ) within the cone that is visited during a camera exposure, given by the equation

$$Ī(\alpha ,{\theta }_0,{\varphi }_0)=\underset{S(\alpha ,{\theta }_0,{\varphi }_0)}{\iint }d\theta d\varphi \text{sin}\theta \eta (\theta ,\varphi )I(\theta ,\varphi )$$ (1)

where α is the half angle of the cone, θ₀ and ϕ₀ are the polar and azimuthal orientation angles of the cone, respectively, S is the surface of the spherical section subtended by the cone and the unit sphere, and η(θ, ϕ) is an image weighting factor that bears the relative contributions of each I(θ, ϕ) to the final image. Full derivations and calculation details related to the evaluation of equation 1 are described in the supporting information; however, we present a brief description here. To compute each I(θ, ϕ) (256×256 pixels, 7.4-nm pixel size in object space), we performed full vectorial diffraction calculations of dipole emitters (emission λ = 609 nm) immersed in index-matched media (n = 1.518) imaged with an oil-immersion microscope objective of 100× magnification and numerical aperture 1.4.^{7, 10} A closed-form expression for the weighting factor η(θ, ϕ) requires a coordinate transformation which is not essential for our discussion here but is given in full detail in the supporting information. More qualitatively, η(θ, ϕ) includes contributions from three relevant probability distribution functions (PDFs). The first describes waiting times for emission after absorption at time t = 0, given by f(t) = e^−t/τ_F /τ_F. Here τ_F is the fluorescence lifetime, which is typically on the order of ~1 ns. In our calculations, we used τ_F = 3.5 ns, corresponding to a typical lifetime of both small molecule dyes and fluorescent proteins.²⁰ The second PDF contributing to η(θ, ϕ) represents photon absorption (Figure 1C) and is proportional to |μ⃑(θ′, ϕ′) · E⃑_inc|², where μ⃑(θ′, ϕ′) is a unit vector with orientation (θ′, ϕ′) (the orientation upon absorption at time t = 0), and E⃑_inc is the incident electric field. Here, we assumed a collimated circularly polarized excitation beam to approximate conditions used in standard widefield fluorescence imaging in which the pumping beam contains negligible amounts of z-polarized light. The last factor contributing to η(θ, ϕ) is the conditional PDF of a SM having rotated to orientation (θ, ϕ) (where it emits) at time t, given that it was at orientation (θ′, ϕ′) (where it absorbed) at time t = 0. This factor is a solution to the rotational diffusion equation subject to the boundary conditions set by the cone edges. Its analytical form is given elsewhere²¹ and depends implicitly on the rotational diffusion coefficient D_rot, which we assumed to be equal to 8.3 × 10⁶ rad²/s (corresponding to a rotational correlation time τ_R = 20 ns) based on previous measurements of GFP in PBS solution.²² Emitters with smaller τ_R typical of small molecule emitters are discussed below. Rotational diffusion has the effect of blurring or smearing η(θ, ϕ), which would otherwise be equal to the absorption PDF in the limit that the excited state lifetime is much shorter than the rotational relaxation time; in other words, if the absorption and emission dipoles are collinear. (While not always strictly true, the assumption of collinear absorption and emission dipoles is justified by the fact that these two vectors are collinear²³ or nearly collinear¹⁹ for many common fluorophores. Allowing for these moments to be nonparallel would require an additional factor to be carried through our calculations, which we choose to omit for simplicity.) Combining these three PDFs, we obtain the image weighting factor η(θ, ϕ) (Figure 1D and Figure S1). Note that, due to rotational mobility, the relative weighting of inclined angles (θ near 90°) and shallow angles (θ near 0°) are decreased and increased, respectively, compared to pure absorption alone. Under certain conditions of fluorophore attachment, small molecule emitters may rotate ~10 or more times faster than fluorescent proteins.²⁴ As expected, η becomes increasingly blurred when we calculate with a diffusion coefficient 10 times larger (Figure S2).

We used custom-written MATLAB routines to calculate η(θ, ϕ), and thus Ī, for various (α, θ₀, ϕ₀) and defocus (z). Resulting single-molecule images were then fit using nonlinear least squares regression to a 2D Gaussian function, and the apparent (x,y) positions were extracted and compared to the true positions to yield apparent lateral shifts, (Δx,Δy). Notably, the symmetry of the dipole image simplifies our simulations in that lateral shifts are always along the molecular tilt direction cos(ϕ₀)î + sin(ϕ₀)ĵ, and images Ī(α, θ₀, ϕ₀ ≠ 0°) are simply rotated versions of Ī(α, θ₀, ϕ₀ = 0°). Thus, we describe the lateral shifts due to constrained rotational diffusion of SMs in terms of radial distance Δr in order to cover all possible cases of lateral shift.

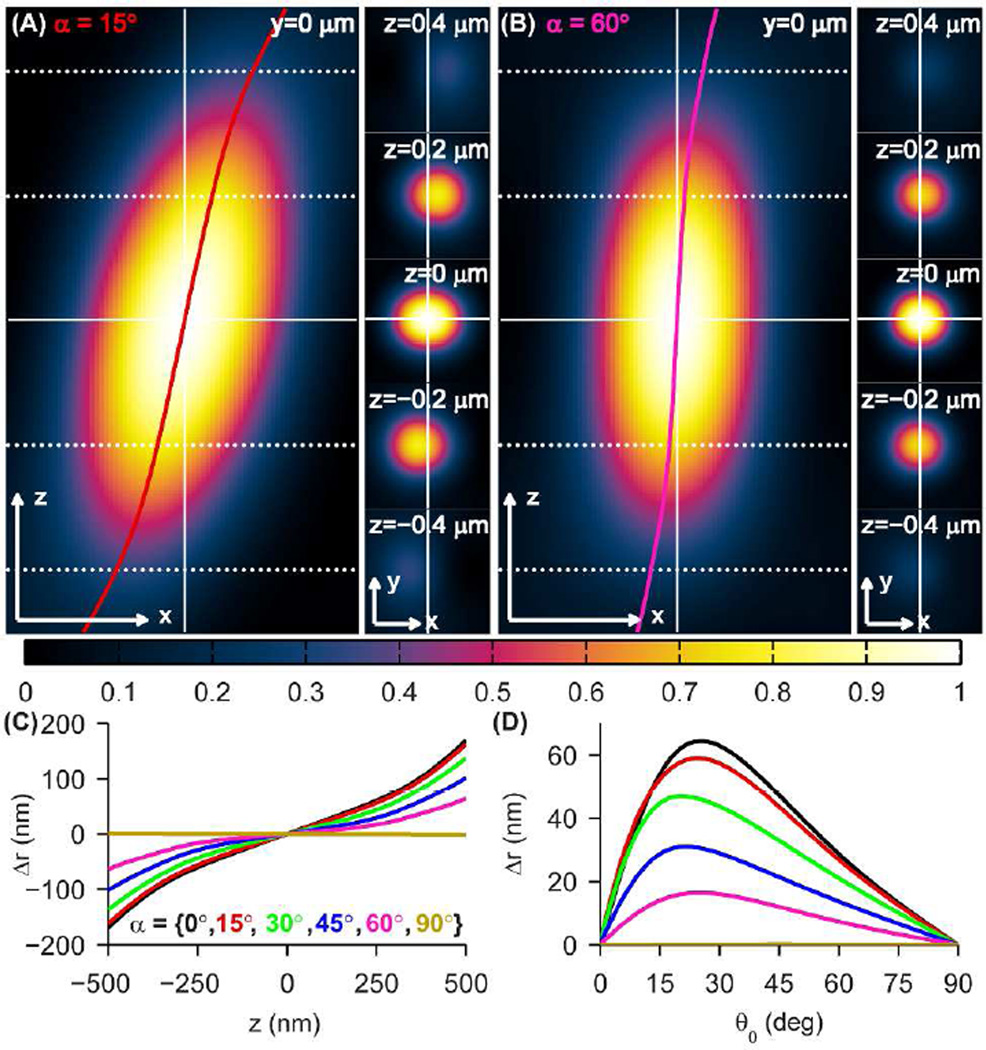
The simulated effect of cone angle on the 3D PSF is shown in Figure 2A–B. For a small cone angle, α = 15°, the 3D PSF is similar to that of a fixed SM and shows a significant lateral shift Δr of ±44 nm at z = ±200 nm up to ±162 nm at z = ±500 nm for cone axis orientation (θ₀, ϕ₀) = (45°,0°) (Figure 2A). In contrast, the vertical (untilted) 3D PSF of an isotropic emitter is mostly recovered for the case of α = 60° (Figure 2B). The effect of defocus on lateral shift Δr(z) for various α between 0° (fixed orientation) and 90° (unconstrained rotation) is shown in Figure 2C for the same cone axis orientation. We observe that the magnitude of lateral shift increases monotonically with defocus, becoming increasingly nonlinear for |Δz| > 200 nm. Figure 2D depicts lateral shift Δr(θ₀) as a function of the cone’s polar orientation at fixed defocus (z = 200 nm) for the same values of α (see Figure S3 for PSF cross-sections for other cone angles α). While the lateral shift is worst for θ₀ near 20°–25°, the relative brightness of SMs at these orientations is 8%–55% compared to SMs at θ₀ = 90° depending on the size of the cone (Figure S3). In particular, for small cone angles, molecules with larger shifts have a smaller probability of being detected in an experiment. In terms of both defocus z and the cone’s polar orientation θ₀, Δr decays nonlinearly as α increases to the limit that Δr = 0 for unconstrained rotation. Therefore, small degrees of rotational diffusion do not effectively reduce lateral shift; rotational diffusion must be largely unconstrained (α > 60°) in order to reduce shift below 10 nm for all orientations.

Figure 2.

SM rotational diffusion effects on 3D PSFs and lateral shifts. (A) xz (left) and xy (right) cross-sections of the 3D PSF for a SM diffusing within the cone (α, θ₀, ϕ₀) = (15°,45°,0°). The lateral shift Δr(z) is overlaid in red. (B) Same as (A) for a SM diffusing within the cone (α, θ₀, ϕ₀) = (60°,45°,0°). The lateral shift Δr(z) is overlaid in magenta. The various z-planes containing the xy cross-sections are denoted by horizontal dotted/solid lines at left. Scale/axes arrows: 200 nm. (C) Lateral shift Δr as a function of axial position z for θ₀ = 45° and cone angles α = {0° (black), 15° (red), 30° (green), 45° (blue), 60° (magenta), 90° (gold)}. (D) Lateral shift Δr as a function of cone axis orientation θ₀ for z = 0.2 µm and the same cone angles α as in (C).

In a super-resolution imaging experiment, however, the 3D PSF is sampled by a detector with nonzero pixel size. Accordingly, we simulated the pixelated 3D PSFs and lateral shifts as they would be measured by a typical camera (65-nm pixel size in object space), shown in Figure S4. Pixelation does not noticeably affect the measured 3D PSFs or lateral shifts within |z| ≤ 300 nm compared to Figure 2, but outside this range, there are small differences in lateral shifts (≤ 30 nm). Overall trends as a function of α and z, however, are unaffected by pixelation. Other experimental noise effects, such as finite photons detected from each single molecule and detector read noise, would cause a variance in the detected position of each single molecule, but the expected position error Δr for each measurement would be unaffected.

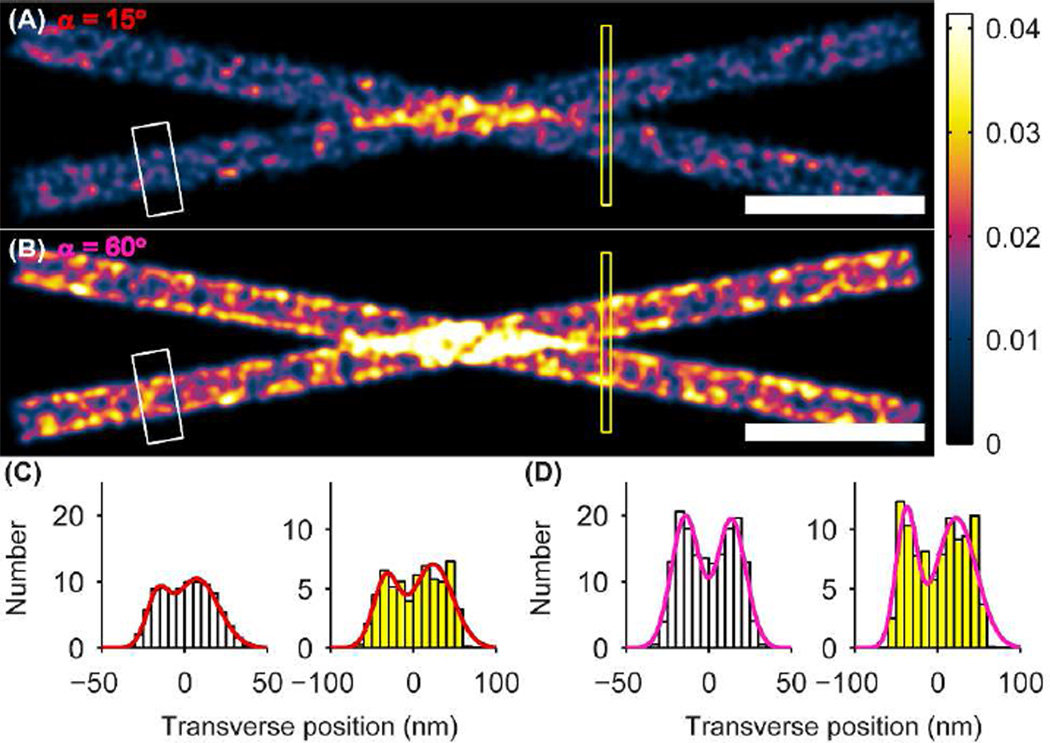
As mentioned, the degree of rotational mobility can potentially have significant effects on a reconstructed super-resolution image. To demonstrate this, we simulated a super-resolution image of two crossing microtubules (Figure 3). The microtubules are each simulated as hollow cylinders oriented perpendicular to the optical axis with diameter 40 nm, consistent with microtubules labeled with small molecule fluorophores via primary and secondary antibodies.²⁵ The microtubule centers are separated in z by a total of 200 nm, with one located 100 nm above the focal plane and the other 100 nm below. We simulated the labeling of each cylinder by producing molecular positions whose density was Poisson distributed with mean dictated by the Nyquist sampling theorem [(2/10 nm)²]. Each molecule was assigned a mean orientation (θ₀, ϕ₀) drawn such that the unit sphere was sampled with uniform probability density. To produce the reconstruction, the modeled lateral shift Δr was added to each molecular position, and then a Gaussian of full width at half maximum of 10 nm was convolved with each position to simulate the effects of localization precision due to finite SNR (each SM was plotted with an identical Gaussian spot). In an actual SMACM experiment each of these Gaussians would be sampled only a few times; however, we include the entire localization distribution function in the image in order to suppress sampling noise in the ensuing histograms (Figure 3C–F) and emphasize the effect of lateral shift errors. This choice corresponds for instance to a STORM experiment in which many molecular switching cycles allow each SM’s position to be sampled many times. An equivalent choice would be to simulate two parallel microtubules, sample each Gaussian a small number of times, then histogram over the full length of the cylinders. We instead elected to simulate crossing microtubules so that we could make use of the variation in separation distance within a single image. Qualitative and quantitative differences are readily apparent between the simulated image corresponding to α = 15° (Figure 3A) and that corresponding to α = 60° (Figure 3B). First, the labeling appears to be less dense in the more restricted case, despite identical labeling positions, number, and density in both images. This effect is due to the fact that in the more constrained case, more molecules are fixed at orientations that render them dimmer and thus harder to detect (Figure S3). In each image, we selected a rectangular area along one of the microtubules (white boxes in Figure 3A–B) and collapsed the data into histograms transverse to the tubules (Figure 3C–D). For the less constrained case (Figure 3D), this histogram contains resolvable peaks near each edge of the microtubule, exemplified by the peaks in the double Gaussian fit overlay. This effect is due to the hollow nature of the microtubule labeling and the fact that near the edges, molecules from many different z contribute to the summed signal.²⁵ By contrast, the corresponding histogram for the more constrained case (Figure 3C) shows no sharp peaks at the edges. The large, stochastic shifts of more constrained, highly oriented molecules blur the edges significantly. Another consideration relevant to real experiments is the additional random sampling noise associated with stochastic switching of SMs. Combining the two aforementioned effects could help explain why the hollow cores of otherwise equivalently labeled microtubules are not always resolvable.²⁶ To highlight another difference between the images, we histogrammed the data within the yellow boxes in Figure 3A–B, where the separation of the microtubules is near the resolution limit set by labeling density and the Gaussian convolution kernel. In the less constrained case the histogram shows two clearly resolvable peaks, especially in the double Gaussian fit (Figure 3D). By contrast, the resolvability of the two microtubules is worsened in the more constrained case (Figure 3C). While the double-peaked behavior is discernible in all of the histograms, the contrast from peak to valley is much smaller in the α = 15° case; the aforementioned SM sampling noise would most likely blur these peaks together to render them unresolvable in an actual experiment. It is also worth noting that in a real experiment one may detect crossing microtubules with even greater depth separation, as large as ~500 nm. In such a case the shifts will be even larger in the highly constrained dipole case and thus the degradation will be even more dramatic.

Figure 3.

SMACM imaging simulation of crossing microtubules separated in z by 200 nm whose SM labels form a hollow cylindrical shell of diameter 40 nm. Molecular dipole orientations of the labels are drawn from a uniform distribution. (A) Microtuble image for SM labels confined to a cone of half angle α = 15°. (B) Same as (A) for SM labels confined to a cone of half angle α = 60°. The white and yellow boxes denote the regions histogrammed in (C)–(D). The color scale is in units of number of SMs/(0.5 nm)². Scale bars: 200 nm. (C) Transverse histograms of one hollow cylindrical microtubule (white, at left) and of the two microtubules near their crossing point (yellow, at right) for α = 15°. Double-Gaussian fits of these histograms are overlaid in red. (D) Same as (C) for α = 60°. Double-Gaussian fits of these histograms are overlaid in magenta.

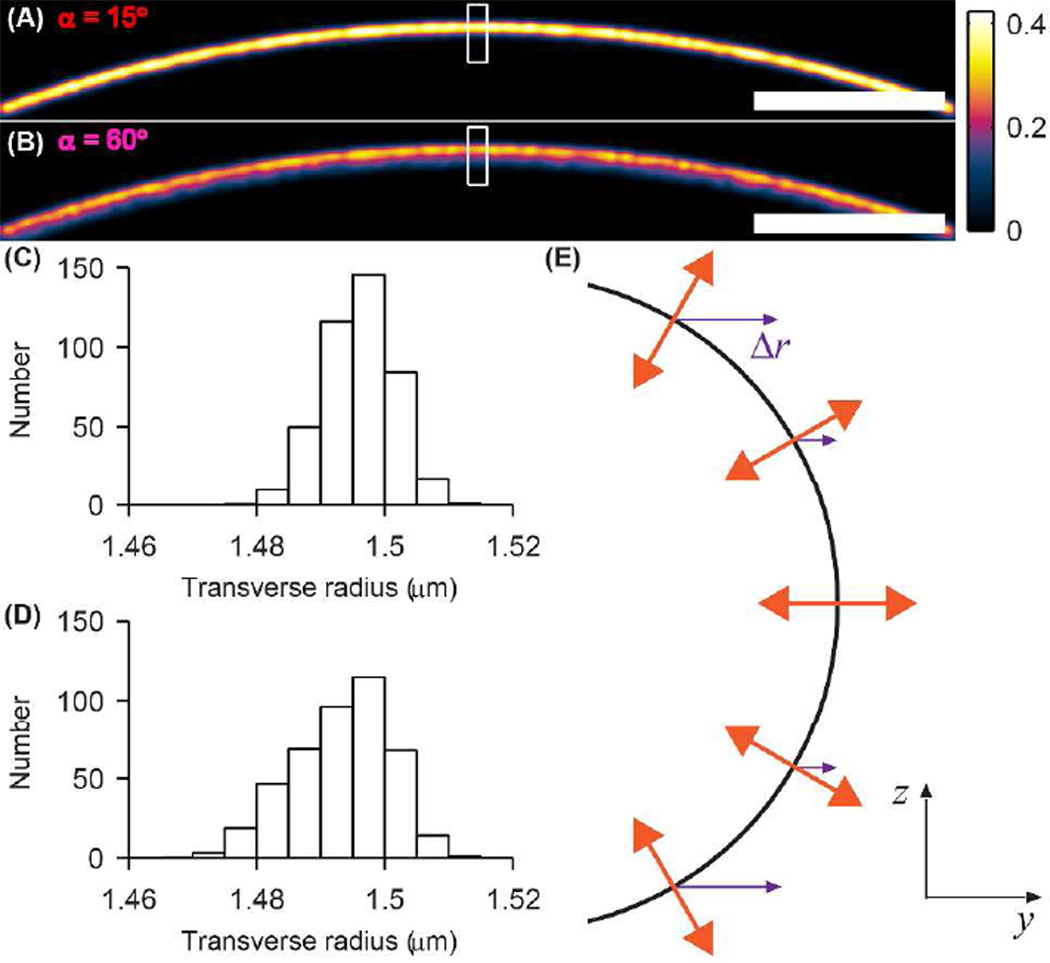
To demonstrate image distortion resulting from insufficient rotational mobility, we simulated a fluorescently labeled hemispherical “cell membrane” (Figure 4) of diameter 3 µm corresponding, for example, to the end cap of a fission yeast cell. The hemisphere is positioned and oriented such that the focal plane divides it into two halves. Molecular positions were produced in the same way as in the microtubule images. Unlike the microtubule case, we chose to assign (θ₀, ϕ₀) of each molecule deterministically. Previous measurements have shown that certain fluorophores embedded within lipid membranes tend to orient themselves such that their dipoles are orthogonal to the surface of the membrane,²⁷ and so we oriented each molecule as such. Since the membrane extends beyond the microscope’s depth of field in the axial direction, only molecules within 260 nm of the focal plane contribute to our analysis here, corresponding to molecules that are at least half the intensity of molecules in the focal plane. The effect of this nonrandom orientation distribution on the α = 15° (Figure 4A) and α = 60° (Figure 4B) images is striking. In the less constrained case (Figure 4B) there is peaking in intensity at the far (distal) edge of the cell, the location of the membrane. Moving inward from the edge, there are molecules above and below the focal plane whose lateral positions, when projected onto the focal plane, lie within the cell and contribute to a smoothly decaying signal. This is further illustrated in the histogram (Figure 4D) of the data within the marked white box. For the more constrained case, the corresponding image (Figure 4A) and histogram (Figure 4C) remarkably show a thinner, brighter cell edge. While the apparent position of the edge has not changed, signal from the smoothly decaying tail has seemingly been shunted back toward the edge. This surprising result is explained in Figure 4E. While dipoles located at the equator of the cell are oriented with θ₀ = 90°, molecules above and below the plane exhibit increasingly shallow θ₀. Thus, the magnitude of Δr increases monotonically for molecules at greater and greater distances from the focal plane. Furthermore, dipoles within a given vertical slice all have the same ϕ₀ and thus the same direction of lateral shift, shown as purple arrows. Hence, as one moves up or down in z away from the focal plane in Figure 4E, though the true y positions of the molecules decrease, the apparent lateral shifts partially compensate to yield apparent positions nearer to the far edge of the membrane. In this case, the dipole mislocalization effect can actually help one detect the edge of the cell membrane.

Figure 4.

SMACM imaging simulation of a cell membrane whose labels form a hollow hemispherical shell of radius 1.5 µm and are orientated normal to the membrane surface. (A) Membrane image for SM labels confined to a cone of half angle α = 15°. (B) Same as (A) for SM labels confined to a cone of half angle α = 60°. The white box denotes the region histogrammed in (C)–(D). The color scale is in units of number of SMs/(0.5 nm)². Scale bars: 200 nm. (C) Transverse histogram of SMs labeling the membrane for α = 15°. (D) Same as (C) for α = 60°. (E) yz schematic depicting the simulated orientation (orange) and relative lateral shift Δr (purple) of SMs labeling the hemispherical cell membrane (black) with the prescribed orientation distribution.

In conclusion, we have shown that significant rotational mobility is needed in order to palliate the localization inaccuracy that otherwise results from the anisotropic emission patterns of single molecules in 2D SMACM experiments. The severity of this mislocalization depends highly on the degree of rotational mobility exhibited by the molecule, here varied by tuning the angle of the cone in which the molecule is allowed to freely rotate. Our results demonstrate that changing the amount of rotational mobility can cause substantial variability in the features of reconstructed SMACM images.

While our calculations were performed assuming a D_rot corresponding to a relatively large probe (GFP), we do not expect the functional form of the mislocalization to depend heavily on this parameter. To corroborate this claim, we re-simulated the case of α = 30° using a 10× larger D_rot (τ_R = 2 ns; e.g. corresponding to a small molecular dye embedded in a neutral micelle²⁴) (Figure S2). Though η(θ, ϕ) is blurred out significantly as compared to the larger D_rot case, the values of Δr(z) and Δr(θ₀) change very little (≤ 8 nm difference in Δr, Figure S2).

Our results make it apparent that in order to accurately bound the amount of mislocalization that can be expected in a given experiment, it may be necessary to measure the apparent lateral shifts or rotational anisotropy directly. For instance, if one wishes to ensure that α > 60° such that Δr ≤ 10 nm, a normalized steady-state anisotropy less than about 0.14 would be sufficient.¹⁴ Larger bulk anisotropies can be tolerated if the fluorophore explores a sufficiently large cone angle on the time scale of single-molecule imaging. Qualitative metrics such as judging the amount of asymmetry exhibited by defocused images may be insufficient to sense localization error since these images are very similar over a large range of α, especially when sampled with a camera of typical pixel size (Figure S5). Our previous report shows that if single molecules are rotationally immobile, the Double-Helix Point Spread Function (DH-PSF) is capable of simultaneously measuring the 3D position and orientation of a molecule, and recovering its true lateral position.¹⁰ In the future this study will be extended to account for varying levels of rotational mobility.

ABBREVIATIONS

SM

single molecule

SMACM

single-molecule active control microscopy

3D

three-dimensional

PSF

point spread function

PDF

probability distribution function

GRP

green fluorescent protein