Precision Sensing by Two Opposing Gradient Sensors: How Does Escherichia coli Find its Preferred pH Level?

Abstract

It is essential for bacteria to find optimal conditions for their growth and survival. The optimal levels of certain environmental factors (such as pH and temperature) often correspond to some intermediate points of the respective gradients. This requires the ability of bacteria to navigate from both directions toward the optimum location and is distinct from the conventional unidirectional chemotactic strategy. Remarkably, Escherichia coli cells can perform such a precision sensing task in pH taxis by using the same chemotaxis machinery, but with opposite pH responses from two different chemoreceptors (Tar and Tsr). To understand bacterial pH sensing, we developed an Ising-type model for a mixed cluster of opposing receptors based on the push-pull mechanism. Our model can quantitatively explain experimental observations in pH taxis for various mutants and wild-type cells. We show how the preferred pH level depends on the relative abundance of the competing sensors and how the sensory activity regulates the behavioral response. Our model allows us to make quantitative predictions on signal integration of pH and chemoattractant stimuli. Our study reveals two general conditions and a robust push-pull scheme for precision sensing, which should be applicable in other adaptive sensory systems with opposing gradient sensors.

Introduction

The survival of living systems relies on their ability to sense their environmental conditions and move to advantageous locations. A classic example is bacterial chemotaxis (1–4): By sensing gradients of chemical stimuli, bacterial cells usually migrate in a unidirectional mode following the gradients, i.e., from low to high attractant concentrations or from high to low repellent concentrations. This strategy allows them to find nutrients (attractant) and escape from toxins (repellent). However, there are other environmental factors such as pH and temperature, for which the physiological optimum may not be the extremes in a gradient but correspond to an intermediate level. For example, extremely acidic or alkaline environments can be detrimental to Escherichia coli cells (5). Interestingly, the same chemotaxis machinery is also used in the bacterial pH taxis and the opposing pH responses by two major types of chemoreceptors to determine the preferred pH level (6–9). Therefore, a push-pull mechanism may be responsible for the pH taxis, which allows cells to invert their responses at a particular pH value. This mode of precision sensing is closely related to, yet quite different from, the traditional concept of chemotaxis, which generates unidirectional response to certain chemical gradients. Instead of directing cells to the extreme levels in a gradient, precision sensing helps cells to find some intermediate, optimal level of stimuli. So far, however, the mechanisms for precision sensing remain poorly understood.

In E. coli, extracellular chemical stimuli are sensed and processed by several types of transmembrane chemoreceptors, among which the aspartate binding receptor (Tar) and serine binding receptor (Tsr) are the most abundant (10). Interaction among different types of receptors enables them to act together and respond cooperatively to specific signals (11–13). Over the past decades, there has been significant progress, both experimental and theoretical, in understanding the role of receptor cooperativity in signal amplification (11–23). In E. coli, Tar and Tsr form hetero-trimers of homo-dimers in cytoplasmic membrane (24–26). These receptors form clusters that associate with the adaptor protein CheW and the histidine kinase CheA (27–29). Binding of attractant (or repellents) to the periplasmic domain of receptors inhibits (or promotes) the autophosphorylation activity of CheA, which in turn decreases (or increases) phosphorylation of the response regulator CheY and eventually regulates the flagellar motor to navigate the cell toward attractant (or away from repellent). The system also contains a phosphatase CheZ, which dephosphorylates CheY-P (the phosphorylated form of CheY).

Sensory adaptation is needed to maintain a short-term memory for temporal comparisons of concentrations when swimming in a gradient (4,30,31). In E. coli, adaptation is achieved by receptor methylation and demethylation, as catalyzed by two cytoplasmic enzymes, methyltransferase CheR and methylesterase CheB, which add and remove methyl group at specific sites of receptors, respectively. Methylation of receptors increases the kinase activity of CheA that phosphorylates both CheY and CheB. Phosphorylation of CheB enhances its enzymatic activity (for demethylation) and helps restore the receptor-kinase activity to its prestimulus level (adaptation) after its initial response to an external stimulus. However, if it is only the total kinase activity that controls the adaptation (methylation/demethylation) process, there will be severe methylation crosstalk (memory contamination) between different types of receptors; for example, both Tar (specific for aspartate) and Tsr (specific for serine) receptors will be methylated to the same degree even when the cell only experiences a change in aspartate concentration. A recent study shows that bacterial cells avoid methylation crosstalk by having the activity of individual receptors locally control their own methylation dynamics (13). This local adaptation mechanism drives each individual receptor to its most responsive state and maintains high sensitivity of the entire receptor cluster (13).

Although the molecular sensing mechanism is unclear, bacterial pH taxis is also mediated by the two major receptors, Tar and Tsr. A recent study showed that Tar gives an attractant response whereas Tsr elicits a repellent response to an increase in pH (9). The competition between these opposing effects results in a particular preferred pH value. Here, we develop a mathematical model to explain the recent experimental data on bacterial pH sensing. We attempt to address the following questions:

• 1.How could the gradient sensing chemotaxis signaling pathway be used to carry out precision sensing in pH taxis?
• 2.What determines (encodes) the preferred pH value?
• 3.How is the pH sensing program integrated with other chemical sensing processes?
• 4.What are the general conditions or constraints for the push-pull mechanism to perform precision sensing?

The Ising-Type Model for pH Sensing

Our model for pH sensing is based on the Ising-type model for a mixed cluster of receptors (Tar and Tsr) as proposed in Lan et al. (13) and Mello and Tu (18). We assume that the environmental pH modulates the receptor-kinase activity primarily by affecting the periplasmic domain of the receptors just like chemoattractants bind to receptors in chemosensing. This assumption is supported by the experiment on a hybrid Tsar receptor, which has the periplasmic domain of Tsr and the signaling domain of Tar but resembles the response of Tsr (9). In light of such analogy, each single receptor can be characterized by four state variables (q,l,s,m) that are labeled as subscripts: q defines the type of receptor with q = 1 for Tar and q = 2 for Tsr; l = 0,1 indicates the proton binding state of the receptor; s = 0,1 represents the inactive or active conformation of the receptor; and m ∈[0,4] records the receptor’s methylation level because Tar and Tsr have up to four or five methyl groups. The process of receptor covalent modification is much slower than that of the ligand binding and activity switching (32). Such separation of timescales allows us to treat the evolution of (l,s,m) with a quasi-equilibrium approximation. The receptor binding/activity states can be described by their equilibrium values for a given m, whereas the slow methylation dynamics is characterized by a system of coupled ordinary differential equations tracing the population distribution of receptors at different methylation levels.

The free energy of an individual receptor in the state (q,l,s,m) is given by

$$H_{q,l,s,m}={\mu }_q·l+\left(E_q^L·l+E_{q,m}^M+E_q^C\right)·s,$$ (1)

where the chemical potentials of the inactive and active proton-bound receptors, μ_q and μ_q + E^L_q, are defined as

$$e^{-{\mu }_q}={10}^{K_q^I-\text{pH}}\text{and}{e}^{-\left({\mu }_q+E_q^L\right)}={10}^{K_q^A-\text{pH}}.$$ (2)

Note that the proton concentration at a given pH is equal to 10^6−pH μM. For convenience, we have expressed the effective dissociation constants K^I_q and K^A_q for the inactive and active type-q receptors in the pH scale. In principle, K^I_q and K^A_q may depend on the receptor methylation level K_q^I,A = K_q^I,A(m), as evidenced by pH sensing experiments for cells with different receptor methylation levels (9). However, we found that the push-pull mechanism for pH taxis works as long as Tar and Tsr dominate different pH regimes, regardless of such methylation level dependence; see the Supporting Material for details. For this reason, we will assume constant K^I_q and K^A_q in the rest of the article and examine the consequence of the methylation level dependence in the Discussion section.

In Eq. 1, E^M_q,m represents the free energy contribution by receptor methylation and is assumed to be a linear function of m for intermediate methylation levels (32),

$$E_{q,m}^M={\alpha }_q·\left(m-m_{q,0}\right),\text{for}0<m<4,$$ (3)

where α_q measures the free energy change by adding one methyl group, and m_q,0 sets the average methylation level in zero ligand background. Note that the methylation energy at the boundary, $\left|E_{q,m=0}^M\right|$ and $\left|E_{q,m=4}^M\right|$, should be large enough to ensure accurate adaptation; see the Supplementary Information of Lan et al. (13) for details. In the Ising model, neighboring receptors in the mixed cluster can interact with each other, as captured by the receptor-receptor coupling energy term E^C_q in Eq. 1, which is assumed to depend linearly on the activity of its neighbors:

$$E_q^C=\sum _{\left(nn\right)}\frac{C_{q{q}^{\prime }}}{N_0}·\left(s_{q^{\prime }}-\frac{1}{2}\right).$$ (4)

The above expression means that the activity of a receptor (s = 0 or 1) in the cluster depends on the activities of its N₀ neighbors with a coupling strength C_qq^′/N₀ < 0 for each cooperative interaction. To preserve symmetry between active and inactive states, we have put 1/2 in Eq. 4. This treatment does not alter our main results or conclusions.

All the aforementioned energies are written in the units of the thermal energy k_BT. In the mean-field approximation, the average activity of a type-q receptor at methylation level m can be written as

$${\langle a\rangle }_{q,m}={\left\{1+\frac{1+{10}^{K_q^I-\text{pH}}}{1+{10}^{K_q^A-\text{pH}}}·\text{exp}\left[E_{q,m}^M+\sum _{q^{\prime }=1,2}{f}_{q^{\prime }}{C}_{q{q}^{\prime }}\left({\langle a\rangle }_{q^{\prime }}-\frac{1}{2}\right)\right]\right\}}^{-1},$$ (5)

where f_q is the fraction of type-q receptor such that f₁ + f₂ = 1 and 〈a〉_q represents the mean-field activity averaged over all type-q receptors, i.e.,

$${\langle a\rangle }_q=\sum _{m=0}^4{P}_{q,m}{\langle a\rangle }_{q,m}.$$ (6)

The symbol P_q,m in Eq. 6 represents the fractional population of type-q receptors with methylation level m, and satisfies the normalization condition ${\sum }_{m=0}^4{P}_{q,m}=1$. Subject to the (slow) methylation-demethylation kinetics, P_q,m values are governed by the following master equations,

$$\frac{d{P}_{q,m}}{dt}=k_R\left(1-{\langle a\rangle }_{q,m-1}\right)P_{q,m-1}+k_B{\langle a\rangle }_{q,m+1}{P}_{q,m+1}-\left[k_R\left(1-{\langle a\rangle }_{q,m}\right)+k_B{\langle a\rangle }_{q,m}\right]P_{q,m},$$ (7)

with the boundary condition P_q,m<0 = P_q,m>4 = 0. Here, we assume that only inactive receptors methylate with rate k_R, and only active receptors demethylate with rate k_B. The timescale is set by k_R = 1. We take constant rates of k_R and k_B by using a linear approximation (32). In general, both k_R and k_B depend on the kinase activity. Such dependence, however, does not change the behavior of our model significantly because accurate adaption maintains the receptor activity near its preferred level, where the linear approximation holds.

Equations 5–7 fully define our pH sensing model. The only parameters specific to pH sensing are K_q^I,A; all the other parameters are the same as in chemotaxis (Table 1). Equation 7 is solved numerically using the Euler discretization method. At each time step, we first solve Eqs. 5 and 6 under the current pH level using the nonlinear equation solver Fsolve in MATLAB (The MathWorks, Natick, MA), and then we plug the new solution of {〈a〉_q,m} and {〈a〉_q} into Eq. 7 and update {P_q,m} over this small time interval using the solver Ode15s in MATLAB. Iterating the above procedure will give us the entire dynamics of receptor activity and methylation distribution.

Table 1.

Parameters used in the Ising-type model

Parameter	Value	Parameter	Value
f1	1/2	f2	1/2
m1,0	1.0	m2,0	2.5
EM1,0	10	EM2,0	10
α1	−1.875	α2	−1.5
C11	−3.5	C12	−3.5
C21	−4.0	C22	−4.0
kR	1	kB	2
KI1	9.0	KI2	6.0
KA1	7.3	KA2	7.8

Results

Tar and Tsr respond oppositely to pH changes

In a recent experiment (9), Yang and Sourjik used the fluorescence resonance energy transfer (FRET) technique to investigate the intracellular response of E. coli chemotaxis pathways to step-like changes of extracellular pH. The energy transfer pair is CheY and CheZ such that the FRET signal is proportional to [CheY-P-CheZ], the concentration of the intermediate species in the enzymatic hydrolysis of CheY-P (11). At steady state, the production rate of CheY-P, catalyzed by CheA, is exactly balanced by its degradation rate, which is proportional to [CheY-P-CheZ]. Therefore, the FRET signal can be viewed as a reporter of the CheA kinase activity. The authors found that mutant cells expressing only Tar, when preadapted at neutral pH of 7.0, exhibit an attractant response to a decrease of pH and a repellent response to an increase of pH. An opposite response was observed for cells expressing only Tsr.

In our Ising-type model, we can set f₁ = 1, f₂ = 0 (or f₂ = 1, f₁ = 0) to model mutant cells expressing only Tar (or Tsr). The opposite responses to pH changes for Tar and Tsr can be described in our model by setting K₁^A < K₁^I for Tar and K₂^A < K₂^I for Tsr. In Fig. 1 A, we plot the receptor activity 〈a〉₁ for cells expressing Tar (f₁ = 1) in response to certain changes of pH stimuli. Indeed, a decrease (or an increase) of pH is like an attractant (or a repellent) to the Tar receptors in our model. The opposite response of Tsr receptors, denoted by 〈a〉₂, to the same pH profile is also plotted in Fig. 1 A, consistent with experimental observations (9).

Figure 1.

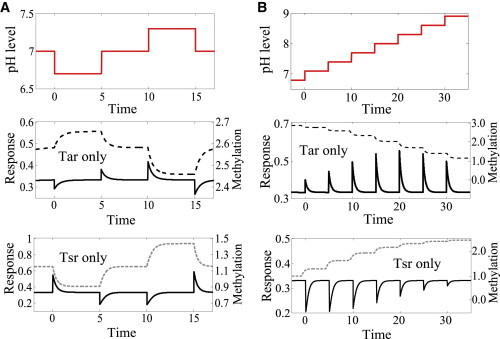
Responses to pH stimulation (solid lines) and dynamics of methylation levels (dashed lines) for the Tar-only mutant (f₁ = 1) and the Tsr-only mutant (f₂ = 1). (A) Tar and Tsr responses to up and down pH steps. (B) Tar and Tsr responses to a series of increased steps, from pH = 6.8 to pH = 8.9 with step size ΔpH = 0.3.

We also studied the receptor activity of Tar and Tsr in response to steps of increasing pH values (Fig. 1 B). Before each step of stimulation, the model system is allowed to adapt to the ambient pH. The simulation was carried out over a broad range of ambient pH values (from pH 6.8 to 8.9 with step size ΔpH = 0.3). As one can see from Fig. 1 B, the Tar response remains relatively strong whereas the Tsr response decreases as the pH level increases in the tested pH range. This pattern results from the different operating regions of Tar and Tsr as determined by their respective dissociation parameters in our model (Table 1), and is qualitatively consistent with the experimental observations (9). Moreover, Tar dominates the response at high pH values and Tsr dominates at low pH regions. Such difference in dominance is critical for the system to invert its response at an intermediate pH value.

Similar to chemotaxis, adaptation to pH changes is achieved by changes in receptor methylation. Specifically, the methylation level increases upon positive (attractant) stimulation and decreases upon negative (repellent) stimulation. As shown in Fig. 1 (dashed lines), Tar (or Tsr) methylation decreases (or increases) at higher pH, in agreement with experiments (9). The observation reported in Yang and Sourjik (9) of distinctive methylation patterns for Tar and Tsr also confirms the local adaptation mechanism (13) that the adaptation processes for individual receptors are affected by their own activities (conformational changes), instead of being solely regulated by the total kinase activity of the receptor cluster.

The reversal of pH response in wild-type cells

The response of wild-type (WT) E. coli cells that express both Tar and Tsr is determined by integration of the two opposing pH responses. Fig. 2 plots the responses for the Tar-only mutant, the Tsr-only mutant, and the WT cell to a series of pH steps with varying step sizes (ΔpH) but the same ambient pH. We denote pH₀ and pH₁(= pH₀ + ΔpH) as the pre- and poststimulation pH levels, respectively. As shown in Fig. 2 B, the WT cell (with the Tar/Tsr ratio f₁/f₂ = 0.5) exhibits a repellent response to a decrease in pH and an attractant response to an increase in pH, similar to the Tsr-only response. This suggests that the WT response at ambient pH 7.0 is dominated by the Tsr-mediated response, consistent with the experimental findings (9). Fig. 2 C plots their initial responses (i.e., the maximum magnitude right after each stimulation) as a function of pH₁ with ambient pH₀ = 7.0. The quantitative values of $K_{1,2}^{A,I}$, as listed in Table 1, are determined by fitting our model to the experimental data for the Tar-only and Tsr-only mutants. These values are then used in the model, now without any free parameters, to predict the pH response for the WT cell. As shown in Fig. 2 C, the modeling results are in good agreement with the experimental observations.

Figure 2.

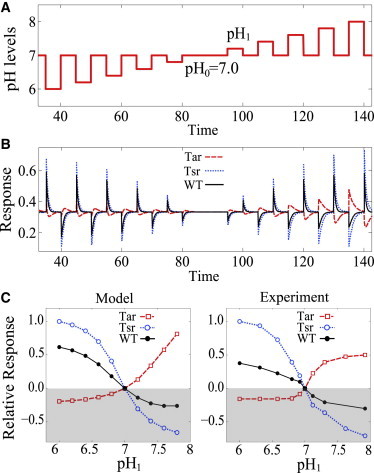
(A and B) Responses of the Tar-only mutant (f₁ = 1, dashed line), the Tsr-only mutant (f₂ = 1, dot-dashed line), and the WT strain (f₁ = f₂ = 0.5, solid line) to a series of pH steps with varying step sizes and but same ambient pH level (pH₀ = 7.0). (C) Their relative responses (normalized by the maximum response value among all the data points in each subfigure) versus the poststimulation pH, denoted as pH₁ = pH₀ + ΔpH. (Left panel) Obtained from our model results in panel B and is compared with the experimental measurements (right panel) in Yang and Sourjik (9).

The response also depends on the ambient pH level, denoted by pH₀. Fig. 3, A and B, plots the response of the WT strain (with f₁/f₂ = 0.5) to steps of first increasing then decreasing pH with the same step size (ΔpH = 0.3). The model exhibits an attractant response of gradually decreasing magnitude for ambient pH level up to pH₀ = 7.7. The response then inverts to a repellent response for pH₀ ≥ 8.0. For the sequence of steps of decreasing pH, the WT system shows an almost mirror-image response of opposite sign (Fig. 3 B). This response pattern again resembles the experimental observation (9). Quantitatively, the inversion point pH^∗ (the preferred pH) lies between 8.0 and 8.3, also agreeing with the experimental finding (9).

Figure 3.

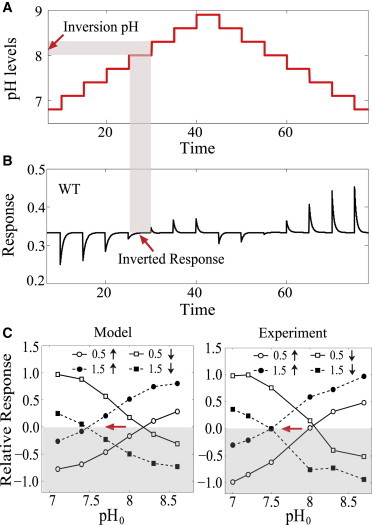
(A and B) Response of the WT cell with f₁/f₂ = 0.5 to steps of first increasing then decreasing pH levels (the ambient pH₀: 6.8 → 8.9 → 6.8 with step size ΔpH = 0.3). As illustrated by the shaded area, the inversion pH can be located by mapping the region where the response becomes inverted. (C) Relative responses versus the ambient pH₀ for increasing pH steps (circles, up arrow) and decreasing pH steps (squares, down arrow) under two different Tar/Tsr ratios: f₁/f₂ = 0.5 (open symbols, solid lines) and f₁/f₂ = 1.5 (solid symbols, dashed line). (Horizontal arrow) Shift of the response inversion point to lower pH upon increasing the Tar/Tsr ratio. (Left panel) Our model results; these are directly compared to the experimental measurements (right panel) in Yang and Sourjik (9). The relative responses were normalized by the maximum response value among all the data points in each subfigure (either model or experiment).

The preferred pH depends logarithmically on the receptor abundance ratio

What determines the inversion point pH^∗ in the pH response of E. coli cells?

Experimentally, it has been found that the relative levels of Tar and Tsr change with the cell density and growth conditions in the medium (33). By tuning the cell density and growth condition, Yang and Sourjik (9) observed a shift of the inversion point, pH^∗, from 8.0 to 7.5, as a result of the increased abundance of Tar relative to Tsr (the Tar/Tsr ratio from 0.5 to 1.5). Taking the same parameters we used in Fig. 2, our model also predicts the response pattern with shifted pH^∗, similar to what was observed in experiment (Fig. 3 C). The solid (or dashed) lines represent the magnitude of response to steps of increasing and decreasing pH given that the Tar/Tsr ratio is 0.5 (or 1.5), as can be obtained from simulations shown in Fig. 3 B.

Analytically, we have simplified our full model (see the Supporting Material for detailed derivation) to provide a quantitative prediction on how this inversion point of pH depends on the relative levels of Tar and Tsr. Specifically, we found that the inversion point could be modulated as a (minus) logarithm of the Tar/Tsr ratio (to base 10):

$${\text{pH}}^{\text{∗}}\approx K_2^A-{\text{log}}_{10}\left(\frac{f_1}{f_2}\right).$$ (8)

Given a change of Tar/Tsr ratio from 0.5 to 1.5, we can estimate that the shift of inversion pH point is roughly: log₁₀(1.5) – log₁₀(0.5) ≈ 0.48, which is quite close to the experimental observation 8.0 – 7.5 = 0.5. This tunability of the preferred pH point can be beneficial for cells to adjust their behavioral responses according to both internal and external physiological conditions. Additional measurements for cells with different receptor population ratios (f₁/f₂) can be used to test our model prediction quantitatively.

Our model has so far focused on the signaling pathway for pH sensing. How does the sensory output (receptor-kinase activity) navigate the cells’ migration toward the preferred pH level?

To answer this question, we have implemented a two-dimensional Monte-Carlo simulation for cells moving in a linear pH gradient (pH from 6.0 to 9.0 in 600 μm). The algorithm is based on an earlier computational model for bacterial chemotaxis (34). Here, we have directly incorporated the pH sensing module (Tar and Tsr) into the original algorithm, using the same parameters given in Table 1. Effects of the pH change on the motor speed have been measured before in Chen and Berg (35) where only weak dependence of the speed on the external pH was observed. Thus, we assumed a constant run speed in the simulations. As shown in Fig. 4, cells (which were uniformly distributed at the beginning) eventually accumulate near a location corresponding to the preferred pH value. Furthermore, as the Tar/Tsr ratio changes from 0.5 to 1.5, the average pH, as sampled by the locations of 100 cells, is found to change from 8.15 to 7.4. Our simulation results demonstrate the capability of the precision sensing mechanism in guiding the cells to their preferred pH level, which can be tuned by changing the relative abundance of the two opposing sensors.

Figure 4.

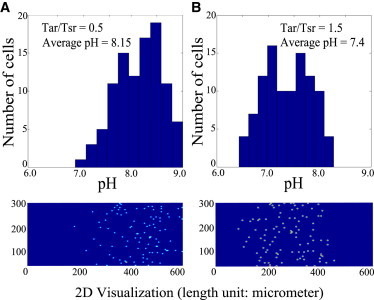
Two-dimensional stimulations for pH taxis with different Tar/Tsr ratios: (A) f₁/f₂ = 0.5 and (B) f₁/f₂ = 1.5. (Top panels) Distribution of 100 cells along the linear pH gradient (pH: 6.0 → 9.0 with ΔpH =1 per 200 μm). (Bottom panels) Two-dimensional visualizations of those WT cells performing pH taxis in steady state. The Monte Carlo simulation uses those key parameters given in Table 1. The detailed algorithm is provided in the Supporting Material.

Two general conditions for precision sensing

What are the general constraints for the precision sensing mechanism via two opposing gradient sensors?

Here, we use our model to answer this question, taking pH sensing as an example. For cells that are adapted to a background pH level (denoted by the variable pH), their average kinase activity changes to a(pH,pH′) directly after the pH level changes to a new level pH′ (before adaptation sets in). The response at the background to an infinitesimal increase of pH is characterized by the sensitivity S defined as

$$S\left(\text{pH}\right)\equiv \underset{\delta \text{pH}\to 0}{\text{lim}}\frac{a\left(\text{pH},\text{pH}+\delta \text{pH}\right)-a\left(\text{pH},\text{pH}\right)}{\delta \text{pH}},$$ (9)

where a(pH,pH) = a₀ is the prestimulus (adapted) activity. In our model, the adapted activity for both Tar and Tsr is a₀ ≡ k_R/(k_R + k_B). Note that S < 0 and S > 0 correspond to attractant and repellent responses, respectively. For precision sensing, S needs to reverse sign and thus the inversion point pH^∗ should satisfy

$$S\left({\text{pH}}^{\text{∗}}\right)=0,$$ (10)

which is the first condition required for precision sensing.

By using a mean-field approximation in our model (see the Supporting Material for details) and assuming C₁₁ = C₁₂ and C₂₁ = C₂₂ for simplicity, we obtain an analytical form for S(pH) and the above condition (Eq. 10) simplifies to

$$f_1\times \frac{y_1^A-y_1^I}{\left(y^{\text{∗}}+y_1^A\right)\left(y^{\text{∗}}+y_1^I\right)}+f_2\times \frac{y_2^A-y_2^I}{\left(y^{\text{∗}}+y_2^A\right)\left(y^{\text{∗}}+y_2^I\right)}=0,$$ (11)

with redefined variables $y^{\text{∗}}\equiv {10}^{{\text{pH}}^{\text{∗}}}$, $y_q^A\equiv {10}^{K_q^A}$, and $y_q^I\equiv {10}^{K_q^I}$ for Tar (q = 1) and Tsr (q = 2). To satisfy the above equation, y^A₁ − y^I₁ should have the opposite sign as y^A₂ − y^I₂, which simply means that Tar and Tsr should have opposite responses to pH. If we further assume that y^A₁ ≈ y^A₂ (i.e., K^A₁ ≈ K^A₂), y^A₂ ≫ y^I₂, y^I₁ ≫ y^A₁, and y^I₁ ≫ y^∗ ≫ y^I₂, then we obtain a simple analytical expression for y^∗ ≈ y^A₂ × (f₂/f₁), which leads to the expression for the inversion point (pH^∗) as shown in Eq. 8.

Although Eq. 10 is necessary for the existence of an inverted response, it is not sufficient to drive precision sensing. This inversion point pH^∗ needs to be attractive, which is only guaranteed by having

$$S^{\prime }\left({\text{pH}}^{\text{∗}}\right)\equiv {\frac{dS}{d\text{pH}}|}_{{\text{pH}}^{\text{∗}}}>0.$$ (12)

Equation 12 is the second condition required for precision sensing. For the particular case a₀ = 1/2, we found that (see the Supporting Material for details)

$$S^{\prime }\left(\text{pH}\right)=\frac{{\text{ln}}^2\left(10\right)}{4}\times \sum _{q=1}^2{f}_q\left[\frac{y{y}_q^A}{{\left(y+y_q^A\right)}^2}-\frac{y{y}_q^I}{{\left(y+y_q^I\right)}^2}\right],$$ (13)

where y ≡ 10^pH. For the case y^I₁ ≫ y^A₁ ≈ y^A₂ ≫ y^I₂ considered in this article and in the range y^I₁ ≫ y ≫ y^I₂, where the inverted response occurs, the above expression can be simplified:

$$S^{\prime }\left(\text{pH}\right)\approx \frac{{\text{ln}}^2\left(10\right)}{4}\times \frac{y{y}_2^A}{{\left(y+y_2^A\right)}^2}>0.$$ (14)

This shows that the inversion pH level in our model is indeed a stable (attractive) fixed point, which is consistent with the experiments as shown in Fig. 3 C. It is also apparent that S′(pH) does not depend on Tar/Tsr. Therefore, tuning the ratio f₁/f₂ can shift the inversion point but does not change the shape of the response curve. This prediction agrees with the experimental data (9) and our simulations (Fig. 3 C): when f₁/f₂ changes from 0.5 to 1.5, the inversion point (as defined by the zero crossing point of the response curves) shifts from 8.0 to 7.5, but the slope of those curves remains roughly the same.

Possible precision sensing schemes

The two general requirements for precision sensing, as summarized by Eqs. 10 and 12, can be used to evaluate different possible scenarios with two opposing sensors. Fig. 5 illustrates six typical combinations of the two sensors with overlapping sensitivity regimes. To establish a stable inversion point, the push-pull mechanism requires that the repellant sensor (Tar, red line) dominates in the high pH regime, whereas the attractant sensor (Tsr, blue line) must dominate in the low pH regime. This stability requirement immediately rule out the scenarios outlined in Fig. 5, D and E. Fig. 5 F illustrates a special case where the operating regime of Tar is contained in the regime of Tsr. This scheme allows for two fixed points, one attractive and the other repulsive; thus a cell starting at high pH levels may not be able to migrate toward the (preferred) low pH level due to the repulsive fixed point.

Figure 5.

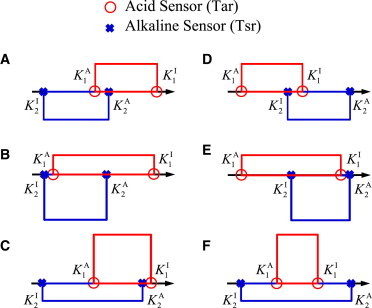
Possible schemes for precision sensing. The height of the upper (red) or lower (blue) boxes represents the maximum magnitude of the response of Tar or Tsr, respectively, which depends on the abundance of each type of sensor. The length of the boxes denotes the range of sensitivity as determined by $K_{1,2}^A$ and $K_{1,2}^I$. (Arrow points toward an increasing pH gradient.) Specifically, we consider six typical combinations of the opposing sensory regimes: (A) K^I₂ < K^A₁ ≤ K^A₂ < K^I₁; (B) K^I₂ ≈ K^A₁ < K^A₂ < K^I₁; (C) K^I₂ < K^A₁ < K^A₂ ≈ K^I₁; (D) K^A₁ < K^I₂ ≤ K^I₁ < K^A₂; (E) K^A₁ < K^I₂ < K^I₁ ≈ K^A₂; and (F) K^I₂ < K^A₁ < K^I₁ < K^A₂.

The scheme in Fig. 5 A with K^I₂ < K^A₁ ≤ K^A₂ < K^I₁ is what we used in this article for pH sensing in E. coli. The inversion point is expected to be defined within the overlapped operating regions of Tar and Tsr. This small overlap is necessary because if there is no overlap, e.g., K^I₂ < K^A₂ < K^A₁ < K^I₁, cells would show no appreciable response to pH changes within the dead-zone (K^A₂, K^A₁), which is inconsistent with experiments (Fig. 3). One advantage of the Fig. 5 A scheme is that it puts no constraints on the relative response strength of Tar and Tsr (which depends on the relative abundance of these receptors). This allows the inversion point to be tunable by freely adjusting the Tar/Tsr ratio as shown in Eq. 8.

The two schemes shown in Fig. 5, B and C, represent the cases where there is a large overlap between the operating ranges of the two opposing sensors. In particular, either the maximums or the minimums of the two operating regimes are close to each other: K^I₂ ≈ K^A₁ < K^A₂ < K^I₁ for Fig. 5 B and K^I₂ < K^A₁ < K^A₂ ≈ K^I₁ for Fig. 5 C. Let us consider the case in Fig. 5 B. By using Eq. 10 and following the same procedure as before (see the Supporting Material for details), we get an estimate of the inversion pH level,

$${\text{pH}}^{\text{∗}}\approx K_2^A+{\text{log}}_{10}\left(\frac{f_2}{f_1}-1\right),$$ (15)

which means that the existence of the inversion point requires tuning the sensor ratio f₁/f₂ < 1. For the particular case a₀ = 1/2, the second condition (Eq. 12) is also satisfied as

$$S^{\prime }\left(\text{pH}\right)\approx f_2\times \frac{{\text{ln}}^2\left(10\right)}{4}\times \frac{y{y}_2^A}{{\left(y+y_2^A\right)}^2}>0,$$ (16)

which suggests that pH^∗ is indeed an attractive fixed point if it exists. However, as measured by S′(pH), the attraction is now weakened by a factor f₂ in comparison with Eq. 14 for the scenario shown in Fig. 5 A. Intuitively, the broadening of the operating regime of one sensor deep into the operating regime of the opposing sensor weakens the system’s precision sensing ability and can even destroy precision sensing if it overpowers the other sensor (f₁ > f₂).

Therefore, based on the experimental observation and our aforementioned analysis, the most robust push-pull scheme seems to be the one illustrated in Fig. 5 A. The parameter condition for this scheme can be simply expressed as K^I₂ < K^A₁ ≤ K^A₂ < K^I₁.

Discussion

A critical challenge for living systems is to find the favorable environment where they can live and prosper. This is usually achieved by continuously sensing the external conditions and performing biased random movements toward those optimal niches. Bacterial chemotaxis serves as an elegant example, because it allows the cells to follow the chemical gradients and navigate unidirectionally toward the highest concentrations of nutrients or lowest levels of toxins. Nonetheless, for many environmental factors such as pH and temperature (5,9,36), the most physiologically favorable conditions do not correspond to the extreme levels of those factors and cells prefer to accumulate around an intermediate level in a gradient. By using a modeling approach, we confirm that this behavior can be achieved by a push-pull mechanism by coordinating two opposing sensors (Tar and Tsr), each dominating in different regimes of pH (Fig. 6).

Figure 6.

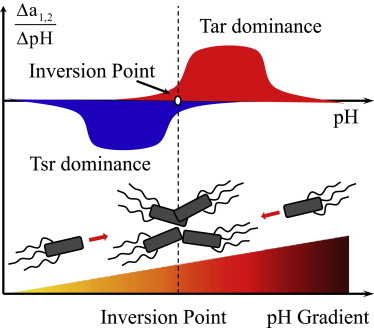
Schematic illustration of the push-pull mechanism for bacterial pH taxis. The two opposing sensors, Tar and Tsr, dominate the response in different pH regions. The balance between their competing effects determines the inversion point of the pH response (i.e., the preferred pH value) at which cells appear to accumulate.

Bacteria can integrate and respond to a multitude of stimuli. For example, responses of the Tsr receptor to combined repellent/attractant signals has been studied before in the Tar-deletion mutant by the simultaneous photorelease of caged protons and serine (8). Depending on the relative levels of these two effectors, the Tsr receptor was observed to produce an attractant or repellent response. Our computational model can also be extended to predict how bacteria might process the pH signals in the presence of other chemical stimuli (see the Supporting Material for details). As a preliminary step, we hypothesize that the external pH modulates the receptor kinase activity but does not directly affect chemoattractant binding to the receptor. Fig. 7 shows the predicted response of Tar-only mutant to a combination of pH and chemical (MeAsp) stimuli. Because Tar generates an attractant response to [MeAsp] but a repellent response to an increase of pH, the model predicts a neutral response curve (dashed line, Fig. 7 B) along which the effects of increasing pH and adding [MeAsp] cancel out with each other. Experiments similar to that of Khan et al. (8) can be carried out to test our prediction for the Tar-only mutant and to reveal whether the pH sensing step is relatively independent of the chemical binding process in the chemoreceptors. The extended model also allows us to study how the presence of chemical attractants affects the pH responses. Our results (see Fig. S1 in the Supporting Material) demonstrate that the pH responses of Tar and Tsr are appreciably weakened when the Tar- and Tsr-only mutants were preadapted to high MeAsp and serine backgrounds, respectively. This is in qualitative agreement with the experimental observations (9).

Figure 7.

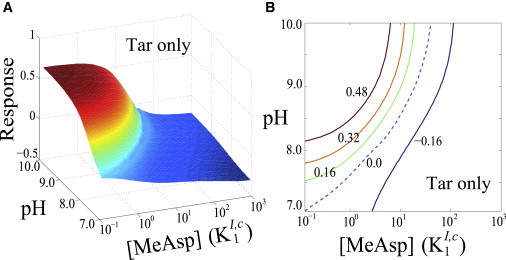
Response of the Tar-only mutant to both pH and chemical (MeAsp) stimuli, as predicted by an extended Ising-type model (with details in the Supporting Material). The mutant was preadapted to pH₀ = 7.0 and [MeAsp]₀ = 10⁻¹K₁^I,c before being stimulated to the new state (pH, [MeAsp]), where the dissociation constant K₁^I,c = 18 μM. (A) Each point in the surface represents the Tar response to a combined stimuli (pH, [MeAsp]). (B) The contour plot of panel A on the space (pH, [MeAsp]) (dashed line corresponds to the neutral response curve along which the responses to the pH and chemoattractant changes cancel out).

Bacteria can also perform precision sensing in thermotaxis as they tend to accumulate at ∼37°C in a temperature gradient. For E. coli, it was found experimentally (38–40) that the Tar receptor can switch from a warm sensor to a cold sensor when the receptor methylation level increases across a critical level. The push-pull mechanism is valid but more subtle in this case as the two balancing effects (push and pull) are provided by the same receptor in different methylation states. The requirements for precision sensing, as summarized by Eqs. 10 and 12 in this article, also apply for thermotaxis. Indeed, based on these general conditions, a theoretical model for thermotaxis by Jiang et al. (41) revealed that imperfect adaptation to temperature changes (in contrast to the perfect adaptation in chemotaxis) is needed to drive the receptor methylation level to cross the critical level where the inverted response occurs.

Despite their similar precision sensing capability, there are some important distinctions between temperature sensing and pH sensing:

• 1.At least two competing sensors are involved for the push-pull mechanism in pH sensing (Fig. 6), whereas Tar alone is able to invert its sensing mode for temperature.
• 2.The inversion of pH response requires appropriate combination of the dominant regimes of Tar and Tsr (Fig. 5). Although a high maximum receptor methylation level could lead to a decrease or even inversion of the pH response (especially for Tsr), the experimentally observed change in methylation level due to the pH change alone (9) is not sufficient to drive the receptors to their inversion methylation level in the absence of additional chemoattractants (see the Supporting Material for details). For thermotaxis, however, temperature-induced methylation level change is essential to drive the receptor across the inversion point (41).
• 3.Although the imperfect adaptation to the temperature is necessary for the inverted response in thermotaxis (41), the push-pull mechanism for pH sensing works with perfect adaptation.

The push-pull mechanism appears to be a general mechanism for precision sensing that enables cells to accumulate at specific intermediate levels of environmental factors. For example, indole, a stationary-phase chemical signal, can also elicit opposite responses via Tar and Tsr. Similar to pH sensing, the response of WT cells to indole gradients gets inverted from the repellent response at low concentrations to attractant response at high concentrations (V. Sourjik, Heidelberg University, personal communication, 2012). Moreover, this inversion is also found to depend on the relative levels of Tar and Tsr. In another example, it was found that two receptors, Tsr and Aer, are responsible for E. coli aerotaxis, which leads to the accumulation of bacteria at a preferred level of oxygen (42). This is again similar to the pH taxis and may be explained by a variant of our model. Finally, the four transmembrane chemoreceptors of E. coli sense phenol as either an attractant (Tar) or a repellent (Tsr, Tap, and Trg) (43). It would be very interesting to test whether the push-pull mechanism studied here for pH taxis serves as a general strategy in bacterial sensory systems.