Theory of Polymer-Nanopore Interactions Refined Using Molecular Dynamics Simulations

Abstract

Molecular dynamics (MD) simulations were used to refine a theoretical model that describes the interaction of single polyethylene glycol (PEG) molecules with α-hemolysin (αHL) nanopores. The simulations support the underlying assumptions of the model, that PEG decreases the pore conductance by binding cations (which reduces the number of mobile ions in the pore) and by volume exclusion, and provide bounds for fits to new experimental data. Estimation of cation binding indicates that four monomers coordinate a single K⁺ in a crown-ether like structure, with, on average, 1.5 cations bound to a PEG 29-mer at a bulk electrolyte concentration of 4 M KCl. Additionally, PEG is more cylindrical and has a larger cross-section area in the pore than in solution, although its volume is similar. Two key experimental quantities of PEG are quantitatively described by the model: the ratio of single channel current in the presence of PEG to that in the polymer’s absence (blockade depth), and the mean residence time of PEG in the pore. The refined theoretical model is simultaneously fit to the experimentally determined current blockade depth and the mean residence times for PEGs with 15 – 45 monomers, at applied transmembrane potentials of -40 to -80 mV, and for three electrolyte concentrations. The model estimates the free energy of the PEG-cation complexes to be -5.3 k_BT. Finally the entropic penalty of confining PEG to the pore is found to be inversely proportional to the electrolyte concentration.

Introduction

Biological nanopores have been used to electrically detect and characterize molecules, thereby potentially enabling a wide range of sensing applications.^1-3 This technology is possible because the pores have dimensions that are commensurate with single molecules,⁴ do not gate,⁵ and retain molecules in the pore far longer than would be expected for freely diffusing species.⁶ Protein nanopores have been used to detect many analyte types including H⁺ and D⁺ ions in solution,^5,7 DNA and RNA polynucleotides,^8-14 therapeutic agents against anthrax toxins,^1,3,15,16 proteins,^17,18 polypeptides,¹⁹ polyethylene glycol (PEG)^6,20-24 and synthetic molecules.^23-27 Recently, the Staphylococcus aureus α-hemolysin (αHL) nanopore was used to discriminate between different size polymers, which provides the basis for a form of single molecule mass spectrometry (SMMS).^23,24

There has been considerable interest in the use of single nanopores to sequence DNA.^1,8,28-32 However, the method remains elusive, in part because it has been difficult to discern small differences between the four DNA mononucleotides to better than 2σ on average.³³ The SMMS technique noted above provides the basis for a nanopore-based DNA sequencing by synthesis (SBS) approach, because polymeric tags can be used as surrogates for mononucleotides and detected by the nanopore with > 6σ separation.³⁴ The ability to use PEG and PEG analogs for this and other applications demands a physically accurate description of their interactions with nanopores.

Here, we use molecular dynamics (MD) simulations to critically test and refine a theoretical model²⁴ that quantifies the interactions between single PEG molecules in the αHL pore (Figure 1). The model assumes that PEG decreases the pore conductance by two physical processes: i) volume exclusion due to the presence of the polymer in the pore, and ii) a decrease in the mobile ion concentration due to the formation of reversible PEG-cation complexes. Newly obtained experimental data measured over a wide range of PEG molecular weights, electrolyte concentrations, and transmembrane potentials are then fit to the refined theoretical model, which leads to a better estimation of the model parameters. The techniques reported here provide the basis to analyze a variety of molecules, for example, labels that can be used in nanopore-based DNA sequencing.³⁴

Figure 1.

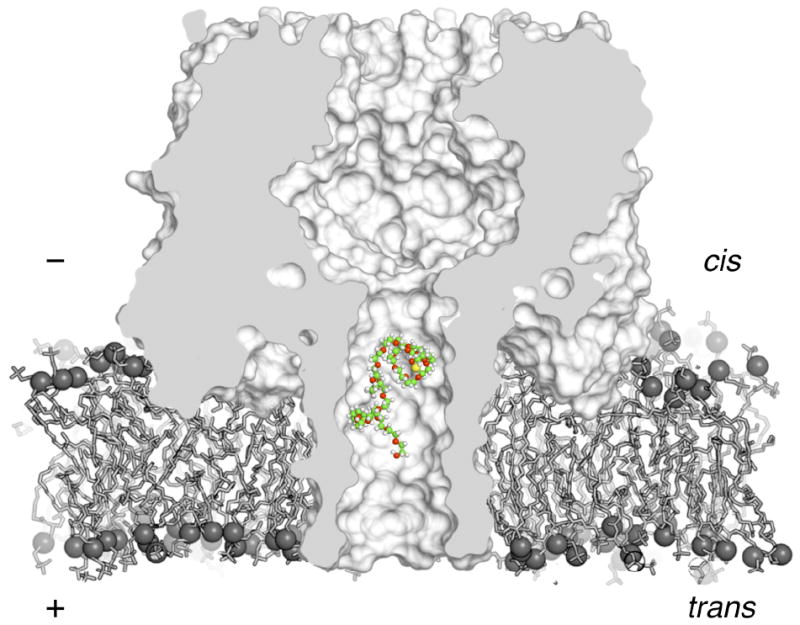
Cross-section of an αHL nanopore in a lipid bilayer. The pore has two major components: the cap region on the cis side with a relatively large vestibule, and the narrower stem portion spanning the membrane that is used in single molecule sensing applications. A potential, applied relative the trans side of the pore to match experiment drives an ionic current across the channel. PEG partitions into the narrow stem region on the trans side, thereby blocking the pore. In the size range studied as part of this work, PEG molecules blocking the pore cause the channel conductance to decrease proportional their size. In contrast, the mean residence time of PEG increases with the size of the molecule. This image was created with PyMol.³⁵

Materials and Methods

Molecular Dynamics Simulation

All simulations were performed using NAMD 2.8³⁶ and the analyses were performed using CHARMM c36b2.³⁷ Force field parameters were from CHARMM and obtained by combining protein parameters from C22 with the CMAP correction,^38,39 ether parameters from C35r,⁴⁰ lipid parameters from C36,⁴¹ and the TIP3P water model.⁴² Pressure control with a Nosé-Hoover Langevin piston,^43,44 was used to maintain a pressure of 1 atm during initial equilibration. Temperature was maintained by coupling the system to a Langevin bath with a damping frequency of 1 ps^-1. Electrostatic forces were calculated using particle mesh Ewald summation⁴⁵ with a real space cutoff of 12 Å. Lennard-Jones forces were switched smoothly to zero between 10 Å and 12 Å. Simulations were performed with a 2 fs time step and coordinates were saved at 2 ps intervals. SHAKE was used to constrain the hydrogen-carbon bonds.⁴⁶

Simulations of a single PEG29 molecule in bulk solution were performed using a cubic periodic simulation cell with edge length 50 Å. Four simulation systems consisting of 3797, 3786, 3526 and 3394 TIP3P water molecules and 0, 69, 206, 275 pairs of K⁺ and Cl⁻ ions were setup to yield electrolyte concentrations of ~ 0 M, 1 M, 3 M and 4 M respectively. One thousand steps of energy minimization were performed, followed by heating the simulation cell from 200 K to a final temperature of 293 K. After 5 ns of equilibration under a constant isotropic pressure (NPT) of 1 atm, the edge length of each simulation cell converged to 48.5 Å, 48.9 Å, 48.6 Å and 48.5 Å respectively for each of the four electrolyte concentrations. After equilibration, pressure control was turned off and the simulations were run under constant volume and constant temperature (NVT) to generate 100 ns trajectories from which average properties were calculated.

Nanopore simulations were setup using CHARMM-GUI.⁴⁷ A single αHL nanopore was incorporated in a square patch of 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) lipid bilayer with an edge length of 120.25 Å. The system includes 344 lipids, 41106 TIP3P water molecules, 3169 pairs of K⁺ and Cl⁻ ions with an additional 7 Cl⁻ counterions to yield a system that was electrostatically neutral. The system was initially run under NPT conditions to allow the bilayer to equilibrate. Additional equilibration for 10 ns was then performed by fixing the bilayer area and maintaining the pressure normal to the bilayer at 1 atm (NPAT). During this stage the simulation cell was heated to a final temperature of 293 K. The final height of the simulation cell after equilibration was 144.57 Å and the final electrolyte concentration was 4 M KCl. After equilibration, the simulations were run under NVT conditions and a transmembrane potential of -40 mV was applied with the trans side at ground (Figure 1). One 250 ns trajectory was generated in the absence of PEG in the nanopore. Two 500 ns trajectories were generated, each with a single PEG29 placed in the transmembrane region of the pore. Ten shorter trajectories (50 ns each) were initialized with snapshots from the two long simulations to yield an additional 500 ns. Lastly, two 100 ns trajectories at electrolyte concentrations of 3 M and 3.5 M KCl were generated using the same initial conditions as the 4 M KCl simulations to obtain a total of 1.7 μs for PEG in αHL.

Single-molecule Nanopore Experiments

Planar solvent-free lipid bilayers were formed with DPhyPC (1,2 diphytanolyl-sn-glycero-3-phosphatidylcholine) in n-decane on quartz capillaries.⁴⁸ The quartz capillary used in this study had an aperture with a diameter of 1.04 μm. The capillary was filled with a mixture of heterogeneous distributions of PEG; 30 μM of each 1000 g/mol and 1500 g/mol, and a calibration standard consisting of 1 μM of highly purified PEG29, Mw. 1251 g/mol. PEG was dissolved in either 3 M KCl, 3.5 M KCl or 4 M KCl, each buffered with 10 mM tris and titrated with 3 M citric acid to pH 7.2. The capillary was first immersed in electrolyte solution (with the same ionic strength as the solution inside the capillary, but with no added PEG) and a pipette tip was used to paint the capillary face with a solution of DPhyPC in n-decane to spontaneously form a membrane. After ≈ 10 min, 0.5 μL of αHL (0.5 mg/mL) was added to the external solution bath. A pressure of 80 mm Hg to 140 mm Hg on the capillary side was used to decrease the membrane thickness and aid in channel incorporation. Once a single channel was incorporated into the membrane, the pressure was reduced to ≈ 40 mm Hg to prevent further channel formation. The measurement was performed at applied transmembrane potentials varying between -40 mV and -80 mV for each electrolyte concentration. Data were sampled at 500 kHz after being filtered with an 8-pole Bessel filter with a cutoff frequency of 100 kHz.

Theory of PEG in an αHL nanopore

We refine an analytical model that describes the interactions of PEG with an αHL nanopore.²⁴ Specifically, the model describes the decrease in channel conductance, and the mean residence time, due to the presence of PEG in the pore. The model assumes PEG decreases the ionic current measured across the pore by two physical processes, volume exclusion and reversible PEG-cation complexes. Ignoring molecular fluctuations, PEG was represented by a charged cylinder with cross-section area A_PEG and length L_PEG. Further, the model assumed that PEG is confined to the transmembrane region of the pore, represented by a cylinder of area A_pore and length L_pore. The expression for the blockade depth (see Reiner et al.²⁴ for a detailed derivation), defined as the ratio of the average ionic current when PEG is present in the pore (<i>) to the average ionic current across an empty channel (<i₀>), is

$$\frac{\langle i\rangle }{\langle i_0\rangle }={\left(1-\frac{L_{\mathit{PEG}}}{L_{\mathit{pore}}}\left(1-\frac{2}{\left(a^{\ast }-b^{\ast }\frac{m_B}{m_T}\right)\left(1-\frac{A_{\mathit{PEG}}}{A_{\mathit{pore}}}\right)}\right)\right)}^{-1},$$ (1)

where $a^{\ast }=({\delta }_{+}^{\mathit{eff}}+{\delta }_{-}^{\mathit{eff}})/D_p$, $b^{\ast }={\delta }_{+}^{\mathit{eff}}/D_p$, ${\delta }_{+}^{\mathit{eff}}$ and ${\delta }_{-}^{\mathit{eff}}$ are concentration-weighted diffusion constants of cations and anions inside the pore and D_p is the diffusion constant of ions in the pore, in the absence of PEG. The blockade depth also depends on the number of cations inside the pore, m_T = C_p L_PEG (A_pore − A_PEG), where C_p is the KCl concentration inside the pore in the presence of PEG. The number of cations bound to the PEG is given by,

$$m_B=\frac{\alpha -\sqrt{{\alpha }^2-4m_{T}n{r}_m^{+}}}{2},$$ (2)

where n is the number of monomers in the PEG, $r_m^{+}$ is the average number of monomers in the chain for each bound cation, $\alpha =m_T+n{r}_m^{+}{K}_A^{-1}$, with an association constant $K_A=\exp \left(-\beta (\mathrm{\Delta }{G}_{\mathit{pore}}+s^{+}e\left|V_{\mathit{app}}\right|)\right)$. Finally, ΔG_pore is the free energy change associated with PEG binding a single cation (Figure 2), β is the thermal energy, e is the electron charge, V_app is the applied transmembrane potential, and s⁺ is a freely adjustable parameter that balances the electroosmotic and electrophoretic forces acting on a single cation.

Figure 2.

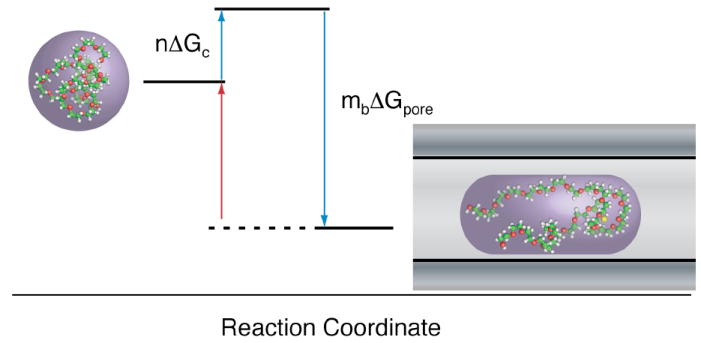
The kinetics of PEG partitioning into the nanopore are described by reversible reactions. PEG kinetics contribute to a description of both the channel conductance and the mean residence time. In order to enter the pore (blue arrows), PEG must overcome an entropic barrier (n ΔG_c). The model also accounts for reversible PEG-cation complexes, formed when PEG adsorbs m_B cations resulting in a free energy change of m_B ΔG_pore. In addition to volume exclusion, the adsorbed ions decrease the local ion concentration and further reduce the channel conductance. The mean residence time of PEG is determined by the free energy of dissociation. PEG exits the pore when m_B cations dissociate from the complex (red arrow) and follows a single exponential distribution.

The mean residence time <τ_n> of PEG is determined by the free energy of dissociation of the molecule from the nanopore and is expressed using the Arrhenius rate equation,

$$\langle {\tau }_n\rangle =\frac{\xi \epsilon L_{\mathit{PEG}}}{m_B\left|V_{\mathit{app}}\right|}\exp \left(-\beta (n\mathrm{\Delta }{G}_c+m_B(\mathrm{\Delta }{G}_{\mathit{pore}}+s^{\mathit{PEG}}e\left|\mathit{Vapp}\right|))\right),$$ (3)

where ΔG_c is the free energy change per monomer associated with confining PEG to the nanopore, ξ is the hydrodynamic drag term acting on PEG, and $s^{\mathit{PEG}}=\gamma \left(1-F_V^{\mathit{PEG}}/F_E^{\mathit{PEG}}\right)$ is an adjustable parameter that balances the electroosmotic and electrophoretic forces $(F_V^{\mathit{PEG}}/F_E^{\mathit{PEG}})$ acting on PEG inside the pore.

Results and Discussion

Ionic current

Ionic currents were calculated from trajectories for a pore in the absence (unblocked) and presence of a single PEG molecule. Assuming the channel conductance is ohmic⁴⁹, the ionic current is i = (N_K⁺-N_Cl⁻) q/Δt, where N_K⁺ and N_Cl⁻ are the accumulated crossings of each ionic species across the channel, q is the charge of the ion and Δt is the time interval of the measurement. The ionic current was calculated across a transverse plane at the geometric center of the membrane, from each saved frame of the trajectory (Figure 3 left, inset and Table 1). For the unblocked pore, the magnitude of the net ionic current <i₀> = 119 ± 11 pA, calculated using 250 ns of simulation data at an applied transmembrane potential, V_app = -40 mV. This value is ~ 20 % lower than the experimentally measured open channel current under identical conditions.^23,50 The systematic error in the simulated ionic currents can be partially attributed to the parameterization of the force field,⁵¹ and is comparable with other simulation studies.^52-55

Figure 3.

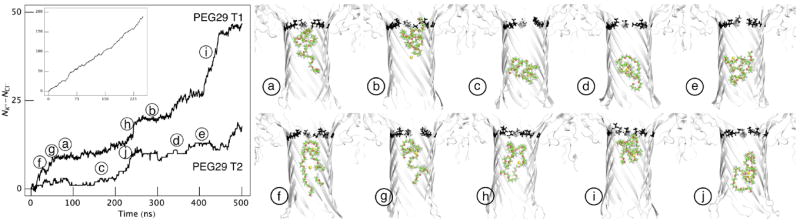
Ionic current calculations from molecular dynamics simulations of PEG in αHL nanopores. (Left) Ion flux across the geometric center of the membrane, as a function of time, with no PEG blocking the pore (250 ns, inset) and two trajectories with PEG29 inside the pore (500 ns each, PEG29 T1 and PEG29 T2). (Right) Starting conformations, sampled from PEG29 T1 and PEG29 T2, for ten 50 ns long simulations are shown, where the channel was either in a non-conducting state (top row) or in a conducting state (bottom row). Only the transmembrane stem region is shown in each figure with atomic representations of Lys 147 and Glu 111 (black) to highlight the constriction in the channel.⁴

Table 1.

Mean Ionic Currents (4 M KCl and -40 mV potential)

		<i> (pA)	<i0> (pA)	<i>/<i0>
MD	Open Pore	--	119±11	--
	PEG29 T1	21±7	--	0.19±0.09
	PEG29 T2	8±4	--	0.07±0.05
	PEG29 T3	26±9	--	0.23±0.09
	Average	19±7	119±11	0.16±0.04
Experiment23		37±1	150±3	0.25±0.005

The ionic current with PEG present in the pore (<i>) was estimated from two all-atom MD simulations (PEG29 T1 and PEG29 T2), each 500 ns long and generated under the same conditions as the open pore case. In each simulation, a single PEG29 was placed in the transmembrane region of the nanopore with a random starting conformation. Figure 3 (left) shows the accumulated ion flux (N_K⁺-N_Cl⁻) as a function of time for the two trajectories. At least two distinct states, delineated by the slopes of the curve, can be observed from this plot. Flat regions of the curve indicate a non-conducting state, where the molecule almost entirely blocks the pore, and regions with steeper slope (> 0.15 q/ns) indicate a conducting state where the ionic current exceeds experiment.²³ We obtain <i> for the trajectories by first calculating the current independently for each conducting and non-conducting segment and then performing a weighted average. Ionic currents and the average blockade depths (<i>/<i₀>) calculated from each trajectory are shown in Table 1. In the case of PEG29 T1, the average blockade depth is 0.19 ± 0.09, consistent with the experimental value of 0.25 ± 0.005 within two standard errors.²³ PEG29 T2 yields a blockade depth of 0.07 ± 0.04, which is systematically lower than experiment.

To further sample PEG conformations in the nanopore, we ran ten additional simulations (Figure 3), each 50 ns long (500 ns total, PEG29 T3), with starting PEG conformations taken equally from the conducting and non-conducting states of PEG29 T1 and PEG29 T2. Combining the ionic currents from the individual segments resulted in a combined blockade depth of 0.23 ± 0.09 that is consistent with experiment. An average of all the simulations resulted in a blockade depth of 0.16 ± 0.04. The simulations demonstrate that the average ionic current is obtained from the superposition of two or more distinct states, which are too short-lived to be presently measured experimentally. Therefore, the theoretical model describes PEG interactions using the long-time average of the ionic currents to enable comparison with experiment.

PEG Geometry

At low molecular weights, PEG acts as an ideal chain in bulk solution.^56,57 The radius of gyration (R_g) then satisfies the relationship R_g ∝ M_w^ν, where M_w is the molecular weight of the molecule and ν is the Flory exponent, which is 0.5 for an ideal chain. This was verified for PEG in water (calculated for the θ-condition) within statistical error using MD simulations.⁴⁰ In contrast, PEG coordinates cations in electrolyte solution forming compact helical crown etherlike structures.⁵⁸ The number of ions bound to the chain scales directly with electrolyte concentration and consequently PEG takes on more compact conformations. Small angle neutron scattering (SANS) measurements of PEG in solution (pure D₂O and 3.6 M KCl) show a decreasing radius of gyration confirming this behavior.⁵⁹

The scaling behavior of PEG with ionic strength was tested with four simulations in bulk solution shown in Figure 4. The simulations were performed in pure water and in electrolyte solutions with concentrations of 1M, 3M, and 4 M KCl. The results were then compared to simulations of PEG inside the pore. Each point in Figure 4 (black curves) represents 100 ns of simulation data after equilibration of the system. Four properties of PEG, relevant to improving the model are compared in the figure, the transverse aspect ratio (a_x/y = x/y, Figure 4A), transverse cross-section area (A_PEG = (π/4) x y, B), longitudinal length of the molecule (L_PEG = z, C), and the number of cations bound to the chain (m_B, D). These properties of PEG were calculated by determining the principal components of the molecule in each simulation frame and assigning the longest component to the z-axis, followed by x and then y; standard errors were calculated by dividing the data into independent blocks that were 10 ns each. Assuming PEG in bulk solution can be represented on average by a cylinder with an elliptical cross-section, the radius of gyration can be expressed in terms of the quantities in Figure 4 as $R_g^2=\frac{1}{\pi }\frac{A_{\mathit{PEG}}}{a_{x/y}}\left(a_{x/y}^2+1\right)+\frac{L_{\mathit{PEG}}^2}{12}$. This equation, combined with the trend of R_g from the experimental data,⁵⁹ implies that increasing the electrolyte concentration will cause a decrease in a_x/y, A_PEG and L_PEG as seen from Figure 4. Furthermore, R_g calculated from simulations in pure water yields a value of 15.5 ± 0.3 Å, consistent with the SANS results, assuming the polymer acts like a Gaussian coil.⁵⁹ The radius of gyration was also calculated for 3.6 M KCl to be 13.3 ± 0.5 Å, by interpolating the curves in Figure 4. This value is ~ 10 % lower than that measured using SANS data at the same electrolyte concentration, partly because the experimental data were fit under the assumption that the molecule acts like an ideal chain,⁵⁹ and the likely suboptimal parameterization of the CHARMM ion parameters at high electrolyte concentrations.

Figure 4.

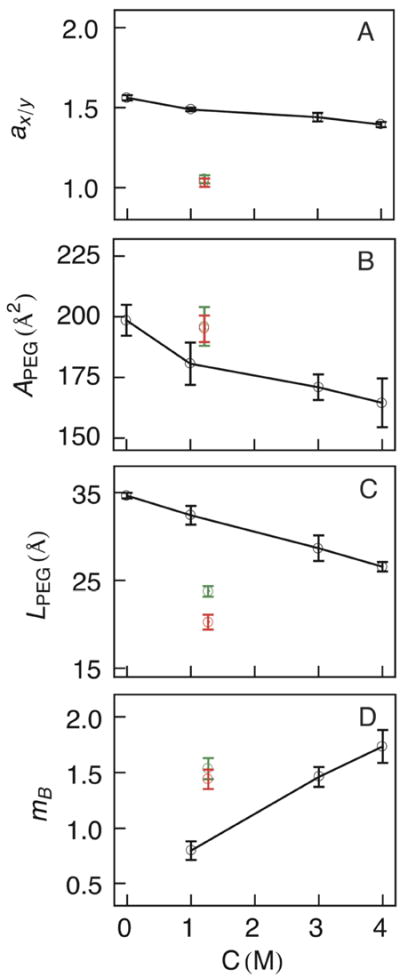
Geometric properties of PEG as a function of electrolyte concentration. Each property was calculated in the reference frame of the molecule with the longest axis designated as the z-coordinate, followed by x and then y. The plots show properties from simulations of PEG in bulk solution (black curves) and from simulations of PEG inside an αHL nanopore (conducting regions are shown in green and non-conducting regions in red). Simulation properties for PEG inside the pore are shown at the effective electrolyte concentration in the transmembrane region of 1.27 M KCl (4 M bulk electrolyte concentration).

The electrolyte concentration inside the pore is lower than the bulk value.⁵² From the MD trajectories at 4 M KCl, we estimate the salt concentration inside the transmembrane region of the pore to average 30 % of the bulk value or 1.27 ± 0.02 M, in the presence of PEG. Inside the pore, PEG conformations have a larger cross-section area and a shorter length than in bulk solution (Figures 4B and 4C). The conducting (green) and non-conducting states (red) of PEG are plotted at the effective salt concentration inside the pore. From Figure 4A, it is evident that inside the nanopore PEG is more cylindrically symmetric (a_x/y ≈ 1), consistent with the symmetry of the pore.⁵³ Interestingly, the volume of PEG in bulk solution is qualitatively similar to that inside the pore. However, confinement causes an increase in A_PEG, relative to simulations in bulk solution, approaching the value in pure water, while L_PEG is ~ 25 % smaller. Thus, confinement of PEG in the pore influences its conformation, contrary to previous assertions.⁴⁰

An essential observation from Figure 4 is that inside the pore, the differences in the PEG geometry between the conducting and non-conducting states are small. While a_x/y and A_PEG are virtually indistinguishable between the two states, L_PEG decreases by ~ 3 Å in the non-conducting state, indicating a more compact conformation. In addition to PEG geometry, the conductance is also influenced by the location of the molecule in the channel. The distribution of the PEG center of mass along the pore axis (Figure 5) shows a strong correlation between channel conductance and pore radius (R_p). Deep channel blockades occur predominantly in narrow regions of the pore with R_p < 12.4 Å. The origin of the two observed states can be further investigated by a more thorough sampling along the pore axis with techniques such as umbrella sampling^60,61 that will be performed in future work. The fact that the non-conducting state of the channel is correlated with a compact PEG geometry in the narrow regions of the pore (with nonspecific interactions between PEG and the channel) has broad implications in the design of solidstate and hybrid solid-state/biological nanopores.

Figure 5.

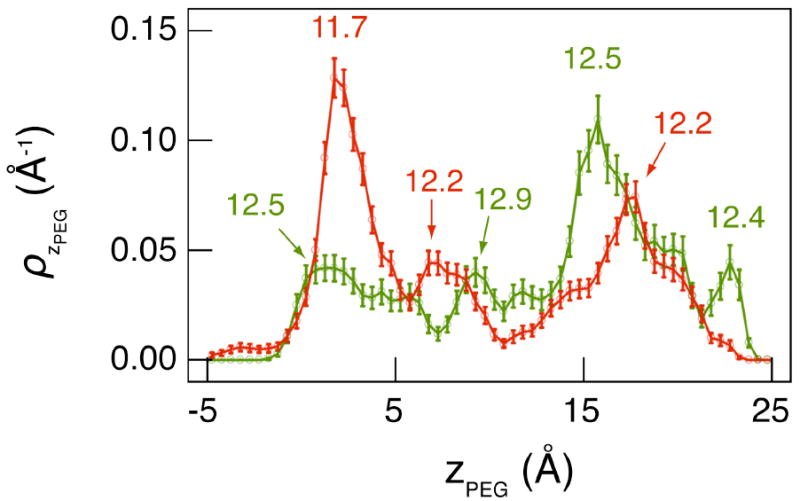
Center of mass distribution of PEG inside the pore for conducting (green) and non-conducting states (red). The labels show the radius of the pore (R_p) at the location of the individual peaks. The distribution indicates a strong correlation between the channel conductance and pore radius, where the non-conducting states primarily occupy the narrowest regions of the channel.

Cation Binding

The coordination of cations by the oxygen atoms in the C-O-C subunit of PEG to form planar crown ether-like structures has been observed experimentally in the gas phase using ion chromatography^62-65 and to a more limited extent in solution using MD simulations.⁵⁸

Simulations performed as part of this work confirm this behavior, as illustrated by the simulation snapshot in Figure 6A. Ion binding was quantified by calculating the radial distribution function (g_K⁺-PEG(r)) between K⁺ ions and the PEG29 oxygen atoms (Figure 6B). The first coordination shell is at 3.9 Å, with no corresponding evidence of coordination between the Cl⁻ ions and PEG (data not shown). The PEG coordination number was calculated by integrating g_K⁺-PEG(r) and found to be 4.1 PEG oxygen atoms for each cation.

Figure 6.

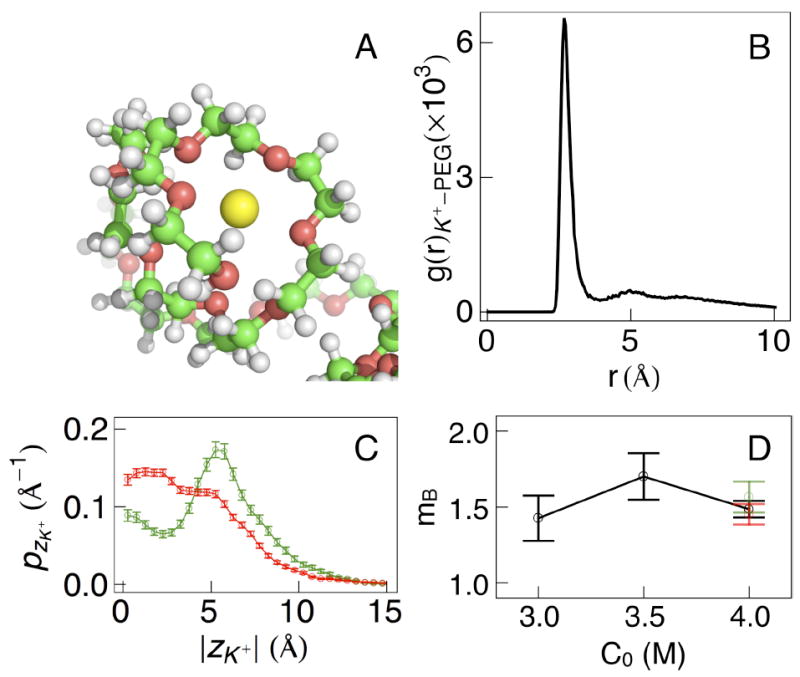
PEG coordinates cations in electrolyte solutions. (A) PEG forms planar helical conformations that are analogous to crown ethers. (B) The radial K⁺-PEG distribution function from simulations of PEG in αHL is shown and is used to calculate the coordination number for each cation. (C) The absolute z-distribution of ions bound to the PEG shows that ions are clustered closer to the center of mass of the molecule in the bound state (red) when compared with the unbound state (green). (D) The number of bound ions does not vary significantly inside the pore for the electrolyte concentrations simulated.

The preceding result was used for a more detailed analysis of ion binding. For each simulation frame, the number of ions bound to the PEG29 chain was estimated from hydrogen bonding between the cations and PEG oxygen atoms. The cutoff distance was selected to be 3.9 Å, to coincide with the first coordination shell, and an ion was considered bound if it was within the cutoff distance of four or more successive PEG oxygen atoms. In bulk solution, the number of bound cations (m_B) scale strongly with electrolyte concentration (Figure 4D). However, inside the pore, the mean number of bound cations for the conducting and non-conducting states is virtually identical (1.57 ± 0.05 and 1.47 ± 0.02 respectively), with a combined average of 1.52 ± 0.03. Figure 6C shows the z-distribution of bound K⁺ ions relative to the center of mass of the PEG inside the nanopore. The denser configurations of PEG in the non-conducting states are further supported by this plot. We observe distinct peaks for each of the two states, with the non-conducting states taking on more compact conformations. Finally, in contrast with simulations of PEG in bulk solution, m_B inside the pore does not change significantly with increasing electrolyte concentration (Figure 6D). From 100 ns trajectories of PEG in αHL at 3 M and 3.5 M bulk electrolyte concentrations, m_B equals 1.43 ± 0.15 and 1.70 ± 0.15 respectively.

Parameter Estimation and Simulation Sampling

The accurate recovery of ionic currents from simulation trajectories (to benchmark against experiment) requires extensive spatial sampling of the pore and several transitions between the PEG conducting and non-conducting states. The aggregated trajectories of PEG in the nanopore (see Figure 3) only sample ~ 20 Å of the transmembrane region of the pore and yield 15 transitions between the conducting and non-conducting states. Therefore, while the simulated ionic currents are statistically consistent with experiment, there is relatively large uncertainty. The experimentally determined mean residence time of PEG29 in the pore (at 4 M KCl and -40 mV applied potential) is ~ 600 μs, which is two orders of magnitude longer than the timescales typically accessible with all-atom MD simulations. However, despite the relatively slow convergence of the ionic currents, we are able to estimate the parameters relevant to refining the theoretical model (for example A_PEG, L_PEG and m_B), which converge on much shorter time scales for the simulations of PEG29 performed here. This is because the difference in these critical model parameters is small between the bound and unbound states of PEG inside the pore.

Experimental data

Polydisperse PEG distributions (pPEG) with mean molecular weight (M_w) of 1000 g/mol and 1500 g/mol were measured experimentally with a single αHL nanopore incorporated in a DPhyPC lipid bilayer. Data were recorded with bulk electrolyte concentrations of 3 M, 3.5 M, and 4 M KCl and with applied transmembrane potentials between -40 mV and -80 mV relative to the trans side of the pore. When no PEG is present in the pore, an average open channel current (<i₀>) was recorded that was sensitive to both the applied transmembrane potential and the electrolyte concentration (4 M KCl data shown in Figure 7, left). PEG, added from the trans side of the pore, caused deep, well-defined transient current blockades.²³ A single PEG partitioning into the pore results in an average ionic current (<i>) that decreases with the size of the molecule. Individual PEG blockade events were analyzed by a thresholding algorithm that determined both the blockade depth (<i>/<i₀>), by scaling <i> with the average open channel current, and the residence time (τ).²⁴

Figure 7.

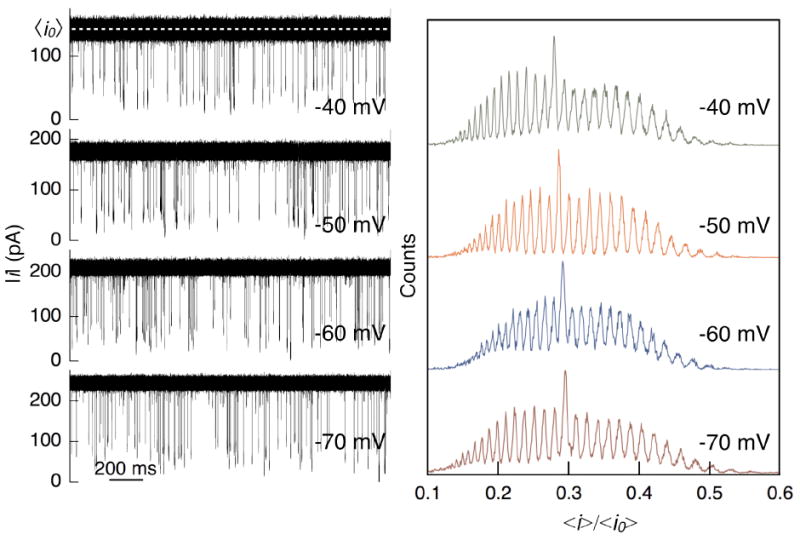
Experimental measurements of PEG mixtures (mean molecular weight of 1000 g/mol and 1500 g/mol in 4 M KCl at pH 7.2) with a single αHL nanopore. (Left) Time-series of ionic currents are shown at four transmembrane potentials. The mean open channel current (<i₀>, dashed white at -40 mV) increases with applied potential. PEG partitions into the channel and reduces its conductance (<i>) proportional to the molecule size. Individual PEG events are then analyzed to estimate the blockade depth (<i>/<i₀>). (Right) Distribution of <i>/<i₀> at four applied transmembrane potentials. The peaks represent uniquely sized polymers, discriminated with single monomer resolution. A systematic shift of the peaks to the right across the four plots highlight the inverse dependence of <i>/<i₀> with applied potential.

Figure 7 (left) shows representative ionic current time-series of pPEG in 4 M KCl (qualitatively similar results were obtained in [KCl] = 3 M and 3.5 M, not shown). The magnitude of the open channel current scaled directly with increasing potential, averaging 141.2 ± 0.1 pA, 176.7 ± 0.1 pA, 210.5 ± 0.2 pA and 242.9 ± 0.1 pA for the applied transmembrane potentials of -40 mV, -50 mV, -60 mV, and -70 mV respectively. The rate of PEG partitioning into the pore was also observed to increase with transmembrane voltage averaging 6.1 events/s, 6.2 events/s, 7.0 events/s and 8.6 events/s. A histogram of <i>/<i₀> resulted in distinct peaks for each of the four applied transmembrane potentials (Figure 7 right). Each peak in the histogram identifies a single sized PEG molecule with single monomer resolution. The blockade depth distribution is calibrated with an internal standard of highly purified monodisperse PEG29 (1251 g/mol) shown by the tallest peak in each plot. Because <i>/<i₀> scales inversely with the polymer size,^23,24 peaks to the left of PEG29 represent larger polymers. The blockade depth histograms (Figure 7, right) clearly resolve PEG molecules ranging in size from PEG16 (722 g/mol) to PEG40 (1778 g/mol). Furthermore, increasing the transmembrane potentials causes the blockade depth to systematically decrease.²⁴

The peak positions in Figure 7 (for the 4 M KCl case) were identified using a peak finder algorithm²⁴ and then plotted as a function of polymer number in Figure 8. A maximum likelihood estimator was used to assign events to individual peaks in each data set. This allowed a ready estimate of the probability density of residence times as a function of polymer size. The residence times of a given size PEG molecule are exponentially distributed.²³ Figure 8 also shows the mean residence time as a function of polymer index number. From the figure, we observe that the mean residence time scales inversely with applied transmembrane potential.

Figure 8.

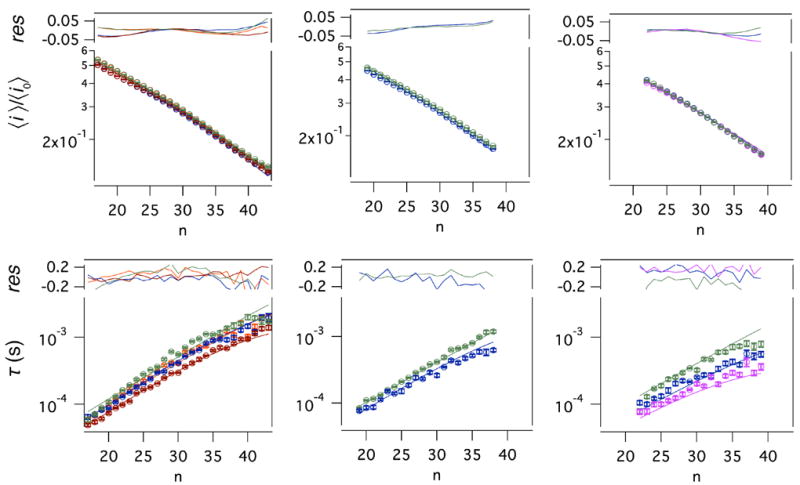
Mean blockade depths (top) and residence times (bottom) as a function of the polymer size (n) were fit to the refined theoretical model simultaneously. PEG molecules with different sizes were measured experimentally at three electrolyte concentrations: 4 M KCl (first column) at four applied transmembrane potentials of -40 mV (green), -50 mV (orange), -60 mV (blue) and -70 mV (brown); 3.5 M KCl (middle column) at -40 mV and -60 mV; 3 M KCl (right column) at -40 mV, -60 mV and -80 mV (magenta). Least squares fits to the data (solid lines) were obtained for the blockade depth, (<i>/<i₀>) from eq 1 and residence time (τ) from eq 3. Normalized residuals (res) were calculated for each curve using the expression 1-(<i>/<i₀>)_model/(<i>/<i₀>)_data for the blockade depth and 1- τ_model/τ_data for the residence times.

Estimation of model parameters

The theoretical model,²⁴ refined by MD simulations here, was fit to the blockade depth and residence time data shown in Figure 8. The blockade depth (eq 1) depends on model parameters such as the local electrolyte concentration inside the pore in the presence of PEG (C_p), the relationship between the electrophoretic and electroosmotic forces acting on cations (s⁺), the concentration weighted diffusion constants (a*and b*) and the free energy of a single cation adsorbing to PEG (ΔG_pore). Because these parameters are invariant with electrolyte concentration and the applied transmembrane potential, they were linked between all data sets in the fit. In addition to the parameters above, the residence time (eq 3) depends on the free energy of confinement (ΔG_c), which was adjusted independently with electrolyte concentration. Equation 3 also depends on parameters that describe the relationship between the electrophoretic and electroosmotic forces acting on PEG (s^PEG) and the hydrodynamic drag on the PEG (ξ). To reduce the number of free parameters, C_p, A_PEG and L_PEG were obtained from MD simulations and therefore fixed in the model. From the simulations, the pore geometry was found to be A_pore = 450 Ų and L_pore = 49.5 Å. Initial values of $r_m^{+}$ were obtained from simulations, but not fixed in the model.

Blockade depths and residence times as a function of polymer index number (n) were simultaneously fit to electrolyte concentrations of 3 M KCl (-40 mV, -60 mV and -80 mV), 3.5 M KCl (-40 mV and -60 mV) and 4 M KCl (-40 mV, -50 mV, -60 mV and -70 mV) using the global optimization program Motofit.⁶⁶ Figure 8 shows the results of the fits to the blockade depth (left) and residence times (right) in each case, together with the fit residuals. Parameters invariant with electrolyte concentration were found to be a* = 1.553 ± 0.001, b* = 1.50 ± 0.02, s⁺= 1.39 ± 0.03, s^PEG = 0.108 ± 0.003, ξ = 1172 ± 16 Vs/m and ΔG_pore = -5.3 ± 0.1 k_BT. Parameters that vary with the bulk electrolyte concentration (C₀) are listed in Table 2. The number of bound ions (m_B) for PEG29 is obtained from eq 2 using the estimated fit parameters, $r_m^{+}$, ΔG_pore and s⁺.

Table 2.

Model Fit Parameters

C0 M	Vapp mV	ΔGc kBT	$r_m^{+}\times {10}^{­3}$	mB (PEG29)
3.0	-40	0.175±0.006	71.5±0.3	2.01±0.01
	-60			1.90±0.02
	-80			1.68±0.03
3.5	-40	0.175±0.006	69.3±0.5	1.95±0.01
	-60			1.85±0.02
4.0	-40	0.156±0.005	67.9±0.3	1.91±0.01
	-50			1.87±0.01
	-60			1.81±0.01
	-70			1.72±0.02

The refined model of PEG interactions with αHL is in excellent agreement with the blockade depth and residence time data (Figure 8). The number of bound ions (m_B) was obtained from the simulations (Figure 6D) at -40 mV for each electrolyte concentration in Table 2. Because the simulations were not run for each transmembrane potential, m_B was not fixed in the model. At 4 M KCl, the model predicts that a PEG29 binds, on average, three fewer cations than previously reported.²⁴ Moreover the excellent fit between the experimental data and the model implies that volume exclusion plays a large role in PEG-nanopore interactions. The values of m_B obtained from the fit are on average 25 % higher than those estimated from the simulations at -40 mV (Figure 6D). This is consistent with the systematic error in the simulations due to incorrect parameterization of the force field, including the lack of induced polarization effects. The presence of PEG in the pore drives an electroosmotic flow that opposes the flow of ions.⁶⁷ The model estimates these forces through s^PEG. Assuming PEG is centered in the pore (γ = 0.5), $F_V^{\mathit{PEG}}/F_E^{\mathit{PEG}}=0.78\pm 0.01$, which agrees with previous experimental studies with PEG²⁴ and solid-state nanopore DNA experiments.^28,67

An important consequence of including the effects of cation binding is that the model estimates both the free energy of binding a single cation (ΔG_pore) and the entropic penalty of confining PEG to the pore (ΔG_c). As expected, the value of ΔG_pore differs considerably from the binding energies of -30 k_BT measured experimentally for K⁺–dimethyl ether (DME) interactions in vacuum.⁶⁴ Solvation has a large effect on the binding energy. While direct measurements of the binding energies for the solvated molecule are difficult, ΔG_pore is in excellent agreement with K⁺–DME binding energies calculated in water using quantum mechanical methods.⁶⁸ Finally from Table 2, ΔG_c is inversely proportional to electrolyte concentration because PEG assumes more compact conformations at higher electrolyte concentration (Figure 4). Interestingly the entropic penalty exceeds the thermal energy at room temperature when n > 6 for all measured electrolyte concentrations. The relatively high entropic penalty will influence the capture rate of PEG by the pore and will need to be considered when designing PEG analogs in applications such as the proposed nanopore-based DNA sequencing by synthesis.³⁴

Conclusions

We refined a model of polymer interactions with nanopores using a combination of analytical theory, MD simulations and new measurements. Predictions made by the simulations are used to test and modify several previous assumptions about the interactions of PEG with the αHL nanopore. In this study, MD simulations of PEG29 in bulk solution were performed in pure water and with electrolyte concentrations of 1 M, 3 M, and 4 M KCl. Additional simulations of PEG29 inside an αHL nanopore were run with an electrolyte concentration of 4 M KCl and a transmembrane potential of -40 mV. Polydisperse PEG (M_w =1000 g/mol and 1500 g/mol) was measured experimentally using an αHL nanopore with electrolyte concentrations between 3 M and 4 M KCl and transmembrane potentials between -40 mV and -80 mV. Molecular interactions estimated from MD simulations were used to refine the theoretical model, which was then fit to experimental data to yield excellent quantitative agreement for all the measured cases.

The MD simulations predict that the PEG geometry is significantly influenced by the nanopore. Consequently, conformations of PEG obtained from simulations in bulk solution, while qualitatively similar, are not adequate when developing a quantitative model of polymernanopore interactions, as had been proposed.⁴⁰ The cross-sectional area of PEG29 is ~ 20 % larger inside the pore, compared with the polymer in bulk solution, and the aspect ratio is commensurate with that of the pore. This is expected, given the lower electrolyte concentration inside the pore and the effects of confinement. The increased cross-sectional area causes volume exclusion to play a greater role in the measured blockade depth, compared with earlier predictions.²⁴ MD simulations also confirm that PEG binds cations in bulk solution as well as inside the pore. The simulations predict that PEG29 binds 1.52 ± 0.02 cations on average inside the pore (4 M KCl, V_app = -40 mV), which is about 3-fold less than that estimated previously.^24,69 An important outcome of using physically accurate parameters obtained from MD simulations is that the free energy of PEG binding a single cation (ΔG_pore) is estimated to be -5.3 k_BT, ~ 2.5-fold lower than previously estimated²⁴ and in quantitative agreement with quantum mechanical calculations.⁶⁸ The effect of confinement on PEG geometry was found to be substantial even for relatively small molecules (n > 6). This is contrary to the conclusions of previous studies where only molecules with volumes substantially larger than the pore were thought to overcome an entropic barrier at the pore entrance.^70,71 The heights of the entropic barrier per monomer (ΔG_c) for the 3 M, 3.5 M and 4 M KCl data are 0.175 ± 0.006 k_BT, 0.175 ± 0.006 k_BT and 0.156 ± 0.005 k_BT respectively.

Finally, the simulations clearly highlight the sensitivity of the ionic currents to the conformation and location of PEG inside the pore. Relatively large differences in the ionic current in the conducting and non-conducting states are the result of subtle differences in PEG conformation, its location in the pore, and ion binding. The microscopic states accessible to MD simulations are not easily measured experimentally. The combination of the molecular detail from MD simulations with analytical theory makes the tools developed here important when designing either molecular tags for DNA sequencing applications³⁴ or in designing biological, solid-state or hybrid nanopores.^72-75