Systematic optimization model and algorithm for binding sequence selection in computational enzyme design

Xiaoqiang Huang; Kehang Han; Yushan Zhu

doi:10.1002/pro.2275

. 2013 May 6;22(7):929–941. doi: 10.1002/pro.2275

Systematic optimization model and algorithm for binding sequence selection in computational enzyme design

Xiaoqiang Huang ¹, Kehang Han ¹, Yushan Zhu ^1,^*

PMCID: PMC3719087 PMID: 23649589

Abstract

A systematic optimization model for binding sequence selection in computational enzyme design was developed based on the transition state theory of enzyme catalysis and graph-theoretical modeling. The saddle point on the free energy surface of the reaction system was represented by catalytic geometrical constraints, and the binding energy between the active site and transition state was minimized to reduce the activation energy barrier. The resulting hyperscale combinatorial optimization problem was tackled using a novel heuristic global optimization algorithm, which was inspired and tested by the protein core sequence selection problem. The sequence recapitulation tests on native active sites for two enzyme catalyzed hydrolytic reactions were applied to evaluate the predictive power of the design methodology. The results of the calculation show that most of the native binding sites can be successfully identified if the catalytic geometrical constraints and the structural motifs of the substrate are taken into account. Reliably predicting active site sequences may have significant implications for the creation of novel enzymes that are capable of catalyzing targeted chemical reactions.

Keywords: computational enzyme design, computational protein design, protein–ligand interaction, binding, active-site recapitulation, global optimization

Introduction

The ultimate goal of computational enzyme design is to generate an in silico amino acid sequence that will fold into a predefined topological structure and run the targeted reaction with levels of activity similar to those of naturally occurring enzymes for their primary substrates. The high efficiency and unsurpassed selectivity, such as chemoselectivity, region and stereospecificity, and the biodegradability of enzymes have made them attractive green catalysts for chemical transformations in the pharmaceutical industry. However, the limited availability of naturally occurring enzymes has restricted their applicability to broader problems in biotechnology. Structure-based enzyme design is a significant alternative that can contribute to the discovery of enzymes that can efficiently catalyze chemical reactions of interest, but that are currently inaccessible via natural enzymes. After the first fully automated design of a novel sequence for an entire protein was reported,¹ various protein variants with appreciable activities for different reactions have been designed. Hellinga and coworkers have designed several metalloenzymes²^–⁴ based on the ligand binding site construction program, DEZYMER, which was initially developed by Hellinga and Richards.⁵ Mayo and coworkers have extended their computational protein design tool, ORBIT, to enzyme active site design.⁶^,⁷ The artificial enzymes that were designed based on Rosetta from Baker, Houk, and coworkers were experimentally confirmed for three different reactions,⁸^–¹⁰ demonstrating that computational enzyme design can be used to generate active catalysts. Naturally occurring enzymes, such as amylase, fumarase, and staphylococcal nuclease, enhance the rates of the reactions that they catalyze by more than 10¹⁴ fold¹¹; however, most computationally designed enzymes provide enhancements of less than 10⁶ and are more than six orders of magnitude below the diffusion limit.¹² To determine why the activities of artificial enzymes fail to reach those of the natural enzymes, various studies have been carried out to investigate the origins of the catalysis,¹³^,¹⁴ to further increase their activity by using directed evolution,¹⁵ and to study the influence of dynamics on evaluation and iterative improvement of the designs.¹⁶

Assuming that the ideal active site description can be completely transferred into the catalytic efficiency of the computationally designed enzyme and the structural recapitulation based on self-assembly folding could be implemented perfectly, we would want to know, whether or not the designed binding sequence is compatible with the matched catalytic sites or, whether or not the binding sequence can stabilize the interface between the active site and the small molecule, and maintain the transition state structure accurately. To address these questions, the design method used in Rosetta⁸^,¹⁷ was first reiterated. After the matching process was finished, the positions and conformations of the catalytic residues and transition state that satisfy the active site description were determined. In the last step for full sequence optimization of the binding positions surrounding the docked transition state model, the catalytic site description was kept fixed. According to the transition state theory for enzymatic reaction¹¹ the conformation of the catalytic site description lies at a maximum point on the free energy surface along the reaction coordinate, and the optimal binding between the transition state and the active site residues lies at a minimum point on the free energy surface of the reaction system. However, the decomposition-based enzyme design method might not find the saddle point for the reaction,¹⁸ because the degrees of freedom of the catalytic site description were neglected during sequence selection for the binding residues. This will result in a high activation energy for the reaction and a low catalytic efficiency for the designed enzymes. Lassila et al.⁷ developed a process for ligand placement in computational enzyme design that allows ligand rotation, translation, and conformational freedom to be explored within the full sequence design calculation, which includes both the catalytic and binding residues.

To identify the saddle point on the free energy surface of the enzymatic reaction system, we constructed a systematic optimization model for sequence selection of the binding residues based on graph-theoretical modeling within the decomposed enzyme design methodology implemented in PRODA,¹⁹ that is, PROtein Design Algorithmic package, and developed a novel global optimization algorithm to solve the hyperscale combinatorial optimization problems for generic sequence selection in computational protein design. The systematic optimization model and global optimization algorithm for enzyme design that we developed were evaluated by the recapitulation of native sites for the two hydrolytic reactions shown in Figure 1. The catalytic geometrical relationships that were obtained are presented in Figure 2.

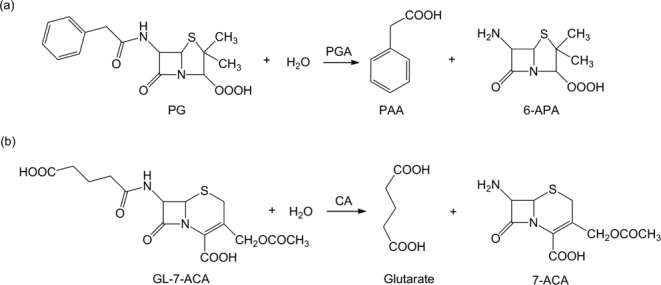
The reaction schemes catalyzed by PGA and CA. PGA: penicillin G acylase; CA: cephalosporin acylase; PG: penicillin G; PAA: phenylacetic acid; 6-APA: 6-aminopenicillanic acid; GL-7-ACA: glutaryl-7-aminocephalosporanic acid; 7-ACA: 7-aminocephalosporanic acid.

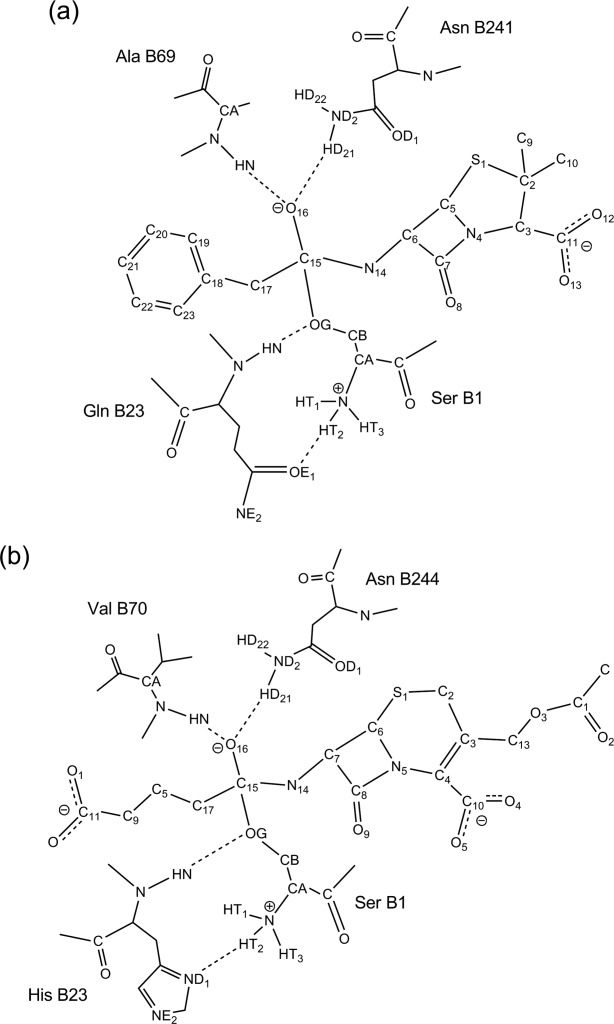
The catalytic geometrical constraints for two reactions catalyzed by PGA and CA, and the exact geometry definitions are included in Supporting Information Tables S1 and S2. (a) PGA; (b) CA.

Results

A heuristic global optimization algorithm for the sequence selection problem

The goal of the optimization problem (P) is to repack the active site as tightly as possible in order to identify the global minimum binding energy between the enzyme active site and the transition state. Our earlier solution to the core sequence selection problem,¹⁹ that is, Algorithm 0, used the following approach: (i) first run the dead-end elimination (DEE) based filters; (ii) construct the MILP problem using the selected rotamers; and (iii) solve the MILP problem. This approach does not work for the binding sequence selection problem because of two differences between it and the core sequence selection problem; namely, (i) a larger backbone independent rotamer library which included 7421 rotamers²⁰ was used in enzyme design and this resulted in a hyperscale combinatorial optimization problem, and (ii) the complex free energy function that was used to compute the interactions between polar residues diminished the energy gap between rotamers and greatly decreased the effectiveness of the DEE theorem-based heuristics.²¹^,²² Therefore, the solution to the optimization problem (P) has become a great challenge. In our previous study¹⁹ of the core sequence selection problem, we found that the gap between the MILP problem and its linear programming (LP) relaxation was quite small, for instance the relative gap of 14 case studies is less than 5.0%, and the maximal relative gap is only 11.49%, although the LP rarely found an integer solution. In the present study, we recalculated the 20 case studies of Zhu,¹⁹ by first solving the LP problem without running the DEE. The results of this calculation are shown in Table I. The LP relaxation solutions for three of the case studies are the same as their global minimum energy conformation (GMEC) solutions and the gap between the LP solution and the GMEC solution for the other case studies is small. After analyzing the LP solution carefully, we found that most of the vertex decision variables converged at their lower bounds. Based on this important finding, we developed a heuristic algorithm for the generic sequence selection problem, Algorithm 1. Algorithm 1 uses the following approach: (i) first solve the LP problem; (ii) eliminate the rotamers for which the LP solutions converge at their lower bounds and construct a small MILP problem using the remaining rotamers; and (iii) solve the small MILP problem. The effectiveness of Algorithm 1 was confirmed by the results in Table I, which show that the heuristic solutions for seven of the case studies are the same as their GMEC solutions. After analyzing the other case studies for which the heuristic solutions are greater than their GMEC solutions, we found that some of the GMEC rotamers for these cases were wrongly eliminated because they were not selected by the LP solution. To overcome this problem and restore these GMEC rotamers, we designed a scoring function to rank all the rotamers at each design site as,

Table I.

Computational Results for 20 Core Sequence Selection Problems

			MILP solution (no. of rotamer of MILP)

PDB	No. of site (no. of rotamer)	LP solution (GMEC)	N = 0, X = 0	N = 20, X = 2	N = 20, X = 5
1aac	20 (1860)	−125.99 (−124.56)	−122.86 (81)	(219)^a	(342)^a
1b9o	23 (2139)	−149.61 (−139.69)	(48)^a	(243)^a	(393)^a
1c5e	18 (1674)	−104.11 (−103.03)	(24)^a	(173)^a	(297)^a
1c9o	12 (1116)	−65.73 (−64.66)	(29)^a	(129)^a	(210)^a
1cc7	11 (1023)	−77.11 (−68.67)	−65.21 (20)	(114)^a	(183)^a
1cex	50 (4650)	−263.41 (−262.26)	−261.14 (69)	(504)^a	(833)^a
1cku	11 (1023)	(−61.86)^a	(11)^a	(111)^a	(193)^a
1ctj	17 (1581)	(−99.14)^a	(17)^a	(181)^a	(290)^a
1cz9	28 (2604)	−149.96 (−147.22)	−142.13 (62)	(286)^a	(462)^a
1czp	18 (1674)	−85.83 (−84.30)	(28)^a	(162)^a	(281)^a
1d4t	20 (1860)	−140.72 (−124.55)	−121.94 (81)	−122.14 (226)	(351)^a
1igd	10 (930)	−70.21 (−66.79)	−60.20 (20)	(108)^a	(170)^a
1pga	10 (930)	(−67.75)^a	(10)^a	(110)^a	(169)^a
1qq4	40 (3720)	−217.88 (−209.39)	−202.98 (66)	(412)^a	(673)^a
1qtn	26 (2418)	−169.08 (−162.60)	−160.92 (58)	(282)^a	(447)^a
1ubq	14 (1302)	−85.45 (−76.81)	−70.19 (66)	(154)^a	(239)^a
2pth	45 (4185)	−235.59 (−222.16)	−216.32 (110)	(471)^a	(750)^a
3lzt	26 (2418)	−157.49 (−142.01)	−138.24 (49)	−141.28 (270)	(443)^a
5p21	45 (4185)	−283.16 (−269.56)	−265.37 (104)	(465)^a	(760)^a
7rsa	15 (1395)	−90.82 (−89.45)	−86.68 (20)	−89.39 (145)	(253)^a

Open in a new tab

The global minimum solution of the sequence selection problem is represented by GMEC, and the LP relaxation solution or the heuristic MILP solution is the same as the GMEC solution.

N refers to the number of top rotamers at the current design site.

X refers to the number of top rotamers having the same amino-acid type at the current design site.

(1)

An example of the ranking effect of this scoring function for all the rotamers at the third design site of case study 1CC7 is shown in Figure 3. The rotamer selected by the LP solution ranked first and, although the GMEC rotamer ranked fourth, it was not selected by the LP solution. To be restored, the rotamers should satisfy three conditions: (i) it is not selected by the LP solution; (ii) it should rank in the top N for all the rotamers at the current design site; and (iii) it should rank in the top X for all the same amino-acid type rotamers at the current design site. N and X are algorithmic parameters that should be set as small as possible in order to minimize the number of rotamers that are selected for the final small MILP problem. The second step of Algorithm 1 was therefore revised as: (ii-a) eliminate the rotamers for which the LP solutions converge at their lower bounds, restore rotamers based on the scoring function described by Eq. ((1)), and finally construct a small MILP problem using all the active rotamers. A close-up view of the top 20 rotamers at the third design site of 1CC7 is shown in the inset in Figure 3, and the top two rotamers for each amino acid type in the top 20 rotamers are indicated by different symbols. The GMEC rotamer at the third design site of 1CC7 was restored successfully using this scoring function. The results for the 20 case studies that were obtained using the revised Algorithm 1 with two different sets of parameters are given in Table I. For N = 20 and X = 2, the heuristic solutions for 17 of the case studies were the same as their GMEC solutions. By increasing X from 2 to 5, the GMEC solutions for all 20 case studies were obtained. The heuristic algorithm has two additional advantages: (i) the LP relaxation problem is polynomial-time tractable even though its size is huge; and (ii) the size of the final MILP problem is small as shown by the number of rotamers of the MILP problems in Table I. For the largest case study 1CEX, the original MILP problem had 4650 rotamers but the small MILP problem constructed using N = 20 and X = 2 had only 504 rotamers, and its solution was the same as that of the original MILP problem, namely the GMEC solution.

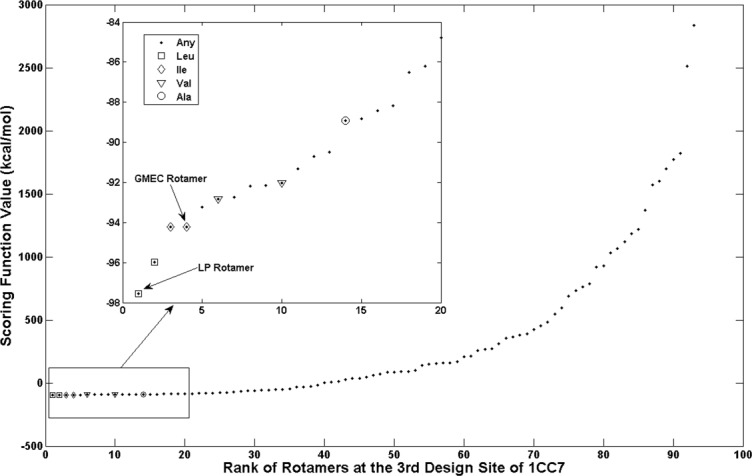
Effect of scoring function on recovery of rotamers which were mistakenly eliminated by LP. The inset figure is the close-up view for the top 20 rotamers at the third design site of 1CC7. The LP rotamer refers to the rotamers saved by the fractional solution of LP relaxation problem, while the GMEC rotamers refer to the rotamers which are taken in the global minimum solution at the current design site.

For the binding sequence selection problem, two preliminary filtering strategies to prune the large number of dead-end rotamers at each design site were applied before running the revised Algorithm 1. The first filter is the intrinsic energy check which eliminates rotamers that either have intrinsic energies 20.0 kcal/mol above the energy of another rotamer of the same amino-acid type or have energies 50.0 kcal/mol above the energy of another rotamer of any amino-acid type at the same design site. The second filter is the single Goldstein DEE criterion.²² It should be noted that the interaction energy between each catalytic rotamer pair was biased to favor those contacts that satisfy the catalytic geometrical relationship.

Sequence recapitulation test of the native enzyme binding site

The systematic optimization approach developed in this study for binding sequence selection was tested using the two enzyme-catalyzed hydrolytic reactions shown in Figure 1, and the catalytic geometrical relationships between catalytic residues and TS small molecules are presented in Figure 2. The parameters for the catalytic geometrical relationships and small molecule placements are presented in Supporting Information Tables S1–S4. The design schemes for scaffolds penicillin G acylase (PGA) and cephalosporin acylase (CA) are presented in Supporting Information Table S5. The total numbers of rotamers for all design sites were 74,089 and 77,586, and the computational complexities reached 9.53 × 10⁷⁴ and 5.15 × 10⁸⁴ for PGA and CA, respectively. To evaluate different binding sequences for a specific reaction, we assumed that the native enzyme was the best catalyst among all the designed proteins. In the crystal structures of the complexes, the side chains of two substrates for two reactions are different, although the catalytic mechanism is identical. The side chain of penicillin G (PG) in the binding pocket of PGA is a phenyl ring, which is hydrophobic, while the side chain of glutaryl-7-amino cephalosporanic acid (GL-7-ACA) in the binding pocket of CA is a linear carboxylic acid, which is hydrophilic and charged. As a consequence of this difference, the active pockets of PGA and CA are different; the binding pocket of PGA mostly contains hydrophobic amino acid side chains, while the binding pocket of CA has more polar amino acid side chains. To characterize such differences in the design sites, we introduced some specific 0–1 linear programming constraints, and added them into the optimization problem (P) to reflect these aspects. For instance, because the side chain of GL-7-ACA is hydrophilic and negatively charged, we assumed that there was one positively charged amino-acid side chain in the active pocket of the designed CA, but no negatively charged amino-acid side chains. These restrictions can be described by two 0–1 equalities as,

(2)

(3)

where SP is the set of primary design sites. The results of binding sequence selection for PGA and CA under different design types are shown in Table II and Figure 4. For scaffold PGA, up to five primary design sites were recovered under different design types, but the compositions of the designed sequences were different. Under design type (*,*,*), this means that there was no restriction on the number of charged and polar residues during the binding sequence selection process, and the designed enzyme had three charged residues, LysB67, AspB154, and ArgB177, which formed salt-bridge networks between their charged groups. The strong pairwise interaction between these residues reduced the total free energy of the protein system, but these residues may not contribute to the binding between the transition state and the active site of PGA, because the side chain of PG in the active pocket is the hydrophobic phenyl ring. After adding the design type restriction constraints to limit the appearance of charged residues in the designed positions, the selected residues at primary sites were all hydrophobic, even when no limit was placed on the number of polar residues. To recover the polar residues at sites B31 and B67, one or two polar residues were forced to appear in the designed sequences under design types (0,0,1) and (0,0,2); however, the B31, B67, and B154 sites were still not recovered. After carefully analyzing the crystal structure of PGA (1GK9), we found that a specific water molecule formed two water-mediated hydrogen bonds with atom OG of SerB67 and atom NE1 of TrpB154. Because we used the implicit solvent model in our free energy function, elaborate structural motifs of this type are rarely recovered, perhaps explaining why sites B67 and B154 were not recovered. Using a Monte Carlo optimization, five binding sites of PGA were recovered, and site B31, although not recovered, was similar to the wild type, that is, TyrB31Phe. These maximum recovered design results are shown in Figure 4(a) and compared with the optimal conformations of the wild type. The results show that the side-chain conformations of the residues at the recovered PheA146, PheB57, PheB24, and IleB177 sites were identical with those of the wild type. For scaffold CA, the designed sequence had four sites with charged residues under design type (*,*,*) when there was no restriction on the number of charged residues; however, just two sites, ArgB57 and ThrB69, were recovered. As for the scaffold PGA case, the active site repacking optimization without considering the specific environment of the binding pocket cannot recapitulate the native sequence. Because the side chain of GL-7-ACA is a negatively charged carboxylic acid, we restricted the appearance of negatively charged residues and the number of positively charged residues in the subsequent design types. The computational results shown in Table II suggest that the binding sequence selection was greatly improved under the restricted design types. The maximum recovered design result was obtained under design type (1,0,4), where six of the primary binding sites were recovered and the remaining three sites were similar to those of the wild type, namely, LeuB24Ile, TyrB33Phe, and AsnB68Gln. This result, shown in Figure 4(b), implies that the side-chain conformations of the recovered residues overlap completely with those of the wild-type residues. The guanidine group of ArgB57 formed a very good salt bridge with the carboxylic group of transition state side chain, and the OH group of TyrA150 formed a good hydrogen bond with the carboxylic group of the transition state side chain. The mutation TyrB33Phe in the design site resulted in the loss of the hydrogen bond with the transition state carboxylic group, but this was replaced by the mutation AsnB68Gln, because the mutated GlnB68 formed two hydrogen bonds, one between the atom NE2 of GlnB68 and the backbone atom O of PheB58, and the other between the atom OE1 of GlnB68 and the guanidine group of ArgB57. These mutations led to a lower free energy of the whole protein system compared with the free energy of the wild type shown in Table II, but the loss of the hydrogen bond with the transition state will impair the binding between the enzyme active site and the transition state, and further affect the catalytic activity.

Table II.

Binding Sequence Selection Results for PGA and CA Under Different Design Types

Scaffold	No. TS rotamer	Design type^a	Primary residues^b									Energy
PGA	25	WT	A142 M	A146 F	B24 F	B31 Y	B56 V	B57 F	B67 S	B154 W	B177 I	−238.29
		(,,*)	+	−	−	F	F	−	K	D	R	−278.98
		(0,0,*)	+	−	−	F	F	−	V	F	F	−273.01
		(0,0,1)	+	−	−	H	F	−	V	F	F	−272.93
		(0,0,2)	F	−	−	F	L	−	Q	Q	−	−267.76
		(0,0,*)^c	+	−	−	F	F	−	V	F	−	−270.59
CA	3455	WT	A149 Y	B24 L	B33 Y	B50 Q	B57 R	B58 F	B68 N	B69 T	B177 F	−307.22
		(,,*)^d	R	N	R	E	−	W	Q	−	E	−329.16
		(1,0,*)	F	I	F	−	−	−	Q	V	−	−325.85
		(1,0,3)	F	L	F	−	−	−	Q	−	−	−325.52
		(1,0,4)	−	I	F	−	−	−	Q	−	−	−323.77
		(1,0,5)	−	I	F	−	−	H	Q	−	−	−319.22

Open in a new tab

The design type is represented by the specified number of positively charged residues, negatively charged residues, and polar residues shown in the parenthesis. The asterisk implies that no restriction is forced on the designated residue type.

The primary residues are those that contact with TS directly and vary type and conformation simultaneously.

This sequence is found by Monte Carlo optimization based on the sequence obtained under design type (0,0,*).

The MILP solution has encountered convergence difficulties, and the sequence was arrived at 8% gap.

+: The type of designed residue is the same as that of WT, but the conformation is different.

−: The type and conformation of designed residue are the same as those of WT.

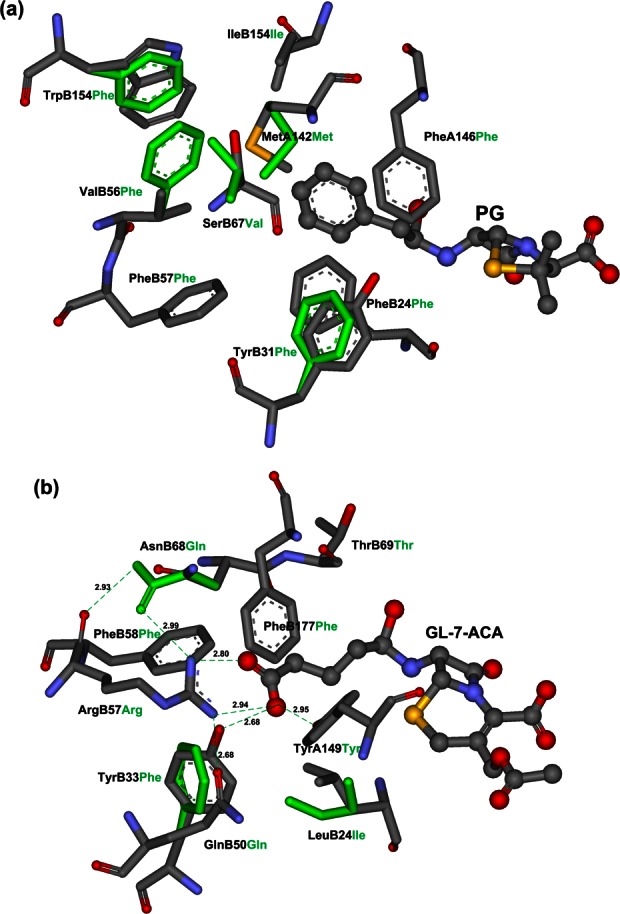
The maximum recovered design results for PGA and CA, and only TS and residues at primary design sites are shown. (a) PGA; (b) CA. The TS small molecules are shown in ball and stick model, and O/N/C/S atoms are shown in red/teal/gray/orange. The primary binding residues are shown in stick models, the wild-type residues are shown in colors of their atoms and labeled in black, and the designed residues are shown in cyan and labeled in cyan. The hydrogen bonds formed in active site of CA are shown by cyan dotted lines, and the distances between donors and acceptors are shown in Å. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

The effect of the degrees of freedom of the transition state on binding sequence recapitulation was investigated further using scaffold CA, because the side chain in its binding pocket is a linear and flexible carboxylic acid; the side chain in the binding pocket of PGA is a rigid phenyl ring. These differences can be corroborated by the small molecule placement results. For scaffold CA, a total of 1,644,463 conformations of GL-7-ACA were obtained based on the placement rules given in Supporting Information Table S4, and 1090, 1868, 3455, and 5762 conformations were collected after root-mean-square deviation (RMSD) screening with parameters 1.0 Å, 0.9 Å, 0.8 Å, and 0.7 Å, respectively. For scaffold PGA, only 1111 conformations of PG were obtained based on the placement rules given in Supporting Information Table S3, and 25, 30, 35, and 46 conformations were collected after RMSD screening with the same parameters as those used for CA. Therefore, we investigated the effect of transition state rotamer library size on binding sequence selection using scaffold CA, and the results of the calculation are shown in Table III. It should be noted that only the design type for maximal sequence recovery was given for each transition state rotamer library. Table III shows that the sequence recapitulation in the binding pocket of CA was greatly improved as the transition state rotamer library size increased, and the design results converged when the transition state rotamer library was big enough. Based on the transition state theory of enzymatic catalysis, these results imply that identification of the saddle point on the free energy surface of the reaction system is critical for high catalytic efficiency, because the lower the saddle point the lower the activation energy along the reaction coordinate.

Table III.

Effect of Rotamer Library Size of Transition State on Binding Sequence Selection

Scaffold	No. TS rotamer	Design type^a	Primary residues^b									Energy
CA		WT	A149 Y	B24 L	B33 Y	B50 Q	B57 R	B58 F	B68 N	B69 T	B177 F
	1090	(1,0,3)	F	W	F	R	F	−	Q	−	−	−323.85
	1868	(1,0,5)	−	N	R	−	F	W	Q	−	W	−314.85
	3455	(1,0,4)	−	I	F	−	−	−	Q	−	−	−323.77
	5762	(1,0,4)	−	W	F	−	−	−	Q	−	−	−319.34

Open in a new tab

Only the design type for maximal sequence recovery is given.

The primary residues are those that contact with TS directly and vary type and conformation simultaneously.

Discussion

Although the volume of sequence space for a protein structure in the core was found to be restricted to a region around the native sequence,²³ the amino acid sequence on the surface or in the boundary area still cannot be predicted accurately in silico if only the protein backbone structures are given.²⁴ The active site of an enzyme is always on the surface or in the boundary area of a protein, and in the present study we found that the binding sequence of an active site can be predicted accurately at most design sites if the catalytic geometrical constraints and the structural motifs of the natural substrates are taken into account simultaneously. The reliable prediction of the active site sequence is of great significance for computational enzyme design,²⁵ because it can help to eliminate the large number of false positives and identify the active mutants for target reactions.

In the systematic optimization model (P) for binding sequence selection, the third set of constraints force the search for repacking to locate the optimal point, which minimizes the binding energy between enzyme active site and transition state, while satisfying the catalytic geometrical relationships. This point is the saddle point on the free energy surface of the enzyme-catalyzed reaction system as shown in Figure 5. The saddle point is a minimum along the binding process, and a maximum along the reaction coordinate. The catalytic efficiency of the designed enzyme can be promoted if the activation energy of the Michaelis complex is lower and the saddle point is the limit. To find the saddle point, the degrees of freedom of the transition state should be explored sufficiently in the sequence selection process for binding sites, and this means that the size of the small molecule transition state rotamer library should be large enough. This hypothesis was confirmed by the recapitulation test of native binding sites for scaffold CA as shown in Table III. Although our experimental results to support this viewpoint are still not available, the same conclusion could be drawn based on the successful design cases reported by Baker's group,⁸^–¹⁰ because all the transition states of their target reactions are, to a large extent, rigid. Their recent paper²⁶ on the computational design of hydrolytic enzymes for three esters also indicates that the designed esterase mutants show less activity toward the tyrosyl ester than the coumarin ester and the p-nitrophenyl ester, though the acyl groups of the three esters are identical.

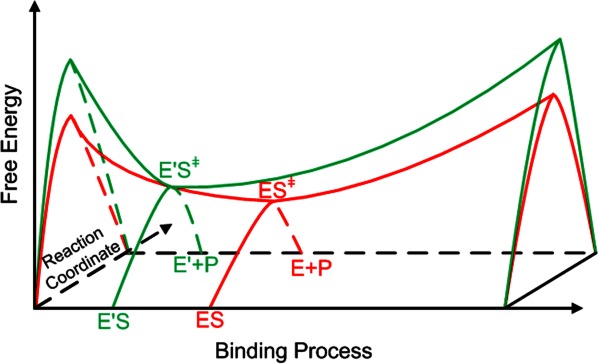
Saddle point on free energy surface for enzymatic reaction system, where ES represents Michaelis complex of native enzyme E and substrate S, and ES^≠ stands for the transition state of ES. E′ represents the designed enzyme and P represents the product of reaction. The valley curve refers to the binding process between enzyme active site and transition state of substrate, and the peak curve refers to the reaction coordinate. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Based on our earlier work on the core sequence selection problem, we developed the heuristic global optimization algorithm to successfully identify high quality near optimum solutions for binding sequence selection in enzyme design. We have shown that this mathematical programming based algorithm can easily handle the catalytic geometrical constraints, as well as the design type constraints. It should be noted that the latter constraints are difficult to be manipulated by DEE theory based algorithms or random algorithms. Similar mathematical optimization-based sequence selection problem was formulated by Floudas and coworkers²⁷^–³⁰ for protein design, and Maranas and coworkers³¹ for enzyme design. Boas and Harbury³² mentioned that a high-resolution rotamer library in which the number of rotamers is 5000 or more is necessary to design a protein–ligand binding site. This suggestion was confirmed by the results of our calculation presented in Supporting Information Table S6, based on a small rotamer library that included only 984 rotamers, and that could only recover very few design sites. Therefore, we used the larger rotamer library of Xiang and Honig,²⁰ which included 7421 rotamers for the binding sequence selection process. This approach, however, produced a hyper-scale optimization problem and presented a great challenge for the development of our algorithm. With the aid of parallel interior-point method for linear programming problem we developed the heuristic algorithm that we have shown can solve the sequence selection problem efficiently and effectively.

The design type constraints that we used greatly influenced the sequence recapitulation test of scaffold CA. We found that the free energy of the wild-type sequence was much higher than that of the design sequences for both the PGA and CA scaffolds shown in Table II. This finding was caused by excessive pairwise interactions, mainly hydrogen bonding between polar or charged residues, between residues in the design sites instead of the binding interaction between the design site and the transition state. We used design type constraints to tackle this problem by restricting the appearance of polar residues at design sites. Similar biological constraints were used by Floudas and coworkers for computational protein design, which have been experimentally validated on a wide variety of different systems and applications.³³^–³⁶ Because the hydrogen-bonding network is critical for the proper design of protein–ligand interactions,³⁷^–³⁹ more elaborate design constraints should be developed and introduced into the computational enzyme design methodology to allow for a more systematic manipulation of the binding sites.

Materials and Methods

The decomposition-based computational enzyme design methodology implemented in PRODA, the PROtein Design Algorithmic package, comprises three stages: (i) matching process for catalytic residue site selection; (ii) small molecule rotamer library generation based on a modified targeted ligand placement approach⁷ for transition state sampling; and (iii) sequence selection for binding residues based on active site repacking calculation. The matching algorithm for catalytic residue site selection was reported earlier.⁴⁰ The focus of the present work was on the latter two stages. The catalytic residues were assumed to take the wild-type positions in all the calculations.

Systematic optimization model for binding sequence selection

As an extension of the sequence selection model for protein core positions,¹⁹ the binding sequence selection problem in computational enzyme design can be formulated as a mixed-integer linear programming (MILP) problem using graph-theoretical modeling. The transition state (TS) is an additional design site and its rotamers are sourced from a small molecule rotamer library produced by the targeted placement approach. The catalytic geometrical relationships between the catalytic residues and transition state are represented by 0–1 linear constraints. If we assume that there are p optimized sites in a sequence selection problem, and this problem can be modeled by an undirected p-partite graph with node set V_i at each design site i for i = 1, 2, …, p. Each node set V_i has n_i rotamers, then a binary vertex variable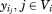 Inline graphic can be used to represent whether or not a rotamer {i_j} is selected at site i, and a binary edge variable 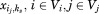can represent whether or not both rotamers {i_j} and {k_s} are selected at sites i and k simultaneously. According to the rigorous proof of Zhu,¹⁹ in computational protein design the binary edge variable 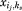Inline graphic can be relaxed to be continuous without affecting the solution and optimum of the sequence selection problem. Therefore, the MILP model for binding sequence selection in computational enzyme design can be represented as follows,

graphic file with name pro0022-0929-mu7.jpg

(4)

where, E(i_j) is the intrinsic energy resulting from the interaction between the template and the rotamer {i_j} at position i, and E(i_j,k_s) represents the pairwise interaction between rotamers {i_j} and {k_s}. The first set of constraints ensures that exactly one rotamer is chosen for each position, and the second set of constraints ensures that the edge variable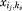 Inline graphic is set to 1 only when both rotamers {i_j} and {k_s} are chosen. The third set of constraints are specific to the enzyme design problem, and each set corresponds to a pair of positions (i, k) that are connected by some catalytic geometrical relationship. S_i(k) is the set of rotamers {i_j} at position i whose catalytic geometrical relationships can be satisfied by at least one rotamer at position k and S_k(i_j) is the set of rotamers {k_s} at position k which can form correct catalytic geometrical relationships with rotamer {i_j} at position i. These two sets of rotamers are produced by checking the catalytic geometrical relationships between each pair of rotamers at (i, k) before the optimization problem (P) is constructed. The third set of rotamer constraints ensures that each pair of catalytic geometrical relationship can be satisfied by the optimum solution. The rotamer library for the transition state was generated using the targeted small molecule placement approach.

Reactions, structures, and transition states

Two hydrolytic reactions shown in Figure 1 for the preparation of important pharmaceutical intermediates were used to exemplify the systematic optimization approach for computational enzyme design. The first reaction is catalyzed by penicillin G acylase (PGA), which converts penicillin G (PG, benzylpenicillin) to 6-amino-penicillanic acid (6-APA) and phenylacetic acid. The second reaction is catalyzed by cephalosporin acylase (CA), which converts glutaryl-7- aminocephalosporanic acid (GL-7-ACA) to 7-aminocephalosporanic acid (7-ACA) and glutaric acid. PGA and CA both belong to the N-terminal nucleophile aminohydrolase superfamily, and share the same catalytic mechanism⁴¹ in which the hydroxyl group of the N-terminal serine of the B-chain is the nucleophilic group. The crystal structures of these enzymes and their substrates were obtained from the Protein Data Bank (PDB) files without minimization. The PGA and PG structures are from 1GK9 and 1GM7,⁴² and the CA and GL-7-ACA structures are from 1JVZ.⁴³ The active site descriptions for the two reactions can be constructed from the catalytic mechanism proposed by Duggleby et al.⁴¹ For the reaction catalyzed by PGA, the four catalytic residues are SerB1, GlnB23, AlaB69, and AsnB241 and for the reaction catalyzed by CA, the four catalytic residues are SerB1, HisB23, ValB70, and AsnB244. The geometrical constraints between the catalytic residues and the transition states for PGA and CA are shown in Figure 2 and the specific ranges of the catalytic geometrical parameters are presented in Supporting Information Tables S1 and S2.

Small molecule rotamer library generation

To consider the rotational, translational, and conformational freedoms of the transition state in the sequence selection process, a slightly modified targeted small molecule placement approach⁵^,⁷ was developed to generate the rotamer library for the transition state in the active site where the catalytic and the binding residues were all truncated to alanine residues. The placement was initiated by selecting a particular catalytic residue as the anchor residue. The anchor residue was always the residue that initiates the nucleophilic or electrophilic attack in the catalytic reaction. Because the sites of the catalytic residues, including the anchor residue, were predetermined in the matching process, each rotamer of the anchor residue was chosen from a rotamer library²⁰ and placed on the backbone position. Any rotamer of the anchor residue that sterically clashed with the truncated backbone atoms was eliminated. For each placed anchor rotamer a set of ligand orientations and conformations was generated by sampling the catalytic geometrical parameters between the anchor residue and the transition state, that is, the bond length, bond angles, and dihedral angles, and the internal conformational parameters of the transition state, that is, the dihedral angles of the rotatable bonds at a defined step interval in the allowed ranges shown in Supporting Information Tables S3 and S4. The small molecule rotamer was stored in a list if the following three criteria were satisfied simultaneously: (i) no steric overlaps inside the small molecule; (ii) no steric clashes between the small molecule and the placed anchor rotamer and the backbone atoms of the protein; and (iii) rotamers exist at each of the other catalytic residue sites that satisfy the defined catalytic geometrical relationship with the placed transition state. The placement process was implemented in a depth-first tree enumerative way, and the branches that violated the above criteria were pruned at the early stage of the process. The first two criteria were measured by a scoring function, where only simplified van der Waals interactions between atoms were considered.³⁸^,⁴⁰ The third criterion was measured by checking if the catalytic geometrical variables lay in the allowed parameter ranges shown in Supporting Information Tables S1 and S2. The numbers of rotamers of the small molecules that were stored in the list can be very large; however, the final small molecule rotamer library was produced by selecting only the rotamers for which the RMSD between each pair of the rotamers in the list was greater than a predefined value.

Sequence selection for binding residues

The design sites in the sequence selection process include (i) catalytic residues sites for which only the conformations of the side chains are variable; (ii) two kinds of binding sites: one, primary sites that are in direct contact with the transition state and for which both the identities and the side-chain conformations vary, and, two, secondary sites that lie far from the transition state but are in direct contact with the primary sites and for which the side-chain conformations are varied during the sequence selection process for the primary sites; and (iii) the transition state, for which the conformations are taken from the small molecule rotamer library that is generated as described in the preceding section. The design schemes for PGA and CA are shown in Supporting Information Table S5. The protein backbone and the side chains of the nonoptimized positions referred to as the template were kept rigid during the sequence selection process,and the identity at each primary design site was selected from all the amino acids except glycine and proline. The side-chain conformations of these amino acids were from the backbone-independent rotamer library of Xiang and Honig,²⁰ which contains 7421 rotamers. We used the CHARMM 22 force field parameters for the atomic radii and internal coordinate parameters,⁴⁴ which consider the explicit positions of all the hydrogen atoms.

A free energy function based on a molecular mechanics energy model and an implicit solvent model was developed in the computational enzyme design methodology for a protein–ligand system, where the reference state refers to the template of the scaffold in solvent and an isolated small molecule in solvent. The free energy function is a linear combination of seven terms: (i) the van der Waals interaction, attractive term; (ii) the van der Waals interaction, repulsive term; (iii) the hydrogen-bonding term; (iv) the electrostatic interaction, desolvation term; (v) the electrostatic interaction, screened Coulomb term; (vi) the hydrophobic term; and (vii) the entropic term. The van der Waals interaction consists of two terms, an attractive term and a repulsive term.²³ E_attr is the attractive portion of a 12-6 Lennard-Jones potential with the van der Waals radii and well depths taken from the CHARMM 22 parameter set,⁴⁴ except that we scaled the van der Waals radii by 0.95 for heavy atoms and 0.5 for hydrogen atoms. E_rep is the repulsive term that reaches the maximum value of 10.0 kcal/mol when two atoms overlap and ramps linearly down to connect with the 12-6 potential at E = 0. This term is less repulsive than a 12-6 potential and compensates for the use of a fixed backbone and a discrete rotamer set. The explicit geometry and hybridization-dependent hydrogen bonding term of Dahiyat and Mayo,⁴⁵ namely, E_HB, was used because it allows some more restrictive angle-dependent and distance dependent terms to be applied to limit the occurrence of unfavorable hydrogen bond geometries. The long-range electrostatic interaction is described by a generalized Born model,⁴⁶ which was developed to become pairwise decomposable, and implemented in a computational protein design protocol⁴⁷ based on the generic side chain method proposed by Zhang et al.⁴⁸ The implicit solvent electrostatic interaction consists of two terms, the desolvation term E_desolv for polar and charged atoms upon burial after design, and the screened Coulomb term E_SC for the Coulomb interaction between atoms with partial charges in a continuum solvent context. The implicit solvation model is augmented with a term that accounts for the hydrophobic effects of the nonpolar atoms. The hydrophobic term, E_HP, uses the pairwise surface area decomposition approach⁴⁸ based on the generic side chain method to reward the buried nonpolar surface areas with a parameter of 26 cal/mol Å²; the solvent-accessible surface area of the overlapping atoms is calculated using the numerical surface calculation (NSC) algorithm.⁴⁹ The contribution of the side-chain entropy loss upon formation of the folded state, E_S, is estimated using a simple model of side-chain flexibility, and the values used in the calculations for the 20 naturally amino acids were those reported by Creamer.⁵⁰

The energy matrix calculation based on the above free energy function and the global optimization algorithm for amino acid sequence selection are implemented in PRODA, which was written in ANSI C language and implemented on a computer cluster with 208 cores. The linear programming problems and the mixed-integer linear programming problems for sequence selection were solved on a workstation with 64 cores sharing 256G RAM using the parallel interior-point LP and branch-and-bound based MILP algorithms.

Supplementary material

Additional Supporting Information may be found in the online version of this article.

pro0022-0929-SD1.doc^{(156.5KB, doc)}

References

1.Dahiyat BI, Mayo SL. De novo protein design: fully automated sequence selection. Science. 1997;278:82–87. doi: 10.1126/science.278.5335.82. [DOI] [PubMed] [Google Scholar]
2.Pinto AL, Hellinga HW, Caradonna JP. Construction of a catalytically active iron superoxide dismutase by rational protein design. Proc Natl Acad Sci USA. 1997;94:5562–5567. doi: 10.1073/pnas.94.11.5562. [DOI] [PMC free article] [PubMed] [Google Scholar]
3.Benson DE, Wisz MS, Hellinga HW. Rational design of nascent metalloenzymes. Proc Natl Acad Sci USA. 2000;97:6292–6297. doi: 10.1073/pnas.97.12.6292. [DOI] [PMC free article] [PubMed] [Google Scholar]
4.Benson DE, Haddy AE, Hellinga HW. Converting a maltose receptor into a nascent binuclear copper oxygenase by computational design. Biochemistry. 2002;41:3262–3269. doi: 10.1021/bi011359i. [DOI] [PubMed] [Google Scholar]
5.Hellinga HW, Richards FM. Construction of new ligand-binding sites in proteins of known structure. 1. Computer-aided modeling of sites with predefined geometry. J Mol Biol. 1991;222:763–785. doi: 10.1016/0022-2836(91)90510-d. [DOI] [PubMed] [Google Scholar]
6.Bolon DN, Mayo SL. Enzyme-like proteins by computational design. Proc Natl Acad Sci USA. 2001;98:14274–14279. doi: 10.1073/pnas.251555398. [DOI] [PMC free article] [PubMed] [Google Scholar]
7.Lassila JK, Privett HK, Allen BD, Mayo SL. Combinatorial methods for small-molecule placement in computational enzyme design. Proc Natl Acad Sci USA. 2006;103:16710–16715. doi: 10.1073/pnas.0607691103. [DOI] [PMC free article] [PubMed] [Google Scholar]
8.Jiang L, Althoff EA, Clemente FR, Doyle L, Röthlisberger D, Zanghellini A, Gallaher JL, Betker JL, Tanaka F, Barbas CF, Hilvert D, Houk KN, Stoddard BL, Baker D. De novo computational design of retro-aldol enzymes. Science. 2008;319:1387–1391. doi: 10.1126/science.1152692. [DOI] [PMC free article] [PubMed] [Google Scholar]
9.Röthlisberger D, Khersonsky O, Wollacott AM, Jiang L, DeChancie J, Betker J, Gallaher JL, Althoff EA, Zanghellini A, Dym O, Albeck S, Houk KN, Tawfik DS, Baker D. Kemp elimination catalysts by computational enzyme design. Nature. 2008;453:190–195. doi: 10.1038/nature06879. [DOI] [PubMed] [Google Scholar]
10.Siegel JB, Zanghellini A, Lovick HM, Kiss G, Lambert AR, St Clair JL, Gallaher JL, Hilvert D, Gelb MH, Stoddard BL, Houk KN, Michael FE, Baker D. Computational design of an enzyme catalyst for a stereoselective bimolecular diels-alder reaction. Science. 2010;329:309–313. doi: 10.1126/science.1190239. [DOI] [PMC free article] [PubMed] [Google Scholar]
11.Fersht A. Structure and mechanism in protein science: a guide to enzyme catalysis and protein folding. New York: WH Freeman; 1998. [Google Scholar]
12.Baker D. An exciting but challenging road ahead for computational enzyme design. Protein Sci. 2010;19:1817–1819. doi: 10.1002/pro.481. [DOI] [PMC free article] [PubMed] [Google Scholar]
13.Lassila JK, Baker D, Herschlag D. Origins of catalysis by computationally designed retroaldolase enzymes. Proc Natl Acad Sci USA. 2010;107:4937–4942. doi: 10.1073/pnas.0913638107. [DOI] [PMC free article] [PubMed] [Google Scholar]
14.Frushicheva MP, Cao J, Chu ZT, Warshel A. Exploring challenges in rational enzyme design by simulating the catalysis in artificial kemp eliminase. Proc Natl Acad Sci USA. 2010;107:16869–16874. doi: 10.1073/pnas.1010381107. [DOI] [PMC free article] [PubMed] [Google Scholar]
15.Khersonsky O, Röthlisberger D, Wollacott AM, Murphy P, Dym O, Albeck S, Kiss G, Houk KN, Baker D, Tawfik DS. Optimization of the in-silico-designed kemp eliminase ke70 by computational design and directed evolution. J Mol Biol. 2011;407:391–412. doi: 10.1016/j.jmb.2011.01.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
16.Privett HK, Kiss G, Lee TM, Blomberg R, Chica RA, Thomas LM, Hilvert D, Houk KN, Mayo SL. Iterative approach to computational enzyme design. Proc Natl Acad Sci USA. 2012;109:3790–3795. doi: 10.1073/pnas.1118082108. [DOI] [PMC free article] [PubMed] [Google Scholar]
17.Zanghellini A, Jiang L, Wollacott AM, Cheng G, Meiler J, Althoff EA, thlisberger D, Baker D. New algorithms and an in silico benchmark for computational enzyme design. Protein Sci. 2006;15:2785–2794. doi: 10.1110/ps.062353106. [DOI] [PMC free article] [PubMed] [Google Scholar]
18.Leach AR. Molecular modelling: principles and applications. London: Prentice Hall; 2001. [Google Scholar]
19.Zhu YS. Mixed-integer linear programming algorithm for a computational protein design problem. Ind Eng Chem Res. 2007;46:839–845. [Google Scholar]
20.Xiang Z, Honig B. Extending the accuracy limits of prediction for side-chain conformations. J Mol Biol. 2001;311:421–430. doi: 10.1006/jmbi.2001.4865. [DOI] [PubMed] [Google Scholar]
21.Desmet J, Demaeyer M, Hazes B, Lasters I. The dead-end elimination theorem and its use in protein side-chain positioning. Nature. 1992;356:539–542. doi: 10.1038/356539a0. [DOI] [PubMed] [Google Scholar]
22.Goldstein RF. Efficient rotamer elimination applied to protein side-chains and related spin glasses. Biophys J. 1994;66:1335–1340. doi: 10.1016/S0006-3495(94)80923-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
23.Kuhlman B, Baker D. Native protein sequences are close to optimal for their structures. Proc Natl Acad Sci USA. 2000;97:10383–10388. doi: 10.1073/pnas.97.19.10383. [DOI] [PMC free article] [PubMed] [Google Scholar]
24.Jaramillo A, Wernisch L, Hery S, Wodak SJ. Folding free energy function selects native-like protein sequences in the core but not on the surface. Proc Natl Acad Sci USA. 2002;99:13554–13559. doi: 10.1073/pnas.212068599. [DOI] [PMC free article] [PubMed] [Google Scholar]
25.Chakrabarti R, Klibanov AM, Friesner RA. Computational prediction of native protein ligand-binding and enzyme active site sequences. Proc Natl Acad Sci USA. 2005;102:10153–10158. doi: 10.1073/pnas.0504023102. [DOI] [PMC free article] [PubMed] [Google Scholar]
26.Richter F, Blomberg R, Khare SD, Kiss G, Kuzin AP, Smith AJT, Gallaher J, Pianowski Z, Helgeson RC, Grjasnow A, Xiao R, Seetharaman J, Su M, Vorobiev S, Lew S, Forouhar F, Kornhaber GJ, Hunt JF, Montelione GT, Tong L, Houk KN, Hilvert D, Baker D. Computational design of catalytic dyads and oxyanion holes for ester hydrolysis. J Am Chem Soc. 2012;134:16197–16206. doi: 10.1021/ja3037367. [DOI] [PMC free article] [PubMed] [Google Scholar]
27.Fung HK, Floudas CA, Taylor MS, Zhang L, Morikis D. Toward full-sequence de novo protein design with flexible templates for human beta-defensin-2. Biophys J. 2008;94:584–599. doi: 10.1529/biophysj.107.110627. [DOI] [PMC free article] [PubMed] [Google Scholar]
28.Fung HK, Welsh WJ, Floudas CA. Computational de novo peptide and protein design: rigid templates versus flexible templates. Ind Eng Chem Res. 2008;47:993–1001. [Google Scholar]
29.Klepeis JL, Floudas CA, Morikis D, Tsokos CG, Lambris JD. Design of peptide analogues with improves activity using a novel de novo protein design approach. Ind Eng Chem Res. 2004;43:3817–3826. [Google Scholar]
30.Fung HK, Rao S, Floudas CA, Prokopyev O, Pardalos PM, Rendl F. Computational comparison studies of quadratic assignment like formulations for the in silico sequence selection problem in de novo protein design. J Combin Optim. 2005;10:41–60. [Google Scholar]
31.Khoury GA, Fazelinia H, Chin JW, Pantazes RJ, Cirino PC, Maranas CD. Computational design of Candida boidinii xylose reductase for altered cofactor specificity. Protein Sci. 2009;18:2125–2138. doi: 10.1002/pro.227. [DOI] [PMC free article] [PubMed] [Google Scholar]
32.Boas FE, Harbury PB. Design of protein-ligand binding based on the molecular-mechanics energy model. J Mol Biol. 2008;380:415–424. doi: 10.1016/j.jmb.2008.04.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
33.Bellows ML, Fung HK, Taylor MS, Floudas CA, Lopez de, Victoria A, Morikis D. New compstatin variants through two de novo protein design frameworks. Biophys J. 2010;98:2337–2346. doi: 10.1016/j.bpj.2010.01.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
34.Bellows ML, Taylor MS, Cole PA, Shen L, Siliciano RF, Fung HK, Floudas CA. Discovery of entry inhibitors for HIV-1 via a new de novo protein design framework. Biophys J. 2010;99:3445–3453. doi: 10.1016/j.bpj.2010.09.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
35.Bellows-Peterson ML, Fung HK, Floudas CA, Kieslich CA, Zhang L, Morikis D, Wareham KJ, Monk PN, Hawksworth OA, Woodruff TM. De novo peptide design with c3a receptor agonist and antagonist activities: theoretical predictions and experimental validation. J Med Chem. 2012;55:4159–4168. doi: 10.1021/jm201609k. [DOI] [PMC free article] [PubMed] [Google Scholar]
36.Klepeis JL, Floudas CA, Morikis D, Tsokos CG, Argyropoulos E, Spruce L, Lambris JD. Integrated computational and experimental approach for lead optimization and design of compstatin variants with improved activity. J Am Chem Soc. 2003;125:8422–8423. doi: 10.1021/ja034846p. [DOI] [PubMed] [Google Scholar]
37.Looger LL, Dwyer MA, Smith JJ, Hellinga HW. Computational design of receptor and sensor proteins with novel functions. Nature. 2003;423:185–190. doi: 10.1038/nature01556. [DOI] [PubMed] [Google Scholar]
38.Luo WJ, Pei JF, Zhu YS. A fast protein-ligand docking algorithm based on hydrogen bond matching and surface shape complementarity. J Mol Model. 2010;16:903–913. doi: 10.1007/s00894-009-0598-7. [DOI] [PubMed] [Google Scholar]
39.Huang XQ, Yang J, Zhu YS. A solvated ligand rotamer approach and its application in computational protein design. J Mol Model. 2013;19:1355–1367. doi: 10.1007/s00894-012-1695-6. [DOI] [PubMed] [Google Scholar]
40.Lei YL, Luo WJ, Zhu YS. A matching algorithm for catalytic residue site selection in computational enzyme design. Protein Sci. 2011;20:1566–1575. doi: 10.1002/pro.685. [DOI] [PMC free article] [PubMed] [Google Scholar]
41.Duggleby HJ, Tolley SP, Hill CP, Dodson EJ, Dodson G, Moody PCE. Penicillin acylase has a single-amino-acid catalytic center. Nature. 1995;373:264–268. doi: 10.1038/373264a0. [DOI] [PubMed] [Google Scholar]
42.McVey CE, Walsh MA, Dodson GG, Wilson KS, Brannigan JA. Crystal structures of penicillin acylase enzyme-substrate complexes: structural insights into the catalytic mechanism. J Mol Biol. 2001;313:139–150. doi: 10.1006/jmbi.2001.5043. [DOI] [PubMed] [Google Scholar]
43.Kim Y, Hol WGJ. Structure of cephalosporin acylase in complex with glutaryl-7-aminocephalosporanic acid and glutarate: insight into the basis of its substrate specificity. Chem Biol. 2001;8:1253–1264. doi: 10.1016/s1074-5521(01)00092-8. [DOI] [PubMed] [Google Scholar]
44.MacKerell AD, Bashford D, Bellott M, Dunbrack RL, Evanseck JD, Field MJ, Fischer S, Gao J, Guo H, Ha S, Joseph-McCarthy D, Kuchnir L, Kuczera K, Lau FTK, Mattos C, Michnick S, Ngo T, Nguyen DT, Prodhom B, Reiher WE, Roux B, Schlenkrich M, Smith JC, Stote R, Straub J, Watanabe M, Wiorkiewicz-Kuczera J, Yin D, Karplus M. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J Phys Chem B. 1998;102:3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
45.Dahiyat BI, Benjamin Gordon D, Mayo SL. Automated design of the surface positions of protein helices. Protein Sci. 1997;6:1333–1337. doi: 10.1002/pro.5560060622. [DOI] [PMC free article] [PubMed] [Google Scholar]
46.Dominy BN, Brooks CL. Development of a generalized born model parametrization for proteins and nucleic acids. J Phys Chem B. 1999;103:3765–3773. [Google Scholar]
47.Vizcarra CL, Zhang NG, Marshall SA, Wingreen NS, Zeng C, Mayo SL. An improved pairwise decomposable finite-difference poisson-boltzmann method for computational protein design. J Comput Chem. 2008;29:1153–1162. doi: 10.1002/jcc.20878. [DOI] [PubMed] [Google Scholar]
48.Zhang N, Zeng C, Wingreen NS. Fast accurate evaluation of protein solvent exposure. Proteins Struct Funct Bioinf. 2004;57:565–576. doi: 10.1002/prot.20191. [DOI] [PubMed] [Google Scholar]
49.Eisenhaber F, Lijnzaad P, Argos P, Sander C, Scharf M. The double cubic lattice method: efficient approaches to numerical integration of surface area and volume and to dot surface contouring of molecular assemblies. J Comput Chem. 1995;16:273–284. [Google Scholar]
50.Creamer TP. Side-chain conformational entropy in protein unfolded states. Proteins Struct Funct Bioinf. 2000;40:443–450. doi: 10.1002/1097-0134(20000815)40:3<443::aid-prot100>3.0.co;2-l. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

pro0022-0929-SD1.doc^{(156.5KB, doc)}

[b1] 1.Dahiyat BI, Mayo SL. De novo protein design: fully automated sequence selection. Science. 1997;278:82–87. doi: 10.1126/science.278.5335.82. [DOI] [PubMed] [Google Scholar]

[b2] 2.Pinto AL, Hellinga HW, Caradonna JP. Construction of a catalytically active iron superoxide dismutase by rational protein design. Proc Natl Acad Sci USA. 1997;94:5562–5567. doi: 10.1073/pnas.94.11.5562. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b3] 3.Benson DE, Wisz MS, Hellinga HW. Rational design of nascent metalloenzymes. Proc Natl Acad Sci USA. 2000;97:6292–6297. doi: 10.1073/pnas.97.12.6292. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b4] 4.Benson DE, Haddy AE, Hellinga HW. Converting a maltose receptor into a nascent binuclear copper oxygenase by computational design. Biochemistry. 2002;41:3262–3269. doi: 10.1021/bi011359i. [DOI] [PubMed] [Google Scholar]

[b5] 5.Hellinga HW, Richards FM. Construction of new ligand-binding sites in proteins of known structure. 1. Computer-aided modeling of sites with predefined geometry. J Mol Biol. 1991;222:763–785. doi: 10.1016/0022-2836(91)90510-d. [DOI] [PubMed] [Google Scholar]

[b6] 6.Bolon DN, Mayo SL. Enzyme-like proteins by computational design. Proc Natl Acad Sci USA. 2001;98:14274–14279. doi: 10.1073/pnas.251555398. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b7] 7.Lassila JK, Privett HK, Allen BD, Mayo SL. Combinatorial methods for small-molecule placement in computational enzyme design. Proc Natl Acad Sci USA. 2006;103:16710–16715. doi: 10.1073/pnas.0607691103. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b8] 8.Jiang L, Althoff EA, Clemente FR, Doyle L, Röthlisberger D, Zanghellini A, Gallaher JL, Betker JL, Tanaka F, Barbas CF, Hilvert D, Houk KN, Stoddard BL, Baker D. De novo computational design of retro-aldol enzymes. Science. 2008;319:1387–1391. doi: 10.1126/science.1152692. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b9] 9.Röthlisberger D, Khersonsky O, Wollacott AM, Jiang L, DeChancie J, Betker J, Gallaher JL, Althoff EA, Zanghellini A, Dym O, Albeck S, Houk KN, Tawfik DS, Baker D. Kemp elimination catalysts by computational enzyme design. Nature. 2008;453:190–195. doi: 10.1038/nature06879. [DOI] [PubMed] [Google Scholar]

[b10] 10.Siegel JB, Zanghellini A, Lovick HM, Kiss G, Lambert AR, St Clair JL, Gallaher JL, Hilvert D, Gelb MH, Stoddard BL, Houk KN, Michael FE, Baker D. Computational design of an enzyme catalyst for a stereoselective bimolecular diels-alder reaction. Science. 2010;329:309–313. doi: 10.1126/science.1190239. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b11] 11.Fersht A. Structure and mechanism in protein science: a guide to enzyme catalysis and protein folding. New York: WH Freeman; 1998. [Google Scholar]

[b12] 12.Baker D. An exciting but challenging road ahead for computational enzyme design. Protein Sci. 2010;19:1817–1819. doi: 10.1002/pro.481. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b13] 13.Lassila JK, Baker D, Herschlag D. Origins of catalysis by computationally designed retroaldolase enzymes. Proc Natl Acad Sci USA. 2010;107:4937–4942. doi: 10.1073/pnas.0913638107. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b14] 14.Frushicheva MP, Cao J, Chu ZT, Warshel A. Exploring challenges in rational enzyme design by simulating the catalysis in artificial kemp eliminase. Proc Natl Acad Sci USA. 2010;107:16869–16874. doi: 10.1073/pnas.1010381107. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b15] 15.Khersonsky O, Röthlisberger D, Wollacott AM, Murphy P, Dym O, Albeck S, Kiss G, Houk KN, Baker D, Tawfik DS. Optimization of the in-silico-designed kemp eliminase ke70 by computational design and directed evolution. J Mol Biol. 2011;407:391–412. doi: 10.1016/j.jmb.2011.01.041. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b16] 16.Privett HK, Kiss G, Lee TM, Blomberg R, Chica RA, Thomas LM, Hilvert D, Houk KN, Mayo SL. Iterative approach to computational enzyme design. Proc Natl Acad Sci USA. 2012;109:3790–3795. doi: 10.1073/pnas.1118082108. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b17] 17.Zanghellini A, Jiang L, Wollacott AM, Cheng G, Meiler J, Althoff EA, thlisberger D, Baker D. New algorithms and an in silico benchmark for computational enzyme design. Protein Sci. 2006;15:2785–2794. doi: 10.1110/ps.062353106. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b18] 18.Leach AR. Molecular modelling: principles and applications. London: Prentice Hall; 2001. [Google Scholar]

[b19] 19.Zhu YS. Mixed-integer linear programming algorithm for a computational protein design problem. Ind Eng Chem Res. 2007;46:839–845. [Google Scholar]

[b20] 20.Xiang Z, Honig B. Extending the accuracy limits of prediction for side-chain conformations. J Mol Biol. 2001;311:421–430. doi: 10.1006/jmbi.2001.4865. [DOI] [PubMed] [Google Scholar]

[b21] 21.Desmet J, Demaeyer M, Hazes B, Lasters I. The dead-end elimination theorem and its use in protein side-chain positioning. Nature. 1992;356:539–542. doi: 10.1038/356539a0. [DOI] [PubMed] [Google Scholar]

[b22] 22.Goldstein RF. Efficient rotamer elimination applied to protein side-chains and related spin glasses. Biophys J. 1994;66:1335–1340. doi: 10.1016/S0006-3495(94)80923-3. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b23] 23.Kuhlman B, Baker D. Native protein sequences are close to optimal for their structures. Proc Natl Acad Sci USA. 2000;97:10383–10388. doi: 10.1073/pnas.97.19.10383. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b24] 24.Jaramillo A, Wernisch L, Hery S, Wodak SJ. Folding free energy function selects native-like protein sequences in the core but not on the surface. Proc Natl Acad Sci USA. 2002;99:13554–13559. doi: 10.1073/pnas.212068599. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b25] 25.Chakrabarti R, Klibanov AM, Friesner RA. Computational prediction of native protein ligand-binding and enzyme active site sequences. Proc Natl Acad Sci USA. 2005;102:10153–10158. doi: 10.1073/pnas.0504023102. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b26] 26.Richter F, Blomberg R, Khare SD, Kiss G, Kuzin AP, Smith AJT, Gallaher J, Pianowski Z, Helgeson RC, Grjasnow A, Xiao R, Seetharaman J, Su M, Vorobiev S, Lew S, Forouhar F, Kornhaber GJ, Hunt JF, Montelione GT, Tong L, Houk KN, Hilvert D, Baker D. Computational design of catalytic dyads and oxyanion holes for ester hydrolysis. J Am Chem Soc. 2012;134:16197–16206. doi: 10.1021/ja3037367. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b27] 27.Fung HK, Floudas CA, Taylor MS, Zhang L, Morikis D. Toward full-sequence de novo protein design with flexible templates for human beta-defensin-2. Biophys J. 2008;94:584–599. doi: 10.1529/biophysj.107.110627. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b28] 28.Fung HK, Welsh WJ, Floudas CA. Computational de novo peptide and protein design: rigid templates versus flexible templates. Ind Eng Chem Res. 2008;47:993–1001. [Google Scholar]

[b29] 29.Klepeis JL, Floudas CA, Morikis D, Tsokos CG, Lambris JD. Design of peptide analogues with improves activity using a novel de novo protein design approach. Ind Eng Chem Res. 2004;43:3817–3826. [Google Scholar]

[b30] 30.Fung HK, Rao S, Floudas CA, Prokopyev O, Pardalos PM, Rendl F. Computational comparison studies of quadratic assignment like formulations for the in silico sequence selection problem in de novo protein design. J Combin Optim. 2005;10:41–60. [Google Scholar]

[b31] 31.Khoury GA, Fazelinia H, Chin JW, Pantazes RJ, Cirino PC, Maranas CD. Computational design of Candida boidinii xylose reductase for altered cofactor specificity. Protein Sci. 2009;18:2125–2138. doi: 10.1002/pro.227. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b32] 32.Boas FE, Harbury PB. Design of protein-ligand binding based on the molecular-mechanics energy model. J Mol Biol. 2008;380:415–424. doi: 10.1016/j.jmb.2008.04.001. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b33] 33.Bellows ML, Fung HK, Taylor MS, Floudas CA, Lopez de, Victoria A, Morikis D. New compstatin variants through two de novo protein design frameworks. Biophys J. 2010;98:2337–2346. doi: 10.1016/j.bpj.2010.01.057. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b34] 34.Bellows ML, Taylor MS, Cole PA, Shen L, Siliciano RF, Fung HK, Floudas CA. Discovery of entry inhibitors for HIV-1 via a new de novo protein design framework. Biophys J. 2010;99:3445–3453. doi: 10.1016/j.bpj.2010.09.050. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b35] 35.Bellows-Peterson ML, Fung HK, Floudas CA, Kieslich CA, Zhang L, Morikis D, Wareham KJ, Monk PN, Hawksworth OA, Woodruff TM. De novo peptide design with c3a receptor agonist and antagonist activities: theoretical predictions and experimental validation. J Med Chem. 2012;55:4159–4168. doi: 10.1021/jm201609k. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b36] 36.Klepeis JL, Floudas CA, Morikis D, Tsokos CG, Argyropoulos E, Spruce L, Lambris JD. Integrated computational and experimental approach for lead optimization and design of compstatin variants with improved activity. J Am Chem Soc. 2003;125:8422–8423. doi: 10.1021/ja034846p. [DOI] [PubMed] [Google Scholar]

[b37] 37.Looger LL, Dwyer MA, Smith JJ, Hellinga HW. Computational design of receptor and sensor proteins with novel functions. Nature. 2003;423:185–190. doi: 10.1038/nature01556. [DOI] [PubMed] [Google Scholar]

[b38] 38.Luo WJ, Pei JF, Zhu YS. A fast protein-ligand docking algorithm based on hydrogen bond matching and surface shape complementarity. J Mol Model. 2010;16:903–913. doi: 10.1007/s00894-009-0598-7. [DOI] [PubMed] [Google Scholar]

[b39] 39.Huang XQ, Yang J, Zhu YS. A solvated ligand rotamer approach and its application in computational protein design. J Mol Model. 2013;19:1355–1367. doi: 10.1007/s00894-012-1695-6. [DOI] [PubMed] [Google Scholar]

[b40] 40.Lei YL, Luo WJ, Zhu YS. A matching algorithm for catalytic residue site selection in computational enzyme design. Protein Sci. 2011;20:1566–1575. doi: 10.1002/pro.685. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b41] 41.Duggleby HJ, Tolley SP, Hill CP, Dodson EJ, Dodson G, Moody PCE. Penicillin acylase has a single-amino-acid catalytic center. Nature. 1995;373:264–268. doi: 10.1038/373264a0. [DOI] [PubMed] [Google Scholar]

[b42] 42.McVey CE, Walsh MA, Dodson GG, Wilson KS, Brannigan JA. Crystal structures of penicillin acylase enzyme-substrate complexes: structural insights into the catalytic mechanism. J Mol Biol. 2001;313:139–150. doi: 10.1006/jmbi.2001.5043. [DOI] [PubMed] [Google Scholar]

[b43] 43.Kim Y, Hol WGJ. Structure of cephalosporin acylase in complex with glutaryl-7-aminocephalosporanic acid and glutarate: insight into the basis of its substrate specificity. Chem Biol. 2001;8:1253–1264. doi: 10.1016/s1074-5521(01)00092-8. [DOI] [PubMed] [Google Scholar]

[b44] 44.MacKerell AD, Bashford D, Bellott M, Dunbrack RL, Evanseck JD, Field MJ, Fischer S, Gao J, Guo H, Ha S, Joseph-McCarthy D, Kuchnir L, Kuczera K, Lau FTK, Mattos C, Michnick S, Ngo T, Nguyen DT, Prodhom B, Reiher WE, Roux B, Schlenkrich M, Smith JC, Stote R, Straub J, Watanabe M, Wiorkiewicz-Kuczera J, Yin D, Karplus M. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J Phys Chem B. 1998;102:3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]

[b45] 45.Dahiyat BI, Benjamin Gordon D, Mayo SL. Automated design of the surface positions of protein helices. Protein Sci. 1997;6:1333–1337. doi: 10.1002/pro.5560060622. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b46] 46.Dominy BN, Brooks CL. Development of a generalized born model parametrization for proteins and nucleic acids. J Phys Chem B. 1999;103:3765–3773. [Google Scholar]

[b47] 47.Vizcarra CL, Zhang NG, Marshall SA, Wingreen NS, Zeng C, Mayo SL. An improved pairwise decomposable finite-difference poisson-boltzmann method for computational protein design. J Comput Chem. 2008;29:1153–1162. doi: 10.1002/jcc.20878. [DOI] [PubMed] [Google Scholar]

[b48] 48.Zhang N, Zeng C, Wingreen NS. Fast accurate evaluation of protein solvent exposure. Proteins Struct Funct Bioinf. 2004;57:565–576. doi: 10.1002/prot.20191. [DOI] [PubMed] [Google Scholar]

[b49] 49.Eisenhaber F, Lijnzaad P, Argos P, Sander C, Scharf M. The double cubic lattice method: efficient approaches to numerical integration of surface area and volume and to dot surface contouring of molecular assemblies. J Comput Chem. 1995;16:273–284. [Google Scholar]

[b50] 50.Creamer TP. Side-chain conformational entropy in protein unfolded states. Proteins Struct Funct Bioinf. 2000;40:443–450. doi: 10.1002/1097-0134(20000815)40:3<443::aid-prot100>3.0.co;2-l. [DOI] [PubMed] [Google Scholar]

PERMALINK

Systematic optimization model and algorithm for binding sequence selection in computational enzyme design

Xiaoqiang Huang

Kehang Han

Yushan Zhu

Abstract

Introduction

Figure 1.

Figure 2.

Results