Translating HIV sequences into quantitative fitness landscapes predicts viral vulnerabilities for rational immunogen design

Summary

A prophylactic or therapeutic vaccine offers the best hope to curb the HIV-AIDS epidemic gripping sub-Saharan Africa, but remains elusive. A major challenge is the extreme viral sequence variability among strains. Systematic means to guide immunogen design for highly variable pathogens like HIV are not available. Using computational models, we have developed an approach to translate available viral sequence data into quantitative landscapes of viral fitness as a function of the amino acid sequences of its constituent proteins. Predictions emerging from our computationally defined landscapes for the proteins of HIV-1 clade B Gag were positively tested against new in vitro fitness measurements, and were consistent with previously defined in vitro measurements and clinical observations. These landscapes chart the peaks and valleys of viral fitness as protein sequences change, and inform the design of immunogens and therapies that can target regions of the virus most vulnerable to selection pressure.

Introduction

A cheap, easily-administered prophylactic or therapeutic vaccine represents the best hope for arresting the global HIV-AIDS epidemic (Baker et al., 2009), but remains elusive after three decades of effort. The recent discovery of antibodies that can neutralize diverse HIV strains (Walker et al., 2011) and evidence that a cytotoxic Tlymphocyte (CTL)-based vaccine has the potential to abort infection (Hansen et al., 2011; Hansen et al., 2009) offer hope, but important challenges remain. Prominent among these is the ability of the virus to mutate to new variants that do not carry a significant penalty in replicative fitness (Autran et al., 2008; Goulder & Watkins, 2004). The replicative fitness of the virus is correlated with disease pathogenesis: infection with low fitness viruses or the emergence of immune pressure-mediated low fitness viruses is associated with improved control of the viral load (Miura et al., 2010). It has been suggested, therefore, that vaccine-induced immune responses should be focused on vulnerable regions of the virus, within which mutations impose a high fitness cost (Goulder & Watkins, 2004; Streeck et al., 2007; Walker et al., 2011).

Highly conserved residues have long been suggested as a target for effective CTL responses (Letourneau et al., 2007; Rolland et al., 2007; Streeck et al., 2007), but studies have shown that viral fitness is also strongly influenced by couplings between multiple simultaneous mutations (Allen et al., 2005; Brockman et al., 2010; Brockman et al., 2007; Brumme et al., 2009; Dahirel et al., 2011; Draenert et al., 2004; Ferrari et al., 2011; Leslie et al., 2004; Letourneau et al., 2007; Martinez-Picado et al., 2006; Miura et al., 2009; Miura et al., 2009; Schneidewind et al., 2008; Schneidewind et al., 2007; Troyer et al., 2009; Walker et al., 2011). These couplings may arise, for example, due to the structural proximity of groups of residues within the three dimensional protein structure, or participation of the group in a particular viral function involving multiple proteins. The coupling between multiple mutations may be compensatory – where in the fitness of the viral strain containing multiple mutations is higher than would be expected from the mutations occurring independently – or deleterious – where in the multiple mutant is less fit than would be predicted from the single point mutations. Rare individuals capable of controlling HIV infection without therapy (elite controllers) naturally target multiple residues in groups of residues within which multiple simultaneous mutations are particularly detrimental to viral fitness (Dahirel et al., 2011). Together, these studies suggest that groups of residues containing deleterious mutational couplings are promising new targets for vaccine-induced immune attack (Dahirel et al., 2011).

A comprehensive knowledge of the fitness of viral strains containing multiple mutations would reveal many more regions of the viral proteome containing groups of residues vulnerable to immune targeting. This would open the possibility of designing immunogens containing these vulnerable regions which could be presented by people with diverse HLAs to induce effective CTL responses (similar to elite controllers). The ability to determine the fitness of any viral strain could also inform the design of therapies based on antibodies and small molecule inhibitors.

Systematic identification of regions where multiple mutations are deleterious requires an approach that assigns a quantitative measure of the replicative fitness to any viral strain containing multiple mutations. First postulated by Sewall Wright in 1932 (Wright, 1932), the fitness landscape describes the replicative capacity of the virus as a function of its amino acid sequence. Effective antibody responses would target epitopes in the Env protein defined by narrow peaks, as they are likely to be conserved across strains. CTL responses should target combinations of epitopes or protein residues where mutations drive the virus from the high-fitness peaks into the valleys where its compromised fitness impairs its ability to replicate and inflict damage to the host. Furthermore, a potent vaccine would also elicit additional responses to block viral escape to nearby high-fitness strains identified by the fitness landscape. Thus, viral fitness landscapes offer an unprecedented means to identify vulnerable regions of the virus, and guide the design of efficacious vaccine immunogens and therapies for diverse viruses. Here, we present a method to determine the fitness landscape of viruses, and apply it to HIV.

The Shannon entropy (a measure of sequence variability) of single residues and targeted epitopes is correlated with the emergence of escape mutations, and has been proposed as a measure of the fitness cost of escape (Allen et al., 2005; Ferrari et al., 2011). This measure, however, is restricted to localized groups of residues, and therefore largely ignores mutational couplings that are known to be important determinants of viral replicative fitness. Dahirel et al. recently presented a means to qualitatively identify groups of sites possessing strong mutational couplings (Dahirel et al., 2011), but this approach does not furnish quantitative measures of viral fitness required to construct the fitness landscape. Regression models have been fitted to in vitro HIV fitness measurements as a function of amino acid sequence (Hinkley et al., 2011; Kouyos et al., 2012). However, such approaches require extensive and laborious in vitro fitness measurements.

In contrast to these approaches, we have devised a method to obtain fitness landscapes by direct analysis of available protein sequence databases, without appealing to experimental fitness measurements. We apply our methodology to proteins within the key HIV-1 structural polyprotein, Gag, and validate the inferred fitness landscape by direct comparison to new and existing experimental data, and clinical observations. To illustrate one utility of the inferred fitness landscapes, we use the landscapes to design a Gag immunogen that is predicted to prime efficacious CTL responses in persons with diverse HLA haplotypes.

Results

Model Development

Only a limited number of full genome HIV sequences are currently available. Analyses of these few sequences do not provide sufficient statistical power for the development of a unified fitness landscape for the entire HIV proteome, necessitating that we pursue models for individual proteins. However, our approach is directly extensible to the translation of full genome sequence data to fitness landscapes as more sequences become available. Conceptually, it is useful to visualize this information as a topographical map (Figure 1), where the amino acid sequence of the virus determines the location of the viral strain on the map, and the height of the landscape prescribes its replicative fitness.

Figure 1.

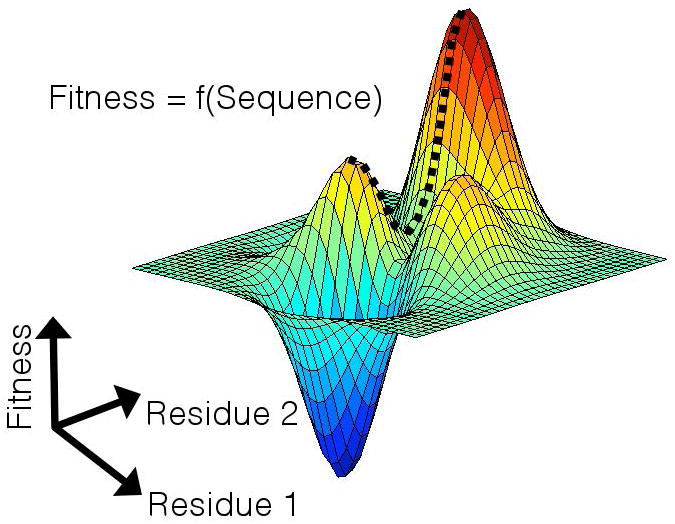
Cartoon schematic of a viral fitness landscape. The replicative fitness of a viral strain is a function of its amino acid sequence. This information can be visualized as a topographical map where the amino acid sequence specifies a location on the landscape, and the height of the landscape prescribes viral fitness. For visualization purposes, this cartoon pertains to a virus consisting of only two residues. For multi-residue viral proteins, the fitness landscape is traced out in higher dimensions. The broken line indicates a hypothetical high-fitness mutational escape pathway from the global fitness maximum, to a nearby local maximum.

The HIV-1 structural polyprotein Gag is a promising target for CTL responses, containing multiple peptides that are presented by HLA class I molecules, and regions that are mutationally restricted by structural and functional restraints (Dahirel et al., 2011; Goulder & Watkins, 2004; Schneidewind et al., 2008; Schneidewind et al., 2007; Troyer et al., 2009). A number of Gag residues exhibit deleterious mutational couplings (Dahirel et al., 2011). Thus, to develop and illustrate the accuracy of our approach, we have inferred fitness landscapes for the four principal Gag proteins: p6, p7 (nucleocapsid), p17 (matrix) and p24 (capsid).

Multiple sequence alignments (MSA) for the four Gag proteins in HIV-1 clade B were downloaded and processed from the Los Alamos National Laboratory HIV database (http://www.hiv.lanl.gov) as described in the Supplemental Computational Procedures. These data are compilations of consensus sequences drawn from infected patients. Our goal is to infer the viral fitness landscape from these data.

We described each sequence in the MSA using a binary code. If the amino acid at a particular residue in a protein sequence is the wild-type amino acid, it is denoted by 0; if the residue is any one of the 19 “mutant” amino acids, it is denoted by 1. Neglecting the particular identity of the mutant amino acid greatly reduces the computational cost of extracting fitness landscapes, and is a good approximation for the relatively well-conserved Gag polyprotein (cf. Supplemental Computational Procedures). The disadvantage is loss of residue-specific resolution, so that the fitness landscapes cannot differentiate between mutant viral strains containing different amino acids in the mutated positions.

The sequence data contain information on the probability of occurrence of each single, double, triple, and higher order mutation. A mathematical model reproducing these probability distributions describes the evolutionary space accessible to HIV. Since each protein comprises tens to hundreds of residues, the number of possible double, triple, quadruple, etc., mutations is extraordinarily large, making it intractable to fit a model describing the probability distributions of mutations of all orders. Instead, we follow the maximum entropy principle (Jaynes, 1957) to seek the least biased model capable of reproducing the observed probabilities of occurrence of every single and double mutation (Mora & Bialek, 2011; Tkacik et al., 2006; Tkacik et al., 2009), and use it to predict higher order mutations. As described in Computational and Experimental Procedures, this leads us to infer a model where the probability of occurrence of a particular sequence is described by a well-studied model in physics, known as the infinite-range Ising spin glass (Binder & Young, 1986).

We found that mathematical models inferred in this way not only reproduce the pattern of single and double mutations, but also predict with high accuracy the observed probabilities of occurrence of triple and quadruple mutants, and the probability of observing a sequence containing any particular number of mutations (cf. Supplemental Computational Procedures). In fact, depending upon the Gag protein, our mathematical models capture 70–99% of the information content on correlated mutational interactions contained in the available sequences derived from patients. Thus, our models have achieved the goal of capturing the mutational patterns exhibited by the virus within the MSA.

Having fitted models for each protein, a quantity, E, can be assigned to viral strains containing any combination of mutations (cf. Computational and Experimental Procedures). In analogy with the physics literature, we refer to E as the “energy”. The value of E corresponding to a particular mutant strain is related to the probability of observing this strain within the population of all possible mutants, whereby low-energy strains are highly prevalent, and high-energy strains comparatively rare. We assume that highly prevalent – and therefore low energy – sequences in the population correspond to strains with high intrinsic replicative fitness. Our model suggests that log(f), where f is the fitness of any mutant strain, should be negatively correlated with its energy (cf. Equation 1). Under relatively restrictive assumptions, Sella and Hirsh have precisely derived the connection between E and fitness (Sella & Hirsh, 2005). However, the complex interactions between HIV and the immune systems of diverse individuals makes it difficult to mathematically demonstrate that our model obtains intrinsic viral fitness landscapes. Accordingly, in the following sections we present strong evidence that E is indeed a good proxy for fitness by testing our model predictions against new and existing in vitro experimental data, and clinical observations from HIV infected persons.

The inferred fitness landscape compares well with in vitro replicative fitness data

If our model for the fitness landscape inferred from sequence data is a measure of intrinsic replicative viral fitness, we should observe a negative correlation between measured in vitro fitness of mutant viral strains and our proposed metric of fitness, the energy, E, corresponding to that strain. This is because our model predicts that low E corresponds to high fitness (see above). To test this hypothesis, we predicted the energy of 19 viral strains with single and double mutations in the p24 protein. These mutations were introduced to the HIV-1 clade B NL4-3 backbone, and the in vitro replicative capacity of each strain was measured (cf. Computational and Experimental Procedures). Each residue was mutated to the most common mutant amino acid at that position observed in the sequence data.

Following the prescription of our model (cf. Equation 1), we plot the energy of strain i relative to the wild-type, (E_i − E_wt), against the logarithm of its measured relative fitness, log (f_i/f_wt). We observe a statistically significant negative correlation (Figure 2A, Pearson correlation coefficient, ρ = −0.52 (p = 0.02, two-tailed Fisher test)). The direct relationship between E_i and f_i also exhibits a strong negative correlation (Figure S1A, ρ = −0.68 (p = 9 × 10⁻⁴)). Since our fitness assays were performed in vitro in the absence of immune pressure, these results suggest that our inferred landscapes describe the intrinsic replicative fitness effects of mutations in Gag.

Figure 2.

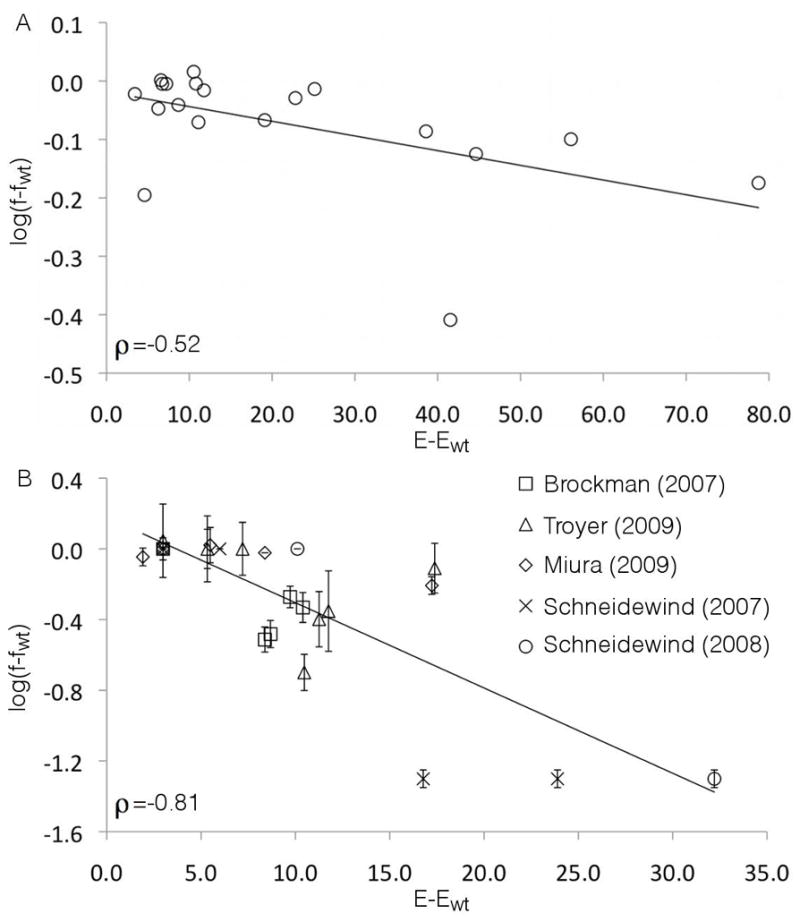
Comparison of our theoretical metric of fitness (E) and experimental in vitro replicative fitness data. (A) In vitro replicative fitness was measured for 19 Gag single and double mutants (cf. Computational and Experimental Procedures). A Pearson correlation coefficient of ρ = −0.52 (p = 0.02) reveals a statistically significant negative correlation between the energy difference of the engineered mutants relative to the wild-type strain computed from our model, (E − E_wt), and the logarithm of the measured relative fitness of the mutant, log (f/f_wt). (B) Replicative fitness data was compiled for 25 engineered Gag mutants containing up to five point mutations (Brockman et al., 2007 (Jurkat cell), Miura et al., 2009, Troyer et al., 2009, Schneidewind et al., 2007, Schneidewind et al., 2008). This data also exhibits a strong negative correlation ρ = −0.81 (p = 2 ×10⁻⁷). In each panel, a linear least squares fit is provided to guide the eye, and error bars delineating estimated uncertainties in the relative fitness are provided where available.

To further test our model, we compiled 50 previously published experimental measurements of the in vitro replicative fitness of engineered p24 Gag mutants containing up to five polymorphisms (Brockman et al., 2007; Crawford et al., 2007; Miura et al., 2009; Schneidewind et al., 2008; Schneidewind et al., 2007; Troyer et al., 2009). Since in inferring our model we do not distinguish between any of the 19 possible mutant amino acids at each position observed in the MSA, our model is statistically most accurate in describing the fitness effects of mutant strains containing the most probable mutant amino acids at mutated positions. Accordingly, we first compared our model to those 25 fitness measurements in which the engineered polymorphism corresponds to the single most probable mutant amino acid at that position observed in the MSA. As for comparisons with our own experimental data, we observed a strong negative correlation between our predictions of the energy of a strain and its measured in vitro replicative fitness (Figure 2B, ρ = −0.81 (p = 2 ×10⁻⁷)). The relationship between E_i and f_i also exhibits a strong negative correlation (Figure S1B, ρ= −0.75 (p = 6 ×10⁻⁶)). Despite the inaccuracy of the binary approximation for the other 25 published data points, the negative correlation was maintained upon considering all 50 data points (Figure S1C–D). In the Supplemental Computational Procedures, we describe an extension of our model that does not require making the binary approximation.

The viral sequences used to parametrize our model were extracted from infected individuals, each of whom possess a unique adaptive immune response targeting different regions of the HIV proteome. Thus, the effectively fittest viral strains in each individual are expected to differ. Why, therefore, do we see good correspondence between E and in vitro intrinsic replicative fitness? Assuming the representation of HLA alleles to approximately follow that of United States Caucasians (Gonzalez-Galarza et al., 2011), the recognition frequencies of the most common HLA restricted p17 and p24 epitopes (Streeck et al., 2009) indicate that, of the 363 residues in p17 and p24, only 46 are targeted by more than 10% of the population, no single residue is targeted by more than 23%, and 146 are not targeted at all. If we may assume that a diverse range of HLA class I haplotypes are represented within the population from which the sequences were obtained, and that infecting strains rapidly revert to replicatively more fit strains if the immune pressure in a new host does not attack the region in which a mutation was forced in the infecting host (Davenport et al., 2008; Friedrich et al., 2004; Henn et al., 2012), then our models represent averages over haplotypes in the population. This averaging may explain why our models appear to reflect the underlying intrinsic viral fitness, rather than “footprints” of adaptive immune pressure (Matthews et al., 2009).

Clinically documented escape strains correspond to high fitness strains

Viral strains can escape CTL recognition by establishing one or more point mutations within, or flanking, the target epitope. It is expected that the clinically observed escape strains will be those that permit the virus to evade immune recognition with minimal cost to its replicative fitness, and should correspond to low-energy strains in our model.

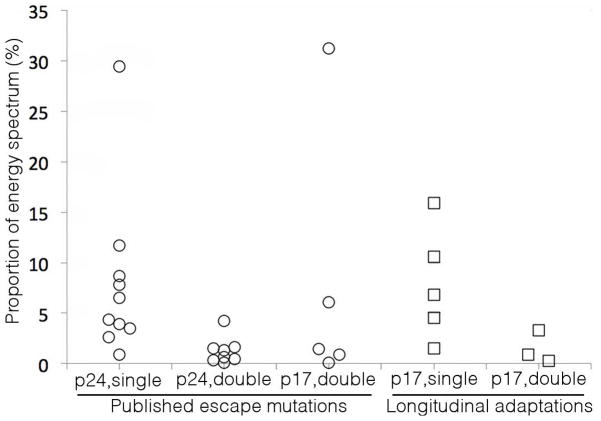
Published accounts of escape strains sequenced from HIV infected individuals and statistical analyses of proximate HLA associated polymorphisms allowed us to compile a list of p17 and p24 escape mutations against which to test our inferred fitness landscape (Brockman et al., 2010; Brockman et al., 2007; Brumme et al., 2009; Draenert et al., 2004; Leslie et al., 2004; Martinez-Picado et al., 2006; Miura et al., 2009; Schneidewind et al., 2008; Schneidewind et al., 2007; Troyer et al., 2009). In p24 we gathered a set of 10 single and 8 double mutants, and in p17, a set of 5 double mutants and 1 triple mutant. In contrast to Shannon entropy-based approaches that consider the variability of single residues or epitopes in isolation (Allen et al., 2005; Ferrari et al., 2011), our method permits quantitative ranking of any multi-residue mutant according to the value of E (proxy for fitness) assigned by our model. The particular mutants, HLA associated epitopes, and computed energies are listed in Table S1. The energy assigned to each mutant by our model is shown in Figure 3.

Figure 3.

Clinically documented mutant strains correspond to low energy (high fitness) states within our inferred model. Circles: Energies assigned by our model to the 10 p24 single mutants, 8 p24 double mutants, and 5 p17 double mutants listed within Table S1, which identifies the particular mutants, HLA associated epitopes, and computed energies. Squares: Energies of the strains of three p17 epitopes observed to undergo sequence adaptation in longitudinal deep sequencing of an HIV infected host (Henn et al., 2012). In all cases, residues outside the epitope are treated as wild-type in the assignment of energies.

Of the p24 single mutants, 9 out of 10 possess energies within the bottom 11.7% of the spectrum of 231 possible single mutant strains (E < 8.4). The remaining candidate, carrying a mutation at position 264, possesses an energy E = 19.4, placing it at the 29^th percentile of the energy spectrum. The low fitness (high energy) apparently tolerated by this mutant is explained by the observation that mutations of this residue are never observed in isolation, but only in concert with a mutation at position 268 (Schneidewind et al., 2007). We find that the interaction coupling between these residues is compensatory, leading to a high-fitness double mutant with a low energy (E = 11.0) corresponding to the bottom 1.3% of the spectrum. A third compensatory mutation is also frequently observed at position 173 (Schneidewind et al., 2007), leading to further compensation, and a highly fit triple mutant (E = 2.9). This progression of compensatory interactions demonstrates the ability of our model to capture couplings between multiple simultaneous mutations throughout the protein, which cannot be achieved by the Shannon entropy of single residues or epitopes.

All 8 of the p24 double mutants reside within the bottom 4.2% of the energy spectrum of all possible 26,565 doubly mutated strains. Similarly, the energies of 4 of the 5 p17 double mutants lie in the bottom 6.1% of the 8,646 possible double mutants. The remaining double mutant resides in the 31^st percentile. While the p17 triple mutant possesses an energy E = 16.99, flipping one particular residue back to wild-type results in a highly fit (E = 1.03) double mutant that is the 13^th lowest energy strain of all 8,646 possible double mutants (0.15% energy percentile) (cf. Table S1). We note that we identified the p17 triple mutant from a statistical analysis of polymorphisms in the vicinity of the A11-TI9 epitope at Gag_84-92 (Brumme et al., 2009), rather than an observation of this strain within an infected person.

By cross-referencing the list of best-defined HIV CTL epitopes (the CTL “A list”) (Frahm et al., 2008), with a compilation of statistically significant HLA associated polymorphisms (Brumme et al., 2009), we identified 25 epitopes in p17 and p24 with defined CTL escape mutations. If we assume that all point mutations within, or flanking, these epitopes lead to equally efficient CTL escape, our inferred fitness landscape predicts that escape mutations should correspond to those residues in epitopes that incur the smallest energy penalty upon mutation, and thus maximally preserve viral fitness.

As illustrated in Figure 4, the well-documented B*57 associated escape mutations at positions 242 and 248 in the TW10 (Gag_240-249) epitope in p24 (Brumme et al., 2009) coincide precisely with the point mutations leading to the lowest fitness penalty (lowest energy cost). Similar results for the 24 remaining examples are presented in Figure S2. In 21 of 25 cases, the observed escape mutation – or one such mutation in epitopes where multiple escapes are observed – occurs at precisely the least costly, or next least costly, position. Of the 4 remaining cases, 2 of the documented escape mutations identified by statistical analyses are defined as “indirect” HLA associations (Brumme et al., 2009), implying that they may exist as compensatory mutations elicited by a prior mutation in other proteins, rather than as primary escapes to evade CTL pressure. Our models have been constructed for single proteins, and are therefore capable of capturing mutational couplings between residues within the same protein. As more whole genome sequences become available, our method can be applied to identify the fitness effects of inter-protein couplings.

Figure 4.

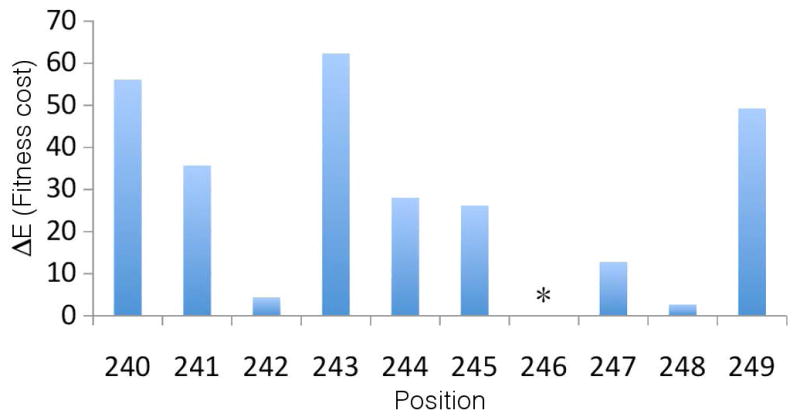
Comparison of point mutant energy costs with documented B*57 associated escape mutations in the TW10 (Gag_240-249) epitope in p24. The 10 residues constituting the epitope are indexed along the abscissa, and the energy cost associated with making a point mutation at each position, ΔE, along the ordinate. The greater the energy cost, the higher the fitness penalty. Mutations at position 246 were not observed within our sequence alignments, leading to the specification within our model of an infinite energy cost of a point mutation at this position, which we denote by *. The observed escape mutations at 242 and 248 (Brumme et al., 2009) occur precisely at the two positions carrying the lowest energy cost (smallest fitness penalty).

The fact that the preponderance of escape mutations observed in people with different genotypes are high fitness (low energy) strains further supports the hypothesis that the inferred fitness landscape reflects intrinsic viral fitness, and not immune footprints of individuals with particular HLAs. Not all high fitness mutant strains are clinically observed, due in part to finite sampling of the circulating strains, redundancy in the genetic code rendering mutations of some amino acids intrinsically more difficult than others, and that not all positions are subject to immune pressure driven mutations.

Temporal patterns of mutations in individual patients follow high-fitness routes

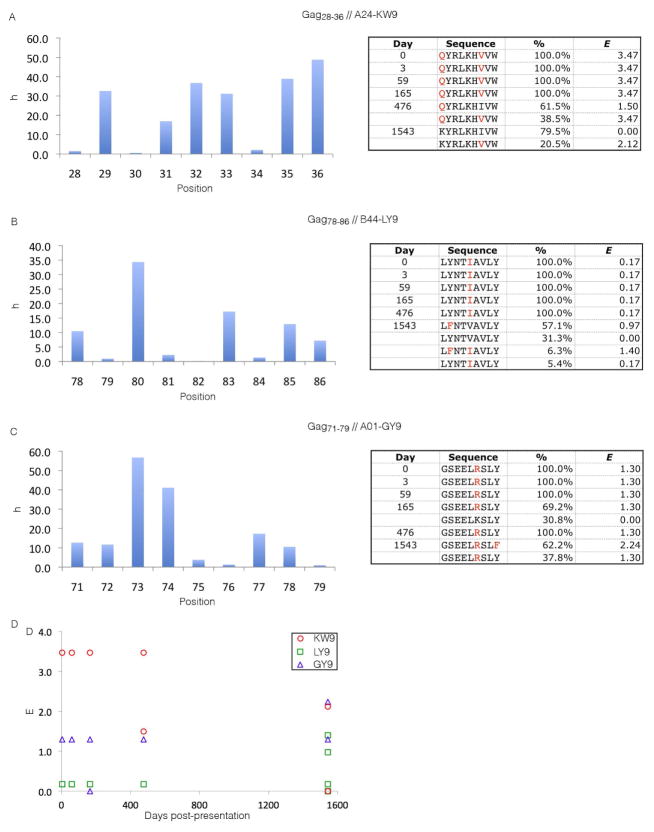
As a further, stringent test of whether our models reflect intrinsic viral fitness, we compared our predictions to recently reported longitudinal deep sequencing within a single host over the first four years of HIV infection (Henn et al., 2012). Three of the six sequenced CTL Gag epitopes in this individual exhibited sequence adaptation over the course of infection. Comparison of the observed sequence adaptations to the fitnesses (energies) computed from our model show that they populate the high fitness (low energy) states of the inferred landscape (Figure 3) and, the temporal adaptation courses follow high fitness (low energy) routes (Figure 5).

Figure 5.

Longitudinal deep sequencing within a single infected host identified three p17 CTL Gag epitopes as undergoing sequence adaptation during the first four years of HIV infection (Henn et al., 2012). In panels A–C, the title provides the location of each CTL epitope within Gag (e.g., Gag_28-36), the HLA association (e.g., A24), and the name of the epitope (e.g., KW9). On the left side we present bar charts illustrating our inferred h parameter (c.f. Computational and Experimental Procedures) at each position in the epitope. On the right, we list the strains observed by deep sequencing at the six time points (Henn et al., 2012), the fraction of the deep sequencing reads corresponding to each strain (Henn et al., 2012), and the energy of each strain assigned by our model. Red letters indicate point mutations relative to our MSA consensus; all residues outside the epitope are treated as wild-type in the computation of energies from our model. In panel D, we present the temporal adaptation courses tracking the energy assigned by our model to the mutant strains of each epitope sequenced at each time point.(A) The infecting strain contains two mutations in the KW9 epitope (Gag_28-36) at positions 28 and 34, corresponding to the positions with the second (h₂₈ = 1.50) and third (h₃₄ = 2.12) lowest h values and a compensatory J coupling (J_28,34 = −0.15, c.f. Computational and Experimental Procedures), lowering the energy of the double mutant relative to the two independent point mutations. By day 476, 61.5% of the viral population has reverted to the lower energy single mutant (h₂₈ = 1.50). By day 1543, 79.5% of viral strains have reverted to the lowest energy (E=0) wild-type state. The remaining 20.5% occupy the third least costly singly mutated state (h₃₄ = 2.12). The lowest (h₃₀ = 0.55), second lowest (h₂₈ = 1.50) and third lowest (h₃₄ = 2.12) singly mutated states are similar in energy.(B) The LY9 epitope (Gag_78-86) enters with a single mutation in the infecting strain at the single lowest energy position (h₈₂ = 0.17). No sequence adaptation is observed until day 1543, at which time 31.3% of the population has reverted to the lowest energy (E=0) wild-type. 57.1% of the population occupy the second lowest energy singly mutated state (h₇₉ = 0.97), while 6.3% occupy a low energy doubly mutated state (h₇₉ = 0.97, h₈₂ = 0.17, J_79,82 = 0.25), and 5.4% remain in the infecting state. (C) The GY9 epitope (Gag_71-79) entered with a single mutation at the second least costly position in the epitope (h₇₆ = 1.30), nearly equi-energetic with the least costly point mutation (h₇₉ = 0.97). By day 165, the wild-type strain transiently emerged in 30.8% of the population, but has vanished by day 476. At day 1543, 37.8% of the population remains in the infecting state. The remaining 62.2% possess mutations at the second least costly (h₇₉ = 0.97) and least costly (h₇₆ = 1.30) positions, and a small compensatory coupling (J_76,79 = −0.04). This double mutant is of very low energy, lying within the lowest 1% of all 8,646 possible p17 double mutants. Of the three epitopes considered, only for GY9 is a significant fraction of the day 1543 population not observed in the lowest energy wild-type state, although it transiently emerges in day 165. Of the three epitopes, GY9 was the only one against which a CTL response was reported (Henn et al., 2012), consistent with a situation in which the wild-type state is effectively less fit than a competing mutant strain capable of evading immune pressure.(D) Temporal adaptation courses follow high fitness (low energy) routes for each of the three epitopes: KW9 (red circles), LY9 (green squares), and GY9 (blue triangles).

As illustrated in Figure 5A, the infecting strain contained two mutations within the KW9 (Gag_28-36) epitope, presumably driven by immune pressure in the previous host (Henn et al., 2012). They occur at the second and third energetically least costly positions predicted by our model, and the energy of this double mutant is in the bottom 3.3% of all double mutants. By day 1543 of infection, 79.5% of the population had reverted to wild-type. The LY9 (Gag_78-86) epitope of the infecting strain (Figure 5B) contained a point mutation at the least costly position. By day 1543, 31.3% of strains had reverted to wild-type, with the remaining strains split between three other states that we predict to be highly fit. The energies of these four states are very close, suggesting that stochastic fluctuations may have populated the marginally less fit states. Finally, the GY9 (Gag_71-79) epitope in the infecting strain (Figure 5C) carried a single mutation at the second least costly position. By day 165 the wild-type transiently emerged in 30.8% of strains, to be replaced in 62.2% of the population by day 1543 with a highly fit double mutant residing within the bottom 1% of all double mutants. In Figure 5D, we show the temporal adaptation courses of the three epitopes. Of the three epitopes, a CTL response was reported against only GY9 (Henn et al., 2012). This response may render the wild-type strain effectively less fit than higher energy mutants that are able to evade immune pressure. Accordingly, in the presence of this immune pressure, the wild-type may be outcompeted by a highly fit double mutant, offering a plausible rationalization for its observed transient emergence and disappearance.

That the strains observed during sequence adaptation within a single host correspond to the high fitness (low energy) mutations predicted by our model, further substantiates our inferred landscapes as reflections of intrinsic viral fitness.

CTL targeting of peptides presented by elite controllers incur the largest fitness costs

A diversity of HIV mutant viral strains exists within an infected host (Lee et al., 2008). Viral populations containing strains with lower replicative fitness have been correlated with better disease control (Miura et al., 2010). We hypothesized that our model may be able to identify effective CTL immune responses as those which give rise to mutations that significantly decrease the average fitness of the viral population within a host.

The results we have reported strongly suggest that the energy, E_i, of a particular viral strain, i, is a good measure of its intrinsic replicative fitness. To simulate the diversity of viral strains that may exist within an infected host, we used the energies predicted by our model to generate a large ensemble of mutant strains in which each is represented in proportion to its fitness (cf. Equation 1 and Supplemental Computational Procedures). The average fitness of an ensemble of sequences should correlate with its average energy, <E> = Σ_i P(i) E_i, where P(i) is the prevalence of strain i in the ensemble.

We suggest that an effective immune response will significantly increase the average energy (decrease the average fitness) of the ensemble of viral strains in an individual. Such responses will preferentially eliminate high-fitness viral strains, leaving behind unfit strains that are less able to replicate and damage the host. Conceptually, this corresponds to deletion of those strains residing near the peaks of the fitness landscape, causing the ensemble as a whole to be pushed into the low-fitness valleys (cf. Figure 1). The fitness cost upon targeting a particular CTL epitope was quantified as the change in <E>,Δ<E>, upon removing from the ensemble all viral strains with wild-type amino acids in the targeted epitope, simulating the effect of CTL elimination of these strains. Our model predicts that targeting epitopes associated with larger values of Δ<E>should result in better control of HIV infection.

Using this criterion, we rank-ordered the 121 p24 epitopes defined in the Los Alamos HIV Molecular Immunology Database (http://www.hiv.lanl.gov/content/immunology) listed in Table S2. We define a particular HLA associated epitope to be immunodominant if its cognate CTL response is observed in more than 50% of patients expressing this HLA in either the chronic or acute phase of infection (Streeck et al., 2009). Available immunodominance data allowed us to identify 12 such epitopes, of which 8 are associated with protective HLA alleles that clinical and genome wide association studies have linked with superior ability to control HIV infection (Hendel et al., 1999; Pereyra et al., 2010; Streeck et al., 2009; Trachtenberg & Erlich, 2001) (Table S2). As illustrated in Figure 6, the 3 immunodominant epitopes that lead to the greatest fitness costs, and 6 of the 7 immunodominant epitopes leading to the greatest fitness costs, are presented by HLA molecules associated with persons who can naturally control HIV infections (Hendel et al., 1999; Miura et al., 2009; Pereyra et al., 2010; Trachtenberg & Erlich, 2001). We find, therefore, that elite controllers target epitopes where mutational escape incurs the largest fitness costs, consistent with the observation that viral strains extracted from these persons have impaired replicative capacity (Miura et al., 2009). Notably, the results in Figure 6 pertain to multiple HLA types, providing further support for the assertion that our landscapes describe intrinsic viral fitness, rather than “footprints” of adaptive immunity (Matthews et al., 2009). Our results also suggest that we can predict disease pathogenesis from knowledge of viral strains in a patient because we can determine the average fitness of the in-host viral population. As an aside, we observe that the negative Δ<E> value corresponding to epitope 121 reflects an immune pressure that preferentially removes unfit strains, allowing the remaining fitter strains to occupy a larger fraction of the population. This effect may suggest a possible interpretation for failed vaccine trials that led to increased viral loads and a reduction in time to antiretroviral treatment resumption (Autran et al., 2008).

Figure 6.

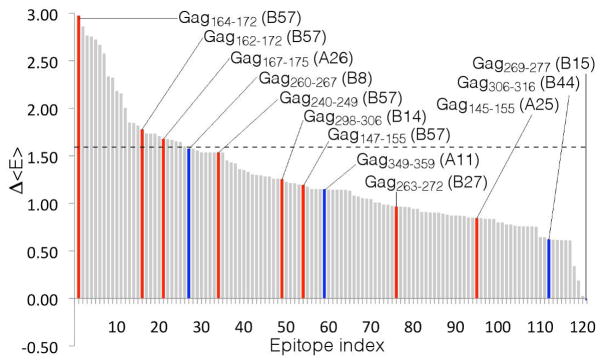
Rank ordered bar chart of 121 p24 class I HLA epitopes according to the computed energy penalty, Δ<E>, imposed upon the viral ensemble. The particular epitopes considered are listed in Table S2. Epitopes associated with a reported immunodominant response within a particular HLA class I allele (Streeck et al., 2009) are designated by colored bars and labeled with the epitope location and HLA association. Red bars indicate that the corresponding HLA allele has been linked with enhanced HIV control, whereas blue bars denote those that have not (Miura et al., 2009; Pereyra et al., 2010; Trachtenberg & Erlich, 2001). The immunodominance data pertaining to the B*57 KF11 epitope Gag_162-172were assumed to also apply to the epitope formed from its nine residue subset, Gag_164-172. Six of the seven immunodominant epitopes leading to the greatest fitness cost are associated with protective HLA alleles; the dashed line at Δ<E> = 1.54 represents the cutoff above which all immunodominant responses are associated with protective alleles.

Dahirel et al. identified groups of residues (“sectors”) in Gag subject to mutational couplings particularly detrimental to viral fitness (Dahirel et al., 2011). The 3 top ranked immunodominant epitopes in our model contain 5, 6 and 7 residues, respectively, within the top sector of Dahirel et al. containing the most detrimental couplings, whereas the 9 remaining epitopes each contain 4 residues or fewer. This suggests that our landscapes are capable of identifying vulnerable protein regions containing deleterious mutational couplings.

Not all immunodominant p24 epitopes associated with protective alleles will lead to large fitness costs, since each allele may mediate its beneficial effect through only a small fraction of the epitopes it targets. For example, B*27 is a protective allele, with chronic phase escape from its KK10 (Gag_263-272) epitope associated with progression to AIDS (Pereyra et al., 2010; Schneidewind et al., 2007; Trachtenberg & Erlich, 2001). The relatively low ranking of this epitope in Figure 6 may be due to (at least) two factors. Firstly, this epitope contains only 3 residues from Dahirel et al.’ s top sector (Dahirel et al., 2011). Nine B*27 epitopes are defined within our list of 121 epitopes, containing a total of 11 residues within this sector. Targeting the KK10 epitope in isolation may lead to only a modest reduction in viral fitness, whereas targeting multiple B*27 epitopes simultaneously may lead to a more substantial fitness loss due to additional deleterious couplings. Secondly, the protective action of B*27 may lie elsewhere in the proteome, as suggested by recent work demonstrating a strong B*27 response to the KY9 Pol epitope (Friedrich et al., 2011; Payne et al., 2010).

The available data allowed us to identify only one immunodominant CTL epitope within p17, and none within p6 and p7, thereby precluding similar analyses for these proteins (Streeck et al., 2009).

The inferred fitness landscapes can be used for in silico immunogen design

As one illustration of the value of fitness landscapes, we consider the design of CTL Gag immunogens that may induce potent immune responses in people with diverse genotypes. We observe that this strategy may be directly extended to guide the design of antibody immunogens, combinations of potent antibodies, or small molecule inhibitors.

Peptides from regions of HIV that are particularly vulnerable to multiple mutations tend to be immunodominantly targeted by CTLs in persons possessing protective HLA molecules (Dahirel et al., 2011). In contrast, non-protective HLA molecules dominantly present epitopes from regions where mutational escape from immune pressure is relatively easy. Non-protective HLAs can target peptides from vulnerable regions only sub-dominantly when the whole proteome is presented (cf. Table S2) (Dahirel et al., 2011; Streeck et al., 2009). The previous section demonstrates that our landscapes can identify vulnerable regions of the viral proteome that can be presented sub-dominantly (or dominantly) by diverse HLAs. An immunogen designed to prime these responses, while excluding dominantly presented regions from which mutational escape is easy, could, if properly delivered as a vaccine, elicit effective immune responses within hosts with diverse haplotypes.

We consider the design of a CTL Gag immunogen for a target population comprising the top 21 haplotypes of North Americans with European ancestry, accounting for 44.6% of this population (http://www.ncbi.nlm.nih.gov/projects/gv/mhc). Cross-referencing with the list of optimally defined “A list” CTL epitopes (Frahm et al., 2008), we found that the class I HLA-A, -B and -C molecules in this population restrict p = 1, 0, 10 and 20 epitopes in p6, p7, p17 and p24, respectively. For each Gag protein, we constructed all possible combinations of 1,2,3,…, p epitopes, where each combination represents an immunogen candidate. There are 1, 1023 and 1,048,575 combinations for p6, p17 and p24, respectively. The efficacy of each candidate in each of the 21 haplotypes was evaluated by identifying those epitopes in the immunogen that could be presented by HLA molecules constituting the haplotype, and the fitness penalties upon simultaneously targeting these epitopes. The penalty, Δ<E>, was calculated in the manner described in the previous section. The fitness penalty exacted by forcing mutations within the epitopes comprising each immunogen candidate, i, in each haplotype, j, is denoted as $\mathrm{\Delta }<\text{E}{>}_{\text{i}}^{\text{j}}$.

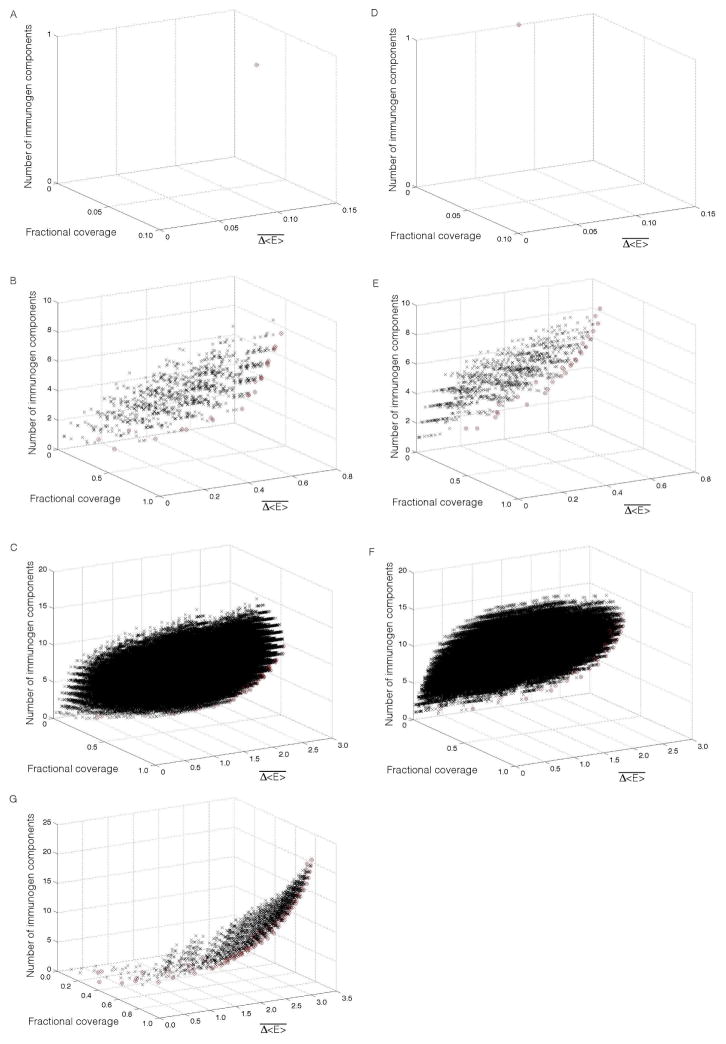
We evaluated each immunogen candidate, i, derived from each of the three proteins according to three criteria: (i) the weighted average fitness impact in the target population, $\overline{\mathrm{\Delta }<\text{E}{>}_{\text{i}}}={\displaystyle \sum _{\text{j}=1}^{21}}{\omega }_{\text{j}}\mathrm{\Delta }<\text{E}{>}_{\text{i}}^{\text{j}}$, where ω_j is the fraction of haplotype j in the target population, (ii) the fraction of the target population that respond to at least one epitope in the immunogen (fractional coverage), and (iii) the number of epitopes in the immunogen. The performance of all p6, p17 and p24 immunogen candidates according to these three criteria are presented in Figure 7A–C. With in this candidate pool for each protein, we identified candidates such that immunogens that are superior to them in any one criterion (increased fitness penalty, higher population coverage, fewer included epitopes) are inferior in one or more of the other criteria. These immunogens constitute the “optimal frontier” (or “Pareto frontier”(Arora, 2011)) of the candidate pool, where improvements in any one criterion are necessarily accompanied by a deterioration in another. Candidates which do not lie on the frontier are sub-optimal, since improvements may be made in any one criteria without incurring a penalty in another. For p6, p17 and p24, we identified 1, 25 and 44 optimal candidates for inclusion in an immunogen. Their epitope compositions are listed in Tables S3–5. The evaluation criteria may be altered without changing the approach. For example, in Figure 7D–F we show the results of calculations in which criterion (ii) was modified to evaluate the fraction of the target population that respond to at least two epitopes.

Figure 7.

Evaluation of immunogen candidates. (A–C) Scatter plots of (A) p6, (B) p17 and (C) p24 vaccine candidates in the three-dimensional design space spanned by: (i) the weighted average fitness impact in the target population, $\overline{\mathrm{\Delta }<\text{E}>}$, (ii) fraction of the target population that respond to at least one epitope in the immunogen (fractional coverage), and (iii) the number of components in the vaccine. The target population comprised the 21 most prevalent haplotypes in North Americans of European ancestry, accounting for 44.6% of this population. Respectively, 1, 1023 and 1,048,575 immunogen candidates were tested for p6, p17 and p24 (black crosses), of which 1, 25 and 44 candidates were located on the Pareto frontier (red circles). The composition of these Pareto efficient immunogens is listed in Tables S3–5. (D–F) Scatter plots analogous to those in panels A–C for (D) p6, (E) p17, and (F) p24, in which criterion (ii) was modified to the fraction of the target population that respond to at least two epitopes in the immunogen; 1, 31 and 62 candidates are located on the Pareto frontier. (G) Scatter plot of the 2,340 combination Gag vaccine candidates in the three-dimensional design space spanned by: (i) the weighted average fitness impact in the target population, $\overline{\mathrm{\Delta }<\text{E}>}$, (ii) fraction of the target population that respond to at least one epitope in the immunogen (fractional coverage), and (iii) the number of components in the vaccine. The compositions of the 95 Pareto efficient candidates are listed in Table S6.

There are (1+1)×(25+1)×(44+1)=2,340 candidate immunogens for the combined [p6, p17, p24] polyprotein formed from the combination of candidates on the optimal frontier for each individual protein, plus the “null” immunogen containing no epitopes in a particular protein. Using the same criteria as before, we identified 95 Gag polyprotein immunogens on the optimal frontier Figure 7G. Their composition is listed in Table S6. As this table shows, our strategy permitted the identification of a 12 component (113 residue) immunogen with 100% coverage of the target population (i.e., all members respond to at least one epitope). In future work, we plan to test the efficacy of our designed Gag immunogens in inducing potent CTL responses in vitro and in animal models.

Discussion

HIV is a highly mutable virus that also replicates very rapidly. The large diversity of viable viral strains makes it difficult for the adaptive immune system to mount natural responses that effectively control the virus (Autran et al., 2008; Goulder & Watkins, 2004). Immune responses or therapeutic agents that target regions of the viral proteome where mutations lead to a large cost in replicative fitness can be very effective for viral control or aborting the infection (Dahirel et al., 2011; Goulder & Watkins, 2004; Streeck et al., 2007). Systematic means to derive the viral fitness landscape permits the identification of such regions. These landscapes, therefore, offer an unprecedented guide for the rational design of vaccine immunogens that could redirect the adaptive immune response towards regions of the virus most vulnerable to attack. They could also help design optimal combinations of passively-administered antibodies and small molecule therapeutic inhibitors that could neutralize diverse strains.

We report a computational method that can translate viral sequence databases into quantitative landscapes of intrinsic fitness of viral strains containing multiple, potentially synergistic, mutations. We have applied this approach to proteins contained in Gag, and positively tested our predictions against experiments and clinical data.

As one illustration of how to leverage the insights furnished by inferred fitness landscapes, we have designed a Gag immunogen to prime CTL immune responses against vulnerable regions of the viral proteome within a target human population. Recent experiments with mousepox virus suggest that such long-peptide immunogens, if properly delivered, can redirect the host immune system to mount CTL responses capable of conferring protective immunity upon mice that are otherwise naturally susceptible to infection (Remakus et al., 2012). Similarly, Melief, van der Burg, and co-workers have reported the efficacy of long-peptide immunogens to kill cancerous tumors if they are delivered in a way that results in highly immunogenic responses (Melief & van der Burg, 2008). We plan to test our immunogen in animal models with optimized delivery approaches that result in sufficient immunogenicity.

Subject to continued validation, the approach we have developed provides a general methodology to translate viral sequence data into fitness landscapes. With both viral sequencing and computational hardware costs rapidly declining, our methodology offers a means to compute full-genome fitness landscapes for diverse viral pathogens – and possibly cancers – as sufficiently large numbers of sequences become available. This methodology may therefore represent a potentially powerful tool to guide the design of improved prophylactic and therapeutic strategies.

Computational and Experimental Procedures

Fitness Landscape Inference

Under the binary approximation, the sequence of an m-residue protein may be specified by the m-dimensional vector z⃗, the elements of which, ${\{{\text{z}}_{\text{i}}\}}_{\text{i}=1}^{\text{m}}$, indicate whether the amino acid at position i is wild-type, z_i = 0, or mutant, z_i = 1. The maximum entropy model that fits the one and two-body mutational probabilities is the Ising spin glass model (Binder & Young, 1986). The probability of observing a particular sequence, z⃗, within the population of all possible mutants is,

$$\text{P}(\overrightarrow{\text{z}})=\frac{1}{\text{Z}}{\text{e}}^{-\text{E}(\overrightarrow{\text{z}})},\text{E}(\overrightarrow{\text{z}})=\sum _{\text{i}=1}^{\text{m}}{\text{h}}_{\text{i}}{\text{z}}_{\text{i}}+\sum _{\text{i}=1}^{\text{m}}\sum _{\text{j}=\text{i}+1}^{\text{m}}{\text{J}}_{\text{ij}}{\text{z}}_{\text{i}}{\text{z}}_{\text{j}}$$ Eqn. 1

In analogy with spin glasses, we refer to E as a dimensionless “energy”, and the normalizing factor $\text{Z}={\displaystyle \sum _{[{\text{z}}_{\text{I}}]=\{0,1\}}}{\text{e}}^{-\text{E}(\overrightarrow{\text{z}})}$ as the partition function. The h_i and J_ij model parameters are inferred from the one and two-point mutational probabilities observed in the protein sequence data using a semi-analytical extension of the iterative gradient descent implemented by Mora and Bialek (Mora & Bialek, 2011). We detail this procedure in the Supplemental Computational Procedures, along with a description of the Monte-Carlo procedure used to sample from the fitted models for each of the four Gag proteins.

Replicative Fitness Assays

The following mutations and mutation combinations were introduced into a HIV-1 subtype B NL4-3 plasmid using the QuikChange II XL Site-Directed Mutagenesis kit (Stratagene, La Jolla, CA), as previously described (Wright et al., 2012): 146P, 147L, 146P/147L, 219Q, 242N, 219Q/242N, 186I, 310T, 295E, 182S, 179G, 229K, 331R, 190I, 302R, 315G, 168I, 326S, 310T/326S. To generate the mutant viruses, 10μg of mutant plasmids were electroporated into an HIV-1-inducible GFP-reporter T cell line using conditions described previously (Huang et al., 2011) and virus growth was subsequently monitored by detection of GFP-positive cells by flow cytometry (Brockman et al., 2010; Wright et al., 2012). Replication capacities of mutant viruses were similarly assayed in the GFP-reporter T cells by flow cytometry (Brockman et al., 2010; Wright et al., 2012). Briefly, cells were infected at a MOI of 0.003 and the exponential slope of increase in the percentage infected cells between days 3 and 6 post-infection was calculated as the measure of viral replication capacity. Replication capacities of mutant viruses were expressed relative to that of the wild-type NL4-3 virus, included as a control in every assay, such that a replication capacity of 1 indicated replication equal to that of NL4-3. Assays were performed in triplicate and the results averaged.

Highlights.

• Quantitative fitness landscapes were extracted from viral sequence databases

• We developed a landscape for HIV Gag using a model from statistical physics

• Predictions show good agreement with new in vitro and existing clinical data