A Modeling Framework for the Evolution and Spread of Antibiotic Resistance: Literature Review and Model Categorization

Abstract

Antibiotic-resistant infections complicate treatment and increase morbidity and mortality. Mathematical modeling has played an integral role in improving our understanding of antibiotic resistance. In these models, parameter sensitivity is often assessed, while model structure sensitivity is not. To examine the implications of this, we first reviewed the literature on antibiotic-resistance modeling published between 1993 and 2011. We then classified each article's model structure into one or more of 6 categories based on the assumptions made in those articles regarding within-host and population-level competition between antibiotic-sensitive and antibiotic-resistant strains. Each model category has different dynamic implications with respect to how antibiotic use affects resistance prevalence, and therefore each may produce different conclusions about optimal treatment protocols that minimize resistance. Thus, even if all parameter values are correctly estimated, inferences may be incorrect because of the incorrect selection of model structure. Our framework provides insight into model selection.

Antibiotic-resistant infections can lead to increased morbidity and mortality and lengthened hospital stays (1, 2) because of inadequate initial therapy and, in some cases, increased virulence. Resistance to first- or even second-line antibiotics forces the use of more expensive second- or third-line antibiotics. These individual-level effects compound at the population level because of transmission; compared with effective treatment and pathogen clearance, treatment failure increases transmission and thereby the total number of cases, the total number of drug prescriptions, and associated morbidity and mortality. In the European Union, the annual cost associated with antibiotic-resistant infections is estimated to be €1.5 billion (based on 2007 euros) (3), while in the United States the value is estimated to be greater than $16 billion (based on 2000 dollars) (4, 5).

Mathematical modeling has played an integral role in improving our understanding of antibiotic resistance (6). These models provide a platform for in silico experiments that help us better understand mechanistic sources of uncertainty, generate refined hypotheses, and interpret empirical observations. Models make empirical experimentation more efficient, and in silico experiments can be conducted at reduced cost and avoid ethical dilemmas. Within-host models have focused on: 1) emergence of antibiotic resistance (7), 2) microbial fitness and selection for antibiotic-resistant strains compared with antibiotic-sensitive strains (8, 9), and 3) antibiotic tolerance (10). Population-level models have been used to better understand and predict the effects of treatment protocols such as antibiotic cycling (11).

Published models of the emergence and spread of antibiotic resistance have progressed from resistance models of abstract agents in abstract settings (12, 13) to resistance models of specific agents such as Mycobacterium tuberculosis (14), Streptococcus pneumoniae (15), Staphylococcus aureus (16), and Enterococcus (17) in more specified settings, such as transmission between hospitals (18), within hospitals and intensive care units (19), and within day-care centers (20). These studies include a multitude of model structures that vary in complexity and inherent assumptions. However, all models of antibiotic resistance include competition between antibiotic-sensitive and antibiotic-resistant strains. To model this competition, a wide array of model structures have been used, each reflecting distinct biological mechanisms of competition, but model structure is rarely justified. One exception to this is a study of S. pneumoniae that extensively compared the effect of using different model structures (21). In general, however, most articles on antibiotic-resistance modeling have provided little justification for the model structure chosen, nor have they considered how alternative model structures affect their investigations' inferences.

To examine the implications of this, we reviewed the peer-reviewed literature on antibiotic-resistance modeling published from 1993 to 2011. PubMed searches were carried out using the search terms “(determinist* or stochast* or compartment* or mathematic* or simulat*) and model* and resist*.” We excluded all exclusively within-host models, pharmacodynamic-pharmacokinetic models, and reviews that did not present novel work. We then grouped these articles into 6 categories based on common features of their structures. This allowed us to create a unifying framework composed of generic model structures that make explicit the variety of model assumptions used with regard to within-host and population-level competition between antibiotic-sensitive and -resistant strains. We used this framework to categorize all published articles into 1 or more of the 6 generic model structures. We also summarized how often each model structure category was used in the literature and each category's threshold properties. We show that choice of model structure affects the nature of inferences that can be drawn in terms of population coexistence and dieout of antibiotic-sensitive and -resistant strains.

FRAMEWORK DEVELOPMENT

This review focuses exclusively on articles that modeled between-host dynamics. These studies all model the spread of antibiotic-resistant and -sensitive bacterial strains from one host to another. Often a distinction is made between infection, defined as rapid bacterial overgrowth leading to disease symptoms, and colonization, where there is stable bacterial presence without disease symptoms. In this context, colonization may sometimes lead to infection. In this paper we are less concerned with these differences, focusing rather on person-to-person spread of agents that either colonize or cause infection. Because of this, we use the term infection when either colonization or infection may apply.

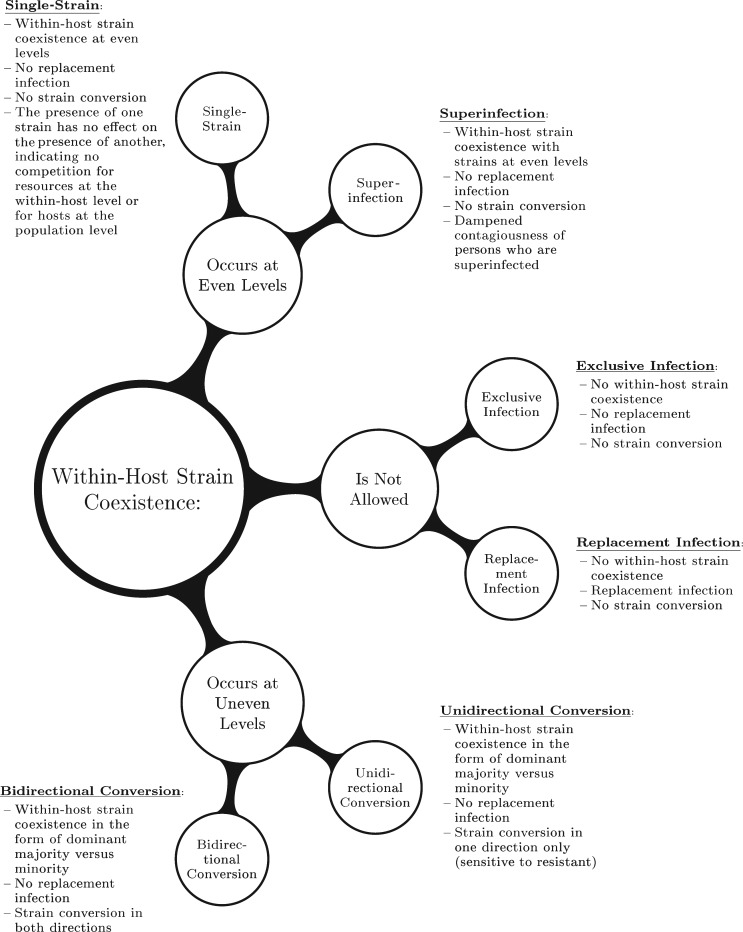
Figure 1 shows how between-host models are categorized on the basis of properties of within-host dynamics. Within a host, resistant and sensitive strains can coexist either at equal levels or where one strain predominates over the other. In contrast, a host may be infected exclusively by a resistant or sensitive strain if coexistence is not permitted. Within-host competition can have differing results; if a host is infected with 1 strain, there is potential for a novel strain to replace the resident strain. If a host is superinfected with both sensitive and resistant strains, a predominant strain may convert from sensitive to resistant or vice versa. Based on these definitions, our model categories are determined by 1) the extent of strain coexistence allowed within a host, 2) the potential for replacement infection when a novel strain challenges a resident strain within a host, and 3) strain conversion when a predominantly antibiotic-sensitive infection converts to being predominantly resistant due to within-host selection.

Figure 1.

Categorization of the antibiotic-resistant model structures found in an exhaustive literature review of between-host resistance models published from 1993 through 2011. Model category was determined by: 1) the level of coexistence allowed within a host, 2) the potential for replacement infection when a novel strain challenges a resident strain within a host, and 3) strain conversion when a predominantly antibiotic-sensitive infection converts to a predominantly antibiotic-resistant infection due to selection within a host.

The extent of within-host strain coexistence can be characterized by 3 possibilities. The top cluster in Figure 1 represents coexistence occurring within a host with strains at even levels. This encompasses both the single-strain and superinfection model structures. Neither of these structures allows replacement infection or strain conversion. These structures differ in terms of reduced contagiousness when both strains are present in a host; the single-strain model assumes no such reduction, while the superinfection model does reduce contagiousness when a host is superinfected. The middle cluster in Figure 1 represents model structures that do not allow within-host coexistence, encompassing the exclusive infection and replacement infection model structures. These structures also do not allow strain conversion. These 2 structures differ when a novel strain challenges an infected host; in the exclusive infection model, the novel strain may not infect and replace the resident strain, while in the replacement infection model it may. Finally, the bottom cluster in Figure 1 represents model structures for which within-host coexistence occurs at uneven levels encompassing both the unidirectional and bidirectional conversion models. In these model structures, there is an implicit majority-minority relationship between the frequency of coexisting sensitive and resistant strains within a host. Neither of these structures allows for replacement infection, while both allow for strain conversion. This conversion can be in 1 direction (unidirectional), usually conversion of sensitive to resistant, or 2 directions (bidirectional), where predominantly sensitive infections may convert to resistant and vice versa.

State transitions and the parameters involved

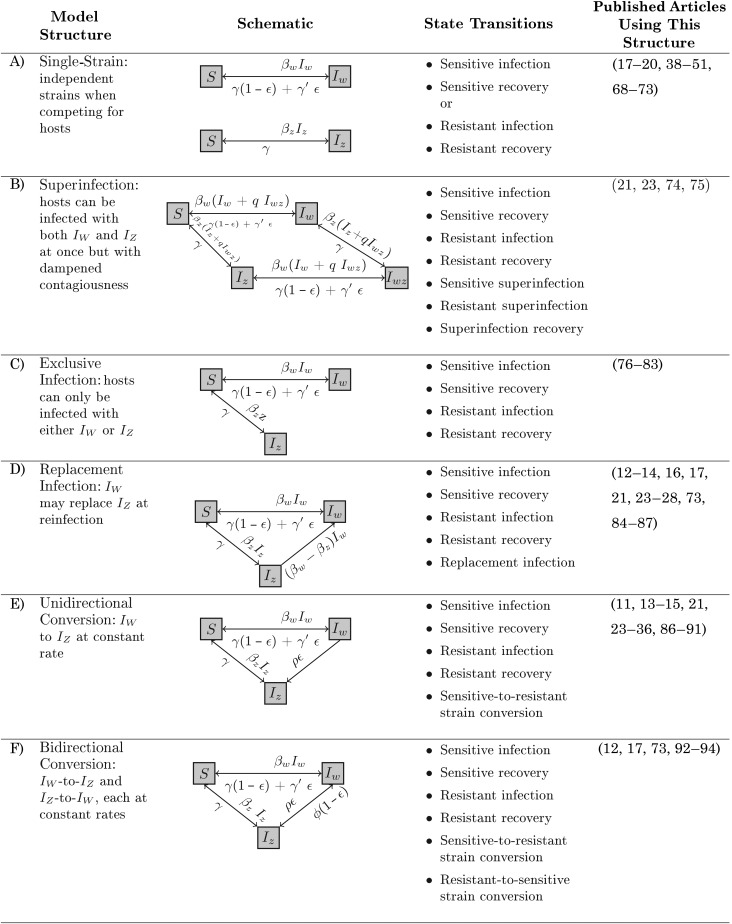
We constructed and analyzed the most generic forms of the model structures presented in Figure 1. To ensure code integrity, we used both Python 2.7.3 (www.python.org) and Mathematica 8 (http://www.wolfram.com/mathematica/) in this process. The first and second columns of Figure 2 provide a description of each model structure as well as a schematic. In these models, hosts belong in one of 4 states: susceptible (S); infectious with antibiotic-sensitive bacteria (I_W); infectious with antibiotic-resistant bacteria (I_Z); and superinfected, dually infected with both sensitive and resistant strains (I_WZ). These models characterize the transition between the 4 possible states using differential equations. The third column of Figure 2 lists the transitions between states for each structure. The final column of Figure 2 lists the published articles from the literature that used each model structure. Each model structure is composed of 2 or more of the 10 types of state transitions described below. The section of the Web Appendix (available at http://aje.oxfordjournals.org/) entitled “Differential equation formulations” has greater detail on each model structure.

Figure 2.

Structures of antibiotic-resistance transmission models used in the literature on between-host antibiotic-resistance modeling, 1993–2011. Each category is defined by its assumptions related to within-host strain coexistence, replacement infection, and strain conversion. Shown are model schematics, the state transitions for each model structure, and the reference numbers of the published articles that used each model structure.

Sensitive infection (S to I_W)

Transmission of antibiotic-sensitive bacteria results from a mass-action process, the product of the densities of people in the S and I_W states and the transmission parameter β_w, assumed to be specific to the sensitive strain.

Resistant infection (S to I_Z)

Transmission of antibiotic-resistant bacteria results from a mass-action process, the product of the densities of people in the S and I_Z states and the transmission parameter β_z, assumed to be specific to the resistant strain. In subsequent analyses, we assume that β_z is smaller than β_w as one way to show that the resistant strain is less fit than the sensitive strain in the absence of antibiotics. Our analysis also considers the condition where β_z and β_w are equal.

Sensitive recovery (I_W to S)

Recovery from infection with the antibiotic-sensitive strain occurs at a constant rate and is modified by the population antibiotic treatment level. Thus, if there is no antibiotic treatment in a population, recovery occurs at the innate recovery rate γ. If the entire population is receiving antibiotic treatment, recovery occurs at a faster rate defined by γ′. When some fraction of the population is taking antibiotics at one time, we assume that the recovery rate from I_W is a function of γ, γ′, and the proportion of the population receiving antibiotic treatment, ε:

Resistant recovery (I_Z to S)

Recovery from infection with the antibiotic-resistant strain occurs at a constant rate, γ, that is not modified by antibiotic treatment.

Resistant superinfection (I_W to I_WZ)

Superinfection transitioning from I_W to I_WZ results from a mass-action process, with the following force of infection:

where q determines the contagiousness of a superinfected host. If q = 0.5, each strain in a superinfected host is excreted at half the rate of that in hosts who are infected with only 1 strain (I_W or I_Z). If q = 1, the contagiousness of each of the strains from a superinfected host is identical to the contagiousness of monoinfected hosts; however, this superinfected host is in effect excreting for 2 people and therefore would be twice as contagious as a monoinfected host.

One biological interpretation of q is the site-specificity of each strain. If the sensitive and resistant strains each infect completely distinct sites, we would expect the value of q to be at or near 1. In this case, the presence of one strain would not use up potential sites for the other; because of this, shedding of both strains would not be altered from the situation where only 1 of the strains is present. If the strains colonize and infect identical sites while still coexisting, the value of q would be at or near 0.5. In this case, the presence of one strain uses up sites that the other would have potentially used; if each strain uses roughly half of the sites (i.e., if there is no fitness advantage of one over the other at this level), we would expect the shedding resulting from each strain to be halved compared with the situation where there is only 1 strain present. If there is somehow antagonism resulting in decreased shedding when both strains are present, the value of q would be less than 0.5.

Sensitive superinfection (I_Z to I_WZ)

Superinfection transitioning from I_Z to I_WZ results from a mass-action process, the product of β_w and (I_W + qI_WZ).

Superinfection recovery (I_WZ to I_W or I_Z)

Recovery from superinfection occurs with loss of one strain at a time (either sensitive or resistant), at rates identical to recovery from each strain alone, determined by γ, γ′, and ε.

Replacement infection (I_Z to I_W)

Replacement infection results from a mass-action process, the product of the densities of people in the I_W and I_Z states and either β_w, if I_W is replacing I_Z, or β_z, if I_Z is replacing I_W. If replacement in both directions is allowed, some replacement will be canceled out by replacement in the opposite direction. The net flow (i.e., the difference between the two) reduces to

In this example, where replacement is allowed in both directions, the strain with the greater β determines the replacement direction. If we assume that the sensitive strain has a higher transmission rate, it may replace the resistant strain.

Sensitive-to-resistant conversion (I_W to I_Z)

Strain conversion from sensitive to resistant depends on population antibiotic treatment ε and the rate at which resistant strains out-compete sensitive strains in the presence of antibiotics, the amplification rate ρ. Underlying this is an assumed mixed infection, composed predominantly of sensitive strains but with a small minority of resistant strains. Under the presence of antibiotics, the resistant minority of bacteria within the host take over at rate ρ as a function of the resistant strain replication rate, the reduced sensitive strain replication rate, and the death rate of sensitive bacteria from antibiotic exposure. This mixed infection could result from either 1) reinfection with 1 or more strains; 2) initial infection with a heterogeneous bacterial population, some with and some without the resistance trait, rather than a homogeneously sensitive population; or 3) de novo within-host resistance acquisition via either mutation or plasmid transfer. In our work, we assume that a mixed infection is already present when strain conversion operates.

One example of resistant conversion is the antibiotic treatment failure of M. tuberculosis (22). Conversion occurs within a host through selection for preexisting resistant agents. A ripe context for resistant conversion is set through poor adherence to treatment protocol, combined with the slow replication rate of the agent; this can effectively expose hosts to no therapy when they are receiving monotherapy or, more importantly for multidrug resistance, to monotherapy when receiving multidrug therapy.

Resistant-to-sensitive conversion (I_Z to I_W)

Strain conversion from resistant to sensitive occurs in a fashion complimentary to conversion from sensitive to resistant. This rate is determined by the product of the proportion of the population not receiving antibiotic treatment, (1 − ε), and the rate parameter φ. φ is interpreted similarly to ρ: Assuming that there is a mixed infection composed predominantly of resistant bacteria with a minority of sensitive bacteria, the absence of antibiotic treatment results in the sensitive bacteria's out-competing the resistant bacteria until they become the predominant strain at rate φ. Here φ is a function of differential replication rates between antibiotic-resistant and -sensitive bacteria, given the absence of antibiotic exposure. The mechanism underlying loss of resistance may operate either through backwards mutation or plasmid loss; again, we leave the modeling of this mechanism to others and assume that when there is sensitive conversion, there is a preexisting mixed infection.

The reverse-mutation rate is slower than the compensatory mutation rate that improves the fitness of a resistant agent in the absence of antibiotics (9). This leads many to argue that emergence of sensitivity from a population that is homogeneously resistant is unlikely. However, this argument only pertains to the emergence of a sensitive strain; the conversion models we use assume that there is always a sensitive minority strain in a majority-resistant infection, and that therefore conversion is still possible.

RESULTS

Choice of model structure varies in the literature

In our analysis, although model structure choice was clustered into a few structures across all articles, the degree of consensus varied by the agent studied (Table 1). The majority of articles (11 of 13) modeling M. tuberculosis resistance used unidirectional conversion models (11, 14, 23–31) allowing for de novo mutation to arise and confer resistance, subsequently outcompeting sensitive strains. Seven of these 11 articles, in addition to strain conversion, also incorporated replacement infection (14, 23–28), allowing a latent sensitive or resistant tuberculosis strain to be replaced by a novel strain. Articles modeling S. pneumoniae often (8 of 13) used unidirectional conversion models, relating to the agent's incremental acquisition of penicillin resistance (15, 32–37); this can be thought of as an extension of the unidirectional conversion resistance acquisition mechanism of M. tuberculosis, where multiple mutations lead to greater resistance, rather than a dichotomous status of sensitive or resistant. Resistance to penicillin, therefore, was modeled as an incremental point mutation process that increases the minimum inhibitory concentration of the resulting strain. Most articles modeling Enterococcus or S. aureus resistance (17 of 23) used single-strain models (7, 18, 19, 38–51), ignoring all competition and assuming independence between sensitive and resistant strains, focusing on transmission of either vancomycin-resistant enterococci or methicillin-resistant S. aureus (MRSA) in isolation.

Table 1.

Characteristics of Articles on Modeling of Between-host Antibiotic Resistance Published From 1993 Through 2011, by Agent Studied and Model Structure Used

Agent	Model Structure
	Single- Strain	Superinfection	Exclusive Infection	Replacement Infection	Unidirectional Conversion	Bidirectional Conversion	Replacement Infection, Unidirectional Conversion	Replacement Infection, Bidirectional Conversion	Replacement Infection, Unidirectional Conversion, Superinfection
Mycobacterium tuberculosis	1	0	1	0	4	0	6	0	1
Streptococcus pneumoniae	1	1	2	0	6	1	0	0	2
Staphyloccus aureus (MRSA)	9	1	2	1	0	0	0	0	0
Enterococcus (VRE)	14	0	1	1	0	2	0	0	0
Unnamed nosocomial agents	3	0	3	1	0	1	0	1	0

Abbreviations: MRSA, methicillin-resistant Staphylococcus aureus; VRE, vancomycin-resistant Enterococcus.

Choice of model structure infers types of competition

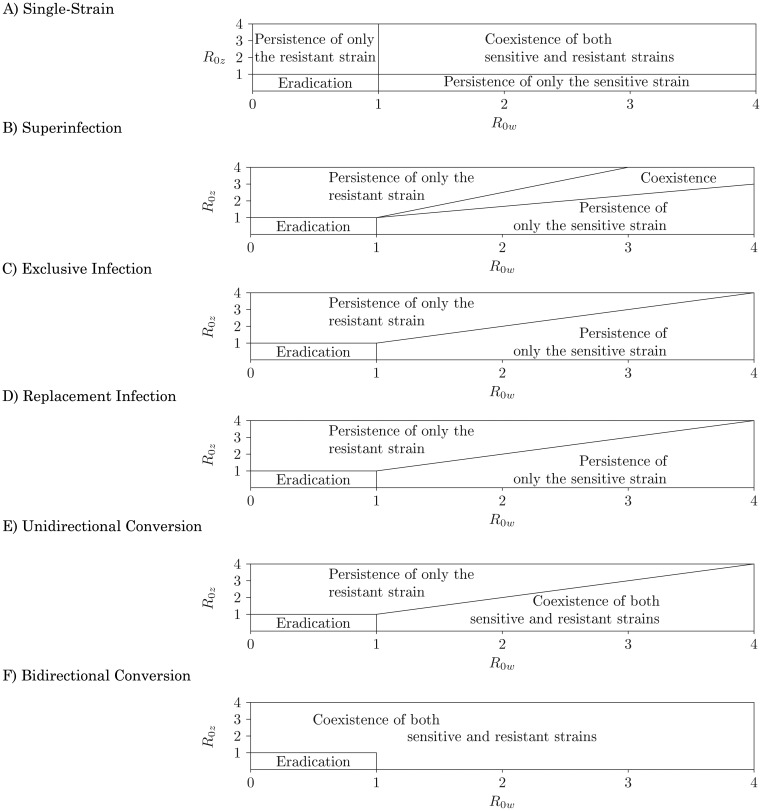
Both within- and between-host competition affects the resulting possibility of coexistence of both strains or persistence of only one strain or the other. Figure 3 represents the global properties of the models as a function of strain-specific R₀'s. These R₀'s are a function of all transmission parameters (Table 2), including the treatment prevalence, ɛ. Population-level strain coexistence is not possible when there is no within-host coexistence. In 2 model structures (exclusive infection, replacement infection) there is no within-host coexistence, and thus there is no possibility for population-level coexistence. In 4 model structures (single-strain, superinfection, unidirectional conversion, and bidirectional conversion), there is some degree of within-host strain coexistence that allows for the potential for population-level coexistence. Both of these cases are the dynamic consequence of within-host competition mechanisms. This section provides an understanding of these dynamic phenomena through a discussion of strain competition in each model structure.

Figure 3.

Bifurcation diagrams of competition between antibiotic-sensitive (I_W) and antibiotic-resistant (I_Z) bacterial strains for 6 model structures. Each axis represents a strain-specific R₀, calculated in the absence of the competing strain (see Web Appendix). Model structure alters the result of competition between sensitive and resistant strains across strain-specific transmission strengths.

Table 2.

Parameter Symbols and Values Used to Calculate the Equilibrium Prevalence of Antibiotic-sensitive and Antibiotic-resistant Strains of Bacteria for Each Model Structure Illustrated in Figure 4

Parameter	Explanation	Default Value	Unit
ε	Percentage of the population using antibiotics	Varied from 0% to 15%	%
βw	Transmission rate of the sensitive IW strain	0.04	t−1
βz	Transmission rate of the resistant IZ strain	0.015	t−1
γ	Innate recovery rate	0.01
γ′	Recovery rate from IW, assuming that antibiotics are being used	0.1	t−1
ρ	Conversion rate from IW to IZ, assuming that antibiotics are being used	0.5	t−1
φ	Conversion rate from IZ to IW, assuming that antibiotics are not being used	0.05	t−1
q	Contagiousness of each strain in superinfected hosts	0.5	Proportion

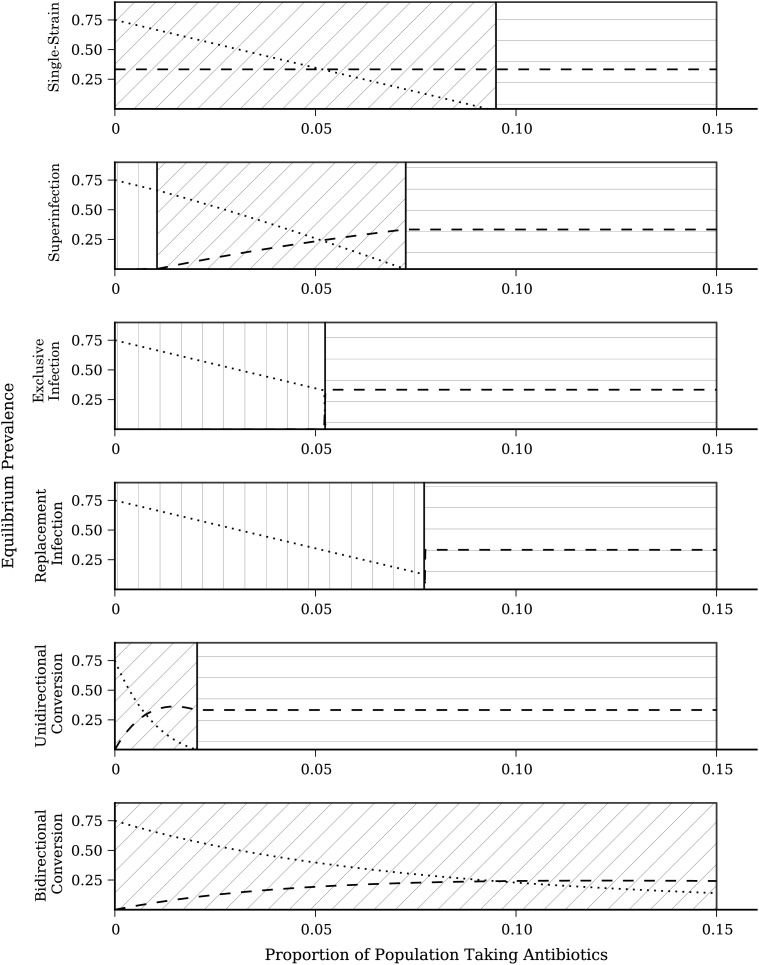
Equilibrium prevalence across model structures

To compare equilibrium prevalence across model structures, we calculated the equilibrium prevalence of sensitive and resistant strains across a range of population antibiotic treatment levels (0 < ε < 0.15) (Figure 4), otherwise using identical parameter values. At ε = 0.05 there is strain coexistence in the single-strain, superinfection, and bidirectional conversion models, persistence of the resistant strain only in the exclusive infection and replacement infection models, and persistence of the resistant strain only in the unidirectional model. Thus, even if all parameter values are correctly estimated, inferences may be incorrect because of incorrect selection of model structure. Even when there is the same general inference (e.g., coexistence of sensitive and resistant strains), the equilibrium prevalence of each strain may differ between model structures.

Figure 4.

Equilibrium prevalence of antibiotic-sensitive (I_W) and antibiotic-resistant (I_Z) bacterial strains for 6 model structures. Dashed lines represent the prevalence of antibiotic-sensitive strains; dotted lines represent the prevalence of antibiotic-resistant strains. Parameter values are held constant across model forms (Table 2). The background hatching denotes regions of antibiotic treatment parameter space. Vertical hatching indicates a region where only the antibiotic-sensitive strain persists; diagonal hatching indicates a region where both strains coexist; and horizontal hatching indicates a region where only the antibiotic-resistant strain persists.

For additional detail discussing these results for each model structure, see the Web Appendix.

Agent features and choice of model structure

Constructing an antibiotic-resistance model that appropriately describes competition between antibiotic-sensitive and -resistant strains for a specific agent requires knowing whether within-host strain coexistence occurs, replacement infection is possible, and strain conversion is possible. Coexistence has been demonstrated for S. pneumoniae (52–54), M. tuberculosis (55–57), and S. aureus (58). In each of these examples, the coexistence of sensitive and resistant strains may occur at either even levels or uneven levels. As Balmer and Tanner explained (59), within-host competition can fall into one of 3 categories: competition for colonization sites or resources, apparent competition caused by a common predator to the strains as mediated by the host immune system, and direct interference in which strains excrete substances to harm one another. In our superinfection model, we model the within-host competition for resources with the parameter q. When q = 1, there is no competition between the strains, and the superinfection model becomes the single-strain model. When q = 0, the superinfection model becomes the exclusive infection model. The superinfection model, therefore, is only required when 0 < q < 1.

In contrast to coexistence, there is limited evidence to support replacement infection. Lipsitch et al. (54) found evidence counter to replacement infection for S. pneumoniae, since resident strain levels within a host were not affected by infection with a challenging strain. Although models commonly assume that replacement infection is possible for M. tuberculosis, it is not clear whether a strain latently infecting a host is pushed out by a challenging strain. In addition to replacement infection, where the challenging strain pushes out the original resident strain, reinfection can occur when 1) both strains coexist at similar levels in the host (single-strain and superinfection models) or 2) the challenging strain persists only as a small minority. The unidirectional and bidirectional conversion models may reflect this last category, but here we have not modeled the actual reinfection process that leads to this kind of mixed infection, although others have (21).

Better data exist for characterizing strain conversion. The emergence of penicillin resistance in S. pneumoniae results from repeated point mutations conferring incremental increases in resistance and gradual subsequent strain conversion (60). For M. tuberculosis, treatment failure of a sensitive infection can result in resistance emergence through de novo chromosomal mutation and subsequent within-host strain conversion (61).

Strain conversion requires a mixed infection resulting from mutation, plasmid acquisition or loss, or reinfection; this mixed infection can have strains either at even levels or in a majority-minority relationship. The group of articles on S. pneumoniae models published by Temime et al. (15, 32, 33) and Opatowski et al. (35, 36) presents one example of strain conversion, in which a sensitive strain gradually becomes more resistant as a result of repeated point mutations. The M. tuberculosis models of Blower et al. (14, 29, 31), among other articles, similarly show conversion of a sensitive strain to a resistant strain resulting from antibiotic treatment failure. Additionally, one must assess the likelihood of resistance loss (conversion in the opposite direction). There is growing empirical evidence (62) suggesting that reversibility is unlikely, possibly because of resistant strains' acquiring additional compensatory mechanisms (perhaps through de novo mutation) to increase and bring even their within-host fitness with antibiotic-sensitive strains in the absence of antibiotic pressure (9).

An additional consideration when choosing a model structure is whether the pathogen is obligate or opportunistic. Most interventions that focus on obligate pathogens (e.g., tuberculosis, salmonella, etc.) decrease the circulation of all pathogen strains associated with particular agents, including antibiotic-resistant and -sensitive strains. When applying antibiotic treatment, however, strain differences become apparent because of the differential effectiveness of antibiotics across resistant and sensitive strains. When antibiotic use is not the focus, single-strain models can make sense for obligate pathogens. On the other hand, it may be important for strain conversion, particularly for tuberculosis, to account for the possibility of treatment failure.

Opportunistic agents such as S. pneumoniae, S. aureus, and Escherichia coli do not always cause disease when there is colonization. For E. coli, it may even be helpful to the host to keep sensitive strains around. When opportunistic agents cause disease, effective antibiotic treatment is necessary. Thus, it may be advantageous to minimize the prevalence of resistance while remaining indifferent to or protecting sensitive strains. Under these circumstances, using multistrain models to inform strain-specific interventions is important if we are interested in preserving levels of sensitive agents.

While we focused here on competition between agents of the same bacterial species, this work could be expanded to model competition or synergism between multiple species. For example, using the superinfection model, we have shown that when q = 1, two species would be assumed to be independent of one another within a host, and when q < 1, they would antagonistically interact, reducing contagiousness; additionally, the two species could interact synergistically, each making the other more contagious within a host, by setting q > 1. Polymicrobial interactions have recently been implicated in the emergence of vancomycin-resistant S. aureus through biofilm interaction with Candida albicans (63, 64). These agents not only affect each other's resistance status but also may affect growth and excretion of one another synergistically, as suggested by synergistic mortality increases in mice (65–67).

CONCLUSION

Models provide insight into the effect of interventions given a set of underlying mechanistic assumptions. Different biological mechanisms of within-host competition allow for different intervention targets and considerations. For example, a primary assumption of single-strain MRSA models is that MRSA emergence occurs outside a hospital, entering the hospital via importation. Only a model with competing strains can provide mechanisms of MRSA emergence. These multistrain models also provide mechanisms in which antibiotic use affects the prevalence of MRSA, relative to methicillin-sensitive S. aureus (MSSA). When developing strategies to control MRSA based on a single-strain model, the assumption is that there is no competition between MRSA and MSSA. Intervention strategies assuming this model structure therefore focus on reducing transmission from persons infected with MRSA through nonpharmaceutical interventions such as hand hygiene, surface decontamination, and isolation that affect resistant and sensitive strains equally. Intervention in an exclusive infection model, on the other hand, allows for the possibility of MSSA to be used against MRSA. Thus, in addition to dampening MRSA transmission through nonpharmaceutical interventions, more judicious use of antibiotics can help promote MSSA transmission, forcing MRSA into extinction in a hospital. Intervention in a unidirectional conversion model not only takes into account transmission from MRSA-infected hosts but also accounts for hosts who convert from MSSA to MRSA; thus, control efforts would have to be broadened not only to persons with MRSA infection but also to those with MSSA.

The presence of strain coexistence, replacement infection, and strain conversion affects the choice of model structure. Some may argue that not having sufficient data to parameterize a mechanistic model is a reason to ignore such a mechanism in a model analysis. However, excluding a potentially important mechanism for the purpose of making a conservative inference has the opposite effect; it hides uncertainty through omission, rather than showing the uncertainty up front as would happen if the mechanism were included. With increasing concern about the spread of antibiotic resistance and increasing use of mathematical models to better understand the mechanisms behind this spread, it is timely to put forth a framework that can help guide model choice for future analyses.