Microsecond folding dynamics of the F13W G29A mutant of the B domain of staphylococcal protein A by laser-induced temperature jump

Abstract

The small size (58 residues) and simple structure of the B domain of staphylococcal protein A (BdpA) have led to this domain being a paradigm for theoretical studies of folding. Experimental studies of the folding of BdpA have been limited by the rapidity of its folding kinetics. We report the folding kinetics of a fluorescent mutant of BdpA (G29A F13W), named F13W^*, using nanosecond laser-induced temperature jump experiments. Automation of the apparatus has permitted large data sets to be acquired that provide excellent signal-to-noise ratio over a wide range of experimental conditions. By measuring the temperature and denaturant dependence of equilibrium and kinetic data for F13W^*, we show that thermodynamic modeling of multidimensional equilibrium and kinetic surfaces is a robust method that allows reliable extrapolation of rate constants to regions of the folding landscape not directly accessible experimentally. The results reveal that F13W^* is the fastest-folding protein of its size studied to date, with a maximum folding rate constant at 0 M guanidinium chloride and 45°C of 249,000 s^-1. Assuming the single-exponential kinetics represent barrier-limited folding, these data limit the value for the preexponential factor for folding of this protein to at least ≈2 × 10⁶ s^-1.

Small single-domain proteins that fold with simple two-state kinetics have played an important role both experimentally and in theory/simulations for delineating models for folding (1-9). While folding with two-state kinetics, this set of proteins fold over a wide range of time scales ranging from 1.2 s^-1 at 37°C for the α/β protein MerP (10) to 8,100 s^-1 at 37°C for the β-sheet WW domain, hYap (11). Small single-domain helical proteins are expected to fold rapidly (12). Accordingly, the wild type (WT) B domain of staphylococcal protein A (BdpA) folds with a rate constant of 120,000 s^-1 at 37°C (13), whereas the designed miniprotein BBA5 has a folding rate constant of 130,000 s^-1 at 25°C (14).

Proteins that fold rapidly on a time scale that approaches that of molecular dynamics simulations provide a unique opportunity for direct comparison of experiment and simulation (14, 15). In addition, studies of rapidly folding proteins can guide estimates of the preexponential factor v^† in a Kramer's description of protein folding. In chemical reaction kinetics, the breaking of covalent bonds in a gas-phase reaction is described with a value for ν^† on the order of 10¹¹ to 10¹³ s^-1. However, this value is not suitable to describe a complex system of noncovalent interactions such as those involved in protein folding. Moreover, ν^† may vary between proteins and may change as folding progresses. Direct experimental measurement of rates close to the magnitude of ν^† for proteins is now becoming possible using laser-induced temperature-jump (T jump) experiments (16). Observations of the folding of small unstructured peptides have provided an estimate for ν^† in the range of 10⁷ to 10⁸ s^-1 (17-19), whereas experiments on the 66-residue cold-shock protein B have suggested an upper limit of 5,000 s^-1 (20). Theoretical computations for the five-helix protein, λ repressor (λ_6-85), suggest a value for of ν^† ≈ 2 × 10⁶ s^-1 (21), whereas recent experimental observations of biexponential folding kinetics of λ_6-85 (16) and a 35-residue subdomain of villin headpiece suggest an upper limit for these proteins of the order 5 × 10⁵ s^-1 (22).

The small size (58 residues) and simple topology of the three-helix protein BdpA have led to this domain becoming a paradigm for theoretical studies of protein folding (23-31). Although differing in detail, these studies have suggested that BdpA folds via a diffusion-collision mechanism, in which both native and nonnative long-range contacts form as the protein progresses toward the native state. Experimental studies of BdpA folding using NMR line-shape analysis have shown that the protein folds extremely rapidly with apparent two-state kinetics (120,000 s^-1 at 37°C) (13). Here we report on the folding kinetics of a fluorescent mutant of BdpA (G29A F13W), named F13W^*, using nanosecond laser-induced T jump experiments. This mutant was designed to fold more rapidly than the WT protein by increasing the helical propensity of helix II and decreasing the entropy of the denatured state. Phe-13 was also substituted with Trp to provide a fluorescence probe of folding (Fig. 1) (32). By measuring both the temperature and denaturant dependence of the folding and unfolding rate constants, we present kinetic landscapes for F13W^* and show that this protein has a maximum folding rate constant in 0 M guanidinium chloride (GuHCl) and at 45°C of 249,000 s^-1. Assuming that the single-exponential relaxation kinetics that are observed for this protein under all conditions reflect barrier-limited folding, these data suggest a minimum value for the preexponential factor of this protein on the order of 2 × 10⁶ s^-1.

Fig. 1.

Structure of BdpA showing the position of the tryptophan residue substituted for Phe at position 13 to provide a fluorescence probe. Gly-29 was also mutated to Ala in this study. The figure is based on the WT crystal structure with PDB coordinates 1BDD, and the mutations were incorporated by using swiss model (www.expasy.org/swissmod/SWISS-MODEL.html).

Materials and Methods

Protein Preparation. The gene encoding F13W^* was created from the gene encoding WT BdpA by using the QuikChange procedure (Qiagen, Chatsworth, CA). DNA sequencing confirmed the gene contained the desired mutations and no others. F13W^* was overexpressed (in the plasmid pAED4) in Escherichia coli BL21 (DE3) cells, as described (13). Pure protein (50-100 mg/liter) was obtained. F13W^* was shown to be pure by using analytical reverse-phase HPLC and SDS/PAGE and of the correct molecular weight by using electrospray ionization mass spectrometry.

Steady-State Equilibrium Measurements. To determine whether the F13W^* mutant of BdpA unfolds at equilibrium with a two-state transition, the protein was titrated with GuHCl and the denaturation of the protein monitored by using far UV CD (222 nm) and fluorescence (λ_ex 290 nm, λ_em 350 nm) at 37°C. CD experiments were performed on an Aviv (Lakewood, NJ) model 202 CD instrument equipped with a Peltier temperature controller and an automatic titrator (13). Fluorescence spectra were obtained by using an SLM model 8100 fluorimeter (SLM-Aminco, Urbana, IL). The data were normalized to the signals of the unfolded and native states (under these conditions, clear pre- and posttransition baselines are obtained) and plotted as the percent denatured state. The protein was also denatured thermally in 2.2 M GuHCl by using a temperature ramp from 2 to 94°C in 2°C increments. Denaturation was followed by far UV CD at 222 nm [by using a Jasco (Easton, MD) J-715 instrument] and tryptophan fluorescence (λ_ex 290 nm, λ_em 350 nm) [PTI (South Brunswick, NJ) Quantamaster C-61 spectrofluorimeter]. The data were normalized to the signals of the unfolded and native states. The data were fitted to a two-state model as described in ref. 33, from which the free energy of folding ΔG_UN and the corresponding GuHCl dependence of ΔG_UN (the equilibrium m value, M_UN) were determined.

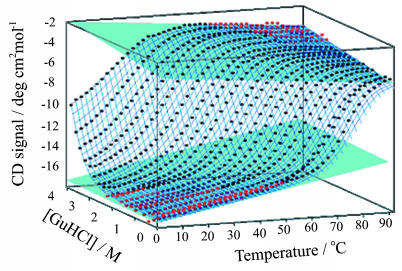
Mapping the Equilibrium Unfolding Free Energy Surface as a Function of Temperature and Denaturant Concentration. Correct interpretation of the T jump relaxation kinetics relies on the ability to determine accurate values for the thermodynamic stability of the protein over a wide range of temperatures and denaturant concentrations. Although under some conditions, analysis of denaturation data as a function of a single variable such as temperature can provide accurate values for ΔG_UN, under many conditions the pre- or posttransition baselines are insufficiently defined for accurate analysis. To overcome this problem, we have adopted an approach in which a 2D surface that is a function of temperature (T) and GuHCl concentration (C) is used (M. A. Daugherty, T. L. Calderone, and T.G.O., unpublished work). By using a surface fit in this manner, base planes (Fig. 3) are well defined in the high T, high C and low T, low C regions of the surface, and reliable equilibrium parameters can be obtained.

Fig. 3.

Equilibrium unfolding of F13W^* as a function of temperature and GuHCl concentration. Native and denatured base planes shown in blue are fitted to the data points shown in red to permit a global surface fit to the data (see Materials and Methods) yielding the thermodynamic parameters listed in Table 2.

A thermodynamic model was used to fit the surface as follows. The CD signal at any temperature and denaturant concentration Θ₂₂₂(T,C) is given by

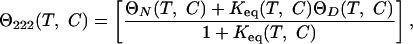1

where K_eq is the equilibrium constant, and Θ_N(T,C) and Θ_D(T,C) are the native and denatured base planes, respectively. These base planes are defined by

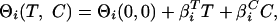2

where i = N for the native base plane, and i = D for the denatured base plane, Θ_i(0, 0) is a common point of reference for the native and denatured planes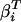, and and 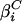are the temperature and denaturant dependencies, respectively, of the base planes. The free energy of folding ΔG_UN is considered a function of both T and C in the following manner:

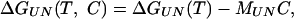3

where ΔG_UN(T) is the temperature dependence of the free energy in the absence of urea, and M_UN (the m value) is the denaturant dependence at a specific temperature. The m value may also have a temperature dependence M_UN(T) and therefore will have an associated temperature-dependent enthalpy h(T) and entropy s(T) (per mol denaturant, i.e., kJ/mol·M), which will themselves have a dependency c on heat capacity of the form

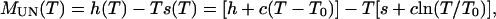4

where T_o is a temperature reference point. To avoid long extrapolations to 0 M GuHCl, a convenient reference condition is set at an intermediate value of temperature and denaturant concentration, referred to as T_hs and C_hs, at which ΔH_UN (T_hs, C_hs) = ΔS_UN (T_hs, C_hs) = 0. The temperature dependence of the change in free energy of folding is therefore given by

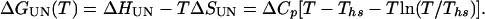5

Combining Eqs. 3-5 yields an expression that describes the free energy of folding of a two-state protein with respect to temperature and denaturant concentration,

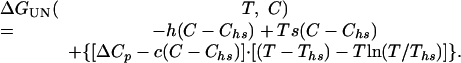6

The fluorescence intensity has a strong temperature dependence, therefore CD was used to follow the thermal denaturation of F13W^* with respect to temperature and GuHCl concentration. Samples at a concentration of ≈15 μM (0.1 mg/ml) in buffer A (20 mM sodium acetate, pH 5.0, containing 100 mM sodium chloride) were incubated at different temperatures in 1-mm path-length cells. Samples were equilibrated for 3 min at each temperature before the CD signal was averaged over a 3-min data collection period. Twenty samples at GuHCl concentrations ranging from 0 to 4.0 M in 0.2 M increments were each incubated from 2 to 94°C in 2°C increments. The resulting data (Fig. 3) were fitted by Eq. 6 by using igor pro 4 (Wave-metrics, Lake Oswego, OR). The data were weighted by using statistical errors calculated at each point from the standard deviation of the average of the CD signal. The dependence c of the m value on heat capacity in Eq. 6 was held equal to zero with no detrimental effect on the quality of the fit, i.e., it was assumed there was no denaturant dependence of ΔC_p. The fitting procedure returned parameters T_hs, C_hs, ΔC_p, h, and s. This analysis allows the equilibrium constant at any temperature or denaturant concentration between 0-100°C and 0-4 M GuHCl to be accurately determined.

T Jump Kinetic Measurements. A T jump apparatus was constructed, based on the design of Gruebele and coworkers (34). The apparatus is capable of generating up to a 25°C increase in sample temperature in 8 ns. The T jump is generated by Raman shifting the 1,064-nm output (1 J per pulse) of a Q switched Nd:YAG laser [Continuum (Santa Clara, CA) Surelite III] in a 1-m-length stainless steel tube of methane at 30 atm (1 atm = 101.3 kPa) to produce an infrared pulse at 1,550 nm with 10-30% conversion efficiency. The protein sample is contained in a quartz cell of path length 0.5 mm [Custom (Custom LC, Hellma, U.K.], thermostated by a Peltier device and Peltier controller [Marlow (Dallas) SE5010] to maintain the sample at constant temperature in the range 0-90 ± 0.1°C. The sample cell is housed in a chamber, which can be evacuated to prevent condensation on optical surfaces. The relaxation kinetics of F13W^* after the T jump were monitored by the change in intrinsic fluorescence intensity of Trp-13. Fluorescence was excited at 287 nm by using <1 mW of the frequency tripled output of a femtosecond mode-locked Ti:Sapphire laser [Coherent (Santa Clara, CA) Mira 900/Verdi V10]. The mode-locked output at 37 MHz was pulse picked to give a pulse separation of ≈130 ns and a pulse width of <200 fs. Fluorescence at the emission λ_max of F13W^* (≈340-350 nm) was selected by using a long-pass filter with cut-off at 310 nm [CVI Optics, Albuquerque, NM] and detected by using a photomultiplier tube (PMT) [Hamamatsu (Hamamatsu City, Japan) R7400U-03] with custom dynode chain. The PMT output signal was digitized by using a digital sampling oscilloscope with a sampling rate of 8GS/s [LeCroy (Chestnut Ridge, NY) LC584AXL]. In the experiments described here, the integrated intensity of 50 consecutive fluorescence pulses was averaged, giving a time resolution of 6.5 μs, and a good signal-to-noise ratio was achieved by averaging 50 experiments of identical T jump magnitude (±0.2°C) (see below). The Q switched laser, a shutter to prevent the sample from photobleaching, an infrared energy meter to measure the size of the T jump, the oscilloscope, and preliminary data analyses were all automated by using control software written in igor pro 4. The relaxation kinetics were measured for up to 12 final temperatures between 10 and 80°C, after T jumps of typically 10°C (±0.5°C) at each of 16 different GuHCl concentrations between 0 and 4 M.

The dead time of the experiment depends on scattered light caused by cavitation after each T jump. A T jump of 10°C was found to give the best tradeoff between signal amplitude change and cavitation for most experiments, resulting in a typical dead time of 5-40 μs, depending on the final temperature of the solution after the T jump. To measure more rapid relaxation kinetics (experiments at 0 M GuHCl at final temperatures of 76 and 80°C), a 5°C T jump was used. In this case, the dead time was approximately the time resolution between two UV pulses (≈130 ns), and 5,000 jumps per final temperature were averaged.

The magnitude of each T jump was determined by splitting off a fraction of each infrared heating pulse onto an energy meter (Coherent Fieldmaster GS with LM-PSLP head), which was calibrated for each experiment by using the temperature-dependent change in fluorescence lifetime of N-acetyl-tryptophan-amide after T jumps.

Analysis of T Jump Kinetic Measurements. All relaxation kinetics were well described by a single exponential decay defined by the observed kinetic rate constant k_obs. The folding and unfolding rate constants k_f and k_u were determined by combining the observed kinetic rate constant k_obs with the equilibrium constants K_eq obtained from the thermodynamic fit to the equilibrium CD data described above.

The kinetic data were fitted to a Kramers model, where the activation free energy for folding ΔG^† is given as a function of temperature and denaturant concentration. The preexponential factor ν^† was assumed to be viscosity and temperature independent and was given a value of 5 × 10⁵ s^-1 (11). An expression similar to that used for the free energy of folding (Eq. 6) is used to describe the free energy of activation. However, the enthalpy of 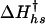and entropy 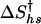of activation at T_hs and C_hs are nonzero, hence the free energy of activation is given by

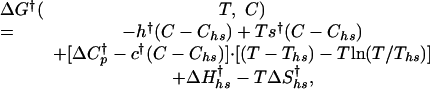7

where the crossed parameters are analogous to those in the equilibrium description of Eq. 6 but refer to changes between the denatured or the native state and the transition state when calculating k_f and k_u, respectively.

The uncertainties in the kinetic folding rate constants were calculated from the standard deviation of the observed rate constants (k_obs) from 50 experiments. A weighted fit of the folding and unfolding rate constant surface shown in Fig. 5 by using Eq. 7 was performed with values of T_hs = -9.33°C and C_hs = 4.15 M determined from the equilibrium data (see Table 2, which is published as supporting information on the PNAS web site). The fit to the kinetic data yields parameters 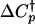, h^†, s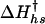^†, , and 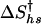c^† is held equal to zero, because it is assumed there is no curvature in the temperature dependence of the activation m values.

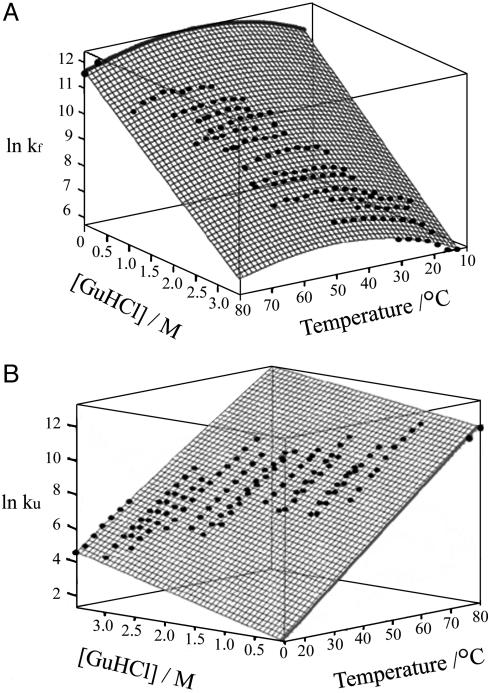
Fig. 5.

Kinetic folding and unfolding surfaces of F13W^*. Shown are k_f (A) and k_u (B) as a function of GuHCl concentration and temperature. The surfaces are fitted to the thermodynamic model described in Materials and Methods. The thick black lines are the extrapolated fits to 0 M GuHCl. The data points at 0 M GuHCl and final temperatures of 76°C and 80°C were determined in a separate pair of T jump experiments and were not used in the fitting of the kinetic surfaces.

Results and Discussion

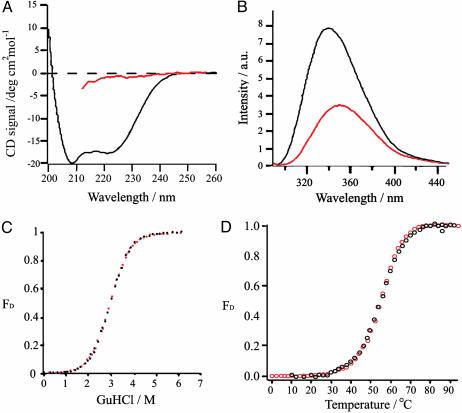
Equilibrium Thermal and Chemical Denaturation of F13W^* Is Two-State. The far UV CD and fluorescence emission spectra of F13W^* in the native state and denatured in 6 M GuHCl are shown in Fig. 2 A and B. Akin to the WT protein (13), the mutant protein is also highly helical and the newly introduced tryptophan residue is buried (λ_max of 340 nm). In 6 M GuHCl, F13W^* unfolds to a species that lacks helical structure, and the tryptophan side chain becomes more exposed (λ_max increases to 350 nm and the fluorescence decreases to ≈60% of the native intensity). WT BdpA unfolds with a two-state transition (13). To determine whether this is the case for F13W^*, the mutant protein was titrated with GuHCl, and denaturation was monitored by both far UV CD (at 222 nm) and by fluorescence intensity (at 350 nm). The data (Fig. 2C) demonstrate that equilibrium unfolding of F13W^* is two state under these conditions. Fitting the data in Fig. 2C to a two-state model (33) yields a ΔG_UN of 17.6 ± 0.8 kJ/mol and M_UN of 5.98 ± 0.42 kJ/mol·M. Overall, therefore, the mutations have little effect on the thermodynamic stability of BdpA (ΔG_UN = 17.9 ± 0.8 kJ/mol for the WT protein) or on the relative compactness of the native and denatured states [M_UN for the WT protein under identical conditions = 6.27 ± 0.42 kJ/mol·M (13)]. CD and fluorescence data in Fig. 2D confirm that F13W^* also undergoes a two-state thermal unfolding transition.

Fig. 2.

Equilibrium unfolding of F13W^* is two-state. (A) CD spectra of F13W^* in 0 M GuHCl (black) and 6 M GuHCl (red). (B) Fluorescence emission spectra (λ_ex = 290 nm) in 0 M (black) and 6 M (red) GuHCl. (C) Equilibrium denaturation of F13W^* vs. GuHCl measured by using CD at 222 nm (red) and the fluorescence emission intensity at 350 nm (black). (D) Equilibrium denaturation of F13W^* vs. temperature in 2.2 M GuHCl by using CD at 222 nm (red) and the fluorescence emission intensity at 350 nm (black). The experiments in A-C were carried out in buffer A at 37°C. The experiment in D was carried out in buffer A containing 2.2 M GuHCl.

Mapping the Equilibrium Free Energy Surface of F13W^*. To obtain accurate values for the free energy of unfolding of F13W^*, the equilibrium unfolding surface of the protein was measured over a wide range of GuHCl concentrations (0-4 M) and temperatures (2-94°C). The equilibrium surface, fitted globally to the two-state model described by Eq. 6, is shown in Fig. 3. The model fits the data well under all conditions, and the fit parameters are summarized in Table 2. The ΔG_UN and M_UN resulting from the fit (Eq. 6) at different temperatures are shown in Table 1.

Table 1. Thermodynamic values for F13W^* in buffer A containing 0 M GuHCI as a function of temperature.

Temperature, °C	kf, × 103 s−1	ku, s−1	mf, kJ/mol·M	mu, kJ/mol·M	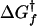, kJ/m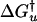ol	, kJ/mol′	MUN, kJ/mol·M	ΔGUN, kJ/mol
10	83 ± 12	2.5 ± 0.4	3.9 ± 0.8	2.3 ± 0.8	− 12.9 ± 4.7	37.4 ± 4.7	6.2 ± 0.1	24.5 ± 1.9
25	177 ± 26	30 ± 4.5	4.0 ± 0.8	2.1 ± 0.8	− 11.7 ± 4.8	33.2 ± 4.8	6.1 ± 0.1	21.5 ± 1.9
37	235 ± 35	211 ± 32	4.1 ± 0.9	1.9 ± 0.9	− 11.5 ± 4.9	29.6 ± 4.9	6.0 ± 0.1	18.1 ± 1.9
50	245 ± 38	1,640 ± 246	4.2 ± 0.9	1.7 ± 0.9	− 11.8 ± 5.0	25.3 ± 5.0	5.9 ± 0.1	13.4 ± 1.9
70	165 ± 25	34,640 ± 5,200	4.4 ± 0.9	1.5 ± 0.9	− 13.7 ± 5.0	18.1 ± 5.0	5.9 ± 0.1	4.5 ± 1.9

Data were obtained from the extrapolated fits of the kinetic data in Fig. 5 (m_s, m_u′ ΔG_S,⁺ ΔG_U⁺) by using the model in Eq. 7 and a value of v⁺ = 5 × 10⁵ s⁻¹ and from the equilibrium data in Fig. 3 (M_UN, ΔG_UN) by using the model in Eq. 6 (see Materials and Methods).

Because the reliability of the values for the kinetic rate constants obtained from the T jump data critically depends on the accuracy of the determination of the equilibrium constant, it is important to validate the results obtained by the surface-fitting approach. This was confirmed by comparing the thermodynamic values determined by using the surface fit with those obtained from a 1D fit of the GuHCl titration (M_UN and ΔG_UN) under conditions where the pre- and posttransition baselines are well defined [e.g., by GuHCl titration at 37°C (Fig. 2C)]. These approaches yielded values of M_UN of 6.1 ± 0.3 kJ/mol·M and 6.0 ± 0.4 kJ/mol·M, and values for ΔG_UN of 18.06 ± 2.1 kJ/mol and 17.6 ± 0.8 kJ/mol for the surface and 1D fits, respectively, demonstrating the consistency of the two approaches. The surface-fitting approach thus provides reliable and accurate values for K_eq, even in regions where the pre- or posttransition baselines are absent or poorly defined.

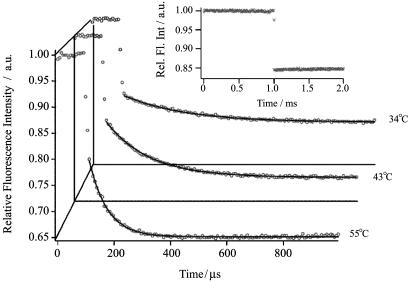
Mapping the Folding and Unfolding Free Energy Surfaces of F13W^* Using T Jump. Fig. 4 shows representative fluorescence relaxation traces for F13W^* after T jumps of 10°C to three different final temperatures in 2.6 M GuHCl. The data show an initial rapid decrease in fluorescence intensity, resulting from the temperature dependence of tryptophan fluorescence. This is also shown in the fluorescence change of N-acetyl tryptophan-amide after a similar T jump from 30°C to 40°C (Fig. 4 Inset). After the initial decrease in signal, the protein fluorescence decays with single-exponential kinetics, from which the observed relaxation rate constant, k_obs, was determined. In no case was there any evidence of more complex exponential decays in the kinetics of F13W^*.

Fig. 4.

Typical relaxation kinetics of F13W^* after T jumps of a magnitude of 10°C to 55°C, 43°C, and 34°C in 2.6 M GuHCl. Each trace represents the average of 50 experiments at the same final temperature, and each point represents the average integrated intensity of 50 consecutive fluorescent pulses that are separated by 130 ns, giving a final temporal resolution in this case of 6.5 μs. The data are normalized to the intensity of the protein fluorescence before the T jump. The relaxation kinetics are fitted to a single-exponential function (solid black lines). (Inset) The fluorescence intensity change of a sample of N-acetyl tryptophan-amide after a 10°C T jump to 50°C.

The relaxation kinetics of F13W^* were measured by T jump over a wide range of temperature and GuHCl concentration so that the folding and unfolding rate constants could be determined accurately by fitting the resulting kinetic surface according to the kinetic model in Eq. 7. Over 100 kinetic traces between 0.8 and 3.8 M GuHCl and 30-80°C were acquired, yielding the kinetic surface plot in Fig. 5. The natural logarithms of k_f and k_u determined from the surface fit are linearly dependent on GuHCl concentration over the range studied at all temperatures, supporting the use of a two-state model to fit the data.

To validate the reliability of the kinetic surface fits, the rates of folding and unfolding at 76 and 80°C in 0 M GuHCl were obtained experimentally by using 5°C T jumps [with a dead time of 130 ns (see Materials and Methods)] and compared with the rate constants predicted by the surface fit to these conditions. At both final temperatures, the measured values of k_u and k_f match precisely the extrapolated line at 0 M GuHCl, confirming the accuracy and validity of the rate constants over the entire surface shown in Fig. 5. The kinetic and thermodynamic parameters for the folding and unfolding of BdpA are shown in Table 1.

F13W^* Folding: Implications for Current Folding Models. The data in Fig. 5 show that F13W^* folds rapidly, with a folding rate constant in 0 M GuHCl at 37°C of 237,000 s^-1; at 45°C in 0 M GuHCl, the maximum folding rate constant is 249,000 s^-1. The data demonstrate, therefore, that F13W^* is the most rapidly folding protein discovered to date (Table 3, which is published as supporting information on the PNAS web site). The protein folds with remarkable rapidity, with a rate constant twice that of the WT protein under the same conditions (13) and more than four times that of the 61-aa all-helical engrailed homeodomain at 25°C (15). The increase in k_f observed for F13W^* relative to WT BdpA is consistent with the increase in helical propensity of helix II caused by substitution of G29 with Ala and the corresponding decrease in entropy of the denatured state (note that the substitution of Phe-13 with Trp has no effect on the hydrophobicity or helicity of helix I) (32). The data suggest, therefore, that helix II is formed in the rate-limiting transition state, consistent with theoretical models of how this protein folds (27).

The equilibrium and kinetic data allow the transition state for the folding of F13W^* to be defined with respect to two reaction coordinates. First, the entropic reaction coordinate (defined as 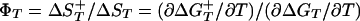, where 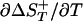is the entropy change associated with the transition from the native to the activated state, and ΔS_T is the entropy change associated with the equilibrium transition between the unfolded and native states). In the case of F13W^*, Φ_T varies between 0.14 and 0.28 over the temperature range studied in 0 M denaturant (using a preexponential factor of 5 × 10⁵ s^-1). The behavior of F13W^* is thus similar to the FBP WW domain for which Φ_T changes by a factor of two for a similar change in reaction temperature of 25°C (35). A second reaction coordinate is Φ_D = m_f/M_UN. At 37°C, Φ_D of F13W^* = 0.7 in both 0 M and 4 M GuHCl, demonstrating that the transition state for folding of F13W^* is relatively compact and independent of denaturant concentration.

At 45°C in 0 M GuHCl, F13W^* folds with a rate constant of 249,000 ± 38,000 s^-1. In a recent study of λ_6-85, Gruebele and coworkers suggest a lower limit for the folding preexponential of this protein of ν^† of 5 × 10⁵ s^-1 (16). Using this value, the ΔG^† for F13W^* at 37°C is -1.9 kJ/mol or 0.75 kT, which would place F13W^* in the regime of downhill folding. However, despite exploring a broad range of conditions, nonexponential kinetics, which are usually associated (36) with barrierless folding, were never observed. Assuming that F13W^* folds with barrier-limited kinetics with an activation barrier of at least 2 kT, our data place a lower limit for the preexponential factor of BdpA of ν^† ≈1.8 × 10⁶ s^-1, a value significantly greater than that of λ_6-85, consistent with the much simpler topology of BdpA. An alternative description of folding landscapes, recently presented by Plotkin and Wolynes (37), describes a buffed surface, which is only weakly funneled in the thermodynamic sense but has many small barriers to reconfigurational motion. Here the search through these shallow traps determines the folding rate constant. Such a landscape does not require the preexponential to be defined by a single activation barrier but is determined by the kinetic search through the many configurational transition states, each separated by a very small free energy difference. Such a model is predicted by Plotkin and Wolynes to be most likely for small proteins. Whether F13W^* folds in this manner remains unknown. Nonetheless, the ability to measure the rate constants of folding and unfolding accurately by using global analysis of the 3D kinetic and thermodynamic surfaces, as demonstrated here for F13W^*, now provides the opportunity to determine how and why this small helical protein folds so rapidly to its native state.

Note Added in Proof. A recent manuscript (38) has shown that the de novo designed three-helix protein α₃D folds rapidly to the native state with a folding time of 3.2 ± 1.2 μs at 50°C. These data also suggest that v⁺ ≈ 1 × 10⁶ s^-1. However, whereas the authors propose that the rapid folding of α₃D may be attributed to its de novo design sequence, the results presented here for F13W^* BdpA show that natural three-helix bundle proteins can also fold rapidly to their native state.