Using Empirical Phase Diagrams to Understand the Role of Intramolecular Dynamics in Immunoglobulin G Stability

Abstract

Understanding the relationship between protein dynamics and stability is of paramount importance to the fields of biology and pharmaceutics. Clarifying this relationship is complicated by the large amount of experimental data that must be generated and analyzed if motions that exist over the wide range of timescales are to be included. To address this issue, we propose an approach that utilizes a multidimensional vector-based empirical phase diagram (EPD) to analyze a set of dynamic results acquired across a temperature-pH perturbation plane. This approach is applied to a humanized immunoglobulin G1 (IgG1), a protein of major biological and pharmaceutical importance whose dynamic nature is linked to its multiple biological roles. Static and dynamic measurements are used to characterize the IgG and to construct both static and dynamic empirical phase diagrams. Between pH 5 and 8, a single, pH-dependent transition is observed that corresponds to thermal unfolding of the IgG. Under more acidic conditions, evidence exists for the formation of a more compact, aggregation resistant state of the immunoglobulin, known as A-form. The dynamics-based EPD presents a considerably more detailed pattern of apparent phase transitions over the temperature-pH plane. The utility and potential applications of this approach are discussed.

Introduction

Proteins are known to be inherently flexible in solution. They exist at equilibrium as a statistical ensemble of interconverting states, with the relative occupancy of these states corresponding to a Boltzmann distribution [1, 2]. These states differ from each other by conformational fluctuations and local unfolding and their dynamics can be approximated by periodic functions, such as harmonic oscillations and normal modes. When fluctuations occur in a concerted fashion, they give rise to a broad range of behavior from local motions, such as aromatic ring flips and bond isomerizations, to larger scale domain motions, such as substrate binding and allosteric rearrangement. The timescale of these motions generally ranges from picoseconds to minutes, though motions involving femtosecond and hour timescales have been reported [3-7].

The importance of protein motions to molecular recognition and enzymatic catalysis is well established [8-12]. Its relationship to stability, however, is not well understood. Lattice models suggest that protein fluctuations increase with temperature and that a reduced range of motions is sampled by more thermostable proteins [13-15]. A growing body of evidence, however, indicates that the relationship between protein dynamics and stability is far more complicated. It is now understood that many thermostable proteins are quite dynamic; moreover, an increase in thermostability does not necessitate a reduction in dynamics [16-21]. Nevertheless, it is reasonable to conclude that unfolding is preceded by an increase in fluctuations that contribute to protein destabilization. Both the nature of these destabilizing motions and their degree of conservation among protein homologues remain unknown.

From a practical standpoint, studying the relationship between protein stability and dynamics is complicated by the large amount of data that must be collected and analyzed during a comprehensive study. Studies of protein (de)stabilization require measurements to be taken over a wide range of one or more external perturbations, such as temperature and pH. Analysis of protein dynamics further increases the experimental demand, since multiple experiments are generally needed to cover the range of timescales over which protein motions occur. For a technique to be ideal given these requirements, it must be rapid and performable in the absence of sample modification. Once such studies are complete, identifying consistent and/or significant trends in the complex data sets can be challenging. To this end, we have developed an empirical phase diagram (EPD) based approach, which enables trends in multiple sets of data to be simultaneously visualized across a two-dimensional perturbation plane [22, 23]. EPDs have been successfully used to study conformational changes in a variety of biomacromolecules employing static measurements of protein stability [22-25]. To date, measurements of protein dynamics have not been included in EPDs.

Immunoglobulin G (IgG) molecules are a biologically and pharmaceutically important class of proteins whose highly dynamic nature makes them ideal for exploring the relationship between dynamics and stability. These antibodies play multiple roles in immune responses, including antigen recognition, complement activation, and effector stimulation. Immunoglobulins have an extended domain structure comprised of four disulphide-linked chains—two heavy (~ 50 kDa each) and two light (~ 22 kDa each). Each of the two antibody binding (Fab) regions contains a single light chain and an N-terminal portion of one of the heavy chains. The remaining C-terminal portion of the heavy chains forms the crystallizable (Fc) region and a flexible hinge region, which connects the Fc region to the two Fab regions. This results in a Y-shaped molecule in which the two Fab “arms” are highly mobile.

The hinge region is responsible for much of the dynamic behavior of immunoglobulins. Immunoglobulin flexibility is known to be intimately linked to biological activity and has been studied by a variety of methods [26-35]. The results of these studies strongly suggest that the presence of the hinge is at least partially responsible for the highly dynamic behavior of the immunoglobulin. Further evidence for intramolecular flexibility is found in the variable portion (Fv) of the Fab region where a significant reduction in backbone dynamics is observed upon antigen binding [34].

To further explore the relationship between protein dynamics and stability, we have performed a series of static and dynamic measurements of a humanized immunoglobulin G1 (IgG1κ) across a broad temperature-pH plane. The static measurements used include steady-state intrinsic fluorescence, far-UV circular dichroism (CD), light scattering, and ANS fluorescence. The main dynamic techniques employed are pressure perturbation calorimetry (PPC), high-resolution ultrasonic velocimetry (HR-US), red-edge excitation shifts (REES), and time-correlated single photon counting (TCSPC) fluorescence anisotropy. The data from these techniques have been used to create static and dynamic empirical phase diagrams and provide a unique picture of IgG dynamics.

Materials and Methods

Sample Preparation

The IgG1κ monoclonal antibody was provided by MedImmune, Inc. (Gaithersburg, MD). The protein was dialyzed using a 3.5 kDa MWCO membrane into 20 mM citrate-phosphate buffer with an ionic strength adjusted to 0.1 using NaCl and pH ranging from 3 to 8. Dialysis was carried out overnight at 4 °C. The protein concentration was calculated from the absorbance at 280 nm at 20.0 °C using an Agilent 8453 UV-Visible spectrophotometer (Palo Alto, CA) fitted with a Peltier temperature controller.

Analytical Ultracentrifugation

A Beckman ProteomeLab XL-A/XL-I analytical ultracentrifuge equipped with a scanning UV/visible optics system was used to conduct sedimentation velocity experiments at 20.0 °C as a function of pH. Samples were prepared at three concentrations (0.25, 0.50 and 0.75 mg/mL) and loaded into a BeckmanCoulter 12 mm flow-through centerpiece assembly with quartz windows. Ultracentrifugation was carried out using a four-position An 50 Ti rotor with a rotational speed of 40,000 rpm. Scans were conducted continuously. Data were analyzed using a continuous distribution model and SEDFIT version 9.3 [36].

Dynamic Light Scattering

Dynamic light scattering (DLS) was used to measure the effective particle size of the IgG at pH 3 and 6 over the temperature range 10 to 85 °C using a 10 °C/h temperature ramp. The experiments were conducted with a Brookhaven BI-9000AT digital autocorrelator and a BI-200SM goniometer (Brookhaven Instruments Corporation, Holtsville, NY) equipped with a 50 mW helium–neon diode laser operating at 532 nm. The data were collected at a 90° scattering angle. The sample concentration was 1 mg/mL. The results were analyzed using the method of cumulants, and the effective diameter was calculated using the Stokes–Einstein equation.

Steady-State Fluorescence Spectroscopy

Fluorescence studies were conducted with a two-channel, four-position PTI Quanta Master Spectrophotometer (Lawrenceville, NJ) with Peltier temperature control. All studies used a temperature ramp from 20.0 to 85.0 °C in 2.5 °C increments with a five minute equilibration time between temperature increases. The IgG concentration used in the fluorescence studies was 0.1 mg/mL. The sample was held in a 1 cm path length quartz cuvette, and the excitation and emission slit widths were set to 4 nm. Intrinsic fluorescence was produced by exciting at 295 nm (> 95% tryptophan emission) and measuring the emission from 300 to 450 nm. The buffer spectrum was subtracted from each sample spectrum, and the intrinsic fluorescence peak position was determined by first derivative analysis. The tryptophan fluorescence intensity was determined by linear interpolation of the emission data about the respective peak position. Static light scattering intensity was simultaneously monitored at 90 ° relative to the fluorescence excitation source using an emission slit width of 0.5 nm.

The fluorescent dye 1-anilino-8-napthalenesulfonate (ANS) was used to detect apolar sites that can result from conformational changes. The IgG concentration used was 0.1 mg/mL (~ 6.7 × 10^-4 mM), and ANS was added to a final concentration of ~ 1.3 × 10^–2 mM. The sample was held in a 1 cm path length quartz cuvette, and the excitation and emission slit widths were set to 4 nm. The samples were excited at 375 nm and the emission was measured from 400 to 600 nm. Sample spectra were corrected for background fluorescence from the very weakly fluorescent unbound ANS by subtracting the spectrum of ANS in buffer alone. The ANS fluorescence peak position was determined by first derivative analysis. The ANS fluorescence intensity was determined by interpolation of the emission data about the respective peak position.

Far-UV Circular Dichroism

Secondary structure was monitored using a Jasco J-720 spectrometer (Tokyo, Japan) equipped with Peltier temperature control. The IgG concentration was 0.2 mg/mL, and the measurements were made using a 0.1 cm path length quartz cuvette. Full spectra of the IgG were measured at 20.0 °C between 190 and 260 nm over the pH range 3–8. The effect of pH and temperature were measured by monitoring the ellipticity at 218 nm over the temperature range 20.0–90.0 °C with a temperature ramp rate of 15 °C/hr. The measurements employed a scanning speed of 50 nm/min, a response time of 1 sec, and a bandwidth of 1 nm. Sample spectra were corrected by subtraction of the buffer spectrum, and molar ellipticity was calculated using a molecular weight of 150 kDa.

Pressure Perturbation Calorimetry

The PPC measurements were performed on a VP-DSC microcalorimeter with a PPC accessory (MicroCal, Northhampton, MA). The sample and reference volumes were 0.5188 mL, and the protein concentration was 5 mg/mL. Both the sample and reference were degassed prior to measurement. Pressure perturbation calorimetry measures the differential heat between a reference and sample as a result of pressurization or depressurization. At each temperature (ranging from 20.0 to 100.0 °C in 2.5 °C increments), the sample underwent six cycles of ~ 5 atmospheres (gage) pressurization and depressurization. The coefficient of thermal expansion, α, defined as

$$\alpha =\left(\frac{1}{V}\right){\left(\frac{\partial V}{\partial T}\right)}_P$$ Eq. 1

and can be related to the measurement by the equation

$${\left(\frac{\partial Q}{\partial P}\right)}_T=-\mathit{TV\alpha }$$ Eq. 2

where Q is the measured heat, P is the pressure, T is the temperature, and V is the volume.

High Resolution Ultrasonic Spectroscopy

Ultrasonic velocimetry measurements were performed on an HR-US 102 Spectrometer (Ultrasonic Scientific, Dublin, Ireland) with a frequency range of 2 to 18 MHz and a resolution of ±0.2 mm/s and 0.2% attenuation. Sample temperature was controlled using a Phoenix P2 water circulator (Thermo Haake), and measurements were measured continuously from 20 °C to 85 °C. The sample and reference volumes were 1 mL, and the protein sample concentration was 5 mg/mL. The sample and buffer were degassed prior to the measurement. Velocity and attenuation were measured at 12 MHz, and the data were processed using HRUS v4.50.27.25 software.

The adiabatic compressibility was calculated using Eq. 3

$${\beta }_S=-\frac{1}{V}{\left(\frac{\partial V}{\partial P}\right)}_S=-\left(\frac{1}{{\nu }_0}\right){\left(\frac{\partial v_0}{\partial P}\right)}_S=\left(\frac{{\beta }_0}{{\nu }_0}\right)\underset{c\to 0}{\lim }\left(\frac{\frac{\beta }{{\beta }_0}-V_0}{c}\right)$$ Eq. 3

where

$$V_0=\frac{\rho -c}{{\rho }_0}\mathrm{and}$$ Eq. 4

$${\nu }_0=\underset{c\to 0}{\lim }\left(\frac{1-V_0}{c}\right).$$ Eq. 5

The adiabatic compressibility of the solution is β, adiabatic compressibility of the buffer β₀, density of the solution ρ, density of the buffer ρ₀, protein concentration c, apparent volume fraction of the buffer V₀, and partial specific volume of the antibody ν₀. The sample and buffer density (ρ) along with the ultrasonic velocity (u) through the sample and buffer are related to the adiabatic compressibility (β and β₀) by the Laplace equation, β = 1/ρu².

Density

Measurements of sample and buffer density were performed with a DMA-5000 high precision densitometer (Anton Paar, Graz, Austria) with a precision of 1 × 10⁻⁶ g/cm³ and 0.001 °C. The instrument was calibrated using dry air and ultrapure, degassed water over the temperature range 20.000−60.000 °C. Densities of the sample (5 mg/ml) and buffer were measured from 20.000 to 55.000 °C in 2.500 °C increments.

Red-Edge Excitation Shifts

Fluorescence measurements used in the determination of red-edge excitation shifts were performed with a four-position PTI Quanta Master Spectrophotometer (Lawrenceville, NJ) with Peltier temperature control. The study was performed using a temperature ramp from 20.0 to 85.0 °C in 2.5 °C increments with a five minute equilibration time between temperature increases. The IgG concentration was 0.5 mg/mL, and the sample was held in a 1 cm path length quartz cuvette. The excitation and emission slit widths were set to 3 nm. Excitation wavelengths of 290, 295, 300, 305 and 310 nm were used, and the emission spectra were collected from 300 to 450 nm. The absolute peak position was determined from the first derivative of a polynomial fit of the emission data. In some cases, the width of the scattering peak at 310 nm inhibited accurate determination of the emission maximum. For these situations, no red-edge shift is reported.

Time-Resolved Fluorescence and Anisotropy

Time-correlated single photon counting was used to measure the tryptophan fluorescence decay and anisotropy of the IgG. The experiments were conducted on a custom built instrument using a mode-locked, cavity-dumped Mira Optima 900f Ti:Sapphire system pumped by a 10W Verdi Laser from Coherent, Inc. (Santa Clara, CA) as the excitation source. The pulses were frequency tripled using an Inrad harmonic separator. A T-format detection system was fitted with Oriel 27320 polarizers, single-pass Sciencetech 9030 monochrometers, and Hamamatsu microchannel plate PMTs. Sample temperature was regulated using a Peltier thermoelectric temperature controller from Quantum Northwest (Spokane, WA). Data collection was performed using an SPC-630 PCI card from Becker and Hickl GmbH (Berlin, Germany) operating at 14.7 ps/channel resolution. Data was collected to at least 30,000 peak counts for all of the decays. Fluorescent lifetime decays were measured with the polarizers set to the magic angle (54.7°) and anisotropy measurements were performed with perpendicularly oriented (0° and 90°) polarizers. The instrument response function (IRF) and G-factor were measured at 10 °C increments through the temperature ramp. The sample used for G-factor measurement was dilute N-acetyl-l-tryptophan in buffer. The IgG concentration was 0.1 mg/mL, and the sample was held in a 1 cm path length quartz cuvette. The experiment was performed using a temperature ramp from 20.0 °C to 85.0 °C in 2.5 °C increments. The IgG was allowed to equilibrate for 5 minutes between temperature increases. The excitation wavelength was 300 nm and the fluorescence emission was measured at 345 nm.

Amplitude averaged tryptophan lifetime, <τ>, was determined from the decay components longer than 50 ps. The rotational correlation times were calculated using the maximum entropy method implemented in Pulse5QT (Maximum Entropy Data Consultants, Inc.) [37, 38]. The analysis used 197 logarithmically spaced exponentials with a maximum of 200 ns. An infinite correlation time was used to account for the existence of any undetectable motions. Due to software limitations, it was possible to use only one of the IRFs collected from each of the two detectors. This was generally not of concern since the two IRFs were very similar. Nevertheless, correlation times less than 100 ps were disregarded to avoid error associated with the IRF deconvolution. Hydrodynamic calculations were performed using the program HYDROPRO [39] and human IgG1, PDB accession number 1HZH [40, 41]. The Fc fragment used for calculations contained residues 243–478 of both heavy chains, and the Fab fragment contained the respective light chain and residues 1–228 of the appropriate heavy chain.

Empirical Phase Diagram

The generation of empirical phase diagrams has been described previously [22, 23]. Briefly, the data are normalized between −0.5 and 0.5 to prevent any technique from dominating the phase diagram. In situations where data are absent for some temperature-pH combinations, a zero was entered. The data are then represented as a vector field on a temperature-pH plane, which is expressed in matrix notation. The temperature-pH matrix is converted to a density matrix, from which eigenvectors and eigenvalues are calculated. The eigenvectors corresponding to the three largest eigenvalues are subsequently used to transform the original vector field into a new, three-dimensional coordinate system. Finally, the transformed vector field is represented as a color map where the three dominant eigenvectors are assigned the colors red, green, and blue (RGB), respectively. The resulting color for each coordinate on the pH-temperature plane was generated using a linear combination of the RGB colors, in which the contribution from each color is based on the magnitude of the appropriate transformed vector. The analysis is performed using MATLAB (Mathworks, Inc., Natick, MA). The static EPD was calculated using molar ellipticity data at 218 nm, intrinsic fluorescence intensity, intrinsic emission maximum, average tryptophan lifetime, light scattering intensity, and ANS fluorescence intensity. The dynamic EPD was calculated using adiabatic compressibility, coefficient of thermal expansion, tryptophan red-edge excitation shift, and the slow rotational correlation time.

Results

Analytical Ultracentrifugation

Analytical ultracentrifugation was used to measure the sedimentation coefficient and verify the homogeneous nature of the IgG after dialysis into citrate-phosphate buffer over the pH range studied. Between 90 and 99 percent of each sample has a sedimentation coefficient in the range of 5.99 ± 0.02 to 6.58 ± 0.03 S (Table 1). There is also a larger component(s) within each sample having a sedimentation coefficient ranging from approximately 9 to 13 S.

Table 1.

IgG sedimentation coefficients measured at 20°C and pH 3–8.

pH	Sedimentation Coefficient (S)	Monomer Fraction (%)
3	5.99±0.02	93.7±2.2
4	6.30±0.03	98.2±0.4
5	6.38±0.04	96.4±1.8
6	6.42±0.03	99.4±0.9
7	6.42±0.07	98.4±0.7
8	6.58±0.03	97.3±2.8

Conventional Static Analysis of the IgG

The results of a conventional static analysis which includes circular dichroism, intrinsic fluorescence, ANS fluorescence, and light scattering, of the IgG as a function of pH and temperature are summarized in Figure 1A–F. Briefly, a single cooperative transition is observed in the temperature range of 60–70 °C over the pH range 5–8. The decrease in molar ellipticity (Figure 1A), the increase in tryptophan fluorescence intensity (Figure 1C) and the red shift of the emission peak (Figure 1B) at the transition temperature are consistent with protein unfolding and solvent exposure of the tryptophan residues. This unfolding event exposes hydrophobic regions of the protein and ultimately leads to aggregation, which is indicated by the respective increases in ANS fluorescence intensity (Figure 1F) and light scattering intensity (Figure 1E). Although temperature increases initially reduce the average tryptophan fluorescence lifetime (τ), increasing the temperature beyond the transition results in aggregation and an increase in the fluorescence lifetime (Figure 1D).

Figure 1.

Static measurements of the IgG collected at pH 3 (black), 4 (red), 5 (green), 6 (yellow), 7 (blue), and 8 (magenta). (A) Molar ellipticity at 218 nm, (B) intrinsic fluorescence peak position and (C) intensity, (D) tryptophan fluorescence lifetime, (E) static light scattering, and (F) ANS fluorescence intensity. Error bars in (A–C and E–F) are ± 1 σ from three independent experiments.

The behavior at pH 3–4 is significantly different from that at higher pH. Each technique shows a lower transition temperature at pH 3 and 4 than it does at higher pH. In addition, the broadness of the transition is much greater at low pH than it is at high pH. The light scattering data (Figure 1E) show that the transition of the IgG at pH 5–8 occurs abruptly over a narrow temperature range; the transition at pH 4 covers a much wider temperature range, and the sample at pH 3 shows no transition. Furthermore, trends in the data indicate that the protein exists in a very different state under acidic conditions. For instance, the molar ellipticity at pH 3 and 4 (Figure 1A) decreases (i.e. becomes more negative) with elevated temperature, implying the protein has gained secondary structure. At pH 3, the initial position of the emission peak is substantially red-shifted and the magnitude of the temperature-induced red-shift is larger, relative to the other pH values (Figure 1B). The initial red shift of the tryptophan emission peak and the large amount of ANS fluorescence indicate that at low temperatures, the tryptophan residues and other apolar regions are probably exposed to solvent. In this state, the absence of an increase in light scattering intensity at high temperatures indicates the IgG is considerably more resistant to aggregation than at higher pH (Figure 1E). At pH 4, the IgG is in a state less prone to aggregation than at higher pH, yet more prone to aggregation at elevated temperature than the IgG at pH 3.

Adiabatic Compressibility

HR-US velocimetry measurements combined with high precision density measurements were used to calculate the adiabatic compressibility of the IgG at pH 3–8 as a function of temperature (Figure 2A). A general positive trend is observed over the entire pH range. The magnitude of the adiabatic compressibility at elevated temperatures (> 65 °C) is slightly higher at pH 7 and 8 than for the lower pH range. Major transitions are observed for some of the conditions at temperatures similar to the transitions detected using the static methods. Most notable are the transitions that occur at pH 7 and 8 near 60 °C. Similar transitions can be seen for the other pH values, but they are much less pronounced. In addition to the major transition observed at elevated temperatures, the data appear to indicate the presence of a minor transition between 20 and 40 °C.

Figure 2.

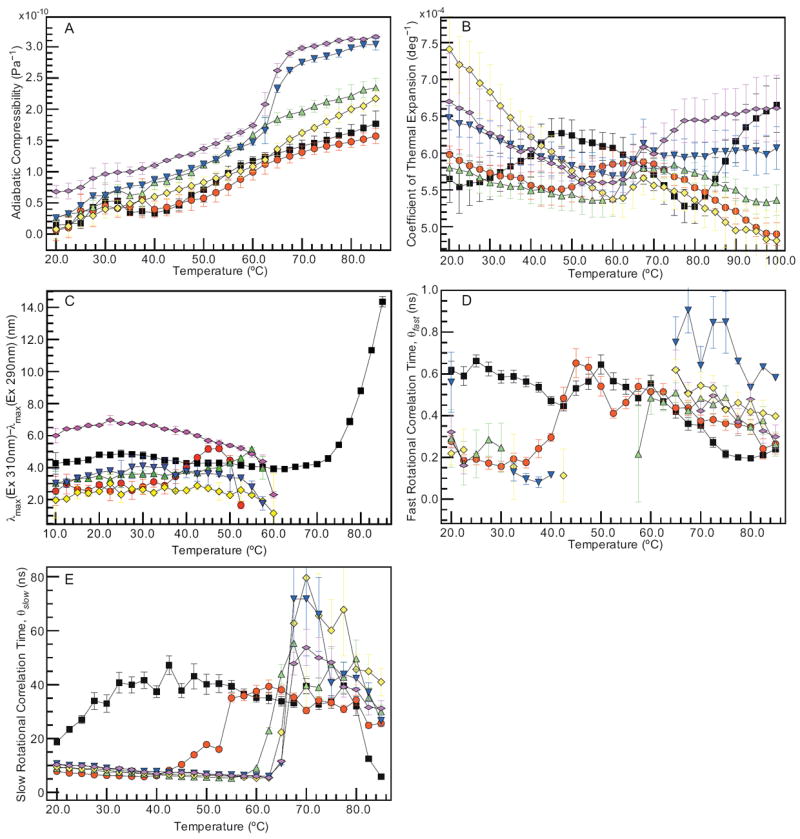
Dynamic measurements of the IgG collected at pH 3 (black), 4 (red), 5 (green), 6 (yellow), 7 (blue), and 8 (magenta). Hydrodynamic measurements of the IgG include (A) adiabatic compressibility and (B) coefficient of thermal expansion. Tryptophanyl dynamics were examined by (C) red-edge excitation shift based on excitation at 290 and 310 nm and both (D) fast and (E) slow rotational correlation times (θ) determined by time-resolved anisotropy. Error bars are ± 1 σ from three (A–B) or two (C) independent experiments. Error bars in (D–E) are determined from maximum entropy analysis.

Coefficient of Thermal Expansion

The coefficient of thermal expansion (α, Eq. 1) is calculated from PPC measurements performed as a function of temperature over the pH range 3–8 (Figure 2B). Although the variability in the data is significant, trends indicate that the expansivity is affected by pH and temperature. For the IgG at pH 5–8, the coefficient of thermal expansion has a negative slope from approximately 20 to 60 °C. Within this range, the magnitude of the slope follows the pH trend 6 > 7 ≈ 8 > 5. From 60 to 65 °C, α increases with temperature. Throughout the remainder of the temperature range, the coefficient of thermal expansion continues to increase for the IgG at pH 8 and decreases at pH 5–7. At pH 4, the trend follows that of pH 5, except that the previously observed transition is shifted from 60 °C to 50 °C, and the temperature dependence of α is more gradual throughout the remainder of the temperature range. At pH 3, there are two transitions, one near 25 °C and one near 80 °C. The coefficient of thermal expansion increases between 25 °C and 45 °C, and the gradual decrease in α between 45 °C and 80 °C is followed by a sharp increase over the remainder of the temperature range.

Red-Edge Excitation Shift

The effect of red-edge excitation on tryptophan fluorescence is quantified here as the shift in the emission peak when excited at 310 relative to 290 nm. The difference in the peak positions is plotted for the IgG at pH 3–8 as a function of increasing temperature in Figure 2C. At 10 °C, the extremes of the pH range appear to have the greatest peak shift: 4.3 ± 0.7 nm for the pH 3 sample and 6.0 ± 0.5 nm at pH 8. The intermediate pH values have peak shifts between 2.0 ± 1.1 and 3.0 ± 0.7 nm. The general trend is a relatively constant peak shift over the low temperature range followed by a decrease in the magnitude of the shift as the temperature increases. This decrease is, in some cases, preceded by an increase in the peak shift (e.g. pH 4 and 5). The exception to the observed trend occurs at pH 3, where the IgG has a relatively constant red-edge shift over the temperature range 10–65 °C, followed by a significant increase to 14.4 ± 0.3 nm at 55 °C.

Time-Resolved Anisotropy

Maximum entropy analysis recovers a mono- or bi-exponential decay fit to the rotational correlation times from the time-resolved fluorescence anisotropy measurements. The resulting correlation times (θ) are divided into two components, fast (θ_fast < 1 ns) and slow (θ_slow ≥ 1 ns). The correlation times (θ_fast and θ_slow) are plotted in Figure 2D–E for pH 3–8 as a function of temperature. The correlation times and error (χ²) are listed at 10 °C intervals from 20 to 80 °C in Table 2. The large error at 70 °C for pH 6 and 7 is probably caused by the effect of protein aggregation on the fluorescence anisotropy decay. For pH 4–8, θ_fast is ~0.1–0.3 ns at low temperatures (20–40 °C) and increases to 0.4–0.9 ns at temperatures above 60 °C. The discontinuity in the fast correlation time (θ_fast) at intermediate temperatures from pH 5–8 is due to overlap with the instrument response function (IRF). Decay components exist in this region (< 100 ps) that are consistent with values expected for fast correlation times, but they were not assigned because they could not be unambiguously distinguished from deconvolution error. At pH 3, θ_fast varies over the range 0.4–0.6 ns from 20 to 60 °C and then decreases thereafter. The slow correlation time (θ_slow) remains relatively constant (~10 ns) for pH 4–8 before the onset of a transition at 45 °C at pH 4 and 60–65 °C at pH 5–8. The behavior of θ_slow at pH 3 is again different, with an increase from 20 to 50 ns over the temperature range 20–45 °C, followed by a gradual decrease until 80 °C. A sharp decrease is then observed for the remaining 5 °C of the temperature range.

Table 2.

IgG rotational time correlation constants between 20 and 80 °C and pH 3–8.

	pH 3			pH 4			pH 5
Temp (°C)a	θfast (ns)b	θslow (ns)	χ2	θfast (ns)	θslow (ns)	χ2	θfast (ns)	θslow (ns)	χ2
20.0	0.62±0.04	18.72±0.80	1.17	0.28±0.03	7.85±0.13	1.19	0.29±0.14	8.93±0.19	1.13
30.0	0.59±0.03	32.97±3.20	1.09	0.16±0.02	6.30±0.10	1.05	0.25±0.12	7.48±0.15	1.09
40.0	0.47±0.02	37.38±2.09	1.05	0.30±0.02	6.21±0.10	1.01	--	6.65±0.11	1.09
50.0	0.64±0.05	40.13±3.72	1.05	0.54±0.05	17.76±0.73	1.07	--	5.68±0.10	1.14
60.0	0.55±0.04	35.10±1.62	1.02	0.51±0.04	37.54±2.13	1.04	0.49±0.08	9.01±0.32	1.08
70.0	0.35±0.03	39.41±2.76	1.13	0.37±0.03	30.39±1.14	1.13	0.48±0.05	39.69±3.27	1.11
80.0	0.20±0.01	32.06±3.43	1.10	0.35±0.03	34.24±1.81	1.12	0.35±0.04	49.61±6.91	1.42
	pH 6			pH 7			pH 8
Temp (°C)	θfast (ns)	θslow (ns)	χ2	θfast (ns)	θslow (ns)	χ2	θfast (ns)	θslow (ns)	χ2
20.0	0.22±0.05	9.49±0.14	1.03	0.56±0.14	10.63±0.21	1.17	0.32±0.08	10.31±0.25	1.04
30.0	--	8.39±0.12	1.01	--	9.01±0.12	1.09	--	8.90±0.15	1.16
40.0	--	6.66±0.10	1.18	0.12±0.00	7.78±0.13	1.15	--	6.95±0.11	1.00
50.0	--	6.31±0.12	1.12	--	6.80±0.10	1.19	--	6.73±0.12	1.03
60.0	--	5.32±0.10	1.07	--	6.18±0.12	1.14	--	5.97±0.05	1.10
70.0	0.54±0.06	79.61±47.69	1.05	0.64±0.09	71.79±21.16	1.13	0.42±0.05	53.74±6.76	1.13
80.0	0.42±0.05	45.63±5.61	1.07	0.53±0.00	42.27±3.45	1.13	0.48±0.08	38.17±3.98	1.13

^(a)Although the data has been acquired every 2.5 °C between 20 and 85 °C it is reported every 10 °C in this table.

^(b)The correlation constants have been divided into categories based on timescales less than one nanosecond (fast) and greater than one nanosecond (slow).

Discussion

The IgG is a monomer with native-like secondary structure

At most pH values, the IgG exists as a relatively homogeneous population with a small amount of oligomers (~ 9–13 S) in the chosen solution conditions at 20 °C (Table 1). The observed distribution of sedimentation coefficients is consistent with those previously reported for IgG [42]. The negative peak at 218 nm in the CD spectra is consistent with a high degree of β-sheet content, as observed for all human immunoglobulins (data not shown) [43, 44].

The IgG undergoes a single conformational transition at high pH

Static measurements detect a single, cooperative transition with a midpoint between 60 and 70 °C at pH 5–8. DSC shows multiple overlapping transitions (data not shown) but these spectroscopic measurements do not resolve them. The transition is particularly evident in the intrinsic fluorescence intensity, emission maximum, and average lifetime measurements (Figure 1B–D). This transition is associated with a loss of tertiary and secondary structure, as demonstrated by the increase in ANS fluorescence intensity at 60–65 °C and subsequent decrease in molar ellipticity at 70–75 °C (Figure 1F and A, respectively). The primary cause of this transition is presumably at least partial unfolding of the Fab region, which is known to occur within this temperature range for several IgG subclasses [45, 46]. The red shift of the intrinsic fluorescence peak position (Figure 1B) indicates the environment of the fluorophores is more polar, further supporting the existence of an unfolding event. The concomitant formation of aggregates is demonstrated by the sharp increase in light scattering intensity at 65 °C. Precipitation of the aggregates is responsible for the decrease in fluorescence and light scattering intensity at very high temperatures (> 70 °C) (Figure 1C and E, respectively).

Evidence for a distinct IgG conformation at acidic pH

Under acidic conditions (pH 3–4), the behavior of the IgG is very different from that at higher pH. The greatest variation is observed at pH 3, with pH 4 displaying characteristics that are intermediate between the flanking pH values (3 and 5). Intrinsic fluorescence intensity, emission maximum, and the average tryptophan lifetime indicate that an initial transition occurs with an onset between 30–35 °C at pH 3 and 40–50 °C at pH 4 (Figure 1B–C). The transition is followed closely by an increase in secondary structure (Figure 1A) at each of the two lower pH values. This observation is consistent with reports that IgG forms a more compact structure at acidic pH, often termed the A-form, although elevated temperatures are not required to induce the structural transition in other reported examples [42, 47, 48]. This alternate structure is believed to be exceptionally aggregation resistant and to have an increased amount of solvent-exposed apolar residues [47], which may explain the absence of an increase in light scattering intensity (Figure 1E), the red-shifted emission maximum (Figure 1B), and the increase in ANS fluorescence intensity (Figure 1F) that are present at pH 3. The red-edge shift and rotational correlation times (discussed below) indicate that the tryptophans have reduced conformational mobility under these conditions, which does not seem consistent with their increased solvent accessibility. This apparent contradiction can be explained in one of two ways: (1) that the red-edge excitation shift and rotational correlation times measured are dominated by buried tryptophans; or (2) that the increase in secondary structure reduces the conformational mobility of even solvent exposed tryptophans.

The increase in β-sheet content (Figure 1A), observed at 40 and 60 °C for pH 3 and 4, respectively, could also be caused by the formation of oligomeric structures. These structures, which do not exclude the existence of A-form IgG, could arise either from the entire IgG or a portion thereof. Under certain conditions, such as low pH and elevated temperatures, some IgG light chains are known to form intermolecular β-sheet structures [49-51]. Furthermore, the C_H3 portion of Fc fragments is believed to create oligomeric complexes at low pH [52]. Dynamic light scattering (data not shown) performed at pH 3 reveals a population with an effective diameter of 30–40 nm is present in small quantities (< 3.0% total) at elevated temperatures (> 60 °C). This is larger in size than the major population, which has an effective diameter ranging from 7 to 18 nm over the entire temperature range, and is much smaller than the large aggregates observed with increasing temperature at higher pH. The population with the 30–40 nm effective diameter is only present at high temperatures, indicating that it arises from a different source than the higher molecular weight component that exists at 20 °C under the same pH (Table 1). Though further characterization of the proposed oligomeric structures is necessary, the structural information obtained thus far indicates their probable presence at pH 3 and elevated temperatures.

Dynamic studies provide complementary information about the IgG

Measurements of IgG dynamics provide information that both supports and complements the results of the static measurements. To avoid redundancy, the ensuing discussion focuses primarily on complementary results, making references to data which are consistent with the trends observed using static measurements. The results of hydrodynamic measurements, such as PPC and HR-US, provide very different views of the effects of temperature and pH on the dynamics of the IgG. It is important to note, however, that the adiabatic compressibility and the coefficient of thermal expansion are thermodynamic constants and thus defined only for a reversible process. Their use herein to study thermal unfolding is not meant to imply that this criterion has been satisfied; rather, it is to identify conditions where alterations occur in the dynamic behavior of the IgG.

Protein compressibility is influenced by internal protein motions and hydration. Increased dynamic motions, conformational flexibility, void volume, and elasticity will result in higher values of adiabatic compressibility. Hydration, which can reduce many of these processes, decreases the magnitude of the compressibility. For instance, the greater adiabatic compressibility observed at pH 7 and 8 compared to lower pH may be due to the effect of deprotonation on hydration. The adiabatic compressibility of this IgG, however, increases with temperature over the entire pH range tested, suggesting that the effects of conformational fluctuations and dynamics are greater than those from hydration (Figure 2A). This trend is similar to that reported for other humanized IgG1κ antibodies [53]. A weak, low temperature transition is present throughout the entire pH range from 25–35 °C, indicating that the IgG may display increased conformational fluctuations throughout this lower temperature range.

The coefficient of thermal expansion (α) is also sensitive to changes in hydration of proteins, solvent accessibility, void volumes, conformational fluctuations, and mechanical elasticity [54, 55]. Increases in these properties are believed to increase the value of the coefficient of thermal expansion. The temperature dependence of α is also affected by the nature of the solvated amino acid side chains, with exposure of aliphatic and hydrophilic side chains leading to a positive and negative temperature dependence, respectively [56]. Based on the variable temperature-dependence of α, it appears that multiple factors are influencing its value (Figure 2B). At pH 5–8, α has an initial negative slope, which can be attributed to decreases in solvation-related dynamics and increases in the exposure of hydrophilic side chains. The slight increase in the coefficient of thermal expansion beginning at 60 °C for this pH range indicates that, as expected, swelling and conformational fluctuations are associated with protein unfolding. At pH 3, the slope of α alternates throughout the temperature range: positive at low temperatures (20–43 °C), negative at intermediate temperatures (43–80 °C), and finally positive at high temperatures (80–100 °C). The behavior at low temperatures indicates that there is an increase in conformational fluctuations and the exposure of aliphatic side chains to solvent, the later of which is consistent with the increased intensity of ANS fluorescence and the red-shift of the intrinsic fluorescence peak position. The trend at intermediate temperatures is consistent with the coincident increase in molar ellipticity at 218 nm (Figure 1A). Although the temperature dependence at high pH is similar to that reported for other IgG1κ antibodies, differences exist at low pH [53]. This result may not be surprising given the potential importance of the relationship between dynamics and antibody specificity. The absence of a transition similar to that observed in the adiabatic compressibility measurements at 25–35 °C (see above) is curious because α is also sensitive to alterations in protein hydration and internal motions. There are two possible explanations for this absence: (1) α is less sensitive to these types of dynamic perturbations; (2) the additional effectors of α, such as conformational fluctuations or changes in void volumes and mechanical elasticity, decrease the value of α in this temperature range, effectively canceling the transition.

In addition to hydrodynamic properties, protein dynamics can be studied by measuring solvent reorientation through red-edge excitation shifts, which are sensitive to the viscosity (i.e. orientational and spatial mobility) of the environment surrounding the fluorophore. In a viscous environment, the reorientation of solvent around the fluorophore is limited, causing a red shift in the emission of fluorophores that absorb a photon at lower energy. In environments where solvent relaxation is more complete, the magnitude of the red-edge shift decreases. In aqueous solution, red-edge shifts for tryptophanyl residues are typically less than 10 nm [57, 58], and there is only one report of a shift greater than 15 nm [59]. The maximum red-edge shift observed for the IgG is 14.4 nm at pH 3 (Figure 2C), which is quite large. Though the IgG has a greater number of tryptophans than most proteins studied by red-edge excitation, the magnitude of these shifts has been shown to be relatively independent of the number of tryptophan residues present [58]. The large red-edge shift is even more intriguing because it is observed at 85 °C. Red-edge effects generally display an inverse temperature dependence because the increased level of solvent reorientation facilitates the exchange of energy between excited state sublevels [58, 60]. The trend observed for the IgG indicates that the viscosity of the surrounding environment increases with temperature, which is consistent with the proposed oligomerization of the immunoglobulins under these conditions.

Both the local and global orientational dynamics of the IgG tryptophanyl residues can be measured using time-resolved anisotropy. Tryptophan rotational correlation times are known to be highly protein dependent [61-63], making comparisons challenging even for local dynamics. Nevertheless, general assignments can be made based on the knowledge that tryptophans in immunoglobulins are generally located in three distinct regions: buried within the β-sheets present in each domain, between domains, and in the antigen-combining site [64]. Tryptophanyl residues present in regions of well-defined secondary structure, such as those containing β-sheets, are expected to be relatively immobile, while those located in very dynamic environments, such as the region between individual domains are probably more mobile. In the absence of an antigen, tryptophans located in the antigen-combining site may also be relatively mobile. Based on these assumptions, tryptophans present in both the antigen combining site and interdomain regions are probably responsible for a majority of the fast component (θ_fast) present in the anisotropy decay (Figure 2D–E and Table 2). Furthermore, the timeframe of θ_fast (0.4–4.0 ns) coincides with motions that are expected to be common in dynamic regions of proteins, such as rotamer isomerizations and localized backbone fluctuations [63]. Tryptophans that are located in more conformationally restricted environments, such as β-sheets, are probably responsible for a large portion of the slow component (θ_slow) of the anisotropy decay and may contribute to some of the fast components as well. The types of motions that coincide with θ_slow could include domain motions, hinge bending, and minor conformational rearrangements. This correlation time, however, is too short to correspond to either molecular tumbling or movement of entire Fab/Fc regions. The global tumbling time is estimated to be ~195 ns for a human IgG1 and the correlation times of isolated Fab or Fc fragments are estimated to be 30–40 ns, which is probably faster than the motions of these regions within an intact IgG [39-41].

Comparison of static and dynamic empirical phase diagrams

In the static EPD, a well-defined transition occurs at 65 °C for pH 5–8 (Figure 3A). At pH 3 and 4, there are two transitions. The first occurs at around 40 °C and 55 °C for pH 3 and 4, respectively. The second is at approximately 70 °C for both pH 3 and 4, although the transition is broader at pH 3. The dynamic EPD is considerably more complicated (Figure 3B). A transition consistent with the one present in the static EPD for pH 5–8 is evident; however, the onset is more variable (55–65 °C). A second transition is also observed at ~ 35 °C for pH 6–8. At pH 3, transitions are observed nearly every 10 °C, demonstrating the extremely variable nature of IgG dynamics under acidic conditions.

Figure 3.

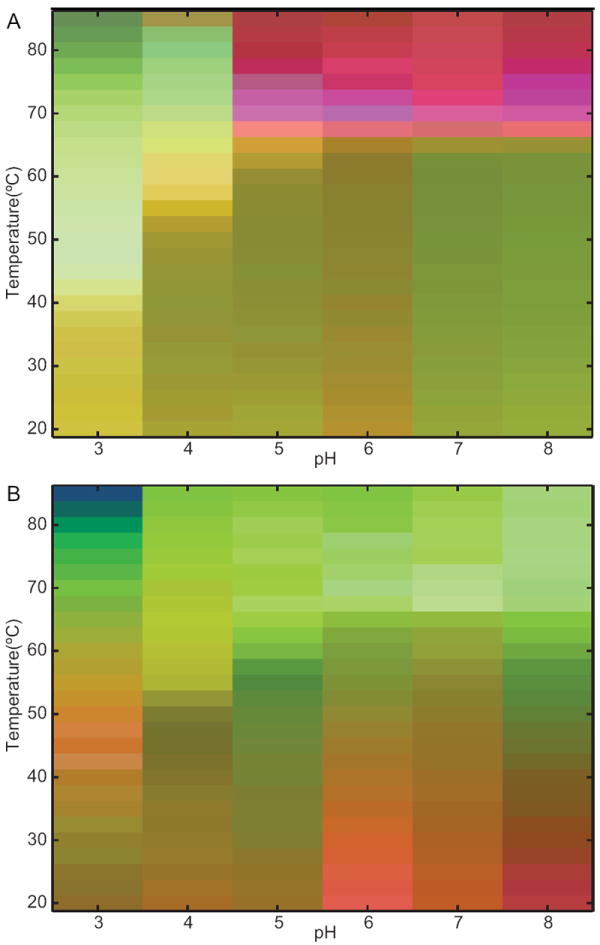
(A) Static and (B) dynamic empirical phase diagrams of the IgG as a function of temperature and pH.

The presence of both new transitions and those with earlier onsets in the dynamic EPD can be explained by the greater variety of solution state alterations that are detectable using dynamic measurements. Static measurements primarily detect changes in the secondary or tertiary structure of a protein. Dynamic measurements, on the other hand, are sensitive to variations in additional protein characteristics such as molecular tumbling, domain movement, rotamer isomerizations, and changes in the void volume or degree of solvation. The alteration(s) that is primarily responsible for a particular transition can be determined by inspecting the data for each of the measurements in the temperature and pH range of interest. The low temperature transition observed for pH 6–8 correlates with a transition present in the adiabatic compressibility of the IgG (Figure 2A), which indicates that alterations in the hydrodynamic properties of the IgG are responsible. The broadening of the high temperature transition at pH 5–8 appears to be caused by a decrease in the tryptophanyl red-edge shift (Figure 2C). As discussed above, this is indicative of increased solvent reorientation around the tryptophan residues, which may be caused by alterations in tertiary structure preceding aggregation or changes in protein solvation. The large number of transitions present in the dynamic EPD at pH 3 probably results from changes in several parameters, including the coefficient of thermal expansion and the orientational dynamics of the IgG (Figure 2B and E). Although it is difficult to interpret changes seen by multiple techniques, this result clearly indicates the high variability in the dynamic properties of the IgG at pH 3.

The methods described herein have several advantages over current techniques and are useful for exploring the relationship between dynamics and protein stability. Although static measurements have been used for this purpose, our observations indicate that measurements of protein dynamics are effectively a more “sensitive” method of determining the conditions under which proteins are most stable. Compared to techniques that are currently used to study protein dynamics, such as NMR and single molecule fluorescence, the methods we describe herein are faster, have no molecular size limit, and do not require sample modification. In addition, we have shown that when incorporated into an EPD, these dynamic measurements provide a detailed view of the sensitivity (or resistance) of a protein to external perturbations. We anticipate this approach may also be useful in the formulation of pharmaceutical biomacromolecular drugs since it allows one to study the impact certain compounds have on both motions that precede structural transitions and those that increase sensitivity to proteases and other methods of degradation.