Abstract
The invasion of red blood cells (RBCs) by malaria parasites is a complex dynamic process, in which the infected RBCs gradually lose their deformability and their ability to recover their original shape is greatly reduced with the maturation of the parasites. In this work, we developed two types of cell model, one with an included parasite, and the other without an included parasite. The former is a representation of real malaria-infected RBCs, in which the parasite is treated as a rigid body. In the latter, where the parasite is absent, the membrane modulus and viscosity are elevated so as to produce the same features present in the parasite model. In both cases, the cell membrane is modeled as a viscoelastic triangular network connected by wormlike chains. We studied the transient behaviors of stretching deformation and shape relaxation of malaria-infected RBCs based on these two models and found that both models can generate results in agreement with those of previously published studies. With the parasite maturation, the shape deformation becomes smaller and smaller due to increasing cell rigidity, whereas the shape relaxation time becomes longer and longer due to the cell’s reduced ability to recover its original shape.
Introduction
Malaria is a mosquito-borne infection induced by parasites of the genus Plasmodium, of which Plasmodium falciparum causes the majority of fatalities and produces the most severe clinical manifestations (1,2). It begins with a bite from an infected female mosquito, transmitting a sporozoite to liver cells through blood vessels. In liver cells, the sporozoite reproduces asexually thousands of merozoites, which rupture the liver cells and return to blood vessels. The merozoites then start to invade healthy red blood cells (hRBCs), where they develop into ring, trophozoite, and schizont forms until more merozoites are produced and the infected red blood cells (iRBCs) burst (3). This article concentrates on these three forms of iRBC caused by P. falciparum, denoted as rRBCs, tRBCs, and sRBCs, respectively.
In malaria disease, the invasion of hRBCs by parasites is a complex dynamic process, accompanied by progressive changes in the shape, size, and mechanical properties of the cell (2,4–7). An hRBC has a biconcave disklike shape with a major diameter of ∼7.8 μm (8). Upon penetration, the parasite develops into a thin ring-shaped disk of diameter 2∼3 μm (9), which is why this is called the ring stage. At this stage, the rRBC shows almost no change in shape and size. At the trophozoite stage, the parasite increases in size to ∼4 μm and becomes more rounded. The tRBC shows obvious changes in shape, with many bumps and depressions on its surface, and its volume increases by ∼17% (5,9,10) compared to the hRBC. At the schizont stage, the parasite undergoes several rounds of mitosis to produce daughter parasites, comprising up to ∼50% of the sRBC volume (11). The sRBC is nearly spherical in shape; its surface area decreases by ∼18% compared to the hRBC (5,9). Mechanically, the iRBC gradually loses its deformability and its ability to recover its original shape greatly decreases with maturation of the parasites (11,12). There are two major reasons for this. One is that the parasites secrete proteins on the cell membrane to modify its structure, thus increasing its shear modulus and viscosity (9). The other is that the presence of the rigidity-producing parasite reduces cell deformability (13) and increases cell viscosity (14). An additional cause has to do with the cell geometry, characterized by the surface area/volume ratio. In most studies, the cell surface area and volume are usually assumed to be conserved, because the cell area dilation modulus is significantly large and the cell penetrability is not considered, leading to a negligible effect of cell geometry. Thus far, few studies (14) have been done on how malaria parasites reduce the shape recoverability of the cell, but there are a number of works (11,15,16) on how the cell loses its deformability due to infestation by malaria parasites. Hosseini and Feng (11) studied the effect of parasite size on the stretching deformation of iRBCs using the smoothed-particle hydrodynamics method, and they pointed out that there is a compensation effect between the elevation of the membrane shear modulus and the size of the parasite in generating the same amount of stretching deformation. This conclusion may explain the difference in membrane shear modulus measured by optical tweezers and micropipette aspirations. In the stretching experiments by optical tweezers (17–19), the iRBC is treated as an entire specimen to be stretched diametrically, such that the effect of the parasite is offset by the elevation of the membrane shear modulus. As a result, the loss of deformability is entirely ascribed to the elevation of the membrane shear modulus, and the shear modulus is measured at ∼5.3, 16, 21.3, and 53.3 μN/m for the hRBC, rRBC, tRBC, and sRBC, respectively. This case can be analyzed by a cell model without an included parasite. In the stretching experiments by micropipette aspiration (13,20,21,22,23), the membrane shear modulus is measured to be ∼6 μN/m for the hRBC and 15 μN/m for the rRBC, tRBC, and sRBC, because the membrane is probed locally and the effect of the parasite is thus considered separately. Hence, this case can only be analyzed by a cell model with an included parasite.
In this work, we developed two cell models, one with and the other without an included parasite. The model with an included parasite was developed directly from a real malaria-infected RBC, where the parasite is modeled as a rigid body. The model without an included parasite is an RBC model in which the membrane modulus and viscosity are elevated to produce the same features present in the parasite model. In both models, the cell membrane is represented by a triangular network formed by nonlinear wormlike chains instead of linear chains to more reasonably model the shape deformation. Moreover, a viscous term is also added into each chain to describe the membrane viscosity. Based on these two models, we investigated the transient behaviors in the stretching deformation and shape relaxation of malaria-infected RBCs.
Model Development
Cell models
Fig. 1 schematically illustrates the models with an included parasite for hRBC, rRBC, tRBC, and sRBC. An hRBC has a biconcave shape, given by (8)
| (1) |
where are the coordinates of the membrane particle; is the hRBC radius of 3.91 μm; , , and are three coefficients with values of 0.81, 7.83, and −4.39 μm, respectively. Since the rRBC has a shape similar to that of the hRBC, we still use Eq. 1 to model it, with the same radius and coefficients as for the hRBC,. However, a rigid ring disk is introduced to represent the parasite, with diameter and thickness set to 2.0 and 1.0 μm (9), as shown in Fig. 1 b. The tRBC is more or less axisymmetric and slightly thicker than the rRBC in shape, although there are many protuberants and depressions on the cell membrane surface (18). Therefore, we still use the biconcave shape described by Eq. 1 to represent the tRBC, but the radius, , is set to 3.80 μm and the three coefficients , , and are 2.10, 7.58, and −5.59 μm to make the cell thicker. The parasite inside the tRBC is also modeled as a biconcave body with the same coefficients, , , and , as the tRBC. However, its radius is set to 2.9 μm so that the parasite occupies ∼40% of the tRBC volume. These values of tRBC and internal parasite are chosen to match the tRBC data reported by Esposito et al. (5), as listed in Table 1. At the schizont stage, because the sRBC exhibits a nearly spherical shape, an oblate spheroid is used to model the sRBC, with radii 3.5 μm × 3.5 μm × 1.685 μm, as shown in Fig. 1 d. The parasite is also modeled as an oblate spheroid of the same aspect ratio as the sRBC. Its radii are chosen as 2.78 μm × 2.78 μm × 1.339 μm so that the parasite occupies ∼50% of the sRBC volume.
Figure 1.
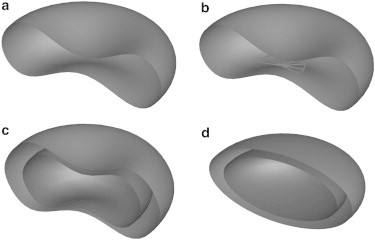
Schematic illustration of cell models. (a) An hRBC with characteristic biconcave shape. (b) An rRBC with the same shape as the hRBC, with a ring-disk parasite of 3.3% volume fraction at the cell center. (c) A tRBC with biconcave shape thicker than that of the hRBC and a biconcave parasite of 40% volume fraction at the cell center. (d) An sRBC with spheroid shape, and a spheroid parasite of 50% volume fraction at the cell center.
Table 1.
Parameters of healthy and infected RBCs used in this and other studies
| Cell type | Surface area (μm2) | Volume (μm3) | Parasite volume fraction | Shear modulus (μN/m) |
Membrane viscosity (μNs/m) |
||
|---|---|---|---|---|---|---|---|
| Model with parasite | Model without parasite | Model with parasite | Model without parasite | ||||
| hRBC | 135 | 94 | — | 6.0 | 6.0 | 0.6 | 0.6 |
| 120 ± 15 (5) | 88 ± 20 (5) | — | 6.0 (22) | — | 0.6–0.8 (27) | — | |
| rRBC | 135 | 94 | 3.3% | 15 | 15 | 1.6a | 1.6 |
| 110 ± 8 (5) | 83 ± 12 (5) | 3–15% (6) | 15.3 (23) | 15 (11) | — | 1.5–2.5 (28) | |
| tRBC | 135 | 116 | 40% | 15 | 35 | 1.6a | 15 |
| 119 ± 14 (5) | 103 ± 26 (5) | 15–50% (6) | 9–18 (13) | 30 (11) | — | 11–19.5 (29) | |
| sRBC | 104 | 86 | 50% | 15 | 40 | 1.6a | 56 |
| 98 ± 13 (5) | 81 ± 8 (5) | 50–80% (6) | 9–14 (13) | 40 (11) | — | — | |
For all four cell types, data in the upper row are from this study, and data in the lower row are from the literature, with individual studies identified by the numbers in parentheses.
No experimental values for membrane viscosity were found in the literature.
The model without an included parasite adopts the same iRBC configuration above, but without the parasite. The absence of a parasite is compensated for by elevating the membrane shear modulus and viscosity. In the model with an included parasite, the membrane shear modulus is set to be 6.0 μN/m for the hRBC and 15 μN/m for the rRBC, the tRBC, and the sRBC, as listed in Table 1. The membrane viscosity is 0.6 μNs/m for the hRBC, and 1.6 μNs/m for the rRBC, the tRBC, and the sRBC. In the model without an included parasite, the membrane shear modulus is 6.0, 15, 35, and 40 μN/m and the membrane viscosity is 0.6, 1.6, 15, and 56 μNs/m for the hRBC, the rRBC, the tRBC, and the sRBC, respectively. In fact, the membrane shear modulus and viscosity in this model cannot be regarded as material properties; they are used only to provide an effective and quick means of producing a stretching and relaxation deformation consistent with the data. We may refer to these as the equivalent membrane shear modulus and equivalent membrane viscosity. It is obvious that the model without an included parasite is more easily implemented in numerical simulations than the model with an included parasite, due to the absence of parasite. For example, the Supporting Material alludes to the simulation of iRBCs in simple shear flow based on the model without an included parasite (24).
Model formulation
The dissipative particle dynamics (DPD) method is used to model the cells, with or without an included parasite. In this method, the whole cell is turned into a system of DPD particles; each particle represents a cluster of molecules on the mesoscopic scale (15). The particles on the cell membrane are connected as a triangular network of nonlinear wormlike chains, and the parasite is treated as a rigid body by a set of constrained particles. All particles move in accordance with Newton's second law,
| (2) |
| (3) |
| (4) |
where and are the mass and location of the particle; is the time; , , and are three sets of internal, membrane, and parasite particles, respectively; and is the number of parasite particles. In Eq. 4, only the translational motion of the parasite is tracked, since it is a rigid body. The DPD force, , is used to describe the interactions between any two particles, which include conservative ,dissipative , and random forces:
| (5) |
The conservative force is related to the compressibility of fluid, and the dissipative force represents the viscous nature of the fluid. The presence of the random force guarantees a constant system temperature (specific kinetic energy) through a fluctuation-dissipation theorem. The membrane force, , is used to describe the behaviors of the cell membrane, including the elastic part, , and the viscous part, :
| (6) |
The elastic part is characterized by a total energy potential (25), consisting of the in-plane energy generated by the stretching deformation, the bending energy by the bending deformation, the area-constraint energy by the surface area change, and the volume-constraint energy by the volume change. The viscous part is modeled by a dissipative and a random part, introduced to determine the membrane viscosity and keep the system temperature constant. The details of all the forces can be found in the Supporting Material.
Results and Discussion
Stretching deformation
In the experiments performed by Suresh et al. (17) using optical tweezers, two silica beads of diameter 2 μm attached to opposite ends of a healthy or infected RBC are pulled apart diametrically, imposing a constant stretching force. Thus, in the simulation, a constant stretching force is acting uniformly on the membrane particles lying inside a circular domain of diameter 2 μm at opposite ends of the cell. Fig. 2 compares the simulation described in this article with the experimental results of Suresh et al. (17) in terms of the variation in the axial (stretching direction) and transverse (width direction) diameters, which are plotted for the hRBC, rRBC, tRBC, and sRBC under different stretching forces from 0 to 200 pN. Note that the variation in diameter is defined as , where and are current and initial diameters of the RBC. Under a 100 pN force, the axial diameter varies from 80% for the hRBC to 44.5%, 31.1%, and 20.3% for the rRBC, tRBC, and sRBC, respectively. Thus, the elongational deformation decreases by 35.5%, 48.9%, and 59.7% for the rRBC, tRBC and sRBC compared with the hRBC. In other words, the cell gradually loses its deformability with maturation of the parasite, as illustrated by the deformed shapes in Fig. 2. Past studies (11,17) have shown that the membrane bending modulus is not significant in the stretching deformation, which is dominated by in-plane elasticity. Here, the bending modulus is set to 2.4 × 10−19 J in all simulation cases. For the cases with included parasites, the shear modulus is set to 6.0 μN/m for the hRBC and 15 μN/m for the rRBC, tRBC, and sRBC, as noted in Table 1. For the cases without included parasites, however, it is set to 6.0, 15, 35, and 40 μN/m for the hRBC, rRBC, tRBC, and sRBC, respectively. In all cases, we find that the numerical results presented here are in good agreement with the experimental data (17). These values also agree with the estimated values of Hosseini and Feng (11), who used the smoothed-particle hydrodynamics method in their estimates to generate a deformation similar to that produced in experiments. In addition, shear modulus values were found to be 5.3, 16, 21.3, and 53.3 μN/m in the work of Suresh et al. (17) and 6.3, 14.5, 29, and 40 μN/m in that of Fedosov et al. (15) for the cases without included parasites.
Figure 2.
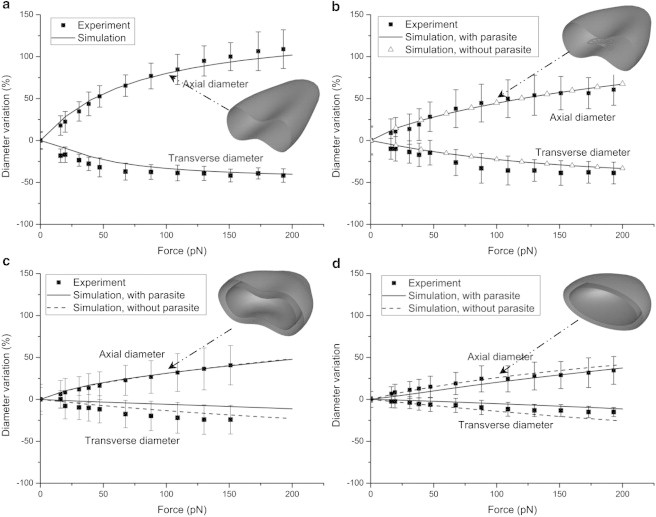
Comparison between numerical results and experimental data (17). Stretching response of the hRBC (a), rRBC(b), tRBC(c), and sRBC (d) subjected to stretching forces from 0 to 200 pN. The deformed shapes are the steady shapes of the hRBC, rRBC, tRBC, and sRBC with included parasites subjected to a stretching force of 100 pN.
In the ring stage, the presence of the parasite does not affect the stretching deformation in any significant way, as shown in Fig. 2 b. As a result, we conclude that the loss of deformability of rRBC is mainly attributed by the increase in shear modulus to 15 μN/m from 6.0 μN/m for the hRBC. In the trophozoite stage, the tRBC with the parasite has an increase in axial diameter similar to that of the tRBC without the parasite but a more gradual decrease in transverse diameter, as plotted in Fig. 2 c. In the schizont stage, the sRBC with the parasite has a more gradual increase in both axial diameter and transverse diameter compared to the sRBC without the parasite, as shown in Fig. 2 d. The large included parasite yields an additional resistance to the squeezing of the cell in the transverse direction, leading to a more gradual decrease in the transverse diameter for both the tRBC and sRBC with included parasites. However, this resistance is much stronger in the schizont stage than in the trophozoite stage due to the increase in size of the parasite, so that the difference in axial diameter between the sRBCs with and without the parasite is more obvious than for the tRBCs with and without the parasite. In addition, the shear modulus of the iRBC with the parasite is smaller than that without the parasite in the trophozoite and schizont stages, implying that the loss of deformability of the tRBC and sRBC also depends on the presence of the large parasite. Compared with the rRBC, the tRBC loses 13.4% elongation deformation under the 100 pN stretching force, whereas the sRBC loses 24.5% elongation deformation. Because they both have the same shear modulus, the additional loss in elongational deformation is due to the size of the parasite: 40% cell volume for the tRBC, and 50% for the sRBC.
Shape relaxation
The ability of the cell to recover its original shape results from the elastic energy storage in the membrane (26). The rate of shape recovery is mainly determined by the viscous dissipation within the membrane (27). Therefore, the cell shape relaxation is also related to the membrane elastic and viscous properties, characterized by a shape relaxation time defined as (27)
| (7) |
where and are the membrane shear modulus and viscosity. To calculate the shape relaxation time from the simulation data, the exponential model of Hochmuth et al. (27) is adopted:
| (8) |
where and are the axial and transverse diameters; is the time variable; is the time at the instant the force is released; and the subscripts max and correspond to the release and recovery states, respectively.
Fig. 3 plots the axial and transverse diameters of hRBC, rRBC, tRBC, and sRBC subject to 100 pN force during stretching and relaxation, from which three conclusions can be drawn. First, the changes in the axial and transverse diameters become smaller with increasing parasite maturation, indicating that the iRBC gradually loses its deformability. Second, both diameters approach their own steady-state values more gradually with increasing parasite maturation in terms of both stretching and relaxation, showing that the iRBC has an increasing membrane viscosity. Therefore, the iRBC recovers to its original shape more slowly with increasing parasite maturation, as shown by the deformed shapes in Fig. 3. This has been observed experimentally (14). Last, the rRBCs with and without an included parasite have about the same axial and transverse diameters during both stretching and relaxation. However, the tRBC and sRBC with included parasites have smaller variations in axial and transverse diameters compared to the tRBC and sRBC without included parasites. This clearly implies that a larger parasite makes the cell more resistant to deformation.
Figure 3.
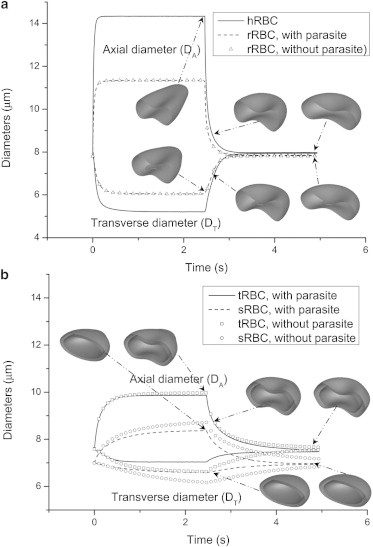
Variation of axial and transverse diameters of hRBC and rRBC (a) and the tRBC and sRBC (b) during stretching and relaxation. The deformed shapes show the shape evolution of the hRBC, rRBC, tRBC, and sRBC with included parasites at 2.465, 2.613, and 4.93 s during relaxation.
Fig. 4 illustrates the best fit, based on Eq. 8, for calculating the shape relaxation time of hRBC, rRBC, tRBC, and sRBC, where is defined as the lefthand side of Eq. 8. With increasing time, gradually approaches zero for all four types of cell, showing that the cell gradually recovers its original shape. Furthermore, approaches zero more slowly with increasing parasite maturation, implying a reduction of cell recoverability. The shape relaxation time is calculated to be 0.111 s for the hRBC, 0.128, 0.368, and 0.5 s for the rRBC, tRBC, and sRBC with parasites, and 0.125, 0.486, and 0.792 s for the rRBC, tRBC, and sRBC without parasites. Hochmuth et al. (27) estimated the shape relaxation time of the hRBC to be 0.1–0.13 s by a micropipette aspiration technique. Cranston et al. (28) measured it to be 0.092–0.15 s for the hRBC, and 0.101–0.173 s for the rRBC, and they also pointed out that the shape relaxation time definitely increases with increasing parasite maturation. Mauritz et al. (29) measured it to be 0.104 s for the hRBC, and 0.4 s for the tRBC by an optical tweezers method. Our values for the hRBC, rRBC, and tRBC agree well with published results. So far, there are no data published on the shape relaxation time of the sRBC infected by P. falciparum. However, Handayani et al. (30) reported the normalized recovery ratio (defined as the ratio of the shape relaxation time of the hRBC to that of the iRBC) to be ∼0.63, 0.43, and 0.32 for the rRBC, tRBC, and sRBC infected by P. vivax. For comparison, the normalized recovery ratio in this work is calculated to be 0.876, 0.302, and 0.222 for the rRBC, tRBC, and sRBC with parasites, and 0.888, 0.228, and 0.14 for the same without parasites. A qualitative agreement is thus found on the decreasing trend of the normalized recovery ratio. The shape relaxation time can also be directly estimated from Eq. 7 by the known membrane shear modulus and viscosity. However, this procedure may not be applicable to the cell model with included parasite, because the iRBC’s relaxation is hampered by the presence of the parasite. For the hRBC, the shape relaxation time is estimated from Eq. 7 to be 0.1 s, as noted in Table 1. For the rRBC, tRBC, and sRBC, it is directly calculated to be 0.107, 0.428, and 1.4 s, respectively. Except for the shape relaxation time of the sRBC, those of the others are relatively close to the values obtained by the best fit. The large difference for the sRBC may be attributed to the small membrane shear modulus (40 μN/m) used in the cell model without included parasite. Note that Suresh et al. (17) used a membrane shear modulus of 53.3 μN/m for the sRBC to simulate stretching deformation of the cell.
Figure 4.
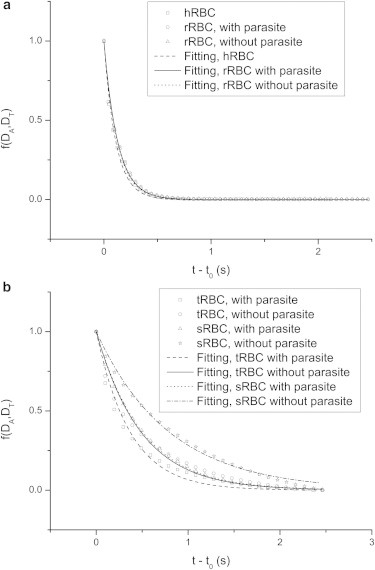
Fitting of the relaxation time of the hRBC and rRBC (a) and the tRBC and sRBC (b) according to Eq. 8, where f(DA, DT) stands for the lefthand side of the equation and t0 is 2.465 s.
Conclusions
In this work, we developed two models for malaria-infected cells, one with and the other without an included parasite. The former is a representation of malaria-infected RBCs, whereas the latter is a model with parameters adjusted to fit experimental data—both the membrane modulus and viscosity are elevated to produce a stretching deformation and a shape relaxation time similar to those observed in other studies. Based on these models, we then investigated the stretching deformation and shape relaxation time of malaria-infected RBCs. In the stretching simulation, the axial and transverse diameters were measured and compared with earlier experimental results. Good agreement was observed for all four types of cells, hRBC, rRBC, tRBC, and sRBC. With increasing parasite maturation, the iRBC gradually loses its deformability, and the effects of the included parasite on iRBC deformability can be emulated in the model without included parasites by simply increasing the membrane shear modulus. In the shape relaxation simulation, the shape relaxation time was calculated and observed to be consistent with previously reported values. With parasite maturation, the iRBC gradually reduces its shape recoverability, and the effect of the included parasite on the iRBC’s shape recoverability can be compensated in the model without included parasites by simply increasing the membrane viscosity.
Acknowledgments
The authors gratefully acknowledge financial support from the Ministry of Education of Singapore through Academic Research Fund (AcRF) Tier 1 under Project No. R-265-000-395-133.
Supporting Material
References
- 1.Rowe J.A., Claessens A., Arman M. Adhesion of Plasmodium falciparum-infected erythrocytes to human cells: molecular mechanisms and therapeutic implications. Expert Rev. Mol. Med. 2009;11:e16. doi: 10.1017/S1462399409001082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Haldar K., Mohandas N. Erythrocyte remodeling by malaria parasites. Curr. Opin. Hematol. 2007;14:203–209. doi: 10.1097/MOH.0b013e3280f31b2d. [DOI] [PubMed] [Google Scholar]
- 3.Tilley L., Dixon M.W.A., Kirk K. The Plasmodium falciparum-infected red blood cell. Int. J. Biochem. Cell Biol. 2011;43:839–842. doi: 10.1016/j.biocel.2011.03.012. [DOI] [PubMed] [Google Scholar]
- 4.Millholland M.G., Chandramohanadas R., Greenbaum D.C. The malaria parasite progressively dismantles the host erythrocyte cytoskeleton for efficient egress. Mol. Cell. Proteomics. 2011;10:010678. doi: 10.1074/mcp.M111.010678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Esposito A., Choimet J.B., Tiffert T. Quantitative imaging of human red blood cells infected with Plasmodium falciparum. Biophys. J. 2010;99:953–960. doi: 10.1016/j.bpj.2010.04.065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Serebrennikova Y.M., Patel J., García-Rubio L.H. Quantitative analysis of morphological alterations in Plasmodium falciparum infected red blood cells through theoretical interpretation of spectral measurements. J. Theor. Biol. 2010;265:493–500. doi: 10.1016/j.jtbi.2010.05.037. [DOI] [PubMed] [Google Scholar]
- 7.Aingaran M., Zhang R., Marti M. Host cell deformability is linked to transmission in the human malaria parasite Plasmodium falciparum. Cell. Microbiol. 2012;14:983–993. doi: 10.1111/j.1462-5822.2012.01786.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Evans E., Fung Y.C. Improved measurements of the erythrocyte geometry. Microvasc. Res. 1972;4:335–347. doi: 10.1016/0026-2862(72)90069-6. [DOI] [PubMed] [Google Scholar]
- 9.Hanssen E., McMillan P.J., Tilley L. Cellular architecture of Plasmodium falciparum-infected erythrocytes. Int. J. Parasitol. 2010;40:1127–1135. doi: 10.1016/j.ijpara.2010.04.012. [DOI] [PubMed] [Google Scholar]
- 10.Li A., Mansoor A.H., Lim C.T. Observations on the internal and surface morphology of malaria infected blood cells using optical and atomic force microscopy. J. Microbiol. Methods. 2006;66:434–439. doi: 10.1016/j.mimet.2006.01.009. [DOI] [PubMed] [Google Scholar]
- 11.Hosseini S.M., Feng J.J. How malaria parasites reduce the deformability of infected red blood cells. Biophys. J. 2012;103:1–10. doi: 10.1016/j.bpj.2012.05.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Suresh S. Mechanical response of human red blood cells in health and disease: Some structure-property-function relationships. J. Mater. Res. 2006;21:1871–1877. [Google Scholar]
- 13.Nash G.B., O’Brien E., Dormandy J.A. Abnormalities in the mechanical properties of red blood cells caused by Plasmodium falciparum. Blood. 1989;74:855–861. [PubMed] [Google Scholar]
- 14.Shelby J.P., White J., Chiu D.T. A microfluidic model for single-cell capillary obstruction by Plasmodium falciparum-infected erythrocytes. Proc. Natl. Acad. Sci. USA. 2003;100:14618–14622. doi: 10.1073/pnas.2433968100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Fedosov D.A., Caswell B., Karniadakis G.E. Systematic coarse-graining of spectrin-level red blood cell models. Comput. Methods Appl. Mech. Eng. 2010;199:1937–1948. doi: 10.1016/j.cma.2010.02.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Fedosov D.A., Caswell B., Karniadakis G.E. Quantifying the biophysical characteristics of Plasmodium-falciparum-parasitized red blood cells in microcirculation. Proc. Natl. Acad. Sci. USA. 2011;108:35–39. doi: 10.1073/pnas.1009492108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Suresh S., Spatz J., Seufferlein T. Connections between single-cell biomechanics and human disease states: gastrointestinal cancer and malaria. Acta Biomater. 2005;1:15–30. doi: 10.1016/j.actbio.2004.09.001. [DOI] [PubMed] [Google Scholar]
- 18.Park Y.K., Diez-Silva M., Suresh S. Refractive index maps and membrane dynamics of human red blood cells parasitized by Plasmodium falciparum. Proc. Natl. Acad. Sci. USA. 2008;105:13730–13735. doi: 10.1073/pnas.0806100105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Liu Y.P., Li C., Lai A.C.K. Experimental study on the deformation of erythrocytes under optically trapping and stretching. Mater. Sci. Eng. A Struct. Mater. 2006;423:128–133. [Google Scholar]
- 20.Glenister F.K., Coppel R.L., Cooke B.M. Contribution of parasite proteins to altered mechanical properties of malaria-infected red blood cells. Blood. 2002;99:1060–1063. doi: 10.1182/blood.v99.3.1060. [DOI] [PubMed] [Google Scholar]
- 21.Paulitschke M., Nash G.B. Membrane rigidity of red blood cells parasitized by different strains of Plasmodium falciparum. J. Lab. Clin. Med. 1993;122:581–589. [PubMed] [Google Scholar]
- 22.Hochmuth R.M. Erythrocyte membrane elasticity and viscosity. Ann. Rev. Physiol. 1987;49:209–219. doi: 10.1146/annurev.ph.49.030187.001233. [DOI] [PubMed] [Google Scholar]
- 23.Maier A.G., Cooke B.M., Tilley L. Malaria parasite proteins that remodel the host erythrocyte. Nat. Rev. Microbiol. 2009;7:341–354. doi: 10.1038/nrmicro2110. [DOI] [PubMed] [Google Scholar]
- 24.Vlahovska P.M., Podgorski T., Misbah C. Vesicles and red blood cells in flow: from individual dynamics to rheology. C. R. Phys. 2009;10:775–789. [Google Scholar]
- 25.Fedosov D.A., Caswell B., Karniadakis G.E. A multiscale red blood cell model with accurate mechanics, rheology, and dynamics. Biophys. J. 2010;98:2215–2225. doi: 10.1016/j.bpj.2010.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Hochmuth R.M., Mohandas N., Blackshear P.L., Jr. Measurement of the elastic modulus for red cell membrane using a fluid mechanical technique. Biophys. J. 1973;13:747–762. doi: 10.1016/S0006-3495(73)86021-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Hochmuth R.M., Worthy P.R., Evans E.A. Red cell extensional recovery and the determination of membrane viscosity. Biophys. J. 1979;26:101–114. doi: 10.1016/S0006-3495(79)85238-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Cranston H.A., Boylan C.W., Krogstad D.J. Plasmodium falciparum maturation abolishes physiologic red cell deformability. Science. 1984;223:400–403. doi: 10.1126/science.6362007. [DOI] [PubMed] [Google Scholar]
- 29.Mauritz J.M.A., Tiffert T., Kaminski C.F. Detection of Plasmodium falciparum-infected red blood cells by optical stretching. J. Biomed. Opt. 2010;15:030517. doi: 10.1117/1.3458919. [DOI] [PubMed] [Google Scholar]
- 30.Handayani S., Chiu D.T., Russell B. High deformability of Plasmodium vivax-infected red blood cells under microfluidic conditions. J. Infect. Dis. 2009;199:445–450. doi: 10.1086/596048. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


