Factors Influencing Ascertainment Bias of Microsatellite Allele Sizes: Impact on Estimates of Mutation Rates

Abstract

Microsatellite loci play an important role as markers for identification, disease gene mapping, and evolutionary studies. Mutation rate, which is of fundamental importance, can be obtained from interspecies comparisons, which, however, are subject to ascertainment bias. This bias arises, for example, when a locus is selected on the basis of its large allele size in one species (cognate species 1), in which it is first discovered. This bias is reflected in average allele length in any noncognate species 2 being smaller than that in species 1. This phenomenon was observed in various pairs of species, including comparisons of allele sizes in human and chimpanzee. Various mechanisms were proposed to explain observed differences in mean allele lengths between two species. Here, we examine the framework of a single-step asymmetric and unrestricted stepwise mutation model with genetic drift. Analysis is based on coalescent theory. Analytical results are confirmed by simulations using the simuPOP software. The mechanism of ascertainment bias in this model is a tighter correlation of allele sizes within a cognate species 1 than of allele sizes in two different species 1 and 2. We present computations of the expected average allele size difference, given the mutation rate, population sizes of species 1 and 2, time of separation of species 1 and 2, and the age of the allele. We show that when the past demographic histories of the cognate and noncognate taxa are different, the rate and directionality of mutations affect the allele sizes in the two taxa differently from the simple effect of ascertainment bias. This effect may exaggerate or reverse the effect of difference in mutation rates. We reanalyze literature data, which indicate that despite the bias, the microsatellite mutation rate estimate in the ancestral population is consistently greater than that in either human or chimpanzee and the mutation rate estimate in human exceeds or equals that in chimpanzee with the rate of allele length expansion in human being greater than that in chimpanzee. We also demonstrate that population bottlenecks and expansions in the recent human history have little impact on our conclusions.

ASCERTAINMENT bias in population genetics is usually studied in two contexts. One is discovery of polymorphic loci and it is best illustrated by the example of single nucleotide polymorphisms (SNPs). As demonstrated in a number of articles, taking into account the ascertainment scheme is a very important aspect of SNP data analysis. For example, Polanski and Kimmel (2003) derived expressions for modeling the way in which ascertainment modified SNP sampling frequencies and distorted inferences concerning the mutation rate. A more recent article (Albrechtsen et al. 2010) considers chip-based high-throughput genotyping, which has facilitated genome-wide studies of genetic diversity. Many studies have utilized these large data sets to make inferences about the demographic history of human populations. However, again, the SNP chip data suffer from ascertainment biases caused by the SNP discovery process in which a small number of individuals from selected populations are used as discovery panels. Albrechtsen et al. (2010) demonstrate that the ascertainment bias distorts measures of human diversity and may change conclusions drawn from these measures in unexpected ways. They also show that details of the genotyping calling algorithms may have a surprisingly large effect on population genetic inferences. This type of ascertainment bias will be of importance in forthcoming genetic and genomic studies.

However, this article is concerned with a different type of ascertainment bias, which occurs in interspecies or interpopulation studies. If a genetic measure of variability or diversity such as heterozygosity, and its underlying causes such as mutation, are studied in more than one species, a careful consideration of the sampling scheme used as basis for comparison is needed. Depending on from which species the polymorphisms are ascertained, the comparison of variability between the two species may be biased in a given direction. We consider a specific scenario in which two extant species, such as human and chimpanzee, are traced to a common ancestral species. We consider microsatellite loci, which can be modeled mathematically in a relatively simple way, so that the forward-time simulations can be compared to analytical computations.

We study ascertainment bias of interspecies (population) studies of microsatellite loci, which occurs when a locus is selected on the basis of its large allele size in the species in which it is first discovered (say, the cognate species 1). This bias is reflected in average allele length in any noncognate species 2 being smaller than that in species 1. This phenomenon was observed in various pairs of species, including human and chimpanzee. Various mechanisms were proposed to explain the observed differences in mean allele lengths between two species. Here, we examine the simplest possible framework: a single-step asymmetric and unrestricted stepwise mutation model with genetic drift. The mathematical model analyzed is based on coalescent theory. The mechanism of ascertainment bias in this model is a tighter correlation of allele sizes within a cognate species 1 than of allele sizes in two different species 1 and 2. We present computations of the expected bias, given the mutation rate, population sizes of species 1 and 2, time of separation of species 1 and 2, and the age of the allele.

Microsatellite polymorphisms, characterized by variations of copy numbers of short motifs of nucleotides, have become a common tool for gene mapping and evolutionary studies since they are abundantly found in genomes of a large number of organisms (Pena et al. 1993; Bowcock et al. 1994; Deka et al. 1994; Primmer and Ellegren 1998). High mutation rate at these loci is the attractive feature of using the microsatellites as tools for molecular evolutionary studies, since consequences of accumulation of past mutation events are seen as differences of allele frequency distributions even in closely related taxa (Weber and Wong 1993; Kimmel and Chakraborty 1996; Chakraborty et al. 1997). However, in cross-species comparisons of allele size distributions at microsatellite loci, some apparently discordant findings (namely, a systematic bias of average allele sizes in one species as compared to another) led some investigators to argue that these repeat loci may not be the most efficient tools for interspecies studies (Rubinsztein et al. 1995; Crawford et al. 1998). In general, for evolutionary studies microsatellite loci as identified in one species (or population) are studied in other species (or populations), making use of their genome homology. Nevertheless, the process of detection (in the cognate species) and its use in a noncognate species may inherently affect the allele size distribution and associated other summary measures of genetic variation (such as heterozygosity, allele size variance, or number of segregating alleles). This discordance, called the ascertainment bias, is claimed to have been observed in sheep (Forbes et al. 1995), swallows, cetaceans, ruminants, turtles, and birds (Ellegren et al. 1995). However, Rubinsztein et al. (1995) and Amos and Rubinsztein (1996) explained such observations as intertaxa differences of rates and patterns of mutations at microsatellite loci.

The goal of this study is to address this issue. Our approach is different from other attempts to study similar problems (see, e.g., Rogers and Jorde 1996). We consider a general model of mutations (called the generalized stepwise mutation model, GSMM) that is shown to be applicable to microsatellites (Kimmel et al. 1996; Kimmel and Chakraborty 1996) on which we superimpose the effects of demographic differences of cognate and noncognate taxa, as both of these factors are known to jointly affect the features of polymorphisms at microsatellite loci in extant taxa (Kimmel et al. 1998). In particular, using coalescent theory, we show that when the past demographic histories of the cognate and noncognate taxa are different, the rate and directionality of mutations affect the allele sizes in the two taxa differently than the simple effect of ascertainment bias.

Materials and Methods

Evolution of a DNA-repeat locus

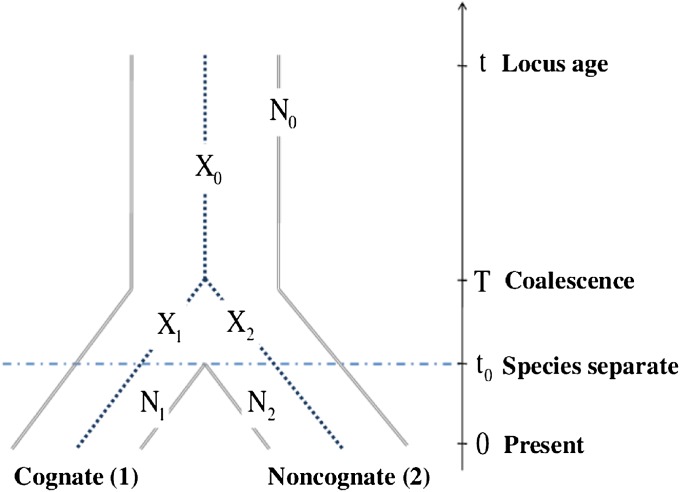
We consider a DNA-repeat locus that has originated t units of time ago (at backward or reverse time t), and observed at present (time 0). The adjective “backward” will usually be omitted. Chromosomes containing the locus belong to one of the two populations (labeled 1 and 2), which diverged t₀ time units before present (time t₀) from an ancestral population (labeled 0). The essentials are depicted in Figure 1.

Figure 1.

Evolutionary history of a locus in two species. Demographic scenario employed in the mathematical model and simuPOP simulations. Notation: N₀, N₁, and N₂, effective sizes of the ancestral, cognate, and noncognate populations, respectively; X₀, X₁, and X₂, increments of allele sizes due to mutations in the ancestral allele, in chromosome 1 and in chromosome 2, respectively.

The ancestral population consists of 2N₀ chromosomes and populations 1 and 2 of 2N₁ and 2N₂ chromosomes, respectively. We assume the time-continuous Fisher–Wright–Moran model (Kimmel et al. 1998). At the locus considered, alleles mutate according to the unrestricted GSMM (Kimmel and Chakraborty 1996). Specifically, the action of genetic drift and mutation can be represented by the following coalescence/mutation model:

1. Chromosomes 1 and 2, sampled at time 0 from populations 1 and 2, respectively, have a common ancestor T units of time before present (Figure 1). Random variable T has exponential distribution with parameter 1/(2N₀), shifted by t₀, i.e.,

   $$\mathrm{Pr}\left[T>\tau \right]=\{\begin{array}{ll}1,\hfill & \tau \le t_0,\hfill \\ \exp \left[-\left(\tau -t_0\right)/\left(2N_0\right)\right],\hfill & \tau >t_0.\hfill \end{array}$$ (1)

   In other words, as long as the two chromosomes or their direct ancestors belong to different populations (i.e., for τ ≤ t₀, in backward time), they cannot coalesce. From the moment the populations converge (i.e., for τ > t₀ in reverse time), the distribution of the time to coalescence is exponential with parameter 1/(2N₀).

2. Chromosomes 1 and 1′, sampled at time 0 from population 1, have a common ancestor T units of time before present, either in population 1, if T ≤ t₀ or in the ancestral population 0, if T > t₀. Therefore, the random variable T has a more complex distribution of the form,

   $$\mathrm{Pr}\left[T>\tau \right]=\{\begin{array}{ll}\exp \left[-\tau /\left(2N_1\right)\right],\hfill & \tau \le t_0,\hfill \\ \exp \left[-t_0/\left(2N_1\right)-\left(\tau -t_0\right)/\left(2N_0\right)\right],\hfill & \tau >t_0.\hfill \end{array}$$ (2)

   In other words, as long as the two chromosomes or their direct ancestors belong to population 1 (i.e., for τ ≤ t₀, in backward time), they coalesce with intensity 1/(2N₁). From the moment the species converge (i.e., for τ > t₀ in backward time), the coalescence intensity is 1/(2N₀).

3. Initial size (number of repeats) at the locus at time (t) of the origin of the locus is equal to a constant. Choosing this constant equal to 0 is not a restrictive assumption. In our model, we assume that before time t there were no mutation events.

4. Mutation epochs along the lines of descent occur according to a Poisson process with constant intensities ν₀, ν₁, and ν₂ in populations 0, 1, and 2, respectively. Each mutation event alters the allele size S by adding to it a random number of repeats U, i.e.,

   $$S\to S+U.$$

U is an integer-valued random variable (rv) with probability generating function (pgf)

$${\varphi }_k\left(s\right)=E\left(s^U\right)={\displaystyle \sum _{i=-\mathrm{\infty }}^{\mathrm{\infty }}\mathrm{Pr}\left[U=i\right]s^i}.$$

The pgf ϕ_k(s) and, equivalently, the distribution of U is generally different in each population k (k = 0, 1, 2). Consequently, the change of the allele size, during a time interval of length Δt spent in population k is a compound Poisson random variable with pgf exp{νΔt[ϕ_k(s) − 1]}. For the asymmetric single-step stepwise mutation model (SSMM), we have

$${\varphi }_k\left(s\right)=b_{k}s+d_k/s,$$ (3)

where b_k = Pr[U = 1] and d_k = Pr[U = −1] = 1 − b_k are the respective probabilities of expansion and contraction of the allele in a single mutation epoch.

Remark. The model is formulated as if the length of generation in species 0, 1, and 2 were identical. However, the mutation rates and populations sizes can be rescaled, to accomodate different generation time as explained in the section concerning modeling (below). Indeed all results in the following section are invariant under rescaling. We return to this issue in the Discussion.

Conditional Distributions and Ascertainment Bias of Allele Sizes

The main purpose of this section is to use the coalescent theory (as reviewed by Tavaré 1984) to derive conditional expected allele size at a chromosome, given the allele size on another chromosome sampled either from a different or from the same population as the original chromosome. This information is crucial for obtaining estimates of the ascertainment bias in conjunction with other effects.

Chromosomes sampled from populations 1 and 2

We use notation as in Figure 1: X₀, X₁, and X₂ denote the incremental changes of allele sizes (or, simply, allele sizes) in the ancestral chromosome 0, and in chromosomes 1 and 2, respectively. Conditionally on T, X₀, X₁, and X₂ are independent random variables. Let us note that while chromosome 0 always lives in population 0, chromosomes 1 and 2 begin their lives in population 0 and then continue in populations 1 and 2. Let Y₁ = X₀ + X₁ and Y₂ = X₀ + X₂ denote the allele sizes at time 0 (present time) at chromosomes 1 and 2, respectively. We first compute the expected allele size at chromosome 2, jointly with the allele size at chromosome 1 being equal to i (conditional on {T = τ}),

$$\begin{array}{c}E\left[Y_2;Y_1=i|T=\tau \right]={\displaystyle {\sum }_{j}E\left[X_0+X_2;X_0=j;X_1=i-j|T=\tau \right]}\\ =E\left[X_2|T=\tau \right]\mathrm{Pr}\left[Y_1=i|T=\tau \right]\\ \hspace{1em}+{\displaystyle {\sum }_{j}j\hspace{0.17em}\mathrm{Pr}\left[X_0=j|T=\tau \right]\mathrm{Pr}\left[X_1=i-j|T=\tau \right]}.\end{array}$$ (4)

In the terms of probability generating functions, we obtain

$${\displaystyle \sum _{i}E\left[Y_2;Y_1=i|T=\tau \right]s^i}=E\left[X_2|T=\tau \right]f_{X_0|T=\tau }\left(s\right)f_{X_1|T=\tau }\left(s\right)+s {f_{X_0}^{\prime }}_{|T=\tau }\left(s\right)f_{X_1|T=\tau }\left(s\right).$$ (5)

For more details, see Supporting Information, File S1 (Derivation of Equations 5 and 6).

Chromosomes sampled from population 1

Using the same reasoning, we obtain

$${\displaystyle \sum _{i}E\left[Y_1^{\prime };Y_1=i|T=\tau \right]s^i}=E\left[X_1^{\prime }|T=\tau \right]f_{X_0|T=\tau }\left(s\right)f_{X_1|T=\tau }\left(s\right)+s {f_{X_0}^{\prime }}_{|T=\tau }\left(s\right)f_{X_1|T=\tau }\left(s\right).$$ (6)

Probability generating functions and expectations of incremental changes of allele sizes

Random variables X₀, X₁, and X₂ result from compounding the Poisson process (Kingman 1993) of mutations, with varying intensities ν₀, ν₁, and ν₂, by distributions of allele size changes with pgf’s ϕ₀(s), ϕ₁(s), and ϕ₂(s) , respectively. Without getting into detail, we obtain

$$f_{X_0|T=\tau }\left(s\right)=\{\begin{array}{ll}\exp \left\{\left(t-t_0\right){\nu }_0\left[{\varphi }_0\left(s\right)-1\right]+\left(t_0-\tau \right){\nu }_1\left[{\varphi }_1\left(s\right)-1\right]\right\},\hfill & \tau \le t_0,\hfill \\ \exp \left\{\left(t-\tau \right){\nu }_0\left[{\varphi }_0\left(s\right)-1\right]\right\},\hfill & t_0<\tau \le t,\hfill \\ 1,\hfill & \tau >t,\hfill \end{array}$$ (7)

$$f_{X_i|T=\tau }\left(s\right)=\{\begin{array}{ll}\exp \left\{\tau {\nu }_i\left[{\varphi }_i\left(s\right)-1\right]\right\},\hfill & \tau \le t_0,\hfill \\ \exp \left\{\left(\tau -t_0\right){\nu }_0\left[{\varphi }_0\left(s\right)-1\right]+t_0{\nu }_i\left[{\varphi }_i\left(s\right)-1\right]\right\},\hfill & t_0<\tau \le t,\hfill \\ \exp \left\{\left(t-t_0\right){\nu }_0\left[{\varphi }_0\left(s\right)-1\right]+t_0{\nu }_i\left[{\varphi }_i\left(s\right)-1\right]\right\},\hfill & \tau >t,\hfill \end{array}$$ (8)

for i = 1, 2. Also, $f_{X_1^{\prime }|T=\tau }\left(s\right)\equiv f_{X_1|T=\tau }\left(s\right)$. The conditional expected values are obtained by differentiation of respective pgf’s and setting s = 1.

Computational expressions for E[Y₂; Y₁ = i] and $E\left[Y_1^{\prime };Y_1=i\right]$

In the SSMM, the pgf’s ϕ₀(s), ϕ₁(s), and ϕ₂(s) have the form as in Equation 3. We note the expansion

$$e^{\nu t\left[bs+d/s-1\right]}={\displaystyle \sum _{i\in Z}{\beta }_i{s}^i}={\displaystyle \sum _{i\in Z}{e}^{-\nu t}{I}_i\left(2\nu t\sqrt{bd}\right){\left(\frac{b}{d}\right)}^{i/2}{s}^i},$$ (9)

valid for |s| = 1, where I_i = I_−i is the modified Bessel function of the first type, of integer order i (Abramowitz and Stegun 1972). Using this expansion, it is possible to represent the right-hand sides of Equations 5 and 6 as power series in variable s. Finally,

$$E\left[Y_2;Y_1=i\right]={\displaystyle {\int }_0^{\mathrm{\infty }}E\left[Y_2;Y_1=i|T=\tau \right]f_T\left(\tau \right)d\tau },$$ (10)

$$E\left[Y_1^{\prime };Y_1=i\right]={\displaystyle {\int }_0^{\mathrm{\infty }}E\left[Y_1^{\prime };Y_1=i|T=\tau \right]f_T\left(\tau \right)d\tau },$$ (11)

where f_T(τ) is the distribution density of the time to coalescence, based on relationships (1) and (2), respectively. A computational expression for Pr[Y₁ = i] can be similarly obtained from

$$\text{Pr}\left[Y_1=i\right]={\displaystyle {\int }_0^{\mathrm{\infty }}\text{Pr}\left[Y_1=i|T=\tau \right]f_T\left(\tau \right)d\tau }.$$ (12)

Suppose that a DNA-repeat locus discovered in a genome search of population 1 is retained for further study if it has a minimum number of x repeats of the motif, i.e., if

$$Y_1\ge x.$$

The number of repeats (allele size) serves here as a substitute measure of the locus’ variability. The reason is that, irrespective of directionality of mutational changes, in the GSMM, the extremes of repeat count are strongly positively correlated with variance of repeat count and heterozygosity at the locus. The latter is a consequence of the random-walk mechanism of mutations in this model (Kimmel and Chakraborty 1996).

If the locus is retained and a sample of n individuals from the noncognate population 2 is typed for this locus, then the expected value of the mean repeat count in the sample is equal to

$$E\left[\frac{1}{n}{\displaystyle \sum _{i=1}^n{Y}_{2i}|Y_1\ge x}\right]=E\left[Y_2|Y_1\ge x\right]=\frac{{\displaystyle {\sum }_{i\ge x}E\left[Y_2;Y_1=i\right]}}{{\displaystyle {\sum }_{i\ge x}\mathrm{Pr}\left[Y_1=i\right]}}.$$ (13)

If a sample of n individuals of the cognate population 1 is typed for this locus, then the expected values of the mean repeat count in the sample is equal to

$$E\left[\frac{1}{n}{\displaystyle \sum _{i=1}^n{Y}_{1i}^{\prime }|Y_1\ge x}\right]=E\left[Y_1^{\prime }|Y_1\ge x\right]=\frac{{\displaystyle {\sum }_{i\ge x}E\left[Y_1^{\prime };Y_1=i\right]}}{{\displaystyle {\sum }_{i\ge x}\mathrm{Pr}\left[Y_1=i\right]}}.$$ (14)

The mean allele size difference, D, which is due to a combined effect of ascertainment bias and intrinsic genetic factors, can be defined as

$$D=E\left[Y_1^{\prime }|Y_1\ge x\right]-E\left[Y_2|Y_1\ge x\right].$$ (15)

Simulation method

Despite the complexity of the theory involved in the study of ascertainment bias, simulation of such a process is straightforward using simuPOP, a general-purpose individual-based forward-time population genetics simulation environment (Peng and Kimmel 2005). We consider a microsatellite locus founder population with N₀ individuals (2N₀ chromosomes). We consider a diploid with initial allele size on each chromosome to be 100. The founder population is evolved for t − t₀ generations before two copies of this population of sizes N₁ and N₂ are created, which are evolved for another t₀ generations.

Direct execution of simulations for tens of thousands of generations is time consuming. The probability that a random allele exceeds a specified threshold may be low; therefore, many attempts may be needed to obtain an estimate of ascertainment bias.

This problem can be addressed through the use of a scaling technique (Hoggart et al. 2007). Compared to a regular simulation that evolves a population of size N for t generations, a scaled simulation with a scaling factor λ evolves a smaller population of size N/λ for t/λ generations with magnified (multiplied by λ) mutation, recombination, and selection forces. This method can be justified by a diffusion approximation to the standard Wright–Fisher process (Ewens 2004; Hoggart et al. 2007); however, because the diffusion approximation applies only to weak genetic forces in the evolution of haploid sequences, it cannot be involved when nonadditive diploid or strong genetic forces are used. Simulation study has been performed with a scaling factor λ, where populations with sizes N_i/λ are evolved for t_i/λ generations, under mutation models with mutation rates λν, where N_i ∼ 10⁴ − 10⁶, t_i ∼ 10³ − 10⁵ and ν_i ∼ 10⁻⁴ are values typical of human and primate effective population sizes, evolutionary history, and microsatellite mutation rates. Running the simulations with different scaling factors yields identical results if λ ≤ 100 (λ = 1000, 500, 100, 50, 10 have been tested).

Results

Summary of modeling results

The purpose of modeling is to determine in what circumstances the presence or absence of differences, observed in sizes of alleles at loci discovered in a cognate species (population 1) and then typed in a noncognate species (population 2), can be attributed to ascertainment bias or alternatively to differential effects of genetic drift or mutation rate and pattern. Let us first review the intuitions concerning these effects. These intuitions are valid independently of a particular model of mutations:

1. The observed difference between allele sizes, Equation 15, results from a stronger correlation between allele states of chromosomes in cognate population 1 as compared to noncognate population 2.

2. Reduced genetic drift in population 1 may reduce the effects of ascertainment bias. Indeed, if the cognate population 1 is much larger than the noncognate population 2, then the coalescence process within population 1 has the star-like structure characterized by reduced dependence of allele states (Tajima 1989). Therefore, the difference between correlations of allele states of chromosomes in cognate population 1 and noncognate population 2 will be reduced. Note that the size of the noncognate population 2 will not influence the difference of expected allele sizes, but it may influence other indices of polymorphism.

3. Mutation rate and pattern, different in populations 1 and 2, influence the differences in allele sizes between different populations.

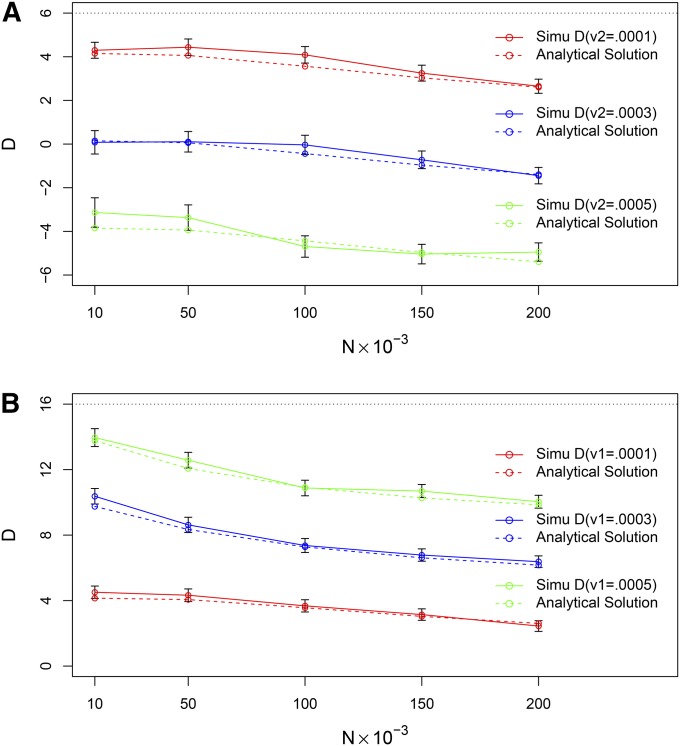
Figure 2 depicts a series of modeling studies of D, the combined effect of ascertainment bias, genetic drift, and differential mutation rate on the mean repeat count, based on simuPOP model, compared to those obtained using Equation 15. The error bar refers to mean ±2 × SEM (standard error of the mean) of simulated D values from 1000 replicates. Parameter values approximate the evolutionary dynamics of dinucleotides in humans and chimpanzees: time from divergence of species t₀ = 4 × 10⁶ years = 2 × 10⁵ generations for Figure 2 (assuming 20 years per generation), the age of the repeat locus t = 1 × 10⁷ years = 5 × 10⁵ generations, mutation rate ν = 1 × 10⁻⁴ per generation, and probability of increase of allele size in a single mutation event, b = 0.55. Effective size of the current human population is 2N = 4 × 10⁵ individuals.

Figure 2.

Observed difference D in allele sizes may be positive or negative. Comparison of simuPOP simulations with computations based on Equation 15. (A) Values of D for the basic parameter values b₀ = b₁ = b₂ = b = 0.55, ν₀ = ν₁ = ν = 0.0001, t₀ = 2 × 10⁵ generations, and t = 5 × 10⁵ generations, with the effective sizes of all populations concurrently varying from 2 × 10⁴ to 4 × 10⁵ individuals and with mutation rates ν₂ varying from ν to 5ν. (B) Values of D for the basic parameter values b₀ = b₁ = b₂ = b = 0.55, ν₀ = ν₂ = ν = 0.0001, t₀ = 2 × 10⁵ generations, and t = 5 × 10⁵ generations, with the effective sizes of all populations concurrently varying from 2 × 10⁴ to 4 × 10⁵ individuals and with mutation rates ν₁ varying from ν to 5ν (assuming 20 years per generation).

Figure 2A depicts the values of D for the basic parameter values b₀ = b₁ = b₂ = b = 0.55, and ν₀ = ν₁ = ν = 0.0001, with the effective sizes of all populations concurrently varying from 2 × 10⁴ to 4 × 10⁵ individuals and with mutation rates ν₂ varying from ν to 5ν. Figure 2B depicts the values of D for the basic parameter values b₀ = b₁ = b₂ = b = 0.55, and ν₀ = ν₂ = ν = 0.0001, with the effective sizes of all populations concurrently varying from 2 × 10⁴ to 4 × 10⁵ individuals and with mutation rates ν₁ varying from ν to 5ν . These two figures make it explicit that the combined effect of ascertainment bias, genetic drift, and differential mutation rate on the mean repeat count can result in a range of D values from positive to negative ones.

For the purpose of obtaining sets of model parameters that yield good fit to the experimental observation of allele length differences, we have applied the genetic algorithm (Mitchell 1996) as a search heuristic to explore an arguably realistic parameter space that specifes a variety of discrete values within a reasonable range to each of the key parameters. We set t to vary in the range from 440,000 to 740,000; t₀ from 250,000 to 400,000; N₀ from 10,000 to 85,000; N₁ from 5,000 to 12,000; N₂ from 10,000 to 25,000; ν₀, ν₁, ν₂ from 5 × 10⁻⁵ to 1 × 10⁻³; b₀, b₁, b₂ from 0.51 to 0.55; x from 12 to 18. Discussion and Conclusions involves more detail about settings of these ranges. In the genetic algorithm of optimization (fitting), each parameter range is encoded by a two- to six-bit vector, yielding 2² to 2⁶ possible values. An initial “pseudo-population” was created by setting X randomly chosen parameter combinations as X “individuals.” The value of each modeling parameter in any individual has been converted to binary format to become a 0–1 sequence. Each sequence can be treated as a “chromosome.” Thus, the genome of an individual consists of a complete heritable parameter setting. By evolving the population under the Wright–Fisher model for Y generations with mutation and crossover, it yields by selection the individuals that can best fit the experimental observation. We compare modeling results to observations of Cooper et al. (1998); see the next section for detail.

In the currently implemented ascertainment scheme, we assume P(L ≥ x) ≤ 0.25 to ensure that the probability of choosing polymorphic loci is relatively small (cf. Table 1B). Given a set of input parameter values (including t, t₀, N, b, and x), P(L ≥ x) can be approximated by the cumulative distribution function of the Gaussian distribution shown in File S1 (section Derivation of the range for the estimate of t). If a parameter set yields P(L ≥ x) > 0.25 then it will be excluded. The cutoff 0.25 has been chosen heuristically. If a cutoff >0.25 is adopted, the parameter values to fit D_CH and D_HC are easier to find. The opposite holds if the cutoff is <0.25. The 0.25 value seems to lead to a parsimonious variant of acceptable parameter values.

Table 1. Parameter settings that yield a good fit, for a range of realistic effective population sizes and mutation rates.

t	t0	N0	N1	N2	ν0	ν1	ν2	b0	b1	b2	x	DHC	DCH
A.
540	270	15	6	15	0.00012	0.00006	0.00002	0.55	0.55	0.55	12	5.17	1.30
550	280	10	9	10	0.00012	0.00006	0.00002	0.55	0.55	0.55	12	5.06	1.10
570	300	15	3	20	0.00030	0.00022	0.00016	0.55	0.55	0.55	12	5.35	1.29
560	290	20	5	20	0.00030	0.00016	0.00010	0.55	0.55	0.55	12	5.27	1.14
460	250	25	10	12	0.00030	0.00055	0.00045	0.55	0.55	0.55	12	5.42	1.24

B.
580	260	10	7	25	0.00075	0.00020	0.00005	0.51	0.51	0.51	18	5.18	1.26
720	250	15	8	23	0.00015	0.00010	0.00005	0.55	0.55	0.55	18	5.17	1.22
620	250	10	10	17	0.00010	0.00010	0.00005	0.55	0.55	0.55	12	5.30	1.44
660	250	10	12	25	0.00055	0.00025	0.00010	0.51	0.51	0.51	18	5.45	1.76
740	260	10	12	25	0.00035	0.00020	0.00010	0.51	0.51	0.51	15	5.02	2.11

C.
720	260	10	11	13	0.00025	0.00010	0.00010	0.51	0.55	0.51	13	5.08	1.20
740	250	10	7	11	0.00020	0.00010	0.00010	0.52	0.55	0.51	14	5.08	1.33
740	260	10	12	18	0.00020	0.00010	0.00010	0.51	0.55	0.51	12	5.17	1.22
740	260	10	10	15	0.00020	0.00010	0.00010	0.51	0.55	0.51	12	5.22	1.30
680	250	10	9	16	0.00025	0.00010	0.00010	0.51	0.55	0.51	15	5.44	1.59

Information of the plausible range of each input parameter was retrieved from the literature (details in Discussion and Conclusions). Times t and t₀ are expressed in thousands of generations (assuming 20 years per generation). Population sizes N₀, N₁, and N₂ are expressed in thousands of individuals. D_HC is the calculated average allele length difference on human loci that are typed in chimpanzee and D_HC is the reciprocal difference. Top (A): best fits from an explorary parameter search given a broad range of mutation rates (from 10⁻⁵ to 10⁻³), with parameters b₀, b₁, b₂, and x set as default values (b₀ = b₁ = b₂ = 0.55, x = 12). The mutation rates in the two best fits are below the generally accepted range. Although the other three fits yield acceptable mutation rate estimates, the parameter combinations result in very high probabilities of finding polymorphic loci, P(L ≥ x) > 0.25 Middle (B): P(L ≥ x) ≤ 0.25 is assumed to ensure that the probability of choosing polymorphic loci is relatively small. Parameters b₀, b₁, b₂ are set equal and range from 0.51 to 0.55. x ranges from 12 to 18. The best fits are obtained when ν₂ is equal to the minimum possible value (5 × 10⁻⁵), while fits become slightly worse if ν₂ is increased (10⁻⁴). Bottom (C): when P(L ≥ x) ≤ 0.25 is still required while b₀, b₁ and b₂ are allowed to vary independently, the parameter search tends to favor b₁ > b₂ and small x (< 15) to yield best fits. In B and C with t, t₀, N, b, and x assuming ranges of possible values when P(L ≥ x) ≤ 0.25, ν₀ is always greater than ν₁ and ν₂; ν₁ is greater than or equal to ν₂; ν₁b₁ is always greater than ν₂b₂.

Comparisons of empirical statistics derived from human and chimpanzee microsatellite data

We apply our model to analyze the well-known data set published by Cooper et al. (1998). These authors examined 40 human microsatellite markers and their homologs in a panel of nonhuman primates and showed that human loci tend to be longer. Such a trend was also confirmed by several other studies. Taken at face value, these data indicated that, since their most recent common ancestor, more microsatellite expansion mutations have occurred in the lineage leading to humans compared with the lineage leading to chimpanzees. Based on this, they suggested that this provided evidence that microsatellites tended to expand with time and were doing so more rapidly in humans. However, an alternative explanation, which attributes the difference to the influence of ascertainment bias, may also result in the observation of allele length difference. Therefore, Cooper et al. (1998) performed the necessary reciprocal experiment showing that human microsatellites tend to be longer than their chimpanzee homologs, regardless of the species from which the loci were cloned.

Dinucleotide (CA) repeat loci discovered and characterized in humans (n = 22) were on average 5.18 repeat units longer than those in chimpanzees, while dinucleotide repeats discovered in chimpanzees (n = 25) were on average 1.23 repeat units longer in humans. Table 1 lists best fits of three independent parameter searching results based on the genetic algorithm, with setup of X = 100, Y = 1000 probability of crossover = 0.6, and mutation rate = 0.02 in each search. Table 1A shows best fits from an exploratory parameter search given a broad range of mutation rates (from 10⁻⁵ to 10⁻³), while b₀, b₁, b₂, and x are set as default values (b₀ = b₁ = b₂ = 0.55, x = 12). The mutation rates in the top two best fits are below generally accepted ranges, ν₂ = 2 × 10⁻⁵ < 5 × 10⁻⁵. Although the other three fits yield feasible mutation rate estimates, the parameter combinations result in very high probabilities of finding polymorphic loci, P(L ≥ x) > 0.25. In Table 1B, P(L ≥ x) ≤ 0.25 is assumed to ensure that the probability of choosing polymorphic loci is relatively small. b₀, b₁, b₂ are set to be equal and range from 0.51 to 0.55. x ranges from 12 to 18. The best fits are obtained when ν₂ is equal to the minimum possible value (5 × 10⁻⁵), while fits become slightly worse if ν₂ is increased (10⁻⁴). In Table 1C, when P(L ≥ x) ≤ 0.25 is still required while b₀, b₁, b₂ are allowed to vary independently, the parameter search tends to favor b₁ > b₂ and small x (< 15) to yield best fits.

For a range of evolutionary times, effective population sizes and mutation rates, higher mutation rates, and rates of allele length expansions are always observed at human microsatellite loci compared to those in chimpanzee (ν₁ ≥ ν₂ and ν₁b₁ > ν₂b₂), consistent with Cooper et al. (1998) data.

Influence of bottlenecks and expansions in human history

While assuming a constant population size for chimpanzee, we explore the influence of bottlenecks and expansions in human history on the observed difference in allele lengths (D). We extend the current modeling scheme and derive the analytical solution to compute D with human cognate population size being arbitrarily varied from one generation to another.

Assume that the lineage of humans has been evolved following a multistep demographic model, where there are L steps with human population size varied from step to step. In the backward direction, we denote the present time in generation units as t_L = 0, the beginning and ending times of the mth step (m = 1, 2, …, L) as t_m−1 and t_m, and the population size of the mth step as N_m. As already defined, t and t₀ are the age of the locus and the time when the two species split, respectively, and N₀ is the ancestral population size.

Chromosomes 1 and 1′ sampled at time 0 from population 1 have a common ancestor T units of time before present, either in population 1 at stage m, if t_m ≤ T ≤ t_m−1 (for m = 1, 2, …, L) or in the ancestral population 0, if T ≥ t₀. Therefore,

$$P\left(T>\tau \right)=\{\begin{array}{ll}\exp \left[-{\displaystyle {\sum }_{k=m+1}^L\left(\frac{t_{k-1}-t_k}{2N_k}\right)-\frac{\tau -t_m}{2N_m}}\right],\hfill & t<\tau \le t_{m-1},\hfill \\ \exp \left[-{\displaystyle {\sum }_{k=1}^L\left(\frac{t_{k-1}-t_k}{2N_k}\right)-\frac{\tau -t_0}{2N_0}}\right],\hfill & \tau >t_{0.}\hfill \end{array}$$ (16)

for m = 1, 2, …, L. For derivation of an analog of Equation 11 in the extended model see File S1.

Taking a set of model parameters that fit the data from Table 1, t = 620,000, t₀ = 250,000, N₀ = N₁ = 10,000, N₂ = 17,000, ν₀ = 0.0001, ν₁ = 0.0001, ν₂ = 0.0005, b₀ = b₁ = b₂ = 0.55, x = 12 we obtain D(H − C) = 5.30 and D(C − H) = 1.44 in the modeling scheme assuming fixed human population size.

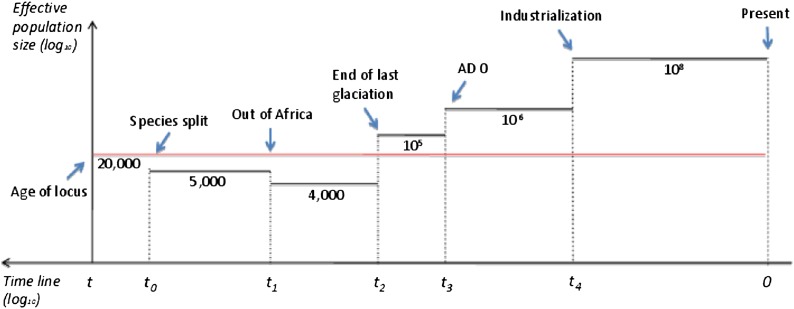
Figure 3 is a schematic representation of major bottlenecks and expansions in the recent human history. The locus was born in the ancestral population, t generations ago. From t₀ when the two species split, effective population sizes for human and chimpanzee were equal to N₁ and N₂ (e.g., 5000 and 20,000; Burgess and Yang 2008), respectively. At t₁ (∼200,000 years ago) when humans evolved to migrate out of Africa, a bottleneck event caused by the fact that a subpopulation of migrants was sampled from a larger African population occurred. Our stratified demographic model assumes that the decreased population size due to that bottleneck was constant until the end of the latest glaciation, t₂ (∼12,000 years ago). More precisely, it grew until the beginning of the last glaciation (∼50,000 years ago; Bond and Lotti 1995) and then dropped, but the influence of this detail is minor. After that, human population underwent a series of expansions, with its effective size being ∼10⁵ from the end of last glaciation (t₂) to 0 AD (t₃ ∼ 2000 years ago), ∼10⁶ from year 0 CE (t₃) to the emergence of industrialization (t₄ ∼ 180 years ago), and ∼10⁸ from t₄ to present time (current generation). Adapting the human demography with varying population sizes, as described above, in the extended model, we have calculated D(H − C) = 5.42 and D(C − H) = 5.42, compared to 5.30 and 1.44 obtained from the original model with fixed human population size. Using another set of model parameters from Table 1, t = 720,000, t₀ = 260,000, N₀ = 10,000, N₁ = 11,000, N₂ = 13,000 ν₀ = 0.00025, ν₁ = 0.0001, ν₂ = 0.0001, b₀ = b₂ = 0.51, b₁ = 0.55 x = 13 results in D(H − C) = 5.17 and D(C − H) = 1.20 obtained from the extended model, compared with 5.08 and 1.20 obtained from the original model. D(C − H) remains the same in the extended model because only the human effective population (N₁) has been varied. D(C − H) does not depend on N₁ but on N₂, which is assumed to be constant in both basic and extended models.

Figure 3.

Scheme of human demographic history with recent bottlenecks and expansions. Black line depicts human population, red line depicts ancestral and chimpanzee populations. t, age of the locus (∼560,000 generations ∼ 11.2 MYA); t₀, species split (∼290,000 generations ∼ 5.8 MYA); t₁, human migration out of Africa (∼10,000 generations ∼ 200,000 years ago); t₂, end of the last glaciation (∼600 generations ∼ 12,000 years ago); t₃, ad 0 (∼100 generations ∼ 2000 years ago); t₄, beginning of industrialization (∼9 generations ∼ 180 years ago).

We conclude that for the range of parameters we considered, population bottlenecks and expansions in the recent human history have little impact on the modeled difference of allele sizes based on the settings of model parameters used in Table 1 to fit the data. Finally, the mutation rate estimate in the ancestral population is consistently greater than that in chimpanzee and in human it is higher than or equal to that in chimpanzee.

Discussion and Conclusions

Computations presented in this article demonstrate that the scaled forward simulations using simuPOP closely match the analytical solution of the evolutionary model used. We note that mathematical derivation of Equation 15 depends on simplicity of the assumed microsatellite discovery criterion Y₁ ≥ x. If this criterion is replaced by a condition on heterozygosity or variance, the theoretical derivations become very difficult. On the other hand, it is easy to use any other microsatellite discovery criterion in simuPOP simulations.

Data of Cooper et al. (1998) indicate that when the human-derived dinucleotide repeat loci are typed in chimpanzee, they show a trend toward smaller mean allele sizes in the chimpanzee as compared to that in human populations. These and other data also suggest that the same holds for other measures of within-population variation (i.e., the chimpanzees showing lower heterozygosity and allele size variance, compared to humans; Vowles and Amos 2006). The theoretical model shows that these observations are in agreement with the presence of ascertainment bias, caused by a selective choice of human loci. In the reciprocal experiment, the chimpanzee-derived dinucleotides, typed in human populations, also show a trend toward smaller mean allele sizes in the chimpanzee as compared to that in human populations.

We adapted a genetic algorithm (Mitchell 1996) to perform an extensive parameter space search by specifying a number of values of each of the key modeling parameters (t, N, ν, b, and x; see Table 1 for details), which are variable within plausible ranges. Patterson et al. (2006) reviewed the estimated times of divergence of the two species (t₀) and determined that divergence occurred approximately between 250,000 and 350,000 generations ago. This corresponds to ∼5 to 7 million years by assuming 20 years per generation. For the purpose of modeling, the time when a particular locus was born (t) is computed to be varying ∼450,000 to 750,000 generations to ensure the threshold of allele size being large enough that the polymorphic locus occurs only relatively rarely (≤25% of loci; see Supporting Information: Derivation of t for details). Using both likelihood and Bayesian methods, Yang (2002), estimated that the ancestral (N₀) and chimpanzee (N₂) effective population sizes ranged from 10,000 to 20,000 individuals, and the human effective population size ranged from 3000 to 12,000 individuals (Burgess and Yang 2008). Chen and Li (2001) suggested a much larger effective population size, 50,000 ∼ 90,000, of the common ancestor of human and chimpanzee. We assign multiple numbers within these ranges as possible values of N₀, N₁, and N₂. Additionally, given that the microsatellite loci mutation rate in any population is >10⁻⁴, as analyzed by Ellegren (2000), ν₀, ν₁, ν₂ are assumed in a wide range starting from 5 × 10⁻⁵. Mutational biases (Sainudiin et al. 2004; Wu and Drummond 2011) b₀, b₁, b₂ range from 0.51 to 0.55. In this model, we assume such bias to be constant within a population. As demonstrated in Table 1, for a range of effective population sizes and evolutionary times, the estimated human mutation rates are always higher than or equal to those in chimpanzee and the mutation rate estimates in the ancestral population are always greater than those in either human or chimpanzee.

These observations imply that ascertainment bias is a significant factor in interpreting interpopulation genetic variation at microsatellite loci, when the loci are selectively chosen for polymorphism in one of the populations compared. Ascertainment bias effect is confounded by other differences in evolutionary dynamics between the cognate and noncognate populations, particularly by interpopulation differences of rates of mutations at the locus. As shown in Figure 2A, increased mutation rate in the noncognate population reduces the effect of the ascertainment bias, while increased mutation rate in the cognate population amplifies the effect of the bias (Figure 2B). On the other hand, the primary cause of ascertainment bias is a tighter correlation of allele sizes within the cognate population. Thus, intuitively it is clear that population size differences between cognate and noncognate populations may reduce or amplify the ascertainment bias. If the cognate population is of larger size or is growing more rapidly than the noncognate one, a reduced bias is expected.

The differences of patterns of biases seen at the dinucleotide loci discovered in human vs. chimpanzee can be explained by our model if the mutation rate is higher for humans. The observed pattern that ascertainment bias is of a lower magnitude for the chimpanzee-specific loci is also consistent with effective population size in chimpanzee being smaller than that in human. In this sense, our observations and theoretical predictions are consistent with the assertion of Rubinsztein et al. (1995), although expansion bias of mutations is not necessary to explain the observed differences in humans and chimpanzees.

As mentioned, when describing the model, the time and mutation rates (as well as effectively the population sizes) are scaled to the unit equal to the human generation length. This is convenient, and the numbers can be rescaled to accomodate different evolutionary parameters in different species. Our theory and data can also be used to explain the apparently discordant conclusions reached by other investigators examining this issue. For example, Ellegren et al. (1995) observed smaller allele sizes in noncognate species compared with cognates of birds, which could be predominantly due to ascertainment bias alone. Crawford et al. (1998), in contrast, found longer median allele sizes in sheep compared with cattle, regardless of the origin of the microsatellites. This may be the case where the ascertainment bias effect is counteracted or even reversed due to mutation rate and/or effective population size differences in sheep and cattle.

There had been discussions with regard to the dependence of interpopulation allele size differences on the absolute repeat lengths of alleles (Ellegren et al. 1995; Amos and Rubinsztein 1996). For microsatellites, there is a general tendency for an increased level of polymorphism at loci harboring larger alleles (Weber 1990). Our theory shows that loci exhibiting higher degrees of polymorphism are likely to be subject to lesser bias of ascertainment (due to lower correlation of allele sizes in the cognate population). Hence, appropriate adjustment of interlocus differences of polymorphism as well as allele sizes should be made in addressing the importance of ascertainment bias.

Vowles and Amos (2006) is an important contribution to the literature on ascertainment bias. Among others, these authors observed that long repeats tend to be interrupted, which contributes an additional bias. They also proposed that the difference D be explained if microsatellites evolve at different rates, with longer microsatellites evolving faster, this latter effect having some statistical rationale. In this article, we offer an explanation that does not rely on interruption nor acceleration, but only on sampling, and demographic and population-genetic effects, under constant though species-dependent mutation rates. However, there is at least some concordance; we find that human microsatellites, which are on average longer, also have higher mutation rates, which might be a hint that both approaches detect the same or similar effect.

In summary, we conclude that ascertainment bias is an important consideration for interpretation of interpopulation differences of genetic variation at microsatellite loci, but this bias can be reduced or even reversed when the past demographic histories of cognate and noncognate populations are different. In addition, mutation rate differences among populations can also influence or mimic ascertainment bias.