Development and application of ab initio QM/MM methods for mechanistic simulation of reactions in solution and in enzymes

Abstract

Determining the free energies and mechanisms of chemical reactions in solution and enzymes is a major challenge. For such complex reaction processes, combined quantum mechanics/molecular mechanics (QM/MM) method is the most effective simulation method to provide an accurate and efficient theoretical description of the molecular system. The computational costs of ab initio QM methods, however, have limited the application of ab initio QM/MM methods. Recent advances in ab initio QM/MM methods allowed the accurate simulation of the free energies for reactions in solution and in enzymes and thus paved the way for broader application of the ab initio QM/MM methods. We review here the theoretical developments and applications of the ab initio QM/MM methods, focusing on the determination of reaction path and the free energies of the reaction processes in solution and enzymes.

INTRODUCTION

Understanding the origin of catalytic power of enzymes is a major aim of biochemical study. Most biological functions are accomplished through the binding of ligands with protein or DNA/RNAs and subsequently a series of chemical reactions catalyzed by specific enzymes. As an essential link of the biomolecular interaction network, each individual enzymatic process contributes to the stability and regulation of the complicated biological processes, whose equilibrium and rate are often refined results from the evolution process. Investigating the origin of the catalytic power of enzymes helps deciphering key events and leads to understanding of complex biological processes. Furthermore, studying enzyme catalysis is also essential for the design of new or better inhibitors and enzymes, which have important practical applications ranging from drug design to the development of novel catalysts in industrial processes [1].

Experimental studies can provide crucial and indispensable information concerning the mechanism, thermodynamics, and kinetics for enzymatic reactions[2]. However, experimental data often provides indirect evidence and is thus insufficient for determining the detailed reaction mechanism [3]. Particularly, experimental study cannot directly determine the structure of the transition state, which is crucial not only for determination of the reaction mechanism but also for biomedicinal research such as inhibitor or drug design.

Complementary to experimental study, simulations can yield atomistic or even electronic information regarding the effects of site-specific interactions on the reaction process, the reaction path, and the structure of the transition state[4, 5, 6, 7, 8, 9, 10, 11]. Simulation studies of many enzymatic processes have addressed and also raised many important issues in enzyme catalysis such as covalent catalytic mechanisms [12, 13], contribution of the pre-organized electrostatic environment of enzymes[14, 15], the effects of strain and conformational dynamics of the enzyme-substrate complex [16, 17], non-equilibrium dynamical effects, and quantum tunnelling effects[18, 19]. Because the structural and dynamic properties of enzymes are complicated and can vary drastically between different enzymes, the origin of enzymatic proficiency remains a current topic of interest [3, 20]. Accurate simulation methods will definitely play a key role in the understanding of those complex interactions in the enzyme catalysis.

Solution reactions are also another important territory for theoretical study: Solution reactions are often defined as references for enzymatic reactions, while many synthesis and manufacturing of daily consumer products are achieved by solution reactions too. It is well known that solvent molecules play significant roles in chemical reactions in solution [21, 22, 23, 19]. Energetically, the complex electrostatic interactions between the solvent and solute molecules create a reaction environment completely different from gas phase, resulting in different chemical equilibrium and reaction rate. Dynamically, thermal fluctuation and diffusion of the solvent molecules serve as an energy bath to the motions of the reaction moieties, leading to different relaxation and barrier-crossing dynamics. In numerous cases, direct participation of the solvent molecule in the reaction not only can create a concentration effect, but may also alter the reaction path.

Compared with enzyme catalysis, simulation of solution reactions with explicit solvent contributions has brought less attention. Solution reactions are often simulated with varying levels of approximation, particularly for simulations employing ab initio QM approaches. One common practice is to simplify the contributions of the solvent molecules by using a continuum representation. This reduces the number of degrees of freedom in the simulation, but the isotropic continuum-medium model cannot always correctly reproduce the anisotropic, site-specific interactions between the solute and solvent molecules. For the same reaction, the key factor responsible for the varied rates and equilibrium between solution and enzyme reactions is the structural and dynamic difference between diffusive solvent molecules and organized enzyme structures. To make reliable comparison, both the solution and enzymatic reactions must be simulated at the same level of accuracy.

Advances in theory and computational resources have made the accurate free energies of gas-phase, small molecular reactions more and more approachable. However, for reactions in solution and enzymes, theoretical study is very difficult and incomprehensive because of the complexity of many degrees of freedom of solvents and/or enzyme. In the present review, we focus on the theoretical development and application of ab initio QM/MM free energy simulation methods for chemical reactions in solution and in enzymes. We will first discuss the calculation of the QM/MM energy, then general aspects of free energy simulation with QM/MM methods, and finally the methods for efficient determination of free energies of reactions in solution and in enzymes. Application examples will also be discussed.

QM/MM METHOD

General overview

To simulate a complex reaction in solution or enzymes, an accurate and computationally efficient energy function is necessary. A straightforward idea is to treat every components of the molecular system with the same accurate theory, e.g., quantum chemistry. Although rigorous on every degrees of freedom, this approach becomes impractical for large molecules due to the polynomially increasing demands for computational resources. Even with the development of linear-scaling quantum chemistry methods such as the divide-and-conquer approach [24, 25], full ab initio QM calculations can only be performed routinely for small molecules with number of atoms no more than a few hundred. The number of atoms of the interesting chemical or biological molecular system, however, usually exceeds thousands and often reaches hundreds of thousand. For system of such a size, a simplified description must be developed to allow efficient energy calculation and broad phase space sampling. This is indeed possible. A closer examination on the nature of the target problem reveals a common feature: Except for the electron transfer reaction which can occur at long distances in the molecular system, in many chemical reactions only a small number of atoms directly participate in the localized bond forming or breaking events. Of course the interactions of these small set of atoms must be described accurately. For other atoms of the system, their valence states do not undergo changes and thus make minimal direct contribution to the change of the electronic structure of the atoms in the active site. These atoms, such as the solvent molecules in the solution, do contribute to the reaction process by serving as a steric and electrostatic environment to influence the properties and reactivity of the active site. The importance of these environmental atoms can be illustrated by the sensitivity of many organic reactions to the chemical and physical properties of the solvents.

A good theory for simulating the reaction process thus needs to strike the balance between the accurate description of the chemical events in the active site and efficient modeling of the contributions of the complex environment. An effective approach in fact has been developed as a multi-resolution approach: The active site of the molecular system is described with highly accurate quantum theory, while the contribution of the rest of the system is described by approximate, yet efficient theories such as molecular mechanics. This combined QM/MM approach, first developed by Warshel and Levitt [26], allows reliable electronic structure calculations for enzymatic reactions with a realistic and atomistic description of the environment. This approach takes advantage of the applicability and accuracy of the QM methods for chemical reactions in systems of several tens of atoms and of the computational efficiency of the MM description for the rest of the enzyme and solvent, which normally consists of many thousands of atoms. Development of combined QM/MM methods has enabled simulations of complex chemical and biological processes, leading to significant advances in our understanding. In particular, simulations have generated considerable insight into chemical reaction mechanisms in solution and in enzymes, as discussed in several recent reviews [5, 8, 7, 27, 4, 10, 28, 11].

According to the level of QM theory used, QM/MM approach can be classified into two types. The first type employed semiempirical QM methods such as MNDO, AM1, PM3, empirical valence bond (EVB), and the recently developed self-consistent charge density functional tight binding (SCC-DFTB) method [21, 29, 30, 6]. Due to the outstanding computational efficiency, the majority of the work in the QM/MM field is carried out with this type of methods. The semiempirical QM calculations are so fast that direct MD sampling is readily affordable, and thus free energy and reaction dynamics calculations can be routinely performed. Nonetheless, the inherent deficiencies of semiempirical QM methods lead to poor reliability of the simulation results and subsequently limit the scope of applicability of the semiempirical QM/MM approaches.

The second type of QM/MM calculation directly employs ab initio QM via wavefunction theory or density functional theory (DFT) [31, 32, 33, 34, 35, 36, 37, 38, 10, 11]. The name “ab initio” already suggests the most important advantage of these methods: They were constructed from first principles. Because of the optimal balance of efficiency and accuracy [39, 40, 41], DFT becomes the most popular choice. Recent developments in approximate functionals have resulted in even better accuracy at a similar computational cost [42]. In general ab initio QM calculations are computationally much more demanding than semiempirical methods, therefore rigorous statistical mechanics sampling and reaction dynamics calculations with an ab initio QM/MM method are most challenging. The present review will focus on the developments and applications of ab initio QM/MM method in the simulation of complex reaction in solution and enzymes.

QM/MM energy function

In the combined QM/MM method [26, 30], usually the system is split into two subsystems: {r_QM}, a QM subsystem containing the active site, and {r_MM}, an MM subsystem containing the rest of the molecular system. Of course this QM/MM partitioning scheme can be extended to more than two subsystems. Unless explicitly stated, we assumed this two-subsystem QM/MM partition in this review. The total potential energy of a QM/MM system can be schematically written as a sum of different interaction terms

$$E_{QM/MM}({\mathbf{r}}_{QM},{\mathbf{r}}_{MM})=E_{QM}({\mathbf{r}}_{QM},{\mathbf{r}}_{MM})+E_{QM/MM,\mathit{\text{ele}}}({\mathbf{r}}_{QM},{\mathbf{r}}_{MM})+E_{QM/MM,\mathit{\text{nucl}}}({\mathbf{r}}_{QM},{\mathbf{r}}_{MM})+E_{QM/MM,vdw}({\mathbf{r}}_{QM},{\mathbf{r}}_{MM})+E_{QM/MM,\mathit{\text{covalent}}}({\mathbf{r}}_{QM},{\mathbf{r}}_{MM})+E_{MM}({\mathbf{r}}_{MM})$$ (1)

The first three terms on the right hand side are the QM internal energy, the electrostatic interaction energy between the QM electrons and MM subsystems, and the electrostatic interaction energy between the QM nuclei and MM subsystems, respectively. The remaining three terms are the van der Waals energy between the QM and MM subsystems, the covalent interaction energy between the two subsystems, and the purely MM interaction energy of the MM subsystem, respectively. In the following sections, we discuss in details computation techniques for each interaction term.

Defining QM subsystem

In a QM/MM simulation, the first important task is to construct the QM subsystem with associated QM Hamiltonian, E_QM(r_QM,r_MM). This process is often far more complicated than a simple task of choosing a QM method, e.g., semiempirical or ab initio. When the QM/MM separation of the entire system creates one or more covalent bonds connecting the QM and MM subsystems, such as the bond linking a QM side chain and the MM backbone of an enzyme, how one defines a QM Hamiltonian best characterizing the QM subsystem becomes a serious problem. Obviously, the QM Hamiltonian has to be self-contained to ensure the closure of the electronic valence state of the QM subsystem. This usually requires modification of the QM Hamiltonian apart from the simple isolation of the QM subsystems from the entire molecule.

Several approaches have been developed to solve the closure of the QM subsystem [43, 30, 31, 44, 45, 37, 46, 38, 47]. Traditionally, “link” hydrogen atoms are added to the MM-bonded QM atoms to saturate the valence orbital of the QM subsystem [30, 43]; the number of the hydrogen atoms depends on the number of QM/MM crossing bonds. Using additional hydrogen atoms to cap the QM subsystem is easy to implement, but the resulting system is thermodynamically different from the original one because the total number of atoms is different. The dynamics of the new hydrogen atoms may also affect the dynamics of other QM atoms in simulations.

In contrast, two other approaches, namely the pseudobond method [31, 44, 48]and the frozen local orbital method [45, 37, 46, 38, 47], do not bear such problems. In the pseudobond method, the MM-bonded QM atoms are assigned a special basis set and an effective core potential that is designed to mimic the correct covalent bonding involving the boundary QM atoms. By making such atoms with a free valence of 1, there is no need for additional atoms to saturate the QM covalent bonds on the QM/MM boundary. The optimization of the basis set and effective core potential can be performed with a small set of “training” molecules, and the optimized parameters have been shown to be applicable in broader chemical situations. Several methods, following the pseudobond method in using effective core potentials, have subsequently been developed, including the quantum capping potential method [49, 50], the effective group potential technique [51], effective Hamiltonians from a minimum principle [52], variational optimization of effective core potentials for molecular properties [53] and multicentered valence-electron effective potentials [54]. In an attempt to extend the pseudobond approach to more general situations, recently a design-atom method has also been developed [55].

In the frozen local orbital method, especially in the most recent extension of generalized hybrid orbital (GHO) method [56, 57, 58, 59, 47], a set of specially designed local orbitals are assigned to the boundary QM or MM atoms to maintain closure of the QM subsystem. Depending on the different implementation schemes, the magnitude of the neighboring MM charges, the positions of the MM point charges, the positions of the frozen orbitals, as well as the interaction model between boundary MM atoms and QM atoms will be adjusted to improve the description of the QM/MM boundary.

QM/MM electrostatic interactions

Computing the first two terms on the right hand side of Eq. (1), specifically E_QM(r_QM,r_MM) and E_QM/MM,ele(r_QM,r_MM), is the core of all QM/MM methods. The third term is usually a simple Coulombic interaction between QM nuclear charges and MM charges and will often be left out in following discussions. A straightforward procedure, often called as “electrostatic embedding” approach, computes the first two terms together by including the electrostatic potential from the MM atoms in the QM calculation; that is

$$E_{QM}({\mathbf{r}}_{QM},{\mathbf{r}}_{MM})+E_{QM/MM,\mathit{\text{ele}}}({\mathbf{r}}_{QM},{\mathbf{r}}_{MM})=<\mathrm{\Psi }|H_{\mathit{\text{eff}}}|\mathrm{\Psi }>,$$ (2)

where H_eff is the effective QM Hamiltonian including contribution of the MM electrostatic potential, and Ψ is electronic wavefunction of the QM subsystem. Since the QM SCF calculation is carried out with MM charges embedded, the polarization of the QM subsystem due to the presence of the MM subsystem is captured at the same level of QM theory. The electrostatic interaction between the QM and MM systems can thus be rigorously defined as

$$E_{QM/MM,\mathit{\text{ele}}}({\mathbf{r}}_{QM},{\mathbf{r}}_{MM})=<\mathrm{\Psi }|{\nu }_{MM}(\mathbf{r},{\mathbf{r}}_{MM})|\mathrm{\Psi }>,$$ (3)

which can be computed in many electronic structure programs. In the above equation, ν_MM(r,r_MM) is the electrostatic potential contributed by the MM environment. When the MM atoms contain only point charges,

$${\nu }_{MM}(\mathbf{r},{\mathbf{r}}_{MM})=\sum _{i\in MM}\frac{q_i}{|\mathbf{r}-{\mathbf{r}}_{MM,i}|}.$$ (4)

in which q_i is the charge and r_MM,i is the coordinate of an MM atom i. Interestingly, in this case the QM/MM electrostatic interaction can also be expressed in another form as a function of the QM electron densities ρ(r),

$$E_{QM/MM,\mathit{\text{ele}}}({\mathbf{r}}_{QM},{\mathbf{r}}_{MM})=\sum _{i\in MM}{q}_i\int \frac{\rho (\mathbf{r})}{|\mathbf{r}-{\mathbf{r}}_{MM,i}|}d\mathbf{r},$$ (5)

The integral on the right hand side is often defined as a component of the QM electrostatic potential at the MM positions

$${\nu }_{QM,ESP}({\mathbf{r}}_{MM})=\int \frac{\rho (\mathbf{r})}{|\mathbf{r}-{\mathbf{r}}_{MM}|}d\mathbf{r}+\sum _{i\in QM}\frac{Z_i}{|{\mathbf{r}}_{QM,i}-{\mathbf{r}}_{MM}|}.$$ (6)

The two equally exchangable representations of the electrostatic interaction between the QM and MM systems provide us much flexbilities in carrying out QM/MM calculations.

This electrostatic embedding scheme considers MM electrostatic contributions in the QM calculations. In comparison, another scheme to compute the QM/MM electrostatic interactions is the mechanical embedding approach represented by the ONIOM methods[60]. In this approach, the molecular system is hierarchically split into different layers that are described with different levels of theory ranging from ab initio QM, to semiempirical QM, and to MM. The energy function of the inner layer, presumably described at a higher level of theory, does not include the contribution of the outer layers; the energy of the outer layer also includes the self-interactions of the inner layer(s), but being described at a lower level of theory. An interpolation scheme is then used to computed the total energy of the system to avoid double counting of the interacting energies. The critical difference between the electrostatic embedding and mechanical embedding schemes is that the polarization effect is modeled with a higher level of theory in the former and with a lower level of theory in the latter.

In the electrostatic embedding scheme, special care needs to be taken to treat the electrostatic interactions between the QM subsystem and the nearby MM atomic charges, in particular those on the MM atoms in covalent contact with the QM atoms. Direct inclusion of those MM point charges in the QM effective Hamiltonian may cause charge penetration and off-balance polarization of the QM electrons. To address this problem, re-scaling of the MM charges [31] has been employed in the pseudo-bond approach. An alternative approach might be smearing the MM charges by Gaussian distributions [61].

QM/MM van der Waals interactions

The van der Waals interactions between the QM and MM subsystems, E_QM/MM,νdw(r_QM,r_MM), are usually described in the same additive form of MM interactions, e.g., Lennard-Jones 6–12 potential. The parameters for the QM atoms were often directly taken from MM force fields. Although this simple practice has been proved to work satisfactorily in many QM/MM simulations, one still needs to take cautions for two considerations. First, the van der Waals parameters of the current MM force fields were fitted together with the MM point charges which on large extent were determined empirically and often over-polarized to compensate the polarization effect in solution. In the QM/MM method with the electrostatic embedding scheme, in principle the polarization of QM atoms are explicitly described as shown in 1. The van der Waals parameters of MM force fields thus might be incompatible with the QM force fields. A carefully examination is needed. Second, the physical origin of the weak dispersion interactions is the instantaneous polarization of the electron density which obviously depends on the chemical environment and the distribution of electron densities. It is thus more desirable to design a smart approach where the van der Waals parameters can be adjusted with the progress of chemical reactions. This has been implemented recently with semi-empirical QM methods [62]. For ab initio QM methods, an efficient implementation is needed to ensure it is computationally applicable.

QM/MM covalent interactions

When one or more covalent bonds connect the QM and MM subsystems, E_{QM/MM;covalent} (r_QM,r_MM), the covalent interactions between QM and MM atoms, need to be considered in the QM/MM energy function. Those interactions are often described in classical MM forms including bonds, bond angles, and dihedrals. Inclusion of the QM/MM covalent interactions is important to prevent the QM subsystem from artificial drifting in the MM environment. In general, any covalent interaction should be retained if it involves both the QM and MM atoms.

MM interactions

It might seems that the MM interactions are the most trivial term in the QM/MM method, nonetheless, this is incorrect. From the beginning the design of MM force fields has been influenced by different philosophies and thus evolved into different flavors with different emphases. Due to the diversity in their forms and parameters, simulations performed with different MM force fields may show somewhat large discrepancies in the results [63]. As discussed earlier, the MM point charges and MM van der Waals parameters were usually fitted together to achieve balanced agreement for vast structural and thermodynamic properties. Therefore, even with the same QM method, employment of different MM force fields may lead to different results of the QM/MM simulations. This poses an important challenge to the future development of MM force fields, maybe toward a direction for compatibility with QM method.

Polarization in MM subsystem

In the electrostatic embedding scheme, the QM polarization effect due to MM electrostatic interactions is explicitly considered as in Eq. 3. The polarization of MM atoms due to QM electrostatic interactions is, nevertheless, absent in the currently popular MM force fields. The polarization of the MM atoms might be split into contributions from two sources. The first contribution stems from the re-distribution of the MM charges, or intra-MM-subsystem charge transfer. The second contribution arises from the probable charge transfer between the QM and MM subsystems.

To treat the intra-subsystem electron polarization, MM atoms can be described by the polarizable model such as polarizable point multipole model [26, 64, 65, 66], fluctuating charge model [67, 68, 69], and the classical charge Drude model [70, 71, 72, 73]. With the recent development of Drude model based MM force fields, simulations have been performed to explore the contribution of MM polarization in QM/MM methods [74, 75]. The development of Drude model possesses several advantages in the QM/MM implementations, including the simplified Drude point charge in computing integrals in QM calculations and several existing approaches to avoid dual-SCF calculations for the QM and MM subsystems [73, 75]. As there are not definite conclusions about the magnitudes of the contribution of polarization on the free energies of reactions,[75] more work is required for further developing and testing other polarizable models.

Charge transfer between the QM and MM subsystems is a difficult issue. Simple charge equilibrium approach has been implemented to allow the charge transfer between subsystems [76]. However, there are two practical issues should be noted. The first is that the current DFT exchange-correlation functionals bear large errors in treating fractional electrons [77, 78, 79, 80]; the second is that the consistence between the electronic affinities of the QM and MM atoms have not been tested. For these reasons, the effects of inter-system charge transfer remains to be carefully examined.

Long-range QM/MM electrostatic interactions

The importance of the correct description of long-range QM/MM electrostatic interactions has not been explored in most simulations, as many QM/MM simulations have been performed with finite and stochastic boundary conditions. The inclusion of long-range QM/MM electrostatic interaction is not trivial because the well-established Ewald summation method may not be directly applicable. In fact, several technical concerns must be addressed. The first issue concerns the treatment of a periodic QM subsystem. In biomolecular simulations, usually the simulation box must be large enough so that the interaction between the QM subsystem, which is often charged, with its images is negligible. The second concern is how to consider the periodically distributed MM charges in the QM calculation if the charge-embedding scheme is used. Even though Ewald-type methods have been developed for semiempirical methods[81, 82], a similar development for ab initio QM/MM methods is still lacking.

No doubt the long-range electrostatic interaction is important for stabilizing the enzyme structures and may also be important for enzyme functions. However, the key question might be whether or not the long-range polarization is significant for QM subsystem. It has been observed that even for a charge-transfer reaction, the QM polarization effects are small when the MM point charges are more than 9 ~ 14 Å from the QM atoms [83]. Beyond this distance, the MM point charges merely contribute by providing a static electrostatic potential. Therefore a simple technical scheme has been adopted in our simulations with periodic boundary condition [84, 85, 83] in which a cutoff of 9 ~ 14 Å was used for selecting MM charges for the QM SCF calculation. The QM calculation yielded polarized QM ESP charges that were in turn used to represent the QM subsystem during MD simulations with the long range electrostatic interactions treated by the Particle-mesh Ewald Method [86].

To avoid the technical difficulties associated with periodic QM/MM systems, important progress has been made to approximate long-range QM/MM electrostatic interactions by implementing a stochastic generalized solvent boundary with the SCC-DFTB method [87, 88]. York and co-workers have developed a variational electrostatic projection method that employs a continuum solvent model for the long-range electrostatic interactions [89].

AB INITIO REACTION PATH POTENTIAL

The calculation of the QM internal energy and QM/MM electrostatic interactions in Eq. (2) is the bottleneck for QM/MM calculations. In the electrostatic embedding scheme, a SCF calculation is required for each different QM or MM conformation, which is quite costly for ab initio QM methods. An approximate, ab initio-based QM/MM energy function without the need for SCF calculations is thus more desirable for phase space sampling and long time dynamics simulations.

To avoid SCF calculation, perturbation theory can be introduced where the energy change of the system is characterized by the response to change of QM or MM configurations. Lu and Yang developed the ab initio reaction path potential (RPP) method [90]. The approach involves separating the QM energy into two components: a QM internal energy and an electrostatic interaction energy between the QM and MM subsystems. Each component is then expanded analytically in terms of both the fluctuations of the QM geometry and the MM electrostatic potential determined by MM coordinates. The resulting RPP provides a simple, analytic expression for the QM/MM total energy that is valid in the vicinity of the initial conformations. Since the polarization of the QM subsystem by the fluctuating MM environment is properly considered, the RPP is particularly useful for QM/MM simulations. A truncation to second-order interactions in RPP was found to be very accurate.

On the basis of the work of ESP fitting of QM atomic charges, RPP approximates the electrostatic term in 5as the Coulombic interactions between the QM ESP charges (and multipoles) and the MM atomic charges, i.e.

$$E_{QM/MM}^{ESP}({\mathbf{r}}_{QM},{\mathbf{r}}_{MM})=\sum _{j\in MM}{q}_j\sum _{i\in QM}\frac{Q_i({\mathbf{r}}_{QM},{\mathbf{r}}_{MM})}{|{\mathbf{r}}_{QM,i}-{\mathbf{r}}_{MM,j}|}$$ (7)

Here, Q_i(r_QM,r_MM) is the ESP fitted charge of QM atom i, and q_j is the point charge of MM atom j from the MM force field. From the many experiences in ESP fitting, it is well known that the above term is a good approximation to the interaction sum of E_QM/MM,ele(r_QM,r_MM)+E_QM/MM,nucl(r_QM,r_MM). If it is necessary, one can further add electrostatic multipoles to each QM atom or bond to improve the accuracy of ESP fitting. Obviously, this term $E_{QM/MM}^{ESP}({\mathbf{r}}_{QM},{\mathbf{r}}_{MM})$ captures the essence of the electrostatic interactions between the QM and MM subsystems. Whereas the MM atomic charges are constant in common force fields, the QM electrostatic charges are clearly dependent on both r_QM and r_MM. The QM internal energy, E₁(r_QM,r_MM), is then defined as

$$E_1({\mathbf{r}}_{QM},{\mathbf{r}}_{MM})=\langle \mathrm{\Psi }|H_{\mathit{\text{eff}}}|\mathrm{\Psi }\rangle -E_{QM/MM}^{ESP}({\mathbf{r}}_{QM},{\mathbf{r}}_{MM})$$ (8)

This QM internal energy is the energy of the QM system in the presence of the electrostatic potential of the MM atoms, minus the Coulombic interactions between the QM ESP charges and MM atomic charges. The QM energy also depends on both r_QM and r_MM.

The most important advantage of this separation scheme is that we can now introduce polarization effects into both terms as high-order perturbations. In the RPP model, the QM ESP charges are assumed to respond linearly to changes in both the external electrostatic potentials at the atomic sites and the geometries of the QM system, as

$$Q_i({\mathbf{r}}_{QM},{\nu }_{MM})=Q_{QM,i}^0+\sum _{j\in QM}{\chi }_{ij}[{\nu }_{MM}({\mathbf{r}}_{QM,j}^0)-{\nu }_{MM}^0({\mathbf{r}}_{QM,j}^0)]+\sum _{j\in QM}{\kappa }_{ij}[{\mathbf{r}}_{QM,j}-{\mathbf{r}}_{QM,j}^0]$$ (9)

where $Q_{QM,i}^0$ is a reference ESP charge for QM atom i. The QM reference charges are determined at a given QM geometry $\left\{{\mathbf{r}}_{QM,j}^0\right\}$ and with a given external MM electrostatic potential $\{{\nu }_{MM}({\mathbf{r}}_{QM,j}^0)\}$ at the position of the QM atoms, which is an equal form for the point charge expression in 7. After the perturbation of the QM geometry and the external MM electrostatic potential, the polarized charges are determined through two response kernels, namely [90, 91],

$${\chi }_{ij}={\left(\frac{\partial Q_i}{\partial {\nu }_{MM}({\mathbf{r}}_{QM,j})}\right)}_N$$ (10)

and [90]

$${\kappa }_{ij}={\left(\frac{\partial Q_i}{\partial {\mathbf{r}}_{QM,j}}\right)}_N$$ (11)

The second kernel can now be computed analytically with a recently introduced ESP fitting method[92]. Just as in the polarization effects introduced in the term $E_{QM/MM}^{ESP}({\mathbf{r}}_{QM},{\mathbf{r}}_{MM})$, we also expand the term E₁(r_QM,r_MM) in a similar manner [90, 85]

$$E_1({\mathbf{r}}_{QM},{\nu }_{MM})=E_1({\mathbf{r}}_{QM}^0,{\nu }_{MM}^0)+\sum _{i\in QM}({\frac{\partial \langle \mathrm{\Psi }|H_{\mathit{\text{eff}}}|\mathrm{\Psi }\rangle }{\partial {\mathbf{r}}_i}|}_{{\mathbf{r}}_{QM}^0,{\nu }_{MM}^0}-\sum _{j\in QM}{\kappa }_{ji}{\nu }_{MM}^0({\mathbf{r}}_j^0)-Q_i^0\frac{\partial {\nu }_{MM}^0({\mathbf{r}}_i^0)}{\partial {\mathbf{r}}_i^0})\mathrm{\Delta }{\mathbf{r}}_i+\frac{1}{2}\sum _{i,j\in QM}\mathrm{\Delta }{\mathbf{r}}_i({\frac{{\partial }^2\langle \mathrm{\Psi }|H_{\mathit{\text{eff}}}|\mathrm{\Psi }\rangle }{\partial {\mathbf{r}}_i\partial {\mathbf{r}}_j}|}_{{\mathbf{r}}_{QM}^0,{\nu }_{MM}^0}-{\kappa }_{ij}\frac{\partial {\nu }_{MM}^0({\mathbf{r}}_i^0)}{\partial {\mathbf{r}}_i^0}-{\kappa }_{ji}\frac{\partial {\nu }_{MM}^0({\mathbf{r}}_j^0)}{\partial {\mathbf{r}}_j^0}-Q_i^0\frac{{\partial }^2{\nu }_{MM}^0({\mathbf{r}}_i^0)}{\partial {\mathbf{r}}_i^0\partial {\mathbf{r}}_j^0}{\delta }_{ij})\mathrm{\Delta }{\mathbf{r}}_j-\sum _{i\in QM}\sum _{j\in QM}{\chi }_{ij}{\nu }_{MM}^0({\mathbf{r}}_i^0)[{\nu }_{MM}({\mathbf{r}}_j^0)-{\nu }_{MM}^0({\mathbf{r}}_j^0)]-\frac{1}{2}\sum _{i\in QM}\sum _{j\in QM}[{\nu }_{MM}({\mathbf{r}}_i^0)-{\nu }_{MM}^0({\mathbf{r}}_i^0)]{\chi }_{ij}[{\nu }_{MM}({\mathbf{r}}_j^0)-{\nu }_{MM}^0({\mathbf{r}}_j^0)]-\sum _{i\in QM}\sum _{j\in QM}\mathrm{\Delta }{\mathbf{r}}_i\frac{\partial {\nu }_{MM}^0({\mathbf{r}}_i^0)}{\partial {\mathbf{r}}_i^0}{\chi }_{ij}[{\nu }_{MM}({\mathbf{r}}_j^0)-{\nu }_{MM}^0({\mathbf{r}}_j^0)]$$ (12)

The approximate QM/MM total energy becomes

$$Ẽ({\mathbf{r}}_{QM},{\mathbf{r}}_{MM})=E_1({\mathbf{r}}_{QM},{\mathbf{r}}_{MM})+\sum _{j\in MM}\sum _{i\in QM}\frac{q_j{Q}_i({\mathbf{r}}_{QM},{\mathbf{r}}_{MM})}{|{\mathbf{r}}_{QM,i}-{\mathbf{r}}_{MM,j}|}+E_{QM/MM,vdw}({\mathbf{r}}_{QM},{\mathbf{r}}_{MM})+E_{QM/MM,\mathit{\text{covalent}}}({\mathbf{r}}_{QM},{\mathbf{r}}_{MM})+E_{MM}({\mathbf{r}}_{MM})$$ (13)

It has been shown that this linearly polarized QM ESP charge model yields quite accurate energetics for reaction systems, given a good initial reference state [90, 84]. In simulations, the reference state was often chosen as a mean electrostatic field of the MM atoms sampled in MD simulations. Such a mean field can provide high quality reference QM charges and response kernels. Moreover, in the limit of sufficient sampling, the QM energy computed with the mean MM electrostatic field converges to the mean of QM energies computed for each individual MM conformation.

It is even possible to simplify this QM ESP charge model by truncating the polarization effects of the QM ESP charges to a zero-order [32, 84, 85]. That is, the QM/MM total energy can be approximated as

$$Ẽ({\mathbf{r}}_{QM}^0,{\mathbf{r}}_{MM})=E_1({\mathbf{r}}_{QM}^0,{\nu }_{MM}^0)+\sum _{j\in MM}\sum _{i\in QM}\frac{q_j{Q}_i({\mathbf{r}}_{QM}^0,{\mathbf{r}}_{MM}^0)}{|{\mathbf{r}}_{QM,i}-{\mathbf{r}}_{MM,j}|}+E_{QM/MM,vdw}({\mathbf{r}}_{QM}^0,{\mathbf{r}}_{MM})+E_{QM/MM,\mathit{\text{covalent}}}({\mathbf{r}}_{QM}^0,{\mathbf{r}}_{MM})+E_{MM}({\mathbf{r}}_{MM})$$ (14)

Without the need for computing two response kernels, this very simplified model is computationally efficient and thus very useful for providing an initial guess for reaction path optimization. This zero-order approximated model [32] shares similarity to the previously developed “ASEP/MD” method [93, 94, 95, 96]. In the latter approach, an mean field of MM electrostatic potentials were used to compute the ESP charges for QM atoms, and the charges were used later for the free energy simulations. The quality of the QM ESP charges thus strongly affects the results of the free energy simulation, thus these charges have to be determined in an iterative fashion. In generall, applications with these simplified QM ESP charge models in the ab initio QM/MM simulation of reaction processes have been successful.

FREE ENERGY SIMULATION

For a molecular system in canonical ensemble, the partition function is

$$Z=\int \mathit{\text{exp}}(-\beta E(X))dX$$ (15)

where β = 1/kT, k is the Boltzmann constant and T is the temperature. The free energy, enthalpy, and entropy are respectively

$$A=-kT\text{ln}ZH=\langle E(X)\rangle +PVS=(H-A)/T$$ (16)

These two equations form the foundation for the computer simulation of the free energies of many important chemical and biological processes.

When one is interested in the free energy change in a reaction process such as bond breaking, the quantity of central focus is the free energy as a function of a reaction coordinate, A(R), also known as potential of mean force (PMF). The corresponding partition function and PMF are

$$Z(R)=\int \text{exp}(-\beta E(X))\delta (R(X)-R)dXA(R)=-kT\text{ln}Z(R)$$ (17)

The partition function can relate to macroscopically observed probability distribution of R through

$$P(R)=Z(R)/Z,$$ (18)

which also relates the calculation of PMF to the determination of P(R) in simulations.

Directly computing the absolute free energy through Eq. 16 requires converged phase space sampling and is thus impractical for complex biological and chemical molecular systems, because the phase space sampling is always limited by the available computer resources.. Of course, experimentally it is also impossible to measure the absolute energy; instead, relative free energies are often more meaningful.

After the pioneer contribution of Kirkwood [97]and Zwanzig [98], various schemes have been developed for efficient simulation of the free energies. Thermodynamic integration and free energy perturbation are two orthodox methods that played important roles in biomolecular applications such as free energy of ligand binding, protein mutation, and drug design. Other relatively newer approaches such as the umbrella sampling, blue-moon constrained sampling, and slow and fast growth methods have also found popularities in solving different free energy problems. With a well-chosen transformation path, which could be a precisely determined reaction path, or a fictitious non-physical transferring of molecules into and out of solvents, applications of these methods should give identical results. However, depending on the nature of the problem, one often has to choose wisely to obtain the best efficiency. This argument is particularly important in QM/MM simulations, in which QM simulations are still very costly with today’s computers and free energy simulation with QM/MM methods are still challenging in the foreseeable future. In the following sections, we briefly review common free energy simulation methods, with comments on the advantage/disadvantages of the applications in QM/MM simulations.

Thermodynamic Integration

Thermodynamic integration (TI) is originally derived in Kirkwoods’ continuous coupling scheme [97]. To compute the free energy difference between two states (0 and 1), ΔA = A₁ −A₀, one may construct a continuous thermodynamic path λ_0→1 between the two states. The free energy difference is thus

$$\mathrm{\Delta }A={\int }_0^1\frac{\partial A(\lambda )}{\partial \lambda }d\lambda .$$ (19)

This equation can be further expressed as

$$\mathrm{\Delta }A={\int }_0^1{<\frac{\partial E(X,\lambda )}{\partial \lambda }>}_{\lambda }d\lambda$$ (20)

where the brackets with a subscript <>_λ indicate ensemble averaging over the state characterized by λ. Because free energy is a state function, there is no restriction on the construction of the path if one is only interested in the free energy difference between the two end states. In the simulation of reaction process, however, we are often interested in the free energies of the entire reaction path, as such we would like to compute the free energy of “intermediate” states on the reaction path too. In this case, the free energy simulation path coincides with the real reaction path, and the parameter λis parallel to the reaction coordinate which normally constitutes of combinations of geometrical terms such as bonds, bond angles, and dihedrals.

As shown in Eq. 20, application of TI requires the energy gradient with respect to the parameter λ, for which the calculation may or may not be easy. If a non-physical path is chosen, which is usually a mixing of the energy functions at two states,

$$E(X,\lambda )=f(\lambda )E_0(X)+g(\lambda )E_1(X),$$ (21)

the gradient is then a function of the derivatives f′(λ) and g′(λ). Series of simulations can be performed for system described by different values of λ, while in each simulation the gradient $\frac{\partial E(X,\lambda )}{\partial \lambda }$ is computed and ensemble-averaged. The free energy difference can be computed by numerical integration instead of Eq. 20. This approach does not add any restriction on the form of the energy function. Therefore, the method can be equally applied to systems described by MM or QM. Indeed, TI simulations with MM force fields have produced fruitful results in biochemical studies, especially in the understanding of ligand binding to proteins and the stability and other physical properties of many protein molecules. Application with QM/MM force fields have also been reported, from early EVB simulation of reaction process to more recent work on electron transfer reaction in solution. Because of the cost of QM calculations, only a small number of ab initio QM/MM simulations have been reported. An additional factor affecting the sampling efficiency is that each sampling step requires two QM calculations, one for the energy function E₀(X) and the other for E₁(X). This further adds the burden to the ab initio QM/MM simulations.

Since the transformation path, described by the parameter λ,is not unique, it is possible to explore different constructions of the path to improve the computational efficiency. In the special case of electron transfer, Yang and coworkers realized that it is possible to choose the fractional number of electrons as the parameter λ which then reduces the number of QM calculations to one at each sampling step. The simulation results have been in good agreement with experiments and other simulations [83].

When a chemical reaction is of interests, in addition to the relative free energies of the reactant and product states, one would also like to know the free energy changes along the reaction process, in particular free energy of the transition state, which often determines the reaction rate in classical transition state theory. In this case, a reaction path with good quality becomes crucial; the determination this path is discussed in next section. If the reaction path can be well described by the combination of geometrical terms, R, one can apply TI type of simulation methods such as blue moon sampling method [99]. It should be reminded in this case, simulations are often performed with constraints on the reaction coordinate. As a consequence, the gradient $\frac{\partial E(X,\lambda )}{\partial \lambda }$ has to include the contribution of the constraints, which in certain circumstances are difficult to compute and thus may limit the applicability of TI method in reaction simulations.

Free Energy Perturbation

Free energy perturbation method was first presented by Zwanzig [98]. It relates the free energy difference between two states to the energy differences sampled at one state [100]

$$\mathrm{\Delta }{A}_{0\to 1}=-kT\mathit{\text{ln}}{<\mathit{\text{exp}}[-\beta (E_1(X)-E_0(X))]>}_0.$$ (22)

Even though this equation is correct in the limit of ensemble convergence, in normal simulations it is found necessary to limit ΔA ≤ 2kT so that there are enough overlapping between the phase spaces of the two states to ensure the convergence. For any processes that the free energy change is larger than this number, one needs to build intermediates state to rely the FEP simulations. The final free energy difference is a sum of the free energy difference determined in each sub-simulations,

$$\mathrm{\Delta }A=\sum _{i=0}^{N-1}\mathrm{\Delta }{A}_{i\to i+1}.$$ (23)

Of course one should also note that this limit is empirical and can be relaxed, for example in the vertical electronic excitation processes.

Comparing FEP Eq. 22 with TI equation 20 clearly shows the difference. TI requires the evaluation of the energy gradient $\frac{\partial E(X,\lambda )}{\partial \lambda }$ while FEP does not. Because of this feature, in FEP simulation of reaction processes, discrete points on the reaction path can be used instead of the entire continuous path [101], which becomes a unique advantage of FEP method, especially in ab initio QM/MM methods.

FEP calculation with ab initio QM/MM methods, however, requires extra considerations. For two conformational states (r_QM,i,r_MM,i) and (r_{QM, j},r_{MM, j}), the energy difference in Eq. 22 can be computed as

$$\mathrm{\Delta }{E}_{QM/MM,i\to j}=E_{QM}({\mathbf{r}}_{QM,j},{\mathbf{r}}_{MM,i})+E_{QM/MM,\mathit{\text{ele}}}({\mathbf{r}}_{QM,j},{\mathbf{r}}_{MM,i})+E_{QM/MM,\mathit{\text{nucl}}}({\mathbf{r}}_{QM,j},{\mathbf{r}}_{MM,i})-E_{QM}({\mathbf{r}}_{QM,i},{\mathbf{r}}_{MM,i})-E_{QM/MM,\mathit{\text{ele}}}({\mathbf{r}}_{QM,i},{\mathbf{r}}_{MM,i})-E_{QM/MM,\mathit{\text{nucl}}}({\mathbf{r}}_{QM,i},{\mathbf{r}}_{MM,i})+E_{QM/MM,vdw}({\mathbf{r}}_{QM,i},{\mathbf{r}}_{MM,i})-E_{QM/MM,vdw}({\mathbf{r}}_{QM,j},{\mathbf{r}}_{MM,i})+E_{QM/MM,\mathit{\text{covalent}}}({\mathbf{r}}_{QM,j},{\mathbf{r}}_{MM,i})-E_{QM/MM,\mathit{\text{covalent}}}({\mathbf{r}}_{QM,i},{\mathbf{r}}_{MM,i}).$$ (24)

As discussed in previous section, accurate calculation for the first six terms on the right hand side requires at least two SCF calculations, one for (r_QM,i,r_MM,i) and one for (r_{QM, j},r_MM,i). This makes the ab initio FEP calculation almost prohibitive. To overcome this difficulty, Yang and coworkers developed an approximate yet effective FEP scheme. Taking the approximate energy function defined in Eq. 14, the energy difference becomes

$$\mathrm{\Delta }{E}_{QM/MM,i\to j}\simeq E_1({\mathbf{r}}_{QM,j},{\nu }_{MM,j})+\sum _{\alpha \in MM,i}\sum _{\beta \in QM,j}\frac{q_{\alpha }{Q}_{\beta }({\mathbf{r}}_{QM,j},v_{MM,j})}{|{\mathbf{r}}_{QM,\beta }-{\mathbf{r}}_{MM,\alpha }|}-E_1({\mathbf{r}}_{QM,i},{\mathbf{r}}_{MM,i})-\sum _{\alpha \in MM,i}\sum _{\beta \in QM,j}\frac{q_{\alpha }{Q}_{\beta }({\mathbf{r}}_{QM,i},{\nu }_{MM,i})}{|{\mathbf{r}}_{QM,\beta }-{\mathbf{r}}_{MM,\alpha }|}+E_{QM/MM,vdw}({\mathbf{r}}_{QM,i},{\mathbf{r}}_{MM,i})-E_{QM/MM,vdw}({\mathbf{r}}_{QM,j},{\mathbf{r}}_{MM,i})+E_{QM/MM,\mathit{\text{covalent}}}({\mathbf{r}}_{QM,j},{\mathbf{r}}_{MM,i})-E_{QM/MM,\mathit{\text{covalent}}}({\mathbf{r}}_{QM,i},{\mathbf{r}}_{MM,i}).$$ (25)

For the accuracy of QM internal energy E₁(r_QM,ν_MM) and QM ESP charges Q_β, it is important to build a good referencing potential ν_MM. Hu et. al. employed a mean MM electrostatic potential from MM sampling which eliminates the fluctuation of E₁(r_QM,ν_MM) and QM ESP charges Q_β [84]. Similar approach has also been employed by Warshel and coworkers [102].

Umbrella Sampling

Umbrella sampling (US) is a useful method for determining the free energies, or the PMF, of a reaction process [103]. The key is to compute the probability distribution of the reaction coordinate from simulations with improved sampling of high-energy, low-probability regions of phase space. After imposing a biasing potential V(R), the observed probability distribution P′(R), of the reaction coordinate R, is computed in the simulation described by the combined energy function of E(X)+V(R). The PMF is thus

$$A(R)=-kT\mathit{\text{ln}}P\prime (R)-V(R)-C,$$ (26)

where C is a constant whose value depends on the biasing potential and is often determined relatively to other simulation windows. The results of umbrella sampling can be processed with the weighted histogram analysis method [104, 105, 106], which provides reduced statistical error. Different schemes have also been developed to improve the sampling efficiency, such as adaptive multi-dimension umbrella sampling approach [107]. Recently, Thiel and co-workers have developed an “umbrella integration” method which combines the advantages of umbrella sampling and thermodynamic integration [108].

Unlike TI, US employs soft restraints instead of constraints in the simulation process, thus essentially the entire R space is sampled in US as compared to only limited points being sampled in TI. An important difference is that there is no need for the computing of constrain force in the US method, which could become a great advantage in complex reactions.

Slow and Fast Growth

Umbrella sampling and thermodynamic integration also served basis for several variant free energy simulation methods. Slow growth is such a variant of TI [109, 110]. Instead of sampling a few fixed points on the reaction/transformation path and computing a converged free energy gradient for each point, slow growth slowly drives the system from one state to the other using a very small step size. The work exerted during this process is summed up to yield an upper-bound estimate of the free energy difference between the two states. The reverse process yields a lower-bound estimate. Together, the results of multiple forward and backward processes yield a good estimate of the free energy difference [111]. When the slow growth method is combined with the coordinate driving technique, a smooth free energy change with respect to the reaction coordinate may be obtained.

In analogy to the slow growth method, recently a “fast growth” method [112, 113]has been developed and has been used to simulate chemical reactions [114, 115]. Unlike the slow growth method in which each simulated work is an estimate of the true free energy, in fast growth the ensemble averaged work is the upper-bound (or lower-bound for the reverse process) estimate of the true free energy. This estimate slowly converges to the true free energy upon the convergence of the ensemble. Since each individual simulation is often only in pico-second timescale range, ab initio QM/MM simulations at this timescale might be possible. However, the main drawback of the fast growth method is that it requires many simulations to yield a good estimate of the free energy, which always possess a large amount of uncertainty [116].

Meta-dynamics method estimates the potential of mean force surface by gradually modulating the potential energy surface. [117] In fact, the method can make good connection to the fast-growth and other non-equilibrium simulation method [118].

AB INITIO QM/MM FREE ENERGY SIMULATION

Direct phase space sampling methods

As we have discussed in the last section, PMF of a reaction process can be simulated with approaches on the basis of direct phase space sampling, such as thermodynamic integration, umbrella sampling, and fast and slow growth methods. It is important to realize that the phase space sampling methods based on PMF calculation along a reaction coordinate usually require converged sampling and of course prior knowledge about the reaction coordinate. The only obstacle is still the cost of ab initio QM calculations required in each sampling step, which limited the system size to a few tens of atoms and the simulation length to a few tens of picosecond. Combination with statistical analysis approaches such as weighted histogram analysis method and maximum likelihood theory can improve the convergence speed and reduce the amount of the computational cost, but nevertheless cannot eliminate the necessity of broad phase space sampling. For this reason, the direct dynamics sampling methods are often only affordable for semiempirical QM/MM methods. As for ab initio QM/MM, few simulations have been reported [119, 85, 75]. Of course, with the steady improvement of computer speed, direct sampling methods may play more important roles in the reaction simulations in the future.

QM/MM-FE

To avoid the high computational costs of ab initio QM calculations in the direct phase space sampling based simulations, another class of free energy simulation methods have been developed to take the advantage of well-defined reaction paths. These methods are usually built on the basis of determination of a representative reaction path and subsequent free energy simulation for the path. An early example is the QM-FE method developed by Jorgensen and coworkers, in which the reaction path optimized for gas-phase reaction process is used to carry out free energy simulation in condensed phase [22].

Also realizing the importance of the reaction path, Yang and co-workers have devoted much effort into developing reaction path optimization and free energy calculation techniques based on ab initio QM/MM methods [32, 84, 85]. The first method, termed QM/MM-FE (or QM/MM-FEP) [32, 120], is carried out in two stages: optimization of the reaction path and calculation of the free energies for the path.

In the QM-FE method, the reaction path is defined as the minimum energy path connecting the reactant state and product state of the molecular system. In principle, such a path can be optimized in a straightforward fashion with the system described in QM/MM energy function. With ab initio QM/MM methods, the computational cost for this direct approach could be very high since the number of QM calculations required for the minimization could exceed a few thousands. To speed this process, the reaction path determination has been designed as a sequential optimization process. To exemplify the advantages of this sequential approach, let us first examine the situation where the QM and MM degrees of freedom are optimized concurrently. In this case, each change of the QM and/or MM geometries will require a new QM evaluation of the energy and gradient. While the energy and gradient calculation is computationally inexpensive for semiempirical QM methods, it is expensive for ab initio QM methods. As it usually takes hundreds to thousands of minimization steps to obtain an adequately converged structure for the whole QM/MM system, the cost for ab initio QM calculations would be prohibitive. Inspired by the fact that in certain types of optimization problems it may be desirable to break up a process into an iterative sequence of two or more steps, we perform the optimization as follows: (i) optimize a subset of the system, A, with the rest of the system, B, held constant; (ii) optimize B with A fixed according to the results obtained in step (i). Thus in the QM/MM-FE method, instead of a concurrent optimization of the QM and MM degrees of freedom, an iterative, sequential optimization protocol was developed that has proven to be effective in reducing the number of QM energy and gradient evaluations. The main idea is that, starting from a given structure of the QM/MM molecular system, the optimization is separated into two processes. One first optimizes r_QM with fixed r_MM, which is at an approximate minimum in the MM degrees of freedom. Afterward, the conformation of the MM subsystem, r_MM, is optimized with fixed r_QM. To reduce the number of QM evaluations, an approximate QM/MM total energy, Ẽ(r_QM,r_MM), is used for the MM optimization. In this approximate QM/MM total energy, the electrostatic interactions between the QM and MM atoms are approximated by the Coulombic interactions between the point charges of the MM atoms and the ESP fitted charges of the QM atoms. This process is then iterated until convergence, which is normally achieved within a few iterations (often less than 10). Expressed as an algorithm, the ab initio QM/MM-FE optimization procedure is as follows:

1. Initiate a structure of the QM subsystem ${\mathbf{r}}_{QM}^{(0)}$, and set the cycle number n = 0;

2. Increase the cycle number n = n+1;

   1. Carry out an MM minimization with QM atoms fixed at ${\mathbf{r}}_{QM}^{(n-1)}$:

      $${\mathbf{r}}_{MM}^{(n)}=\text{arg}{\mathit{\text{min}}}_{{\mathbf{r}}_{MM}}Ẽ({\mathbf{r}}_{QM}^{(n-1)},{\mathbf{r}}_{MM})$$ (27)
   2. Carry out a QM optimization with MM atoms fixed at ${\mathbf{r}}_{MM}^{(n)}$:

      $${\mathbf{r}}_{QM}^{(n)}=\text{arg}{\mathit{\text{min}}}_{{\mathbf{r}}_{QM}}E({\mathbf{r}}_{QM},{\mathbf{r}}_{MM}^{(n)})$$ (28)

3. Go to Step (2) until converged

This process can be carried out individually for a single point on the reaction path, e.g. the reactant and product states, or simultaneously for a chain of conformations along the reaction coordinate with a chain-of-states optimization algorithm such as the NEB method, the Ayala-Schlegel method, or the superlinearly convergent QSM.

Once the reaction path is determined, a FEP simulation with the approximate QM/MM energy function Ẽ(r_QM,r_MM) can be carried out for the optimized QM conformations on the reaction path 25, similar to the QM-FE method [22]. The validity of QM/MM-FE has been confirmed by other laboratories [121, 122, 123].

QM/MM-MFEP: Path optimization on a QM PMF surface

The development of the QM/MM-FE method has provided a viable way for computing accurate free energies of reactions in enzymes. But one limitation has hampered the application of this method to the simulation of solution reactions. In the QM/MM-FE method, the reaction path is optimized on the QM/MM PES, starting from a given initial structure. As a result, the optimized path is influenced by the choice of the initial conformation [124]. In many enzyme-substrate complexes, the dependence of the initial conformation may not cause problems because the active site of the enzyme is usually protected from bulk solvent. When the reaction occurs in solution, or the enzyme active site is exposed to solvent, this dependence will be significant. The rapid exchange of solvent molecules can also cause difficulty for the convergence of the path optimization process. Similar observations have been made for the enzymatic reactions in which the enzyme undergoes significant conformational changes during the reaction process.

To overcome this problem, the QM/MM-MFEP method has been developed in which the reaction path is optimized on the PMF surface of the QM degrees of freedom, instead of the total energy surface [84]. Within the QM/MM context, the thermodynamics of the entire system is simplified by defining the PMF of a QM/MM system in terms of the QM conformation as

$$A({\mathbf{r}}_{QM})=-\frac{1}{\beta }\mathit{\text{ln}}[\int d{\mathbf{r}}_{MM}\mathit{\text{exp}}(-\beta E({\mathbf{r}}_{QM},{\mathbf{r}}_{MM})]$$ (29)

where E(r_QM,r_MM) is the total energy of the entire system expressed as a function of the coordinates of the QM and MM subsystems, r_QM and r_MM, respectively. The gradient of the PMF, also known as the free energy gradient, is then

$$\frac{\partial A({\mathbf{r}}_{QM})}{\partial {\mathbf{r}}_{QM}}={\langle \frac{\partial E({\mathbf{r}}_{QM},{\mathbf{r}}_{MM})}{\partial {\mathbf{r}}_{QM}}\rangle }_{E({\mathbf{r}}_{QM},{\mathbf{r}}_{MM})}$$ (30)

which appears conveniently as the ensemble average of the gradient of the QM atoms, obtained from MD simulations of the MM atoms. In practice, we used the free energy perturbation method and its associated gradient, instead of Eqs. (29–30) [84, 85].

Our construction of the PMF and PMF gradient is different from other work in terms of the variables of the PMF. We allow all of QM degrees of freedom to contribute to the reaction coordinate whereas others have often used one or a few predefined geometric terms. In the latter case, a Jacobian term may be required to correctly include the effects of geometrical constraints on the reaction coordinates.

Because the QM degrees of freedom are coupled with the MM degrees of freedom in the total energy equation (Eq. 1), a straightforward minimization algorithm requires each step in the optimization of the QM conformations to be associated with converged sampling of the MM ensemble. In this optimization scheme, every QM optimization step to a new conformation on the PMF surface is followed by a course of MD sampling of the MM conformations, usually with a simulation time of 100 ~ 1000 ps. Such extensive MM sampling is required so that the QM PMF and gradient obtained are sufficiently accurate for successful structure and reaction path optimization of the QM subsystem. Thus, this method is less efficient in practical simulations. First, 100 ~ 1000 ps of MD simulations on a system of ~ 10,000 atoms is expensive. Second, such MD simulations must be repeated for each step in the QM optimization process. The intrinsic fluctuations and limited simulation times for the MD sampling may also contribute to slow convergence in the path optimization if a new MD simulation is always begun immediately after every QM geometry optimization step.

Sequential sampling and optimization for QM/MM-MFEP method

As in the QM/MM-FE method, to improve the efficiency of the QM/MM-MFEP method, we can reformulate the concurrent optimization of the QM subsystem and the statistical sampling of the MM subsystem into an iterative step of sequential MD sampling of the MM system at a fixed QM structure and subsequent optimization of the QM subsystem within the fixed MM conformational ensemble [85]. The approximate energy function Ẽ(r_QM,r_MM), introduced in the QM/MM-FE method and well described in the RPP model, plays a crucial role in reducing the number of QM energy and gradient evaluations required. In the MD sampling of the MM conformations, Ẽ(r_QM,r_MM) acts as a reference sampling energy function to drive the motion of the MM atoms without performing a QM calculation at every MD step. In the optimization of the QM subsystem within the fixed-size MM conformational ensemble, it can be used to avoid QM calculations associated with each new conformation in the MM ensemble.

The algorithm of the QM/MM-MFEP method can be described as follows.

1. Initiate a structure of the QM subsystem, ${\mathbf{r}}_{QM}^{(0)}$, and set cycle number n = 0.

2. Increase cycle number n = n+1;

   1. Carry out MD sampling of the MM ensemble with QM atoms fixed at ${\mathbf{r}}_{QM}^{(n-1)}$:

      $$\{{\mathbf{r}}_{MM}^{(n)}(\tau ),\tau =1,\dots ,N\}\Leftarrow \mathrm{M}\mathrm{D}\text{sampling based on}{E}_{\mathit{\text{ref}}}({\mathbf{r}}_{MM})$$ (31)

      where τ is the step of the MD simulation, N is the number of MD steps, the reference QM structure is derived from ${\mathbf{r}}_{QM}^{(n-1)}$, the QM geometry from the previous iteration.
   2. Carry out a QM optimization with the MM ensemble fixed at $\{{\mathbf{r}}_{MM}^{(n)}(\tau )\}$ where the object of minimization is the QM PMF (or QM free energy) in the n-th iteration given by a finite sum representation of free energy perturbation as

      $$A^{(n)}({\mathbf{r}}_{QM})=A_{\mathit{\text{ref}}}-\frac{1}{\beta }\text{ln}\{\frac{1}{N}\sum _{\tau =1}^N\text{exp}\{-\beta \mathrm{\Delta }E\}\},$$ (32)

      and the corresponding gradient with respect to the i-th QM coordinate is also given by the finite sum

      $$\frac{\partial A^{(n)}({\mathbf{r}}_{QM})}{\partial {\mathbf{r}}_{QM,i}}=\frac{\sum _{\tau =1}^N\partial Ẽ({\mathbf{r}}_{QM},{\mathbf{r}}_{MM}^{(n)}(\tau ))/\partial {\mathbf{r}}_{QM,i}\text{exp}\{-\beta \mathrm{\Delta }E\}}{\sum _{\tau =1}^N\text{exp}\{-\beta \mathrm{\Delta }E\}},$$ (33)

      where

      $$\mathrm{\Delta }E=Ẽ({\mathbf{r}}_{QM},{\mathbf{r}}_{MM}^{(n)}(\tau ))-E_{\mathit{\text{ref}}}({\mathbf{r}}_{MM}^{(n)}(\tau ))$$ (34)

      which accounts for the fact that the samples were obtained from a fixed MD simulation of a reference state. E_{re f} and A_{re f} are the reference energy function and reference free energy in the free energy perturbation expression.
   3. Update the reference structure based on the minimized QM structure ${\mathbf{r}}_{QM}^{(n)}$.

3. Go to Step (2) until converged.

The key feature of our new QM/MM-MFEP algorithm is the iterative QM optimization in a fixed MM ensemble, Eq. (31) above. Because the MM ensemble, $\{{\mathbf{r}}_{MM}^{(n)}(\tau ),\tau =1,\dots ,N\}$, is finite and remains fixed throughout the course of the QM optimization for ${\mathbf{r}}_{QM}^{(n)}$, one can obtain the precise PMF, Eq. (32), and its gradient, Eq. (33), defined within this ensemble. The PMF so obtained is precise because it does not have statistical fluctuation. But it is approximate because of the finite and hence incomplete ensemble. This circumvents the difficult and costly convergence problems associated with MM sampling. The optimization of the PMF can be carried out efficiently using classical numerical optimization tools. Each optimized QM structure ${\mathbf{r}}_{QM}^{(n)}$ in turn provides the next reference QM structure and its energy function, ${\mathbf{r}}_{QM}^{\mathit{\text{ref}}(n)}$, for the next round of MD sampling of the MM conformations. Each optimized QM structure should improve on the previous one by providing a better QM geometry and corresponding ESP charges for the MM simulation in the next cycle.

The use of a finite, fixed-size ensemble of MM conformations improves the utilization of the MM conformations and avoids repetitive MD sampling at each step of the QM structure optimization. Thus, instead of performing excessive MD samplings that likely have significant overlap with each other, a few cycles of MD simulation are sufficient to yield converged results in the current method. Applications have shown that our QM/MM-MFEP method converges as efficiently as the QM/MM-FE method as shown in Fig 1.

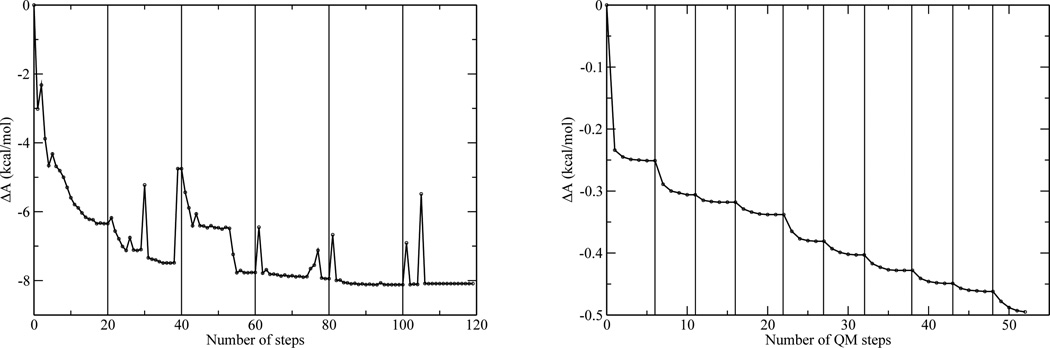
Figure 1.

Convergence of the iterative QM/MM-MFEP and QSM optimizations for the 4OT and S_N2 reactions. Left: Convergence of the relative free energies in the optimization of the reactant state of 4OT. Each vertical line indicates the start of a new cycle. The X-axis is the accumulated number of QM steps made by the QM optimization algorithm. Vertical lines indicate the onset of a new cycle of sequential MM sampling and QM optimization. The number of vertical lines is the number of times MM ensembles are generated; right: Convergence of the relative free energies in the optimization of the reactant state for the S_N2 reaction.

Even though the QM/MM-MFEP was designed for the purpose of optimizing free energy path for reaction processes, we note that this method also has great potential in other general problems in which the free energy difference between two states is the target of interests. In this case, QM/MM-MFEP can be applied to the optimization of structures of the two end states, and then QM/MM free energy purturbation can be carried out with interpolated intermediate states as many as necessary. Even though the structure of the intermediate states can be non-physical, the free energy difference between the two end states can be very accurate as free energy is a state function and is path independent. This scheme will allow very efficient QM/MM free energy simulations for many important molecular processes such as solvation and enzyme/substrate binding.

Other ab initio QM/MM free energy methods

Several other groups have also made important contributions to the development of ab initio QM/MM free energy simulation methods, most of which were developed on the basis of free energy perturbation approach. Warshel and co-workers have developed a QM(ai)/MM method, the key of which is that the sampling and free energies calculation are first carried out with a simplified EVB potential, and then corrected to ab initio QM level with FEP combined with the linear response approximation [125, 126].

Rod et. al. have developed an approach termed quantum mechanical thermodynamic cycle perturbation (QTCP) method which combines features from QM/MM-FE and QM(ai)/MM methods. The reaction path was optimized using QM/MM method for a selected number of configurations of the QM region along the reaction process. Afterward, QM ESP charges were used to compute a MM-like free energy difference between QM configurations, while an MM → QM free energy change was computed for each QM configuration. Both free energy computations were carried out with the free energy perturbation approach. The sole difference between the QTCP approach and the original QM/MM-FE approach is the MM → QM free energy simulation developed in the QM(ai)/MM method, which presumably includes polarization of the QM subsystem due to the fluctuations of the MM subsystem. This has also been achieved in the ab initio QM/MM reaction path potential method with even cheaper computational cost and possible dynamics sampling of the QM region [90].

APPLICATIONS

Many enzymatic reactions have been studied with ab initio QM/MM methods, as summarized in the review by Senn and Thiel [28]. We summarize here the main enzymes recently studied at our Duke University laboratory.

4-oxalocrotonate tautomerase (4OT)

4OT catalyzes the conversion between 2-oxo-4-hexenedioate and 2-oxo-3-hexenedioate. Extensive ab initio QM/MM calculations have been performed to examine several hypothesized mechanisms of 4OT, with the effects of different substrates and point mutations being explored too. The simulation successfully reproduced the experimental barrier, moreover, it predicted the effects of mutations on the catalytic rate in terms of reaction barrier heights.

Specifically, theoretical calculations for the 4OT reaction mechanism suggested that a hydrogen-bond provided by the amide peptide bond between Ile-7 and Leu-8 of 4OT helps properly position the substrate in the active site [34]. To probe the energetic contribution of this backbone group, a 4OT analogue was designed to contain a backbone amide to ester bond mutation between Ile-7 and Leu-8 [(OL8)4OT]. The amide to ester bond mutation in (OL8)4OT effectively deleted a putative hydrogen bonding interaction between the enzyme’s protein backbone and its substrate. Theoretical calculations suggested a 1.0 kcal/mol increase for the barrier height, which is in good agreement with experimental results of 1.8 kcal/mol increase.

Theoretical calculations also suggested the hydrogen bond deletion in (OL8)4OT resulted in a rearrangement of the substrate in the active site. In this rearrangement, an ordered water molecule loses its ability to stabilize the transition state (TS), and Arg-61 gains the ability to stabilize the TS. The predicted role of Arg-61 in (OL8)4OT catalysis was confirmed in kinetic experiments with an analogue of (OL8)-4OT containing an Arg to Ala mutation at position 61: For (OL8)4OT(R61A), the theoretical ΔΔG^‡=1.5 kcal/mol, which was lately confirmed by the experimental result of ΔΔG^‡=1.2 kcal/mol [127].

The different catalytic efficiencies of two substrates of 4OT, 2-hydroxy-muconate (2HM) and 2-oxo-4-hexenedioate (2o4hex) have also been investigated with ab initio QM/MM-FE method. Potential and free energy paths for both substrates were calculated to determine the free energy barriers and compared to the experimental values obtained from the kinetic studies via the transition state theory. For both substrates, ΔG is about 13 kcal/mol, in agreement with experimental determinations. The calculated free energy barrier difference (ΔΔG^‡), or $\mathrm{\Delta }{G}_{2o4\mathit{\text{hex}}}^{‡}-\mathrm{\Delta }{G}_{2HM}^{‡}$ is 0.87 kcal/mol. The subsequent experimental measurement is of 0.85 kcal/mol, in remarkable agreement with theoretical calculations [128].

Cell-division cycle25 phosphatase isomer B (Cdc25b)

Cdc25b is a dual-specificity phosphatase enzyme that catalyzes the dephosphorylation of the Cdk2/CyclinA protein complex. Being a member of the protein tyrosine phosphatases (PTPases) family, Cdc25b is an important regulator of the human cell cycle, and as a result has been identified as a potential anti-cancer target. Since no crystallographic data currently exists for the complex of Cdc25b with Cdk2/CycA, ab initio QM/MM MFEP simulations have been carried out to explore the mechanism of Cdc25b with a small molecule phosphate substrate [129]. The simulation results revealed novel insights into the phosphate transfer mechanism in Cdc25b, with potential implications on other phosphate transfer enzymes too.

The active sites of most PTPases contain the conserved (H/V)CX₅R(S/T) sequence motif, as well as a sequence of residues known as the WPD-loop. In general, PTPases are thought to bind the dianionic form of their phosphate substrates and to employ general acid catalysis via the Asp residue located in the WPD-loop. As in other PTPases, the active site of Cdc25b is characterized by the HCX₅R motif. However, it lacks the WPD-loop presumed to be responsible for acid catalysis. Cdc25b is also missing a Ser/Thr residue immediately following the Arg residue in the catalytic motif. Thus, Cdc25 appears to have unique structural and possibly mechanistic characteristics that distinguish it from all other known PTPases.

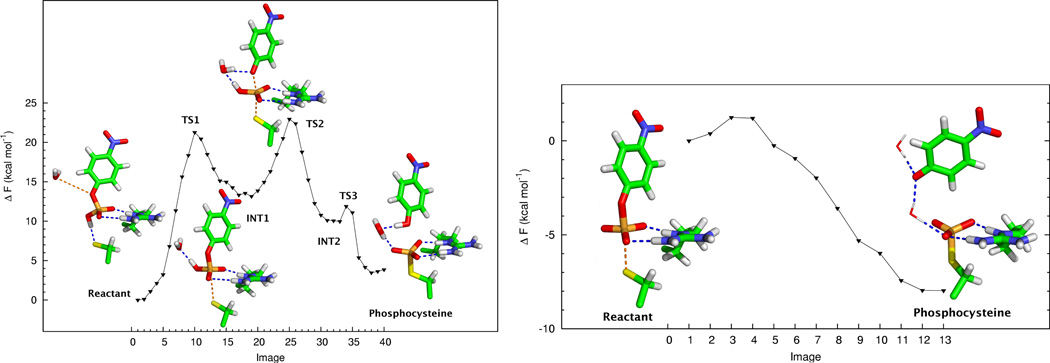
In an effort to understand the dephosphorylation mechanism of Cdc25b with a commonly used small molecule substrate, the rate-limiting step of the reaction catalyzed by Cdc25b with the substrate p-nitrophenyl phosphate (pNPP) was recently simulated using the ab initio QM/MM-MFEP method [85]. The free energy profiles for the reaction of Cdc25b with the pNPP monoanion and dianion are shown in Fig. 2. The mechanism involving monoanionic pNPP yielded an experimental free energy barrier (22.9 kcal mol⁻¹) that is closer to the experimental value $(\mathrm{\Delta }{G}_{298K}^{‡}=18.5{\text{kcal mol}}^{-1})$ than that of dianionic pNPP. The transition state structure of the rate-determining step (TS2) for the pNPP monoanion reaction is characterized by a dissociative, protonated metaphosphate-like species, as shown in Fig. 3. Additionally, the dissociation of the phosphoryl group has occurred without protonation of the p-nitrophenoxide leaving group. Both of these predictions are in agreement with experimental kinetic isotope, pH-rate profile and Bronsted analysis data [130] stating that the transition state in the rate-limiting step is dissociative and that Cdc25 is the only known PTPase that does not utilize acid catalysis in the dephosphorylation reaction of pNPP. The simulation results raised an interesting question to the broader issue of drug design. For example, phosphate mimetics, which are often thought to be a good starting point for the design of protein phosphatase inhibitors, may need to have a charge of −1, rather than −2, for effective binding and inhibition of Cdc25.

Figure 2.

Free energy profiles and stationary points for the dephosphorylation of pNPP in the monoanionic (left) and dianionic forms catalyzed by Cdc25.

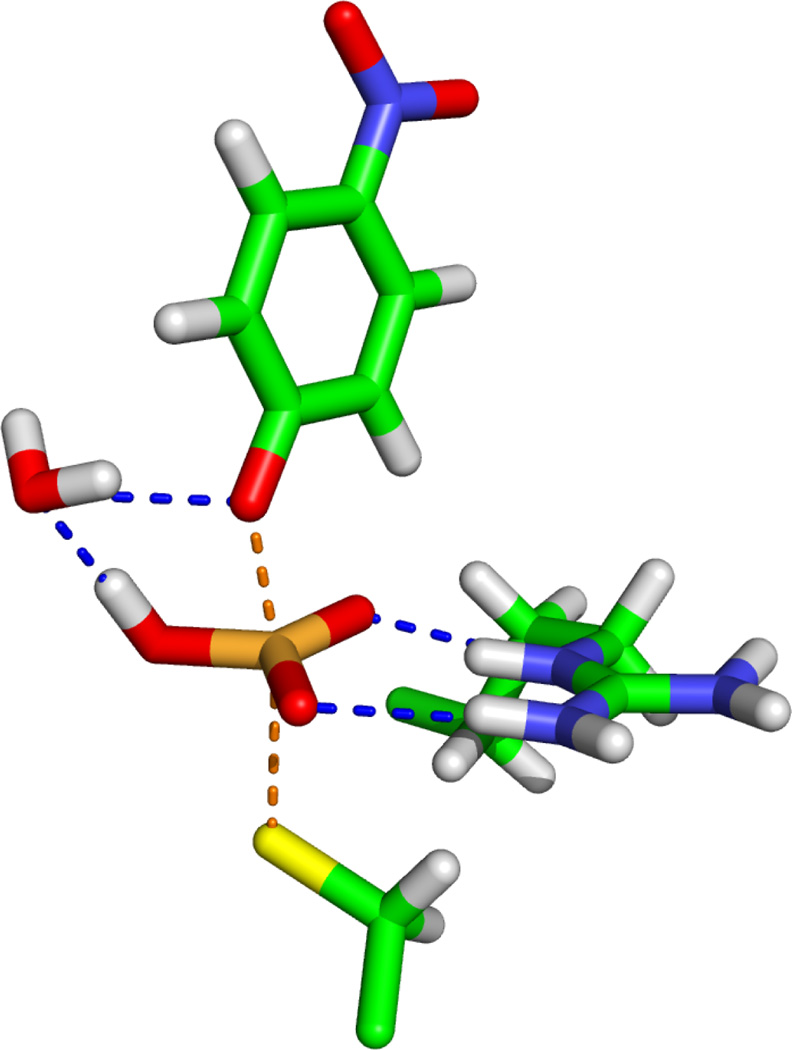
Figure 3.

Transition state for the dephosphorylation of pNPP catalyzed by Cdc25.

Orotidine-5’-monophosphate decarboxylase (ODCase)

Orotidine-5’-monophosphate decarboxylase (ODCase) gains its fame as one of the most proficient enzymes known [131]. It catalyzes the decarboxylation reaction converting orotidine-5’-monophosphate (OMP) to uridine 5’-monophosphate (UMP). The rate of uncatalyzed decarboxylation of 1-methyl orotate molecule in solution (k_non) was determined to be 2.8×10⁻¹⁶s⁻¹ [131]. Compared to the uncatalyzed reaction in solution, ODCase catalyzes the decarboxylation of OMP with a rate (k_cat) of 39s⁻¹ [132], speeding up the process by an unprecedented factor of 1.4×10¹⁷ without the assistance of any metal ions or cofactors.

Several catalytic mechanisms of ODCase have been proposed and examined in detail theoretically and experimentally [133, 134, 135, 136, 137, 138], but no agreement has been made. The heart of the debates is if the enzyme utilizes a covalent mechanism, such as protonation of the pyrimidine ring [137, 138]. Even though theoretical study has suggested that protonations of the pyrimidine ring can lower the reaction barrier substantially, this proposal has not gained much support from experiments. One of the major challenges for mechanistic schemes involving protonated-pyrimidine ring is that available enzyme structures do not reveal good and definite candidates for a proton donor.

To clarify if the non-covalent interactions alone can be responsible for such a large degree of stabilization inferred by the classical transition state theory, extensive theoretical simulations have been carried out, including pure classical MM simulations [139], QM calculations for gas-phase model systems [137, 140], and combined QM/MM simulations [141, 142, 138, 115, 143]. Some simulations have supported the direct decarboxylation mechanism, while some have not been able to reach a definite conclusion. Even for those simulations that support the direct decarboxylation mechanism, the causes for the mechanism, i.e., the driving force for the catalysis, have not been agreed on. For example, whether the electrostatic stress interaction or a desolvation effect drives the catalytic reaction has been under extensive debate.

A somewhat unexpected observation is that several calculations employing DFT and/or other ab initio QM methods have predicted barriers significantly higher than the experimental value [138, 143, 115, 140]. Particularly, simulations combining Car-Parrinello molecular dynamics [144] with the Jarzynski non-equilibrium method [112]yielded a barrier of 21.5 kcal/mol for direct decarboxylation and 33 kcal/mol for C6-protonation assisted decarboxylation [115]. Even though this work provided the strongest theoretical evidence for the direct decarboxylation mechanism, the computed barrier is still too high. Recently, this result was challenged by Houk and coworkers whose simulations again combined DFT calculations with a meta-dynamics sampling method [143]. In the latter study, however, simulations using two differently sized QM subsystems both yielded barriers significantly higher than experimental data.

One reason that may be responsible for the failure of QM/MM simulation is that many previous simulations included a crystallographic water molecule in the active site, whose presence was only confirmed in the structures of enzyme bound with an inhibitor such as 6-hydroxyUMP (BMP) and 6-AzaUMP. Simply considering the fact that the decarboxylation reaction proceeds extremely slowly in water solution, one wonders why and how ODCase utilizes this water molecule in the catalytic process. If stabilizing the transition state requires some charged groups, direct interaction between the reacting moieties of OMP and those charged groups of enzyme would be more effective than the indirect interaction through this water molecule. Furthermore, the position of this water molecule is in fact obstructive to the catalytic process. In ODCase/BMP structure, this water is very close to a hydrophobic pocket, presumably a site to which the leaving CO₂ molecule will bind favorably. The existence of this water molecule would thus only increase the difficulty of CO₂ leaving as it will probable jam the exit path. The existence of this water may also disturb the hydrogen-bond network of Lys-Asp-Lys-Asp(B) and consequently destabilizes the transition state. From these two considerations, we hypothesize that this water molecule may in fact appear only as a cofactor for the binding of the BMP molecule or in some cases the side reactions catalyzed by ODCase, and should not appear in the normal course of the catalytic process of OMP decarboxylation. To examine the validity of this hypothesis, we carried out accurate ab initio QM/MM simulations on the direct decarboxylation processes of OMP in solution and in ODCase without the presence of the BMP bound water molecule. The simulations were performed with the recently developed QM/MM minimum free energy path (QM/MM-MFEP) method which allows the use of very large basis sets and accurate but costly ab initio QM methods.

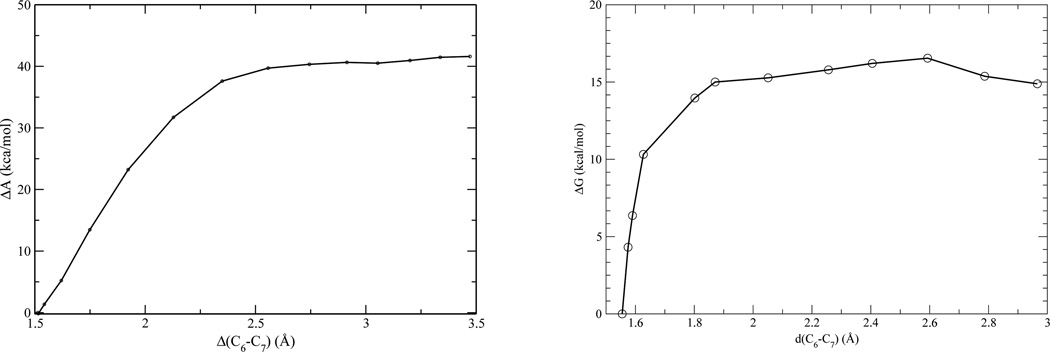
By comparing results of gas-phase reaction computed at different level of QM theories and/or basis sets, we determined that B3LYP/6-31+G* is the least basis set for geometry optimization, while B3LYP/6-311+G* is a basis set perhaps required for accurate energy calculations. At the QM level of B3LYP/6-311+G*, we obtained a barrier of 40.2 kcal/mol, shown in Fig. 4 for the decarboxylation reaction in solution, in good agreement with the experimental measurement of 37.5 kcal/mol. This result supported the use of the QM methods in our QM/MM simulation of enzyme process. In the absence of the crystallographic water molecule, our QM/MM-MFEP method yielded a barrier of 16.5 kcal/mol for reaction in ODCase Fig. 4, in excellent agreement with experiments. The optimized reaction path indicated that the reaction was initiated by the rotation of the ε-NH₃group of Lys72 toward the C6 atom of the pyrimidine ring.

Figure 4.

Free energy profiles for the OMP decarboxylation in solution (left) and in ODCase (right).

By comparing the QM energy cost for breaking the C6–C7 bond in gas phase, water solution, and ODCase, it is clear that due to special structure of the active site of ODCase, breaking C6–C7 bond is intrinsically much easier in enzyme than in solution. In other words, water is a very poor solvent for this process. The transition state of the decarboxylation has a negtive charge spread out over the entire pyrimidine ring, clearly water does not like this negatively charge large size group. In contrary, in the enzyme several hydrogen bonds can provide much stronger stabilization to the transition state. In ODCase, the energy difference for the QM subsystem in the reactant and transition state is merely 22.6 kcal/mol, significantly lower than solution process, and more closely resemble a gas-phase process.

Electron transfer reaction

Electron transfer (ET) is a fundamental process in chemical and biological reactions. Because of the quantum nature of electrons, QM theory is required for theoretical simulation of ET process. The most important theory for studying ET is Marcus theory, in which a linearly polarized solvent model is used to derive the mostly symbolized quadrature curves. Simulations have been performed to explore the contribution of solvent and protein structures beyond the simple linear-response model. Many previous QM/MM simulations employed a thermodynamic integration approach in which the energy surfaces of two states are mixed together to probe the redox process [145, 146, 147, 148, 149, 150]. The relative weights of two energy surfaces thus become a reaction coordinate. Recently, Zeng et. al. employed a “fractional electron” approach to simulate the ET reactions in solution [83]. In this approach, the number of electrons of the QM system was chosen as the reaction coordinate and thermodynamic integration with direct ab initio QM/MM sampling was employed to compute the redox free energies. The results are in good agreement with experimental and previous studies. This approach method thus creates a new venture for the simulation of ET processes in solution and in enzymes.

CLOSING REMARKS

Unique advantages such as broad applicability and reliability, make ab initio QM/MM methods extremely promising and attractive in the simulation of complicated chemical processes in solution and in enzyme. The computational costs often limited the application of ab initio QM in the simulation of large systems and/or of long timescale events. Recent developments in ab initio QM/MM free energy simulation methods, however, paved the way for accurate modeling of these processes. It is expected that the application of ab initio QM/MM free energy simulation methods can make important contribution to the ultimate understanding of enzyme catalysis, including the long sought question about the relationship between enzyme dynamics and catalysis.

Figure 5.

Transition state for the OMP decarboxylation catalyzed by ODCase