Abstract
Association rates for interactions between folded proteins have been investigated extensively, allowing the development of computational and theoretical prediction methods. Less is known about association rates for complexes where one or more partner is initially disordered, despite much speculation about how they may compare to those for folded proteins. We have attached a fluorophore to the N-terminus of the 25 amino acid cMyb peptide used previously in NMR and equilibrium studies (termed FITC-cMyb), and used this to monitor the kinetics of its interaction with the KIX protein. We have investigated the ionic strength and temperature dependence of the kinetics, and conclude that the association process is extremely fast, apparently exceeding the rates predicted by formulations applicable to interactions between pairs of folded proteins. This is despite the fact that not all collisions result in complex formation (there is an observable activation energy for the association process). We propose that this is partially a result of the disordered nature of the FITC-cMyb peptide itself.
Introduction
The protein structure–function paradigm was widely accepted for more than 100 years. However, in recent years, unstructured but biologically active proteins have been the focus of intense research. Much of the work has involved computational predictions of disorder based on amino acid sequences.1 Estimates gained from these approaches suggest that 33% of proteins in eukaryotes might have intrinsically disordered regions.2 In particular, disordered regions appear to be highly represented in proteins involved in signaling and transcriptional processes.2
CBP, and its paralogue p300, are general coactivators that act as a bridge/scaffold between transcriptional factors bound to DNA, and other coactivators and elements of the basal transcriptional machinery.3 The KIX domains of CBP and p300 are known to have many binding partners, which can bind at one or more of two distinct sites on KIX, named the pKID and MLL sites after two of the binding partners.4,5 Several of the partner proteins have disordered regions that undergo coupled folding and binding.5−8 One such protein, which is known to bind in vivo and in vitro, is cMyb.9
cMyb is a 75–89 kDa transcription factor involved in the proliferation, survival, and differentiation of hematopoetic cells.10 It consists of three functional domains: an N-terminal region consisting of three folded DNA binding domains, a central transactivation domain (TAD), and a C-terminal negative regulatory domain. The TAD of cMyb is reported to bind to the KIX region of CBP/p300, and an NMR structure of the complex, obtained using a 25 amino acid peptide from the TAD, has been published8 (Figure 1). This structure shows that the cMyb peptide folds to form a single amphipathic helix that binds along the shallow hydrophobic groove created by the α1 and α2 helices of KIX, and has a single bend at Leu302 which allows this residue to penetrate into a hydrophobic pocket. The pKID domain of CREB is known to bind in the same shallow hydrophobic groove.6 There are no obvious sequence similarities between cMyb and pKID, apart from the conserved leucine residue in the hydrophobic pocket. However, cMyb does contain a known binding motif for KIX φXXφφ, where φ represents a bulky hydrophobic residue and X represents any amino acid.4
Figure 1.
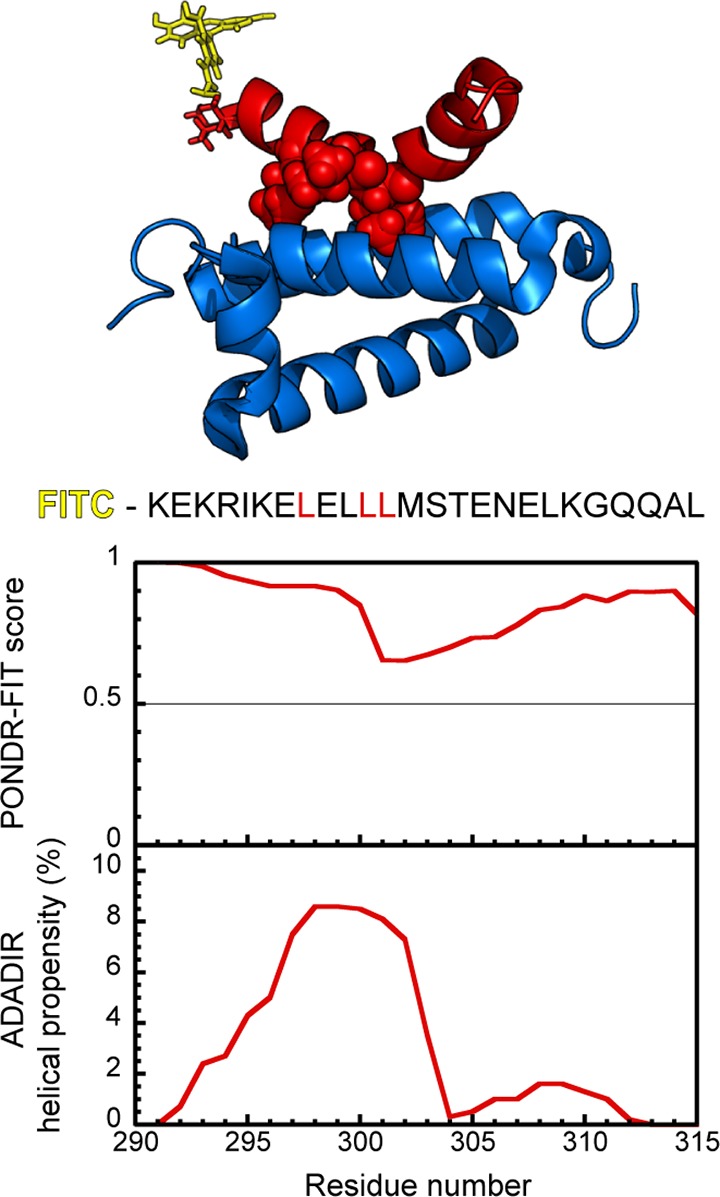
(upper) Cartoon of the complex between FITC-cMyb peptide (red) and KIX (blue). An FITC moiety (yellow) has been superimposed on the NMR structure (PDB 1SB0)8 to show its relative position and size. The leucine residues of the KIX binding motif are shown as red spheres. (lower) cMyb peptide amino acid sequence, shown with its PONDR-FIT28 and AGADIR29 scores displayed at residue level. Residue numbers correspond to position within the full cMyb protein.
There has been much speculation about the importance of disorder to a protein such as cMyb.11 It is frequently stated that one advantage of intrinsic disorder to a protein is the potential for higher association rates with its partners.11−13 However, there is no experimental evidence that in general intrinsically disordered proteins bind significantly faster to their target proteins than their folded counterparts. Reported association rate constants span many orders of magnitude for both folded proteins and unfolded proteins, and there is no statistically significant difference between the two groups.14 In fact, this may not be particularly surprising. Theoretical considerations of increased capture radius, and simulations with lowered free energy barriers, both of which have been proposed to lead to high association rates for IDPs, predict only modest rate enhancements (of under 2.5-fold).13,15 These are likely to be masked entirely by the rate enhancement (or retardation) caused by long-range electrostatic effects, which undoubtedly explains a substantial amount of the variation observed in association rates. Testing for such trends would therefore require comparison of rates collected under conditions where long-range electrostatic effects are corrected for, i.e., at infinite ionic strength.
In investigating the potential role for disorder in proteins, the mechanism by which coupled folding and binding takes place is also of interest.11 Two extreme cases are apparent. First, the disordered protein could bind to the partner and then fold (induced-fit mechanism). Second, the unbound protein could exist in a variety of conformations, of which only those that have a structure resembling the bound form can bind (conformational-selection mechanism). Of course, in actuality, a mixture of the two could also operate where only some partially formed conformations are able to bind and subsequently rearrange to form the final. It has also been noted that, if both mechanisms operate, the flux through each pathway might be changed with protein concentration, as well as with conditions such as pH and temperature.16,17
Despite the interest in kinetic differences between folded and disordered protein binding, and the capability of kinetic measurements to provide mechanistic information, there have so far been relatively few kinetic studies. Here we aim to extend the characterization of the kinetics of a coupled folding-and-binding process. We have attached a fluorophore to the N-terminus of the 25 amino acid cMyb peptide used previously in NMR and equilibrium studies (termed FITC-cMyb), and used this to monitor the kinetics of its fast interaction with the KIX domain of CBP. In particular, we investigate the dependence of the association rate upon ionic strength and temperature to shed light on the mechanism of this coupled folding and binding process.
Methods
Preparation of KIX Protein
The synthetic gene for the KIX domain of mouse CBP (Uniprot 45481, residues 586–672) was obtained from Genscript. The gene was inserted into a modified version of the pRSET A vector that encodes an N-terminal hexahistidine tag with a thrombin cleavage site between the tag and the protein. Protein expression was carried out in Escherichia coli C41 (DE3) grown in 2xTY media at 37 °C. Expression was induced once the cells reached an optical density of 0.4–0.6 AU at 600 nm, by adding IPTG to a final concentration of 0.1 mM and reducing the temperature to 18 °C. The cells were grown overnight and harvested by centrifugation. The centrifuged cells were resuspended in 25 mM imidazole, sonicated and centrifuged, and the protein from the soluble fraction was purified by affinity chromatography on Ni2+ agarose resin. Bound protein was eluted with 250 mM imidazole, and the his-tag cleaved by overnight incubation with thrombin at room temperature. The protein was further purified by gel filtration using a Superdex G75 column in pH 7.4 100 mM sodium phosphate buffer. For ionic strength studies, KIX protein was buffer exchanged and stored in ddH2O. The concentration of KIX stocks was determined using an extinction coefficient of 12 009 M–1 cm–1 at 280 nm obtained by the method of Gill von Hippel.18
Peptides and Reagents
N-terminally labeled FITC-cMyb peptide (Uniprot P06876, residues 291–315) was purchased from Biomatik. 1 mg aliquots were dissolved at 1–2 mg/mL in ddH2O as required. The stock concentration was determined from the absorbance at 493 nm of a 20-fold dilution into biophysical buffer, using an extinction coefficient of 75 000 M–1 cm–1. Sodium phosphate, MOPS, and sodium chloride were purchased from Sigma.
Biophysical Buffers and Dilutions
Two separate buffer types were utilized in these studies. First, 100 mM sodium phosphate buffer, pH 7.4, the pH of which is relatively insensitive to temperature changes, was used for the temperature studies. Second, 20 mM MOPS (pH 7.30 ± 0.02 at 10 °C) with a range of sodium chloride concentrations was used in ionic strength studies. MOPS buffers in the same range as phosphate but has a lower ionic strength because of its lower valency, enabling a larger range of ionic strengths to be investigated. We observed that the rate of association was slightly lower in phosphate buffer, considering our estimates of its ionic strength. In addition, 0.05% tween-20 was included in all biophysical buffers to avoid nonspecific interactions with plastic-ware.
In preparing solutions for kinetic assays, dilutions of KIX and FITC-cMyb stocks were weighed, so that accurate concentrations (accounting for solution density) were obtained.
Circular Dichroism
Circular dichroism (CD) scans were performed with an Applied Photophysics Chirascan, in cuvettes of 1 or 0.2 mm path length. In mixing experiments, individual solutions of FITC-cMyb and KIX in pH 7.4 100 mM sodium phosphate (0.05% tween-20) were prepared, and aliquots removed for mixing in a 1:1 ratio. Spectra were obtained for all three solutions and buffer subtracted. The expected spectrum in the absence of protein interaction was calculated as the average of the two spectra for the individual protein solutions. Helical content for FITC-cMyb alone was variously estimated as 28, 30, and 37% using the methods of Perez-Iratxeta et al.,19 Morriset et al.,20 and Chen et al.,21 respectively.
Equilibrium Anisotropy Binding Curves
FITC-cMyb (1 μM) samples were incubated at the relevant temperature for 1 h in the presence of varying concentrations of KIX, and fluorescence anisotropy measurements performed using a Cary Eclipse Spectrophotometer with fluorescence polarization accessory. The sample holder was maintained at temperature with a Peltier device. Excitation and emission wavelengths were 493 ± 5 and 517 ± 5 nm, respectively. Fluorescence intensity measurements, IVV and IVH, were recorded with polarizing filters in VV and VH format, respectively, and anisotropy R calculated according to eq 1:
| 1 |
where the G-factor (=IHV/IHH) of the experimental setup is used to correct for differences in sensitivity to horizontally and vertically polarized light.22
An estimate of the equilibrium dissociation constant (Kd) was obtained from each binding curve by fitting to eq 2
| 2 |
where Rfree and (Rfree+ ΔR) are the anisotropy of free and bound FITC-cMyb, and [KIX] and [cMyb] are the protein and peptide concentration, respectively.
Kinetic Anisotropy Measurements
Association kinetics were monitored by following the change in anisotropy of FITC-cMyb on binding using a SX20 stopped-flow spectrometer (Applied Photophysics) with an FP1 fluorescence polarization accessory. Under each condition, 10–40 traces were collected and then averaged. Data collected before the first 1 ms were removed before fitting. Anisotropy values reported from stopped-flow have not been corrected for background fluorescence.
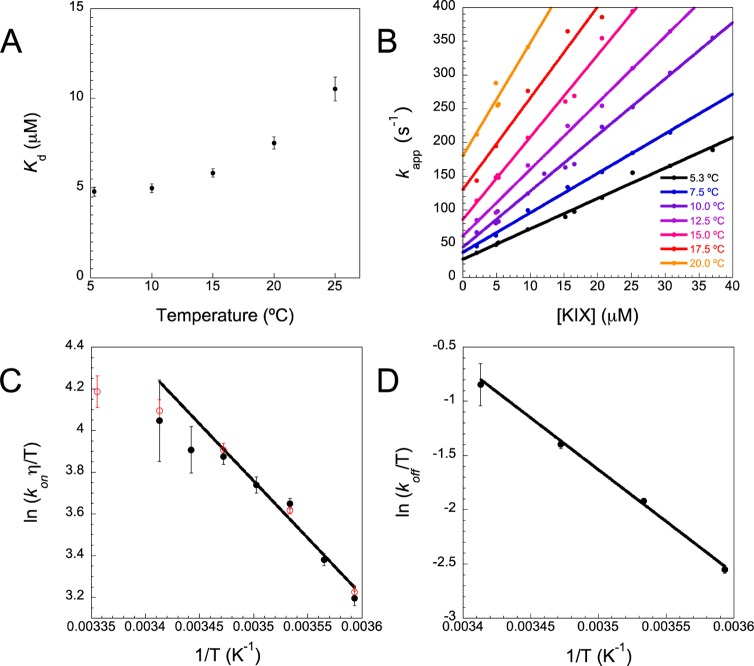
In temperature studies, KIX solutions of various concentrations were mixed 1:1 with 1 μM FITC-cMyb. Three independent KIX stocks were used in the experiments. Kinetics were fit to a single exponential decay function to extract an apparent rate constant, kapp. Rates above 400 s–1 were not included for further analysis. For each temperature, the concentration-dependent kapp estimates were fit with a straight line, the gradient of which was used to estimate the association rate constant (kon). Dissociation rate constants (koff) were calculated from the relation koff = Kdkon, which is appropriate for two-state bimolecular reactions (see Results). In analyzing the association kinetic data, the viscosity of the solutions was assumed to be the same as that for water at each temperature.23
In ionic strength studies, 5–10 μM KIX in MOPS buffer was mixed 1:1 with 5 μM FITC-cMyb in MOPS buffer of equal ionic strength at 10 °C. Kinetic traces were fit to eq 3, which is appropriate for fitting association kinetics collected under reversible conditions
| 3 |
where b = −(Kd + (1 + x)[cMyb]), z = (Kd2 + 2(1 + x)Kd[cMyb] + (x2 – 2x + 1)[cMyb]2)1/2, and x = [KIX]/[cMyb]. This is an adaptation of the fitting strategy we recently reported,14 to account for different mixing ratios. The value of Kd obtained from equilibrium measurements was used as a fixed parameter for the fit.
Calculating Basal Rate Constants
The variation in association rate constant with ionic strength (I) was modeled with a Debye–Huckel-like approximation that has been determined empirically (eq 4).24
| 4 |
where kon,basal, U, and a are fitting parameters, R is the gas constant, T is the temperature, and κ is given by κ = (2NAe2I/ε0εrkBT)1/2, where NA and kB are the Avogadro and Boltzmann constants, respectively, and ε0 and εr are the electrical permittivity of the vacuum and the dielectric constant of water. The variable kon,basal represents the expected kon in the absence of long-range electrostatic effects.
In collating basal association rate constants from the literature for Figure 6, originally reported values were used wherever possible. If basal rates were not reported, the data were fit to eq 4. If the error in the estimated basal rate was larger than the value itself, we excluded the data from the figure.
Figure 6.
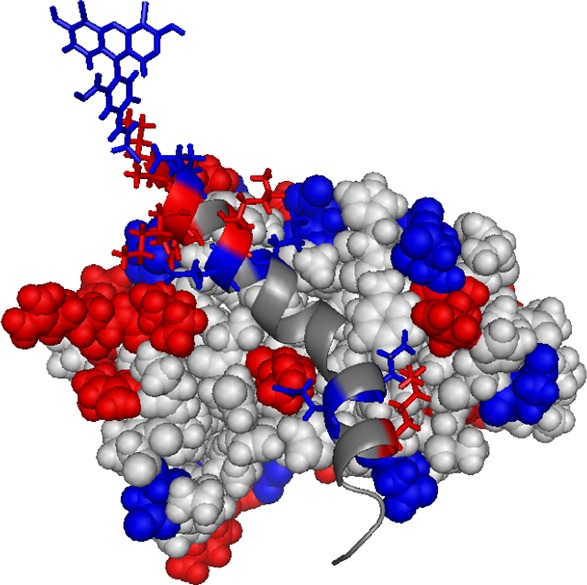
The charge distribution for FITC-cMyb (ribbon) and KIX (spheres) is shown on the structure for the complex, based on pdb 1SB0. Positively charged residues are shown as red spheres (KIX) or sticks (cMyb). Negatively charged residues are shown as blue spheres (KIX) or sticks (cMyb). The fluorophore FITC, which is superimposed on the structure, is expected to be predominantly in its dianionic form, and is shown in blue sticks. Figure prepared using PyMol (The PyMOL Molecular Graphics System, version 1.6, Schrödinger, LLC).
Estimation of Smoluchowski Limit for Association Rate
Expected hydrodynamic radii for cMyb and KIX based on an empirical fit gained for a range of folded and denatured proteins, respectively, using pulse gradient field NMR are 1.38 and 1.66 nm.25 These radii were used in eq 6 to estimate the Smoluchowki limit.26
Estimation of Protein Charge
The charge on KIX and cMyb at pH 7.4 was estimated using average pKa values reported for amino acids in globular proteins and model peptides.54 The charge for FITC-cMyb was corrected to account for N-terminal addition of FITC. At pH 7.3–7.4 and 25 °C, fluoroscein exists predominantly as a dianion (∼90%), with some anion (∼10%), the equilibrium between the two species being described by a protolytic constant of 6.43.27
Results
Coupled Folding and Binding of cMyb Peptide to KIX
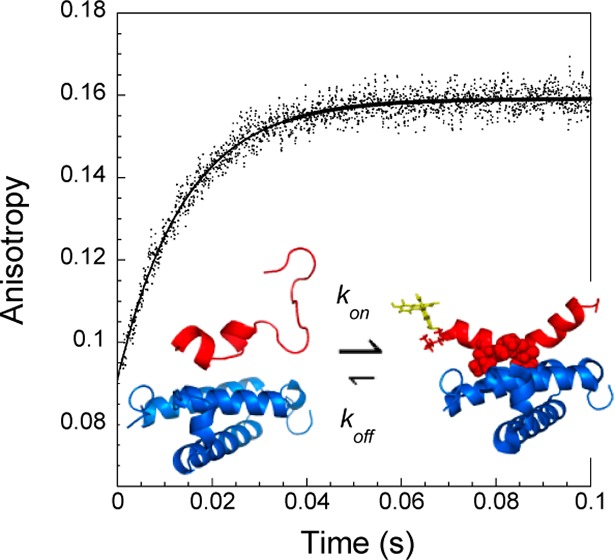
To monitor the formation of cMyb-KIX complex, we used a version of the peptide with a fluorophore, FITC, attached to the N-terminus (termed FITC-cMyb). Otherwise, the cMyb peptide and the KIX protein are identical to those used in generating the NMR structure of the complex (Figure 1).8
We tested this version of the peptide to ensure we had not significantly perturbed the system by addition of the dye molecule. First, the secondary structure of the unbound peptide was very similar to that of the unlabeled cMyb peptide (Figure S1, Supporting Information) though a little more helical. Circular dichroism (CD) spectra of free FITC-cMyb (Figure 2A, red line) showed the peptide to be mostly unstructured, with around 30% residual α-helical content (see Methods). Second, the peptide was still observed to bind to KIX protein. On mixing FITC-cMyb with KIX, a reliable increase in the anisotropy of the FITC is observed, which reflects the slower tumbling of FITC-cMyb in solution on formation of the complex. Such measurements were performed with various concentrations of KIX (Figure 2B), and the curve fit to eq 2 to estimate the equilibrium dissociation constant, Kd, of the complex of 10.5 ± 0.7 μM at 25 °C. This is in good agreement with previous estimates of 10 and 12.5 μM obtained for unlabeled cMyb by isothermal titration calorimetry under very similar conditions (pH 7, 27 °C).8,30 These results indicate that there has been no significant perturbation of the system on dye addition.
Figure 2.
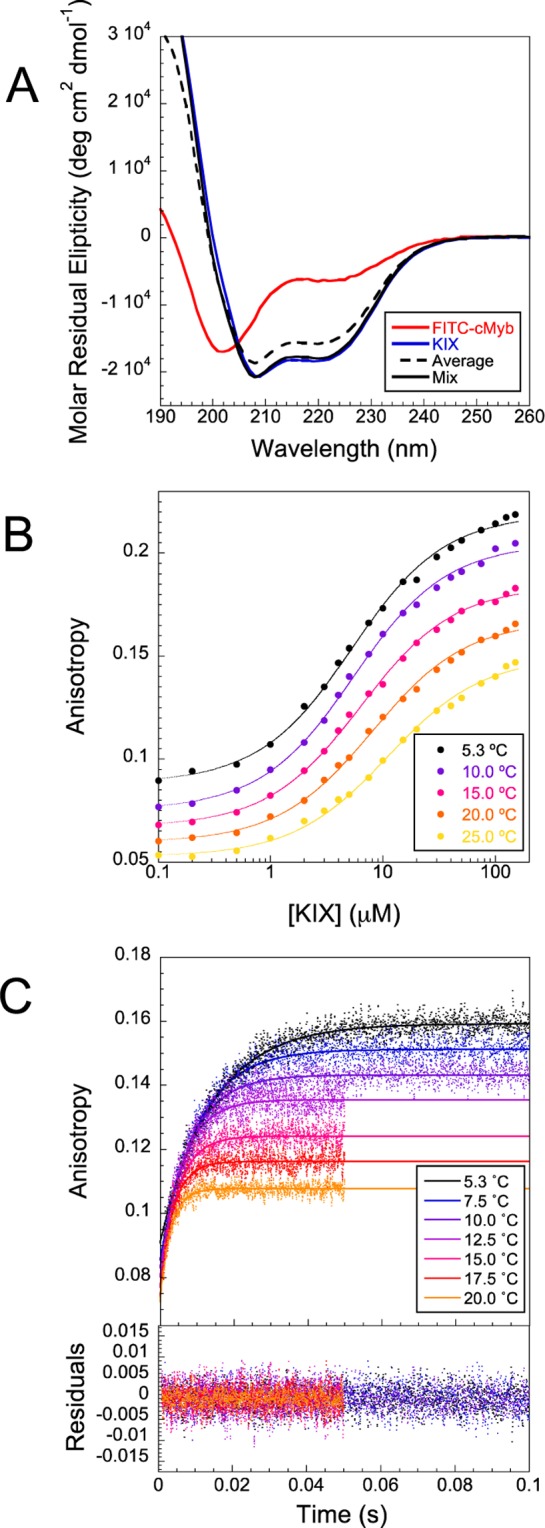
Coupled folding and binding of FITC-cMyb with KIX domain. (A) CD spectra of mixtures of FITC-cMyb and KIX indicate higher helical content than the arithmetic mean of spectra obtained for the individual proteins. Spectra are the average of three repeats. (B) Apparent binding affinity for KIX protein with FITC-cMyb assessed using anisotropy measurements at various temperatures. Only small (<10%) changes in fluorescence intensity were observed with increasing concentrations of KIX protein. (C) Stopped-flow anisotropy changes on mixing were used to monitor the association of FITC-cMyb with KIX. Final concentrations of FITC-cMyb and KIX were 0.5 and 10 μM, respectively. Curves represent the average of around 10–30 traces. Lines represent the best fit to a single exponential, from which an apparent rate constant was extracted.
Although computational predictors such as PONDR28 and AGADIR29 suggest that the peptide should be almost completely disordered prior to binding (Figure 1), the CD spectra suggest that cMyb has around 30% residual helicity in its unbound state. The NMR structure of the complex published previously estimated that 70% of the amino acids are in a helix in the bound form,8 suggesting that this protein–protein interaction falls into the coupled-folding and binding category. We confirmed this increase in helicity on binding by comparing CD measurements of the individual components and mixtures performed at 25 °C (Figure 2A). CD spectra were recorded for 100 μM FITC-cMyb (red line) and 100 μM KIX (blue line), and for mixtures obtained by direct 1:1 mixing of these solutions (black line). This experiment was performed in triplicate, and in each case, the mixture had a more helical spectrum than the one that would be obtained if the two protein components did not interact (solid and dotted black lines, respectively). Note that under these conditions 64 ± 2% of the proteins are expected to be in complex due to the relatively high, 10.5 μM, Kd. At lower concentrations, where less protein is in complex, the difference between the two spectra is reduced as expected (Figure S2, Supporting Information).
Temperature Dependence of Association Kinetics Monitored Using Anisotropy
Equilibrium anisotropy measurements were performed at various concentrations of KIX to determine the binding affinity at temperatures ranging from 5 to 25 °C. The binding affinity decreased significantly with temperature (Figure 3A). Both the association and dissociation processes can reasonably be expected to occur faster at higher temperatures. This result suggests that the dissociation rate increases more relative to the association rate in this temperature range. However, in order to determine the effect of temperature on the processes separately, and to check for the presence of any intermediates in the process, it is necessary to perform kinetics measurements (Figure 2C, Figure 3).
Figure 3.
Temperature dependence of the rate and equilibrium constants for the interaction between FITC-cMyb and KIX in pH 7.4 100 mM sodium phosphate buffer. (A) Kd at various temperatures obtained from the data in Figure 2B. (B) Apparent rate constants from single exponential fits of kinetic anisotropy traces, such as those in Figure 2C, obtained under pseudo-first-order conditions. The gradient of the line of best fit for each temperature was used to estimate kon which is shown as black circles in an Eyring-type plot in part C. η at each temperature was calculated according to the empirical relation described by Kestin et al:31 ln(η/η293) = [(293 – T)/(T – 177)][1.2364 – 1.37 × 10–3(20 – T) + 5.7 × 10–6(20 – T)2], where η293 is 1.002 × 10–3 Pa s. (D) Eyring-type plot for koff, calculated according to koff = Kdkon. In generating the straight line fits in parts C and D, data were weighted inversely according to their variance. In part C, the open red circles represent estimates of kon obtained using the straight line fit for koff in part D and measured Kd values in part A.
Solutions of FITC-cMyb were mixed rapidly with higher concentration solutions of KIX, and the resulting anisotropy increase of FITC monitored using stopped-flow anisotropy. Under these pseudo-first-order conditions, the observed anisotropy increase was observed to fit well to a single exponential (Figure 2c). The dependence of the apparent rate constant on the KIX concentration could then be used to provide estimates for the association rate constant and dissociation rate constant.
Initial attempts to follow the kinetics of the binding process using stopped-flow anisotropy at 25 °C had mixed results. Although it was clear that in principle a change could be observed, the reaction was too rapid to reliably measure rates under the conditions required in order to populate the complex sufficiently for a reasonable signal change (data not shown). Instead, these experiments were performed at a range of temperatures between 5 and 20 °C. As can be seen from Figure 2, as the temperature is decreased, the observed signal change increases, predominantly as a result of higher final complex concentrations.
The kinetic data are consistent with a two-state equilibrium, with no populated intermediates. Stopped-flow anisotropy kinetics traces were all fit well by a single exponential. There was a small decrease in FITC fluorescence upon mixing FITC-cMyb with KIX, which did not take place on mixing with buffer alone. This change reflects a difference in quantum yield, related to the fluorophore environment, between the free and bound forms of the peptide. Although subject to higher error, the rates obtained fitting these kinetic traces agreed with those from anisotropy (Figure S3A, Supporting Information), which also suggests there are no populated intermediates. Finally, the Kd estimates obtained purely from kinetic data using (kon/kapp,0M) are similar to those obtained from equilibrium measurements (Figure S3B, Supporting Information). The apparent rate constants for each temperature are plotted against concentration in Figure 3B. The data fit well to straight lines, with no evidence of plateau toward the higher concentrations. In the case of a two-state equilibrium, the intercept (kapp,0M) and gradient in these plots simply represent the dissociation and association rate constants, respectively.
Both the association and dissociation rate constants increase with temperature (Figure 3B). The temperature dependence of the dissociation process, which is first-order, is expected to stem solely from the free energy difference between the bound state and the transition state, in analogy with results from protein folding.32 According to transition state theory, an Eyring plot (Figure 3C) may therefore be used to determine the enthalpic barrier for dissociation. Over such a short temperature range, ln(koff/T) appears linear with 1/T, and it is not possible to estimate any change in heat capacity. However, the gradient of the straight line provides an estimate for the enthalpic barrier, ΔHTS-b = 19.7 ± 1.2 kcal/mol.
The temperature dependence of the bimolecular association process is likely to be more complex. In interactions between two folded proteins, the rate constant for association can be considered to be the product of three terms; the proportion of collisions with the correct orientation to proceed (A), the collision frequency which is proportional to T/η, and an activation term to account for the proportion of collisions with sufficient thermal energy, to form the transition state (e–EA/RT), as shown in eq 5.
| 5 |
The maximum value of kon is therefore equal to the frequency of collisions between correctly aligned molecules, and occurs when the activation energy is zero. In this case, the reaction is simply diffusion-limited. In such a situation, once the association rate constant is corrected for the collision rate, there should be no further dependence upon the temperature. This is clearly not the case for the association between FITC-cMyb and KIX, since the gradient of the line in Figure 3C is nonzero. The gradient of the line might be used to form an estimate of the apparent activation energy for the association process under the conditions used of 10.9 ± 0.7 kcal/mol. This is not, however, necessarily the same as the enthalpy difference between the free state and transition state.33
In this case, the two proteins are not both folded initially. This could further complicate analysis of the association rate because the starting structure of the peptide could also alter with temperature. Changes in the secondary structure of FITC-cMyb and KIX were examined using CD for temperatures between 10 and 80 °C (Figure S4, Supporting Information). Apparent nonreversibility for the process, indicative of aggregation that occurred at higher temperatures, makes the results difficult to interpret quantitatively. However, it is clear that even over the small temperature range we conducted kinetic experiments over there are changes in the secondary structure of the FITC-cMyb, and remarkably also in KIX. The latter undergoes a cooperative unfolding transition but with a folded baseline indicative of helix fraying in the temperature range used in these studies.
Ionic Strength Dependence
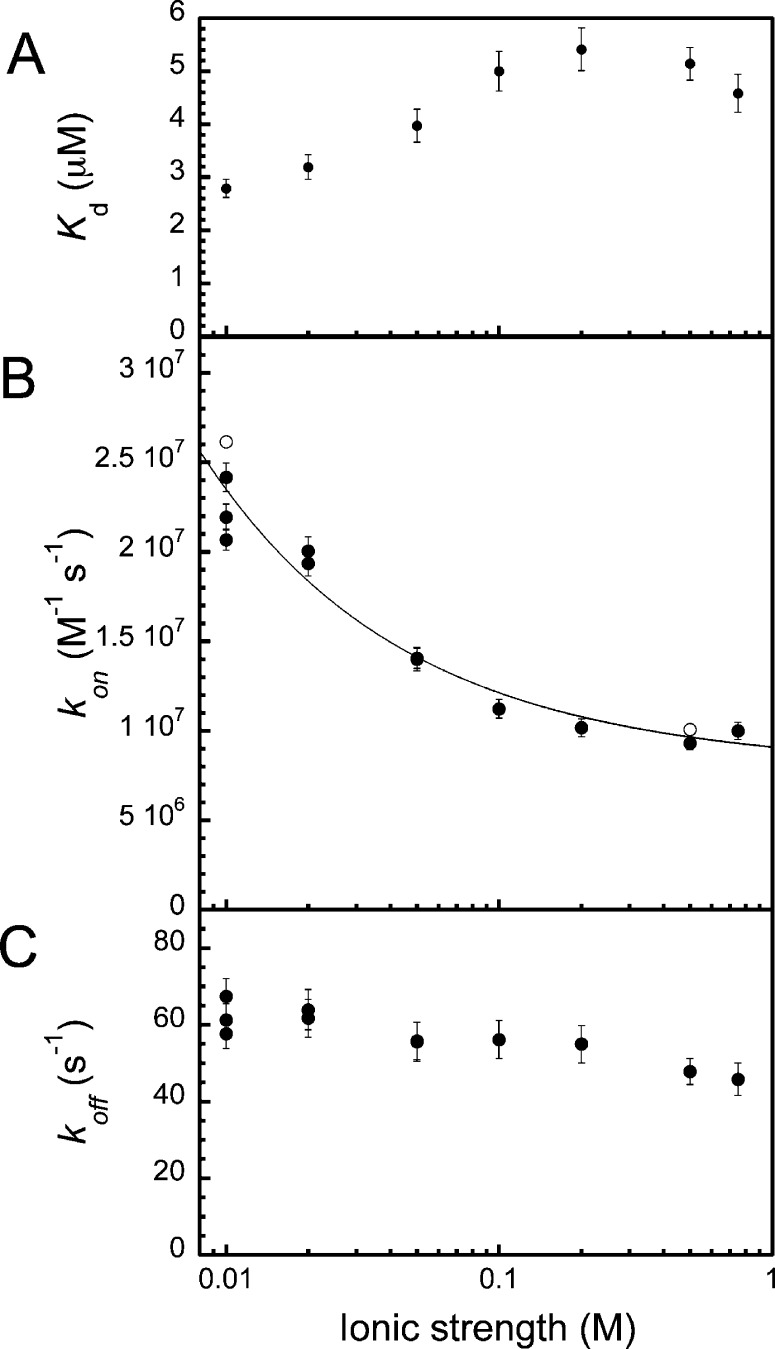
At the pH values used in these studies, FITC-cMyb and KIX are expected to be opposite in charge (−2.9 and 3.1, respectively). To determine the influence of nonspecific long-range electrostatics upon the association rate constant, further experiments were performed at a range of ionic strengths.
Separate solutions of FITC-cMyb and KIX were incubated in MOPS buffers of equal ionic strength at 10 °C. The solutions were rapidly mixed and association monitored using stopped-flow fluorescence anisotropy. The ratio of FITC-cMyb to KIX was around 1:1 or 1:2. Pseudo-first-order conditions clearly do not apply in this case. Kinetics traces were fit instead to eq 3 (Methods), by fixing Kd to the value estimated using equilibrium titration curves (Figure 4A and Figure S5A, Supporting Information) for each of the buffer conditions. This strategy was chosen because it enabled estimates of the association rate constant to be obtained from single kinetic traces and relatively low concentrations of KIX.14 Evidence in support of extracting kon using this approach (Figure 4B, closed circles), which depends upon the two-state nature of the process, is provided by estimates obtained using a pseudo-first-order strategy at both low and high ionic strengths (Figure 4B, open circles) which are very similar. Example traces with associated residuals, which demonstrate the quality of the fit, are shown in Figure S6 (Supporting Information). The equilibrium and association rate constants were surprisingly insensitive to the ionic strength of the solution. Over a 75-fold increase in ionic strength (from 10 to 750 mM), kon, decreases just over 2-fold, rapidly approaching a plateau value. Fitting these data to a Debye–Huckel-like approximation (Figure 4B, eq 4, black line) enables extrapolation of the rate constant to infinite ionic strength of (7.7 ± 0.5) × 106 M–1 s–1,34 thereby removing the effect of long-range electrostatic interactions. A smaller relative decrease in the dissociation rate constant with increased ionic strength was also observed.
Figure 4.
Equilibrium and rate constants for the interaction between FITC-cMyb and KIX in pH 7.30 ± 0.02 MOPS buffers of varying ionic strength at 10.0 °C. (A) Equilibrium dissociation constants extracted from binding affinity experiments (Figure S5A, Supporting Information). (B and C) Association and dissociation rate constants extracted from fitting stopped-flow kinetic traces obtained by mixing FITC-cMyb and KIX in approximately equal concentrations to eq 3. Error bars represent the error in the fit. In part B, the open circles represent independent estimates obtained using an alternative pseudo-first-order approach (Figure S7, Supporting Information). The solid line represents the best fit to a Debye–Huckel-like approximation of charge screening (eq 4).
Over this range of ionic strength, there was no significant change in the secondary structure of the KIX or FITC-cMyb as assessed by CD spectroscopy (Figure S5B, Supporting Information).
Evaluation of Previous Experimental Estimates of Basal Association Rates
There have been relatively few studies of the ionic strength dependence of protein–protein association rates.35−45 We summarize the observed basal association rate constants in Figure 5, and a short paragraph concerning each system is included in the Supporting Information. As yet, the sample size is too small to make fair comparisons between complexes of folded proteins, as compared with those from IDPs. This is especially the case because we expect some bias in the data, as ionic strength tests for electrostatic steering are more likely to be performed where fast association has been observed. Figure 5 demonstrates that, despite this potential bias toward fast associating systems, the basal association rate for the apparently two-state association between cMyb and KIX is the highest we have found reported for protein–protein association. As a result of the apparent activation energy required for association, the basal kon will have a significant temperature dependence. Since the majority of basal kon were determined at 25 °C, the results of the temperature dependence study were used to estimate the basal kon at 25 °C to facilitate comparison (open red circles, Figure 3C, see Methods).
Figure 5.
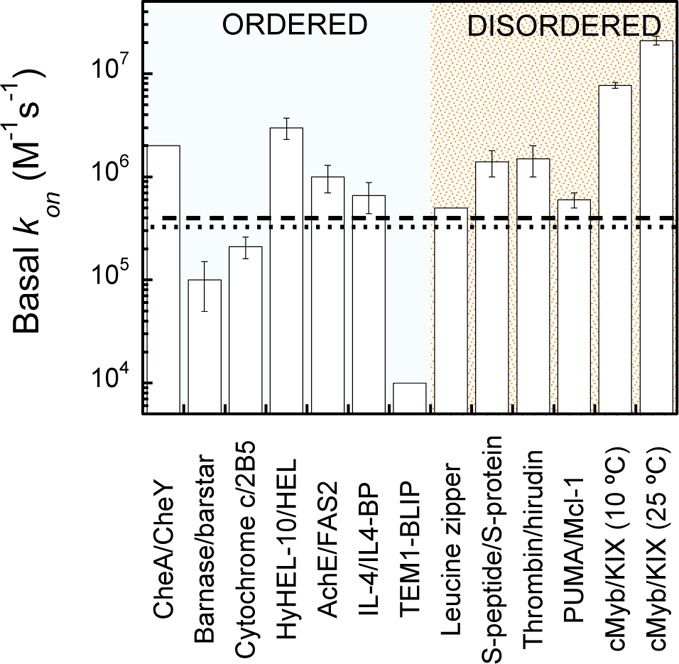
Estimated values for the basal association rate constant collated from studies where protein–protein association was studied over a range of ionic strengths (see Methods). Dotted and dashed lines represent the median association rate constants for complexes of folded and disordered proteins, respectively.14
Taking a separate approach to estimating basal rate constants, we can consider simply all reported association rate constants for complexes formed from folded proteins and IDPs. Values collated previously show these vary over many orders of magnitude; however, the distribution peaks at around 105–106 M–1 s–1.14 The median values are shown as dotted and dashed lines, respectively, in Figure 5. Of course, this may represent an overestimate of the basal rate, since pairs of interacting proteins with opposite charges are likely to be favored.
Discussion
Fast Association of cMyb and KIX
Association kinetics for this complex have recently been reported by Gianni et al., for a pseudo-wild-type of KIX with a single point tryptophan mutation in the binding site (and an attached his-tag).46 The complex formed has a 3-fold lower binding affinity than that reported here at 25 °C, and relatively similar buffer conditions. We tested the effect of a his-tag attached to KIX and found that it caused only a very modest increase in association and dissociation rates under these ionic strength conditions (Figure S8, Supporting Information).
A relatively short extrapolation of our temperature-dependent estimates of koff suggests that at this temperature we would expect koff = 230 ± 20 s–1, which combined with our equilibrium measurements suggests that kon will be around (2.2 ± 0.2) × 107 M–1 s–1. This compares very favorably with the estimate of (2.5 ± 0.1) × 107 M–1 s–1 obtained by Gianni et al.,46 and potentially suggests that neither perturbation, i.e., point mutation or fluorophore labeling, has significantly affected the association binding kinetics.
Although these rates are fast, they are nothing remarkable in themselves. Electrostatic rate enhancement is known to significantly increase association rates, in some cases by several orders of magnitude, and at the pH values used in these studies cMyb and KIX are expected to be oppositely charged. The most famous example of such rate enhancement is for the two folded proteins barnase and barstar, which have been described as “ultrafast” associating proteins. At low ionic strengths, the reported kon is over 5 × 109 M–1 s–1; however, extrapolation to infinite ionic strength to obtain an estimate for the basal rate in the absence of long-range electrostatic forces reduces this to only around 105 M–1 s–1.39 However, our investigation of the ionic strength dependence has shown that for cMyb and KIX there is a surprisingly small degree of electrostatic rate enhancement. In the absence of electrostatic rate enhancement, the association rate constant is (7.7 ± 0.5) × 106 M–1 s–1 at 10 °C, despite the presence of an activation barrier. To make this more comparable to the results of similar studies, which are mostly conducted at 25 °C, we note that the results of the temperature dependence study suggest that at 25 °C the rate will be around 2.7 times higher than that at 10 °C, i.e., (2.1 ± 0.2) × 107 M–1 s–1 (Figure 3C, open red circles). This value is remarkably high. Previous experimental results (Figure 5), Brownian dynamics simulations,47 and theoretical considerations48 with pairs of ordered proteins have all concluded that diffusion-controlled processes have association rates in the range 104–106 M–1 s–1.
Previous Theoretical and Computational Insights into Basal Association Rates
In the absence of applied external forces, such as those provided by an electric field, the Smoluchowski limit for the association rate constant of two spherical particles that form a complex whenever they collide is around 109–1010 M–1 s–1. However, in the absence of long-range interactions, protein–protein associations never reach these rates, because proteins are not equally “reactive” over their whole surface. For protein associations between two freely diffusing folded proteins, the following equation has been suggested to provide an upper limit to the association rate
| 6 |
where A is a factor introduced to account for the proportion of collisions where the correct relative orientations are obtained, D is the relative translational diffusion coefficient, and R is the sum of the radii. Again, the upper limit is reached when all collisions result in complex formation. Simply modeling A as the proportion of collisions where the proteins are observed to contact in the complex structure, to form a so-called geometric rate, is known to underestimate observed rate constants, which are in the range 104–106 M–1 s–1, by around 2 orders of magnitude.34 This apparent discrepancy was solved after observations from Brownian dynamics simulations, where proteins were frequently seen to recollide shortly after an initial collision, potentially having had time to change in their orientation, a so-called diffusive entrapment effect.49 Of course, further complications arise from the fact that proteins are not spherical, and do not have charges distributed evenly over their surfaces. As a result of this, Brownian dynamics simulations to predict association rates are an attractive option.47 Northrupp and Erickson used simulations of this type and found that, for spherical molecules with four contact points arranged in a 17 Å by 17 Å square, the basal association rate was around 105 M–1 s–1.49 We note that the computational calculations required by this approach would be significantly more complicated for a disordered protein. More recently, Qin et al. developed a web server, TransComp, to which protein complex structures can be uploaded.50 They obtain an overall prediction for the association rate (based on transient-complex theory), which is the product of a basal-rate constant calculated from force-free Brownian dynamics simulations and a Boltzmann factor to account for electrostatic rate enhancement. In the authors’ assessment of over 100 protein complexes, the basal association rate estimations range from 3 × 104 to 4 × 106 M–1 s–1. This range also seems to correspond quite well with the values for kon we have collated from the literature (Figure 5).
A more theoretical approach to prediction of rates is taken by Schlosshauer and Baker, who apply an analytical expression they developed for association of spherical molecules with anisotropic reactivity.48 Reactions are assumed to occur once orientations are within specified limits as favorable short-range interactions “guide” molecules into the bound complex. The association rates obtained using their angular constraints again range from 104 to 106 M–1 s–1.
Mechanism for Association
This extremely high association rate constant is apparently inconsistent with a pure conformational selection mechanism for coupled folding and binding of FITC-cMyb to KIX. This mechanism can be considered as an extension of the standard protein association of two ordered proteins, where the concentration of “active” peptide is lower, and thus acts to slow the association process. If the transition between folded and unfolded states in the ensemble is faster than the time scale for association, then the association rate is simply multiplied by the proportion of the IDP that exists in the correct conformation. It is difficult to estimate what this proportion might be; however, a good upper limit may be provided by our CD measurements, which suggest around 30% α-helix exists in the peptide ensemble. If 30% of the peptide is in a fully helical state (the correct conformation), then this maximizes the proportion of binding competent species to 0.3. We should therefore expect the association rate to be more than 3-fold lower than the upper limit for diffusion-controlled interactions between folded proteins, whereas the rate we observe is higher than any reported experimentally obtained or computationally predicted values we have found.
In contrast, the induced-fit (or dock-and-coalesce) mechanism provides a theoretical basis for modest rate enhancement over the situation for folded–folded protein interactions.
In transient complex theory, the protein pairs move diffusively (possibly enhanced by electrostatics) until they come within some capture radius and form an encounter complex, from which they may reach the bound complex if they have sufficient energy. The term fly casting has been used to describe a mechanism whereby unstructured protein molecules may have greater capture radii than their ordered counterparts.12 As Wolynes and coauthors of this original fly casting paper themselves point out, the fly casting effect only contributes a rate acceleration of around a factor of 1.6.12 This modest effect might be enough to explain the enhancement we have observed for the cMyb/KIX system. However, it has been noted that an unstructured protein also has slower translational diffusion than a folded one, which will act to counteract this increase in rate.15 Huang et al. performed simulations of the association of variably structured versions of the peptide pKID with KIX. They observed that, despite greater effective capture radii, the capture rate was actually reduced as a result of disorder. Despite this, they did observe faster association when pKID was more disordered. The 2.5-fold increase in binding rate was instead due to a significant reduction in the binding free energy barrier (which is crossed after capture) as the peptide became more disordered. This effect could explain faster association rates in general for disordered proteins than ordered ones.
Our temperature dependence data clearly indicate that some additional activation energy is required for complex formation. After correction for the expected number of molecule collisions, the rate is still temperature dependent (Figure 3), which indicates the presence of an activation barrier that slows the association process. We stop short of interpreting the gradient of this plot (10.9 ± 0.7 kcal/mol) as the enthalpic barrier for folding. First, from CD denaturation studies (Figure S4, Supporting Information), it is clear that even over this narrow range of temperature there are conformational changes in the FITC-cMyb peptide and KIX. Such changes in KIX with temperature have been observed previously.51 We therefore cannot be confident that the observed changes are not due to structural differences in one or both of the free subunits. Second, more in-depth theoretical derivations for equations such as eq 5 suggest such results be interpreted cautiously.33 We do not know how the entropy changes during this transition, so it is not possible to estimate the fraction of successful collisions from our data; however, the presence of a barrier has certainly been demonstrated. Thus, flexibility in cMyb may increase the chance of conversion from any encounter complex (over that for an ordered peptide) and cause rate enhancement over that expected if cMyb were in a fully folded state. This could explain the underestimation of the basal association rate provided for cMyb/KIX by the TransComp webserver. The algorithm assumes rigid structures for the two proteins, and predicts a basal association rate (3.6 × 105 M–1 s–1 at 298 K) for this complex—around 2 orders of magnitude lower than that obtained, where 12 residues are in contact in the encounter complex. In the authors’ assessment of the predictive power of their algorithm, 85% of rates are within 1 order of magnitude of that predicted (including electrostatic corrections), and no values are over- or underestimated to this extent, so this overestimation does appear to be an outlier.50 We note again that such an interpretation, which relies on the flexible nature of the peptide, seems to exclude a pure conformational selection mechanism. This is consistent with the results of Gianni et al., who found that the association rate of cMyb peptide with KIX only increased around 1.4-fold on partial stabilization of the cMyb helix by TFE, whereas the dissociation rate decreased around 5-fold.46
Rationale for the Fast Association
Reducing the activation barrier increases the fraction of successful collisions, rather than altering the upper limit obtained considering the geometry. The rate we have reported is around an order of magnitude higher than the standardly quoted realistic upper limit for protein–protein association. The simplest explanation for the data might therefore be that the upper limit for association is underestimated in this case. This could arise if the encounter complex for cMyb/KIX requires fewer contacts than average. Alternatively, it might be a result of the relatively large interface size (in comparison with the cMyb peptide). The upper limit for association rates of diffusional processes is relatively insensitive to both the actual size of the interacting proteins and their relative sizes. This can be seen by substitution of Stokes–Einstein relations into the expression for the Smoluchowski diffusion-limited rate for bimolecular reactions31
| 7 |
where η is the solution viscosity and RA and RB are the radii of the proteins A and B. In other words, the effects of diffusional rate and “target area” largely counteract each other. Using the equation, the predicted upper limit is 7 × 109 M–1 s–1 for our system (see Methods), which falls well within the range 109–1010 M–1 s–1 usually quoted. However, this argument applies for the original version of the Smoluchowski limit, which the cMyb/KIX system has not exceeded. The adapted version includes the factor A that corresponds to the fraction of correctly aligned collisions. Attempts to estimate the value of A have been for protein–protein association between folded proteins, where the “reactive patches” constitute a small proportion of the protein surface. In contrast, the cMyb peptide used here forms a single helix when bound, a large proportion of which contacts KIX, so the proportion of reactive surface may be higher.
Ionic Strength Dependence of Rate Constants
Ionic strength was observed to have little effect on the association rate, despite the proteins having opposite charge. This suggests that the amount of translational and rotational electrostatic steering (due to the charges and dipoles of the proteins, respectively) is marginal. The latter is certainly not surprising; cMyb does not have a significant dipole moment even when bound in the complex. In fact, the contact between the two is primarily between hydrophobic residues (Figure 6), which may explain the relative insensitivity of the association rate to ionic strength. The importance of hydrophobic residues in the association process has previously been highlighted by mutational studies, where single and double point mutation of hydrophobic residues Ile 295, Leu298, and Leu302 of cMyb to alanine, isoleucine, or valine caused partial disruption of binding, whereas mutations of charged residues (to alanine) within the same region had only minimal effects.52
There is a gradual decrease of koff with ionic strength; however, as has been observed in previous work with protein–protein complexes, the ionic strength had a relatively small effect on the dissociation rate constant.34
Biological Consequences of Rate Constants
The rate constants for association and dissociation must both be consistent with the requirements for the biological function of the complex. In order to respond to changing environments, the transcription machinery needs to assemble and disassemble quickly. The dissociation rate, which will exceed 300 s–1 under physiological conditions, clearly meets this requirement. Association rates depend upon local physiological concentrations of the proteins, which will in turn depend on factors such as expression and spatial arrangement within the nucleus.53 However, the association rate constant we have observed is remarkably high. This means that under physiological conditions the complex might well achieve local pseudoequilibrium, so that the cell controls the extent of transcription directly through protein concentrations or post-transcriptional modifications to complex binding affinity. The high kon we observed is very similar to that reported for the interaction between the competing ligand pKID with KIX of 7 × 106 M–1 s–1, which is also proposed to bind by an induced fit mechanism.6
Conclusion
From equilibrium CD measurements, we were able to confirm that the peptide cMyb does undergo some folding upon binding to its partner KIX domain from CBP. This interaction is therefore an example of a coupled folding-and-binding process. After correction for long-range electrostatic effects, the association process is the fastest published protein–protein interaction. This is of interest because of speculation in the field regarding the relative association rates for folded and disordered proteins with their partners. The rate is considerably higher than that predicted by an algorithm designed for folded proteins which accounts for effects such as size and interface size. This could be rationalized if the disordered nature of the peptide were to result in a lower activation barrier for the conversion from encounter complex to bound complex, as has been reported from simulations between pKID and KIX.15 Since this system shows very little ionic strength dependence, it is a good candidate for investigations of the effects of disorder and protein size on association rates.
Acknowledgments
This work was supported by the Wellcome Trust (Grant No. WT095195MA). J.C. is a Wellcome Trust Senior Research Fellow. The authors wish to thank J. M. Rogers for useful discussions.
Glossary
Abbreviations
- CD
circular dichroism
- NMR
nuclear magnetic resonance
- TAD
transactivation domain
- KIX
CREB binding domain
- CBP
CREB binding protein
- IDP
intrinsically disordered protein
- FITC
fluorescein isothiocyanate
- MOPS
3-(N-morpholino)propanesulfonic acid
- TFE
trifluoroethanol
- pKID
phosphorylated kinase inducible domain
Supporting Information Available
Eight additional figures and comments regarding previous ionic strength dependence studies of protein–protein association. This material is available free of charge via the Internet at http://pubs.acs.org.
The authors declare no competing financial interest.
Supplementary Material
References
- Meszaros B.; Simon I.; Dosztanyi Z., The Expanding View of Protein-Protein Interactions: Complexes Involving Intrinsically Disordered Proteins. Phys. Biol. 2011, 8. [DOI] [PubMed] [Google Scholar]
- Ward J. J.; Sodhi J. S.; McGuffin L. J.; Buxton B. F.; Jones D. T. Prediction and Functional Analysis of Native Disorder in Proteins from the Three Kingdoms of Life. J. Mol. Biol. 2004, 337, 635–645. [DOI] [PubMed] [Google Scholar]
- Goodman R. H.; Smolik S. CBP/P300 in Cell Growth, Transformation, and Development. Gene Dev. 2000, 14, 1553–1577. [PubMed] [Google Scholar]
- Lee C. W.; Arai M.; Martinez-Yamout M. A.; Dyson H. J.; Wright P. E. Mapping the Interactions of the p53 Transactivation Domain with the KIX Domain of CBP. Biochemistry 2009, 48, 2115–2124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang F.; Marshall C. B.; Yamamoto K.; Li G. Y.; Gasmi-Seabrook G. M. C.; Okada H.; Mak T. W.; Ikura M. Structures of KIX Domain of CBP in Complex with Two FoxO3a Transactivation Domains Reveal Promiscuity and Plasticity in Coactivator Recruitment. Proc. Natl. Acad. Sci. U.S.A. 2012, 109, 6078–6083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sugase K.; Dyson H. J.; Wright P. E. Mechanism of Coupled Folding and Binding of an Intrinsically Disordered Protein. Nature 2007, 447, 1021–1025. [DOI] [PubMed] [Google Scholar]
- Vendel A. C.; Lumb K. J. Molecular Recognition of the Human Coactivator CBP by the HIV-1 Transcriptional Activator Tat. Biochemistry 2003, 42, 910–916. [DOI] [PubMed] [Google Scholar]
- Zor T.; De Guzman R. N.; Dyson H. J.; Wright P. E. Solution Structure of the KIX Domain of CBP Bound to the Transactivation Domain of c-Myb. J. Mol. Biol. 2004, 337, 521–534. [DOI] [PubMed] [Google Scholar]
- Dai P.; Akimaru H.; Tanaka Y.; Hou D. X.; Yasukawa T.; KaneiIshii C.; Takahashi T.; Ishii S. CBP as a Transcriptional Coactivator of c-Myb. Gene Dev. 1996, 10, 528–540. [DOI] [PubMed] [Google Scholar]
- Greig K. T.; Carotta S.; Nutt S. L. Critical Roles for c-Myb in Hematopoietic Progenitor Cells. Semin. Immunol. 2008, 20, 247–256. [DOI] [PubMed] [Google Scholar]
- Dyson H. J.; Wright P. E. Coupling of Folding and Binding for Unstructured Proteins. Curr. Opin. Struct. Biol. 2002, 12, 54–60. [DOI] [PubMed] [Google Scholar]
- Shoemaker B. A.; Portman J. J.; Wolynes P. G. Speeding Molecular Recognition by Using the Folding Funnel: The Fly-Casting Mechanism. Proc. Natl. Acad. Sci. U.S.A. 2000, 97, 8868–8873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou H. X. Intrinsic Disorder: Signaling via Highly Specific but Short-Lived Association. Trends Biochem. Sci. 2012, 37, 43–48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shammas S. L.; Rogers J. M.; Hill S. A.; Clarke J. Slow, Reversible, Coupled Folding and Binding of the Spectrin Tetramerization Domain. Biophys. J. 2012, 103, 2203–2214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang Y.; Liu Z. Kinetic Advantage of Intrinsically Disordered Proteins in Coupled Folding-Binding Process: A Critical Assessment of the “Fly-Casting” Mechanism. J. Mol. Biol. 2009, 393, 1143–1159. [DOI] [PubMed] [Google Scholar]
- Hammes G. G.; Chang Y. C.; Oas T. G. Conformational Selection or Induced Fit: A Flux Description of Reaction Mechanism. Proc. Natl. Acad. Sci. U.S.A. 2009, 106, 13737–13741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weikl T. R.; von Deuster C. Selected-Fit Versus Induced-Fit Protein Binding: Kinetic Differences and Mutational Analysis. Proteins 2009, 75, 104–110. [DOI] [PubMed] [Google Scholar]
- Gill S. C.; von Hippel P. H. Calculation of Protein Extinction Coefficients from Amino Acid Sequence Data. Anal. Biochem. 1989, 182, 319–326. [DOI] [PubMed] [Google Scholar]
- Perez-Iratxeta C.; Andrade-Navarro M. A.. K2D2: Estimation of Protein Secondary Structure from Circular Dichroism Spectra. BMC Struct. Biol. 2008, 8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morriset Jd; David J. S. K.; Pownall H. J.; Gotto A. M. Interaction of an Apolipoprotein (apoLP-alanine) with Phosphatidylcholine. Biochemistry 1973, 12, 1290–1299. [DOI] [PubMed] [Google Scholar]
- Chen Y. H.; Yang J. T.; Martinez H. M. Determination of Secondary Structures of Proteins by Circular-Dichroism and Optical Rotatory Dispersion. Biochemistry 1972, 11, 4120–4131. [DOI] [PubMed] [Google Scholar]
- Lakowicz J. R.Principles of Fluorescence Spectroscopy, 3rd ed.; Springer: New York, 2006. [Google Scholar]
- Kestin J.; Sokolov M.; Wakeham W. A. Viscosity of Liquid Water in Range −8° C to 150 °C. J. Phys. Chem. Ref. Data 1978, 7, 941–948. [Google Scholar]
- Vijayakumar M.; Wong K. Y.; Schreiber G.; Fersht A. R.; Szabo A.; Zhou H. X. Electrostatic Enhancement of Diffusion-Controlled Protein-Protein Association: Comparison of Theory and Experiment on Barnase and Barstar. J. Mol. Biol. 1998, 278, 1015–1024. [DOI] [PubMed] [Google Scholar]
- Wilkins D. K.; Grimshaw S. B.; Receveur V.; Dobson C. M.; Jones J. A.; Smith L. J. Hydrodynamic Radii of Native and Denatured Proteins Measured by Pulse Field Gradient Nmr Techniques. Biochemistry 1999, 38, 16424–16431. [DOI] [PubMed] [Google Scholar]
- von Smoluchowski M. Three Presentations on Diffusion, Molecular Movement According to Brown and Coagulation of Colloid Particles. Phys. Z. 1916, 17, 557–571. [Google Scholar]
- Sjoback R.; Nygren J.; Kubista M. Absorption and Fluorescence Properties of Fluorescein. Spectrochim. Acta, Part A 1995, 51, L7–L21. [Google Scholar]
- Xue B.; Dunbrack R. L.; Williams R. W.; Dunker A. K.; Uversky V. N. Pondr-Fit: A Meta-Predictor of Intrinsically Disordered Amino Acids. Biochim. Biophys. Acta 2010, 1804, 996–1010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Munoz V.; Serrano L. Elucidating the Folding Problem of Helical Peptides Using Empirical Parameters. Nat. Struct. Biol. 1994, 1, 399–409. [DOI] [PubMed] [Google Scholar]
- Goto N. K.; Zor T.; Martinez-Yamout M.; Dyson H. J.; Wright P. E. Cooperativity in Transcription Factor Binding to the Coactivator Creb-Binding Protein (CBP) - the Mixed Lineage Leukemia Protein (Mll) Activation Domain Binds to an Allosteric Site on the KIX Domain. J. Biol. Chem. 2002, 277, 43168–43174. [DOI] [PubMed] [Google Scholar]
- Laidler K. J.Physical Chemistry with Biological Applications; Benjamin/Cummings Publishing Company, Inc.: 1978. [Google Scholar]
- Oliveberg M.; Tan Y. J.; Fersht A. R. Negative Activation Enthalpies in the Kinetics of Protein Folding. Proc. Natl. Acad. Sci. U.S.A. 1995, 92, 8926–8929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou H. X. Rate Theories for Biologists. Q. Rev. Biophys. 2010, 43, 219–293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schreiber G.; Haran G.; Zhou H. X. Fundamental Aspects of Protein-Protein Association Kinetics. Chem. Rev. 2009, 109, 839–860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldberg J. M.; Baldwin R. L. Kinetic Mechanism of a Partial Folding Reaction. 1. Properties of the Reaction and Effects of Denaturants. Biochemistry 1998, 37, 2546–2555. [DOI] [PubMed] [Google Scholar]
- Radic Z.; Kirchhoff P. D.; Quinn D. M.; McCammon J. A.; Taylor P. Electrostatic Influence on the Kinetics of Ligand Binding to Acetylcholinesterase - Distinctions between Active Center Ligands and Fasciculin. J. Biol. Chem. 1997, 272, 23265–23277. [DOI] [PubMed] [Google Scholar]
- Raman C. S.; Jemmerson R.; Nall B. T.; Allen M. J. Diffusion-Limited Rates for Monoclonal-Antibody Binding to Cytochrome-C. Biochemistry 1992, 31, 10370–10379. [DOI] [PubMed] [Google Scholar]
- Rogers J. M.; Steward A.; Clarke J. Folding and Binding of an Intrinsically Disordered Protein: Fast, but Not ’Diffusion-Limited’. J. Am. Chem. Soc. 2013, 135, 1415–1422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schreiber G.; Fersht A. R. Rapid, Electrostatically Assisted Association of Proteins. Nat. Struct. Biol. 1996, 3, 427–431. [DOI] [PubMed] [Google Scholar]
- Selzer T.; Albeck S.; Schreiber G. Rational Design of Faster Associating and Tighter Binding Protein Complexes. Nat. Struct. Biol. 2000, 7, 537–541. [DOI] [PubMed] [Google Scholar]
- Shen B. J.; Hage T.; Sebald W. Global and Local Determinants for the Kinetics of Interleukin-4/Interleukin-4 Receptor Alpha Chain Interaction - a Biosensor Study Employing Recombinant Interleukin-4-Binding Protein. Eur. J. Biochem. 1996, 240, 252–261. [DOI] [PubMed] [Google Scholar]
- Stewart R. C.; Van Bruggen R. Association and Dissociation Kinetics for CheY Interacting with the P2 Domain of CheA. J. Mol. Biol. 2004, 336, 287–301. [DOI] [PubMed] [Google Scholar]
- Stone S. R.; Dennis S.; Hofsteenge J. Quantitative-Evaluation of the Contribution of Ionic Interactions to the Formation of the Thrombin-Hirudin Complex. Biochemistry 1989, 28, 6857–6863. [DOI] [PubMed] [Google Scholar]
- Wendt H.; Leder L.; Harma H.; Jelesarov I.; Baici A.; Bosshard H. R.; Rapid Very Ionic Strength-Dependent Association and Folding of a Heterodimeric Leucine Zipper. Biochemistry 1997, 36, 204–213. [DOI] [PubMed] [Google Scholar]
- Xavier K. A.; Willson R. C. Association and Dissociation Kinetics of Anti-Hen Egg Lysozyme Monoclonal Antibodies HyHEL-5 and HyHEL-10. Biophys. J. 1998, 74, 2036–2045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gianni S.; Morrone A.; Giri R.; Brunori M.; Folding-after-Binding A. Mechanism Describes the Recognition between the Transactivation Domain of c-Myb and the KIX Domain of the CREB-Binding Protein. Biochem. Biophys. Res. Commun. 2012, 428, 205–209. [DOI] [PubMed] [Google Scholar]
- Gabdoulline R. R.; Wade R. C. Biomolecular Diffusional Association. Curr. Opin. Struct. Biol. 2002, 12, 204–213. [DOI] [PubMed] [Google Scholar]
- Schlosshauer M.; Baker D. Realistic Protein-Protein Association Rates from a Simple Diffusional Model Neglecting Long-Range Interactions, Free Energy Barriers, and Landscape Ruggedness. Protein Sci. 2004, 13, 1660–1669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Northrup S. H.; Erickson H. P. Kinetics of Protein-Protein Association Explained by Brownian Dynamics Computer Simulation. Proc. Natl. Acad. Sci. U.S.A. 1992, 89, 3338–3342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qin S.; Pang X.; Zhou H. X. Automated Prediction of Protein Association Rate Constants. Structure 2011, 19, 1744–1751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wei Y.; Horng J. C.; Vendel A. C.; Raleigh D. P.; Lumb K. J. Contribution to Stability and Folding of a Buried Polar Residue at the CARM1Methylation Site of the KIX Domain of CBP. Biochemistry 2003, 42, 7044–7049. [DOI] [PubMed] [Google Scholar]
- Parker D.; et al. Role of Secondary Structure in Discrimination between Constitutive and Inducible Activators. Mol. Cell. Biol. 1999, 19, 5601–5607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McManus K. J.; Stephens D. A.; Adams N. M.; Islam S. A.; Freemont P. S.; Hendzel M. J. The Transcriptional Regulator CBP Has Defined Spatial Associations within Interphase Nuclei. PLoS Comput. Biol. 2006, 2, 1271–1283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pace C. N.; Grimsley G. R.; Scholtz J. M. Protein Ionizable Groups: pK Values and Their Contribution to Protein Stability and Solubility. J. Biol. Chem. 2009, 284, 13285–13289. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.