Abstract
Understanding the role of rhythmic dynamics in normal and diseased brain function is an important area of research in neural electrophysiology. Identifying and tracking changes in rhythms associated with spike trains present an additional challenge, because standard approaches for continuous-valued neural recordings—such as local field potential, magnetoencephalography, and electroencephalography data—require assumptions that do not typically hold for point process data. Additionally, subtle changes in the history dependent structure of a spike train have been shown to lead to robust changes in rhythmic firing patterns. Here, we propose a point process modeling framework to characterize the rhythmic spiking dynamics in spike trains, test for statistically significant changes to those dynamics, and track the temporal evolution of such changes. We first construct a two-state point process model incorporating spiking history and develop a likelihood ratio test to detect changes in the firing structure. We then apply adaptive state-space filters and smoothers to track these changes through time. We illustrate our approach with a simulation study as well as with experimental data recorded in the subthalamic nucleus of Parkinson's patients performing an arm movement task. Our analyses show that during the arm movement task, neurons underwent a complex pattern of modulation of spiking intensity characterized initially by a release of inhibitory control at 20-40 ms after a spike, followed by a decrease in excitatory influence at 40-60 ms after a spike.
Brain rhythms associated with neurological disease have been attracting attention from both neuroscientists and statisticians. Many methods have been proposed and used to study rhythmic dynamics in continuous-valued recordings, but models suitable for the discrete electrical impulse data that are typically recorded from individual neurons are still under active development to address additional challenges. In this paper, we propose a statistical modeling approach that describes neural rhythms by predicting the probability of an electrical impulse at any instant, given the recent past history of impulses. We allow these models to adapt in time in order to track changes in rhythmic spiking dynamics. We apply these methods to data examples obtained from deep brain structures in Parkinson's patients, which helps us understand rhythmic dynamics associated with movement planning and execution in the disease state.
INTRODUCTION
Over recent years, a great appreciation of brain rhythms has emerged in the field of neurological disease. Gradual shifts in lower frequency activity in alpha (7–12 Hz) and beta (12–30 Hz) band oscillations are a well-known hallmark of Alzheimer's disease.1, 2, 3, 4, 5, 6 Low frequency oscillations (3–10 Hz) may contribute to Parkinsonian tremor, whereas enhanced beta band oscillations in the basal ganglia and cortex correlate to bradykinesia and rigidity in Parkinson's disease (PD)7, 8 and may result from amplification of normal striatal network dynamics.9 Patients with schizophrenia have shown a reduced amplitude of gamma (30–200 Hz) and theta (4–7 Hz) oscillations in frontal regions.10, 11, 12, 13, 14
To study such rhythmic dynamics in patients with various neurological diseases, a number of statistical data analysis techniques are common, many of which focus on spectral estimation methods, such as the periodogram or multi-taper estimation, or on autoregressive modeling. However, this wide array of signal processing tools is most appropriately applied to continuous-valued recordings of electrophysiological activities, such as magnetoencephalography (MEG), scalp electroencephalography (EEG), surface electromyography (EMG), and local field potentials (LFP),7, 8, 15, 16, 17, 18 rather than spike trains, which take on discrete values in time. Similarly, deterministic computational modeling methods for neural electrophysiological rhythms are often formulated in terms of differential equations or difference equations, which are more appropriate for continuous-valued signals. Many standard analysis methods available for neural spike train data assume that the firing structure is static in time, limiting their ability to identify and track dynamic transitions. Hence, there is a considerable need for dynamic statistical methods explicitly designed to analyze neural spike train data.19, 20
The analysis of the dynamic properties of spike data presents a number of critical statistical challenges. First, as opposed to continuous-valued measurements, statistical estimation and inference procedures for neural spike train data are most appropriately developed based on the theory of point processes. Inferences based on standard methods developed for continuous valued signals can lead to a reduction in the statistical power available in the data or to inappropriate or incorrect conclusions about associations in the data. For example, spectral analysis methods applied to point process data present particular issues not present for continuous valued signals. An idealized spike contains power at all frequencies,21 making it difficult to interpret the structure of stochastic spiking properties from spectral estimates in a narrow frequency band. Often, analyses of spike train data using spectral methods assume that the data arise from a Poisson process, restricting the types of dynamics that can be captured, and often resulting in smaller than expected power in the low frequencies.22, 23 Such spectral distortion makes it difficult to identify rhythms in the low frequencies.24 Additionally, neural spike train data exhibits a wide variety of history dependent behaviors, such as refractoriness, bursting, and intrinsic rhythms. It has been shown that the autocorrelation function (ACF) of the high-frequency discharge in globus pallidus cells contains many small peaks that do not necessarily reflect bursting activity, and could be inappropriately interpreted as rhythmic spiking.25 However, the majority of the continuous-valued data analysis methods, such as tests based on spectral estimators, is performed under an assumption of stationarity. Such assumptions are rarely true of history-dependent point processes. The violation of stationarity by history-dependent neural spike train data can lead to false detections of changes in the rhythmic dynamics or reduced power in classic testing methods.
Second, the probability of a neuron firing a spike in any time interval is often influenced by many factors occurring simultaneously. These can include influences from external biological or behavioral signals, from the neuron's past activity, or from the activity of other interacting neurons. Many data analysis techniques for spike train data, which focus on the influence of a single factor without regard for others, can lead to incorrect inferences. For example, the coherence between a spike train and an LFP is influenced by the average firing intensity.26 An increase in neural firing rate can also have the effect of increasing the maximum oscillatory frequency that can be transmitted by a neural spike train, as observed in LFP recordings from the subthalamic nucleus (STN) of Parkinson's patients.8 Therefore, spike trains in STN can form robust rhythms by modulating their firing intensity by small amounts. This makes detecting and tracking neural dynamics difficult.
To address these issues, we propose a state-space point process approach for identifying and tracking changes in rhythmic neural dynamics in spike train data. The approach uses history dependent point process models, as rhythmic spiking dynamics are closely related to the history-dependent firing activity. In terms of the statistical point process model, rhythmic neural activity related to physiological oscillations is reflected as a structured history dependence between past and current spiking. This is true for continuous valued signals, such as LFPs, where spectral characteristics are reflected in the autocovariance of past and current signal values. Whereas the autocovariance function accounts for history dependence in the signal at a single temporal lag, a statistical model might account for such dependence across multiply lags. Similarly, the point process model that we develop here characterizes the rhythmic spiking activity in terms of history dependence across a range of temporal lags. Here, we fit rhythmic spiking in Parkinsonian STN neurons to a point process model that captures the modulation of the firing probability as a function of previous spiking across multiple lags. We uncover a consistent dynamic pattern of modulation that characterizes the structure of and suggests potential mechanisms for beta frequency oscillations in the spiking data.
The proposed approach is as follows: First, we construct a point process model with two sets of parameters defining the influence of past history in two distinct physiological states. We estimate these parameters as well as the state transition times that maximize the likelihood of the observed data. We then develop a maximum likelihood ratio test to determine whether such a model provides a significant improvement over one that has only a single set of history parameters and no dynamical transitions. Then, if there exists a statistically significant difference between the two models, we apply a point process filtering and smoothing algorithm to track the temporal dynamics of the transition through time. This two-step approach is illustrated with simulated data and with real spike train data recorded in the STN of Parkinson's patients performing a hand movement task.
METHODS
Experimental data were obtained from single neurons in the STN of patients undergoing surgery for the treatment of PD. Details of the patient selection, basic recording protocols and behavioral paradigm, and previous analyses of this experimental data are discussed in Ref. 27 The patients viewed a computer monitor and used a contralaterally mounted joystick to perform a hand movement task. At the beginning of each trial, a small fixation point appeared in the center of the monitor. After a 200 ms delay, four small grey targets appeared circularly around the fixation point. After another 300 ms delay, a randomly selected target turned green and a small cursor appeared in the center of the monitor. The patient then used the joystick to guide the cursor from the center of the monitor toward the green target. The patient typically reached the target within 1 s of the green cue. Between trials, there was an interval of 1 s and the patients were required to return the joystick to the center position. Patients typically performed 12–24 correct trials in each direction at a given site and 1–4 sites were recorded simultaneously. The initial recording run lasted about 3–5 min for each trial, but in this study, we only used recordings of 1.6 s before and after the start of hand movement, which was determined by an initial 1 degree deflection of the joystick (from a possible range of 18°). Spikes were sorted using a template-matching algorithm refined by principal component analysis and cluster cutting. Seventy percent of cells either had clear single units or represented multiunit recordings that were dominated by a single cell. The remaining 30% represented multiunit recordings that could not be refined further. Because we expected to see history dependent structures reflected in both single unit and multiunit recordings, we included both of the groups in our analyses.
While this movement task included trials in four different directions, our interest here is in the transitions between dynamic rhythmic states, which we posit to be similar for all trials. We therefore pooled all of the trials across all directions, and examined the firing properties of each neuron relative to movement initiation.
For each neuron, we constructed raster plots, peri-stimulus time histograms (PSTH), autocorrelation function plots, and spectrograms (periodogram estimators over 100 ms sliding windows) for all trials. We proceeded to examine 22 neurons that exhibited some degree of rhythmic spiking dynamics based on preliminary results from these standard feature detection methods.
Detecting changes in history-dependent firing patterns
In this section, we introduce the statistical methods to assess whether there has been a significant change in rhythmic spiking dynamics. First, we formulated a point process model with history dependent firing properties, under the assumption that a sudden change in dynamic states occurs at some unknown point in time during the observed spike train time series, and then transitions back to the original dynamic state back at some later time point. We call this a two-state point process model. We used maximum likelihood methods to estimate model parameters related to a background firing rate, to the history dependent firing properties, and to the time points of the transitions. We then performed a maximum likelihood ratio test to determine whether there was a significant difference between this two-state model and a single state model that assumes no change occurs in the neuron's firing properties.
In order to reduce the dimension of the statistical model, both to explain the data parsimoniously and to limit the chance of model overfitting, we developed a statistical model that related the instantaneous probability of a spike at any time point to the past spiking history using a set of cardinal spline basis functions. Splines are locally defined third-order polynomial functions that flexibly approximate arbitrary smooth functions using a small number of basis functions.28 Because our study focused on rhythmic activity, we chose a spline basis set that had been previously used to successfully characterize the desired rhythms in neural spiking activity.29 In this previous study, we constructed a point process model that assumed that the history dependent modulation was constant over known time intervals for each trial. This previous model was developed to visualize specific features of the history dependent structure, but not to determine whether the modulation parameters underwent statistically significant changes during movement or to fully characterize the time course of these changes. In this study, we extended the previous model in two ways: first, we estimate the transitions between the non-movement and movement state and use a nested set of models to determine whether the data show statistically significant changes in the modulation parameters; second, we develop a state space model and a point process filtering and smoothing algorithm to track the dynamic properties of changes in the modulation parameters through time.
A statistical model for point process data is defined by a conditional intensity function , which characterizes the instantaneous spiking probability at any time, t, as a function of t, the past history of spiking Ht, and any other factors that may influence spiking activity.30 In this case, the conditional intensity model was defined as follows:
| (1) |
where Ht is the neuron's spiking history going back 100 ms, relates to a background intensity of spiking, is the binary indicator function that is equal to 0 during an initial non-movement state, becomes equal to 1 when the neuron transitions to a movement planning and execution state, and returns to 0 when the neuron transitions back to the non-movement state. is the parameter multiplying the spline basis functions at the ith control point. When exponentiated, can be interpreted as modulation of the intensity due to a previous spike at the specified lag during the non-movement period. represents the baseline and history modulation coefficients for this indicator function, p is the number of spline control points, and Gi are a set of spline basis functions at multiple selected temporal lags. Here, we assumed the history-dependent spiking activity before and after the movement planning and execution state was the same, thus was expressed by the same set of model parameters, while the rhythmic activity during the movement state is fitted with a different set of parameters. Moreover, p was set to 10 based on previous spline-based models developed with this data.29
If is known, this formula describes a generalized linear model (GLM) for the spike train data.31 Such GLMs have a number of nice properties, including convexity of the likelihood surface and asymptotic normality of the parameter estimates. However, there are two additional unknown parameters, the transition times into and back from the movement state. We computed maximum likelihood estimators for these parameters numerically by computing all model parameter estimates over a grid of possible values for these transition times. The rows of the grid contained the possible transition start times, which spanned a minimum value of 700 ms before movement onset to a maximum value of 500 ms before movement onset, with stepwise increments of 50 ms. The columns of the grid contained the possible transition end times, which spanned a minimum value of 800 ms after movement onset to a maximum value of 1000 ms after movement onset, with stepwise increments of 50 ms. At each point in the grid, we calculated the log-likelihood of the corresponding transition start and end times, maximized over the remaining baseline rate and modulation parameters. This provides a log-likelihood surface for the transition times. We identified the start and end transition times that maximized this log-likelihood surface and used those as point estimates for the fit model. Confidence intervals were computed from the estimated Fisher information for the baseline and history modulation parameters and by computing a local quadratic approximation of the log-likelihood surface for the transition times.32, 33 Using these maximum likelihood estimates to identify the movement period, we compared the two different sets of parameter estimates for history dependent modulation of firing intensity in the movement and non-movement states. In particular, we focused on changes in the background firing rate parameter, as well as changes of modulation at time lags 2 ms, 30 ms, and 50 ms, which may relate to bursting behavior and to rhythmic spiking in the beta frequency band. We also computed the ratios of those parameter estimates between the two states.
To assess whether the two states are significantly different, we tested the hypothesis that the neurons go through a different dynamic state during movement planning and execution than before and after movement against the null hypothesis that there is no transition of dynamic states throughout the experiment. The hypotheses can be formulated as follows:
| (2) |
Because the null model is nested under the proposed model, we performed a maximum likelihood ratio test where the test statistic is defined as follows:
| (3) |
where is the log-likelihood for null model and is the log-likelihood for alternative model. Here, the test statistic follows an asymptotic chi-square distribution with 11 degrees of freedom.32, 33
To assess goodness-of-fit of the two-state model, we constructed Kolmogorov-Smirnov (K-S) plots of time-rescaled inter-spike intervals (ISIs).34 The time-rescaling theorem produces a set of rescaled ISIs that are independent with an exponential distribution with mean 1 if the proposed model accurately describes the structure in the observed spiking activity. To construct the K-S plot, we plot the empirical cumulative distribution of the rescaled ISIs against the theoretical cumulative distribution of the Exponential(1) distribution. The better the quality of the model fit, the closer the K-S plot should be to a 45 degree line.35
In addition to the observed data, we also applied the two-state model to simulated data. Two hundred spike trains were simulated discretely from a Poisson process with unit rate and then the spike times were rescaled according to a model conditional intensity function.34 The parameters of this simulation model were chosen to reflect features observed in the real data. We then estimated the model parameters from the simulated data, and compared these estimates to the known model parameters used to generate the data.
Additionally, in order to study how large a change in history dependent modulation can be detected by the maximum likelihood ratio test procedure in Eqs. 2, 3, we conducted a power analysis using the simulated spike train data. We sampled a variety of different values of modulation parameters related to the beta rhythm ( corresponding to lag 30 ms and 50 ms) and in each case generated 40 simulations of 200 trials of spike trains. We then calculated the proportion of simulations for which we were able to successfully reject the null hypothesis.
State-space smoothing algorithm to track the change through time
The two-state model described above assumes that the transitions between dynamic states occur suddenly and at identical times across all trials. To allow for more gradual and trial dependent transitions between dynamic states, we developed an alternate, adaptive model, where the modulation parameters, , are allowed to change smoothly from one time point to the next. That is, we assumed that the parameters responsible for the rhythmic spiking dynamics are time-varying and we estimated the parameters at each point in time. The conditional intensity function for this adaptive model is
| (4) |
Here, the modulation parameters are time dependent. We estimate the set of parameters at each time point on a millisecond timescale using a stochastic state point process filtering and smoothing algorithm.36 The algorithm recursively estimates the parameters based on the previous estimates and the instantaneous data at each time point. It can be broken down into an initial filtering component,
| (5) |
| (6) |
| (7) |
| (8) |
following by a smoothing component,
| (9) |
| (10) |
where represents the estimated mean of the vector of parameters at time t1 using all of the data up to time t2, and represents the estimated covariance matrix of these parameter estimates at time t1 using all of the data up to time t2. Σ represents a one-step covariance matrix that defines the possible evolution of the modulation parameter vector from one time step to the next. The first and second partial derivatives of with respect to the parameter vector θ are all evaluated at . We initialized the algorithm by setting and to be our estimates and covariance matrix from the two-state model.
To evaluate the adaptive changes, we plotted the estimates for the background firing rate and the estimates for the modulations due to past spiking between 11 ms and 100 ms in the past against time. In order to highlight statistically significant features of these estimates, we compute point-wise significance levels for the estimates of the modulation at each lag and time point. These point-wise bounds are computed by pre- and post-multiplying the posterior covariance estimates, , with the matrix of spline basis functions, and taking the diagonal elements. Note, since these are point-wise estimates, a number of these will achieve significance by chance alone. While one could develop more stringent criteria to account for this multiplicity, here our goal is simply to highlight large statistically significant regions where the modulation properties have undergone dynamic changes. To quantify the uncertainty of the estimated parameter transitions, we also plotted the standard deviations of estimates of background firing rate, and select history-dependent parameters at time lags of 2 ms, 30 ms, and 50 ms against time.
As with the two-state model, we used the resulting model estimates to construct K-S plots of the time-rescaled ISIs for the adaptive model, both for the real data, and for simulated data from 200 simulated spike trains to illustrate that the parameters of the adaptive model could be successfully recovered.
RESULTS
Preliminary analysis
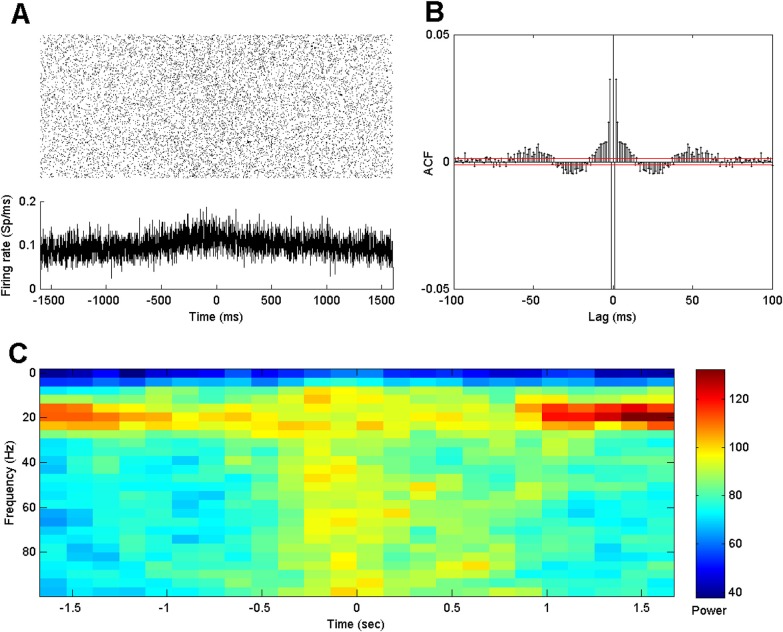
Figure 1a shows a raster plot of the spiking activity across all trials for an example neuron. Below these rasters is a PSTH aligned to the onset of the joystick movement. Visual inspection of the PSTH shows that the firing rate increases slightly at about 600 ms before onset of hand movement and then subsides back to its previous value about 600 ms after the onset. Changes in the rhythmic firing properties are not obvious, either in the individual rasters or in the histograms averaged over trials.
Figure 1.
(a) Raster and PSTH of 3.2 s recordings from a single neuron before and after onset of hand movement (time 0) for all trials. (b) Trial-averaged autocorrelation functions. The red lines denote pointwise 95% significance bounds. (c) Trial-averaged spectrograms of spike trains as a function of time relative to movement onset on the x-axis and frequency between 0 and 100 Hz on the y-axis.
Since it is difficult to visualize rhythmic activity in single trials, we examined a variety of standard visualizations, including trial-averaged autocorrelation plots and spectrograms averaged across all trials. Figure 1b displays the ACF of the example neuron. The ACF shows a clear negative value at lag 1 ms, followed by a sequence of large positive values extending to 10 ms. The dip at lag 1 ms can be explained by the refractory period of the neuron, and the following increased autocorrelation may correspond to a period during which rapid bursts of spikes tend to appear. More subtle fluctuations in the autocorrelation function are observed for lags between 10 ms and 100 ms, which are associated with spiking rhythms. The autocorrelation is significantly positive for lags between 2–15 ms and 40–60 ms, and is significantly negative for lags between 20 and 40 ms.
Figure 1c shows an estimated spectrogram of the spike train as a function of time on the x-axis and frequency between 0 and 100 Hz on the y-axis. There is clear beta band activity, illustrated by the increased power between 10 and 30 Hz, which starts to diminish around 0.7 s before the onset of the hand movement, and returns around 0.7 s after movement initiation. Power in the gamma band, between 60 and 100 Hz, exhibits the opposite trend. It intensifies around 0.5 s before movement onset and then recedes around 0.9 s after movement onset. This high frequency behavior is not limited to a narrow band of frequencies in the Gamma range but is also present at higher frequencies up to the Nyquist cut-off (500 Hz). This likely reflects, in part, an increase in the expected firing rate during movement. Looking across time, we can visually segment the activity into two seemingly distinct rhythmic states. One state is present during a short planning period before the movement onset and during the movement, where the beta rhythm is diminished and high frequency activity is present. The other state occurs before the movement planning period and returns after movement. Commonly, for spike train data analysis, the spectrogram is used as a descriptive technique to visualize rhythmic data rather than as the basis for statistical inference. However, statistical significance of spectral estimators can be evaluated in a number of ways, including using short sliding windows on surrogate data.37, 38 We do note that inferential procedures based on spectral estimators of spiking data raise a number of issues as discussed in Jarvis and Mitra.39 Here, our goal is instead to develop a model based approach to characterize the influence of past history on the firing intensity directly.
To address this question, we developed a statistical test based on a two-state point-process model, whose application we illustrate both in simulation and to the STN data.
Identifying significant changes in spiking dynamics—Simulation study
In order to characterize the properties of the parameter estimation and hypothesis test based on the two-state point process model, we performed a simulation study by generating spike train data from the model with parameter values that capture expected history dependent structure and that undergo different amounts of change between the two dynamic states.
For each parameter set, we simulated 200 spike trains of length 3.2 s using the time-rescaling algorithm described in Sec. 2. We chose the start and end points of the movement state to be from 400 ms before to 400 ms after movement initiation, and we chose the baseline firing rate to be a constant 50 spikes per second. Both the non-movement and movement states included identical parameters for the first 10 ms of history dependence, which were designed to capture a refractory period and bursting activity typical of these neurons. For the movement state, the remaining history parameters were set to 0, indicating no modulation of intensity based on previous spiking at these lags. For the non-movement state, the modulation parameter at 30 ms lag was set to and the modulation parameter at 50 ms lag was set to , for different values of α, indicating beta frequency modulation of the sort observed previously in the STN.29
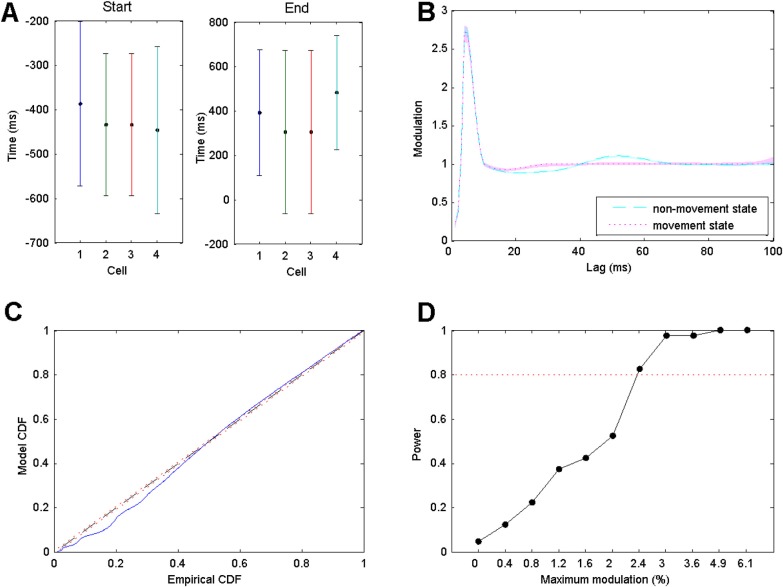
From the simulated spike trains, we estimated the parameters for the start and end points of the transition between the states as well as all of the model parameters for the conditional intensity function in Eq. 1. Figure 2a shows estimates and confidence bounds for the transition points between the states for four simulation examples where the parameter α was set to 0.1. This represents a maximum modulation at lags above 30 ms of 10.5% above the baseline firing intensity. In each case, the true transition times of −400 ms and +400 ms were accurately captured by the 95% confidence intervals. However, the confidence bounds are quite large, spanning periods from −600 ms to −200 ms for the transition to the movement state, and −50 ms to 750 ms for transitions from the movement state. This suggests that estimation of sharp transitions between dynamic states can be inaccurate, even with a large amount of data.
Figure 2.
(a) Estimates and 95% confidence bounds for estimated transition times for the start and end points of the movement spiking state for simulated spike trains of four neurons under the two-state model. Actual transions occurred at −400 ms and 400 ms for start and end transitions, respectively. (b) 95% confidence bounds for the estimated history dependent modulation parameters as a function of lag and the true parameter values for simulated spike data from a single neuron. Cyan dashed line and magenta dotted line represent true modulation during non-movement state and during movement state, respectively. The transparent regions in cyan and magenta correspond to the estimated 95% confidence regions. These regions are narrow and tend to contain the true value at every lag. (c) K-S plot comparing empirical and model CDFs of rescaled simulated ISIs from estimated point process model. (d) Power of the maximum likelihood ratio test as a function of the modulation of the history parameters at 30 ms and 50 ms lags between the non-movement and movement states. The test detects as little as 2.4% modulation in these parameters with 82.5% probability.
Figure 2b shows a comparison between the true history dependent modulation function of firing intensity and the estimated modulation function with 95% confidence bounds for a single simulated neuron. The cyan dashed line represents true modulation during non-movement state and the magenta dotted line represents true modulation during movement state. The cyan transparent region represents 95% confidence bounds for the estimated modulation during the non-movement state and the magenta transparent region represents 95% confidence bounds for the estimated modulation during the movement state. The estimates tend to follow the true parameter values closely, and as opposed to the estimates of the transition times between states, the confidence intervals for the actual history dynamics are very narrow.
Figure 2c shows a K-S plot of the rescaled ISIs for the estimated point process model. The K-S plot follows the 45° line closely, with the largest deviation coming from the smallest rescaled ISIs. This could indicate some minor model misfit associated with the refractoriness and bursting. Indeed, when simulated at a temporal rate higher than 1 ms, the deviations at lower rescaled ISIs disappeared (not shown).
Running the maximum likelihood ratio test on the data from this simulation example gives a test statistic of . If the null hypothesis of no difference between the movement and non-movement states was true, we would expect the value of this test statistic to come from an approximate Chi-square distribution with 11 degrees of freedom. The p-value for the observed test statistic is extremely small (10−8), indicating that there is considerable evidence of a real change in the history dependent spiking dynamics in this data. This is not surprising, given the difference in the estimates and the high degree of confidence in the history dependent parameters between the two states.
Figure 2d shows the power of the test procedure as a function of the amount of modulation in the history parameters related to the beta rhythm between the two states (achieved by varying the α parameter). In each case, 40 simulations of 200 trials were used to perform the test. The x-axis indicates the modulation level at the 30 and 50 ms history parameters in the non-movement state and the y-axis indicates the proportion of tests that were able to successfully reject the null hypothesis. It is evident that even for small value of the modulation parameters (2.4%), we are very likely to identify actual changes in rhythmic dynamics, with the amount of data we recorded for this task.
Identifying significant changes in spiking dynamics—STN data
Next, we applied the two-state model to our observed spike train data. Once again, we used maximum likelihood to estimate all of the model parameters and obtain confidence bounds on those estimates. For the transition times between states, we estimated the maximum likelihood values numerically and used a local quadratic approximation to the log likelihood to estimate the Fisher information and confidence bounds, as described in Sec. 2.
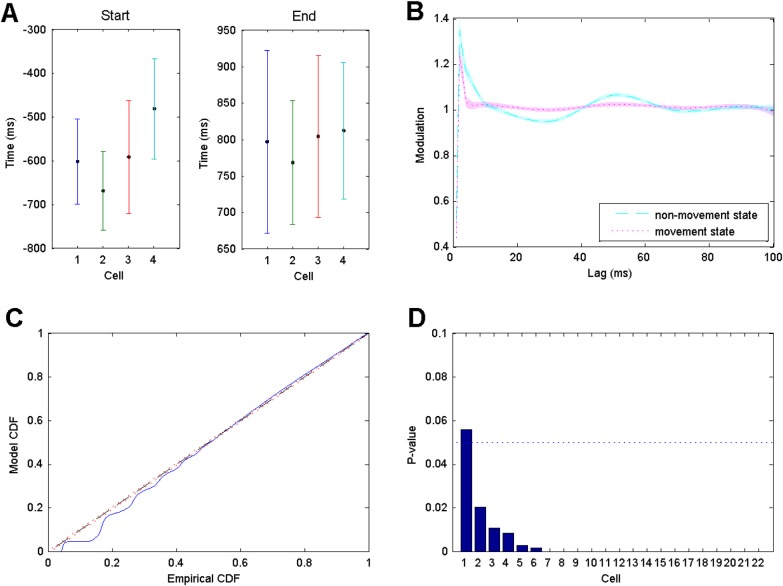
The estimated transition points for the start and end of the movement periods for a set of four representative cell are shown in Figure 3a along with 95% confidence bounds. These estimated values and confidence levels are fairly consistent across all of the neurons we analyzed. The confidence intervals for the transition points are all relatively large, spanning about 200 ms for the transition to the movement state and about 300 ms for transitions back. This could arise for multiple reasons, including variability in the transition times between trials or a slow rather than sudden change in the firing properties. We will explore the latter possibility in Secs. 3D, 3E below. However, it is noteworthy that the size of these confidence bounds is not larger than those estimated in the simulation study, where the transitions were instantaneous and consistent across trials. This suggests another possibility—that the state changes associated with altered spiking history dependence are simply difficult to estimate accurately with the amount of data collected in this experiment.
Figure 3.
(a) Estimates and 95% confidence bounds for transition points between non-movement and movement states for four representative neurons. (b) Estimated history dependent modulation parameters as a function of lag with 95% confidence bounds for a single representative neuron. Cyan dashed line and magenta dotted line represent modulation estimates during non-movement state and during movement state, respectively. Transparent regions represent the corresponding 95% confidence regions. (c) K-S plot comparing empirical and model CDFs of rescaled ISIs from estimated point process model. (d) P-values for the maximum likelihood ratio test for significant changes in modulation between states for all 22 cells, in descending order.
Though the confidence intervals are relatively large for the transition points, the confidence intervals on the model parameters reflecting history dependent dynamics are much smaller and illustrate a clear change between the movement and non-movement states. Figure 3b shows the estimated modulation of the firing rate on the y-axis based on a previous spike at any time lag on the x-axis. The estimated modulation during the non-movement state is shown as a cyan dashed line, and the 95% confidence levels are illustrated by the surrounding transparent cyan region. For the movement state, the estimated parameters are given by the dotted magenta line with a 95% confidence level given by the magenta transparent region. Visually, the non-movement state displays a longer bursting period that ranges from a 2 ms to a 10 ms time lag, a modulation significantly less than 1 for time lags between 10 ms and 40 ms, and a modulation significantly larger than 1 for lags between 40 ms and 60 ms. During the movement state, the estimated modulation exhibits a significant reduction in the parameters above 10 ms related to rhythmic activity. The clear visual separation between the transparent 95% confidence regions between these two states from 10 ms to 60 ms lags suggest that this likely represents a statistically significant change in dynamics.
Figure 3c shows an example K-S plot for the model fit of the neuron whose estimated history dependent properties are shown in Figure 6b. As with the simulation study, the model and empirical cumulative distribution functions (CDFs) demonstrate a good overall fit, with some evidence of misfit in the smallest rescaled ISIs. This may suggest some model misfit related to our assumptions of consistent and sudden state changes or may be related to the difficulty in estimating the transition times with a high level of accuracy.
Figure 6.
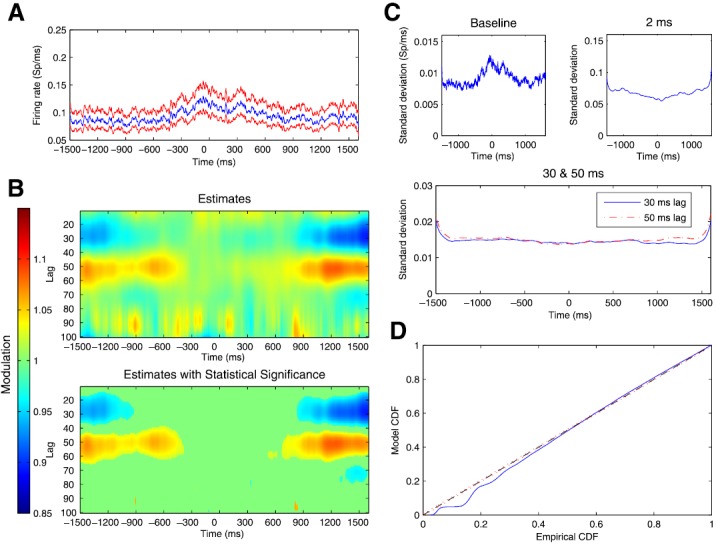
(a) Estimated trajectory and uncertainty of baseline firing rate parameter for observed spiking data from a representative STN neuron. Blue line represents the estimates and red lines denote 95% confidence regions at each time. (b) Estimated values of history dependent modulation of firing intensity as a function of time relative to movement onset on the x-axis and lag between 10 and 100 ms on the y-axis. Blue regions at beginning and end of trial from 20 to 35 ms lags indicate regions of negative modulation and red regions at beginning and end of trial from 40 to 60 ms lags indicate regions positive modulation. (c) Standard deviations for parameter estimates for baseline firing rate and modulation at lag 2 ms, 30 ms, and 50 ms. (d) K-S plot comparing empirical and model CDFs of rescaled ISIs from estimated point process model.
Figure 3d shows the p-values for the significance tests for each of the 22 rhythmic neurons whose firing properties were analyzed. In 21 of these 22 hypothesis tests, we obtained p-values below 0.05 and in 15 of these 22 cells, we obtained p-values below 10−8.
In addition, we analyzed the modulation in the estimated model history parameters between the non-movement and movement states for parameters related to the baseline firing intensity, bursting, and the 30 ms and 50 ms lags related to beta rhythmicity across all 22 STN neurons. Figure 4 shows a set of histograms across cells for each parameter, where a value of 1 represents no modulation in the estimated parameter value between non-movement and movement states, a value greater than 1 indicates an increase in that parameter for a particular neuron with movement, and a value less than 1 indicates a decrease in that parameter with movement. The upper right panel shows that the baseline firing intensity tends to increase in the majority of cells with movement, with a mean increase in 5.6% from the non-movement baseline firing. The upper right panel shows that modulations 2 ms after a spike related to bursting behavior tend to decrease for all but two cells when entering movement state, with a mean decrease in 10.8% from the non-movement state. The lower panels show changes in the parameters related to rhythmic firing in the beta range related to 30 ms lags (left) and 50 ms lags (right). Most neurons show an increase in the 30 ms lag modulation parameter corresponding to an attenuation of the previously observed inhibition at this lag during movement. The average increase in modulation across all cells is 6.6%. For the parameter related to a 50 ms lag, there are a large fraction of neurons that increase their modulation during movement and a larger percentage that decrease their modulation. The average change in modulation is a decrease in only 0.5%. These results suggest that rhythmic spiking in the beta frequency range is associated with a process of inhibition and excitation, and that change in the inhibitory component leads to modulation of beta firing more robustly across the neurons we examined. Overall, even though the parameters responsible for rhythmic firing activity represent fairly small modulation in the firing probability at any instant, the two-state model is able to detect these differences accurately.
Figure 4.

Histograms of ratio of estimated model parameters for baseline intensity and modulation at lags of 2, 30, and 50 ms across all 22 neurons analyzed. A value of 1 indicates no change in modulation between the two states, a value above 1 indicates an increased estimate in the movement state, relative to the non-movement state, and a value below 1 indicates a decreased estimate in the movement state.
Tracking changes in spiking dynamics—Simulation study
In order to characterize the ability of the state-space framework to track evolving rhythmic spiking dynamics, we generated simulated spike train data that smoothly transitioned from the dynamics of the non-movement and movement states observed when we applied the above two-state model to the data. We simulated 200 spike trains of length 3.2 s using the time-rescaling algorithm described in Sec. 2. We chose a constant baseline firing rate of 50 spikes per second for all trials. Parameters for the first 10 ms of history dependence were set to constant values across time, selected to capture the refractory period and bursting activity observed previously in STN neurons.29 We simulated changes in rhythmic spiking in the beta frequency range by letting the parameter associated with the 30 ms lag vary quadratically from a starting point of a maximum modulation that represents a 10% decrease in firing probability for a spike 30 ms in the past during non-movement to no modulation for a previous spike 30 ms in the past at the start of movement, and then back to a 10% negative modulation by the end of trial. At the same time, we set the modulation parameter associated with the 50 ms lag to vary quadratically from a 10% increase in the firing probability for a spike 50 ms in the past to no modulation, back to a 10% increase. The remaining history parameters were set to 0, indicating no modulation of intensity based on previous spiking at these lags.
From the simulated spike trains, we used the point process filter and smoother described in Eqs. 4, 5, 6, 7, 8, 9, 10 to estimate the trajectory of the state process representing all of the model parameters at each instant in time. Figure 5a shows estimates and confidence bounds for the parameter related to the baseline firing rate. The true baseline firing rate, shown as the black line, was held constant at 0.05 spikes/ms. The estimated baseline parameter evolves in time, but hovers at a value close to the true value, with a 95% confidence bound that contains the true value at all times.
Figure 5.
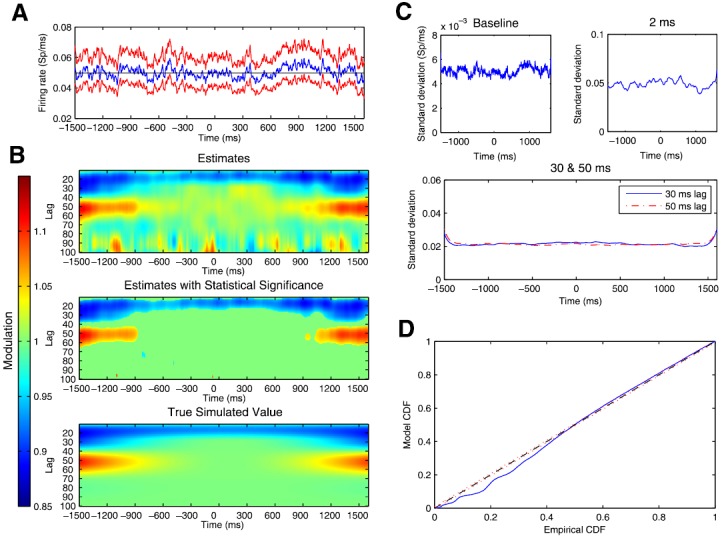
(a) Estimated trajectory and uncertainty of baseline firing rate parameter for simulated spiking data. Blue line represents the estimates and red lines denote 95% confidence regions at each time. Black line represents the true constant baseline firing rate parameter used to simulate the data. (b) Estimated and true values of history dependent modulation of firing intensity as a function of time relative to movement onset on the x-axis and lag between 10 and 100 ms on the y-axis. (c) Standard deviations for parameter estimates for baseline firing rate, and modulation at lag 2 ms, 30 ms, and 50 ms lags. In each case, estimated standard deviations are small compared with estimated mean parameter values, indicating high confidence in estimates. (d) K-S plot comparing empirical and model CDFs of rescaled simulated ISIs from estimated point process model.
Figure 5b shows both the true and estimated history dependent modulation of firing intensity as a function of time relative to movement onset on the x-axis and lags between 10 and 100 ms on the y-axis. The bottom panel shows the true modulation parameter values used to simulate the data. The top panel shows the estimated modulation parameter values at each lag and time point. The middle panel shows only those parameters whose point-wise significance, computed using the estimated posterior covariance matrix, attained a p-value less than p = 0.05, with the rest of the modulation values set to 1. For each of the plots, modulation higher than 1, representing an increase in firing probability based on a previous spike at that lag, is shown in red, whereas modulation lower than 1, representing a decrease in firing probability, is shown in blue. Visually, we find that the estimated trajectories of the modulation values are very close to the true simulated values at all lags and times, although the estimates show some noisy fluctuations, especially at the higher time lags. By considering only those points whose point-wise significances achieved a p-value below 0.05, the noisy changes at higher lags disappear as shown in the middle panel. The important dynamic features of the simulation model relating to the attenuation of the negative modulation around the 30 ms lag and of the positive modulation at the 50 ms lag are well captured.
To assess the confidence of the state-space adaptive model, we tracked the standard deviations of parameter estimates associated with the baseline intensity, bursting propensity (2 ms lag), and beta rhythmic firing (30 and 50 ms lags) through time. Figure 5c displays the estimated standard deviations of these parameters. They all show relatively small and stable standard deviations, indicating a high degree of confidence in the estimates through time. The estimated standard deviation is large at the beginning and the end of the trial, because the smoothing algorithm has less data with which to compute the estimates at these points. However, within 100 ms, the variability quickly drops to a consistent value. Additionally, we find that the estimated confidence in the parameters related to the 30 and 50 ms lags is much smaller than those related to the baseline or bursting parameters, suggesting that these dynamics can be tracked with a high degree of confidence.
Figure 5d shows a K-S plot of the rescaled ISIs for the estimated state-space adaptive model. The K-S plot follows the 45° line closely, with the majority of the larger rescaled ISIs falling inside the 95% confidence bounds. Similar to the K-S plot for the two-state model, the largest deviations from the smallest ISIs perhaps indicate some minor model misfit associated with the refractoriness and bursting of the STN neurons, which disappear if simulated at a higher temporal rate (not shown).
Tracking changes in spiking dynamics—STN data
Next, we applied the adaptive model to the spike train data recorded in STN from Parkinson's patients. Figure 6 shows the results for a representative, rhythmically firing neuron. Figure 6a shows the adaptive estimate of the baseline firing intensity, along with pointwise 95% confidence bounds, at each time. Visually, we can identify an increase in the baseline firing intensity that begins around 400 ms before the initiation of the hand movement. The baseline intensity keeps rising up until the movement begins, remains relatively stable for around 300 ms, and then decreases back to the pre-movement level by around 800 ms after movement began.
Figure 6b shows the estimated history dependent modulation of firing intensity as a function of time relative to movement onset on the x-axis and lag between 10 and 100 ms on the y-axis. The top panel shows the estimated modulation parameter values at each lag and time point. The bottom panel shows only those parameters whose point-wise significance, computed using the estimated posterior covariance matrix, attained a p-value less than p = 0.05, with the rest of the modulation values set to 1. The large blue regions between lags of 20 ms and 35 ms at the beginning and end of the trial represent negative modulation, or a decrease in the firing probability as a function of previous spiking at these lags, which is attenuated starting around 1100 ms before the onset of hand movement and returns around 800 ms after movement onset. Notice that this change is detectable well in advance of the change in the baseline firing rate, which does not begin until around 400 ms prior to movement onset. The large red regions between lags of 40 ms and 60 ms indicate positive modulation, or an increase in instantaneous firing probability as a function of previous spikes at these lags, which is attenuated around 400 ms before movement onset and returns to its initial level around 800 ms after movement onset. The time course of the change in this parameter is more similar to that of the baseline rate than the 30 ms modulation parameter.
This suggests a dynamic pattern of transition between spiking states, whereby the change in rhythmic spiking at beta frequencies initially comes about by a reduction in inhibitory control of spiking, which is followed by reduction in excitatory control at the beta period and a simultaneous increase in baseline firing rate. The top panel also shows short noisy changes in the estimated modulation parameters at higher time lags, which disappear when considering modulation estimates below the point-wise 5% significance level, as shown in the bottom panel, consistent with the simulation study.
Figure 6c shows the estimated standard deviations for the background rate and modulation parameters at lags of 2 ms, 30 ms, and 50 ms. The standard deviation of the baseline firing rate shows dynamic behavior that mimics that of the estimated mean baseline rate. This is not surprising; the estimated mean and variance of the baseline rate of a point process are typically associated. The standard deviation for the modulation parameter at a 2 ms lag related to bursting is small relative to the mean modulation that takes values near 1. The standard deviation is minimal during the movement, where bursting behavior decreases. As with the simulation study, the standard deviation of the parameters related to the rhythmic firing at beta frequencies is small compared with other lags, suggesting that these dynamics can be tracked with a high degree of confidence.
Figure 6d shows the K-S plot of the time-rescaled ISIs for the adaptive model. The model fits well and provides a slight improvement over the two-state model shown in Figure 3. There is still a small but significant lack of fit associated with the smallest rescaled ISIs. This suggests that there may still be some unmodelled features of the dynamics not represented in these models. For example, the model we used does not account for changes in firing as a function of movement direction. Typically, model identification for point process spiking models involves an iterative search across multiple classes of models incorporating different covariates and functional forms. Here, we have presented a simplified model to highlight changes in the rhythmic spiking dynamics rather than attempting to find a single model that completely describes all features of the spiking structure in the data.
DISCUSSION
Increasingly, researchers studying the electrophysiological origins and mechanisms of various neurological diseases are acknowledging the importance of characterizing the dynamic properties of neural rhythms. The most prevalent methods for studying such dynamics typically focus on continuous brain signals, such as LFPs, EEG, MEG, and the like. When applied to spike train data, these methods can lead to results that are difficult to interpret, or inappropriate because of incorrect modeling assumptions. Here, we have presented a state-space point process framework that allows us to first identify dynamics associated with rhythmic spiking and then characterize the transitions between distinct dynamic states.
Specifically, we applied the point process modeling framework to characterize the transition of history-dependent firing activity in STN during a hand movement task. Model estimates showed that the effect of past spiking on the instantaneous probability of firing a spike was small on a single trial, but easily detectable across trials for dataset of the size typically collected in these experiments. We showed that a maximum likelihood ratio test was able to identify very subtle but statistically significant changes in these dynamics.
Furthermore, using a state-space adaptive algorithm, we were able to track and characterize the time course of the changes in modulation of the firing intensity as a function of past spiking history. Although the trajectory of the parameter estimates varied slightly depending on the regions of STN where the signals were recorded, we observed consistent trends across neurons in the time course of the modulation. The modulation of the baseline firing rate on average began to increase around 500 ms before movement onset, reached a maximum around 150 ms before movement onset, fluctuated around the peak value until 100 ms after movement onset, and finally returned to its original value until about 700 ms after movement onset. The parameter related to modulation due to past spiking 50 ms in the past followed a similar time course. However, the estimated influence of past spiking at a 30 ms lag showed more consistent dynamics across neurons and had a temporal trajectory that began to attenuate at earlier times in the planning period, suggesting that movement initiation begins with a release of inhibitory control. These results corroborate previous physiological findings that have characterized the role of the basal ganglia in the disinhibition of selected motor programs.40, 41
The proposed framework has several important features. First, by proposing an explicit point process model, we obtain estimators that have clear interpretations in terms of the probability of observing a spike at any time. By working in the time domain, we need not assume a stationary spiking process, as is common in frequency domain analyses. We also avoid common errors in interpretation that can occur when frequency domain analyses fail to consider the effects of point process data on power spectral estimates across all frequencies.21
Second, the point process modeling framework provides a great deal of flexibility in assessing relationships between the instantaneous probability of spiking, the past spiking history, and other covariates that may influence neural spiking. In this case, we chose to model the effect of past spiking history using cubic spline basis functions. This model formulation allowed us to examine the effects of multiple temporal lags simultaneously with a relatively small number of degrees-of-freedom. This has the advantage of reducing the chance of overfitting in our models, improving the computational efficiency of the estimation algorithms, and increasing the statistical power of the hypothesis tests.
Third, the point process modeling framework allows us to examine the effects of multiple model components simultaneously. Simple visualization methods, such as autocorrelation function, typically examine the effect of previous spiking at a single time lag and can therefore fail to account for influences of one covariate on the estimated influence of another.25 More recently, point process models have been used to study multiple features of rhythmic neural spiking in the STN of Parkinson's patients.42, 43 These models similarly incorporate history dependent modulation to capture features, such as bursting and beta band oscillations, and include task dependent components, such as movement direction and information related to movement cues. However, these models assume constant parameter values and do not attempt to capture rhythmic neural dynamics as a function of movement planning and execution. Forth, the parametric modeling approach provided for a powerful hypothesis test for identifying subtle changes in the firing dynamics. The parametric approach in conjunction with the time rescaling theorem also provides a simple method for rapid simulation of data. We took advantage of this to compute the power of the maximum likelihood ratio hypothesis test. This will also be critical in expanding these analysis methods to study interactions between large neural ensembles.34
Finally, the state-space smoothing algorithm allowed us to track the time course of the change in history dependence, and therefore characterize a critical transition in rhythmic spiking dynamics. We were able to maintain adaptive estimates of both the parameter mean and variance-covariance structure, permitting the construction of confidence intervals and the identification of interactions between covariates.36
We foresee several potential improvements and extensions of this framework. The algorithm we described can be applied to a single trial of data or to multiple trials that share common dynamical properties. Here, we assumed that the spiking dynamics were identical across all trials. This allows us to combine data over trials to detect very subtle changes in the modulation structure through time. If the changes to the modulation parameters as a function of movement are large, then we expect to be able to detect those changes using a single trial of data. For the STN data we analyzed in this paper, we found that movement is associated with very subtle changes in the modulation parameters. In this case, assuming these changes are consistent across trials allows us to detect these small changes with confidence. If the assumption that these changes are consistent across trials is not true, then our model is misspecified, which will affect the bias and variance characteristics of the estimates. In general, we would expect such misfit to manifest as a loss of statistical power, making the identification of significant changes more difficult, and to manifest as a reduction in the goodness-of-fit measures. While no model is completely correct, the fact that our models capture the structure of the data well suggests that the effect of the model misspecification on the analysis results is not substantial.
Here, we used a simplified model of neural spiking to illustrate the problem of identifying and tracking transitions in rhythmic spiking dynamics. In a more complete study, we would develop more accurate and physiologically realistic models by iteratively refining the model class to incorporate other covariates or other functional relationships between covariates. The question of relating statistical models that describe the structure of neural spiking patterns and physiologically realistic models that describe the mechanisms of spike generation is the one of increasing importance. As our models become more complex, estimation and testing methods will need to adapt to accurately identify dynamic transitions. Finally, here we limited ourselves to modeling the spiking activity of a single neuron because in our experimental dataset, very few neurons were simultaneously recorded. Typically, neural ensembles work together to generate and maintain rhythmic activity. We can extend the point process framework by modeling the firing probability of each neuron based on its own history as well as the activity of other simultaneously active neurons in the same or in different brain regions. The methods we developed here can be easily extended to address issues of synchronization by incorporating the past history of simultaneously recorded neurons with parameters related to coupling between neurons into the conditional intensity model with parameters related to coupling between neurons.
As we learn more about the electrophysiological processes underlying neurological disease, the role of rhythms and transitions will continue to grow. One important front in our pursuit to understand these processes is the development of useful statistical estimation and inference procedures—procedures that respect the structure of the data, that rely on appropriate modeling assumptions, and that provide a high degree of statistical power. Point process methods, such as the ones explored here, provide a powerful approach for understanding dynamic structure in spike train data, both in the healthy and diseased brain.
ACKNOWLEDGMENTS
This work was supported by grants from the National Science Foundation [IIS-0643995] and the National Institute of Neurological Disorders and Stroke [R01 NS073118].
References
- Berendse H. W., Verbunt J. P., Scheltens P., van Dijk B. W., and Jonkman E. J., “ Magnetoencephalographic analysis of cortical activity in Alzheimer's disease: A pilot study,” Clin. Neurophysiol. 111, 604 (2000). 10.1016/S1388-2457(99)00309-0 [DOI] [PubMed] [Google Scholar]
- Coben L. A., Danziger W. L., and Berg L., “ Frequency analysis of the resting awake EEG in mild senile dementia of Alzheimer type,” Electroencephalogr. Clin. Neurophysiol. 55, 372 (1983). 10.1016/0013-4694(83)90124-4 [DOI] [PubMed] [Google Scholar]
- Huang C., Wahlund L., Dierks T., Julin P., Winblad B., and Jelic V., “ Discrimination of Alzheimer's disease and mild cognitive impairment by equivalent EEG sources: A cross-sectional and longitudinal study,” Clin. Neurophysiol. 111, 1961 (2000). 10.1016/S1388-2457(00)00454-5 [DOI] [PubMed] [Google Scholar]
- Osipova D., Ahveninen J., Jensen O., Ylikoski A., and Pekkonen E., “ Altered generation of spontaneous oscillations in Alzheimer's disease,” Neuroimage 27, 835 (2005). 10.1016/j.neuroimage.2005.05.011 [DOI] [PubMed] [Google Scholar]
- Penttila M., Partanen J. V., Soininen H., and Riekkinen P. J., “ Quantitative analysis of occipital EEG in different stages of Alzheimer's disease,” Electroencephalogr. Clin. Neurophysiol. 60, 1 (1985). 10.1016/0013-4694(85)90942-3 [DOI] [PubMed] [Google Scholar]
- Schreiter-Gasser U., Gasser T., and Ziegler P., “ Quantitative EEG analysis in early onset Alzheimer's disease: A controlled study,” Electroencephalogr. Clin. Neurophysiol. 86, 15 (1993). 10.1016/0013-4694(93)90063-2 [DOI] [PubMed] [Google Scholar]
- Brown P., Oliviero A., Mazzone P., Insola A., Tonali P., and Di Lazzaro V., “ Dopamine dependency of oscillations between subthalamic nucleus and pallidum in Parkinson's disease,” J. Neurosci. 21, 1033 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levy R., Ashby P., Hutchison W. D., Lang A. E., Lozano A. M., and Dostrovsky J. O., “ Dependence of subthalamic nucleus oscillations on movement and dopamine in Parkinson's disease,” Brain 125, 1196 (2002). 10.1093/brain/awf128 [DOI] [PubMed] [Google Scholar]
- McCarthy M. M., Moore-Kochlacs C., Gu X., Boyden E. S., Han X., and Kopell N., “ Striatal origin of the pathologic beta oscillations in Parkinson's disease,” Proc. Natl. Acad. Sci. U.S.A. 108, 11620 (2011). 10.1073/pnas.1107748108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haenschel C., Bittner R. A., Waltz J., Haertling F., Wibral M., Singer W., Linden D. E., and Rodriguez E., “ Cortical oscillatory activity is critical for working memory as revealed by deficits in early-onset schizophrenia,” J. Neurosci. 29, 9481 (2009). 10.1523/JNEUROSCI.1428-09.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmiedt C., Brand A., Hildebrandt H., and Basar-Eroglu C., “ Event-related theta oscillations during working memory tasks in patients with schizophrenia and healthy controls,” Brain Res. Cognit. Brain Res. 25, 936 (2005). 10.1016/j.cogbrainres.2005.09.015 [DOI] [PubMed] [Google Scholar]
- Cho R. Y., Konecky R. O., and Carter C. S., “ Impairments in frontal cortical gamma synchrony and cognitive control in schizophrenia,” Proc. Natl. Acad. Sci. U.S.A. 103, 19878 (2006). 10.1073/pnas.0609440103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winterer G., Ziller M., Dorn H., Frick K., Mulert C., Wuebben Y., Herrmann W. M., and Coppola R., “ Schizophrenia: Reduced signal-to-noise ratio and impaired phase-locking during information processing,” Clin. Neurophysiol. 111, 837 (2000). 10.1016/S1388-2457(99)00322-3 [DOI] [PubMed] [Google Scholar]
- Uhlhaas P. J. and Singer W., “ Abnormal neural oscillations and synchrony in schizophrenia,” Nat. Rev. Neurosci. 11, 100 (2010). 10.1038/nrn2774 [DOI] [PubMed] [Google Scholar]
- Salenius S., Avikainen S., Kaakkola S., Hari R., and Brown P., “ Defective cortical drive to muscle in Parkinson's disease and its improvement with levodopa,” Brain 125, 491 (2002). 10.1093/brain/awf042 [DOI] [PubMed] [Google Scholar]
- Pfurtscheller G., “ Central beta rhythm during sensorimotor activities in man,” Electroencephalogr. Clin. Neurophysiol. 51, 253 (1981). 10.1016/0013-4694(81)90139-5 [DOI] [PubMed] [Google Scholar]
- Marsden J. F., Limousin-Dowsey P., Ashby P., Pollak P., and Brown P., “ Subthalamic nucleus, sensorimotor cortex and muscle interrelationships in Parkinson's disease,” Brain 124, 378 (2001). 10.1093/brain/124.2.378 [DOI] [PubMed] [Google Scholar]
- Foffani G., Ardolino G., Meda B., Egidi M., Rampini P., Caputo E., Baselli G., and Priori A., “ Altered subthalamo-pallidal synchronisation in Parkinsonian dyskinesias,” J. Neurol., Neurosurg. Psychiatry 76, 426 (2005). 10.1136/jnnp.2004.043547 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown E. N., Mitra P. P., and Kass R. E., “ Multiple neural spike train data analysis: State-of-the-art and future challenges,” Nat. Neurosci. 7, 456 (2004). 10.1038/nn1228 [DOI] [PubMed] [Google Scholar]
- Brown E. N., “ Signal processing and statistical challenges in neuroscience data,” SIAM News 40, 13 (2007). [Google Scholar]
- Brillinger D. R., “ The identification of point processes systems,” Ann. Probab. 3, 909 (1975). 10.1214/aop/1176996218 [DOI] [Google Scholar]
- Bair W., Koch C., Newsome W., and Britten K., “ Power spectrum analysis of bursting cells in area MT in the behaving monkey,” J. Neurosci. 14, 2870 (1994). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franklin J. and Bair W., “ The effect of a refractory period on the power spectrum of neuronal discharge,” SIAM J. Appl. Math. 55, 1074 (1995). 10.1137/S0036139993258691 [DOI] [Google Scholar]
- Rivlin-Etzion M., Ritov Y., Heimer G., Bergman H., and Bar-Gad I., “ Local shuffling of spike trains boosts the accuracy of spike train spectral analysis,” J. Neurophysiol. 95, 3245 (2006). 10.1152/jn.00055.2005 [DOI] [PubMed] [Google Scholar]
- Bar-Gad I., Ritov Y., and Bergman H., “ The neuronal refractory period causes a short-term peak in the autocorrelation function,” J. Neurosci. Methods 104, 155 (2001). 10.1016/S0165-0270(00)00335-6 [DOI] [PubMed] [Google Scholar]
- Lepage K. Q., Kramer M. A., and Eden U. T., “ The dependence of spike field coherence on expected intensity,” Neural Comput. 23, 2209 (2011). 10.1162/NECO_a_00169 [DOI] [PubMed] [Google Scholar]
- Amirnovin R., Williams Z. M., Cosgrove G. R., and Eskandar E. N., “ Visually guided movements suppress subthalamic oscillations in Parkinson's disease patients,” J. Neurosci. 24, 11302 (2004). 10.1523/JNEUROSCI.3242-04.2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramsay J. O. and Silverman B. W., Functional Data Analysis, 2nd ed. (Springer, New York, 2010). [Google Scholar]
- Eden U. T., Gale J. T., Amirnovin R., and Eskandar E. N., “ Characterizing the spiking dynamics of subthalamic nucleus neurons in Parkinson's disease using generalized linear models,” Front. Integr. Neurosci. 6, 28 (2012). 10.3389/fnint.2012.00028 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daley D. and Vere-Jones D., An Introduction to the Theory of Point Processes (Springer-Verlag, New York, 2003). [Google Scholar]
- Truccolo W., Eden U. T., Fellows M. R., Donoghue J. P., and Brown E. N., “ A point process framework for relating neural spiking activity to spiking history, neural ensemble, and extrinsic covariate effects,” J. Neurophysiol. 93, 1074 (2005). 10.1152/jn.00697.2004 [DOI] [PubMed] [Google Scholar]
- Le Cam L., “ Locally asymptotically normal families of distributions,” Univ. Calif. Publ. Stat. 3, 37 (1960). [Google Scholar]
- van der Vaart A. W., Asymptotic Statistics (Cambridge University Press, New York, 1998). [Google Scholar]
- Brown E. N., Barbieri R., Ventura V., Kass R. E., and Frank L. M., “ The time-rescaling theorem and its application to neural spike train data analysis,” Neural Comput. 14, 325 (2002). 10.1162/08997660252741149 [DOI] [PubMed] [Google Scholar]
- Johnson A. and Kotz S., Distributions in Statistics: Continuous Univariate Distributions (Wiley, New York, 1980). [Google Scholar]
- Eden U. T., Frank L. M., Barbieri R., Solo V., and Brown E. N., “ Dynamic analysis of neural encoding by point process adaptive filtering,” Neural Comput. 16, 971 (2004). 10.1162/089976604773135069 [DOI] [PubMed] [Google Scholar]
- Hurtado J. M., Rubchinsky L. L., and Sigvardt K. A., “ Statistical method for detection of phase-locking episodes in neural oscillations,” J. Neurophysiol. 91, 1883 (2004). 10.1152/jn.00853.2003 [DOI] [PubMed] [Google Scholar]
- Hurtado J. M., Rubchinsky L. L., Sigvardt K. A., Wheelock V. L., and Papps C. T. E., “ Temporal evolution of oscillations and synchrony in GPi/muscle pairs in Parkinson's disease,” J. Neurophysiol. 93, 1569 (2005). 10.1152/jn.00829.2004 [DOI] [PubMed] [Google Scholar]
- Jarvis M. R. and Mitra P. P., “ Sampling properties of the spectrum and coherency of sequences of action potentials,” Neural Comput. 13, 717 (2001). 10.1162/089976601300014312 [DOI] [PubMed] [Google Scholar]
- Mink J. W. and Thach W. T., “ Basal ganglia intrinsic circuits and their role in behavior,” Curr. Opin. Neurobiol. 3, 950 (1993). 10.1016/0959-4388(93)90167-W [DOI] [PubMed] [Google Scholar]
- Mink J. W., “ The basal ganglia: Focused selection and inhibition of competing motor programs,” Prog. Neurobiol. 50, 381 (1996). 10.1016/S0301-0082(96)00042-1 [DOI] [PubMed] [Google Scholar]
- Sarma S. V., Cheng M. L., Williams Z. M., Hu R., Eskandar E. N., and Brown E. N., “ Using point process models to determine the impact of visual cues on basal ganglia activity and behavior of Parkinson's patients,” in Proceedings of Joint 48th IEEE Conference on Decision and Control and 28th Chinese Control Conference, Shanghai, P. R. China, 2009.
- Sarma S. V., Eden U. T., Cheng M. L., Williams Z. M., Hu R., Eskandar E. N., and Brown E. N., “ Using point process models to compare neural spiking activity in the subthalamic nucleus of Parkinson's patients and a healthy primate,” IEEE Trans. Biomed. Eng. 57, 1297 (2010). 10.1109/TBME.2009.2039213 [DOI] [PMC free article] [PubMed] [Google Scholar]