Bidirectional Best Hits Miss Many Orthologs in Duplication-Rich Clades such as Plants and Animals

Abstract

Bidirectional best hits (BBH), which entails identifying the pairs of genes in two different genomes that are more similar to each other than either is to any other gene in the other genome, is a simple and widely used method to infer orthology. A recent study has analyzed the link between BBH and orthology in bacteria and archaea and concluded that, given the very high consistency in BBH they observed among triplets of neighboring genes, a high proportion of BBH are likely to be bona fide orthologs. However, limited by their analysis setup, the previous study could not easily test the reverse question: which proportion of orthologs are BBH? In this follow-up study, we consider this question in theory and answer it based on conceptual arguments, simulated data, and real biological data from all three domains of life. Our analyses corroborate the findings of the previous study, but also show that because of the high rate of gene duplication in plants and animals, as much as 60% of orthologous relations are missed by the BBH criterion.

Two genes are called orthologs if they evolved from their last common ancestor after a speciation event, and paralogs if they arose by a gene duplication event (Fitch 1970). The accurate identification of orthologs and paralogs is a prerequisite for many analyses in comparative genomics and an active area of research (Dessimoz et al. 2012). One simple and widespread approach to identifying orthology is the bidirectional best hit (BBH) method (also known as reciprocal best hit or reciprocal Blast hit): call as orthologs all pairs of genes between two species that are more similar (i.e., with highest alignment score) to one another than to any other gene in the other species (Overbeek et al. 1999). We and others have previously observed that despite its simplicity, and substantial conceptual limitations (elaborated below), results obtained by BBH are at times surprisingly robust compared with more sophisticated methods (Hulsen et al. 2006; Altenhoff and Dessimoz 2009; Salichos and Rokas 2011).

In a recent article published in Genome Biology and Evolution, Wolf and Koonin (2012) investigated the link between BBH and orthology, using conserved gene order in bacterial and archaeal genomes. They observed a high consistency in BBH pairing among neighboring genes and concluded that “at least in prokaryotes, genes for which independent evidence of orthology is available typically form BBH and, conversely, BBH can serve as a strong indication of gene orthology.” Indeed, in their evaluation framework, almost all BBH tested appeared to be bona fide orthologs. However, this does not necessarily mean that the converse (“almost all orthologs are BBH”) is true. In other words, the observation that BBH as a predictor of orthology has a high precision rate says nothing about its recall rate.

Here, we revisit the question of the link between BBH and orthology using three lines of investigation. First, we present conceptual arguments on the advantages and limitations of BBH as predictor of orthology. Second, we exploit the recent availability of a genome evolution simulation tool to assess the performance of BBH as a function of the rate of gene duplication. Finally, we evaluate the performance of BBH on real biological data across clades from all three domains of life. These different lines confirm the high precision of BBH observed by Wolf and Koonin (2012), but also demonstrate that BBH can miss a substantial portion of the orthologs in presence of duplicated genes and is thus suboptimal in animals and plants where the rate of gene duplications is comparatively high.

Conceptual Advantages and Limitations of BBH

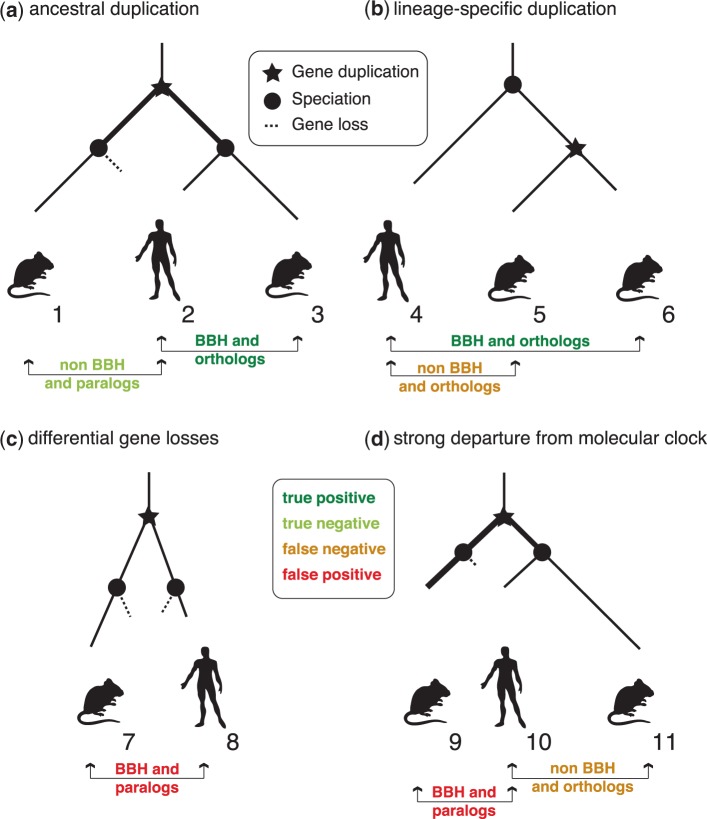
As a first step, we try to understand from first principles in which scenarios BBH performs well and in which it fails. To see where BBH works, let us consider the motivation behind the method. Assuming that genes evolve along trees in which splits are caused by either speciation or gene duplication, note that between any two species, orthologous genes start diverging after all out-paralogous genes (i.e., after all paralogous genes that span across the two species in question). Indeed, by definition, out-paralogs result from a gene duplication necessarily ancestral to the speciation. Under a molecular clock or near-molecular clock assumption, we can expect pairs of genes having started diverging later to have accumulated fewer changes, and therefore to have generally higher alignment score, which motivates the use of BBH (fig. 1a).

Fig. 1.—

Performance of BBH in conceptual examples. (a) BBH recovers the orthologous pair, because the orthologous pair is closer than the paralogous pair due to evolution accrued between the duplication and speciation events (highlighted in bold). (b) BBH only identifies one of the two orthologous pairs, namely the one with higher score. This scenario is common if duplication occurs after speciations of interest. (c) BBH identifies paralogs if the orthologous counterpart is missing in both species. This might happen if the rate of gene losses is high (e.g., following a whole genome duplication). (d) BBH identifies paralogs if the departure from the molecular clock is so strong that paralogs are closer in sequence despite having started diverging before the orthologs.

One important limitation of BBH is that it can only detect 1-to-1 orthology: in presence of a duplication after the last common ancestor of the species in question, some species might contain more than one orthologous gene. Because it only picks the highest scoring pair, BBH will at best identify a subset of the orthologous relationships, thereby causing “false negatives” (fig. 1b).

Note that in terms of orthology and paralogy, there is no distinction between the “original” and “copy” of a gene duplication. In the toy example of figure 1b, Mouse₅ could be the result of a duplication of Mouse₆ into another genomic locus. Although this might make Mouse₅ more or less interesting than Mouse₆ from a functional point of view, this makes no difference in terms of orthology, as orthology is exclusively defined in terms of the ancestral relationships of the genes, not their location in the genome or functional considerations.

To see how problematic lineage-specific duplications can be for BBH, consider a gene that undergoes independent duplications in two species, resulting in m copies in one species and n copies in another. As a result, all m copies in the first species are orthologous to all n copies in the other (m-to-n orthology), leading to orthologous gene pairs. Of these, BBH can at most identify 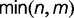pairs. Therefore, if lineage-specific duplications are common, BBH will miss a large proportion of the orthologs.

What about false positives (BBH that are paralogs)? First, there is the case of differential gene losses, which leads to the absence of orthologous genes in the two species and can cause the BBH to be between paralogs (fig. 1c; see also Dessimoz et al. 2006; Scannell et al. 2006). Second, departure from a molecular clock can result in paralogous pairs appearing to be closer than the actual ortholog (fig. 1d). Finally, the highest scoring pairs are not always the evolutionary closest pairs (Koski and Golding 2001). For instance, we recently demonstrated the disruptive effect of artifacts caused by sequencing and assembly errors: ambiguous characters lead to perturbations of the alignment scores, lowering the accuracy of BBH (Dalquen et al. 2013).

These theoretical considerations provide us an idea of the potential successes and failures of BBH, but to gauge the performance of BBH in practice we turn to empirical analyses.

Performance of BBH on Simulation Data

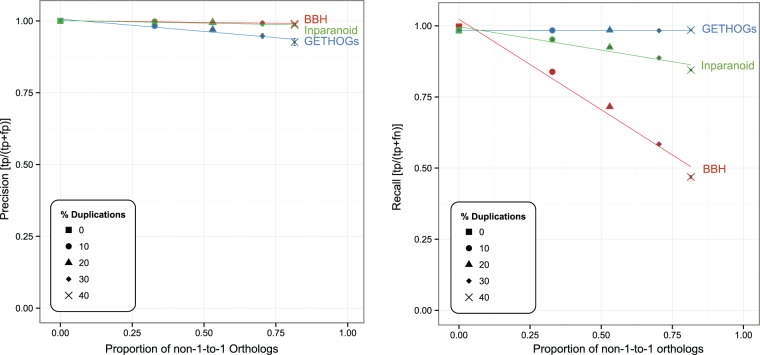
In order to quantify the effect of gene duplication on the proportion of orthologs that are BBH, we simulated datasets of 30 genomes with different duplication rates using the software package ALF (Dalquen et al. 2012; see also Materials and Methods). We then used Basic Alignment Search Tool (Blast) (Altschul et al. 1990) to identify BBH gene pairs and compared these with the true orthologs as given by the simulation program. For comparison, we also analyzed the predictions of Inparanoid (Ostlund et al. 2010) and OMA/GETHOGs (Altenhoff et al. 2013). We computed the trends of the precision (proportion of predicted orthologs that are true orthologs) and the recall (proportion of true orthologs that are correctly predicted) as a function of the true proportion of non-1-to-1 orthology relations, which increases as the gene duplication rate increases. In line with the other two methods, the precision of BBH remained at a very high level with increasing duplication rate, indicating that almost all genes forming BBH are bona fide orthologs (fig. 2a). This part of our analysis corroborates the results of Wolf and Koonin (2012). In contrast and unlike the behavior of the more sophisticated methods, the recall of BBH decreased rapidly with increasing duplication rate (fig. 2b). This behavior indicates that the proportion of orthologs that are BBH decreases as the number of non-1-to-1 orthology relations increases.

Fig. 2.—

Relationship between the proportion of non-1-to-1 orthology and precision/recall for BBH (in red) on simulated data sets with different proportions of genes with a history of duplications. Results for Inparanoid (green) and OMA/GETHOGs (blue) are given for comparison. Each point corresponds to the mean value of five replicates. Error bars give the 95% confidence interval of the mean values in both dimensions.

To ensure that our results hold for varying loss rates, we repeated the analysis on eight scenarios with different combinations of gene loss and duplication rates (see Materials and Methods). Results were highly consistent across all control conditions (supplementary figs. S1–S5, Supplementary Material online).

As BBH are sometimes used to seed orthologous groups, for instance in Inparanoid, we also investigated the coverage of orthologous groups (i.e., clusters of n:m orthologs with 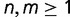) achieved by BBH, OMA/GETHOGs, and Inparanoid. We observed that even under high rates of gene gains and losses, all three methods almost always recover at least one of the orthologous pairs associated with each orthologous group (supplementary fig. S7, Supplementary Material online).

The Limits of BBH on Real Data

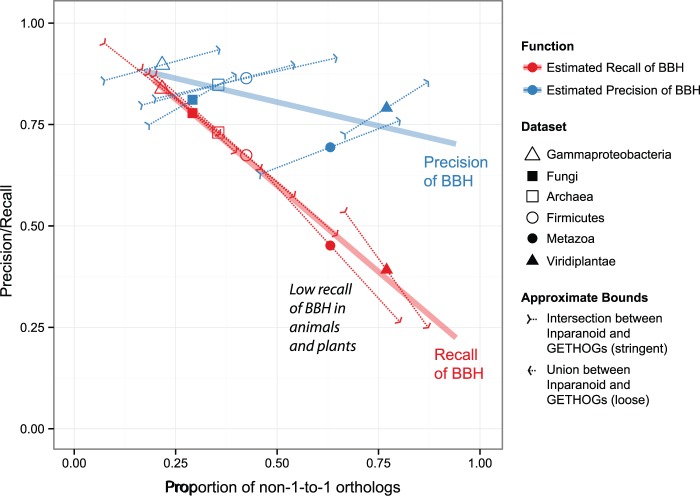
Finally, we sought to assess the performance of BBH on six nonoverlapping sets of real genomes (20 archaea, 20 firmicutes, 20 γ-proteobacteria, 23 fungi, 20 animals, and 12 plants; see also Materials and Methods). As the true evolutionary relationships in this case are unknown, we used orthologs inferred by the GETHOGs and Inparanoid algorithms as reference: by considering the intersection and union sets of orthologs inferred by the two methods, we can get approximate lower and upper bound estimates for the performance of BBH. We tested this approach on the simulated data sets, for which we know the truth, and observed that the resulting trendlines are very close to the truth (supplementary fig. S6, Supplementary Material online).

The results of this analysis on the six biological data sets are provided in figure 3 and table 1. Consistent with the simulation results, recall (red) drops rapidly as the proportion of duplicated genes increases. The drop is more pronounced than for simulated data, probably due to the additional difficulties of modeling real sequences. Interestingly, although our estimation approach yields relatively large uncertainty ranges (reflected in the long dotted arrows in the plot), the favorable direction of the uncertainty is such that we get a very consistent trendline between the results obtained from the union and the intersection of GETHOGs and Inparanoid. As noted above, however, BBH is an adequate way to seed orthologous groups (supplementary fig. S8, Supplementary Material online).

Fig. 3.—

Precision and recall of BBH on real biological data sets, estimated from the intersection and union sets of orthologs inferred by Inparanoid and GETHOGs—the intersection yielding a lower bound for precision and recall and the union yielding an upper bound for precision and recall. The trendlines depict regression over the mid-points.

Table 1.

Statistics Obtained by Comparing BBH to the Intersection and Union of Inparanoid and GETHOGs Predictions on Real Data

Data Set	−
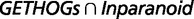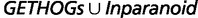	No. Orthologous Pairs	% Non-1-to-1 Orthologs	% Missed by BBH
Archaea	116,187–202,117	16.73–54.28	11.30–42.66
Firmicutes	193,354–395,959	20.08–64.73	12.93–52.25
Fungi	753,147–1,126,046	18.46–39.84	12.51–31.86
γ-Proteobacteria	126,865–180,691	7.48–35.88	5.0–27.40
Metazoa	1,049,129–3,089,297	45.93–80.30	35.98–73.69
Viridiplantae	883,507–2,231,018	66.73–87.25	46.59–75.09

The precision of BBH on real data (blue) is more difficult to assess due to the unfavorable orientation of the uncertainty ranges, which yield more uncertainty in the slope of the overall trendline. Still, the results are largely consistent with simulated data in that precision remains relatively high in all data sets even by the conservative estimates obtained through the intersection of GETHOGs and Inparanoid.

Conclusions

Given the importance of the concept of orthology in many genomic studies, reliable identification of orthologous genes is crucial for many downstream analyses. Often, methods based on BBH are used for orthology inference, sometimes assuming an equivalence between the two. Our results confirm the findings of Wolf and Koonin (2012) that gene pairs which are BBH are indeed quite likely to be orthologous. But at the same time, our conceptual and empirical analyses show that, even for relatively simple evolutionary scenarios, BBH can miss a large proportion of orthologous relations. On real biological data, we furthermore observe that the proportion of duplicated genes and therefore of missed orthologs is considerable even in bacteria and archaea (5–50% missed orthologs depending on the data set and stringency of the analysis). In plants and animals, where gene duplication rates are considerably higher, BBH misses a large proportion of the orthologs (an estimated 55–60% missed orthologs).

In particular circumstances, the use of BBH can nevertheless be justified. For instance, we have shown above that BBH is effective at recovering orthologous group seeds. Likewise, in experiments that only require few but trusted orthologs, the performance of BBH is sufficient.

However, if completeness of orthology prediction is important, methods correctly dealing with many-to-many orthology should be preferred over the convenient but inherently limited BBH approach.

Materials and Methods

Simulated Data Sets

We simulated data with ALF (Dalquen et al. 2012) using the same basic setup as in a previous simulation-based benchmarking study of orthology prediction (Dalquen et al. 2013): we used a topology with 30 species sampled from the tree of 224 γ-proteobacteria as estimated by the OMA project (Altenhoff et al. 2011). The ancestral genome consisted of 1,000 amino acid sequences sampled from the stationary distribution of the WAG substitution model (Whelan and Goldman 2001), which was also used to simulate substitutions. Sequence length was sampled from a gamma distribution fitted on gene lengths of bacterial genomes. Rates for insertions and deletions were 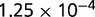per PAM per site, and the length of each insertion and deletion was sampled from a Zipfian distribution with exponent parameter 1.821 (Benner and Cohen 1993).

We created five scenarios with different rates of gene duplications, based on the resulting proportion of genes with a duplication background. Apart from a baseline with no duplications or losses, we chose four proportions that lie within the range believed to be present in real species (Zhang 2003), between 10% and 40%. The gene loss rate was kept constant, coinciding with the duplication rate of the data set with 10% duplications (0.003 per gene per PAM unit). All simulations were repeated five times to get an estimate of the sampling variance (given fixed parameters). A summary of parameters and key statistics is given in table 2.

Table 2.

Key Statistics for Simulated Data Sets

	% Duplications
	0	10	20	30	40
Parameters values
No. of sequences	1,000
Distr. of seq. length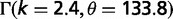
Min. sequence length	50
Substitution model	WAG
Insertion and deletion rate	0.000125
Gene duplication rate	0	0.003	0.0056	0.009	0.0125
Gene loss rate	0		0.003
No. of species			30
Key statistics
Seq. length (mean)	316.6	326.4	323.3	325.0	320.3
Seq. length (stderr)	201.7	211.6	207.4	213.1	203.6
Avg. % gap chars in MSA	24.27	23.25	24.64	26.23	28.65
Variance of % gap chars	58.0	62.8	66.4	72.4	80.5
Total species tree length			763.6
Minimum species tree height			31.70
Maximum species tree height			77.80
Average species tree height			41.36
Average distance between species pairs			72.60

In addition, we created eight scenarios where we varied also the loss rate. In four scenarios, duplication and loss rates were set to be equal. Of the remaining scenarios, one had a proportion of genes with a duplication background of 10% and a loss rate that was three times the duplication rate. Two had a proportion of 30% of genes with a duplication background and a loss rate of either one-third of or three times the duplication rate. For the last scenario, we set the loss rate to zero and the proportion of genes with a duplication background to 40%. Finally, we repeated all simulations on a smaller set of 20 genomes, using as underlying species tree a random subsample of the tree of 37 mammalian species from the OMA project (Altenhoff et al. 2011).

Real Data Sets

We assembled six data sets, covering all kingdoms of the tree of life. With two exceptions, we used the trees of different classes as inferred by the OMA project and pruned them to 20 leaves by repeatedly identifying the most closely related pair of species and removing one of them. For the Fungi data set, we used all 23 fungi species available in OMA, and for the data set of Viridiplantae, we used all 12 species that are part of OMA (see supplementary tables S1–S6, Supplementary Material online, for the list of species in each data set). We did not assume any species tree, as the methods tested do not require one as input.

Orthology Inference

For the computation of BBH, we followed the methodology described by Wolf and Koonin (2012). For each data set, we performed pairwise all-against-all protein sequence alignments of all genomes, using Blast with an E-value of 0.01. Blast hits were considered BBH if they scored 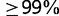of the top-scoring hit. Alongside BBH, we also ran Inparanoid 4.1 (Ostlund et al. 2010) and GETHOGs (Altenhoff et al. 2013) on the data sets. For the latter method, we used the option of inferring the species tree from the data and derived the set of induced orthologous gene pairs from the hierarchical groupings.

On the simulated data sets, we compared the set of inferred pairwise orthologs of all three methods with the set of true orthologs given by the simulation. To assess the performance of BBH on real data, we compared its output with the union and intersection sets of orthologous pairs from Inparanoid and GETHOGs, which we considered bona fide orthologs.

Supplementary Material

Supplementary figures S1–S8 and tables S1–S6 are available at Genome Biology and Evolution online (http://www.gbe.oxfordjournals.org/).