Accelerating ordered subsets image reconstruction for X-ray CT using spatially non-uniform optimization transfer

Abstract

Statistical image reconstruction algorithms in X-ray CT provide improved image quality for reduced dose levels but require substantial computation time. Iterative algorithms that converge in few iterations and that are amenable to massive parallelization are favorable in multiprocessor implementations. The separable quadratic surrogate (SQS) algorithm is desirable as it is simple and updates all voxels simultaneously. However, the standard SQS algorithm requires many iterations to converge. This paper proposes an extension of the SQS algorithm that leads to spatially non-uniform updates. The non-uniform (NU) SQS encourages larger step sizes for the voxels that are expected to change more between the current and the final image, accelerating convergence, while the derivation of NU-SQS guarantees monotonic descent. Ordered subsets (OS) algorithms can also accelerate SQS, provided suitable “subset balance” conditions hold. These conditions can fail in 3D helical cone-beam CT due to incomplete sampling outside the axial region-of-interest (ROI). This paper proposes a modified OS algorithm that is more stable outside the ROI in helical CT. We use CT scans to demonstrate that the proposed NU-OS-SQS algorithm handles the helical geometry better than the conventional OS methods and “converges” in less than half the time of ordinary OS-SQS.

I. Introduction

Statistical image reconstruction methods can improve resolution and reduce noise and artifacts by minimizing either penalized likelihood (PL) [1]–[3] or penalized weighted least-squares (PWLS) [4]–[6] cost functions that model the physics and statistics in X-ray CT. The primary drawback of these methods is their computationally expensive iterative algorithms. This paper describes new accelerated minimization algorithms for X-ray CT statistical image reconstruction.

There are several iterative algorithms for X-ray CT. Coordinate descent (CD) algorithms [7] (also known as Gauss Siedel algorithms [8, p. 507]) and block/group coordinate descent (BCD/GCD) algorithms [9]–[11], update one or a group of voxels sequentially. These can converge in few iterations but can require long computation time per iteration [6], [12]. Considering modern computing architectures, algorithms that update all voxels simultaneously and that are amenable to parallelization are desirable, such as ordered subsets based on separable quadratic surrogate (OS-SQS) [13]–[15] and preconditioned conjugate gradient (PCG) algorithms [16]. However, those highly parallelizable algorithms require more iterations than CD algorithms [6], [12], and thus it is desirable to reduce the number of iterations needed to reach acceptable images. Splitting techniques [17] can accelerate convergence [18], but require substantial extra memory.

In this paper, we propose an enhanced version of a highly parallelizable SQS algorithm that accelerates convergence. SQS algorithms are optimization transfer methods that replace the original cost function by a simple surrogate function [19], [20]. Here we construct surrogates with spatially non-uniform curvatures that provide spatially non-uniform step sizes to accelerate convergence.

Spatially non-homogeneous (NH) approach [7] accelerated the CD algorithm by more frequently visiting the voxels that need updates. This approach is effective because the differences between the initial and final images are non-uniform. Inspired by such ideas, we propose a spatially non-uniform (NU) optimization transfer method that encourages larger updates for voxels that are predicted to be farther from the optimal value, using De Pierro’s idea in SQS [21]. We provide a theoretical justification for the acceleration of NU method by analyzing the convergence rate of SQS algorithm (in Section II-D). The NH approach also balanced homogeneous and non-homogeneous updates for fast overall convergence rate [7]. Section III-C discusses similar considerations for the proposed NU approach.

Ordered subsets (OS), also known as incremental gradient methods [22], [23] or block iterative methods [24], can accelerate gradient-based algorithms by grouping the projection data into (ordered) subsets and updating the image using each subset. OS algorithms are most effective when a properly scaled gradient of each subset data-fit term approximates the gradient of the full data-fidelity term, and then it can accelerate convergence by a factor of the number of subsets. However, standard OS algorithms usually approach a limit-cycle where the sub-iterations loop around the optimal point. OS algorithms can be modified so that they converge by introducing relaxation [25], reducing the number of subsets, or by using incremental optimization transfer methods [26]. Unfortunately, such methods converge slower than ordinary OS algorithms in early iterations. Therefore, we investigated averaging the sub-iterations when the algorithm reaches a limit-cycle, which improves image quality without slowing convergence. (There was a preliminary simulation study of this idea in [27].)

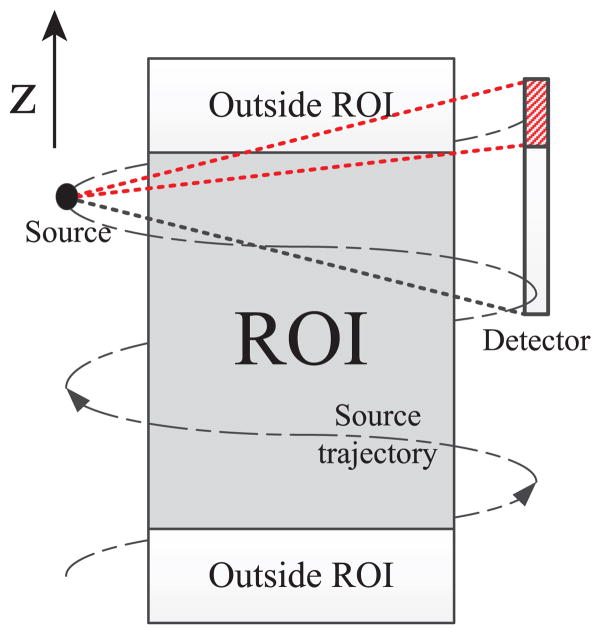
In cone-beam CT, the user must define a region-of-interest (ROI) along the axial (z) direction for image reconstruction (see Fig. 1). Model-based reconstruction methods for cone-beam CT should estimate many voxels outside the ROI, because parts of each patient usually lie outside the ROI yet contribute to some measurements. However, accurately estimating non-ROI voxels is difficult since they are incompletely sampled, which is called the “long-object problem” [28]. Reconstructing the non-ROI voxels adequately is important, as they may impact the estimates within the ROI. Unfortunately in OS algorithms, the sampling of these extra slices leads to very imbalanced subsets particularly for large number of subsets, which can destabilize OS algorithm outside the ROI. This paper proposes an improved OS algorithm that is more stable for 3D helical CT by defining better scaling factors for the subset-based gradient [29].

Fig. 1.

Diagram of helical CT geometry. A (red) dashed region indicates the detector rows that measure data with contributions from voxels both within and outside the ROI.

The paper is organized as follows. Section II reviews PL and PWLS problems for X-ray CT image reconstruction. We review the optimization transfer methods including the SQS algorithm and analyze its convergence rate. Section III presents the proposed spatially non-uniform SQS algorithm (NU-SQS). Section IV reviews the standard OS algorithm and refines it for 3D helical CT. Section V shows the experimental results on various data sets, quantifying the convergence rate and reconstructed image quality. Finally, Section VI offers conclusions. The results show that the NU approach more than doubles the convergence rate, and the improved OS algorithm provides acceptable images in helical CT.

II. Statistical image reconstruction

A. Problem

We reconstruct a non-negative image $x=(x_1,\dots ,x_{N_p})\in {ℝ}_{+}^{N_p}$ from noisy measured transmission data Y ∈ IR^N_d by minimizing either penalized likelihood (PL) or penalized weighted least-squares (PWLS) cost functions:

$$\widehat{x}=arg\underset{x\succcurlyeq 0}{min}\mathrm{\Psi }(x),$$ (1)

$$\mathrm{\Psi }(x)\triangleq L(x)+R(x)=\sum _{i=1}^{N_d}{h}_i({[Ax]}_i)+\sum _{k=1}^{N_r}{\psi }_k({[Cx]}_k),$$ (2)

where x̂ is a minimizer of Ψ(x) subject to a non-negativity constraint. The function L(x) is a negative log-likelihood term (data-fit term) and R(x) is a regularizer. The matrix A = {a_ij} is a projection operator (a_ij ≥ 0 for all i, j) where ${[Ax]}_i\triangleq {\sum }_{j=1}^{N_p}{a}_{ij}{x}_j$, and C = {c_kj} is a finite differencing matrix considering 26 neighboring voxels in 3D image space.¹ The function ψ_k(t) is a (convex and typically non-quadratic) edge-preserving potential function. The function h_i(t) is selected based on the chosen statistics and physics:

• Penalized likelihood (PL) for pre-log data Y_i with Poisson model [1]–[3] uses:

  $$h_i(t)=(b_i{e}^{-t}+r_i)-Y_{i}log(b_i{e}^{-t}+r_i),$$ (3)

  where b_i is the blank scan factor and r_i is the mean number of background events. The function h_i(·) is non-convex if r_i ≠ 0, or convex otherwise. A shifted Poisson model [30] that partially accounts for electronic recorded noise can be used instead.

• Penalized weighted least squares (PWLS) for post-log data y_i = log (b_i/(Y_i − r_i)) with Gaussian model [4]–[6] uses a convex quadratic function:

  $$h_i(t)=\frac{1}{2}{w}_i{(t-y_i)}^2,$$ (4)

  where w_i = (Y_i − r_i)²/Y_i provides statistical weighting. We use the PWLS cost function for our experiments in Section IV and V.

The proposed NU-SQS algorithm, based on optimization transfer methods (in Section II-B), decreases the cost function Ψ(x) monotonically for either (3) or (4).

B. Optimization transfer method

When a cost function Ψ(x) is difficult to minimize, we replace Ψ(x) with a surrogate function φ⁽ⁿ⁾(x) at the nth iteration for computational efficiency. This method is called optimization transfer [19], [20], which is also known as a majorization principle [31], and a comparison function [32]. There are many optimization transfer algorithms such as expectation maximization (EM) algorithms [33], [34], separable surrogate algorithms based on De Pierro’s lemma [35]–[37] and surrogate algorithms using Lipschitz constants [38], [39].

The basic iteration of an optimization transfer method is

$$x^{(n+1)}=arg\underset{x\succcurlyeq 0}{min}{\phi }^{(n)}(x).$$ (5)

To monotonically decrease Ψ(x), we design surrogate functions φ⁽ⁿ⁾(x) that satisfy the following majorization conditions:

$$\begin{array}{l}\mathrm{\Psi }(x^{(n)})={\phi }^{(n)}(x^{(n)}),\\ \mathrm{\Psi }(x)\le {\phi }^{(n)}(x),\forall x\in {ℝ}_{+}^{N_p}.\end{array}$$ (6)

Constructing surrogates with smaller curvatures while satisfying condition (6) is the key to faster convergence in optimization transfer methods [11].

Optimization transfer has been used widely in tomography problems. De Pierro developed a separable surrogate (SS) approach in emission tomography [35], [36]. Quadratic surrogate (QS) functions have been derived for non-quadratic problems, enabling monotonic descent [1]. SQS algorithms combine SS and QS [14], and are the focus of this paper. Partitioned SQS methods for multi-core processors have been proposed for separating the image domain by the number of processors and updating each of them separately while preserving the monotonicity [40]. In addition, replacing ${ℝ}_{+}^{N_p}$ in (6) by an interval that is known to include the minimizer x̂ can reduce the surrogate curvature [7], [41].

Building on this history of optimization transfer methods that seek simple surrogates with small curvatures, we propose a spatially non-uniform SQS (NU-SQS) algorithm that satisfies condition (6) and converges faster than the standard SQS. We review the derivation of the SQS algorithm next.

C. Separable quadratic surrogate (SQS) algorithm

We first construct a quadratic surrogate at the nth iteration for the non-quadratic cost function in (2):

$$\mathrm{\Psi }(x)=L(x)+R(x)\le Q_L^{(n)}(x)+Q_R^{(n)}(x),$$ (7)

where $Q_L^{(n)}(x)$ and $Q_R^{(n)}(x)$ are quadratic surrogates for L(x) and R(x). Based on (2), the quadratic surrogate for L(x) has the form:

$$\begin{array}{l}{Q}_L^{(n)}(x)=\sum _{i=1}^{N_d}{q}_i^{(n)}({[{Ax}^{(n)}]}_i),\\ q_i^{(n)}(t)\triangleq h_i(t_i^{(n)})+{\stackrel{.}{h}}_i(t_i^{(n)})(t-t_i^{(n)})+\frac{{\stackrel{⌣}{c}}_i^{(n)}}{2}{(t-t_i^{(n)})}^2,\end{array}$$ (8)

where $t_i^{(n)}\triangleq {[{Ax}^{(n)}]}_i$, and ${\stackrel{⌣}{c}}_i^{(n)}=max\left\{{\stackrel{⌣}{c}}_i^{(n)},\eta \right\}$ is the curvature of $q_i^{(n)}(t)$ for some small positive value η that ensures the curvature ${\stackrel{⌣}{c}}_i^{(n)}$ positive [1]. In PWLS problem, h_i (·) is quadratic already, so $q_i^{(n)}(t)=h_i(t)$. The quadratic surrogate $Q_R^{(n)}(x)$ for R(x) is defined similarly.

We choose curvatures $\left\{{\stackrel{⌣}{c}}_i^{(n)}\right\}$ that satisfy the monotonicity conditions in (6). For PL, the smallest curvatures:

$${\stackrel{⌣}{c}}_i^{(n)}\triangleq \{\begin{array}{ll}{\left[2\frac{h_i(0)-h_i(t_i^{(n)})+t_i^{(n)}{\stackrel{.}{h}}_i(t_i^{(n)})}{{[t_i^{(n)}]}^2}\right]}_{+},\hfill & t_i^{(n)}>0,\hfill \\ {[{\ddot{h}}_i(0)]}_{+},\hfill & t_i^{(n)}=0,\hfill \end{array}$$ (9)

where [t]₊ = max{t, 0}, called “optimal curvatures,” lead to the fastest convergence rate but require an extra back-projection each iteration for non-quadratic problems [1]. Alternatively, we may use “maximum curvatures”:

$${\stackrel{⌣}{c}}_i\triangleq \underset{t\ge 0}{max}{\ddot{h}}_i(t)$$ (10)

that we can precompute before the first iteration [1].

Next, we generate a separable surrogate of the quadratic surrogate. For completeness, we repeat De Pierro’s argument in [14]. We first rewrite forward projection [Ax]_i as follows:

$${[Ax]}_i=\sum _{j=1}^{N_p}{a}_{ij}{x}_j=\sum _{\begin{array}{c}j=1\\ a_{ij}\ne 0\end{array}}^{N_p}{\pi }_{ij}^{(n)}\left(\frac{a_{ij}}{{\pi }_{ij}^{(n)}}(x_j-x_j^{(n)})+{[{Ax}^{(n)}]}_i\right),$$ (11)

where a non-negative real number ${\pi }_{ij}^{(n)}$ is zero only if a_ij is zero for all i, j, and satisfies ${\sum }_{j=1}^{N_p}{\pi }_{ij}^{(n)}=1$ for all i. Using the convexity of $q_i^{(n)}(·)$ and the convexity inequality yields

$$q_i^{(n)}({[Ax]}_i)\le \sum _{\begin{array}{c}j=1\\ a_{ij}\ne 0\end{array}}^{N_p}{\pi }_{ij}^{(n)}{q}_i^{(n)}\left(\frac{a_{ij}}{{\pi }_{ij}^{(n)}}(x_j-x_j^{(n)})+{[{Ax}^{(n)}]}_i\right).$$ (12)

Thus we have the following separable quadratic surrogate ${\phi }_L^{(n)}(x)$ (with a diagonal Hessian) for the data-fit term L(x):

$$L(x)\le Q_L^{(n)}(x)\le {\phi }_L^{(n)}(x)\triangleq \sum _{j=1}^{N_p}{\phi }_{L,j}^{(n)}(x_j),$$ (13)

$${\phi }_{L,j}^{(n)}(x_j)\triangleq \sum _{\begin{array}{c}i=1\\ a_{ij}\ne 0\end{array}}^{N_d}{\pi }_{ij}^{(n)}{q}_i^{(n)}\left(\frac{a_{ij}}{{\pi }_{ij}^{(n)}}(x_j-x_j^{(n)})+{[{Ax}^{(n)}]}_i\right).$$ (14)

The second derivative (curvature) of the surrogate ${\phi }_{L,j}^{(n)}(x_j)$ is

$$d_j^{L,(n)}\triangleq \frac{{\partial }^2}{\partial x_j^2}{\phi }_{L,j}^{(n)}(x_j)=\sum _{\begin{array}{c}i=1\\ a_{ij}\ne 0\end{array}}^{N_d}{\stackrel{⌣}{c}}_i^{(n)}\frac{a_{ij}^2}{{\pi }_{ij}^{(n)}}.$$ (15)

We can define a separable quadratic surrogate ${\phi }_{R,j}^{(n)}(x_j)$ for the regularizer similarly, and it has the curvature:

$$d_j^{R,(n)}\triangleq \frac{{\partial }^2}{\partial x_j^2}{\phi }_{R,j}^{(n)}(x_j)=\sum _{\begin{array}{c}k=1\\ c_{kj}\ne 0\end{array}}^{N_r}{\ddot{\psi }}_k(0)\frac{c_{kj}^2}{{\pi }_{kj}^{(n)}},$$ (16)

where ${\pi }_{kj}^{(n)}$ have similar constraints as ${\pi }_{ij}^{(n)}$, ψ̈_k(0) = max_t ψ̈_k(t) for maximum curvature [14], or ψ̈_k(0) can be replaced by ψ̇_k([Cx⁽ⁿ⁾]_k)/[Cx⁽ⁿ⁾]_k for Huber’s optimal curvature [32, Lemma 8.3, p.184].

Combining the surrogates for the data-fit term and regularizer and minimizing it in (5) leads to the following separable quadratic surrogate (SQS) method [14] that updates all voxels simultaneously with a “denominator” $d_j^{(n)}\triangleq d_j^{L,(n)}+d_j^{R,(n)}$:

$$x_j^{(n+1)}={\left[x_j^{(n)}-\frac{1}{d_j^{(n)}}\frac{\partial }{\partial x_j}\mathrm{\Psi }(x^{(n)})\right]}_{+},$$ (17)

where a clipping [·]₊ enforces the non-negativity constraint. This SQS decreases the cost function Ψ(x) monotonically, and it converges based on the proof in [20]. If Ψ(x) is convex, a sequence {x⁽ⁿ⁾} converges to x^(∞) that is a global minimizer x̂. Otherwise, {x⁽ⁿ⁾} converges to a local minimizer x^(∞) which may or may not be a global minimizer x̂ depending on the initial image x⁽⁰⁾.

The implementation and convergence rate of SQS depend on the choice of ${\pi }_{ij}^{(n)}$. A general form for ${\pi }_{ij}^{(n)}$ is

$${\pi }_{ij}^{(n)}\triangleq \frac{{\lambda }_{ij}^{(n)}}{{\sum }_{\begin{array}{c}l=1\\ a_{il}\ne 0\end{array}}^{N_p}{\lambda }_{il}^{(n)}},$$ (18)

where a non-negative real number ${\lambda }_{ij}^{(n)}$ is zero only if a_ij is zero. Then (15) can be re-written as

$$d_j^{L,(n)}=\sum _{\begin{array}{c}i=1\\ a_{ij}\ne 0\end{array}}^{N_d}{\stackrel{⌣}{c}}_i^{(n)}\frac{a_{ij}^2}{{\lambda }_{ij}^{(n)}}\left(\sum _{\begin{array}{c}l=1\\ a_{il}\ne 0\end{array}}^{N_p}{\lambda }_{il}^{(n)}\right).$$ (19)

Summations involving the constraint a_ij ≠ 0 require knowledge of the projection geometry, and thereby each summation can be viewed as a type of forward or back projection.

The standard choice [11], [14]:

$${\overline{\lambda }}_{ij}=a_{ij},{\overline{\lambda }}_{kj}=\mid c_{kj}\mid ,$$ (20)

leads to

$${\overline{d}}_j^{L,(n)}=\sum _{i=1}^{N_d}{\stackrel{⌣}{c}}_i^{(n)}{a}_{ij}\left(\sum _{l=1}^{N_p}{a}_{il}\right),$$ (21)

and

$${\overline{d}}_j^{R,(n)}=\sum _{k=1}^{N_r}{\ddot{\psi }}_k(0)\mid c_{kj}\mid \left(\sum _{l=1}^{N_p}\mid c_{kl}\mid \right).$$ (22)

This choice is simple to implement, since the (available) standard forward and back projections can be used directly in (21). (Computing ${\overline{d}}_j^{R,(n)}$ in (22) is negligible compared with (21).) The standard SQS generates a sequence {x⁽ⁿ⁾} in (17) by defining the denominator as

$${\overline{d}}_j^{(n)}\triangleq {\overline{d}}_j^{L,(n)}+{\overline{d}}_j^{R,(n)}.$$ (23)

However, we prefer choices for ${\lambda }_{ij}^{(n)}$ (and ${\lambda }_{kj}^{(n)}$) that provide fast convergence. Therefore, we first analyze the convergence rate of the SQS algorithm in terms of the choice of ${\lambda }_{ij}^{(n)}$ in the next section. Section III introduces acceleration by choosing better ${\lambda }_{ij}^{(n)}$ (and ${\lambda }_{kj}^{(n)}$) than the standard choice (20).

D. Convergence rate of SQS algorithm

The convergence rate of the sequence {x⁽ⁿ⁾} generated by the SQS iteration (17) depends on the denominator $D^{(n)}\triangleq \text{diag}\left\{d_j^{(n)}\right\}$. This paper’s main goal is to choose ${\lambda }_{ij}^{(n)}$ so that the sequence {x⁽ⁿ⁾} converges faster.

The asymptotic convergence rate of a sequence {x⁽ⁿ⁾} that converges to x^(∞) is measured by the root-convergence factor defined as R₁{x⁽ⁿ⁾} ≜ lim sup_n→∞ ||x⁽ⁿ⁾ − x^(∞)||^1/n in [31, p. 288]. The root-convergence factor at x^(∞) for SQS algorithm is given as R₁ {x⁽ⁿ⁾}= ρ(I − [D^(∞)]⁻¹H^(∞)) in [31, Linear Convergence Theorem, p. 301] and [42, Theorem 1], where the spectral radius ρ(·) of a square matrix is its largest absolute eigenvalue and H^(∞) ≜ ∇²Ψ(x^(∞)), assuming that D⁽ⁿ⁾ converges to D^(∞). For faster convergence, we want R₁{x⁽ⁿ⁾} and ρ(·) to be smaller. We can reduce the root-convergence factor based on² [42, Lemma 1], by using a smaller denominator D⁽ⁿ⁾ subject to the majorization conditions in (6) and (13).

However, the asymptotic convergence rate does not help us design D⁽ⁿ⁾ in the early iterations, so we consider another factor that relates to the convergence rate of SQS:

Lemma 1

For a fixed denominator D (using the maximum curvature (10)), a sequence {x⁽ⁿ⁾} generated by an SQS algorithm (17) satisfies

$$\mathrm{\Psi }(x^{(n+1)})-\mathrm{\Psi }(x^{(\infty )})\le \frac{{\mid \mid x^{(0)}-x^{(\infty )}\mid \mid }_D^2}{2(n+1)},$$ (24)

for any n ≥ 0, if Ψ (x) is convex. Lemma 1 is a simple generalization of Theorem 3.1 in [39], which was shown for a surrogate with a scaled identity Hessian (using Lipschitz constant). The inequality (24) shows that minimizing ||x⁽⁰⁾−x^(∞)||_D with respect to D will reduce the upper bound of Ψ(x⁽ⁿ⁾)−Ψ(x^(∞)), and thus accelerate convergence. (Since the upper bound is not tight, there should be a room for further acceleration by choosing better D, but we leave it as future work.)

We want to adaptively design D⁽ⁿ⁾ to accelerate convergence at the nth iteration. We can easily extend Lemma 1 to Corollary 1 by treating the current estimate x⁽ⁿ⁾ as an initial image for the next SQS iteration:

Corollary 1

A sequence {x⁽ⁿ⁾} generated by an SQS algorithm (17) satisfies

$$\mathrm{\Psi }(x^{(n+1)})-\mathrm{\Psi }(x^{(\infty )})\le \frac{{\mid \mid x^{(n)}-x^{(\infty )}\mid \mid }_{D^{(n)}}^2}{2}$$ (25)

for any n ≥ 0, if Ψ(x) is convex. The inequality (25) motivates us to use $\mid x_j^{(n)}-x_j^{(\infty )}\mid$ when selecting $d_j^{(n)}$ (and ${\lambda }_{ij}^{(n)}$) to accelerate convergence at nth iteration. We discuss this further in Section III-A. We fix D⁽ⁿ⁾ after the n_fix number of iterations to ensure convergence of SQS iteration (17), based on [20]. In this case, D⁽ⁿ⁾ must be generated by the maximum curvature (10) to guarantee the majorization condition (6) for subsequent iterations.

From (17) and (19), the step size ${\mathrm{\Delta }}_j^{(n)}$ of the SQS iteration (17) has this relationship:

$${\mathrm{\Delta }}_j^{(n)}\triangleq x_j^{(n+1)}-x_j^{(n)}\propto \frac{1}{d_j^{(n)}},$$ (26)

where smaller $d_j^{(n)}$ (and relatively larger ${\lambda }_{ij}^{(n)}$) values lead to larger steps. Therefore, we should encourage $d_j^{(n)}$ to be small ( ${\lambda }_{ij}^{(n)}$to be relatively large) to accelerate the SQS algorithm. However, we cannot reduce $d_j^{(n)}$ simultaneously for all voxels, due to the majorization conditions in (6) and (13). Lemma 1 (and Corollary 1) suggest intuitively that we should try to encourage larger steps ${\mathrm{\Delta }}_j^{(n)}$ (smaller $d_j^{(n)}$) for the voxels that are far from the optimum to accelerate convergence.

III. Spatially non-uniform separable quadratic surrogate (NU-SQS)

We design surrogates that satisfy condition (6) and provide faster convergence based on Section II-D. We introduce the “update-needed factors” and propose a spatially non-uniform SQS (NU-SQS) algorithm.

A. Update-needed factors

Based on Corollary 1, knowing $\mid x_j^{(n)}-x_j^{(\infty )}\mid$ would be helpful for accelerating convergence at the nth iteration, but $x_j^{(\infty )}$ is unavailable in practice. NH-CD algorithm [7] used the difference between the current and previous iteration instead:

$$u_j^{(n)}\triangleq max\left\{\mid x_j^{(n)}-x_j^{(n-1)}\mid ,{\delta }^{(n)}\right\},$$ (27)

which we call the “update-needed factors” (originally named a voxel selection criterion (VSC) in [7]). Including the small positive values {δ⁽ⁿ⁾} ensures all voxels to have at least a small amount of attention for updates. This $u_j^{(n)}$ accelerated the NH-CD algorithm by visiting voxels with large $u_j^{(n)}$ more frequently.

B. Design

For SQS, we propose to choose ${\lambda }_{ij}^{(n)}$ to be larger if the jth voxel is predicted to need more updates based on the “update-needed factors” (27) after the nth iteration. We select

$${\stackrel{\sim }{\lambda }}_{ij}^{(n)}=a_{ij}{u}_j^{(n)},$$ (28)

which is proportional to $u_j^{(n)}$ and satisfies the condition for ${\lambda }_{ij}^{(n)}$. This choice leads to the following NU-based denominator:

$${\stackrel{\sim }{d}}_j^{L,(n)}=\frac{1}{u_j^{(n)}}\sum _{i=1}^{N_d}{\stackrel{⌣}{c}}_i^{(n)}{a}_{ij}\left(\sum _{l=1}^{N_p}{a}_{il}{u}_l^{(n)}\right),$$ (29)

which leads to spatially non-uniform updates ${\mathrm{\Delta }}_j^{(n)}\propto u_j^{(n)}$.

If it happened that

$$\mid x_j^{(n)}-x_j^{(\infty )}\mid \approx B\mid x_j^{(n)}-x_j^{(n-1)}\mid \text{for}\text{all}j,$$ (30)

where B is a constant, then the NU denominator ${\stackrel{\sim }{d}}_j^{L,(n)}$ would minimize the upper bound of Ψ(x⁽ⁿ⁺¹⁾) − Ψ(x^(∞)) in Corollary 1:

Lemma 2

The proposed choice ${\stackrel{\sim }{d}}_j^{L,(n)}$ in (29) minimizes the following weighted sum of the denominators

$$\sum _{j=1}^{N_p}{\left(u_j^{(n)}\right)}^2{d}_j^{L,(n)}$$ (31)

over all possible choices of the $d_j^{L,(n)}$ in (19).

Proof

In Appendix A.

The proposed ${\stackrel{\sim }{d}}_j^{L,(n)}$ in (29) reduces to the standard choice ${\overline{d}}_j^{L,(n)}$ in (21) when $\left\{u_j^{(n)}\right\}$ is uniform. Similar to the standard choice ${\overline{d}}_j^{L,(n)}$, the proposed choice ${\stackrel{\sim }{d}}_j^{L,(n)}$ can be implemented easily using standard forward and back projection. However, since ${\stackrel{\sim }{d}}_j^{L,(n)}$ depends on iteration (n), additional projections required for ${\stackrel{\sim }{d}}_j^{L,(n)}$ at every iteration would increase computation. We discuss ways to reduce this burden in Section III-F.

Similar to the data-fit term, we derive the denominator of NU-SQS for the regularizer term to be:

$${\stackrel{\sim }{d}}_j^{R,(n)}=\frac{1}{u_j^{(n)}}\sum _{k=1}^{N_r}{\ddot{\psi }}_k(0)\mid c_{kj}\mid \left(\sum _{l=1}^{N_p}\mid c_{kl}\mid u_l^{(n)}\right),$$ (32)

from the choice ${\stackrel{\sim }{\lambda }}_{kj}^{(n)}=\mid c_{kj}\mid u_j^{(n)}$ and the maximum curvature method in [14]. Alternatively, we may use Huber’s optimal curvature [32, Lemma 8.3, p.184] replacing ψ̈_k(0) in (32) by ψ̇_k([Cx⁽ⁿ⁾]_k)/[Cx⁽ⁿ⁾]_k. The computation of (32) is much less than that of the data-fit term.

Defining the denominator in the SQS iteration (17) as

$${\stackrel{\sim }{d}}_j^{(n)}\triangleq {\stackrel{\sim }{d}}_j^{L,(n)}+{\stackrel{\sim }{d}}_j^{R,(n)}$$ (33)

leads to the accelerated NU-SQS iteration, while the algorithm monotonically decreases Ψ(x) and is provably convergent [20]. We can further accelerate NU-SQS by ordered subsets (OS) methods [13], [14], while losing the guarantee of monotonicity. This algorithm, called ordered subsets algorithms based on a spatially non-uniform SQS (NU-OS-SQS), is explained in Section IV.

C. Dynamic range adjustment (DRA) of $u_j^{(n)}$ In reality, (30) will not hold, so (27) will be suboptimal. We could try to improve (27) by finding a function f⁽ⁿ⁾(·): [δ⁽ⁿ⁾, ∞) → [ε, 1] based on the following

$$arg\underset{f^{(n)}(·)}{min}\sum _{j=1}^{N_p}{\left(f^{(n)}(u_j^{(n)})-\frac{\mid x_j^{(n)}-x_j^{(\infty )}\mid }{{max}_j\mid x_j^{(n)}-x_j^{(\infty )}\mid }\right)}^2,$$ (34)

where ε is a small positive value. Then we could use $f^{(n)}(u_j^{(n)})$ as (better) update-needed factors. However, solving (34) is intractable, so we searched empirically for good candidates for a function f⁽ⁿ⁾(·).

Intuitively, if the dynamic range of the update-needed factors $u_j^{(n)}$ in (27) is too wide, then there will be too much focus on the voxels with relatively large $u_j^{(n)}$, slowing the overall convergence rate. On the other hand, a narrow dynamic range of $u_j^{(n)}$ will provide no speed-up, since the algorithm will distribute its efforts uniformly. Therefore, adjusting the dynamic range of the update-needed factors is important to achieve fast convergence. This intuition corresponds to how the NH-CD approach balanced between homogeneous update orders and non-homogeneous update orders [7].

To adjust the dynamic range and distribution of $u_j^{(n)}$, we first construct their empirical cumulative density function:

$$F_{\text{cdf}}^{(n)}(u)\triangleq \frac{1}{N_p}\sum _{j=1}^{N_p}{I}_{\left\{u_j^{(n)}\le u\right\}}$$ (35)

to somewhat normalize their distribution, where I_B = 1 if B is true or 0 otherwise. Then we map the values of $F_{\text{cdf}}^{(n)}(u)$ by a non-decreasing function g(·): [0, 1] → [ε, 1] as follows

$${\stackrel{\sim }{u}}_j^{(n)}\triangleq f^{(n)}(u_j^{(n)})=g\left(F_{\text{cdf}}^{(n)}(u_j^{(n)})\right),$$ (36)

which controls the dynamic range and distribution of ${\left\{{\stackrel{\sim }{u}}_j^{(n)}\right\}}_{j=1}^{N_p}$, and we enforce positivity in g(·) to ensure that the new adjusted parameter ${\stackrel{\sim }{\lambda }}_{ij}^{(n)}=a_{ij}{\stackrel{\sim }{u}}_j^{(n)}$ is positive if a_ij is positive. (We set δ⁽ⁿ⁾ in (27) to zero here, since a positive parameter ε ensures the positivity of ${\stackrel{\sim }{\lambda }}_{ij}^{(n)}$ if a_ij is positive.) The transformation (36) from $u_j^{(n)}$ to ${\stackrel{\sim }{u}}_j^{(n)}$ is called dynamic range adjustment (DRA), and two examples of such ${\stackrel{\sim }{u}}_j^{(n)}$ are presented in Fig. 2. Then we use ${\stackrel{\sim }{u}}_j^{(n)}$ instead of $u_j^{(n)}$ in (28).

Fig. 2.

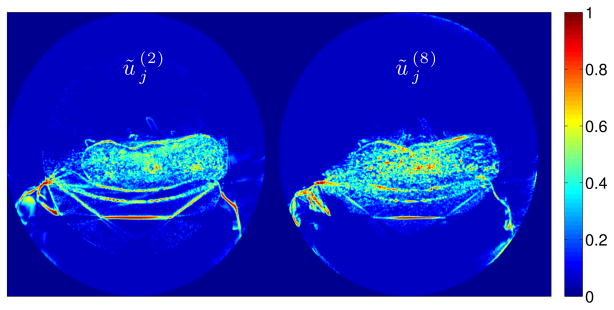
A shoulder region scan: ${\stackrel{\sim }{u}}_j^{(2)}$ and ${\stackrel{\sim }{u}}_j^{(8)}$ after dynamic range adjustment (DRA) for NU-OS-SQS(82 subsets), with the choice g(v) = {max v¹⁰, 0.05}. NU-OS-SQS updates the voxels with large ${\stackrel{\sim }{u}}_j^{(n)}$ more, whereas ordinary OS-SQS updates all voxels equivalently.

Here, we focus on the following function for adjusting the dynamic range and distribution:

$$g(v)\triangleq max\{v^t,\epsilon \}$$ (37)

where t is a non-negative real number that controls the distribution of ${\stackrel{\sim }{u}}_j^{(n)}$ and ε is a small positive value that controls the maximum dynamic range of ${\stackrel{\sim }{u}}_j^{(n)}$. The function reduces to the ordinary SQS choice in (20) when t = 0. The choice of g(·), particularly the parameters t and ε here, may influence the convergence rate of NU-SQS for different data sets, but we show that certain values for t and ε consistently provide fast convergence for various data sets.

D. Related work

In addition to the standard choice (20), the choice

$${\lambda }_{ij}^{(n)}=a_{ij}max\left\{x_j^{(n)},\delta \right\},$$ (38)

with a small non-negative δ, has been used in emission tomography problems [35], [36] and in transmission tomography problems [11], [37]. This choice is proportional to $x_j^{(n)}$, and thereby provides a relationship ${\mathrm{\Delta }}_j^{(n)}\propto x_j^{(n)}$. This classical choice (38) can be also viewed as another NU-SQS algorithm based on “intensity”. However, intensity is not a good predictor of which voxels need more update, so (38) does not provide fast convergence based on the analysis in Section II-D.

E. Initialization of $u_j^{(0)}$

Unfortunately, $u_j^{(n)}$ in (27) is available only for n ≥ 1, i.e., after updating all voxels once. To define the initial update factors $u_j^{(0)}$, we apply edge and intensity detectors to an initial filtered back-projection (FBP) image. This is reasonable since the initial FBP image is a good low-frequency estimate, so the difference between initial and final image will usually be larger near edges. We investigated one particular linear combination of edge and intensity information from an initial image. We used the 2D Sobel operator to approximate the gradient of the image within each transaxial plane. Then we normalized both the approximated gradient and the intensity of the initial image, and computed a linear combination of two arrays with a ratio 2: 1 for the initial update-needed factor $u_j^{(0)}$, followed by DRA method. We have tried other linear combinations with different ratios, but the ratio 2 : 1 provided the fastest convergence rate in our experiments.

F. Implementation

The dependence of ${\lambda }_{ij}^{(n)}$ on iteration (n) increases computation, but we found two practical ways to reduce the burden. First, we found that it suffices to update ${\stackrel{\sim }{u}}_j^{(n)}$ (and ${\stackrel{\sim }{d}}_j^{(n)}$) every n_loop > 1 iterations instead of every iteration. This is reasonable since the update-needed factors usually change slowly with iteration. In this case, we must generate a surrogate with the maximum curvature (10) to guarantee the majorization condition (6) for all iterations. Second, we compute the NU-based denominator (29) simultaneously with the data-fit gradient in (17). In 3D CT, we use forward and back-projectors that compute elements of the system matrix A on the fly, and those elements are used for the gradient ∇L(x) in (17). For efficiency, we reuse those computed elements of A for the NU-based denominator (29). We implemented this using modified separable footprint projector subroutines [43] that take two inputs and project (or back-project) both. This approach required only 25% more computation time than a single forward projection rather than doubling the time (see Table I). Combining this approach with n_loop = 3 yields a NU-SQS algorithm that required only 13% more computation time per iteration than standard SQS, but converges faster.

TABLE I.

Run time of one iteration of NU-OS-SQS(82 subsets) for different choice of n_loop for GE performance phantom.

	SQS	OS-SQS(82)	NU-OS-SQS(82)
nloop	·	·	1	3	5
1 Iter. [sec]	82	125	161	139	133

Computing ${\stackrel{\sim }{u}}_j^{(n)}$ and the corresponding NU-based denominator requires one iteration each. In the proposed algorithm, we computed ${\stackrel{\sim }{u}}_j^{(n)}$ during one iteration, and then computed the NU-based denominator (29) during the next iteration combined with the gradient computation ∇L(x). Then we used the denominator for n_loop iterations and then compute ${\stackrel{\sim }{u}}_j^{(n)}$ again to loop the process (see outline in Appendix B).

IV. Improved ordered subsets (OS) algorithm for helical CT

Ordered subsets (OS) methods can accelerate algorithms by a factor of the number of subsets in early iterations, by using a subset of the measured data for each subset update. However, in practice, OS methods break the monotonicity of SQS and NU-SQS, and typically approach a limit-cycle looping around the optimum. This section describes a simple idea that reduces this problem, only slightly affecting the convergence rate unlike previous convergent OS algorithms. In helical CT geometries, we observed that conventional OS algorithms for PL and PWLS problem are unstable for large subset numbers as they did not consider their non-uniform sampling. Thus, we describe an improved OS algorithm that is more stable for helical CT.

A. Ordinary OS algorithm

An OS algorithm (with M subsets) for accelerating the SQS or NU-SQS updates (17) has the following mth sub-iteration within the nth iteration using the denominator³ ${\stackrel{\sim }{d}}_j^{(n)}$ in (33):

$$x_j^{(n+\frac{m+1}{M})}={\left[x_j^{(n+\frac{m}{M})}-\frac{1}{{\stackrel{\sim }{d}}_j^{(n)}}\left({\widehat{\gamma }}_j^{(n+\frac{m}{M})}\frac{\partial }{\partial x_j}{L}_m\left(x^{(n+\frac{m}{M})}\right)+\frac{\partial }{\partial x_j}R\left(x^{(n+\frac{m}{M})}\right)\right)\right]}_{+},$$ (39)

where ${\widehat{\gamma }}_j^{(n+\frac{m}{M})}$ scales the gradient of a subset data-fit term L_m(x) = Σ_i∈Sm h_i([Ax]_i), and S_m consists of projection views in mth subset for m = 0, 1, ···, M − 1. We count one iteration when all M subsets are used once, since the projection A used for computing data-fit gradients is the dominant operation in SQS iteration.

If we use many subsets to attempt a big acceleration in OS algorithm, some issues arise. The increased computation for the gradient of regularizer in (39) can become a bottleneck (this has been relieved in [44]). Also having less measured data in each subset will likely break the subset balance condition

$$\nabla L_0(x)\approx \nabla L_1(x)\approx \cdots \approx \nabla L_{M-1}(x).$$ (40)

The update in (39) would accelerate the SQS algorithm by exactly M if the scaling factor ${\widehat{\gamma }}_j^{(n+\frac{m}{M})}$ satisfied the condition:

$${\widehat{\gamma }}_j^{(n+\frac{m}{M})}=\frac{\frac{\partial }{\partial x_j}L(x^{(n+\frac{m}{M})})}{\frac{\partial }{\partial x_j}{L}_m(x^{(n+\frac{m}{M})})}.$$ (41)

It would be impractical to compute this factor exactly, so the conventional OS approach is to simply use the constant γ = M. This “approximation” often works well in the early iterations when the subsets are suitably balanced, and for small number of subsets. But in general, the errors caused by the differences between ${\widehat{\gamma }}_j^{(n+\frac{m}{M})}$ and a constant scaling factor γ cause two problems in OS methods. First, the choice γ = M causes instability in OS methods in a helical CT that has limited projection views outside ROI, leading to very imbalanced subsets. Therefore, we propose an alternative choice γ_j that better stabilizes OS for helical CT in Section IV-B. Second, even with γ replaced by γ_j, OS methods approach a limit-cycle that loops around the optimal point within sub-iterations [25]. Section IV-C considers a simple averaging idea that reduces this problem.

B. Proposed OS algorithm in helical CT

The constant scaling factor γ = M used in the ordinary regularized OS algorithm is reasonable when all the voxels are sampled uniformly by the projection views in all the subsets. But in geometries like helical CT, the voxels are non-uniformly sampled. In particular, voxels outside the ROI are sampled by fewer projection views than voxels within the ROI (see Fig. 1). So some subsets make no contribution to such voxels, i.e., very imbalanced subsets. We propose to use a voxel-based scaling factor γ_j that considers the non-uniform sampling, rather than a constant factor γ.

After investigating several candidates, we focused on the following scaling factor:

$${\gamma }_j=\sum _{m=0}^{M-1}{I}_{\left\{{\sum }_{i\in S_m}{\stackrel{⌣}{c}}_i^{(n)}{a}_{ij}\left({\sum }_{l=1}^{N_p}{a}_{il}{\stackrel{\sim }{u}}_l^{(0)}\right)>0\right\}},$$ (42)

where I_B = 1 if B is true or 0 otherwise. As expected, γ_j < M for voxels outside the ROI and γ_j = M for voxels within the ROI. The scaling factor (42) has small compute overhead as it can be computed simultaneously with the precomputation of the initial data-fit denominator (29) by rewriting it as

$${\stackrel{\sim }{d}}_j^{L,(0)}\triangleq \frac{1}{{\stackrel{\sim }{u}}_j^{(0)}}\sum _{m=0}^{M-1}\left(\sum _{i\in S_m}{\stackrel{⌣}{c}}_i^{(n)}{a}_{ij}\left(\sum _{l=1}^{N_p}{a}_{il}{\stackrel{\sim }{u}}_l^{(0)}\right)\right).$$ (43)

We store (42) as a short integer for each voxel outside the ROI only, so it does not require very much memory.

We evaluated the OS algorithm with the proposed scaling factors (42) using the GE performance phantom. Fig. 3 shows that the OS algorithm using the proposed scaling factors (42) leads to more stable reconstruction than the ordinary OS approach which diverges outside the ROI. The instability seen with the ordinary OS approach may also degrade image quality within the ROI as seen by the noise standard deviations in Fig. 3. The results in Fig. 4 further show that the ordinary OS algorithm exhibits more variations within the ROI due to the instability outside ROI, whereas the proposed OS algorithm is robust.

Fig. 3.

Effect of gradient scaling in regularized OS-SQS algorithm with GE performance phantom (GEPP) in helical CT: Each image is reconstructed after running 20 iterations of OS algorithm with 328 subsets, using ordinary and proposed scaling approaches. Standard deviation σ of a uniform region (in white box) is computed for comparison. We compute full-width half maximum (FWHM) of a tungsten wire (red arrow) to measure the resolution. (The result of a convergent algorithm is shown for reference. Images are cropped for better visualization.)

Fig. 4.

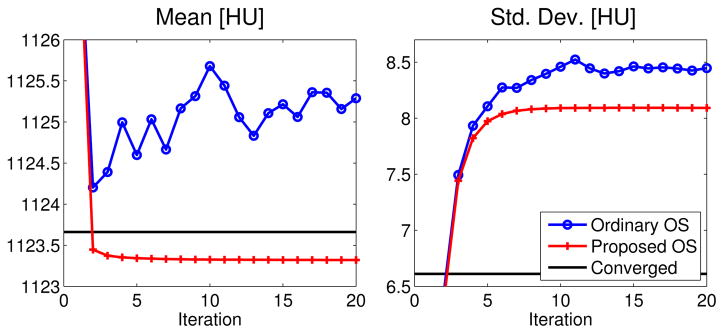
GE performance phantom: mean and standard deviation within a uniform region in the first slice of the ROI (see Fig. 3) vs. iteration, showing the instability of ordinary OS approach with 328 subsets, compared with the proposed OS approach. Also shown is the result from a converged image x^(∞) generated from several iterations of a convergent algorithm.

C. OS algorithm with averaging

Although the new scaling factors (42) stabilize OS in helical CT and reduce artifacts, the final noise level is still worse than a convergent algorithm (see Fig. 3 and 4) because any OS method with constant scaling factors will not converge [45]. This section discusses one practical method that can reduce noise without affecting the convergence rate. This approach helps the OS algorithm come closer to the converged image, reducing the undesirable noise in images reconstructed using OS algorithms with large M.

To ensure convergence, the incremental optimization transfer method [26] was proposed, which involves a form of averaging, but the greatly increased memory space required has prevented its application in 3D X-ray CT. As a practical alternative, we investigated an approach where the final image is formed by averaging all of the sub-iterations at the final iteration n_end of the OS algorithm (after it approaches its limit cycle). A memory-efficient implementation of this approach uses a recursive in-place calculation:

$${\overline{x}}^{\left(\frac{m+1}{M}\right)}=\frac{m}{m+1}{\overline{x}}^{\left(\frac{m}{M}\right)}+\frac{1}{m+1}{x}^{(n_{\text{end}}-1+\frac{m+1}{M})},$$ (44)

where x̄⁽⁰⁾ is an initial zero image, and x̄⁽¹⁾ is the final averaged image. There was a preliminary simulation investigation of averaging the final iteration in [27], and we applied the averaging technique to CT scans here. In Table II, we investigated this averaging method using a scan of the GEPP phantom and quantified the noise and resolution properties (as described in Fig. 3), and evaluated root mean square difference (RMSD⁴) between current and converged image within ROI. Table II shows that the averaging technique successfully reduces the noise and RMSD.

TABLE II.

GE performance phantom: Noise, resolution and RMSD behavior of OS-SQS(328 subsets) after 20 iterations followed by averaging.

	Smoothed FBP	OS-SQS(328)		Conv.
		w/o averaging	w/ averaging
Mean [HU]	1127.7	1123.3	1123.8	1123.7
Std. Dev. [HU]	2.3	8.0	7.2	6.6
FWHM [mm]	1.4	0.7	0.7	0.7
RMSD [HU]	9.4	3.4	0.8	·

Overall, we have enhanced the standard OS-SQS algorithm into the NU-OS-SQS method for 3D helical CT. First, we accelerated the standard OS-SQS algorithm by non-uniform (NU) approach, encouraging larger step sizes for the voxels that need more updates. We modified the algorithm to handle the helical CT geometry by introducing the scaling factor γ_j. We also averaged all sub-iterations at the final iteration to reduce noise. The outline of the proposed algorithm is presented in Appendix B. We investigate the performance of the NU-OS-SQS algorithm for various CT scans in the next section.

V. Experimental results

We investigated the proposed NU-OS-SQS algorithm for PWLS image reconstruction with a non-negativity constraint. The PWLS cost function is strictly convex and has a unique global minimizer [46]. We implemented the NU-OS-SQS algorithm in C and executed it on a Mac with two 2.26GHz quad-core Intel Xeon processors and a 16GB RAM. We used 16 threads, and projection views were grouped and assigned to each thread.

Three 3D helical CT data sets are used in this section to compare the proposed NU-OS-SQS algorithm to the ordinary OS-SQS algorithm, and we used the GE performance phantom (GEPP) to measure the resolution. We used two other clinical data sets to investigate the performance of NU approach. We investigated tuning the DRA function g(·) in (37) to provide fast convergence rate for various data sets. We also provide results from a simulation data set in a supplementary material for reproducibility.⁵

We chose the parameters of the cost function Ψ(x) in (2) to provide a good image. We defined an edge-preserving potential function as ψ_k([Cx]_k) ≜ ω̄_kψ([Cx]_k), where the function:⁶

$$\psi (t)=\frac{{\delta }^2}{b^3}\left(\frac{{ab}^2}{2}{\left|\frac{t}{\delta }\right|}^2+b(b-a)\left|\frac{t}{\delta }\right|+(a-b)log\left(1+b\left|\frac{t}{\delta }\right|\right)\right)$$ (45)

is a generalized version of a Fair potential function in [47], and the spatial weighting ω̄_k [48] provides resolution properties that emulate the GE product “Veo”. We used M = 82 subsets for the OS algorithms, assigning 12 out of 984 projection views per rotation to each subset. We used the maximum curvature (10) for generating the denominator of surrogate function of the cost function Ψ(x), and focused on n_loop = 3 which balances the convergence rate and run time, based on Table I.

In Section II-D, we recommended fixing the denominator ${\stackrel{\sim }{d}}_j^{(n)}$ (generated by the maximum curvature (10)) after n_fix iterations in NU-SQS algorithm to guarantee convergence. This condition is less important theoretically when we accelerate the NU-SQS algorithm with OS methods that break the convergence property. However, we still recommend fixing ${\stackrel{\sim }{d}}_j^{(n)}$ after n_fix iterations (before approaching the limit-cycle) in the NU-OS-SQS algorithm, because we observed some instability from updating ${\stackrel{\sim }{d}}_j^{(n)}$ (and ${\stackrel{\sim }{u}}_j^{(n)}$) every n_loop iterations near the limit-cycle in our experiments. We selected n_fix = 7 for GEPP, but we did not use n_fix for other two cases because the algorithm did not reach a limit-cycle within n_end = 20 iterations, and we leave optimizing n_fix as a future work.

In Section IV-B, we stabilized the OS-SQS algorithm outside ROI in helical geometry by using the factor γ_j in (42). However, we experienced some instability outside ROI in NU-OS-SQS methods even with (42), because a small NU denominator ${\stackrel{\sim }{d}}_j^{(n)}$ outside ROI is more likely to lead to instability than for voxels within the ROI due to the incomplete sampling outside ROI. Therefore, we prevent the denominator ${\stackrel{\sim }{d}}_j^{(n)}$ outside ROI from being very small. We empirically modified the DRA function in Section III-C, and used it for our experiments, improving stability outside ROI. We first modified the function (35) as follows:

$$F_{\text{cdf}}^{(n)}(u)\triangleq \frac{1}{N_p}\sum _{j=1}^{N_p}{I}_{\left\{{\gamma }_j{u}_j^{(n)}\le u\right\}},$$ (46)

since the value of $u_j^{(n)}$ in (27) outside ROI was found to be relatively large due to the incomplete sampling. We further modified (36) and (37) to prevent ${\stackrel{\sim }{d}}_j^{(n)}$ from becoming very small outside ROI as follows with g(v; α) ≜ max {αv^t, ε}:

$${\stackrel{\sim }{u}}_j^{(n)}\triangleq \{\begin{array}{ll}g\left(F_{\text{cdf}}^{(n)}({\gamma }_j{u}_j^{(n)});1\right),\hfill & \text{if}j\text{th}\text{voxel}\text{within}\text{ROI},\hfill \\ g\left(F_{\text{cdf}}^{(n)}({\gamma }_j{u}_j^{(n)});0.5\right),\hfill & \text{otherwise}.\hfill \end{array}$$ (47)

A. GE performance phantom (GEPP)

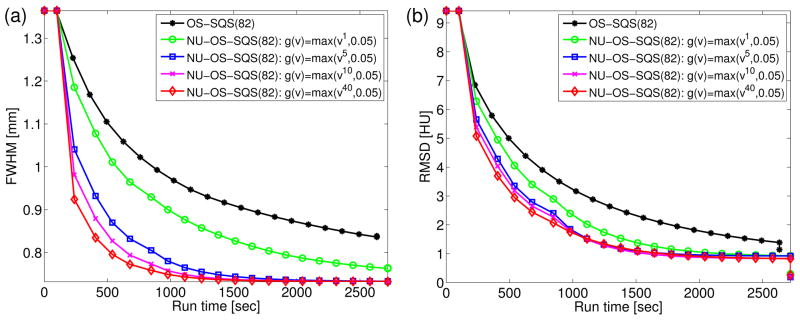
We reconstructed 512 × 512 × 47 images of the GEPP from a 888 × 64 × 3071 sinogram (the number of detector columns × detector rows × projection views) with pitch 0.5. We evaluated the full width at half maximum (FWHM) of a tungsten wire (see Fig. 3). Fig. 5(a) shows the resolution versus run time and confirms that non-uniform (NU) approach accelerates the SQS algorithm. This dramatic speed-up in FWHM is promising since SQS-type algorithms are known to have slow convergence rate of high frequency components [6]. We also evaluated the convergence rate by computing RMSD between current and converged⁷ image versus run time, within ROI.

Fig. 5.

GE performance phantom: plots of (a) FWHM and (b) RMSD as a function of run time for different choice of DRA parameters t for ε = 0.05. The plot markers show each iteration. There are no changes during first iterations, since we consider precomputing the denominator using one forward and back projections as one iteration.

Fig. 5(a) and 5(b) illustrate that increasing t in g(·) in (37) accelerates the convergence of “update-needed” region, particularly the wire and edges in GEPP. However, highly focusing the updates on few voxels will not help speed up the overall convergence for all objects. Therefore, we further investigate the choice of g(·) using various patient CT scans.

The RMSD plots⁸ of NU-OS-SQS in Fig. 5(b) reached a limit-cycle after 1500 sec that did not approach zero. Averaging the sub-iterations at the final iteration improved the final image with small computation cost, yielding the drop in RMSD at the last 20th iteration in Fig. 5(b). The reduced noise was measurable in the reconstructed image as seen in Table II.

B. A shoulder region scan

In this experiment, we reconstructed a 512 × 512 × 109 image from a shoulder region scan 888 × 32 × 7146 sinogram with pitch 0.5. Fig. 6(a) and 6(b) show that the non-uniform approach accelerates convergence, depending on the choice of parameters in g(·). We investigated the relationship between the convergence rate and the DRA function g(·) by tuning both the parameters t and ε in (37). Fig. 6(a) shows that increasing t to 10 accelerated convergence, but larger t values did not help as the choice of t = 40 was slower than t = 10. In Fig. 6(b), decreasing ε to 0.01 accelerated the algorithm in this shoulder region scan, but not for the data set in Section V-C, so ε = 0.05 appears to be a reasonable choice overall.

Fig. 6.

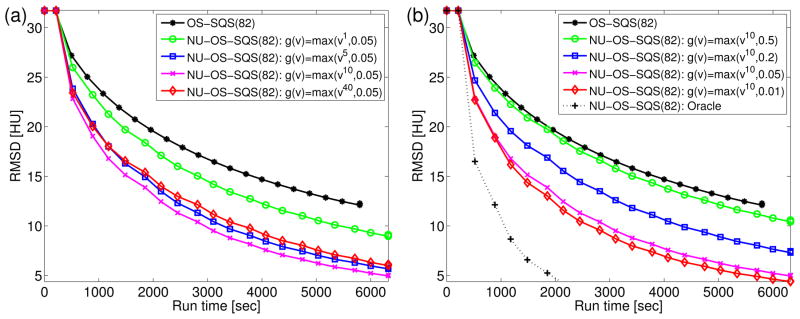
A shoulder region scan: plot of RMSD versus run time for different choice of parameters (a) t and (b) ε in g(v) = max {v^t, ε}.

We averaged the sub-iterations at the last iteration, but Fig. 6(a) and 6(b) did not show a drop at the final iteration (which appeared in Fig. 5(b)), because the algorithm had not yet reached a limit-cycle. Even though averaging did not noticeably decrease the RMSD, the reconstructed image had measurable noise reduction in regions that already reached a limit-cycle like uniform regions. (Results not shown.)

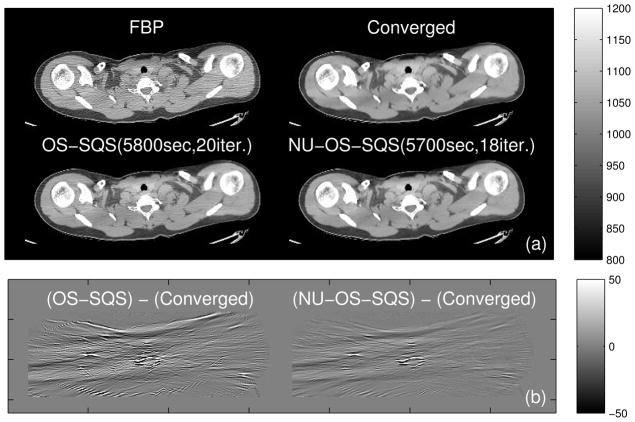
In Fig. 7(a), we illustrate that statistical image reconstruction can reduce noise and preserve image features compared to analytical FBP reconstruction. The reconstructed images of (NU-)OS-SQS show that NU approach helps OS-SQS to approach the converged image faster than the ordinary method. After the same computation (95 min.), the reconstructed image of OS-SQS still contains streaks from the initial FBP image, while NU-OS-SQS has reduced the streaks. This is apparent in the difference images between the reconstructed and converged images in Fig. 7(b).

Fig. 7.

A shoulder region scan: (a) A center slice of initial FBP, converged image and reconstructed image by OS-SQS(82) and NU-OS-SQS(82)-g(v) = max {v¹⁰, 0.05} after about 95 min. (b) Difference between the reconstructed and converged images are additionally shown to illustrate the acceleration of NU approach. (Images are cropped for better visualization.)

By analyzing NU-OS-SQS in two CT scans, we observed that the parameters t = 10 and ε = 0.05 consistently accelerated the algorithm by about a factor of more than two.⁹ (The choice ε = 0.01 was too aggressive in our other experiments.) We also have observed more than two-fold accelerations in other experiments. (Results not shown.) Fig. 6(b) shows the RMSD plot using the (practically unavailable) oracle update-needed factor ${\widehat{u}}_j^{(n)}\triangleq \mid x_j^{(n)}-x_j^{(\infty )}\mid$ instead of our heuristic choice ${\stackrel{\sim }{u}}_j^{(n)}$. This result suggests that additional optimization of the DRA method and initialization of ${\stackrel{\sim }{u}}_j^{(0)}$ could further speed up the NU algorithm in future work.

C. A truncated abdomen scan

We also reconstructed a 390 × 390 × 239 image from a 888 × 64 × 3516 sinogram with pitch 1.0. This scan contains transaxial truncation and the initial FBP image has truncation artifacts [49] that can be reduced by iterative reconstruction. The choice of $u_j^{(0)}$ described in Section III-E did not consider truncation effects, and we found that NU-OS-SQS did not reduce such artifacts faster than standard OS-SQS. (The large patient size may also have reduced the possible speed-up by the NU method, compared to the previous two scans.) Therefore, we investigated an alternative NU method that can reduce truncation artifacts faster than standard algorithm.

We designed a modified NU method using a few (m_sub) sub-iterations of standard OS-SQS to generate the initial update-needed factor $u_j^{(0)}$, which may also be a reasonable approach for other scans. We perform initial sub-iterations $x_{\text{sub}}^{(m/M)}$ in (39) efficiently using two-input projectors (in Section III-F) and replacing the all-view denominator ${\stackrel{\sim }{d}}_j^{L,(n)}$ in (29) by a standard subset-based denominator [25]:

$${\stackrel{\sim }{d}}_{j,\text{sub}}^{L_m,\left(\frac{m}{M}\right)}\triangleq \gamma \sum _{i\in S_m}{\stackrel{⌣}{c}}_i^{(\frac{m}{M})}{a}_{ij}\left(\sum _{l=1}^{N_p}{a}_{il}\right),$$ (48)

where S_m consists of projection views in mth subset. The scaling factor γ_j in (42) is unavailable at this point, so we use γ = M instead. After m_sub sub-iterations, we compute the following initial update-needed factors:

$${\stackrel{\sim }{u}}_j^{(0)}\triangleq f_{\text{sub}}^{\left(\frac{m_{\text{sub}}}{M}\right)}\left(\left|x_{j,\text{sub}}^{\left(\frac{m_{\text{sub}}}{M}\right)}-x_j^{(0)}\right|\right),$$ (49)

where $f_{\text{sub}}^{\left(\frac{m_{\text{sub}}}{M}\right)}(·)$ is a DRA function in (36), and we use these to compute the NU denominators ${\stackrel{\sim }{d}}_j^{L,(0)}$ and ${\stackrel{\sim }{d}}_j^{R,(0)}$ that we use for first n_loop outer iterations.

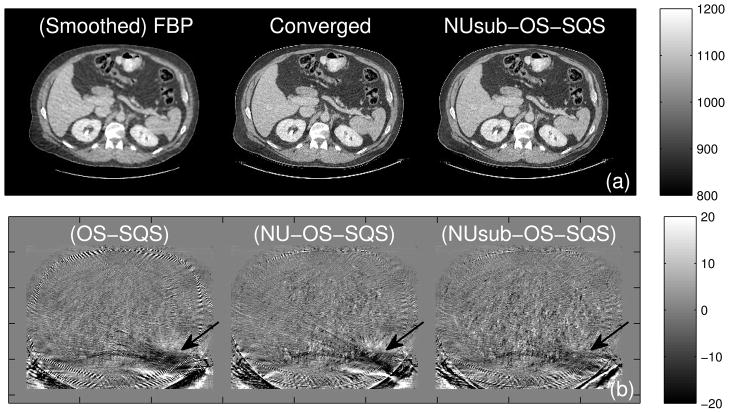
Fig. 8(a) shows that statistical image reconstruction provides better image quality than FBP reconstruction. Fig. 8(b) illustrates that this NUsub-OS-SQS approach reduces the truncation artifacts faster than the standard OS-SQS and NU-OS-SQS. Although standard OS-SQS reduces noise faster than other two algorithms in Fig. 8(b), both NU-OS-SQS and NUsub-OS-SQS show better convergence near the spine, the boundary of patient, and other internal structures than OS-SQS at the same computation time (90 min.).

Fig. 8.

A truncated abdomen scan: (a) A center slice of FBP, converged image, and reconstructed image by NUsub-OS-SQS(82 g(v) = {max v¹⁰, 0.05} using ${\stackrel{\sim }{u}}_j^{(0)}$ in (49) generated from sub-iterations. (b) Difference between the reconstructed and converged images, where images are reconstructed by OS-SQS(82) after 5400sec (20iter.), NU-OS-SQS(82) after 5230sec (18iter.) using ${\stackrel{\sim }{u}}_j^{(0)}$ extracted from FBP based on Section III-E, and NUsub-OS-SQS(82) after 5220sec (17iter.) using ${\stackrel{\sim }{u}}_j^{(0)}$ in (49). The (black) arrows indicate truncation artifacts. Images are cropped for better visualization.

VI. Conclusion

This paper has presented a spatially non-uniform SQS algorithm that can efficiently minimize both PL and PWLS problems monotonically. The experimental results show that the proposed NU-SQS approach converged more than twice as fast as SQS. The OS algorithm, further applied to SQS method for acceleration, was enhanced to handle non-uniformly sampled geometries such as helical CT. The improvements showed promising results on large 3D helical CT data sets.

The key of the NU-SQS approach is designing “update-needed” factors $u_j^{(n)}$ in (27) that encourage larger step sizes for voxels that are predicted to need larger changes to reach the final image. Further optimization of these factors, e.g., by improving the initialization of ${\stackrel{\sim }{u}}_j^{(0)}$ and the DRA function in (36), should lead to further acceleration and stability of the proposed NU-SQS and NU-OS-SQS methods.

Appendix A. Proof of Lemma 2

The proposed choice ${\stackrel{\sim }{\lambda }}_{ij}^{(n)}=a_{ij}{u}_j^{(n)}$ in (28) and its corresponding ${\stackrel{\sim }{d}}_j^{L,(n)}$ in (29) are a choice that minimizes ${\sum }_{j=1}^{N_p}{\left(u_j^{(n)}\right)}^2{d}_j^{L,(n)}$ among all possible $d_j^{L,(n)}$ in (19), i.e.,

$$\left\{{\stackrel{\sim }{\lambda }}_{ij}^{(n)}\right\}=arg\underset{\{{\lambda }_{ij}^{(n)}\}}{min}\sum _{j=1}^{N_p}{\left(u_j^{(n)}\right)}^2\left(\sum _{\begin{array}{c}i=1\\ a_{ij}\ne 0\end{array}}^{N_d}{\stackrel{⌣}{c}}_i^{(n)}\frac{a_{ij}^2}{{\lambda }_{ij}^{(n)}}\sum _{\begin{array}{c}l=1\\ a_{il}\ne 0\end{array}}^{N_p}{\lambda }_{il}^{(n)}\right),$$

subject to the positivity constraint on ${\lambda }_{ij}^{(n)}$ if a_ij ≠ 0.

Proof

By the Schwarz inequality 〈s, t〉² ≤ ||s||²||t||², we have

$${\left(\sum _{\begin{array}{c}j=1\\ a_{ij}\ne 0\end{array}}^{N_p}{a}_{ij}{u}_j^{(n)}\right)}^2\le \sum _{\begin{array}{c}j=1\\ a_{ij}\ne 0\end{array}}^{N_p}{\left(u_j^{(n)}\right)}^2\frac{a_{ij}^2}{{\lambda }_{ij}^{(n)}}\sum _{\begin{array}{c}l=1\\ a_{il}\ne 0\end{array}}^{N_p}{\lambda }_{il}^{(n)},$$

where $s_j=\sqrt{\frac{{\lambda }_{ij}^{(n)}}{{\sum }_{l=1}^{N_p}{\lambda }_{il}^{(n)}}}$ and $t_j=a_{ij}{u}_j^{(n)}\sqrt{\frac{{\sum }_{l=1}^{N_p}{\lambda }_{il}^{(n)}}{{\lambda }_{ij}^{(n)}}}$. Then,

$$\begin{array}{l}\sum _{j=1}^{N_p}{\left(u_j^{(n)}\right)}^2{d}_j^{L,(n)}=\sum _{i=1}^{N_d}{\stackrel{⌣}{c}}_i^{(n)}\left(\sum _{\begin{array}{c}j=1\\ a_{ij}\ne 0\end{array}}^{N_p}{\left(u_j^{(n)}\right)}^2\frac{a_{ij}^2}{{\lambda }_{ij}^{(n)}}\sum _{\begin{array}{c}l=1\\ a_{il}\ne 0\end{array}}^{N_p}{\lambda }_{il}^{(n)}\right)\\ \ge \sum _{i=1}^{N_d}{\stackrel{⌣}{c}}_i^{(n)}{\left(\sum _{\begin{array}{c}j=1\\ a_{ij}\ne 0\end{array}}^{N_p}{a}_{ij}{u}_j^{(n)}\right)}^2\\ =\sum _{j=1}^{N_p}\left(\sum _{\begin{array}{c}i=1\\ a_{ij}\ne 0\end{array}}^{N_d}{\stackrel{⌣}{c}}_i^{(n)}{a}_{ij}{u}_j^{(n)}\sum _{\begin{array}{c}l=1\\ a_{il}\ne 0\end{array}}^{N_p}{a}_{il}{u}_l^{(n)}\right)\\ =\sum _{j=1}^{N_p}{\left(u_j^{(n)}\right)}^2\left(\frac{1}{u_j^{(n)}}\sum _{\begin{array}{c}i=1\\ a_{ij}\ne 0\end{array}}^{N_d}{\stackrel{⌣}{c}}_i^{(n)}{a}_{ij}\sum _{\begin{array}{c}l=1\\ a_{il}\ne 0\end{array}}^{N_p}{a}_{il}{u}_l^{(n)}\right)\\ =\sum _{j=1}^{N_p}{\left(u_j^{(n)}\right)}^2{\stackrel{\sim }{d}}_j^{L,(n)}.\end{array}$$

Appendix B. Outline of the proposed NU-OS-SQS algorithm]

Set M, nend, nloop and initialize x by an FBP image.

Generate uj from an FBP image by edge and intensity detectors.

Compute the maximum curvature či = max {ḧi(0), η}.

$d_j^L=0$, γj = 0, xj,ref = xj, and the final image x̄;j = 0.

$${\stackrel{\sim }{d}}_j^R=\frac{1}{u_j}\sum _{k=1}^{N_r}{\ddot{\psi }}_k(0)\mid c_{kj}\mid \left(\sum _{l=1}^{N_p}\mid c_{kl}\mid u_l\right)$$ (50)

n = 0

for m = 0, 1, …, M − 1

$$\begin{array}{l}{d}_{j,\text{sub}}^L=\frac{1}{u_j}\sum _{i\in S_m}{\stackrel{⌣}{c}}_i{a}_{ij}\left(\sum _{l=1}^{N_p}{a}_{il}{u}_l\right)\\ d_j^L+=d_{j,\text{sub}}^L\text{and}{\gamma }_j+=I_{\left\{d_{j,\text{sub}}^L>0\right\}}\end{array}$$ (51)

end

for n = 1, 2, …, nend − 1

if n mod nloop = 1 and n ≤ nfix

$${\stackrel{\sim }{d}}_j^L=d_j^L,\text{and}\text{compute}{\stackrel{\sim }{d}}_j^R\text{by}(50)$$

elseif n mod nloop = nloop − 1 and n ≤ nfix − 2

$$x_{j,\text{ref}}=x_j$$

elseif n mod nloop = 0 and n ≤ nfix − 1

$$d_j^L=0,\text{and}{u}_j=g(F_{\text{cdf}}(x_j-x_{j,\text{ref}}))$$

end

for m = 0, 1, …, M − 1

$$x_{j,\text{prev}}=x_j$$

if n mod nloop ≠ 0 or n ≥ nfix

$$g_{j,\text{sub}}^L=\frac{\partial }{\partial x_j}{L}_m(x_{\text{prev}})$$ (52)

else

compute both $d_{j,\text{sub}}^L$ by (51) and $g_{j,\text{sub}}^L$ by (52)

simultaneously using two-input projection function, and

$$d_j^L+=d_{j,\text{sub}}^L$$

end

$$x_j={\left[x_{j,\text{prev}}-\frac{{\gamma }_j{g}_{j,\text{sub}}^L+\frac{\partial }{\partial x_j}R(x_{\text{prev}})}{{\stackrel{\sim }{d}}_j^L+{\stackrel{\sim }{d}}_j^R}\right]}_{+}$$ (53)

if n = nend − 1

$${\overline{x}}_j=\frac{m}{m+1}{\overline{x}}_j+\frac{1}{m+1}{x}_j$$

end

end

end