Significance
The eukaryotic flagellum is a best-seller of nature: These slender cell appendages propel sperm and many other microswimmers, including disease-causing protists. In mammalian airways or the oviduct, collections of flagella beat in synchrony to pump fluids efficiently. Flagellar synchronization was proposed to rely on mechanical feedback by hydrodynamic forces, but the details are not well understood. Here, we used theory and experiment to elucidate a mechanism of synchronization in the model organism Chlamydomonas, a green algal cell that swims with two flagella like a breaststroke swimmer. Our analysis shows how synchronization arises by a coupling of swimming and flagellar beating and characterizes an exemplary force–velocity relationship of the flagellar beat.
Keywords: flagellar force–velocity relation, low-Reynolds-number hydrodynamics
Abstract
The unicellular green alga Chlamydomonas swims with two flagella that can synchronize their beat. Synchronized beating is required to swim both fast and straight. A long-standing hypothesis proposes that synchronization of flagella results from hydrodynamic coupling, but the details are not understood. Here, we present realistic hydrodynamic computations and high-speed tracking experiments of swimming cells that show how a perturbation from the synchronized state causes rotational motion of the cell body. This rotation feeds back on the flagellar dynamics via hydrodynamic friction forces and rapidly restores the synchronized state in our theory. We calculate that this “cell-body rocking” provides the dominant contribution to synchronization in swimming cells, whereas direct hydrodynamic interactions between the flagella contribute negligibly. We experimentally confirmed the two-way coupling between flagellar beating and cell-body rocking predicted by our theory.
Eukaryotic cilia and flagella are long, slender cell appendages that can bend rhythmically and thus present a prime example of a biological oscillator (1). The flagellar beat is driven by the collective action of dynein molecular motors, which are distributed along the length of the flagellum. The beat of flagella, with typical frequencies ranging from 20–60 Hz, pumps fluids, for example, mucus in mammalian airways (2), and propels unicellular microswimmers such as Paramecia, spermatozoa, and algae (3). The coordinated beating of collections of flagella is important for efficient fluid transport (2, 4, 5) and fast swimming (6). This coordinated beating represents a striking example for the synchronization of oscillators, prompting the question of how flagella couple their beat. Identifying the specific mechanism of synchronization can be difficult because synchronization may occur even for weak coupling (7). Further, the effect of the coupling is difficult to detect once the synchronized state has been reached.
Hydrodynamic forces were suggested to play a significant role for flagellar synchronization already in 1951 by Taylor (8). Since then, direct hydrodynamic interactions between flagella were studied theoretically as a possible mechanism for flagellar synchronization (9–12). Another synchronization mechanism that is independent of hydrodynamic interactions was recently described in the context of a minimal model swimmer (13–15). This mechanism crucially relies on the interplay of swimming motion and flagellar beating.
Here, we address the hydrodynamic coupling between the two flagella in a model organism for flagellar coordination (16–19), the unicellular green alga Chlamydomonas reinhardtii. Chlamydomonas propels its ellipsoidal cell body, which has typical diameter of 10 μm, using a pair of flagella, whose lengths are about 10 μm (16). The two flagella beat approximately in a common plane, which is collinear with the long axis of the cell body. In that plane, the two beat patterns are nearly mirror-symmetric with respect to this long axis. The beating of the two flagella of Chlamydomonas can synchronize, that is, adopt a common beat frequency and a fixed phase relationship (16–19). In-phase synchronization of the two flagella is required for swimming along a straight path (19). The specific mechanism leading to flagellar synchrony is unclear.
Here, we use a combination of realistic hydrodynamic computations and high-speed tracking experiments to reveal the nature of the hydrodynamic coupling between the two flagella of free-swimming Chlamydomonas cells. Previous hydrodynamic computations for Chlamydomonas used either resistive force theory (20, 21), which does not account for hydrodynamic interactions between the two flagella, or computationally intensive finite element methods (22). We employ an alternative approach and represent the geometry of a Chlamydomonas cell by spherical shape primitives, which provides a computationally convenient method that fully accounts for hydrodynamic interactions between different parts of the cell. Our theory characterizes flagellar swimming and synchronization by a minimal set of effective degrees of freedom. The corresponding equation of motion follows naturally from the framework of Lagrangian mechanics, which was used previously to describe synchronization in a minimal model swimmer (13, 15). These equations of motion embody the key assumption that the flagellar beat speeds up or slows down according to the hydrodynamic friction forces acting on the flagellum, that is, if there is more friction and therefore higher hydrodynamic load, then the beat will slow down. This assumption is supported by previous experiments that showed that the flagellar beat frequency decreases when the viscosity of the surrounding fluid is increased (23, 24). The simple force–velocity relationship for the flagellar beat employed by us coarse-grains the behavior of thousands of dynein molecular motors that collectively drive the beat. Similar force–velocity properties have been described for individual molecular motors (25) and reflect a typical behavior of active force generating systems.
Our theory predicts that any perturbation of synchronized beating results in a significant yawing motion of the cell, reminiscent of rocking of the cell body. This rotational motion imparts different hydrodynamic forces on the two flagella, causing one of them to beat faster and the other to slow down. This interplay between flagellar beating and cell-body rocking rapidly restores flagellar synchrony after a perturbation. Using the framework provided by our theory, we analyze high-speed tracking experiments of swimming cells, confirming the proposed two-way coupling between flagellar beating and cell-body rocking.
Previous experiments restrained Chlamydomonas cells from swimming, holding their cell body in a micropipette (17–19). Remarkably, flagellar synchronization was observed also for these constrained cells. This observation seems to argue against a synchronization mechanism that relies on swimming motion. However, the rate of synchronization observed in these experiments was faster by an order of magnitude than the rate we predict for synchronization by direct hydrodynamic interactions between the two flagella in the absence of any motion. In contrast, we show that rotational motion with a small amplitude of a few degrees only, which may result from either a residual rotational compliance of the clamped cell or an elastic anchorage of the flagellar pair, provides a possible mechanism for rapid synchronization, which is analogous to synchronization by cell-body rocking in free-swimming cells.
Results and Discussion
High-Precision Tracking of Confined Chlamydomonas Cells.
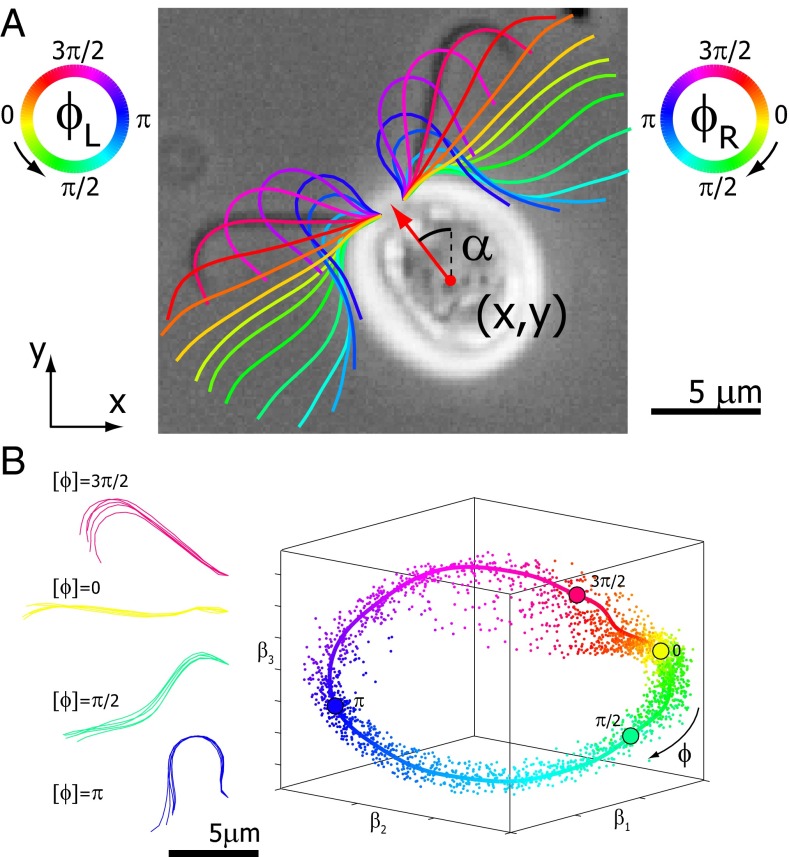
To study the interplay of flagellar beating and swimming motion, we recorded single wild-type C. reinhardtii cells swimming in a shallow observation chamber using high-speed phase-contrast microscopy (1,000 frames per second). The chamber heights were only slightly larger than the cell diameter so that the cells did not roll around their long body axis, but only translated and rotated in the focal plane. This confinement of cell motion to two space dimensions and the fact that the approximately planar flagellar beat was parallel to the plane of observation greatly facilitated data acquisition and analysis. From high-speed recordings we obtained the projected position and orientation of the cell body as well as the shape of the two flagella (Fig. 1A and Fig. S1).
Fig. 1.
Five degrees of freedom for Chlamydomonas. (A) In our experiments, conducted in shallow observation chambers, Chlamydomonas cells swim in a plane. At each time, the position and orientation of the cell body is characterized by its center position 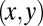 and the angle α of its long axis with respect to the laboratory frame. The beating of each flagellum is characterized by a single periodic phase variable,
and the angle α of its long axis with respect to the laboratory frame. The beating of each flagellum is characterized by a single periodic phase variable, 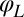 and
and 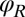 for the left and right flagellum, respectively. The flagellar shapes shown in different colors were tracked from high-speed recordings and correspond to a time-difference of
for the left and right flagellum, respectively. The flagellar shapes shown in different colors were tracked from high-speed recordings and correspond to a time-difference of 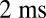 . This beat pattern was used for all computations. (B) Binning of tracked flagellar shapes according to shape similarity defines a flagellar phase angle as shown on the left. More precisely, we employed a nonlinear dimensionality reduction technique as specified in Supporting Information to represent each tracked planar flagellar shape as a point in an abstract shape space. This representation reveals the periodicity of the flagellar beat and supports our description of the flagellar beat as a fixed sequence of flagellar shapes parameterized by a single phase variable φ.
. This beat pattern was used for all computations. (B) Binning of tracked flagellar shapes according to shape similarity defines a flagellar phase angle as shown on the left. More precisely, we employed a nonlinear dimensionality reduction technique as specified in Supporting Information to represent each tracked planar flagellar shape as a point in an abstract shape space. This representation reveals the periodicity of the flagellar beat and supports our description of the flagellar beat as a fixed sequence of flagellar shapes parameterized by a single phase variable φ.
In the reference frame of the cell body, each flagellum undergoes periodic shape changes. To formalize this observation, we defined a flagellar phase variable by binning flagellar shapes according to shape similarity (Fig.1B and Fig. S2). A time series of flagellar shapes is represented by a point cloud in an abstract shape space. This point cloud comprises an effectively one-dimensional shape cycle, which reflects the periodicity of the flagellar beat. Each shape point can be projected on the centerline of the point cloud. We define a phase variable φ running from 0 to 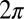 that parameterizes this limit cycle by requiring that the phase speed
that parameterizes this limit cycle by requiring that the phase speed 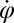 be constant for synchronized beating. Approximately, we determine this parameterization from the condition that the averaged phase speed is independent of the location along the limit cycle. This defines a unique flagellar phase for each tracked flagellar shape. The width of the point cloud shown in Fig. 1B is a measure for the variability of the flagellar beat during subsequent beat cycles. We find that the variations of flagellar shapes for the same value of the phase variable are much smaller than the shape changes during one beat cycle. For our analysis, we therefore neglect these variations of the flagellar beat. In this way, we characterize a swimming Chlamydomonas cell by 5 degrees of freedom: its position
be constant for synchronized beating. Approximately, we determine this parameterization from the condition that the averaged phase speed is independent of the location along the limit cycle. This defines a unique flagellar phase for each tracked flagellar shape. The width of the point cloud shown in Fig. 1B is a measure for the variability of the flagellar beat during subsequent beat cycles. We find that the variations of flagellar shapes for the same value of the phase variable are much smaller than the shape changes during one beat cycle. For our analysis, we therefore neglect these variations of the flagellar beat. In this way, we characterize a swimming Chlamydomonas cell by 5 degrees of freedom: its position 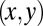 in the plane, the orientation angle α of its cell body, and the two flagellar phase variables
in the plane, the orientation angle α of its cell body, and the two flagellar phase variables 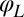 and
and 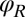 for the left and right flagellum, respectively. Our theoretical description will employ the same 5 degrees of freedom and use flagellar shapes tracked from experiment for the hydrodynamic computations.
for the left and right flagellum, respectively. Our theoretical description will employ the same 5 degrees of freedom and use flagellar shapes tracked from experiment for the hydrodynamic computations.
Hydrodynamic Forces and Interactions.
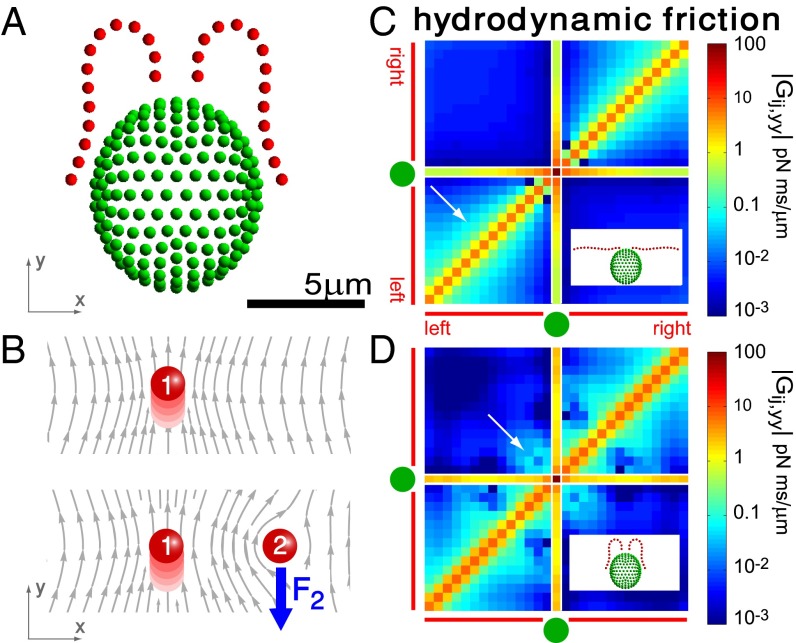
For a swimming Chlamydomonas cell, inertial forces are negligible [as characterized by a low Reynolds number of 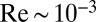 (22)], which implies that the hydrodynamic friction forces exerted by the cell depend only on its instantaneous motion (26). To conveniently compute hydrodynamic friction forces and hydrodynamic interactions, we represented the geometry of a Chlamydomonas cell by 300 spherical shape primitives (Fig. 2A). The spheres constituting the cell body are treated as a rigid cluster. For simplicity, we consider free-swimming cells and do not include wall effects in our hydrodynamic computations. Flagellar beating and swimming corresponds to a simultaneous motion of all 300 spheres of our cell model. The dependence of the corresponding hydrodynamic friction forces and torques on the velocities of the individual spheres is characterized by a grand hydrodynamic friction matrix G. We computed this friction matrix G using a Cartesian multipole expansion technique (27); Materials and Methods gives details. Fig. 2 C and D shows a submatrix that relates force and velocity components parallel to the long axis of the cell. The entries of the color matrix depict the force exerted by any of the flagellar spheres or by the cell-body cluster (row index), if a single flagellar sphere or the cell-body cluster is moved (column index). The indexing of flagellar spheres is indicated by cartoon drawings of the cell next to the color matrix. The diagonal entries of this friction matrix are positive and account for the usual Stokes friction of a single “flagellar sphere” (or of the cell body). Off-diagonal entries are negative and represent hydrodynamic interactions. We find considerable hydrodynamic interactions between spheres of the same flagellum, as well as between each flagellum and the cell body. However, interactions between the two flagella are comparably weak.
(22)], which implies that the hydrodynamic friction forces exerted by the cell depend only on its instantaneous motion (26). To conveniently compute hydrodynamic friction forces and hydrodynamic interactions, we represented the geometry of a Chlamydomonas cell by 300 spherical shape primitives (Fig. 2A). The spheres constituting the cell body are treated as a rigid cluster. For simplicity, we consider free-swimming cells and do not include wall effects in our hydrodynamic computations. Flagellar beating and swimming corresponds to a simultaneous motion of all 300 spheres of our cell model. The dependence of the corresponding hydrodynamic friction forces and torques on the velocities of the individual spheres is characterized by a grand hydrodynamic friction matrix G. We computed this friction matrix G using a Cartesian multipole expansion technique (27); Materials and Methods gives details. Fig. 2 C and D shows a submatrix that relates force and velocity components parallel to the long axis of the cell. The entries of the color matrix depict the force exerted by any of the flagellar spheres or by the cell-body cluster (row index), if a single flagellar sphere or the cell-body cluster is moved (column index). The indexing of flagellar spheres is indicated by cartoon drawings of the cell next to the color matrix. The diagonal entries of this friction matrix are positive and account for the usual Stokes friction of a single “flagellar sphere” (or of the cell body). Off-diagonal entries are negative and represent hydrodynamic interactions. We find considerable hydrodynamic interactions between spheres of the same flagellum, as well as between each flagellum and the cell body. However, interactions between the two flagella are comparably weak.
Fig. 2.
Hydrodynamic interactions between the two flagella are weak. (A) Model Chlamydomonas cell represented by an ensemble of 300 spheres used to compute hydrodynamic friction forces at low Reynolds numbers. In our calculations, the model cell was assumed to be far from any surfaces. (B) Illustration of hydrodynamic interactions between spheres. A single sphere (labeled 1) moving with velocity 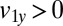 along the y axis will drag fluid alongside and thus exert a total hydrodynamic friction force
along the y axis will drag fluid alongside and thus exert a total hydrodynamic friction force 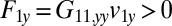 on the fluid. If a second sphere (labeled 2) is held fixed close to the first one, it will locally slow down this fluid flow. The force
on the fluid. If a second sphere (labeled 2) is held fixed close to the first one, it will locally slow down this fluid flow. The force 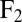 required to hold the second sphere equals the force exerted by this sphere on the fluid; its y component
required to hold the second sphere equals the force exerted by this sphere on the fluid; its y component 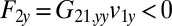 defines a friction coefficient
defines a friction coefficient 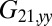 that characterizes hydrodynamic interactions between the two spheres. (C) Hydrodynamic interactions between different parts of the model cell. Analogous to B, one defines a matrix
that characterizes hydrodynamic interactions between the two spheres. (C) Hydrodynamic interactions between different parts of the model cell. Analogous to B, one defines a matrix 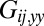 of hydrodynamic friction coefficients for the ensemble of
of hydrodynamic friction coefficients for the ensemble of 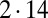 flagellar spheres and the rigid sphere cluster constituting the cell body that together represent a Chlamydomonas cell (Inset). Each column of the color-coded matrix shows the magnitude of hydrodynamic friction exerted by a flagellar sphere (or the cell body), if a single sphere or the cell body is moved parallel to the long cell body axis. Off-diagonal entries characterize hydrodynamic interactions, which are particularly pronounced along a single flagellum (white arrow), or between one flagellum and the cell body (central column). Hydrodynamic interactions between the two flagella are very weak and partly screened by the cell body. (D) Same as in C, but for a recovery stroke configuration. There are weak hydrodynamic interactions between the proximal segments of the two flagella (white arrow). All friction coefficients shown scale with the viscosity of the fluid, which was taken as the viscosity of water at 20 °C,
flagellar spheres and the rigid sphere cluster constituting the cell body that together represent a Chlamydomonas cell (Inset). Each column of the color-coded matrix shows the magnitude of hydrodynamic friction exerted by a flagellar sphere (or the cell body), if a single sphere or the cell body is moved parallel to the long cell body axis. Off-diagonal entries characterize hydrodynamic interactions, which are particularly pronounced along a single flagellum (white arrow), or between one flagellum and the cell body (central column). Hydrodynamic interactions between the two flagella are very weak and partly screened by the cell body. (D) Same as in C, but for a recovery stroke configuration. There are weak hydrodynamic interactions between the proximal segments of the two flagella (white arrow). All friction coefficients shown scale with the viscosity of the fluid, which was taken as the viscosity of water at 20 °C, 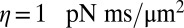 .
.
Theoretical Description of Flagellar Beating and Swimming.
We now present dynamical equations for the minimal set of 5 degrees of freedom shown in Fig. 1A to describe flagellar beating, swimming, and later flagellar synchronization in Chlamydomonas. These equations of motion follow naturally from the framework of Lagrangian mechanics of dissipative systems, which defines generalized forces conjugate to effective degrees of freedom.
Motivated by our experiments, we describe the progression through subsequent beat cycles of each of the two flagella by respective phase angles 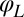 and
and 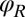 (Fig. 1A). The angular frequency
(Fig. 1A). The angular frequency 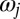 of flagellar beating is given by the time-averaged phase speed
of flagellar beating is given by the time-averaged phase speed 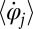 , so we can think of the phase speed as the instantaneous beat frequency. We are interested in variations of the phase speed that can restore a synchronized state after a perturbation. We introduce the key assumption that changes in hydrodynamic friction during the flagellar beat cycle can increase or decrease the phase speed of each flagellum. Specifically, we assume that for both the left and right flagellum,
, so we can think of the phase speed as the instantaneous beat frequency. We are interested in variations of the phase speed that can restore a synchronized state after a perturbation. We introduce the key assumption that changes in hydrodynamic friction during the flagellar beat cycle can increase or decrease the phase speed of each flagellum. Specifically, we assume that for both the left and right flagellum, 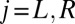 , the respective flagellar phase speed
, the respective flagellar phase speed 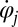 is determined by a balance of an active driving force
is determined by a balance of an active driving force 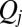 that coarse-grains the active processes within the flagellum and a generalized hydrodynamic friction force
that coarse-grains the active processes within the flagellum and a generalized hydrodynamic friction force 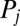 , which depends on
, which depends on 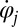 . Note that in addition to hydrodynamic friction, dissipative processes within the flagella may contribute to the friction forces
. Note that in addition to hydrodynamic friction, dissipative processes within the flagella may contribute to the friction forces 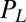 and
and 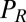 . We do not consider such internal friction in our description because it does not change our results qualitatively. The hydrodynamic friction forces
. We do not consider such internal friction in our description because it does not change our results qualitatively. The hydrodynamic friction forces 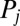 have to be computed self-consistently for a swimming cell. We restrict our analysis to planar motion in the “xy” plane and thus consider the position
have to be computed self-consistently for a swimming cell. We restrict our analysis to planar motion in the “xy” plane and thus consider the position 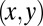 and the orientation α of the cell body with respect to a fixed laboratory frame (Fig. 1A).
and the orientation α of the cell body with respect to a fixed laboratory frame (Fig. 1A).
Any change of the degrees of freedom x, y, α, 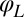 , or
, or 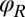 results in the dissipation of energy into the fluid at some rate
results in the dissipation of energy into the fluid at some rate 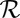 . This dissipation rate
. This dissipation rate 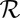 characterizes the mechanical power output of the cell and plays the role of a Rayleigh dissipation function known in Lagrangian mechanics; it can be written as
characterizes the mechanical power output of the cell and plays the role of a Rayleigh dissipation function known in Lagrangian mechanics; it can be written as 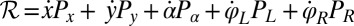 , which defines the generalized friction forces
, which defines the generalized friction forces 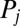 conjugate to the different degrees of freedom. The forces
conjugate to the different degrees of freedom. The forces 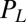 ,
, 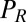 , and
, and 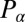 are conjugate to an angle and have physical unit, piconewtons times micrometer. We compute the generalized friction forces using the grand hydrodynamic friction matrix G introduced above. In brief, the superposition principle of low-Reynolds-number hydrodynamics relevant for Chlamydomonas swimming (26) implies that the generalized friction forces relate linearly to the generalized velocities,
are conjugate to an angle and have physical unit, piconewtons times micrometer. We compute the generalized friction forces using the grand hydrodynamic friction matrix G introduced above. In brief, the superposition principle of low-Reynolds-number hydrodynamics relevant for Chlamydomonas swimming (26) implies that the generalized friction forces relate linearly to the generalized velocities, 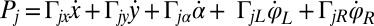 . This defines the generalized hydrodynamic friction coefficients
. This defines the generalized hydrodynamic friction coefficients 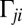 , which are suitable linear combinations of the entries of the grand hydrodynamic friction matrix G (Materials and Methods and Figs. S3 and S4).
, which are suitable linear combinations of the entries of the grand hydrodynamic friction matrix G (Materials and Methods and Figs. S3 and S4).
The friction force 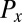 conjugate to the x coordinate of the cell position represents just the x component of the total force exerted by the cell on the fluid, and an analogous statement applies for
conjugate to the x coordinate of the cell position represents just the x component of the total force exerted by the cell on the fluid, and an analogous statement applies for 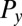 ;
; 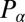 is the total torque associated with rotations around an axis normal to the plane of swimming. If the swimmer is free from external forces and torques, we have
is the total torque associated with rotations around an axis normal to the plane of swimming. If the swimmer is free from external forces and torques, we have 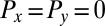 and
and 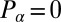 . Together with the proposed balance of flagellar friction and driving forces,
. Together with the proposed balance of flagellar friction and driving forces, 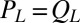 and
and 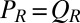 , we have a total of five force balance equations, which allow us to solve for the time derivatives of the 5 degrees of freedom. We obtain an equation of motion that combines swimming and flagellar phase dynamics
, we have a total of five force balance equations, which allow us to solve for the time derivatives of the 5 degrees of freedom. We obtain an equation of motion that combines swimming and flagellar phase dynamics
The phase dependence of the active driving forces 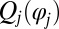 is uniquely specified by the condition that the phase speeds should be constant,
is uniquely specified by the condition that the phase speeds should be constant, 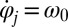 , for synchronized flagellar beating with zero flagellar phase difference
, for synchronized flagellar beating with zero flagellar phase difference 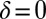 , where
, where 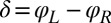 .
.
In essence, this generic description implies that the phase speed of one flagellum is determined by hydrodynamic friction forces, which in turn depend on the swimming motion of the cell. Because the swimming motion is determined by the beating of both flagella, Eq. 1 effectively defines a feedback loop that couples the two flagellar oscillators.
Theory and Experiment of Chlamydomonas Swimming.
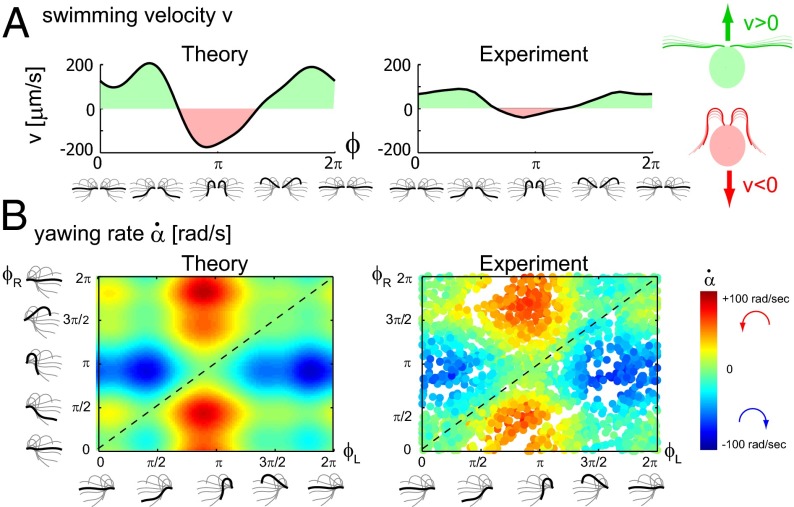
Using the equation of motion (Eq. 1), we can compute the swimming motion of our model cell. For mirror-symmetric flagellar beating with zero flagellar phase difference 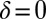 , the model cell follows a straight path with an instantaneous velocity that is positive during the effective stroke but becomes negative during a short period of the recovery stroke (Fig. 3A, Left). Chlamydomonas swims two steps forward, one step back. This saltatory motion is also observed experimentally by us (Fig. 3A, Right) and others (16, 28, 29). In our computation, the instantaneous swimming velocity reaches values up to 200 μm/s, which agrees with experimental measurements for free-swimming cells (29), but overestimates the observed translational swimming speeds in shallow chambers, in which wall effects are expected to reduce the speed of translational motion (compare left and right panels in Fig. 3A). If the two flagella are beating out of phase, the cell will not swim straight anymore, but the cell body yaws (Fig. 3B). Cell-body yawing is observed experimentally (Fig. 3B, Right), with measured yawing rates that agree well with our computations (Fig. 3B, Left). The proximity of boundary walls is known to reduce translational motion but to affect rotational motion to a much lesser extent for a given distance from the wall (21). This is indeed observed in our experiments with cells swimming in shallow chambers: Whereas the observed translational speed is smaller than predicted (Fig. 3A and Fig. S5), the observed yawing rates are very similar to the predicted ones (Fig. 3B). The good agreement between theory and experiment for the yawing rate supports our hydrodynamic computation as well as our description of flagellar beating using a single phase variable. In the next section, we show that rotational motion is crucial for flagellar synchronization, whereas translational motion is less important.
, the model cell follows a straight path with an instantaneous velocity that is positive during the effective stroke but becomes negative during a short period of the recovery stroke (Fig. 3A, Left). Chlamydomonas swims two steps forward, one step back. This saltatory motion is also observed experimentally by us (Fig. 3A, Right) and others (16, 28, 29). In our computation, the instantaneous swimming velocity reaches values up to 200 μm/s, which agrees with experimental measurements for free-swimming cells (29), but overestimates the observed translational swimming speeds in shallow chambers, in which wall effects are expected to reduce the speed of translational motion (compare left and right panels in Fig. 3A). If the two flagella are beating out of phase, the cell will not swim straight anymore, but the cell body yaws (Fig. 3B). Cell-body yawing is observed experimentally (Fig. 3B, Right), with measured yawing rates that agree well with our computations (Fig. 3B, Left). The proximity of boundary walls is known to reduce translational motion but to affect rotational motion to a much lesser extent for a given distance from the wall (21). This is indeed observed in our experiments with cells swimming in shallow chambers: Whereas the observed translational speed is smaller than predicted (Fig. 3A and Fig. S5), the observed yawing rates are very similar to the predicted ones (Fig. 3B). The good agreement between theory and experiment for the yawing rate supports our hydrodynamic computation as well as our description of flagellar beating using a single phase variable. In the next section, we show that rotational motion is crucial for flagellar synchronization, whereas translational motion is less important.
Fig. 3.
(A) For synchronized flagellar beating, we compute saltatory forward swimming with positive instantaneous velocity during effective stroke beating, and a backward motion during the recovery stroke (Left); this behavior is summarized by cartoon drawings (Extreme Right). A typical experimental velocity profile of a Chlamydomonas cell in a shallow observation chamber measured during a cycle of synchronized beating is shown for comparison in the middle panel. (B) Flagellar asynchrony causes cell-body yawing, both in theory and experiment. Shown is the instantaneous rotation rate 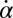 of the cell body in color code as a function of the respective phase of the two flagella. For in-phase synchronized flagellar beating (dashed line), the cell body does not rotate (green). For out-of-phase flagellar beating, however, we find significant cell-body rocking (blue, clockwise; red, counter-clockwise).
of the cell body in color code as a function of the respective phase of the two flagella. For in-phase synchronized flagellar beating (dashed line), the cell body does not rotate (green). For out-of-phase flagellar beating, however, we find significant cell-body rocking (blue, clockwise; red, counter-clockwise).
Theory of Flagellar Synchronization by Cell-Body Yawing.
We now demonstrate how yawing of the cell body leads to flagellar synchronization. We first examine the flagellar phase dynamics after a perturbation of in-phase flagellar synchrony. Fig. 4A shows numerical results for a free-swimming cell obtained from solving the equation of motion (Eq. 1). The initial flagellar asynchrony causes a yawing motion of the model cell, which is characterized by periodic changes of the cell’s orientation angle 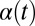 . The phase difference δ between the left and right flagellum decays approximately exponentially as
. The phase difference δ between the left and right flagellum decays approximately exponentially as 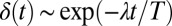 with a rate constant λ (measured in beat periods
with a rate constant λ (measured in beat periods 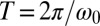 ) that will serve as a measure of the strength of synchronization.
) that will serve as a measure of the strength of synchronization.
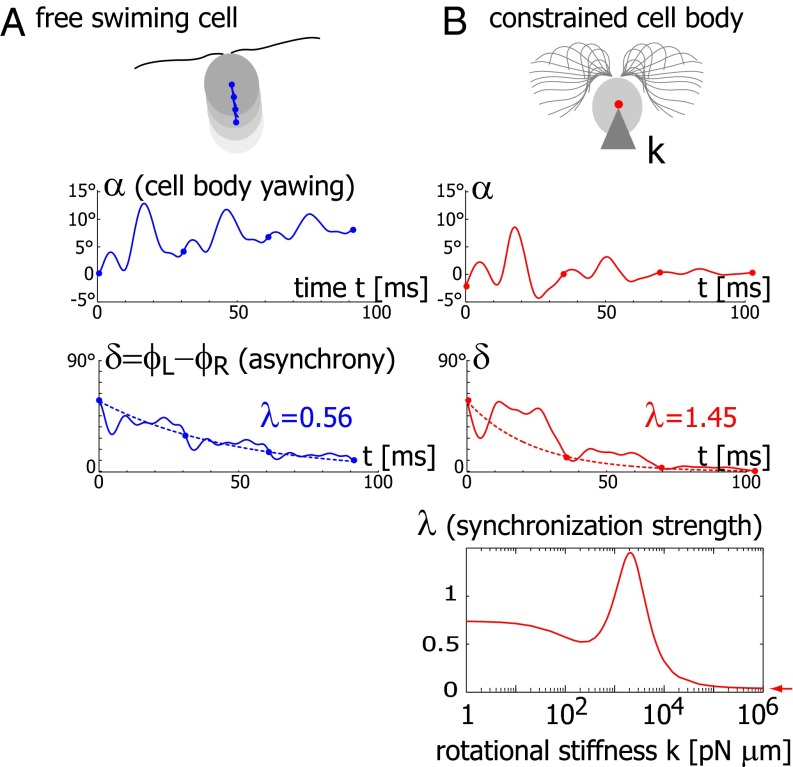
Fig. 4.
Flagellar synchronization by cell-body yawing. (A) For a free-swimming cell (Top), the equation of motion (Eq. 1) predicts a yawing motion of the cell body characterized by 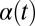 if the two flagella are initially out of synchrony (Middle). The flagellar phase difference δ is found to decrease with time (Bottom, solid line), approximately following an exponential decay
if the two flagella are initially out of synchrony (Middle). The flagellar phase difference δ is found to decrease with time (Bottom, solid line), approximately following an exponential decay 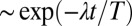 (dotted line), where T is the period of the flagellar beat and λ defines a dimensionless synchronization strength. Thus, in-phase synchronized beating is stable with respect to perturbations. Dots mark the completion of a full beat cycle of the left flagellum. (B) To mimic experiments where external forces constrain cell motion, we simulated the idealized case of a cell that cannot translate, while cell-body yawing is constricted by an elastic restoring torque
(dotted line), where T is the period of the flagellar beat and λ defines a dimensionless synchronization strength. Thus, in-phase synchronized beating is stable with respect to perturbations. Dots mark the completion of a full beat cycle of the left flagellum. (B) To mimic experiments where external forces constrain cell motion, we simulated the idealized case of a cell that cannot translate, while cell-body yawing is constricted by an elastic restoring torque 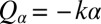 that acts at the cell body center (Top). Again, the two flagella synchronize (Middle) with a synchronization strength λ that can become even larger than in the case of a free swimming as shown here for
that acts at the cell body center (Top). Again, the two flagella synchronize (Middle) with a synchronization strength λ that can become even larger than in the case of a free swimming as shown here for 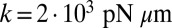 , which is close to the rotational stiffness for which the synchronization strength λ is maximal (Bottom). For very large clamping stiffness k, the cell body cannot move and the synchronization strength λ attenuates to a basal value
, which is close to the rotational stiffness for which the synchronization strength λ is maximal (Bottom). For very large clamping stiffness k, the cell body cannot move and the synchronization strength λ attenuates to a basal value 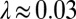 , which arises solely from direct hydrodynamic interactions between the two flagella (arrow). Parameters:
, which arises solely from direct hydrodynamic interactions between the two flagella (arrow). Parameters: 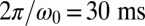 .
.
To mimic experiments in which external forces constrain cell motion, we now consider the idealized case of a cell that cannot translate, while cell-body yawing is constrained by an elastic restoring force 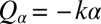 . Again, the two flagella synchronize in-phase, provided some residual cell-body yawing is allowed (Fig. 4B). In the absence of an elastic restoring force
. Again, the two flagella synchronize in-phase, provided some residual cell-body yawing is allowed (Fig. 4B). In the absence of an elastic restoring force 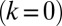 , when the model cell cannot translate, but can still freely rotate, its yawing motion and synchronization behavior is very similar to the case of a free-swimming cell that can rotate and translate. For a fully clamped cell body, however, the synchronization strength is strongly attenuated and is solely due to the direct hydrodynamic interactions between the two flagella. In this case of synchronization by hydrodynamic interactions, the time constant for synchronization is decreased approximately 20-fold compared to the case of free swimming. These numerical observations point to a crucial role of cell-body yawing for flagellar synchronization. The underlying mechanism of synchronization can be explained as follows. For in-phase synchronization, the flagellar beat is mirror-symmetric and the cell swims along a straight path. If, however, the left flagellum has a small head-start during the effective stroke, this causes a counter-clockwise rotation of the cell (Fig. 3B). This cell-body yawing increases (decreases) the hydrodynamic friction encountered by the left (right) flagellum, causing the left flagellum to beat slower and the right one to beat faster. As a result, flagellar synchrony is restored.
, when the model cell cannot translate, but can still freely rotate, its yawing motion and synchronization behavior is very similar to the case of a free-swimming cell that can rotate and translate. For a fully clamped cell body, however, the synchronization strength is strongly attenuated and is solely due to the direct hydrodynamic interactions between the two flagella. In this case of synchronization by hydrodynamic interactions, the time constant for synchronization is decreased approximately 20-fold compared to the case of free swimming. These numerical observations point to a crucial role of cell-body yawing for flagellar synchronization. The underlying mechanism of synchronization can be explained as follows. For in-phase synchronization, the flagellar beat is mirror-symmetric and the cell swims along a straight path. If, however, the left flagellum has a small head-start during the effective stroke, this causes a counter-clockwise rotation of the cell (Fig. 3B). This cell-body yawing increases (decreases) the hydrodynamic friction encountered by the left (right) flagellum, causing the left flagellum to beat slower and the right one to beat faster. As a result, flagellar synchrony is restored.
Next, we present a formalized version of this argument using a reduced equation of motion. We thus arrive at a simple theory for biflagellar synchronization, which will later allow for quantitative comparison with experiments. As in Fig. 4B, we assume that the cell is constrained such that it cannot translate 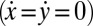 . The cell can still yaw, possibly being subject to an elastic restoring force
. The cell can still yaw, possibly being subject to an elastic restoring force 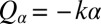 . This leaves only 3 degrees of freedom:
. This leaves only 3 degrees of freedom: 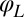 ,
,  , and α. Neglecting direct hydrodynamic interactions between the flagella, we can reduce the equations of motion for a clamped cell (Eq. 1 with constraint
, and α. Neglecting direct hydrodynamic interactions between the flagella, we can reduce the equations of motion for a clamped cell (Eq. 1 with constraint 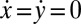 ) to a set of three coupled equations for the three remaining degrees of freedom:
) to a set of three coupled equations for the three remaining degrees of freedom:
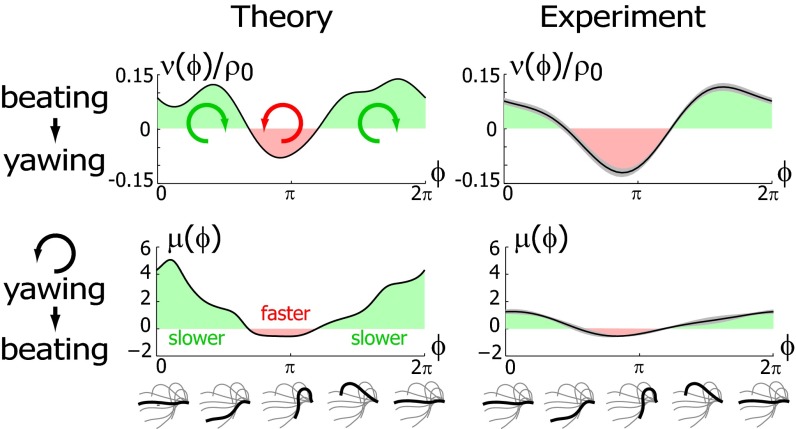
The coupling function μ in Eq. 2 characterizes the effect of cell-body yawing on the flagellar beat as detailed below, and ν describes how asynchronous flagellar beating results in yawing; ρ is the hydrodynamic friction coefficient for yawing of the whole cell. The coupling functions μ, ν, and ρ can be computed using our hydrodynamic model.* Their dependence on the flagellar phase is shown in Fig. 5 (Left). The physical significance of Eqs. 2–4 can be explained as follows. Eq. 2 implies that during the effective stroke of the left flagellum 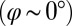 , a counter-clockwise rotation of the whole cell slows down the flagellar beat, whereas a clockwise rotation speeds it up (Fig. 5B,
, a counter-clockwise rotation of the whole cell slows down the flagellar beat, whereas a clockwise rotation speeds it up (Fig. 5B, 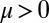 ). Eq. 3 implies the converse for the right flagellum. During the recovery stroke
). Eq. 3 implies the converse for the right flagellum. During the recovery stroke 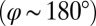 , the effect is opposite and a counter-clockwise rotation of the cell would speed up the beat of the left flagellum
, the effect is opposite and a counter-clockwise rotation of the cell would speed up the beat of the left flagellum 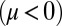 . Eq. 4 states that flagellar beating causes the cell body to yaw: If the right flagellum were absent, the model cell would rotate clockwise
. Eq. 4 states that flagellar beating causes the cell body to yaw: If the right flagellum were absent, the model cell would rotate clockwise 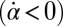 during the effective stroke of the left flagellum (Fig. 5A,
during the effective stroke of the left flagellum (Fig. 5A, 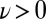 ), and counter-clockwise during its recovery stroke
), and counter-clockwise during its recovery stroke 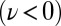 . This swimming behavior is observed for uniflagellar mutants (21). For synchronized beating of the two flagella, the right-hand side of Eq. 4 cancels to zero and the model cell swims straight. For asynchronous flagellar beating with a finite phase difference
. This swimming behavior is observed for uniflagellar mutants (21). For synchronized beating of the two flagella, the right-hand side of Eq. 4 cancels to zero and the model cell swims straight. For asynchronous flagellar beating with a finite phase difference 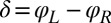 , the phase dependence of the coupling function
, the phase dependence of the coupling function 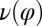 results in an imbalance of the torques generated by the left and right flagellum, respectively, which is balanced by a rotation of the whole cell.
results in an imbalance of the torques generated by the left and right flagellum, respectively, which is balanced by a rotation of the whole cell.
Fig. 5.
Flagellar beating and cell-body yawing are coupled in a bidirectional way. (Upper Left) In our theory, the beat of the left flagellum generates a torque, which, in the absence of the right flagellum, has to be counterbalanced by a yawing motion of cell body (Eq. 4). This effect is quantified by the coupling function 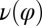 shown, normalized here by
shown, normalized here by 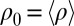 : The effective stroke
: The effective stroke 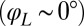 of the left flagellum causes the cell to yaw clockwise. (Lower Left) Conversely, yawing of the cell changes the hydrodynamic friction force that opposes the flagellar beat, which, in our theory, speeds up or slows down the beat (Eq. 2). This effect is quantified by the coupling function
of the left flagellum causes the cell to yaw clockwise. (Lower Left) Conversely, yawing of the cell changes the hydrodynamic friction force that opposes the flagellar beat, which, in our theory, speeds up or slows down the beat (Eq. 2). This effect is quantified by the coupling function 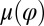 shown: a counter-clockwise yawing during the effective stroke of the left flagellum slows down its beat. The coupling of beating and yawing allows for flagellar synchronization in a free-swimming cell. (Right) By fitting Eqs. 2 and 4 to experimental time-series data, we can recover the coupling functions
shown: a counter-clockwise yawing during the effective stroke of the left flagellum slows down its beat. The coupling of beating and yawing allows for flagellar synchronization in a free-swimming cell. (Right) By fitting Eqs. 2 and 4 to experimental time-series data, we can recover the coupling functions 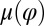 and
and 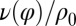 (1 cell,
(1 cell, 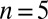 time series of 0.5-s duration; gray regions denote mean ± SE).
time series of 0.5-s duration; gray regions denote mean ± SE).
We study the dynamical system given by Eqs. 2–4 after a small perturbation of the synchronized state at 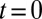 with initial flagellar phase difference
with initial flagellar phase difference 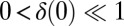 . For simplicity, we assume equal intrinsic beat frequencies,
. For simplicity, we assume equal intrinsic beat frequencies, 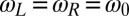 . The synchronization strength λ is given by
. The synchronization strength λ is given by 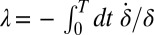 . In the limit of a small elastic constraint, we find (Supporting Information)
. In the limit of a small elastic constraint, we find (Supporting Information)
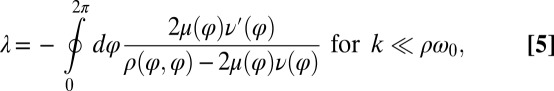 |
where a prime denotes differentiation with respect to φ. Using the coupling functions μ, ν, and ρ computed above, we obtain 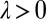 , which implies stable in-phase synchronization (Fig. 4). In the case of a stiff elastic constraint, we obtain a different result for λ:
, which implies stable in-phase synchronization (Fig. 4). In the case of a stiff elastic constraint, we obtain a different result for λ:
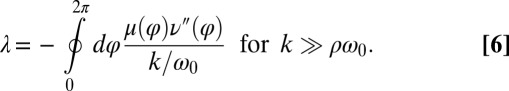 |
Synchronization in the absence of an elastic restoring force as characterized by Eq. 5, and synchronization involving a strong elastic coupling as characterized by Eq. 6 shows interesting differences, which relate to the fact that in the first case the flagellar phase dynamics depends only on the yawing rate 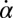 , but not on α itself. The difference between these two synchronization mechanisms is best illustrated in a special case, in which both the ratio
, but not on α itself. The difference between these two synchronization mechanisms is best illustrated in a special case, in which both the ratio 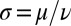 and ρ are constant. A constant σ correspond to an active flagellar driving force that does not depend on the flagellar phase, whereas for constant ρ the angular friction for yawing would not depend on the flagellar configuration. In the limit of a stiff elastic constraint,
and ρ are constant. A constant σ correspond to an active flagellar driving force that does not depend on the flagellar phase, whereas for constant ρ the angular friction for yawing would not depend on the flagellar configuration. In the limit of a stiff elastic constraint, 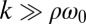 , we readily find
, we readily find 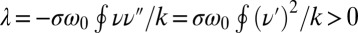 , which indicates stable in-phase synchronization. In the limit of a weak elastic constraint,
, which indicates stable in-phase synchronization. In the limit of a weak elastic constraint, 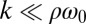 , however, the integral on the right-hand side of Eq. 5 evaluates to zero, which implies that synchronization does not occur. Hence, synchronization in the absence of an elastic restoring force requires that either
, however, the integral on the right-hand side of Eq. 5 evaluates to zero, which implies that synchronization does not occur. Hence, synchronization in the absence of an elastic restoring force requires that either 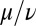 or ρ depend on the flagellar phase.
or ρ depend on the flagellar phase.
For our realistic Chlamydomonas model, μ and ν differ (Fig. 5A), and also ρ is not constant (Fig. S3). This allows for rapid synchronization also in the absence of elastic forces. Previous work on synchronization in minimal systems showed that elastic restoring forces can facilitate synchronization (11, 30). Here, we have shown that elastic forces can increase the synchronization strength (Fig. 4), but they are not required for flagellar synchronization in swimming Chlamydomonas cells, even if hydrodynamic interactions are neglected.
Our discussion of flagellar synchronization can be extended to the case, where the intrinsic beat frequencies of the two flagella do not match. If the frequency mismatch 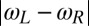 is small compared to the inverse time scale of synchronization
is small compared to the inverse time scale of synchronization 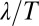 , a general result implies that the two flagellar oscillators will still synchronize (7). For a frequency mismatch that is too large, the two flagella display phase drift with a phase difference that increases monotonously (18).
, a general result implies that the two flagellar oscillators will still synchronize (7). For a frequency mismatch that is too large, the two flagella display phase drift with a phase difference that increases monotonously (18).
Experiments Show Coupling of Beating and Yawing.
We reconstructed the coupling functions 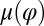 and
and 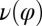 between beating and yawing from experimental data using the theoretical framework developed in the previous section. In brief, (i) we extracted the instantaneous yawing rate
between beating and yawing from experimental data using the theoretical framework developed in the previous section. In brief, (i) we extracted the instantaneous yawing rate 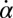 and flagellar phase speeds
and flagellar phase speeds 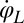 and
and 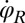 from high-speed videos of swimming Chlamydomonas cells, (ii) we represented the coupling functions by a truncated Fourier series, and (iii) we obtained the unknown Fourier coefficients by linear regression using Eqs. 2–4. The high temporal resolution of our imaging enabled us to accurately determine phase speeds as time derivatives of flagellar phase angle data. Fig. 5B displays averaged coupling functions obtained by fitting for a typical Chlamydomonas cell; fits for five more cells are shown in Figs. S6 and S7. We find a significant coupling between flagellar phase speeds and yawing rates, which are in good qualitative agreement with the theoretical predictions.
from high-speed videos of swimming Chlamydomonas cells, (ii) we represented the coupling functions by a truncated Fourier series, and (iii) we obtained the unknown Fourier coefficients by linear regression using Eqs. 2–4. The high temporal resolution of our imaging enabled us to accurately determine phase speeds as time derivatives of flagellar phase angle data. Fig. 5B displays averaged coupling functions obtained by fitting for a typical Chlamydomonas cell; fits for five more cells are shown in Figs. S6 and S7. We find a significant coupling between flagellar phase speeds and yawing rates, which are in good qualitative agreement with the theoretical predictions.
For the experimental conditions used, we commonly observed cells that displayed a large frequency mismatch between the two flagella. In the cells selected for analysis, this frequency mismatch exceeded 30%. This large frequency mismatch caused flagellar phase drift, which resulted in pronounced cell-body yawing and enabled us to accurately measure the coupling of yawing and flagellar beating. Experiments were done using either white-light illumination, which gave maximal image quality, or red-light illumination, which reduces a possible phototactic stimulation of the cells.
The observed modulation of flagellar phase speed according to the rate of yawing is consistent with a force–velocity dependence of flagellar beating, for which the speed of the beat decreases if the hydrodynamic load increases. We propose that a similar load characteristic of the flagellar beat holds also in cases of small frequency mismatch, where it allows for flagellar synchronization.
Conclusion and Outlook
We have presented a theory on the hydrodynamic coupling underlying flagellar synchronization in swimming Chlamydomonas cells. We have shown that direct hydrodynamic interactions between the two flagella as considered in refs. 9–11 give only a minor contribution to the computed synchronization strength and are unlikely to account for the rapid synchronization observed in experiments (16–19). In contrast, rotational motion of the swimmer caused by asynchronous beating imparts different hydrodynamic friction forces on the two flagella, which rapidly brings them back in tune: Chlamydomonas rocks to get into synchrony.
Using high-speed tracking experiments, we could confirm the two-way coupling between flagellar beating and cell-body yawing predicted by our theory. The striking reproducibility of our fits for the corresponding coupling functions and their favorable comparison to our theory is highly suggestive of a regulation of flagellar phase speed by hydrodynamic friction forces that depend on rotational motion. Thus, coupling of flagellar beating and cell-body yawing provides a strong candidate for the mechanism that underlies flagellar synchronization of swimming Chlamydomonas cells. A similar mechanism may account for synchronization in isolated flagellar pairs (31) (Fig. S8).
To explain a previously observed synchronization for cells held in a micropipette (17–19), we propose a finite clamping compliance that still allows for residual cell-body yawing with an amplitude of a few degrees, which is sufficient for rapid synchronization. Alternatively, a compliant basal anchorage of the flagellar pair or bending deformations of the elastic cell body would allow for flagellar synchronization by a completely analogous mechanism. In fact, the simple theory for biflagellar synchronization by rotational motion presented here (Eqs. 2–4) applies analogously to a pivoting motion of an elastically anchored flagellar pair (Figs. S9 and S10). From the observed value 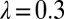 for the synchronization strength in clamped cells (19), we estimate a rotational stiffness of
for the synchronization strength in clamped cells (19), we estimate a rotational stiffness of 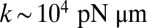 for either of these two cases.
for either of these two cases.
Finally, the coupling of two phase oscillators by a third degree of freedom, in this case rotational motion, could allow for synchronization also in other contexts. For example, one may consider that synchronization in ciliar arrays (2) is mediated by an elastic coupling through the matrix with elastic deformations playing the role of the third degree of freedom.
Materials and Methods
Hydrodynamic Computation of Swimming Chlamydomonas.
We represent a Chlamydomonas cell by an ensemble of 300 spheres of radius 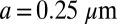 (Fig. 2A) and use a freely available hydrodynamic library based on a Cartesian multipole expansion technique (27) to compute the grand hydrodynamic friction matrix G (26) for this ensemble of spheres. We assume a rigid cell body, and hence that the spheres constituting the cell body move as a rigid unit, which results in
(Fig. 2A) and use a freely available hydrodynamic library based on a Cartesian multipole expansion technique (27) to compute the grand hydrodynamic friction matrix G (26) for this ensemble of spheres. We assume a rigid cell body, and hence that the spheres constituting the cell body move as a rigid unit, which results in 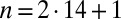 independently moving objects. The matrix G has dimensions
independently moving objects. The matrix G has dimensions 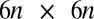 and relates the components of the translational and rotational velocities,
and relates the components of the translational and rotational velocities, 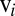 and
and 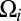 , of each of the n objects to the hydrodynamic friction forces and torques,
, of each of the n objects to the hydrodynamic friction forces and torques, 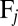 and
and 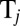 , exerted by the j-th object on the fluid,
, exerted by the j-th object on the fluid, 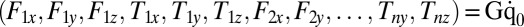 with
with 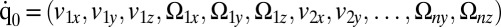 . Fig. 2 C and D shows a submatrix of G that relates force and velocity components parallel to the long axis of the cell body. The reduced friction matrix
. Fig. 2 C and D shows a submatrix of G that relates force and velocity components parallel to the long axis of the cell body. The reduced friction matrix 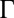 for a set of m effective degrees of freedom q is computed from G as
for a set of m effective degrees of freedom q is computed from G as 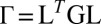 with
with 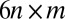 transformation matrix
transformation matrix 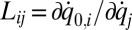 , where
, where 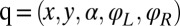 (13). Initial tests confirmed that the friction matrix of only the cell body gave practically the same result as the analytic solution for the enveloping spheroid; similarly, the computed friction matrix of only a single flagellum matched the prediction of resistive force theory (26).
(13). Initial tests confirmed that the friction matrix of only the cell body gave practically the same result as the analytic solution for the enveloping spheroid; similarly, the computed friction matrix of only a single flagellum matched the prediction of resistive force theory (26).
Imaging Chlamydomonas Swimming in a Shallow Observation Chamber.
For cell culture, C. reinhardtii cells (CC-125 wild-type mt+ 137c, R. P. Levine via N. W. Gillham, 1968) were grown in 300 mL TAP+P buffer (32) (with 4× phosphate) at 24 °C for 2 d under conditions of constant illumination (two 75-W fluorescent bulbs) and constant air bubbling to a final density of 106 cells/mL.
For high-speed video microscopy, an assay chamber was made of precleaned glass and sealed using Valap, a 1:1:1 mixture of lanolin, paraffin, and petroleum jelly, heated to 70 °C. The surface of that chamber was blocked using casein solution (solution of casein from bovine milk, 2 mg/mL, for 10 min) prior to the experiment. Single, noninteracting cells were visualized using phase-contrast microscopy set up on a Zeiss Axiovert 100 TV Microscope using a 63× Plan-Apochromat NA1.4 PH3 oil lens in combination with an 1.6× tube lens and an oil phase-contrast condenser N.A. 1.4. The sample was illuminated using a 100-W tungsten lamp. For red-light imaging, an e-beam-driven luminescent light pipe (Lumencor) with spectral range of 640–657 nm and power of 75 mW was used. The sample temperature was kept constant at 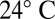 using an objective heater (Chromaphor). For image acquisition, an EoSens Cmos high-speed camera was used. Videos were acquired at a rate of 1,000 frames per second with exposure times of 1 ms (white light) and 0.6 ms (red light). Finally, cell positions and flagellar shapes were tracked using custom-build Matlab software (Supporting Information gives details).
using an objective heater (Chromaphor). For image acquisition, an EoSens Cmos high-speed camera was used. Videos were acquired at a rate of 1,000 frames per second with exposure times of 1 ms (white light) and 0.6 ms (red light). Finally, cell positions and flagellar shapes were tracked using custom-build Matlab software (Supporting Information gives details).
Supplementary Material
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
*Specifically, 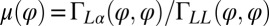 ,
, 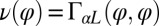 ,
, 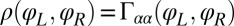 . For simplicity, the active flagellar driving forces were approximated as
. For simplicity, the active flagellar driving forces were approximated as 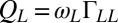 and
and 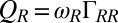 for constrained translational motion.
for constrained translational motion.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1300895110/-/DCSupplemental.
References
- 1.Alberts B, et al. Molecular Biology of the Cell. 4th Ed. New York: Garland Science; 2002. [Google Scholar]
- 2.Sanderson MJ, Sleigh MA. Ciliary activity of cultured rabbit tracheal epithelium: beat pattern and metachrony. J Cell Sci. 1981;47:331–347. doi: 10.1242/jcs.47.1.331. [DOI] [PubMed] [Google Scholar]
- 3.Gray J. Ciliary Movements. Cambridge, UK: Cambridge Univ Press; 1928. [Google Scholar]
- 4.Osterman N, Vilfan A. Finding the ciliary beating pattern with optimal efficiency. Proc Natl Acad Sci USA. 2011;108(38):15727–15732. doi: 10.1073/pnas.1107889108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Elgeti J, Gompper G. Emergence of metachronal waves in cilia arrays. Proc Natl Acad Sci USA. 2013;110(12):4470–4475. doi: 10.1073/pnas.1218869110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Brennen C, Winet H. Fluid mechanics of propulsion by cilia and flagella. Annu Rev Fluid Mech. 1977;9:339–398. [Google Scholar]
- 7.Pikovsky A, Rosenblum M, Kurths J. Synchronization. Cambridge, UK: Cambridge Univ Press; 2001. [Google Scholar]
- 8.Taylor GI. Analysis of the swimming of microscopic organisms. Proc R Soc Lond A Math Phys Sci. 1951;209(1099):447–461. [Google Scholar]
- 9.Gueron S, Levit-Gurevich K. Energetic considerations of ciliary beating and the advantage of metachronal coordination. Proc Natl Acad Sci USA. 1999;96(22):12240–12245. doi: 10.1073/pnas.96.22.12240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Vilfan A, Jülicher F. Hydrodynamic flow patterns and synchronization of beating cilia. Phys Rev Lett. 2006;96(5):058102. doi: 10.1103/PhysRevLett.96.058102. [DOI] [PubMed] [Google Scholar]
- 11.Niedermayer T, Eckhardt B, Lenz P. Synchronization, phase locking, and metachronal wave formation in ciliary chains. Chaos. 2008;18(3):037128. doi: 10.1063/1.2956984. [DOI] [PubMed] [Google Scholar]
- 12.Golestanian R, Yeomans JM, Uchida N. Hydrodynamic synchronization at low Reynolds number. Soft Matter. 2011;7:3074. [Google Scholar]
- 13.Friedrich BM, Jülicher F. Flagellar synchronization independent of hydrodynamic interactions. Phys Rev Lett. 2012;109(13):138102. doi: 10.1103/PhysRevLett.109.138102. [DOI] [PubMed] [Google Scholar]
- 14.Bennett RR, Golestanian R. Emergent run-and-tumble behavior in a simple model of Chlamydomonas with intrinsic noise. Phys Rev Lett. 2013;110(14):148102. doi: 10.1103/PhysRevLett.110.148102. [DOI] [PubMed] [Google Scholar]
- 15.Polotzek K, Friedrich BM. A three-sphere swimmer for flagellar synchronization. New J Phys. 2013;15(4):045005. [Google Scholar]
- 16.Rüffer U, Nultsch W. High-speed cinematographic analysis of the movement of Chlamydomonas. Cell Motil. 1985;5(3):251–263. [Google Scholar]
- 17.Rüffer U, Nultsch W. Flagellar coordination in Chlamydomonas cells held on micropipettes. Cell Motil Cytoskeleton. 1998;41(4):297–307. doi: 10.1002/(SICI)1097-0169(1998)41:4<297::AID-CM3>3.0.CO;2-Y. [DOI] [PubMed] [Google Scholar]
- 18.Polin M, Tuval I, Drescher K, Gollub JP, Goldstein RE. Chlamydomonas swims with two “gears” in a eukaryotic version of run-and-tumble locomotion. Science. 2009;325(5939):487–490. doi: 10.1126/science.1172667. [DOI] [PubMed] [Google Scholar]
- 19.Goldstein RE, Polin M, Tuval I. Noise and synchronization in pairs of beating eukaryotic flagella. Phys Rev Lett. 2009;103(16):168103. doi: 10.1103/PhysRevLett.103.168103. [DOI] [PubMed] [Google Scholar]
- 20.Tam D, Hosoi AE. Optimal feeding and swimming gaits of biflagellated organisms. Proc Natl Acad Sci USA. 2011;108(3):1001–1006. doi: 10.1073/pnas.1011185108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Bayly PV, et al. Propulsive forces on the flagellum during locomotion of Chlamydomonas reinhardtii. Biophys J. 2011;100(11):2716–2725. doi: 10.1016/j.bpj.2011.05.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.O’Malley S, Bees MA. The orientation of swimming biflagellates in shear flows. Bull Math Biol. 2012;74(1):232–255. doi: 10.1007/s11538-011-9673-1. [DOI] [PubMed] [Google Scholar]
- 23.Brokaw CJ. Effects of viscosity and ATP concentration on the movement of reactivated sea-urchin sperm flagella. J Exp Biol. 1975;62(3):701–719. doi: 10.1242/jeb.62.3.701. [DOI] [PubMed] [Google Scholar]
- 24.Garcia M, Berti S, Peyla P, Rafaï S. Random walk of a swimmer in a low-Reynolds-number medium. Phys Rev E Stat Nonlin Soft Matter Phys. 2011;83(3 Pt 2):035301. doi: 10.1103/PhysRevE.83.035301. [DOI] [PubMed] [Google Scholar]
- 25.Hunt AJ, Gittes F, Howard J. The force exerted by a single kinesin molecule against a viscous load. Biophys J. 1994;67(2):766–781. doi: 10.1016/S0006-3495(94)80537-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Happel J, Brenner H. Low Reynolds Number Hydrodynamics. Boston: Kluwer; 1965. [Google Scholar]
- 27.Hinsen K. HYDR0LIB : A library for the evaluation of hydrodynamic interactions in colloidal suspensions. Comput Phys Commun. 1995;88(2-3):327–340. [Google Scholar]
- 28.Racey TJ, Hallett R, Nickel B. A quasi-elastic light scattering and cinematographic investigation of motile Chlamydomonas reinhardtii. Biophys J. 1981;35(3):557–571. doi: 10.1016/S0006-3495(81)84812-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Guasto JS, Johnson KA, Gollub JP. Oscillatory flows induced by microorganisms swimming in two dimensions. Phys Rev Lett. 2010;105(16):168102. doi: 10.1103/PhysRevLett.105.168102. [DOI] [PubMed] [Google Scholar]
- 30.Reichert M, Stark H. Synchronization of rotating helices by hydrodynamic interactions. Eur Phys J E Soft Matter. 2005;17(4):493–500. doi: 10.1140/epje/i2004-10152-7. [DOI] [PubMed] [Google Scholar]
- 31.Hyams JS, Borisy GG. Flagellar coordination in Chlamydomonas reinhardtii: isolation and reactivation of the flagellar apparatus. Science. 1975;189(4206):891–893. doi: 10.1126/science.1098148. [DOI] [PubMed] [Google Scholar]
- 32.Gorman DS, Levine RP. Cytochrome f and plastocyanin: their sequence in the photosynthetic electron transport chain of Chlamydomonas reinhardi. Proc Natl Acad Sci USA. 1965;54(6):1665–1669. doi: 10.1073/pnas.54.6.1665. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.