Case-only method for cause-specific hazards models with application to assessing differential vaccine efficacy by viral and host genetics

Abstract

Cause-specific proportional hazards models are commonly used for analyzing competing risks data in clinical studies. Motivated by the objective to assess differential vaccine protection against distinct pathogen types in randomized preventive vaccine efficacy trials, we present an alternative case-only method to standard maximum partial likelihood estimation that applies to a rare failure event, e.g. acquisition of HIV infection. A logistic regression model is fit to the counts of cause-specific events (infecting pathogen type) within study arms, with an offset adjusting for the randomization ratio. This formulation of cause-specific hazard ratio estimation permits immediate incorporation of host-genetic factors to be assessed as effect modifiers, an important area of vaccine research for identifying immune correlates of protection, thus inheriting the estimation efficiency, and cost benefits of the case-only estimator commonly used for assessing gene–treatment interactions. The method is used to reassess HIV genotype-specific vaccine efficacy in the RV144 trial, providing nearly identical results to standard Cox methods, and to assess if and how this vaccine efficacy depends on Fc-γ receptor genes.

1. Introduction

Competing risks data occur in medical studies when there are multiple causes of a failure event. For estimating covariate effects on cause-specific hazard functions, a standard analysis approach uses a proportional hazards model (Prentice and others, 1978). An example of cause-specific hazards modeling includes assessment of how vaccine protection varies against distinct circulating pathogen types in preventive vaccine efficacy (VE) trials (Gilbert and others, 1998; Gilbert, 2000). This type of analysis, termed “sieve analysis” (Gilbert and others, 1998), was an important component of assessing immune correlates of protection in a recent HIV VE trial (Rolland and others, 2012). This trial, namely the RV144 trial, randomized 16 395 HIV negative volunteers to receive an HIV vaccine regimen or placebo regimen over a 24-week period, and monitored participants for the primary endpoint of HIV infection (Rerks-Ngarm and others, 2009). The primary analysis assessed VE against HIV infection with any viral genotype using the standard Cox model, and a secondary sieve analysis assessed VE against HIV infection with particular HIV genotypes defined by match or mismatch to the HIV strains represented in the vaccine construct at HIV Envelope amino acid positions 169 or 181. The standard cause-specific Cox model (Prentice and others, 1978) was used to assess VE against the particular HIV genotypes, and a simple augmented data extension of this model was used to compare the genotype-specific VEs (Lunn and McNeil, 1995).

In this article, we present a novel and easily implementable method for estimating pathogen type or strain-specific VE in vaccine trials, which also applies to general clinical trials with rare competing risks failure time endpoints. As does the method of Gilbert and others (1998), the proposed method ignores failure times and is based on counts of HIV infections in vaccine and placebo recipients. The difference is, rather than using a multinomial logistic regression (MLR) model, we regress the vaccine or placebo assignment on the indicator of a specific virus strain, which allows the inference of interest without the restrictive proportional baseline hazard assumption. Because HIV infection is a rare event in preventive HIV VE trials, ignoring the failure times leads to minimal, if not negligible, loss of statistical precision for estimating treatment effects.

Our formulation of strain-specific vaccine effects resembles the case-only estimator widely used to estimate gene–environment interactions or gene–treatment interactions (Piegorsch and others, 1994; Vittinghoff and Bauer, 2006; Dai and others, 2012). Indeed, we show that the strain-specific VE within a host-genetic subgroup can be estimated similarly in this form of case-only estimator, exploiting the independence between treatment assignment and host genes. This development of competing risks modeling contributes to HIV vaccine research, because assessing if and how vaccine protection against HIV infection varies with viral and host genotypes helps to better understand the mechanisms of vaccine protection and to design more efficacious HIV vaccines in the future. Beyond HIV vaccine trials, the niche for the method is clinical trials with rare competing risks failure time endpoints for which it is of interest to assess treatment effects in expensive-to-identify subgroups, for which the case-only method is highly appealing for its statistical and measurement efficiency.

2. Case-only method for cause-specific competing risks models with rare events

2.1. Background and existing methods

Consider an observed continuous failure time T with a failure cause J, where J is a discrete categorical variable with m possible levels, 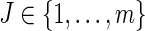; T can be viewed as the minimum of the latent failure times 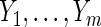corresponding to each type of the m causes. We are interested in the effect of a randomized binary treatment indicator Z ( 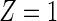denotes the treatment condition and 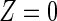denotes the control condition) on the m cause-specific hazard functions (Prentice and others, 1978), defined by

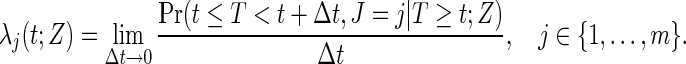Suppose that there is right censoring in the failure time. Let C denote the censoring time, and the data consist of independent and identically distributed observations 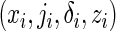for 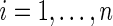study subjects, where z_i is the treatment assignment, x_i is the minimum of the failure time t_i and the censoring time c_i, δ_i is the censoring indicator with 1 indicating a failure event, and j_i is the cause of the failure if 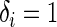and arbitrarily defined otherwise. We assume the usual independent censoring mechanism for the minimum cause-specific failure time, i.e.

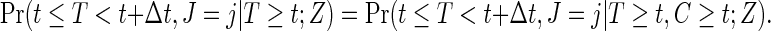(2.1)

Assume a proportional cause-specific hazards model for the effect of Z,

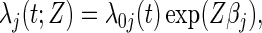(2.2)

where β_j is the vaccine effect expressed as the cause-j specific log hazard ratio and 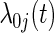is an arbitrary baseline hazard function for cause j. In preventive VE trials, the competing causes are J pathogen strains circulating in the geographic region of the trial that study participants may be exposed to and hence acquire. The parameter of interest is VE to reduce susceptibility to infection with strain j, typically defined as 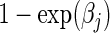. Based on data from all n subjects, the usual Cox partial likelihood can be employed to estimate β_j, treating failures of all other causes as being censored. A data duplication method can be used to simultaneously estimate differences 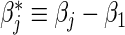for j=2,…,m, and hence to estimate ratios of strain-specific vaccine versus control relative risks (Lunn and McNeil, 1995; Gilbert, 2000). In the simplest case with two failure types, for each observed failure or censoring event two records are created: one for the observed failure type, and one for the other failure type but coded as being censored. Both β_j and 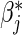are useful for understanding strain variations in vaccine protection. In addition, these methods may be implemented with the additional assumption of proportional baseline cause-specific hazards (Holt, 1978; Prentice and others, 1978; Lunn and McNeil, 1995),

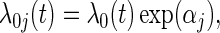(2.3)

which may provide more efficient estimation of β_j and 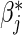, along with estimation of α_j.

A convenient feature following the proportional baseline hazard assumption is that, ignoring the failure time data, the relative treatment effect 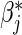, and the relative baseline hazard ratio, defined as 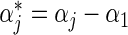, can be estimated using an MLR model,

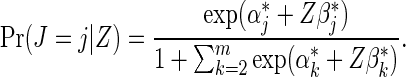(2.4)

Only count data from failure cases are used in this estimation. Gilbert and others (1998) developed assumptions under which the MLR model can be used to estimate ratios of strain-specific hazard ratios, based on counts of infecting strains from vaccine and placebo recipients. The proportional baseline cause-specific hazard ratio assumption made by this model can be overly restrictive; for example, the assumption would be violated if the relative prevalence of different circulating viral strains exposing trial participants shifts during the follow-up period of a vaccine trial. In HIV vaccine trials, the comparison of the above failure time and counts-only estimation methods suggested that optimal evaluation of strain-specific VE will not require the knowledge of infection times (Gilbert, 2000).

2.2. Case-only method for assessing strain-specific vaccine effects

In the rare event setting and as an alternative counts-only method to the MLR model, cause-specific treatment effects can be estimated by a case-only type of estimator, incorporating the randomization ratio to treatment and control. The probability of treatment assignment for a failure event with cause j occurring at time t can be expressed as

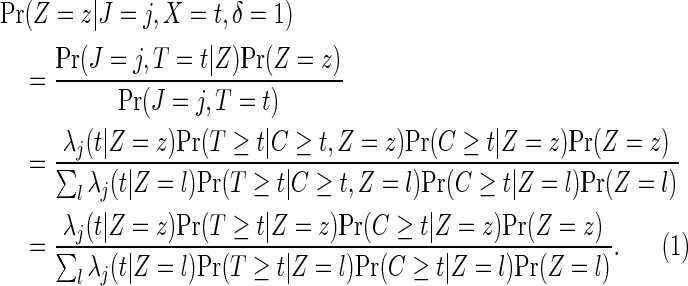(2.5)

The last equation (2.5) holds because of (2.1), since

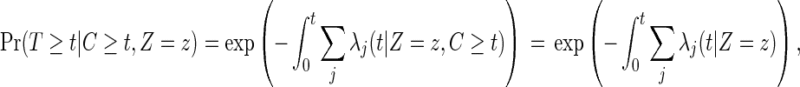where 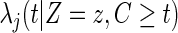is defined as

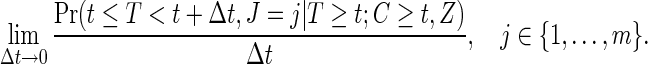If the failure event is rare, 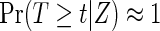for all t, and the censoring time C is independent of treatment assignment Z, it follows that

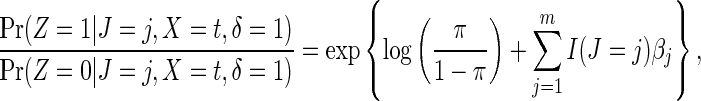(2.6)

where π is the probability a trial participant is randomized to the vaccine arm and 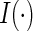is an indicator function. This result suggests that the cause-specific hazard ratio can be estimated by a simple logistic model regressing Z on m indicator variables 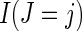among participants who have an event, entering 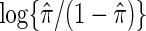as an offset, where 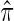is the fraction of randomized subjects assigned to the vaccine arm. Reparameterization of β_j to 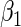and 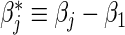enables the estimation of ratios of strain-specific hazard ratios. The variance of the estimated β_j can be estimated by the inverse of the observed information matrix derived from (2.6). Advantageously, compared with the MLR model (2.4), the proportional baseline hazards assumption (2.3) is not needed in (2.6); both the strain-specific treatment effect β_j and the relative treatment effect 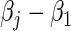are directly estimated.

2.3. Case-only method for assessing strain-specific vaccine effects within host-genetic subgroups

The estimator derived in (2.6) is analogous to case-only estimators for assessing gene–treatment interactions in randomized clinical trials (Vittinghoff and Bauer, 2006; Dai and others, 2012). See, for example, (Dai and others, 2012, Appendix), where the treatment assignment is regressed on the genetic factor among all disease cases with the logarithm of the randomization ratio as an offset. The case-only estimator of gene–treatment interaction is nearly as efficient as the full cohort analysis with all participants being genotyped, and is much more efficient than the case-cohort approach (Vittinghoff and Bauer, 2006). In vaccine research, host-genetic subgroup analysis is of keen interest for assessing strain-specific vaccine protection, as certain host genes may be required for the vaccine to stimulate immune responses protective against certain pathogen strains. Interestingly, as we discuss next, this case-only formulation of cause-specific treatment effects permits straightforward incorporation of host-genetic factors as effect modifiers, such that strain-specific genetic-subgroup treatment effects can be estimated efficiently and economically.

In addition to the data 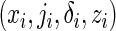previously defined, suppose that a host-genetic factor G is ascertained for all cases, with 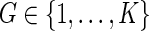. Interest is in estimating VE against the 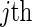viral strain in the 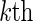host-genetic subgroup. Define the cause-specific hazard function for the 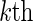subgroup to be

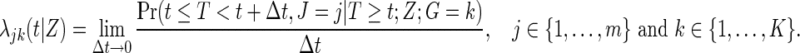For the j strain-specific vaccine effect in the subgroup k, assume a proportional cause-specific hazards model:

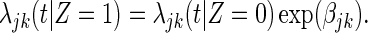We assume the usual independent censoring similar to (2.1), now conditional on both Z and G. For every failure event, observe that

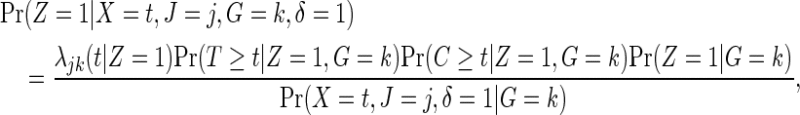because of independent censoring. By randomization, Z is independent of G, so that 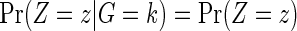. If the failure event is rare and the censoring time C is independent of treatment assignment in each genetic subgroup, it follows that

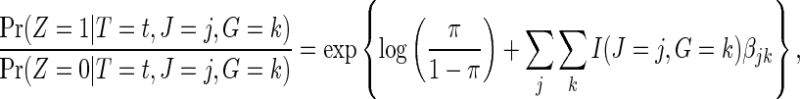(2.7)

where π is the fraction assigned to the vaccine arm. Therefore, the strain-specific vaccine effect among host-genetic subgroups can be obtained by fitting a logistic regression in all infected participants, in which the randomized assignment is regressed on the indicator variable 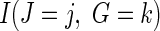and 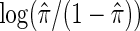is treated as an offset. As for previous case-only methods (Piegorsch and others, 1994; Dai and others, 2012), a vital assumption is Z being independent of G, which holds in randomized studies.

3. An example: the RV144 trial

RV144, a randomized double-blind preventive HIV VE trial conducted by the US Military HIV Research Program and the Thai Ministry of Health in Thailand, was the first HIV vaccine trial to show positive VE to prevent HIV infection, estimated at 31.2% using the standard Cox model (Rerks-Ngarm and others, 2009). In vaccine recipients, levels of vaccine-induced IgG binding antibodies to the V1–V2 region of the HIV Envelope protein measured 2 weeks after the vaccinations were inversely correlated with the subsequent rate of HIV infection (Haynes and others, 2012). This generated the hypothesis that V1–V2-directed antibodies played a role in the modest level of protection observed, and, to help test this hypothesis, HIV viral sequences in the V1–V2 region were measured at the time of HIV infection diagnosis and compared among vaccine and placebo recipients. For each of eight preselected amino acid positions in V1–V2 (Rolland and others, 2012), two causes of HIV infection were considered: 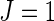() is infection with an HIV with matching (mismatching) the residue at the same site in the vaccine construct. Using the standard competing risks data fitting approach (Lunn and McNeil, 1995), Rolland and others (2012) found that VE was significantly different when comparing matched HIV with mismatched HIV at amino acid positions 169 and 181 (Table 1). Biological interpretation of these findings, including the unexpected sieve effect against 181 mismatched HIV, was discussed in Rolland and others (2012).

Table 1.

Comparison of the case-only estimator (2.6) and the estimator using failure time data (Lunn and McNeil, 1995) in the RV144 trial

	Failure time data (Lunn and McNeil, 1995)				Case-only data (2.6)
	VE† (%)	95% CI	p-value‡	p-value§	VE† (%)	95% CI	p-value‡	p-value§
169 match	47.57	(18.42, 66.30)	0.0036	—	47.37	(18.11, 66.17)	0.0044	—
Mismatch	−54.80	(−257.6, 33.00)	0.3000	0.0342	−55.56	(−100, 32.67)	0.3011	0.0249
181 match	17.02	(−26.2, 45.46)	0.3800	—	16.67	(−26.78, 45.22)	0.3944	—
Mismatch	77.85	(34.54, 92.50)	0.0028	0.0237	77.78	(34.35, 92.48)	0.0065	0.0257

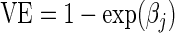^† as defined in (2.2).

^‡p-value assessing the significance of strain-specific VE.

^§p-value comparing VE between two virus strains.

Here, we fit the case-only logistic model (2.6) considering position 169 and 181 separately, and we compare the results to those of Rolland and others (2012) (Table 1). For each position, the estimates of VE, the 95% confidence intervals, and the p-values comparing VE between the two virus strains are all numerically close, suggesting that the case-only estimation in (2.6) yields similar results as the full failure time approach in Lunn and McNeil (1995). The reason is that, in the RV144 trial, the HIV infection rate over the 3.5-year follow-up period was well below 1% in both randomized arms, rendering the rare disease approximation in the derivation of (2.6) quite satisfactory.

Many IgG antibody functions depend on Fc-γ receptor genetics, and therefore it was of interest to assess whether and how strain-specific VE was modified by host-genetic subgroups defined by single nucleotide polymorphisms (SNPs) covering the five Fc-γ receptor genes Fc-γR2a, Fc-γR2b, Fc-γR2c, Fc-γR3a, and Fc-γR3b. For all 125 of the RV144 cases, 148 SNPs covering these receptors were genotyped. SNPs that have minor allele frequency 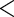5% or highly correlated with another SNP (Pearson correlation 0.80) were screened out, leaving 21 SNPs for analysis. See Li and others (2013) for details about how the SNPs were measured and screened. For each SNP, the case-only method was applied to estimate VE against 169 matched HIV and against 181 mismatched HIV, which were the two strains with evidence of positive VE in Table 1, with main questions of interest whether and how VE differed by SNP levels. Table 2 shows the strain-specific VE estimates in genetic subgroup defined by three SNPs, as an example. After adjusting for multiple testing among 21 Fc-γ receptor SNPs against 169 matched and 181 mismatched viral strains (42 tests in total), the VE against 169 matched virus strain in participants who carry CT or TT in the SNP rs138747765 of Fc-γ receptor 2c gene appears significantly different from the VE in participants with CC genotype (91% vs 15%, FWER-adjusted p-value 0.0414). FWER-adjusted p-values were computed using the resampling method (Westfall and Young, 1993). The protection conferred by the vaccine regimen appeared restricted to 169 matched viruses, and the present result suggests that this 169 matched protection was stronger in or restricted to the SNP rs138747765 CT/TT genotype subgroup. Results for all SNPs are presented in Li and others (2013).

Table 2.

Strain-specific VE in several host-genetics subgroups in the RV144 trial

SNP	Genotype	VE (%)	95% CI	p-value†	p-value‡	Adjusted p-value§
169 match virus strain
Fc-γR2b/rs145835719	CC	32.50	(−9.98, 58.57)	0.1146	—	—
	CA/AA	82.35	(39.78, 94.83)	0.0056	0.0465	0.5826
Fc-γR2c/rs138747765	CC	15.15	(−40.40, 48.72)	0.5225	—	—
	CT/TT	90.91	(61.34, 97.86)	0.0012	0.0043	0.0414
Fc-γR3a/rs147342954	GG	60.98	(30.46, 78.1)	0.0014	—	—
	GA/AA	12.50	(−79.28,57.29)	0.7152	0.0857	0.8186
181 mismatch virus strain
Fc-γR2b/rs145835719	CC	66.67	(−3.35, 89.25)	0.0571	—	—
	CA/AA	100	(−100,100)	0.9944	0.9948	1
Fc-γR2c/rs138747765	CC	69.23	(5.63, 89.97)	0.0393	—	—
	CT/TT	100	(−100,100)	0.9961	0.9963	1
Fc-γR3a/rs147342954	GG	84.62	(31.82, 96.53)	0.0137	—	—
	GA/AA	50	(−100,90.84)	0.4235	0.3062	0.9999

^†p-value assessing the significance of strain-specific VE within a genetic subgroup.

^‡p-value comparing strain-specific VE between two genetic subgroups.

^§p-value adjusting for the family-wise error rate.

4. Discussion

The rare disease assumption is required for the approximation in (2.6) so that Pr(T≥t|Z=1)/Pr(T≥t|Z=0)≈1, and similarly in (2.7) that Pr(T≥t|Z=1,G=k)/Pr(T≥t|Z=0,G=k)≈1. A similar approximation was made for the case-only estimator for assessing gene–treatment interactions. In a simulation study, Vittinghoff and Bauer (2006) showed that the bias and the type I error of the case-only estimator are satisfactory when the cumulative event rate is 10% or less. This suggests that the proposed case-only methods are quite applicable to current HIV prevention trials, in which the infection probability during the follow-up is typically much lower than 10%.

In addition to the usual independent censoring assumption for standard Cox proportional hazards models, as the full cohort analysis would require, the case-only methods also require that censoring is independent of treatment assignment Z (2.6), possibly conditional on the host genotype G (2.7). This is quite plausible in the placebo-controlled, double-blind vaccine trials. If it is questionable, censoring being independent of treatment assignment Z can always be verified by a log-rank test comparing censoring between treatment arms. Testing censoring being independent of Z given G, however, would require genotypic data in all participants or a random subset, and thus is not feasible for a host-genetic study with only cases genotyped. If censoring is indeed differential between arms, one may add an estimated adjustment factor 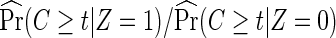in (2.6), and similarly 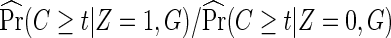in (2.7).

If the required conditions are met, case-only methods yield nearly equivalent estimators to those derived from the full cohort analysis where every participant is measured for expensive subgroup variables (Vittinghoff and Bauer, 2006). The niche for the case-only method is clinical trials with rare competing risks failure time endpoints, e.g. HIV vaccine trials we presented here. Other applications include trials with rare but serious adverse events, and the interest is in finding patient subgroups that suffer from these adverse events. For such settings the case-only method is appealing for its statistical efficiency and for minimizing the number of subjects from whom the requisite expensive subgroup covariates are measured.

Funding

This work was supported by National Institute of Health [grant number P01 CA53996 and R01 HL114901 to J.Y.D., 2 R37 AI054165-10 to P.B.G.].