Temperature sculpting in yoctoliter volumes

Abstract

The ability to perturb large ensembles of molecules from equilibrium led to major advances in understanding reaction mechanisms in chemistry and biology. Here, we demonstrate the ability to control, measure, and make use of rapid temperature changes of fluid volumes that are commensurate with the size of single molecules. The method is based on attaching gold nanoparticles to a single nanometer-scale pore formed by a protein ion channel. Visible laser light incident on the nanoparticles causes a rapid and large increase of the adjacent solution temperature, which is estimated from the change in the nanopore ionic conductance. The temperature shift also affects the ability of individual molecules to enter into and interact with the nanopore. This technique could significantly improve sensor systems and force measurements based on single nanopores, thereby enabling a method for single molecule thermodynamics and kinetics.

Introduction

The equilibrium state of a chemical or biological system is determined by many physical and chemical variables. Changes in one or more of these drives the system to a new steady state and relaxation time measurements can provide information about its properties. Recent work suggests that the behavior of molecules along the reaction pathway and the inter- and intramolecular dynamics are best obtained using single molecule measurement techniques ^1-6. A less explored regime involves the isolation of the thermodynamic perturbation (e.g., temperature, pressure, chemical binding) on a single molecule and the subsequent observation of that same molecule. This represents the ultimate sensitivity in reaction measurements because it isolates the internal degrees of freedom of a single molecule.

Over the last century, a variety of techniques were developed to measure reaction rates in chemistry and biology. The most influential of these techniques relied on rapid mixing of reactant solutions (e.g., continuous flow/quenched flow ⁷, and stopped-flow methods ⁸). In the latter, solutions containing different molecular species are driven into a mixing chamber within milliseconds, and the flow of reactants is abruptly stopped. The progress of the reaction is then monitored by following either an optical property (e.g., absorption ⁹, circular dichroism ¹⁰, and fluorescence emission ¹¹), the NMR signature of a reactant ¹², or calorimetry ¹³. The stopped-flow method has been a seminal tool to probe enzyme activity kinetics ¹⁴, protein folding ¹⁵, proton pumping ¹⁶, polymerization ¹⁷, and drug interactions ¹⁸. The technique was initially limited to reactions that proceed with relatively slow time constants (τ > 1 s) ¹⁹. However, variations on techniques to deliver the reactants in different ratios ²⁰, and the ability to mix liquids together more rapidly promises to enhance the method’s utility and increase its bandwidth ²¹.

Other techniques were developed to study more rapid chemical and polymer kinetics. These include microfluidic ²² and nanofluidic ²³ mixing, and relaxation methods that rapidly perturb a system from equilibrium by changes in pressure, or local chemical species concentration induced by pulses of laser light ^9,24, ionic current ²⁵, electrostatic potential ²⁶, or mechanical force ^27-29. The latter three methods allowed for kinetic analysis at the molecular (nanometer) length scale.

In the late 1950s, a novel method to rapidly perturb the solution temperature (T-jump) ³⁰ provided yet another means to measure what were considered at the time to be “immeasurably fast” diffusion-controlled reactions ³¹. In the early T-jump studies, the discharge of capacitors rapidly heated relatively large volumes of solution in microseconds ^30,31. Rapid heating technology was brought to the nanosecond domain with Q-switched lasers ^32-34, and the temperature was estimated via a change in the optical absorbance of a tracer molecule ³⁵. Infrared absorbing dyes ³⁶ or thin metal films ³⁷were used to convert laser energy into heat over picosecond timescales , which enabled the study of protein unfolding (e.g., RNaseA) ³⁸ and folding (e.g., apomyoglobin) ³⁹ or interfacial electron transfer reactions ^40,41. More recently, an infrared laser (1445 nm) was used to directly excite an OH-stretch mode in water, leading to increase the temperature of picoliter volumes.⁴²

Most of these laser-based techniques require post processing (i.e., pump-probe, fluorescence lifetime) to deduce the local temperature changes, which limits the ability to accurately measure the solution temperature in real time. In addition, each pulse from a Q-switched ultrafast laser represents an entire experiment, where the solution temperature initially increases to a predefined value and then relaxes to room temperature. A major improvement in the technique would expand the laser induced T-jump method to longer timescales in which a complex temporal profile of the temperature could be precisely controlled. This requires a much more localized heat source and the means to estimate the temperature of exceptionally small fluid volumes. The capability demonstrated below represents a first step towards this goal, and is achieved using a combination of gold nanoparticles and single nanometer-scale pores.

The highly confined surface plasmon resonance effect ^43-45 in gold nanoparticles enhances the absorption of light by the particle, thereby increasing its temperature ^44,46-49 essentially instantaneously (i.e., ps to ns timescales) compared to heating water with an infrared laser (μs to ms timescales) ^42,50, a property that has been used in many bio-related applications including imaging ^48,49,51, and cancer therapies ^51-53. We show here that by attaching gold nanoparticles to individual nanometer-scale pores, and optically exciting the plasmon mode of the nanoparticles, the time dependence of the pore solution temperature can be controlled. It follows that the temporal temperature profile can be sculpted and estimated, in real-time, via the change in the nanopore ionic conductance. The temperature change is highly localized near the pore, which allows the nanopore to probe the thermodynamic and kinetic properties of single molecules.

Experimental Section

Modification of Au nanoparticles and N293C

Forty nm diameter Au nanoparticles were attached to a genetically engineered version of the pore forming protein α-hemolysin, N293C, with high melting temperature DNA oligonucleotides (T_m ~ 120 °C). Ten μL of 3.4 mM disulfide-protected DNA1 (5′-(5′-thiol)-GCGGCGCTCGCGGGCGCTGCGGCGGCGGCG-3′) and its complimentary strand DNA2 (5′-(5′-thiol)-CGCCGCCGCCGCAGCGCCCGCGAGCGCCGC-3′) (Midland Certified Reagent Company, Midland, TX) in TE buffer (10 mM tris, 1 mM EDTA at pH 8.25), was mixed with 10 μL of 0.1 M dithiothreitol (DTT) and allowed to react at room temperature for 30 min. The deprotected DNA was then dialyzed with a 2 kDa molecular weight cut-off dialysis membrane (slide-a-lyzer mini Pierce/Thermo Scientific) into Milli-Q water (Millipore). To attach DNA1 to the pore-forming protein, 2 μL of deprotected DNA1 diluted to ~300 μM with 3.4 mg/mL bovine serum albumen (Sigma-Aldrich) was added to 5 μL of 0.25 mg/mL (~78 μM) N293C. To attach DNA2 to the Au nanoparticles, 10 μL of DNA2 was added to 20 μL of unprotected Au nanoparticles (Naked Gold; Bioassay Works, Ijamsville, MD) (40 ± 7) nm diameter with an optical density, OD = 15 (Figure SI 1A). The DNA conjugated protein and Au were stored in the refrigerator and used within one week.

SEM experiments

To image nanoparticle clusters attached to N293C, a lipid bilayer membrane was tethered to a gold electrode ^54,55 (see SI section for detailed methods). About 1 nM DNA-modified αHL N293C was added to the solution, and allowed to form nanopores in the membrane for ≈ 24 hours. The DNA-modified Au nanoparticles were subsequently injected into the solution and allowed to react for < 1 min prior to vigorous rinsing with milli-Q water. The surfaces were then removed from solution and dried with streaming N₂, and loaded into the SEM chamber for imaging.

Membrane formation and single nanopore capture

Planar lipid bilayer membranes were formed on a ca. 100 μm diameter hole in 25 μm thick PTFE, following the method of Mueller and Rudin ⁵⁶ using a prepaint mixture of 2 mg/mL DPhyPC in pentane that was injected onto both sides of the hole and allowed to dry for ca. 10 min. The partition was then adhered to a glass-bottomed teflon holder, allowing microscopic visualization of the membrane. Electrolyte solution (3M KCl, 10 mM TRIS, pH 7.2) was added to the upper well and a femtotip (Eppendorf North America, Long Island, NY) was positioned with a micromanipulator in close proximity to the hole. Several pL of lipid solution (5 mg/mL DPhyPC in hexadecane) was ejected from the tip onto the Teflon surface, and a membrane was formed by dragging this solution across the hole with a small fire-polished glass rod. A second femtotip containing the DNA-N293C solution was positioned in close proximity to the membrane. After positioning, a small backing pressure was applied to the femtotip (ca. 10 to 100 hPa) and a small transmembrane voltage was applied (typically 20 mV) to monitor the formation of nanopores in the membrane. After the insertion of ca. 100 to 1000 nanopores, the backing pressure was reduced to zero and the tip was removed from the solution. DNA-modified Au nanoporticles were injected at the membrane surface in a similar fashion.

Finally, a ca. 1 μm diameter glass pipette silanized with Sigmacote (Sigma Aldrich) containing a Ag/AgCl wire and matching electrolyte solution was brought into contact with the membrane until a single protein nanopore was located in the tip. That action localizes the nanopore to a well-defined location and allows near-diffraction-limited laser excitation of the gold-modified nanopore. A 532 nm CW laser (Crystalaser, Reno, NV) operating at 300 mW was focused into the aperture of an acousto optic modulator (Crystal Technology, Palo Alto, CA). The modulator has a 20 ns risetime and the intensity of the first Bragg diffracted beam was modulated with a 15 MHz function generator (Agilent Technologies, Santa Clara, CA). An adjustable iris selected the first Bragg diffracted beam and this beam was launched into the back aperture of an inverted microscope (Axiovert 200, Zeiss). The beam was focused onto the end of the pipette with a 40×objective (EC Plan-Neofluar NA 0.9 Zeiss, Thornwood, NY) to excite the plasmon mode of the nanoparticle and heat the surrounding solution. Measurement of the pore ionic conductance was performed with an Axopatch 200B and Digidata 1440A (Molecular Devices, Sunnyvale, CA). Unless reported otherwise, the ionic current data was sampled at 50 kHz with a 10 kHz low pass filter.

Results and Discussion

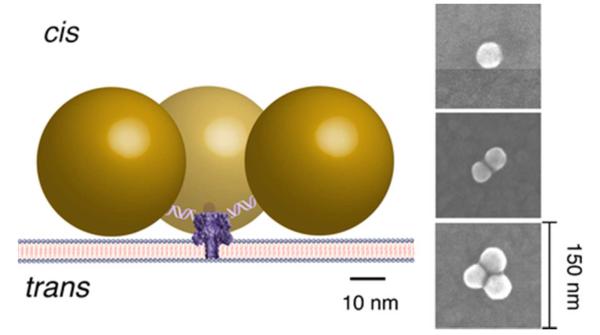
The feasibility of this approach is demonstrated by linking one or more gold nanoparticles (40 nm diameter), via a DNA tether, to nanopores formed by the protein toxin Staphylococcus aureus alpha hemolysin in a planar lipid bilayer membrane (Figure 1). Relatively short (30-nucleotide) DNA polynucleotides with a thiol group at the 5′ end were bound to the nanoparticles. Complementary polynucleotides with a thiol group at the 3′ end were attached to the genetically engineered αHL protein with a single asparagine (N) to cysteine (C) point mutation at the amino-terminus (N293C) located on the cap domain of the ion channel ⁵⁷. The duplex DNA should separate each nanoparticle ca. 10 nm from the N terminus of the protein, and allow the attachment of up to three nanoparticles per channel, due to steric limitations. Although electrostatic repulsion can affect the configuration of the tethered Au nanoparticles in close proximity to each another ⁵⁸, SEM imaging suggests this does not appear to be problematic (Figure 1 and Figure S1).

Figure 1.

Schematic illustration of the ca. yoctoliter volume heating and measurement system. Forty nanometer diameter gold nanoparticles are attached to a single nanopore formed by a genetically engineered version of αHL protein toxin via 30 base pair duplex DNA. Continuous wave green laser light (532 nm) incident on the nanoparticles is strongly absorbed at or near the surface plasmon resonance, and raises their temperature ⁴⁶. The temperature increase is estimated from the measured change in the nanopore ionic conductance. (Right) SEM images of typical Au clusters. Statistical details of the SEM experiments are in Figure S1 and in the SI text.

The rapid temperature jumps made by exciting surface plasmons of the gold nanoparticles with continuous wave 532 nm laser light changes the adjacent electrolyte’s viscosity (and thus bulk conductivity). Thus, the temperature in and near the nanopore can be estimated from the channel ionic conductance. The relative change in the bulk conductivity is related to the temperature change by Δσ/σ = A ΔT, where A = 0.02 °C⁻¹ for initial temperatures T₀ = 21 °C ⁵⁹ and is essentially independent of the electrolyte concentration ⁶⁰. Because the αHL single channel conductance increases in proportion to the bulk conductivity^61,62, it too should increase in a like manner with temperature.

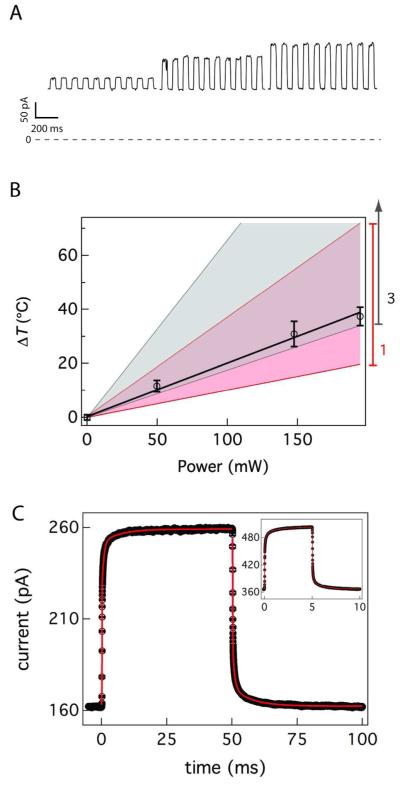
Figure 2A shows a typical single nanopore ionic current time series at three different laser power levels. In each segment, the conductance steps are caused by cycling the laser beam on and off at a frequency of 10 Hz with an acousto-optic modulator. Figure 2B illustrates the linear increase in the nanopore temperature with the laser power, determined from the pore conductance. The calculated temperature change is overlaid for one (pink) and three (gray) nanoparticles attached to a nanopore. These data are suggestive of single particle attachment, but uncertainty in the calculation does not rule out either two or three particles bound to the channel. As expected, in the absence of gold nanoparticles, there was no laser-induced increase in channel conductance (see SI text and Figure S2 for this and other controls). In the presence of the nanoparticles, the mean ionic current (Figure 2C) shows that there are at least two relaxations in this particular system. The time constant for the heating and cooling phases of the experiment were determined by aligning and averaging multiple T-jumps, and fitting the resultant data to a function that includes up to 3 series time constants (see SI text for details). With a 10 Hz switching frequency a steady-state can be clearly observed within ≈ 15 ms suggesting that the experiment is well controlled. Fitting these data produces two observable time constants, one at the bandwidth of the amplifier (0.1 ms) and a slower time constant of (1.16 ± 0.05) ms for heating and (1.10 ± 0.02) ms for the cooling (see SI table S1 for the full fitting parameters). The rise time for the change in temperature of the solution adjacent to a nanopore is τ ≈ 50 ns ⁶³. The higher frequency switching data (100 Hz Figure 2C inset) required a third time constant to produce a reliable fit. With τ₁ held at the filter bandwidth (10 μs), additional time constants of (46.2 ± 0.1) μs and (348 ± 1) σs for the heating and (16.4 ± 0.1) μs and (307 ± 1) μs for the cooling. While the observed time constants are much longer than the actual time it takes to heat the volume (ca. 50 ns), these results demonstrate the ability to directly observe, in real time, rapid changes of the temperature in a single nanopore. These long (relative to the solution rise time) relaxations are likely due to several nearly degenerate open states of the αHL nanopore^64,65, that may differ slightly from pore to pore, and do not impede the use of this method with suitably designed or chosen nanopores.

Figure 2.

Control and measurement of the temperature in and around the nanopore. (A) Conductance changes of a single nanopore caused by laser excitation of 40 nm diameter gold nanoparticles. The applied voltage was 40 mV and the on/off chopping frequency is 10 Hz. The detection bandwidth and sampling frequency are 10 kHz and 50 kHz respectively. For the highest power setting a second nanopore with an identical conductance appeared, and the current from that part of the data was divided by two. The slow variation in conductance in the heated states is likely caused by the movement of the system in the laser beam profile. (B) Estimated temperature change with the applied laser power. The pink shaded region shows the calculated heating with on SD error estimate for a single nanoparticle attachment and the grey shaded region shows the three particle heating calculation and error estimate (see text). (C) 390 currents steps were aligned and averaged. These data were fit a sigmoidal function in series with an exponential function (red solid line, see SI for details) to yield two time constants. The excitation power was 147.5 mW and the ionic current was sampled at 50 kHz after filtering the data with a 10 kHz 4-pole low pass Bessel filter (inset). 3,000 current steps of two nanopores were aligned and averaged to improve the signal to noise ratio and then fit to three time constants from a sigmoidal function in series with two exponential functions (red solid line). The excitation power was 180 mW, and the ionic current was sampled at 250 kHz after filtering the data with a 100 kHz 4-pole low pass Bessel filter.

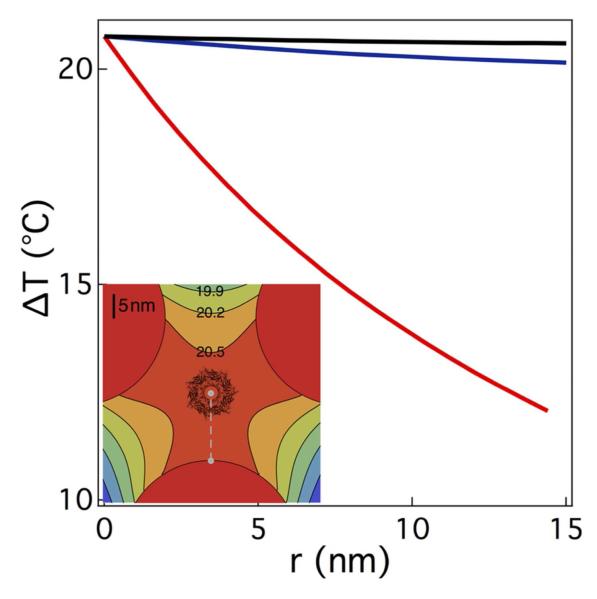
To confirm that the temperature changes result from heating nanoparticles directly attached to the nanopore, we calculate the temperature rise with one, two, or three gold nanoparticles attached to the nanopore. The steady state heat equation, ∇²T+ κ ⁻¹q = 0 is used to calculate the increase in the solvent temperature above ambient, where κ is the thermal conductivity of the surrounding fluid and q is the power density absorbed by the gold particles. Here, convective and radiative heat transfer are ignored. Beginning with a single spherical nanoparticle, the temperature change above ambient is calculated to be ΔT = P_abs/[4πκ(r+a)] where P_abs is the power absorbed by the particle, r is the radial distance measured from the surface of the nanoparticle, and a is the radius of the nanoparticle. In the Rayleigh limit, the temperature increase at the surface of the particle is ΔT_particle = (0.4 °C/mW) P (see SI for details), where P is the power incident on the nanoparticle. Using this result we extend the analysis to the two and three particle cases by numerically solving the heat equation. For multiple particles, the temperature profile is calculated in the plane parallel to the membrane and defined by the centers of the particles (see Figure 1), approximately 10 nm above the cis entrance of the nanopore. The profile of the calculated temperature increase above ambient for one, two, or three attached particles and P = 49.7 mW is shown in Figure 3. For the one particle case, the agreement between the estimated and calculated temperature is better than 5%. However, because of uncertainties in some of the measured parameters (see Figure 3 caption), the calculated temperature for two and three particles is also consistent with our measurements. Moreover for two or more particles, the temperature gradient from the particle surface is greatly reduced leading to an almost uniform temperature distribution adjacent to the nanopore. The net increase in nanopore conductance in proportion to the incident laser power is not due to smoothly-varying changes to the pore’s structure. The latter is comprised of seven anti-parallel β-sheets⁵⁷ that are relatively stable over a wide range of temperatures (−10 °C < T < 90 °C)^62,65,66.

Figure 3.

Theoretical temperature profile adjacent to a single αHL nanopore with three tethered 40 nm diameter gold nanoparticles, irradiated with 49.7 mW of 532 nm wavelength continuous wave laser light. Temperature change above ambient as a function of distance from the surface of a nanoparticle assuming one (red), two (blue), or three (black) nanoparticles attached to a pore. Due to spherical symmetry, the temperature estimate for a single particle is a function of the radial distance from the surface of the particle to the entrance of the pore. The temperature change estimate for two or three particles is limited to the plane of the calculation described in the text, and provides the upper limit of the expected temperature in the pore. The estimated temperature changes at the cis mouth of the pore for a single Au particle is 13.8 °C, 41.1 °C and 54.3 °C for 49.7 mW, 147.5 mW and 195 mW excitation, respectively and 20.6 °C, 61.4 °C and 81.5 °C for the same excitation power range for three Au particles. The uncertainty of this calculation is ca. 58% based on the uncertainty of 25 % for the focal spot size, 10 % for the particle size and 7 % for the beam power, precluding an estimate of the number of particles attached for the experiments herein. (Inset) The illustration shows the top view of the nanopore superimposed upon the temperature profile above ambient for three attached gold particles, calculated for the plane that connects the geometrical center of each particle. This plane is ca. 10 nm above the cis entrance of the pore.

Controlling the temperature in the vicinity of the nanopore detector enables single molecule thermodynamic and kinetic measurements because the ability of any polymer to enter the pore, and transport in it, should depend on the solution viscosity, and the polymer’s thermodynamic properties. For example, an αHL nanopore can separate, with single monomer resolution, poly(ethylene glycol), PEG ^67,68. Specifically, individual PEGs that enter the pore reduce the ionic conductance in proportion to their size ^67,68, and the amount of charge adsorbed to it ⁶⁸. PEG is an ideal candidate molecule with which to test this heating technique. It is currently the only polymer which has a detailed temperature-dependent physical model of the polymer inside the pore ⁶⁸. Specifically, the residence time of PEGs inside the pore is strongly dependent on the ionic strength of the electrolyte solution ^69-71. Weak chelation of cations by PEG plays a crucial role in this phenomenon⁶⁸. As such, this low energy barrier interaction is sensitive to temperature changes. Thus, the residence time of the PEG in the nanopore provides a continuous probe of the solution temperature within the nanopore and thus provides a secondary verification of the nanopore interior temperature independent of the open state current discussed earlier.

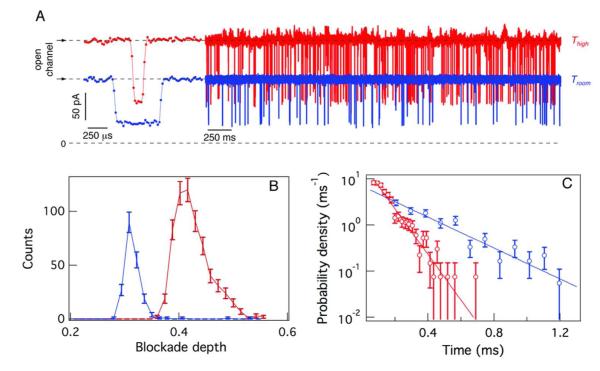
To test this hypothesis, monodisperse PEG (n = 29, where n is the degree of polymerization) was added to the trans side of the membrane, and the incident heating laser power was cycled on and off at 10 Hz. Figure 4A shows the low and high conductance states of the open channel for T_room = (21 ± 1) °C (blue) and T = (54 ± 2) °C (red), respectively (the temperature steps have been removed and the high and low temperature segment have been concatenated for visual clarity), Previous work has shown that an increase in the applied electrostatic potential increases the rate at which charged polymers enter the αHL nanopore ^68,72-74. The ionic current time series (Figure 4A) shows that the rate at which the PEGs enter the pore was greater at the elevated temperature (64 events/s and 24 events/s at T = 54 °C and T_room = 21 °C , respectively). A representative single event from each temperature state is shown to the left. In addition, both the degree to which the PEG molecules blocked the pore conductance (Figure 4B), and their mean residence time in the pore ((260 ± 30) μs and (88 ± 4) μs, respectively, Figure 4C), were less at the elevated temperature.

Figure 4.

Effect of a temperature jump on PEG-induced effects on the single nanopore conductance. (A) Ionic current time series for a single nanopore at T = 21 °C (blue) and T = 54 °C (red) illustrating the transient PEG-induced decreases in nanopore conductance. A typical current blockade for each temperature state is shown (left). The pore conductance and PEG capture rate (events/sec) are greater at elevated temperature. (B) The histogram of relative current blockades shift to a lesser occluded state at elevated temperature. (C) The histogram of the PEG residence times in the nanopore shifts to shorter-lived states, as predicted by theory ⁶⁸. The transmembrane potential was 40 mV.

Curiously, the PEG capture rate increased by 2.7-fold while the nanopore conductance only increased by 1.6 fold in the higher temperature state (Figure 4A). Thus, the enhanced polymer capture rate cannot be described solely by the decrease in solution viscosity. Another process or processes such as structural changes in the polymer or thermophoresis ⁷⁵ may contribute to this effect. Regardless of the source of the enhanced polymer capture rate, the large temperature gradients present in these experiments should provide new means for developing and characterizing the thermodynamic properties of these and other polymer systems under as yet unexplored conditions.

Cations bound to PEG molecules in the pore ^67,68 have a profound effect on both the degree by which PEG reduces the pore conductance and the mean residence times for the polymers in the pore ⁶⁸. Specifically, they cause a greater current blockade depth than PEG volume exclusion alone ^68,76 and they markedly increase the polymer residence time in the pore ⁶⁸. Thus, the results in Figures 4B and 4C suggest that the increase in temperature decreases the number of cations bound to the PEG in the nanopore. Based on previous experimental results and a theoretical model for cation-PEG interactions ⁶⁸, the residence time of PEG29 in 3M solution should be (203 ± 7) μs and (85 ± 4) μs at the low and high temperatures used here, which is consistent with the data in Figure 4. In contrast to the results shown here (Figure 4), the magnitude of the current blockade predicted by the model is relatively insensitive to the temperature. This change in conductance is likely due to a change in the PEG conformation in the pore.

Nanopore-based sensors ^77-79 are capable of detecting, identifying, and characterizing a wide range of molecular species, including ions ^80,81, single-stranded RNA and DNA ^82,83, double-stranded DNA ^84-87, synthetic polymers ^67,68, proteins ^88,89, and proteins as they transition from the folded to the unfolded state both chemically ^90,91 and thermally ⁹². These results and the observation that single-stranded DNA and RNA can be driven electrophoretically through single αHL nanopores ⁸² stimulated research efforts into nanopores as single molecule sensors. Nanopores have been developed with a wide range of different chemistries from naturally-occurring protein nanopores ^57,89,93-95 or semiconductor based synthetic nanopores ^84,96-99. A useful property of nanopore detectors is that they are ca. yoctoliter volume devices that can measure single molecule-induced ionic current blockades at high signal-to-noise ratios. The ability to solely heat this volume could bring single molecule T-jump methods to bear on nanopore-based analytical measurements and provide a marked advance in the technology. Using diffraction limited laser focal spots, which are considerably larger than nanopores (10⁻¹⁶ L vs. 10⁻²³ L, respectively), is problematic because they require high powers to initiate heating, comparable to the heating reported herein, and could lead to a number of problems including the rupture of the membrane supporting the nanopore.

One difficulty when heating samples with gold nanoparticles is accurately measuring the temperature surrounding the optically excited nanoparticles. Previous methods for deducing the temperature include measuring position fluctuations of an optically trapped gold nanoparticle ⁴⁶, observing phase transitions in a bilayer membrane ^48,49 or other matrix ¹⁰⁰, or monitoring intensity fluctuations in laser-induced fluorescence ^101,102. These optical methods require post-processing of data, which limits the ability to rapidly observe temperature changes and provide real-time estimates for, and control of the temperature. Our approach is different because it is electrical and provides a measurement of the temperature adjacent to the nanoparticle. This allows for thermometry over timescales set by the integration time of the electrophysiology apparatus. More importantly, it only measures the temperature of the solution within the ca. 10⁻²³ L volume defined by the nanopore, which is the single molecule sensing region of interest.

Conclusion

By combining nanopore-based sensing with gold nanoparticle plasmon heating, we have developed a new approach for studying the thermodynamics and kinetics at the single molecule limit. One can easily imagine experiments where the properties of molecules are modified, via changes in temperature, within the vicinity of the nanopore for purposes of analysis and control. Such rapid changes would be impossible with standard heating technology. The method reported here overcomes these limitations by isolating the heating to a small volume (ca. yoctoliter) within a region of interest (nanopore sensor) for single molecule sensing.

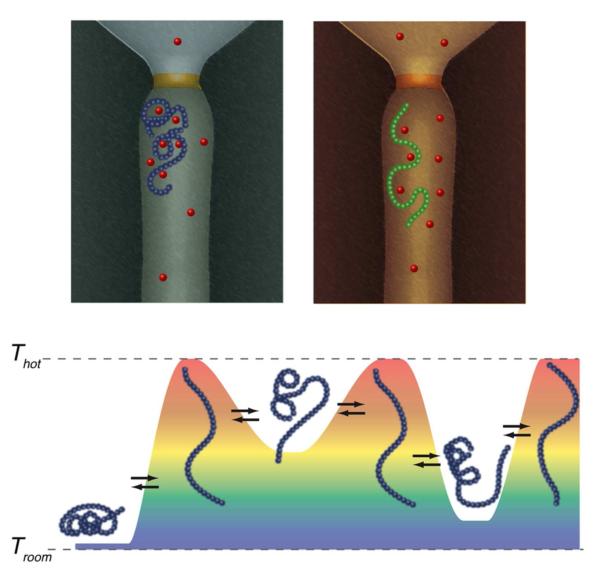
We have demonstrated the attachment of gold nanoparticles to single modified αHL nanopores and that this system is both an effective single molecule heater and a nanometer-scale thermometer. In addition, we have shown that the gold-modified nanopore can perform single molecule sensing measurements with the temperature of the solution within the vicinity of the nanopore as a new variable under rapid control. Because the kinetics of reversibly heating such small volumes is extremely rapid (ca. 50 ns) ⁶³ compared to the residence times of polymers in single nanopores (ca. 1 ms) ^67,68,82, the novel method can clearly probe reversible equilibrium processes between different species and molecules that can fully or partially enter the pore (Figure 4), which could provide additional control of nanopore-based DNA sequencing-by-synthesis methods ¹⁰³. It also has the potential to study the kinetics of structural changes that occur in synthetic and biological polymers by the use of complex temporal temperature profiles (Figure 5) and to identify or discriminate between different molecules in solution, as has been demonstrated for the identification of gaseous species using micro-hotplates ^104-106. For example, applying a complex temperature time series (i.e. temperature sculpting) to the system should identify regimes of rapid or persistent rapid structural dynamics in different segments of the polymer. In this way, a convergence of single molecule kinetics and thermodynamics will reveal information about a polymer’s identity, function, or both.

Figure 5.

The potential use of rapid temperature-jump kinetics for single molecule thermodynamic analysis. (Top) A polymer is drawn in the nanopore adopting two (of many) conformations that are affected by temperature. In this illustrative example, the polymer interacts with cations, forming a tightly coiled structure. At elevated temperature the binding is relaxed and the polymer forms a less compact structure. (Bottom) The ability to rapidly change the temperature profile (magnitude, duration, etc.) while a polymer is in the nanopore could help discriminate between subtly different molecules. Here, an experiment is envisioned where the equilibrium structure of a polymer is perturbed and measured with a well-defined but variable thermal history.